07. Работа и Энергия — Физика это просто!!! 2016
Взглянем с «точки зрения Джоуля» на работу и энергию. Попробуем понять, почему они одной размерности.
Термином «работа» в механике определяется физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением:
Рисунок 5
Работа равна нулю, если тело движется по инерции (F = 0), если нет перемещения (s = 0) или, если угол между перемещением и силой равен 90° (cos α = 0). Единицей работы в СИ служит Джоуль (Дж).
1 джоуль — это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы.
Для определения количества совершения работы в единицу времени вводят величину «мощность».
Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:
Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт — мощность, при которой совершается работа в 1 Дж за 1 секунду.
Рассмотрим действие на тело некоторой постоянной силы F. И пусть она действует вдоль перемещения. Одномерный случай. На участке пути s будет произведена работа А. В результате у тела изменится скорость:
И пусть она действует вдоль перемещения. Одномерный случай. На участке пути s будет произведена работа А. В результате у тела изменится скорость:
Я надеюсь, все поняли, почему ?
И почему это справедливо только для прямолинейного равноускоренного движения? Движения под действием постоянной силы.
Величину (m * v2)/2 для материальной точки называют кинетической энергией тела. Ее размерность, как видно из формулы, совпадает с размерностью работы.
!!! Вообще говоря, энергия – это такая величина, которая своим изменением характеризует величину работы. И еще она (энергия) сохраняется в замкнутой системе. Это все, что мы знаем про энергию. (Подробности у Фейнмана в первом томе его «Лекций по физике»!)
Кинетическая энергия — энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета.
Кроме этого, существует и другой вид механической энергии — потенциальная энергия. Рассмотрим систему двух взаимодействующих тел. Например, тела, приподнятого над Землей, и саму Землю. Так как Земля очень-очень большая и тяжелая, а тело маленькое и относительно легкое и, к тому же, оно не сильно меняет свою высоту над уровнем поверхности Земли, то можно считать, что тело находится в поле постоянной силы. Силы тяжести.
Работа силы тяжести при перемещении тела на отрезке |h1 — h2| будет равна:
Величину m*g*h в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести.
Из формулы (21) вытекает, что работа не зависит от траектории движения в поле силы тяжести, а определяется лишь изменением высоты.
Потенциальная энергия характеризует и другие взаимодействующие тела. Потенциальной энергией обладает сжатая пружина:
где k — модуль упругости, х — смещение от положения равновесия.
Потенциальная энергия, как и кинетическая, является величиной относительной. И высота, и скорость зависят от выбора системы координат.
Дополнительное образование
Начальные классы Расписание занятий дополнительной образовательной услуги «Гимназист»
5-11 классы Расписание занятий дополнительной образовательной услуги «Гимназист»
1-11 классы Расписание дополнительных образовательных услуг различных направлений
Положение об оказании платных образовательных и иных услуг
Документы о порядке оказания платных образовательных и иных услуг в 2021-2022 учебном году:
Приказ об утверждении прейскуранта стоимости платных образовательных и иных услуг на 2021-2022 учебный год
Договор об оказании платных дополнительных образовательных услуг
Договор об оказании платных дополнительных образовательных услуг на второе полугодие (в случае изменения перечня услуг)
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 1-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 2-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 3-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 4-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 5-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 6-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 7-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 8-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 9-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 10-х классов на второе полугодие 2021-2022 учебного года
- Договор об оказании платных дополнительных образовательных услуг для обучающихся 11-х классов на второе полугодие 2021-2022 учебного года
Дополнительное соглашение о расторжении договора об оказании платных дополнительных образовательных услуг
Дополнительное соглашение о смене реквизитов
Договор на оказание услуг общественного питания
Прейскурант цен на услуги общественного питания
Бланк заявления на выбор услуг общественного питания для обучающихся 1-4 класов
Бланк заявления на выбор услуг общественного питания для обучающихся 5-11 класов
Договор на оказание услуг психологической службой гимназии
Договор на оказание услуг по индивидуальному собеседованию
Договор на оказание услуг дошкольного обучения
- Договор об оказании услуг «Подготовка к школе» (обучение в будние дни)
- Договор об оказании услуг «Подготовка к школе» (обучение по субботам)
Потенциальная энергия: определение, виды, формулы
Определение потенциальной энергии
Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.
Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии.
Виды потенциальной энергии
Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.
Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.
Знакомьтесь: наш мир. Физика всего на свете.
Книга адресована школьникам старших классов, студентам, преподавателям и учителям физики, а также всем тем, кто хочет понять, что происходит в мире вокруг нас, и воспитать в себе научный взгляд на все многообразие явлений природы. Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
Каждый раздел книги представляет собой, по сути, набор физических задач, решая которые читатель укрепит свое понимание физических законов и научится применять их в практически интересных случаях.
Формулы потенциальной энергии
Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.
А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:
А = F*s = mg*s = mg*(h1
— h2) = mgh1
— mgh2
= Eп1
— Еп
Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп < 0.
Отметим также и то, что в формуле работы отсутсвовал cosa. Это не случайно. Ведь если тело движется по сложной траектории, то, какой бы сложной она ни была, её можно разбить на множество вертикальных и горизонтальных участков. Но на горизонтальных участках работа силы тяжести будет равна нулю, так как угол между силой тяжести и перемещением будет прямым, а значит работа будет совершаться только на вертикальных участках траектории, для которых cosa = 1 или cosa = −1.
Тогда можно сделать ещё один важный вывод — работа силы тяжести не зависит от формы траектории, а только от расположения начальной и конечной точки. А это не случайность — это свойство любых сил, сообщающих телам потенциальную энергию. Такие силы называют потенциальными и сила тяжести — одна из них. К потенциальным силам относится и сила упругости.
Б) Чтобы вывести формулу потенциальной энергии упругой деформации, рассмотрим, какую работу нужно совершить, чтобы растянуть пружину, изменив её длину на х (х =
А = –Fупр(ср.)*s,
Во-первых, знак минус в формуле стоит потому, что угол между силой упругости и перемещением свободного конца пружины равен 180 градусов и cosa = −1.
Во-вторых, возникающая при растяжении пружины сила упругости является переменной силой, в отличие от силы тяжести, поэтому в формуле работы стоит средняя сила упругости. При этом величина силы упругости, в соответствии с законом Гука, прямо пропорциональна изменению длины пружины, а значит её среднее значение можно определить так:
Fупр(ср.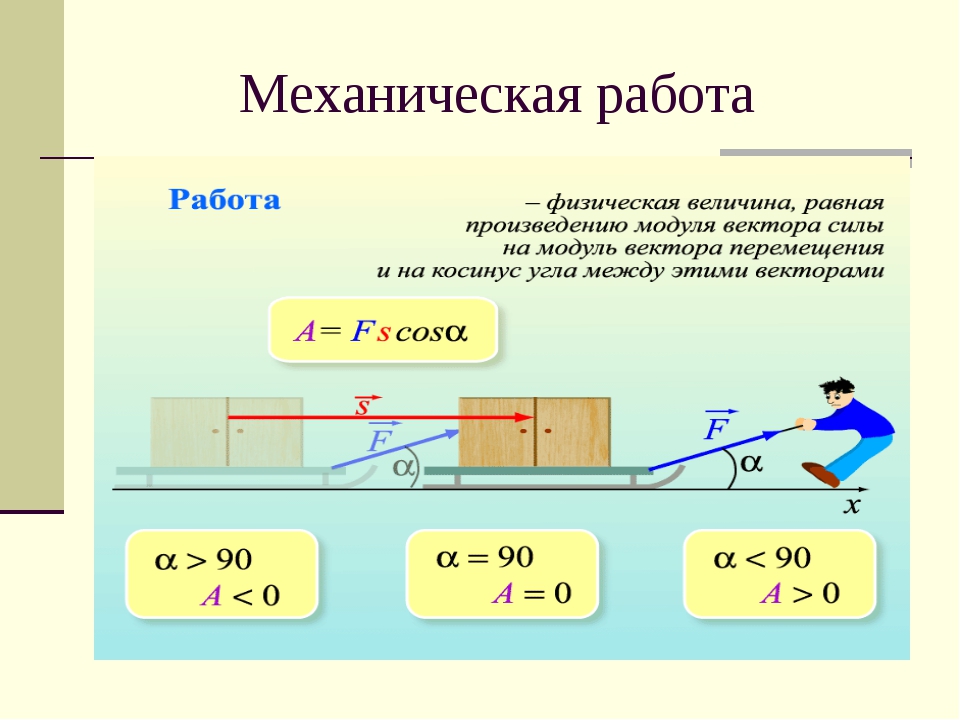 ) = (Fупр(нач.) + Fупр(конеч.))/2
) = (Fупр(нач.) + Fупр(конеч.))/2
И так как Fупр(нач.) = 0, а Fупр(конеч.) = kх, то:
А = —kх*s/2
Но s = x, поэтому: А = —kx2/2 = 0 — kх2/2 = Еп1 — Еп2.
В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx2/2.
Что еще почитать?
Методические советы учителям
1) Обязательно обратите внимание учащихся на связь энергии и работы.
2) Не давайте учащимся формулы потенциальной энергии без вывода.
3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.
4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.
5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.
Физика. Механика
Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).
Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.
Рис 4.1. Элементарная работа
Элементарная работа силы равна скалярному произведению вектора силы на вектор перемещения её точки приложения
Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина
Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина
— это проекция силы F на направление перемещения. Следовательно,
Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:
При перемещении вдоль оси x работу графически можно представить как площадь под кривой Fx(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.
Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = Fx(x)
Если перемещение ортогонально силе, то = 0 и работа равна нулю:
Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.
Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.
Если на тело действует несколько сил, то
то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью . Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины.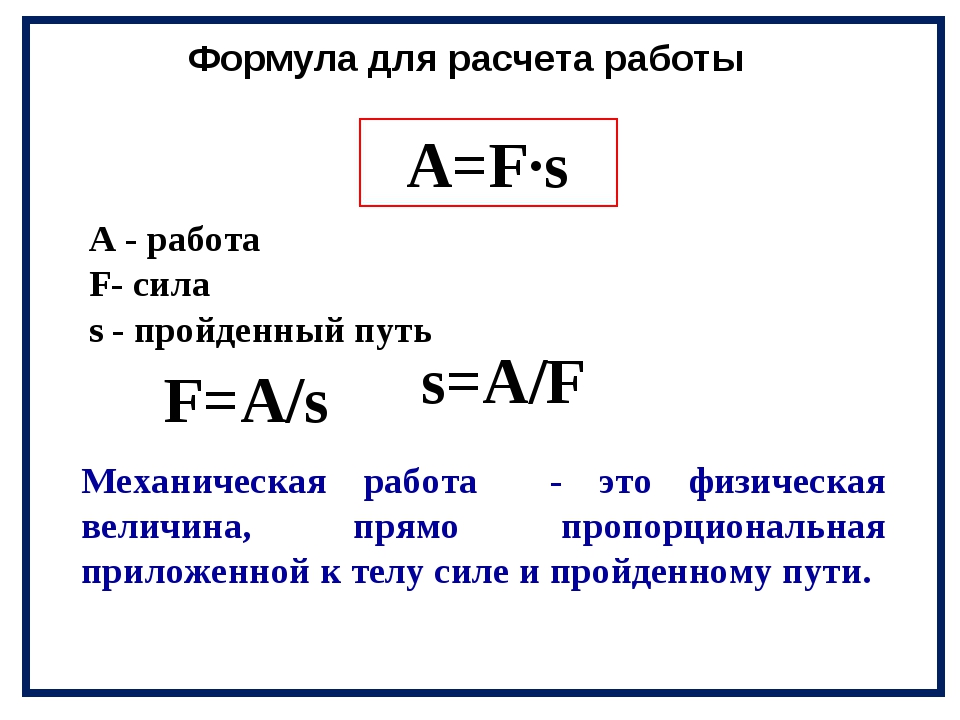 Тогда согласно закону Гука
Тогда согласно закону Гука
где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).
Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины
Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид
так что для полной работы упругой деформации пружины получаем
Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.
Дополнительная информация
http://www.plib.ru/library/book/17833.html – Хайкин С.Э. Физические основы механики, Наука, 1971 г.– стр. 476–479 (§ 111): выведено выражение для потенциальной энергии упруго деформированного тела.
Как обозначается полезная работа в физике. Механическая работа: определение и формула
При взаимодействии
тел импульс одного тела может
частично или полностью передаваться
другому телу. Если на систему тел не
действуют внешние силы со стороны других
тел, такая система называетсязамкнутой .
Если на систему тел не
действуют внешние силы со стороны других
тел, такая система называетсязамкнутой .
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьегозаконов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через и По третьему закону Ньютона Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: Применим к этим телам второй закон Ньютона:
где и – импульсы тел в начальный момент времени, и – импульсы тел в конце взаимодействия. Из этих соотношений следует:
Это равенство означает,
что в результате взаимодействия двух
тел их суммарный импульс не изменился.
Рассматривая теперь всевозможные парные
взаимодействия тел, входящих в замкнутую
систему, можно сделать вывод, что
внутренние силы замкнутой системы не
могут изменить ее суммарный импульс,
то есть векторную сумму импульсов всех
тел, входящих в эту систему.
Механическая работа и мощность
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения (рис. 1.1.9):
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α джоулях (Дж).
Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
Если проекция силы на направление перемещения не остается постоянной, работу следует вычислять для малых перемещений и суммировать результаты:
Примером силы, модуль которой зависит от координаты, может служить упругая сила пружины, подчиняющаяся закону Гука . Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины (рис. 1.1.11).
Зависимость модуля
внешней силы от координаты x изображается
на графике прямой линией (рис. 1.1.12).
1.1.12).
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами, и равна работе равнодействующей приложенных сил.
Работа силы, совершаемая в единицу времени, называется мощностью . Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа.
Каждое тело, совершающее движение, можно охарактеризовать работой. Иными словами, она характеризует действие сил.
Работа определяется как:
Произведение модуля силы и пути пройденного телом, умноженное на косинус угла между направлением силы и движения.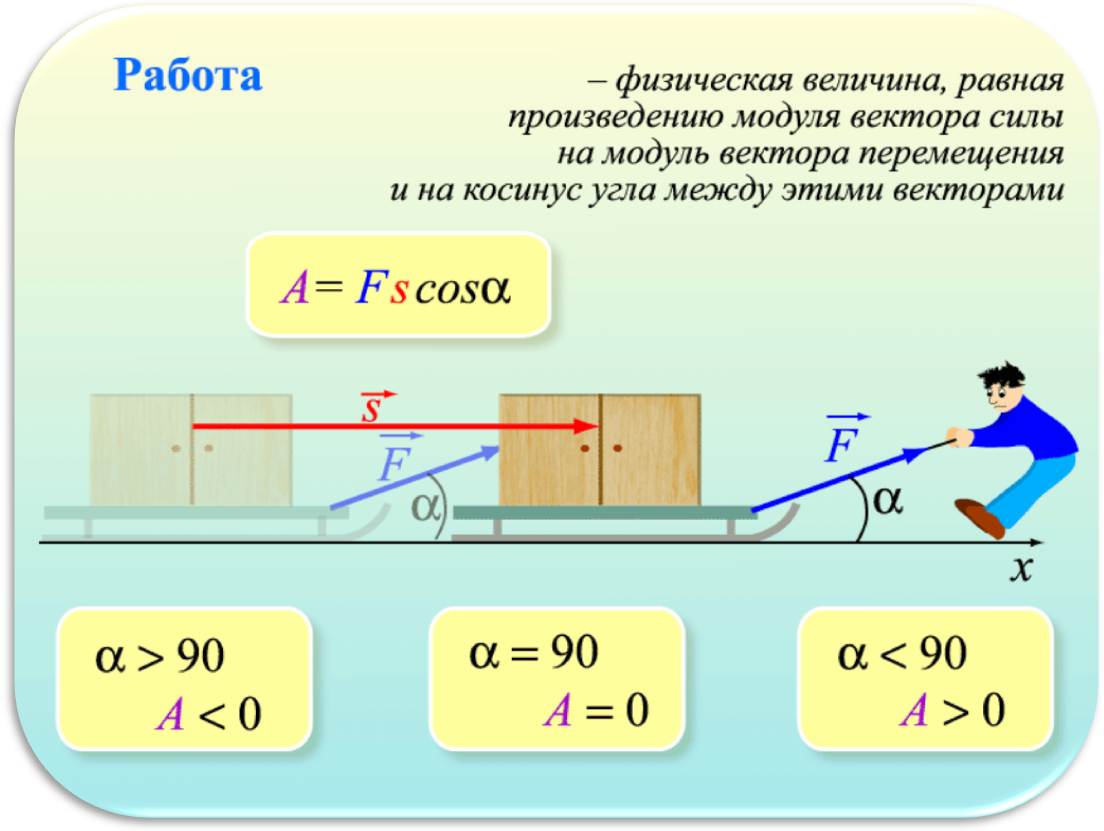
Работа измеряется в Джоулях:
1 [Дж] = = [кг* м2/c2]
К примеру, тело A под действием силы в 5 Н, прошло 10 м. Определить работу совершенную телом.
Так как направление движения и действия силы совпадают, то угол между вектором силы и вектором перемещения будет равен 0°. Формула упроститься, потому что косинус угла в 0° равен 1.
Подставляя исходные параметры в формулу, находим:
A= 15 Дж.
Рассмотрим другой пример, тело массой 2 кг, двигаясь с ускорением 6 м/ с2, прошло 10 м. Определить работу проделанную телом, если оно двигалось по наклоненной плоскости вверх под углом 60°.
Для начала, вычислим какую силу нужно приложить, что бы сообщить телу ускорение 6 м/ с2.
F = 2 кг * 6 м/ с2 = 12 H.
Под действием силы 12H, тело прошло 10 м. Работу можно вычислить по уже известной формуле:
Где, а равно 30°. Подставляя исходные данные в формулу получаем:
A= 103, 2 Дж.
Мощность
Множество машин механизмов выполняют одну и ту же работу за различный промежуток времени. Для их сравнения вводится понятие мощности.
Для их сравнения вводится понятие мощности.
Мощность – это величина, показывающая объем работы выполненный за единицу времени.
Мощность измеряется в Ватт, в честь Шотландского инженера Джеймса Ватта.
1 [Ватт] = 1 [Дж/c].
К примеру, большой кран поднял груз весом 10 т на высоту 30 м за 1 мин. Маленький кран на эту же высоту за 1 мин поднял 2 т кирпича. Сравнить мощности кранов.
Определим работу выполняемую кранами. Груз поднимается на 30м, при этом преодолевая силу тяжести, поэтому сила, затрачиваемая на поднятие груза, будет равна силе взаимодействия Земли и груза(F = m * g). А работа – произведению сил на расстояние пройденное грузами, то есть на высоту.
Для большого крана A1 = 10 000 кг * 30 м * 10 м / с2 = 3 000 000 Дж, а для маленького A2 = 2 000 кг * 30 м * 10 м / с2 = 600 000 Дж.
Мощность можно вычислить, разделив работу на время. Оба крана подняли груз за 1 мин (60 сек).
Отсюда:
N1 = 3 000 000 Дж/60 c = 50 000 Вт = 50 кВт.
N2 = 600 000 Дж/ 60 c = 10 000 Вт = 10 к Вт.
Из выше приведенных данных наглядно видно, что первый кран в 5 раз мощнее второго.
В нашем повседневном опыте слово «работа» встречается очень часто. Но следует различать работу физиологическую и работу с точки зрения науки физики. Когда вы приходите с уроков, вы говорите: «Ой, как я устал!». Это работа физиологическая. Или, к примеру, работа коллектива в народной сказке «Репка».
Рис 1. Работа в повседневном смысле слова
Мы же будем говорить здесь о работе с точки зрения физики.
Механическая работа совершается, если под действием силы происходит перемещение тела. Работа обозначается латинской буквой А. Более строго определение работы звучит так.
Работой силы называется физическая величина, равная произведению величины силы на расстояние, пройденное телом в направлении действия силы.
Рис 2. Работа — это физическая величина
Формула справедлива, когда на тело действует постоянная сила.
В международной системе единиц СИ работа измеряется в джоулях.
Это означает, что если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа 1 джоуль.
Единица работы названа в честь английского ученого Джеймса Прескотта Джоуля.
Рис 3. Джеймс Прескотт Джоуль (1818 — 1889)
Из формулы для вычисления работы следует, что возможны три случая, когда работа равна нулю.
Первый случай — когда на тело действует сила, но тело не перемещается. Например, на дом действует огромная сила тяжести. Но она не совершает работы, поскольку дом неподвижен.
Второй случай — когда тело перемещается по инерции, то есть на него не действуют никакие силы. Например, космический корабль движется в межгалактическом пространстве.
Третий случай — когда на тело действует сила, перпендикулярная направлению движения тела. В этом случае, хотя и тело перемещается, и сила на него действует, но нет перемещения тела в направлении действия силы .
Рис 4. Три случая, когда работа равна нулю
Следует также сказать, что работа силы может быть отрицательной. Так будет, если перемещение тела происходит против направления действия силы . Например, когда подъемный кран с помощью троса поднимает груз над землей, работа силы тяжести отрицательна (а работа силы упругости троса, направленная вверх, наоборот, положительна).
Предположим, при выполнении строительных работ котлован необходимо засыпать песком. Экскаватору для этого понадобится несколько минут, а рабочему с помощью лопаты пришлось бы трудиться несколько часов. Но и экскаватор, и рабочий при этом выполнили бы одну и ту же работу .
Рис 5. Одну и ту же работу можно выполнить за разное время
Чтобы охарактеризовать быстроту выполнения работы в физике используется величина, называемая мощностью.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
Мощность обозначается латинской буквой N .
Единицей измерения мощности я системе СИ является ватт.
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Единица мощности названа в честь английского ученого, изобретателя паровой машины Джеймса Уатта.
Рис 6. Джеймс Уатт (1736 — 1819)
Объединим формулу для вычисления работы с формулой для вычисления мощности.
Вспомним теперь, что отношение пути, пройденного телом, S , ко времени движения t представляет собой скорость движения тела v .
Таким образом, мощность равна произведению численного значения силы на скорость движения тела в направлении действия силы .
Этой формулой удобно пользоваться при решении задач, в которых сила действует на тело, движущееся с известной скоростью.
Список литературы
- Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7-9 классов общеобразовательных учреждений. — 17-е изд.
 — М.: Просвещение, 2004.
— М.: Просвещение, 2004. - Перышкин А.В. Физика. 7 кл. — 14-е изд., стереотип. — М.: Дрофа, 2010.
- Перышкин А.В. Сборник задач по физике, 7-9 кл.: 5-е изд., стереотип. — М: Издательство «Экзамен», 2010.
- Интернет-портал Physics.ru ().
- Интернет-портал Festival.1september.ru ().
- Интернет-портал Fizportal.ru ().
- Интернет-портал Elkin52.narod.ru ().
Домашнее задание
- В каких случаях работа равна нулю?
- Как находится работа на пути, пройденном в направлении действия силы? В противоположном направлении?
- Какую работу совершает сила трения, действующая на кирпич, при его перемещении на 0,4 м? Сила трения равна 5 Н.
Основные теоретические сведения
Механическая работа
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы . Работой, совершаемой постоянной силой F , называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла между векторами силы F и перемещения S :
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α α
≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Она может быть как положительна (0° ≤ α α
≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 ньютон на перемещении 1 метр в направлении действия силы.
Если же сила изменяется с течением времени, то для нахождения работы строят график зависимости силы от перемещения и находят площадь фигуры под графиком – это и есть работа:
Примером силы, модуль которой зависит от координаты (перемещения), может служить сила упругости пружины, подчиняющаяся закону Гука (F упр = kx ).
Мощность
Работа силы, совершаемая в единицу времени, называется мощностью . Мощность P (иногда обозначают буквой N ) – физическая величина, равная отношению работы A к промежутку времени t , в течение которого совершена эта работа:
По этой формуле рассчитывается средняя мощность , т.е. мощность обобщенно характеризующая процесс.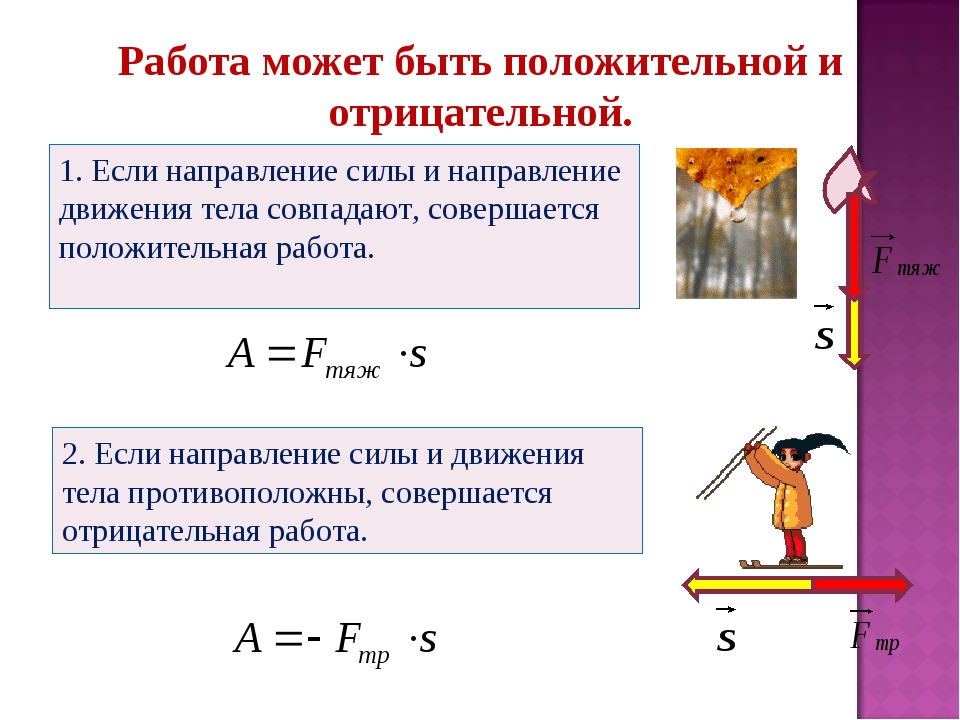 Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
Итак, работу можно выражать и через мощность: A = Pt (если конечно известна мощность и время совершения работы). Единица мощности называется ватт (Вт) или 1 джоуль за 1 секунду. Если движение равномерное, то:
По этой формуле мы можем рассчитать мгновенную мощность (мощность в данный момент времени), если вместо скорости подставим в формулу значение мгновенной скорости. Как узнать, какую мощность считать? Если в задаче спрашивают мощность в момент времени или в какой-то точке пространства, то считается мгновенная. Если спрашивают про мощность за какой-то промежуток времени или участок пути, то ищите среднюю мощность.
КПД – коэффициент полезного действия , равен отношению полезной работы к затраченной, либо же полезной мощности к затраченной:
Какая работа полезная, а какая затраченная определяется из условия конкретной задачи путем логического рассуждения. К примеру, если подъемный кран совершает работу по подъему груза на некоторую высоту, то полезной будет работа по поднятию груза (так как именно ради нее создан кран), а затраченной – работа, совершенная электродвигателем крана.
Итак, полезная и затраченная мощность не имеют строгого определения, и находятся логическим рассуждением. В каждой задаче мы сами должны определить, что в этой задаче было целью совершения работы (полезная работа или мощность), а что было механизмом или способом совершения всей работы (затраченная мощность или работа).
В общем случае КПД показывает, как эффективно механизм преобразует один вид энергии в другой. Если мощность со временем изменяется, то работу находят как площадь фигуры под графиком зависимости мощности от времени:
Кинетическая энергия
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела (энергией движения) :
То есть если автомобиль массой 2000 кг движется со скоростью 10 м/с, то он обладает кинетической энергией равной Е к = 100 кДж и способен совершить работу в 100 кДж. Эта энергия может превратиться в тепловую (при торможении автомобиля нагревается резина колес, дорога и тормозные диски) или может быть потрачена на деформацию автомобиля и тела, с которым автомобиль столкнулся (при аварии). При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
При вычислении кинетической энергии не имеет значения куда движется автомобиль, так как энергия, как и работа, величина скалярная.
Тело обладает энергией, если способно совершить работу. Например, движущееся тело обладает кинетической энергией, т.е. энергией движения, и способно совершать работу по деформации тел или придания ускорения телам, с которыми произойдёт столкновение.
Физический смысл кинетической энергии: для того чтобы покоящееся тело массой m стало двигаться со скоростью v необходимо совершить работу равную полученному значению кинетической энергии. Если тело массой m движется со скоростью v , то для его остановки необходимо совершить работу равную его первоначальной кинетической энергии. При торможении кинетическая энергия в основном (кроме случаев соударения, когда энергия идет на деформации) «забирается» силой трения.
Теорема о кинетической энергии: работа равнодействующей силы равна изменению кинетической энергии тела:
Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.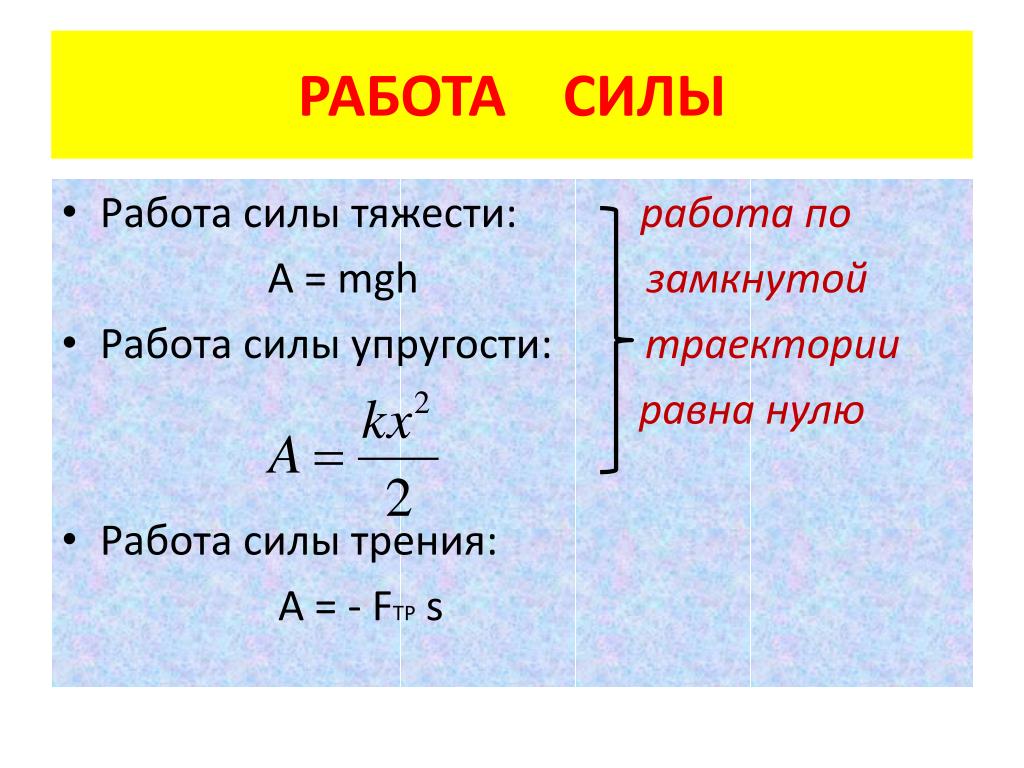 Применять данную теорему удобно в задачах на разгон и торможение тела.
Применять данную теорему удобно в задачах на разгон и торможение тела.
Потенциальная энергия
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел .
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями (так называемые консервативные силы ). Работа таких сил на замкнутой траектории равна нулю. Таким свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести Земли рассчитывается по формуле:
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень (h – расстояние от центра тяжести тела до нулевого уровня). Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Если тело обладает потенциальной энергией, значит оно способно совершить работу при падении этого тела с высоты h до нулевого уровня. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
Часто в задачах на энергию приходится находить работу по поднятию (переворачиванию, доставанию из ямы) тела. Во всех этих случаях нужно рассматривать перемещение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. В каждой задаче нулевой уровень выбирается из соображения удобства. Физический смысл имеет не сама потенциальная энергия, а ее изменение при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Следовательно, такая пружина обладает запасом энергии. Растяжение или сжатие х надо рассчитывать от недеформированного состояния тела.
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x 1 , тогда при переходе в новое состояние с удлинением x 2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком (так как сила упругости всегда направлена против деформации тела):
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Работа силы трения зависит от пройденного пути (такой вид сил, чья работа зависит от траектории и пройденного пути называется: диссипативные силы ). Понятие потенциальной энергии для силы трения вводить нельзя.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
Он определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой (формула уже приведена выше).
КПД можно рассчитывать как через работу, так и через мощность. Полезная и затраченная работа (мощность) всегда определяются путем простых логических рассуждений.
В электрических двигателях КПД – отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника. В тепловых двигателях – отношение полезной механической работы к затрачиваемому количеству теплоты. В электрических трансформаторах – отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т.д.
Из–за неизбежных потерь энергии на трение, на нагревание окружающих тел и т. п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
п. КПД всегда меньше единицы. Соответственно этому КПД выражается в долях затрачиваемой энергии, то есть в виде правильной дроби или в процентах, и является безразмерной величиной. КПД характеризует как эффективно работает машина или механизм. КПД тепловых электростанций достигает 35–40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением – 40–50%, динамомашин и генераторов большой мощности – 95%, трансформаторов – 98%.
Задачу, в которой нужно найти КПД или он известен, надо начать с логического рассуждения – какая работа является полезной, а какая затраченной.
Закон сохранения механической энергии
Полной механической энергией называется сумма кинетической энергии (т.е. энергии движения) и потенциальной (т.е. энергии взаимодействия тел силами тяготения и упругости):
Если механическая энергия не переходит в другие формы, например, во внутреннюю (тепловую) энергию, то сумма кинетической и потенциальной энергии остаётся неизменной. Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Если же механическая энергия переходит в тепловую, то изменение механической энергии равно работе силы трения или потерям энергии, или количеству выделившегося тепла и так далее, другими словами изменение полной механической энергии равно работе внешних сил:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему (т.е. такую в которой не действует внешних сил, и их работа соответственно равна нолю) и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной:
Это утверждение выражает закон сохранения энергии (ЗСЭ) в механических процессах . Он является следствием законов Ньютона. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой силами упругости и тяготения. Во всех задачах на закон сохранения энергии всегда будет как минимум два состояния системы тел. Закон гласит, что суммарная энергия первого состояния будет равна суммарной энергии второго состояния.
Алгоритм решения задач на закон сохранения энергии:
- Найти точки начального и конечного положения тела.
- Записать какой или какими энергиями обладает тело в данных точках.
- Приравнять начальную и конечную энергию тела.
- Добавить другие необходимые уравнения из предыдущих тем по физике.
- Решить полученное уравнение или систему уравнений математическими методами.
Важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими силами действуют силы трения или силы сопротивления среды. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
Часть механической энергии превращается во внутреннюю энергию тел (нагревание). Таким образом энергия в целом (т.е. не только механическая) в любом случае сохраняется.
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии .
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Разные задачи на работу
Если в задаче требуется найти механическую работу, то сначала выберите способ её нахождения:
- Работу можно найти по формуле: A = FS ∙cosα . Найдите силу, совершающую работу, и величину перемещения тела под действием этой силы в выбранной системе отсчёта.
 Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Обратите внимание, что угол должен быть выбран между векторами силы и перемещения. - Работу внешней силы можно найти, как разность механической энергии в конечной и начальной ситуациях. Механическая энергия равна сумме кинетической и потенциальной энергий тела.
- Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh , где h – высота, на которую поднимается центр тяжести тела .
- Работу можно найти как произведение мощности на время, т.е. по формуле: A = Pt .
- Работу можно найти, как площадь фигуры под графиком зависимости силы от перемещения или мощности от времени.
Закон сохранения энергии и динамика вращательного движения
Задачи этой темы являются достаточно сложными математически, но при знании подхода решаются по совершенно стандартному алгоритму. Во всех задачах Вам придется рассматривать вращение тела в вертикальной плоскости. Решение будет сводиться к следующей последовательности действий:
- Надо определить интересующую Вас точку (ту точку, в которой необходимо определить скорость тела, силу натяжения нити, вес и так далее).

- Записать в этой точке второй закон Ньютона, учитывая, что тело вращается, то есть у него есть центростремительное ускорение.
- Записать закон сохранения механической энергии так, чтобы в нем присутствовала скорость тела в той самой интересной точке, а также характеристики состояния тела в каком-нибудь состоянии про которое что-то известно.
- В зависимости от условия выразить скорость в квадрате из одного уравнения и подставить в другое.
- Провести остальные необходимые математические операции для получения окончательного результата.
При решении задач надо помнить, что:
- Условие прохождения верхней точки при вращении на нити с минимальной скоростью – сила реакции опоры N в верхней точке равна 0. Такое же условие выполняется при прохождении верхней точки мертвой петли.
- При вращении на стержне условие прохождения всей окружности: минимальная скорость в верхней точке равна 0.
- Условие отрыва тела от поверхности сферы – сила реакции опоры в точке отрыва равна нулю.

Неупругие соударения
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел.
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).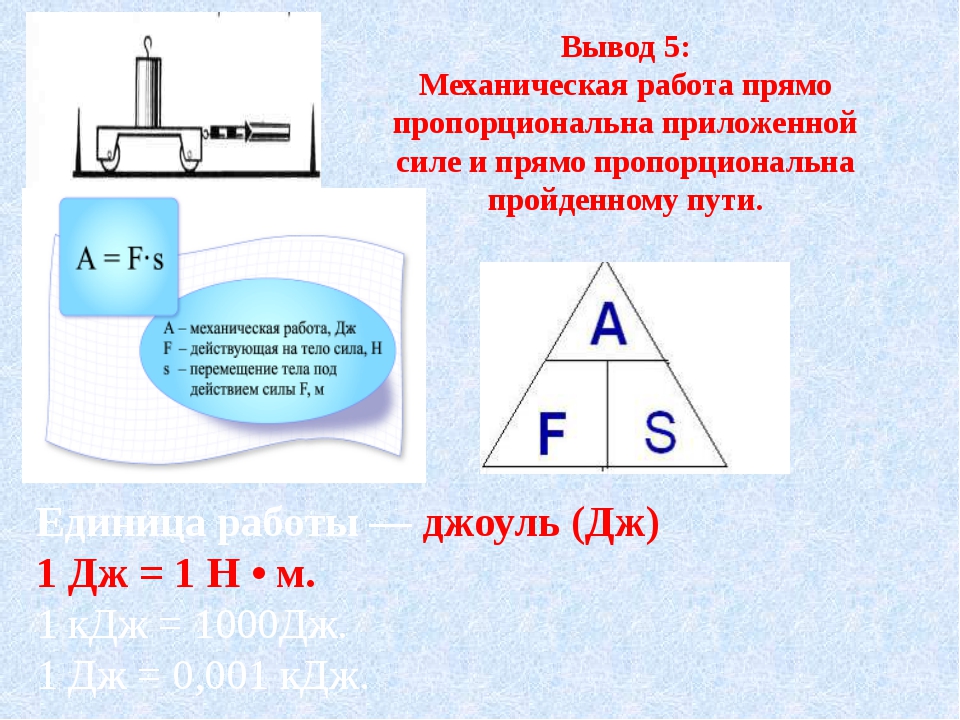 В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары .
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары .
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание). Для описания любых ударов Вам нужно записать и закон сохранения импульса, и закон сохранения механической энергии с учетом выделяющейся теплоты (предварительно крайне желательно сделать рисунок).
Абсолютно упругий удар
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел. Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя.
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров. В этом случае векторы скоростей шаров после упругого соударения всегда направлены перпендикулярно друг к другу.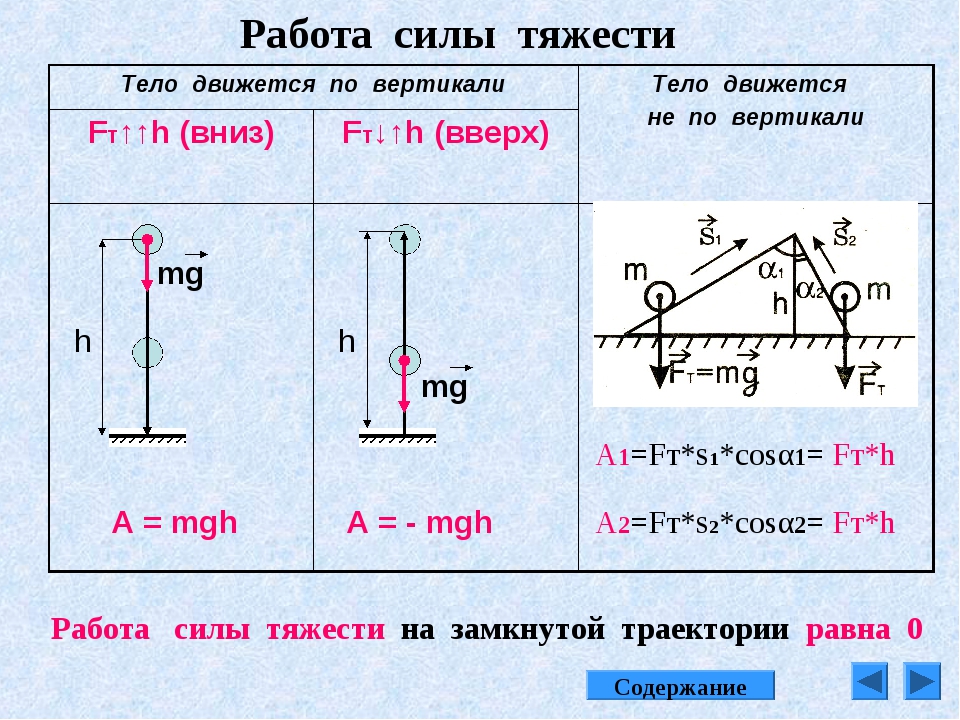
Законы сохранения. Сложные задачи
Несколько тел
В некоторых задачах на закон сохранения энергии тросы с помощью которых перемещаются некие объекты могут иметь массу (т.е. не быть невесомыми, как Вы могли уже привыкнуть). В этом случае работу по перемещению таких тросов (а именно их центров тяжести) также нужно учитывать.
Если два тела, соединённые невесомым стержнем, вращаются в вертикальной плоскости, то:
- выбирают нулевой уровень для расчёта потенциальной энергии, например на уровне оси вращения или на уровне самой нижней точки нахождения одного из грузов и обязательно делают чертёж;
- записывают закон сохранения механической энергии, в котором в левой части записывают сумму кинетической и потенциальной энергии обоих тел в начальной ситуации, а в правой части записывают сумму кинетической и потенциальной энергии обоих тел в конечной ситуации;
- учитывают, что угловые скорости тел одинаковы, тогда линейные скорости тел пропорциональны радиусам вращения;
- при необходимости записывают второй закон Ньютона для каждого из тел в отдельности.

Разрыв снаряда
В случае разрыва снаряда выделяется энергия взрывчатых веществ. Чтобы найти эту энергию надо от суммы механических энергий осколков после взрыва отнять механическую энергию снаряда до взрыва. Также будем использовать закон сохранения импульса, записанный, в виде теоремы косинусов (векторный метод) или в виде проекций на выбранные оси.
Столкновения с тяжёлой плитой
Пусть навстречу тяжёлой плите, которая движется со скоростью v , движется лёгкий шарик массой m со скоростью u н. Так как импульс шарика много меньше импульса плиты, то после удара скорость плиты не изменится, и она будет продолжать движение с той же скоростью и в том же направлении. В результате упругого удара, шарик отлетит от плиты. Здесь важно понять, что не поменяется скорость шарика относительно плиты . В таком случае, для конечной скорости шарика получим:
Таким образом, скорость шарика после удара увеличивается на удвоенную скорость стены. Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
Аналогичное рассуждение для случая, когда до удара шарик и плита двигались в одном направлении, приводит к результату согласно которому скорость шарика уменьшается на удвоенную скорость стены:
По физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ.
 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Определение работы в физике. Механическая работа
А что это значит?
В физике «механической работой» называют работу какой-нибудь силы (силы тяжести, упругости, трения и т.д.) над телом, в результате действия которой тело перемещается.
Часто слово «механическая» просто не пишется.
Иногда можно встретить выражение » тело совершило работу», что в принципе означает «сила, действующая на тело, совершила работу».
Я думаю — я работаю.
Я иду — я тоже работаю.
Где же здесь механическая работа?
Если под действием силы тело перемещается, то совершается механическая работа.
Говорят, что тело совершает работу.
А точнее будет так: работу совершает сила, действующая на тело.
Работа характеризует результат действия силы.
Cилы, действующие на человека совершают над ним механическую работу, а в результате действия этих сил человек перемещается.
Работа — физическая величина, равная произведению силы, действующей на тело, на путь, совершенный телом под действием силы в направлении этой силы.
А — механическая работа,
F — сила,
S — пройденный путь.
Работа совершается
, если соблюдаются одновременно 2 условия: на тело действует сила и оно
перемещается в направлении действия силы.
Работа не совершается
(т.е. равна 0),если:
1. Сила действует, а тело не перемещается.
Например: мы действуем с силой на камень, но не можем его сдвинуть.
2. Тело перемещается, а сила равна нулю, или все силы скомпенсированы (т.е. равнодействующая этих сил равна 0).
Например: при движении по инерции работа не совершается.
3. Направление действия силы и направление движения тела взаимно перпендикулярны.
Например: при движении поезда по горизонтали сила тяжести работу не совершает.
Работа может быть положительной и отрицательной
1. Если направление силы и направление движения тела совпадают, совершается положительная работа.
Например: сила тяжести, действуя на падающую вниз каплю воды, совершает положительную работу.
2. Если направление силы и движения тела противоположны, совершается отрицательная работа.
Например: сила тяжести, действующая на поднимающийся воздушный шарик, совершает отрицательную работу.
Если на тело действует несколько сил, то полная работа всех сил равна работе результирующей силы.
Единицы работы
В честь английского ученого Д.Джоуля единица измерения работы получила название 1 Джоуль.
В международной системе единиц (СИ):
[А] = Дж = Н м
1Дж = 1Н 1м
Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.
При перелете с большого пальца руки человека на указательный
комар совершает работу — 0, 000 000 000 000 000 000 000 000 001 Дж.
Сердце человека за одно сокращение совершает приблизительно 1 Дж работы, что соответствует работе, совершенной при поднятии груза массой 10 кг на высоту 1 см.
ЗА РАБОТУ, ДРУЗЬЯ!
Механическая работа это энергетическая характеристика движения физических тел, имеющая скалярный вид. Она равна модулю силы действующей на тело, умноженной на модуль перемещения вызванного этой силой и на косинус угла между ними.
Формула 1 — Механическая работа.
F — Сила, действующая на тело.
s — Перемещение тела.
cosa — Косинус угла между силой и перемещением.
Данная формула имеет общий вид. В случае если угол между прикладываемой силой и перемещением равен нулю, то косинус равен 1. Соответственно работа будет равна только произведению силы на перемещение. Проще говоря, если тело движется в направлении приложения силы, то механическая работа равна произведению силы на перемещение.
Второй частный случай, когда угол между силой, действующей на тело и его перемещением равен 90 градусов. В этом случае косинус 90 градусов равен нулю, соответственно работа будет равна нулю. И действительно, что происходит мы, прикладываем силу в одном направлении, а тело движется перпендикулярно ему. То есть тело движется явно не под действием нашей силы. Таким образом, работа нашей силы по перемещению тела равна нулю.
Рисунок 1 — Работа сил при перемещении тела.
В случае если на тело действует больше одной силы, то рассчитывают суммарную силу, действующую на тело. И далее ее подставляют в формулу как единственную силу. Тело под действием силы может перемещаться не только прямолинейно, но и по произвольной траектории. В этом случае работа вычисляется для малого участка перемещения, который можно считать прямолинейным и далее суммируется по всему пути.
Работа может быть как положительной, так и отрицательной. То есть если перемещение и сила совпадают по направлению, то работа положительна. А если сила приложена в одном направлении, а тело перемещается в другом, то работа будет отрицательна. Примером отрицательной работы может служить работа силы трения. Так как сила трения направлена встречно движению. Представьте себе, тело движется по плоскости. Сила, приложенная к телу, толкает его в определенном направлении. Эта сила совершает положительную работу по перемещению тела. Но при этом сила трения совершает отрицательную работу. Она тормозит перемещение тела и направлена навстречу его движению.
Рисунок 2 — Сила движения и трения.
Работа в механике измеряется в Джоулях. Один Джоуль это работа совершаемая силой в один Ньютон при перемещении тела на один метр. Кроме направления движения тела может меняться и величина прилагаемой силы. К примеру, при сжатии пружины, сила прилагаемой к ней будет увеличиваться пропорционально пройденному расстоянию. В этом случае работу вычисляют по формуле.
Формула 2 — Работа сжатия пружины.
k — жесткость пружины.
x — координата перемещения.
С механической работой (работой силы) вы уже знакомы из курса физики основной школы. Напомним приведенное там определение механической работы для следующих случаев.
Если сила направлена так же, как перемещение тела, то работа силы
В этом случае работа силы положительна.
Если сила направлена противоположно перемещению тела, то работа силы
В этом случае работа силы отрицательна.
Если сила f_vec направлена перпендикулярно перемещению s_vec тела, то работа силы равна нулю:
Работа – скалярная величина. Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:
1 Дж = 1 Н * м.
1. Брусок массой 0,5 кг переместили по столу на 2 м, прикладывая к нему силу упругости, равную 4 Н (рис. 28.1). Коэффициент трения между бруском и столом равен 0,2. Чему равна работа действующей на брусок:
а) силы тяжести m?
б) силы нормальной реакции ?
в) силы упругости ?
г) силы трения скольжения тр?
Суммарную работу нескольких сил, действующих на тело, можно найти двумя способами:
1. Найти работу каждой силы и сложить эти работы с учетом знаков.
2. Найти равнодействующую всех приложенных к телу сил и вычислить работу равнодействующей.
Оба способа приводят к одному и тому же результату. Чтобы убедиться в этом, вернитесь к предыдущему заданию и ответьте на вопросы задания 2.
2. Чему равна:
а) сумма работ всех действующих на брусок сил?
б) равнодействующая всех действующих на брусок сил?
в) работа равнодействующей? В общем случае (когда сила f_vec направлена под произвольным углом к перемещению s_vec) определение работы силы таково.
Работа A постоянной силы равна произведению модуля силы F на модуль перемещения s и на косинус угла α между направлением силы и направлением перемещения:
A = Fs cos α (4)
3. Покажите, что из общего определения работы следуют к выводы, показанные на следующей схеме. Сформулируйте их словесно и запишите в тетрадь.
4. К находящемуся на столе бруску приложена сила, модуль которой 10 Н. Чему равен угол между этой силой и перемещением бруска, если при перемещении бруска по столу на 60 см эта сила совершила работу: а) 3 Дж; б) –3 Дж; в) –3 Дж; г) –6 Дж? Сделайте пояснительные чертежи.
2. Работа силы тяжести
Пусть тело массой m движется вертикально от начальной высоты h н до конечной высоты h к.
Если тело движется вниз (h н > h к, рис. 28.2, а), направление перемещения совпадает с направлением силы тяжести, поэтому работа силы тяжести положительна. Если же тело движется вверх (h н
В обоих случаях работа силы тяжести
A = mg(h н – h к). (5)
Найдем теперь работу силы тяжести при движении под углом к вертикали.
5. Небольшой брусок массой m соскользнул вдоль наклонной плоскости длиной s и высотой h (рис. 28.3). Наклонная плоскость составляет угол α с вертикалью.
а) Чему равен угол между направлением силы тяжести и направлением перемещения бруска? Сделайте пояснительный чертеж.
б) Выразите работу силы тяжести через m, g, s, α.
в) Выразите s через h и α.
г) Выразите работу силы тяжести через m, g, h.
д) Чему равна работа силы тяжести при движении бруска вдоль всей этой же плоскости вверх?
Выполнив это задание, вы убедились, что работа силы тяжести выражается формулой (5) и тогда, когда тело движется под углом к вертикали – как вниз, так и вверх.
Но тогда формула (5) для работы силы тяжести справедлива при движении тела по любой траектории, потому что любую траекторию (рис. 28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).
Таким образом,
работа силы тяжести при движении но любой траектории выражается формулой
A т = mg(h н – h к),
где h н – начальная высота тела, h к – его конечная высота.
Работа силы тяжести не зависит от формы траектории.
Например, работа силы тяжести при перемещении тела из точки A в точку B (рис. 28.5) по траектории 1, 2 или 3 одинакова. Отсюда, в частности, следует, что рибота силы тяжести при перемещении по замкнутой траектории (когда тело возвращается в исходную точку) равна нулю.
6. Шар массой m, висящий на нити длиной l, отклонили на 90º, держа нить натянутой, и отпустили без толчка.
а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 28.6)?
б) Чему равна работа силы упругости нити за то же время?
в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?
3. Работа силы упругости
Когда пружина возвращается в недеформированное состояние, сила упругости совершает всегда положительную работу: ее направление совпадает с направлением перемещения (рис. 28.7).
Найдем работу силы упругости .
Модуль этой силы связан с модулем деформации x соотношением (см. § 15)
Работу такой силы можно найти графически.
Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8).
На рисунке 28.9 изображен график зависимости F(x) для силы упругости. Разобьем мысленно все перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.
Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках.
Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).
7. Используя рисунок 28.10, докажите, что
работа силы упругости при возвращении пружины в недеформированное состояние выражается формулой
A = (kx 2)/2. (7)
8. Используя график на рисунке 28.11, докажите, что при изменении деформации пружины от x н до x к работа силы упругости выражается формулой
Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины, Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.
9. В начальный момент растяжение пружины жесткостью 400 Н/м равно 3 см. Пружину растянули еще на 2 см.
а) Чему равна конечная деформация пружины?
б) Чему равна работа силы упругости пружины?
10. В начальный момент пружина жесткостью 200 Н/м растянута на 2 см, а в конечный момент она сжата на 1 см. Чему равна работа силы упругости пружины?
4. Работа силы трения
Пусть тело скользит по неподвижной опоре. Действующая на тело сила трения скольжения направлена всегда противоположно перемещению и, следовательно, работа силы трения скольжения отрицательно при любом направлении перемещения (рис. 28.12).
Поэтому если сдвинуть брусок вправо, а пегом на такое же расстояние влево, то, хотя он и вернется в начальное положение, суммарная работа силы трения скольжения не будет равна нулю. В этом состоит важнейшее отличие работы силы трения скольжения от работы силы тяжести и силы упругости. Напомним, что работа этих сил при перемещении тела по замкнутой траектории равна нулю.
11. Брусок массой 1 кг передвигали по столу так, что его траекторией оказался квадрат со стороной 50 см.
а) Вернулся ли брусок в начальную точку?
б) Чему равна суммарная работа действовавшей на брусок силы трения? Коэффициент трения между бруском и столом равен 0,3.
5. Мощность
Часто важна не только совершаемая работа, но и скорость совершения работы. Она характеризуется мощностью.
Мощностью P называют отношение совершенной работы A к промежутку времени t, за который эта работа совершена:
(Иногда мощность в механике обозначают буквой N, а в электродинамике – буквой P. Мы считаем более удобным одинаковое обозначение мощности.)
Единица мощности – ватт (обозначают: Вт), названная в честь английского изобретателя Джеймса Уатта. Из формулы (9) следует, что
1 Вт = 1 Дж/c.
12. Какую мощность развивает человек, равномерно поднимая ведро воды массой 10 кг на высоту 1 м в течение 2 с?
Часто мощность удобно выражать не через работу и время, а через силу и скорость.
Рассмотрим случай, когда сила направлена вдоль перемещения. Тогда работа силы A = Fs. Подставляя это выражение в формулу (9) для мощности, получаем:
P = (Fs)/t = F(s/t) = Fv. (10)
13. Автомобиль едет по горизонтальной дороге со скоростью 72 км/ч. При этом его двигатель развивает мощность 20 кВт. Чему равна сила сопротивления движению автомобиля?
Подсказка. Когда автомобиль движется по горизонтальной дороге с постоянной скоростью, сила тяги равна по модулю силе сопротивления движению автомобиля.
14. Сколько времени потребуется для равномерного подъема бетонного блока массой 4 т на высоту 30 м, если мощность двигателя подъемного крана 20 кВт, а КПД электродвигателя подъемного крана равен 75%?
Подсказка. КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.
Дополнительные вопросы и задания
15. Мяч массой 200 г бросили с балкона высотой 10 и под углом 45º к горизонту. Достигнув в полете максимальной высоты 15 м, мяч упал на землю.
а) Чему равна работа силы тяжести при подъеме мяча?
б) Чему равна работа силы тяжести при спуске мяча?
в) Чему равна работа силы тяжести за все время полета мяча?
г) Есть ли в условии лишние данные?
16. Шар массой 0,5 кг подвешен к пружине жесткостью 250 Н/м и находится в равновесии. Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия?
в) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия?
г) Чему равна работа равнодействующей всех приложенных к шару сил за время, в течение которого шар движется к положению равновесия?
17. Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.
а) Чему равен модуль силы трения при движении санок по горизонтальной поверхности?
б) Чему равна работа силы трения при движении санок по горизонтальной поверхности на пути 20 м?
в) Чему равен модуль силы трения при движении санок по горе?
г) Чему равна работа силы трения при спуске санок?
д) Чему равна работа силы тяжести при спуске санок?
е) Чему равна работа равнодействующей сил, действующих на санки, при их спуске с горы?
18. Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м 3 , а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя? Есть ли в условии лишние данные?
Подсказка. КПД теплового двигателя равен отношению совершенной двигателем работы к количеству теплоты, которое выделилось при сгорании топлива.
Энергия — универсальная мера различных форм движения и взаимодействия. Изменение механического движения тела вызывается силами , действующими на него со стороны других тел. Работы силы — процесс обмена энергией между взаимодействующими телами.
Если на тело движуещаеся прямолинейно действует постоянная сила F, которая составляет некоторый угол с направлением перемещения, то работа этой силы равна произведению проекции силы F s на направление перемещения, умноженной на перемещение точки приложения силы: (1)
В бщем случае сила может изменяться как по модулю, так и по направлению, поэтому скалярная величина элементарной работоы силы F на перемещении dr:
где — угол между векторами F и dr; ds = |dr| — элементарный путь; F s — проекция вектора F на вектор dr рис. 1
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути: (2)
где s — пройденный телом. При /2 работа силы отрицательна. При =/2 (сила перпендикулярна перемещению) работа силы равна нулю.
Единица работы — джоуль (Дж): работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н м).
Мощность – величина скорости совершения работы: (3)
За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент ремени:(4)
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт (Вт): мощность, при которой за время 1с совершается работа 1Дж (1Вт = 1Дж/с).
Кинетическая и потенциальная энергии
Кинетическая энергия механической системы — энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а изм-е энергии движущегося тела(dT ) возрастает на величину затраченной работы dA . Т. е. dA = dТ
Используя второй закон Ньютона(F=mdV/dt) и ряд др-х преобразований получаем
(5) — кинетическая энергия тела массой m, движущееся со скоростью v .
Кинетическая энергия зависит только от массы и скорости тела.
В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Т. о., кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
В сл-е взаимодействия тел осуществл-х посредством силовых полей(поля упругих, гравитационных сил), работа, совершаемая действующими силами при перемещении тела, не зависит от траектории этого перемещения, а зависит только от начального и конечного положений тела. Такие поля называются потенциальными , а силы, действующие в них, — консервативными . Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (сила трения). Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном(бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус: dA= — dП (6)
Работа dA — скалярное произведение силы F на перемещение dr и выражение (6) можно записать: Fdr= -dП (7)
При расчётах потенциальную энергию тела в каком-то определенном положении считают равной нулю(выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна (8)
где высота h отсчитывается от нулевого уровня, для которого П 0 =0.
Т. к. начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение(кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты(глубина h » ), П= — mgh «.
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы равна сумме кинетической и потенциальной энергий: E=T+П.
Занимательная физика
1. Сформированность познавательных интересов, интеллектуальных и творческих способностей учащихся;
2. Убежденность в возможности познания природы, в необходимости разумного использования достижений науки и технологий для дальнейшего развития человеческого общества, уважение к творцам науки и техники, отношение к физике как элементу общечеловеческой культуры;
3. Самостоятельность в приобретении новых знаний и практических умений;
4. Готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями;
5. Формирование ценностных отношений друг к другу, учителю, авторам открытий и изобретений, результатам обучения.
6. Овладение навыками самостоятельного приобретения новых знаний, организации учебной деятельности, постановки целей, планирования, самоконтроля и оценки
результатов своей деятельности, умениями предвидеть возможные результаты своих действий;
7. Понимание различий между исходными фактами и гипотезами для их объяснения, теоретическими моделями и реальными объектами, овладение универсальными учебными действиями на примерах гипотез для объяснения известных фактов и экспериментальной проверки выдвигаемых гипотез, разработки теоретических моделей процессов или явлений;
8. Формирование умений воспринимать, перерабатывать и предъявлять информацию в словесной, образной, символической формах, анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами, выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его;
9. Освоение приемов действий в нестандартных ситуациях, овладение эвристическими методами решения проблем;
10. Формирование умений работать в группе с выполнением различных социальных ролей, представлять и отстаивать свои взгляды и убеждения, вести дискуссию.
11.Формирование представлений о закономерной связи и познаваемости явлений природы, об объективности научного знания; о системообразующей роли физики для развития других естественных наук, техники и технологий; научного мировоззрения как результата изучения основ строения материи и фундаментальных законов физики;
12. Знания о природе важнейших физических явлений окружающего мира и понимание смысла физических законов, раскрывающих связь изученных явлений;
13. Формирование первоначальных представлений о физической сущности явлений природы (механических, тепловых, электромагнитных и квантовых), видах материи (вещество и поле), движении как способе существования материи; усвоение основных идей механики, атомно-молекулярного учения о строении вещества, элементов электродинамики и квантовой физики; овладение понятийным аппаратом и символическим языком физики;
14. Применять полученные знания для объяснения принципов действия важнейших
технических устройств, (работы) машин и механизмов, средств передвижения и связи, бытовых приборов, промышленных технологических процессов, решения практических задач повседневной жизни, обеспечения безопасности своей жизни, рационального природопользования и охраны окружающей среды; влияния технических устройств на окружающую среду; осознание возможных причин техногенных и экологических катастроф.
15. Осознание необходимости применения достижений физики и технологий для рационального природопользования;
16. Овладение основами безопасного использования естественных и искусственных электрических и магнитных полей, электромагнитных и звуковых волн, естественных и искусственных ионизирующих излучений во избежание их вредного воздействия на окружающую среду и организм человека;
17. Формирование убеждения в закономерной связи и познаваемости явлений природы, в объективности научного знания, в высокой ценности науки в развитии материальной и духовной культуры людей;
18. Развитие теоретического мышления на основе формирования умений устанавливать факты, различать причины и следствия, строить модели и выдвигать гипотезы, отыскивать и формулировать доказательства выдвинутых гипотез, выво- дить из экспериментальных фактов и теоретических моделей физические законы;
19. Развитие умения планировать в повседневной жизни свои действия с применением полученных знаний законов механики, электродинамики, термодинамики и тепловых явлений с целью сбережения здоровья;
20. Формирование представлений о нерациональном использовании природных ресурсов и энергии, загрязнении окружающей среды как следствие несовершенства машин и механизмов.
21. Коммуникативные умения докладывать о результатах своего исследования, участвовать в дискуссии, кратко и точно
отвечать на вопросы, использовать справочную литературу и другие источники информации.
Работа
Сила без движения или сила, перпендикулярная движению, не работает
Эти два примера сил, которые не работают, парадоксальны. Вы определенно можете почувствовать усталость, выполняя любое из этих действий, так как же вы можете сказать, что работа не выполняется?
В случае, показанном слева, независимо от того, насколько сильно и как долго вы толкали ящик, если ящик не двигается, значит, вы не работали с ящиком. Он сидит на том же месте! Почему тогда вы чувствуете усталость (а также разочарование и т. Д.)). Решение этой дилеммы приходит в том случае, если учесть, что, когда ваши мышцы используются для приложения силы к чему-либо, отдельные мышечные волокна находятся в непрерывном процессе сокращения и освобождения, чтобы поддерживать общий коллективный результат постоянной силы, воздействующей на внешний объект. Это сокращение и отпускание включает в себя силу и движение и составляет внутреннюю работу в вашем теле. Энергия проявляется в нагревании ваших мышечных тканей, но если ящик не двигается, сетка по-прежнему не работает.
Пример справа — еще один стандартный парадокс в определении работы. Если ящик переносится с постоянной скоростью, то для его движения не требуется никакой чистой силы. Сила, прикладываемая человеком, направлена вверх, равная весу коробки, и эта сила перпендикулярна движению. Если нет движения в направлении силы, то эта сила не совершает никакой работы. Тем не менее, вы определенно чувствуете, что делаете работу, если несете тяжелую коробку. Разрешение парадокса аналогично первому примеру — ваши мышцы должны сохранять дополнительное напряжение, чтобы оставаться в вертикальном положении под нагрузкой.Это требует большего внутреннего сокращения и высвобождения наших мышечных волокон и, следовательно, внутренней работы нашего тела. Но работа, проделанная с коробкой, равна нулю, поскольку при движении по прямой с постоянной скоростью его энергия остается той же самой.
Есть много важных примеров сил, которые не работают, потому что действуют перпендикулярно движению. При круговом движении центростремительная сила всегда действует перпендикулярно движению. Он меняет направление движения, но не воздействует на объект.Это можно применить к любой круговой орбите.
Определение работы по химии, биологии, физике.
Примеры работ по темам:
Негативная работа и общая работа
Свободная энергия и работа
- Свободная энергия Гиббса — это максимальное количество работы без расширения , которое может быть извлечено из закрытой системы.
- Работа выполняется за счет внутренней энергии системы.
- Энергия, которая не извлекается при работе , обменивается с окружающей средой в виде тепла.
- «Полезный» в данном случае относится к работе , не связанной с расширением системы.
- Чаще всего это электрическая работа (перемещение электрического заряда через разность потенциалов), но возможны и другие формы работы .
Работа
- Термодинамическая работа включает механическую работу (расширение газа) плюс многие другие типы работы , например электрические.
- Как таковая, термодинамическая работа является обобщением концепции работы в механике.
- Тем не менее, нагрев и работа могут дать одинаковые результаты.
- И нагрев, и работают. может вызвать повышение температуры.
- Поскольку давление постоянно, работа , выполненная , равна PΔV.
MLA: Работы, цитируемые в разделе
Flextime
- При гибком графике работникам разрешено определять свой график работы вместо графика работы в течение стандартных часов 9 часов утра.м. до 17:00
- Flextime хорошо работает для родителей, когда оба родителя работают .
- Ее муж может пойти на работу, позже, чтобы проводить детей в школу, и, таким образом, остаться на работе позже.
- Flexitime — это изменяемый график работы , в отличие от традиционного графика работы , требующего от сотрудников работы с 9:00 до 17:00. день.
- При гибком графике обычно существует основной период (примерно 50% от общего количества рабочих дней / рабочих дней) дня, когда ожидается, что сотрудники будут на рабочих днях (например, между 11 часами утра.м. и 15:00).
Работающие бедняки
- работающих бедных — это работающих человек, чьи доходы ниже заданной черты бедности.
- работающих бедных — это работающих человек, чьи доходы ниже заданной черты бедности.
- Из этих семей 5,19 миллиона, или 58,9%, имели хотя бы одного человека, который был классифицирован как работающих
- Один из ключевых продолжающихся споров касается различия между работающими и неработающими (безработными) бедными.
- Некоторые из этих препятствий могут включать в себя поиск доступного жилья, организацию транспорта на работу и обратно, покупку предметов первой необходимости, организацию ухода за детьми, наличие непредсказуемого графика работы , совмещение двух или более работ и совладание с работой с низким статусом .
Теорема о кинетической энергии и работе-энергии
- Работа , -энергетическая теорема утверждает, что работа , , совершаемая всеми силами, действующими на частицу, равна изменению кинетической энергии частицы.
- Принцип работы , и кинетической энергии (также известный как работа , -энергетическая теорема) утверждает, что работа , , совершаемая суммой всех сил, действующих на частицу, равна изменению кинетической энергии частицы.
- Сила выполняет работы на блок.
- Кинетическая энергия блока увеличивается в результате на величину работы .
- Это соотношение обобщено в работе , -энергетической теореме.
Рабочий класс
- Секретари, фермеры и стилисты могут считаться членами рабочего класса .
- Рабочие классы в основном встречаются в промышленно развитых странах и в городских районах неиндустриальных экономик.
- В США параметры рабочего класса остаются нечетко определенными и спорными.
- Из-за различий между средними и работающими культурами класса , работающих студентов колледжа могут столкнуться с «культурным шоком» при поступлении в систему послесреднего образования с его культурой «среднего класса».
- Исследование, показывающее, что работающих студентов класса учат ценить послушание выше лидерства и творческих способностей, может частично объяснить трудности, с которыми сталкиваются многие работающих студентов класса при поступлении в колледжи и университеты.
Важность оплачиваемой и неоплачиваемой работы
- Хотя мы обычно считаем работу оплачиваемой, неоплачиваемая работа не менее важна для экономики.
- В большинстве случаев, когда мы думаем о работе , мы думаем об оплачиваемой работе .
- Неоплачиваемые рабочие работают без оплаты.
- Другой важный вид неоплачиваемой работы — это работа , выполняемая членами семьи по ведению домашнего хозяйства.
- По мере того, как все больше женщин попадают на оплачиваемую рабочую силу, многие из них возвращаются домой после дня оплачиваемой работы , чтобы продолжить работу «вторую смену» неоплачиваемой домашней работы .
Анализ управления оборотным капиталом
- Чистый оборотный капитал рассчитывается как оборотные активы за вычетом текущих обязательств.
- Если оборотные активы меньше текущих обязательств, у предприятия имеется дефицит оборотного капитала , также называемый дефицитом оборотного капитала .
- Решения, относящиеся к оборотному капиталу, и краткосрочному финансированию, именуются оборотным управлением капиталом.
- Если бы деньги росли на деревьях, у компаний никогда не было бы рабочих нехватки капитала.
- Определите оборотного капитала и обсудите, как компания будет использовать его
Определение работы | Определить работу
Определение работы
«Работа выполняется, когда объект движется (смещается) в направлении приложения силы.«
ИЛИ Работа определяется как сила � смещение.
W = F x S
Подробнее о работе:
Для выполнения работы необходимо выполнение двух условий.
Необходимо приложить силу
Объект должен сместиться на определенное расстояние .
Даже после приложения силы к объекту, если объект не двигается, проделанная работа равна нулю.
Сила — причина движения. Без использования силы объекты не будут перемещаться из-за инерции (тенденции тела оставаться в своем состоянии).
Механическая энергия, используемая при приложении силы, называется работой.
Единица измерения S.I — джоуль.
W = F X S = (Сила измеряется в Ньютонах, а перемещение — в метрах). Следовательно, проделанная работа = Ньютон X метр = 1 Джоуль.
Пример 1: Ребенок толкает стул вперед, и стул падает назад (неправильно сбалансированный). Теперь работа, выполняемая ребенком, равна нулю, потому что стул не движется вперед.
Для выполнения работы Тело / Объект должны смещаться в направлении силы
Пример 2: Три человека работали на железнодорожном пути и хотели переместить железный стержень на расстояние в 1 метр.Три человека прикладывают усилие 400 Н, но стержень не смещается. Какую работу проделали эти три человека?
Ответ: Ноль
Причина: Поскольку смещения нет (железный стержень не сдвинулся). Сила X нуля = 0
Примеры работ
Магнит, притягивающий железный гвоздь.
Пружина в тяге.
Решенный пример из работы
К телу w приложена сила 30 Н, и тело переместится на некоторое расстояние.10 м, то работы
А. 30J
Б. 30J
С. 300J
D. 0,3J
Правильный ответ: C.
Решение:
Шаг 1: Запишите уравнение работы. W = f.dx
Шаг 2 : Шаг 2: Вставьте значение силы и смещения в Ньютонах и расстояние в метрах = 30.10
Шаг 3: Запишите окончательный ответ в джоулях.
Шаг 4 : W = 300j
Работа, энергия и сила
ОпределенияРабота может быть определена как передача энергии.В физике мы говорим, что работа выполняется с объектом, когда вы передаете ему энергию. Если один объект передает (отдает) энергию второму объекту, то первый объект работает со вторым объектом.
Работа — это приложение силы на расстоянии. Поднять какой-нибудь груз с земли и положить его на полку — хороший пример работы. Сила равна весу объекта, а расстояние равно высоте полки (W = Fxd).
Принцип работы-энергии — Изменение кинетической энергии объекта равно чистой работе, проделанной с ним.2.
Виды энергии
Есть два типа энергии во многих формах:
Кинетическая энергия = Энергия движения
Потенциальная энергия = Накопленная энергия
Формы энергии
Солнечное излучение — инфракрасное тепло, радиоволны, гамма-лучи, микроволны, ультрафиолетовый свет
Атомная / ядерная энергия — энергия, выделяемая в ядерных реакциях.Когда нейтрон расщепляет ядро атома на более мелкие части, это называется делением. Когда два ядра соединяются под воздействием миллионов градусов тепла, это называется слиянием
.Электрическая энергия — Производство или использование электроэнергии в течение периода времени, выраженное в киловатт-часах (кВтч), мегаватт-часах (NM) или гигаватт-часах (ГВтч).
Химическая энергия — Химическая энергия — это форма потенциальной энергии, связанная с разрывом и образованием химических связей. Он накапливается в продуктах питания, топливе и батареях и выделяется в виде других форм энергии во время химических реакций.
Механическая энергия — Энергия движущихся частей машины. Также относится к движениям людей
Тепловая энергия — форма энергии, которая передается за счет разницы температур
Что такое Power
Мощность — это работа, выполненная за единицу времени. Другими словами, мощность — это мера того, насколько быстро можно выполнить работу. Единица мощности — ватт = 1 джоуль / 1 секунда.
Одной из распространенных единиц энергии является киловатт-час (кВтч).Если мы используем один кВт мощности, одного кВтч энергии хватит на один час.
Расчет работы, энергии и мощности
РАБОТА = W = Fd
Поскольку энергия — это способность выполнять работу, мы измеряем энергию и работу в одних и тех же единицах (Н * м или джоули).
МОЩНОСТЬ (P) — скорость производства (или поглощения) энергии с течением времени: P = E / t
Единицей измерения СИPower является ватт, представляющий выработку или поглощение энергии со скоростью 1 Джоуль / сек.Единицей измерения мощности в английской системе является мощность в лошадиных силах, что эквивалентно 735,7 Вт.
См. Также: Работа, энергия и мощность — Как понять и рассчитать счет за энергию.
Попробуйте это упражнение!
1) Сила в 20 ньютонов, толкающая объект на 5 метров в направлении силы. Сколько работы сделано?
Пожалуйста, введите свой ответ в отведенное для этого поле:
2) Если вы выполняете 100 джоулей работы за одну секунду (используя 100 джоулей энергии).Сколько энергии используется?
3) 1 лошадиная сила равна сколько ватт?
Работа и энергия
Концепции работы и энергии тесно связаны с концепцией силы, потому что приложенная сила может работать с объектом и вызывать изменение энергии. Энергия определяется как способность выполнять работу.Работа
Понятие работы в физике определяется гораздо более узко, чем обычное использование этого слова. Работа выполняется с объектом, когда приложенная сила перемещает его на расстояние. На нашем повседневном языке работа связана с затратами мышечных усилий, но это , а не на языке физики. Человек, держащий тяжелый предмет, не выполняет никакой физической работы, потому что сила не перемещает предмет на расстояние. Согласно физическому определению работа выполняется, пока тяжелый объект поднимается, но не когда объект неподвижен. Другой пример отсутствия работы — это масса на конце струны, вращающаяся по горизонтальному кругу на поверхности без трения.Центростремительная сила направлена к центру круга и, следовательно, не перемещает объект на расстояние; то есть сила направлена не в направлении движения объекта. (Однако была проделана работа, чтобы привести массу в движение.) Математически работа равна Вт, = F · x, где F, — приложенная сила, а x — это пройденное расстояние, то есть смещение. Работа — это скаляр. Единицей измерения работы в системе СИ является джоуль (Дж), то есть ньютон-метр или кг м / с 2 .
Если работа выполняется с помощью переменной силы, приведенное выше уравнение использовать нельзя. На рисунке показан график зависимости силы от смещения для объекта, на который действуют три различных последовательных силы. Сила увеличивается в сегменте I, постоянна в сегменте II и уменьшается в сегменте III. Работа, выполняемая над объектом каждой силой, представляет собой область между кривой и осью x . Общая проделанная работа — это общая площадь между кривой и осью x . Например, в этом случае работа, выполняемая тремя последовательными силами, показана на рисунке 1.
Рисунок 1
Действующая сила изменяется в зависимости от положения.
В этом примере общая выполненная работа равна (1/2) (15) (3) + (15) (2) + (1/2) (15) (2) = 22,5 + 30 + 15; работа = 67,5 Дж. Для постепенно изменяющейся силы работа выражается в интегральной форме: Вт = ∫ F · d x.
Кинетическая энергия
Кинетическая энергия — это энергия движущегося объекта. Выражение для кинетической энергии может быть получено из определения работы и кинематических соотношений.Рассмотрим силу, приложенную параллельно поверхности, которая перемещает объект с постоянным ускорением.
Исходя из определения работы, второго закона движения Ньютона и кинематики, W = Fx = max и v f 2 = v o 2 + 2 ax или a = ( v f 2 — v o 2 ) / 2 x .Подставьте последнее выражение для ускорения в выражение для работы, чтобы получить W = м ( v f 2 — v o 2 ) или W = (1/2) мв f 2 — (1/2) мв o 2 . Правая часть последнего уравнения дает определение кинетической энергии: K . Е . = (1/2) мв 2 Кинетическая энергия — это скалярная величина с теми же единицами, что и работа, джоулями (Дж). Например, масса 2 кг, движущаяся со скоростью 3 м / с, имеет кинетическую энергию 9 Дж.
Приведенный выше вывод показывает, что чистая работа равна изменению кинетической энергии. Это соотношение называется теоремой работы-энергии: Вт нетто = К . Е . f — К . Е . o , где K . Е . f — конечная кинетическая энергия и K . Е . o — исходная кинетическая энергия.
Потенциальная энергия
Потенциальная энергия, , также называемая накопленной энергией, — это способность системы выполнять работу, обусловленную ее положением или внутренней структурой. Примерами могут служить энергия, запасенная в сваях в верхней части его пути, или энергия, запасенная в спиральной пружине.Потенциальная энергия измеряется в джоулях.
Гравитационная потенциальная энергия — энергия положения. Во-первых, рассмотрим потенциальную энергию гравитации вблизи поверхности Земли, где ускорение свободного падения (g) приблизительно постоянно. В этом случае гравитационная потенциальная энергия объекта относительно некоторого опорного уровня составляет P.E . = mgh , где h — вертикальное расстояние над опорным уровнем.Чтобы поднять объект медленно, сила, равная его весу (мг) , прилагается через высоту (h) . Совершенная работа равна изменению потенциальной энергии: Вт = P . Е . f — P . Е . o = mgh f — mgh o , где нижние индексы (f и o) относятся к окончательной и исходной высоте корпуса.
Запуск ракеты в космос требует работы, чтобы разделить массу Земли и ракеты для преодоления силы тяжести. Для больших расстояний от центра Земли вышеприведенное уравнение неадекватно, потому что g непостоянно. Общая форма гравитационной потенциальной энергии — это P.E . = — GMm / r , где M и m обозначают массы двух разделенных тел, а r — расстояние между центрами масс.Отрицательный знак является результатом выбора нулевого задания при r равным бесконечности, то есть при очень большом расстоянии .
Упругая потенциальная энергия — это энергия, запасенная в пружине. Величина силы, необходимой для растяжения пружины, определяется как F = — kx , где x — это расстояние растяжения (или сжатия) пружины из ненагруженного положения, а k — это . пружинная постоянная. Жесткость пружины — это мера жесткости пружины, при этом более жесткие пружины имеют большие значения k .Потенциальная энергия, запасенная в пружине, задается P . Е . = (1/2) kx 2 .
Изменение потенциальной энергии равно работе. Сила тяжести и сила растяжения пружины — это разные силы; следовательно, приведенные выше уравнения потенциальной энергии для этих двух случаев также могут быть выведены из интегральной формы работы Δ P . Е . = W = ∫ F · d x.
Мощность
Мощность — скорость выполнения работы, средняя P = Вт / т , где t — временной интервал, в течение которого выполняется работа (Вт) .Другая форма мощности находится из Вт = F Δ x и замены средней скорости объекта за время t на Δ x / t : среднее P = F Δ x / Δ t = F (в среднем v ).
Сохранение энергии
Принцип сохранения энергии — один из самых далеко идущих общих законов физики.В нем говорится, что энергия не создается и не уничтожается, а может быть преобразована из одной формы в другую только в изолированной системе.
Поскольку полная энергия системы всегда остается постоянной, закон сохранения энергии является полезным инструментом для анализа физической ситуации, когда энергия меняет форму. Представьте себе качающийся маятник с незначительными силами трения. На вершине его подъема вся энергия является гравитационной потенциальной энергией из-за высоты над неподвижным положением.Внизу качелей вся энергия преобразована в кинетическую энергию движения. Полная энергия — это сумма кинетической и потенциальной энергий. Он поддерживает одно и то же значение во время движения качелей вперед и назад (см. Рисунок 2).
Рисунок 2
Маятник подчиняется закону сохранения энергии.
В точке C потенциальная энергия зависит от высоты, а остальная часть полной энергии — кинетическая энергия.
Хотя полная энергия сохраняется, кинетическая энергия не требуется. Столкновение двух объектов с сохранением кинетической энергии называется упругим столкновением . Сталкивающиеся объекты, взаимодействующие с потерями кинетической энергии из-за потерь на трение или деформации объекта, называются неупругими столкновениями. В макроскопическом мире большинство столкновений неупругие; однако потери кинетической энергии незначительны в почти упругих столкновениях между атомными частицами и субатомными частицами.Для этих случаев закон сохранения количества движения и кинетической энергии дает полезные уравнения.
Рассмотрим простое лобовое упругое столкновение, когда одна масса ( м 1 ) с заданной скоростью ( v 1 ) сталкивается со второй массой ( м 2 ), которая изначально находится в состоянии покоя. Примените законы сохранения количества движения и кинетической энергии, чтобы получить м 1 v 1 = м 1 ′ v 1 + m 2 v 2 ′ и (1/2) м 1 v 1 2 = (1/2) m 1 v 1 ′ 2 + (1 / 2) м 2 v ′ 2 2 , где штрихи относятся к скоростям после столкновения.Решение уравнений дает скорости двух масс после взаимодействия:
Поучительны три особых случая:
Для равных масс, где м 1 = м 2 , обратите внимание, что v 1 ′ становится равным нулю, а v 2 ′ равно v 1 ; таким образом, при равных массах объекты просто обмениваются скоростями, как это иногда наблюдается с шарами для пула. (Шары для пула имеют энергию вращения и несколько неупругие столкновения, поэтому их поведение только приближается к примеру.)
Если м 2 массивно, числитель и знаменатель почти совпадают в уравнении для v 1 ′. Тогда v 1 ′ примерно равно v 1 , но в противоположном направлении. Знаменатель выражения для v 2 ′ будет настолько большим, что скорость второй массы после столкновения будет небольшой. Другими словами, входящая масса ( м, 1 ) отскочит от второй массы почти с начальной скоростью, а ударная масса ( м, 2 ) будет медленно перемещаться после столкновения.
Если m 1 массивно, то v 1 ′ приблизительно равно v 1 , а v 2 ′ почти вдвое больше v 1 ; или падающая массивная частица продолжает двигаться почти с той же скоростью, а ударная масса движется вперед почти с удвоенной начальной скоростью первой массы после столкновения.
Центр масс
Концепция центра масс (CM) полезна для анализа движения системы частиц.Система частиц действует так, как будто вся ее масса сосредоточена в КМ. В отсутствие внешней силы, если ЦМ системы находится в состоянии покоя, тогда он будет оставаться в покое, а если он изначально находится в движении, он будет поддерживать это движение. Другими словами, КМ движется в соответствии со вторым законом Ньютона. Координаты центра масс x и y равны
.Рассмотрим предыдущий пример лобового столкновения двух равных масс, которые слиплись после столкновения.КМ изначально движется с постоянной скоростью и сохраняет ту же скорость после столкновения. Когда первая масса катится ко второй массе, CM всегда находится посередине между двумя массами. Перед столкновением CM покрывает половину расстояния приближающегося объекта за одно и то же время, и, следовательно, скорость CM составляет половину начальной скорости приходящей массы. В тот момент, когда две массы взаимодействуют, CM находится прямо между двумя объектами. После столкновения массы слипаются и имеют половину начальной скорости, потому что эффективная масса удвоилась.CM продолжает оставаться на полпути между массами. Он сохраняет ту же скорость (1/2) v o после столкновения. На рисунке движущийся белый шар ударяется о неподвижный черный шар. Пронумерованные и обведенные позиции CM соответствуют пронумерованным позициям шаров.
Рисунок 3
Неупругое столкновение двух шаров.
Урок 38: Работа и сила
Работа
Обыденное определение «работа» и то, что мы используем в физике, сильно отличаются друг от друга.
- Когда большинство людей думают о «работе», они думают о своей работе.
- В физике мы определяем работу двумя разными способами.
Определение 1:
Работа — это передача энергии либо от объекта к объекту, либо от одного типа энергии к другому.
Определение 2:
Работа — это сила, действующая на объект, вызывающая его смещение в том же направлении.
- Этому второму определению соответствует формула.Хотя это просто, относитесь к нему с уважением. Это что-то вроде формулы F = ma; простой, но применимый во многих различных ситуациях.
W = F d
W = работа (Джоули)
F = сила (Ньютоны)
d = перемещение (метры)
По определению, 1 Дж работы выполняется путем приложения силы 1 Н для перемещения объекта на 1 м.
- Работа не имеет направления, поэтому это скалярная величина.
- Кроме того, направление движения должно быть , в том же направлении (параллельно), что и направление силы, иначе никакая работа не выполняется.
Пример 1: Я держу в руках кусок сыра весом 2 кг. Я прохожу 12 метров в другую сторону комнаты. Объясните , работал ли я.
Поскольку я держу сыр против силы тяжести, сила, которую я должен приложить к нему, будет направлена вверх. Я двигался горизонтально, поэтому два вектора (сила и смещение) перпендикулярны друг другу. Я не работал.
Пример 2: Я решаю заставить своего питомца лягушку сделать небольшой подъем тяжестей (но я собираюсь начать его медленно!).Он поднимает 10 кг с пола, над головой и обратно на пол. Объясните , работал ли он.
Ну, в этом случае сила должна быть направлена вверх, когда он поднимает гири, и сначала он поднимает их, так что пока все кажется хорошо. Но подождите … Я сказал, что он затем опускает гири на пол. В целом смещение этих грузов равно нулю! Поэтому он не работал.
Пример 3: Прошлой зимой моя машина попала в сугроб.Я обещаю одному из моих друзей, что, если он придет поработать для меня, я куплю ему Whopper (с дополнительным луком … он действительно любит лук). Садимся за машину и выталкиваем ее из снега. Объясните , если я должен ему Whopper.
В этой ситуации мы оба двигались в одном направлении (параллельно друг другу), и машина двигалась в том же направлении. Так что ответ будет «Да!» Я в долгу перед ним за работу, которую он проделал … но я разрежу ее пополам и съеду часть сам, так как половину работы сделал я.
На самом деле, выполнить любые стандартные расчеты работы с помощью формулы довольно просто.
- Просто убедитесь, что, начиная любой вопрос, вы убедитесь, что сила и смещение имеют одинаковое направление.
Пример 4: Моя дочь Катриен хватает моего сына Нильса за ногу и тащит его на 2,3 м по полу. Если для этого она приложила силу 18,1 Н, определит, сколько работы она сделала.
W = F d = 18.1 Н (2,3 м) = 42 Дж
Когда вы посмотрите на только что рассчитанный ответ, вы также захотите иметь в виду первое определение работы.
- Поскольку работа — это передача энергии, это применимо к приведенному выше примеру. Катриен переводит химическую энергию, хранящуюся в ее теле, в кинетическую энергию Нильса, движущуюся по полу.
- Это определение также полезно, если вы знаете что-то о том, как энергия меняет формы.
Иногда мы называем полную энергию объекта (потенциальную и кинетическую) механической энергией объекта.
- Это будет означать, что выполнение работы с объектом каким-то образом изменяет механическую энергию объекта.
- «Механическая» энергия не означает, что она всегда должна задействовать машины.
- На самом деле большую часть времени это не имеет ничего общего с машиной.
- Яблоко, падающее со скалы, обладает потенциальной и кинетической энергией, а значит, и механической энергией.
- Мы подробно рассмотрим механическую энергию в следующем уроке.
Мощность
В повседневной жизни слово «мощность» чаще всего ассоциируется с электричеством, но в физике это не так.
- Мощность — это скорость выполнения работы.
- Это означает, что мощность измеряет, насколько быстро используется энергия.
- Поскольку это скорость, с которой что-то происходит, время должно каким-то образом быть задействовано.
- Если вы посмотрите на основную формулу силы, вы увидите, что она такая же, как и многие формулы, в которых учитывается время.
P = мощность (Вт)
Вт = Δ E = работа (Джоули)
t = время (секунды)
Иногда в приведенной выше формуле вы увидите Δ E вместо W.
- Δ E просто означает изменение энергии, в чем и заключается вся работа.
Мощность — это действительно то, насколько быстро вы потребляете энергию, поэтому ее можно измерять в Джоулях в секунду.
- В честь его поисков более эффективного двигателя (который лучше преобразовывал энергию!) Единица измерения мощности названа ватт в честь Джеймса Ватта.
- Представьте себе лампочку … вы всегда говорите о том, сколько ватт у лампы, как у лампочки на 60 Вт.
- Это просто означает, что лампочка потребляет 60 Джоулей энергии каждую секунду.
Пример 5: Я оставил лампочку мощностью 150 Вт на 2,5 часа. Определите , сколько электроэнергии я использовал.
В этом случае электричество (электрическая энергия) превращается в тепло и свет… вот и работа! «Электричество» — это НЕ мощность.Это энергия.
Вы израсходовали более миллиона Джоулей энергии !!!
| Работа и энергия | ||
| Когда сила перемещается на в направлении, в котором она действует, работа выполняется этим сила. | ||
| Итак, можно задать вопрос… что именно работа ? | ||
| Работа — это процесс преобразования энергии из одной формы в другую (электрическая энергия в тепловую энергию, химическая энергия в кинетическую энергию и т. д.) | ||
| Итак, что такое энергия? | ||
| Хорошо… энергия — это то, что вам нужно, если вы хотите работать …! | ||
| (Немного больше формальное звучащее заявление: Энергия — это способность делать работу.) | ||
| Если эти два взаимозависимых определения кажутся менее чем удовлетворительными, посмотрите на это с «практической» точки зрения. Знаем ли мы, что мы подразумеваем под энергией? | ||
| Да; энергия — это полезная вещь, которую мы получаем от электричества, химических реакций, таких как горение, движущая сила ветра (кинетическая энергия), потенциал накопленной воды за плотиной, чтобы дать нам электричество (гравитационная потенциальная энергия) и т. д. | ||
| Другими словами, два условия: выполненная работа, и преобразованная энергия , означают то же самое. | ||
| количество выполненной работы (или преобразованной энергии) с помощью силы, когда
сила движется, зависит от двух очевидных факторов: — пройденное расстояние (в том направлении, по которому сила актов) и — величина (сила) силы | ||
| Чтобы убедиться в этом, подумайте сначала о том, чтобы подняться на 20 ступенек, а затем позже. подъем на 200 ступенек; в каком случае вы устали больше? | ||
| Большее расстояние; ты будешь больше уставать. | ||
| Точно так же рассмотрите возможность первого подъема по этой лестнице. ничего не неся, а потом поднялся по той же лестнице с Мешок картофеля 50 кг * на спине. | ||
| Требуется большее усилие; опять утомительно. | ||
| Мы используем эту идею, чтобы определить количество работы, выполненной в данной ситуации следующее уравнение: | ||
| выполненная работа = расстояние силы, перемещенное в направлении силы | ||
| обратите внимание, что, хотя и сила, и смещение (расстояние, пройденное за заданном направлении) — векторные величины, работа (энергия) — скаляр количество.Вышеупомянутое уравнение представляет собой скалярное произведение двух векторов. | ||
| Приведенное выше уравнение также приводит нас к единице измерения количества работы, Ньютонметр. | ||
| Однако в честь ученого, который много поработал над работой (извините за that), Джеймс Прескотт Джоуль (1818 — 1889), 1 ньютонметр называется 1 Джоуль | ||
| 1Джоуль — это количество работы, выполненной при сила 1Н перемещает направление 1 м по своей линии действия. | ||
| Если направление смещения не совпадает с направлением силы, мы используем составляющую силы, которая на параллельна смещение. | ||
| Например, когда тело ускоряется вниз по наклонная плоскость под действием силы тяжести, как показано здесь. | ||
| Величина составляющая силы тяжести, действующая параллельно смещению, равна дается величиной силы, умноженной на косинус угол между силой и перемещением. | ||
| Таким образом, мы можем сформулировать более общее уравнение: | ||
| Один из самых полезных фактов об энергии заключается в том, что общее количество энергии в Вселенная считается постоянной. | ||
| Эта идея выражена в законе сохранения энергии : | ||
| Энергия в любой закрытой системе никогда не теряется, но может быть изменена из одной формы к другому. | ||
| Этот закон может помочь нам упростить многие вычисления / прогнозы в физике, нажмите вот для примера. | ||
| Примеры преобразования энергии: | ||
| — Аккумулятор преобразует химическую энергию в электрическую энергию | ||
| — Электродвигатель подъема лифта преобразует электроэнергии в гравитационная потенциальная энергия | ||
| — Ядерный реактор преобразует ядерной энергии в тепловой энергии. | ||
| — Когда движущееся транспортное средство использует тормоза для остановки, кинетическая энергия автомобиля преобразуется в тепловую энергию в тормозах. | ||
| (Это это интересный случай, потому что тепловая энергия — это просто кинетическая энергия, но обладает множеством беспорядочно движущихся частиц …) | ||
| Мощность | ||
| Рассмотрим два автомобильных двигателя. | ||
| Можно охарактеризовать как более мощный чем другой. | ||
| Оба двигателя способны выполнение того же объема работы , но более мощный мотор может делать работу быстрее . | ||
| Это соображение приводит нас к следующее определение слова власть: | ||
| Мощность — это скорость выполнения работы (или преобразования энергии) или | ||
| Мощность — это выполненная работа (или преобразованная энергия) в единицу времени | ||
| единицей мощности, следовательно, является Джоуль в секунду, Дж -1 | ||
| Однако мощность 1 Дж -1 называется 1 Вт (1 Вт) в честь Джеймса Ватта и
18 -й век инженер-механик, работавший на паровых машинах. | ||




 — М.: Просвещение, 2004.
— М.: Просвещение, 2004. Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
Обратите внимание, что угол должен быть выбран между векторами силы и перемещения.
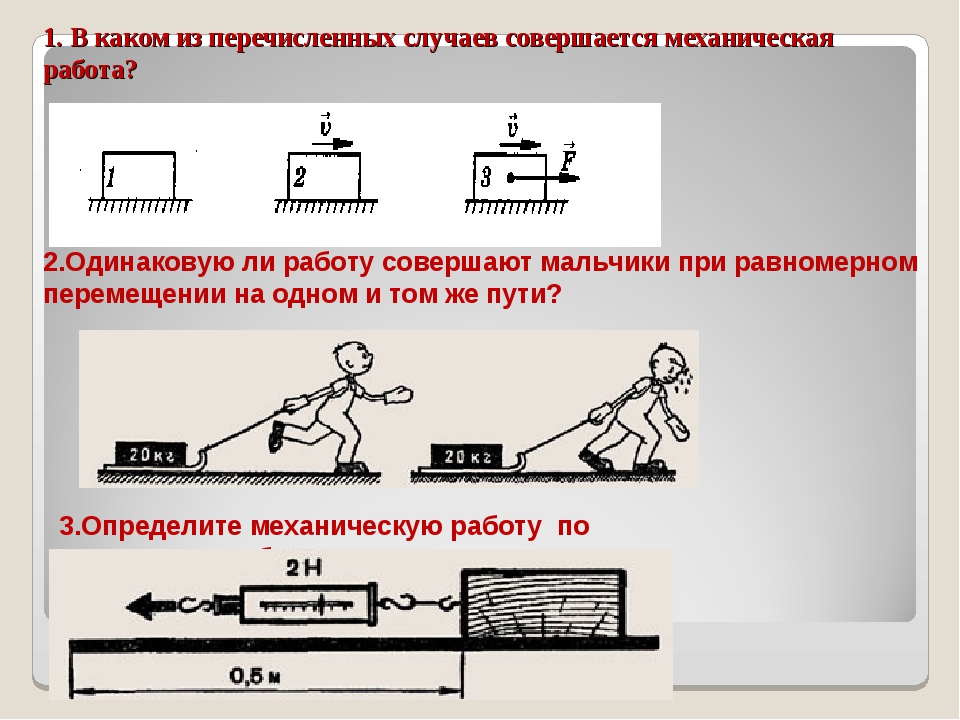

 После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами.