Урок 11. Лекция 11. Работа. Мощность. Энергия. Закон сохранения энергии
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.
Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости).
A = Fs cos α
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
[1 Дж=1 Н·м]
Работа силы, совершаемая в единицу времени, называется мощностью.
Мощность N –
N=A/t
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Внесистемная единица мощности 1 л.с.=735 Вт
Связь между мощностью и скоростью при равномерном движении:
N=A/t так как A=FScosα тогда N=(FScosα)/t, но S/t = v следовательно
N=Fvcos α
В технике используются единицы работы и мощности:
1 Вт·с = 1 Дж; 1Вт·ч = 3,6·103 Дж; 1кВт·ч = 3,6·106 Дж
Если тело способно совершить работу, то говорят, что оно обладает энергией.
Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.
Обозначается Е Единица энергии в СИ [1Дж = 1Н*м]
Механическая работа есть мера изменения энергии в различных процессах А = ΔЕ.
Различают два вида механической энергии – кинетическая Ек и потенциальная Еp энергия.
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергий
Е = Ек + Еp
Кинетическая энергия – это энергия тела, обусловленная его движением.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
Если тело движется со скоростью , то для его полной остановки необходимо совершить работу
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятиепотенциальной энергии
Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела.
Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия
Ep = mgh
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
где k – жесткость пружины.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
A = Ek2 – Ek1
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1) или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией.
Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.
Е = Ек + Еp = const
Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
Законы сохранения. Работа и мощность. Теория, Формулы, Шпаргалка
Законы сохранения. Работа и мощность.
(теория и формулы для ЕГЭ)
Законы сохранения
Импульсом тела (материальной точки) называют произведение массы тела на вектор его скорости. Единица модуля импульса тела – 1 кг·м/c.
Импульсом силы называют произведение вектора скорости на интервал времени её действия ∆t. Единица модуля импульса силы – 1 кг·м/c.
[F·∆t] = Н·м.

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются друг с другом и движутся дальше как одно тело. Механическая энергия не сохраняется (она частично или полностью переходит во внутреннюю энергию тел).
Закон сохранения импульса.
Замкнутая (изолированная) система – система тел, взаимодействующих только между собой и не взаимодействующих с телами, не входящими в эту систему.
Закон сохранения импульса: векторная сумма импульсов тел, составляющих замкнутую систему, не изменяется.
Энергия – скалярная физическая величина, являющаяся мерой способности тела (или системы тел) совершить работу. Существует кинетическая и потенциальная энергия.
Закон сохранения энергии в механических процессах – сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Е = Еk1
Если Fтр≠ 0, механическая энергия переходит во внутреннюю (тепловую) энергию тела:
Q = Е2 – Е1, где Q =Атр

Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными (силы тяжести и силы упругости)
Работа силы.
Механической работой A, совершаемой постоянной силой, называется скалярная физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения.
А = F∙s∙cos α [А] = Дж 1Дж =1Н∙1м
Работа зависит от угла α.

Работа силы тяжести не зависит от формы траектории и равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Атяж. = mg(h1 – h2) = — ( mgh1 — mgh2) = — (Ер2 – Ер1)
Работа силы тяжести по замкнутой траектории равна нулю.
Мощность – скалярная физическая величина, равная отношению совершенной работы к промежутку времени, за который она совершена.
Коэффициент полезного действия механизмов КПД – величина, равная отношению полезной работы к полной работ, выраженная в процентах.

Конспект урока «Законы сохранения. Работа и мощность. Теория и формулы для ЕГЭ».
Еще конспекты для 10-11 классов:
Механическая работа. Мощность (Побединский Д.М.). Видеоурок. Физика 10 Класс
На данном уроке, тема которого: «Механическая работа. Мощность», мы поговорим о работе: четко определим понятие работы в физике, решим несколько задач по данной теме урока, а также поговорим о том, что такое мощность.
Тема урока – работа. Мы часто используем это понятие. Например, рабочий устал, потому что проделал большую работу: перенес 200 кирпичей с первого этажа на второй (см. рис. 1).

Рис. 1. Совершение работы
Мы знаем, почему он устал: он в это время прикладывал к кирпичам силу. Но только ли в силе дело? Наверняка, если бы он переносил кирпичи на третий этаж, он бы выполнил бόльшую работу, а если он бы толкал неподвижную стену, никакой работы выполнено бы не было, хотя рабочий бы устал. Значит, дело не только в силе, перемещение тоже играет роль. Сегодня мы четко определим понятие работы в физике.
Оно близко к бытовому понятию работы, но нужно понимать важный момент.
В бытовом представлении работу выполняет человек, двигатель или другой субъект. В физике определение должно быть четким: субъект работы – сила. Поэтому работа, выполненная при действии нескольких сил, равна сумме работ, выполненных каждой силой по отдельности.
Как мы увидели на примере, работа тем больше, чем больше приложенная сила и чем больше пройденный путь. И сила, и перемещение – векторы, они имеют направления. Рассмотрим пока случай, когда направления векторов силы и перемещения совпадают (см. рис. 2), работа в физике определяется именно так:

т. е. как физическая величина, пропорциональная силе и перемещению.

Рис. 2. Направления векторов силы и перемещения совпадают
Соответственно, единицей работы является произведение единицы силы на единицу пути, т. е.  . У этой единицы есть собственное наименование – джоуль (Дж).
. У этой единицы есть собственное наименование – джоуль (Дж).

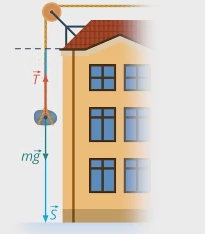
Рассмотрим такой пример: с крыши дома высотой 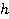 упал камень массой
упал камень массой  . Вычислите работу, которую выполнила сила тяжести (см. рис. 3).
. Вычислите работу, которую выполнила сила тяжести (см. рис. 3).

Рис. 3. Падение камня с крыши дома
Работа – это сила, умноженная на перемещение. Сила тяжести, действовавшая на камень, равна  , перемещение равно
, перемещение равно 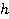 (камень упал с крыши на землю), работа равна
(камень упал с крыши на землю), работа равна  (см. рис. 4).
(см. рис. 4).

Рис. 4. Определение работы
Важно заметить, что нам безразлично, придавала ли данная сила ускорение телу. Рассмотрим ту же задачу, но с условием, что камень не падает, а осторожно, с постоянной скоростью опускается на веревке. Сила тяжести будет та же, как и перемещение, поэтому работа будет та же,  (см. рис. 5).
(см. рис. 5).

Рис. 5. Камень опускают с крыши дома
Нам важно лишь то, как сила участвует в движении, в какой степени она на него влияет. Но не всегда сила направлена туда же, куда и перемещение. Рассмотрим нашу задачу с новым условием: камень опускают по наклонной траектории под углом 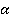 к вертикали (см. рис. 6).
к вертикали (см. рис. 6).

Рис. 6. Камень опускают по наклонной траектории
На перемещение  влияет только та составляющая силы тяжести, которая направлена вдоль перемещения, т. е. проекция силы тяжести на направление перемещения (см. рис. 7).
влияет только та составляющая силы тяжести, которая направлена вдоль перемещения, т. е. проекция силы тяжести на направление перемещения (см. рис. 7).

Рис. 7. Составляющая силы тяжести
Из прямоугольного треугольника проекция силы тяжести равна  и работа равна
и работа равна 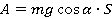 (см. рис. 8).
(см. рис. 8).

Рис. 8. Прямоугольный треугольник
Поскольку перемещение увеличилось,  , окончательно работа равна:
, окончательно работа равна:

Мы получили формулу для работы в общем виде
, где косинус угла между силой и перемещением показывает степень участия силы в данном перемещении, насколько сила выполняет работу по перемещению тела в данном направлении. Работа – это скалярное произведение силы и перемещения.
Формула  показывает частный случай: сила и перемещение сонаправлены (см. рис. 9), т. е. угол между ними равен 0 и
показывает частный случай: сила и перемещение сонаправлены (см. рис. 9), т. е. угол между ними равен 0 и  .
.
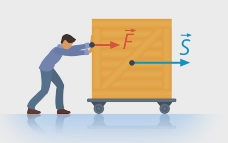
Рис. 9. Сила и перемещение сонаправлены
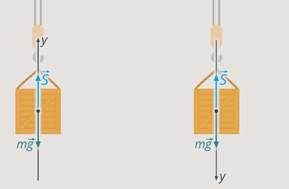
Вернемся к задаче о камне и рассмотрим другой частный случай, когда сила и перемещение направлены в противоположные стороны. Найдем теперь работу силы натяжения веревки, на которой камень спускают вертикально (см. рис. 10).

Рис. 10. Найдем силу натяжения веревки
Находим работу по той же формуле 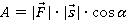 . Перемещение равно все той же высоте дома. Сила натяжения веревки по модулю равна
. Перемещение равно все той же высоте дома. Сила натяжения веревки по модулю равна  .
.
Почему 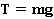
|
Откуда мы взяли, что
Рис. 11. Сила натяжения компенсирует силу тяжести |
Угол между противоположно направленными векторами  и
и  равен 180°. Теперь у нас все есть для нахождения работы:
равен 180°. Теперь у нас все есть для нахождения работы:
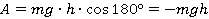
Результат согласуется с нашими представлениями: когда сила и перемещение направлены противоположно, мы получили отрицательную работу, и действительно, сила не способствует движению, а противодействует ему. Сила натяжения веревки «тащит» камень вверх, а он опускается вниз.
О выборе системы координат
|
Посмотрим, влияет ли на знак работы выбор системы координат. У нас есть тело, которое поднимается, т. е. движется вверх. Рассмотрим работу силы тяжести. Сила тяжести направлена вниз. Попробуем направить ось координат вверх и вниз (см. рис. 12).
Рис. 12. Выбор направления оси y
В первом случае перемещение положительно, сила отрицательна. Работа будет равна:
Во втором случае перемещение отрицательно, сила положительна. Работа будет равна:
Таким образом, если сила выполняет отрицательную работу в данном направлении, то это происходит независимо от выбора системы координат, поэтому выбор делаем, как удобнее для решения задачи. |
Об отрицательной работе
|
Отрицательные числа – это модель. В природе нет отрицательного количества. Есть количество, к примеру, 5 монет. -5 монет может значить, что эти же 5 монет забрали от начального количества. В физике мы часто сталкиваемся с векторными величинами: скорость, перемещение, сила и т. д. Их проекции на оси координат могут быть отрицательными. Если проекция скорости равна -5 м/с, это значит, что тело движется со скорость 5 м/с против направления оси координат (см. рис. 13).
Рис. 13. Направление скорости против оси координат Знак показывает направление относительно выбранной оси координат. Что значит отрицательная работа? Работа не вектор, у нее нет направления и ее нельзя рассматривать в проекции на оси координат. Что тогда значит минус? Работа – это произведение двух векторов, силы и перемещения, и знак работы тоже показывает направление одного вектора относительно другого, без привязки к оси координат. |
Рассмотрим еще один случай: камень не опускали, а переместили горизонтально на расстояние  (см. рис. 14).
(см. рис. 14).
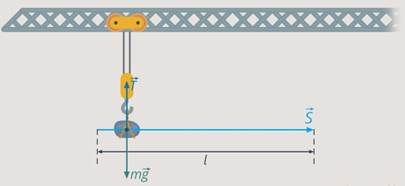
Рис. 14. Сила натяжения нити работу не совершает
Глава 3 Работа и энергия §11. Энергия, работа, мощность
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Если тело движется прямолинейнои на него действует постоянная сила F, которая составляет некоторый уголс направлением перемещения, то работа этой силы равна произведению проекции силыFsна направление перемещения (Fs=Fcos), умноженной на перемещение точки приложения силы:
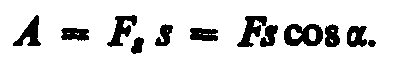 (11.1)
(11.1)
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным.Элементарной работойсилы F на перемещении dr называетсяскалярнаявеличина
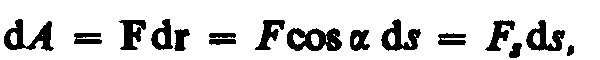
где — угол между векторами F и dr;ds= |dr| — элементарный путь;Fs —проекция вектора F на вектор dr (рис. 13).
Работа силы на участке траектории от точки 1до точки2равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
 (11.2)
(11.2)

Для вычисления этого интеграла надо знать зависимость силы Fs,от путиsвдоль траектории1—2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работаАопределяется на графике площадью заштрихованной фигуры. Если, например, тело движется прямолинейно, силаF=constи=const, то получим

где s— пройденный телом путь (см. также формулу (11.1)).
Из формулы (11.1) следует, что при </2 работа силы положительна, в этом случае составляющаяFsсовпадает по направлению с вектором скорости движенияv (см. рис. 13). Если>/2, то работа силы отрицательна. При=/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю.
Единица работы — джоуль(Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Нм).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
 (11.3)
(11.3)
За время dt сила Fсовершает работуFdr, и мощность, развиваемая этой силой, в данный момент времени
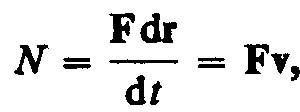
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N —величинаскалярная.
Единица мощности — ватт(Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
§ 12. Кинетическая и потенциальная энергии
Кинетическая энергиямеханической системы — это энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dAсилы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергииdTтела, т. е.

Используя второй
закон Ньютона  и умножая на перемещениеdrполучаем
и умножая на перемещениеdrполучаем


Так как 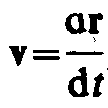 тоdA =mvdv=mvdv=dT, откуда
тоdA =mvdv=mvdv=dT, откуда
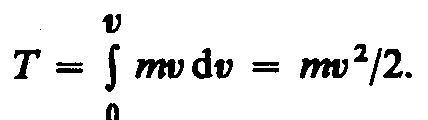
Таким образом, тело массой т, движущееся со скоростью v,обладает кинетической энергией
 (12.1)
(12.1)
Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.
При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия— механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, —консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называетсядиссипатнвной; ее примером является сила трения.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
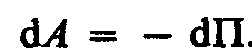 (12.2)
(12.2)
Работа dAвыражается как скалярное произведение силыFна перемещениеdrи выражение (12.2) можно записать в виде
 (12.3)
(12.3)
Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению.
Потенциальная энергия может быть определена исходя из (12.3) как

где С— постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Для консервативных сил
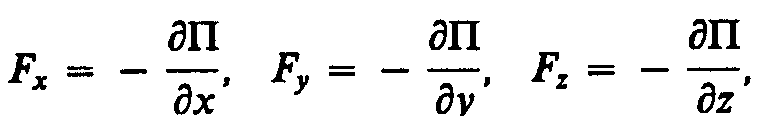
или в векторном виде
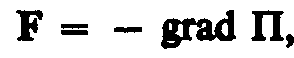 (12.4)
(12.4)
где
 (12.5)
(12.5)
(i,j,k— единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называетсяградиентом скаляраП.
Для него наряду с обозначением gradП применяется также обозначениеП.(«набла») означает символический вектор, называемый оператором Гамильтона* или набла-оператором:
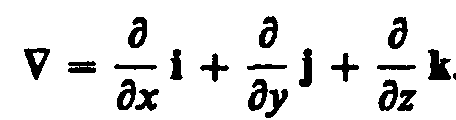 (12.6)
(12.6)
* У. Гамильтон (1805—1865) — ирландский математик и физик.
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т,поднятого на высотуhнад поверхностью Земли, равна
 (12.7)
(12.7)
где высота hотсчитывается от нулевого уровня, для которого П0=0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высотыhна поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!).Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубинаh‘ ), П=—mgh‘.
Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

где Fx упp —проекция силы упругости на осьх; k —коэффициент упругости(для пружины —жесткость), а знак минус указывает, чтоFx упp направлена в сторону, противоположную деформацииx.
По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.

Элементарная работа dA,совершаемая силойFxпри бесконечно малой деформацииdx, равна

а полная работа

идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела

Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы— энергия механического движения и взаимодействия:

т. е. равна сумме кинетической и потенциальной энергий.
Урок 11. Лекция 11. Работа. Мощность. Энергия. Закон сохранения энергии
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.
Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости).
A = Fs cos α
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
[1 Дж=1 Н·м]
Работа силы, совершаемая в единицу времени, называется мощностью.
Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
N=A/t
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Внесистемная единица мощности 1 л.с.=735 Вт
Связь между мощностью и скоростью при равномерном движении:
N=A/t так как A=FScosα тогда N=(FScosα)/t, но S/t = v следовательно
N=Fvcos α
В технике используются единицы работы и мощности:
1 Вт·с = 1 Дж; 1Вт·ч = 3,6·103 Дж; 1кВт·ч = 3,6·106 Дж
Если тело способно совершить работу, то говорят, что оно обладает энергией.
Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.
Обозначается Е Единица энергии в СИ [1Дж = 1Н*м]
Механическая работа есть мера изменения энергии в различных процессах А = ΔЕ.
Различают два вида механической энергии – кинетическая Ек и потенциальная Еp энергия.
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергий
Е = Ек + Еp
Кинетическая энергия – это энергия тела, обусловленная его движением.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
Если тело движется со скоростью , то для его полной остановки необходимо совершить работу
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятиепотенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела.
Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй):
Ep = mgh
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
где k – жесткость пружины.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
A = Ek2 – Ek1
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1) или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией.
Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.
Е = Ек + Еp = const
Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
4.3. Работа, мощность, энергия
Работа А силы  – скалярная физическая величина,
характеризующая меру действия силы,
приложенной к телу. Работа постоянной
силы на конечном перемещении
– скалярная физическая величина,
характеризующая меру действия силы,
приложенной к телу. Работа постоянной
силы на конечном перемещении :
: где
где — угол между
— угол между и
и .
За единицу измерения работы в СИ принят
джоуль:
.
За единицу измерения работы в СИ принят
джоуль: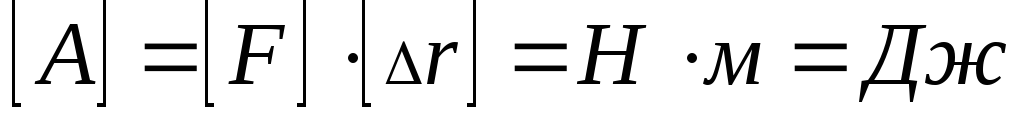 .
.
Мощность N
– скалярная физическая величина,
характеризующая быстроту (скорость)
совершения работы:  ,
Вт.
,
Вт.
Энергия – скалярная физическая величина, характеризующая общую количественную меру движения и взаимодействия всех видов материи. В механике используют также более краткое определение: механическая энергия – скалярная физическая величина, характеризующая способность тела совершать работу.
Один
из видов механической энергии –
кинетическая энергия  –
энергия движения, определяемая массой
тела и его скоростью. При
–
энергия движения, определяемая массой
тела и его скоростью. При
 .
Положительная работа внешних сил
увеличивает кинетическую энергию тела:
.
Положительная работа внешних сил
увеличивает кинетическую энергию тела:  .
.
Другой
вид механической энергии – потенциальная
энергия,  –
скалярная физическая величина,
характеризующая взаимодействие тел,
зависящее от их взаимного расположения.
Для тел, удаленных друг от друга на
бесконечно большое расстояние, их
потенциальная энергия равна нулю.
–
скалярная физическая величина,
характеризующая взаимодействие тел,
зависящее от их взаимного расположения.
Для тел, удаленных друг от друга на
бесконечно большое расстояние, их
потенциальная энергия равна нулю.
При
положительной работе сил взаимодействия
потенциальная энергия уменьшается:  .
Для тел массой
.
Для тел массой  ,
расположенных на Земле или в близи неё
,
расположенных на Земле или в близи неё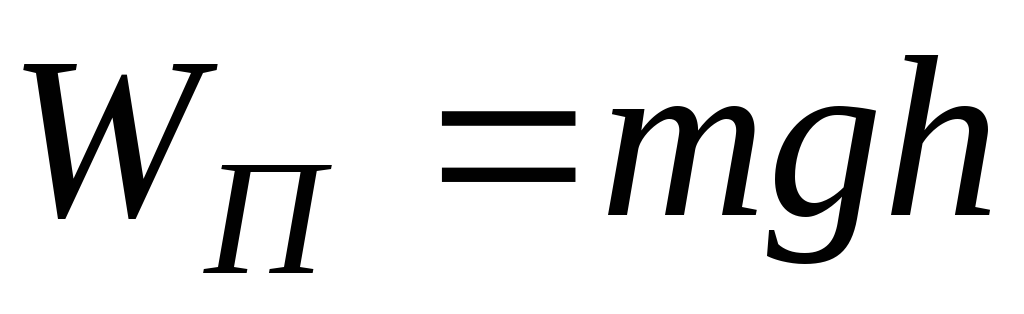 .
.
Потенциальная
энергия гравитационного притяжения
двух материальных точек (см.п. 6.4)  отрицательна; для увеличения
отрицательна; для увеличения необходимо воздействие внешних сил.
необходимо воздействие внешних сил.
4.4. Закон сохранения механической энергии
Механическая
энергия  системы
материальных точек, находящихся под
действием консервативных сил, остается
постоянной. В такой системе могут происходить лишь
превращения потенциальной энергии
системы
материальных точек, находящихся под
действием консервативных сил, остается
постоянной. В такой системе могут происходить лишь
превращения потенциальной энергии  в
кинетическую
в
кинетическую и обратно, но полный запас энергии
системы измениться не может. При наличии
неконсервативных сил (например, сил
трения, сил сопротивления…) механическая
энергия системы не сохраняется, она
уменьшается, что приводит к нагреванию
системы. Такой процесс называетсядиссипацией (рассеянием) энергии.
и обратно, но полный запас энергии
системы измениться не может. При наличии
неконсервативных сил (например, сил
трения, сил сопротивления…) механическая
энергия системы не сохраняется, она
уменьшается, что приводит к нагреванию
системы. Такой процесс называетсядиссипацией (рассеянием) энергии.
Силы
называют консервативными,
если их работа зависит только от
начального и конечного положений тела.
Работа консервативной силы по замкнутой
траектории равна нулю. Примером
консервативной силы является сила
тяготения  .
материальных точек массами
.
материальных точек массами и
и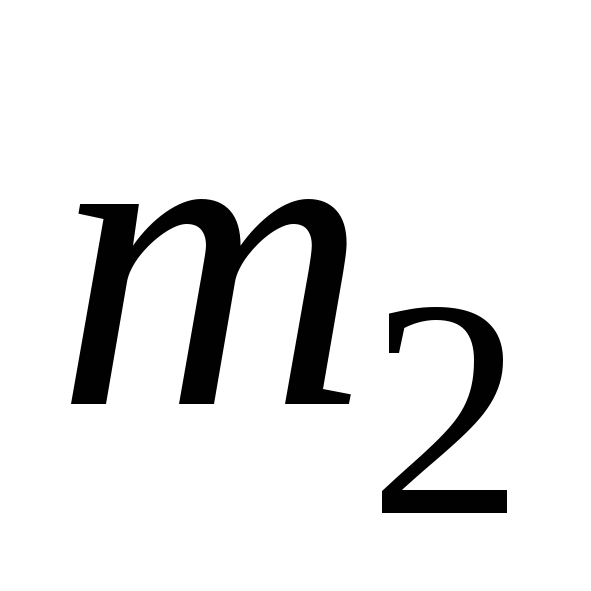 (см.
закон всемирного тяготения п. 4.2).
(см.
закон всемирного тяготения п. 4.2).
Закон сохранения механической энергии математически выглядит так:
 ,
,
где  –
механическая энергия материальной
точки.
–
механическая энергия материальной
точки.
Этот закон связан с однородностью времени, то есть с инвариантностью физических законов относительно выбора начала отсчета времени.
4.5. Общефизический закон сохранения энергии
Классическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннего атомистического строения вещества. При ударе, трении и аналогичных процессах кинетическая энергия видимого движения тел не пропадает. Она только переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии получила название внутренней энергии.
Беспорядочное движение атомов и молекул воспринимается нашими органами чувств в виде тепла. Таково физическое объяснение кажущейся потери механической энергии при ударе, трении и пр.
В физике закон сохранения энергии распространяют не только на явления, рассматриваемые в механике, но и на все без исключения процессы, происходящие в природе.
Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую.
Идея этого закона принадлежит Ломоносову, изложившему закон сохранения материи и движения.
 ,
,
где  ,(
,( –
количество теплоты,
–
количество теплоты, –
энергия излучения света)
–
энергия излучения света)
Общефизический закон сохранения энергии не может быть выведен из уравнений механики и должен рассматриваться как одно из наиболее широких обобщений опытных фактов.
Работа, энергия, мощность — ДИНАМИКА — МЕХАНИКА — ФИЗИКА
ФИЗИКА
МЕХАНИКА
ДИНАМИКА
Работа, энергия, мощность
Работа
А — механическая работа постоянной силы, [Н · м], [Дж];
F — сила, [Н];
S — перемещение, [м];
α — угол между направлениями векторов силы и перемещения
Кинетическая энергия
Ек — кинетическая энергия, [Дж];
m — масса тела, [кг];
υ — скорость тела, [м/с].
Теорема об кинетическую энергию
А — работа, [Дж];
ΔEк — изменение кинетической энергии, [Дж].
Потенциальная энергия тела, поднятого над Землей
Ег — потенциальная энергия, [Дж];
m — масса тела, [кг];
g — ускорение свободного падения, g = 9,8 м/с2;
h — высота тела над Землей, [м].
Потенциальная энергия упруго деформированного тела
х = 0 — нулевой уровень
х — величина деформации , [м];
k — коэффициент жесткости пружины [Н/м];
li —длина недеформованої пружины (х = 0), [м].
Потенциальная энергия гравитационного взаимодействия
m1.2 — массы материальных точек, [кг];
R — расстояние между точками, [м];
G — гравитационная постоянная,
Закон сохранения механической энергии
Е — полная механическая энергия [Дж];
Ек — кинетическая энергия, [Дж];
Ег — потенциальная энергия, [Дж].
Мощность
N — мощность, [Дж/c], [Вт];
t — время, [с].
КПД
η — коэффициент полезного действия
Ак полезная работа, [Дж];
Аиз — затрачена работа, [Дж].




 , где косинус угла между силой и перемещением показывает степень участия силы в данном перемещении, насколько сила выполняет работу по перемещению тела в данном направлении. Работа – это скалярное произведение силы и перемещения.
, где косинус угла между силой и перемещением показывает степень участия силы в данном перемещении, насколько сила выполняет работу по перемещению тела в данном направлении. Работа – это скалярное произведение силы и перемещения.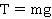 ? Задача на движение тела, на которое действуют силы. Нам не важны размеры камня, поэтому можем считать его материальной точкой и применить второй закон Ньютона. По условию камень опускается равномерно, ускорение равно нулю, значит, и равнодействующая действующих на него сил равна нулю, т. е. сила натяжения компенсирует силу тяжести,
? Задача на движение тела, на которое действуют силы. Нам не важны размеры камня, поэтому можем считать его материальной точкой и применить второй закон Ньютона. По условию камень опускается равномерно, ускорение равно нулю, значит, и равнодействующая действующих на него сил равна нулю, т. е. сила натяжения компенсирует силу тяжести,