Мощность переменного тока. Работа переменного тока

Господа, всех вас в очередной раз приветствую! В сегодняшней статье я бы хотел поднять темы, касающиеся мощности и энергии (работы) в цепях переменного тока. Сегодня мы узнаем, что это такое и научимся их определять. Итак, погнали.

Прежде чем начать что-либо обсуждать про переменный ток, давайте-ка вспомним, как мы определяли мощность в случае постоянного тока. Да-да, у нас была отдельная статейка на эту тему, помните? Если нет, то напоминаю, что в случае постоянного тока мощность в цепи считается очень просто, по одной из этих трех замечательных формул:

где P – искомая мощность, которая выделяется на резисторе R;

I – сила тока в цепи через резистор R;

U – напряжение на резисторе R.

Это все здорово. Но как быть в случае переменного тока, а в частности – синусоидального? Ведь там у нас колбасится синус, значения тока и напряжения все время меняются, сейчас они одни, через мгновение – уже другие, т.е., выражаясь научным языком, они являются

функциями времени. Пользуясь знаниями, полученными нами в предыдущей вводной статье, мы можем записать вот такой закон изменения силы тока:

Мы не будем сейчас повторять что здесь есть что, все это было досконально рассмотрено в прошлый раз.

Абсолютно аналогично можно записать зависимость напряжения от времени для переменного синусоидального тока

Пока что считаем, что у нас в цепи только резисторы (конденсаторы и индуктивности отсутствуют), следовательно, напряжение и ток совпадают по фазе между собой. Не понятно почему так? Ничего, в будущем разберем это подробно. Пока же для нас это значит только то, что фазы как в законе изменения тока, так и в законе изменения напряжения можно выкинуть.

И вот глядя на эти три строчки с формул и сопоставляя их между собой, не приходит ли вам на ум какая-либо идея? Например, что можно бы подставить ток или напряжение в формулу для мощности… Такая идея пришла? Это просто замечательно! Давайте ее сейчас же реализуем! Поскольку у нас и ток, и напряжения зависят от времени, все три полученные новые формула для мощности абсолютно также будет зависеть от времени.

Ох, прям в глазах рябит от синусов . Но ведь все довольно просто и очевидно откуда, что получилось, не так ли? По вот этим вот самым формулам можно

рассчитать мгновенную мощность в определенный момент времени. Фишка в том, что если через резистор течет переменный ток, то в каждое мгновение времени на нем будет выделяться вообще говоря разная мощность: иначе и быть не может, раз амплитуда тока через резистор все время разная. Другое дело, что визуально, при большой частоте изменения тока, мы скорее всего это не заметим: температура резистора не будет хаотично скакать в такт изменения мощности, которая на нем выделяется. Это будет потому, что сам резистор благодаря его массе и теплоемкости синтегрирует эти перепады температуры.

Итак, с мощностью более-менее понятно. А как быть с энергией? Ну, то есть с теплом, которое выделяется на резисторе? Как оценить эту самую энергию? Для этого нам надо вспомнить, как же связаны между собой мощность и энергия. Мы уже затрагивали эту тему в статье про мощность в цепи постоянного тока. Тогда этот вопрос решился просто: при постоянном токе достаточно умножить мощность (которая там не зависит от времени и все время одинакова) на время наблюдения и получить выделяющуюся за это самое время наблюдения энергию. С переменным током все посложнее, потому что тут мощность зависит от времени. И, увы, тут не обойтись без интегралов… Что это вообще такое этот самый интеграл? Как, вероятно, многие из вас знают,

интеграл – это просто площадь под графиком . В данном конкретном случае под графиком зависимости мощности от времени P(t). Да, вот так вот все просто.

Итак, энергия (или работа, что по сути одно и то же) в цепи переменного тока считается следующим образом

В этой формуле Q – это искомая работа (энергия) переменного тока (измеряется все так же в джоулях), P(t) – закон изменения мощности от времени, а Т – собственно, сам отрезок времени, который мы рассматриваем, и в течении которого ток работает.

Вообще говоря, это выражение можно рассматривать как общий случай и для постоянного тока, и для переменного (при этом переменный ток может быть любой формы, не обязательно синусоидальный). Во всех эих случаях можно считать энергию через вот этот вот интеграл. Если же мы подставим сюда P(t)=const (случай постоянного тока), то исходя из особенности взятия интеграла от константы результат расчета будет абсолютно таким же, как если бы мы просто умножили мощность на время, поэтому нет никакого смысла так заморачиваться и рассматривать интегралы в теме постоянного тока. Но полезно это знать, что бы была некая единая картина. Сейчас же, господа, я прошу вас запомнить главный вывод из всей этой болтовни –

если мы хотим найти выделившуюся энергия за время T (без разницы какой ток – постоянный или переменный), то это можно сделать, найдя площадь под графиком зависимости мощности от времени на интервале от 0 до Т.

Если брать токи синусоидальные и подставлять конкретные выражения для зависимости мощности от времени, то энергию можно посчитать по одной из следующих формул

Господа, скажу сразу, в своих статьях я не буду рассказывать, как брать интегралы. Я надеюсь, что вы это знаете. А если нет – ничего страшного, не спешите закрывать статью. Я буду стараться строить изложение таким образом, чтобы незнание интегралов не привело в вашем сознании к fatal error . Очень часто их вообще не требуется считать ручками, а можно посчитать в специализированных программах или даже онлайн на многочисленных сайтах.

Давайте теперь разберем все вышесказанное на конкретном примере. Господа, специально для вас я подготовил рисуночек 1. Взгляните на него. Изображение кликабельно.

Рисунок 1 – Зависимость мощности от времени для переменного и постоянного тока

Там два графика: на верхнем показана зависимость мощности от времени для случая переменного синусоидального тока, а на нижнем – для случая постоянного тока. Как я их построил? Очень просто. Для первого графика я взял вот эту ранее написанную нами формулу.

Будем полагать, что амплитуда синусоидального тока равна I_m=1 A, сопротивление резистора, на котором рассеивается мощность, равно

R=5 Ом, а частота синуса равна f = 1 Гц, что соответствует круговой частоте

То есть формула, по которой мы строим график мощности переменного тока, имеет вид

Именно по этой формуле построен верхний график на рисунке 1.

А как быть с нижним графиком? Господа, ну тут совсем все просто. Я исходил из того, что через тот же самый резистор R=5 Ом течет постоянный ток величиной I=1 А. Тогда, как должно быть понятно из закона Джоуля-Ленца, на данном резисторе будет рассеиваться вот такая вот мощность

Поскольку ток постоянный, то эта мощность будет одинаковой в любой момент времени. А для таких замечательнейших случаев эталонной стабильности великая и могучая математика предусматривает график в виде прямой. Что мы и видим на нижнем графике рисунка 1.

Понятное дело, что раз через наши пятиомные резисторы течет ток, то на них выделяется некоторая мощность и рассеивается некоторое количество энергии. Иными словами, резистор греется за счет выделяющейся на нем энергии. Мы уже обсуждали, что эта энергия считается через интеграл. Но, как мы уже говорили, есть и графическое представление этого интеграла – он равен площади под графиком. Эту площадь я заштриховал на рисунке 1. То есть, если мы найдем, чему равна площадь под верхним и нижним графиками, то мы определим, какое количество энергии выделилось в первом и втором случае.

Ну, с нижним графиком вообще все просто. Там – прямоугольник высотой 5 Вт и шириной 2 секунды. Поэтому площадь (то бишь энергия) находится элементарно

Отметим, что этот результат в точности совпадает с формулой, полученной нам для расчета энергии постоянного тока в одной из прошлых статей.

Со верхним графиком все не так просто. Там у нас неправильная форма и просто так сразу нельзя сказать, чему равна эта площадь. Вернее, сказать можно – она равна вот такому вот интегралу

Результат вычисления этого интеграла равен конкретному числу и это число – как раз наша искомая энергия, которая выделилась на резисторе. Мы не будем расписывать взятие этого интеграла. Посчитать такой интеграл ручками не составит труда для человека, хотя бы поверхностного знакомого с математикой. Если же все-таки это вызывает затруднение, или просто лень самому считать – есть огромное количество САПРа, которое сделает это за вас. Либо можно посчитать этот интеграл на каком-либо сайте: по запросу в гугле «интегралы онлайн» выдается достаточное количество результатов. Итак, сразу переходим к ответу и он равен

Вот так вот. Энергия, которая выделяется на резисторе при протекании синусоидального тока с амплитудой 1 А почти в два раза меньше энергии, которая будет выделяться в случае, если течет постоянный ток величиной 1 А. Оно и понятно – даже визуально на рисунке 1 площадь под верхним графиком заметно ниже, чем под нижним.

Как-то так, господа. Теперь вы знаете, как рассчитать мощность и энергию в цепи переменного тока. Однако сегодня мы рассмотрели довольно сложный путь. Оказывается, есть методы попроще, с использованием так называемых действующих величин тока и напряжения. Но об этом в следующей статье.

А пока что – всем вам огромной удачи, спасибо, что прочитали, и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

» Работа и мощность переменного электрического тока . Коэффициент мощности «

План-конспект урока по физике в 11 классе

на ……………

Тема урока : Работа и мощность переменного электрического тока.Коэффицент мощности

Цели: рассмотреть фазовые соотношения между током и напряжением в цепи переменного тока с катушкой

Тип урока: урок изучения нового материала

План занятия 

1.Орг момент

2.Опрос дом.задания

Явление резонанса

Явление резонанса в цепи переменного тока

3.Обьяснение новой темы

Как вам известно, работа, выполненная постоянным током, определяется как произведение напряжения, силы тока и времени прохождения тока:

A= U· I · t. (3–28)

Для определения работы, выполненной переменным током за короткий промежуток времени, его значение рассматриваем как постоянное. В таком случае мгновенное значение выполненной работы переменного тока тоже находится из похожей формулы:

A= u · i · t. (3–29)

Если напряжение, приложенное к концам цепи, изменяется согласно закономерности

u=U_m cosωt, то сила тока в нем тоже меняется по гармоническому закону со сдвигом

по фазе: i = I _m cos(ωt + φ). (3–30)

мгновенное значение мощности переменного тока можно записать в виде

p = u · i = U_m · I _m cosωt · cos(ωt +φ) (3–31)

Здесь мощность с истечением времени меняется и по модулю, и по знаку. В первой половине периода, если мощность передается в цепь (р > 0), то во второй половине часть мощности обратно передается в сеть питания (р < 0).

В некоторых случаях очень важно знать среднее значение мощности в течение длительного времени. Для этого достаточно определить мощность, приходящуюся на один период.

Для определения мощности, приходящейся на один период, формулу (3–31) преобразуем в вид, чтобы она не зависела от времени. Для этого используем формулу из курса математики – произведение двух косинусов:

cosαcosβ=(cos(α – β) + cos(α + β))/2

В рассматриваемом нами случае α = ωt и β = ωt + φ. Поэтому,мощность

P= U_m I_m (cosω+ cos(2ωt + φ)/2= U_м I_m cosω/2 + U_м I_m cos(2ωt + φ)/2

Среднее значение второго слагаемого в данном выражении в течение одного периода равно нулю. Значит, независимо от времени, средняя мощность, приходящаяся на один период, будет

P= U_м I_m cosω/2

Если учитывать выражение эффективных значений тока и напряжения,

мы имеем: P= U I cosω/2

Эта величина называется мощностью переменного тока для участка цепи:

P = U· I cosφ. (3–32)

Согласно этому, работа, выполненная переменным током, определяется следующей формулой: A = U· I · t cosφ. (3–33)

Таким образом, мощность и работа, выполненная переменным током участка цепи, определяется эффективными значениями силы тока и напряжения. Она также зависит от фазовых смещений между напряжением и силой тока. Множитель cosφ в формуле (3–32) называется коэффициентом мощности.

4.Решение задач

Катушка с индуктивностью 0,5 Гн и активным сопротивлением 100 Ом и конденсатор емкостью 10 мкФ соединены с источником переменного напряжения u = 300 sin200 πt. Найдите мощность тока и коэффициент мощности

5.Подведение итогов

6.Дом.задание : §20

Баязитов Р.И.

Работа и мощность переменного тока

Мгновенная мощность в цепи переменного тока (частный случай)

Допустим, что цепь имеет только активное сопротивление. Пусть напряжение на концах цепи изменяется по гармоническому закону:

Мы помним, что сдвига фаз между током и напряжением в нашей цепи (только $R$) не будет, следовательно, запишем, что:

Если рассмотреть маленький промежуток времени, то переменный ток можно рассмотреть как постоянный, значит мгновенная мощность переменного тока ($P_{tR}$) равна:

Работа в цепи переменного тока (частный случай)

Работа переменного тока на маленький промежуток времени $dt$ равна (${dA}_t$):

Следовательно, работа за один период полного колебания ($A_T$) может быть определена как:

Рассмотрим общий случай цепи переменного напряжения, когда она содержит и активное и реактивное сопротивление. Теперь между током и напряжением существует разность фаз. Работа, совершенная во внешней цепи за время $dt$, равна:

Напряжение $U$, можно разложить на две составляющие: активную ($U_a$) и реактивную ($U_r$).

Активная составляющая совершает колебания в одной фазе с током, она равна:

Реактивная составляющая смещена по фазе относительно тока на $\pm \frac{\pi }{2}$ и имеет вид:

При вычислении работы за период, получится два слагаемых. Учитывая, что реактивная составляющая за полный период равна нулю, следовательно, полная работа определена только активной составляющей напряжения:

Средняя мощность

Чаще, чем понятием мгновенная мощность, оперируют понятием среднее значение мощности. Причем рассматривают большой промежуток времени, который включает множество периодов колебаний. Так как мы рассматривает периодический процесс, то нам будет достаточно найти среднее значение мощности на один полный период.

Ее легко найти как:

где $cos\varphi $- коэффициент мощности. Формула (10) показывает, что в общем случае выделяемая в цепи мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между ними.

Замечание

Зависимость мощности от коэффициента мощности учитывают при проектировании линий электропередачи для переменного тока. Если нагрузки вцепи имеют большое реактивное сопротивление, то $\varphi \ne 0$ и $cos\varphi $ может быть заметно меньше единицы. В таких случаях для передачи нужной мощности необходимо учесть силу тока, что ведет к возрастанию выделения тепла Джоуля — Ленца или требует увеличения сечения проводов, что увеличивает стоимость линии электропередач. На практике всегда стремятся распределить нагрузки так, чтобы $cos\varphi \ $был как можно ближе к единице.

Средняя мощность при наличии в цепи только активного сопротивления, равна:

Пример 1

Задание: Пусть сила тока изменяется в соответствии с законом: $I=I_m{sin \left(\omega t\right)\ }.$ Запишите выражения для мгновенных мощностей, развиваемых током на разных элементах цепи ($C,L$).

Решение:

Используя соотношение:

\[U=\frac{q}{C}(1.1)\]

и выражение:

\[I=\frac{dq}{dt}\to q=\int{Idt}=-\frac{I_m}{\omega }{cos \left(\omega t\right)\ }+q_0=-\frac{I_m}{\omega }{cos \left(\omega t\right)\ }\left(1.2\right),\]

где мы можем положить $q_0=0,$ так как эта постоянная интегрирования с колебаниями тока не связана, запишем уравнение для колебания напряжения на конденсаторе:

\[U_C=-\frac{I_m}{C\omega }{cos \left(\omega t\right)\ }=\frac{I_m}{C\omega }{sin \left(\omega t-\frac{\pi }{2}\right)\ }\left(1.3\right).\]

Мгновенная мощность на конденсаторе равна:

\[P_{tC}=U_CI=\frac{I_m}{C\omega }{sin \left(\omega t-\frac{\pi }{2}\right)\ }\ I_m{sin \left(\omega t\right)\ }=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)\ }\ }.\]

Изменение напряжения на индуктивности выразим как:

\[U_L=L\frac{dI}{dt}=LI_m\omega {cos \left(\omega t\right)\left(1.5\right).\ }\]

Мгновенная мощность тока на индуктивности:

\[P_{tL}=U_LI=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)\ }.\ }\]

Мгновенные мощности на емкости и индуктивности меняют знак. Часть времени ток совершает положительную работу, то есть передает энергию на элементы, другая часть времени работа отрицательна, то есть энергия этих элементов возвращается к источнику сторонних ЭДС. Происходит обмен энергиями между индуктивностями, емкостями и источниками ЭДС в процессе которого емкости и индуктивности выполнят роль источников ЭДС.

Ответ: $P_{tC}=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)\ }\ },$ $P_{tL}=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)\ }.\ }$

Пример 2

Задание: Чему равна средняя мощность на сопротивлении, емкости и индуктивности?

Решение:

Для того чтобы получить средние мощности тока за период колебаний необходимо усреднить выражения:

\[P_{tC}=-\frac{I^2}{C\omega }{sin \left(\omega t\right){cos \left(\omega t\right)(2.1)\ }\ },\] \[P_{tR}={I^2}_mR{sin}^2\left(\omega t\right)\left(2.2\right),\] \[P_{tL}=L{I^2}_m\omega {cos \left(\omega t\right){sin \left(\omega t\right)(2.3)\ }.\ }\]

Учтем, что за период колебаний выполняются соотношения:

\[\left\langle {cos \left(\omega t\right){sin \left(\omega t\right)\ }\ }\right\rangle =0\ \left(2.4\right).\] \[\left\langle {s{in}^2 \left(\omega t\right)\ }\right\rangle =\frac{1}{2}\left(2.5\right).\]

Используя (2.5) и (2.4) из (2.1) — (2.2) получим:

\[\left\langle P_{tC}\right\rangle =0,\] \[\left\langle P_{tL}\right\rangle =0,\] \[\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR.\]

Ответ: $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR.$

Мощность переменного тока. Мощность тока через катушку, резистор, конденсатор

 

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

 

Мощность тока через резистор

 

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

 

Мощность тока через конденсатор

 

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

 

Мощность тока через катушку

 

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

 

Мощность тока на произвольном участке

 

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Работа и мощность переменного тока — Мегаобучалка

Энергия, поставляемая источником электродвижущей силы во внешнюю цепь, испытывает превращения в другие виды энергии. Если в цепи имеется только активное сопротивление, то вся энергия превращается в тепло, выделяемое на сопротивлении . Между током и напряжением сдвиг фаз отсутствует. Кроме того, в течение малого промежутка времени переменный ток можно рассматривать как постоянный. Поэтому мгновенная мощность, развиваемая переменным током на сопротивлении:

.

Хотя ток и напряжение бывают как положительными, так и отрицательными, мощность, равная их произведению, всегда положительна. Однако она пульсирует, изменяясь от нуля до максимального значения с частотой, равной удвоенной частоте переменного тока. На рис. 7.12 показана временная зависимость тока, напряжения и мощности переменного тока, выделяемой на активном сопротивлении. Ясно, что средняя передаваемая мощность меньше максимальной и равна половине максимальной мощности. Среднее значение и за период равно . Это можно объяснить следующим образом: , а за полный цикл среднее значение равно среднему значению . Поэтому среднее значение мощности будет равно

.

В общем случае, когда цепь содержит не только активное сопротивление, но и индуктивность и емкость, между током и напряжением существует сдвиг фаз, и это сказывается на величине мощности. В цепи с индуктивностью энергия источника переходит в энергию магнитного поля, равную , изменяющуюся с течением времени. Мощность, которая требуется для создания магнитного поля в катушке индуктивности, равна произведению силы тока и разности потенциалов на катушке:

.

Из последней формулы видно, что в том интервале времени, когда , мощность положительна. Это означает, что источник передает энергию во внешнюю цепь, она идет на увеличение энергии магнитного поля. Когда же , мощность отрицательна, в эти промежутки времени энергия, запасенная в магнитном поле, возвращается из внешней цепи в источник. Таким образом, в цепи, содержащей индуктивность, знак мощности периодически изменяется. Так же будет и в случае, когда внешняя цепь содержит конденсатор емкостью . Однако в этом случае происходит переход энергии источника в энергию электрического поля конденсатора, равную . Развиваемая мощность также меняет знак в зависимости от знака .

В катушке индуктивности с нулевым активным сопротивлением или в конденсаторе напряжение сдвинуто по фазе на относительно тока, и поэтому энергия вообще не поглощается. Например, как видно из рис. 7.13, мгновенная мощность в чисто емкостном сопротивлении колеблется между положительными и отрицательными значениями, что соответствует поглощению мощности и затем возвращению ее к источнику. В результате средняя мощность за период равна нулю.

В общем случае полная мощность, развиваемая источником сторонних сил, равна . Эту величину называют мощностью тока, а величины , , – мощностями тока на сопротивлении, индуктивности и емкости соответственно. При силе тока падение напряжения на активном сопротивлении равно , падение напряжения на индуктивности – , падение напряжения на емкости – . Мгновенные значения мощностей соответственно равны

Интерес представляет среднее значение мощности за период. Так как синус и косинус сдвинуты относительно друг друга по фазе на , то среднее значение их произведения равно нулю: . Средние значения квадратов синуса и косинуса . Поэтому , , . Таким образом, отлична от нуля только средняя мощность на активном сопротивлении R, поэтому его и называют активным сопротивлением. На индуктивности и емкости средние мощности равны нулю. Эти элементы в среднем энергетически нейтральны, их называют реактивными сопротивлениями.

Работа и мощность переменного тока. Действующее значение тока и напряжения.

⇐ ПредыдущаяСтр 6 из 6

Найдем мощность, выделяемую в цепи переменного тока. Мгно­венное значение мощности равно произведению мгновенных значе­ний напряжения и силы тока:

***
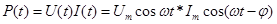Воспользуемся формулой :

 

Выражению *** можно придать вид:

**

 

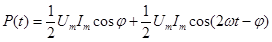Практический интерес представляет среднее по времени значе­ние Р(t), которое мы обозначим просто Р. Так как среднее значе­ние 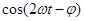равно нулю,

*

 

Из * *следует , что мгновенная мощность колеблется около среднего значения с частотой, в 2 раза превышающую частоту тока.

 

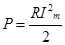Подставив это значение 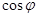в формулу * и учтя, что 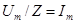, получим

 

 

Такую же мощность развивает постоянный ток, сила которого равна — действующее значение силы тока. 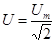— действующее значение напряжения.

Выражение средней мощности через действующие значения силы тока и напряжения имеет вид

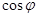— коэффициент мощности. В технике стремятся сделать 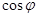как можно больше. При малом 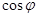для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.

 

Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Напряженность электростатического поля. Принцип суперпозиции. Расчет напряженности поля тон­кого заряженного стержня.

Электрический диполь и его поле.

Силовые линии электростатического поля. Поток вектора. Электростатическая теорема Гаусса и ее применение для расчета полей.

Работа электростатического поля. Теорема о циркуляции напряженности электростатического поля. Потенциал. Эквипотенциальная поверхность. Связь потенциала с напряженностью.

Проводники в электростатическом поле. Распределение заряда в проводнике. Электростатическое по­ле в полости.

Поверхностная плотность заряда. Граничные условия на границе проводника с вакуумом.

Дифференциальная форма теоремы Гаусса. Уравнение Пуассона. Общая задача электростатики.

Емкость уединенного проводника. Конденсатор. Емкость конденсаторов различной конфигурации. Соединение конденсаторов.

Энергия конденсатора. Плотность энергии электростатического поля.

Поляризация диэлектриков. Связанные заряды. Вектор поляризации. Диэлектрическая проницае­мость.

Теорема Гаусса для электростатических полей в веществе. Электрическое смещение. Граничные условия на границе раздела диэлектриков.

Электрический ток и его характеристики. Условия существования тока. Законы Ома и Джоуля- Ленца в дифференциальной форме.

Сторонние силы. ЭДС. Закон Ома для участка цепи с источником ЭДС. Закон Джоуля-Ленца в ин­тегральной форме.

Правила Кирхгофа и расчет электрических цепей.

Магнитное поле. Сила Лоренца и сила Ампера. Вектор магнитной индукции.

Закон Био-Савара. Принцип суперпозиции. Магнитное поле прямолинейного тока и кругового тока.

Виток с током в магнитном поле. Момент сил, действующих на виток с током в магнитном поле.

Теорема Гаусса для магнитного поля. Закон полного тока. Магнитное поле соленоида.

Магнитная энергия тока. Плотность энергии магнитного поля.

Движение заряженных частиц в электрическом и магнитном полях.

Масс-спектрометр. Принцип работы и применение.

Эффект Холла. Постоянная Холла.

Явление электромагнитной индукции. ЭДС индукции, возникающая в движущихся проводниках. Закон электромагнитной индукции. Правило Ленца.

Явление самоиндукции. Индуктивность. Индуктивность длинного соленоида.

Магнитное поле в веществе. Молекулярные токи. Намагниченность. Магнитная проницаемость.

Пара- и диамагнетики и их свойства. Элементарная теория диамагнетизма.

Ферромагнетики и их свойства.

Максвелловская трактовка закона электромагнитной индукции. Обобщение теоремы о циркуляции

электростатического поля на случай переменных полей.

Ток смещения. Обобщение закона полного тока на случай переменных полей.

Система уравнений Максвелла в интегральной форме. Материальные уравнения. Скорость распро­странения электромагнитных возмущений.

Скин-эффект и его элементарная теория.

Генератор переменного тока. Емкость, индуктивность и активное сопротивление в цепи переменно­го тока. Закон Ома для переменных токов.

Затухающие колебания в колебательном контуре. Коэффициент затухания и логарифмический дек­ремент затухания колебаний.

Вынужденные колебания в колебательном контуре. Резонанс.

Работа и мощность переменного тока. Действующее значение тока и напряжения.

 



ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ Работа и мощность переменного тока

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ

Работа и мощность переменного тока • В случае, когда сила тока изменяется во времени по произвольному закону, ток называется переменным. • Колебания тока называются гармоническими, если они описываются уравнениями вида – циклическая частота, (ωt+φ) – фаза колебания, φ — начальная фаза, Im – амплитуда силы тока.

• В цепях переменного тока возникает разность фаз в колебаниях силы тока и напряжения, которая зависит от параметров ω, L, C, R. С учетом этого уравнения колебаний для некоторого участка цепи запишем в виде • Мгновенная мощность тока на этом участке Преобразуем произведение синусов.

• Практический интерес представляет среднее значение мощности тока за период колебаний. При этом учтем, что среднее значение cos(2ωt – φ) равно нулю. Тогда – действующие значения силы тока и напряжения.

• Работа тока на участке цепи за время t • Если на участке цепи имеется только резистор, то φ = 0, и средняя мощность тока

Индуктивность в цепи переменного тока Катушка идеальная: R=0. Пусть ток в цепи изменяется по закону I = Imsinωt. (1) Напряжение между точками 1 и 2 равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:

Анализ: 1. Напряжение опережает силу тока на φ=π/2. 2. Амплитудные значения силы тока и напряжения связаны соотношением Um= Im·ωL XL=ωL — индуктивное сопротивление катушки. 3. Мощность тока в цепи

Емкость в цепи переменного тока Пусть напряжение на клеммах генератора изменяется по закону Тогда заряд на конденсаторе Сила тока, текущего в цепи

Анализ: 1. Сила тока, изменяясь, опережает напряжение на φ=π/2. 2. Амплитудные значения силы тока и напряжения связаны соотношением — емкостное сопротивление цепи. 3. Средняя мощность тока в цепи равна нулю (cosφ=0).

Электрический колебательный контур состоит из катушки и конденсатора, образующих замкнутую цепь.

В интервале времени 0 – Т/4 конденсатор разряжается, сила тока возрастает, ЭДС самоиндукции препятствует возрастанию тока. Энергия электрического поля конденсатора переходит в энергию магнитного поля катушки.

В интервале времени Т/4 – Т/2 сила тока уменьшается, ЭДС самоиндукции поддерживает убывающий ток. В результате происходит перезарядка конденсатора. При этом энергия магнитного поля катушки переходит в энергию электрического поля конденсатора.

Теоретическое рассмотрение дает: 1. В идеальном контуре, содержащем конденсатор и катушку индуктивности, должны происходить незатухающие электромагнитные колебания, циклическая частота которых 2. Период собственных колебаний в контуре (Формула У. Томсона).

3. Полная энергия идеального контура с течением времени не изменяется: q, I – мгновенные значения заряда на конденсаторе и силы тока в контуре. 4. Для амплитудных значений справедливо равенство

Закон Ома для цепи переменного тока • КС: последовательное соединение элементов цепи, вынужденные колебания, частота колебаний. • В любой момент времени сила тока во всех элементах цепи одинакова. Как зависит амплитуда силы тока от параметров цепи?

• Решение задачи с использованием метода векторных диаграмм приводит к следующему результату:

• Выражение (2) – закон Ома для последовательной цепи переменного тока. Величина имеет смысл полного сопротивления цепи.

Резонанс напряжений Если то

Электромагнитные волны

Ток смещения В цепи переменного тока, содержащей конденсатор, ток проводимости на обкладках конденсатора обрывается. Дж. Максвелл высказал удивительную идею о том, что процесс, происходящий между обкладками конденсатора следует рассматривать как особый вид тока, который создает такое же магнитное поле, как и ток проводимости. Этот ток был назван током смещения.

• По гипотезе Максвелла ток смещения создает магнитное поле, т. е. при изменении электрического поля в пространстве появляется поле магнитное.

• Наиболее весомый вклад внес в молекулярную физику и электродинамику. В 1859 г. установил статистический закон, описывающий распределени молекул газа по скоростям. В 1860 -65 гг. создал теорию электромагнитного поля. В 1865 г. теоретически обосновал существование ЭМ волн и высказал гипотезу об ЭМ природе света. Максвелл Джеймс Клерк (1831 – 1879, англ. )

• Переменный электромагнитный процесс распространяется в пространстве. Он имеет волновой характер. • Вывод о существовании электромагнитных волн Дж. Максвелл сделал в 1865 г. • Г. Герц экспериментально обнаружил электромагнитные волны и исследовал их свойства в 1887 -88 гг.

Генрих Герц (1857 – 1894, нем. ) • Является одним из основоположников электродинамики. В 1888 г. экспериментально доказал существование электромагнитных волн Придал уравнениям Максвелла современную форму. В 1887 г. обнаружил внешний фотоэффект.

• Следствия из уравнений Максвелла (в дифференциальной форме): 1. Скорость распространения ЭМВ: с ≈ 3· 108 м/с.

2. Вектор Умова-Пойнтинга для ЭМВ (определяет мгновенное значение энергии, переносимой волной за единицу времени через единичную площадку): S = S(t). Интенсивность ЭМВ – среднее значение S.

3. Электромагнитная волна является поперечной:

Геометрический образ плоской волны Длина волны видимого излучения: 400(ф) – 760(кр) нм.

4. ЭМВ производит давление на тела. В 1873 г. Дж. Максвелл рассчитал давление света на основе электромагнитной теории: Здесь I — интенсивность ЭМВ, r — коэффициент ее отражения. Справедливость этой формулы была экспериментально подтверждена выдающимся русским физиком П. Н. Лебедевым в 1898 г.

П. Н. Лебедев (1866 – 1912, рус. ) Известен как блестящий экспериментатор-виртуоз, автор исследований, выполненных скромными средствами на грани технических возможностей того времени, но поражающих глубокой интуицией и гениальностью. .

5. На границе диэлектриков ЭМВ отражаются и преломляются. Известные законы отражения и преломления света являются прямым следствием уравнений Максвелла. 6. Имеют место такие явления, как поглощение, интерференция, дифракция, дисперсия ЭМВ и др.