Механическая работа и мощность

Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы. Другими словами, работа — мера воздействия силы.

Определение механической работы

Определение 1

Работа А, совершаемая постоянной силой F→, — это физическая скалярная величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F→ и перемещением s→.

Данное определение рассматривается на рисунке 1.

Формула работы записывается как,

A=Fs cos α.

Работа – это скалярная величина. Единица измерения работы по системе СИ — Джоуль (Дж).

Джоуль равняется работе, совершаемой силой в 1 Н на перемещение 1 м по направлению действия силы.

Рисунок 1. Работа силы F→: A=Fs cos α=Fss

При проекции Fs→ силы F→ на направление перемещения s→ сила не остается постоянной, а вычисление работы для малых перемещений Δsi

суммируется и производится по формуле:

A=∑∆Ai=∑Fsi∆si.

Данная сумма работы вычисляется из предела (Δsi→0), после чего переходит в интеграл.

Графическое изображение работы определяют из площади криволинейной фигуры, располагаемой под графиком Fs(x)рисунка 2.

Рисунок 2. Графическое определение работы ΔAi=FsiΔsi.

Примером силы, зависящей от координаты, считается сила упругости пружины, которая подчиняется закону Гука. Чтобы произвести растяжение пружины, необходимо приложить силу F→, модуль которой пропорционален удлинению пружины. Это видно на рисунке 3.

Рисунок 3. Растянутая пружина. Направление внешней силы F→ совпадает с направлением перемещения s→. Fs=kx, где k обозначает жесткость пружины.

F→упр=-F→

Механическая работа. Мощность – FIZI4KA

1. Механическая работа ​\( A \)​ — физическая величина, равная произведению вектора силы, действующей на тело, и вектора его перемещения: ​\( A=\vec{F}\vec{S} \)​. Работа — скалярная величина, характеризуется числовым значением и единицей.

За единицу работы принимают 1 джоуль (1 Дж). Это такая работа, которую совершает сила 1 Н на пути 1 м.

\[ [\,A\,]=[\,F\,][\,S\,]; [\,A\,]=1Н\cdot1м=1Дж \]

2. Если сила, действующая на тело, составляет некоторый угол ​\( \alpha \)​ с перемещением, то проекция силы ​\( F \)​ на ось X равна ​\( F_x \)​ (рис. 42).

Поскольку ​\( F_x=F\cdot\cos\alpha \)​, то \( A=FS\cos\alpha \).

Таким образом, работа постоянной силы равна произведению модулей векторов силы и перемещения и косинуса угла между этими векторами.

3. Если сила ​\( F \)​ = 0 или перемещение ​\( S \)​ = 0, то механическая работа равна нулю ​\( A \)​ = 0. Работа равна нулю, если вектор силы перпендикулярен вектору перемещения, т.е. ​\( \cos90^\circ \)​ = 0. Так, нулю равна работа силы, сообщающей телу центростремительное ускорение при его равномерном движении по окружности, так как эта сила перпендикулярна направлению движения тела в любой точке траектории.

4. Работа силы можетбыть как положительной, так и отрицательной. Работа положительная ​\( A \)​ > 0, если угол 90° > ​\( \alpha \)​ ≥ 0°; если угол 180° > ​\( \alpha \)​ ≥ 90°, то работа отрицательная ​\( A \)​ < 0.

Если угол ​\( \alpha \)​ = 0°, то ​\( \cos\alpha \)​ = 1, ​\( A=FS \)​. Если угол ​\( \alpha \)​ = 180°, то ​\( \cos\alpha \)​ = -1, ​\( A=-FS \)​.

5. При свободном падении с высоты ​\( h \)​ тело массой ​\( m \)​ перемещается из положения 1 в положение 2 (рис. 43). При этом сила тяжести совершает работу, равную:

​

\[ A=F_тh=mg(h_1-h_2)=mgh \]

​При движении тела вертикально вниз сила и перемещение направлены в одну сторону, и сила тяжести совершает положительную работу.

Если тело поднимается вверх, то сила тяжести направлена вниз, а перемещение вверх, то сила тяжести совершает отрицательную работу, т.е.

\[ A=-F_тh=-mg(h_1-h_2)=-mgh \]

6. Работу можно представить графически. На рисунке изображён график зависимости силы тяжести от высоты тела относительно поверхности Земли (рис. 44). Графически работа силы тяжести равна площади фигуры (прямоугольника), ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс
в точке ​\( h \)​.

Графиком зависимости силы упругости от удлинения пружины является прямая, проходящая через начало координат (рис. 45). По аналогии с работой силы тяжести работа силы упругости равна площади треугольника, ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс в точке ​\( x \)​.
​\( A=Fx/2=kx\cdot x/2 \)​.

\[ F=kx^2/2 \]

7. Работа силы тяжести не зависит от формы траектории, по которой перемещается тело; она зависит от начального и конечного положений тела. Пусть тело сначала перемещается из точки А в точку В по траектории АВ (рис. 46). Работа силы тяжести в этом случае

\[ A_{AB}=mgh \]

Пусть теперь тело движется из точки А в точку В сначала вдоль наклонной плоскости АС, затем вдоль основания наклонной плоскости ВС. Работа силы тяжести при перемещении по ВС равна нулю. Работа силы тяжести при перемещении по АС равна произведению проекции силы тяжести на наклонную плоскость ​\( mg\sin\alpha \)​ и длины наклонной плоскости, т.е. ​\( A_{AC}=mg\sin\alpha\cdot l \)​. Произведение ​\( l\cdot\sin\alpha=h \)​. Тогда \( A_{AC}=mgh \). Работа силы тяжести при перемещении тела по двум различным траекториям не зависит от формы траектории, а зависит от начального и конечного положений тела.

Работа силы упругости также не зависит от формы траектории.

Предположим, что тело перемещается из точки А в точку В по траектории АСВ, а затем из точки В в точку А по траектории ВА. При движении по траектории АСВ сила тяжести совершает положительную работу, при движении по траектории В А работа силы тяжести отрицательна, равная по модулю работе при движении по траектории АСВ. Следовательно работа силы тяжести по замкнутой траектории равна нулю. То же относится и к работе силы упругости.

Силы, работа которых не зависит от формы траектории и по замкнутой траектории равна нулю, называют консервативными. К консервативным силам относятся сила тяжести и сила упругости.

8. Силы, работа которых зависит от формы пути, называют неконсервативными. Неконсервативной является сила трения. Если тело перемещается из точки А в точку В (рис. 47) сначала по прямой, а затем по ломаной линии АСВ, то в первом случае работа силы трения ​\( A_{AB}=-Fl_{AB} \)​, а во втором ​\( A_{ABC}=A_{AC}+A_{CB} \)​, \( A_{ABC}=-Fl_{AC}-Fl_{CB} \).

Следовательно, работа ​\( A_{AB} \)​ не равна работе ​\( A_{ABC} \)​.

9. Мощностью называется физическая величина, равная отношению работы к промежутку времени, за который она совершена. Мощность характеризует быстроту совершения работы.

Мощность обозначается буквой ​\( N \)​.

\[ N = A/t \]

Единица мощности: ​\( [N]=[A]/[t] \)​. ​\( [N] \)​ = 1 Дж/1 с = 1 Дж/с. Эта единица называется ватт (Вт). Один ватт — такая мощность, при которой работа 1 Дж совершается за 1 с.

10. Мощность, развиваемая двигателем, равна: ​\( N = A/t \)​, ​\( A=F\cdot S \)​, откуда ​\( N=FS/t \)​. Отношение перемещения ко времени представляет собой скорость движения: ​\( S/t = v \)​. Откуда ​\( N = Fv \)​.

Из полученной формулы видно, что при постоянной силе сопротивления скорость движения прямо пропорциональна мощности двигателя.

В различных машинах и механизмах происходит преобразование механической энергии. За счёт энергии при её преобразовании совершается работа. При этом на совершение полезной работы расходуется только часть энергии. Некоторая часть энергии тратится на совершение работы против сил трения. Таким образом, любая машина характеризуется величиной, показывающей, какая часть передаваемой ей энергии используется полезно. Эта величина называется коэффициентом полезного действия (КПД).

Коэффициентом полезного действия называют величину, равную отношению полезной работы ​\( (A_п) \)​ ко всей совершённой работе \( (A_с) \): ​\( \eta=A_п/A_с \)​. Выражают КПД в процентах.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Работа определяется по формуле

1) ​\( A=Fv \)​
2) \( A=N/t \)​
3) \( A=mv \)​
4) \( A=FS \)​

2. Груз равномерно поднимают вертикально вверх за привязанную к нему верёвку. Работа силы тяжести в этом случае

1) равна нулю
2) положительная
3) отрицательная
4) больше работы силы упругости

3. Ящик тянут за привязанную к нему верёвку, составляющую угол 60° с горизонтом, прикладывая силу 30 Н. Какова работа этой силы, если модуль перемещения равен 10 м?

1) 300 Дж
2) 150 Дж
3) 3 Дж
4) 1,5 Дж

4. Искусственный спутник Земли, масса которого равна ​\( m \)​, равномерно движется по круговой орбите радиусом ​\( R \)​. Работа, совершаемая силой тяжести за время, равное периоду обращения, равна

1) ​\( mgR \)​
2) ​\( \pi mgR \)​
3) \( 2\pi mgR \)​
4) ​\( 0 \)​

5. Автомобиль массой 1,2 т проехал 800 м по горизонтальной дороге. Какая работа была совершена при этом силой трения, если коэффициент трения 0,1?

1) -960 кДж
2) -96 кДж
3) 960 кДж
4) 96 кДж

6. Пружину жёсткостью 200 Н/м растянули на 5 см. Какую работу совершит сила упругости при возвращении пружины в состояние равновесия?

1) 0,25 Дж
2) 5 Дж
3) 250 Дж
4) 500 Дж

7. Шарики одинаковой массы скатываются с горки по трём разным желобам, как показано на рисунке. В каком случае работа силы тяжести будет наибольшей?

1) 1
2) 2
3) 3
4) работа во всех случаях одинакова

8. Работа по замкнутой траектории равна нулю

А. Силы трения
Б. Силы упругости

Верным является ответ

1) и А, и Б
2) только А
3) только Б
4) ни А, ни Б

9. Единицей мощности в СИ является

1) Дж
2) Вт
3) Дж·с
4) Н·м

10. Чему равна полезная работа, если совершённая работа составляет 1000 Дж, а КПД двигателя 40 %?

1) 40000 Дж
2) 1000 Дж
3) 400 Дж
4) 25 Дж

11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами.

РАБОТА СИЛЫ
A. Работа силы упругости при растяжении пружины
Б. Работа силы трения
B. Работа силы тяжести при падении тела

ЗНАК РАБОТЫ
1) положительная
2) отрицательная
3) равна нулю

12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Работа силы тяжести не зависит от формы траектории.
2) Работа совершается при любом перемещении тела.
3) Работа силы трения скольжения всегда отрицательна.
4) Работа силы упругости по замкнутому контуру не равна нулю.
5) Работа силы трения не зависит от формы траектории.

Часть 2

13. Лебёдка равномерно поднимает груз массой 300 кг на высоту 3 м за 10 с. Какова мощность лебёдки?

Ответы

Механическая работа. Мощность

Оценка

Механическая работа: определение и формула

 

Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?

Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое

механическая работа с точки зрения физики. В физике механическая работа – это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом. Как так? Сейчас разберемся.

Механическая работа в физике

Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример – это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть.

В каком случае совершается механическая работа?

Определение механической работы

Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.

Формула механической работы

Определяется механическая работа формулой:

A=Fs,

где A – работа,
F – сила,

s – пройденный путь.

Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние,  на которое мы передвинули тело.

Единица работы – 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример – это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения, то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.

Нужна помощь в учебе?

Предыдущая тема: Воздухоплавание в физике
Следующая тема:&nbsp&nbsp&nbspМощность: формула и применение в физике

Все неприличные комментарии будут удаляться.

Механическая работа в физике. Формула и примеры задач

При рассмотрении перемещений тел и их систем в пространстве часто приходится рассчитывать работу тех или иных сил. В данной статье дадим определение механической работы в физике, объясним, как она связана с энергией, а также приведем примеры решения задач на эту тему.

В чем различие между энергией и работой?

При изучении работы в физике (9 класс общеобразовательных школ) многие ученики путают данную величину с энергией. Понять это можно: ведь обе характеристики определяются в джоулях. Тем не менее, энергия — это фундаментальная характеристика. Она не может появляться или исчезать, а способна лишь переходить в разные состояния и формы. В этом заключается суть закона ее сохранения в изолированной системе. Работа же — это одна из форм реализации энергии, которая приводит к пространственному перемещению тел.

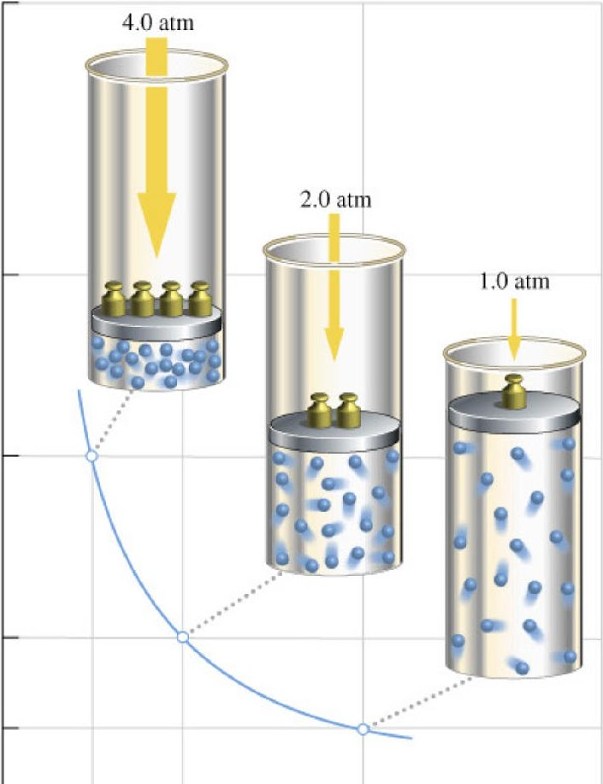
Так, при нагреве газа увеличивается его внутренняя энергия, то есть система получает возможность за счет нее совершить некоторую механическую работу. Последняя возникнет, когда газ начнет расширяться, увеличивать свой объем.

Строгое определение работы в физике

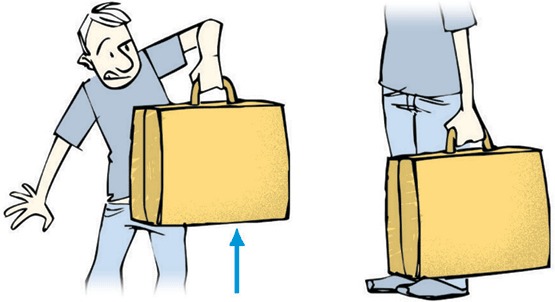
Строгим определением в физике является такое, которое предполагает четкое математическое обоснование. Применительно к рассматриваемой величине можно сказать следующее: если на тело действует некоторая сила F¯, в результате которой оно начинает перемещаться на вектор S¯, то работой A называется такая величина:

A = (F¯*S¯)

Поскольку A — это величина скалярная, то круглые скобки в правой части равенства говорят о том, что оба вектора умножаются скалярно.

Из записанного выражения следует важный факт: если сила действует перпендикулярно перемещению, то работы она не совершает. Так, многие школьники при решении по физике контрольных работ в 10 классе, например, допускают частую ошибку. Они полагают, что перемещать горизонтально тяжелый груз трудно именно из-за силы тяжести. Как показывает формула работы, сила тяжести при горизонтальном перемещении совершает нулевую работу, поскольку она направлена вертикально вниз. В действительности, трудность перемещения тяжелого груза связана с действием силы трения, которая прямо пропорциональна силе тяготения.

Выражение для A в явном виде может быть записано так:

A = F*cos(φ)*S

Произведение F*cos(φ) представляет собой проекцию вектора силы на вектор перемещения.

Работа и КПД

Каждому известно, что создать механизм, который бы всю затраченную энергию переводил в полезную работу, оказывается невозможным на практике. В связи с этим ввели понятие коэффициента полезного действия (КПД). Рассчитать его несложно, если воспользоваться следующим выражением:

КПД = А_п/А_з*100 %

Здесь А_п, А_з — полезная и затраченная работы соответственно. При этом А_з всегда больше, чем А_п, поэтому КПД всегда меньше 100 %. Например, двигатель внутреннего сгорания имеет КПД в пределах 25-40 %. Эти цифры говорят о том, что большая часть топлива при сгорании расходуется на нагрев окружающей среды, а не на движение автомобиля.

В абсолютном большинстве случаев невозможность получить КПД = 100 % связано с постоянным присутствием сил трения. Даже в таком простом механизме, как рычаг, эти силы, действующие в области опоры, приводят к снижению КПД до 80-90 %.

Далее в статье решим пару задач по рассмотренной теме.

Задача с телом на наклонной плоскости

Тело массой 4 кг движется вертикально вверх по наклонной плоскости. Угол ее наклона относительно горизонта составляет 20^o. На тело действует внешняя сила, которая равна 80 Н (она направлена горизонтально), а также сила трения, которая составляет 10 Н. Необходимо вычислить работу каждой из сил и общую работу, если тело двигалось вдоль плоскости 10 метров.

Прежде чем начать решать задачу, напомним, что, кроме указанных сил, на тело еще действует сила тяжести и реакции опоры. Последнюю можно не рассматривать, поскольку ее работа будет равна нулю. Сила же тяжести выполняет отрицательную работу, поскольку тело движется вверх по наклонной.

Сначала вычислим работу внешней силы F_0. Она составит:

A₀ = F₀*S*cos(20^o) = 751,75 Дж.

Заметим, что рассчитанная работа будет положительной, поскольку вектор внешней силы имеет острый угол с направлением перемещения.

Работы сил тяжести F_g и трения F_f будут отрицательными. Рассчитаем их с учетом угла наклона плоскости и направления перемещения тела:

A₁ = -F_g*S*sin(20^o) = -m*g*S*sin(20^o) = -134,21 Дж;

A₂ = -F_f*S = -10*10 = -100 Дж.

Общая работа всех сил будет равна сумме рассчитанных величин, то есть:

A = A₀ + A₁ + A₂ = 751,75 — 134,21 — 100 = 517,54 Дж.

Эта работа тратится на увеличение кинетической энергии тела.

Задача со сложной зависимостью силы

Известно, что материальная точка движется вдоль прямой, изменяя свои координаты от x = 2 до x = 5 м. В процессе движения на нее оказывает действие сила F, которая изменяется по следующему закону:

F = 3*x² + 2*x — 5 Н.

Полагая, что F действует вдоль линии перемещения точки, необходимо вычислить работу, которую она совершает.

Поскольку сила постоянно изменяется, то в лоб не получится использовать записанную в статье формулу для A. Чтобы рассчитать эту величину поступим следующим образом: вычислим на каждом элементарном отрезке пути dx работу dA, а затем, сложим все результаты. Рассуждая так, мы приходим к интегральной формуле для работы в физике:

A = ∫_x(F*dx).

Теперь осталось вычислить этот интеграл для нашего случая:

A = ∫⁵₂((3*x² + 2*x — 5)*dx) = (x³ + x² — 5*x)|⁵₂ = 123 Дж.

Мы получили результат в джоулях, поскольку координата x выражается в метрах, а сила F в ньютонах.

Формула работы

Цели:

• сформировать представление о величине «производительность», выявить зависимость между величинами: объем выполненной работы (А), производительность (V) и время (t), построить формулу работы А = V * t, V = A : t, t = A : V.
• повторить и закрепить решение примеров на порядок действий, соотношение между единицами дины, времени, массы.

ХОД УРОКА

I.

– Кто из Вас знает, кем работают ваши родители и на каком предприятии они трудятся?
– А кто из Вас знает пословицы о труде?

• Работа силушку копит, а лень ее топит.
• Под лежачий камень вода не течет.
• Трудолюбив, как муравей.
• Не спеши языком, торопись делом.
• Кто мало говорит, тот много делает.
• Без труда не вытащишь рыбку из пруда.
• Рабочие руки не знают скуки.
• Дело мастера боится.
• Всякое умение трудом дается.
• Без труда нет добра.
• Без труда день годом станет.
• Горька работа, да сладок мед.

II. Актуализация знаний

(На доске таблица и формулы. Дети придумывают задачи и решают устно)

S	V	t
? км	60 км/ч	4 ч
720 км	? км/ч	6 ч
57 км	19 км/ч	? ч

– Найдите среди формул те, которые показывают, как найти неизвестные значения пути, скорости и времени. (Формулы выставляются на доске и комментируются)

– А зачем вообще нужны формулы? (Показывают, как решать похожие между собой задачи).
– Подберите формулы для решения первой задачи. (S = V * t)
– Придумайте по этой формуле задачу, аналогичную первой задачи.
– Запишите формулу, подходящую к задаче: «Один всадник проскакал 70 км за 2 ч, а второй – 90 км за 3 ч. Какой из них скакал быстрее?» (V = S: t)
– Решите эту задачу, пользуясь формулой.
(1. 70 : 2 = 35 (км/ч) – скорость первого всадника.
2. 90 : 3 = 30 (км/ч) – скорость второго всадника.
3. 35 км/ч > 30 км/ч => 1 всадник скакал быстрее)

III. Постановка проблемы

– Подберите формулу к задаче: «Один мастер сделал 2 детали за 4 часа, а  второй – 21 деталь за 3 часа. Кто из них работал быстрее?» (Подходящей формулы среди данных нет)
– Сформулируйте цель урока – установить, какие величины описывают процесс выполнения работы, и установить взаимосвязь между ними.
– Тема урока – Формула работы.

IV. «Открытие» детьми нового знания.

– О каких величинах идет речь в последней задаче – о площади, объеме, пройденном пути? (Нет. В задаче говориться о количестве деталей, сделанных рабочими, о скорости и времени их работы

).
– Как найти скорость работы мастеров? (Надо количество сделанных деталей разделить на время работы).
– Скорость работы называют производительностью и обозначают (V), всю выполненную работу – А, время работы – t.
– Попробуйте установить взаимосвязь между этими величинами. (А = V * t, V = A : t, t = A : V)
– Теперь, зная формулу работы, давайте решим задачу.

V = A : t
1. 24 : 4 = 6 (дет./ч) – производительность первого мастера.
2. 21 : 3 = 7 (дет./ч) – производительность второго мастера.
3. Второй мастер работал быстрее.

Практическая работа на производительность

– Решите устно в течение 2 минут следующие уравнения.

9 + х = 12                               х – 27 = 8                    5 * х = 25
8 * х = 480                             52 : х = 13                   420 : х = 7
40 – х = 12                             х : 19 = 4                     800 + х = 823
90 : х = 5                                34 – х = 17                  х – 36 = 15
х * 50 = 250                           18 + х = 110               х – 25 = 118

– Давайте проверим количество правильных ответов и вычислим производительность каждого из вас.
– Как это сделать? (Количество верных ответов разделить на 2).
– А какая у вас производительность за урок? (То что получилось умножить на 45 минут).

Закрепление понятия «производительность»

V. Первичное закрепление

• С.44, №2
• С. 44, №3
• С.44, №4 (а)

VI. Самостоятельная работа с самопроверкой по эталону

VII. Закрепление пройденного

VIII. Итог

– Что сегодня на уроке было самым интересным?
– Что сегодня на уроке было главным?
– Где нам могут пригодиться эти знания?
– Какую поговорку выберем своим девизом?

IX. Домашнее задание

Приложение 1