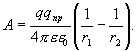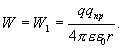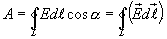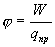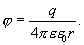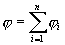11.6. Работа сил электростатического поля по перемещению зарядов.

В однородном поле (рис.11.12). Однородное поле создают, например, большие металлические пластины, имеющие заряды противоположного знака. Найдем работу по перемещению заряда q’ на расстояние d:

Таким образом, работа, совершаемая силами поля, не зависит от формы пути, по которому перемещался заряд, а зависит только от расстояния d, измеряемого вдоль силовой линии меж­ду начальным и конечным положением заряда.

В неоднородном поле точечного заряда q (рис.11.13).

Найдем работу по перемещению пробного заряда q’ из точки 1 в точку 2 в поле, создаваемом точечным зарядом q:

. (11-23)

И в этом случае работа сил не зависит от формы пути. Она является только функцией начального и конечного положения заряда.

Для замкнутой траектории L она равна нулю, т. к. , т. е.

или (11-24)

т.е. циркуляция вектора напряженности по любому замкнутому контуру равна нулю.

В механике было приведено следующее определение: «Силы, работа которых не зависит от формы пути, называются консервативными силами, а поля, работа сил которых не зави­сит от формы пути, называются потенциальными полями». Таким образом, рассмотренное нами электростатическое поле является потенциальным,

а кулоновские силы — консерватив­ными.

11.6. Потенциал. Разность потенциалов. Потенциал точечного заряда, диполя, сферы.

Известно, что работа сил потенциального поля может быть представлена как убыль потенциальной энергии, т. е.

. (11-25)

Отсюда следует, что потенциальная энергия пробного заряда в поле заряда q будет

При потенциальная энергия должна обращаться в нуль, поэтому значение постоян­ной С полагаем равным нулю. В итоге получаем, что

(11-26)

Величину

(11-27)

называют потенциалом электрического поля в данной точке. Потенциал , наряду с напря­женностью электрического поля, используется для описания электрического поля. Потенциал точечного зарядаq, как следует из (11-26) и (11-27),

, (11-28)

т. е. (прямо пропорционален величине заряда и обратно пропорционален расстоя­нию от него). Потенциал в СИ измеряется в вольтах:

1 В= 1Дж/1 Кл.

Если поле создает система точечных зарядов то потенциал

. (11-29)

Из формулы (11-27) вытекает, что заряд q’, находящийся в точке поля с потенциалом , обладает потенциальной энергией

. (11-30)

Следовательно, работу сил поля над зарядом q’ можно выразить через разность потен­циалов

, (11-31)

здесь — разность потенциалов между двумя точками поля, которая называется на­пряжением. Напряжение тоже измеряется в вольтах.

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, назы­вается

эквипотенциальной поверхностью.

Ее уравнение имеет вид .

Для точечного заряда

и эквипотенциальная поверхность является сферической. При перемещении заряда q’ вдоль эквипотенциальной поверхности на отрезок dl по­тенциал не изменяется, т. е. = 0, следовательно,

.

Вектор напряжен­ности электрического поля , перпендикулярен эквипотенциальной поверхности.

39.Работа сил электростатического поля по перемещению зарядов. Циркуляция вектора напряженности. Потенци­альный характер электростатического поля.

Работа по перемещению электрического заряда

Вычислим работу при перемещении электрического заряда в однородном электрическом поле с напряженностью . Если перемещение заряда происходило по линии напряженности поля на расстояние 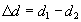(рис. 134), то работа равна A = Fэ(d1 — d2) = qE(d1 — d2),

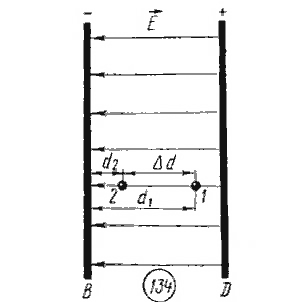
где d1 и d2 — расстояния от начальной и конечной точек до пластины В.

В механике было показано, что при перемещении между двумя точками в гравитационном поле работа силы тяжести не зависит от траектории движения тела. Силы гравитационного и электростатического взаимодействия имеют одинаковую зависимость от расстояния, векторы сил направлены вдоль прямой, соединяющей взаимодействующие точечные тела. Отсюда следует, что и при перемещении заряда в электрическом поле из одной точки в другую работа сил электрического поля не зависит от траектории его движения.

Этот вывод подтверждается самыми точными экспериментами.

При изменении направления перемещения на 180° работа сил электрического поля, как и работа силы тяжести, изменяет знак на противоположный. Если при перемещении заряда q из точки В в точку С силы электрического поля совершили работу А, то при перемещении заряда q по тому же самому пути из точки С в точку В они совершают работу — А. Но так как работа не зависит от траектории, то и при перемещении по траектории CKB тоже совершается работа — А. Отсюда следует, что при перемещении заряда сначала из точки В в точку С, а затем из точки С в точку В, т. е. по замкнутой траектории, суммарная работа сил электростатического поля оказывается равной нулю (рис. 135).

Работа сил электростатического поля при движении электрического заряда по любой замкнутой траектории равна нулю.

Циркуляция вектора напряженности.

Поле, работа сил которого по любой замкнутой траектории равна нулю, называется потенциальным полем. Гравитационное и электростатическое поля являются потенциальными полями.

В случае, если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль какой-либо траектории (рис. 1) двигается другой точечный заряд Q0, то сила, которая приложена к заряду, совершает некоторую работу. Работа силы F на элементарном перемещении dl равна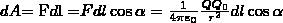

Так как dl/cosα=dr, то

Работа при перемещении заряда Q0 из точки 1 в точку 2 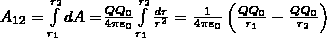(1)

от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы —консервативными

Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е.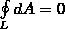

(2)

Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Еdl = Eldl, где El = Ecosα — проекция вектора Е на направление элементарного переме¬щения. Тогда формулу (2) можно представить в виде 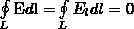(3)

Интеграл называется циркуляцией вектора напряженности.Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называется

потенциальным.Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность.

Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля).

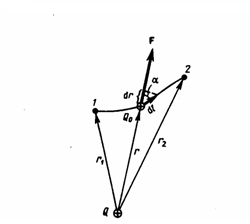
Рис.1

Потенци­альный характер электростатического поля

Потенциал. Работа по перемещению заряда в электростатическом поле.

2. 1. Потенциал, разность потенциалов электростатического поля?

Потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля:

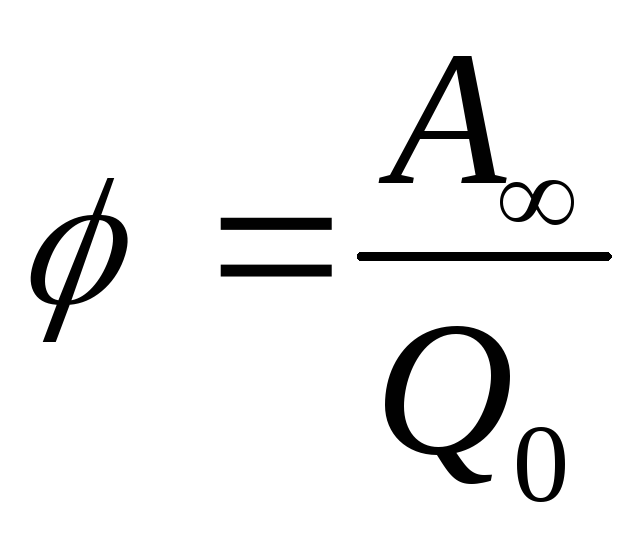(1.6)

Разность потенциалов:

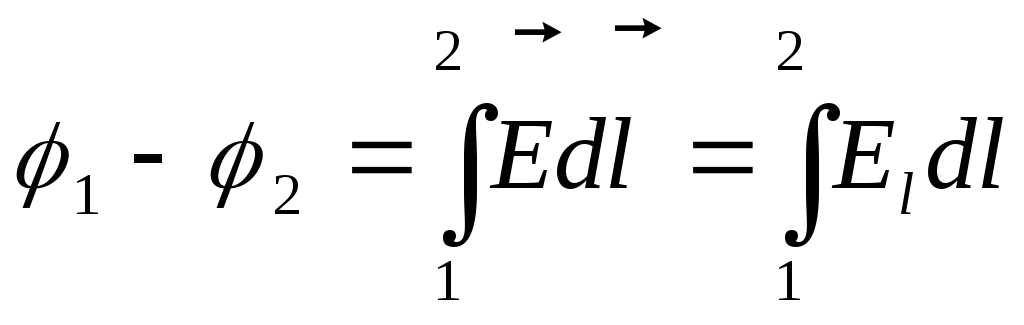(1.7)

1. 2. Связь между напряженностью и потенциалом электростатического поля.

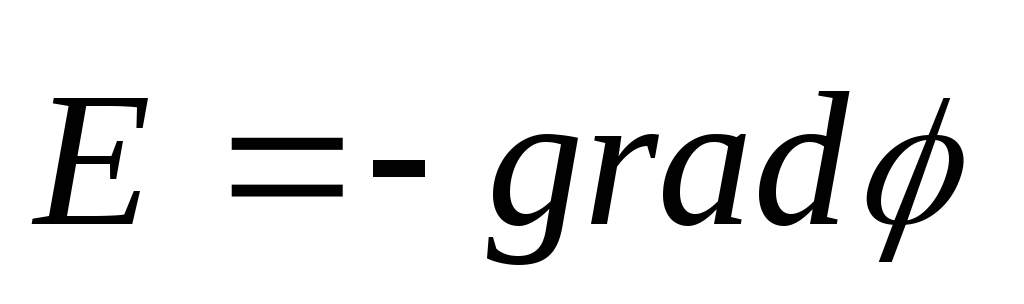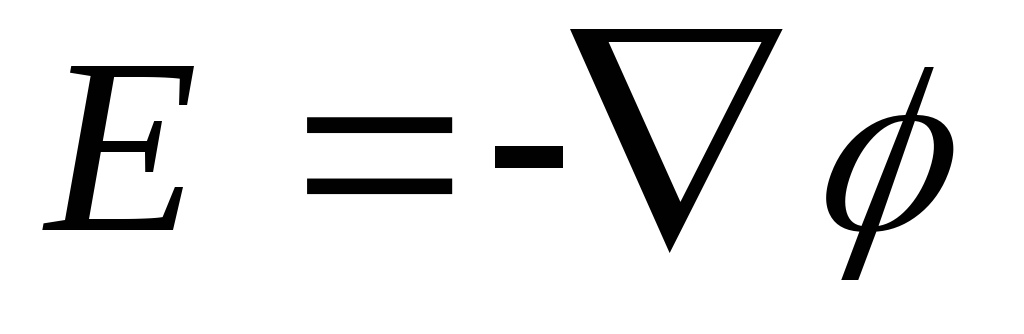, или (1.8)

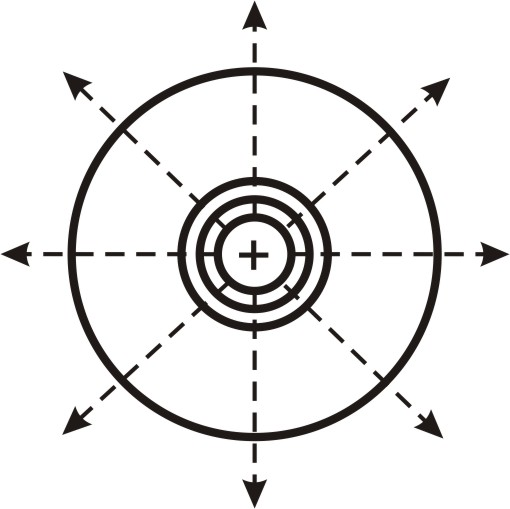
Рис. 1.7

т. е. напряженность поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал имеет одно и то же значение (рис. 1.7).

2. 3. Работа электростатического поля при перемещении заряда.

Работа при перемещении заряда Q₀ из точки 1 в точку 2 находится (рис. 1.13) из определения работы электростатического поля 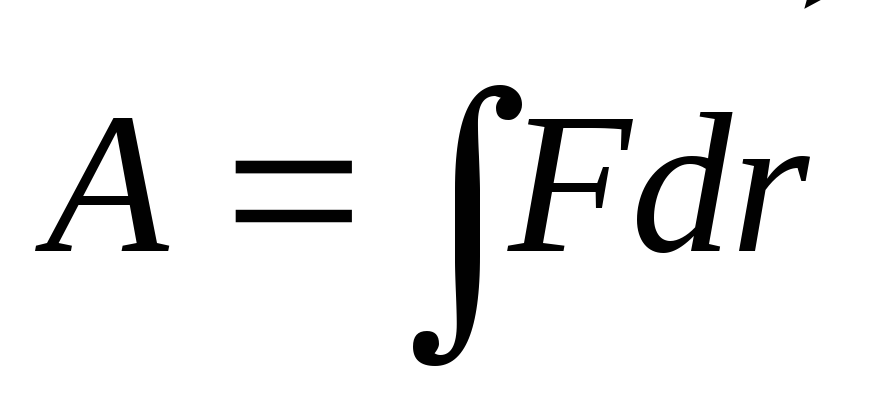и закона Кулона , тогда

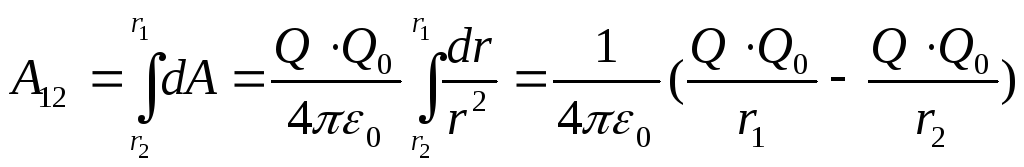(1.14)

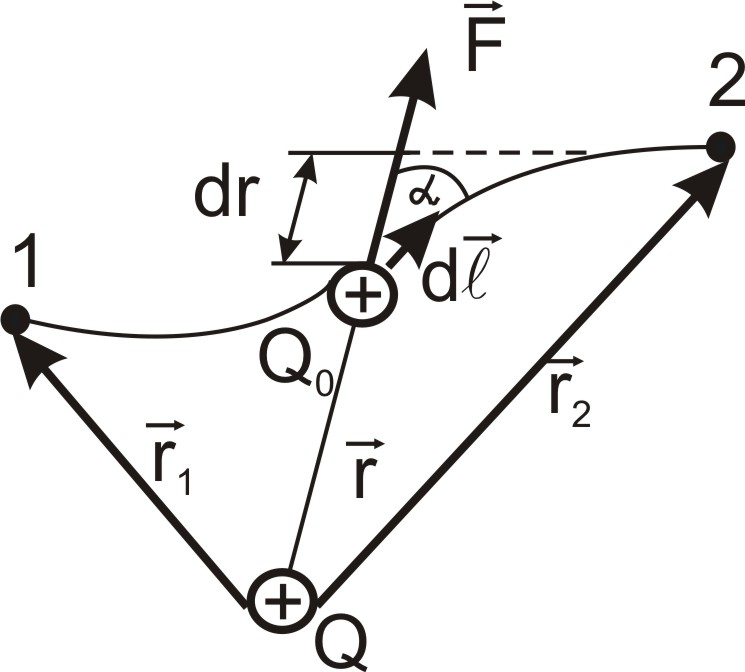
Рис. 1.13

Работа сил поля при перемещении заряда Q₀ из точки 1 в точку 2 может быть записана также в виде

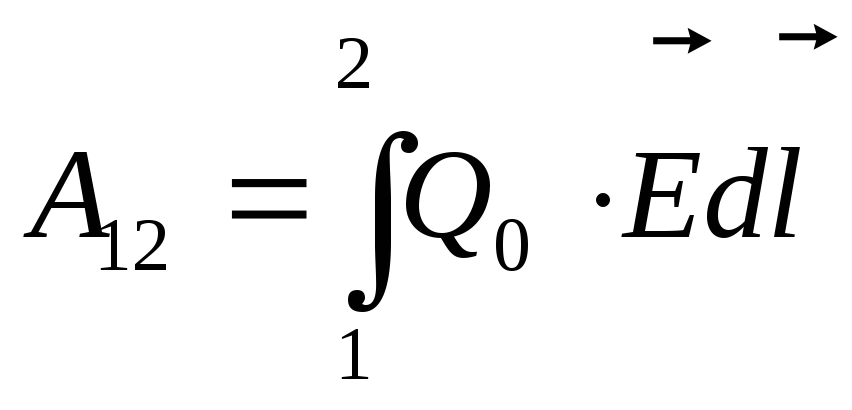(1.16)

Работа электростатического поля не зависит от траектории движения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

2. 4. Циркуляция вектора напряженности электростатического поля.

Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути равна , где 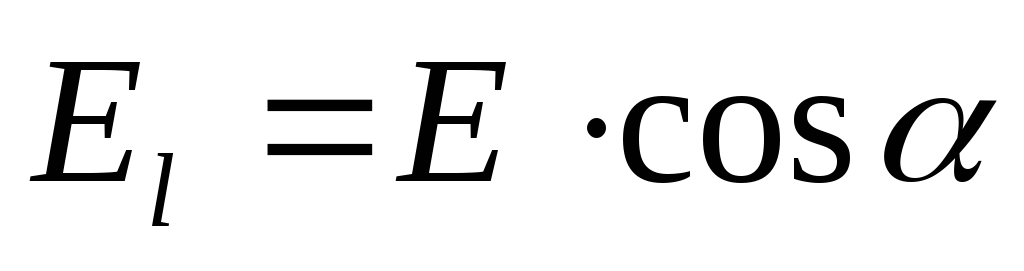— проекция вектора Е на направление элементарного перемещения.

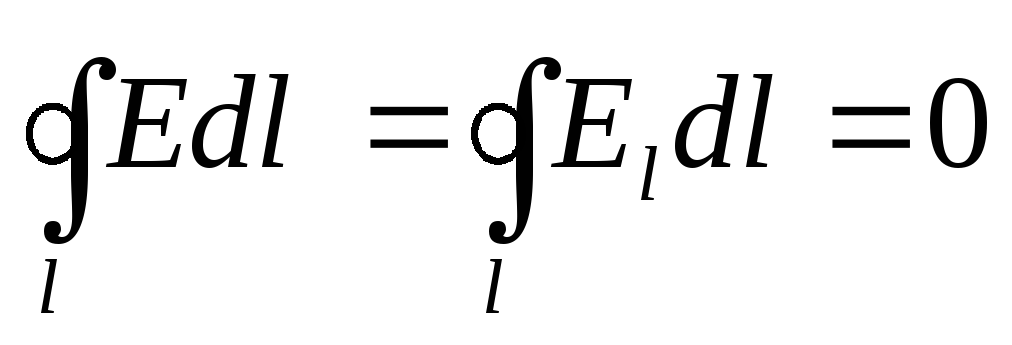(1.15)

Интеграл 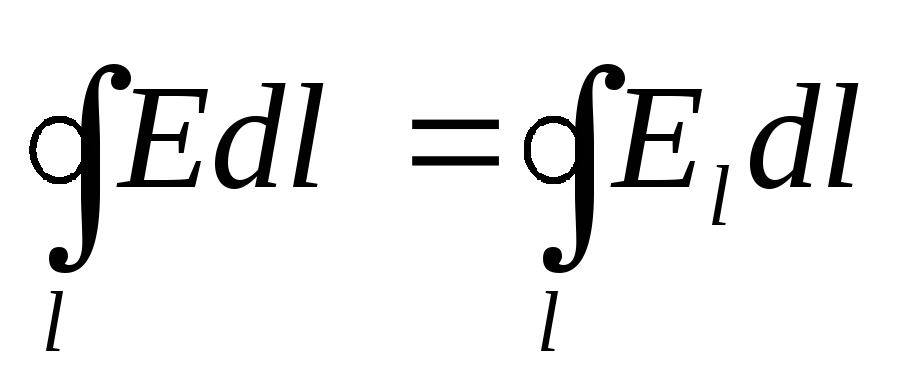называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным. Из обращения в нуль циркуляции вектора следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.

Работа электростатического поля, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути , равна нулю, т. е.

2. 5. Вектор электрического смещения.

Вектор электрического смещения для электрически изотропной среды равен

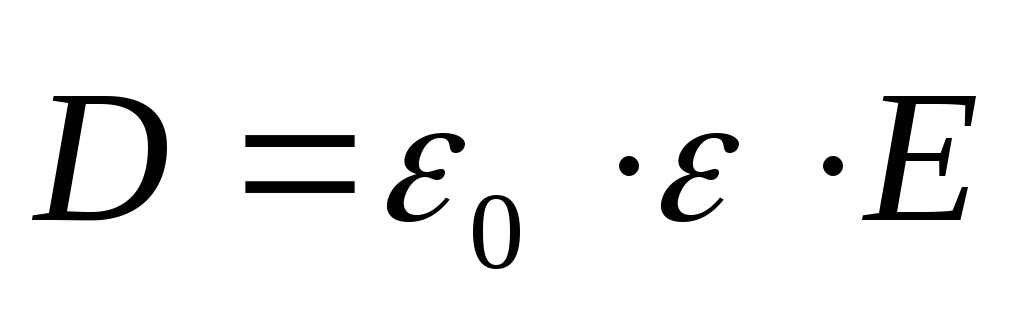(1.17)

где -диэлектрическая проницаемость среды, показывающая как слоем диэлектрика ослабляется поле по сравнению с вакуумом.

Вектор напряженности , переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Линии вектора могут начинаться и заканчиваться на любых зарядах – свободных и связанных, в то время как линии вектора – только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора проходят не прерываясь.

Работа электростатического поля при перемещении заряда

Тела, способные совершать работу за счет сил взаимодействия друг с другом, обладают потенциальной энергией. Взаимодействие электрических зарядов осуществляется посредством электрического поля. Следовательно, находящийся в электростатическом поле заряд обладает потенциальной энергией, которую называют электростатической.

В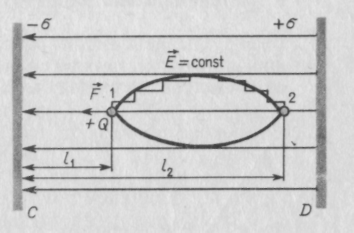 однородном поле на заряд действует постоянная по модулю и направлению сила F = qE. Работа постоянной силы определяется по формуле А = Fℓcos. Направление силы F, действующей на заряд q, со стороны электрического поля противоположно направлению перемещения заряда (т.е. =180°), поэтому А = -Fℓ. Из рисунка ℓ = ℓ₂ — ℓ₁, тогда работа силы электростатического поля A = —qE(ℓ₂ — ℓ₁).

Перемещение по плавной кривой можно представить в виде перемещения по ступенчатой ломаной линии со сколь угодно малыми участками. При перемещении заряда вдоль вертикальных участков ломаной, перпендикулярных направлению вектора напряженности поля, сила поля работу не совершает (так как =90°). Следовательно, работа переноса заряда по кривой из точки 1 в точку 2 равна сумме работ, совершаемых силой поля при перемещении заряда по горизонтальным участкам ломаной. Но сумма всех таких участков равна расстоянию ℓ₂— ℓ₁ между точками 1 и 2 вдоль силовой линии. Следовательно, работа поля, совершаемая при перемещении заряда по любой кривой, соединяющей точки 1 и 2, определяется так же, как и работа переноса заряда по прямой между этими точками, т.е. не зависит от формы траектории.

Вывод о независимости работы электростатических сил от траектории движения заряда справедлив не только для однородного, но и для произвольного электростатического поля. Это следует из закона сохранения энергии: после возвращения заряда q в исходное положение первоначальное состояние системы полностью восстанавливается и, следовательно, должно восстановиться исходное значение энергии системы. Следовательно, в любом электростатическом поле работа, совершаемая при перемещении заряда из одной точки поля в другую, не зависит от того, по какой траектории движется заряд, а зависит только от положения этих точек в поле. Силы, обладающие подобным свойством, называют консервативными, а поля этих сил — потенциальными. Следовательно, электростатическое поле является потенциальным, а электростатические силы — консервативными. Работа сил потенциального поля при перемещении заряда по замкнутому контуру равна нулю.

Потенциальная энергия заряда в однородном электростатическом поле.

Работа консервативных сил равна изменению потенциальной энергии, взятому с противоположным знаком, т. е. A = -W_П = -(W_П2-W_П1) = -qE(ℓ₂ — ℓ₁). Следовательно, в однородном электростатическом поле потенциальная энергия заряда W_П = qE ℓ, где ℓ — кратчайшее расстояние заряда от начала отсчета.

Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо не только для однородного, но и для любого электростатического поля. Поэтому отношение потенциальной энергии заряда, помещенного в какую-либо точку электростатического поля, к значению этого заряда не зависит от заряда, а является характеристикой поля в данной точке, его называют электрическим потенциалом  в этой точке  =W_П/q.

Потенциал электростатического поля в данной точке есть скалярная величина, численно равная потенциальной энергии единичного заряда, помещенного в эту точку поля. Потенциал есть энергетическая характеристика поля, т.е. энергия заряда в точке поля с потенциалом : W_П = q.

Работа поля по перемещению заряда А = -(W_П2— W_П1) = —q(₂ — ₁) = q

Величину  = ₁ — ₂ называют разностью потенциалов. Единица потенциала и разности потенциалов 1В = 1Дж/1Кл.

Потенциал в данной точке электростатического поля может быть определен лишь с точностью до некоторой постоянной величины, числовое значение которой зависит от выбора начала отсчета потенциала. При переносе начала отсчета потенциалы всех точек электростатического поля меняются на одно и то же значение, а разность потенциалов остается неизменной. Работа перемещения заряда в электростатическом поле зависит от разности потенциалов, поэтому для ее подсчета безразлично, где было выбрано начало отсчета потенциала.

Следовательно, выбирать начало отсчета потенциала можно произвольно. В теоретических расчетах потенциалы бесконечно удаленных точек принято считать равными нулю. В электро- и радиотехнике за начало отсчета потенциала принимают поверхность Земли.

Потенциал электростатического поля, созданного точечным электрическим зарядом, определяют в данной точке по формуле .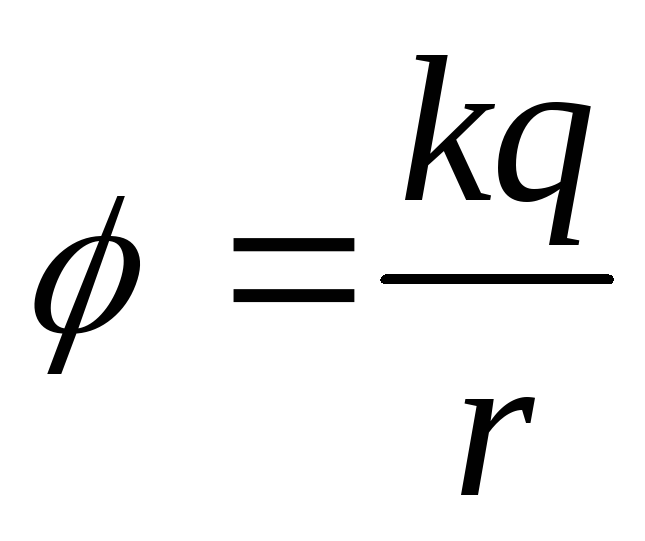

Потенциалы точек поля, созданного точечным положительным зарядом, положительны и уменьшаются при удалении от него, а в поле отрицательного точечного заряда потенциалы отрицательны и возрастают при удалении от заряда. В случае, если за нулевой принят потенциал бесконечно удаленных точек, потенциал поля точечного заряда имеет простой физический смысл: т. е. потенциал данной точки электростатического поля, созданного точечным зарядом, численно равен работе, совершаемой силой, действующей со стороны поля, при перемещении единичного положительного заряда из данной точки в бесконечно удаленную.

Формула справедлива также и для определения потенциала в точках поля, создаваемого равномерно заряженной сферой или шаром на расстояниях, больших или равных его радиусу, так как поле такой сферы вне ее и на ее поверхности совпадает с полем точечного заряда.

Если заряд не является точечным, то для определения потенциала поля, создаваемого им, поступают следующим образом. Разбивают этот заряд на сколь угодно малые заряды, каждый из которых можно считать точечным. Тогда потенциал в произвольной точке поля определится как сумма потенциалов, созданных в этой точке каждым отдельным точечным зарядом, т.е.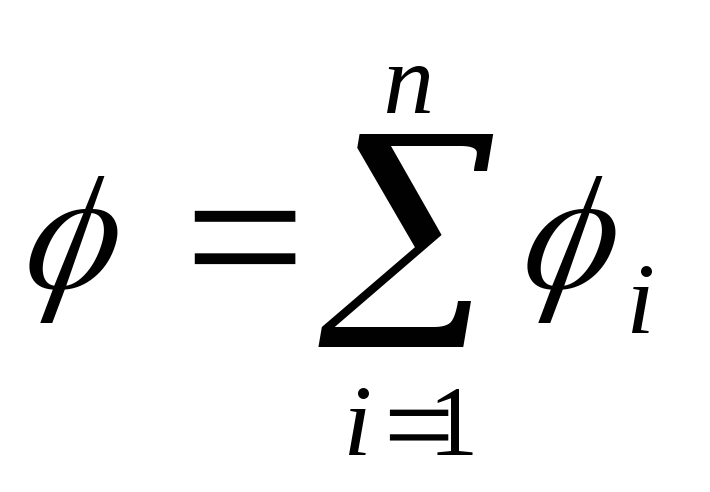

Поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной. Например, в поле точечного заряда эквипотенциальными являются поверхности сфер, описанные вокруг этого заряда с центром в той точке, где он находится.

Пересечение эквипотенциальных поверхностей с плоскостью чертежа образует эквипотенциальные линии. С их помощью мы можем графически изображать электрическое поле, подобно тому, как это мы делали с помощью линий напряженности.

Линии напряженности электростатического поля направлены перпендикулярно эквипотенциальным поверхностям и показывают направление наибыстрейшего убывания потенциала. Поэтому при перемещении заряда вдоль эквипотенциальной поверхности электрические силы работу не совершают, т.е. работа равна нулю.

Работа при перемещении заряда в однородном поле перпендикулярно эквипотенциальным поверхностям 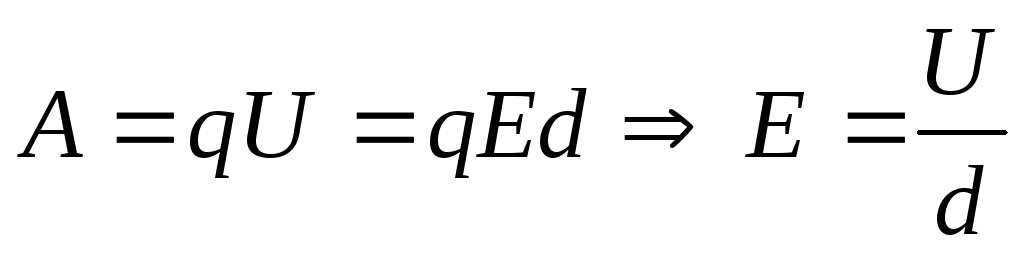— в однородном поле.

1.6. Работа электрического поля по перемещению электрического заряда. Циркуляция вектора напряженности электрического поля

Е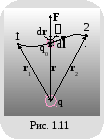сли в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд q_o (рис. 1.11), то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна

(1.22)

где dr = dlcos.

Работа при перемещении заряда q из точки 1 в точку 2

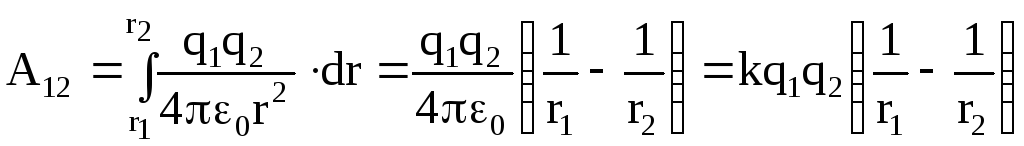, (1.23)

где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ k = 1/4₀;

q₁ – заряд, создающий электрическое поле;

q₂ – заряд, перемещаемый в электрическом поле;

r₁, r₂ – начальное и конечное расстояния между зарядами.

Из формулы (1.23) видно, что работа сил электрического поля по перемещению электрического заряда не зависит от траектории перемещения, а определяется только начальным и конечным положением зарядов. Следовательно, электростатическое поле электрических зарядов является потенциальным, а электростатические силы – консервативными силами.

Кроме того, из формулы (1.23) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.

. (1.24)

Если в качестве заряда, переносимого в электростатическом поле, взять положительный единичный точечный заряд, то элементарная работа сил поля на пути dl равна dA = Edl = E_ldl, где E_l = Ecos — проекция вектора E на направление элементарного перемещения. Тогда формулу (1.24) можно записать в виде

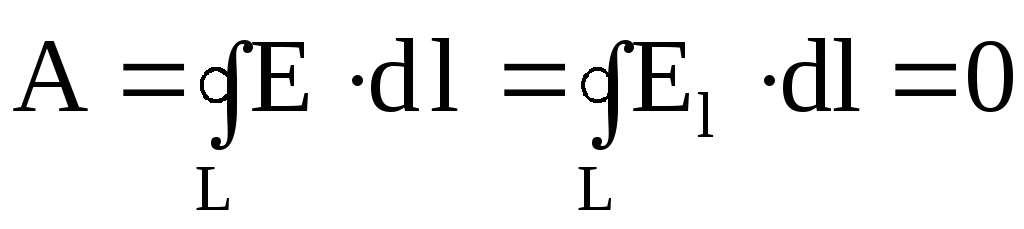. (1.25)

Интеграл

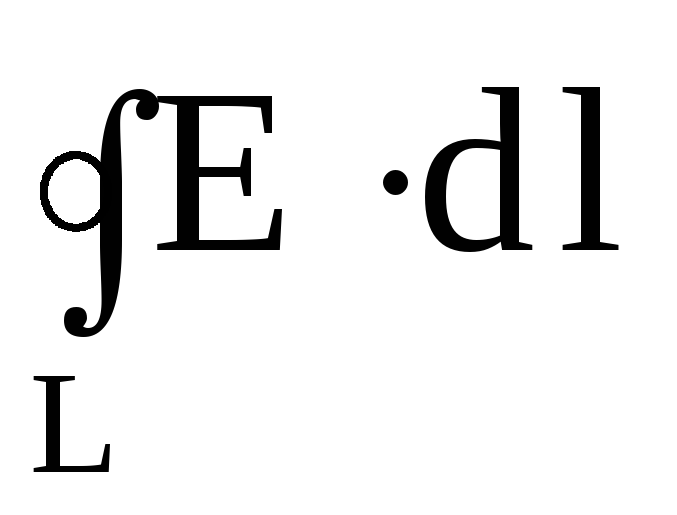(1.26)

называют циркуляцией вектора напряженности электростатического поля. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура (1.25) равна нулю. Равенство нулю циркуляции вектора напряженности электростатического поля еще раз подтверждает, что оно является потенциальным. Из потенциальности электростатического поля следует, что линии напряженности электростатического поля не могут быть замкнутыми – они начинаются и заканчиваются на зарядах или же уходят в бесконечность.

Надо отметить, что формула (1.25) справедлива лишь только для электростатического поля. Для электрических полей движущихся зарядов условие равенства нулю циркуляции вектора напряженности не выполняется. Для таких полей она отлична от нуля.

1.7. Энергия электрического заряда в электрическом поле

При перемещении электрического заряда под действием сил электрического поля происходит изменение его первоначального положения, что влечет за собой изменение потенциальной энергии системы. Поэтому можно утверждать, что работа сил электрического поля совершается за счет изменения (уменьшения) потенциальной энергии:

A = W₁ — W₂ = W. (1.27)

Формула (1.27) определяет изменение потенциальной энергии, а не её величину. Следовательно, можно условно выбрать такое положение электрического заряда, при котором потенциальная энергия системы равна нулю. Принято считать потенциальную энергию системы зарядов, равной нулю, в том случае, когда один из них удален от другого на бесконечность, т.е., например, W₂ = W = 0. Тогда W₁ = A.

Таким образом, потенциальная энергия заряда, находящегося в электрическом поле другого заряда (потенциальная энергия двух электрических зарядов, системы из двух электрических зарядов), измеряется (численно равна) работой, которую совершают силы электрического поля по удалению одного из зарядов из данной точки поля в бесконечность.

Так как

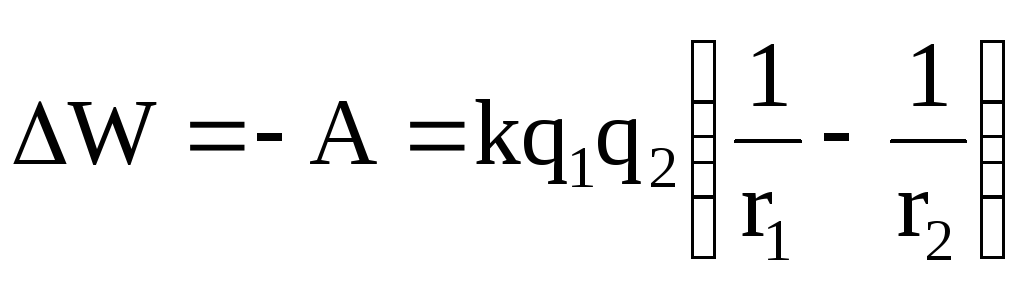(1.28)

и при r₂, W₂0, в предельном случае при r₂ = , W₂ = 0, то

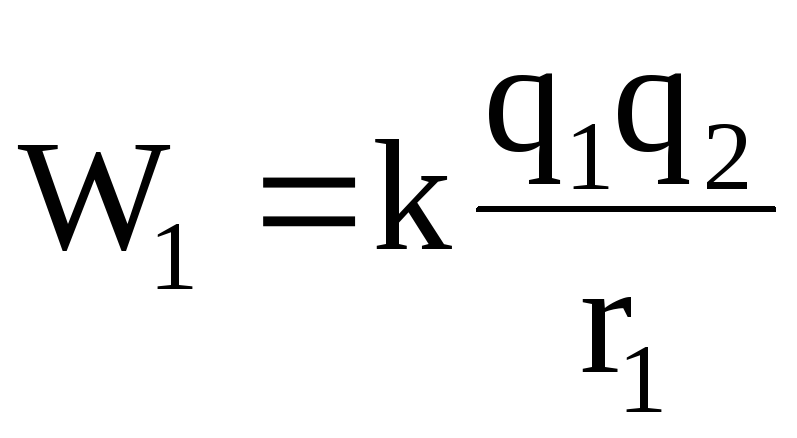. (1.29)

Выражение (1.29) определяет потенциальную энергию заряда, находящегося в электрическом поле другого заряда (потенциальную энергию двух электрических зарядов, системы из двух электрических зарядов).

Так как положение зарядов было выбрано произвольно, то в общем случае потенциальная энергия заряда, находящегося в электрическом поле другого заряда (потенциальная энергия двух электрических зарядов, системы из двух электрических зарядов) определяется так:

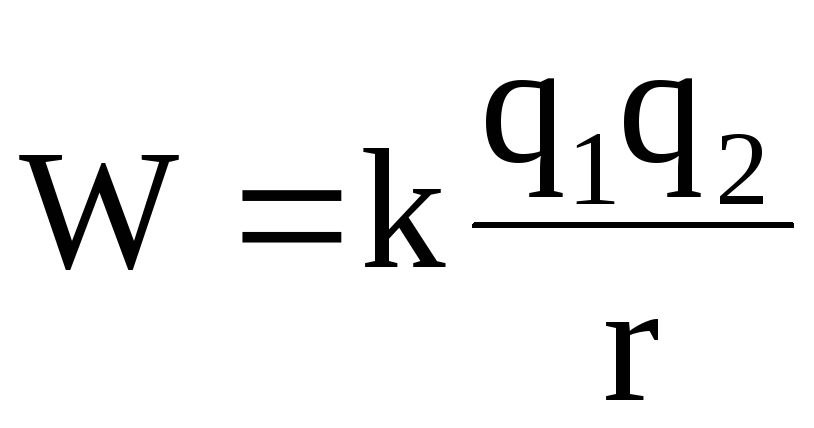, (1.30)

где r – расстояние между центрами взаимодействующих зарядов или до рассматриваемой точки поля, в которую помещается электрический заряд.

13.9. Работа сил электростатического поля при перемещении заряда

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда 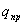из одной точки электростатического поля в другую на отрезке пути 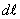 , по определению равна

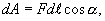
где 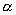 — угол между вектором силы F и направлением движения 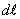. Если работа совершается внешними силами, то dA0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда 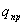 из точки “а” в точку “b” будет равна

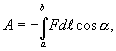
где 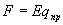 — кулоновская сила, действующая на пробный заряд  в каждой точке поля с напряженностью Е. Тогда работа

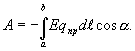
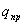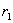Пусть заряд  перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии  в точку “b”, удаленную от q на расстоянии 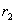 (рис 1.12).

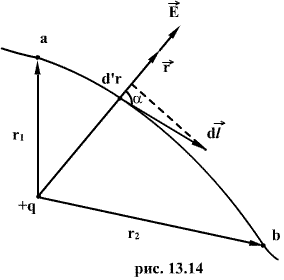
Как видно из рисунка  тогда получим

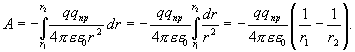
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно

(13.16)

13.10. Потенциальная энергия электростатического поля

Полученный результат свидетельствует о том, что работа не зависит от пути, по которому перемещался в электростатическом поле пробный заряд 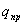 , и зависит только от положений точек “а” и “b”. Такое поле называется потенциальным. Поэтому работа, очевидно, равна убыли потенциальной энергии W этого заряда

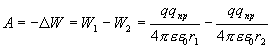
Перенесем пробный заряд на бесконечность. Напряженность поля Е на бесконечности принимается равной нулю, следовательно 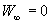 . Но так как  , то второе слагаемое тоже будет равно нулю и тогда

(13.17)

13.11. Циркуляция вектора напряженности

Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

(13.18)

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

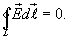
13.12. Потенциал электростатического поля

Внося в данную точку поля различные пробные заряды 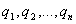 мы будем, соответственно, изменять потенциальную энергию, т.е. получим различные 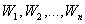 . Но отношение потенциальной энергии к заряду остается величиной постоянной. Следовательно для характеристики поля можем использовать это отношение. Обычно оно обозначается буквой 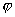 и называется потенциалом поля в данной точке

(13.19)

Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала — вольт. С учетом (1.16)

(13.20)

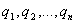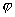Когда поле образовано несколькими произвольно расположенными зарядами  , потенциал его  в данной точке равен алгебраической сумме потенциалов 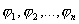 , создаваемых каждым зарядом в отдельности, т.е.

(13.21)

Если из точки “а” в точку “b” электрического поля перемещается заряд q’, то при этом совершается работа против электрических сил, равная

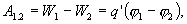
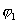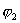где  и  — потенциалы поля в точках “а” и ” b”.

В СИ за единицу разности потенциалов принимают Вольт (В), Разность потенциалов между двумя точками поля равна одному Вольту, если для перемещения между ними заряда в один Кулон нужно совершить работу в один Джоуль

В атомной физике и электронике часто употребляют для измерения работы и энергии, величину называемую электронвольтом (эВ). Один электронвольт равен работе, совершаемой при перемещении заряда, равного заряду электрона, между двумя точками поля с разностью потенциалов один вольт.

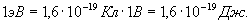
Работа перемещения заряда в электростатическом поле. Потенциал поля. Разность потенциалов

Если в электростатическом поле точечного заряда qиз точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд q₀, то сила, приложенная к заряду, совершает работу. Работа силы на элементарном перемещении dlравна

Работа при перемещении заряда q₀из точки 1 в точку 2

Работа A₁₂не зависит от траектории перемещения, а определяется только положениями начальной и конечной точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными.

Таким образом, работа перемещения заряда в электростатическом поле по любому замкнутому контуру Lравна нулю

Интеграл называется циркуляцией вектора напряженности. Из обращения ее в нуль следует, что линии напряженности электростатического поля никогда не могут быть замкнуты сами на себя. Они начинаются и кончаются на зарядах, либо уходят в бесконечность. Это свидетельствует о наличии в природе двух родов электрических зарядов. Формула справедлива только для электростатического поля.

При перемещении зарядов изменяется их взаимное расположение, поэтому работа, совершаемая электрическими силами, в этом случае равна изменению потенциальной энергии перемещаемого заряда:

Потенциальная энергия заряда q₀, находящегося в поле заряда qна расстоянии r от него равна

Считая, что при удалении заряда на бесконечность, потенциальная энергия обращается в нуль, получаем: const = 0.

Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов потенциальная энергия из взаимодействия (притяжения) отрицательна.

В любой точке поля потенциальная энергия W заряда численно равна работе, которую необходимо совершить для перемещения заряда из бесконечности в эту точку.

Отношение зависит только от q и r. Эту величину называют потенциалом:

Единица электрического потенциала – вольт (В).

Она характеризует потенциальную энергию, которой обладал бы по­ложительный единичный заряд, помещенный в данную точку поля.Для поля точечного заряда: . Потенциал данной точки поля равен работе перемещения единичного положительного заряда из данной точки в бесконечность.

Потенциал поля, создаваемого системой точечных зарядов, равен алгебраической сумме потенциалов всех этих зарядов: .

Работа сил поля при перемещении заряда q’ из точки 1 в точку 2 может быть записана в виде:

Величину называют разностью потенциалов (напряжением) электрического поля.