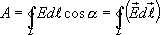Работа по перемещению заряда в электрическом поле

Одним из основных понятий в электричестве является электростатическое поле. Его важным свойством считается работа по перемещению заряда в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Условия выполнения работы Сила, находящиеся в электростатическом поле, перемещает заряд из одного места в другое. На нее совершенно не влияет форма траектории. Определение силы зависит только от положения точек в начале и конце, а также, от общей величины заряда. Исходя из этого, можно сделать следующий вывод: Если траектория при перемещении электрозаряда является замкнутой, то вся работа сил в электростатическом поле имеет нулевое значение. При этом, форма траектории не имеет значения, поскольку кулоновские силы производят одинаковую работу. Когда направление, в котором перемещается электрозаряд, изменяется на противоположное, то сама сила также изменяет свой знак. Поэтому, замкнутая траектория, независимо от своей формы, определяет всю работу, производимую кулоновскими силами, равной нулю. Если в создании электростатического поля принимает участие сразу несколько точечных зарядов, то их общая работа будет складываться из суммы работ, производимых кулоновскими полями этих зарядов. Общая работа, независимо от формы траектории, определяется исключительно местом расположения начальных и конечных точек. Понятие потенциальной энергии заряда Потенциальность, свойственная электростатическому полю, позволяет определять потенциальную энергию какого-либо заряда. Кроме того, с ее помощью более точно устанавливается работа по перемещению заряда в электрическом поле. Чтобы получить это значение, в пространстве необходимо выбрать определенную точку и потенциальную энергию заряда, размещаемого в данной точке. Заряд, помещаемый в любую точку, имеет потенциальную энергию, равной работе, совершаемой электростатическим полем, во время перемещения заряда из одной точки в другую. В физическом смысле, потенциальная энергия представляет собой значение для каждой из двух разных точек пространства. При этом, работа по перемещению заряда находится вне зависимости от путей его перемещения и выбранной точки. Потенциал электростатического поля в данной пространственной точке, равняется работе, совершаемой электрическими силами, когда единичный положительный заряд удаляется из этой точки в бесконечное пространство. Работа электрического поля

1.3. Работа электрического поля по перемещению электрического заряда. Движение заряженных частиц в электрических полях

Элементарная работа сил электрического поля по перемещению электрического заряда на dr,

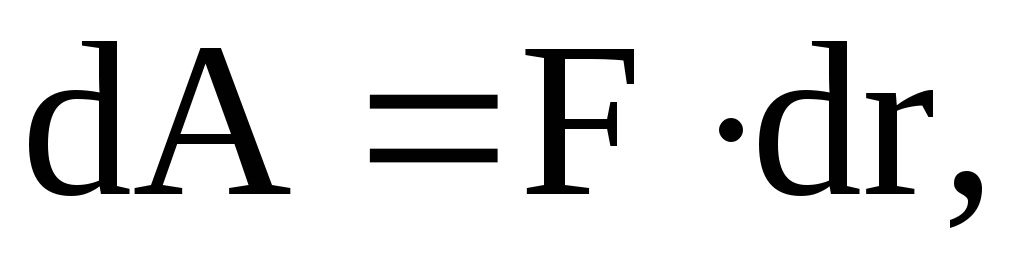
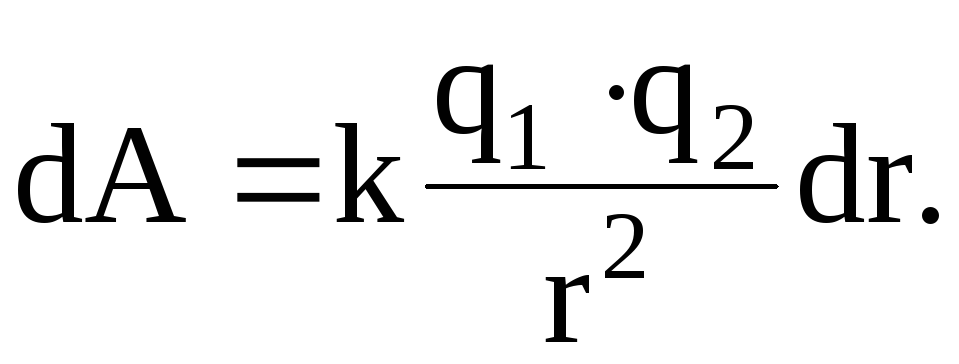
Если перемещение заряда q₂ было совершено из точки, находящейся на расстоянии r₁ от центра заряда, создающего поля в точку, расположенную на расстоянии r₂ от него, то работа, совершаемая силами электрического поля

.

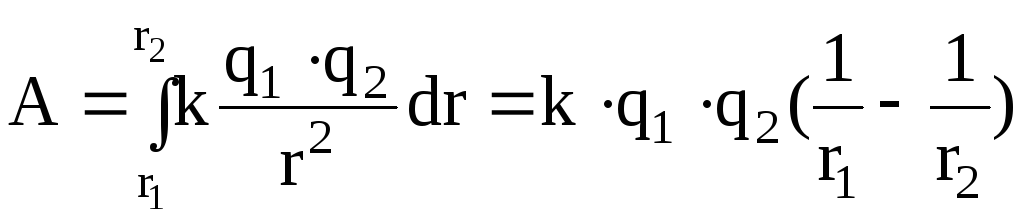Из выражения видно, что работа не зависит от траектории перемещения, а определяется только начальным и конечным положениями перемещаемого заряда. Кроме того, работа, по перемещению электрического заряда во внешнем электрическом поле по любому замкнутому пути ℓ , равна нулю, т.е.

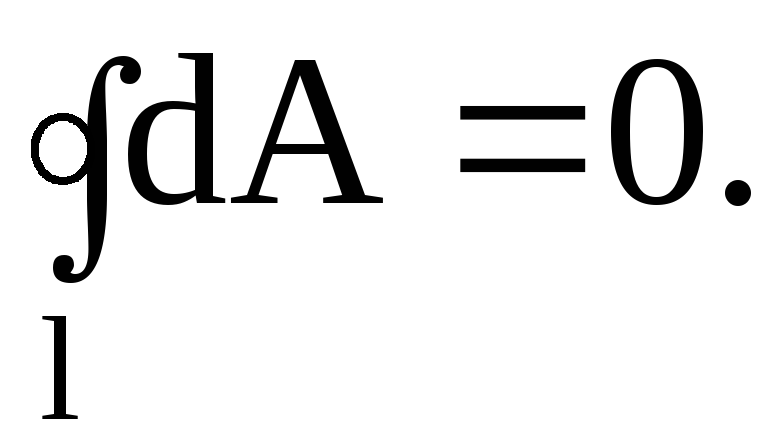
Это подтверждает, что электрическое поле является потенциальным, а электрические силы-консервативными.

Работа сил электрического поля совершается за счет изменения (уменьшение) потенциальной энергии

A=W_p1-W_p2=-DW_p.

Принято считать потенциальную энергию системы зарядов равной нулю в том случае, когда один из них удален от другого на бесконечность, т.е., например, W

p₂=W_p=0. Тогда W_p1=A.

Потенциальная энергия заряда, находящегося в электрическом поле другого заряда, измеряется работой, которую совершают силы электрического поля по удалению одного из зарядов из данной точки поля в бесконечность:

.

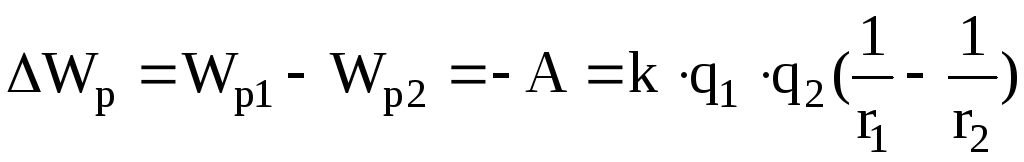при r₂=, W_p2=0,

В общем случае

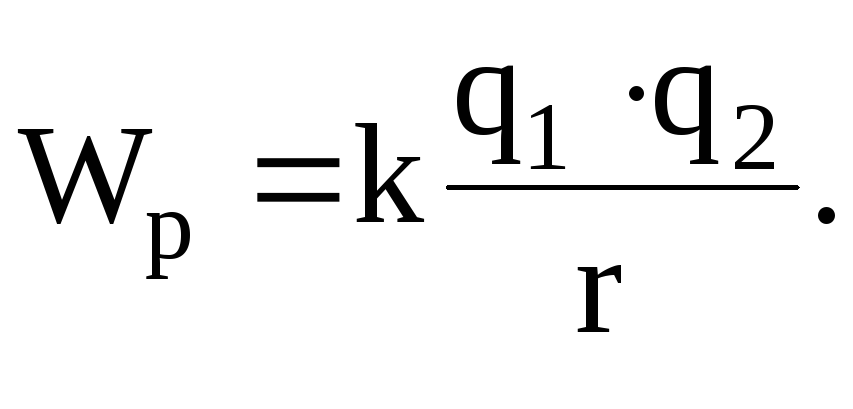
Разность потенциалов между двумя точками электрического поля, которое создано бесконечно длинным равномерно заряженным стержнем (цилиндром) с линейной плотностью заряда t:

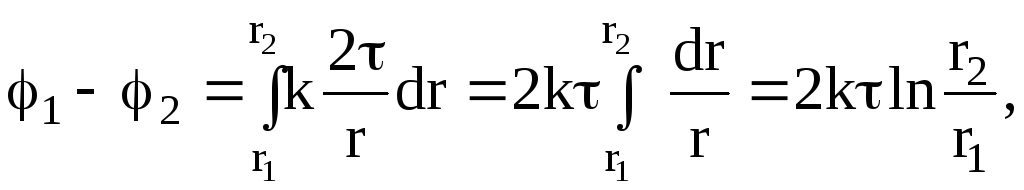
где r₁ и r₂-соответственно расстояние от оси стержня (цилиндра) до рассматриваемых точек электрического поля.

Разность потенциалов между двумя точками электрического поля, которое создано бесконечно длинной, равномерно заряженной плоскостью с поверхностной плотностью заряда s:

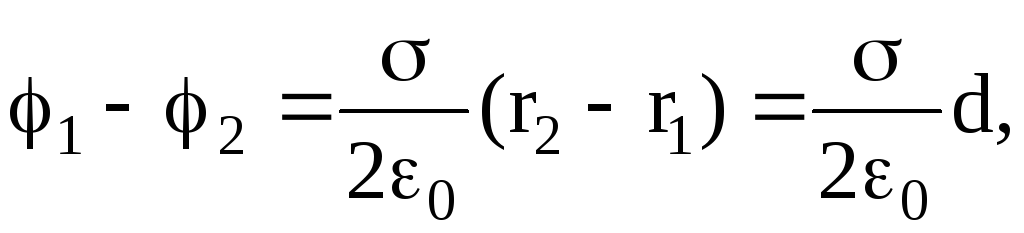
где r₂-r₁=d-расстояние между рассматриваемыми точками. Разность потенциалов между двумя точками поля, которое создано равномерно заряженной сферической поверхностью радиусом R, расстояние от рассматриваемых точек до центра сферы r₁>R и r₂>R:

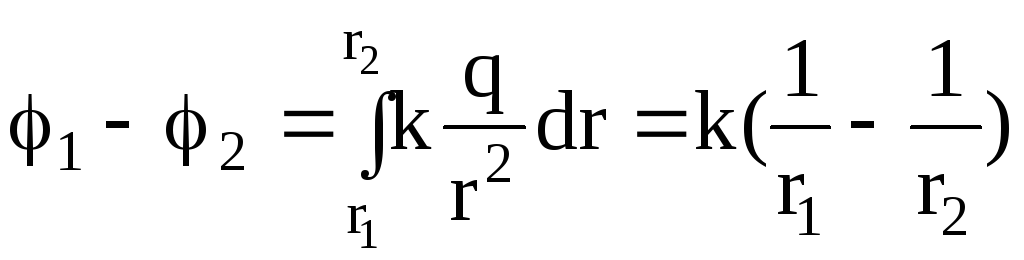
Если принять r₁₌r и r₂=

, то потенциал поля вне сферической поверхности что совпадает с ранее полученным соотношением для потенциала поля точечного заряда.

.

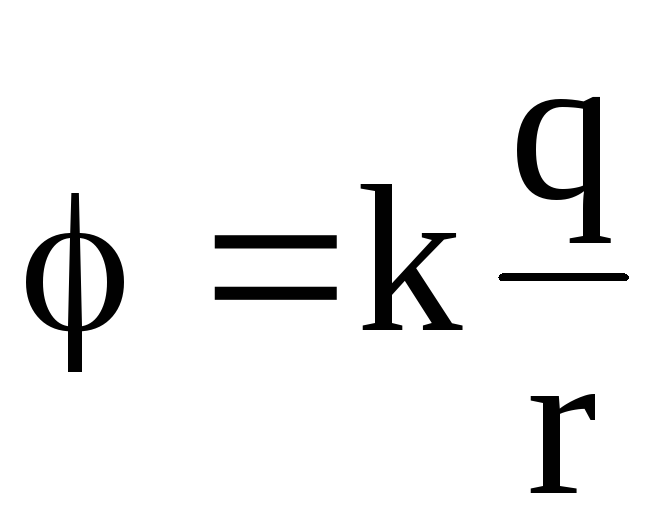Внутри сферической поверхности потенциал всюду одинаков и равен

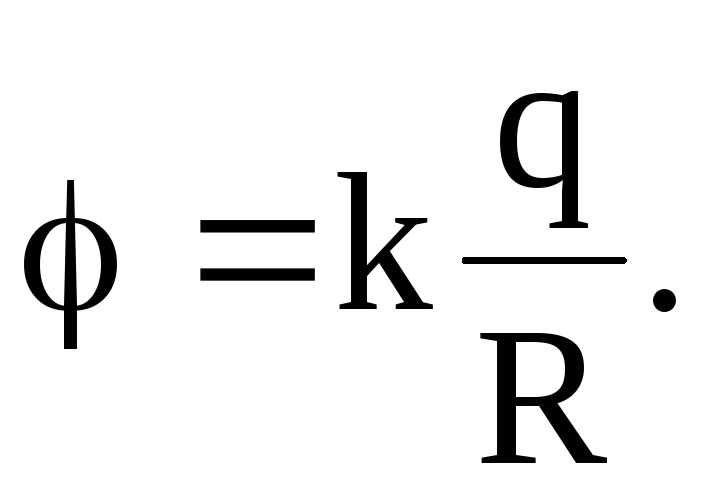
Разность потенциалов между двумя точками поля, которое создано равномерно заряженным по объёму шаром радиусом R, если расстояние от рассматриваемых точек поля до центра шара r₁>R и r₂

>R , объёмная плотность заряда r:

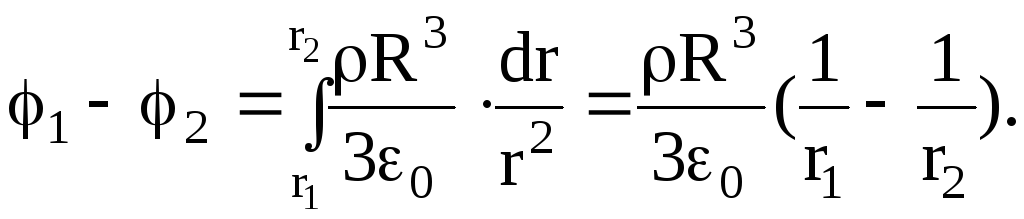
Если принять r₂=и r₁=R , то потенциал поля в этом случае:

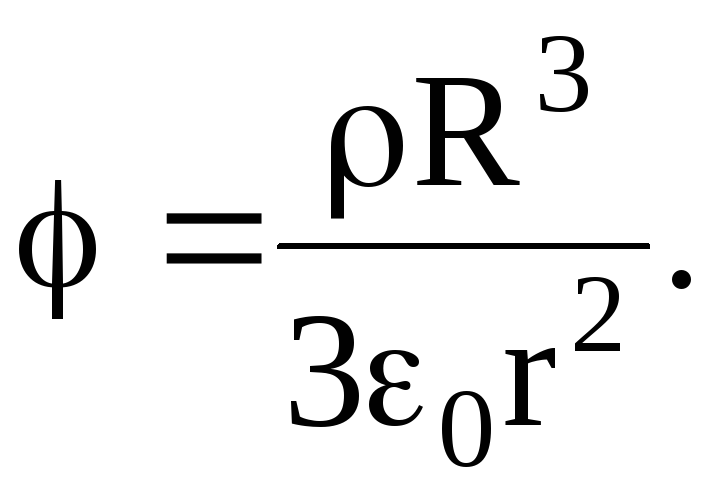
На поверхности шара (r=R)

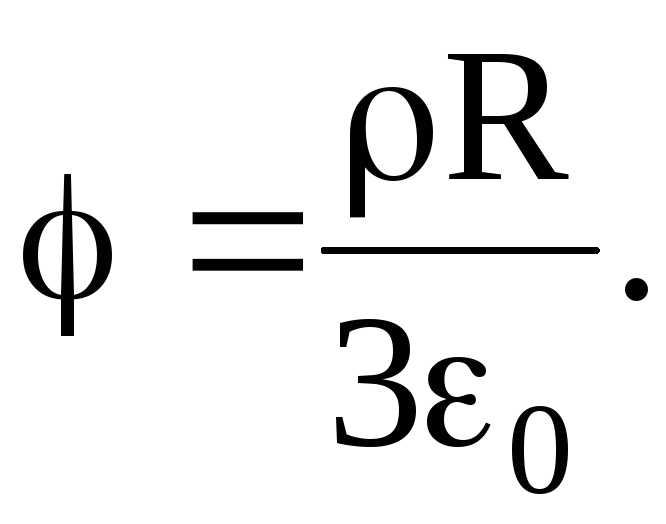
В центре шара (R=0): j=0.

Эквипотенциальные поверхности – поверхности равного потенциала.

Так как A=q(j

1–j₂), то при перемещении заряда по эквипотенциальной поверхности работа не совершается (A=0). Работа совершается лишь тогда, когда перемещение заряда происходит с одной эквипотенциальной поверхности на другую. В этом случае j₁¹j₂

A=q(j₁-j₂).

1.3.1. Примеры решения задач

1.3.1.1. Задача. Какой скоростью сближения должны обладать протоны, находясь на расстоянии 5 см, чтобы они могли сблизиться друг с другом до расстояния 10^-11 см?

Решение. При решении задачи можно рассматривать один протон неподвижным, а второй – движущимся по направлению к первому.

Так как между протонами существуют силы отталкивания, то движение второго протона будет замедленным. Его скорость уменьшится от искомой скорости v

1 до скорости v₂=0 в момент остановки протона. При этом будет уменьшаться и кинетическая энергия протона от начального значения T₁ до значения T₂=0 в момент остановки протона.

За счет кинетической энергии протона будет совершена работа против сил поля. На основании закона сохранения энергии

А=DT,

или

e(j₁-j₂)=T₂-T₁,(1)

где e – заряд протона,

j₁ и j₂ – потенциалы поля, созданного неподвижными

протонами в точках, соответствующих начальному и конечному положению движущегося протона.

Приняв во внимание, что T₂=0, и поменяв знаки в обеих частях равенства (1) на обратные, получим:

e (j₁-j₂)=T₁.

Подставим в формулу (2) выражения потенциала, создаваемого точечным зарядом, и кинетической энергии:

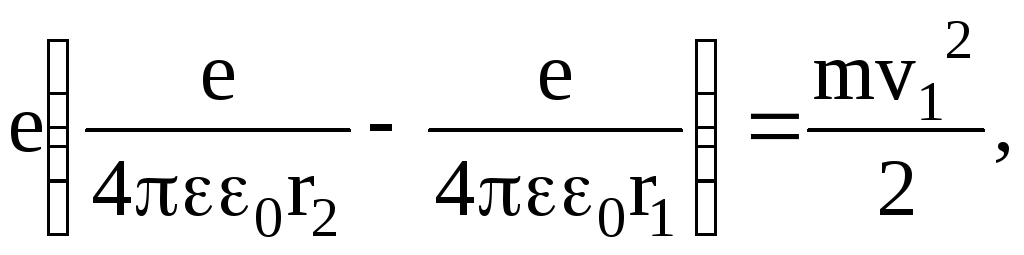
или

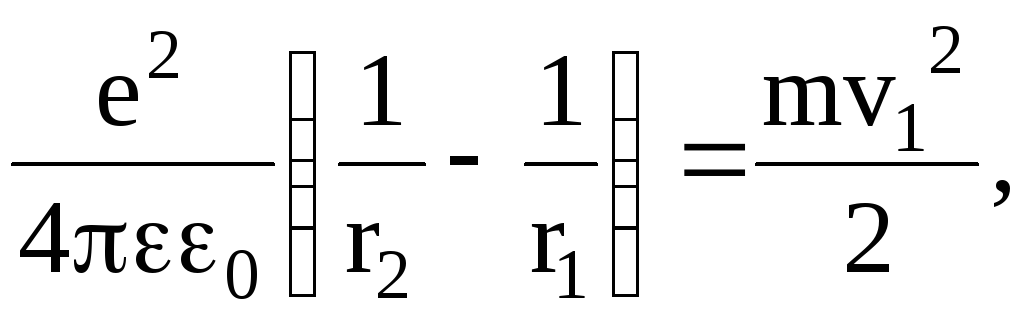
Отсюда

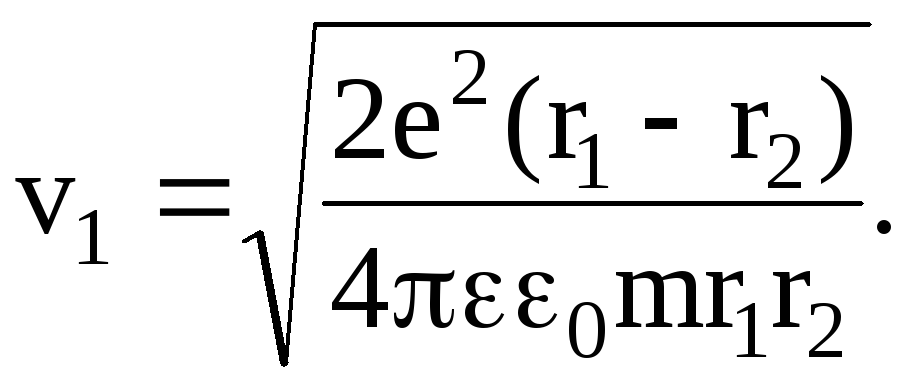
Подставив числовые значения, произведя вычисления, будем иметь:

v₁=1,66×10⁶ (м/с).

1.3.1.2. Задача. Определить начальную скорость v_o сближения протонов, находящихся на достаточно большом расстоянии друг от друга, если минимальное расстояние r_мин, на которое они могут сблизиться, равно 10^-11 см.

Решение. Между двумя протонами действуют силы отталкивания, вследствие чего движение протонов будет замедленным. Поэтому задачу можно решить как в инерциальной системе отсчета (связанной с центром масс двух протонов), так и в неинерциальной (связанной с одним из ускоренно движущихся протонов). Во втором случае законы Ньютона не могут быть применимыми. Применение же принципа Даламбера затруднительно из-за того, что ускорение системы будет переменным. Поэтому удобно рассмотреть задачу в инерциальной системе отсчета.

Поместим начало координат в центр масс протонов. Поскольку мы имеем дело с одинаковыми частицами, то центр масс будет находиться в точке, делящей пополам отрезок, соединяющий частицы. Относительно центра масс частицы будут иметь в любой момент времени одинаковые по абсолютной величине скорости v₁ и v₂. Скорость каждой частицы будет равна половине скорости сближения

v₁=v₂=v/2. (1)

Для решения задачи применим закон сохранения энергии, согласно которому полная механическая энергия E изолированной системы постоянна, т.е.

E=T+П,

где T – кинетическая энергия;

П – потенциальная энергия.

Выразим потенциальную энергию в начальный и конечный моменты движения.

В начальный момент, согласно условию задачи, протоны находились на большом расстоянии, поэтому потенциальной энергией можно пренебречь. Следовательно, для начального момента полная энергия будет равна кинетической энергии T₀ протонов, т.е.

E=T₀. (2)

В конечный момент, когда протоны максимально сблизятся, скорость и кинетическая энергия равны нулю, а полная энергия E будет равна потенциальной энергии П_кон:

E=П_кон. (3)

Приравняв правые части равенств (2) и (3), получим

T₀=П_кон. (4)

Кинетическая энергия равна сумме кинетических энергий протонов

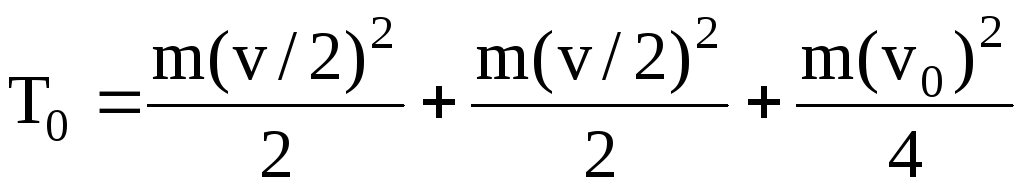. (5)

Потенциальная энергия системы двух зарядов q₁ и q₂, находящихся в вакууме, определяется по формуле:

где r – расстояние между зарядами.

Воспользовавшись этой формулой, получим

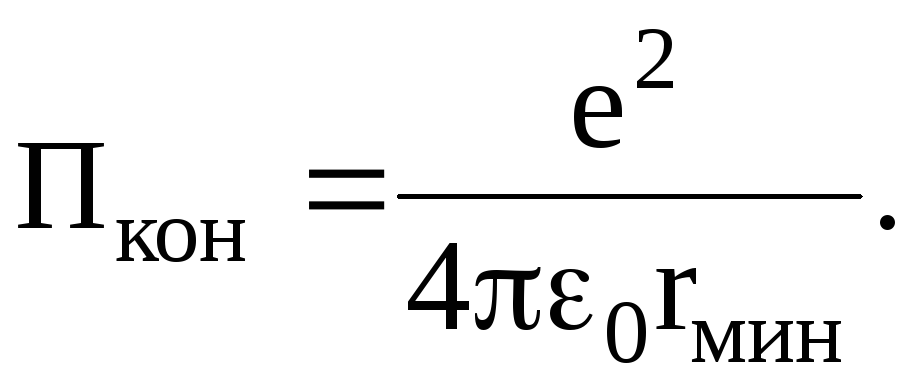(6)

С учетом выражений (5) и (6) формула (4) примет вид

.

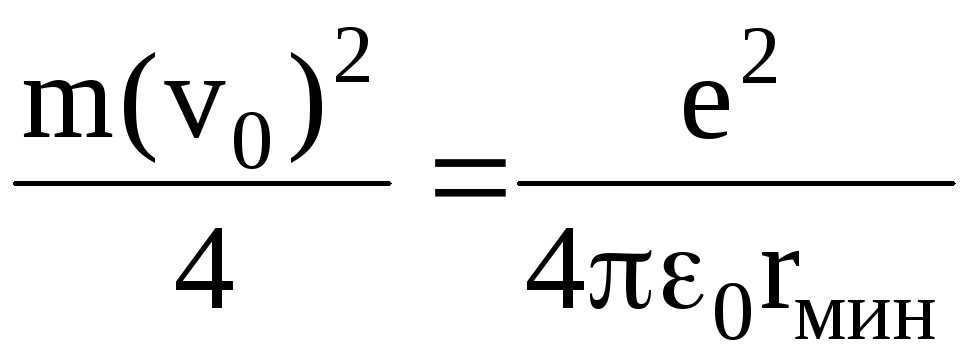Откуда

.

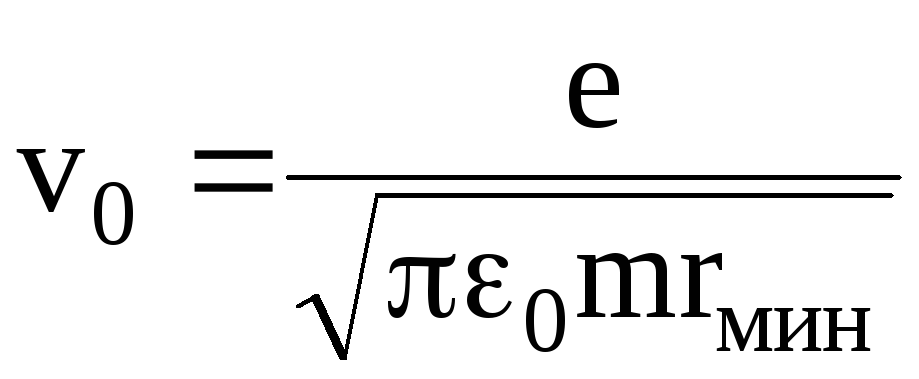Подставив числовые значения, получим

v₀= 2,35×10⁶ (м/с).

1.3.1.3. Задача. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью v₁=10⁶ м/с, чтобы скорость его возросла в n=2 раза.

Решение. Ускоряющую разность потенциалов можно найти, вычислив работу A сил электростатического поля. Эта работа определяется произведением заряда электрона e на разность потенциалов U:

A=eU. (1)

Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:

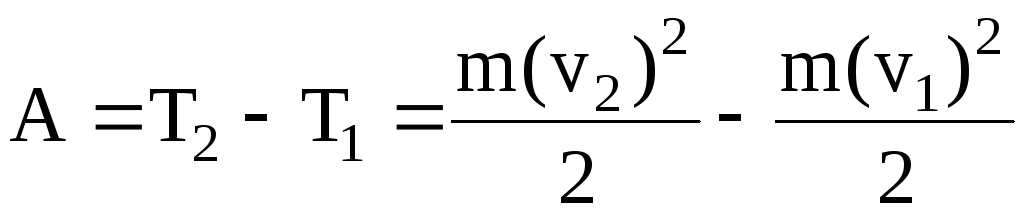, (2)

где T₁ и T₂ – кинетические энергии электрона до и после прохождения ускоряющего поля;

m-масса электрона;

v₁ и v₂ – начальная и конечная его скорости.

Приравняв правые части равенств (1) и (2), получим

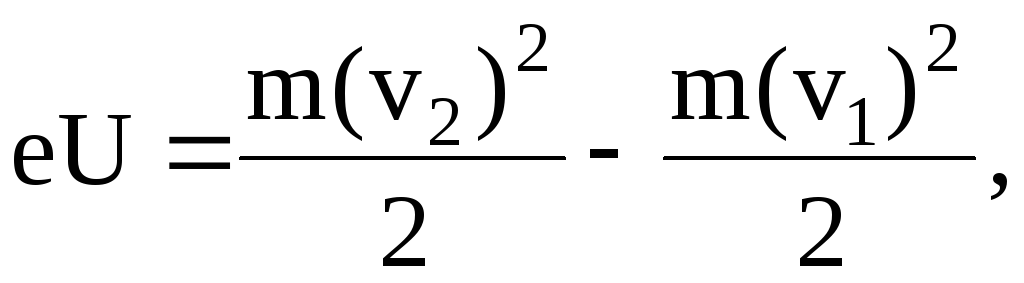
или

где n=v₂/v₁.

Отсюда искомая разность потенциалов

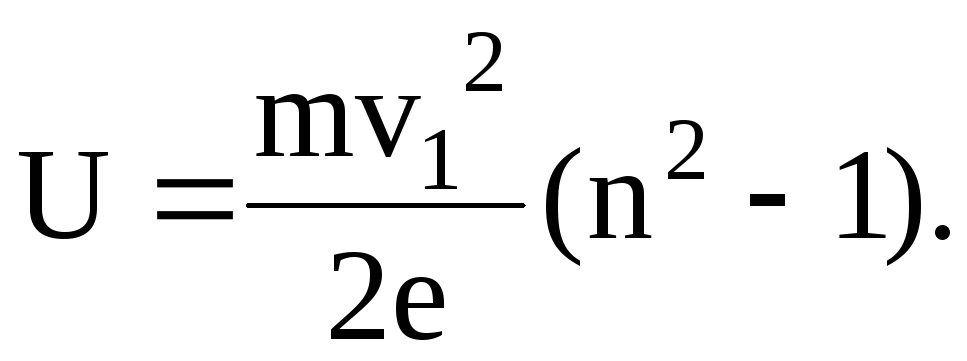(3)

Подставив численные значения физических величин и выполнив вычисления, будем иметь:

U=8,53 (В).

1.3.1.4. Задача. Электрическое поле создается двумя зарядами Q₁=4 мкКл и Q₂=-2 мкКл, находящимися на расстоянии а=0,1 м друг от друга. Определить работу А_1,2 сил поля по перемещению заряда Q=50 нКл из точки 1 в точку 2.

Решение. Для определения работы А_1,2 сил поля воспользуемся соотношением

А_1,2=Q(j₁ – j₂).

Применяя принцип суперпозиции электрических полей, определим потенциалы j₁ и j₂ точек 1 и 2 поля:

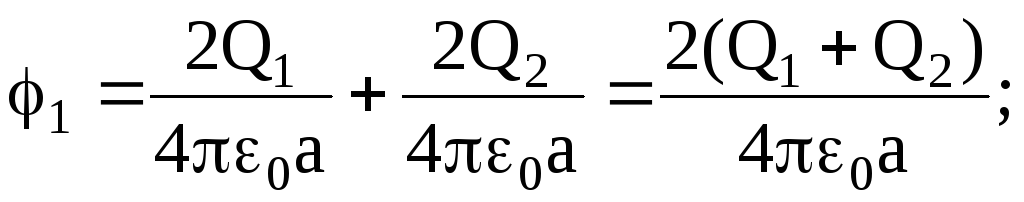
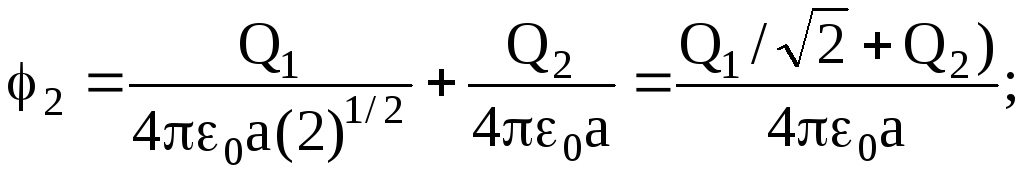
Тогда

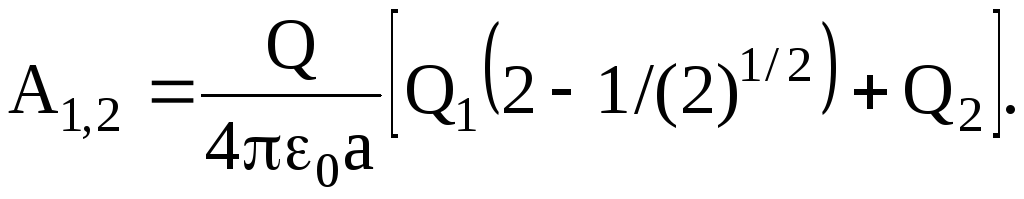
Подставив числовые значения величин в единицах системы СИ, произведя вычисления, получим

А_1,2=14,3 (мДж).

1.3.1.5. Задача. С поверхности бесконечного равномерно заряженного (t=50 нКл/м) прямого цилиндра вылетает a-частица (v₀=0). Определить кинетическую энергию T₂ a-частицы (кэВ) в точке на расстоянии 8R от поверхности цилиндра.

Решение. Так как силы электростатического поля являются консервативными, то для определения кинетической энергии a-частицы в заданной точке воспользуемся законом сохранения энергии, записанном в виде

E₁=E₂,

где E₁ – полная энергия -частицы на поверхности цилиндра;

E₂-полная энергия -частицы в заданной точке.

Так как

E₁=T₁+U₁; E₂=T₂+U₂,

где T₁ и T₂ – кинетические энергии a-частицы в соответствующих состояниях;

U₁ и U₂ – потенциальные энергии -частицы в соответствующих состояниях.

Учитывая, что T₁=0 (v₀=0), можно записать

U₁=T₂+U₂,

откуда

T₂=U₁ – U₂=Q(j₁ – j₂),

где Q – заряд a-частицы;

j₁ и j₂— потенциалы на поверхности цилиндра и в рассматриваемой точке.

Используя решение примера (1.5), для разности потенциалов, будем иметь

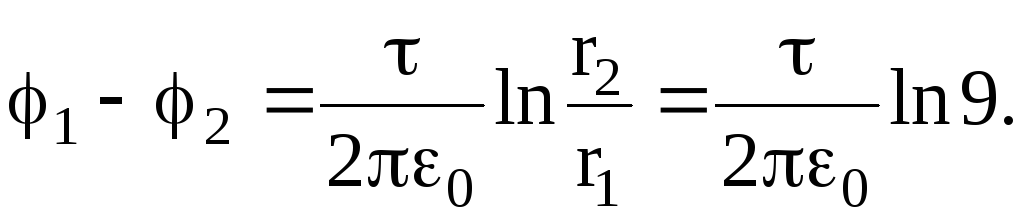
Тогда

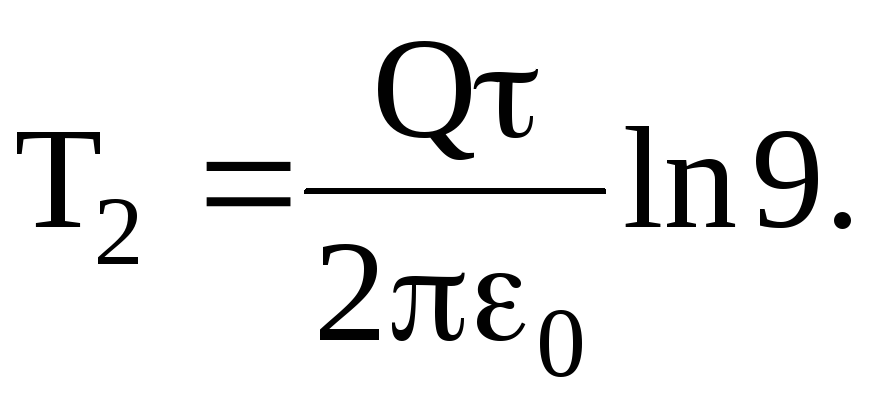
Подставив все величины в единицах системы СИ, произведя вычисления, получим

T₂=3,96 (кэВ).

1.3.1.6. Задача. Две частицы, обладающие массами m₁, m₂ и зарядами q₁ и q₂, движутся навстречу друг другу, имея вдалеке относительную скорость vотн. На какое минимальное расстояние сблизятся частицы?

Решение. Эту задачу можно решить тремя способами, различающимися выбором системы отсчета:

1. Рассмотрим движение частиц в какой-либо «лабораторной» системе отсчета, например связанной с Землей. Полагая систему двух заряженных частиц изолированной, воспользуемся законом сохранения энергии

W=const, (1)

где W-полная энергия частиц, которые в каждый момент времени обладают кинетической энергией, а также потенциальной знергией кулоновского взаимодействия.

Когда частицы находятся вдалеке друг от друга, то, как это следует из формулы

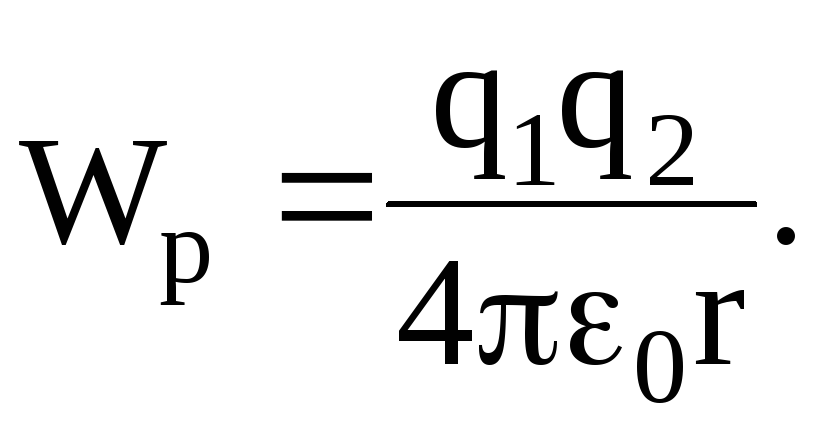
их потенциальной энергией можно пренебречь.

Тогда полная энергия системы

W₁₌m₁ v₁ ²/2+m₂v₂²/2, (2)

где v₁, v₂-скорости частиц в выбранной системе отсчета.

Так как векторы v₁ и v₂ направлены противоположно, то значения v₁ и v₂ связаны с заданной величиной v_отн соотношением

v_отн=ôv₁-v₂ô=v₁+v₂. (3)

При сближении частиц потенциальная энергия их кулоновского взаимодействия (отталкивания), будучи величиной положительной, начнет увеличиваться. Следовательно, суммарная кинетическая энергия частиц станет уменьшаться. Частицы не могут, как угодно близко подойти друг к другу, иначе их потенциальная энергия оказалась бы больше полной энергии W₁, что противоречит условия (1).

При наибольшем сближении частиц, когда расстояние между ними равно r_мин, полная энергия

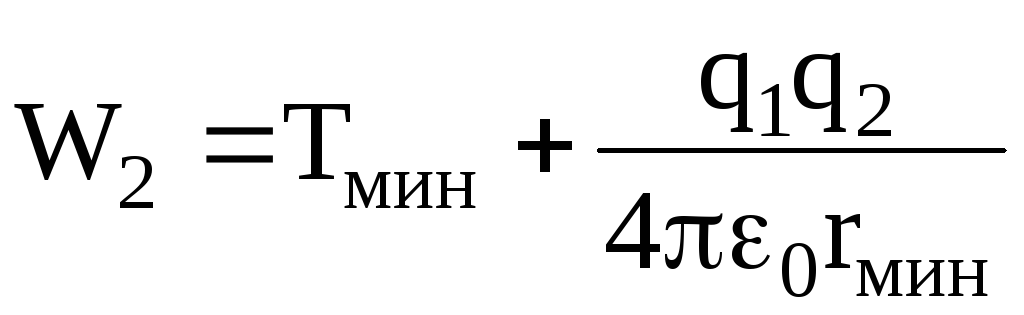. (4)

Чтобы найти кинетическую энергию T_мин системы, учтем, что в момент наибольшего сближения частиц их скорости будут одинаковыми: v_1мин=v_2мин=v. Действительно, когда скорости частиц неодинаковые, расстояние между ними растет или уменьшается и, следовательно, не является минимальным.

Применив к системе закон сохранения импульса, запишем:

m₁ v₁ – m₂v₂=(m₁+m₂)v, (5)

где (m₁ v₁-m₂v₂)-импульс удаленных частиц;

(m₁+m₂)v-импульс системы при наибольшем сближении частиц.

При этом вектор v предположительно выбран совпадающим по направлению с вектором v₁ (очевидно, при подсчете кинетической энергии направление скорости несущественно). Из уравнения (5) имеем

v=(m₁ v₁ – m₂v₂)/(m₁+m₂).

Тогда для величины T_мин, получим

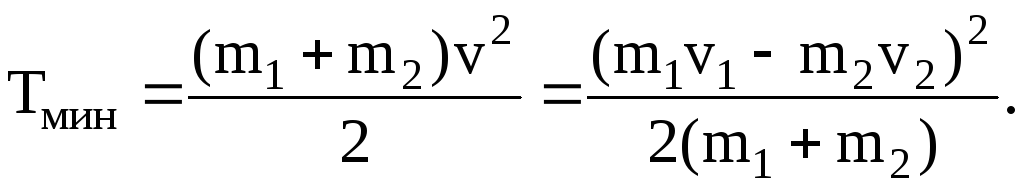
Подставив это значение T_мин в формулу (4), приравняв на основании закона сохранения энергии правые части формул (2) и (4), а также учитывая соотношение (3), найдем

2. Выберем систему отсчета, связанную с центром инерции системы двух частиц. Пусть скорости частиц в этой системе отсчета равны v₁ ‘ и v₂‘. Сначала выразим каждую из величин v₁ ‘ и v₂‘ через относительную скорость v_отн. Так как частицы движутся навстречу друг другу, то

v_отн=v₁ ‘+v₂‘. (1)

Поскольку в данной системе отсчета скорость центра инерции частиц равна нулю, то, согласно утверждению, что импульс системы материальных точек равен произведению массы M системы на скорость движения v_с ее центра инерции, суммарный импульс частиц p=0. Тогда, применив к системе частиц закон сохранения импульса и учитывая противополжные направления векторов v₁ и v₂, получим

m₁ v₁ ‘ – m₂v₂‘=0. (2)

Решив систему (1) и (2) относительно v₁ ‘ и v₂‘, найдем:

v₁‘=[m₂/(m₁+m₂)]v_отн; v₂‘=[m₁/(m₁+m₂)]v_отн.

Полная энергия системы частиц в начальный момент равна сумме их кинетических энергий. В момент наибольшего сближения частицы имеют одинаковые по модулю и направлению скорости. При этом каждая из скоростей равна нулю, так как в противном случае оказалось бы нарушенным условие p=0. Следовательно, частицы будут сближаться до тех пор, пока вся кинетическая энергия не превратится в энергию кулоновского взаимодействия. Таким образом,

.

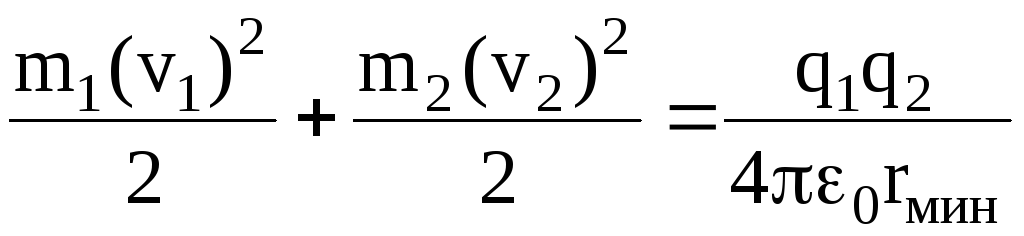Подставив сюда найденные значения v₁‘ и v₂‘, получим

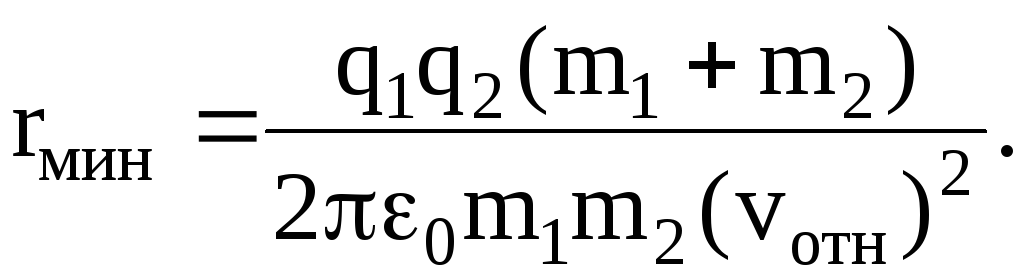
3. Выберем систему отсчета, движущуюся поступательно вместе с одной из заряженных частиц, например с первой. Эта система отсчета является неинерциальной. В ней первая частица неподвижна, а вторая движется навстречу первой с начальной скоростью vотн. Теперь начальная энергия системы частиц равна кинетической энергии второй частицы:

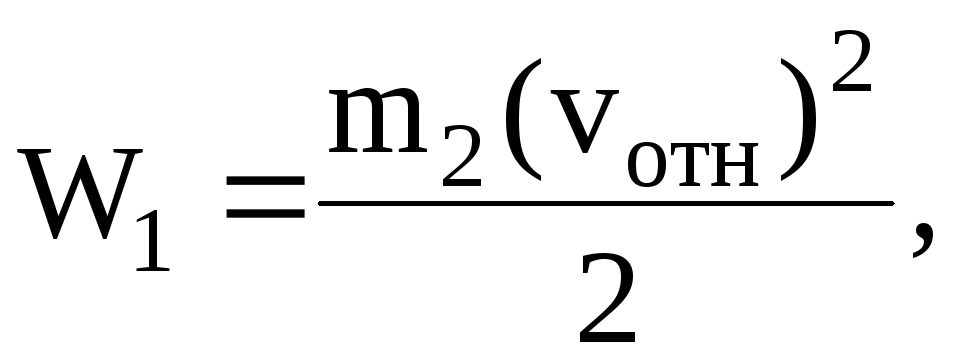(1)

а конечная энергия (при r=r_мин) равна лишь потенциальной энергии кулоновского взаимодействия, т.е.

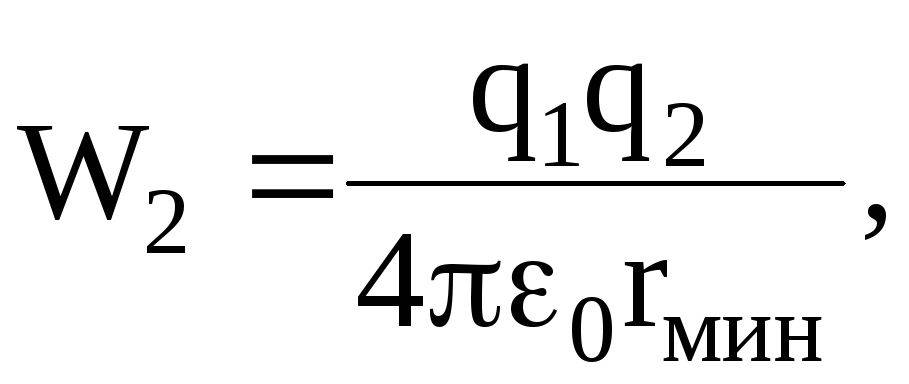(2)

поскольку в момент наибольшего сближения вторая частица имеет нулевую скорость.

В данном случае система взаимодействующих частиц является незамкнутой, так как на нее действуют силы инерции, которые следует считать внешними по отношению к системе. Поэтому ни полный импульс, ни полная энергия системы частиц в неинерциальной системе отсчета не сохраняются.

Согласно закону сохранения энергии, изменение энергии системы, должно быть равно работе A силы инерции F_ин, действующей на частицу m₂ во время ее приближения к частице m₁:

W₂-W₁=A, (3)

и задача сводится к нахождению величины A. Для силы инерции, имеем

F_ин=-m₂a₁, (4)

где a₁-ускорение частицы m₁ в инерциальной системе отсчета.

Это ускорение можно определить с помощью второго закона Ньютона и закона Кулона:

.

Поскольку ускорение a₁ первой частицы, обусловленное кулоновской силой отталкивания, направлено в одну сторону, то сила инерции, как это следует из (4), направлена в другую и равна

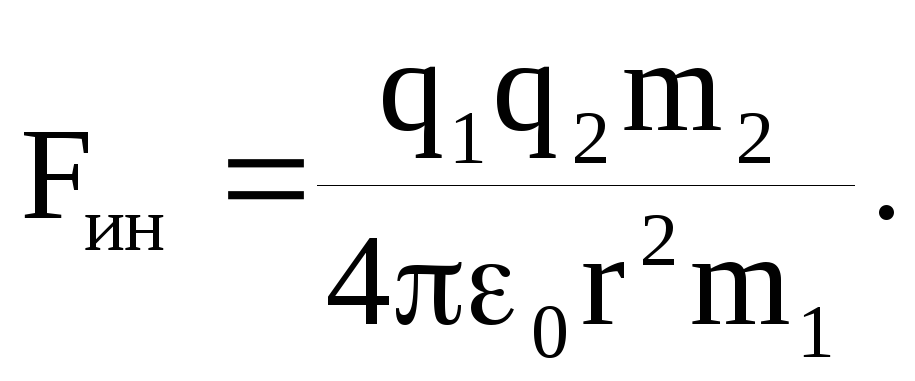(5)

Так как частица m₂ перемещается в сторону противоположную направлению силы инерции, то сила инерции совершает над ней отрицательную работу, значение которой найдем, учитывая соотношение (5):

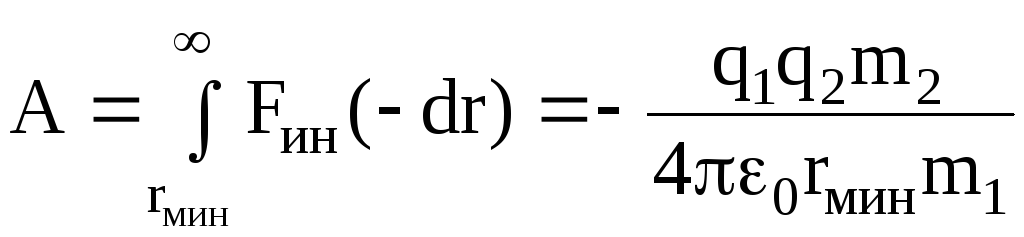. (6)

Подставив в (3) значения W₁, W₂, A из уравнений (1), (2), (6), найдем

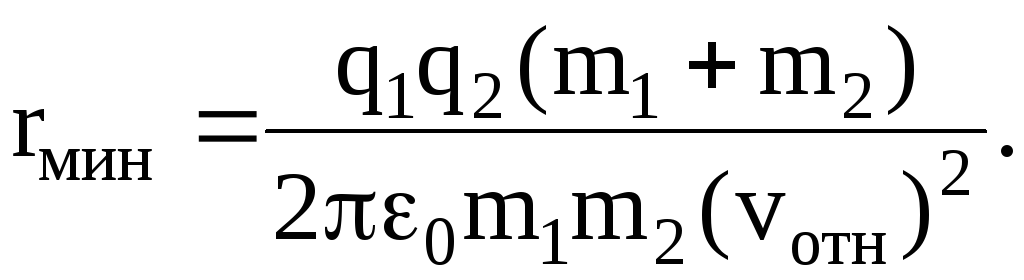
1.4. Проводники и диэлектрики в электрическом поле. Электроемкость. Конденсаторы и их емкость. Энергия электрического поля

3. Работа электрического поля по перемещению заряда на замкнутом пути. Циркуляция напряженности. Эдс

Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила  F = q E. При перемещении заряда на отрезке dl силами поля совершается работа

dA = F dl = q E dl cos (E, dl).

При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна

 .

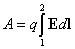Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого 

 .

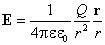Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:

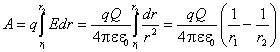
Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

(13.18)

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

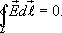
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил в источникахпостоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительногозаряда вдоль контура.

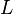ЭДС можно выразить через напряжённость электрического поля сторонних сил (). В замкнутом контуре () тогда ЭДС будет равна:

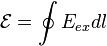, где 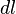— элемент длины контура.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

Источник ЭДС (идеальный источник напряжения) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.

В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.

4. Электроемкость. Конденсатор. Емкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия электрического поля в вакууме и в диэлектрике.

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В Международной системе единиц (СИ) ёмкость измеряется в фарадах. В системе СГС в сантиметрах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводникибесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид

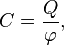 где 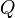—заряд, 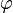— потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):

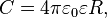
где ε₀ — электрическая постоянная, ε — относительная диэлектрическая проницаемость.

Известно, что 

Так как , то подставив сюда найденный, получим, что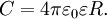

Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омическойпроводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкции состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного токаон проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.

С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом

,

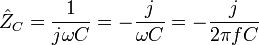где j — мнимая единица, ω — циклическая частота (рад/с) протекающего синусоидального тока, f — частота в Гц, C — ёмкость конденсатора (фарад). Отсюда также следует, что реактивное сопротивление конденсатора равно: 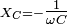. Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).

При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственнойиндуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью C, собственной индуктивностью L_C и сопротивлением потерь R_n.

Резонансная частота конденсатора равна

При f >f_p конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f <f_p, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.

Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:

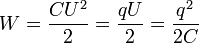
где U — напряжение (разность потенциалов), до которого заряжен конденсатор.

Работа сил электростатического при перемещении заряда

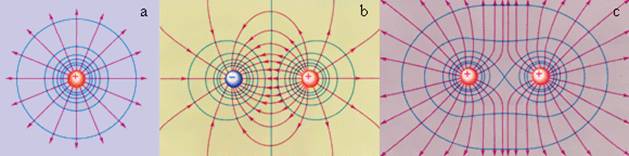
При перемещении точечного электрического заряда q_пр электростатического поля из одной точки в другую на расстояние dS элементарная работа, совершаемая силой F, будет равна:

Где α это угол между направлением движения и силой F.

В случае, когда работа совершается силами поля, то dA>0, а если внешними силами, то dA<0. Проинтегрировав последнее выражение, получим выражение работы против сил поля при перемещении точечного заряда q_пр из точки a в точку b:

Где F = Eq_пр – кулоновская сила, которая действует на «пробный» заряд q_пр в каждой точке поля с напряженностью Е. В токам случае работа будет равна:

Предположим, что от пути перемещения или интегрирования точечного заряда будет зависеть результат интегрирования. Но если бы интеграл (формула 2) зависел только от пути, то можно было бы перемещать точечный заряд с точки а в точку b по пути где А меньше, а возвращать по пути где А больше, и в итоге «получить» энергию больше, чем было затрачено в первом случае. Однако «извлекать» энергию из поля можно только при условии перемещения зарядов, создающих само поле, то есть электрическое поле тоже будет изменяться. Но, создающие электрическое поле заряды в электростатике неподвижны, что делает невозможным извлечение из поля энергии при условии, что в электростатике закон сохранения энергии справедлив.

Теперь давайте докажем, что совершаемая при перемещении заряда работа в электростатическом поле зависит только от конечного и начального положений электрического заряда.

Пусть «пробный» заряд q_пр перемещается в поле заряда q из точки а, которая удалена на расстояние r₁ от q, в точку b, удаленную на расстояние r₂ от q, по пути аа^/b (рисунок ниже а)):

Так как поле точечного заряда радиально, то на участке аа^/ работа не производится, поскольку перемещение осуществляется перпендикулярно вектору Е. Отсюда следует, что работа по переносу «пробного» заряда от точки а к точке b будет равна:

Теперь выберем более сложный путь движения точечного заряда (рисунок выше б)).  Траекторией его движения будет то радиус, то дуга окружности. Каждый раз, когда путь будет пролегать по радиусу, интегрируется dr/r². Интеграл берется в пределах от r_a до r_a^/  по первому радиальному участку, по следующему от r_a^/ до r_a^// и так далее. Общий интеграл в пределах от r₁ до r₂ будет равна сумме интегралов, то есть ответ получится тот же, что и в первом случае. Отсюда следует, что и для любого пути, составленного из произвольного числа участков такого же вида, получится аналогичный результат. Расчет перемещения заряда в электростатическом поле для любых траекторий более сложен, но приводит к аналогичному результату, а именно:

Где интеграл берется от начальной точки a до конечной точки b по любому пути.

Работа электрического поля по перемещению заряда

На любой заряд, который находится в электрическом поле, воздействует сила. В связи с этим при передвижении заряда в поле происходит определенная работа электрического поля. Как же произвести расчет этой работы?

Работа электрического поля состоит в переносе электрозарядов вдоль проводника. Она будет равняться произведению напряжения, силы тока и времени, потраченного на работу.

Применив формулу закона Ома, мы можем получить несколько различных вариантов формулы для проведения подсчета работы тока:

A = U˖I˖t = I²R˖t = (U²/R)˖t.

В соответствии с законом сохранения энергии работа электрического поля равняется изменению энергии отдельно взятого участка цепи, в связи с чем энергия, выделяемая проводником, будет равняться работе тока.

Выразим в системе СИ:

[А] = В˖А˖с = Вт˖с = Дж

1 кВт˖час = 3600000 Дж.

Проведем опыт. Рассмотрим передвижение заряда в одноименном поле, которое образовано двумя параллельно расположенными пластинами А и В и заряженными разноименными зарядами. В таком поле силовые линии на всем своем протяжении перпендикулярны этим пластинам, и когда пластина А будет заряжена положительно, тогда напряженность поля Е будет направлена от А к В.

Предположим, что позитивный заряд q передвинулся из точки a в точку b по произвольному пути ab = s.

Так как сила, которая действует на заряд, который находится в поле, будет равняться F = qE, то работа, совершенная при передвижении заряда в поле согласно заданному пути, определится по равенству:

A = Fs cos α, или A = qFs cos α.

Но s cos α = d, где d – дистанция между пластинами.

Отсюда следует: A = qEd.

Допустим, теперь заряд q переместится из a и b по сути acb. Работа электрического поля, совершенная на этом пути, равняется сумме работ, совершенных на отдельных участках его: ac = s₁, cb = s₂, т.е.

A = qEs₁ cos α₁ + qEs₂ cos α₂,

A = qE(s₁ cos α₁ + s₂ cos α₂,).

Но s₁ cos α₁ + s₂ cos α₂ = d, а значит, и в данном случае A = qEd.

Кроме того, предположим, что заряд q передвигается из a в b по произвольной кривой линии. Чтобы подсчитать работу, совершенную на данном криволинейном пути, необходимо расслоить поле между пластинами А и В некоторым количеством параллельных плоскостей, которые будут настолько близки одна к другой, что отдельные участки пути s между данными плоскостями можно будет считать прямыми.

В таком случае работа электрического поля, произведенная на каждом из данных отрезков пути, будет равняться A₁ = qEd₁, где d₁ — дистанция между двумя сопредельными плоскостями. А полная работа на всем пути d будет равняться произведению qE и суммы расстояний d₁, равной d. Таким образом, и в результате криволинейного пути совершенная работа будет равняться A = qEd.

Примеры, рассмотренные нами, показывают, что работа электрического поля по перемещению заряда из какой-либо точки в другую не зависит от формы пути передвижения, а зависит исключительно от положения данных точек в поле.

Кроме того, мы знаем, что работа, которая совершается силой тяжести при передвижении тела по наклонной плоскости, имеющей длину l, будет равняться работе, которую совершает тело при падении с высоты h, и высоте наклонной плоскости. Значит, работа силы тяжести или, в частности, работа при передвижении тела в поле тяжести, тоже не зависит от формы пути, а зависит только от разности высот первой и последней точек пути.

Так можно доказать, что таким важным свойством может обладать не только однородное, а и всякое электрическое поле. Похожим свойством обладает и сила тяжести.

Работа электростатического поля по перемещению точечного заряда из одной точки в другую определяется линейным интегралом:

A₁₂ = ∫ L₁₂q (Edl),

где L₁₂ – траектория движения заряда, dl – бесконечно малое перемещение вдоль траектории. Если контур замкнутый, то для интеграла используется символ ∫; в этом случае предполагается, что выбрано направление обхода контура.

Работа электростатических сил не зависит от формы пути, а только лишь от координат первой и последней точек перемещения. Следовательно, силы поля консервативны, а само поле – потенциально. Стоит отметить, что работа любой консервативной силы по замкнутому пути будет равняться нулю.

Работа по перемещению заряда в электростатическом поле (задачи)

Задачи, связанные связанные с работой электрического поля, угадываются по условию движения заряда в самом поле. Чаще всего нам заданы начальные/конечные параметры системы (потенциалы, точки начала/конца движения, перемещение тела). При этом важно выяснить какое поле предложено в задаче. В случае:

(1)

• неоднородного поля (задан источник поля — точечный заряд, шар)

(2)

Общим для обоих типов полей является нахождение работы электростатического поля из теоремы об изменении кинетической энергии:

(3)

• — работа по перемещению заряда,
• — изменение кинетической энергии тела.

1. Отрицательный заряд, модуль которого…
2. Точечный заряд перемещают в однородном электростатическом поле…
3. Работа, совершённая силами электростатического поля при переносе…
4. Электрон и протон из состояния покоя ускоряются в одном…
5. Какую работу совершают электрические силы, перемещая заряд…
6. В электронных часах за сутки перемещается заряд…
7. В электроприборе при напряжении за одну минуту перемещается заряд…
8. С помощью какого напряжения можно разогнать неподвижный электрон…
9. Силы электростатического поля совершают работу…
10. Электрон из состояния покоя ускоряется в электростатическом поле…
11. Два маленьких шарика, электрические заряды которых находятся…

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

Работа в электрическом поле. Потенциал

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении 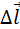  равна (рис. 1.4.1):

Рисунок 1.4.1. Работа электрических сил при малом перемещении  заряда q

Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

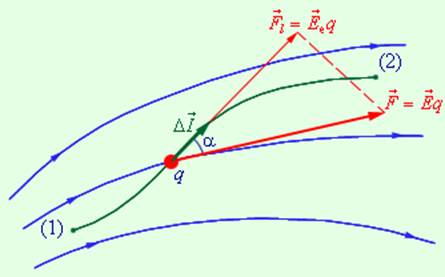
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение 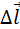. Работа ΔA кулоновских сил на этом перемещении равна

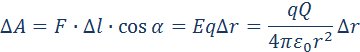
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r₁ до r = r₂, то можно получить

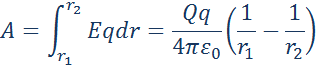
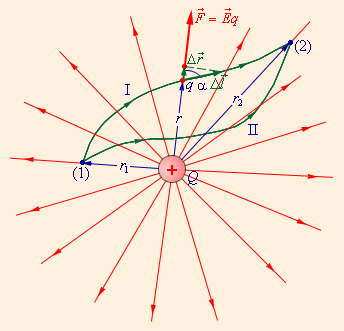Рисунок 1.4.2. Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории

Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.

Если электростатическое поле создается совокупностью точечных зарядов 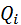, то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ  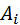кулоновских полей точечных зарядов:  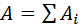 Так как каждый член суммы  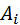не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.

Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.

Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A₁₀, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):

(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)

Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.

Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).

A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2.

Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

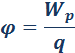
Потенциал φ является энергетической характеристикой электростатического поля.

Работа A₁₂ по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ₁ – φ₂) начальной и конечной точек:

A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2).

В Международной системе единиц (СИ) единицей потенциала является Вольт (В).

1 В = 1 Дж / 1 Кл

Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

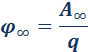
Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.

Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

Рисунок 1.4.3. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

Если пробный заряд q совершил малое перемещение 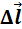 вдоль силовой линии из точки (1) в точку (2), то можно записать:

ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ,

где Δφ = φ₁ – φ₂ – изменение потенциала. Отсюда следует

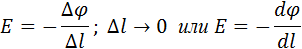
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:

φ = φ₁ + φ₂ + φ₃ + …