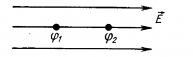
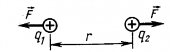
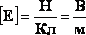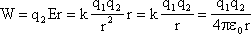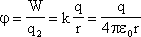Формула работы электростатического взаимодействия двух точечных зарядов.
⇐ ПредыдущаяСтр 5 из 11Следующая ⇒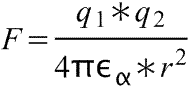 где
где
F — сила взаимодействия двух точечных зарядов
q1, q2— величины зарядов
εα — абсолютная диэлектрическая проницаемость среды
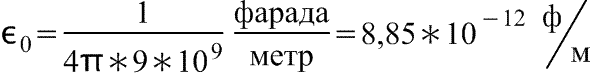 r — расстояние между точечными зарядами
r — расстояние между точечными зарядами
Консервативность электростатического взаимодействия.
Вычислим работу, которую совершает электростатическое поле, созданное зарядом q´ по перемещению заряда q из точки 1 в точку 2.
Работа на пути dl равна:
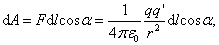
где d
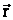 при перемещении на dl;
при перемещении на dl; 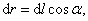 т. е.
т. е.
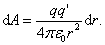
Тогда полная работа при перемещении q´ из точки 1 в точку 2 равна интегралу:
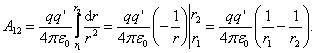 |
Работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения
Потенциал электростатического поля.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду: 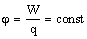
— энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Потенциал электростатического поля точечного заряда.
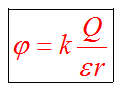

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле. 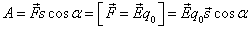
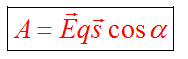

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Связь напряженности электростатического поля с потенциалом.

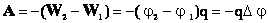
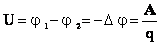
Электроемкость проводника и конденсатора.
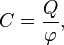 Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд
Формула электроемкости плоского конденсатора.
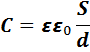
Энергия электрического поля.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. 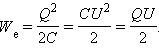
2.5.
Электрический ток.
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц
Условия возникновения и существования электрического тока.
1. наличие свободных носителей зарядов,
3. замкнутая цепь,
4. источник сторонних сил, который поддерживает разность потенциалов.
Сторонние силы.
Сторонние силы — силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил.
Э.д.с. Напряжение.
Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока.
ЭДС можно выразить через напряжённость электрического поля сторонних сил
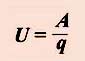 Напряжение ( U ) равно отношению работы электрического поля по перемещению заряда
Напряжение ( U ) равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.
Единица измерения напряжения в системе СИ:
[ U ] = 1 B
Сила тока.
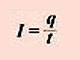
Плотность тока.
Плотность тока j — вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярно направлению тока, к величине этой площадки.
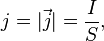
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).
Работа и энергия в электростатическом поле
Часть задач школьного уровня связана с поиском работы и энергии в электростатическом поле.
Работа по перемещению заряда в электростатическом поле.
- Поле однородно
Однородным называется поле, напряжённость которого во всех точках одинакова (
). Поместим в данное поле заряд . Тогда, исходя из определения напряжённости электростатического поля, модуль силы, действующей на заряд: (1)Вспомним определение механической работы:
(2)Подставим (1) в (2):
(3)Соотношение (3) удобно для поиска работы, в случае заряда в однородном электростатическом поле.
Важно: в задачах однородное поле должно быть задано самим выражением «считать поле однородным», также электростатическое поле плоского конденсатора можно считать однородным.
- Поле неоднородно
Неоднородным называется поле, напряжённость которого непостоянно в различных точках пространства. В случае неоднородности поля, воспользуемся выражением (3):
= = (4)Мы воспользовались определением перемещения: разность конечного (
) и начального () положения тела.Исходя из определения потенциала:
= = (5)- где
- — проекция вектора на выбранную ось,
- — потенциал в точке.
Тогда, если ввести
и , получим: (6)Т.е. в неоднородном электростатическом поле (а на самом деле, в любом), работа по переносу заряда численно равна переносимому заряду, умноженному на разность потенциалов между точками переноса.
Важно: неоднородное поле в задаче вводится через саму фразу «поле неоднородное» и через источники: точечный заряд, шар, которые также создают неоднородные поля.
Вывод: в задачах на нахождение работы по переносу заряда необходимо выяснить характер поля (однородное или неоднородное) и применить соответствующее выражение (3) или (6).
Энергия взаимодействия зарядов
А теперь обсудим энергию взаимодействия зарядов. Энергия взаимодействие зарядов на школьном уровне даётся без вывода, поэтому мы тоже ещё просто зафиксируем:
(7)Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
Работа электростатического поля. Потенциал. Эквипотенциальные поверхности
Работа электростатического поля. Потенциал. Эквипотенциальные поверхности
Электростатическое поле — это электрическое поле неподвижного заряда.
Сила F эл, действующая на заряд, перемещает его, совершая раборту.
В однородном электрическом поле Fэл = qE — постоянная величина
Работа поля (электрической силы) не зависит от формы траектории и на замкнутой траектории равна нулю.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Электростатическая энергия — потенциальная энергия системы заряженных тел (т.к. они взаимодействуют и способны совершить работу).
Так как работа поля не зависит от формы траектории, то одновременно
Сравнивая формулы работы, получим потенциальную энергию заряда в однородном электростатическом поле
Если поле совершает положительную работу ( вдоль силовых линий ), то потенциальная энергия заряженного тела уменьшается (но согласно закону сохранения энергии увеличивается кинетическая энергия ) и наоборот.
ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
-энергитическая характеристика электрического поля.
— скалярная величина, определяющая потенциальную энергию заряда в любой точке электрического поля.
Величина потенциала считается относительно выбранного нулевого уровня.
РАЗНОСТЬ ПОТЕНЦИАЛОВ ( или иначе НАПРЯЖЕНИЕ )
— это разность потенциалов в начальной и конечной точках траектории заряда.
Напряжение между двумя точками ( U ) равно разности потенциалов этих точек и равно работе поля по перемещению единичного заряда.
СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ
Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.
ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
— поверхности, все точки которых имеют одинаковый потенциал
для однородного поля — это плоскость
для поля точечного заряда — это концентрические сферы
Эквипотенциальная поверхность имеется у любого проводника в электростатическом поле, т.к. силовые линии перпендикулярны поверхности проводника.
Все точки внутри проводника имеют одинаковый потенциал ( =0).
Напряженность внутри проводника = 0, значит и разность потенциалов внутри = 0.
Электростатика и законы постоянного тока — Класс!ная физика
Электрический заряд. Электризация. Закон сохранения электрического заряда. Закон Кулона. Единица электрического заряда —
Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля —
Проводники и диэлектрики в электростатическом поле. Поляризация диэлектриков
—
Потенциальная энергия тела в электростатическом поле. Потенциал электростатического поля и разность потенциалов. Связь между напряженностью электростатического поля и разхностью потенциалов —
Электроемкость. Конденсаторы. Энергия заряженного конденсатора —
Электрический ток. Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление —
Работа и мощность тока
Вывод формулы для расчета работы сил поля
Рис. 3.17. Рис. 3.18.
Как вы считаете: случайно ли это совпадение?
Тесты к лекции №3.
Тест 3.1. Дайте формулировку теоремы Остроградского-Гаусса:
£ поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме заключенной внутри этой поверхности зарядов, деленной на ε0.
£ поток вектора напряженности электрического поля через замкнутую поверхность равен 0.
£ поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности.
£ поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенной внутри этой поверхности зарядов, умноженной на ε0.
Тест 3.2. Какой формулой описывается поле заряженной нити?
£
£
£
£
Тест 3.3. Чему равен суммарный поток, создаваемый при пересечении линиями напряженности “морщин”?
£
£
£
£
Тест 3.5. Объемная плотность заряда выражается формулой:
£
£
£
£
£
Работа электрического поля по перемещению заряда. Потенциал. Потенциальный характер электростатического поля[11]
4.1. Вывод формулы для расчета работы сил поля при перемещении заряда.
4.2. Понятие потенциала, потенциальный характер электростатического поля.
4.3. Связь между напряженностью и потенциалом.
4.4. Потенциал поля плоского конденсатора, заряженной нити, цилиндрического и сферического конденсаторов.
4.1. Вывод формулы для расчета работы сил поля при перемещении заряда
Пусть имеется точечный положительный заряд. Рассчитаем работу по его перемещению из точки 1 в точку 2.
Рис. 4.1.
Вывод: работа по перемещению заряда из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов начальной и конечной точек траектории.
4.2. Понятие потенциала, потенциальный характер электростатического поля
может служить характеристикой поля.
Т. к. при функциональная часть выражения (4.2) , то примем const = 0. Получим:
Эта величина получила название: потенциал поля точечного заряда:
, тогда и
(4.5)
Потенциалом поля в данной точке называется физическая величина, численно равная работе по переносу единичного положительного заряда из данной точки поля в бесконечность.
Работа сил электростатического поля равна убыли потенциальной энергии, т. е.:
Тогда, сравнив (4.4) и (4.6), получим:
Т. к. при , то :
Потенциалом поля в данной точке называется физическая величина, численно равная потенциальной энергии, которая приобретается единичным положительным зарядом при переносе его из бесконечности в данную точку поля.
Выясним свойства потенциального электростатического поля.
Рис. 4.2.
1. Работа по переносу заряда из одной точки электрического поля в другую не зависит от формы траектории.
2. Работа по переносу заряда вдоль замкнутой траектории равна нулю.
,
4. Работа сил электростатического поля при перемещении заряда.
При перемещении заряда в электростатическом поле, действующие на заряд кулоновские силы, совершают работу. Пусть заряд q00 перемещается в поле заряда q0 из точки С в точку В вдоль произвольной траектории (рис.1.12). На q0 действует кулоновская сила
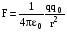 .
При элементарном перемещении заряда
dl,
эта сила совершает работу dA
.
При элементарном перемещении заряда
dl,
эта сила совершает работу dA
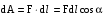 ,
где
— угол между векторами
,
где
— угол между векторами 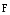 и
и 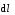 .
Величина dlcos=dr
является проекцией вектора
.
Величина dlcos=dr
является проекцией вектора 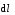 на
направление силы
на
направление силы 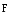 .
Таким образом, dA=Fdr,
.
Таким образом, dA=Fdr, 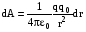 .
Полная работа по перемещению заряда из
точки С в В определяется интегралом
.
Полная работа по перемещению заряда из
точки С в В определяется интегралом 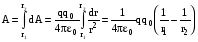 ,
где r1 и
r2 —
расстояния заряда q до точек С и В. Из
полученной формулы следует, что работа,
совершаемая при перемещении электрического
заряда q0 в
поле точечного заряда q, не
зависит от формы траектории перемещения,
а зависит только от начальной и конечной
точки перемещения.
,
где r1 и
r2 —
расстояния заряда q до точек С и В. Из
полученной формулы следует, что работа,
совершаемая при перемещении электрического
заряда q0 в
поле точечного заряда q, не
зависит от формы траектории перемещения,
а зависит только от начальной и конечной
точки перемещения.
В разделе динамики показано, что поле, удовлетворяющее этому условию, является потенциальным. Следовательно, электростатическое поле точечного заряда — потенциальное, а действующие в нем силы — консервативные.
Если заряды q и q0 одного знака, то работа сил отталкивания будет положительной при их удалении и отрицательной при их сближении (в последнем случае работу совершают внешние силы). Если заряды q и q0 разноименные, то работа сил притяжения будет положительной при их сближении и отрицательной при удалении друг от друга (последнем случае работу также совершают внешние силы).
Пусть
электростатическое поле, в котором
перемещается заряд q0,
создано системой зарядов q1,
q2,…,qn.
Следовательно, на q0 действуют
независимые силы 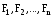 , равнодействующая
которых равна их векторной сумме. Работа
А равнодействующей силы равна
алгебраической сумме работ составляющих
сил,
, равнодействующая
которых равна их векторной сумме. Работа
А равнодействующей силы равна
алгебраической сумме работ составляющих
сил, 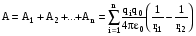 ,
где ri1 и
ri2 —
начальное и конечное расстояния между
зарядами qi и
q0 .
,
где ri1 и
ri2 —
начальное и конечное расстояния между
зарядами qi и
q0 .
Циркуляция вектора напряженности.
При
перемещении заряда по произвольному
замкнутому пути L работа сил
электростатического поля равна нулю.
Поскольку, конечное положение заряда
равно начальному r1=r2,
то 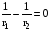 и
и 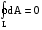 (кружок
у знака интеграла указывает на то, что
интегрирование производится по замкнутому
пути). Так как
(кружок
у знака интеграла указывает на то, что
интегрирование производится по замкнутому
пути). Так как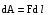 и
и 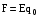 ,
то
,
то 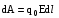 .
Отсюда получаем
.
Отсюда получаем 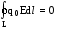 .
Сократив обе части равенства на q0,
получим
.
Сократив обе части равенства на q0,
получим 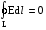 или
или 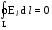 ,
где El=Ecos
— проекция вектора Е на направление
элементарного перемещения
,
где El=Ecos
— проекция вектора Е на направление
элементарного перемещения 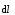 .
Интеграл
.
Интеграл 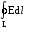 называется циркуляцией
вектора напряженности.
Таким образом,циркуляция
вектора напряженности электростатического
поля вдоль любого замкнутого контура
равна нулю.
Это заключение есть условие потенциальности
поля.
называется циркуляцией
вектора напряженности.
Таким образом,циркуляция
вектора напряженности электростатического
поля вдоль любого замкнутого контура
равна нулю.
Это заключение есть условие потенциальности
поля.
Потенциальная энергия заряда.
В потенциальном поле тела обладают потенциальной энергией и работа консервативных сил совершается за счет убыли потенциальной энергии.
Поэтому работу A12 можно представить, как разность потенциальных энергий заряда q0 в начальной и конечной точках поля заряда q :
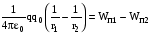
Потенциальная энергия заряда q0 , находящегося в поле заряда q на расстоянии r от него равна
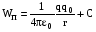
Считая, что при удалении заряда на бесконечность, потенциальная энергия обращается в нуль, получаем: const = 0 .
Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов потенциальная энергия из взаимодействия (притяжения) отрицательна.
Если поле создается системой n точечных зарядов, то потенциальная энергия заряда q0 , находящегося в этом поле, равна сумме его потенциальных энергий, создаваемых каждым из зарядов в отдельности:
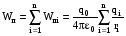
Потенциал электростатического поля.
Отношение 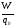 не
зависит от пробного заряда q0 и
является, энергетической
характеристикой поля, называемой потенциалом:
не
зависит от пробного заряда q0 и
является, энергетической
характеристикой поля, называемой потенциалом:
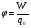
Потенциал ϕ в какой-либо точке электростатического поля есть скалярная физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
5.
Потенциал электростатического
поля — скалярная величина, равная
отношению потенциальной энергии
заряда в поле к этому заряду: — энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
| |
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
| |
— следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
| |
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В
СИ потенциал измеряется в вольтах: |
| |
Разность потенциалов | ||
|
| |
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
| |
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
| |
Связь между напряженностью и напряжением. | ||
Из
доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
| |
Из этого соотношения видно:
|
| |
Эквипотенциальные поверхности. ЭПП — поверхности равного потенциала. Свойства ЭПП: — работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; — вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
| |
|
| |
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
| |
Потенциальная энергия взаимодействия зарядов. |
| |
|
| |
Потенциал поля точечного заряда |
| |
|
| |
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
| |
Перераспределение зарядов при контакте заряженных проводников. | ||
ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ
Электрический
диполь —
система двух равных по модулю разноименных
точечных зарядов (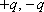 ),
расстояние
),
расстояние 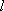 между
которыми значительно меньше расстояния
до рассматриваемых точек поля. Плечо
диполя —
вектор
между
которыми значительно меньше расстояния
до рассматриваемых точек поля. Плечо
диполя —
вектор 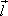 ,
направленный по оси диполя (прямой,
проходящей через оба заряда) от
отрицательного заряда к положительному
и равный расстоянию между
зарядами. Электрический
момент диполя (дипольный
момент):
,
направленный по оси диполя (прямой,
проходящей через оба заряда) от
отрицательного заряда к положительному
и равный расстоянию между
зарядами. Электрический
момент диполя (дипольный
момент): 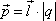 . Напряженность
поля диполя в
произвольной точке (согласно принципу
суперпозиции):
. Напряженность
поля диполя в
произвольной точке (согласно принципу
суперпозиции): 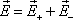 где
где 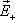 и —
напряженности полей, создаваемых
соответственно положительным и
отрицательным зарядами.
и —
напряженности полей, создаваемых
соответственно положительным и
отрицательным зарядами.
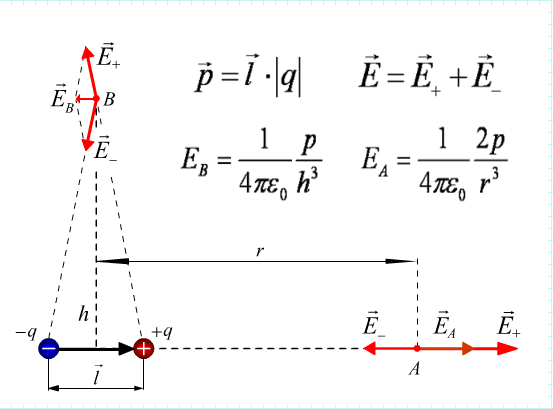
 Напряженность
поля диполя на продолжении оси диполя
в точке А:
Напряженность
поля диполя на продолжении оси диполя
в точке А: 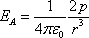 .
Напряженность
поля диполя на перпендикуляре,
восставленном к оси из его середины в
точке B:
.
Напряженность
поля диполя на перпендикуляре,
восставленном к оси из его середины в
точке B: 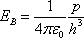 .
.
§ 12.3 Работа сил электростатического поля. Потенциал. Эквипотенциальные поверхности
На заряд qпр помещённый в произвольную точку электростатического поля с напряжённостью Е, действует сила F= qпр E. Если заряд не закреплён, то сила заставит его перемещаться и, значит, будет совершаться работа. Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда qпр из точки а электрического поля в точку b на отрезке пути dℓ, по определению, равна
dA = Fdℓcosα
(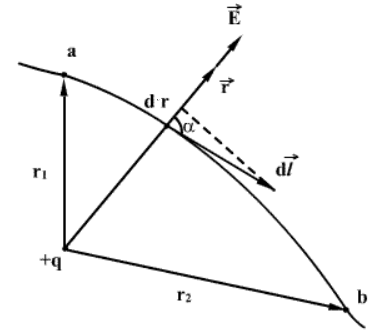 α
— угол между F
и направлением движения) (рис.12.13).
α
— угол между F
и направлением движения) (рис.12.13).
Если работа совершается внешними силами, то dA< 0 , если силами поля, то dA > 0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении qпр из точки a в точку b
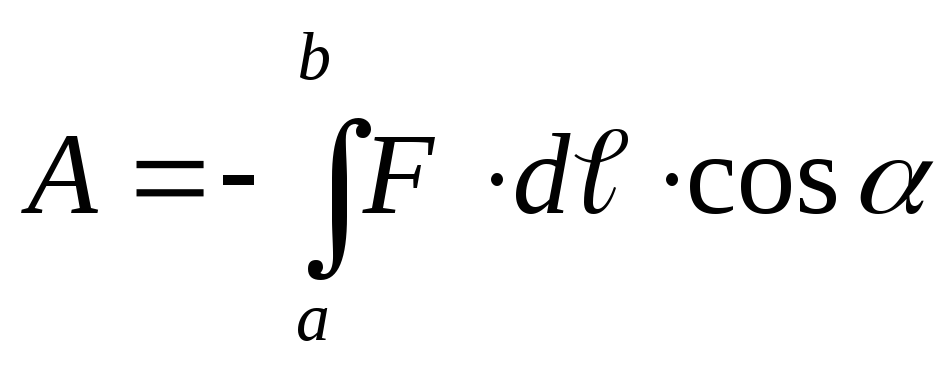 (12.20)
(12.20)
Рисунок -12.13
(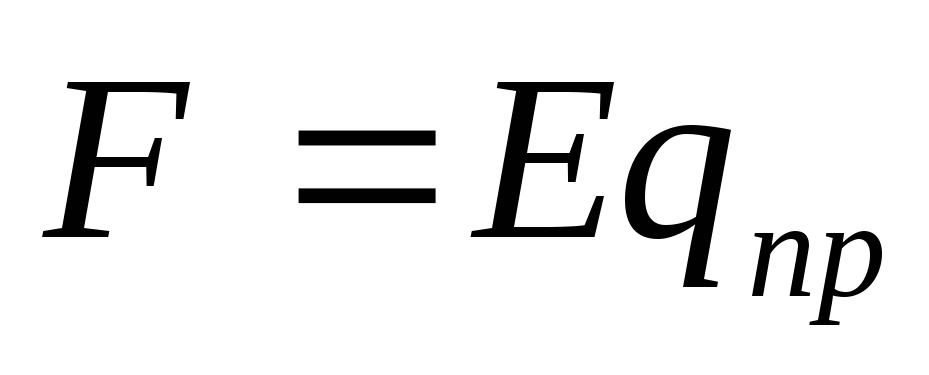 — кулоновская сила, действующая на
пробный заряд qпр в каждой точке поля с напряжённостью
E).
— кулоновская сила, действующая на
пробный заряд qпр в каждой точке поля с напряжённостью
E).
Тогда работа
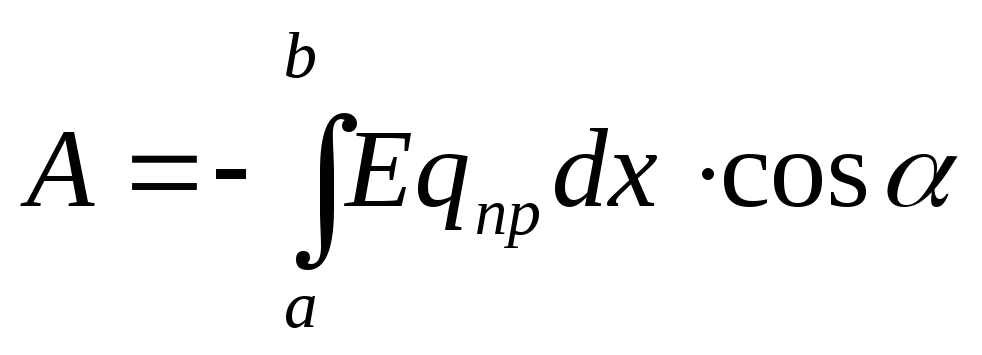 (12.21)
(12.21)
Перемещение
совершается перпендикулярно вектору  ,
следовательно cosα
=1, работа переноса пробного заряда qпр от a к b равна
,
следовательно cosα
=1, работа переноса пробного заряда qпр от a к b равна
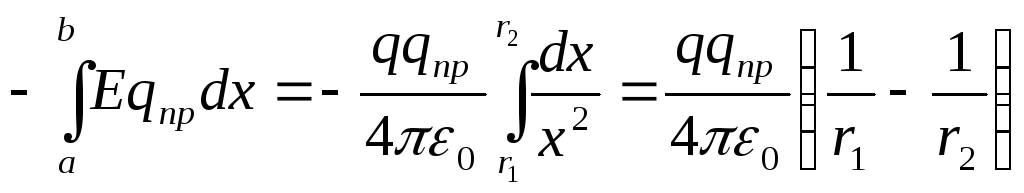 (12.22)
(12.22)
Работа сил электрического поля при перемещении заряда не зависит от формы пути, а зависит лишь от взаимного расположения начальной и конечной точек траектории.
Следовательно, электростатического поля точечного заряда является потенциальным , а электростатические силы – консервативными.
Это свойство потенциальных полей. Из него следует, что работа совершаемая в электрическом поле по замкнутому контуру, равна нулю:
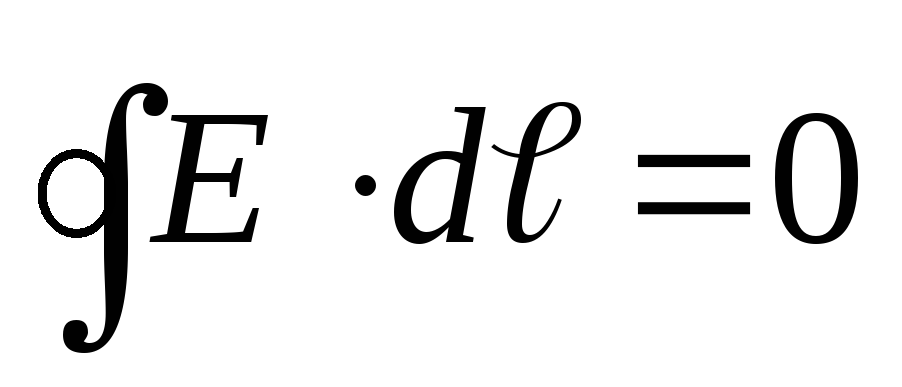 (12.23)
(12.23)
Интеграл 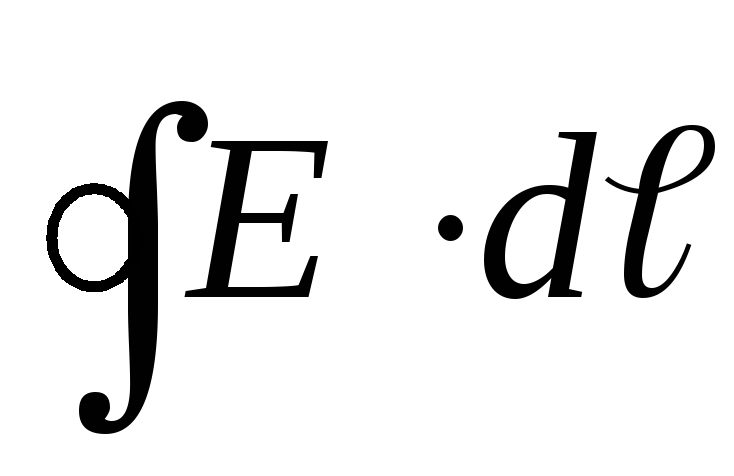 называется циркуляцией
вектора напряженности.
Из обращения в нуль циркуляции вектора
Е следует, что линии напряжённости
электростатического поля не могут быть
замкнутыми, они начинаются на положительных
и кончаются на отрицательных зарядах.
называется циркуляцией
вектора напряженности.
Из обращения в нуль циркуляции вектора
Е следует, что линии напряжённости
электростатического поля не могут быть
замкнутыми, они начинаются на положительных
и кончаются на отрицательных зарядах.
Как известно, работа консервативных сил совершается за счёт убыли потенциальной энергии. Поэтому, работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд qпр в начальной и конечной точках поля заряда q:
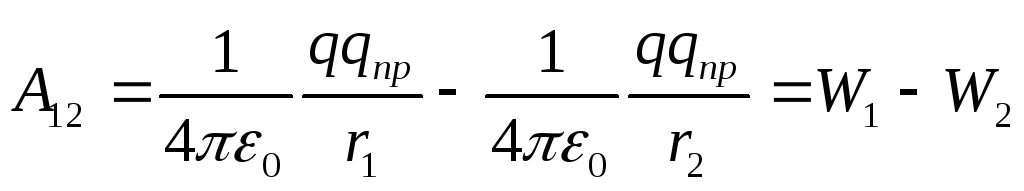 (12.24)
(12.24)
откуда следует, что потенциальная энергия заряда qпр в поле заряда q равна
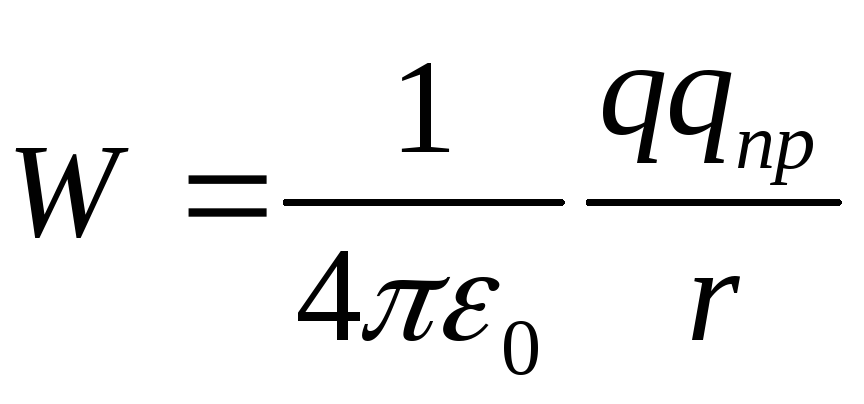 (12.25)
(12.25)
Для одноименных зарядов qпрq>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноимённых зарядов qпрq< 0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
Если поле создаётся системой n точечных зарядов q1, q2, …. qn, то потенциальная энергия U заряда qпр, находящегося в этом поле, равна сумме его потенциальных энергий Ui, создаваемых каждым из зарядов в отдельности:
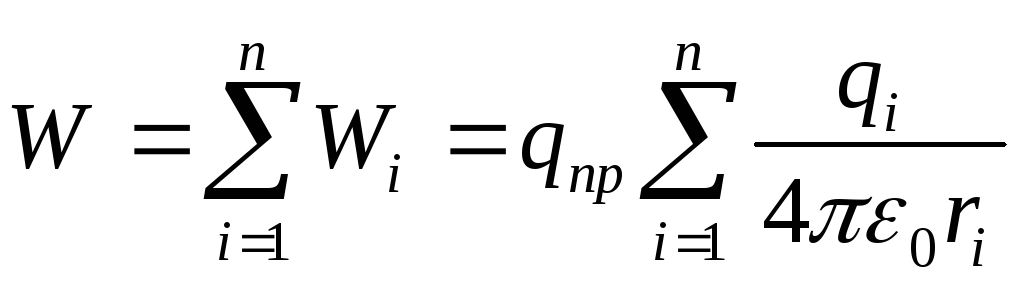 (12.26)
(12.26)
Отношение 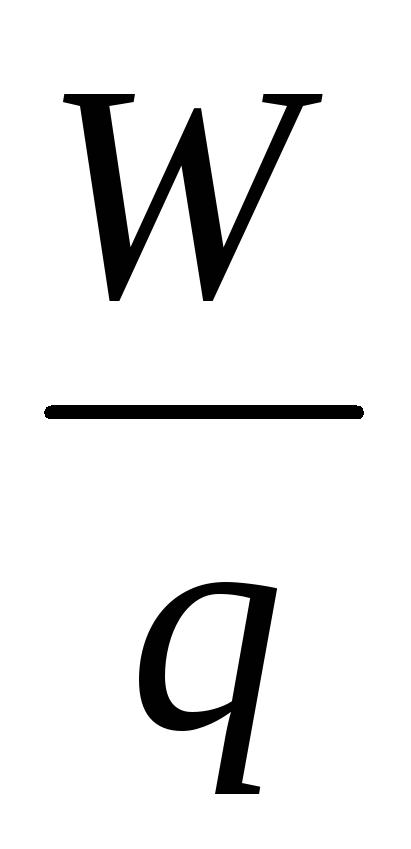 не зависят от заряда q
и является энергетической характеристикой
электростатического поля.
не зависят от заряда q
и является энергетической характеристикой
электростатического поля.
Скалярная физическая величина, измеряемая отношением потенциальной энергии пробного заряда в электростатическом поле к величине этого заряда, называется потенциалом электростатического поля.
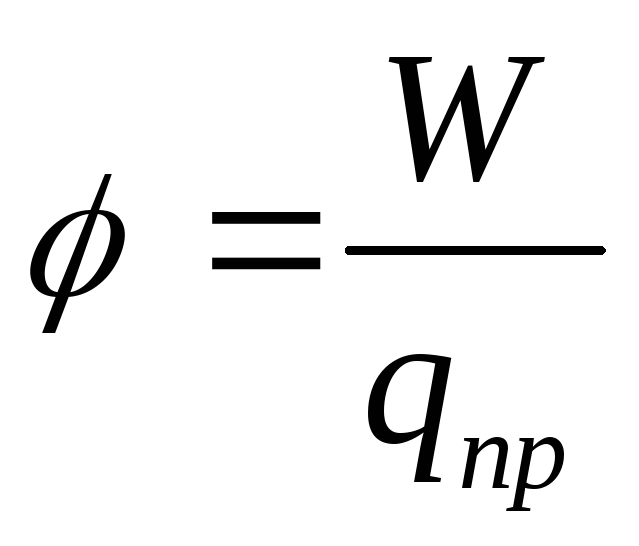 (12.27)
(12.27)
Потенциал поля, создаваемый точечным зарядом q, равен
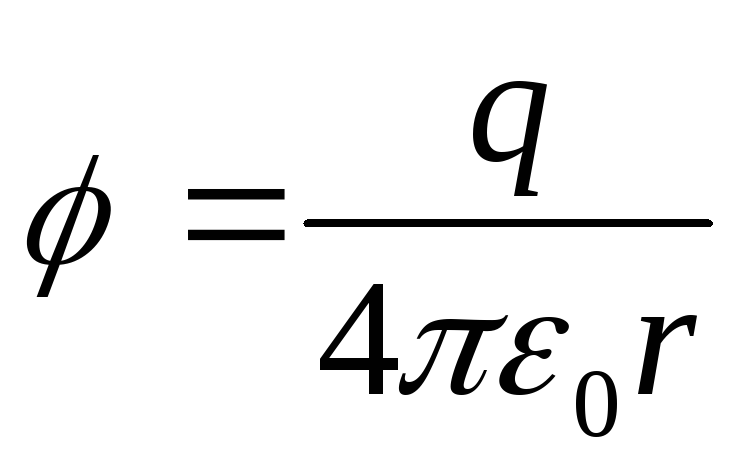 (12.28)
(12.28)
Единица потенциала – вольт.
Работа, совершаемая силами электростатического поля при перемещении заряда qпр из точки 1 в точку 2 может быть представлена как
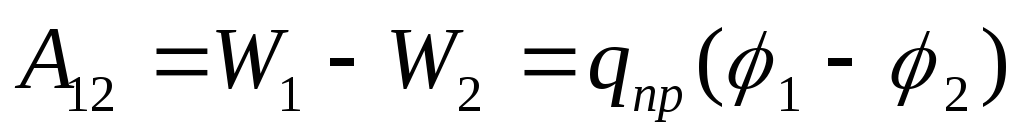 (12.29)
(12.29)
т.е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.
Разность потенциалов двух точек электростатического поля φ1-φ2 равна напряжению. Тогда
Отношение работы, совершаемой электростатическим полем при перемещении пробного заряда из одной точки поля в другую, к величине этого заряда называется напряжением между этими точками.
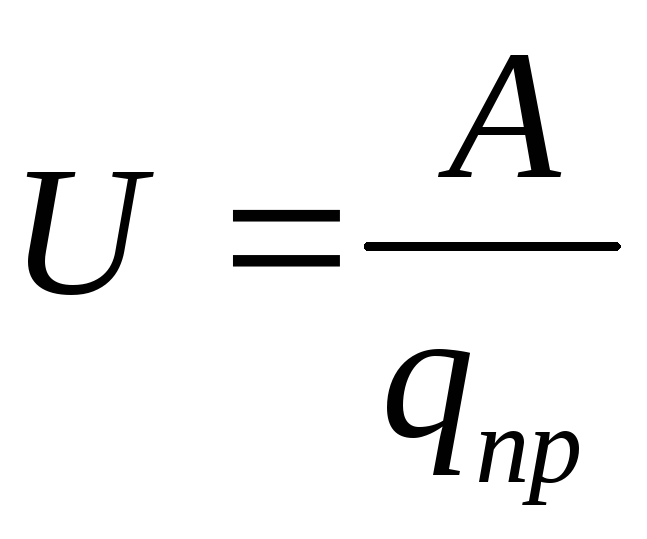 (12.30)
(12.30)
Графически электрическое поле можно изображать не только с помощью линий напряжённости, но и с помощью эквипотенциальных поверхностей.
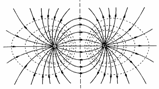
Эквипотенциальные поверхности – совокупность точек, имеющих одинаковый потенциал. Из рисунка видно, что линии напряжённости (радиальные лучи) перпендикулярны эквипотенциальным линиям.
Э квипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесчисленное множество
(рис.12.14).
Однако их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
одинаковы. Тогда густота эквипотенциальных
поверхностей наглядно характеризует
напряжённость поля в разных точках.
Там, где эти поверхности расположены
гуще, напряжённость поля больше. Зная
расположение эквипотенциальных линий
(поверхностей), можно построить линии
напряжённости или по известному
расположению линий напряжённости можно
построить эквипотенциальные поверхности.
квипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесчисленное множество
(рис.12.14).
Однако их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
одинаковы. Тогда густота эквипотенциальных
поверхностей наглядно характеризует
напряжённость поля в разных точках.
Там, где эти поверхности расположены
гуще, напряжённость поля больше. Зная
расположение эквипотенциальных линий
(поверхностей), можно построить линии
напряжённости или по известному
расположению линий напряжённости можно
построить эквипотенциальные поверхности.
Работа электрического тока. Видеоурок. Физика 8 Класс
На данном уроке мы рассмотрим вольтметр и амперметр, узнаем, что такое работа электрического тока и как она вычисляется.
Сам по себе электрический ток не нужен. Важным является не сам ток, а его действие.
Действие электрического тока характеризуется работой электрического тока.
Работа – это величина, которая характеризует превращение энергии из одного вида в другой.
Например, была энергия кинетическая, стала энергия потенциальная, т. е. тело находилось в состоянии движения, затем оно остановилось, поднявшись при этом на некоторую высоту.
Что касается электрического тока, то мы уже знаем о движении электрических зарядов по проводнику и что движение это происходит под действием электрического поля, т. е. работу совершает электрическое поле. И работа в данном случае показывает, как энергия одного вида, например, энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д.
Работа электрического тока связана, в первую очередь, с понятием электрического напряжения и силы тока.
Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику.

Это утверждение получено из соотношения для электрического напряжения.
Электрическое напряжение – это работа электрического поля по переносу электрического заряда q.

Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.

Это утверждение следует из соотношения для силы тока.
Сила тока – это отношение заряда ко времени, в течение которого протекает заряд по проводнику через поперечное сечение проводника.

Подставив в формулу определения работы  , получим выражение для вычисления работы электрического тока, работы электрического поля по перемещению электрического заряда.
, получим выражение для вычисления работы электрического тока, работы электрического поля по перемещению электрического заряда.

Работа – 1 Джоуль или 1 Дж;
Напряжение – 1 Вольт или 1 В;
Сила тока – 1 Ампер или 1 А;
Время – 1 секунда или 1 с.

Определение
Работа электрического тока равна произведению силы тока на участке цепи, напряжению на концах этого участка и времени, в течение которого протекает ток по проводнику.
Работа электрического тока связана с приборами, позволяющими определять значения указанных величин.
Напряжение определяется по прибору, который называется вольтметр. А для измерения силы тока используют амперметр (рис. 1).

Рис. 1. Изображения вольтметра и амперметра
Включив эти два прибора в электрическую цепь, наблюдая за показаниями этих приборов, определив время, в течение которого производятся измерения, определяем значение работы электрического тока. .
.
Обратите внимание на то, что плата, которую мы производим за электроэнергию, – это плата именно за работу электрического тока. Действие электрического тока – это те самые действия, которые используются в технике, такой как нагревательные устройства, устройства, которые используются в быту (телевизоры, радиоприемники и т. д.).
Работа измеряется при помощи амперметра и вольтметра, но, тем не менее, есть отдельный прибор, который сразу способен измерять работу электрического тока
На следующем уроке мы познакомимся с понятием мощности.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Stoom.ru (Источник).
- Physics.ru (Источник).
- Class-fizika.narod.ru (Источник).
Домашнее задание
- П. 50, вопросы 1–4, стр. 119, задание 24 (1). Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Через реостат с сопротивлением 5 Ом протекает ток силой 0,5 А. Нужно определить, какую работу произведет ток в течение 4 часов (14 400 сек.).
- С помощью каких приборов можно измерить работу электрического поля?




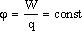
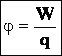
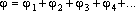
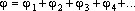
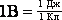
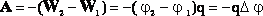
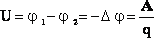
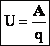
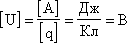
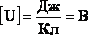
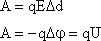 →
→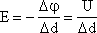
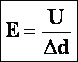
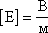 —Напряженность
поля равна 1 В/м, если между двумя
точками поля, находящимися на расстоянии
1 м друг от друга существует разность
потенциалов 1 В.
—Напряженность
поля равна 1 В/м, если между двумя
точками поля, находящимися на расстоянии
1 м друг от друга существует разность
потенциалов 1 В.