Работа электрического поля при перемещении заряда.

 ??? Вопросы

1. Формула работы электрического поля по перемещению заряда?

2. Единица измерения работы электрического поля?

3. В каких случаях работа электрического поля А=0, А>0, A<0?

4. Зависит ли работа электрического поля по перемещению заряда от формы траектории?

5. Какое электрическое поле называют однородным? Приведите пример?

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным .

Потенциал

Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

Работа в электрическом поле. Потенциал

Работа сил электростатического поля. Понятие потенциала

Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.

Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.

Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.

Определение 1

При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.

У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.

Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:

Определение 2

Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.

Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→  на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:

∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.

Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от r=r1 до r=r2 и получим следующее:

A=∫r1r2E·q·dr=Qq4πε01r1-1r2.

Рисунок 1.4.2. Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.

Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак.

А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.

Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.

Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0.

Определение 3

Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.

Обозначив энергию как W, а работу, совершаемую зарядом, как A10, запишем следующую формулу:

Wp1=A10.

Обратите внимание, что энергия обозначается именно буквой W, а не E, поскольку в электростатике E – это напряженность поля.

Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.

Определение 4

Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2, нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.

A12=A10+ A02= A10 – A20 =Wp1 – Wp2.

Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.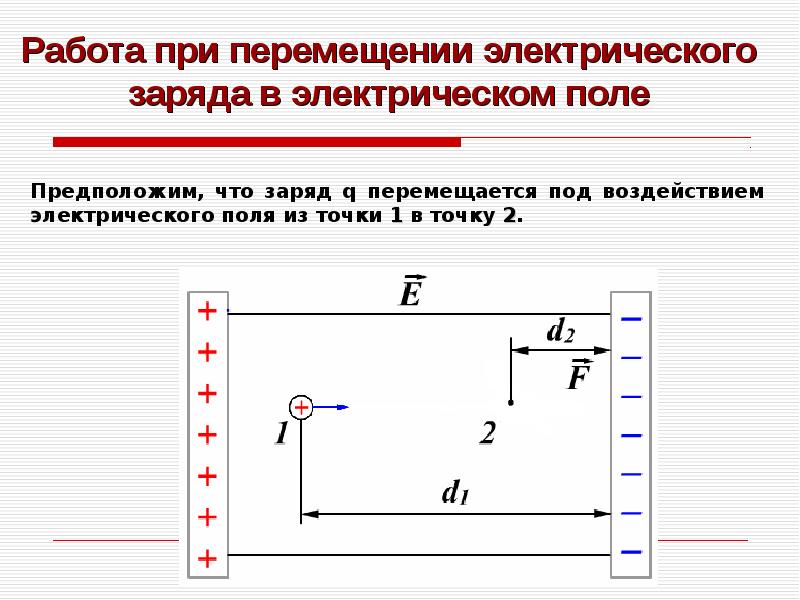

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Понятие потенциала электрического поля

Определение 5

Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.

Он обозначается буквой φ. Это важная энергетическая характеристика электростатического поля.

φ=Wpq.

Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.

A12=Wp1–Wp2=qφ1–qφ2=q(φ1 – φ2).

Потенциал электрического поля измеряется в вольтах (В).

1 В=1 Дж1 Кл.

Разность потенциалов в формулах обычно обозначается Δφ.

Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:

Определение 6

Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.

φ∞=A∞q.

Чтобы вычислить потенциал точечного заряда на расстоянии r, на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:

φ=φ∞=1q∫r∞Edr=Q4πε0∫r∞drr2=14πε0Qr

С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r≥R, что следует из теоремы Гаусса.

Изображение электрических полей с помощью эквипотенциальных поверхностей

Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.

Определение 7

Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.

Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.

Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.

Рисунок 1.4.3. Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.

Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.

В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:

ΔA12=qEΔl=q(φ1–φ2)=–qΔφ,

где Δφ=φ1-φ2 – изменение потенциала. Отсюда выводится, что: 

E=-∆φ∆l, (∆l→0) или E=-dφdl.

Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.

Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:

φ=φ1+φ2+φ3+. ..

1.5 Работа сил электростатического поля

Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила
F = q E. При перемещении заряда на отрезке dl силами поля совершается работа

dA = F dl = q E dl cos (E, dl).

При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна

.

Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого 

.

Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:

Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.

Для электрического поля, созданного системой зарядов Q₁, Q₂,¼, Q_n, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:

.

Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q.

Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.

.

Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле — потенциальным.

---

Вопросы

1)   Как доказать, что электростатическое поле является потенциальным.

2)   Напишите выражение для работы, совершаемой силами однородного поля напряженностью Е над зарядом q при его перемещении из точки 1 заданной радиус вектором r₁ в точку 2 с радиус вектором r₂ по произвольной траектории

наверх

Работа электрического поля. (10 класс)

1. Работа электрического поля

10 класс
Работа электростатического поля
Знак потенциальной энергии в механике
Знак потенциальной энергии в электростатике
Независимость работы от траектории
Потенциал электрического поля
Напряженность и напряжение
Энергия и потенциал точечного заряда
Заряды и массы. Аналогия.
Эквипотенциальные поверхности
выход

3. Работа электростатического поля

+
+
+
+
+
+
+
+
d1
+
+ F
S
d2
—
Из
Поместим
рисунка находим:
заряд +q в
электрическое
S = d1 – dполе.
2
Под
Во время
действием
движения
поляна
заряд переместится
действует сила
по
F =qE,
направлению
которая
силовых
совершает
линий.
работу:
A = FScos(0°) = qE(d1 – d2) = -(qEd2 – qEd1) = — ΔWp
Wp = qEd

4. Аналогия с работой силы тяжести

Заряд q перемещается
в электрическом поле
Тело массы m перемещается
в поле силы тяжести
+
F = qE
d1
F = mg
h2
+
d2
———-
Wp = qEd
Aэл.поля = -ΔWp
h3
A = FScos(0)
= mg(h2 – h3)
Wp = mgh
= -(mgh3 – mgh2) = — ΔEp
Aтяж = -ΔWp

5. Знак потенциальной энергии

m>0
h>0
Wp = mgh > 0
h
«0» высоты
h
m>0
h
Wp = mgh
Знак потенциальной энергии
зависит только от знака высоты
(от выбора «0» уровня)

6.

Знак потенциальной энергии Пример 3
1
2
+ + + +
F = qE
F = qE
+-
— — — —
d
«0» уровень
Wp = -|qEd|
+|qEd| 00
d
«0» уровень
Знак энергии заряда, находящегося в электрическом
поле, зависит: от направления поля, знака заряда и
выбора «0» уровня

7. Знак потенциальной энергии

Знак потенциальной энергии равен знаку
работы электрического поля при
перемещении заряда на «0» уровень.
A = -ΔWp = — (Wp2 – Wp1) = — (0 – Wp1) = Wp1
Пример 1
+
F = qE
A = FScos(0°) > 0
S
Wp = +|qEd|
«0» уровень

8. Знак потенциальной энергии

Второе
Знак
потенциальной
правило:
энергии равен знаку
работы
Если
сила,
электрического
действующая поля
на заряд,
при
перемещении
направлена
назаряда
«0» уровень,
на «0» то
уровень
Wp > 0
A = -ΔWp = — (Wp2 – Wp1) = — (0 – Wp1) = Wp1
Пример 2
+
S
«0» уровень
F = qE
Для
A =перемещения
FScos(180°)на
«0» уровень необходимо
на заряд подействовать
внешней
Wp = силой
-|qEd|
(на рисунке не указана).

9. Работа при перемещении по разным траекториям

электрического поля
A231 =Работа
FS231cos(α)
= =F*FBC
cos(0°)==F=F*AB
cos(90°)
cos(0°)
=*BC
0
**cos(α)
*FCB
*AC
*cos(90°)
не зависит от траектории.
A
+
S2
F
α
A1 = F*BC
A2= 0
A3 = F*BC
S1
S3 α
C
B
A2+ A3 = A1

10. Работа электрического поля не зависит от траектории

A12 = -ΔW12 = — (W2 – W1)
1
II
+
F
Энергии заряда W1 и W2 не
зависят от траектории.
Следовательно, при
перемещении заряда по
траекториям I и II работа
одинакова.
I
2

11. Работа при перемещении по замкнутой траектории

При перемещении заряда по замкнутой линии
A
=
FS
cos(α)
=
F
AB
cos(α)
=
F
cos(180°)
cos(90°)
=
F
= 0= — F BC
*=
*BC
*FCA
**BC
*cos(90°)
*cos(180°)
1
1
2
3
2
3
работа электрического поля равна нулю. *
A
+
F
α
S3
C
A1 = F*BC
S1
+
F
S2 α
F
B
A2 = — F*BC
A3= 0
A123= 0

12. Потенциал электрического поля

На заряд, находящийся в электрическом поле,
действует сила F
1
+
q
FE1
Если удалить заряд, то в
точке «останется»
напряженность
F
E
q
Напряженность – силовая
характеристика
электрического поля

13. Потенциал электрического поля

Заряд, находящийся
Потенциал –вэнергетическая
электрическом поле,
характеристика
обладает потенциальной
электрического
энергией.
поля
«0» уровень
d1
1
?
+
q
φ1F1
Что «осталось»
Если
удалить заряд,
в точке?
то в
точке «остался»
Wp = |qEd|
потенциал
Wp qEd
Ed
q
q
[Wp ] Дж
[ ]
В
[q]
Кл

14. Напряженность и напряжение

1 — 2 Uзаряд из точки
[U 1
] в точку
В
Переместим
2
E
E
d
φ
q1 F
d
φ2
+
1
Δd
2
[ d ]
м
Работа электрического поля:
A = FS= qEΔd
A = — (Wp2 – Wp1) = Wp2 – Wp1
Wp1 = qφ1; Wp2 = qφ2
A = qEΔd = q(φ1 – φ2) = qU
U = φ1 – φ2 — разность
потенциалов или напряжение

15.

Энергия и потенциал точечного заряда F – изменяется,
следовательно, разобьем
Qq
Q
Переместим
заряд
q
из
точки
a
в
точку
b
Wp k
Wp q k
путь на
r небольшие участки Δr Si
Работа электрического поля:
A = F1ΔS1 + F2ΔS2 + …
+
q ΔSF1 ΔS
S ΔS …
a 2 3
+
Q φa
+
φb
Fb
Qq
Qq
A k 2 S1 k 2 S 2 …
r1
r2
Qq
Qq
A k
k
ra
rb

16. Заряды и массы. Аналогия.

Взаимодействие зарядов
q1
+ F
F — q2
r
q1q2
F k 2
r
q1q2
Wp k
r
q2
→ Wp
Взаимодействие масс
m1
F
F
r
m1m2
F G 2
r
m1m2
Wp G
r
m2

17. Эквипотенциальные поверхности

При перемещении заряда перпендикулярно силовым
Поверхность,
все точки которой
линиям электрического
поля A = имеют
q(φ1 – φравный
2) = 0,
потенциал, называется эквипотенциальной
следовательно, φ1 = φ2
Однородное поле
Поле точечного заряда
+
+
Q
+

Работа электрического поля — презентация онлайн

Работа электрического поля

2.

РАБОТА И ЭНЕРГИЯ в механике РАБОТА И ЭНЕРГИЯ В МЕХАНИКЕ
Работа совершается тогда, когда под
действием силы тело перемещается
A = Fs·cosα
Знак работы зависит от угла α
Потенциальная энергия определяется
взаимным расположением
взаимодействующих тел ( например, тело у
поверхности Земли)

3. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА

E = const
A=Fs cosα
F=Eq
s·cosα=d
●3
s
α
A = qEd
1
d
d – расстояние вдоль
силовой линии
1. Работа не зависит от формы траектории
А12 + А23), А23 = 0
2. Работа по замкнутому пути равна нулю
●2
(А13 =

4. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА

1. Работа не зависит от формы пути
2. Работа по замкнутой траектории
в неоднородном поле равна нулю

5. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Если работа не зависит от формы траектории, то
она равна изменению потенциальной энергии,
взятой с противоположным знаком
A = — (W2 – W1) = — ∆Wp
Если поле совершает положительную работу, то
потенциальная энергия заряженного тела
уменьшается, и наоборот
(аналогично в гравитационном поле)

6.

ПОТЕНЦИАЛ Потенциалом электрического поля называют
отношение энергии заряда в поле к этому заряду
W
φ > 0 , если q>0
q
φ
Потенциал поля точечного заряда
kq
на бесконечности φ = 0
r

7. Разность потенциалов. НАПРЯЖЕНИЕ

РАЗНОСТЬ ПОТЕНЦИАЛОВ. НАПРЯЖЕНИЕ
Разность потенциалов в начальной и конечной
точках траектории называется напряжением
U = φ1 – φ 2
Единица измерения напряжения и
потенциала 1В (вольт)
Работа по перемещению заряда в
неоднородном поле
A = qU
или
A = q (φ1 – φ2)

8. Связь между напряженностью и напряжением.

СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И
НАПРЯЖЕНИЕМ.
A = qE(d1 – d2) = q (ϕ1– ϕ2)
qE ∆d = q (ϕ1– ϕ2)
qE ∆d = q U
U
E=
∆d
В
[E] =
м
Из этого соотношения видно:
1.Вектор напряженности направлен в сторону уменьшения потенциала.
2.Электрическое поле существует, если существует разность потенциалов.
3.Единица напряженности:
Напряженность поля равна 1 В/м, если между двумя точками поля,
находящимися на расстоянии 1 м друг от друга существует
разность потенциалов 1 В.

9. Эквипотенциальные поверхности – поверхности равного потенциала

ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ –
ПОВЕРХНОСТИ РАВНОГО ПОТЕНЦИАЛА
Вектор напряженности перпендикулярен
эквипотенциальной поверхности и
направлен в сторону уменьшения потенциала
Эквипотенциальные поверхности (синие линии) и силовые линии
(красные линии) простых электрических полей: a – точечный заряд; b –
электрический диполь; c – два равных положительных заряда
Из принципа суперпозиции напряженностей полей,
создаваемых электрическими зарядами, следует принцип
суперпозиции для потенциалов:
φ = φ1 + φ2 + φ3 + …

11. Аналогия с работой силы тяжести

АНАЛОГИЯ С РАБОТОЙ СИЛЫ ТЯЖЕСТИ
Заряд q перемещается
в электрическом поле
Тело массы m перемещается
в поле силы тяжести
+
F = qE
d1
F = mg
h2
+
d2
———-
Wp = qEd
Aэл. поля = -ΔWp
h3
Wp = mgh
Aтяж = -ΔWp

12. Заряды и массы. Аналогия.

ЗАРЯДЫ И МАССЫ. АНАЛОГИЯ.
Взаимодействие зарядов
q1 + F
F — q2
r
q1q2
F k 2
r
q1q2
Wp k
r
q2
→
Wp
Взаимодействие масс
m1
F
F
r
m1m2
F G 2
r
m1m2
Wp G
r
m2

14. Задача 1

ЗАДАЧА 1
Ртутный шарик, потенциал которого 1,2 кВ.
разбивается на 27 одинаковых капелек. Определите
потенциал каждой капельки. Ответ округлите до
целого числа.
РЕШЕНИЕ
ДАНО:
ϕ = 1,2•103 В ϕ = N ϕ m = N m q = N q

Найти работу сил поля по перемещению заряда. Работа в электрическом поле

Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд q 0 , то сила, приложенная к заряду, совершает работу. Работа силы на элементарном перемещении dl равна

Работа при перемещении заряда q 0 из точки 1 в точку 2

Работа A 12 не зависит от траектории перемещения, а определяется только положениями начальной и конечной точек . Следовательно, электростатическое поле точечного заряда является потенциальным , а электростатические силы — консервативными .

Таким образом, работа перемещения заряда в электростатическом поле по любому замкнутому контуру L равна нулю

Интеграл называется циркуляцией вектора напряженности. Из обращения ее в нуль следует, что линии напряженности электростатического поля никогда не могут быть замкнуты сами на себя. Они начинаются и кончаются на зарядах, либо уходят в бесконечность. Это свидетельствует о наличии в природе двух родов электрических зарядов. Формула справедлива только для электростатического поля.

При перемещении зарядов изменяется их взаимное расположение, поэтому работа, совершаемая электрическими силами, в этом случае равна изменению потенциальной энергии перемещаемого заряда:

Потенциальная энергия заряда q 0 , находящегося в поле заряда q на расстоянии r от него равна

Считая, что при удалении заряда на бесконечность, потенциальная энергия обращается в нуль, получаем: const = 0.

Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна , для разноименных зарядов потенциальная энергия из взаимодействия (притяжения) отрицательна .

В любой точке поля потенциальная энергия W заряда численно равна работе, которую необходимо совершить для перемещения заряда из бесконечности в эту точку.

Отношение зависит только от q и r . Эту величину называют потенциалом:

Единица электрического потенциала – вольт (В).

Она характеризует потенциальную энергию, которой обладал бы по­ложительный единичный заряд, помещенный в данную точку поля.Для поля точечного заряда: . Потенциал данной точки поля равен работе перемещения единичного положительного заряда из данной точки в бесконечность.

Потенциал поля, создаваемого системой точечных зарядов, равен алгебраической сумме потенциалов всех этих зарядов : .

Работа сил поля при перемещении заряда q’ из точки 1 в точку 2 может быть записана в виде:

Величину называют разностью потенциалов (напряжением) электрического поля.

Чем на самом деле является напряжение? Это способ описания и измерения напряженности электрического поля. Само по себе напряжение не может существовать без электронного поля вокруг положительных и отрицательных зарядов. Так же, как магнитное поле окружает Северный и Южный полюса.

По современным понятиям, электроны не оказывают взаимного влияния. Электрическое поле – это нечто, что исходит от одного заряда и его присутствие может ощущаться другим.

О понятии напряженности можно сказать то же самое! Просто это помогает нам представить, как электрическое поле может выглядеть. Честно говоря, оно не обладает ни формой, ни размером, ничем подобным. Но поле функционирует с определённой силой на электроны.

Силы и их действие на заряженную частицу

На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее.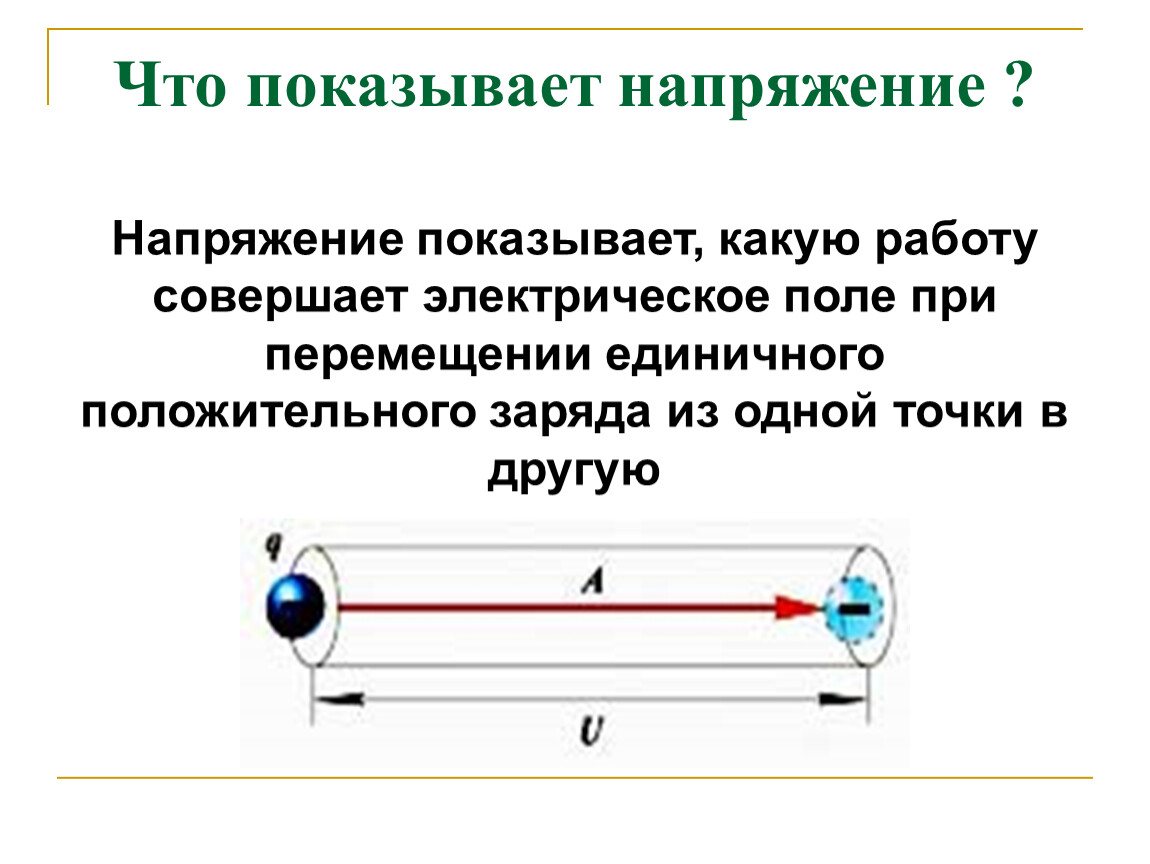 Этой силой совершается работа по передвижению электрона.

Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.

Свойства силовых линий:

• путешествуют с севера на юг;
• не имеют взаимных пересечений.

Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.

Силовые линии демонстрируют:

• направления электрических полей;
• напряженность. Чем ближе линии, тем больше сила поля и наоборот.

Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.

Что такое потенциал?

Потенциалом называется энергия, которая затрачивается на передвижение заряженной частицы из первой точки, имеющей нулевой потенциал во вторую точку.

Разность потенциалов меж пунктами А и Б – это работа, производимая силами для передвижения некоего положительного электрона по произвольной траектории из А в Б.

Чем больший потенциал у электрона, чем больше плотность потока на единицу площади. Такое явление подобно гравитации. Чем больше масса, тем больше потенциал, тем интенсивнее и плотнее гравитационное поле на единицу площади.

Небольшой заряд с низким потенциалом, с прореженной плотностью потока показан на следующем рисунке.

А ниже показан заряд с большим потенциалом и плотностью потока.

Например: во время грозы электроны истощаются в одной точке и собираются в другой, образуя электрическое поле. Когда сила станет достаточной, чтобы сломать диэлектрическую проницаемость, получается удар молнии (состоящий из электронов). При выравнивании разности потенциалов электрическое поле разрушается.

Электростатическое поле

Это разновидность электрического поля, неизменного повремени, образуемого зарядами, которые не двигаются. Работа передвижения электрона определяется соотношениями,

где r1 и r2 – расстояния заряда q до начальной и конечной точки траектории движения. По полученной формуле видно, что работа при перемещении заряда из точки в точку не зависит от траектории, а зависит лишь от начала и конца перемещения.

На всякий электрон действует сила, и поэтому при перемещении электрона в поле выполняется определенная работа.

В электростатическом поле работа зависит лишь от конечных пунктов следования, а не от траектории. Поэтому, когда движение происходит по замкнутому контуру, заряд приходит в исходное положение, и величина работы становится равной нулю. Это происходит потому, что падение потенциала нулевое (поскольку электрон возвращается в ту же самую точку).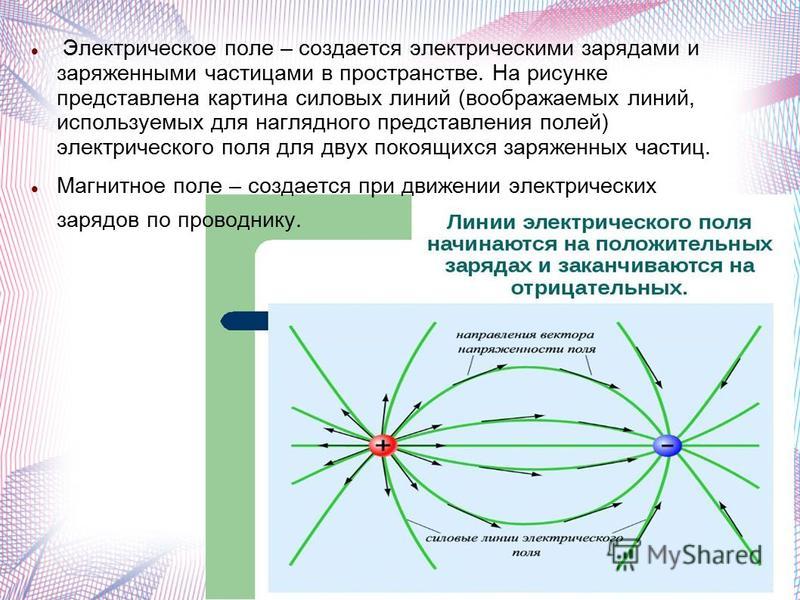 Так как разность потенциалов нулевая, чистая работа будет также нулевой, ведь потенциал падения равен работе, деленной на значение заряда, выраженное в кулонах.

Об однородном электрическом поле

Однородным называется электрическое поле меж двух противоположно заряженных плоских металлических пластин, где линии напряженности параллельны между собой.

Почему сила действия на заряд в таком поле всегда одинаковая? Благодаря симметрии. Когда система симметрична и есть только одна вариация измерения, всякая зависимость исчезает. Есть много других фундаментальных причин для ответа, но фактор симметрии – самый простой.

Работа по передвижению положительного заряда

Электрическое поле – это поток электронов от «+» до «-», приводящий к высокой напряженности области.

Поток – это количество линий электрического поля, проходящих через него. В каком направлении будут положительные электроны двигаться? Ответ: по направлению электрического поля от положительного (высокого потенциала) к отрицательному (низкому потенциалу). Поэтому положительно заряженная частица будет двигаться именно в этом направлении.

Интенсивность поля во всякой точке определяется как сила, воздействующая на положительный заряд, помещенный в эту точку.

Работа заключается в переносе электронных частиц по проводнику. По закону Ома, можно определить работу разными вариациями формул, чтобы провести расчет.

Из закона сохранения энергии следует, что работа – это изменение энергии на отдельном отрезке цепи. Перемещение положительного заряда против электрического поля требует совершения работы и в результате получается выигрыш в потенциальной энергии.

Заключение

Из школьной программы мы помним, что электрическое поле образуется вокруг заряженных частиц. На любой заряд в электрическом поле воздействует сила, и вследствие этого при движении заряда выполняется некоторая работа. Большим зарядом создается больший потенциал, который производит более интенсивное или сильное электрическое поле. Это означает, что возникает больший поток и плотность на единицу площади.

Важный момент заключается в том, что должна быть выполнена определенной силой работа по перемещению заряда от высокого потенциала к низкому. Тем самым уменьшается разница заряда между полюсами. Перемещение электронов от токи до точки требует энергии.

Пишите комментарии, дополнения к статье, может я что-то пропустил. Загляните на , буду рад если вы найдете на моем еще что-нибудь полезное.

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ.

Электрический заряд q — физическая величина, определяющая интенсивность электромагнитного взаимодействия.

[q] = l Кл (Кулон).

Атомы состоят из ядер и электронов. В состав ядра входят положительно заряженные протоны и не имеющие заряда нейтроны. Электроны несут отрицательный заряд. Количество электронов в атоме равно числу протонов в ядре, поэтому в целом атом нейтрален.

Заряд любого тела: q = ±Ne , где е = 1,6*10 -19 Кл — элементарный или минимально возможный заряд (заряд электрона), N — число избыточных или недостающих электронов. В замкнутой системе алгебраическая сумма зарядов остается постоянной:

q 1 + q 2 + … + q n = const.

Точечный электрический заряд — заряженное тело, размеры которого во много раз меньше расстояния до другого наэлектризованного тела, взаимодействующего с ним.

Закон Кулона

Два неподвижных точечных электрических заряда в вакууме взаимодействуют с силами, направленными по прямой, соединяющей эти заряды; модули этих сил прямо пропорциональны произведению зарядов и обратно пропорциональны квадрату расстояния между ними:

Коэффициент пропорциональности

где — электрическая постоянная.

где 12 — сила, действующая со стороны второго заряда на первый, а 21 — со стороны первого на второй.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля — материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке — это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

Принцип суперпозиции полей

Напряженность поля системы зарядов равна векторной сумме напряженностей полей каждого из зарядов системы:

Диэлектрическая проницаемость среды равна отношению напряженностей поля в вакууме и в веществе:

Она показывает во сколько раз вещество ослабляет поле. Закон Кулона для двух точечных зарядов q и Q , расположенных на расстоянии r в среде c диэлектрической проницаемостью:

Напряженность поля на расстоянии r от заряда Q равна

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРО-СТАТИЧЕСКОМ ПОЛЕ

Между двумя большими пластинами, заряженными противоположными знаками и расположенными параллельно, поместим точечный заряд q .

Так как электрическое поле между пластинами с напряженностью однородное, то на заряд во всех точках действует сила F = qE , которая при перемещении заряда на расстояние вдоль совершает работу

Эта работа не зависит от формы траектории, то есть при перемещении заряда q вдоль произвольной линии L работа будет такой же.

Работа электростатического поля по перемещению заряда не зависит от формы траектории, а определяется исключительно начальным и конечным состояниями системы. Она, как и в случае с полем сил тяжести, равна изменению потенциальной энергии, взятому с противоположным знаком:

Из сравнения с предыдущей формулой видно, что потенциальная энергия заряда в однородном электростатическом поле равна:

Потенциальная энергия зависит от выбора нулевого уровня и поэтому сама по себе не имеет глубокого смысла.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И НАПРЯЖЕНИЕ

Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.

Работа, совершаемая потенциальным полем, равна изменению потенциальной энергии системы, взятой с противоположным знаком:

Потенциал — отношение потенциальной энергии заряда в поле к величине этого заряда:

Потенциал однородного поля равен

где d — расстояние, отсчитываемое от некоторого нулевого уровня.

Потенциальная энергия взаимодействия заряда q с полем равна .

Поэтому работа поля по перемещению заряда из точки с потенциалом φ 1 в точку с потенциалом φ 2 составляет:

Величина называется разностью потенциалов или напряжением.

Напряжение или разность потенциалов между двумя точками — это отношение работы электрического поля по перемещению заряда из начальной точки в конечную к величине этого заряда:

[U]=1Дж/Кл=1В

НАПРЯЖЕННОСТЬ ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ

При перемещении заряда q вдоль силовой линии электрического поля напряженностью на расстояние Δ d поле совершает работу

Так как по определению, то получаем:

Отсюда и напряженность электрического поля равна

Итак, напряженность электрического поля равна изменению потенциала при перемещении вдоль силовой линии на единицу длины.

Если положительный заряд перемещается в направлении силовой линии, то направление действия силы совпадает с направлением перемещения, и работа поля положительна:

Тогда , то есть напряженность направлена в сторону убывания потенциала.

Напряженность измеряют в вольтах на метр:

[E]=1 B/м

Напряженность поля равна 1 В/м, если напряжение между двумя точками силовой линии, расположенными на расстоянии 1 м, равна 1 В.

ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ

Если независимым образом измерять заряд Q , сообщаемый телу, и его потенциал φ, то можно обнаружить, что они прямо пропорциональны друг другу:

Величина С характеризует способность проводника накапливать электрический заряд и называется электрической емкостью. Электроемкость проводника зависит от его размеров, формы, а также электрических свойств среды.

Электроёмкостъ двух проводников — отношение заряда одного из них к разности потенциалов между ними:

Емкость тела равно 1 Ф , если при сообщении ему заряда 1 Кл оно приобретает потенциал 1 В.

КОНДЕНСАТОРЫ

Конденсатор — два проводника, разделенные диэлектриком, служащие для накопления электрического заряда. Под зарядом конденсатора понимают модуль заряда одной из его пластин или обкладок.

Способность конденсатора накапливать заряд характеризуется электроемкостью, которая равна отношению заряда конденсатора к напряжению:

Емкость конденсатора равна 1 Ф, если при напряжении 1 В его заряд равен 1 Кл.

Емкость плоского конденсатора прямо пропорциональна площади пластин S , диэлектрической проницаемости среды, и обратно пропорциональна расстоянию между пластинами d :

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА.

Точные эксперименты показывают, что W=CU 2 /2

Так как q = CU , то

Плотность энергии электрического поля

где V = Sd — объем, занимаемый полем внутри конденсатора. Учитывая, что емкость плоского конденсатора

а напряжение на его обкладках U=Ed

получаем:

Пример. Электрон, двигаясь в электрическом поле из точки 1 через точку 2, увеличил свою скорость от 1000 до 3000 км/с. Определите разность потенциалов между точками 1 и 2.

Одним из основных понятий в электричестве является электростатическое поле. Его важным свойством считается работа по перемещению заряда в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени.

Условия выполнения работы

Сила, находящиеся в электростатическом поле, перемещает заряд из одного места в другое. На нее совершенно не влияет форма траектории. Определение силы зависит только от положения точек в начале и конце, а также, от общей величины заряда.

Исходя из этого, можно сделать следующий вывод: Если траектория при перемещении электрозаряда является замкнутой, то вся работа сил в электростатическом поле имеет нулевое значение. При этом, форма траектории не имеет значения, поскольку кулоновские силы производят одинаковую работу. Когда направление, в котором перемещается электрозаряд, изменяется на противоположное, то сама сила также изменяет свой знак. Поэтому, замкнутая траектория, независимо от своей формы, определяет всю работу, производимую кулоновскими силами, равной нулю.

Если в создании электростатического поля принимает участие сразу несколько точечных зарядов, то их общая работа будет складываться из суммы работ, производимых кулоновскими полями этих зарядов. Общая работа, независимо от формы траектории, определяется исключительно местом расположения начальных и конечных точек.

Понятие потенциальной энергии заряда

Свойственная электростатическому полю, позволяет определять потенциальную энергию какого-либо заряда. Кроме того, с ее помощью более точно устанавливается работа по перемещению заряда в электрическом поле. Чтобы получить это значение, в пространстве необходимо выбрать определенную точку и потенциальную энергию заряда, размещаемого в данной точке.

Заряд, помещаемый в любую точку, имеет потенциальную энергию, равной работе, совершаемой электростатическим полем, во время перемещения заряда из одной точки в другую.

В физическом смысле, потенциальная энергия представляет собой значение для каждой из двух разных точек пространства. При этом, работа по перемещению заряда находится вне зависимости от путей его перемещения и выбранной точки. Потенциал электростатического поля в данной пространственной точке, равняется работе, совершаемой электрическими силами, когда единичный положительный заряд удаляется из этой точки в бесконечное пространство.

Работа электрического поля

На любой заряд, который находится в электрическом поле, воздействует сила. В связи с этим при передвижении заряда в поле происходит определенная работа электрического поля. Как же произвести расчет этой работы?

Работа электрического поля состоит в переносе электрозарядов вдоль проводника. Она будет равняться произведению напряжения, и времени, потраченного на работу.

Применив формулу закона Ома, мы можем получить несколько различных вариантов формулы для проведения подсчета работы тока:

A = U˖I˖t = I²R˖t = (U²/R)˖t.

В соответствии с законом сохранения энергии работа электрического поля равняется изменению энергии отдельно взятого участка цепи, в связи с чем энергия, выделяемая проводником, будет равняться работе тока.

Выразим в системе СИ:

[А] = В˖А˖с = Вт˖с = Дж

1 кВт˖час = 3600000 Дж.

Проведем опыт. Рассмотрим передвижение заряда в одноименном поле, которое образовано двумя параллельно расположенными пластинами А и В и заряженными разноименными зарядами. В таком поле силовые линии на всем своем протяжении перпендикулярны этим пластинам, и когда пластина А будет заряжена положительно, тогда Е будет направлена от А к В.

Предположим, что позитивный заряд q передвинулся из точки a в точку b по произвольному пути ab = s.

Так как сила, которая действует на заряд, который находится в поле, будет равняться F = qE, то работа, совершенная при передвижении заряда в поле согласно заданному пути, определится по равенству:

A = Fs cos α, или A = qFs cos α.

Но s cos α = d, где d — дистанция между пластинами.

Отсюда следует: A = qEd.

Допустим, теперь заряд q переместится из a и b по сути acb. Работа электрического поля, совершенная на этом пути, равняется сумме работ, совершенных на отдельных участках его: ac = s₁, cb = s₂, т.е.

A = qEs₁ cos α₁ + qEs₂ cos α₂,

A = qE(s₁ cos α₁ + s₂ cos α₂,).

Но s₁ cos α₁ + s₂ cos α₂ = d, а значит, и в данном случае A = qEd.

Кроме того, предположим, что заряд q передвигается из a в b по произвольной кривой линии. Чтобы подсчитать работу, совершенную на данном криволинейном пути, необходимо расслоить поле между пластинами А и В некоторым количеством которые будут настолько близки одна к другой, что отдельные участки пути s между данными плоскостями можно будет считать прямыми.

В таком случае работа электрического поля, произведенная на каждом из данных отрезков пути, будет равняться A₁ = qEd₁, где d₁ — дистанция между двумя сопредельными плоскостями. А полная работа на всем пути d будет равняться произведению qE и суммы расстояний d₁, равной d. Таким образом, и в результате криволинейного пути совершенная работа будет равняться A = qEd.

Примеры, рассмотренные нами, показывают, что работа электрического поля по перемещению заряда из какой-либо точки в другую не зависит от формы пути передвижения, а зависит исключительно от положения данных точек в поле.

Кроме того, мы знаем, что работа, которая совершается силой тяжести при передвижении тела по наклонной плоскости, имеющей длину l, будет равняться работе, которую совершает тело при падении с высоты h, и высоте наклонной плоскости. Значит, работа или, в частности, работа при передвижении тела в поле тяжести, тоже не зависит от формы пути, а зависит только от разности высот первой и последней точек пути.

Так можно доказать, что таким важным свойством может обладать не только однородное, а и всякое электрическое поле. Похожим свойством обладает и сила тяжести.

Работа электростатического поля по перемещению точечного заряда из одной точки в другую определяется линейным интегралом:

A₁₂ = ∫ L₁₂q (Edl),

где L₁₂ — траектория движения заряда, dl — бесконечно малое перемещение вдоль траектории. Если контур замкнутый, то для интеграла используется символ ∫; в этом случае предполагается, что выбрано направление обхода контура.

Работа электростатических сил не зависит от формы пути, а только лишь от координат первой и последней точек перемещения. Следовательно, силы поля консервативны, а само поле — потенциально. Стоит отметить, что работа любой по замкнутому пути будет равняться нулю.

Работа сил электрического поля — Энциклопедия по машиностроению XXL

В механике было показано, что при перемещении между двумя точками в гравитационном поле работа силы тяжести не зависит от траектории движения тела. Силы гравитационного и электростатического взаимодействия имеют одинаковую зависимость от расстояния, векторы сил направлены вдоль прямой, соединяющей взаимодействующие точечные тела. Отсюда следует, что и при перемещении заряда в электрическом поле из одной точки в другую работа сил электрического поля не зависит от траектории его движения.  [c.137]
При изменении направления перемещения на 180° работа сил электрического поля, как и работа силы тяжести, изменяет знак на противоположный. Если при перемещении заряда q из точки В в точку С силы электрического поля совершили работу А, то при перемещении заряда q по тому же самому пути из точки С в точку В они совершают работу — А. Но так как работа не зависит  [c.137]

Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю. Это означает, что вектор силы F3 в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности.  [c.139]

Отсюда работа сил электрического поля при перемещении заряда равна произведению напряжения и между точками на заряд q  [c.139]

Работа и мощность электрического тока. Работу сил электрического поля, создающего электрический ток, называют работой тока. Работа А сил электрического поля или работа электрического тока на участке цепи с электрическим сопротивлением R за время At равна  [c.149]

Теперь можно поставить вопрос о том или ином ограничении объема V. Если поверхность а охватывает полностью тот объем, где имеется электромагнитное поле, то поток энергии сквозь нее равен нулю. В этом случае мы приходим к знакомому выражению закона сохранения изменение электромагнитной энергии равно работе сил электрического поля. Впрочем, такое утверждение нетривиально если j = с (Е + Ес р), то получается выражение для работы сторонних сил и джоулевой теплоты и мы убе-  [c.39]

Термоэлектронный ток. Поток свободных электронов, так называемая электронная эмиссия, возникает при нагревании электрода до высокой температуры. При достаточно высокой температуре кинетическая энергия части электронов становится больше работы сил электрического поля в поверхностном слое, и такие электроны вылетают из металла. Чем выше температура электрода, тем больше электронов вылетает за его пределы. Зависи-  [c.541]

Так как кинетическая энергия электрона обусловлена работой сил электрического поля еУ, то из закона сохранения энергии следует, что  [c.98]

Работа сил электростатического поля при движении электрического заряда по любой замкнутой траектории равна нулю.  [c.137]

Электродвижущая сила. Полная работа сил электростатического поля при движении зарядов по замкнутой цепи постоянного тока равна нулю. Следовательно, вся работа электрического тока в замкнутой электрической цепи оказывается совершенной за счет действия сторонних сил, вызывающих разделение зарядов внутри источника и поддерживающих постоянное напряжение на выходе источника тока. Отношение работы совершаемой сторонними силами по перемещению заряда q вдоль цепи, к значению этого заряда называется электродвижущей силой источника (ЭДС) W  [c.150]

Итак, работа сил тяготения, упругих сил и сил электрического поля, созданного электрическими зарядами, не зависит от пути и определяется только начальным и конечным положением точки приложения силы. Но в таком случае работа этих сил по любому замкнутому пути всегда должна быть равна нулю. Действительно, пусть  [c.127]

Всякая система тел, в которой действуют силы тяжести, упругие силы и силы электрического поля, созданного электрическими зарядами, обладает определенны.м ограниченным запасом работы, которую эти силы могут совершить. Этот запас работы, обусловленный конфигурацией тел системы, представляет собой потенциальную энергию системы.  [c.129]

Действительно, напряжение на пластинах при постоянном заряде пропорционально емкости конденсатора, емкость же обратно пропорциональна расстоянию между пластинами. Раздвигая их, мы затрачиваем работу по преодолению сил электрического поля, притягивающих разноименно заряженные пластины друг к другу, и уменьшаем тем самым емкость конденсатора. Но величина заряда на его пластинах остается постоянной,значит, повышается напряжение. Следовательно, количество электроэнергии, запасенной в конденсаторе, возрастает. Конечно, раздвигать и сдвигать пластины не очень удобно для этого нужна сложная механическая система, какой-то специальный двигатель. Нельзя ли обойтись и. без него Взглянув еще раз на формулу для подсчета емкости конденсатора, мы увидим, что емкость можно менять, не только раздвигая и сдвигая пластины, но и за счет диэлектрической постоянной прокладки. А эта величина меняется при изменении температуры. Попеременно нагревая и охлаждая конденсатор, мы можем менять его емкость и вырабатывать электроэнергию точно так же, как при раздвигании его пластин. Именно по такому пути пошли американцы.  [c.126]

Будем полагать, что изменение полной энергии жидкости в объеме V происходит благодаря переносу полной энергии втекающей и вытекающей массой, переносу тепла через границу молекулярным путем (теплопроводностью), работе внешних массовых и поверхностных сил, наличию внутренних источников теплоты. Другие возможные причины изменения полной энергии — перенос лучистой энергии, работа сил электрических или магнитных полей и т. д. — для простоты не учитываются. В соответствии со сказанным можно записать следую-  [c.14]

Это замечательное свойство силы тяжести позволяет значительно упростить решение задач, связанных с расчетом работы этой силы. Таким свойством обладают и многие другие силы, например силы всемирного тяготения (частным случаем которых является сила тяжести), силы упругости, силы электрического поля, создаваемого неподвижными зарядами, и др.  [c.230]

Работа внешних источников, идущая на преодоление сил электрического поля, при увеличении заряда на dq равна iA = q dq.  [c.57]

Электромеханические распылители работают следующим образом. На внутреннюю поверхность быстро вращающейся насадки подается дозированное количество лакокрасочного материала, растекающегося тонким слоем по поверхности и поступающего на коронирующую кромку. Под действием центробежных сил лакокрасочный материал срывается с кромки и дробится в плоскости, перпендикулярной оси вращения насадки. Дальнейшее высокодисперсное распыление и движение частиц лакокрасочного материала к окрашиваемому изделию обеспечивается электростатическими силами электрического поля.  [c.97]

При работе чашечных и грибковых распылителей направление сил электрического поля не совпадает с направлением действия центробежных сил (рис. 3.5). Если пренебречь влиянием гравитационных сил, то на частицу распыленного лакокрасочного материала в момент ее отрыва от кромки действуют следующие основ-  [c.98]

При работе генератора к селену и покровному сплаву поочередно подводится то отрицательный, то положительный потенциал переменного тока. В первом случае свободные электроны из покровного сплава под действием сил электрического поля в большом количестве проходят через запирающий слой в селен. В этот момент от выпрямителя поступает постоянный ток в цепь включенных потребителей.  [c.111]

Напряжение — отношение работы, совершаемое частицей, обладающей электрическим зарядом, и перемещаемой силами электрического поля из одной его точки в другую, к величине заряда этой частицы создается и поддерживается источниками тока (генератором, аккумулятором и т. п.) и вызывает в присоединенных к источнику цепях ток.  [c.430]

Разность потенциалов. Мерой изменения энергии при взаимодействиях тел является работа. Мы выяснили, что при перемещении электрического заряда q работа А сил электростатического поля равна изменению потенциальной энергии AWp заряда, взятому с противоположным знаком, поэтому из выражений (40.1) и (40.3) получаем  [c.138]

При перемещении электрического заряда в электростатическом поле работа сил поля равна произведению заряда на разность потенциалов начальной и конечной точек траектории движения заряда.  [c.138]

Как будет показано далее, равенство (40.9) может не вы полняться, если электрическое поле непотенциальное. В непотенциальных электрических полях работа сил поля при перемещении электрического заряда зависит от траектории движения заряда из одной точки в другую.  [c.139]

Так как кинетическая энергия электрона равна работе сил ускоряющего электрического поля, проекцию скорости электрона Vx можно найти из выражения  [c.204]

Дело сводится к явлениям электромагнитной индукции. Пусть в отсутствие магнитного поля скорость электрона на орбите была По- При включении магнитного поля за то время, пока напряженность поля меняется от нуля до Н, действует электродвижущая сила индукции, т. е. вихревое электрическое поле, линии которого расположены в плоскости, перпендикулярной к направлению изменяющегося магнитного потока. Это поле действует на электрон и в силу своего вихревого характера совершает некоторую работу даже при замкнутом пути электрона, изменяя кинетическую энергию его орбитального движения.  [c.626]

Этот случай совершенно аналогичен движению под действием постоянной силы тяжести. Работа зависит только от расстояния между перпендикулярными к направлению поля плоскостями, на которых лежат начальная и конечная точки перемещения. Если направление электрического поля условно считать направлением вниз , то работа силы зависит только от разности высот начальной и конечной точек перемещения. В частном случае, когда перемещение заряда происходит от одной обкладки конденсатора до другой, работа силы  [c.126]

Что касается работы силы, действующей со стороны магнитного поля на движущиеся в этом поле электрические заряды, т. е. силы  [c.128]

Выражение, аналогичное (4.9), мы уже получили выше, когда определяли скорость электрически заряженных частиц, ускоряемых электрическим полем (3.27). Была также найдена работа электрических сил в этом случае (4.5). Таким образом, мы уже получили выше вырал ение для кинетической энергии заряженной частицы, но не толковали его с этой точки зрения.  [c.138]

Запишем выражение для моп1ности, рассеиваемой в объеме V, которая равна работе сил электрического поля в единицу времени  [c.38]

Так как работа сил электростатического поля при перемещении заряда из одной точки пространства в другую не зависит от траектории движения заряда рлежду этими точками, то разность потенциалов ф — (р2 двух точек электрического поля является величиной, не зависящей от траектории движения заряда. Разность потенциалов, следовательно, может служить энергети-  [c.138]

В системе тел, в которой действуют только силы тяжести, упругие силы и силы электрического поля, созданного электрическими зарядами, всякая работа этих сил связана с изменгнием конфигурации (так как, когда система вернулась к прежней конфигурации, работа всех этих сил должна быть равна нулю). Если силы, действующие в системе, совершаЕОт положительную работу, то конфигурация при этом всегда изменяется так, что в конце концов способность системы совершагь работу оказывается исчерпанной. Например, если сила растянутой пружины совершает положительную работу, то при этом пружина сокращается. В конце концов пружина сократится до нормальной длины и не сможет далее совершать работу. Растянутая пружина обладает определенным ограниченным запасом работы, которую она мол-сет совершить. Величина этого запаса работы определяется начальным растяжением пружины, т. е. ее начальной конфигурацией.  [c.129]

При рассмотрении в рамках механики движений электрически заряженных частиц в электрических и магнитных полях мы, как уже указывалось, вынуждены пренебрегать эффектом излучения электромагнитной энергии этими частицами и теми тормозящими силами, которые при этом действуют со стороны излучаемого поля на частицы. (Что эти силы должны тормозить движение частиц, ясно из энергетических соображений на создание энергии излучения затрачивается часть работы сил ускоряющего поля, т. е. часть работы этих сил идет на преодоление сил, действующих со стороны излучаемого поля.) В ускорителях больших энергий потери энергии на алектрбмагнитное излучение могут играть существенную роль и положить предел  [c.222]

Потенциал (у), напряжение, электро-движующая сила (и, Е, э. д. с.). Потенциал (точки представляет собой отношение работы, совершаемой силами электрического поля при переносе заряда Q из данной точки в бесконечность, к величине заряда. Разность потенциалов двух точек, или напряжение между ними, есть отношение энергии, затрачиваемой зарядом Q при перемещении между заданными точками, к величине заряда, т. е. tp] — tf2 = Ы12. Часто за точку нулевого потенциала принимают потенциал земли и относительно его определяют разность потенциалов.  [c.513]

Первый из них основан на генерации электрической энергии в результате работы, совершаемой продуктами радиоактивного распада (заряженными частицами) против сил электрического поля. Электрическая энергия в таком устройстве получается непосредственно, без преобразования других видов энергии. По конструкции эти батареи представляют собой две концентрические или парал-лельныеповерхности, разделенные зазором, который может быть или отвакуумирован, или заполнен диэлектриком. Одна из поверхностей, на которую наносится радиоактивный изотоп, служит излучателем, а другая — коллектором. Электроны, испускаемые излучателем, собираются на коллекторе и заряжают его отрицательно по отношению к излучателю. Максимальная разность потенциалов на электродах ограничивается энергией заряженных частиц и обычно достигает нескольких киловольт. Сила тока батареи зависит от интенсивности радиоактивного источника.  [c.142]

Работа, совершенная электрическим полем Е в направлении х при увеличении на бд (координаты остаются фиксированными при 5 г), равна Е8рх = Еа бд,.. Поэтому обобщенная сила, соответствующая г-й моде, равна а Ео ехр (гсо ). Координата д удовлетворяет уравнению  [c.565]

Пламли [612] учел силы инерции, поле вязкого потока и распределение плотности заряда на поверхности взаимодействующих капель, а также внешнее электрическое поле. Его результаты представлены на фиг. 10.14 в виде зависимости эффективности столкновений между заряженными каплями от их заряда. Для заряда был выбран закон пропорциональности квадрату радиуса капли, предложенный в работе [296] [уравнение (10.6)].  [c.478]

Природа сил Xj различная, могут быть силы электрического или магнитного поля, механические и другие силы. Соответственно под координатами понимается не только положение системы в пространстве, но и состояние ее деформации, электризации, намагниченности и др. Речь идет, таким образом, об обобщенных силах X,- и обобщенных внешних координатах системы Vj. Обобш,ение состоит, в частности, в том, что в отличие от истинных механических сил и координат обобщенные силы и координаты могут иметь иную размерность при условии, что их произведение имеет размерность энергии. Например, сила, деленная на площадь, равняется давлению (Р), а изменение расстояния в направлении действия этой силы, умноженное на площадь граничной поверхности, — это изменение объема системы (dl ). Поэтому элементарная механическая работа против сил изотропного внешнего давления записывается в термодинамике как работа расширения системы  [c.43]

Вихрелое олектричсское поле отличается от электростатического поля тем, что оно не связано с электрическими зарядами, его линии напряженности прадстав-ляют собой замкнутые линии. Работа сил вихревого электрического поля при движении электри-  [c.189]

Магнитное поле при включении не сразу достигает своей конечной величины, а устанавливается в течение определенного промежутка времени. Этот промежуток времени настолько велик по сравнению с периодом обращения эле Строна, что весь процесс можно рассматривать как очень медленный, подобно квазистатическим процессам в термодинамике. Поэтому в каждый момент времени должно соблюдаться равенство между суммой квазиупругой силы и силы Лоренца, с одной стороны, и центростремительной силой — с другой. Однако центростремительная сила будет меняться, потому что возрастание магнитного поля по закону электромагнитной индукции влечет за собой появление вихревого электрического поля с осью симметрии, совпадающей с направлением магнитного поля. Именно это электрическое поле в силу своего вихревого характера ускоряет электрон, изменяя кинетическую энергию его орбитального движения. Сила Лоренца не может изменить частоту обращения, так как она направлена перпендикулярно к скорости и, следовательно, никакой работы совершить не может.  [c.108]

---

B5: Работа, совершаемая электрическим полем и электрическим потенциалом

Когда заряженная частица перемещается из одного положения в электрическом поле в другое положение в том же самом электрическом поле, электрическое поле действует на частицу. Проделанная работа консервативна; следовательно, мы можем определить потенциальную энергию для случая силы, действующей со стороны электрического поля. Это позволяет нам использовать концепции работы, энергии и сохранения энергии при анализе физических процессов с участием заряженных частиц и электрических полей.

Мы определили работу, совершаемую над частицей силой, как силу на пути, умноженную на длину пути, с оговоркой, что когда составляющая силы вдоль пути различается на разных участках пути необходимо разделить путь на сегменты, на каждом из которых сила вдоль пути имеет одно значение для всего сегмента, вычислить работу, проделанную на каждом сегменте, и сложить результаты.

Давайте исследуем работу, совершаемую электрическим полем над заряженной частицей, когда она движется в электрическом поле, в довольно простом случае однородного электрического поля.Например, давайте посчитаем работу, совершаемую над положительно заряженной частицей заряда q, когда она движется из точки \ (P_1 \) в точку \ (P_3 \)

по пути: «От \ (P_1 \) прямо в точку \ (P_2 \), а оттуда прямо в \ (P_3 \) ». Обратите внимание, что нам не говорят, что заставляет частицу двигаться. В этой проблеме нас это не волнует. Возможно, заряженная частица находится на конце кварцевого стержня (кварц — хороший изолятор), и человек, который держит стержень за другой конец, перемещает стержень так, чтобы заряженная частица двигалась, как указано.

Вдоль первой части пути, от \ (P_1 \) до \ (P_2 \), сила, действующая на заряженную частицу, перпендикулярна пути.

У силы нет составляющей на пути, поэтому она вообще не действует на заряженную частицу, когда заряженная частица движется из точки \ (P_1 \) в точку \ (P_2 \).

\ [W_ {12} = 0 \]

Из \ (P_2 \) частица направляется прямо в \ (P_3 \).

На этом участке пути (от \ (P_2 \) до \ (P_3 \)) сила точно совпадает с направлением движения частицы.

Таким образом, работа — это просто величина силы, умноженная на длину сегмента пути:

\ [W_ {23} = Fb \]

Величина силы — это заряд частицы, умноженный на величина электрического поля \ (F = qE \), поэтому,

\ [W_ {23} = qEb \]

Таким образом, работа, совершаемая электрическим полем над заряженной частицей, когда частица движется из точки \ (P_1 \) к \ (P_3 \) по указанному пути:

\ [W_ {123} = W_ {12} + W_ {23} \]

\ [W_ {123} = 0 + qEb \]

\ [W_ {123} = qEb \]

Теперь давайте посчитаем работу, совершаемую над заряженной частицей, если она претерпевает такое же смещение (от \ (P_1 \) к \ (P_3 \)), но делает это, двигаясь прямой путь, прямо из \ (P_1 \) в \ (P_3 \).

Сила, действующая на положительно заряженную частицу, находящаяся в том же направлении, что и электрическое поле, вектор силы составляет угол \ (\ theta \) с направлением пути и выражением

\ [W = \ vec { F} \ cdot \ vec {\ Delta r} \]

для работы становится

\ [W_ {13} = F c \, cos \ theta \]

\ [W_ {13} = qE c \, cos \ theta \]

Анализируя заштрихованный треугольник на следующей диаграмме:

, мы обнаруживаем, что \ (cos \ theta = \ frac {b} {c} \).Подставляя это в наше выражение для работы (\ (W_ {13} = qE c \, cos \ theta \)), получаем

\ [W_ {13} = qEc \ frac {b} {c} \]

\ [W_ {13} = qEb \]

Это тот же результат, который мы получили для работы, совершаемой над заряженной частицей электрическим полем, когда частица перемещалась между теми же двумя точками (от \ (P_1 \) к \ (P_3 \)) по другому пути (от \ (P_1 \) до \ (P_2 \) до \ (P_3 \)). Оказывается, работа выполняется одинаково, независимо от того, какой путь проходит частица от \ (P_1 \) к \ (P_3 \).Я не хочу тратить время на то, чтобы доказать это здесь, но я хотел бы исследовать еще один путь (не столько для получения результата, сколько для того, чтобы рассмотреть важный момент о том, как рассчитать трудозатраты). Ссылаясь на схему:

Рассчитаем работу, совершаемую над частицей с зарядом \ (q \) электрическим полем, когда частица движется от \ (P_1 \) к \ (P_3 \) по пути “ из \ (P_1 \) прямо в \ (P_4 \), из \ (P_4 \) прямо в \ (P_5 \) и из \ (P_5 \) прямо в \ (P_3 \).”От \ (P_1 \) до \ (P_4 \) сила в том же направлении, что и направление, в котором движется частица по траектории, поэтому

\ [W_ {14} = F (b + d ) \]

\ [W_ {14} = qE (b + d) \]

От точки \ (P_4 \) до \ (P_5 \) сила, действующая на заряженную частицу электрическим полем, находится справа под углом к ​​траектории, поэтому сила не действует на заряженную частицу на отрезке от \ (P_4 \) до \ (P_5 \).

\ [W_ {45} = 0 \]

На отрезке от \ (P_5 \) до \ (P_3 \),

сила действует прямо противоположно направлению, в котором движется частица. .Это означает, что работа, совершаемая силой электрического поля на заряженной частице при движении частицы от \ (P_5 \) к \ (P_3 \), является отрицательной величиной силы, умноженной на длину отрезка пути. Таким образом,

\ [W_ {53} = — Fd \]

\ [W_ {53} = — qEd \]

и

\ [W_ {1453} = W_ {14} + W_ {45} + W_ {53} \]

\ [W_ {1453} = qE (b + d) +0 + (- qEd) \]

\ [W_ {1453} = qEb \]

Как указано в рекламе, мы получаем то же результат работы, проделанной над частицей, когда она движется от \ (P_1 \) к \ (P_3 \) по «\ (P_1 \) к \ (P_4 \) к \ (P_5 \) к \ (P_3 \)» как мы сделали на двух других путях.

Всякий раз, когда работа, выполняемая над частицей силой, действующей на эту частицу, когда эта частица перемещается из точки \ (P_1 \) в точку \ (P_3 \), остается неизменной, независимо от того, какой путь принимает частица на пути из точки \ (P_3 \). \ (P_1 \) to \ (P_3 \), мы можем определить функцию потенциальной энергии для силы. Функция потенциальной энергии — это присвоение значения потенциальной энергии каждой точке пространства. Такое назначение позволяет нам вычислить работу, совершаемую частицей силой, когда частица движется из точки \ (P_1 \) в точку \ (P_3 \), просто вычитая значение потенциальной энергии частицы в точке \ (P_1 \) от значения потенциальной энергии частицы в \ (P_3 \) и взятия отрицательного результата.Другими словами, работа, совершаемая над частицей силой электрического поля, когда частица переходит из одной точки в другую, является просто отрицательной величиной изменения потенциальной энергии частицы.

При определении функции потенциальной энергии для случая частицы заряда \ (q \) в однородном электрическом поле \ (\ vec {E} \), (бесконечный набор векторов, каждый из которых указывает на одно и то же и каждый из них имеет одну и ту же величину \ (E \)), мы в значительной степени полагаемся на ваше понимание гравитационной потенциальной энергии у поверхности Земли.Вблизи поверхности Земли, как мы говорили в первом томе этой книги, существует однородное гравитационное поле (векторное поле силы на массу), направленное вниз. На частицу с массой \ (m \) в этом поле действует сила «\ (mg \), направленная вниз» в любом месте вблизи поверхности Земли. В этом случае потенциальная энергия частицы массы \ (m \) определяется выражением \ (mgy \), где \ (mg \) — величина направленной вниз силы, а \ (y \) — высота, на которой частица выше произвольно выбранного контрольного уровня.Для простоты сравнения со случаем электрического поля мы теперь описываем опорный уровень для гравитационной потенциальной энергии как плоскость, перпендикулярную гравитационному полю \ (g \), векторному полю силы на массу; а также; мы называем переменную \ (y \) «чистым» расстоянием (расстояние в направлении, противоположном направлению гравитационного поля), на котором частица находится от плоскости отсчета. (Итак, мы называем направление, в котором указывает гравитационное поле, направление, которое, как вы знаете, должно быть нисходящим, направлением «слабого поля».)

Теперь перейдем к случаю однородного электрического поля. Как и в случае с гравитационным полем у поверхности Земли, сила, действующая на жертву со стороны однородного электрического поля, имеет одну и ту же величину и направление в любой точке пространства. Конечно, в случае электрического поля сила равна \ (qE \), а не \ (mg \), и характеристика жертвы, которая имеет значение, — это заряд \ (q \), а не масса \ (m \). Мы называем направление, в котором направлено электрическое поле, направлением «слабого поля», а противоположное направление — направлением «сильного поля».Теперь мы произвольно определяем плоскость, перпендикулярную электрическому полю, как плоскость отсчета для электрической потенциальной энергии частицы заряда \ (q \) в электрическом поле. Если мы назовем \ (d \) расстояние, на котором заряженная частица находится от плоскости в направлении сильного поля, то потенциальная энергия частицы с зарядом \ (q \) будет равна

\ [U = qEd \]

, где

\ (U \) — электрическая потенциальная энергия заряженной частицы,

\ (q \) — заряд частицы,

\ (E \) — величина каждого вектора электрического поля, создающего вверх по однородному электрическому полю, а

\ (d \) — это «сильное поле», на котором частица находится от плоскости отсчета \ (U = 0 \).

Давайте убедимся, что это выражение для функции потенциальной энергии дает результат, который мы получили ранее для работы, проделанной над частицей с зарядом \ (q \) однородным электрическим полем, изображенным на следующей диаграмме, когда частица движется из \ (P_1 \) — \ (P_3 \)

Как вы можете видеть, я выбрал (для моего удобства), чтобы опорная плоскость находилась в самом нижнем положении, имеющем отношение к проблеме. При таком выборе частица с зарядом \ (q \), когда она находится в \ (P_1 \), имеет потенциальную энергию \ (qEb \) (поскольку точка \ (P_1 \) находится на расстоянии \ (b \) «в поле» от плоскости отсчета) и, когда она находится в \ (P_3 \), частица заряда \ (q \) имеет потенциальную энергию \ (0 \), поскольку \ (P_3 \) находится на плоскости отсчета.

\ [W_ {13} = — \ Delta U \]

\ [W_ {13} = — (U_3-U_1) \]

\ [W_ {13} = — (0-qEb) \]

\ [W_ {13} = qEb \]

Это действительно результат, который мы получили (для работы, совершаемой электрическим полем над частицей с зарядом \ (q \), когда эта частица перемещалась из \ (P_1 \) to \ (P_3 \)) другими тремя способами, которыми мы рассчитали эту работу.

Авторы и авторство

Электрическое поле и движение заряда

Возможно, одним из самых полезных, но само собой разумеющихся достижений последних веков является разработка электрических цепей.Поток заряда по проводам позволяет нам готовить пищу, освещать дома, кондиционировать нашу работу и жилое пространство, развлекать нас фильмами и музыкой и даже позволяет нам безопасно ездить на работу или в школу. В этом разделе Физического класса мы исследуем причины, по которым заряд течет по проводам электрических цепей, и переменные, которые влияют на скорость, с которой он течет. Средства, с помощью которых движущийся заряд передает электрическую энергию приборам для их работы, будут подробно рассмотрены.

Один из фундаментальных принципов, который необходимо понять, чтобы понять электрические цепи, относится к концепции того, как электрическое поле может влиять на заряд внутри цепи, когда он перемещается из одного места в другое. Понятие электрического поля впервые было введено в разделе «Статическое электричество». В этом блоке электрическая сила описывалась как неконтактная сила. Заряженный воздушный шар может оказывать притягивающее воздействие на противоположно заряженный воздушный шар, даже когда они не находятся в контакте.Электрическая сила действует на расстоянии, разделяющем два объекта. Электрическая сила — это сила, действующая на расстоянии.

Силы действия на расстоянии иногда называют полевыми силами. Концепция полевой силы используется учеными для объяснения этого довольно необычного явления силы, которое происходит при отсутствии физического контакта. На пространство, окружающее заряженный объект, влияет наличие заряда; в этом пространстве устанавливается электрическое поле.Заряженный объект создает электрическое поле — изменение пространства или поля в окружающей его области. Другие заряды в этой области почувствовали бы необычное изменение пространства. Независимо от того, входит заряженный объект в это пространство или нет, электрическое поле существует. Пространство изменяется присутствием заряженного объекта; другие объекты в этом пространстве испытывают странные и таинственные качества космоса. По мере того, как другой заряженный объект входит в пространство и перемещается на все глубже и глубже в поле, действие поля становится все более и более заметным.

Электрическое поле — это векторная величина, направление которой определяется как направление, в котором положительный тестовый заряд будет выдвигаться при помещении в поле. Таким образом, направление электрического поля около положительного заряда источника всегда направлено от положительного источника. И направление электрического поля около отрицательного заряда источника всегда направлено в сторону отрицательного источника.

Электрическое поле, работа и потенциальная энергия

Электрические поля подобны гравитационным полям — оба связаны с силами, действующими на расстоянии.В случае гравитационных полей источником поля является массивный объект, а силы воздействия на расстоянии действуют на другие массы. Когда концепция силы тяжести и энергии обсуждалась в Блоке 5 Физического Класса, было упомянуто, что сила тяжести является внутренней или консервативной силой. Когда гравитация воздействует на объект, перемещая его с высокого места на более низкое, общее количество механической энергии объекта сохраняется. Однако во время падающего движения произошла потеря потенциальной энергии (и увеличение кинетической энергии).Когда гравитация воздействует на объект, перемещая его в направлении гравитационного поля, объект теряет потенциальную энергию. Потенциальная энергия, изначально запасенная внутри объекта в результате его вертикального положения, теряется, когда объект движется под действием гравитационного поля. С другой стороны, для перемещения массивного объекта против его гравитационного поля потребуется энергия. Стационарный объект не будет естественно двигаться против поля и получать потенциальную энергию. Энергия в форме работы должна быть передана объекту внешней силой, чтобы он достиг этой высоты и соответствующей потенциальной энергии.

Важный момент, который следует сделать из этой аналогии с гравитацией, заключается в том, что внешняя сила должна совершать работу, чтобы переместить объект против природы — от энергии с низким потенциалом к ​​энергии с высоким потенциалом. С другой стороны, объекты естественным образом переходят от энергии с высоким потенциалом к ​​энергии с низким потенциалом под действием силы поля. Для объектов просто естественно переходить от высокой энергии к низкой; но требуется работа, чтобы переместить объект с низкой энергии на высокую.

Аналогичным образом, чтобы переместить заряд в электрическом поле против его естественного направления движения, потребуется работа. Работа внешней силы, в свою очередь, добавит объекту потенциальной энергии. Естественное направление движения объекта — от высокой энергии к низкой энергии; но работа должна быть проделана, чтобы переместить объект против натуры . С другой стороны, не потребуется работы, чтобы переместить объект из места с высоким потенциалом энергии в место с низким потенциалом энергии.Когда этот принцип логически распространяется на движение заряда в электрическом поле, связь между работой, энергией и направлением движения заряда становится более очевидной.

Рассмотрим диаграмму выше, на которой положительный заряд источника создает электрическое поле, а положительный тестовый заряд движется против поля и вместе с ним. На диаграмме A положительный тестовый заряд перемещается против поля из точки A в точку B. Перемещение заряда в этом направлении было бы подобно движению против природы.Таким образом, потребуется работа, чтобы переместить объект из местоположения A в местоположение B, и положительный тестовый заряд будет приобретать потенциальную энергию в процессе. Это было бы аналогично перемещению массы в восходящем направлении; потребовалась бы работа, чтобы вызвать такое увеличение потенциальной гравитационной энергии. На схеме B положительный тестовый заряд перемещается с полем из точки B в точку A. Это движение было бы естественным и не требовало работы внешней силы. Положительный тестовый заряд будет терять энергию при перемещении из точки B в точку A.Это было бы аналогично падению массы вниз; это произойдет естественным образом и будет сопровождаться потерей гравитационной потенциальной энергии. Из этого обсуждения можно сделать вывод, что место с высокой энергией для положительного тестового заряда — это место, ближайшее к положительному исходному заряду; а место с низким энергопотреблением находится дальше всего.

Вышеупомянутое обсуждение относилось к перемещению положительного тестового заряда в электрическом поле, созданном положительным зарядом источника. Теперь рассмотрим движение того же положительного пробного заряда в электрическом поле, создаваемом отрицательным зарядом источника.Тот же принцип в отношении работы и потенциальной энергии будет использоваться для определения местоположений высокой и низкой энергии.

На схеме C положительный тестовый заряд движется из точки A в точку B в направлении электрического поля. Это движение было бы естественным — как масса, падающая на Землю. Для того, чтобы вызвать такое движение, не потребуется работа, и это будет сопровождаться потерей потенциальной энергии. На схеме D положительный тестовый заряд движется из точки B в точку A против электрического поля.Потребуется работа, чтобы вызвать это движение; это было бы аналогично увеличению массы в гравитационном поле Земли. Поскольку энергия передается испытательному заряду в виде работы, положительный испытательный заряд будет приобретать потенциальную энергию в результате движения. Из этого обсуждения можно сделать вывод, что место с низкой энергией для положительного испытательного заряда — это место, ближайшее к отрицательному заряду источника, а место с высокой энергией — это место, наиболее удаленное от отрицательного заряда источника.

Когда мы начнем обсуждать схемы, мы применим эти принципы, касающиеся работы и потенциальной энергии, к движению заряда по цепи. Как мы здесь рассуждали, перемещение положительного тестового заряда против электрического поля потребует работы и приведет к увеличению потенциальной энергии. С другой стороны, положительный тестовый заряд будет естественным образом перемещаться в направлении поля без необходимости работы с ним; это движение приведет к потере потенциальной энергии.Прежде чем применять это к электрическим цепям, нам нужно сначала изучить значение концепции электрического потенциала.

Да, вы можете нанести на карту электрическое поле дома

Но как насчет численного значения электрического поля между этими проводящими пластинами? Если я просто пройду прямо посередине от одной пластины к другой, я могу получить значения электрического потенциала для разных значений y.Вот как это выглядит:

Вспомните взаимосвязь между электрическим полем и потенциалом. Электрическое поле — это отрицательная величина изменения потенциала, деленная на изменение положения. Если вы построите график зависимости потенциала от положения, это то же самое, что и наклон. Обратите внимание, что график выше является линейной функцией. Это означает, что наклон и, следовательно, электрическое поле постоянны. По наклону я получаю постоянное электрическое поле 0,713 вольт на см (0,00713 В / м). О, 1 В / м — это ньютон на кулон.Оба являются эквивалентными единицами измерения электрического поля.

Но подождите! Электрическое поле связано с электрической силой, а это значит, что оно должно быть вектором. Вычисленное выше значение основано на наклоне, поэтому это просто скалярное значение. Что ж, это легко исправить. Поскольку я построил потенциал относительно положения y , это дает мне y компонент электрического поля. Чтобы найти компонент x , мне также нужно построить электрический потенциал в этом направлении.

Но в этом случае потенциал действительно не сильно меняется в направлении x . Это означает, что x-компонента электрического поля будет равна нулю В / м. Честно говоря, это хорошая особенность этих параллельных проводящих пластин — они создают постоянное электрическое поле в одном направлении.

Зачем нам бумага?

Итак, это краткое введение в электрические поля и разность электрических потенциалов. Теперь ответ на важный вопрос, который вы не задавали:

Предположим, я возьму 9-вольтовую батарею и с помощью нескольких проводов соединю клеммы с двумя параллельными полосами из алюминиевой фольги, разделенными расстоянием 10 см — без каких-либо бумага.Могу ли я повторить этот эксперимент, чтобы рассчитать электрическое поле между этими пластинами?

Ответ — нет. Я имею ввиду, это должно работать . Теория состоит в том, что у вас есть изменение потенциала на двух кусках алюминия и изменение расстояния. Поскольку у вас две параллельные пластины, электрическое поле должно быть довольно постоянным. Но это не сработает. Если вы возьмете вольтметр и подключите один щуп к отрицательной полосе, а второй поместите прямо посередине, он должен показать 4.5 вольт. Вместо этого он будет показывать ноль вольт.

Электрическая потенциальная энергия (U) и электрический потенциал (V): (Примечания из C

Электрическая потенциальная энергия (U) и электрический потенциал (V): ( Записи лекций К. Эркалса PHYS 221 )

Рассмотрим конденсатор с параллельными пластинами, который производит однородную электрическое поле между его большими пластинами. Это достигается путем подключения каждой пластины к одному из выводов источник питания (например, аккумулятор).

Рисунок 1: Электрическое поле создается заряженными пластинами. разделенные расстоянием l. Обвинения на пластинах стоят + Q и Q.

Рисунок 2: Электрический заряд q перемещается из точки A в сторону точка B с внешней силой T против электрической силы qE.

Рис. 3, 4: Когда он перемещается на расстояние d, его потенциальная энергия в точке B равна qEd относительно точки A.

Рисунок 5: При отпускании из B (T = 0) он будет ускоряться к нижней пластине. Как он движется по направлению к нижней пластине его потенциальная энергия уменьшается, а кинетическая энергия увеличивается. Когда он достигает нижнего пластина (где мы можем выбрать потенциальную энергию равной нулю), ее потенциал энергия в точке A полностью преобразуется в кинетическую энергию в точке B:

Обратите внимание, что qEd — это работа, выполняемая полем в качестве заряда движется под действием силы qE от B к A.Здесь m — масса заряда q, а v — его скорость при достижении точка А. Здесь мы предположили, что электрическая поле однородное! Работы по E field:

Давайте вспомним теорему о кинетической энергии-работе (Work Energy принцип):

, где мы ввели понятие потенциальной энергии и консервативная сила (сила, под которой можно определить потенциальную энергию так что проделанная работа зависит только от разницы потенциальной энергии функция оценивается в конечных точках).

Практическое правило определения того, является ли EPE увеличение:

Если заряд движется в том направлении, при нормальном движении его электрическая потенциальная энергия уменьшается. Если заряд движется в противоположном направлении к тому, что он обычно двигался бы, его электрическая потенциальная энергия увеличивается. Эта ситуация похожа на ситуацию постоянное гравитационное поле (g = 9,8 м / с ² ). Когда вы поднимаете предмет, вы увеличивая его гравитационную потенциальную энергию.Аналогичным образом, когда вы опускаете объект, его гравитационная энергия равна уменьшается.

Общая формула потенциальной разницы:

Работа, выполняемая полем E, когда оно действует на заряд q для перемещения. он от точки A до точки B определяется как разность электрических потенциалов между точки A и B:

Ясно, что потенциальную функцию V можно сопоставить каждому точка в пространстве, окружающем распределение заряда (например, параллельное тарелки).Приведенная выше формула обеспечивает простой рецепт для расчета работы, проделанной при перемещении заряда между двумя точками где мы знаем значение разности потенциалов. Приведенные выше утверждения и формула действительны независимо от путь, по которому перемещается заряд. Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив интегрирование по простому пути (например, по прямой) из точки A расстояние от Q которого равно r до бесконечности.Путь выбирается по радиальной линии, так что становится просто Edr. Поскольку электрическое поле Q равно kQ / r ² ,

Этот процесс определяет электрический потенциал точечного плата. Обратите внимание, что потенциальная функция скалярная величина в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал энергия системы зарядов или зарядовых распределений.Предположим, мы вычисляем проделанную работу относительно электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от заряд Q. Работу выдал:

Обратите внимание, что если q отрицательное, его знак должен использоваться в уравнение! Следовательно, система состоящий из отрицательного и положительного точечного заряда, имеет отрицательный потенциальная энергия.

Отрицательная потенциальная энергия означает, что работа должна быть выполнена против электрического поля при раздвижении зарядов!

Теперь рассмотрим более общий случай, связанный с потенциал в окрестности ряда зарядов, как показано на рисунке ниже:

Пусть r ₁ , r ₂ , r ₃ будет расстояния зарядов до точки поля А, а r ₁₂ , r ₁₃ , r ₂₃ представляют собой расстояние между зарядами.Электрический потенциал в точке А равен:

.

Пример:

Если мы принесем заряд Q из бесконечности и поместим его в точку A проделанная работа будет:

Суммарная электрическая потенциальная энергия этой системы обвинения, а именно, работа, необходимая для того, чтобы довести их до их нынешних должностей, может быть рассчитывается следующим образом: сначала приведите q1 (нулевая работа, так как нет заряда еще), затем в поле q1 вывести q2, затем в поля q1 и q2 принести q3.Добавьте всю работу, необходимую для вычислить общую работу. Результат будет:

Обнаружение электрического поля по электрическому потенциалу:

Компонент E в любом направлении является отрицательным скорость изменения потенциала с расстоянием в этом направлении:

Символ называется Градиент. Электрическое поле — это градиент электрического потенциала.Линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.

Поверхности равных хвостов:

Это воображаемые поверхности, окружающие заряд. распределение. В частности, если распределение заряда сферическое (точечный заряд или однородно заряженная сфера), поверхности сферические, концентрические с центром заряда распределение. Линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.Уравнение означает, что из-за отрицательный знак, направление E противоположно направлению, в котором V увеличивается; E направлен с более высоких уровней V на более низкие (с более высоких потенциал для снижения потенциала). Другой словами, градиент скаляра (в данном случае E-поля) нормален к поверхности постоянного значения (эквипотенциальная поверхность) скаляра и в направлении максимальная скорость изменения постоянного скаляра. Запомните это утверждение, когда мы проводим эксперимент.

Электрическая потенциальная энергия

Электрическая потенциальная энергия
следующий: Электрический потенциал Up: Электрический потенциал Предыдущее: Электрический потенциал

Электрическая потенциальная энергия Рассмотрим заряд, помещенный в однородное электрическое поле. ( например, , поле между двумя противоположно заряженными, параллельными проводящие пластины).Предположим, что мы очень медленно перемещаем заряд векторным смещением по прямой. Сколько работы мы должны выполнить чтобы добиться этого? Что ж, сила, которую мы должны приложить к заряду, равной и противоположной электростатической силе, испытываемой зарядом ( т.е. , мы должны преодолеть электростатическую силу, действующую на заряд, прежде чем мы свободно перемещать). Объем работы, которую мы выполняем при перемещении заряда, — это просто произведение силы. мы оказывают, и смещение заряда в направлении этой силы .Предположим, что вектор смещения образует угол с электрическое поле. Следует, что

(76)

Таким образом, если мы перемещаем положительный заряд в направлении электрического поля, мы делаем отрицательную работу ( т.е. , мы получаем энергию). Так же, если мы переместим положительный заряд в направлении, противоположном электрическому полю затем мы делаем положительную работу (, т.е. , мы теряем энергию).

Рассмотрим набор точечных зарядов, распределены в пространстве, которые жестко зажаты в таком положении, что не могут двигаться.Мы уже знаем, как рассчитать электрическое поле, создаваемое таким распределение заряда (см. раздел 3). В общем, этот электрический поле будет неоднородный. Предположим, что мы помещаем заряд в поле, скажем, в точке а также затем медленно переместите его по кривой в другую точку. Сколько работы мы должны выполнить, чтобы добиться этого? Разделим путь заряда от точки к точке в серию отрезков прямой, где ый отрезок имеет длину и образует угол с местное электрическое поле.Если мы сделаем достаточно большим, мы сможем адекватно представить любой изогнутый путь между и, и мы также можем гарантировать что примерно одинаково на всем отрезке пути. Простым обобщение уравнения. (76) работа, которую мы должны выполнять при перемещении заряд от точки к точке

(77)

Наконец, переходя к пределу, уходящему в бесконечность, правая часть вышеприведенное выражение становится линейным интегралом:

(78)

Давайте теперь рассмотрим частный случай, когда точка идентична точке .Другими словами, случай, когда мы перемещаем заряд по замкнутому контуру в электрическом поле. Сколько работы мы должны выполнить, чтобы этого добиться? На самом деле можно доказать, используя довольно мощную математику, что чистая работа, выполняемая, когда заряд перемещается по замкнутому контуру в электрическое поле, создаваемое фиксированными зарядами, составляет ноль . Тем не мение, нам не нужно быть математическими гениями, чтобы понять, что это разумный результат. Предположим, ради аргумента, что сетевая работа выполняется, когда мы берем на себя заряд некоторого замкнутый контур в электрическом поле не равен нулю.Другими словами, мы теряем энергию каждый раз, когда мы проводим заряд по петле в одном направлении, но получаем энергию каждый раз проводим заряд по петле в обратном направлении. Этот следует из уравнения. (77), потому что, когда мы меняем направление циркуляции вокруг петли электрическое поле на -м участке пути не изменяется, но, поскольку заряд движется по отрезку в обратном направлении, , и, следовательно, . Выберем перемещение заряда по петле в направлении в котором мы получаем энергию.Итак, мы перемещаем заряд один раз по петле, и в процессе мы получаем определенное количество энергии. Откуда эта энергия? Позволь нам рассмотреть возможности. Может быть, электрическое поле подвижного заряда отрицательно влияет на фиксированные расходы, поэтому что последние заряды теряют энергию, чтобы компенсировать энергию, которая мы получаем? Но фиксированные платежи не могут двигаться, и поэтому с ними невозможно работать. Может электрическое поле теряет энергию, чтобы компенсировать энергию, которая мы получаем? (Напомним, из предыдущего раздела, что существует энергия, связанная с с электрическим полем, заполняющим пространство).Но все обвинения (, т.е. , фиксированные сборы и движимый сбор) находятся в одном и том же положении до и после того, как мы возьмем подвижный заряд вокруг петли, и поэтому электрическое поле то же самое до и после (поскольку по закону Кулона электрическое поле зависит только от положений и величины зарядов), а значит, энергия поля должна быть то же до и после. Таким образом, мы имеем ситуацию, когда мы берем заряжаются вокруг замкнутого контура в электрическом поле и в процессе получают энергию, но ничего не теряет энергию.Другими словами, энергия появляется из « разреженный воздух », что явно нарушает первый закон термодинамики. Единственный способ избежать этого абсурдного вывода — это если мы примем следующее правило:

Работа, выполненная при взятии заряда по замкнутому контуру в электрическом поле, создаваемое фиксированными платежами, равно нулю.

Одним из следствий приведенного выше правила является то, что работа, выполняемая при перемещении заряд между двумя точками и в таком электрическом поле независимый пути между этими точками.Это легко доказать. Рассмотреть возможность два разных пути, 1 и 2, между точками и. Пусть работа сделана, взяв на себя ответственность от и до путь 1 быть, и работа, проделанная при принятии заряда от до вдоль путь 2 быть. Давайте возьмем на себя ответственность от до по пути 1, а затем от по пути 2. Сеть работа, проделанная для принятия заряда по этому замкнутому контуру, составляет. Поскольку мы знаем, что эта работа должна быть равна нулю, отсюда сразу следует это. Таким образом, у нас есть новое правило:

Работа, выполняемая при переносе заряда между двумя точками в электрическом поле. генерируемые фиксированными зарядами, не зависят от пути, пройденного между точками.

Сила, обладающая особым свойством, заключающимся в том, что работа по ее преодолению для перемещения тела между двумя точками в пространстве не зависит от Путь между этими точками называется консервативной силой . Очевидно, что электростатическая сила между неподвижными зарядами консервативная сила. Другой пример консервативной силы — сила силы тяжести (работа, выполняемая при подъеме груза, зависит только от разницы по высоте между начальной и конечной точками, а не на пути взяты между этими точками).Трение — очевидный пример неконсервативной сила.

Предположим, что мы очень медленно перемещаем заряд от точки к точке. в электрическом поле, создаваемом фиксированными зарядами. Работа, которую мы должны выполнить, чтобы достичь этого можно рассчитать используя уравнение. (78). Поскольку мы теряем энергию, когда заряд движется от к , что-то должно получить эту энергию. Давайте пока предположим, что это что-то есть заряд. Таким образом, заряд получает энергии, когда мы перемещаем его от точки к точке.Какова природа этого прироста энергии? Конечно, это не выигрыш в кинетической энергии, поскольку мы перемещаем частицу медленно : , то есть , так что он всегда обладает незначительной кинетической энергией. На самом деле, если хорошенько подумать, мы увидим, что выигрыш в энергии заряд зависит только от его позиции . Для фиксированной отправной точки работа при переходе от одной точки к другой зависит только от положение точки, а не, например, на маршруте между а также .Обычно мы называем энергию, которой обладает тело в силу своего положения. потенциальная энергия : например. , масса имеет определенную гравитационную потенциальную энергию что зависит от его высоты над землей. Таким образом, мы можем сказать, что когда заряд переносится из точки в точку в электрическом поле, создаваемом фиксированными зарядами. электрическая потенциальная энергия увеличивается на величину:

(79)

Здесь обозначает электрическую потенциальную энергию заряда в точке, и др. Это определение однозначно определяет разность в потенциальной энергии между точками и (поскольку не зависит от пройденного пути между этими точками), но абсолютное значение потенциальной энергии на данный момент остается произвольным.

Мы видели, что когда заряженная частица переносится из точки в точку в электрическом поле, ее электрическая потенциальная энергия увеличивается на указанную величину. в формуле. (79). Но как частица хранит эту энергию? Фактически, частица совсем не накапливает энергию.Вместо этого энергия хранится в электрическом поле. окружающие частицу. Можно рассчитать это увеличение энергия поля напрямую (как только мы знаем формулу, которая связывает плотность энергии электрического поля до величины поля), но это очень утомительно расчет. Гораздо проще рассчитать проделанную работу, взяв заряд от точки к точке, по формуле. (78), а затем использовать закон сохранения энергии, чтобы заключить, что энергия электрического поля должна увеличились на сумму.Тот факт, что мы условно приписываем эту энергию возрастают к частице, а не к полю, с помощью концепции электрического потенциальная энергия не имеет значения для всех практических целей. Например, мы называем деньги, которые у нас есть в банке, « наши », несмотря на то, что они принадлежат банку, потому что мы знаем, что банк вернет нам деньги в любое время, когда мы их попросим. Аналогичным образом, когда мы перемещаем заряженную частицу в электрическое поле от точки к точке, тогда энергия поля увеличивается на величину (работа, которую мы выполняем при перемещении частицы из в), но мы можем безопасно ассоциировать эта энергия увеличивается вместе с частицей, потому что мы знаем, что если частица переместится обратно в точку, тогда поле отобразит все энергия возвращается частице без потерь .Между прочим, мы можем быть уверены, что поле возвращает энергию частице без потерь, потому что если есть были бы какие-либо потери, это означало бы, что ненулевая работа выполняется при снятии заряженных частица вокруг замкнутого контура в электрическом поле, создаваемом фиксированными зарядами. Мы называем силовое поле, которое сохраняет энергию без потерь в консервативном поле . Таким образом, электрическое поле, а точнее электростатическое поле ( т.е. , электрическое поле, генерируемое стационарные заряды), является консервативным.Это должно быть ясно из вышеизложенного обсуждение, что концепция потенциальной энергии имеет смысл только в том случае, если поле который генерирует рассматриваемую силу, является консервативным.

Гравитационное поле — еще один пример консервативного поля. Оказывается что когда мы поднимаем тело на определенную высоту, увеличивается гравитационная потенциальная энергия тела фактически хранится в окружающей среде. гравитационного поля ( то есть , в искажениях пространства-времени вокруг тело).Можно определить увеличение энергии гравитационного поле напрямую, но это очень сложно расчет с использованием общей теории относительности. С другой стороны, очень легко рассчитать работу, проделанную при подъеме тела. Таким образом, удобно рассчитать прирост энергии поля от проделанной работы, и затем приписать это увеличение энергии телу с помощью концепции гравитационно потенциальная энергия.

В заключение, мы можем оценить увеличение электрической потенциальной энергии заряда при он снимается между двумя разными точками в электростатическом поле из проделанная работа по перемещению заряда между этими двумя точками.Энергия на самом деле хранится в электрическом поле, окружающем заряд, но мы можем смело приписать эту энергию к заряду, потому что мы знаем, что поле хранит энергию без потерь, и будет возвращать энергию заряду всякий раз, когда этого требует законы физики.

---

следующий: Электрический потенциал Up: Электрический потенциал Предыдущее: Электрический потенциал

Ричард Фицпатрик 2007-07-14

Электрическая потенциальная энергия — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Определите работу, выполняемую электрической силой
• Определить электрическую потенциальную энергию
• Применение рабочей и потенциальной энергии в системах с электрическими зарядами

Когда свободный положительный заряд q ускоряется электрическим полем, ему придается кинетическая энергия ((Рисунок)).Этот процесс аналогичен ускорению объекта гравитационным полем, как если бы заряд спускался с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую, хотя, конечно, источники сил очень разные. Давайте исследуем работу, совершаемую электрическим полем над зарядом q в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.

Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма.В обоих случаях потенциальная энергия уменьшается с увеличением кинетической энергии. Работа выполняется силой, но поскольку эта сила консервативна, мы можем писать.

Электростатическая или кулоновская сила является консервативной, что означает, что работа, проделанная на q , не зависит от пройденного пути, как мы продемонстрируем позже. Это в точности аналог силы тяжести. Когда сила консервативна, можно определить потенциальную энергию, связанную с силой. Обычно легче работать с потенциальной энергией (потому что она зависит только от положения), чем рассчитывать работу напрямую.

Чтобы показать это явно, рассмотрим электрический заряд, зафиксированный в начале координат, и переместим другой заряд к q таким образом, чтобы в каждый момент приложенная сила точно уравновешивала электрическую силу на Q ((Рисунок)). Работа, совершаемая силой, приложенной к заряду Q , изменяет потенциальную энергию Q . Мы называем эту потенциальную энергию электрической потенциальной энергией Q .

Смещение «тестового» заряда Q при наличии фиксированного «исходного» заряда q .

Работа, совершаемая приложенной силой, когда частица перемещается из точки в, может быть рассчитана с помощью

.

Поскольку приложенная сила уравновешивает электрическую силу на Q , две силы имеют равную величину и противоположные направления. Следовательно, приложенная сила составляет

, где мы определили положительное значение, указывающее от начала координат, а r — это расстояние от начала координат. Направления как смещения, так и приложенной силы в системе на (Рисунок) параллельны, и, таким образом, работа, выполняемая в системе, является положительной.

Мы используем букву U для обозначения электрической потенциальной энергии, которая измеряется в джоулях (Дж). Когда консервативная сила выполняет отрицательную работу, система получает потенциальную энергию. Когда консервативная сила выполняет положительную работу, система теряет потенциальную энергию. В системе на (Рисунок) кулоновская сила действует в направлении, противоположном смещению; поэтому работа отрицательная. Однако мы увеличили потенциальную энергию в двухзарядной системе.

Проверьте свое понимание Если Q имеет массу, равную скорости Q при

В этом примере работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери U или отрицательной.Значение для U можно найти в любой точке, взяв одну точку в качестве ориентира и вычислив работу, необходимую для перемещения заряда в другую точку.

Электрическая потенциальная энергия

Работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и возникает в результате потери U или отрицательной. Математически

Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное понимание энергии и преобразования энергии без необходимости иметь дело с силой напрямую.Например, гораздо более распространено использование концепции электрической потенциальной энергии, чем непосредственное рассмотрение кулоновской силы в реальных приложениях.

В полярных координатах с q в начале координат и Q , расположенным на r , вектор элемента смещения равен, и, таким образом, работа становится равной

Обратите внимание, что этот результат зависит только от конечных точек и в остальном не зависит от выбранного пути. Чтобы изучить это дальше, сравните путь к с путем на (рисунок).

Сегменты и представляют собой дуги окружностей с центром q . Поскольку сила на Q направлена ​​либо в сторону q , либо от нее, сила, уравновешивающая электрическую силу, не совершает никакой работы, поскольку она перпендикулярна смещению вдоль этих дуг. Таким образом, работа выполняется только на отрезке, идентичном

.

Одним из следствий этого расчета работы является то, что, если бы мы пошли по пути, сетевая работа была бы равна нулю ((Рисунок)).Напомним, что так мы определяем, консервативна сила или нет. Следовательно, поскольку электрическая сила связана с электрическим полем посредством, электрическое поле само по себе является консервативным. То есть

Обратите внимание, что Q — постоянная величина.

Замкнутый путь в электрическом поле. Чистая работа вокруг этого пути равна нулю.

Другое значение состоит в том, что мы можем определить электрическую потенциальную энергию. Напомним, что работа, совершаемая консервативной силой, также выражается как разница в потенциальной энергии, соответствующей этой силе.Следовательно, работу по приведению заряда от опорной точки к интересующей можно записать как

.

и, согласно (Рисунок), разница в потенциальной энергии пробного заряда Q между двумя точками составляет

Следовательно, мы можем записать общее выражение для потенциальной энергии двух точечных зарядов (в сферических координатах):

Мы можем принять второй член за произвольный постоянный эталонный уровень, который служит нулевым эталоном:

Удобный выбор ссылки, основанный на нашем здравом смысле, состоит в том, что, когда два заряда бесконечно далеко друг от друга, между ними нет взаимодействия.(Вспомните обсуждение эталонной потенциальной энергии в книге «Потенциальная энергия и сохранение энергии».) Принятие потенциальной энергии этого состояния равной нулю исключает член из уравнения (точно так же, как когда мы говорим, что земля является нулевой потенциальной энергией в гравитационной потенциальной энергии проблема), а потенциальная энергия Q , когда он отделен от q расстоянием r , принимает вид

Эта формула симметрична относительно q и Q , поэтому ее лучше всего описать как потенциальную энергию двухзарядной системы.

Согласно закону Кулона силы, возникающие от нескольких зарядов на пробном заряде Q , накладываются друг на друга; они могут быть рассчитаны индивидуально, а затем добавлены. Это означает, что рабочие интегралы и, следовательно, результирующие потенциальные энергии демонстрируют одинаковое поведение. Чтобы продемонстрировать это, рассмотрим пример сборки системы из четырех зарядов.

Сборка четырех положительных зарядов Найдите объем работы, который внешний агент должен проделать для сборки четырех зарядов в вершинах квадрата со стороной 1.0 см, начиная каждый заряд с бесконечности ((Рисунок)).

Сколько работы необходимо для сборки этой конфигурации заряда?

Стратегия Мы вводим заряды по одному, давая им исходные местоположения в бесконечности и вычисляя работу, чтобы доставить их из бесконечности в их конечное местоположение. Делаем это в порядке увеличения заряда.

Решение Шаг 1. Сначала довести заряд до ориджина. Поскольку на конечном расстоянии от этого заряда еще нет других зарядов, не производится никакой работы по его выводу из бесконечности,

Шаг 2.Удерживая заряд в исходной точке, переместите заряд в ((Рисунок)). Теперь приложенная сила должна работать против силы, создаваемой зарядом, зафиксированным в начале координат. Проделанная работа равна изменению потенциальной энергии заряда:

Шаг 2. Работайте, чтобы вывести заряд из бесконечности.

Шаг 3. Удерживая заряды и закрепив на своих местах, внести заряд в ((рисунок)). На этом шаге проделано

работы. Шаг 3. Работа по выводу заряда из бесконечности.

Шаг 4. Наконец, оставив первые три заряда на своих местах, поднесите их к ((Рисунок)). Здесь проделано

работ. Шаг 4. Работа по выводу заряда из бесконечности.

Следовательно, общая работа, выполняемая приложенной силой при сборке четырех зарядов, равна сумме работы по перемещению каждого заряда из бесконечности в его конечное положение:

Значение. Работа над каждым зарядом зависит только от его попарного взаимодействия с другими зарядами.Нет необходимости рассматривать более сложные взаимодействия; работа над третьим зарядом зависит только от его взаимодействия с первым и вторым зарядами, взаимодействие между первым и вторым зарядами не влияет на третий.

Проверьте свое понимание Является ли электрическая потенциальная энергия двух точечных зарядов положительной или отрицательной, если заряды одного знака? Противоположные знаки? Как это соотносится с работой, необходимой для сближения зарядов из бесконечности?

положительных, отрицательных, и эти количества такие же, как работа, которую вам нужно будет проделать, чтобы перенести заряды из бесконечности

Обратите внимание, что электрическая потенциальная энергия положительна, если два заряда одного типа, положительного или отрицательного, и отрицательная, если два заряда имеют противоположные типы.Это имеет смысл, если вы думаете об изменении потенциальной энергии, когда вы приближаете два заряда или отдаете их друг от друга. В зависимости от относительных типов зарядов вам, возможно, придется работать с системой, или система будет работать на вас, то есть ваша работа будет либо положительной, либо отрицательной. Если вам нужно произвести положительную работу с системой (фактически подтолкнуть заряды ближе), тогда энергия системы должна увеличиться. Если вы приблизите два положительных заряда или два отрицательных заряда, вы должны произвести положительную работу с системой, которая повысит их потенциальную энергию.Поскольку потенциальная энергия пропорциональна 1/ r , потенциальная энергия возрастает, когда r опускается между двумя положительными или двумя отрицательными зарядами.

С другой стороны, если вы приближаете положительный и отрицательный заряды, вы должны выполнять отрицательную работу с системой (заряды тянут вас), что означает, что вы забираете энергию у системы. Это снижает потенциальную энергию. Поскольку потенциальная энергия отрицательна в случае пары положительного и отрицательного зарядов, увеличение 1/ r делает потенциальную энергию более отрицательной, что аналогично уменьшению потенциальной энергии.

Результат из (Рисунок) может быть распространен на системы с любым произвольным количеством зарядов. В этом случае удобнее всего записать формулу как

Коэффициент 1/2 учитывает двойное сложение каждой пары зарядов.

Сводка

• Работа, выполняемая для перемещения заряда из точки A ​​ в B в электрическом поле, не зависит от пути, и работа вокруг замкнутого пути равна нулю. Следовательно, электрическое поле и электрическая сила консервативны.
• Мы можем определить электрическую потенциальную энергию, которая между точечными зарядами равна, с нулевой точкой отсчета, взятой на бесконечности.
• Для электрической потенциальной энергии действует принцип суперпозиции; потенциальная энергия системы нескольких зарядов — это сумма потенциальных энергий отдельных пар.

Концептуальные вопросы

Была бы электрическая потенциальная энергия значимой, если бы электрическое поле не было консервативным?

№Мы можем определить потенциальные энергии только для консервативных полей.

Почему нам нужно проявлять осторожность в отношении работы, выполненной на системе, в сравнении с работой, выполненной на системой в вычислениях?

Влияет ли порядок, в котором мы собираем систему точечных начислений, на общую выполненную работу?

Нет, хотя некоторые порядки проще вычислить.

Проблемы

а.
г.

Для образования атома водорода протон фиксируется в точке, а электрон переносится издалека на расстояние, равное среднему расстоянию между протоном и электроном в атоме водорода.Сколько работы сделано?

(a) Какова средняя выходная мощность дефибриллятора сердца, который рассеивает 400 Дж энергии за 10,0 мс? (б) Учитывая высокую выходную мощность, почему дефибриллятор не вызывает серьезных ожогов?

Глоссарий

электрическая потенциальная энергия

потенциальная энергия, запасенная в системе заряженных объектов за счет зарядов

Электрическое поле — HowToMechatronics

В этой лекции мы узнаем об электрическом поле, свойствах силовых линий электрического поля и принципе суперпозиции.Вы можете посмотреть следующее видео или прочитать письменное руководство ниже.

РЕКОМЕНДУЕТСЯ

Два электрически заряженных объекта действуют друг на друга. Они также оказывают давление друг на друга, даже когда не находятся в контакте. Эта сила называется действием на расстоянии .

Что такое электрическое поле?

Если у нас есть заряженный объект, мы действительно можем предсказать, что случится с другими электрическими зарядами, когда они будут поднесены близко к этому объекту.

Заряженный объект изменяет пространство вокруг себя, образуя электрическое поле. Электрическое поле может воздействовать силой на другой электрический заряд, находящийся в любой точке поля.

Когда мы говорили о законе Кулона, мы наблюдали силу между двумя зарядами как действие между двумя объектами, а теперь мы будем наблюдать силу как действие, которое электрическое поле оказывает на заряд, входящий в это поле.

Майкл Фарадей был британским ученым и первым представил понятие электрического поля.Поле может быть:

• Любая величина, которой можно присвоить значение во всех точках пространства вокруг источника поля; или
• «Область влияния».

Как работают электрические поля?

Прежде всего, напряженность электрического поля — это векторная величина, имеющая величину и направление. Направление поля в точке на самом деле совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.

Допустим, имеется положительный точечный заряд, обозначенный заглавной буквой Q.Чтобы увидеть эффект, который этот заряд оказывает на другие заряды, мы введем в его сферу влияния небольшой положительный тестовый заряд, обозначенный q.

Причина, по которой мы вносим небольшой тестовый заряд, заключается в том, что нам нужно значение, которое не зависит от размера тестового заряда и зависит только от источника поля и расстояния от этого источника.

Тестовый заряд по определению всегда положительный. Оба заряда создают электрические поля, но большой Q имеет гораздо большую величину, чем маленький q.Точечный заряд Q изменяет пространство вокруг себя и создает электрическое поле.

Формула электрического поля

Теперь мы можем измерить поле.

Электрическое поле, создаваемое заряженным объектом, фактически представляет собой электрическую силу между объектом и испытательным зарядом, деленную на величину этого испытательного заряда. Закон Кулона поможет нам найти силу.

Итак, вместо заглавной F мы воспользуемся уравнением закона Кулона.

Здесь мы можем заметить, что малое q появляется дважды в этом уравнении, поэтому оно сокращается, и мы получаем уравнение, которое включает только точечный заряд.

Наконец, напряженность электрического поля, создаваемого точечным зарядом, равна кулоновской постоянной, умноженной на заряд объекта, создающего поле, деленному на квадрат расстояния между этим объектом и испытательным зарядом.

Здесь у нас есть положительный точечный заряд и положительный тестовый заряд, а результат имеет положительный знак, что означает, что положительно заряженный объект будет отражать положительный тестовый заряд. Вот почему на диаграмме электрического поля есть стрелки, направленные наружу.

Для отрицательного точечного заряда и положительного тестового заряда у нас есть сила притяжения, которая показана отрицательным знаком в уравнении.

Схема силовых линий отрицательно заряженного объекта будет выглядеть как диаграмма положительно заряженного объекта, но со стрелками, направленными внутрь, что означает, что отрицательно заряженный объект Q будет притягивать положительные испытательные заряды.

Единицей измерения электрического поля является ньютон / кулон или вольт / метр.

Электрическое поле существует, даже если поблизости нет тестового заряда для его измерения. Точно так же гравитационное поле окружает Землю, даже если поблизости нет «тестовой массы» для ее измерения.

Если мы знаем значение точечного заряда и значение напряженности электрического поля, мы можем легко вычислить силу, просто умножив эти значения.

Пример

Например, у нас есть точечный заряд Q, равный 1 × 10-8 Кулонов.Также у нас есть пробный заряд в 1 кулон на расстоянии 50 см. Итак, какое электрическое поле находится в 50 см от точечного заряда?

Электрическое поле в этой точке будет представлять собой постоянную Кулона, умноженную на заряд, генерирующий поле, и разделенное на квадрат расстояния между точечным зарядом и пробным зарядом. Это равно 9 × 109 Нм2 / C2, умноженным на 1 × 10-8 C, разделенным на (0,5 м) 2.

Здесь мы можем сократить количество метров и кулонов, что дает нам ньютоны / кулоны.Это равно 90, разделенному на 0,25 Ньютона / кулон. Наконец, величина электрического поля, создаваемого точечным зарядом на расстоянии 50 см, составляет 360 Ньютонов на кулон.

Сила, приложенная к испытательному заряду, будет равна испытательному заряду, умноженному на величину электрического поля, которая равна 1 кулону, умноженному на 360 ньютонов / кулон. Здесь кулоны уравновешиваются, и сила, действующая на этот 1 кулон заряда, составит 360 ньютонов.

Здесь мы можем заметить, что и точечный, и тестовый заряд положительны, поэтому сила будет отталкивающей, что означает, что направление силы будет наружу.

Принцип суперпозиции

Принцип суперпозиции применим также к электрическим полям.

Допустим, у нас есть два точечных заряда Q1 и Q2, и мы подносим рядом положительный тестовый заряд q. Q1 — положительный заряд, а Q2 — отрицательный заряд. Сила, которую Q1 применяет к q, является отталкивающей, а сила, которую Q2 применяет к q, является притягивающей.

Принцип суперпозиции может помочь нам вычислить полное электрическое поле, создаваемое множественными точечными зарядами, которое представляет собой просто сумму всех отдельных полей.

Другими словами, полное электрическое поле в точке от системы зарядов, действующих на пробный заряд, равно векторной сумме электрических полей в этой точке от каждого из отдельных зарядов.

Используя уравнение, мы можем вычислить полное электрическое поле E, которое равно E1 + E2:

Линии электрического поля

Небольшой положительный тестовый заряд q, помещенный в различные точки рядом с Q, будет отталкиваться (или притягиваться) Q и перемещаться по линиям.Эти векторы называются силовыми линиями или линиями электрического поля, концепция, впервые введенная Майклом Фарадеем.

Они показывают направление и величину силы, приложенной к ближайшему положительному испытательному заряду. На самом деле это направление, в котором перемещался бы мобильный положительный заряд, если бы его поместили в поле.

Свойства линий электрического поля

Давайте посмотрим на поле между двумя зарядами одинаковой величины, но противоположного знака. Они образуют электрический диполь.

Теперь давайте соединим их электрические поля и создадим полное электрическое поле.

Если мы обратим внимание на это полное электрическое поле, то обнаружим четыре важных свойства силовых линий электрического поля.

1. Линии всегда начинаются с положительных зарядов и заканчиваются отрицательными. В нашем примере линии начинаются от положительно заряженного объекта и движутся к отрицательно заряженному. Из каждой частицы выходит одинаковое количество линий, потому что величина их зарядов одинакова и противоположна.
2. Линии поля должны касаться направления поля в любой точке.
3. Сходство линий указывает на напряженность поля. Чем больше плотность линий, тем больше величина поля, и наоборот.