Проводники и диэлектрики

Все материалы, существующие в природе, различаются своими электрическими свойствами. Таким образом, из всего многообразия физических веществ в отдельные группы выделяются диэлектрические материалы и проводники электрического тока.
Что представляют собой проводники?
Проводник – это такой материал, особенностью которого является наличие в составе свободно передвигающихся заряженных частиц, которые распространены по всему веществу.
Проводящими электрический ток веществами являются расплавы металлов и сами металлы, недистиллированная вода, раствор солей, влажный грунт, человеческое тело.
Металл – это самый лучший проводник электрического тока. Также и среди неметаллов есть хорошие проводники, например, углерод.
Все, существующие в природе проводники электрического тока, характеризуются двумя свойствами:
- показатель сопротивления;
- показатель электропроводности.
Электропроводность – это характеристика (способность) физического вещества проводить ток. Поэтому свойствами надежного проводника являются низкое сопротивление потоку движущихся электронов и, следовательно, высокая электропроводность. То есть, лучший проводник характеризуется большим показателем проводимости.
Например кабельная продукция: медный кабель обладает большей электропроводностью по сравнению с алюминиевым.
Что представляют собой диэлектрики?
Диэлектрики – это такие физические вещества, в которых при заниженных температурах отсутствуют электрические заряды. В состав таких веществ входят лишь атомы нейтрального заряда и молекулы. Заряды нейтрального атома имеют тесную связь друг с другом, поэтому лишены возможности свободного перемещения по всему веществу.
Самым лучшим диэлектриком является газ. Другие непроводящие электрический ток материалы – это стеклянные, фарфоровые, керамические изделия, а также резина, картон, сухое дерево, смолы и пластмассы.
Диэлектрические предметы – это изоляторы, свойства которых главным образом зависимы от состояния окружающей атмосферы. Например, при высокой влажности некоторые диэлектрические материалы частично лишаются своих свойств.
Проводники и диэлектрики широко используются в сфере электротехники для решения различных задач.
Например, вся кабельно-проводниковая продукция изготавливается из металлов, как правило, из меди или алюминия. Оболочка проводов и кабелей полимерная, также, как и вилках всех электрических приборов. Полимеры – отличные диэлектрики, которые не допускают пропуска заряженных частиц.
Серебряные, золотые и платиновые изделия – очень хорошие проводники. Но их отрицательная характеристика, которая ограничивает использование, состоит в очень высокой стоимости.
Поэтому применяются такие вещества в сферах, где качество гораздо важнее цены, которая за него уплачивается (оборонная промышленность и космос).
Медные и алюминиевые изделия также являются хорошими проводниками, при этом имеют не столь высокую стоимость. Следовательно, использование медных и алюминиевых проводов распространено повсеместно.
Вольфрамовые и молибденовые проводники имеют менее хорошие свойства, поэтому используются в основном в лампочках накаливания и нагревательных элементах высокой температуры. Плохая электропроводность может существенно нарушить работу электросхемы.
Диэлектрики также различаются между собой своими характеристиками и свойствами. Например, в некоторых диэлектрических материалах также присутствуют свободные электрически заряды, пусть и в небольшом количестве. Свободные заряды возникают из-за тепловых колебаний электронов, т.е. повышение температуры все-таки в некоторых случаях провоцирует отрыв электронов от ядра, что понижает изоляционные свойства материала. Некоторые изоляторы отличаются большим числом «оторванных» электронов, что говорит о плохих изоляционных свойствах.
Самый лучший диэлектрик – полный вакуум, которого очень трудно добиться на планете Земля.
Полностью очищенная вода также имеет высокие диэлектрические свойства, но таковой даже не существует в реальности. При этом стоит помнить, что присутствие каких-либо примесей в жидкости наделяет ее свойствами проводника.
Главный критерий качества любого диэлектрического материала – это степень соответствия возложенным на него функциям в конкретной электрической схеме. Например, если свойства диэлектрика таковы, что утечка тока совсем незначительная и не приносит никакого ущерба работе схемы, то диэлектрик является надежным.
Что такое полупроводник?
Промежуточное место между диэлектриками и проводниками занимают полупроводники. Главное отличие проводников заключается в зависимости степени электропроводности от температуры и количества примесей в составе. При том материалу свойственны характеристики и диэлектрика, и проводника.
С ростом температуры электропроводность полупроводников растет, а степень сопротивления при этом падает. При понижении температуры сопротивление стремится к бесконечности. То есть, при достижении нулевой температуры полупроводники начинают вести себя как изоляторы.
Полупроводниками являются кремний и германий.
Статья по теме: Электрический ток и его скорость

Определения понятий проводник, полупроводник и диэлектрик в электрическом поле. Какое отличие между перечисленными материалами.
В электричестве выделяют три основных группы материалов – это проводники, полупроводники и диэлектрики. Основным их отличием является возможность проводить ток. В этой статье мы рассмотрим, чем отличаются эти виды материалов и как они ведут себя в электрическом поле. Содержание:
Что такое проводник
Вещество, в котором присутствуют свободные носители зарядов, называют проводником. Движение свободных носителей называют тепловым. Основной характеристикой проводника является его сопротивление (R) или проводимость (G) – величина обратная сопротивлению.
G=1/R
Говоря простыми словами – проводник проводит ток.

К таким веществам можно отнести металлы, но если говорить о неметаллах то, например, углерод – отличный проводник, нашел применение в скользящих контактах, например, щетки электродвигателя. Влажная почва, растворы солей и кислот в воде, тело человека – тоже проводит ток, но их электропроводность зачастую меньше, чем у меди или алюминия, например.
Металлы являются отличными проводниками, как раз таки благодаря большому числу свободных носителей зарядов в их структуре. Под воздействием электрического поля заряды начинают перемещаться, а также перераспределяться, наблюдается явление электростатической индукции.
Что такое диэлектрик
Диэлектриками называют вещества, которые не проводят ток, или проводят, но очень плохо. В них нет свободных носителей зарядов, потому что связь частиц атома достаточно сильная, для образования свободных носителей, поэтому под воздействием электрического поля тока в диэлектрике не возникает.
Газ, стекло, керамика, фарфор, некоторые смолы, текстолит, карболит, дистиллированная вода, сухая древесина, резина – являются диэлектриками и не проводят электрический ток. В быту диэлектрики встречаются повсеместно, например, из них делаются корпуса электроприборов, электрические выключатели, корпуса вилок, розеток и прочее. В линиях электропередач изоляторы выполняются из диэлектриков.

Однако, при наличии определенных факторов, например повышенный уровень влажности, напряженность электрического поля выше допустимого значения и прочее – приводят к тому, что материал начинает терять свои диэлектрические функции и становится проводником. Иногда вы можете слышать фразы типа «пробой изолятора» — это и есть описанное выше явление.
Если сказать кратко, то основными свойствами диэлектрика в сфере электричества являются электроизоляционные. Именно способность препятствовать протеканию тока защищает человека от электротравматизма и прочих неприятностей. Основной характеристикой диэлектрика является электрическая прочность – величина равная напряжению его пробоя.
Что такое полупроводник
Полупроводник проводит электрический ток, но не так как металлы, а при соблюдении определенных условий – сообщении веществу энергии в нужных количествах. Это связано с тем, что свободных носителей (дырок и электронов) зарядов слишком мало или их вовсе нет, но если приложить какое-то количество энергии – они появятся. Энергия может быть различных форм – электрической, тепловой. Также свободные дырки и электроны в полупроводнике могут возникать под воздействием излучений, например в УФ-спектре.

Где применяются полупроводники? Из них изготавливают транзисторы, тиристоры, диоды, микросхемы, светодиоды и прочее. К таким материалам относят кремний, германий, смеси разных материалов, например арсенид-галия, селен, мышьяк.
Чтобы понять, почему полупроводник проводит электрический ток, но не так как металлы, нужно рассматривать эти материалы с точки зрения зонной теории.
Зонная теория

На изображении ниже показаны три вида материалов с их энергетическими уровнями:

Обратите внимание, что у проводника энергетические уровни от валентной зоны до зоны проводимости объединены в неразрывную диаграмму. Зона проводимости и валентная зоны накладываются друг на друга, это называется зоной перекрытия. В зависимости от наличия электрического поля (напряжения), температуры и прочих факторов количество электронов может изменяться. Благодаря вышеописанному, электроны могут передвигаться в проводниках, даже если сообщить им какое-то минимальное количество энергии.
У полупроводника между зоной валентности и зоной проводимости присутствует определенная запрещенная. Ширина запрещенной зоны описывает, какое количество энергии нужно сообщить полупроводнику, чтобы начал протекать ток.
У диэлектрика диаграмма похожа на ту, которая описывает полупроводники, однако отличие лишь в ширине запрещенной зоны – она здесь во много раз большая. Различия обусловлены внутренним строением и вещества.
Мы рассмотрели основные три типа материалов и привели их примеры и особенности. Главным их отличием является способность проводить ток. Поэтому каждый из них нашел свою сферу применения: проводники используются для передачи электроэнергии, диэлектрики – для изоляции токоведущих частей, полупроводники – для электроники. Надеемся, предоставленная информация помогла вам понять, что собой представляют проводники, полупроводники и диэлектрики в электрическом поле, а также в чем их отличие между собой.
Напоследок рекомендуем просмотреть полезное видео по теме:
Наверняка вы не знаете:
- Причины потерь электроэнергии на больших расстояниях
- Зависимость сопротивления проводника от температуры
- Что такое диэлектрические потери
- Что такое электрический заряд
Нравится
 0)Не нравится
0)Не нравится 0)
0)Проводники и диэлектрики в электрическом поле
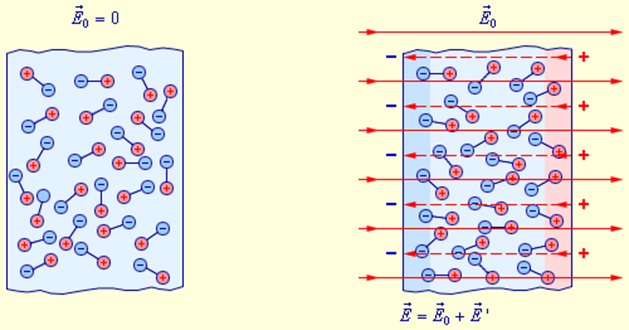
Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. При наличии внешнего поля происходит перераспределение заряженных частиц, и в веществе возникает собственное электрическое поле. Полное электрическое поле  складывается в соответствии с принципом суперпозиции из внешнего поля
складывается в соответствии с принципом суперпозиции из внешнего поля  и внутреннего поля
и внутреннего поля 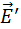 , создаваемого заряженными частицами вещества.
, создаваемого заряженными частицами вещества.
Вещество многообразно по своим электрическим свойствам. Наиболее широкие классы вещества составляют проводники и диэлектрики.
Основная особенность проводников – наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника. Типичные проводники – металлы.
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают не скомпенсированные положительные и отрицательные заряды (рис. 1.5.1). Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами.
Индукционные заряды создают свое собственное поле 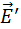 , которое компенсирует внешнее поле
, которое компенсирует внешнее поле  во всем объеме проводника:
во всем объеме проводника:
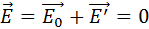
(внутри проводника).
Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.
|
Рисунок 1.5.1. Электростатическая индукция |
Все внутренние области проводника, внесенного в электрическое поле, остаются электронейтральными. Если удалить некоторый объем, выделенный внутри проводника, и образовать пустую полость, то электрическое поле внутри полости будет равно нулю. На этом основана электростатическая защита – чувствительные к электрическому полю приборы для исключения влияния поля помещают в металлические ящики (рис. 1.5.2).
|
Рисунок 1.5.2. Электростатическая защита. Поле в металлической полости равно нулю |
Так как поверхность проводника является эквипотенциальной, силовые линии у поверхности должны быть перпендикулярны к ней.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
При внесении диэлектрика во внешнее электрическое поле  в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.
в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.
Связанные заряды создают электрическое поле 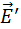 которое внутри диэлектрика направлено противоположно вектору напряженности
которое внутри диэлектрика направлено противоположно вектору напряженности  внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле
внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле 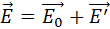 внутри диэлектрика оказывается по модулю меньше внешнего поля
внутри диэлектрика оказывается по модулю меньше внешнего поля 
Физическая величина, равная отношению модуля напряженности 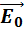 внешнего электрического поля в вакууме к модулю напряженности
внешнего электрического поля в вакууме к модулю напряженности 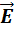 полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.
полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.
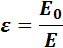
Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная и электронная поляризации. Эти механизмы проявляются главным образом при поляризации газообразных и жидких диэлектриков.
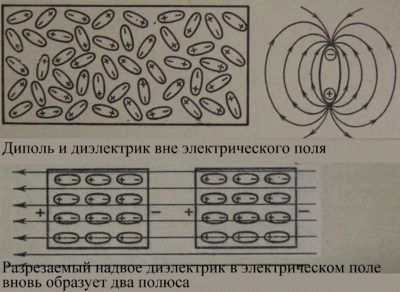
Ориентационная или дипольная поляризация возникает в случае полярных диэлектриков, состоящих из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы представляют собой микроскопические электрические диполи – нейтральную совокупность двух зарядов, равных по модулю и противоположных по знаку, расположенных на некотором расстоянии друг от друга. Дипольным моментом обладает, например, молекула воды, а также молекулы ряда других диэлектриков (H2S, NO2 и т. д.).
При отсутствии внешнего электрического поля оси молекулярных диполей из-за теплового движения ориентированы хаотично, так что на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем равен нулю.
При внесении диэлектрика во внешнее поле  возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле
возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле 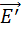 направленное навстречу внешнему полю
направленное навстречу внешнему полю  (рис. 1.5.3).
(рис. 1.5.3).
|
Рисунок 1.5.3. Ориентационный механизм поляризации полярного диэлектрика |
Поляризация полярных диэлектриков сильно зависит от температуры, так как тепловое движение молекул играет роль дезориентирующего фактора.
Электронный или упругий механизм проявляется при поляризации неполярных диэлектриков, молекулы которых не обладают в отсутствие внешнего поля дипольным моментом. Под действием электрического поля молекулы неполярных диэлектриков деформируются – положительные заряды смещаются в направлении вектора  а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свое поле
а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля. На поверхности диэлектрика появляются нескомпенсированные связанные заряды, создающие свое поле 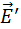 , направленное навстречу внешнему полю
, направленное навстречу внешнему полю  Так происходит поляризация неполярного диэлектрика (рис. 1.5.4).
Так происходит поляризация неполярного диэлектрика (рис. 1.5.4).
Деформация неполярных молекул под действием внешнего электрического поля не зависит от их теплового движения, поэтому поляризация неполярного диэлектрика не зависит от температуры. Примером неполярной молекулы может служить молекула метана CH4. У этой молекулы четырехкратно ионизированный ион углерода C4– располагается в центре правильной пирамиды, в вершинах которой находятся ионы водорода H+. При наложении внешнего электрического поля ион углерода смещается из центра пирамиды, и у молекулы возникает дипольный момент, пропорциональный внешнему полю.
|
Рисунок 1.5.4. Поляризация неполярного диэлектрика |
Электрическое поле 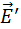 связанных зарядов, возникающее при поляризации полярных и неполярных диэлектриков, изменяется по модулю прямо пропорционально модулю внешнего поля
связанных зарядов, возникающее при поляризации полярных и неполярных диэлектриков, изменяется по модулю прямо пропорционально модулю внешнего поля  . В очень сильных электрических полях эта закономерность может нарушаться, и тогда проявляются различные нелинейные эффекты. В случае полярных диэлектриков в сильных полях может наблюдаться эффект насыщения, когда все молекулярные диполи выстраиваются вдоль силовых линий. В случае неполярных диэлектриков сильное внешнее поле, сравнимое по модулю с внутриатомным полем, может существенно деформировать атомы или молекулы вещества и изменить их электрические свойства. Однако, эти явления практически никогда не наблюдаются, так как для этого нужны поля с напряженностью порядка 1010–1012 В/м. Между тем, гораздо раньше наступает электрический пробой диэлектрика.
. В очень сильных электрических полях эта закономерность может нарушаться, и тогда проявляются различные нелинейные эффекты. В случае полярных диэлектриков в сильных полях может наблюдаться эффект насыщения, когда все молекулярные диполи выстраиваются вдоль силовых линий. В случае неполярных диэлектриков сильное внешнее поле, сравнимое по модулю с внутриатомным полем, может существенно деформировать атомы или молекулы вещества и изменить их электрические свойства. Однако, эти явления практически никогда не наблюдаются, так как для этого нужны поля с напряженностью порядка 1010–1012 В/м. Между тем, гораздо раньше наступает электрический пробой диэлектрика.
У многих неполярных молекул при поляризации деформируются электронные оболочки, поэтому этот механизм получил название электронной поляризации. Этот механизм является универсальным, поскольку деформация электронных оболочек под действием внешнего поля происходит в атомах, молекулах и ионах любого диэлектрика.
В случае твердых кристаллических диэлектриков наблюдается так называемая ионная поляризация, при которой ионы разных знаков, составляющие кристаллическую решетку, при наложении внешнего поля смещаются в противоположных направлениях, вследствие чего на гранях кристалла появляются связанные (нескомпенсированные) заряды. Примером такого механизма может служить поляризация кристалла NaCl, в котором ионы Na+ и Cl– составляют две подрешетки, вложенные друг в друга. В отсутствие внешнего поля каждая элементарная ячейка кристалла NaCl (см. Часть I § 3.6 ) электронейтральна и не обладает дипольным моментом. Во внешнем электрическом поле обе подрешетки смещаются в противоположных направлениях, т. е. кристалл поляризуется.
При поляризации неоднородного диэлектрика связанные заряды могут возникать не только на поверхностях, но и в объеме диэлектрика. В этом случае электрическое поле 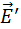 связанных зарядов и полное поле
связанных зарядов и полное поле  могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле
могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле  в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем
в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем  строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:
строго справедливо только в случае однородного диэлектрика, заполняющего все пространство, в котором создано внешнее поле. В частности:
Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд Q, то напряженность поля 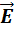 создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
 Проводники и диэлектрики — основные вещества которые широко используются в электротехнике и имеют прямо противоположное назначение.
Проводники и диэлектрики — основные вещества которые широко используются в электротехнике и имеют прямо противоположное назначение.
Проводники это вещества, в которых достаточное количество свободных электронов. При наличии разности потенциалов они проводят электрический ток.
Хорошими проводниками являются металлы, растворы кислот, щелочей, солей и просто вода с примесями.
Наиболее распространенными металлами, которые используются в качестве проводников, являются медь, алюминий, цинк, железо.
В измерительных приборах и дорогостоящей технике в качестве проводников применяют серебро. Иногда ним для улучшения проводимости покрывают только поверхность медных проводников.
Сопротивление проводников зависит от диаметра провода. Чем больше диаметр, тем меньше сопротивление, ниже потери и проводник меньше нагревается. Чем больше ток, тем толще должны быть проводники.
Чтобы медный проводник не перегревался, плотность тока не должна превышать норму. Эта норма зависит от условий охлаждения провода. Например, в открытых проводах она выше, в закрытых или рядом расположенных — ниже. В обмотках трансформаторов, где условия охлаждения намного хуже, плотность тока, как правило, не должна превышать 3 А/мм2. При этом диаметр медного провода для требуемого значения тока рассчитывают по формуле:
D(мм) = 0,8 × √I(А)
D – диаметр, в мм, I – ток, в А.
Если нет на замену перегоревшего предохранителя, то его можно восстановить, запаяв в предохранитель медный провод, диаметр которого рассчитывают по формуле:
D(мм) = 0,034 × Iпл (А) + 0,005
Эту формула применяют если рассчитанное значение диаметра не превышает 0,2 мм.
Для удобства ниже в таблице приведена информация для быстрого определения диаметра провода используемого в качестве предохранителя:
Ток, А | Диаметр провода в мм | |||
Медь | Алюминий | Сталь | Олово | |
1 | 0,039 | 0,066 | 0,132 | 0,183 |
2 | 0,07 | 0,104 | 0,189 | 0,285 |
3 | 0,107 | 0,137 | 0,245 | 0,380 |
5 | 0,18 | 0,193 | 0,346 | 0,53 |
7 | 0,203 | 0,250 | 0,45 | 0,66 |
10 | 0,250 | 0,305 | 0,55 | 0,85 |
| 15 | 0,32 | 0,40 | 0,72 | 1,02 |
20 | 0,39 | 0,485 | 0,87 | 1,33 |
| 25 | 0,46 | 0,56 | 1,0 | 1,56 |
| 30 | 0,52 | 0,64 | 1,15 | 1,77 |
35 | 0,58 | 0,70 | 1,26 | 1,95 |
40 | 0,63 | 0,77 | 1,38 | 2,14 |
45 | 0,68 | 0,83 | 1,5 | 2,3 |
50 | 0,73 | 0,89 | 1,6 | 2,45 |
В следующей таблице для информации приведены основные параметры, часто применяемых материалов:
| Материал | Удельное сопротивление, Ом*мм2 м(р) | Удельный вес, г/см3 | Температура плавления, oС |
| Медь | 0,0175 | 8,9 | 1085 |
| Алюминий | 0,0281 | 2,7 | 658 |
| Железо | 0,135 | 7,8 | 1530 |
| Никелин | 0,4 | 8,8 | 1100 |
| Константан | 0,49 | 8,9 | 1200 |
| Манганин | 0,43 | 8,4 | 910 |
| Нихром | 1.1 | 8,2 | 1550 |
Чтобы не считать по формуле, сечение монтажного медного провода можно выбрать в зависимости от тока по таблице:
| Сечение провода, мм2 | 0,05 | 0,07 | 0,1 | 0,2 | 0,3 | 0,5 | 0,7 | 1 | 1,5 | 2 | 4 | 6 | 10 |
| Допустимый ток, А | 0,7 | 1 | 1,3 | 2,5 | 3,5 | 5 | 7 | 10 | 14 | 17 | 25 | 30 | 45 |
Сечение провода связано с диаметром следующим образом:
S = 0,785 D2
Алюминиевый провод, при том же диаметре, что и медный, допускает ток в среднем на 23% меньший.
Диэлектрики это вещества, в которых отсутствуют свободные электроны. Они не проводят электрический ток, их еще называют изоляторами.
К ним относятся: слюда, пластмассы, стекло, гетинакс, стеклотекстолит, фарфор, каучук, смолы, дистиллированная вода, воздух и т.д.
Основными электрическими характеристиками диэлектриков являются удельное сопротивление «ρ» и электрическая прочность «Епр».
Удельное сопротивление показывает величину сопротивления в Ом, при его толщине величиной 1 см.
Электрическая прочность показывает предельную величину напряжения в вольтах, при которой диэлектрик не разрушается, (не наступает пробой) и он сохраняет свои изоляционные свойства.
Удельное сопротивление ρ и электрическая прочность Епр некоторых твёрдых диэлектриков, используемых в качестве изоляционных материалов приведена ниже в таблице:
| Диэлектрический материал | Удельное сопротивление, ρ, ом·см | |Диэлектрическая проницаемость, Епр, в/см |
| Кварцевое стекло | 1016-1018 | 2-3·105 |
| Полиэтилен | 1015-1016 | 4·105 |
| Слюда | 1014-1016 | 1-2·106 |
| | Электрофарфор | 1013-1014 | 3·105 |
| Мрамор | 108-109 | 2-3·105 |
Так же для диэлектриков важны и другие их свойства, а именно:
Физико – химические
Нагревостойкость – способность выдерживать повышение температуры
Холодностойкость – способность переносить перепады температур
Смачиваемость – способность отторгать влагу
Химические
Противостояние агрессивной среде
Способность склеиваться
Растворение в растворителях
Механические
Способность выдерживать механические нагрузки
Защита от коррозии
Гибкость, элластичность
Что такое проводник?
Проводник – это вещество или материал, которое отлично проводит электрический ток.
Как вы все знаете, любое вещество состоит из атомов. Атомы в свою очередь состоят из электронов и ядер

Давайте для понимания рассмотрим вот такую картинку. Предположим, что пастух – это ядро, а овцы вокруг него – это электроны.

Те овцы, которые находятся рядом с пастухом, не могут от него просто так взять и убежать, так как он присматривает за ними. Иначе останется без мяса и шерсти к осени. Но вот те овцы, которые находятся поодаль от пастуха, имеют все шансы от него убежать.
То же самое можно сказать и про атомы и электроны. Электроны, которые находятся на самой дальней орбите от ядра менее зависимы, чем те, которые расположены ближе к ядру.

В результате, такие электроны могут “оторваться” от ядра и начать самостоятельное путешествие по веществу. Такие электроны называются свободными электронами.


Чем больше свободных электронов, тем лучше проводимость вещества.
Сопротивление проводника
Удельное сопротивление
И вот мы плавно переходим к другому вопросу, что такое сопротивление проводника? Как я уже говорил выше, чем больше свободных электронов в веществе, тем лучше такое вещество проводит электрический ток. Следовательно, сопротивление проводника зависит от того, сколько свободных электронов содержит такой проводник. Поэтому, в физике есть такое понятие, как удельное сопротивление вещества.
Еще раз. Если в каком-либо веществе полно свободных электронов, то такое вещество будет хорошо проводить электрический ток. Если электронов еще меньше, то такое вещество будет плохо проводить электрический ток. А если свободных электронов почти нет, то такое вещество совсем не будет проводить ток. Поэтому, удельное сопротивление вещества показывает способность этого вещества препятствовать электрическому току, проходящему через него.
Удельное сопротивление выражается в единицах Ом × м.
Формула удельного сопротивления проводника

где
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Площадь поперечного сечения проводника – это что-то типа этого:
 площадь поперечного сечения проводника
площадь поперечного сечения проводника
Формула сопротивления проводника
Итак, мы теперь знаем такую физическую величину, как удельное сопротивление. Теперь мы с легкостью можем найти сопротивление проводника.

где
ρ – это удельное сопротивление, Ом × м
R – сопротивление проводника, Ом
S – площадь поперечного сечения, м2
l – длина проводника, м
Длина проводника
Допустим перед нами стоит задача: у нас есть медный провод с поперечным сечением в 0,1 мм2 . Нам надо получить сопротивление проводника в 1 Ом. Какая длина проводника должна быть?
Оказывается, эта задачка решается очень просто. Достаточно вспомнить формулу выше.

Отсюда получаем, что

Удельное сопротивление меди можно узнать из таблицы. Оно равняется 0,017 Ом × мм2 /м.
Получаем, что

Проводники на печатных платах
Как вы знаете, все схемы состоят из проводов или печатных дорожек, которые соединяют различные радиоэлементы в единое целое. Например, в статье “самый простой усилитель звука“, я с помощью проводов соединял различные радиоэлементы, и у меня получилась схема, которая усиливала звуковые частоты.
Для того, чтобы все было красиво, эстетично и занимало мало пространства, прямо на платах создают “проводки”, которые уже называются “печатными дорожками”.

В домашних условиях все это делается с помощью технологии ЛУТ (Лазерно-Утюжная-Технология).
На другой стороне печатной платы уже располагаются радиоэлементы

Так как радиолюбители стараются делать свои устройства как можно меньше по габаритам, то и плотность монтажа возрастает. Поэтому, в некоторых случаях радиоэлементы и печатные дорожки располагают по обе стороны платы.
Промышленные печатные платы уже делают многослойными. Они состоят из слоев, как торт из коржей:

Бум SMD технологий вызвал в свою очередь нужду в многослойных печатных платах.
Сверхпроводимость
Также в природе существует и такой эффект, как сверхпроводимость. Сверхпроводимость – это когда некоторые материалы и их сплавы вообще не обладают сопротивлением. То есть их сопротивление очень и очень близко к нулю. Но, спешу вас разочаровать, в простых условиях это получить невозможно, так как это достигается только при критических температурах.
Если желаете больше узнать про материалы, которые используются в электронике и электротехнике, скачайте эту книгу.

Проводники и диэлектрики в электрическом поле
Электростатическая индукция
Любое тело, помещенное в электрическом поле, электризуется. Однако процесс электризации для различных веществ будет разным.
Электрические характеристики электронейтрального тела зависят от подвижности заряженных частиц в нем, которая определяется строением атомов вещества и их взаимным расположением.
По концентрации свободных заряженных частиц в веществе все вещества делятся на три основных класса: проводники, диэлектрики и полупроводники. К проводникам относятся вещества, содержащие заряженные частицы, способные двигаться упорядоченно по всему объему тела под действием электрического поля, — так называемые свободные заряды. Проводниками являются все металлы, водные растворы солей, кислот, щелочей, расплавы солей, ионизованные газы.
Рассмотрим поведение в электрическом поле только твердых металлических проводников. В металлах носителями свободных зарядов являются свободные электроны. Их называют электронами проводимости. Свободные электроны участвуют в тепловом движении и могут перемещаться по куску металла в любом направлении.
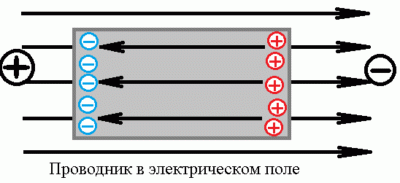
Поместим незаряженный металлический проводник в однородное электростатическое поле.
Под действием поля в нем возникнет упорядоченное движение свободных электронов в направлении, противоположном направлению напряженности Ē этого поля. Электроны будут накапливаться на одной стороне проводника и образуют там избыточный отрицательный заряд, а их нехватка на другой стороне проводника повлечет образования там избыточного положительного заряда, то есть в проводнике произойдет разделение зарядов. Эти нескомпенсированные разноименные заряды появляются в проводнике только под действием внешнего электрического поля, то есть такие заряды являются индуцированными (приведенными). А в целом проводник остается незаряженным. В этом мы убеждаемся, вынимая проводник из электрического поля.
Вид электризации, при котором под действием внешних электрических полей происходит перераспределение зарядов между частями определенного тела, называют электростатической индукцией.
Нескомпенсированные электрические заряды, появившиеся на противоположных частях проводника, создают внутри проводника собственное электрическое поле напряженностью Ēвн. Направления внешнего и внутреннего полей — противоположные:

 Проводник во внешнем электрическом поле
Проводник во внешнем электрическом полеВ результате перемещения свободных носителей заряда и накопления их на противоположных частях проводника напряженность Ē внутреннего поля увеличивается и, наконец, уравнивается по модулю с напряженностью Ēвн внешнего поля. Это приводит к тому, что напряженность результирующего поля внутри проводника равна нулю. К тому же на проводнике устанавливается равновесие зарядов.
Электростатическая защита
При равновесия зарядов на проводнике все нескомпенсированный заряд размещается только на внешней поверхности проводника, а внутри него электрического поля нет. Это явление используют для создания электростатической защиты — защиты от действия электрического поля. В отличие от гравитационного поля, от электрического поля можно защититься, если окружить проводник, например, медной сеткой. На практике это используют, чтобы защититься от мощного электрического поля радиолокаторов и радиостанций, излучения которых может навредить здоровью человека; чтобы предотвратить действия электрического поля на чувствительные приборы.
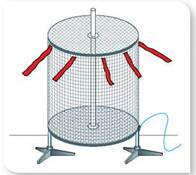
 Электрическое поле, сконцентрированное извне
Электрическое поле, сконцентрированное извнеВиды диэлектриков
Диэлектриками, или изоляторами, называют такие тела, через которые электрические заряды не могут переходить от заряженного тела к незаряженному. Это свойство диэлектриков обусловлена тем, что в них при определенных условиях нет свободных носителей заряда. Если условия меняются, например, при нагревании, в диэлектрике могут возникнуть свободные носители заряда, и он начнет проводить электричество. Итак, разделение веществ на проводники и диэлектрики является условным.
К диэлектрикам относятся все газы при нормальных условиях, жидкости (керосин, спирты, ацетон, дистиллированная вода и др.), твердые тела (стекло, пластмассы, сухое дерево, бумага, резина и т.д.).
В диэлектриках электрические заряды не могут перемещаться под действием электрического поля по всему объему тела так, как свободные заряды проводника.
Диэлектрики делят на два вида:
- полярные, состоящие из молекул, в которых центры распределения положительных и отрицательных зарядов не совпадают (вода, спирты и др.)
- неполярные, состоящие из атомов или молекул, в которых центры распределения положительных и отрицательных зарядов совпадают (бензол, инертные газы, полиэтилен и др.).

 Виды диэлектриков: а — полярные; б — неполярные
Виды диэлектриков: а — полярные; б — неполярныеПоляризация диэлектриков
Внутри диэлектрика электрическое поле может существовать. Притяжение незаряженного тела (диэлектрика) и заряженного тела объясняется тем, что в электрическом поле происходит поляризация диэлектрика, то есть смещение по сторонам разноименных зарядов, входящих в состав атомов и молекул таких веществ, но здесь смещение происходит в пределах каждого атома или молекулы.
Молекулы полярных диэлектриков — это электрические диполи, имеющих постоянный дипольный момент вследствие асимметрии центра масс положительных и отрицательных зарядов.
Если полярный диэлектрик поместить в электрическое поле, то эти диполи начинают возвращаться своими положительно заряженными концами к отрицательно заряженной пластины, а отрицательно заряженными — к положительно заряженной пластине. В результате на поверхности диэлектрика у положительной пластины возникает достаточно тонкий слой отрицательных зарядов, а у отрицательной — положительных, которые и создают встречное поле. (Внутри диэлектрика положительные и отрицательные заряды соседних диполей компенсируют действие друг друга.) Однако, в отличие от проводников, это поле уже не способно полностью компенсировать внешнее, а лишь ослабляет его в ε раз.

 Поляризация полярного диэлектрика
Поляризация полярного диэлектрикаМолекулы неполярных диэлектриков, если отсутствует внешнее электрическое поле, дипольного момента не имеют. Если же неполярный диэлектрик поместить в электрическое поле, его молекулы деформируются, в результате чего образуются диполи, которые ведут себя, как и диполи полярного диэлектрика. В полярных диэлектриках также происходит поляризация молекул, вследствие чего в электрическом поле дипольный момент каждой молекулы несколько увеличивается. Но поляризация неполярных диэлектриков объясняется возникновением дипольного момента в молекуле вследствие ее деформации во внешнем электрическом поле. В зависимости от химической связи она может быть результатом деформации электронных оболочек отдельных атомов и ионов (электронная поляризация) или следствием смещения положительных и отрицательных ионов в разные стороны вдоль силовых линий внешнего электрического поля (ионная поляризация). Приведенный дипольный момент возрастает с увеличением напряженности электрического поля.

 Деформация и ориентация молекул неполярного диэлектрика в электрическом поле
Деформация и ориентация молекул неполярного диэлектрика в электрическом полеТаким образом, в диэлектриках, как и в проводниках, наблюдается индукция электрических зарядов. Однако, если в электрическом поле разделить диэлектрик на две части, то мы не получим разноименно заряженных тел. В этом заключается отличие индукции в диэлектрике от индукции в проводниках.
Диэлектрическая проницаемость вещества
Для характеристики электрических свойств диэлектриков введена особая величина, которую называют диэлектрической проницаемостью. Это физическая постоянная, которая показывает, во сколько раз модуль напряженности электрического поля внутри диэлектрика Евн меньше модуля напряженности Е0 в вакууме:


Диэлектрическая проницаемость определена для всех диэлектриков и занесена в таблицы. Для дистиллированной воды ε = 81, а для керосина ε = 2.
Диэлектрики и проводники в электрическом поле – тема статьи. Ниже рассмотрены физические процессы, происходящие внутри тел и снаружи. Рекомендуется ознакомиться с обзорами на тему электрического потенциала и электрического напряжения.
Электричество и магнетизм
Электричество известно с давних времён, но иных сведений, кроме признания существования, о явлении не приводилось. Узнали лишь, что статический заряд удаётся получить трением, и дело застопорилось. Сложно сказать, что открыто раньше, но геологи считают, что магнетизм известен людям по крайней мере с V века до нашей эры. Находки указывают, что намагниченные куски породы использовались в неизвестных целях на территории современной Турции.
Известно, что систематизация данных по магнетизму началась раньше. Первопроходцем стал известный ныне, благодаря единственному документу, Перегрин. В 1269 году он написал манускрипт, где описал и систематизировал данные по магнитам, предложил методику ориентации для путешественников в пространстве. С латинского «перегринус», «пилигрим» – путешественник. Уже в первые века нашей эры свойство магнита активно эксплуатировалось китайскими мореходами. Перегрин вскрывал ряд свойств:
- Магнит всегда располагается по направлению с севера на юг. Следовательно, обнаруживает два полюса. Одноименные отталкиваются, а разноимённые притягиваются.
- Если магнит разломить пополам, получается два совершенно отдельных куска, обладающие в полной мере свойствами первоначального. Получить полюс по отдельности простыми средствами не получится.
Что касается электричества, физики отдают несомненный приоритет Гильберту. Этот человек создал трактат, где собрал и систематизировал имеющиеся данные, много экспериментировал самостоятельно. Гильберт, по странному совпадению занялся сравнением магнетизма и электричества. К 1600 году никто не задумывался о связи материй и ничего не мог доказать. Гильберт установил, что электричество – в его понимании – считается слабой субстанцией: заряд легко смывается водой, экранируется и характеризуется малой силой взаимодействия. Для теории и будущих поколений сделал важное наблюдение:
- Магнитный шар из руды – Гильберт назвал его Тереллой – ведёт себя подобно Земному в смысле действия на стрелку компаса.
- Электрическое взаимодействие распространяется по прямой. Следовательно, Гильберт оказался первым, кто правильно охарактеризовал силовые линии поля.
Два века понадобилось человечеству, чтобы подобный эффект обнаружить в проводе с током. Сказанное приводит к выводу, что исследования тормозились, вдобавок к инквизиции, отсутствием генератора электричества – не с чем проводить эксперименты. Тереть янтарь шерстью утомительно и малоэффективно. Иллюстрации Гильберта (см. рис.) подтолкнули исследователей к изучению структуры силовых линий, что в будущем помогло объяснить поведение диэлектриков и проводников в магнитном поле.

Гильберту приписывают первую систематизации материалов. Он искал вещества, демонстрирующие способности к электризации, составил списки отличающихся. В последний класс попало большинство металлов, в первый – диэлектрики. Сегодня установлено, что статический заряд распределить возможно практически на любом теле. Но трением приобретают необычные свойства преимущественно диэлектрики. Таким образом, Гильберт первым систематизировал материалы, хотя на момент 1600 года не смог дать удовлетворительные объяснения.
Считается, что первый электростатический генератор изобрёл Отто фон Герике. Серный шар, вращающийся на железной оси, натирали ладонями, наблюдая искры электрического разряда. Герике обнаружил перераспределение статического электричества по поверхности различных тел. На основе созданного генератора стали ставить опыты, к середине XVIII века материалы оказались поделены на классы (проводники и диэлектрики) и по знаку получаемого трением заряда. Появилось смоляное (отрицательное) и стеклянное (положительное) электричество.
Дальнейшие эксперименты позволили при помощи крутильных весов (на тонкой нити) установить закон притяжения и отталкивания между зарядами. Это сделал Шарль Кулон. Он описал количественно силу взаимодействия, подтвердив предположение Гильберта о линейности силовых линий электрических зарядов. На это ушло без малого два века. Закон Кулона позволил учёным дать первые объяснения касательно поведения диэлектриков и проводников в электрическом поле. Уже тогда присутствовало любопытное приспособление, способное удивить и скептика…
Электрофорус
Если поведение диэлектриков в электрическом поле долгое время оставалось неизученным, благодаря металлам Вольта узнал больше об электричестве и позже смог изобрести знаменитый гальванический источник питания. Речь идёт об электрофорусе. Прибор, не слишком известный в России, будоражил умы западных учёных, сегодня служит непременным элементом развлечения студентов. Прибор сейчас покажет (и докажет), как ведут себя проводники в электрическом поле.
Электрофорус – статический генератор с ручным взводом, металлическая печать солидного размера, лучший способ демонстрации статического электричества. Представим, что на круглую подложку из древесины наклеен тончайший лист резины. Вольта говорил, что толстый кусок проявляет худшие свойства. Но не сумел объяснить причину. В давнее время люди не знали, что диэлектрики обладают способностью запасать энергию электрического поля во внутренней структуре. Принцип теперь используется в большинстве конденсаторов.
Тонкий кусок меньше энергии поля поглощал и больше оставлял на поверхности в виде заряда. Трением быстрее доводился до кондиции. Указанный факт отметил Вольта. Требовалось резину натереть. Вольта делал это добрым куском шерсти в течение ряда минут.
Заключительным штрихом конструкции служил тонкий металлический диск, полностью покрывавший резиновый. Толщина выбиралась меньшей, чтобы свойства проводника в электрическом поле проявились ярче. Что происходило в электрофорусе:
- Оператор натирал резину до образования плотного статического заряда электронов.
- Убирал шерсть и опускал сверху металлический диск.
- Проводник электризовался влиянием. Из-за шероховатости поверхности точек соприкосновения оказывалось мало, низ диска заряжался положительно. Это вызвано оттоком электронов, вытолкнутых полем наверх (см. ниже).
- Потом оператор кратковременно заземлял верхнюю часть диска лёгким касанием и разрывал поверхности.
- На нижней стороне металлической «печати» оставался свободный статический положительный заряд.
Опыт повторялся десятки раз. Очевидцы заявляют о сотнях, а Вольта говорил, что «сложно избавить резину от флюида» и предлагал делать это солнечными лучами, пламенем свечи и прочими сильными средствами. Чтобы понять, как работает электрофорус, нужно иметь представление о поведении проводника в электрическом поле.
Поведение проводника в электрическом поле
Деление на проводники, полупроводники и диэлектрики условное. Нет чёткой границы, градация ведётся по удельной проводимости веществ. Проводники хорошо проводят ток, диэлектрики практически лишены указанного качества.
Рассмотрим случай однородного поля с прямыми и параллельными друг другу силовыми линиями, как в большинстве учебников физики. Помещённый в постоянное поле металл начинает заряжаться статическим электричеством, как описано выше. Смысл: линии напряжённости идут в направлении, куда двигался бы положительный заряд – так решил Франклин. Но электроны отрицательны, плывут против течения.
В результате на образце проводника со стороны истока поля скапливается избыток носителей со знаком минус. А противоположный конец металла положителен. Процесс происходит так:
- Поле проникает внутрь металла.
- Проводник полон свободных носителей заряда, двигающихся вдоль силовых линий.
- Процесс перераспределения идёт, пока собственное поле электронов и свободных орбит атомов не уравновесит внешнее воздействие.
- На этом влияние постоянного электрического поля исчерпывается.
Что происходит, если напряжённость поля непостоянна во времени? Допустим, на поверхность падает электромагнитная волна, вызывая попеременное движение электронов в обе стороны, что вызовет ответную электромагнитную волну. Получается, проводник обладает экранирующими свойствами. Отразится лишь половина, это доказывается в теории динамики распространении радиоволн. Чтобы эффект экранирования стал полным, требуется металл заземлить. Что делается на практике.
Поведение диэлектрика в электрическом поле
Стройной теории по поводу поведения диэлектриков в электрическом поле сегодня нет. Физики объясняют происходящее так: в толще вещества присутствуют диполи, образованные сложным строением полимера или аморфного вещества. Размер структур лежит в области нанотехнологий. Молекулы обладают упругими свойствами, проникающее внутрь поле ориентирует их соответствующим образом. Положительная часть смещается по направлению поля, а отрицательная – против.
Диэлектрик способен накапливать энергию поля. Это используется в конденсаторах. Показано, что ёмкость их увеличивается в количество раз, равное диэлектрической проницаемости материала, помещённого между обкладками (для воздуха и вакуума величина равняется 1). Опишем происходящее:
- Конденсатор способен зарядиться лишь до уровня приложенного напряжения.
- Между обкладками создаётся поле. Уровень его напряжённости вычисляется через разницу электрических потенциалов.
- Поле действует на диэлектрик. Диполи внутри начинают ориентироваться так, чтобы с лёгкостью ослабить напряжённость поля.
- Как результат, напряжение на обкладках понижается, процесс заряда возобновляется, до достижения лимита, определяемого типом диэлектрика. Речь идёт о проницаемости вещества.
Диэлектрики в свободном состоянии не имеют выраженного заряда, описываемый эффект назван поляризацией – созданием поля. Вращение диполей считается лишь механизмом, проявляющимся при внешнем воздействии. Во вторую очередь, элементарные заряды начинают вдобавок отдаляться друг от друга. Диполь растягивается. Силы упругости вносят лепту в запасание диэлектриком энергии поля.
Статический заряд на материалы нельзя нанести влиянием. Они хорошо электризуются трением и прикосновением. О чем осведомлены инженеры из нефтяного бизнеса. Масса усилий уходит, чтобы не допустить электризации горючего, приводящей к взрывоопасной ситуации. Задача облегчается тем, что заряд стремится расположиться на поверхности вещества. И специальными гребёнками легко производится нейтрализации. Их ставят на пути потока нефти и снимают на заземлитель избыточный заряд.
90000 PPT — Conductors and Dielectrics PowerPoint Presentation, free download 90001 90002 90003 90004 Conductors and Dielectrics 90005 • Conductors • Current, current density, drift velocity, continuity • Energy bands in materials • Mobility, micro / macro Ohm’s Law • Boundary conditions on conductors • Methods of Images • dielectrics • Polarization, displacement, electric field • permittivity, susceptibility, relative permittivity • dielectrics research • Boundary conditions on dielectrics 90006 90007 90008 90003 90004 Conductors and dielectrics 90005 • Polarization • Static alignment of charge in material • Charge aligns when voltage applied, moves no further • Charge proportional to voltage • Conduction • Continuous motion of charge through material • Enters one side, exits another • Current proportional to voltage • Real-world materials • Plastics, ceramics, glasses -> dielectrics (maybe some conductivity) • Metals -> conductors, semiconductors, superconductors • Cement, Bi osystems -> Both (water high dielectric, salt conductivity) 90006 90007 90014 90003 90004 n 90005 Current and current density • Basic definition of current C / s = Amps • Basic current density (J perp.surface) • Vector current density 90006 90007 90020 90003 90004 Current density and charge velocity 90005 • Basic definition of current • Combining with earlier expression • Gives current density 90006 90007 90026 90003 90004 Charge and current continuity 90005 • Current leaving any closed surface is time rate of change of charge within that surface • Using divergence theorem on left • Taking time derivative inside integral • Equating integrands Qi (t) 90006 90007 90032 90003 90004 Example — charge and current continuity 90005 • Given spherically symmetric current density • Current increasing from r = 5m to r = 6m at t = 1s • Current density from continuity equation • Charge density ρ integral w.Why is current increasing? << Some central repulsive force! 90006 90007 90038 90003 90004 Energy Band Structure in Three Material Types 90005 • Discrete quantum states broaden into energy bands in condensed materials with overlapping potentials • Valence band - outermost filled band • Conduction band - higher energy unfilled band • Band structure determines type of material • Insulators show large energy gaps, requiring large amounts of energy to lift electrons into the conduction band.When this occurs, the dielectric breaks down. • Conductors exhibit no energy gap between valence and conduction bands so electrons move freely • Semiconductors have a relatively small energy gap, so modest amounts of energy (applied through heat, light, oran electric field) may lift electrons from valence to conduction bands. 90006 90007 90044 90003 90004 Free electrons are accelerated by an electric field. The 90005 applied force on an electron of charge Q = -e is But in reality the electrons are constantly bumping into things (like a terminal velocity) so they attain an equilibrium or drift velocity: where eis the electron mobility, expressed in units of m2 / Vs.The drift velocity is used in the current density through: So Ohm's Law in point form (material property) With the conductivity given as: S / m (electrons / holes) Ohm's Law (microscopic form) S / m (electrons) 90006 90007 90050 90003 90004 Ohm's Law (macroscopic form) 90005 • For constant electric field • Ohm's Law becomes • Rearranging gives • Or • Variation with geometry • Conductance vs. Resistance 90006 90007 90056 90003 90004 Ohm's Law example 1 90005 • Checking ohms law microscopic form • Mobility of copper is 0.0032 m2 / Vs • Charge density 90006 90007 90062 90003 90004 Ohm's Law example 2 90005 90006 90007 90068 90003 90004 Boundary conditions for conductors 90005 • No electric field in interior • Otherwise charges repel to the surface • No tangential electric field at surface • Otherwise charges redistribute along surface • Normal electric field at surface • Displacement Normal equals Charge Density (Gauss's Law) 90006 90007 90074 90003 90004 or 90005 Over the rectangular integration path, we use To find: dielectric n These become negligible as h approaches zero.Therefore conductor More formally: Boundary Condition for Tangential Electric Field E 90006 90007 90080 90003 90004 Gauss 'Law is applied to the cylindrical surface shown 90005 below: dielectric This reduces to: as h approaches zero n Therefore s conductor More formally: Boundary Condition for the Normal Displacement D 90006 90007 90086 90003 90004 Tangential E is zero 90005 At the surface: Normal D is equal to the surface charge density Summary 90006 90007 90092 90003 90004 Example - Boundary Conditions for Conductors 90005 • Potential given by • Potential at (2 , -1,3) is 300 V.Also 300 V along entire surface where • Thus we can "insert" conductor in region provided the conductor follow hyperbola • The Electric Field is at all times normal to conducting surface • Electric field at point 2, -1,3) • Ex = - 400 V / m, Ey = -200 V / m • Down and to left 90006 90007 90098 90003 90004 Example - Streamlines of Electric Field 90005 • Slope of line equals electric field ratio • Rearranging • Evaluate at P (2, -1,3 ) -2 90006 90007 90104 90003 90004 Boundary condition example (from my phone) * 90005 * www.mathstudio.net 90006 90007 90110 90003 90004 The Theorem of Uniqueness states that if we are given a 90005 configuration of charges and boundary conditions, there will exist only one potential and electric field solution. In the electric dipole, the surface along the plane of symmetry is an equipotential with V = 0. The same is true if a grounded conducting plane is located there. So the boundary conditions and charges are identical in the upper half spaces of both configurations (not in the lower half).In effect, the positive point charge images across the conducting plane, allowing the conductor to be replaced by the image. The field and potential distribution in the upper half space is now found much more easily! Method of Images 90006 90007 90116 90003 90004 Each charge in a given configuration will have its own image 90005 Forms of Image Charges 90006 90007 90122 90003 90004 Want to find surface charge density on conducting plane at 90005 the point (2,5,0). A 30-nC line of charge lies parallel to the y axis at x = 0, z = 3.First step is to replace conducting plane with image line of charge -30 nC at z = -3. Example of the Image Method 90006 90007 90128 90003 90004 Vectors from each line charge to observation point: 90005 Electric Fields from each line charge Add both fields to get: (x component cancels) Example of the Image Method (continued) - 90006 90007 90134 90003 90004 Electric Field at P is thus: 90005 Displacement is thus Charge density is n D Example of the Image Method (continued) 90006 90007 90140 90003 90004 Image Method using Potentials 90005 • Conducting plane at x = 4 with vertical wire in front.• Potential for wire in front at x = 6, y = 3: • Boundary condition for wire in front at x = 6, y = 3: • Boundary condition for image wire in back at x = 2, y = 3: 90006 90007 90146 90003 90004 Image Method using Potentials (cont) 90005 • Total potential becomes • At point (7, -1,5) gives • To get electric field must write V (ρ) as V (x, y) and take gradient 90006 90007 90152 90003 90004 Dielectrics 90005 • Material has random oriented dipoles • Applied field aligns dipoles (negative at (+) terminal, positive at (-) terminal • Effect is to cancel applied field, lower voltage • OR, increase charge to maintain voltage • Either increases capacitance C = Q / V 90006 90007 90158 90003 90004 Review Dipole Moment 90005 • Define dipole moment • Potential for dipole • Written in terms of dipole moment and position • Dipole moment determines "strength" of polar molecule amount of charge (Q) and offset (d) of charge 90006 90007 90164 90003 90004 Introducing an electric field ma y increase the charge 90005 separation in each dipole, and possibly re-orient dipoles so that there is some aggregate alignment, as shown here.The effect is small, and is greatly exaggerated here! E The effect is to increase P. n = charge / volume p = polarization of individual dipole P = polarization / volume Polarization as sum of dipole moments (per volume) 90006 90007 90170 90003 90004 E 90005 Polarization near electrodes positive • From diagram • Excess positive bound charge near top negative electrode • Excess negative bound charge near bottom positive electrode • Rest of material neutral • Excess charge in bound (red) volumes • Writing in terms of polarization • Writing similar to Gauss's law (Note dot product sign, outward normal leaves opposite charge enclosed) - - - - - - - - - - - - - - - - neutral negative + + + + + + + + + + + + + 90006 90007 90176 90003 90004 E 90005 Combining total, free, and bound charge positive • Total, free, and bound charge • Total • Free • Bound • Combining - - - - - - - - - - - - - - - - neutral negative + + + + + + + + + + + + + 90006 90007 90182 90003 90004 D, P, and E in Dielectric 90005 • D continuous • Polarization incr eases • E decreases • C / m2 90006 90007 90188 90003 90004 Bound Charge: 90005 Total Charge: Free Charge: Charge Densities Taking the previous results and using the divergence theorem, we find the point form expressions: 90006 90007 90194 90003 90004 A stronger electric field results in a larger polarization 90005 in the medium.In a linear medium, the relation between P and E is linear, and is given by: where e is the electric susceptibility of the medium. We may now write: where the dielectric constant, or relative permittivity is defined as: Leading to the overall permittivity of the medium: where Electric Susceptibility and the Dielectric Constant 90006 90007 90200 90003 90004 In an isotropic medium, the dielectric constant is invariant 90005 with direction of the applied electric field. This is not the case in an anisotropic medium (usually a crystal) in which the dielectric constant will vary as the electric field is rotated in certain directions.In this case, the electric flux density vector components must be evaluated separately through the dielectric tensor. The relation can be expressed in the form: Isotropic vs. Anisotropic Media 90006 90007 90206 90003 90004 Permittivity of Materials 90005 • Typical permittivity for various solids and liquids. • Teflon - 2 • Plastics - 3-6 • Ceramics 8-10 • Titanates> 100 • Acetone 21 • Water 78 • Actual dielectric «constant» varies with: • Temperature • Direction • Field Strength • Frequency • Real & Imaginary components 90006 90007 90212 90003 90004 Variation with frequency 90005 • Charge polarization due to: • Ionic (low frequency) • Orientation (medium, microwave) • Atomic (IR) • Electronic (Visible, UV) • Dielectric relaxation • As frequency is raised, molecule can no longer «track».• Real permittivity decreases and imaginary permittivity peaks • In medium and microwave range • Rotation, reorientation, etc >> • Modeling: • Permittivity & impedance diagrams. • Statistical relaxation functions (Debye, Cole Davidson). 90006 90007 90218 90003 90004 Application to Polymer Composites 90005 • Dielectric Permittivity in Epoxy Resin 10Hz -10 MHz • Polar-group rotation in epoxy resin. • Low-frequency range 10 Hz — 10 MHz. • Permittivity-loss transition at 1 MHz, at -4 ° C.• Transition frequency increases with temperature. www.msi-sensing.com 90006 90007 90224 90003 90004 Dielectric Permittivity in Epoxy Resin 1 MHz -1 GHz 90005 • Aerospace resin Hexcel 8552. • High frequency range 1 MHz — 1 GHz. • Temperature constant 125 ° C, transition decreases with cure. • TDR measurement method. www.msi-sensing.com 90006 90007 90230 90003 90004 Permittivity in Epoxy Resin during Complete Cure Cycle 90005 www.msi-sensing.com 90006 90007 90236 90003 90004 Application to cement hydration 90005 • Cement Conductivity — Variation with Cure • Imaginary counterpart of real permittivity ( »).• Multiply by to remove power law (o »). • Decrease in ion conductivity, growth of intermediate feature with cure • Frequency of intermediate feature does not match permittivity www.msi-sensing.com 90006 90007 90242 90003 90004 Cement Cure -Dielectric Relaxation Model 90005 Requirements: • Provide free-relaxation, two intermediate -frequency relaxations • Provide conductivity and electrode polarization Debye for free & medium. Cole-Davidson for low. (Literature, biosystems) Combined 9 variables fit over entire range, real & imaginary, 2-stage fit, f = 8.2 ps www.msi-sensing.com 90006 90007 90248 90003 90004 Cement Cure — Model Fitting 90005 • Fits permittivity — both low and free relaxation. • Fits conductivity — both medium and free relaxation. • Fits permittivity polarization. • Fits conductivity baseline. www.msi-sensing.com 90006 90007 90254 90003 90004 Other applications 90005 • Other Applications • Bio • Liquid Crystal • Composite polymers • Titanates • Wireless characterization • MRI dyes • Ground water monitoring • Oil Drilling fluid characterization (GPR) 90006 90007 90260 90003 90004 Since E is conservative, we setup line integral straddling 90005 both dielectrics: Left and right sides cancel, so Leading to Continuity for tangential E Boundary Condition for Tangential Electric Field E And Discontinuity for tangential DE same, D higher in high permittivity material 90006 90007 90266 90003 90004 n 90005 Apply Gauss ‘Law to the cylindrical volume straddling both dielectrics s Flux enters and exits only through top and bottom surfaces, zero on sides Boundary Condition for Normal Displacement D Leading to Continuity for normal D (for ρS = 0) And Discontinuity for normal ED same.E lower in high permittivity material 90006 90007 90272 90003 90004 Bending of D at boundary 90005 • Boundary conditions • DN continuous • Trigonometry • Eliminating DN high low 90006 90007 90278 90003 90004 Example 90005 • Teflon εr = 2.1 • Displacement and Polarization outside • Displacement and Polarization inside • At boundary D is continuous, so inside 90006 90007 90284 90003 90004 Example (continued) 90005 • Polarization up, E field down, D maintains continuity 90006 90007 90290 90003 90004 Example 90005 90006 90007 90296 90003 90004 Quiz 2 — Problem 4.21 90005 90006 90007.90000 electricity | Definition, Facts, & Types 90001 90002 Electrostatics is the study of electromagnetic phenomena that occur when there are no moving charges-i.e., After a static equilibrium has been established. Charges reach their equilibrium positions rapidly because the electric force is extremely strong. The mathematical methods of electrostatics make it possible to calculate the distributions of the electric field and of the electric potential from a known configuration of charges, conductors, and insulators.Conversely, given a set of conductors with known potentials, it is possible to calculate electric fields in regions between the conductors and to determine the charge distribution on the surface of the conductors. The electric energy of a set of charges at rest can be viewed from the standpoint of the work required to assemble the charges; alternatively, the energy also can be considered to reside in the electric field produced by this assembly of charges. Finally, energy can be stored in a capacitor; the energy required to charge such a device is stored in it as electrostatic energy of the electric field.90003 90004 Examine what happens to the electrons of two neutral objects rubbed together in a dry environment 90005 Explanation of static electricity and its manifestations in everyday life. 90006 Encyclopædia Britannica, Inc. 90007 See all videos for this article 90002 Static electricity is a familiar electric phenomenon in which charged particles are transferred from one body to another. For example, if two objects are rubbed together, especially if the objects are insulators and the surrounding air is dry, the objects acquire equal and opposite charges and an attractive force develops between them.The object that loses electrons becomes positively charged, and the other becomes negatively charged. The force is simply the attraction between charges of opposite sign. The properties of this force were described above; they are incorporated in the mathematical relationship known as Coulomb’s law. The electric force on a charge 90009 Q 90010 90011 1 90012 under these conditions, due to a charge 90009 Q 90010 90011 2 90012 at a distance 90009 r 90010, is given by Coulomb’s law, 90003 90002 The bold characters in the equation indicate the vector nature of the force, and the unit vector 90009 90004 r 90005 90010 is a vector that has a size of one and that points from charge 90009 Q 90010 90011 2 90012 to charge 90009 Q 90010 90011 1 90012.The proportionality constant 90009 k 90010 equals 10 90035 -7 90036 90009 c 90010 90035 2 90036, where 90009 c 90010 is the speed of light in a vacuum; 90009 k 90010 has the numerical value of 8.99 × 10 90035 9 90036 newtons-square metre per coulomb squared (Nm 90035 2 90036 / C 90035 2 90036). Figure 1 shows the force on 90009 Q 90010 90011 1 90012 due to 90009 Q 90010 90011 2 90012. A numerical example will help to illustrate this force. Both 90009 Q 90010 90011 1 90012 and 90009 Q 90010 90011 2 90012 are chosen arbitrarily to be positive charges, each with a magnitude of 10 90035 -6 90036 coulomb.The charge 90009 Q 90010 90011 1 90012 is located at coordinates 90009 x 90010, 90009 y 90010, 90009 z 90010 with values of 0.03, 0, 0, respectively, while 90009 Q 90010 90011 2 90012 has coordinates 0, 0.04, 0. All coordinates are given in metres. Thus, the distance between 90009 Q 90010 90011 1 90012 and 90009 Q 90010 90011 2 90012 is 0.05 metre. 90003 90004 electric force between two charges 90005 Figure 1: Electric force between two charges. 90006 Courtesy of the Department of Physics and Astronomy, Michigan State University 90007 Get exclusive access to content from our тисяча сімсот шістьдесят вісім First Edition with your subscription.Subscribe today 90002 The magnitude of the force 90009 90004 F 90005 90010 on charge 90009 Q 90010 90011 1 90012 as calculated using equation (1) is 3.6 newtons; its direction is shown in Figure 1. The force on 90009 Q 90010 90011 2 90012 due to 90009 Q 90010 90011 1 90012 is — 90009 90004 F 90005 90010, which also has a magnitude of 3.6 newtons; its direction, however, is opposite to that of 90009 90004 F 90005 90010. The force 90009 90004 F 90005 90010 can be expressed in terms of its components along the 90009 x 90010 and 90009 y 90010 axes, since the force vector lies in the 90009 x 90010 90009 y 90010 plane.This is done with elementary trigonometry from the geometry of Figure 1, and the results are shown in Figure 2. Thus, in newtons. Coulomb’s law describes mathematically the properties of the electric force between charges at rest. If the charges have opposite signs, the force would be attractive; the attraction would be indicated in equation (1) by the negative coefficient of the unit vector 90009 90004 r. 90005 90010 Thus, the electric force on 90009 Q 90010 90011 1 90012 would have a direction opposite to the unit vector 90009 90004 r 90005 90010 and would point from 90009 Q 90010 90011 1 90012 to 90009 Q 90010 90011 2 90012.In Cartesian coordinates, this would result in a change of the signs of both the 90009 x 90010 and 90009 y 90010 components of the force in equation (2). 90003 90004 components of Coulomb force 90005 Figure 2: The 90009 x 90010 and 90009 y 90010 components of the force 90009 90004 F 90005 90010 in Figure 4 (see text). 90006 Courtesy of the Department of Physics and Astronomy, Michigan State University 90007 90002 How can this electric force on 90009 Q 90010 90011 1 90012 be understood? Fundamentally, the force is due to the presence of an electric field at the position of 90009 Q 90010 90011 1 90012.The field is caused by the second charge 90009 Q 90010 90011 2 90012 and has a magnitude proportional to the size of 90009 Q 90010 90011 2 90012. In interacting with this field, the first charge some distance away is either attracted to or repelled from the second charge, depending on the sign of the first charge. 90003 .90000 Page Not Found | MIT 90001 Skip to content ↓ 90002 90003 Education 90004 90003 Research 90004 90003 Innovation 90004 90003 Admissions + Aid 90004 90003 Campus Life 90004 90003 News 90004 90003 Alumni 90004 90003 About MIT 90004 90003 More ↓ 90002 90003 Admissions + Aid 90004 90003 Campus Life 90004 90003 News 90004 90003 Alumni 90004 90003 About MIT 90004 90031 90004 90031 Menu ↓ Search Menu Uh oh, looks like we couldnt find what you were looking for! 90034 Try searching for something else! What are you looking for? See More Results 90035 Suggestions or feedback? 90036 .90000 Dielectrics under Electric Field | IntechOpen 90001 \ n 90002 2.1. Conductivity 90003 \ n 90004 The main properties for dielectric under electric field are conduction, polarization, dissipation, and breakdown. Although normally a dielectric material is a good insulator, there are still some charge carries flowing through the whole material under electric field, which is called leakage current. Under a direct current (dc) field, the current could be a constant for a material. If the detected current is 90005 I 90006 when a voltage 90005 U 90006 is applied to a material, the conduction 90005 G 90006 of the materials is 90005 I / U 90006.If the material has a regular plate structure with surface 90013 A 90014 and thickness 90013 t 90014, the conductivity 90005 σ 90006 of the material is: 90019 \ n 90004 \ n \ n \ nσ \ nDC \ n \ n = \ n \ nI \ nU \ n \ n \ nd \ nA \ n \ n \ nE1 90019 \ n 90004 The property can also be expressed by bulk resistivity 90013 ρ 90014, which is reciprocal of conductivity: 90019 \ n 90004 \ n \ nρ \ n = \ n \ nU \ nI \ n \ n \ nA \ nd \ n \ n \ nE2 90019 \ n 90004 Both conductivity and resistivity are electrical properties for all materials, that is, conductor, semiconductor, and insulator.Because of different mechanism of conduction, there is a huge gap between conductivities of dissimilar materials, which has been well understood by energy band theory. The conductivity of a conductor could be big as 10 90029 9 90030 S / m; the conductivity of good insulating dielectrics could be small as 10 90029 -18 90030 S / m. 90019 \ n 90004 The DC conductivity in dielectrics is related to the hopping transition of defect charge carries, and thus, it is strongly temperature dependent: 90019 \ n 90004 \ n \ n \ nσ \ nDC \ n \ n = \ n \ nσ \ n0 \ n \ n \ ne \ n \ n- \ nEa \ n / \ n \ nk \ nB \ n \ nT \ n \ n \ n \ nE3 90019 \ n 90004 Here 90013 kB 90014 is Boltzmann constant, 90013 T 90014 is temperature, and 90013 Ea 90014 is thermal activity energy.By fitting experimental date with Eq. 3, the fitted activation energy 90013 Ea 90014 gives information about current carriers. 90019 \ n 90004 The conductivity of dielectrics under alternative current (ac) field is related to the imaginary part of dielectric constant, which is introduced in Section 3. Since insulating is prerequired for dielectrics, the conductivity is less considered in the study of dielectrics. However, in some cases, it is crucial for dielectric properties [7]. 90019 \ n \ n 90002 2.2. Polarization 90003 \ n 90004 Polarization is the unique electrical properties for dielectrics, depending on which concept is defined. There are diverse types of polarization, that is, electronic polarization, ionic polarization, orientation polarization, interface polarization, spontaneous polarization, and so on. 90019 \ n 90004 In dielectrics, if one positive charge + 90013 q 90014 and the corresponding negative charge — 90013 q 90014 are separated by a distance 90005 d 90006, an electric dipole is produced with magnitude 90005 p 90006 90013 = qd 90014.It is a vector with direction from negative charge toward positive charge. This dipole could be the one induced by electric field like in electronic polarization or ionic polarization, but it could also be one permanent like in polar molecules and ferroelectrics. After introducing electric dipole, the polarization in a material can be defined as the sum of individual dipole moments 90005 p 90006 divided by volume 90013 V 90014 of the material: 90019 \ n 90004 \ n \ nP \ n = \ n \ n \ n Σ \ np \ n \ nV \ n \ n \ nE4 90019 \ n 90004 From this definition, we can see that the magnitude of polarization equals to the surface charge density, in fact depending on which the spontaneous polarization of ferroelectrics is measured by Sawyer -Tower electrical bridge.90019 \ n 90004 For all dielectrics under electric field, the mutual shifts of nuclei and electrons induce electronic polarization, which occur within very short time, that is, 10 90029 -14 90030 -10 90029 -16 90030 s. Electronic polarization exists for all materials. In ionic crystals, the relative separation of cation and anion is induced by electric field, which is called ionic polarization. The ionic polarization also builds at a very short time, that is, 10 90029 -12 90030 -10 90029 -13 90030 s.90019 \ n 90004 In some molecules, the center of positive charge and negative charge does not coincide, which is called polar molecule. In polar molecules, permanent dipoles exist and can somehow rotate under electric field. In thermal equilibrium state, the dipoles randomly orient, and thus, there is no net polarization. When an external electric field applied, these dipoles align to it in some extent. Thus, orientation polarization is induced. The response time of these permanent dipoles changes from material to material, that is, 10 90029 -2 90030 -10 90029 -12 90030 s.For example, in water at 300 K, the response time is around 5 × 10 90029 -11 90030 s. 90019 \ n 90004 Interface polarization, which is also called space charge polarization, builds at interface between two or more heterogeneous medium, i.e., between electrodes and dielectrics, between different dielectrics, between grain boundaries in ceramics, etc. The electrons, ions, and other defects trap at these sites, which have a slow response toward AC electric field. The response time varies from case to case, that is, 10 90029 7 90030 -10 90029 -6 90030 s.90019 \ n 90004 In ferroelectrics, from high-temperature paraelectric phase to low-temperature ferroelectric phase, a permanent dipole is present because of symmetry break without electric field, which is called spontaneous polarization. The spontaneous polarization can be reversed by an external electric field, which makes ferroelectrics a smart material with lots of interesting properties. 90019 \ n 90004 In general, the relation between polarization 90005 P 90006 and electric field 90005 E 90006 follows [12]: 90019 \ n 90004 \ n \ nP \ n = \ nεχE \ n + \ nhigher terms in \ n \ nE \ n \ nE5 90019 \ n 90004 where 90013 ε0 90014 is the permittivity of free space, and 90013 χ 90014 is the susceptibility.The equation does not include spontaneous polarization of ferroelectrics. For most dielectrics, the first term is dominant. Higher terms are commonly omitted except for nonlinear dielectrics. 90019 \ n 90004 From Eq. (5), we can see that 90013 χ 90014 represents the polarizability. But the most widely used parameter is dielectric permittivity 90013 ε 90014: 90019 \ n 90004 \ n \ nε \ n = \ n \ nD \ nE \ n \ n \ nE6 90019 \ n 90004 Here 90005 D 90006 is electric displacement. And in engineering, the relative dielectric permittivity 90013 εr = ε / ε0 90014, or more generally called dielectric constant, is used because 90013 ε 90014 is too small in SI unit.90019 \ n 90004 For a capacitor, electric displacement equals to the surface charge density. Assume a planar capacitor consisting of two parallel electrodes with surface 90013 S 90014 and distance 90013 d 90014. When a voltage 90005 V 90006 is applied and there is no dielectric material between electrodes, the surface charge density 90005 Q 90006 90139 90005 0 90006 90142 = 90013 ε0V / t 90014 appears according to Gauss ‘law. If a dielectric material with susceptibility 90013 χ 90014 is filled in between two electrodes, it contributes surface charge density 90005 Q 90006 90139 90005 d 90006 90142 90013 = P = ε0χV / t 90014.As a result, the total surface charge equals the sum of two: 90013 Q = ε0 (1 + χ) V / t. 90014 As a result, combining Eqs. (5) and (6), we can get the relation between relative dielectric permittivity 90013 εr 90014 and susceptibility 90013 χ 90014: 90019 \ n 90004 \ n \ n \ nε \ nr \ n \ n = \ n \ n \ n1 \ n + \ nχ \ n \ n \ n \ nE7 90019 \ n 90004 Both 90013 εr 90014 and 90013 χ 90014 are parameters describing the polarizable property of dielectrics under electric field. 90019 \ n.