провод ас 50 цена, провод ас 50 характеристики вес провода ас 50 8 кабель оптом
Цена провода АС 50/8 указана усредненная и зависит от объема заказа, окончательную цену уточняйте у менеджеров.
Купить провод АС вы можете подав заявку по телефону 8-800-775-3150(звонок по России бесплатный), либо нажав на кнопку «рассчитать» оформить заказ, заполнив бланк заявки. Также для вашего удобства у нас работает онлайн консультант(в правом нижнем углу), который ответит на все ваши вопросы. Доставка осуществляется автотранспортом, при оформлении заявки на провод укажите ваш населенный пункт и наши менеджеры рассчитают цену с доставкой с ближайшего склада, в данный момент действует акция по которой вы экономите от 50% до 100% стоимости доставки.
Главным предназначением не изолированных алюминиевых проводов марки АС 50/8 является передача электроэнергии по линиям воздушных передач. Использованы они могут быть в самых разных климатических поясах при температуре окружающей среды не ниже — 40 и не выше +60.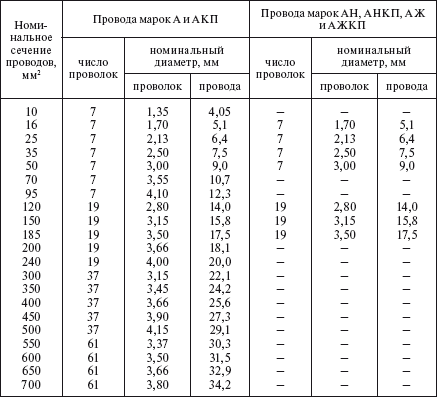 Единственным ограничением для применения этих проводов является количество сернистого газа в воздухе, которое должно быть не больше 150 мг/м2. Также нельзя использовать провод АС 50/8 для прокладывания линий электропередач через водоемы.
Единственным ограничением для применения этих проводов является количество сернистого газа в воздухе, которое должно быть не больше 150 мг/м2. Также нельзя использовать провод АС 50/8 для прокладывания линий электропередач через водоемы.
Цена на провод зависит исключительно от качества алюминия, который применялся для его изготовления. Производители проводов гарантируют их бесперебойную работу в течение четырех лет после начала применения. А максимальный срок использования при строгом выполнении всех норм и стандартов может достигать 45 лет. Нельзя допускать нагрева провода до температуры выше 90 в течение длительного времени.
КОНСТРУКЦИЯ Провода АС 50/8
Провод АС 50/8 представляет собой несколько плотно скрученных друг с другом алюминиевых проволок. В середине скрутки проходит стальной сердечник. Проволоки соединяются таким образом, что соседние повивы идут в противоположные стороны, а самая крайняя наружная проволока всегда наматывается в правую сторону.
Технические характеристики провода АC 50/8 | |
|---|---|
| Наименование характеристики: | Показатели: |
| Сечение провода номинальное | 50/8 мм2 |
| Количество алюминиевых проволок | 6 шт |
| Количество стальных проволок | 1 штука |
| Диаметр алюминиевой проволоки | 3,2 мм |
| Диаметр стальной проволоки | 3,2 мм |
| Диаметр провода | 9,6 мм |
| Диаметр стального сердечника | 3,2 мм |
| Сопротивление на 1 км провода при температуре 20 | 0,5951 Ом |
| Усилие на разрыв | 17112 Н |
| Максимальная температура эксплуатации | 90 |
| Вес провода АC 50/8 (1 км) | 195 кг |
Расчёт веса Эмальпровода
Табличный расчет веса обмоточного провода
У нас вы можете заказать провод на отмот, минимальная норма заказа 500 грамм
|
Диаметр проволоки мм. |
Вес 1 км. Провода |
Диаметр |
Вес 1 км. Провода |
|
|
0,033 |
0,600 |
2,620 |
|
0,071 |
0,040 |
0,630 |
2,870 |
|
0,080 |
0,051 |
0,670 |
3,250 |
|
0,090 |
0,063 |
0,710 |
3,650 |
|
0,100 |
0,077 |
0,750 |
4,070 |
|
0,112 |
0,095 |
0,800 |
4,630 |
|
0,125 |
0,109 |
0,850 |
5,220 |
|
0,140 |
0,147 |
0,900 |
5,840 |
|
0,150 |
0,169 |
0,950 |
6,500 |
|
0,160 |
0,195 |
1,000 |
7,190 |
|
0,170 |
0,220 |
1,060 |
8,090 |
|
0,180 |
0,244 |
|
9,010 |
|
0,200 |
0,299 |
1,180 |
9,990 |
|
0,224 |
0,375 |
1,250 |
11,200 |
0,236 |
0,417 |
1,320 |
12,500 |
|
0,250 |
0,466 |
1,400 |
14,000 |
|
0,265 |
0,524 |
1,450 |
15,100 |
|
0,280 |
0,591 |
1,500 |
16,100 |
|
0,300 |
0,667 |
1,560 |
16,400 |
|
0,315 |
0,708 |
1,600 |
18,300 |
|
0,335 |
0,800 |
1,700 |
20,600 |
|
0,355 |
0,895 |
1,800 |
23,100 |
|
0,380 |
1,030 |
1,900 |
25,700 |
|
0,400 |
1,170 |
2,000 |
28,500 |
|
0,425 |
1,320 |
2,120 |
31,900 |
|
0,450 |
1,490 |
|
35,700 |
|
0,475 |
1,660 |
2,360 |
39,600 |
|
0,500 |
1,830 |
2,440 |
|
|
0,530 |
2,050 |
2,500 |
44,400 |
|
0,560 |
2,280 |
|
|
Провод ППСРВМ, ППСРВМ-1, ППСРМ, ППСРМ-1
КОНСТРУКЦИЯ
- Медная токопроводящая жила (класс гибкости 5), многопроволочная, круглой формы соответствует классу 4 по ГОСТ 22483-77.

- Обмотка из полиэтилентерефталатной пленки.
- Изоляция из резины.
- Разделительный слой — изолированные жилы сечением более 10 мм2 , предназначенные для присоединения к подвижным токоприемникам, поверх изоляции имеют сепаратор из неэлектропроводящей прорезиненной тканевой ленты или полиэтилентерефталатной пленки.
- Оболочка из ПВХ пластиката.
ПРИМЕНЕНИЕ
Данные провода предназначены для внутренних и наружных соединений в тепловозах в качестве комплектующих изделий (для достройки спроектированных единиц подвижного состава и ремонта) и троллейбусов, на напряжение 660, 1500, 3000, 4000 В переменного тока частотой до 400 Гц или 1000, 2500, 4500, 6000 В постоянного тока соответственно, для присоединения к подвижным токоприемникам, монтажа при ограниченных перемещениях и для фиксированного монтажа при воздействии смазочных масел и дизельного топлива. Кабели предназначены и для эксплуатации в районах с тропическим климатом. Провода в тропическом исполнении устойчивы к воздействию плесневых грибов. Провода не распространяют горение. Провода устойчивы к вертикальным колебаниям, вибрациям, изгибам и изгибам с одновременным закручиванием. Провода стойки к воздействию дождя, динамическому воздействию пыли, выпадению инея и воздействию озона.
Провода не распространяют горение. Провода устойчивы к вертикальным колебаниям, вибрациям, изгибам и изгибам с одновременным закручиванием. Провода стойки к воздействию дождя, динамическому воздействию пыли, выпадению инея и воздействию озона.
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Условия эксплуатации и технические характеристики | |
Диапазон температур эксплуатации: | от -50 до +60°С |
Относительная влажность воздуха при температуре до: | + 40°С…. до 98 % |
Монтаж проводов должен производиться при температуре: | не ниже -15°С |
Радиус изгиба при монтаже должен быть: | не менее 3 диаметров провода |
Радиус изгиба при эксплуатации должен быть: | не менее 5 диаметров провода |
Допускается монтаж с отключением и подключением при отсутствии ударов к токоприемникам при плавном изгибе на радиус, равный пятикратному диаметру провода, при температуре: | -50°С |
Длительно допустимая температура на жилах проводов должна быть: | не более 65°С |
Допускается эксплуатация проводов при температуре на жиле: | 75°С |
Провода на номинальное напряжение 660, 1500, 3000, 4000 В переменного тока выдерживают испытание напряжением переменного тока частоты 50 Гц величиной 3000, 6000, 12000, 16000 В соответственно в течение 15 мин после 24 ч пребывания в воде. | |
Число жил и номинальное сечение, мм2 | Номинальный наружный диаметр, мм | Масса 1 км провода, кг | ||||||
660 В | 1500 В | 3000 В | 4000 В | 660 В | 1500 В | 3000 В | 4000 В | |
ППСРВМ | ||||||||
1х1,0 | 5,7 | 6,5 | 7,3 | 10,3 | 44,8 | 57,5 | 72,0 | 140,0 |
1х1,5 | 6,0 | 6,8 | 7,6 | 10,6 | 52,8 | 66,2 | 81,5 | 151,0 |
1х2,5 | 6,7 | 7,5 | 8,3 | 11,3 | 70,6 | 85,8 | 103,0 | 179,0 |
1х4,0 | 7,3 | 8,1 | 9,5 | 11,9 | 88,7 | 105,0 | 135,0 | 204,0 |
1х6,0 | 7,9 | 9,3 | 10,1 | 12,5 | 113,0 | 142,0 | 163,0 | 237,0 |
1х10 | 10,0 | 10,8 | 11,6 | 14,0 | 186,0 | 208,0 | 233,0 | 317,0 |
1х16 | 11,5 | 12,4 | 13,2 | 15,6 | 262,0 | 289,0 | 318,0 | 417,0 |
1х25 | 13,2 | 14,0 | 14,8 | 16,8 | 379,0 | 410,0 | 443,0 | 535,0 |
1х35 | 14,9 | 15,7 | 16,5 | 18,9 | 500,0 | 535,0 | 572,0 | 689,0 |
1х50 | 16,5 | 17,3 | 18,5 | 20,5 | 659,0 | 698,0 | 754,0 | 868,0 |
1х70 | 19,7 | 20,5 | 21,3 | 23,3 | 899,0 | 946,0 | 995,0 | 1125,0 |
1х95 | 21,6 | 22,4 | 23,2 | 25,2 | 1195,0 | 1246,0 | 1300,0 | 1433,0 |
1х120 | 24,6 | 25,3 | 26,1 | 27,7 | 1460,0 | 1519,0 | 1579,0 | 1706,0 |
1х150 | 27,5 | 28,3 | 29,1 | 30,7 | 1815,0 | 1881,0 | 1949,0 | 2092,0 |
1х185 | 28,8 | 29,6 | 30,4 | 31,6 | 2199,0 | 2268,0 | 2339,0 | 2449,0 |
1х240 | 32,6 | 33,4 | 34,6 | 35,8 | 2786,0 | 2869,0 | 2973,0 | 3098,0 |
1х300 | 35,5 | 36,3 | 37,1 | 37,9 | 3438,0 | 3522,0 | 3610,0 | 3700,0 |
ППСРВМ-1 | ||||||||
1х16 | 11,6 | 12,4 | 13,2 | 15,6 | 263 | 290 | 319 | 419 |
1х25 | 13,3 | 14,1 | 14,9 | 16,9 | 380 | 412 | 445 | 537 |
1х35 | 14,9 | 15,7 | 16,5 | 18,9 | 502 | 538 | 575 | 692 |
1х50 | 16,6 | 17,4 | 18,5 | 20,6 | 661 | 698 | 757 | 871 |
1х70 | 19,7 | 20,5 | 21,3 | 23,3 | 901 | 948 | 997 | 1129 |
1х95 | 21,6 | 22,4 | 23,2 | 25,2 | 1198 | 1249 | 1303 | 1436 |
1х120 | 24,5 | 25,3 | 26,1 | 27,7 | 1464 | 1522 | 1582 | 1710 |
1х150 | 27,6 | 28,4 | 29,2 | 30,8 | 1818 | 1885 | 1953 | 2095 |
1х185 | 28,8 | 29,6 | 30,4 | 21,6 | 2202 | 2271 | 2343 | 2454 |
1х240 | 32,6 | 33,4 | 34,6 | 35,8 | 2790 | 2869 | 2977 | 3104 |
1х300 | 35,6 | 36,4 | 37,2 | 38,0 | 3442 | 3527 | 3614 | 3704 |
Габариты и вес кабельных барабанов
Габариты и вес кабельных барабановГабариты и вес кабельных барабанов
Габариты и вес деревянных кабельных барабанов
Данная информация является справочной.
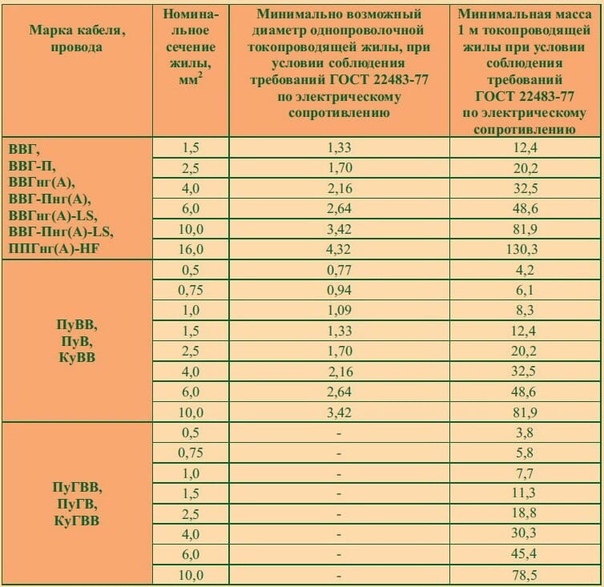 Изготовлением кабельных барабанов не занимаемся
Изготовлением кабельных барабанов не занимаемся| Номера барабанов | Высота | Ширина | Масса барабана, с обшивкой | Масса барабана | Площадь | Объем |
|---|---|---|---|---|---|---|
Барабан №8 | 838 мм | 350 мм | 43 кг | 34 кг | 0,29 м² | 0,2 м³ |
Барабан №8а | 838 мм | 520 мм | 51 кг | 36,5 кг | 0,44 м² | 0,3 м³ |
Барабан №8б | 838 мм | 620 мм | 53,5 кг | 36,5 кг | 0,52 м² | 0,34 м³ |
Барабан №10 | 1044 мм | 646 мм | 56 кг | 39 кг | 0,67 м² | 0,55 м³ |
Барабан №10а | 1044 мм | 864 мм | 75 кг | 55 кг | 0,9 м² | 0,74 м³ |
Барабан №12 | 1264 мм | 650 мм | 132 кг | 99 кг | 0,82 м² | 0,8 м³ |
Барабан №12а | 1264 мм | 864 мм | 151 кг | 107 кг | 1,1 м² | 1,1 м³ |
Барабан №12б | 1264 мм | 746 мм | 145 кг | 110 кг | 0,94 м² | 0,94 м³ |
Барабан №14 | 1444 мм | 875 мм | 217 кг | 165 кг | 1,26 м² | 1,42 м³ |
Барабан №14а | 1444 мм | 665 мм | 200 кг | 152 кг | 0,96 м² | 1,09 м³ |
Барабан №14б | 1444 мм | 770 мм | 234 кг | 186 кг | 1,11 м² | 1,3 м³ |
Барабан №14в | 1444 мм | 904 мм | 226 кг | 172 кг | 1,31 м² | 1,48 м³ |
Барабан №14г | 1444 мм | 1065 мм | 266 кг | 202 кг | 1,54 м² | 1,74 м³ |
Барабан №16 | 1664 мм | 770 мм | 308 кг | 241 кг | 1,28 м² | 1,67 м³ |
Барабан №16а | 1664 мм | 970 мм | 323 кг | 237 кг | 1,61 м² | 2,11 м³ |
Барабан №17 | 1764 мм | 944 мм | 367 кг | 277 кг | 1,67 м² | 2,28 м³ |
Барабан №17а | 1764 мм | 1094 мм | 390 кг | 295 кг | 1,93 м² | 2,67 м³ |
Барабан №17г-01 | 1744 мм | 920 мм | 319 кг | 229 кг | 1,6 м² | 2,2 м³ |
Барабан №17д-01 | 1744 мм | 1070 мм | 342 кг | 247 кг | 1,87 м² | 2,56 м³ |
Барабан №18 | 1864 мм | 1120 мм | 535 кг | 422 кг | 2,1 м² | 3 м³ |
Барабан №18а | 1880 мм | 1122 мм | 606 кг | 422 кг | 2,11 м² | 3,11 м³ |
Барабан №18б | 1864 мм | 1222 мм | 594 кг | 470 кг | 2,1 м² | 3 м³ |
Барабан №18в | 1864 мм | 950 мм | 434 кг | 342 кг | 1,77 м² | 2,59 м³ |
Барабан №18г | 1864 мм | 1130 мм | 540 кг | 427 кг | 2,14 м² | 3,1 м³ |
Барабан №18д | 1864 мм | 1230 мм | 494 кг | 370 кг | 2,29 м² | 3,35 м³ |
Барабан №18е | 1864 мм | 1230 мм | 504 кг | 380 кг | 2,29 м² | 3,35 м³ |
Барабан №18ж | 1864 мм | 1230 мм | 524 кг | 400 кг | 2,29 м² | 3,35 м³ |
Барабан №18з | 1864 мм | 1230 мм | 554 кг | 430 кг | 2,29 м² | 3,35 м³ |
Барабан №18к-01 | 1846 мм | 1090 мм | 474 кг | 361 кг | 2,01 м² | 2,92 м³ |
Барабан №18л-01 | 1846 мм | 1090 мм | 474 кг | 361 кг | 2,01 м² | 2,92 м³ |
Барабан №18к-01 | 1846 мм | 1090 мм | 479 кг | 366 кг | 2,01 м² | 2,92 м³ |
Барабан №20 | 2080 мм | 1250 мм | 763 кг | 584 кг | 2,6 м² | 4,25 м³ |
Барабан №20а | 2080 мм | 1302 мм | 725 кг | 555 кг | 2,72 м² | 4,42 м³ |
Барабан №20б | 2080 мм | 1242 мм | 941 кг | 720 кг | 2,58 м² | 4,22 м³ |
Барабан №20в | 2080 мм | 1150 мм | 700 кг | 560 кг | 2,39 м² | 3,91 м³ |
Барабан №22 | 2280 мм | 1298 мм | 985 кг | 759 кг | 3 м² | 5,3 м³ |
Барабан №22а | 2280 мм | 1348 мм | 1029 кг | 763 кг | 3,07 м² | 5,42 м³ |
Барабан №22б | 2280 мм | 1398 мм | 1110 кг | 833 кг | 3,19 м² | 5,63 м³ |
Барабан №17в с брус | 1764 мм | 944 мм | 380 кг | 290 кг | 1,67 м² | 2,28 м³ |
Барабан №18и с брус | 1864 мм | 1122 мм | 619 кг | 435 кг | 2,11 м² | 3,11 м³ |
Барабан №20в с брус | 2080 мм | 1250 мм | 779 кг | 600 кг | 2,6 м² | 4,25 м³ |
Габариты и вес металлических кабельных барабанов
| Барабан | Ширина | Высота | Масса барабана | Площадь | Объем |
|---|---|---|---|---|---|
Барабан №7МС | 310 мм | 35 мм | 700 кг | 10,85 м² | 0,38 м³ |
Барабан №8МС | 340 мм | 42 мм | 800 кг | 14,28 м² | 0,60 м³ |
Барабан №10МС | 620 мм | 79 мм | 1000 кг | 48,98 м² | 3,87 м³ |
Барабан №12МС | 640 мм | 100 мм | 1200 кг | 64 м² | 6,40 м³ |
Барабан №14МС-7 | 880 мм | 130 мм | 1420 кг | 114,4 м² | 14,87 м³ |
Барабан №18МС-7Б | 872 мм | 200 мм | 1800 кг | 174,4 м² | 34,88 м³ |
Барабан №18МС-7В | 1042 мм | 220 мм | 1800 кг | 229,24 м² | 50,43 м³ |
Барабан №18МС-7А | 1170 мм | 220 мм | 1800 кг | 257,4 м² | 56,63 м³ |
Аутфорс
Поставка кабельно-проводниковой продукцииУфа, ул.
 Российская, д. 37 помещение 50-70
Российская, д. 37 помещение 50-70450104
Россия
Phone: 8 800 777 28 80
Обзор игровой мыши Razer Basilisk V3 / Overclockers.ua
Начиная ещё с появления самой первой версии мыши Razer Basilisk четыре года назад, данная серия всегда была и остается прямым ответом компании на Logitech G502. Начиная с формы и заканчивая характеристиками. Но был один момент, который не был повторен в мыши от Razer, а именно — колесо инерциальной прокрутки. Возможно, из-за патента Logitech на данную технологию. А может быть потому, что в играх от такой функции толку мало и она намного удобнее в офисном сценарии использования. Сложно сказать точно, тем более, что в первом Basilisk была более полезная вещь в виде настраиваемого сопротивления колеса (от еле ощутимого, до жесткого и щелкающего при каждом микродвижении). Тем не менее, в мыши Razer Basilisk V3, которую мы изучим в данном обзоре, инерциальное колесо появилось и теперь, как пишут в официальных документах, — «копия верна».
Технические характеристики
| Модель | Razer Basilisk V3 |
|---|---|
| Сайт производителя | Basilisk V3 |
| Интерфейс | Проводной (USB) |
| Тип | Геймерская (FPS/MMO/RTS-игры) |
| Тип сенсора | Оптический |
| Модель сенсора | Razer Focus+ |
| Разрешение, cpi | 100 – 26 000 |
| Количество кнопок | 11 кнопок (левая, средняя, правая, две дополнительные клавиши сверху, два наклона колеса в стороны, три боковые кнопки, переключатель профиля на основании) + прокрутка вверх/вниз |
| Максимальное ускорение, g | 50 |
| Высота отрыва от поверхности (LOD), мм | 1, 2, 3 |
| Максимальная скорость, м/сек | 16,51 |
| Частота опроса USB-порта, Гц | 125 / 500 / 1000 |
| Частота кадров, fps | Вариативная |
| Внутренняя память | + (5 профилей) |
| Скролл | 1 |
| Прокрутка вертикальная/горизонтальная | +/+ |
| Длина шнура, м | 1,8 |
| Возможность изменения массы | – |
| Возможность регулировки формы корпуса | – |
| Материал кабеля | Нейлоновая оплетка |
| Материал поверхности корпуса | Пластмасса |
| Цвет | Черный |
| Подсветка | + (RGB, 16,8 млн. цветов) цветов) |
| Зоны подсветки | Колесо прокрутки, логотип на корме, полоса светодиодов на основании |
| Материал ножек | Тефлон (PTFE) |
| Программное обеспечение | + (Razer Synapse 3) |
| Размеры, (Д х Ш х В) мм | 130 x 75 x 42,5 |
| Вес, г | 101 |
| Совместимость с ОС | Windows 10 x64 (или новее) |
| Дополнительно | Оптические переключатели Razer второго поколения под ЛКМ и ПКМ с ресурсом наработки на отказ в 70 млн. нажатий. Инерциальное колесо прокрутки Razer HyperScroll с электронным переключением ступенчатого и бесступенчатого режима работы, мягкий кабель Razer Speedflex |
| Средняя стоимость | 2499 грн |
Комплект поставки
Упаковки у Razer в последнее время движутся в сторону упрощения и экологичности используемых материалов, что есть хорошо. По части красоты внешнего вида и информативности у них тоже все в порядке.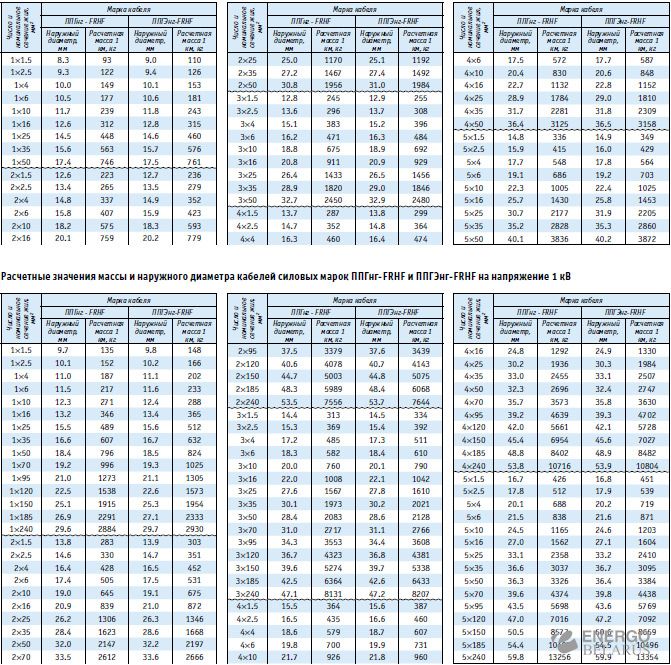
В комплекте поставки кроме мыши есть инструкция, набор наклеек и традиционный листок с приветствием от Мин-Лианг Тана (основателя, исполнительного и творческого директора в одном лице).
Внешний вид
Во внешности и форме Razer Basilisk V3 не поменялось практически ничего относительно Basilisk V2 или Basilisk Ultimate. Матовое, цепкое и немаркое покрытие верхней панели поделено глянцевыми вставками на основные клавиши, корму и боковины. Под панелями ЛКМ и ПКМ по-прежнему установлены фирменные оптические переключатели Razer (но теперь второго поколения), с ресурсом наработки на отказ 70 млн. нажатий и скоростью срабатывания 0,2 мс. Нажимаются со средним усилием и таким же средним по громкости щелчком. В панелях есть микролюфт, но он малозаметен, и нет свободного хода, что гораздо важнее. Две дополнительные клавиши за колесом прокрутки по умолчанию отвечают за смену режимов его работы и за переключение текущего уровня разрешения. Средняя кнопка легкая и тихая в нажатии.
На левой боковине произошел небольшой редизайн. Третья боковая клавиша перестала быть съемной педалью и теперь жестко зафиксирована на своем месте и выполнена из пластика. Кроме того, она переехала на один сантиметр назад и разместилась на передней грани резиновой накладки. Срабатывает эта кнопка тихо и со средним усилием. Две остальные боковые кнопки из глянца наоборот, нажимаются легко, а щелкают громко. Мелкая шестиугольная резиновая текстура накладки осталась без изменений. Лента светодиодов удачно замаскирована в корпусе и пролегает от третьей кнопки и вдоль всей окружности основания, мимо кормы и до конца правой панели.
Сигнальный провод мыши расположен по центру и довольно высоко. Он защищен там от перегиба 20-мм накладкой. Колесо прокрутки внешне не изменилось, но зато его функциональность значительно расширилась. Как и ранее, оно может наклоняться в стороны, с хрустом и громким щелчком нажимая два скрытых переключателя по бокам. И имеет целых три режима работы. В обычном режиме обеспечивается очень тактильная пошаговая прокрутка, колесо отщелкивает тактильно и озвучивает каждую позицию вращения. В режиме инерциальной прокрутки колесо быстро, долго и бесшумно вращается в заданном направлении. Если же включен гибридный режим работы, то в режим инерции колесо перейдет, если его быстро дернуть, и вернется в обычный режим после остановки. Переключение вариантов работы можно назначить на любую кнопку. Само колесо закреплено не жестко и имеет люфт в стороны.
В обычном режиме обеспечивается очень тактильная пошаговая прокрутка, колесо отщелкивает тактильно и озвучивает каждую позицию вращения. В режиме инерциальной прокрутки колесо быстро, долго и бесшумно вращается в заданном направлении. Если же включен гибридный режим работы, то в режим инерции колесо перейдет, если его быстро дернуть, и вернется в обычный режим после остановки. Переключение вариантов работы можно назначить на любую кнопку. Само колесо закреплено не жестко и имеет люфт в стороны.
Мягкий и гибкий шнур Razer Speedflex в оплетке имеет длину в 1,8 метра. Кабель не мешает движениям мыши и позволяет обойтись без использования держателя. Ферритовой накладки на нем нет, зато есть резиновая многоразовая стяжка для регулировки длины и колпачок, для защиты разъема при перевозке мыши.
Правая боковина мыши, как и раньше, покрыта резиновой текстурированной накладкой под пальцы. Вдоль её нижней грани и в упор до передней части ПКМ пролегает лента светодиодной подсветки.
На корме мыши особых изменений нет. Подсвечиваемый логотип Razer остался на своем месте. В самом низу появилась светодиодная вставка.
Эргономика корпуса мыши рассчитана на правшей с ладонями крупного или среднего размера под любой тип хвата. Общий вес без учета кабеля подрос до 101 грамма, что некритично, хоть и считается уже многовато по современным меркам. Баланс веса по осям симметрии слегка смещен вперед.
На основании Razer Basilisk V3 есть пять ножек из белого тефлона — две спереди, по одной сбоку, сзади и по центру. Сенсор Razer Focus+ (он же, вероятно, Pixart PMW3399) находится строго по центру. Посередине задней ножки встроена клавиша переключения бортовых профилей, а над ней — RGB-индикатор текущего активного профиля мыши.
Производитель изрядно постарался с подсветкой Razer Basilisk V3. В добавок к привычному колесу прокрутки и логотипу в основание мыши была встроена лента на девять светодиодов, свечение которой красиво отражается в поверхности вокруг устройства. 16,8 млн. вариантов цветов, высокая яркость, множество световых эффектов и корректная передача белого цвета — тут есть все, что может понадобиться любителю RGB.
16,8 млн. вариантов цветов, высокая яркость, множество световых эффектов и корректная передача белого цвета — тут есть все, что может понадобиться любителю RGB.
Функциональные возможности
Без участия программного обеспечения на мыши можно переключать пять уровней предустановленного по умолчанию разрешения в диапазоне 400, 800, 1600, 3200 и 6400 cpi. Можно менять режим работы колеса и клавишей на основании переключать пять бортовых профилей памяти.
Фирменное ПО
В качестве программного обеспечения Razer Basilisk V3 использует универсальный драйвер Razer Synapse 3 (актуальная версия — 3.6.1018.101823). Драйвер устанавливается вместе с программой контроля учетных записей и фирменных приложений Razer Central. Через нее происходит и старт Synapse. ПО обновляется как автоматически, так и принудительно.
Стартовый экран Synapse 3 имеет «модульную» структуру расположения программ. В новой версии программы появился гостевой режим (без необходимости регистрации учетной записи) и возможность отказаться от загрузки лишних модулей, например студии визуальных эффектов Chroma или редактора макросов. Форма обратной связи с разработчиками, гарантийная форма, информация о поддерживаемых устройствах, ссылка на магазин Razer, и ссылка на фирменную валютную систему Razer Gold & Silver остались на своем месте. Все модули, которые не являются простыми ссылками, дублируются в привычном перечне меню в верхнем левом углу окна приложения. В правом верхнем углу есть доступ в учетную запись текущего пользователя.
Форма обратной связи с разработчиками, гарантийная форма, информация о поддерживаемых устройствах, ссылка на магазин Razer, и ссылка на фирменную валютную систему Razer Gold & Silver остались на своем месте. Все модули, которые не являются простыми ссылками, дублируются в привычном перечне меню в верхнем левом углу окна приложения. В правом верхнем углу есть доступ в учетную запись текущего пользователя.
На вкладке настройки кнопок мыши есть возможность переназначить любые команды для 11 клавиш и двух направлений прокрутки. Полный перечень доступных команд обозначен на выпадающей вкладке слева. Кроме того, можно назначить дополнительные функции для режима Hypershift, в котором при зажатии определенной клавиши и активации режима, функции всех кнопок меняются на альтернативный набор команд. Вкладка выбора и привязки профиля находится сверху по центру. Правее от нее есть значок доступа к встроенной памяти, который разворачивает вкладку с пятью бортовыми профилями. Внизу расположена вкладка настройки колеса прокрутки. Здесь есть программное ускорение скорости прокрутки, переключатель между режимами тактильной прокрутки и свободного вращения, а ещё интеллектуальный режим работы колеса, в котором свободное вращение включается автоматически, если пользователь провернет колесо достаточно быстро.
Здесь есть программное ускорение скорости прокрутки, переключатель между режимами тактильной прокрутки и свободного вращения, а ещё интеллектуальный режим работы колеса, в котором свободное вращение включается автоматически, если пользователь провернет колесо достаточно быстро.
В настройках «эффективности» регулируется разрешение сенсора в пределах от 100 до 26000 cpi с шагом в 50 единиц. Возможна раздельная настройка горизонтальной и вертикальной оси, причем для каждого уровня разрешения индивидуально. Можно настроить пять отдельных уровней чувствительности, либо оставить лишь один уровень (отключив соответствующий ползунок). На выбор есть три частоты опроса в 125, 500 или 1000 Гц. Есть тут и прямая ссылка на стандартную программу для базовой настройки мыши Windows.
В базовых настройках подсветки мыши присутствует возможность регулировки яркости (в пределах от 0 до 100%). Есть ползунок, позволяющий отключить подсветку полностью. Можно настроить время отключения подсветки в случае отключения экрана или при бездействии мыши в диапазоне от 1 до 15 минут. В быстрых эффектах можно выбрать восемь вариантов: волну, динамическую подсветку, дыхание, индикацию громкости, пламя, свет звезд, статическую или циклическую смену спектр. Цвет и настройки эффектов выбираются отдельно, с разными опциями в зависимости от текущего режима. Эффекты можно синхронизировать для других устройств, поддерживающих Chroma-подсветку. Для более сложных настроек нужно щелкнуть на вкладку «расширенные эффекты» и перейти в редактор Chroma Studio, устанавливаемый в виде отдельного модуля.
В быстрых эффектах можно выбрать восемь вариантов: волну, динамическую подсветку, дыхание, индикацию громкости, пламя, свет звезд, статическую или циклическую смену спектр. Цвет и настройки эффектов выбираются отдельно, с разными опциями в зависимости от текущего режима. Эффекты можно синхронизировать для других устройств, поддерживающих Chroma-подсветку. Для более сложных настроек нужно щелкнуть на вкладку «расширенные эффекты» и перейти в редактор Chroma Studio, устанавливаемый в виде отдельного модуля.
В разделе калибровки высоты отрыва сенсора от поверхности есть интеллектуальное отслеживание, которое предполагает фиксированную высоту отрыва на выбор в диапазоне от 1 до 3 мм. Еще можно раздельно задать высоту приземления сенсора, которая будет на 1 или 2 мм меньше высоты отрыва. Альтернативно в разделе ручной калибровки выбирается фирменный коврик Razer из перечня, где тоже появится опция ручной настройки высоты отрыва в пределах от 1 до 10 единиц. Либо калибруется свой вариант поверхности.
Удобный макроредактор позволяет записывать все команды с мыши и клавиатуры, в том числе направления колеса прокрутки и траекторию движения курсора. Задержки записываются как есть или на определенные предустановленные значения. Все макросы можно переименовывать, удалять, импортировать, экспортировать и копировать. Здесь же их можно напрямую привязать к нужной клавише, задав параметры и условия воспроизведения.
Эргономика и тестирование
Тестирование мыши Razer Basilisk V3 проводилось на тканевом коврике монотонного черного цвета SteelSeries QcK Edge XL. Манипулятор обладает удобной формой и весом чуть больше среднего (в 101 грамм), со слегка смещенным вперед центром тяжести, что с лихвой компенсируется цепкими резиновыми боковинами. Подойдет под правую руку с ладонью среднего или большого размера в любом типе хвата. Покрытие верхней панели приятно на ощупь и устойчиво к загрязнению. Ножки скользят плавно, мягкий кабель вообще никак не мешает движениям мыши и создает ощущение работы без провода. Основные клавиши срабатывают четко, имеют хорошую тактильную отзывчивость. К остальным переключателями на устройстве претензий тоже нет.
Основные клавиши срабатывают четко, имеют хорошую тактильную отзывчивость. К остальным переключателями на устройстве претензий тоже нет.
Новое колесо прокрутки с инерциальным режимом работы в большей мере оценят те, кому часто требуется работать с большими документами или длинными веб-страницами. Игрокам оно вряд ли сможет хоть как-то помочь. Хотя последним понравится очень четкая отдача в тактильном режиме работы. Но не понравится люфт колеса в стороны. В любом случае, функция интересная и я рад, что теперь её можно найти не только у Logitech. Единственное, что не стоит включать интеллектуальную прокрутку, поскольку она срабатывает далеко не всегда, когда это требуется. Или скорее склонна включаться, когда это совсем не было нужно. Потому используйте ручное переключение по нажатию клавиши и все будет хорошо. А вот хорошо или нет, то, что компания отказалась от съемной боковой панели третьей клавиши — это вопрос. Мне, например, она нравилась. Зато взамен пользователи получили намного больше подсветки по периметру основания. Которая не особо полезна, но красиво выглядит. Мышь имеет пять бортовых профилей, которые переключаются клавишей на основании (по умолчанию). А программное обеспечение Razer предоставляет широкие возможности по настройке устройства и с годами становится более стабильным и простым.
Которая не особо полезна, но красиво выглядит. Мышь имеет пять бортовых профилей, которые переключаются клавишей на основании (по умолчанию). А программное обеспечение Razer предоставляет широкие возможности по настройке устройства и с годами становится более стабильным и простым.
В мыши установлен фирменный датчик Razer Focus+, представляющий собой переименованный и доработанный PixArt PMW3399. Возможности семейства этих сенсоров уже давно вышли за пределы человеческих способностей и потребностей. Максимальное разрешение составляет 26 000 cpi (не то, что у Logitech G502 с его 25 600 cpi), а предельная скорость достигает 16,51 метра в секунду. Сенсор работает идеально на любых скоростях и поверхностях, а его высоту отрыва и «посадки» можно отрегулировать по своему желанию. Интересно, что несмотря на небольшую просадку точности по мере роста разрешения, снижается уровень сглаживания.
Итоги
Игровая мышь Razer Basilisk V3 представляет собой дальнейшее эволюционное развитие серии в проводном варианте подключения. Среди его безусловных преимуществ особо выделяется крепкий и удобный корпус, четкие оптические переключатели, великолепный сенсор и отличный кабель. Из существенных изменений можно отметить появление нового инерциального колеса прокрутки (достаточно удачного, как по мне), переработку концепции боковой педали третьей кнопки в сторону упрощения и добавку в виде полосы подсветки по периметру основания. Еще устройство прибавило 9 грамм к весу относительно модели V2. Хотя опять же, вес в 101 грамм все еще находится в пределах условной нормы для игровой мыши.
Среди его безусловных преимуществ особо выделяется крепкий и удобный корпус, четкие оптические переключатели, великолепный сенсор и отличный кабель. Из существенных изменений можно отметить появление нового инерциального колеса прокрутки (достаточно удачного, как по мне), переработку концепции боковой педали третьей кнопки в сторону упрощения и добавку в виде полосы подсветки по периметру основания. Еще устройство прибавило 9 грамм к весу относительно модели V2. Хотя опять же, вес в 101 грамм все еще находится в пределах условной нормы для игровой мыши.
Существенных недостатков мне обнаружить в устройстве не удалось. Люфт колеса прокрутки связан во многом с его новой функциональностью. Смещение баланса веса вперед незначительно. Наверное, можно было бы придраться к ещё каким-то мелочам, но эти моменты были бы уже чисто субъективными.
Razer Basilisk V3 может быть рекомендован к приобретению как отличная игровая мышь за свою цену, обладающая расширенными возможностями для офисного применения за счет обновленного колеса инерциальной прокрутки.
Модуль упругости Юнга, напряжения, деформации: численные задачи
Наука> Физика > Упругость > Численные задачи о напряжении, деформации и модуле ЮнгаВ этой статье мы изучим применение концепции и численные задачи о продольном напряжении, продольной деформации, модуле упругости Юнга.
Коэффициенты преобразования :
из | С по | Фактор |
мм | кв.м. | х 10 -3 |
см | кв.м. | х 10 -2 |
кв. | мм | х 10 3 |
кв.м. | см | х 10 2 |
dyne | N | х 10 -5 |
N | dyne | х 10 5 |
см 2 | м 2 | х 10 -4 |
м 2 | см 2 | х 10 4 |
кПа | Па | х 10 3 |
МПа | Па | х 10 6 |
ГПа | Па | х 10 9 |
Формулы:
Пример — 1:
Проволока длиной 2 м и диаметром 2 мм при растяжении на вес 8 кг увеличивает длину на 0. 24 мм. Найдите напряжение, деформацию и модуль Юнга материала проволоки. g = 9,8 м / с²
24 мм. Найдите напряжение, деформацию и модуль Юнга материала проволоки. g = 9,8 м / с²
Дано: Начальное длина проволоки = L = 2 м, Диаметр проволоки = 2 мм, Радиус проволоки 2/2 = 1 мм = 1 × 10 -3 м, присоединенный вес = м = 2 кг, увеличение длины = l = 0,24 мм = 0,24 × 10 -3 м, g = 9,8 м / с².
Найти: Напряжение =? Напряжение =? Модуль Юнга материала = Y =?
Раствор:
Напряжение = F / A = мг / π r²
∴
Напряжение = (8 × 9.8) /(3,142 × (1 × 10 -3 ) ²)
∴
Напряжение = (8 × 9,8) /( 3,142 × 1 × 10 -6 )
∴
Напряжение = 2,5 × 10 7 Н / м²
Деформация = л / л = 0,24 × 10 -3 /2
∴ Деформация
= 0,12 × 10 -3 = 1,2 × 10 -4
Итак, модуль упругости Юнга = Y = напряжение / деформация
∴ Y = (2,5 × 10 7 ) / (1,2 × 10 -4 )
∴ Y = 2,08 × 10 11 Н / м²
Ответ: Напряжение = 2,5 × 10 7 Н / м², деформация = 1. 2 × 10 -4 , модуль упругости Юнга = 2,08 × 10 11 Н / м²
2 × 10 -4 , модуль упругости Юнга = 2,08 × 10 11 Н / м²
Пример — 2:
Провод длиной 2 м и площадью сечения 10 -4 м² растягивается грузом 102 кг. Проволока растягивается на 0,1 см. Рассчитайте продольное напряжение, продольную деформацию и модуль Юнга материала проволоки.
Дано: Начальное длина провода = L = 2 м, Площадь поперечного сечения = A = 10 -4 м, растяжка = 102 кг, масса = 102 × 9.8 Н, увеличение длины = l = 0,1 см = 0,1 × 10 -2 м = 1 × 10 -3 м, g = 9,8 м / с².
Найти: Стресс знак равно Деформация =?, Модуль Юнга материала = Y =?
Раствор:
Напряжение = F / A = мг / А
∴ Напряжение = (102 × 9,8) / 10 -4
∴ Напряжение = 1 × 10 7 Н / м²
Напряжение = л / л = 1 × 10 — 3 /2
∴ Деформация = 0,5 × 10 -3 = 5 × 10 -4
Итак, модуль упругости Юнга = Y = напряжение / деформация = (1 × 10 7 ) / (5 × 10 -4 )
∴ Y = 2 × 10 10 Н / м²
Отв. : Напряжение = 1 × 10 7 Н / м², деформация = 5 × 10 -4 , модуль упругости Юнга = Y = 2 × 10 10 Н / м²
: Напряжение = 1 × 10 7 Н / м², деформация = 5 × 10 -4 , модуль упругости Юнга = Y = 2 × 10 10 Н / м²
Пример — 3:
Проволока из низкоуглеродистой стали радиусом 0,5 мм и длиной 3 м растягивается силой 49 Н. Рассчитайте a) продольное напряжение, b) продольную деформацию c) удлинение, возникающее в теле, если Y для стали составляет 2,1 × 10 11 Н / м².
Дано: Начальная длина провода = L = 3 м, радиус провода = 0.5 мм = 0,5 × 10 -3 м = 5 × 10 -4 м, приложенная сила = 49 Н, модуль Юнга для стали = Y = 2,1 × 10 11 Н / м².
Найти: Напряжение =? Напряжение =? удлинение =?
Раствор:
Напряжение = F / A = мг / π r²
∴ Напряжение = 49 /(3,142 × (5 × 10 -4 ) ²)
∴ Напряжение = 49 /(3,142 × 25 × 10 -8 )
∴ Напряжение = 6,238 × 10 7 Н / м²
Теперь Y = напряжение / деформация
∴ Деформация = напряжение / Y = (6. 238 × 10 7 ) / (2,1 × 10 11 )
238 × 10 7 ) / (2,1 × 10 11 )
∴ Деформация = 2,970 × 10 -4
Теперь, деформация = l / L
∴ l = Деформация × L
∴ l = 2,970 × 10 -4 × 3
∴ l = 8,91 × 10 -4 м = 0,891 × 10 -3 м = 0,891 мм
Ответ: напряжение = 6,238 × 10 7 Н / м², деформация = 2,970 × 10 -4 , удлинение = 0,891 мм.
Пример — 4:
Металлическая проволока длиной 1 м и диаметром 2 мм растягивается под нагрузкой 40 кг.Если Y = 7 × 10 10 Н / м² для металла, найдите (1) напряжение (2) деформацию и (3) силовую постоянную материала проволоки.
Дано: Начальное длина проволоки = L = 1 м, Диаметр проволоки = 2 мм, Радиус проволоки = 2/2 = 1 мм = 1 × 10 -3 м, приложенная нагрузка = м = 40 кг, модуль Юнга материала = Y = 7 × 10 10 Н / м².
Найти: Стресс знак равно Напряжение =?, Постоянная силы =?
Решение:
Напряжение = F / A = мг / π r²
∴ Напряжение = (40 × 9. 8) /(3,142 × (1 × 10 -3 ) ²)
8) /(3,142 × (1 × 10 -3 ) ²)
∴ Напряжение = (40 × 9,8) /(3,142 × 1 × 10 -6 )
∴ Напряжение = 1,25 × 10 8 Н / м²
Сейчас, Y = Напряжение / Деформация
∴ Деформация = Напряжение / Y = 1,25 × 10 8 /7 × 10 10
∴ Деформация = 1,78 × 10 -3
Сейчас, Деформация = l / L
∴ удлинение = l = деформация × длина
∴ l = 1,78 × 10 -3 × 1
∴ l = 1,78 × 10 -3 м
Теперь силовая постоянная K = F / l = мг / л = (40 × 9.8) /(1,78 × 10 -3 )
∴ Постоянная силы K = 2,2 × 10 5 Н / м
Ответ: Напряжение = 1,25 × 10 8 Н / м², деформация = 1,78 × 10 -3 , постоянная силы = 2,2 × 10 5 Н / м
Пример — 5:
Каким должно быть удлинение провода длиной 5 м, чтобы напряжение составляло 1% от 0,1? Если проволока имеет поперечное сечение 1 мм² и растягивается на 10 кг веса, каково напряжение?
Дано: Начальное
длина провода = L = 5 м, деформация = 1% от 0. 1 = 1 × 10 -2 ×
0,1 = 1 × 10 -3 , площадь поперечного сечения = 1 мм² = 1
× 10 -6 м², присоединенная нагрузка = F = 10 кг-масса = 10 × 9,8 Н
.
1 = 1 × 10 -2 ×
0,1 = 1 × 10 -3 , площадь поперечного сечения = 1 мм² = 1
× 10 -6 м², присоединенная нагрузка = F = 10 кг-масса = 10 × 9,8 Н
.
Найти: Удлинение = l =? Напряжение =?,
Раствор:
Напряжение = л / л
∴ удлинение
= l = деформация × L
∴
l = 1 × 10 -3 × 5
∴
l = 5 × 10 -3 м = 5 мм
Напряжение = F / A = мг / π r²
∴
Напряжение = (10 × 9,8) / (1 × 10 -6 )
∴
Стресс = 9.8 × 10 7 Н / м²
Ответ: Удлинение = 5 мм и напряжение = 9,8 × 10 7 Н / м²
Пример-6:
Латунный провод длиной 2 м одним концом закреплен на жесткой опоре, а с другого конца подвешен груз массой 4 кг. Если радиус проволоки составляет 0,35 мм, найдите удлинение проволоки. g = 9,8 м / с², Y = 11 × 10 10 Н / м²
Дано: Начальное
длина провода = L = 2 м, радиус провода = 0. 35 мм = 0,35 × 10 -3 м = 3,5 × 10 -4 м, прилагаемая нагрузка = F = 4 кг, масса = 4 × 9,8 Н, г = 9,81
м / с², Y = 11 × 10 10 Н / м².
35 мм = 0,35 × 10 -3 м = 3,5 × 10 -4 м, прилагаемая нагрузка = F = 4 кг, масса = 4 × 9,8 Н, г = 9,81
м / с², Y = 11 × 10 10 Н / м².
Найти: добавочный номер знак равно
Раствор:
Y = FL / A л
∴
l = F L / π r² Y
∴
l = (4 × 9,8 × 2) /(3,142 × (3,5 × 10 -4 ) ² × 11 × 10 10 )
∴
l = (4 × 9,8 × 2) /( 3,142 × 12,25 × 10 -8 × 11 × 10 10 )
∴
l = 1,85 × 10 -3 м = 0.185 × 10 -2 м =
0,185 см
Ответ: Удлинение провода 0,185 м
Пример-7:
Проволока длиной 1,5 м и радиусом 0,4 мм при нагрузке растягивается на 1,2 мм. Если модуль Юнга его материала равен 12,5 × 10 10 Н / м². Найдите растягивающую силу.
Дано: Начальное
длина провода = L = 1,5 м, радиус провода = 0,4 мм = 0,4 × 10 -3 м = 4 × 10 -4 м, удлинение = l = 1. 2 мм = 1,2 × 10 -3 м, г
= 9,8 м / с², модуль Юнга = Y = 12,5 × 10 10 Н / м².
2 мм = 1,2 × 10 -3 м, г
= 9,8 м / с², модуль Юнга = Y = 12,5 × 10 10 Н / м².
Найти: Растяжка сила = F =?
Раствор:
Y = FL / A л
∴
F = AY л / л
∴
F = π r² Y л / л
∴
F = (3,142 × (4 × 10 -4 ) ² × 12,5 × 10 10 × 1,2 × 10 -3 )
/1,5
∴
F = (3,142 × 16 × 10 -8 × 12,5 × 10 10 × 1,2 × 10 -3 )
/1,5
∴
F = 50.27 Н
Ответ: Требуемая сила растяжения = 50,27 Н
Пример — 8:
Какая сила требуется, чтобы растянуть стальную проволоку в поперечном сечении на 1 см2, чтобы ее длина удвоилась? Y = 2 × 10 11 Н / м². Предположим закон Гука.
Дано: Начальное
длина провода = L, Конечная длина = 2L, Следовательно, удлинение провода = l = 2L — L =
L, Площадь поперечного сечения = 1 см² = 1 × 10 -4 м²,
Модуль упругости Юнга = Y = 2 × 10 11 Н / м².
Найти: Растяжка сила = F =?
Раствор:
Y = FL / A l
∴ F = AY l / L
∴ F = (1 × 10 -4 × 2 × 10 11 × L) / L
∴ F = 2 × 10 7
О: Требуемая сила растяжения = 2 × 10 7 Н
Пример — 9:
Найдите максимальную нагрузку, которую можно приложить к вольфрамовой проволоке диаметром 2 мм, чтобы допустимая деформация не превышала 1/1000. Модуль Юнга для вольфрама = Y = 35 × 10 10 Н / м².
Дано: Деформация = 1/1000 = 10 -3 , модуль упругости Юнга = Y = 35 × 10 10 Н / м², диаметр проволоки = 2 мм, радиус проволоки = 2/2 = 1 мм = 1 × 10 -3 м,
Найти: Максимальная нагрузка = F =?
Раствор:
Y = напряжение / деформация = (F / A) / деформация
Y = F / (A × деформация)
∴
F = π r² × Y × деформация
∴
F = 3,142 × (1 × 10 -3 ) ² × 35 × 10 10 × 10 -3
∴
F = 3. 142 × 1 × 10 -6 × 35 × 10 10 × 10 -3
142 × 1 × 10 -6 × 35 × 10 10 × 10 -3
∴
F = 1100 Н
Ответ: Максимальная нагрузка составляет 1100 Н
Задача — 10:
Масса 2 кг подвешена на стальной проволоке радиусом 0,5 мм и длиной 3 м. Вычислите произведенное расширение. Каким должен быть минимальный радиус проволоки, чтобы не превышался предел упругости? Предел упругости для стали составляет 2,4 × 10 8 Н / м², Y для стали = Y = 20 × 10 10 Н / м²
Дано: Радиус провода = 0.5 мм = 0,5 × 10 -3 м = 5 × 10 -4 м. Исходный длина проволоки = L = 3 м, присоединенная масса = м = 2 кг, Y для стали = Y = 20 × 10 10 Н / м²
Чтобы найти: Удлинение = l = ?, Минимальный радиус проволоки = r =?
Раствор:
Часть — I:
Y = FL / A l
∴ l = FL / AY
∴ l = мг л / π r² Y
∴ l = (2 × 9,8 × 3) /(3,142 1 × (5 × 10 -4 ) ² × 20 × 10 10 )
∴ l = (2 × 9. 8 × 3) /( 3,142 × 25 × 10 -8 × 20 × 10 10 )
8 × 3) /( 3,142 × 25 × 10 -8 × 20 × 10 10 )
∴ l = 3,743 × 10 -4 м = 0,3743 мм
Часть — II:
Дано: Предел упругости для стали = напряжение = 2,4 × 10 8 Н / м², масса прикреплено = m = 2 кг,
Найти: радиус проволоки на пределе упругости = r =?
Напряжение = F / A = F / π r²
∴ r² = мг / (π × напряжение)
∴ r² = (2 × 9,8) / (3,142 × 2,4 × 10 8 )
∴ r² = 2.599 × 10 -8
∴ r = 1,612 × 10 -4 м = 0,1612 × 10 -3 м = 0,1612 мм
Ответ: Часть — I: Изменение длины проволоки на 0,3743 мм
Часть — II: Радиус проволоки при пределе упругости = 0,1612 мм
Пример — 11:
Проволока растягивается с приложением силы 50 кг масс / кв. см. На сколько процентов увеличилась длина провода? Y = 7 × 10 10 Н / м², g = 9. 8 м / с²
8 м / с²
Дано: Напряжение = 50 кг масс / кв. см = 50 × 9,8 Н / 10 -4 м² = 50 × 9,8 × 10 4 Н / м², модуль упругости Юнга = Y = 7 × 10 10 Н / м². g = 9,8 м / с²
Найти: % удлинение =% l / L =?
Раствор:
Теперь, Y = напряжение / деформация
∴
Деформация = Напряжение / Y = (50 × 9,8 × 10 4 ) /
(7 × 10 10 )
∴
Деформация = 7 × 10 -5
% удлинение = деформация × 100 = 7 × 10 -5 × 100
% удлинение = деформация × 100 = 0.007
Отв .: Относительное удлинение 0,007%
Задача — 12:
Сжимающая сила 4 × 10 4 Н прилагается к концу кости длиной 30 см и площадью поперечного сечения 4 см². Что будет с костью? Рассчитайте изменение длины кости. Прочность на сжатие кости составляет 7,7 × 10 8 Н / м², а модуль Юнга кости составляет 1,5 × 10 10 Н / м²
Дано: Начальное
длина провода = L = 30 см = 0. 30 м, площадь поперечного сечения = 4 см²
= 4 × 10 -4 м², присоединенная нагрузка = F = 4 × 10 4 N. Y = 1,5 × 10 10 Н / м². Максимальное напряжение = 7,7 × 10 8 Н / м².
30 м, площадь поперечного сечения = 4 см²
= 4 × 10 -4 м², присоединенная нагрузка = F = 4 × 10 4 N. Y = 1,5 × 10 10 Н / м². Максимальное напряжение = 7,7 × 10 8 Н / м².
Найти: Эффект загрузки =? Изменение длины = l =?,
Раствор:
Приложенное напряжение = Приложенная сила / Площадь
поперечного сечения
Прикладное напряжение = (4 × 10 4 ) / (4 × 10 -4 ) =
1 × 10 8 Н / м²
Это напряжение меньше максимально допустимого напряжения (7.7 × 10 8 Н / м²)
Следовательно, кость не сломается, а сожмется, и ее длина уменьшится
Y = F L / A l
∴
l = (4 × 10 4 × 0,3) / (4 × 10 -4 × 1,5 × 10 10 )
∴
l = 2 × 10 -3 м = 2 мм
Ответ: Длина кости уменьшается на 2 мм
Пример — 13:
Радиус медного стержня 4 мм. Какая сила требуется, чтобы растянуть стержень на 20% от его длины при условии, что предел упругости не превышен? Y = 12 × 10 10 Н / м².
Какая сила требуется, чтобы растянуть стержень на 20% от его длины при условии, что предел упругости не превышен? Y = 12 × 10 10 Н / м².
Дано: Радиус проволоки = r = 4 мм = 4 × 10 -3 м,% удлинения = Деформация = 20% = 20 × 10 -2 , модуль упругости Юнга = Y = 12 × 10 10 Н / м².
Найти: Растяжка сила = F =?
Раствор:
Y = напряжение / деформация = (F / A) / деформация
Y = F / (A × деформация)
∴
F = AY × деформация
∴
F = π r² × Y × деформация
∴
F = 3,142 × (4 × 10 -3 ) ² × 12 × 10 10 × 20 × 10 -2
∴
F = 3.142 × 16 × 10 -6 × 12 × 10 10 × 20 × 10 -2
∴
F = 1,207 × 10 6 Н
Ответ: Требуемая сила растяжения = 1,207 × 10 6 Н
Пример — 14:
Найдите изменение длины провода длиной 5 м и поперечного сечения 1 мм² при растягивающей силе 10 кг-вес. Y = 4,9 × 10 11 Н / м², а g = 9,8 м / с².
Y = 4,9 × 10 11 Н / м², а g = 9,8 м / с².
- Решение:
- Дано: Начальная длина провода = L = 5 м, площадь поперечного сечения = 1 мм² = 1 × 10 -6 м², приложенная нагрузка = F = 10 кг- вес = 10 × 9.8 с. Y = 4,9 × 10 11 Н / м², а g = 9,8 м / с².
- Найти: Изменение длины = l =?
Y = FL / A л
∴ л
= F L / A Y
∴
l = (10 × 9,8 × 5) / (1 × 10 -6 × 4,9 × 10 11 )
∴
l = 1 × 10 -3 м = 1 мм
Ответ: Изменение длины провода на 1 мм
Пример — 15:
Предел упругости превышен, если деформация проволоки (Y = 14 × 10 11 Н / м²) превышает 1/2000.Если площадь поперечного сечения провода составляет 0,02 см², найдите максимальную нагрузку, которую можно использовать для растяжения провода без постоянного затвердевания.
Дано: Штамм = 1/2000 = 5 × 10 -4 , модуль упругости Юнга = Y = 14 × 10 11 Н / м², площадь поперечного сечения = A = 0,02 см² = 0,02 × 10 -4 м² = 2 × 10 -6 м²
Найти: Растяжка сила = F =?
Раствор:
Y = напряжение / деформация = (F / A) / деформация
Y = F / (A × деформация)
∴
F = AY × деформация
∴
F = 2 × 10 -6 × 14 × 10 11 × 5 × 10 -4
∴
F = 1400 N
Ответ.: Требуемая сила растяжения = 1400 Н
Пример — 16:
Предел упругости стали превышен, когда напряжение на данной стальной проволоке превышает 8,26 × 10 8 Н / м². Можно ли растянуть стальную проволоку (Y = 2 × 10 11 Н / м²) длиной 2 м на 10 мм без превышения предела упругости?
Дано: Начальное
длина провода = L = 2 м, предел упругости = напряжение = 8,26 × 10 8 Н / м², модуль упругости Юнга = Y = 2 × 10 11 Н / м².
Найти: Кому выяснить, можно ли растянуть проволоку на 10 мм.
Раствор:
Y = Напряжение / Деформация = Напряжение / (л / л)
∴
Y = (напряжение × L) / Y
∴
Y = (8,26 × 10 8 × 2) / 2 × 10 11
∴
Y = 8,26 × 10 -3 м = 8,26 мм
Ответ: Проволоку нельзя растянуть до 10 мм из-за эластичного
предел будет пересечен при расширении 8,26 мм.
Пример — 17:
Модуль Юнга материала проволоки равен 9.68 × 10 10 Н / м². Проволока из этого материала диаметром 0,95 мм растягивается с приложением определенного усилия. Каким должен быть предел этой силы, если деформация не превышает 1: 1000?
Дано: Штамм = 1/1000 = 10 -3 , модуль упругости Юнга = Y = 9,68 × 10 10 Н / м², Диаметр проволоки = 0,95 мм, Радиус проволоки = 0,95 / 2 = 0,475 мм = 0,475 × 10 -3 м = 4,75 × 10 -4 м
Найти: Растяжка сила = F =?
Раствор:
Y = напряжение / деформация = (F / A) / деформация
Y = F / (A × деформация)
∴
F = π r² × Y × деформация
∴
F = 3. 142 × (4,75 × 10 -4 ) ² × 9,68 × 10 10 × 10 -3
142 × (4,75 × 10 -4 ) ² × 9,68 × 10 10 × 10 -3
∴
F = 68,62
Ответ: Предел необходимого усилия растяжения = 68,62 Н
Пример — 18:
Предел упругости меди составляет 1,5 × 10 8 Н / м². Медный провод следует растягивать с нагрузкой 10 кг. Найдите минимальный диаметр проволоки, который должен иметь предел упругости.
Дано: эластичный Предел = Напряжение = 1.5 × 10 8 Н / м², нагрузка = F = 10 кг, вес = 10 × 9,8.
Найти : минимальный диаметр проволоки.
Раствор:
Напряжение = F / A
∴
Напряжение = F / π r²
∴
r² = F / (π × напряжение)
∴
r² = (10 × 9,8) / (3,142 × 1,5 × 10 8 )
∴
r² = 20,79 × 10 -8
∴
r = 4,56 × 10 -4 м = 0,456 × 10 -3 м = 0,456 мм
Диаметр проволоки = 2 × r = 2 × 0,456 мм = 0,912 мм
Ответ. : Диаметр проволоки 0,912 мм
: Диаметр проволоки 0,912 мм
Пример — 19:
Какой была бы наибольшая длина стальной проволоки, которая при закреплении на одном конце может свободно свисать, не ломаясь? Плотность стали = 7800 кг / м³. Разрушающее напряжение для стали = 7,8 × 10 8 Н / м².
Дано: Плотность стали = ρ = 7800 кг / м³. Напряжение = 7,8 × 10 8 Н / м².
Найти: Наибольшая длина провода = ?.
Раствор:
Напряжение = F / A = мг / А = V ρ г / А
∴ Напряжение = AL ρ г / А
∴ Напряжение = L ρ г
∴ L = Напряжение / ρ г
∴ L = 7,8 × 10 8 / (7800 × 9,8)
∴ L = 7,8 × 10 8 / (7800 × 9,8)
∴ L = 1,021 × 10 4 м
Ответ: Максимальная длина медного провода составляет 1,021 × 10 4 м
Проволочный канат — прочность
Минимальная прочность на разрыв и безопасная нагрузка для стального каната из светлой проволоки, без покрытия, с волокнистым сердечником (FC), улучшенная сталь для плугов (IPS):
| Диаметр каната | Минимальная прочность на разрыв | Безопасная нагрузка | Масса | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (дюйм) | (мм) | (фунт 41 | | | (фунт f ) | (кН) | (фунт м / фут) | (кг / м) | | |
| 5480 | 24,4 | 1100 | 4,89 | 0,11 | 0,16 | ||||
| 5/16 | 8 | 8520 | 37,9 | 1700 | 7,56 | 0,16 0,24 | |||
| 3/8 | 9,5 | 12200 | 54,3 | 2440 | 10,9 | 0,24 | 0,36 | ||
| 7/16 | 11,5 | 16540 | 73,681 | 3310 | 14.7 | 0,32 | 0,48 | ||
| 1/2 | 13 | 21400 | 95,2 | 4280 | 19,0 | 0,42 | 0,63 | ||
| 9/16 | 14,5 | 9/16 | 14,5 | 120 | 5400 | 24,0 | 0,53 | 0,79 | |
| 5/8 | 16 | 33400 | 149 | 6680 | 29,7 | 0.66 | 0,98 | ||
| 3/4 | 19 | 47600 | 212 | 9520 | 42,3 | 0,95 | 1,41 | ||
| 7/8 | 22 | 64400 | 22 | 64400 | 12900 | 57,4 | 1,29 | 1,92 | |
| 1 | 26 | 83600 | 372 | 16700 | 74,3 | 1,68 | 2. 50 50 | ||
| 1 1/8 | 29 | 105200 | 468 | 21000 | 93,4 | 2,13 | 3,17 | ||
| 1 1/4 | 32 | 129200 | 575 | 115 | 2,63 | 3,91 | |||
| 1 3/8 | 35 | 155400 | 691 | 31100 | 138 | 3,18 | 4,73 | ||
| 1 1/2 | 184000 | 818 | 36800 | 164 | 3.78 | 5,63 | |||
| 1 5/8 | 42 | 214000 | 852 | 42800 | 190 | 4,44 | 6,61 | ||
| 1 3/4 | 45 | 248000 110026 | 248000 | 49600 | 221 | 5,15 | 7,66 | ||
| 1 7/8 | 48 | 282000 | 1250 | 56400 | 251 | 5,91 | 8.80 | ||
| 2 | 52 | 320000 | 1420 | 64000 | 285 | 6,72 | 10,0 | ||
Пример — максимальная безопасная масса для троса 3/8 дюйма
Взаимосвязь между масса и сила (вес) могут быть выражены как
м = F / г (1)
где
F = сила, вес (Н)
м = масса (кг)
g = ускорение свободного падения (9. 81 м / с 2 )
81 м / с 2 )
Максимальная безопасная масса каната 3/8 « при допустимой нагрузке 10,9 кН можно рассчитать как
м = (10,9 10 3 Н) / (9,81 м / с 2 )
= 1111 кг
Скачать и распечатать Таблицу безопасной нагрузки на трос
Вес стали и формула для расчета удельного веса стали
Удельный вес стали | Расчет веса стали и формула удельного веса стали и калькулятор веса стали | Удельный вес стали на метр | Удельный вес стали для опор | Удельный вес стали в фунтах на кубический фут Привет, ребята, в этой статье мы знаем об удельном весе стали, формуле расчета веса стали и о том, как рассчитать вес стали на метр или на фут
Как мы знаем, сталь используется для изготовления конструктивных элементов, таких как колонны, балки, опоры, плиты и т. Д. Здания.Вы знаете, что поставщик поставляет стальной пруток разных размеров длиной 12 метров, как мы рассчитываем общую длину стального прутка в килограммах.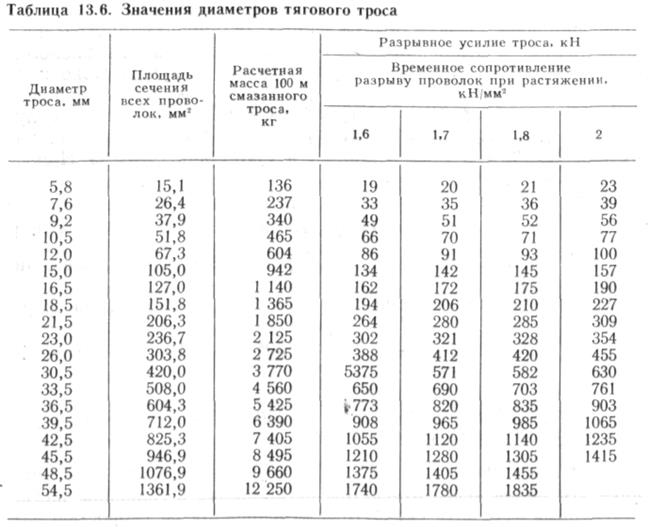
Удельный вес стали: — Удельный вес стали определяется как отношение веса стали к единице объема стали, удельный вес стали обычно измеряется в кг на кубический метр и составляет 7850 кг / м3, измеряется в кН на куб. метр составляет 78,5 кН / м3 или измеряется в граммах на кубический сантиметр и составляет 7,85 г / см3, что примерно равно 490 фунтам на кубический фут в фунтах на кубический фут или 13231 фунт / ярд3 в фунтах на кубический ярд.
Единица массы стали — это отношение массы стали к ее единице объема. Обычно он выражается в килограммах на кубический метр или фунтах на кубический фут. Удельная масса стали составляет 7850 кг / м3 (килограммов на кубический метр) или 490 фунтов / фут3 (фунтов на кубический фут).
Удельный вес стали Существуют различные калькуляторы веса стали для расчета веса стали различных размеров: стальных стержней 8 мм, 6 мм, 10 мм, 12 мм и других. И калькулятор веса стали на основе удельного веса стали и объема стального прутка круглого сечения. По этой статье вы должны рассчитать следующие
По этой статье вы должны рассчитать следующие
1) штанга стальная
2) формула для веса стали
3) d2 / 162 вывод
4) разные размеры стального стержня
5) Вес стали 8 мм на метр
6) 10 мм стальной груз
7) 12 мм стальной груз
8) Вес стального стержня 16 мм
9) 20 мм стальной груз
Удельный вес стали на метрУдельный вес стали на метр для 6 мм равен 0.222 кг, для стального стержня 8 мм — 0,395 кг, для стального стержня 10 мм — 0,617 кг, для стального стержня 12 мм — 0,89 кг, для стального стержня 16 мм — 1,58 кг, для стального стержня 20 мм — 2,47 кг, для стального стержня 25 мм — 3,86 кг, для стального стержня 32 мм — 6,32 кг, для стального стержня 40 мм — 9,87 кг.
Удельный вес стали на фут Удельный вес стали на ножку для 6 мм составляет 0,067 кг, для 8 мм — 0,120 кг, для 10 мм — 0,188 кг, для 12 мм — 0,270 кг, для 16 мм — 0,480 кг, для 20 мм — 0,751 кг, для 25 мм — 1. 174 кг, а для 32 мм — 1,925 кг.
174 кг, а для 32 мм — 1,925 кг.
Вес единицы стали: — Вес единицы стали определяется как масса на единицу длины, если вес арматурного стержня / арматурного стержня измеряется в фунтах на фут, известный как удельный вес арматуры / стали в фунтах / футах.
Удельный вес арматуры / стали 8 мм или № 2,5 составляет 0,265 фунта / фут, для арматуры / стали 10 мм или № 3 это может быть 0,376 фунта / фут, для арматуры / стали 12 мм или № 4 это может быть 0,668 фунта / фут для арматуры / стали 16 мм или № 5 это может быть 1,043 фунта / фут, для арматуры / стали 20 мм или № 6 это может быть 1.502 фунта / фут, для арматуры / стали 22 мм или № 7, это может быть 2,044 фунта / фут, для арматуры / стали 25 мм или № 8, это может быть 2,67 фунта / фут, для арматуры / стали 28 мм или № 9 это может быть 3,40 фунта / фут, для арматуры / стали 32 мм или № 10 это может быть 4 303 фунта / фут, а удельный вес для арматуры / стали 36 мм или № 11 — 5,313 фунта / фут.
Удельный вес стали / стержня / арматуры / стального стержня / арматурного стержня В Индии, во всех штатах, Махараштра, Телангана, Карнатака, Тамилнад, Западная Бенгалия и в крупных городах Дели, Мумбаи, Калькутта, Хайдарабад, Ченнаи, Бангалор, стальные прутки разного размера производятся различными компаниями, а также поставляются и продаются стальной стержень / стержень tmt / арматура / стальной стержень размером 6 мм, 8 мм, 10 мм, 12 мм, 16 мм, 20 мм, 25 мм, 32 мм, 40 мм и т. д.
д.
Удельный вес стали определяется как отношение веса стали к единице ее объема, вес стали измеряется в килограммах (кг), а ее объем измеряется в кубических метрах (м3), тогда ее удельный вес = единице массы / единице объема, представлен как W = m / V, где W — удельный вес стали, м для массы и V для объема, он также известен как удельный вес стали или плотность стали, а их единица СИ — килограмм на кубический метр (кг / м3). . Сталь является наиболее часто используемым элементом в гражданском строительстве для строительства конструкций. Зная единицу веса стали, легко рассчитать количество стали, необходимое для проектов.
Обычно при измерении в кг / м3 его удельный вес в кг на кубический метр (кг / м3) составляет около 7850 кг, при измерении в г / см3 его удельный вес в граммах на кубический сантиметр (г / см3) равен около 7,850 грамма, при измерении в кН / м3 его удельный вес в килоньютонах на кубический метр (кН / м3) составляет около 78,50 кН, при измерении в фунтах / дюйм3 его удельный вес в фунтах на кубический дюйм (фунт / дюйм3) составляет около 0,28 фунта, а при измерении в фунтах / фут3 его удельный вес в фунтах на кубический фут (фунт / фут3) составляет около 490. 74 фунта.
74 фунта.
Вес стальной единицы измеряется в различных единицах, таких как кг / м3, кН / м3, г / см3, фунт / дюйм3 и фунт / фут3, значение веса стальной единицы составляет около 7850 кг / м3, когда оно измеряется в килограммах на кубический метр, 78,50 кН / м3 при измерении в килоньютон на кубический метр, 7,850 г / см3 при измерении в граммах на кубический сантиметр, 0,28 фунта / дюйм3 при измерении в фунтах на кубический дюйм и 490,059 фунта / фут3 при измерении в фунтах на кубический фут.Формула 2L / 533, вес = (10 × 10 × 1) / 533 = 0,188 кг / фут, это вес стального стержня 10 мм в кг на фут.
Как рассчитать вес стального стержня Поскольку мы знаем, что на рынке доступны стальные стержни другой формы, круглый / круглый сплошной стержень, стальной стержень квадратной формы, шестиугольный стержень и т. Д., Сталь является наиболее важным строительным материалом, используемым в строительстве, теперь возникает вопрос: «как рассчитать вес стального стержня », зная вес стального стержня, легко рассчитать количество стали, необходимое для любых проектов, таких как промышленное строительство, многоэтажное здание, малоэтажное здание, мост, плотины, школы, больницы, коммерческие здания и т. д. .
д. .
Для расчета веса стального стержня или стержня мы используем некоторую формулу, которая очень полезна для инженера, начальника участка и обычных людей.
Формула веса стальных стержнейДля расчета веса стальных стержней или стержней формулы следующие: —
● для круглого / круглого сплошного прутка — Диаметр 2 × 0,006165 при измерении в килограммах на метр (кг / м).
● для круглого / круглого сплошного стержня — Диаметр 2 × 0,004143 при измерении в фунтах на фут (фунт / фут).
● для шестиугольного сплошного стержня — размер мм2 × 0,006798 при измерении в килограммах на метр (кг / м).
● для шестиугольного сплошного стержня — размер мм2 × 0,006165 при измерении в фунтах на фут (фунт / фут).
● для сплошного стержня квадратной формы — размер мм2 × 0,00785, когда он измеряется в килограммах на метр (кг / м).
● для сплошного стержня квадратной формы — размер мм2 × 0,00527 при измерении в фунтах на фут (фунт / фут).
Это очень тонкий стальной стержень, который не используется для каких-либо строительных работ, он используется только как проволочный стержень, он слишком тонкий, он известен как стержень для карандаша.
Круглый / круглый Стальной стержень, измеренный в разных единицах измерения, удельный вес 6 мм Стальной стержень, измеренный в килограммах на метр (кг / м), составляет около 0,22 кг, когда он измеряется в килограммах на фут (кг / фут), их вес должен быть равен приблизительно 0,067 кг, при измерении в фунтах на фут (фунт / фут) их вес должен составлять приблизительно 0,1478 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен составлять приблизительно 0,0123 фунта.
Удельный вес 8-миллиметрового стального стержня / стержня / арматурного стержня / арматуры Это тонкий стальной стержень по размеру, он используется в качестве распределительной балки при разливке кровли и балки перемычки, он не подходит для работы RCC балки и колонны.
Круглый / круглый Стальной стержень, измеренный в разных единицах измерения, удельный вес 8 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 0,390 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен составлять приблизительно 0,12 кг, при измерении в фунтах на фут (фунт / фут) их вес должен составлять приблизительно 0,262 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен составлять приблизительно 0,0218 фунта .
Удельный вес 10 мм Стальной стержень / стержень / арматурный стержень / стерженьЭто стальной стержень среднего размера, он используется в качестве основной балки или распределительной балки при разливке крыши и балке перемычки, он не подходит для RCC балок и колонн.
Круглый / круглый Стальной стержень, измеренный в различных единицах измерения, удельный вес 10 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 0,617 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен составлять приблизительно 0,188 кг, при измерении в фунтах на фут (фунт / фут) их вес должен составлять приблизительно 0,414 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен составлять приблизительно 0,0345 фунта .
Размер стального стержня, он используется в качестве распределительного стержня при разливке кровли и балки перемычки, это минимальный размер стержня, необходимый для работы RCC балки и колонны.
Круглый / круглый Стальной стержень, измеренный в различных единицах измерения, удельный вес 12 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 0,889 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен быть примерно 0,271 кг, при измерении в фунтах на фут (фунт / фут) их вес должен быть примерно 0,597 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен быть примерно 0,04978 фунта .
Удельный вес 16 мм Стальной стержень / стержень / арматурный стержень / стерженьСтальной стержень 16 мм, используемый во всех типах конструкционных работ RCC при проектировании конструкции балки, колонны, фундамента и плиты.
Круглый / круглый Стальной стержень, измеренный в разных единицах измерения, удельный вес 16 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 1,58 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен быть приблизительно 0,482 кг, при измерении в фунтах на фут (фунт / фут) их вес должен быть приблизительно 1,061 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен быть приблизительно 0,0884 фунта .
Удельный вес 20 мм Стальной стержень / стержень / арматурный стержень / арматурный стерженьСтальной стержень 20 мм, используемый во всех типах конструкционных работ RCC при проектировании конструкции балки, колонны, фундамента и плиты.
Круглый / круглый Стальной стержень, измеренный в разных единицах измерения, удельный вес 20 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 2,469 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен быть примерно 0,752 кг, при измерении в фунтах на фут (фунт / фут) их вес должен быть примерно 1,659 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен быть примерно 0,138 фунта .
Удельный вес 25 мм стального стержня / стержня / арматурного стержня / арматурыСтальной стержень 25 мм, используемый во всех типах конструкционных работ RCC при проектировании конструкции балки, колонны, фундамента и плиты.
Круглый / круглый Стальной стержень, измеренный в различных единицах, удельный вес 25 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 3,858 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен быть примерно 1,176 кг, при измерении в фунтах на фут (фунт / фут) их вес должен быть примерно 2,592 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен быть примерно 0,216 фунта .
Удельный вес 32 мм Стальной стержень / стержень / арматурный стержень / стержень32 мм Стальной стержень, используемый во всех типах конструкционных работ RCC для проектирования конструкции балки, колонны, фундамента и плиты.
Круглый / круглый Стальной стержень, измеренный в различных единицах измерения, удельный вес 32 мм Стальной стержень / стержень / арматурный стержень, измеренный в килограммах на метр (кг / м), составляет около 6,32 кг, когда он измеряется в килограммах на фут (кг / фут), тогда их вес должен составлять приблизительно 1,926 кг, при измерении в фунтах на фут (фунт / фут) их вес должен составлять приблизительно 4,25 фунта, а при измерении в фунтах на дюйм (фунт / дюйм) их вес должен составлять приблизительно 0,354 фунта .
Что такое добавка в бетон и ее виды
Зачем нужен расчет удельного веса стальных прутковВы знаете, что стальной стержень имеет длину 12 метров различного размера, например 8 мм, 10 мм, 12 мм, 16 мм, 20 мм, 25 мм, 32 мм, 40 мм, 45 мм и 50 мм.поэтому нам нужно преобразовать длину стального стержня в вес в килограммы.
| Стальной стержень |
| Стальной стержень |
, вы знаете, что стальной стержень используется в строительных работах и гражданском строительстве, таких как создание плотин, водопропускных труб, мостов, столбов и т. Д.
| Стальной стержень |
Существуют разные размеры стальных стержней, такие как 6 мм, 8 мм, 10 мм, 12 мм, 16 мм, 20 мм, 25 мм и т.д., где диаметр круглого стержня 6, 8, 10, 12, 16, и вопрос, задаваемый в одной связке, сколько стержней и количество Пруток стальной в одной связке марки
Диаметр.Длина номера
8 мм —– 10 шт. —– 12 м
10 мм —- 7 шт. ——– 12 м
12 мм —- 5 шт. ——– 12 м
16мм —— 3 шт. —– 12 м
20мм —— 2 шт. —— 12 м
25 мм —— 1 шт. —— 12 м
32 мм —— 1 шт. —— 12 м
40мм ——- 1 шт. —– 12м
45 мм —— 1 шт. —— 12 м
50 мм —— 1 шт. —— 12 м
| Формула расчета веса стали |
Удельный вес стальных стержней рассчитывается по двум единицам: 1) вес стали на метр в кг и 2) вес стали на фут в кг.уникальная формула и простой расчет различных размеров стального прутка длиной 12 метров. Формула веса стали следующая:
Формула расчета веса стали бывает двух типов — вес стали на метр в кг и вес стали на фут в кг
Формула веса стали на метр в кг следующая:
Вес стали = (диаметр) * 2/162 × длина
W = (D) * 2 л / 162 кг
А формула веса стали на фут в кг следующая:
Вес стали = (диаметр) * 2/533 × длина
W = (D) * 2 л / 533 кг
Масса / вес стали на 1 фут: — Масса стали на 1 фут толщиной 6 мм примерно равна 0.067 кг, 8 мм — 0,120 кг, 10 мм — 0,188 кг, 12 мм — 0,270 кг, 16 мм — 0,480 кг, 20 мм — 0,751 кг, 25 мм — 1,174 кг и 32 мм — 1,925 кг.
Формула веса стали на метр или фут в кг используется для расчета удельного веса стали. Например удельный вес стали 8 мм на метр или на фут в кг —
Вес стали 8 мм на метр = (8 × 8) / 162 кг / м
Удельный вес стали 8 мм = 0,395 кг / м
Удельный вес стали 8 мм = (8 × 8) / 533 кг / фут
Удельный вес стали 8 мм = 0.12 кг / фут
Удельный вес 8-миллиметровой стали на метр составляет 0,395 кг / м, а на фут 0,12 кг / фут
● Как рассчитать материал, необходимый для кровли здания площадью 1800 квадратных футов
● Как рассчитать материал, необходимый для заливки кровли на 1000 квадратных футов постройка
Вывод формулы d2 / 162 для веса единицы стали на метрНам необходимо рассчитать удельный вес стальных стержней в килограммах на метр, и мы знаем, что удельный вес стального стержня составляет 7850 кг / м3.2/162
Мы знаем, что вес стали = объем стали × плотность стали, а объем = площадь поперечного сечения × длина, поэтому вес стали = площадь поперечного сечения × длина × плотность
Формула веса стали = πD * 2/4 × L × плотность, где w = вес стали, π = 3,14, D = диаметр стального стержня в мм, L = длина стального стержня = 1 м и плотность = 7850 кг / м3 .
Подставляя все значения, получаем вес = 3,14 × D мм * 2/4 × 1 м × 7850 кг / м3, теперь нам нужно преобразовать квадратный миллиметр в квадратный метр, 1 мм ^ 2 = 1/1000 м × 1/1000 м = 1/1000000 м. 2
Рассчитав это, мы получим вес = 3.2 × 0,006162 кг, и это может быть записано следующим образом: вес = D * 2/1 / 0,006162 кг, когда мы разделим 1 / 0,006162, мы получим 162, поэтому окончательная формула веса стальных стержней в кг на метр равна весу = D * 2 × L / 162 кг / м3.
Следовательно, формула веса единицы стали для кг на метр равна вес = D * 2 × L / 162 кг / м
Вывод формулы d2 / 533 для веса стальной единицы на футМы знаем, что вес стали = объем × плотность, например, w = πD * 2/4 × L × плотность, продолжаем w = 3,14 × D мм * 2/4 × 1 фут × 222 кг / фут3.2/533 × L кг / фут, полученная по формуле. Эта формула используется для расчета веса стали на фут.
Вес стали на фут: — вес стали на фут для 6 мм составляет 0,067 кг, 8 мм — 0,120 кг, 10 мм — 0,188 кг, 12 мм — 0,270 кг, 16 мм — 0,480 кг, 20 мм — 0,751 кг, 25 мм — 1,174 кг и 32 мм — 1,925 кг
Вес стали 8 мм на метр● найдите 8-миллиметровую стальную массу на метр и длину 12 метров и 10 единиц стали в одной связке: —
Рассчитать вес стального стержня |
| Стальной стержень 8 мм |
● вес = D2 × L / 162
1) Вес стали 8 мм на метр
Вес = 8 × 8 × 1 ÷ 162 = 0.39 кг
2) Стальной груз 8 мм на 12 м
Вт = 8 × 8 × 12 ÷ 162 = 4,74 кг
3) Стальной груз 8 мм для 1 связки
= 8 × 8 × 12 × 10 ÷ 162 = 47,407 кг
0,39 кг — это удельный вес 8 мм стали на метр, 4,74 кг — для 12 метров и 47,407 кг — для 1 пачки стали 8 мм.
Вес стальных стержней 10 мм на метр● как рассчитать вес стального прутка размером 10 мм длиной 12 метров и количеством стальных листов в одной связке: —
Рассчитать вес стального стержня |
| Стальной стержень 10 мм |
● расчет веса: —
1) Масса стальных стержней 10 мм на 1м = 10 × 10 × 1 ÷ 162 = 0.617 кг
2) Вес стальных стержней 10 мм для 12 м W = 10 × 10 × 12 ÷ 162 = 7,407 кг
3) Масса стального стержня 10 мм для 1 связки = 10 × 10 × 12 × 7 ÷ 162 = 51,85 кг
0,617 кг — удельный вес стали 10 мм на метр, 7,407 кг — для 12 метров и 51,85 кг — для 1 пачки стали 10 мм.
Вес стального прутка 12 мм на метр● как рассчитать массу стального стержня 12 мм длиной 12 метров и 5 стальных стержней в одной связке: —
Рассчитать вес стального стержня● расчет веса: —
1) Груз из стального прутка 12 мм на 1 м = 12 × 12 × 1 ÷ 162 = 0.889 кг
2) Вес стального стержня 12 мм для 12 м = 12 × 12 × 12 ÷ 162 = 10,667 кг
3) Груз стальной пруток 12 мм для 1 связки
= 12 × 12 × 12 × 5 ÷ 162 = 53,333 кг
0,889 кг — это удельный вес стали толщиной 12 мм на метр, 10,667 кг — для 12 метров и 53,34 кг — для 1 пачки стали толщиной 8 мм.
Вес стального прутка 16 мм● как рассчитать вес размера 16 мм Стальной стержень длиной 12 м и 3 шт. Стальных стержней в одной связке
Рассчитать вес стального стержня● расчет веса: —
1) Вес стального стержня 16 мм на 1 м W = 16 × 16 × 1 ÷ 162 = 1.58 кг
2) Вес стального стержня 16 мм для 12 м W = 16 × 16 × 12 ÷ 162 = 18,96 кг
3) Груз стальной пруток 16мм на 1 пачку
= 16 × 16 × 12 × 3 ÷ 162 = 56,889 кг
1,58 кг — это удельный вес стали 16 мм на метр, 18,96 кг — для 12 метров и 56,889 кг — для 1 пачки стали 16 мм.
20 мм стальной груз● как рассчитать вес размера 20 мм Стальной стержень длиной 12 метров и 2 количества стальных стержней в одной связке: —
Рассчитать вес стального стержня● расчет веса: —
1) Стальной груз 20 мм на 1 м W = 20 × 20 × 1 ÷ 162 = 2.469 кг
2) 20 мм стальной груз для 12 м W = 20 × 20 × 12 ÷ 162 = 29,629 кг
3) Вес стали 20 мм на 1 пучок = 20 × 20 × 12 × 2 ÷ 162 = 59,259 кг
2,469 кг — это удельный вес 20 мм стали на метр, 29,629 кг — для 12 метров и 59,259 кг — для 1 пачки стали 20 мм.
Вес стального стержня 25 мм● как рассчитать вес стального прутка размером 25 мм и длиной 12 метров: —
Рассчитать вес стального стержня● расчет веса: —
1) Вес стального стержня 25 мм на 1 м W = 25 × 25 × 1 ÷ 162 = 3.858 кг
2) Вес стального стержня 25 мм для 12 м W = 25 × 25 × 12 ÷ 162 = 46,296 кг
Вес стального стержня 32 мм● как рассчитать вес стального стержня размером 32 мм длиной 12 метров: —
Рассчитать вес стального стержня● расчет веса: —
1) для 1 м W = 32 × 32 × 1 ÷ 162 = 6,32 кг
2) для 12 м W = 32 × 32 × 12 ÷ 162 = 75,85 кг
Вес стального стержня 40 мм● Пример 8: — ● как рассчитать вес стального стержня размером 40 мм и длиной 12 метров: —
Рассчитать вес стального стержня● расчет веса: —
1) для 1 м W = 40 × 40 × 1 ÷ 162 = 9.876 кг
2) для 12 м W = 40 × 40 × 12 ÷ 162 = 118,518 кг
● Пример 9
● как рассчитать вес стального прутка размером 45 мм и длиной 12 метров
● расчет веса: —
1) для 1 м W = 45 × 45 × 1 ÷ 162 = 12,5 кг
2) для 12 м W = 45 × 45 × 12 ÷ 162 = 150 кг
● Пример 10
● как рассчитать вес стального прутка размером 50 мм длиной 12 метров
● расчет веса: —
1) для 1 м W = 50 × 50 × 1 ÷ 162 = 15.432 кг
2) для 12 м W = 50 × 50 × 12 ÷ 162 = 185,185 кг
● Как рассчитать вес стального стержня разного размера в килограммах на фут (кг / фут)
● в футах и удельный вес стали в кг / фут
формула веса = D * 2/533 × L
кг / фут
● Примечание: —
D = диаметр стального стержня в миллиметрах
L = длина стального стержня в футах = 39 футов
Плотность = 222 кг / фут3
Вес = Объем × плотность
W = πD * 2/4 × L × плотность
W = 3.14 × Dмм * 2/4 × 1 фут × 222 кг / фут3
1 мм * 2. = 1 / 304,80 × 304,80 футов * 2
W = (3,14 × Dft × 1 фут / 4 × 304,80 × 304,80) × 222 кг / фут3
W = D * 2 × 0,001878 кг / фут
Вес = D * 2/1 / 0,001878 кг / фут
Вес = D * 2/533 × L кг / фут
● Пример 1: —
● как рассчитать вес стального прутка размером 8 мм длиной 39 футов и количеством стальных стержней в одной связке —
Рассчитать вес стального стержня● расчет веса: —
1) 1 фут
Вт = 8 × 8 × 1 ÷ 533 = 0.12 кг
2) для 39 футов W = 8 × 8 × 39 ÷ 533 = 4,68 кг
3) на 1 пучок W = 8 × 8 × 39 × 10 ÷ 533 = 46,80 кг
● Example2
● как рассчитать вес стального стержня размером 10 мм и длиной 39 футов, имеющего 7 стальных стержней в одной связке
● решить: —
1) на 1 фут W = 10 × 10 × 1 ÷ 533 = 0,1876 кг
2) для 39 футов W = 10 × 10 × 39 ÷ 533 = 7,317 кг
3) для 1 пучка W = 10 × 10 × 39 × 7 ÷ 533 = 51,219 кг
● Example3
● как рассчитать вес стального стержня размером 12 мм и длиной 39 футов и 5 стальных стержней в одной связке: —
● решить: —
1) Для 1 фут W = 12 × 12 × 1 ÷ 533 = 0.270 кг
2) Для 39 футов W = 12 × 12 × 39 ÷ 533 = 10,53 кг
3) Для 1 пучка W = 12 × 12 × 39 × 5 ÷ 533 = 52,68 кг
● Пример 4
● как рассчитать вес стального стержня размером 16 мм, имеющего длину 39 футов и 3 количества стальных стержней, присутствующих в одной связке
● решить: —
1) для 1 фут W = 16 × 16 × 1 ÷ 533 = 0,80 кг
2) для 39 футов W = 16 × 16 × 39 ÷ 533 = 18,73 кг
3) для 1 пучка W = 16 × 16 × 39 × 3 ÷ 533 = 56,195 кг
● Example5
● как рассчитать вес стального стержня размером 20 мм длиной 39 футов и 2 стальных стержней в одной связке
● Решить : —
1) для 1 фут W = 20 × 20 × 1 ÷ 533 = 0.75 кг
2) для 39 футов W = 20 × 20 × 39 ÷ 533 = 29,268 кг
3) для 1 пучка W = 20 × 20 × 39 × 2 ÷ 533 = 58,536 кг
● Теперь ваша очередь: — любые причуды, вопросы по этой теме расчет различных размеров стального стержня, пожалуйста, комментируйте, делитесь и задавайте вопросы, ваши вопросы приветствуются 🙏 в этом блоге
● спасибо, что присоединились к нам
■ Теперь вы можете подписаться на меня на Facebook и подписаться на мой канал youtube
9.3 простых машины | Texas Gateway
Простые машины
Простые машины облегчают работу, но не уменьшают объем работы, которую вы должны выполнять. Почему простые машины не могут изменить объем выполняемой вами работы? Напомним, что в закрытых системах сохраняется общее количество энергии. Машина не может увеличить количество энергии, которую вы в нее вкладываете. Итак, чем полезна простая машина? Хотя он не может изменить объем выполняемой вами работы, простой механизм может изменить количество силы, которую вы должны приложить к объекту, и расстояние, на котором вы прикладываете силу.В большинстве случаев используется простая машина, чтобы уменьшить силу, которую вы должны приложить для выполнения работы. Обратной стороной является то, что вы должны приложить силу на большем расстоянии, потому что произведение силы и расстояния, f d , (что равняется работе), не меняется.
Давайте посмотрим, как это работает на практике. На рис. 9.8 (а) рабочий использует рычаг для приложения небольшой силы на большом расстоянии, в то время как монтировка тянет гвоздь с большой силой на небольшом расстоянии.На рис. 9.8 (b) показано, как работает рычаг математически. Сила усилия, приложенная в точке F e , поднимает нагрузку (силу сопротивления), которая толкает вниз в точке F r . Треугольный шарнир называется точкой опоры; часть рычага между опорой и рычагом F e является рычагом усилия, L e ; а часть слева — рычаг сопротивления, L r . Механическое преимущество — это число, которое говорит нам, во сколько раз простая машина умножает силу усилия.Идеальное механическое преимущество IMA — это механическое преимущество совершенной машины без потери полезной работы, вызванной трением между движущимися частями. Уравнение для IMA показано на рисунке 9.8 (b).
Рис. 9.8 (a) Монтировка — это разновидность рычага. (b) Идеальное механическое преимущество равно длине плеча усилия, деленному на длину плеча сопротивления рычага.
В общем случае IMA = сила сопротивления, F r , деленная на силу усилия, F e . IMA также равно расстоянию, на которое прилагается усилие, d e , деленному на расстояние, на которое проходит груз, d r .
IMA = FrFe = dedrIMA = FrFe = dedrВозвращаясь к экономии энергии, для любой простой машины работа, вложенная в машину, W i , равна работе, которую производит машина, W o . Объединив это с информацией в параграфах выше, мы можем написать
Wi = WoFede = Frdr Если FeFr, то de> dr.Wi = WoFede = Frdr Если FeFr, то de> dr.Уравнения показывают, как простая машина может производить такое же количество работы, уменьшая при этом величину силы усилия за счет увеличения расстояния, на котором прилагается сила усилия.
Watch Physics
Введение в Mechanical Advantage
В этом видео показано, как рассчитать IMA рычага тремя различными методами: (1) исходя из силы усилия и силы сопротивления; (2) от длины плеч рычага, и; (3) от расстояния, на которое приложена сила, и расстояния, на которое перемещается груз.
Проверка захвата
Двое детей разного веса катаются на качелях. Как они позиционируют себя относительно точки поворота (точки опоры), чтобы быть уравновешенными?
- Более тяжелый ребенок сидит ближе к точке опоры.
- Более тяжелый ребенок сидит дальше от точки опоры.
- Оба ребенка сидят на равном расстоянии от точки опоры.
- Поскольку оба имеют разный вес, они никогда не будут уравновешены.
Некоторые рычаги оказывают большое усилие на плечо с коротким усилием. Это приводит к меньшей силе, действующей на большем расстоянии на конце рычага сопротивления. Примерами рычага этого типа являются бейсбольные биты, молотки и клюшки для гольфа. В рычаге другого типа точка опоры находится на конце рычага, а нагрузка — в середине, как в конструкции тачки.
Простая машина, показанная на рис. 9.9, называется колесом и осью . На самом деле это рычаг.Разница в том, что рычаг усилия может вращаться по полной окружности вокруг точки опоры, которая является центром оси. Сила, приложенная к внешней стороне колеса, вызывает большее усилие, прилагаемое к веревке, намотанной вокруг оси. Как показано на рисунке, идеальное механическое преимущество рассчитывается путем деления радиуса колеса на радиус оси. Любое кривошипно-шатунное устройство — это пример колеса и оси.
Рис. 9.9 Сила, приложенная к колесу, действует на его ось.
Наклонная плоскость и клин — две формы одной и той же простой машины. Клин — это просто две наклонные плоскости вплотную друг к другу. На рисунке 9.10 показаны простые формулы для расчета IMA s этих машин. Все наклонные, мощеные поверхности для прогулок или езды являются наклонными плоскостями. Ножи и головки топоров являются примерами клиньев.
Рисунок 9.10 Слева показана наклонная плоскость, а справа — клин.
Винт, показанный на рисунке 9.11 фактически представляет собой рычаг, прикрепленный к круглой наклонной плоскости. Саморезы по дереву (конечно) также являются примерами шурупов. Рычажная часть этих винтов представляет собой отвертку. В формуле для IMA расстояние между резьбами винтов называется шагом и имеет обозначение P .
Рис. 9.11 Показанный здесь винт используется для подъема очень тяжелых предметов, например, угла автомобиля или дома на небольшое расстояние.
На рис. 9.12 показаны три разные системы шкивов.Из всех простых машин механическое преимущество легче всего рассчитать для шкивов. Просто посчитайте количество веревок, поддерживающих груз. Это IMA . И снова мы должны приложить силу на большем расстоянии, чтобы увеличить силу. Чтобы поднять груз на 1 метр с помощью шкивной системы, вам нужно потянуть N метров веревки. Шкивные системы часто используются для подъема флажков и оконных жалюзи и являются частью механизма строительных кранов.
Рисунок 9.12 Здесь показаны три системы шкивов.
Watch Physics
Механическое преимущество наклонных плоскостей и шкивов
В первой части этого видео показано, как рассчитать IMA систем шкивов. В последней части показано, как рассчитать IMA наклонной плоскости.
Проверка захвата
Как можно использовать систему шкивов для подъема легкого груза на большую высоту?
- Уменьшите радиус шкива.
- Увеличьте количество шкивов.
- Уменьшите количество веревок, поддерживающих груз.
- Увеличьте количество веревок, поддерживающих груз.
Сложная машина — это комбинация двух или более простых машин. Кусачки на рис. 9.13 сочетают в себе два рычага и два клина. Велосипеды включают колеса и оси, рычаги, винты и шкивы. Автомобили и другие транспортные средства представляют собой комбинации многих машин.
Рисунок 9.13 Кусачки — обычная сложная машина.
11,5: Магнитная сила на проводнике с током
Движущиеся заряды испытывают силу в магнитном поле. Если эти движущиеся заряды находятся в проводе, то есть если по проводу проходит ток, на провод также должна действовать сила. Однако, прежде чем обсуждать силу, действующую на ток со стороны магнитного поля, мы сначала исследуем магнитное поле, создаваемое электрическим током. Здесь мы изучаем два отдельных эффекта, которые тесно взаимодействуют: провод с током создает магнитное поле, а магнитное поле оказывает силу на провод с током.
Магнитные поля, создаваемые электрическим током
Обсуждая исторические открытия в области магнетизма, мы упомянули открытие Эрстеда о том, что провод, по которому проходит электрический ток, вызывает отклонение расположенного поблизости компаса. Было установлено, что электрические токи создают магнитные поля. (Эта связь между электричеством и магнетизмом более подробно обсуждается в Источниках магнитных полей.)
На стрелку компаса около провода действует сила, которая выравнивает касательную стрелки к окружности вокруг провода.Следовательно, токоведущий провод создает кольцевые петли магнитного поля. Чтобы определить направление магнитного поля, создаваемого проводом, мы используем второе правило правой руки. В RHR-2 ваш большой палец указывает в направлении тока, в то время как ваши пальцы охватывают провод, указывая в направлении создаваемого магнитного поля (рисунок \ (\ PageIndex {1} \)). Если магнитное поле попадало на вас или выходило за пределы страницы, мы обозначаем это точкой. Если магнитное поле попадало на страницу, мы обозначаем это знаком ×.
Эти символы получены с учетом векторной стрелки: стрелка, направленная к вам, с вашей точки зрения будет выглядеть как точка или кончик стрелки. Стрелка, направленная от вас, с вашей точки зрения будет выглядеть как крест или знак ×. Составной эскиз магнитных кругов показан на рисунке \ (\ PageIndex {1} \), где показано, что напряженность поля уменьшается по мере удаления от провода петлями, которые расположены дальше друг от друга.
Рисунок \ (\ PageIndex {1} \): (a) Когда провод находится в плоскости бумаги, поле перпендикулярно бумаге.Обратите внимание на символы, используемые для поля, указывающего внутрь (например, хвоста стрелки), и поля, указывающего наружу (например, кончика стрелки). (б) Длинный и прямой провод создает поле с силовыми линиями магнитного поля, образующими кольцевые петли.Расчет магнитной силы
Электрический ток — это упорядоченное движение заряда. Следовательно, провод с током в магнитном поле должен испытывать силу, создаваемую этим полем. Чтобы исследовать эту силу, давайте рассмотрим бесконечно малое сечение провода, как показано на рисунке \ (\ PageIndex {3} \).Длина и площадь поперечного сечения секции равны дл и A соответственно, поэтому ее объем равен \ (V = A \ cdot dl \). Проволока сформирована из материала, который содержит n носителей заряда в единице объема, поэтому количество носителей заряда в секции равно \ (nA \ cdot dl \). Если носители заряда движутся со скоростью дрейфа \ (\ vec {v} _d \), ток I в проводе равен (от тока и сопротивления)
\ [I = neAv_d. \]
Магнитная сила, действующая на любой отдельный носитель заряда, равна \ (e \ vec {v} _d \ times \ vec {B} \), поэтому общая магнитная сила \ (d \ vec {F} \) на \ (nA \ cdot dl \) носителей заряда в сечении провода
\ [d \ vec {F} = (nA \ cdot dl) e \ vec {v} _d \ times \ vec {B}.\]
Мы можем определить dl как вектор длиной dl , указывающий вдоль \ (\ vec {v} _d \), что позволяет нам переписать это уравнение как
\ [d \ vec {F} = neAv_dd \ vec {l} \ times \ vec {B}, \] или
\ [d \ vec {F} = Id \ vec {l} \ times \ vec {B}. \ label {11.12} \]
Это сила магнитного поля на отрезке провода. Обратите внимание, что на самом деле это результирующая сила, действующая со стороны поля на сами носители заряда. Направление этой силы задается RHR-1, где вы указываете пальцами в направлении тока и сгибаете их к полю.Затем ваш большой палец указывает в направлении силы.
Рисунок \ (\ PageIndex {2} \): бесконечно малое сечение токоведущего провода в магнитном поле.Чтобы определить магнитную силу \ (\ vec {F} \) на проводе произвольной длины и формы, мы должны интегрировать уравнение \ ref {11.12} по всему проводу. Если сечение провода прямое, а B однородный, дифференциалы уравнения становятся абсолютными величинами, давая нам
\ [\ vec {F} = I \ vec {l} \ times \ vec {B}.\]
Это сила, действующая на прямой провод с током в однородном магнитном поле.
Пример \ (\ PageIndex {1} \): уравновешивание гравитационных и магнитных сил на проводе с током
Провод длиной 50 см и массой 10 г подвешен в горизонтальной плоскости с помощью пары гибких проводов (рисунок \ (\ PageIndex {3} \)). Затем на проволоку действует постоянное магнитное поле величиной 0,50 Тл, которое направлено, как показано. Каковы величина и направление тока в проводе, необходимые для снятия напряжения в опорных выводах?
Рисунок \ (\ PageIndex {3} \): (a) Проволока, подвешенная в магнитном поле.(б) Схема свободного тела для проволоки.Стратегия
Из диаграммы свободного тела на рисунке, натяжения в опорных выводах стремятся к нулю, когда гравитационная и магнитная силы уравновешивают друг друга. Используя RHR-1, мы обнаруживаем, что магнитная сила направлена вверх. Затем мы можем определить текущее значение I , приравняв две силы.
Решение
Приравняйте две силы веса и магнитного поля к проводу:
\ [мг = IlB.2)} {(0,50 \, m) (0,50 \, T)} = 0,39 \, A. \]
Значение
Это сильное магнитное поле создает значительную силу на длине провода, чтобы противодействовать его весу.
Пример \ (\ PageIndex {2} \): Расчет магнитной силы на токоведущем проводе
По длинному жесткому проводу, проложенному вдоль оси y , проходит ток 5,0 А, протекающий в положительном направлении y . (а) Если постоянное магнитное поле величиной 0.30 Тл направлено вдоль положительной оси x , какова сила магнитного поля на единицу длины провода? (b) Если постоянное магнитное поле 0,30 Тл направлено на 30 градусов от оси + x к оси + y , какова магнитная сила на единицу длины на проводе?
Стратегия
Магнитная сила, действующая на провод с током в магнитном поле, определяется выражением \ (\ vec {F} = I \ vec {l} \ times \ vec {B} \). Что касается части а, поскольку ток и магнитное поле в этой задаче перпендикулярны, мы можем упростить формулу, чтобы дать нам величину и найти направление через RHR-1.Угол θ составляет 90 градусов, что означает \ (sin \, \ theta = 1. \). Кроме того, длину можно разделить на левую часть, чтобы найти силу на единицу длины. Для части b текущая длина, умноженная на длину, записывается в обозначении единичного вектора, а также магнитное поле. После взятия перекрестного произведения направленность очевидна по результирующему единичному вектору.
Решение
- Начнем с общей формулы магнитной силы на проводе. Мы ищем силу на единицу длины, поэтому мы делим ее на длину, чтобы вывести ее в левую часть.Мы также устанавливаем \ (sin \, \ theta \). Следовательно, решением будет \ [F = IlB \, sin \, \ theta \] \ [\ frac {F} {l} = (5.0 \, A) (0.30 \, T) \] \ [\ frac {F} {l} = 1,5 \, Н / м. \] Направленность: Укажите пальцами в положительном направлении y и согните пальцы в положительном направлении x . Ваш большой палец будет указывать в направлении \ (- \ vec {k} \). Следовательно, с учетом направленности решение будет \ [\ frac {\ vec {F}} {l} = -1,5 \ vec {k} \, Н / м. \]
- Текущее значение, умноженное на длину, и магнитное поле записываются в виде единичного вектора.o) \ hat {i} \] \ [\ vec {F} / l = -1.30 \ hat {k} \, Н / м. \]
Значение
Это большое магнитное поле создает значительную силу на небольшой длине провода. По мере того, как угол магнитного поля становится более близким к току в проводе, на него действует меньшая сила, как видно из сравнения частей a и b.
Упражнение \ (\ PageIndex {1} \)
Прямой гибкий медный провод погружается в магнитное поле, направленное внутрь страницы.(а) Если ток в проводе течет в направлении + x , в каком направлении будет изгибаться провод? (b) В какую сторону изгибается провод, если ток течет в направлении — x ?
Решение
а. наклоняется вверх; б. наклоняется вниз
Пример \ (\ PageIndex {3} \): сила на круглом проводе
Круговая токовая петля радиусом R , по которой проходит ток I , расположена в плоскости xy . Постоянное однородное магнитное поле пересекает контур параллельно оси y (рисунок \ (\ PageIndex {4} \)).Найдите магнитную силу на верхней половине петли, нижней половине петли и общую силу на петле.
Рисунок \ (\ PageIndex {4} \): петля из провода, по которой течет ток в магнитном поле.Стратегия
Магнитная сила на верхнем контуре должна быть записана в терминах дифференциальной силы, действующей на каждый сегмент контура. Если мы интегрируем по каждому дифференциальному элементу, мы решаем общую силу на этом участке петли. Сила, действующая на нижнюю петлю, определяется аналогичным образом, и общая сила складывается из этих двух сил.
Решение
Дифференциальное усилие на произвольном отрезке проволоки, расположенном на верхнем кольце, составляет:
\ [dF = I B \, sin \, \ theta \, dl, \], где \ (\ theta \) — угол между направлением магнитного поля (+ y ) и отрезком провода. Дифференциальный сегмент расположен на том же радиусе, поэтому, используя формулу длины дуги, мы имеем:
\ [dl = Rd \ theta \]
\ [dF = IBR \, sin \, \ theta \, d \ theta. \]
Чтобы найти силу на отрезке, мы интегрируем по верхней половине круга от 0 до \ (\ pi \).0 sin \, \ theta \, d \ theta = IBR (-cos 0 + cos \ pi) = -2 IBR. \]
Чистая сила — это сумма этих сил, которая равна нулю.
Значение
Полная сила на любом замкнутом контуре в однородном магнитном поле равна нулю. Несмотря на то, что каждая часть петли имеет силу, действующую на нее, результирующая сила, действующая на систему, равна нулю. (Обратите внимание, что на петле есть чистый крутящий момент, который мы рассмотрим в следующем разделе.)
Поддержание здорового веса | Национальный институт старения
Поддержание здорового веса важно для общего здоровья и благополучия.
По мере того, как вы становитесь старше, если вы продолжаете есть те же виды и количество пищи, но не становитесь более активными, вы, вероятно, наберете вес. Это потому, что ваш метаболизм (то, как ваше тело получает энергию из пищи) может замедляться с возрастом, а состав вашего тела (количество жира и мышц) может отличаться от того, когда вы были моложе.
Энергия, которую ваше тело получает от питательных веществ, содержащихся в пище, измеряется в калориях. Как показывает практика, чем больше калорий вы потребляете, тем более активными вы должны быть, чтобы поддерживать свой вес.Точно так же верно и обратное: чем больше вы активны, тем больше калорий вам нужно. С возрастом вашему организму может потребоваться меньше пищи для получения энергии, но ему все равно нужно то же количество питательных веществ.
Как мне сохранить здоровый вес?
Прочтите и поделитесь этой инфографикой, чтобы узнать, как правильно выбирать продукты для здорового старения.На ваш вес могут влиять многие факторы, включая генетику, возраст, пол, образ жизни, семейные привычки и культуру, сон и даже место, где вы живете и работаете. Некоторые из этих факторов могут затруднить похудание или сбросить вес.
Но активный образ жизни и выбор здоровой пищи полезны для здоровья для всех, независимо от вашего возраста и веса. Важно выбирать продукты, богатые питательными веществами, и вести активный образ жизни не менее 150 минут в неделю. Как показывает опыт:
- Чтобы сохранить прежний вес, вам нужно сжигать столько же калорий, сколько вы едите и пьете.
- Чтобы похудеть, сжигайте больше калорий, чем едите и пьете.
- Чтобы набрать вес, сжигайте меньше калорий, чем вы едите и пьете.
Советы по поддержанию здорового веса
Что мне есть, чтобы поддерживать здоровый вес?
Выбирайте продукты, в которых много питательных веществ, но мало калорий. У NIA есть информация, которая поможет вам сделать выбор в пользу здорового питания и купить продукты, которые вам нравятся.
Сколько мне нужно физической активности?
Стремитесь заниматься аэробной нагрузкой средней интенсивности не менее 150 минут в неделю.Необязательно делать это сразу — разбейте это на целую неделю, как вам нравится. Если вы не можете сделать столько активности сразу, постарайтесь быть как можно более физически активным. Лучше делать что-то, чем вообще ничего не делать.
Польза упражнений заключается не только в весе. Регулярные упражнения помогут вам заниматься повседневными делами, участвовать в прогулках, водить машину, не отставать от внуков, избегать падений и оставаться независимыми.
Совет: физическая активность
Большинство пожилых людей могут быть умеренно активными.Но вы можете поговорить со своим врачом, если вы не привыкли к активной физической активности и хотите начать интенсивную программу упражнений или значительно увеличить свою физическую активность. Вам также следует проконсультироваться с врачом, если у вас есть следующие проблемы со здоровьем:
- Головокружение
- Одышка
- Боль или давление в груди
- Нерегулярное сердцебиение
- Сгустки крови
- Отек сустава
- Грыжа
- Недавняя операция на бедре или спине
Ваш врач может дать вам несколько советов по безопасности или порекомендовать вам определенные виды упражнений.
Вам не нужно тратить много денег, посещая тренажерный зал или нанимая личного тренера. Подумайте о видах физической активности, которые вам нравятся, например, ходьба, бег, езда на велосипеде, садоводство, уборка дома, плавание или танцы. Старайтесь уделять время тому, что вам нравится, большую часть дней недели. А затем увеличьте продолжительность или добавьте еще одно веселое занятие.
Прочтите эту тему на испанском языке. Lea sobre este tema en español.
Дополнительные сведения о поддержании здорового веса
Этот контент предоставлен Национальным институтом старения NIH (NIA).Ученые NIA и другие эксперты проверяют этот контент, чтобы убедиться, что он точен и актуален.
Проверено содержание:
29 апреля 2019 г.,
Равновесие и статика
Когда все силы, действующие на объект, уравновешены, то говорят, что объект находится в состоянии равновесия . Силы считаются сбалансированными , если правые силы уравновешиваются левыми, а восходящие силы уравновешиваются нисходящими силами.Однако это не обязательно означает, что все силы равны друг другу. Рассмотрим два объекта, изображенных на силовой диаграмме, показанной ниже. Обратите внимание, что два объекта находятся в равновесии, потому что силы, действующие на них, уравновешены; однако отдельные силы не равны друг другу. Сила 50 Н не равна силе 30 Н.
Если объект находится в равновесии, силы уравновешены. Сбалансированный — ключевое слово, используемое для описания ситуаций равновесия.Таким образом, результирующая сила равна нулю, а ускорение равно 0 м / с / с. Объекты в состоянии равновесия должны иметь ускорение 0 м / с / с. Это происходит из первого закона движения Ньютона. Но наличие ускорения 0 м / с / с не означает, что объект находится в состоянии покоя. Объект в состоянии равновесия — это либо …
- в состоянии покоя и в состоянии покоя, или
- в движении и продолжает движение с той же скоростью и направлением.
Это тоже происходит от первого закона движения Ньютона.
Анализ ситуации статического равновесия
Если объект находится в состоянии покоя и находится в состоянии равновесия, то мы бы сказали, что объект находится в «статическом равновесии». «Статический» означает стационарный или в состоянии покоя . Обычная физическая лаборатория заключается в том, чтобы подвесить объект на двух или более нитях и измерить силы, действующие под углом на объект, чтобы выдержать его вес. Состояние объекта анализируется с точки зрения сил, действующих на объект. Объект — точка на веревке, на которую действуют три силы. См. Диаграмму справа. Если объект находится в состоянии равновесия, то результирующая сила, действующая на объект, должна быть 0 Ньютонов. Таким образом, если все силы складываются вместе как векторы, то результирующая сила (векторная сумма) должна быть 0 Ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или результат сложения всех отдельных сил по направлению «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения равнодействующей.Ниже приведены примеры данных для такой лаборатории.
|
Для большинства студентов результат был 0 Ньютонов (или, по крайней мере, очень близок к 0 Н).Это то, что мы ожидали — поскольку объект находился в состоянии равновесия, результирующая сила (векторная сумма всех сил) должна быть 0 Н.
Другой способ определения чистой силы (векторной суммы всех сил) включает использование тригонометрических функций для разделения каждой силы на ее горизонтальную и вертикальную составляющие. Как только компоненты известны, их можно сравнить, чтобы увидеть, сбалансированы ли вертикальные силы и горизонтальные силы.На схеме ниже показаны векторы A, B и C и их соответствующие компоненты. Для векторов A и B вертикальные компоненты могут быть определены с использованием синуса угла, а горизонтальные компоненты могут быть проанализированы с помощью косинуса угла. Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Данные в таблице выше показывают, что силы почти уравновешивают сил.Анализ горизонтальных компонентов показывает, что левый компонент A почти уравновешивает правый компонент B. Анализ вертикальных компонентов показывает, что сумма восходящих компонентов A + B почти уравновешивает нисходящий компонент C. Векторная сумма всех сил ( почти ) равна 0 Ньютону. Но как насчет разницы в 0,1 Н между направленными вправо и влево силами и разницы в 0,2 Н между силами, направленными вверх и вниз? Почему компоненты силы только почти уравновешивают? Данные образца, используемые в этом анализе, являются результатом данных измерений на реальной экспериментальной установке.Разница между фактическими результатами и ожидаемыми результатами связана с ошибкой, возникшей при измерении силы A и силы B. Мы должны сделать вывод, что этот низкий предел экспериментальной ошибки отражает эксперимент с превосходными результатами. Можно сказать, что это «достаточно близко для работы правительства».
Приведенный выше анализ сил, действующих на объект в состоянии равновесия, обычно используется для анализа ситуаций с объектами в состоянии статического равновесия.Наиболее распространенное применение включает анализ сил, действующих на знак, который находится в состоянии покоя. Например, рассмотрите картину справа, висящую на стене. Картина находится в состоянии равновесия, и поэтому все силы, действующие на картину, должны быть уравновешены. То есть все горизонтальные компоненты должны составлять 0 Ньютонов, а все вертикальные компоненты должны составлять 0 Ньютонов. Натяжение троса А влево должно уравновешивать натяжение троса В вправо, а сумма натяжения троса А и троса В вверх должна уравновешивать вес знака.
Предположим, что измеренное натяжение обоих кабелей составляет 50 Н, а угол, который каждый кабель образует с горизонталью, составляет 30 градусов. Какой вес у знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих компонентов натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопроводительные работы показаны ниже.
Поскольку каждый трос тянет вверх с силой 25 Н, общая сила тяги знака вверх составляет 50 Н. Следовательно, сила тяжести (также известная как вес) составляет 50 Н вниз. Знак весит 50 Н.
В приведенной выше задаче натяжение кабеля и угол кабеля относительно горизонтали используются для определения веса знака .Идея в том, что натяжение, угол и вес связаны. Если известны любые два из этих трех, то третья величина может быть определена с помощью тригонометрических функций.
В качестве еще одного примера, иллюстрирующего эту идею, рассмотрим симметричный вывешивание знака, как показано справа. Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в состоянии равновесия (хорошее предположение, если он остается в состоянии покоя), два троса должны обеспечивать достаточную восходящую силу, чтобы уравновесить нисходящую силу тяжести.Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m * g), поэтому каждый из двух тросов должен тянуть вверх с силой 24,5 Н. Поскольку угол между кабелями составляет 100 градусов, каждый кабель должен составлять 50 градусов с вертикалью и 40 градусов с горизонталью. Набросок этой ситуации (см. Диаграмму ниже) показывает, что натяжение кабеля можно определить с помощью синусоидальной функции. Треугольник ниже иллюстрирует эти отношения.
Концептуальное мышлениеЕсть важный принцип, который вытекает из некоторых из тригонометрических вычислений, выполненных выше.Принцип состоит в том, что по мере увеличения угла к горизонтали величина силы натяжения, необходимая для удержания знака в состоянии равновесия, уменьшается. Чтобы проиллюстрировать это, рассмотрим картинку с напряжением 10 Ньютон, удерживаемую тремя разными ориентациями проводов, как показано на схемах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол между проводами и горизонтом варьируется от 60 до 15 градусов. Используйте эту информацию и приведенную ниже диаграмму, чтобы определить натяжение проволоки для каждой ориентации.По завершении нажмите кнопку, чтобы просмотреть ответы.
В заключение, равновесие — это состояние объекта, в котором все силы, действующие на него, уравновешены. В таких случаях чистая сила равна 0 Ньютонам. Зная силы, действующие на объект, тригонометрические функции могут использоваться для определения горизонтальных и вертикальных компонентов каждой силы. В случае равновесия все вертикальные компоненты должны уравновешиваться, а все горизонтальные компоненты должны уравновешиваться.
Следующие вопросы предназначены для проверки вашего понимания ситуаций равновесия. Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.
1.На стене висит следующая картина. Используйте тригонометрические функции, чтобы определить вес изображения.
2. Табличка внизу висит снаружи класса физики, рекламируя самую важную истину, которую можно найти внутри. Знак опирается на диагональный трос и жесткий турник. Если вывеска имеет массу 50 кг, то определите натяжение диагонального троса, поддерживающего его вес.
3. Следующий знак можно найти в Гленвью. Знак имеет массу 50 кг. Определите натяжение тросов.
4. После самой последней доставки печально известный аист объявляет хорошие новости. Если знак имеет массу 10 кг, то какова сила натяжения в каждом тросе? Используйте тригонометрические функции и эскиз, чтобы помочь в решении.
5. Предположим, что ученик тянет с двумя большими силами (F 1 и F 2 ), чтобы поднять книгу весом 1 кг на двух тросах. Если кабели образуют угол в 1 градус с горизонталью, то каково натяжение кабеля?
.






 м.
м.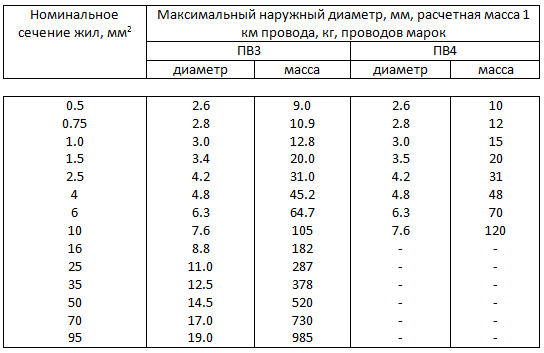 4
4