Вопрос №2. Параллельное соединение приемников в однофазных цепях (10 мин.)
Расчет цепи с параллельным соединением проводников (рис. 7,а) можно осуществить различными способами: методом векторных диаграмм, методом проводимостей и методом комплексных чисел. Первый метод не позволяет с большой точностью осуществить расчеты (рис. 7, б), поэтому были введены методы комплексных чисел и метод проводимостей. Рассмотрим метод проводимостей подробнее.
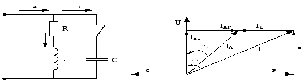
а) б)
Рис. 7. Схема разветвленной цепи и векторная диаграмма
резонанса напряжений
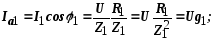
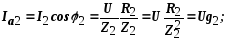
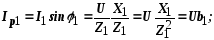
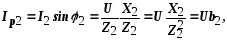
где g1, g2 – активные проводимости ветвей;
b1, b2 – реактивные проводимости ветвей.
Необходимо
отметить, что знак реактивных проводимостей
получается автоматически, т.к. 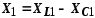
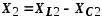 .
Т. к.XL2 и XC1 равны нулю, то b1>0, b2<0.
.
Т. к.XL2 и XC1 равны нулю, то b1>0, b2<0.Общий ток
 где
где  – полная проводимость цепи, См.
– полная проводимость цепи, См.
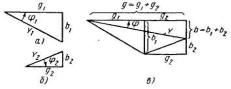
Рис. 8. Треугольники проводимостей
Функции угла φ определяют так:
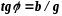 ;
; 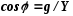
Выражения для мощностей принимают такой вид:
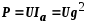
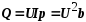
Выводы по второму вопросу: таким образом, для расчета цепей с параллельным соединением приемников используются методы векторных диаграмм, проводимостей и комплексных чисел.
Вопрос №3. Резонанс напряжений и токов (20 мин.)
Резонансным режимом работы цепи – режим, при котором ее сопротивление является чисто активным.
Различают два основных режима: резонанс напряжений и резонанс токов.
3.1. Резонанс напряжений
Резонанс напряжений – это явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.
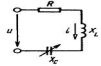
Рис. 9. Схема последовательного колебательного контура
Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление должно быть равно нулю, так как tgφ=X/R.
Условие резонанса
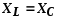
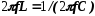
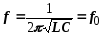
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение является формулой Томсона, определяющей зависимость собственной частоты колебаний контура от параметров L и С. Следует вспомнить, что если конденсатор контура зарядить от источника постоянного тока, а затем замкнуть его на индуктивную катушку, то в контуре возникнет переменный ток частоты f0. Вследствие потери колебания в контуре будут затухать, время
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис. 10.
Признаки резонанса напряжений:
а) сопротивление цепи Z=R минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.
Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на катушке и конденсаторе обусловлено накопленной в них энергией, значение которой

Рис. 10. Векторная диаграмма и резонансная
кривая последовательного контура
Характеристики резонанса:
1)
Волновое сопротивление контура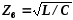
2)
Добротность контура 
3) Резонансная кривая характеризует способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот (рис. 10, б).
4) Полное сопротивление цепи при резонансе
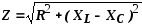
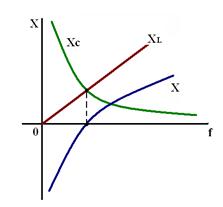
На рис. 11 показана зависимость реактивного сопротивления Х=ХL —Хс от частоты источника f. Анализ этого графика показывает, что при низких и высоких частотах реактивное сопротивление велико и ток в контуре мал. При частотах, близких к
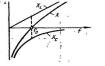
Рис. 11
Резонанс напряжений широко используется в радиотехнике и электронике для выделения сигналов заданной частоты.
6 Резонансные режимы в электрических цепях синусоидального тока » СтудИзба
ЛЕКЦИЯ 6
Резонансные режимы в электрических цепях синусоидального тока.
Резонанс напряжений
Режим работы RLC цепи или LC—цепи, при условии равенства реактивных сопротивлений XC= XL, когда общее напряжение цепи совпадает по фазе с её током  , называется резонансом напряжения.
, называется резонансом напряжения.
XC= XL – условие резонанса

RLC цепь LC цепь.
Признаки резонанса напряжения:
1. Напряжение на входе совпадает по фазе с током, т.е. сдвиг фаз между I и U φ = 0, cos φ = 1
2. Ток в цепи будет наибольшим и как следствие Pmax= I2maxR тоже максимальна, а реактивная мощность равна нулю.
3. Резонансная частота 
4. 
Резонанс можно достигнуть, изменяя L, C или ω.
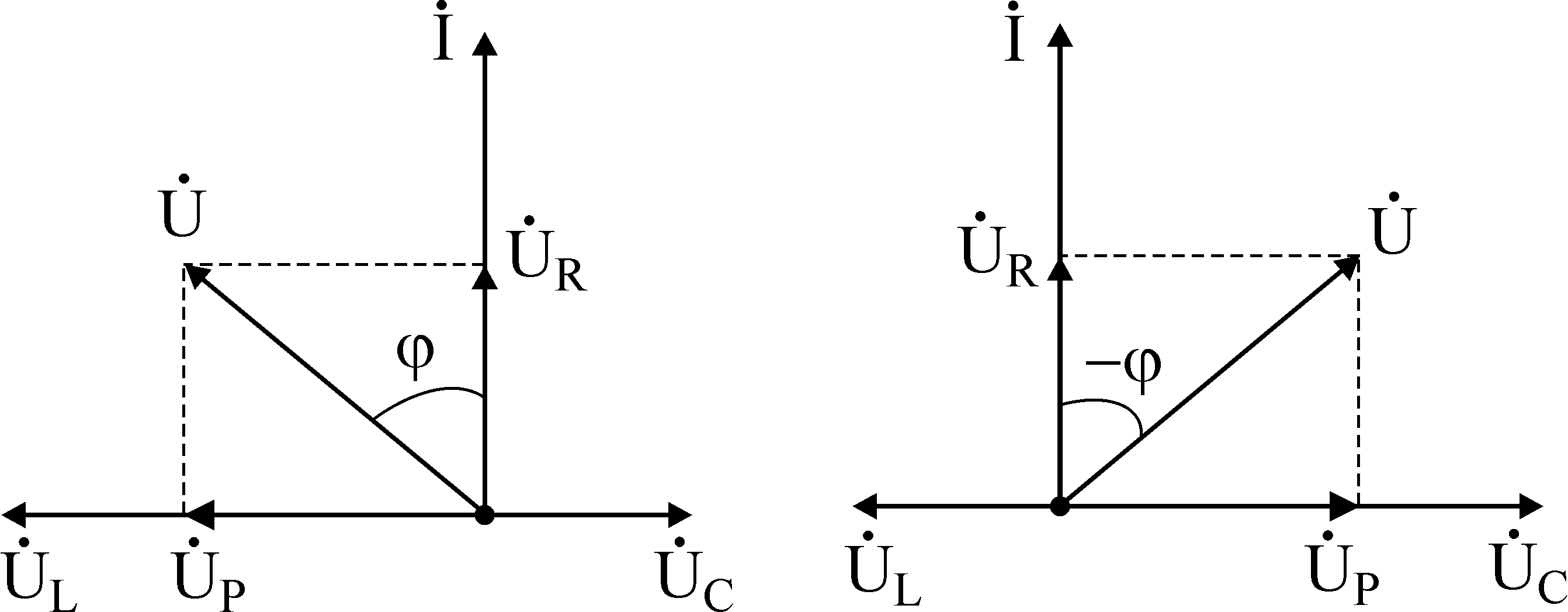
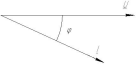
Векторные диаграммы при резонансе напряжений
LC цепь RLC цепь


Случаи других режимов работы RLC цепи
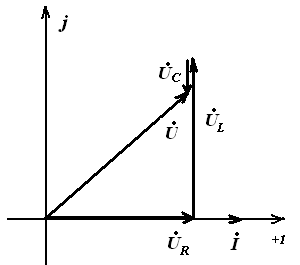
- Если XL>XC т.е.


 U опережает I, значит цепь имеет активно-индуктивный характер
U опережает I, значит цепь имеет активно-индуктивный характер
 напряжение на катушке больше напряжения на конденсаторе.
напряжение на катушке больше напряжения на конденсаторе.
Векторная диаграмма
- Если XL<XC , т.е.


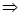 U отстает от I, значит цепь имеет активно-емкостной характер
U отстает от I, значит цепь имеет активно-емкостной характер
 напряжение на конденсаторе больше напряжения на катушке.
напряжение на конденсаторе больше напряжения на катушке.
Векторная диаграмма

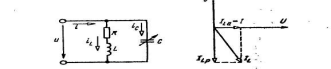
Параллельное соединение элементов в цепи синусоидального тока
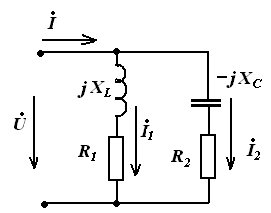
На входе параллельной цепи напряжение 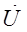
Закон Ома
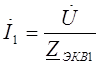

Эквивалентные сопротивления ветвей:

Запишем эквивалентные проводимости:
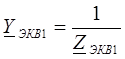 ;
; 
по первому закону Кирхгофа: 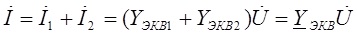
где 
 , где
, где 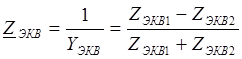
Треугольники проводимостей и токов
 алгебраическая форма
алгебраическая форма
G – действительная часть, активная составляющая
B – мнимая часть, реактивная составляющая.
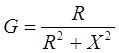 ;
; 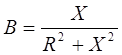
или 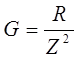 ;
; 
Треугольник тока
Резонанс токов
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
 Условие резонанса токов:
Условие резонанса токов: 
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви
Признаки резонанса токов:
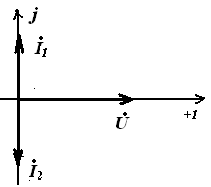
- Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
- Токи ветвей превышают общий ток цепи, который имеет минимальное значение;
 и
и  совпадают по фазе
совпадают по фазе
RLC – цепь Векторная диаграмма
LC – цепь Векторная диаграмма

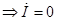
Резонансная частота
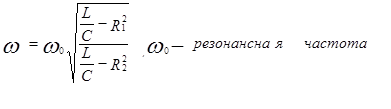 |
Случаи резонансных цепей
цепей
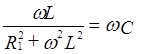 |
Если R2=0 резонанс наступит, при
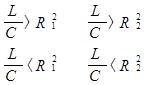 Случаи резонанса токов
Случаи резонанса токов
Случай 1. Один резонанс в цепи, при условии:
Случай 2. Два резонанса в цепи, при определенном соотношении сопротивлений элементов
 Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при
Случай 3. Нет резонанса в цепи – частота является величиной неопределенной, при
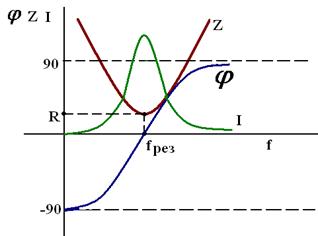
Частотные характеристики колебательного контура
Баланс мощностей в цепях переменного тока
 |
Коэффициент мощности
• Генератор или электрооборудование энергетически выгодно эксплуатировать, если оно совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р.
• Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование
λ=P/S=cosφ≤1
С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает .
Способы увеличения коэффициента мощности
• Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи.
• Генератор осуществляет только необратимые преобразования энергии и не участвует в колебательных процессах обмена энергией с электромагнитным полем приемников, в режиме максимальной мощности.
• Потребители электрической энергии в основном имеют схему замещения RL элемента, поэтому увеличение коэффициента мощности возможен с помощью компенсации реактивной мощности подключением емкостного элемента (QL—QС), подключение емкостного элемента снижает ток в линии электропередачи, что позволяет уменьшить сечение электропроводов, а это приводит к экономии электропроводящих материалов.
• Значение коэффициента мощности в энергосистемах зависит насколько грамотно эксплуатируется электротехнические установки и приборы.
• сosφ может снижаться, если установки работают в режиме холостого хода, или недогружены.
20. (?????)Резонанс напряжений. Условия резонанса. Добротность контура. Основные частотные характеристики.
Резонанс напряжений – явление, при котором цепь содержащая активные и реактивные сопротивления, будет только активное сопротивление (XL — XC = 0). При этом ток в цепи совпадает по фазе с напряжением. Условие возникновение резонанса напряжений – равенство нулю реактивного сопротивления.
Обычно наблюдается в цепях, содержащих катушку и конденсатор, включенные последовательно.



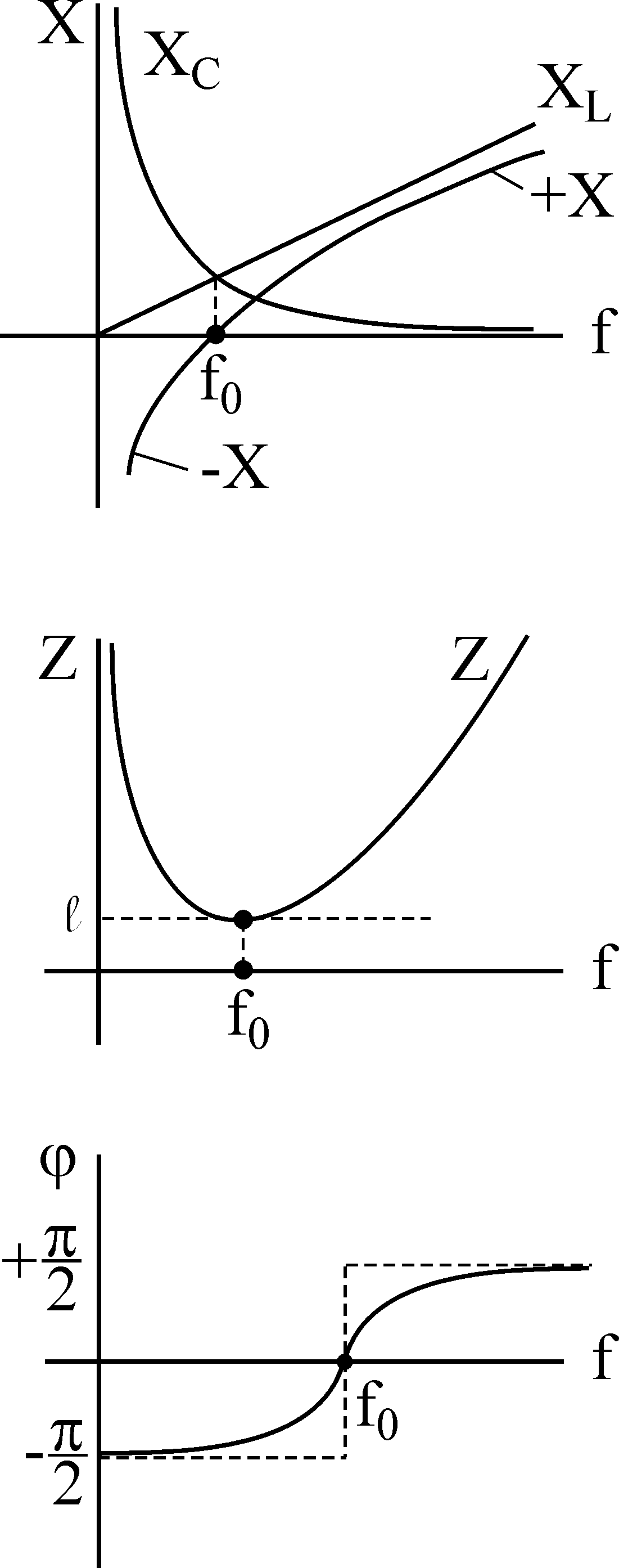






Таким образом:
 –резонансная
частота
–резонансная
частота
При резонансе напряжений ток максимален, так как сопротивление минимально, а
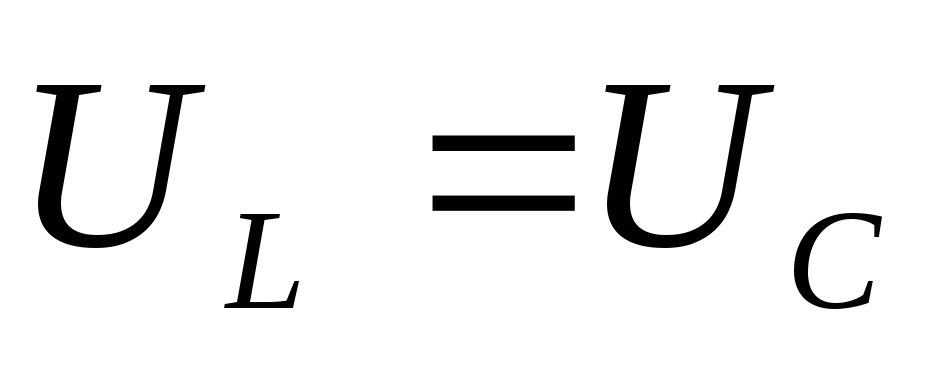
и
таким образом 
Часто для оценки цепи в режиме резонанса применяют такие характеристики как характеристическое сопротивление и добротность контура.
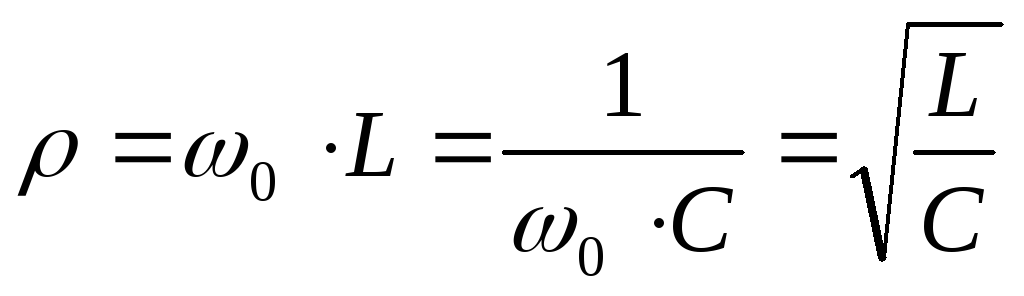 —
характеристическое сопротивление
контура. В простейшем случае это
сопротивление на одном из реактивных
элементов.
—
характеристическое сопротивление
контура. В простейшем случае это
сопротивление на одном из реактивных
элементов.
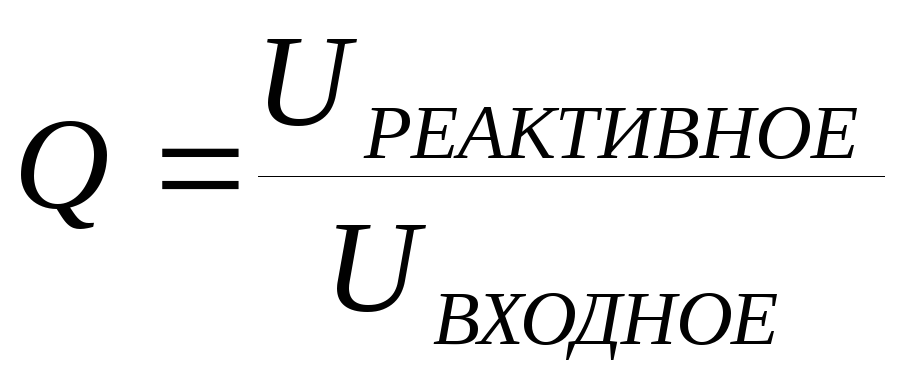
Добротностью контура называется отношение модуля реактивной составляющей напряжения в цепи к модулю входного напряжения в момент резонанса.
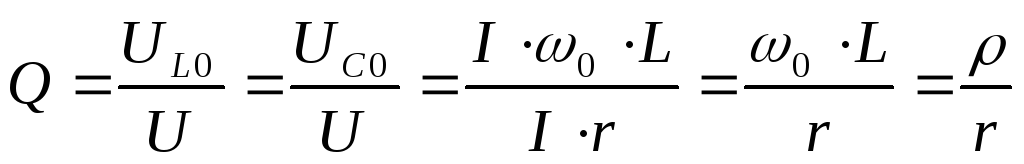
Зависимость от частоты параметров цепи называют частотными характеристиками
21. Резонанс напряжений. Основные частотные характеристики. Векторные диаграммы.
Ч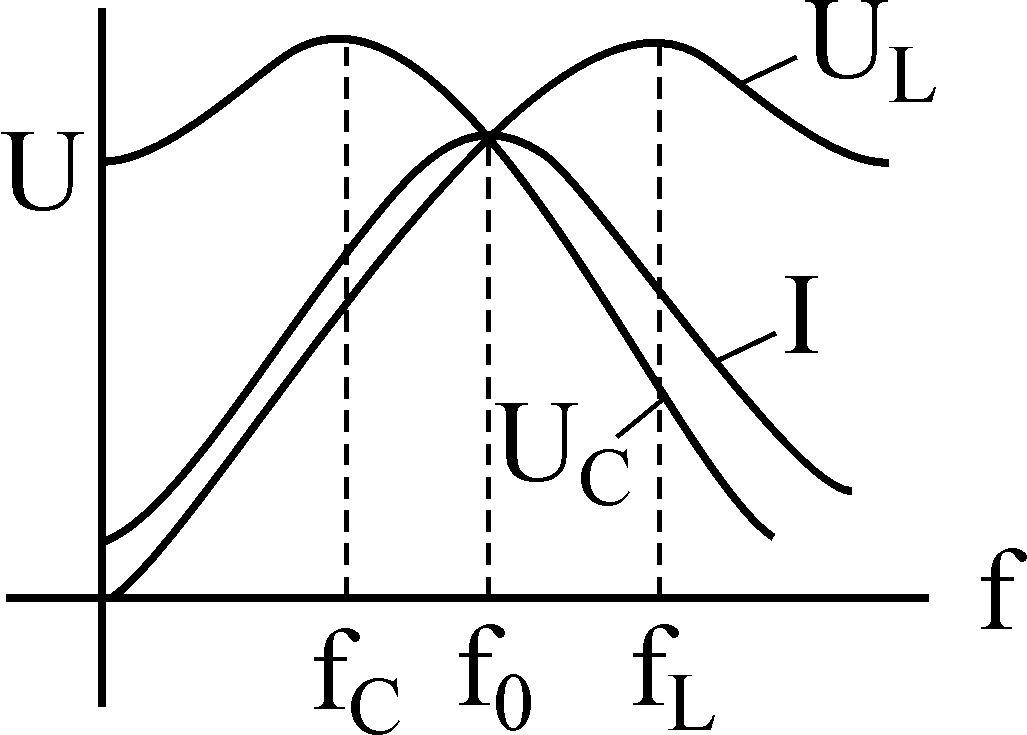 астотными
характеристиками называются зависимости
от частоты параметров, характеризующих
свойства цепи. Зависимости тока и
напряжения в цепи от частоты принято
называть резонансными кривыми.
астотными
характеристиками называются зависимости
от частоты параметров, характеризующих
свойства цепи. Зависимости тока и
напряжения в цепи от частоты принято
называть резонансными кривыми.
резонансная
частота — 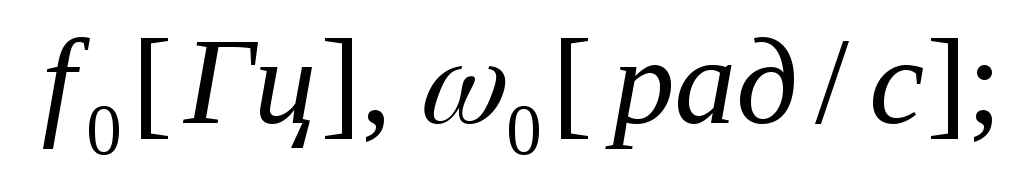
абсолютная
настройка по частоте — 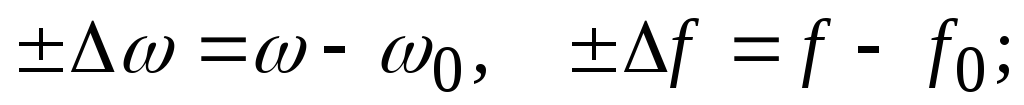
относительная
настройка — 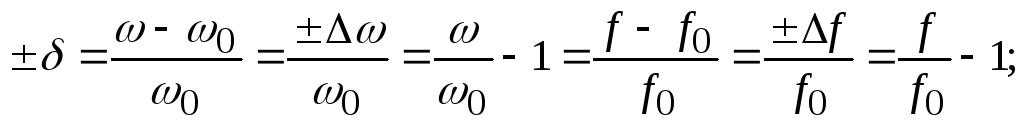
обобщенная
настройка (кси)
– 
(при
этом все настройки положительны, при
ff0,
отрицательны при f
f0,
при очень малых настройках (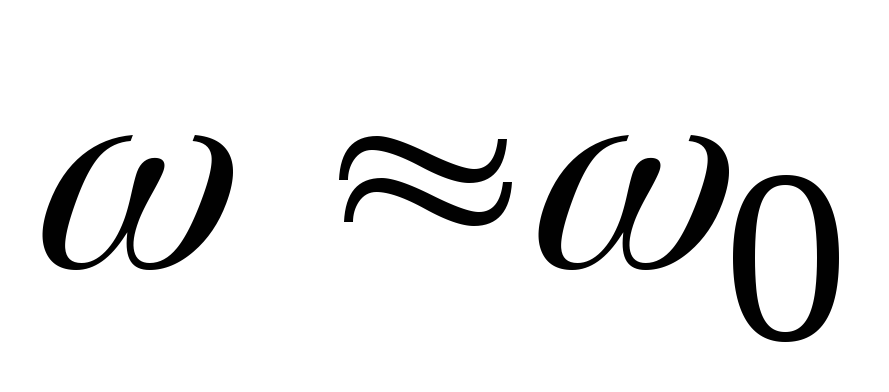 ),
),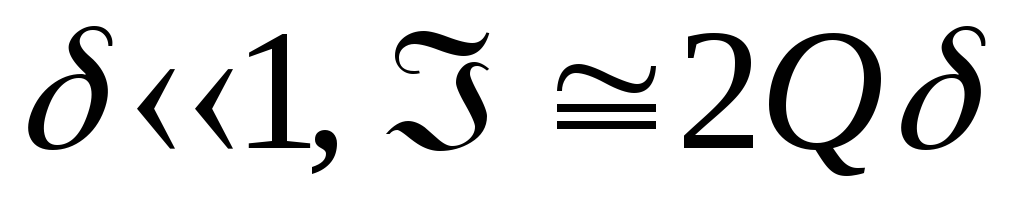 ).
).
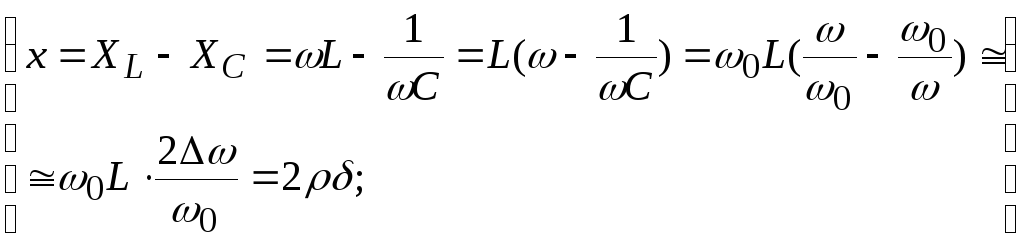
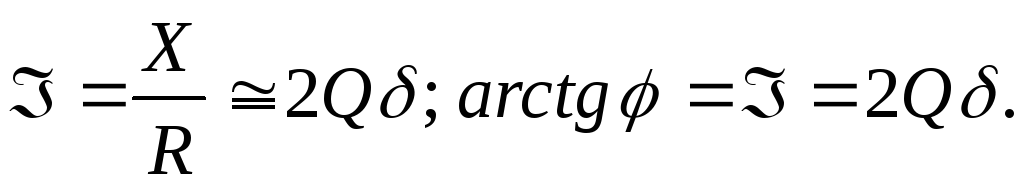
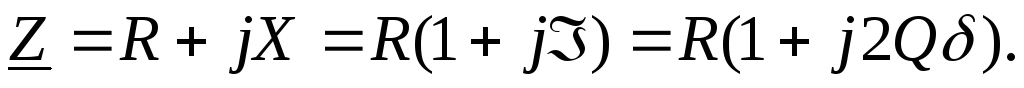
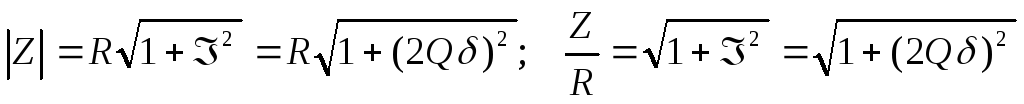
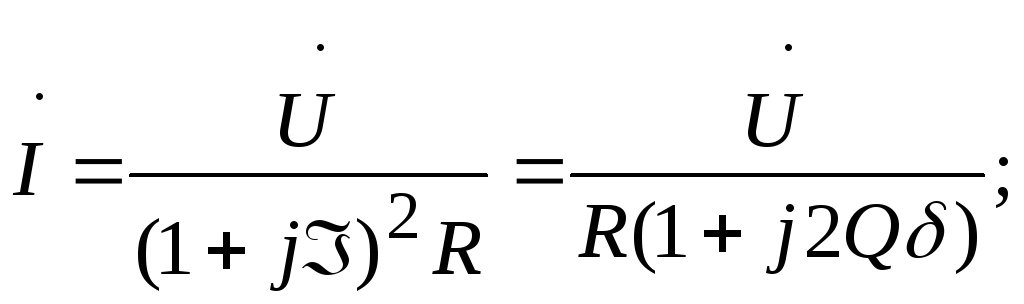
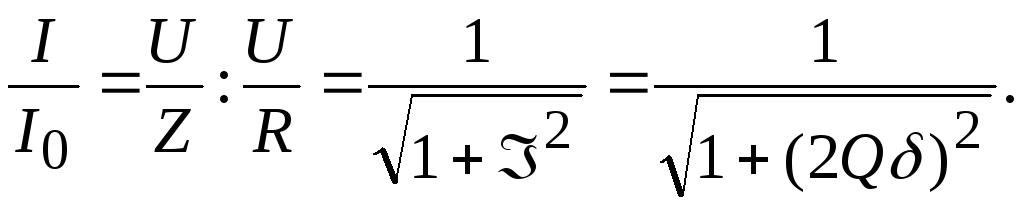
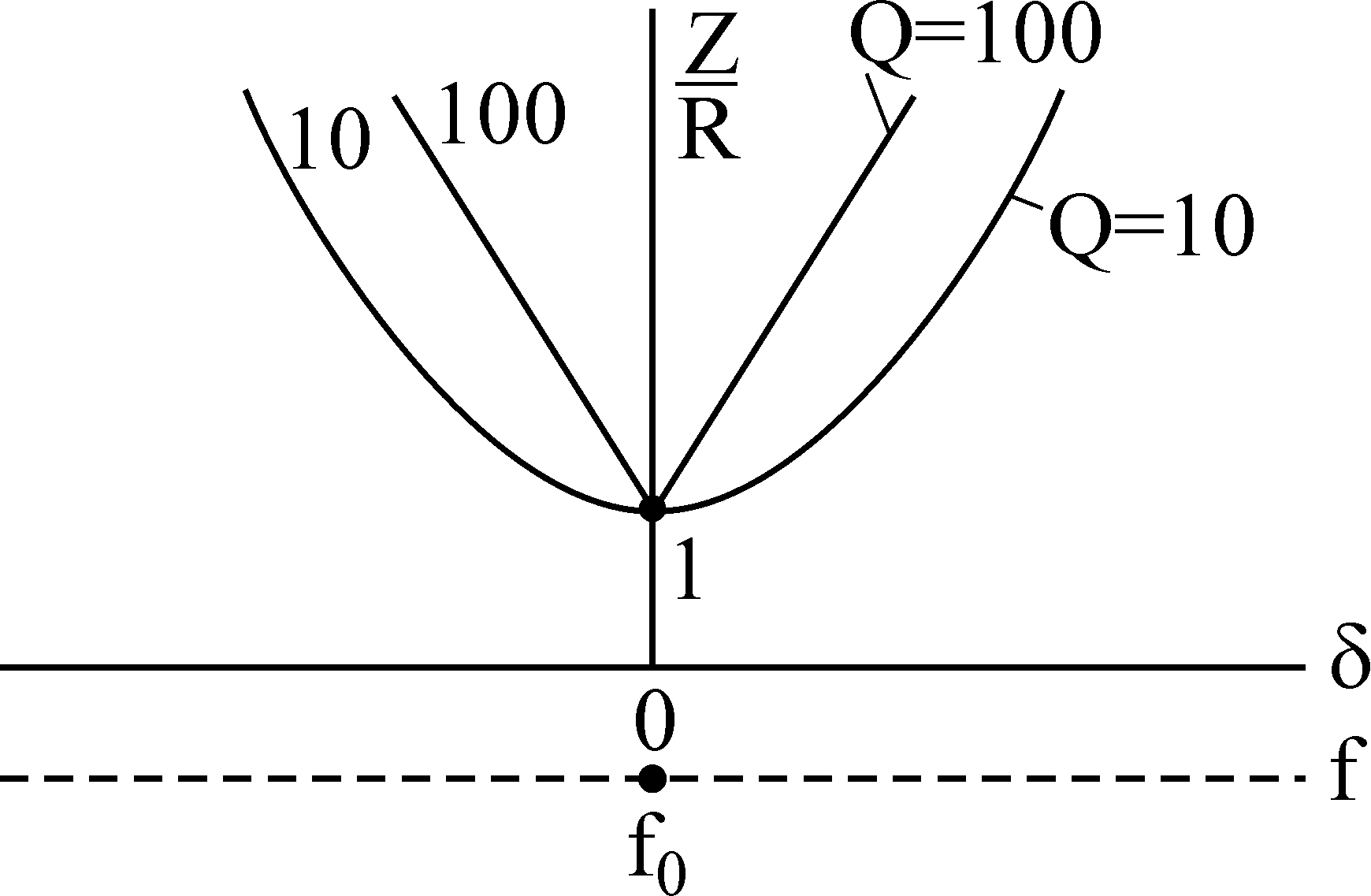
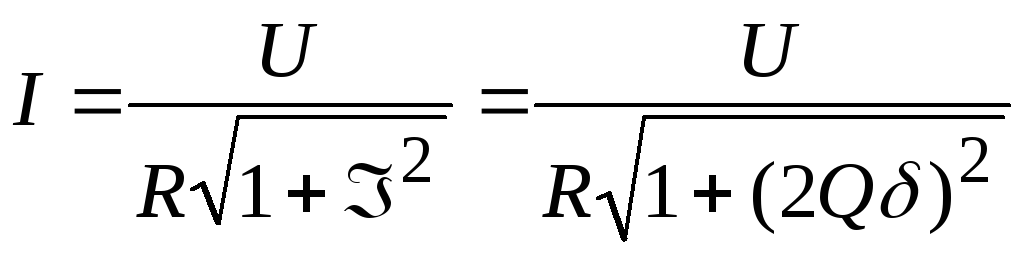
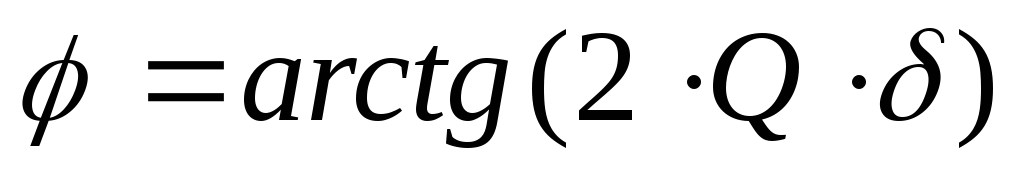
Теперь
можно построить характеристики I,
Z,
в зависимости от 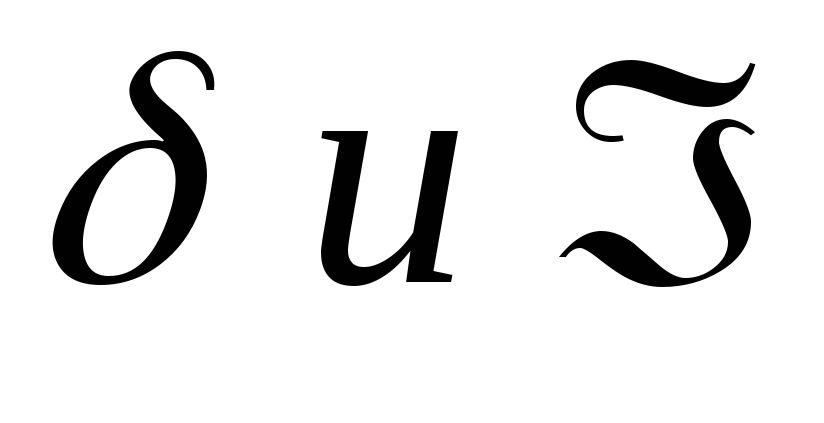 .
.
При
этом можно видеть, что зависимости от
относительной настройки  различаются
по величине добротности
различаются
по величине добротности
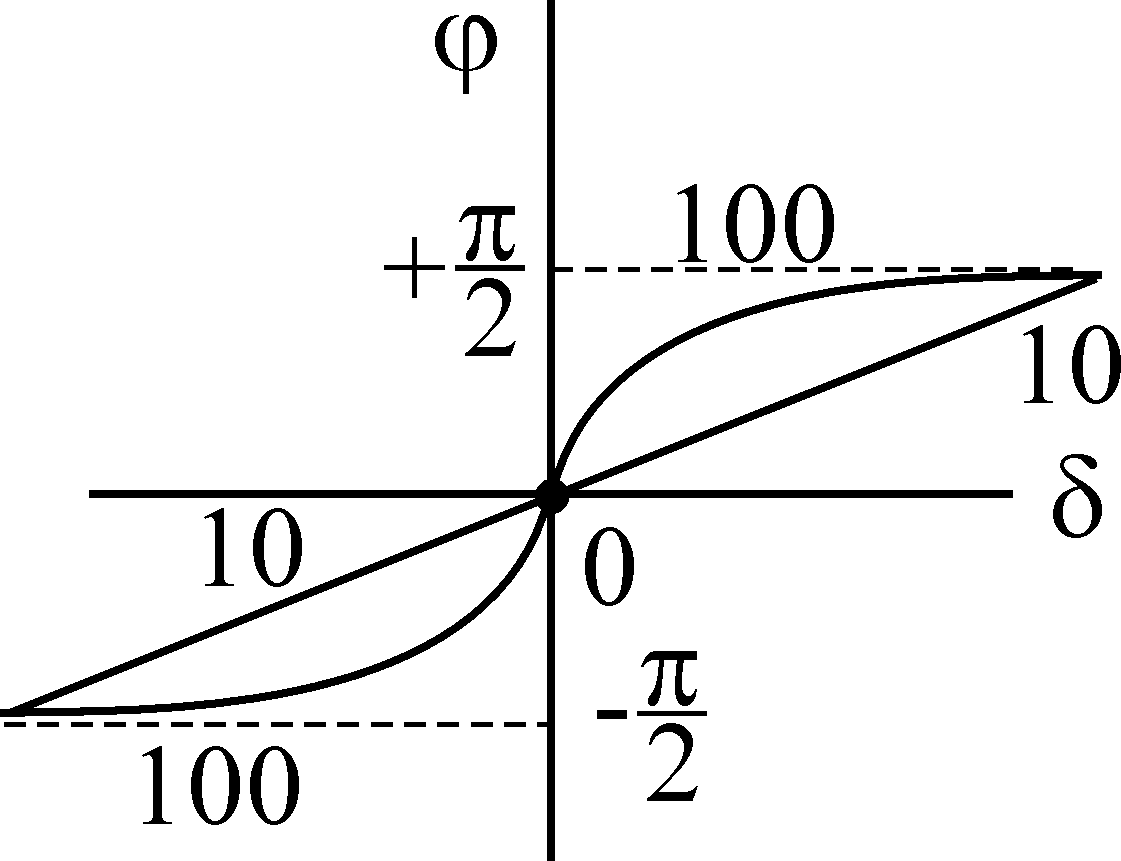
Q, а зависимости от обобщенной настройки одинаковы для всех контуров.
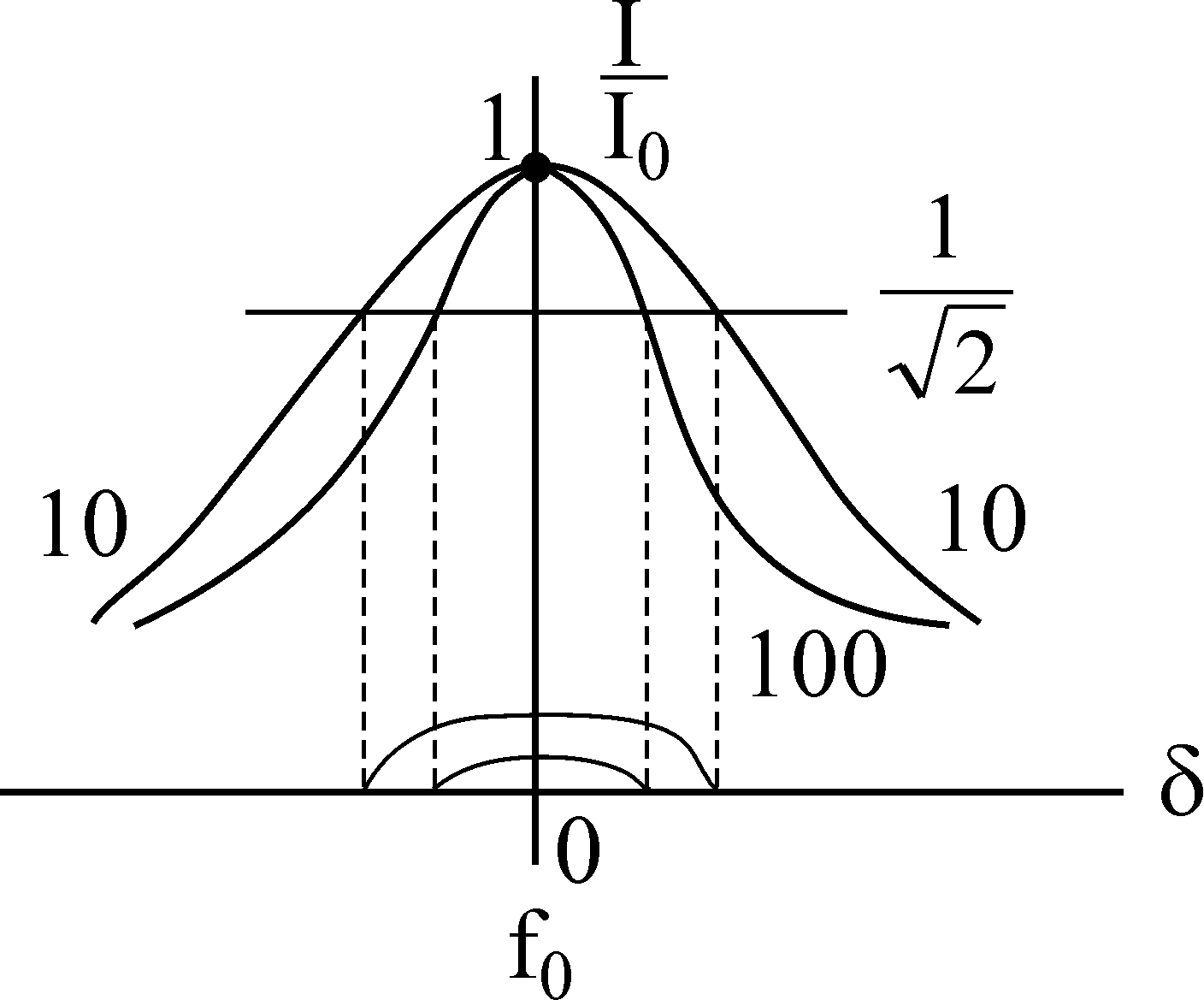
Полосу
частот вблизи резонанса, на границах
которой ток снижается до величины 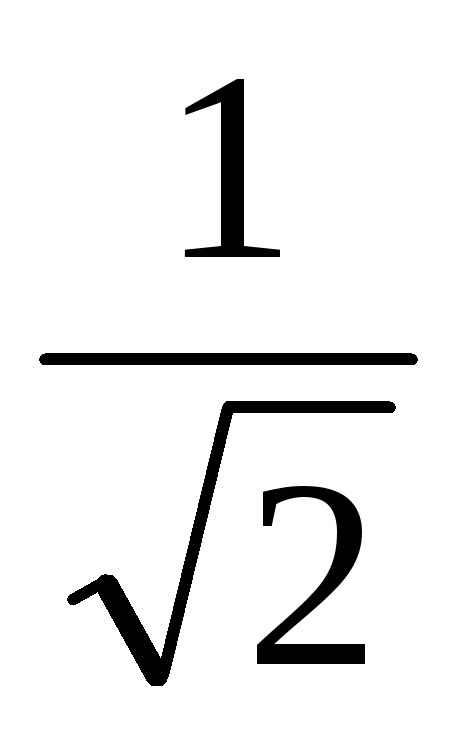 от
от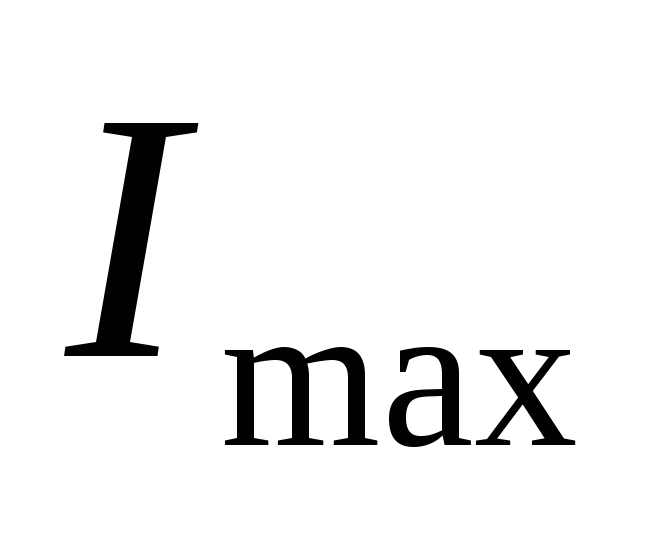 принято
называтьполосой
пропускания резонансного тока.
принято
называтьполосой
пропускания резонансного тока.
Чем больше добротность, тем острее кривая и уже полоса пропускания
Векторные
диаграммы при 
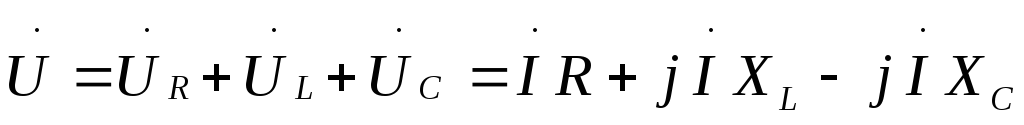

Если источник не идеален и имеет своё внутреннее сопротивление, то это сопротивление фактически добавляется к активному сопротивлению цепи и влияет на добротность и полосу пропускания контура. Чем больше внутреннее сопротивление источника, тем меньше добротность и шире полоса пропускания. Поэтому, с точки зрения сокращения полосы пропускания контура, выгоден источник с малым внутренним сопротивлением.
Если колебательный контур идеален и в нём нет активного сопротивления, то общее сопротивление контура приравнивается к 0, а ток в цепи и добротность возрастают до бесконечности. Однако в реальной цепи такого быть не может.
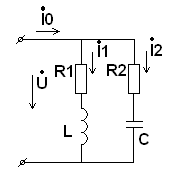
22.Условие резонанса токов
Резонанс токов наблюдается в цепях с параллельным включением L и C. Условием резонанса токов является равенство 0 реактивной проводимости цепи.
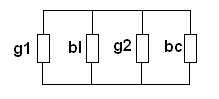
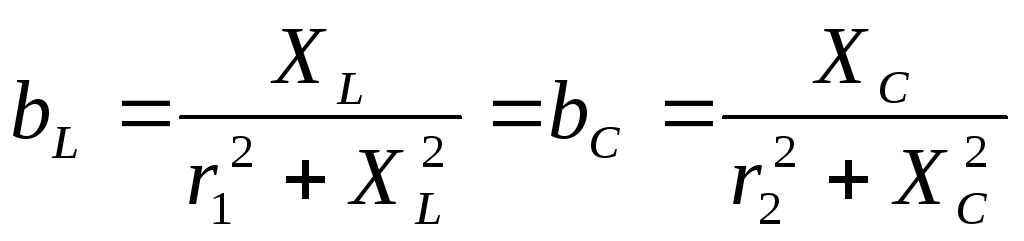
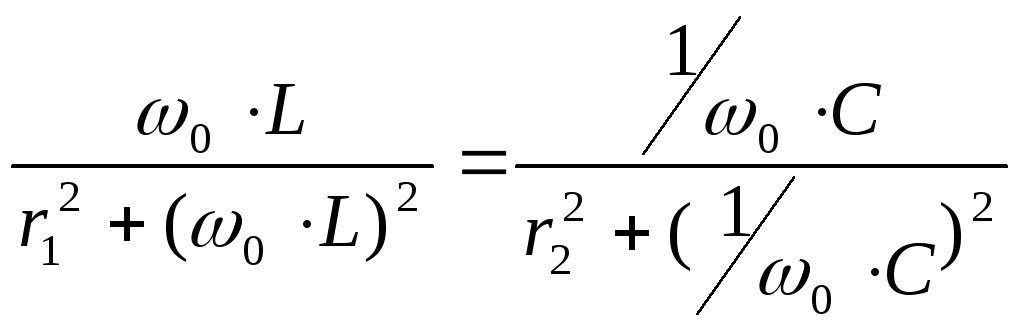
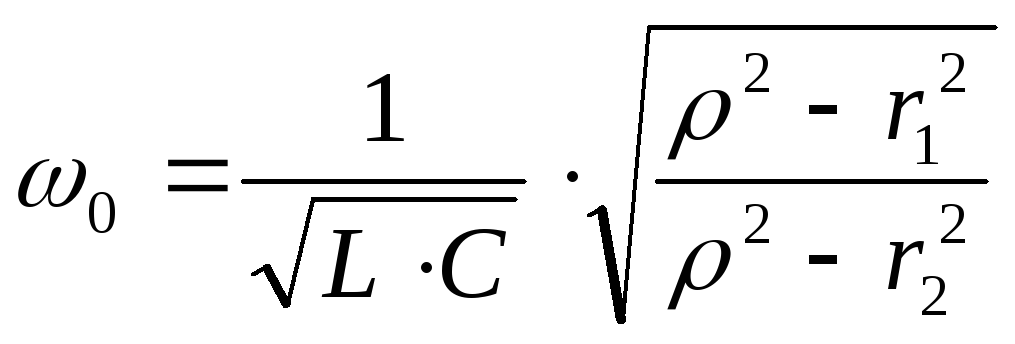
Это уравнения для более общего случая. Резонанс в таком контуре не всегда возможен. В идеализированном случае, когда активными свойствами катушки и конденсатора пренебрегают. Резонансная частота контура определяется формулой:
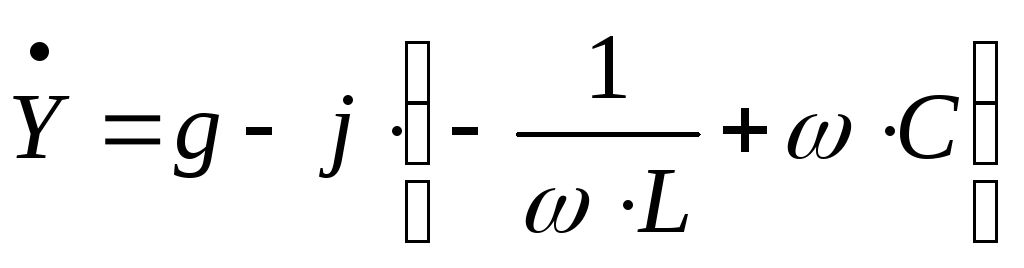 ,
, 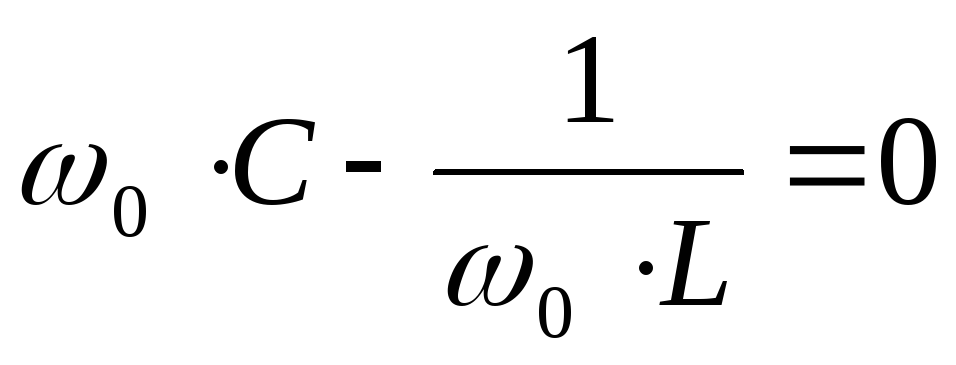 ,
,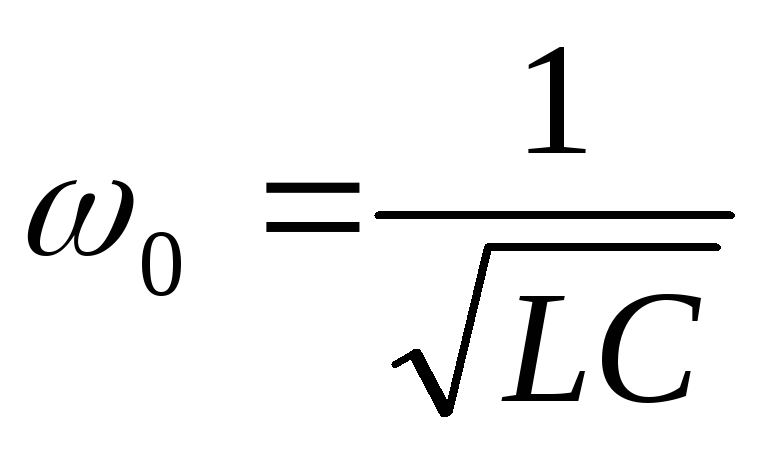 .
.
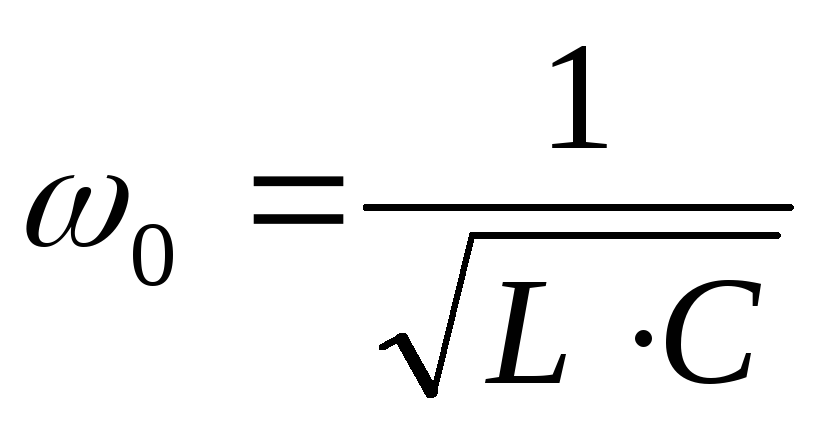
В момент резонанса ток достигает своего минимального значения и совпадает по фазе с напряжением.
Добротность – отношение модуля тока в реактивном элементе к модулю тока в неразветвлённой части схемы.
 ,
,
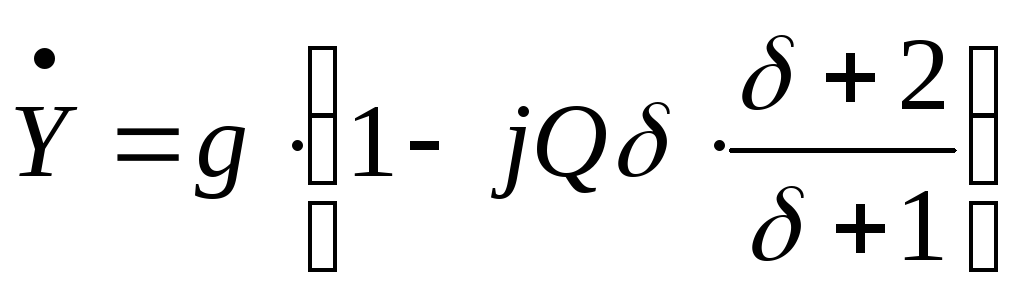 ,
, 

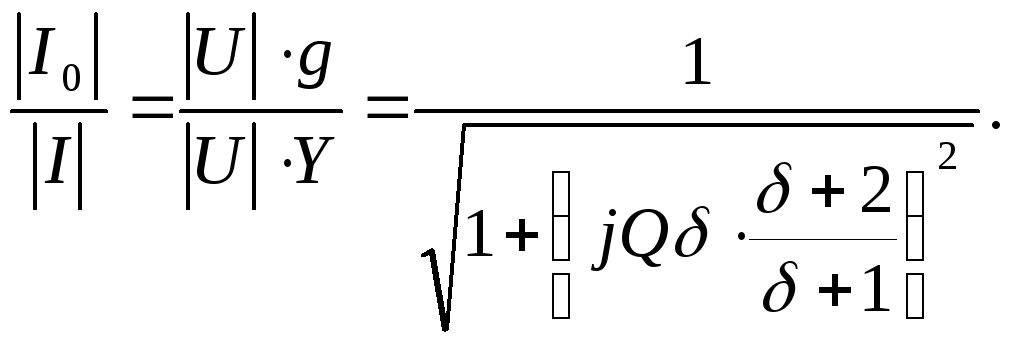

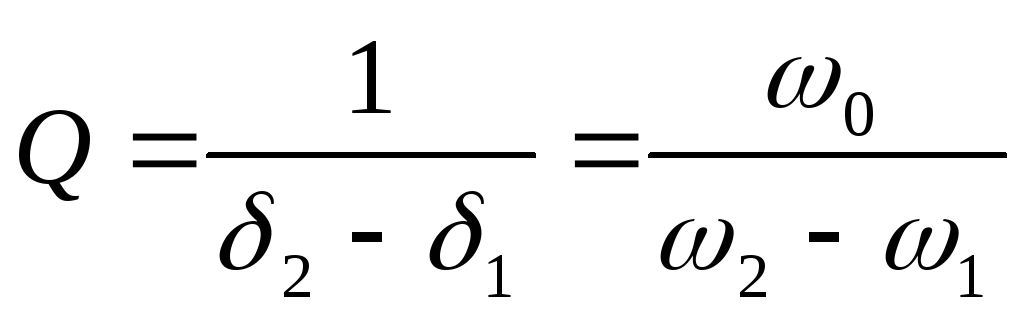
В отличие от последовательного колебательного контура с точки зрения сокращения полосы пропускания и колебательного контура выгоден источник тока с большим Ri.(внутренним сопротивлением источника), так как чем меньше Ri , присоединяемое к параллельному контуру, тем ниже добротность и шире полоса пропускания.
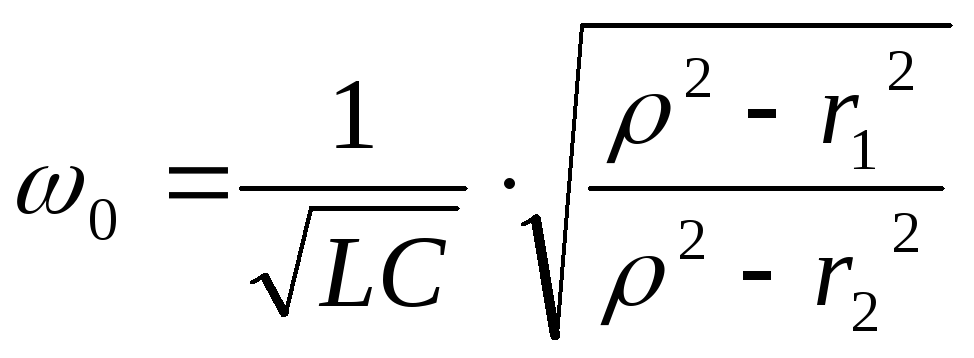
Анализируя полученную нами формулу для резонансной частоты резонанса тока, можно выделить 3 основных случая:
Есть резонанс если
 и
и одного знака
одного знакаБезразличный резонанс

Нет резонанса если
 и
и различного знака
различного знака
Диаграмма:
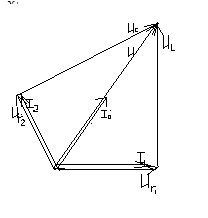
3.2. Резонанс токов
Резонанс токов – это явление в цепи с параллельным колебательным контуром, когда ток в неразветвленной части цепи совпадает по фазе с напряжением источника.
На рис. 12 представлена схема параллельного колебательного контура. Сопротивление R в индуктивной ветви обусловлено тепловыми потерями на активном сопротивлении катушки. Потерями в емкостной ветви можно пренебречь.
Условие резонанса токов: равенство нулю реактивной проводимости контура b=0.
Для выяснения признаков резонанса токов построим векторную диаграмму.
Для того чтобы ток I в неразветвленной части цепи совпадал по фазе с напряжением, реактивная составляющая тока индуктивной ветви ILp должна быть равна по модулю току емкостной ветви IC (рис. 12,б). Активная составляющая тока индуктивной ветви IL, оказывается равной току источника IC .
IC
а) б)
Рис. 12. Схема параллельного колебательного контура и векторная
диаграмма при резонансе токов
Признаки резонанса токов:
а)
сопротивление контура  максимальное и чисто активное;
максимальное и чисто активное;
б) ток в неразветвленной части цепи совпадает по фазе с напряжением источника и достигает практически минимального значения;
в) реактивная составляющая тока в катушке равна емкостному току, причем эти токи могут во много раз превышать ток источника.
Физически это объясняется тем, что при малых потерях в контуре (при малом R) ток источника требуется только для покрытия этих потерь. Ток в контуре обусловлен обменом энергией между катушкой и конденсатором. В идеальном случае (контур без потерь) ток источника отсутствует.
Критерием возникновения резонансного явления в цепи, содержащей индуктивные и емкостные элементы, является…
равенство нулю угла сдвига фаз φ между напряжением и током на входе цепи
равенство 90° угла сдвига фаз φ между напряжением и током на входе цепи
равенство 180° угла сдвига фаз φ между напряжением и током на входе цепи
равенство 270° угла сдвига фаз φ между напряжением и током на входе цепи
Режим резонанса напряжений может быть установлен в цепи…
К возникновению режима резонанса напряжений ведет выполнение условия…
Для случая, соответствующего приведенной векторной диаграмме, характер сопротивления пассивной электрической цепи…
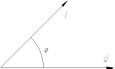
активно-емкостной
активно-индуктивный
активный
емкостной
Характер сопротивления пассивной электрической цепи для случая, соответствующего приведенной векторной диаграмме…
активно-емкостной

активно-индуктивный
активный
емкостной
Если
величина начальной фазы синусоидального
тока
,
а величина начальной фазы синусоидального
напряжения ,
то угол сдвига фаз
,
то угол сдвига фаз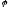 между напряжением и током составляет…
между напряжением и током составляет…
Полное
сопротивление Z
приведенной цепи при 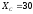 Ом
и
Ом
и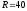 Ом
составляет…
Ом
составляет…
50 Ом

60 Ом
100 Ом
50 Гц
Вывод по третьему вопросу: в заключение необходимо отметить, что явление резонанса токов сложнее и многообразнее явления резонанса напряжений. Фактически был рассмотрен только частный случай радиотехнического резонанса. Резонансы токов и напряжений широко используются в радиотехнических цепях (установках автоматики, телемеханики, связи). Резонанс токов позволяет улучшить коэффициент мощности электроустановок промпредприятий.
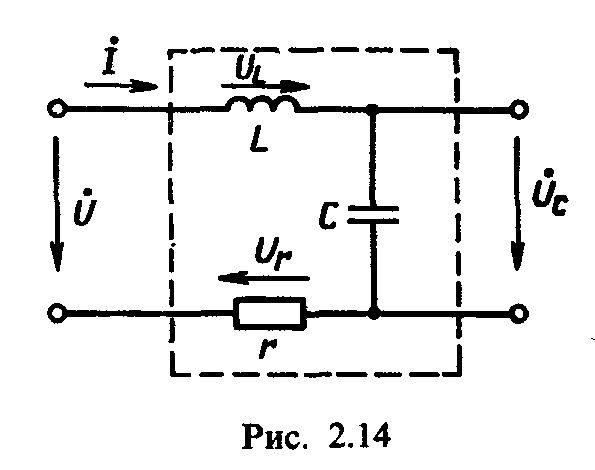
2.9. Последовательный колебательный контур. Резонанс напряжений
Последовательным колебательным контуром называют такую цепь, в которой катушка и конденсатор соединены последовательно относительно входных зажимов (рис. 2.14). В такой цепи можно наблюдать резонанс напряжений. При резонансе напряжений индуктивное и емкостное сопротивления взаимно компенсируются и в результате этого реактивные сопротивление и мощность цепи равны нулю.
При резонансе
напряжений, возникающем в цепи с
последовательным соединением индуктивных
и емкостных элементов, ток и напряжение
цепи совпадают по фазе. В этом случае
угол сдвига фаз между током и напряжением
равен нулю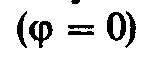 и
полное сопротивлениецепи равно ее
активному сопротивлению. Если
и
полное сопротивлениецепи равно ее
активному сопротивлению. Если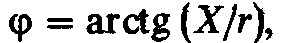 то угол
то угол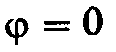 при
при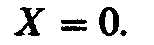
Следовательно,
при резонансе 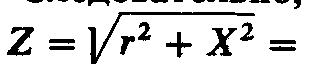
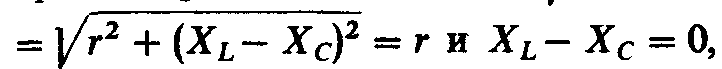 или
или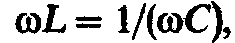 откуда угловая частота при резонансе
откуда угловая частота при резонансе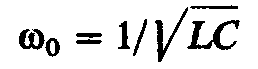 и резонансная частота
и резонансная частота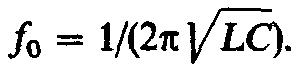
Таким образом,
основным условием возникновения
резонанса напряжений в цепи является
равенство реактивных сопротивлений  так как в этом случае частота колебательного
контура
так как в этом случае частота колебательного
контура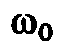 равна частоте сети ω, питающей данную
цепь.
равна частоте сети ω, питающей данную
цепь.
Итак, индуктивное и емкостное сопротивления при резонансе равны, т. е.
 (2.59)
(2.59)
так как 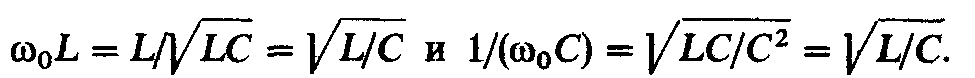
Величину ρ называют характеристическим сопротивлением контура.
Отношение напряжения на индуктивности или на емкости к напряжению, приложенному к цепи при резонансе, называют добротностью контура или коэффициентом резонанса:
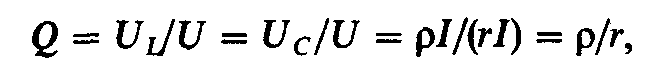 (2.60)
(2.60)
откуда 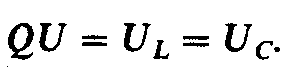
Коэффициент
резонанса показывает во сколько раз
напряжение на индуктивных или емкостных
элементах при резонансе больше, чем
напряжение, приложенное к цепи.
Добротностью контура называют также
отношение характеристического
сопротивления контура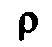 к
его активному сопротивлениюr.
Так как характеристическое сопротивление
обычно составляет в среднем сотни Ом,
а сопротивление r
— несколько Ом, то добротность
колебательных контуров, состоящих
из индуктивных катушек и конденсаторов,
находится в пределах 200-500.
к
его активному сопротивлениюr.
Так как характеристическое сопротивление
обычно составляет в среднем сотни Ом,
а сопротивление r
— несколько Ом, то добротность
колебательных контуров, состоящих
из индуктивных катушек и конденсаторов,
находится в пределах 200-500.
Величину, обратную добротности, называют затуханием контура:
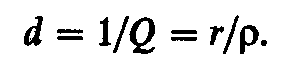 (2.61)
(2.61)
Сопротивление r в радиотехнических контурах является, как правило, собственным сопротивлением катушек и конденсаторов. Его иногда называют сопротивлением потерь контура.
Понятие «затухание контура» связано с тем, что при отключении колебательного контура от источника питания, когда контур накоротко замкнут, колебательный процесс затухает тем быстрее, чем больше коэффициент d.
Рассмотрим схему
рис. 2.14 без нагрузки (UC = UCхх).
Тогда 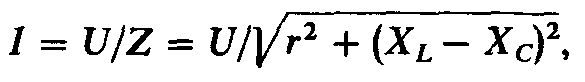
а ток при резонансе
напряжений 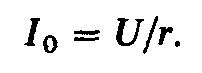 (2.62)
(2.62)
Ток при резонансе
напряжений значительно больше тока
цепи в отсутствие резонанса, так как
при резонансе его значение ограничено
только сопротивлением r.
При резонансе напряжение на индуктивности
и емкости при больших по сравнению с r
значениях  может быть во много раз больше напряжения
сети:
может быть во много раз больше напряжения
сети:
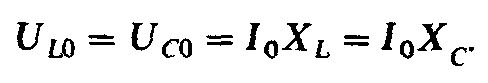
Напряжение на активном сопротивлении при резонансе равно напряжению, приложенному к цепи:

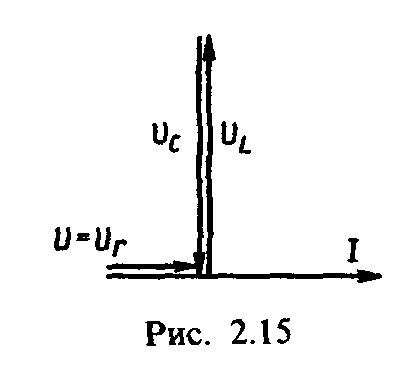
На рис. 2.15 представлена
векторная диаграмма напряжений цепи
рис. 2.14 при резонансе напряжений. Так
как при резонансе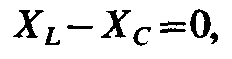 то в этом случае и
то в этом случае и 
Рассмотрим
энергетические процессы, наблюдаемые
в данной цепи при резонансе напряжений.
Для этого определим сумму мгновенных
значений энергий магнитного и
электрического полей цепи, т. е. 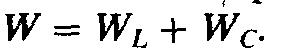 Если принять при резонансе ток
в контуре
Если принять при резонансе ток
в контуре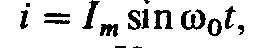 то напряжение на емкости
то напряжение на емкости
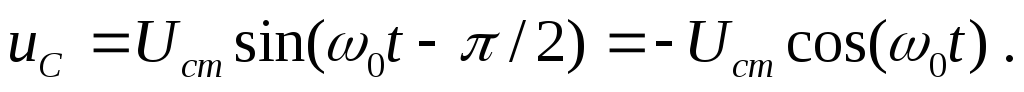
Тогда суммарная энергия
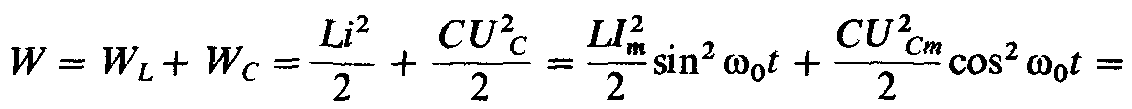
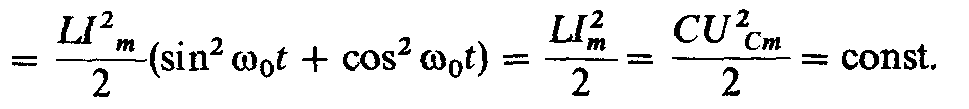 (2.63)
(2.63)
Следовательно, при резонансе напряжений суммарная энергия магнитного и электрического полей остается постоянной, при этом непрерывно происходит перераспределение энергии магнитного и электрического полей, т. е. увеличение энергии магнитного поля сопровождается уменьшением энергии электрического поля и наоборот.
Таким образом, энергия, первоначально запасенная в контуре от источника (сети), колеблется при резонансе между индуктивностью и емкостью, причем без участия в этом процессе источника. Поэтому такой контур называют колебательным.
Итак, при резонансе на долю источника остается лишь покрытие расхода энергии в активном сопротивлении; следовательно, полная мощность равна активной мощности
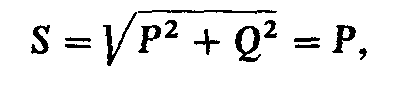
так как реактивная мощность при резонансе равна нулю:
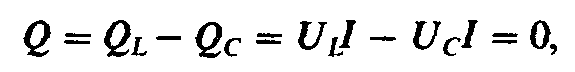 где
где 
Коэффициент мощности при резонансе
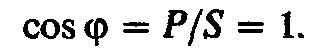
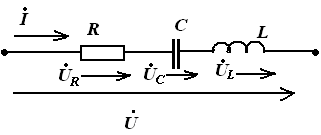
Вопрос 3. В чем заключается явление резонанса напряжений и при каких условиях оно возникает?
Ответ
3.1: В данной
цепи при равенстве индуктивного 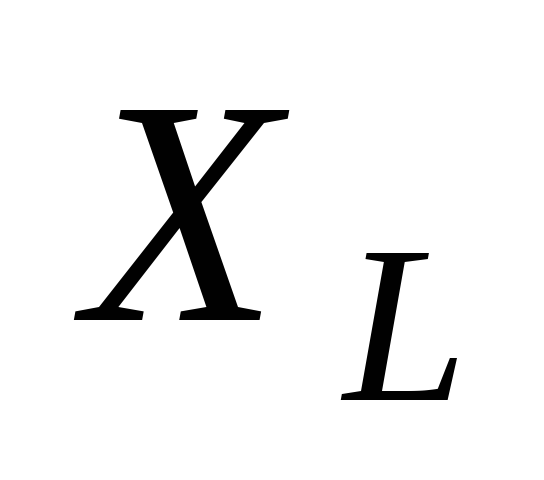 и емкостного
и емкостного 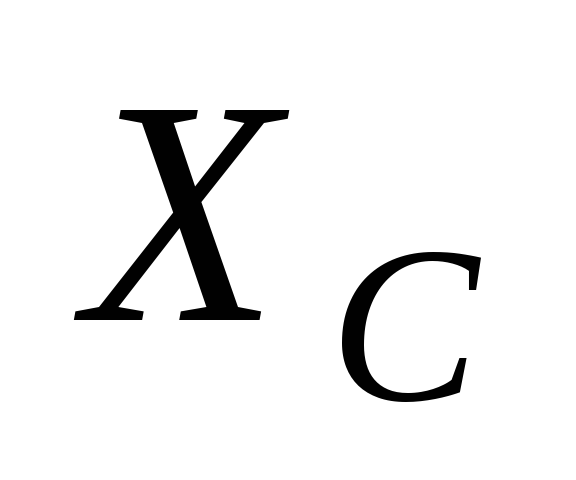 сопротивлений
сопротивлений 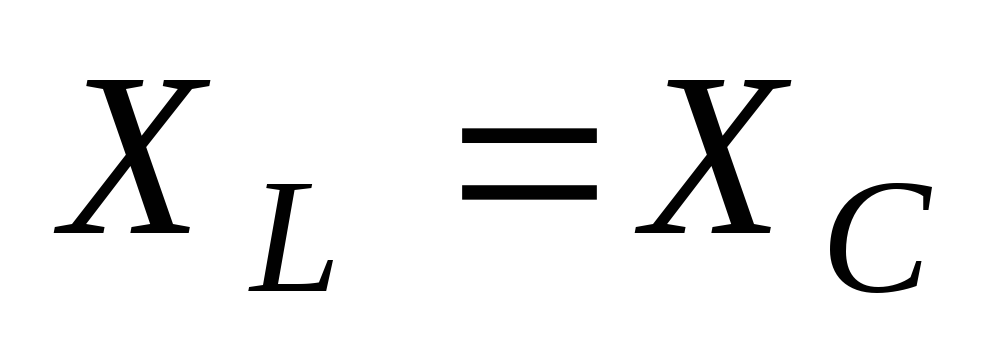 полное сопротивление
полное сопротивление  цепи будет минимальным и чисто активным Z=R,
а ток – максимальным
цепи будет минимальным и чисто активным Z=R,
а ток – максимальным  .
.
Падения
напряжения на индуктивном и емкостном
элементах рассчитываются по закону
Ома:  ,
, 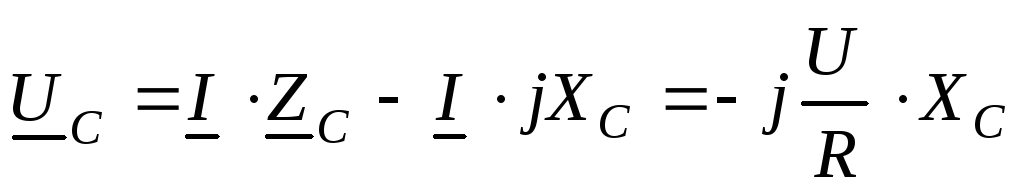 и т.к.
и т.к.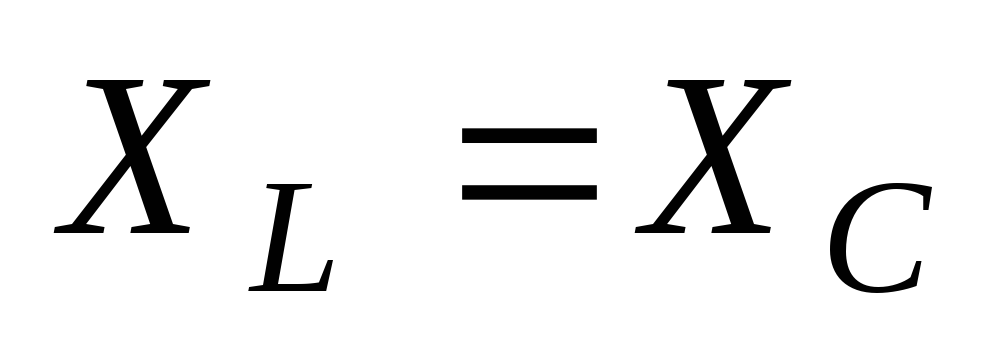 величина
напряжения на идеальной индуктивности ULравнанапряжению
на емкости UC.
величина
напряжения на идеальной индуктивности ULравнанапряжению
на емкости UC. 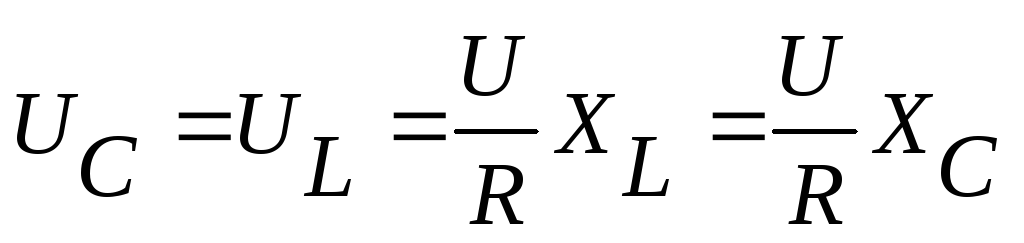 ,
но фазы напряженийULи UC противоположны
(сдвинуты на 180°).
,
но фазы напряженийULи UC противоположны
(сдвинуты на 180°).
Режим
работы цепи c
последовательным соединением R,L,C
элементов при котором 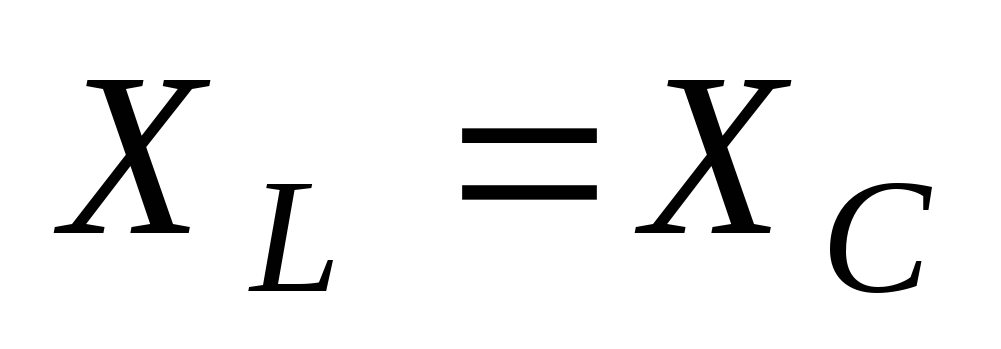 и
и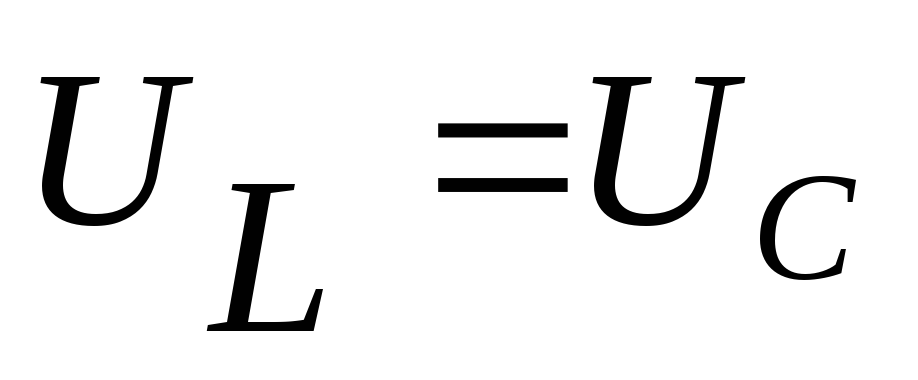 (или
(или 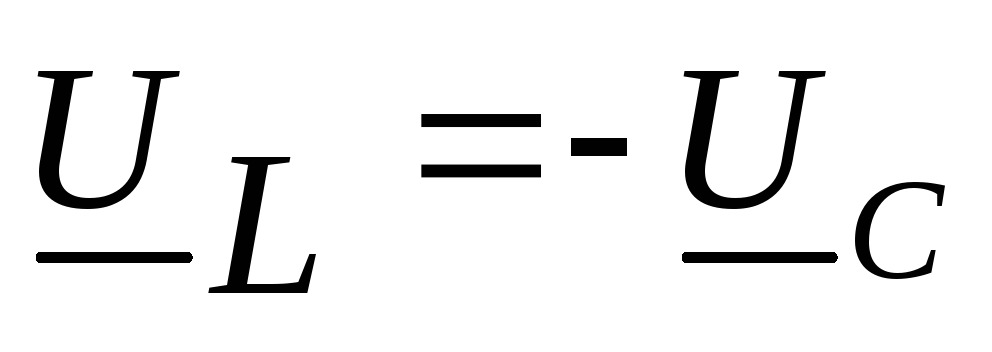 )называют резонансом
напряжений.
)называют резонансом
напряжений.
Сумма
комплексов напряжений ŪLи ŪC равна нулю,
следовательно и модуль суммы будет
равен нулю. Вольтметр, измеряющий падение
напряжения (модуль
комплекса напряжения) на участке цепи с идеальной индуктивностью
и емкостью, покажет значение =0. При этом
ток 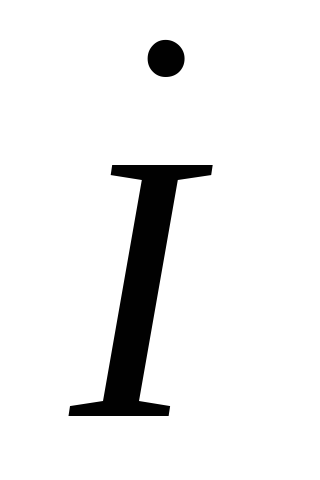 и напряжение
и напряжение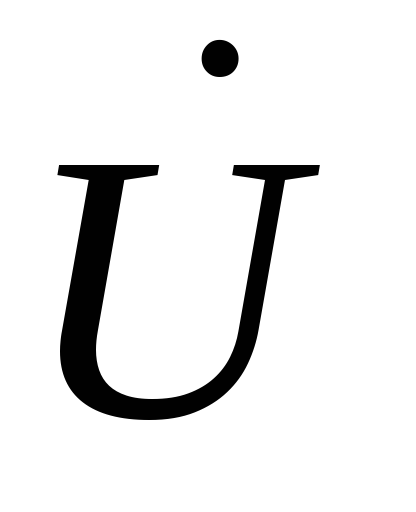 ВХ совпадает по фазе (коэффициент мощности
ВХ совпадает по фазе (коэффициент мощности  ,φ0 =0). Активная
мощность
,φ0 =0). Активная
мощность 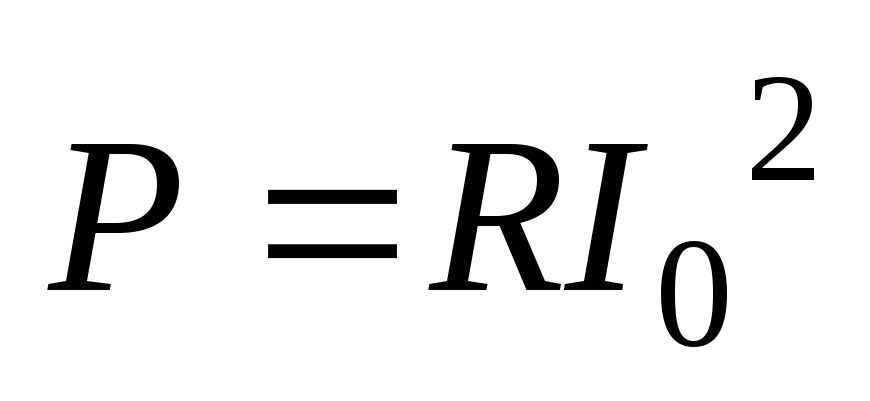 имеет наибольшее значение, равное полной
мощностиS,
в то время как реактивная мощность цепи
оказывается равной нулю:
имеет наибольшее значение, равное полной
мощностиS,
в то время как реактивная мощность цепи
оказывается равной нулю: 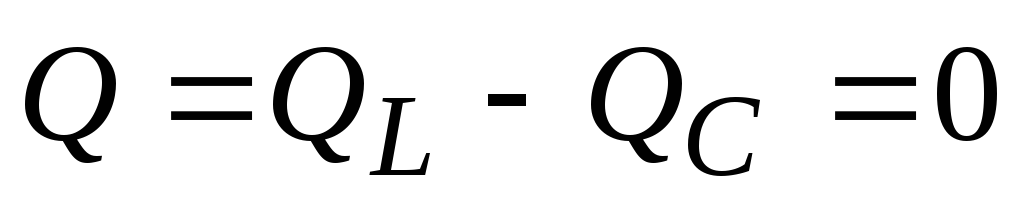 .
.
При
резонансе напряжения на емкости и на
индуктивности могут значительно
превышать подводимое напряжение U,
если 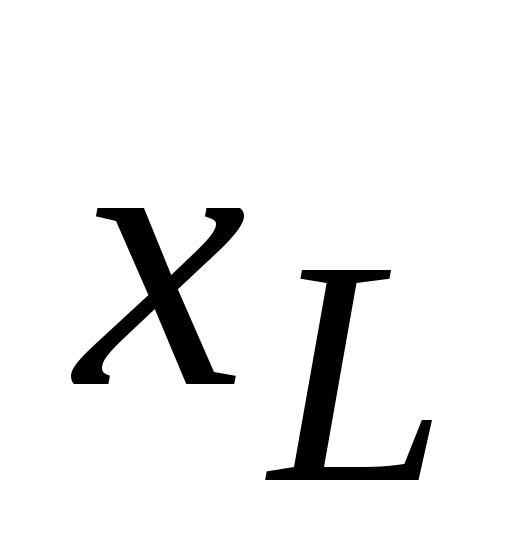 и
и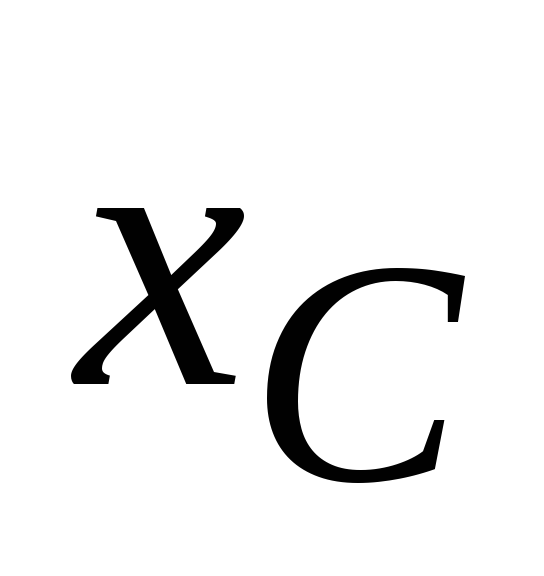 значительно
превышают R:
значительно
превышают R:
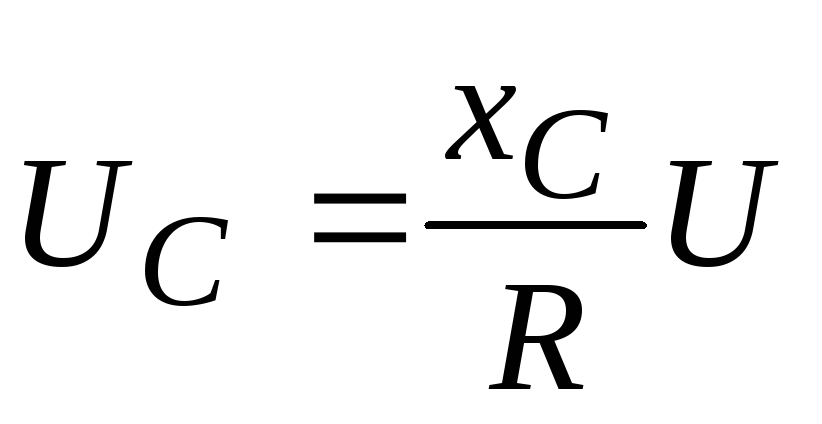 ,
, 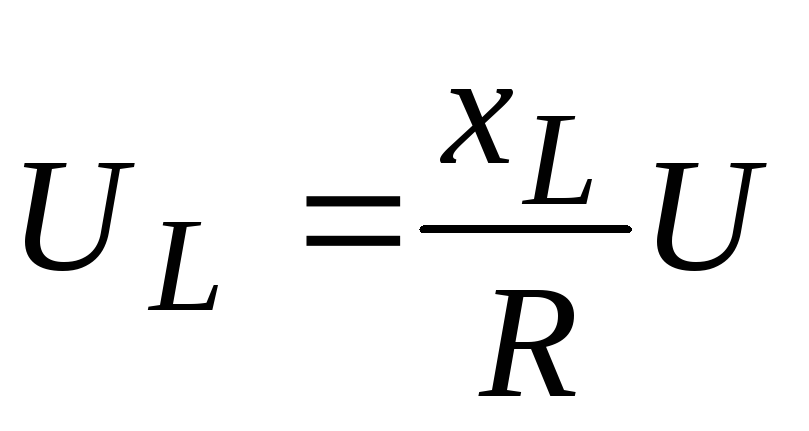 .
.
Физическая причина возникновения повышенных напряжений – это колебания значительной энергии, запасаемой попеременно в электрическом поле емкостного и магнитном поле индуктивного элементов. При резонансе напряжений малые количества энергии, поступающей от источника и компенсирующие потери энергии в активном элементе – сопротивлении R, достаточны для поддержания незатухающих колебаний в системе относительно больших количеств энергии электрического и магнитного полей. Причем в любой момент времени суммарная энергия электрического и магнитного полей остается постоянной.
Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции.
**) Для мощных двигателей отношение сопротивлений обмоток XL/R на промышленной частоте составляет несколько десятков. Напряжение питания двигателей обычно <380В. Поэтому в случае резонанса, напряжение на обмотке UL превысит напряжение питания в деcятки раз (UL>>3800В).
В тоже время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике в различных приборах и устройствах, основанных на резонансных явлениях.
Вопрос 4. Изменением каких параметров электрической цепи (см. Рис.1) можно получить резонанс напряжений ?
Ответ 4: При резонансе напряжений выравниваются реактивные сопротивления ХL=XC.
Т.к. ХL=ω·L , а XC=1/ωС , то равенства сопротивлений можно добиться тремя способами:
при постоянных ω и L изменяя величину емкости С;
при постоянных ω и С изменяя величину индуктивности L;
при постоянных L и С изменяя частоту ω. При резонансе
 .
.
Вопрос 5. С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений в электрической цепи?
Ответ
5: 1) В данной
лабораторной установке опыты проводятся
при постоянных величинах ω и L.
По мере увеличения емкости от минимального
до резонансного значения С0=1/ωXL,
полное сопротивление цепи  будет уменьшаться, при этом ток в цепи
согласно формуле для тока
будет уменьшаться, при этом ток в цепи
согласно формуле для тока 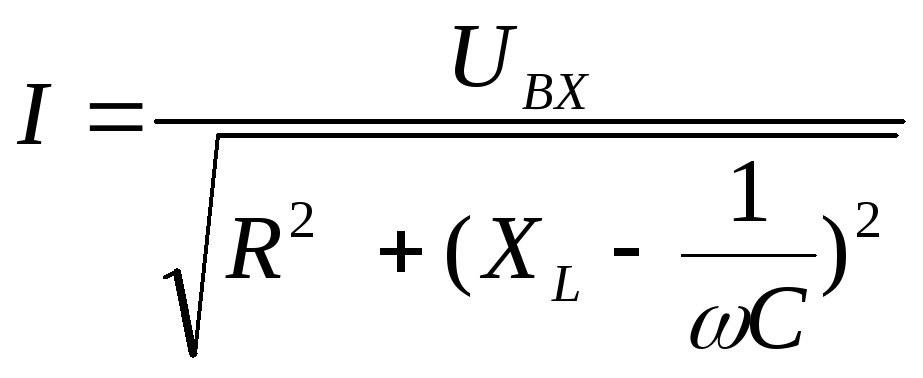 будет расти. При резонансе он достигнет
максимального значения
будет расти. При резонансе он достигнет
максимального значения 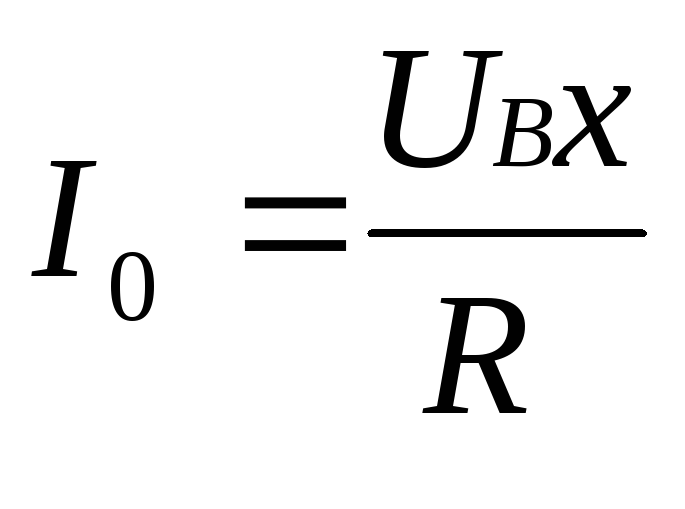 .
.
Вывод 1
1: Амперметр покажет максимальное значение тока.
2) Т.к. UL=I·XL, топадение напряжения на индуктивности UL будет расти пропорционально росту тока. При резонансе напряжений, это напряжение будет максимальным. Однако вольтметр PVК измеряет, согласно схеме замещения, падение напряжения на участке цепи из 2-х последовательно соединенных элементов: сопротивлений катушки R и индуктивности ХL. Падение напряжения на сопротивлении Rравно UR= I·R=Uвх, следовательнопри резонансе это напряжение также будет максимальным.
Вывод 2:
1)Вольтметр
PVК также
покажет максимальное значение 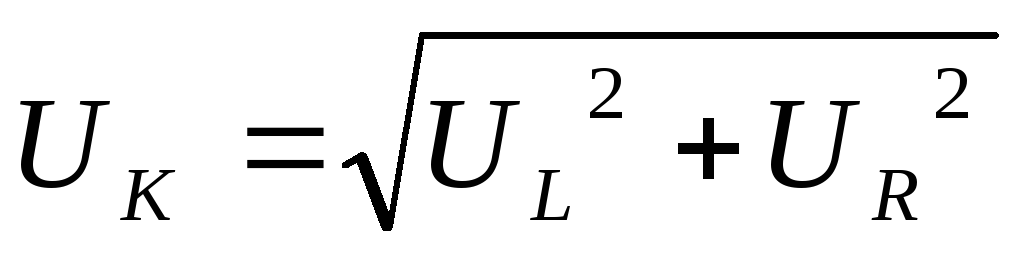
2)Падение
напряжения на емкости С, измеряемое
вольтметром PVC, равно: 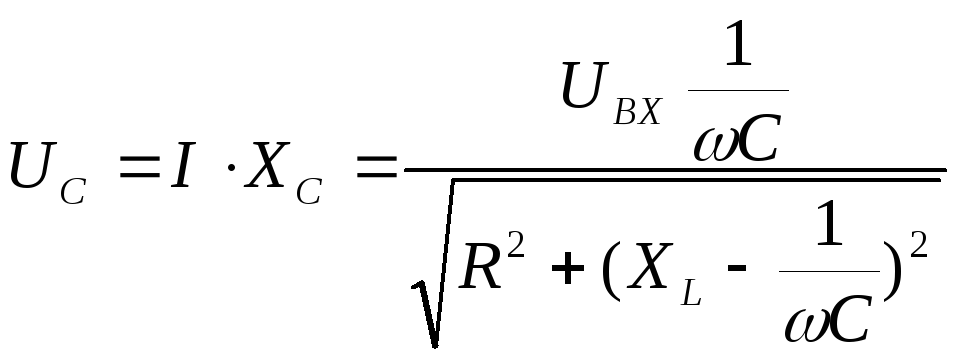 .
.
Т.к
. ток в цепи один , а величины сопротивлений
ХL,
XC при резонансе одинаковы, то и напряжения
одинаковы UL =UС.
При этом Uвх
= UR. При резонансе 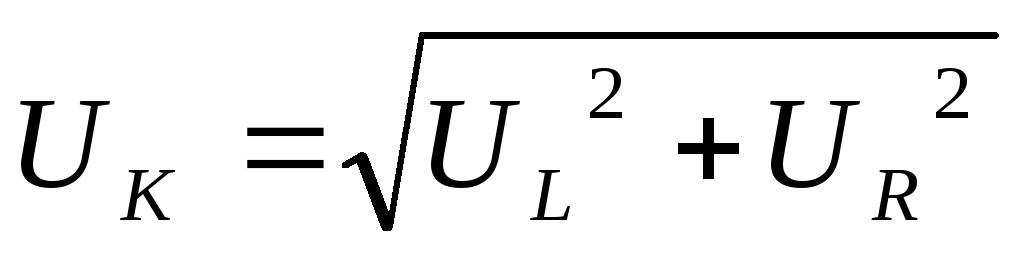 =
=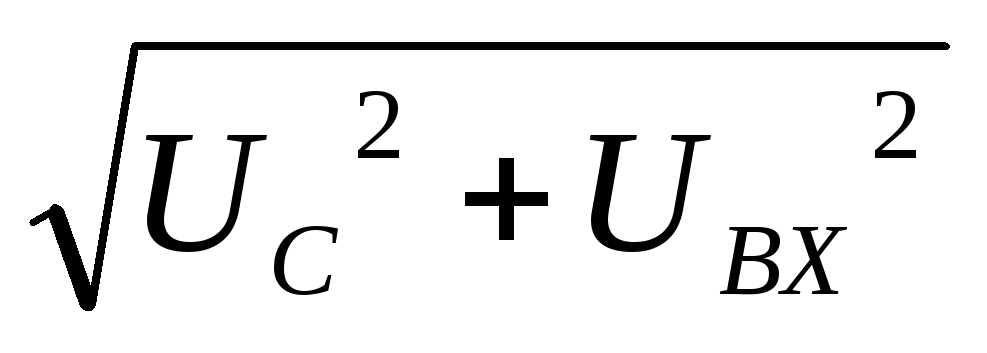 .Следовательно
показания вольтметров PVК и PVCбудут
разными. Очевидно, что UК > UC.
.Следовательно
показания вольтметров PVК и PVCбудут
разными. Очевидно, что UК > UC.
Вывод 3: при резонансе показания вольтметра PVК больше показания вольтметра PVC .
4) Ваттметр PW измеряет активную мощность потребляемую цепью. Т.к. при резонансе ток максимальный, а активная мощность Р = I2·R, то и мощность P будет максимальной.
Вывод 4: Ваттметр покажет максимальное значение Рмакс = I02·R= U2вх / R.
Контрольные вопросы
1. Записать выражение закона Ома для цепи с последовательным соединением конденсатора и индуктивной катушки. Чему равны полное сопротивление цепи и коэффициент мощности cos ?
I=U/Z
Коэффициент мощности cosφ при резонансе напряжений равен единице.
Cosφ=P/s= UR/U
2. Условие, признак и применение резонанса напряжений. В каком случае резонанс напряжений вреден? Почему?
Режим, при котором в цепи с последовательным соединением индуктивного и емкостного элемента напряжение на входе совпадает по фазе с током, резонанс напряжения.
внезапное возникновение резонансного режима в цепях большой мощности может вызывать аварийные ситуацию, привести к пробою изоляции проводов и кабелей и создать опасность для персонала.
3. Какими способами можно достичь резонанса напряжений?
При подключении колебательного контура, состоящего из катушки индуктивности и конденсатора, к источнику энергии могут возникнуть резонансное явление. Возможны два основных типа резонанса: при последовательном соединение катушки и конденсатора- резонанс напряжений, при их параллельном соединении- резонансов токов.
4. Почему при резонансе напряжений U2>U1?
Где R – активное сопротивление
I – сила тока
XL – индуктивное сопротивление катушки
XC – емкостное сопротивление конденсатора
Z – полное сопротивление переменного тока
При резонансе: UL = UС,
Где UС – напряжение катушки,
UL – напряжение конденсатора
Напряжение можно найти:
U=UR+UL+UC =>U=UR,
Где UR – напряжение катушки, к которой подключен вольтметр V2, значит напряжение V2=V1
5. Какова особенность резонанса напряжений? Объяснить ее.
Следовательно, режим резонанса может быть достигнут изменением индуктивности катушки L, емкости конденсата С или частоты входного напряжения ω.
6. Записать выражение закона Ома через проводимости для цепи с параллельным соединением конденсатора и индуктивной катушки. Чему равна полная проводимость?
Закон Ома через проводимости для цепи переменного тока с параллельным соединение ветвей.
7. Условие, признак и применение резонанса токов.
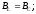
т.е равенство индуктивной и емкостной проводимостей.
8. Какими способами можно достичь резонанса токов?
Режим, при котором в цепи, содержащей параллельное ветви с индуктивным и емкостным элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением , резонансом токов.
9. Почему при резонансе токов I2>I1?
Потому что, исходя из векторной диаграммы токов при резонансе график будет представлять собой прямоугольный треугольник, где токи I и I1 будут являться катетами, а ток I2 – гипотенузой. Следовательно, и I2 будет больше чем I1.
10. Какова особенность резонанса токов? Объяснить ее.
При резонансе токов токи в ветвях значительно больше тока неразветвленной части цепи. Это свойство-усилие тока- является важнейшей особенностью резонанса токов.
11. Объяснить построение векторных диаграмм.
Целью ее построения является определение активной и реактивной составляющих напряжения на катушке и угла сдвига фаз между напряжением на входе цепи и током
Расчеты
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — B 3-х кн.: кн.1 /В. Г. Герасимов и др.; Под ред. В. Г. Герасимова. М.: Энергоатомиздат, 1996. – 288 с.
Касаткин А. С., Немцов М. В. Электротехника. М.: Высш. шк., 1999. – 542 с.
Электротехника /Под ред. Ю. Л. Хотунцева. М.: АГАР, 1998. – 332с.
Борисов Ю. М., Липатов Д. Н., Зорин Ю. Н. Электротехника. Энергоатомиздат, 1985. – 550 с.
ГОСТ 19880-74. Электротехника. Основные понятия. Термины и определения. М.: Издательство стандартов, 1974.
ГОСТ 2.710-81 ЕСКД. Обозначения буквенно-цифренные в электрических схемах.







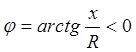
 и
и  совпадают по фазе
совпадают по фазе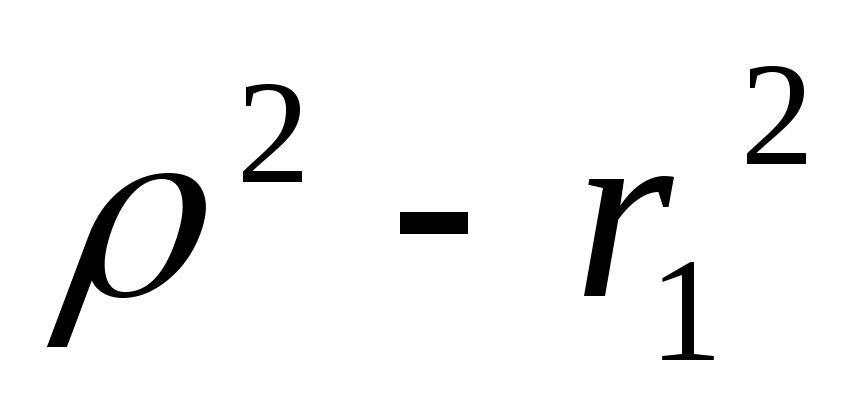 и
и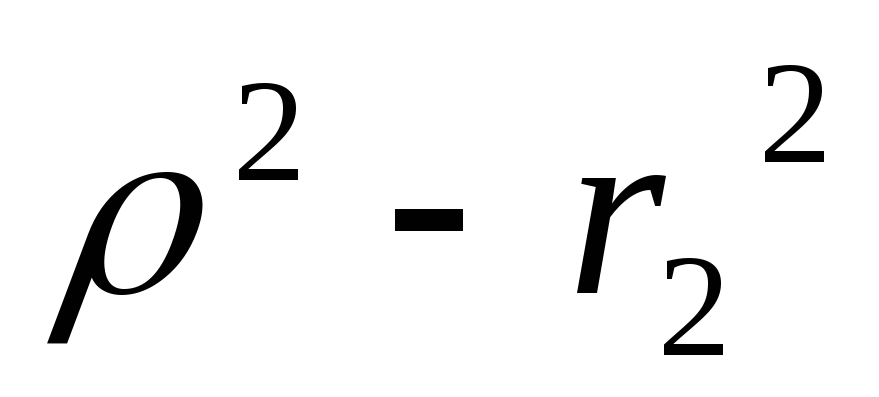 одного знака
одного знака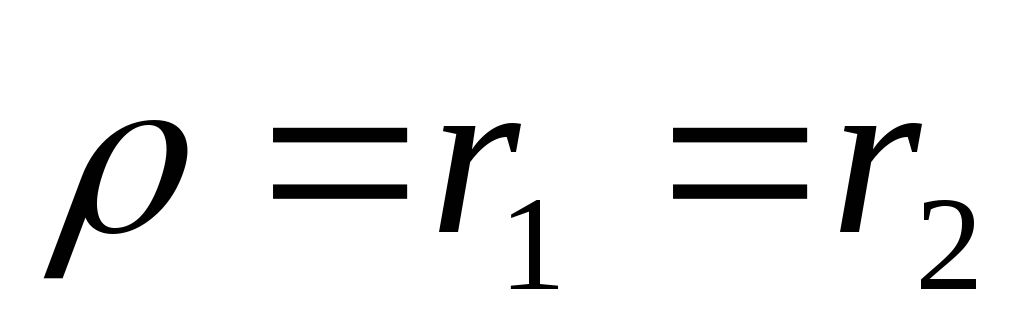
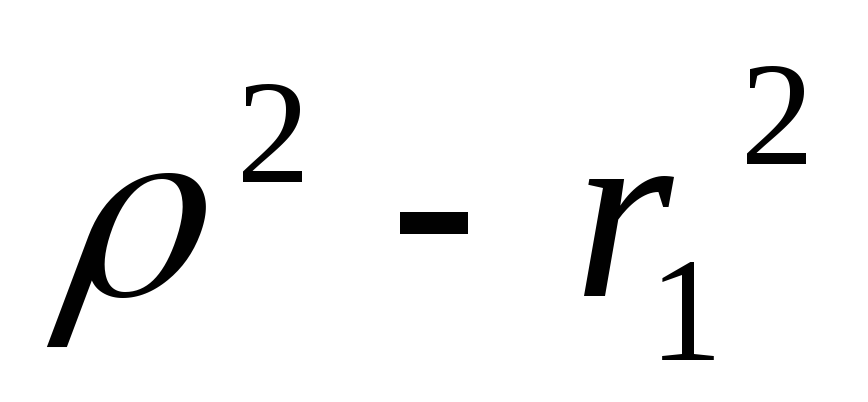 и
и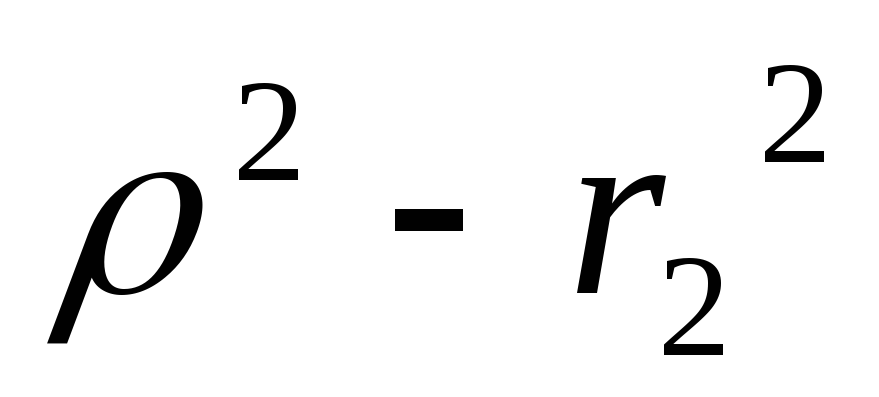 различного знака
различного знака


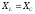

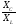
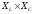

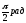
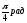
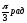
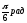

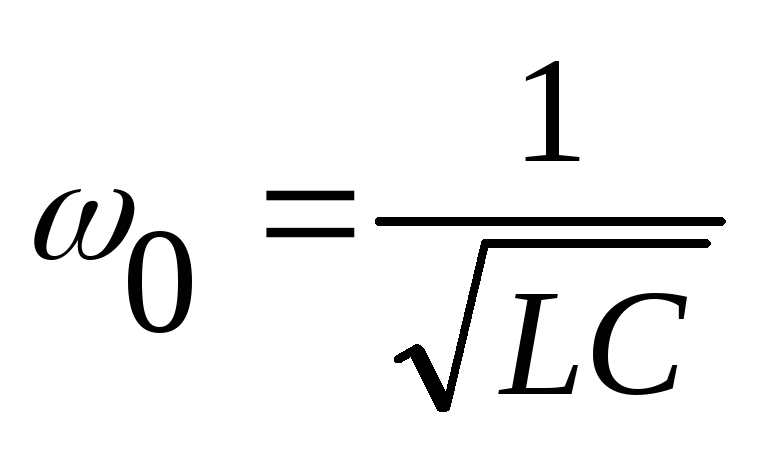 .
.