принцип работы, теория, формула, применение

Принцип эффекта Холла — одна из самых популярных теорий измерения магнитного поля. В этом посте будут обсуждаться Эффект Холла, принцип его работы, объяснение теории, формула, применение, включая расчеты для напряжения Холла, коэффициента Холла, концентрации носителей заряда, подвижности Холла и плотности магнитного поля.

Принцип эффекта Холла объясняет поведение носителей заряда при воздействии электрического и магнитного полей. Этот принцип можно рассматривать как расширение силы Лоренца, которая является силой, действующей на носители заряда (электроны и отверстия), проходящие через магнитное поле.

Датчики, работающие по этому принципу, называются датчиками Холла. Эти датчики Холла пользуются большим спросом и имеют очень широкое применение, например, датчики приближения, переключатели, датчики скорости вращения колес, датчики положения и так далее.

История эффекта Холла

Принцип эффекта Холла был назван в честь американского физика Эдвина Холла (1855–1938). Впервые он был представлен миру в 1879 году.

В 1879 году он обнаружил, что когда проводник / полупроводник с током расположен перпендикулярно магнитному полю, генерируется напряжение, которое можно измерить под прямым углом к ​​пути тока. В течение этого времени электрический ток в проводе считался чем-то похожим на текущую жидкость в трубе.

Принцип эффекта Холла предполагает, что магнитная сила в токе приводит к скученности на конце трубы или (провода). Электромагнитный принцип теперь объясняет науку, лежащую в основе эффекта Холла, гораздо лучше. Теория этого зала, безусловно, намного опередила свое время. Лишь два десятилетия спустя, с введением полупроводников, работа и использование эффекта Холла были эффективно использованы.

Первоначально этот принцип использовался для классификации химических образцов. Позднее датчики Холла (с использованием полупроводниковых соединений арсенида индия) стали источником для измерения постоянного или статического магнитного поля, не поддерживая датчик в движении. После десятилетия в 1960-х годах появились кремниевые полупроводники. Это было время, когда элементы Холла были объединены со встроенными усилителями, и таким образом, выключатель Холла был представлен миру.

Принцип работы эффекта Холла

Принцип эффекта Холла гласит, что когда проводник или полупроводник с током, текущим в одном направлении, вводится перпендикулярно магнитному полю, напряжение может быть измерено под прямым углом к ​​пути тока.

Эффект получения измеримого напряжения, как сказано выше, называется эффектом Холла.

Теория за принципом эффекта Холла

Прежде всего, мы должны понять, что такое электрический ток. Электрический ток — это в основном поток заряженных частиц через проводящий путь. Эти заряженные частицы могут быть «отрицательно заряженными электронами» или даже «положительно заряженными отверстиями» (пустоты, в которых должны находиться электроны). Теперь давайте перейдем к теме.

Если мы возьмем тонкую проводящую пластину (как показано выше на рис. 1 и повторено ниже для простоты считывания) и подключим ее к цепи с батареей (источником напряжения), то ток начнет течь по ней. Носители заряда будут течь по прямой линии от одного конца пластины к другому концу.

Поскольку носители заряда находятся в движении, они будут создавать магнитное поле. Теперь, когда вы поместите магнит рядом с пластиной, его магнитное поле будет искажать магнитное поле носителей заряда. Это расстроит прямой поток носителей заряда. Сила, которая нарушает направление потока носителей заряда, называется силой Лоренца.

Из-за искажения в магнитном поле носителей заряда отрицательные заряженные электроны будут отклоняться на одну сторону пластины, а положительные заряженные дыры — на другую сторону. Вот почему разность потенциалов (также называемая напряжением Холла) будет генерироваться между обеими сторонами пластины, что можно измерить с помощью измерителя.

Этот эффект известен как эффект Холла. Чем сильнее магнитное поле, тем больше электронов будет отклоняться. Это означает, что чем выше ток, тем больше электронов будет отклоняться. И чем больше будут отклоняться электроны, тем больше будет разность потенциалов между обеими сторонами пластины. Поэтому мы можем сказать, что:

• Напряжение Холла прямо пропорционально электрическому току, и прямо пропорционально приложенному магнитному полю.

Формула эффекта Холла

Вот некоторые математические выражения, которые широко используются в вычислениях эффекта Холла:

Напряжение Холла

Напряжение Холла представлена V _H. Формула для напряжения Холла:

Где:

I — Ток, протекающий через датчик

B — напряженность магнитного поля

q — заряд

n — количество носителей заряда на единицу объема

d — толщина датчика

Коэффициент Холла

Оно представлено R_H. Формула для коэффициента Холла (R _H ) равно 1 / (qn) . Коэффициент Холла (R _H ) положителен, если число отверстий положительного заряда больше, чем число электронов отрицательного заряда. Аналогично, коэффициент Холла (RH) отрицателен, если число отрицательных зарядовых электронов больше, чем число отверстий положительного заряда.

Концентрация несущей заряда

Концентрация электронов в носителе заряда обозначена как «n», а «дырки» — как «p». Математическое выражение для концентрации носителей заряда:

Холловская  мобильности

Холловская мобильность для электронов представлена ​​как « μ _n », а для отверстий — как « μ _p ». Математическое выражение для мобильности Холла:

Где:

μ _n — проводимость за счет электронов

μ _p — проводимость благодаря отверстиям

Плотность магнитного потока

Плотность магнитного потока обозначена буквой «B». Формула для плотности магнитного потока:

Применение принципа эффекта Холла

Принцип эффекта Холла используется в:

• Оборудование для измерения магнитного поля.
• Множитель приложений для обеспечения фактического умножения.
• Тестер Эффекта Холла для измерения постоянного тока.
• Измерение фазового угла. Например — при измерении углового положения коленчатого вала, чтобы точно выровнять угол зажигания свечей зажигания
• Датчики линейных или угловых перемещений. Например — определить положение автомобильных сидений и ремней безопасности и выступить в роли блокировки для управления подушкой безопасности.
• Датчики приближения.
• Датчики с эффектом Холла
• Для определения скорости вращения колеса и, соответственно, помощи антиблокировочной тормозной системы (ABS).

Как эффект Холла можно использовать для определения типа используемого полупроводника?

Коэффициент Холла говорит обо всем. Если коэффициент Холла отрицателен, это означает, что основными носителями заряда являются электроны. И поскольку число электронов больше по сравнению с отверстиями в полупроводниках n-типа, это ясно указывает на то, что испытываемый полупроводник n-типа. Аналогичным образом, если коэффициент Холла положительный, это означает, что основными носителями заряда являются дырки. И поскольку число отверстий больше по сравнению с электронами в полупроводниках p-типа, это ясно указывает на то, что испытываемый полупроводник p-типа.

в чём заключается явление, измерения датчиками, основанными на элементах Холла, формула расчетов

Изучение влияния друг на друга электричества и магнетизма привело к открытию явления, названого впоследствии именем его исследователя, эффектом Холла. Благодаря экспериментам учёного был создан датчик, получивший широкое применение в электрических схемах. Его используют в мобильной и бытовой технике совместно с двигателями, в измерительном оборудовании за счет способности преобразовывать магнитную индукцию в разность потенциалов.

Открытие эффекта Холла

Будущий физик Эдвин Герберт Холл родился в американском городе Горем в 1855 году. Получив начальное образование, он в 1875 году поступил в университет, где и ставил свои первые эксперименты. Так, изучая труды Максвелла об электричестве и магнетизме, Холл заинтересовался двумя фактами.

Первый заключался в том, что силы, возникающие в проводнике, расположенном поперечно линиям магнитной индукции, прикладываются непосредственно к веществу. Второй же сообщал, что значение этих сил зависит от скорости движения зарядов. В 1879 году вышла статья учёного Эдмунда Холла, доказывающая факт, что магнитное поле действует с одинаковым усилием как на подвешенный, так и зафиксированный объект.

Анализируя, какая сила может управлять движением заряженных частиц, он пришёл к выводу, что это может быть только напряжение. Для первого опыта физик использовал согнутую в спираль проволоку зажатую между диэлектриков. Эту конструкцию он поместил между двумя магнитами и запитал её от химического элемента тока. В качестве регистратора использовался мост Витстона с гальванометром Кельвина. В совокупности было проведено около тринадцати экспериментов и более четырёхсот измерений с разными условиями. Результатами экспериментов стало утверждение, что магнитный поток может изменять сопротивление материала.

По совету профессора Роуланда было выработано направление нового эксперимента, заключающее в следующем:

1. К проводящей пластине подводился электрический ток.
2. Гальванометр подключался к краям проводника.
3. Включался электромагнит так, чтобы линии напряжённости поля лежали перпендикулярно плоскости пластины.

Предполагалось обнаружить условия для изменения протекания тока. Но опыт не получался, пока в качестве пластины не попробовали использовать тонкий лист из золота. Поставленный новый опыт оказался удачным. Гальванометр чётко зафиксировал появившееся напряжение.

В результате был обнаружено, что при подаче на проводник электрического тока заряд в ней распределяется равномерно по всей её поверхности.

Но как только на пластину воздействует магнитное поле, линии индукции которой перпендикулярны направлению тока, заряд перераспределяется к краям, и возникает разность потенциалов. В этом и заключается эффект Холла, на базе которого были после построены одноимённые датчики.

Физико-математическое определение

Эффект Холла — это явление, которое можно наблюдать при помещении вещества проводящего электрический ток под действие магнитного поля. Физик Холл открыл, что в проводнике, при пропускании по нему постоянного тока появляется электродвижущая сила (ЭДС) если его поместить в поперечное магнитное поле. Физически это обозначает возникновение напряжения на боковых гранях проводящего вещества при поднесении к нему магнита. Используя это, можно регистрировать магнитное излучение. Возникшее напряжение зависит от трёх факторов:

• силы тока;
• напряжённости поля;
• типа проводника.

Сила, с которой электромагнитное поле действует на точечный заряд в веществе, называется силой Лоренца. Частным её случаем является сила Ампера. Математически напряжённость электрического поля описывается выражением:

E h = R*H*j*sinα, где:

• H — напряжённость магнитного поля;
• j — плотность тока;
• α — векторный угол между силовыми линиями H и j;
• R — постоянная Холла.

Если к пластине прямоугольной формы, имеющую длину L, которая намного будет превышать ширину b и толщину d, подвести ток, то его значение будет определяться формулой: I = j*b*d. Когда же её переместить в магнитное поле, направленное перпендикулярно этому току, то на боковых гранях пластины возникнет ЭДС, равная:

V h = E h* b = R*H*I/d.

Так как эффект объясняется влиянием поля на элементарные частички (дырки или электроны) то сила действующая на них описывается законом Лоренца: F =e * [H*υ], где υ — усреднённая скорость носителей зарядов, зависящая от концентрации и величины носителей. Под влиянием этой силы носители начинают прижиматься к боковым поверхностям пластины перпендикулярно j и H. Там они накапливаются, и возникает явление Холла, уравновешивающее силу Лоренца.

При этом коэффициент Холла равен: R = 1/n*e. Например, для металлов он составляет около 10^-3 см³/Кл, а у полупроводников от 10 до 10⁵ см³/Кл.

Постоянную Холла также можно выразить через способность носителей заряда реагировать на внешнее воздействие (подвижность). Так, она равна: R = µ/σ, где: µ — дрейфовая скорость носителей, а σ — удельная электропроводность. Но это в большей мере справедливо для поликристаллов. В то же время для анизотропных проводников будет верней формула: R = r/e*n. Здесь r принимается равной единице и обозначает оценку силы магнитного поля.

Разновидности явления

По мере исследования эффекта был обнаружен ряд особенностей появления электрического поля, отличающий от классического понимания. Так, учёными были выявлены факторы, приводящие к появлению напряжения без пропускания через пластинку тока. Такие явления получили название:

• аномальное;
• квантовое;
• спиновое.

Для аномального эффекта необходимым условием является нарушение T-симметрии, то есть уравнений, описывающих физические законы при обращении времени. Наиболее часто этот эффект наблюдается в материалах, имеющих остаточную намагниченность (ферромагнетики).

Квантовое же отклонение возникает в квазидвумерном электронном газе, где пренебрегают кулоновским взаимодействием. В нём носители заряда обладают слабой связью с ионами кристаллической решётки. В такой системе работают законы квантовых теорий.

При этом чем сильнее магнитное поле, тем более выражено дробное явление Холла, связанное с трансформированием структуры всего электронного газа.

В 1971 году учёные Дьяконов и Перель, изучающие механизм спиновой релаксации, обнаружили, что перпендикулярно направлению линий электромагнитного поля наблюдается отклонение носителей зарядов, имеющих противоположные спины. Этот эффект был связан со спин-гальваническим рассеянием и взаимодействием между спиновыми и орбитальными магнитными моментам.

Способы использования явления

На основе эффекта Холла создаются устройства и приборы, обладающие нужными и часто уникальными свойствами. Эти приборы занимают важное место в измерительно-контрольной технике, автоматизации, радиотехнике и т. д. Приспособления, использующие в своей работе явление Холла, называются элементами Холла (датчиками).

Эти датчики дают возможность измерять силу магнитного поля, так как при неизменной величине тока электродвижущая сила прямо пропорциональна линиям магнитной индукции. Прямая зависимость этих величин для элементов Холла является неоспоримым преимуществом перед другими типами измерителей индукции, основанных на контроле магнетосопротивления.

Приборы Холла позволяют проводить измерения электрических и магнитных характеристик не только металлов, но и полупроводников. Из-за простоты своего действия, несложности в изготовлении, а также высокой точности и надёжности они широко применяются в различных отраслях науки и техники. Датчики используются для измерения силы, давления, углов, перемещения и других неэлектрических величин. Этот эффект используют и при изготовлении полупроводников для контроля подвижности носителей зарядов и подсчёта их концентрации.

Для этого используется формула эффекта Холла: V h = j*B*H / n*q = B*I / (q*n*α) = R*B*I/α,

из которой число носителей находится как N = (I*B) / (q*α* V h). Таким образом, можно определить не только количество носителей, но и также их тип (знак).

Элементы Холла применяются в автомобилестроении из-за их невысокой стоимости, точности показаний, надёжности и способности не зависеть от условий окружающей среды. Их используют в конструкции бесконтактных однополярных и биполярных прерывателей. Благодаря их миниатюрному исполнению электронные гаджеты можно автоматически включать или выключать экран при открытии или закрытии чехла с магнитом. Они помогают в GPS-навигации, улучшая геопозирование.

С каждым годом эффект Холла находит всё более новое применение. Свидетельством тому служит появление устройства виртуальной реальности — Google Card Board, в основе работы которого лежит взаимодействие магнита с датчиком Холла.

Магнитные датчики

Основное преимущество использования датчиков магнитного поля, заключается в их бесконтактной работе. Они бывают аналоговыми и дискретными. Первый тип считается классическим. В его основе лежит принцип, что чем сильнее будет магнитное поле, тем больше будет величина напряжения. В современных приборах и устройствах такой тип уже практически не используется из-за значительных размеров. Цифровой же датчик построен на режиме работы «ключ» и имеет два устойчивых положения. Если сила индукции недостаточна он не срабатывает.

Разделяются дискретные элементы Холла на два типа:

• униполярные — срабатывание которых зависит от полюса магнитного поля;
• биполярные — переключения состояния датчика происходит при изменении магнитного полюса;
• омниполярные — реагируют на действие магнитной индукции любого направления.

Конструктивно датчик представляет собой электронный прибор с тремя выводами. Он может выпускаться как в стандартном исполнении DIP, DFN или SOT, так и в герметичном: например, 1GT101DC (герметичный), A1391SEHLT-T (DNF6), SS39ET (SOT), 2SS52M (DIP).

Характеристики устройства

Выпускаемые датчики, использующие явление Холла, как и любые электронные радиокомпоненты характеризуются своими параметрами. Главным из них является тип прибора и напряжение питания. Но, кроме этого, выделяют следующие технические характеристики:

1. Величина измеряемой индукции. Измеряется она в гауссах или миллитеслах.
2. Чувствительность — определяется значением магнитного потока, на который реагирует датчик, единица измерения мВ/Гс или мВ/мТл.
3. Нулевое напряжение магнитного поля — значение разности потенциалов, соответствующее отсутствию магнитного поля.
4. Дрейф нуля — изменение напряжения, зависящее от температуры. Указывается в процентном отклонении от температуры 25 °C.
5. Дрейф чувствительности — изменение чувствительности, вызванное изменением температуры.
6. Полоса пропускания — уровень снижения чувствительности с шагом в 3 дБ.
7. Индукция включения и выключения — это значение напряжённости поля, при котором датчик устойчиво срабатывает.
8. Гистерезис — разность между индукциями включения и выключения;
9. Время срабатывания — характеризуется промежутком времени перехода из одного устойчивого состояния в другое.

Изготовление приборов

Материал, из которого выполняется элемент Холла, должен обладать большой подвижностью носителей зарядов. Для получения наибольшего значения напряжения вещество не должно иметь высокую электропроводностью. Поэтому при производстве устройств используется: селенид, теллурид ртути, антимонид индия. Тонкопленочные датчики получаются методом испарения вещества и осаждения его на подложку. В качестве её служит слюда или керамика.

Изготавливают датчики также из полупроводников — германия и кремния. Их легируют мышьяком или фосфорной сурьмой. Такие устройства обладают низкой зависимостью от изменения температуры, а величина образуемой на них ЭДС может достигать одного вольта.

Типовой процесс производства пластинчатого датчика Холла состоит из следующих операций:

• обрезка пластины нужного размера;
• шлифовка поверхности;
• формирование с помощью пайки либо сварки симметричных выводов;
• герметизация.

Таким образом, применение эффекта Холла нашло широкое применение в магнитометрии, смартфонах, автомобилях, выключателях и охранных системах.

Одним из главных преимуществ датчиков, выполненных на этом эффекте, является электрическая изоляция (гальваническая развязка) делающие их применение удобным и безопасным.

Эффект Холла.

Эффект Холла относится к группе гальваномагнитных явлений и заключается в том, что под действием магнитного поля, перпендикулярного к электрическому току, электроны в материале отклоняются перпендикулярно как направлению электрического тока, так и магнитного поля. С помощью эффекта Холла стало возможным понять суть процессов проводимости в полупроводниках и провести грань между полупроводниками и другими типами плохо проводящих материалов. Это обусловлено тем, что измерение ЭДС (разности потенциалов) Холла, возникающей в материале перпендикулярно направлению электрического тока и внешнего магнитного поля, дает возможность непосредственно определить концентрацию и знак носителей заряда. Последнее позволяет определить принадлежность материала к тому или иному типу полупроводников (p или n–типа). Измерения эффекта Холла дают возможность отделить случай ионной проводимости от случая электронной проводимости. Наличие эффекта Холла в проводниках и полупроводниках свидетельствует об электронном характере проводимости. С помощью эффекта Холла возможно получить данные и о подвижности носителей заряда (так называемая «холловская» подвижность). Таким образом, можно считать, что эффект Холла – один из наиболее эффективных методов исследования электрических свойств полупроводниковых материалов.

Этот эффект был открыт Е.Холлом в 1879 г.. Сущность явления заключается в следующем. Если металлическую или полупроводниковую пластину, по которой проходит ток, поместить в магнитное поле, направленное перпендикулярно линиям тока (рис.5), то в ней возникает разность потенциалов в направлении перпендикулярном току и магнитному полю.

В основе эффекта лежит взаимодействие между электрическими зарядами и магнитными полями. Любая заряженная частица, движущаяся в магнитном поле, испытывает действие силы Лоренца, направление которой перпендикулярно направлению движения частицы и направлению магнитного поля. Величина этой силы прямо пропорциональна величине заряда q, скорости частицыv и индукции магнитного поля:

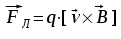(0.1)

Для металлов и для полупроводников n-типа q = -|e|, где |e|— модуль заряда электрона.

Модуль векторного произведения:

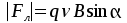(0.2)

У

Рис. 5. Схема возникновения эффекта Холла в полупроводнике n-типа.

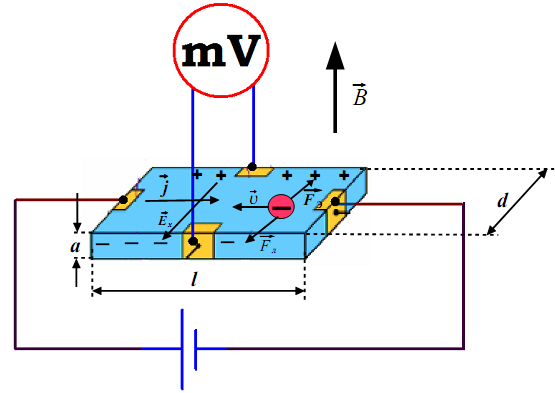словимся, что магнитное поле направлено строго перпендикулярно вектору скорости частиц. Т. е. угол α между векторам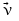и и равен 90⁰, а sin(90⁰)=1 Тогда: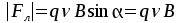

(1)

Под действием силы Лоренца электроны отклоняются к ближней боковой грани пластины рис. 5 и заряжают ее отрицательно. На противоположной грани остается нескомпенсированный положительный заряд ионов кристаллической решетки. В результате этого в пластине возникает поперечное электрическое поле 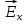, направленное от дальней боковой грани к ближней. Обозначим напряженность образовавшегося электрического поля через 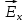. Сила , действующая со стороны электрического поля на заряд, направлена в сторону, противоположную направлению силы Лоренца (рис. 5). Возникшая вследствие этого поперечная разность потенциалов U_x называется ЭДС Холла.

Разделение зарядов в образце продолжается до тех пор, пока силы магнитного и электрического полей не уравновесят друг друга, т. е.:

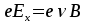(2)

Откуда находим:

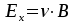(3)

Считаем поле 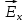, образовавшееся в пластинке однородным. Тогда находим:

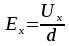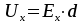→ (4)

где d – толщина пластинки в направлении поля E_x (рис. 5).

С учетом выражения (3) получаем, что:

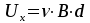(5)

Сила тока, протекающего через единицу поверхности образца, т. е. плотность тока, равна:

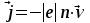(5.1)

А модуль выражения (5.1) найдем как:

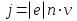(5.2)

где n – число носителей тока в единице объема образца (концентрация носителей тока).

С другой стороны, модуль вектора плотности тока 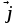определяется как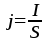, где S – площадь поперечного сечения пластины, перпендикулярная направлению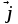. Тогда:

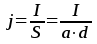(5.3)

где а— ширина пластины в направлении векторарис. 5.

Сопоставляя формулы (5.2) и (5.3), находим:

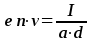(5.4)

Выражая из (5.4) скорость электронов v, находим:

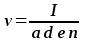(6)

Подставив (6) в (5), получим:

(7)

Обозначим гдеR_х — постоянная или коэффициент Холла. (Условно считают, что знак постоянной Холла совпадает со знаком заряда носителей тока. У электронных полупроводников постояннаяRотрицательна, у дырочных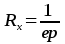— положительна, гдеp– концентрация дырок).

Тогда выражение (7) записывается в виде:

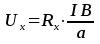(8)

Таким образом, ЭДС Холла зависит от величины проходящего тока, индукции магнитного поля, ширины пластины и концентрации носителей заряда. Зависимость от концентрации говорит о том, что в металлах ЭДС Холла по сравнению с полупроводниками намного меньше, и поэтому использование эффекта Холла началось только с применением полупроводников.

При выводе формулы для U мы полагали, что все носители заряда имеют одинаковую скорость. Если учитывать распределение носителей заряда по скоростям, то необходимо ввести числовой множительA,отличный от единицы:

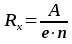
где А– постоянная, зависящая от механизма рассеяния носителей заряда:А=1,93 … 0,99. Практически для большинства металлов можно считать A≈1.

При рассеянии электронов на тепловых колебаниях решетки:

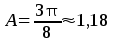
Откуда получаем:

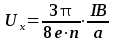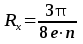,(8.1)

Наглядная иллюстрация эффекта Холла в полупроводниках c n-типом и p-типом проводимости приведена на рис. 6 a), б). По сравнению с рисунком 5 здесь пластина повернута на угол к наблюдателю вокруг оси.

Рис. 6. Эффект Холла в полупроводниках с n-проводимостью а) и p-проводимостью б)

Квантовый эффект Холла — Википедия

Ква́нтовый эффе́кт Хо́лла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа в сильных магнитных полях и при низких температурах. Квантовый эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом (совместно с Г. Дордой и М. Пеппером) в 1980 году^[1], за что впоследствии, в 1985 году, он получил Нобелевскую премию^[2].

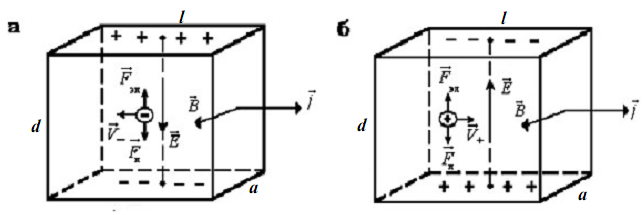
Рис. 1. Зависимости холловского сопротивления и удельного сопротивления от магнитного поля при постоянной концентрации носителей. На зависимости холловского сопротивления наблюдаются «плато»^[3].

Эффект состоит в том, что при достаточно низких температурах в сильных магнитных полях на графике зависимости поперечного сопротивления (отношения возникающего поперечного напряжения к протекающему продольному току) вырожденного двумерного электронного газа (ДЭГ) от величины нормальной составляющей к поверхности ДЭГ индукции магнитного поля (или от концентрации при фиксированном магнитном поле) наблюдаются участки с неизменным поперечным сопротивлением или «плато».

Фон Клитцинг обнаружил так называемый нормальный (или целочисленный) квантовый эффект Холла (КЭХ), когда значения сопротивления на «плато» равно ρxy=h/νe2{\displaystyle \rho _{xy}=h/\nu e^{2}}, где e — заряд электрона, h — постоянная Планка, ν — натуральное число, называемое фактором заполнения уровней Ландау (рис. 1).

В 1982 году Д. Цуи и Х. Штёрмер открыли дробный квантовый эффект Холла (фактор заполнения при этом становится меньше единицы)^[4].

Уже первая работа^[1] по КЭХ, названная «Новый метод определения постоянной тонкой структуры с высокой точностью по квантованию холловского сопротивления» показала, что возможно его применение в качестве стандарта сопротивления. В настоящее время известно, что значения квантованного сопротивления Холла не зависят от качества образца и его материала. Поэтому, начиная с 1990 года, калибровки сопротивлений основаны на КЭХ с фиксированным значением R_э = 25812.807557(18) Ом.

Для наблюдения КЭХ существует ряд условий, которые должны выполняться, чтобы квантование было точным. Ниже приведены основные предпосылки возникновения плато.

Двумерный электронный газ[править | править код]

Если ограничить трёхмерный электронный газ в одном из направлений, таким образом, что в потенциальной яме (например, с ограничивающим потенциалом по оси Z) заполнен только один уровень размерного квантования, то говорят, что электронный газ стал двумерным. В этом случае движение в плоскости, перпендикулярной оси Z остаётся свободным и энергетический спектр ДЭГ выражается формулой:

E=ℏ22m(kx2+ky2)+En,{\displaystyle E={\frac {\hbar ^{2}}{2m}}(k_{x}^{2}+k_{y}^{2})+E_{n},}

где n = 0, 1, 2…, m{\displaystyle m} — эффективная масса квазичастиц (электронов или дырок). Только если заполнен основной уровень размерного квантования (первая подзона размерного квантования) говорят о формировании ДЭГ^[5].

Энергетический спектр носителей заряда в магнитном поле[править | править код]

На классические заряженные частицы, движущиеся в магнитном поле, действует сила Лоренца. Эта сила заставляет частицу двигаться по окружности с угловой скоростью ωc=eB/mc{\displaystyle \omega _{c}=eB/mc}, называемой циклотронной частотой (система единиц СГС). Согласно квантовой теории частицы, совершающие периодическое движение, обладают только дискретными значениями энергии, поэтому у заряженных частиц в магнитном поле появляются уровни энергии, называемые уровнями Ландау. Энергия k-го уровня, если пренебречь составляющей импульса pz{\displaystyle p_{z}} и наличием спина у частицы, определяется выражением^[6]

Ek=(k+12)ℏωc.{\displaystyle E_{k}=\left(k+{\frac {1}{2}}\right)\hbar \omega _{c}.}

Энергетический спектр двумерного электронного газа становится полностью дискретным и каждый энергетический уровень обладает следующим вырождением (число орбит, которые могут принадлежать уровню Ландау)

NH=S2s0=SeBℏc=S2πlB2=BSΦ0,{\displaystyle N_{H}={\frac {S}{2s_{0}}}={\frac {SeB}{\hbar c}}={\frac {S}{2\pi l_{B}^{2}}}={\frac {BS}{\Phi _{0}}},} (1)

где Ф₀ — квант магнитного потока. Это аналогично плотной упаковке циклотронных орбит в двумерном слое. Эту же величину можно получить, если представить, что из всех частиц ДЭГ, расположенных в интервале энергий, равных ħω_с (то есть произведение двумерной плотности состояний D0=mπℏ2{\displaystyle D_{0}={\frac {m}{\pi \hbar ^{2}}}} на энергию ħω_с), формируется отдельный уровень Ландау.

Концентрация электронов в ДЭГ в магнитном поле определяется по формуле ns=NNH{\displaystyle n_{s}=NN_{H}}, если уровень Ферми попадает в щель между уровнями Ландау. В общем случае частичное заполнение одного из уровней Ландау характеризуется так называемым фактором заполнения ν=nsNH=nsheB{\displaystyle \nu ={\frac {n_{s}}{N_{H}}}={\frac {n_{s}h}{eB}}} — отношение концентрации ДЭГ к вырождению уровней Ландау. Он может принимать как целые, так и дробные значения^[5].

Эффект Холла[править | править код]

Явление, открытое Холлом в 1879 году, состоит в том, что в проводнике с током, помещённом в магнитное поле, перпендикулярное направлению тока, возникает электрическое поле в направлении, перпендикулярном направлениям тока и магнитного поля. Сила Лоренца F_L = eBv заставляет электроны отклоняться в направлении, перпендикулярном их скорости v. В результате происходит накопление разноимённых зарядов на краях проводника, и между боковыми гранями образца возникнет разность потенциалов V_H, а внутри него — электрическое поле E_H, называемое полем Холла и уравновешивающее силу Лоренца.

Ток через образец равен I = nevS, где n — концентрация электронов, S — площадь поперечного сечения проводника: S = bd, где b — его ширина, d — толщина.

Условие равенства силы Лоренца и силы, вызванной холловским полем, есть eE_H = eV_H/b = evB. Отсюда следует, что V_H = bvB = IvB/nevd = IB/end = IR_H, где R_H называется холловским сопротивлением. В двумерных системах R_H = B/en_s, где n_s — поверхностная концентрация электронов.

Важно отметить, что R_H — это отношение возникающей поперечной разности потенциалов к продольному току, R_H = R_xy = V_y/I_x. При этом продольное сопротивление R_L = R_xx = V_x/I_x, слабо зависит от индукции магнитного поля, оставаясь по величине близким к своему значению при B = 0^[7].

Целочисленный квантовый эффект Холла[править | править код]

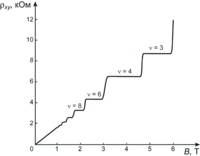Рис. 2. Зависимости холловского сопротивления от магнитного поля. На зависимости холловского сопротивления указаны факторы заполнения для некоторых «плато».

Как было замечено Клитцингом^[1], при измерении эффекта Холла в инверсном слое кремниевого МОП транзистора при низких температурах (Т ~ 1 K) и в сильных магнитных полях (B > 1 Тл) линейная зависимость холловского сопротивления сменяется чередой ступеней (плато) как показано на Рис. 2. Величина сопротивления на этих ступеньках равна комбинации фундаментальных физических констант, делённой на целое число ν{\displaystyle \nu }:

RH=hνe2{\displaystyle R_{H}={\frac {h}{\nu e^{2}}}}

Когда на зависимости холловского сопротивления R_H наблюдается плато, продольное электрическое сопротивление становится очень малой величиной (оно равно нулю с высокой экспериментальной точностью). При низких температурах ток в образце может течь без диссипации (рассеяния).

Прецизионные измерения также показали, что на точности квантования R_H не сказываются такие существенные параметры эксперимента, как размеры образцов, влияние границ и важное в обычном эффекте Холла закорачивание холловского напряжения омическими контактами, а также степень совершенства структур, то есть наличие большого количества примесей и дефектов, тип материала, в котором находится 2D-электронный газ, температура и сила измерительного тока. Экспериментальная точность квантования так высока, что встал вопрос о метрологических применениях КЭХ: проверке формул квантовой электродинамики с помощью прецизионного определения постоянной тонкой структуры или создания нового эталона сопротивления.

Экспериментальная установка[править | править код]

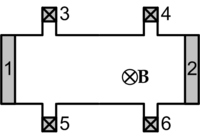Геометрия измерения квантового эффекта Холла. R_H=V₃₅/I₁₂ R_L=V₃₄/I₁₂

Для наблюдения эффекта гетероструктуру со сформированным двумерным электронным газом помещают в однородное магнитное поле, перпендикулярное плоскости электронного газа. При пропускании тока через образец измеряют ток, а также возникающее напряжение вдоль и поперёк образца.

Качественная интерпретация целочисленного квантового эффекта Холла[править | править код]

Электроны дрейфуют вдоль линий постоянной энергии, формируя локализованные и краевые токовые состояния

Целочисленный квантовый эффект Холла может быть просто интерпретирован на основе модели краевых состояний. Как правило, экспериментальный образец с двумерным электронным газом имеет границу, задаваемую литографическим краем или краем области под затвором. Возле края формируется обедняющее электрическое поле, направленное к краю (речь идёт об отрицательно заряженных электронах). Оно приводит к зависимости нуля отсчёта уровней Ландау от координаты, поэтому уровни Ландау «изгибаются» вверх вблизи края. Как известно в скрещенных магнитном и электрическом полях заряженная частица дрейфует вдоль линии постоянной энергии — эквипотенциали. Электроны заполняют состояния согласно статистике Ферми — Дирака до некоторого уровня Ферми, и при факторе заполнения ν{\displaystyle \nu }, близком к целочисленному значению вдали от краёв формируются локализованные состояния, не участвующие в проводимости, а вблизи краёв — краевые токовые состояния. Причем ток на противоположных берегах двумерного электронного газа имеет противоположное направление, а направление обхода однозначно задаётся знаком квантующего магнитного поля. Ток переносимый каждым краевым состоянием квантован и равен e2hμ{\displaystyle {\frac {e^{2}}{h}}\mu }, где μ{\displaystyle \mu } — значение электрохимического потенциала. А число краевых каналов целое и определяется фактором заполнения ν{\displaystyle \nu }. В этом случае, когда локализованные и подвижные состояния на уровне Ферми пространственно разделены и обратное рассеяние подавлено, реализуется режим квантового эффекта Холла.

Влияние неоднородностей[править | править код]

Дефекты, примеси и другие неоднородности в кристалле, которые локализуют, «изолируют» отдельные электроны в «ловушках», являются причиной возникновения широких плато на графиках холловского сопротивления и широких минимумов омического сопротивления. На поверхности кристалла остаются дефекты и примеси, которые порождают энергетические «долины» и «холмы». Когда уровень Ландау оказывается заполненным, некоторые из них попадают в ловушку и изолируются. Они больше не принимают участие в процессах электропроводности через кристалл. Локализованные электроны первыми заполняют и освобождают уровни Ландау при изменении магнитного поля, поддерживая точное заполнение уровней Ландау в энергетически гладкой области кристалла для протяженных интервалов величины магнитного поля. При этом холловское сопротивление образца и магнитосопротивление остаются постоянными. Локализованные благодаря дефектам кристалла электроны представляют собой хранилище необходимых для точного заполнения уровней Ландау носителей в энергетически гладкой области кристалла для конечного интервала напряженностей магнитных полей. Само существование целочисленного квантового эффекта Холла зависит от наличия дефектов в кристалле. Без неоднородностей в кристалле, «идеально чистая» система приводила бы к линейному эффекту Холла, без квантованности^[8].

О сопротивлении, проводимости и потенциале в условиях квантования холловского сопротивления[править | править код]

Эквипотенциали в образце с двумя контактами в условиях квантового эффекта Холла.

В 1982 году Даниэль Цуи (Daniel Tsui) и Хорст Штёрмер (Horst Störmer) заметили, что «плато» в холловском сопротивлении наблюдаются не только при целых значениях n, но и в существенно более сильных магнитных полях^[4] при n=1/3. В дальнейшем были обнаружены плато электрического сопротивления и при других дробных значениях n, например при n=2/5, 3/7…

Природа дробного квантового эффекта Холла была объяснена Р. Лаффлином в 1983 году^[9]. В 1998 году Цуи, Штёрмер и Лаффлин получили Нобелевскую премию по физике за открытие и объяснение этого явления^[10]

Качественное объяснение дробного квантового эффекта Холла[править | править код]

Суть явления заключается в том, что группа электронов «объединяются» в новую «частицу», заряд которой меньше заряда электрона. Дробный квантовый эффект Холла нельзя объяснить на основе поведения одиночных электронов в магнитном поле. Причина заключается во взаимодействии между электронами. Магнитное поле создает «вихри», по одному на каждый квант магнитного потока. Принцип Паули требует, чтобы каждый электрон был окружен одним «вихрем». Когда магнитные поля превышают величину, соответствующую ЦКЭХ с i=1, вихрей становится больше, чем электронов. Принцип Паули выполняется при размещении нескольких вихрей на электроне, которые уменьшают межэлектронное кулоновское отталкивание. Электрон «захватывает» квант магнитного потока и становится «составной частицей». С точки зрения теории, такие «составные частицы» описывать гораздо легче, чем «свободные» электроны. Захваченный квант потока меняет природу частиц, «превращая» фермионы в бозоны. Электрон, захвативший четное число квантов потока, становится фермионом, а нечетное число квантов потока — бозоном. При заполнении на 1/3 нижнего уровня Ландау каждый электрон принимает три кванта магнитного потока. Таким образом получается композитный бозон. Он находится в условиях нулевого магнитного поля (оно уже включено в новую частицу) и в состоянии бозе-конденсации в новом энергетическом состоянии. Можно определить энергетическую щель, необходимую для возникновения квантования холловского сопротивления и для обращения в ноль обычного сопротивления, экспериментальными методами. Когда часть вихрей магнитного поля не захвачена, возникает дробный дефицит заряда в каждом из этих вихрей. По сравнению с электронами, это положительные дробные заряды. Квазичастицы могут свободно двигаться и проводить электрический ток. Образование плато на графиках происходит как и в целочисленном квантовом эффекте Холла, из-за флуктуаций потенциала на дефектах кристалла. Отличие в том, что носители электрического тока — не электроны, а частицы с дробным зарядом. Дробный квантовый эффект Холла объясняется захватом нечетного числа вихрей магнитного потока каждым электроном^[11].

1. ↑ ^{1 2 3} K. v. Klitzing, G. Dorda, M. Pepper New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance Phys. Rev. Lett. 45, 494 (1980) DOI:10.1103/PhysRevLett.45.494
2. ↑ Нобелевский лауреат по физике за 1985 год
3. ↑ К. фон Клитцинг «Квантовый эффект Холла: Нобелевские лекции по физике — 1985 г.» УФН 150, 107 (1986).
4. ↑ ^{1 2} D. C. Tsui, H. L. Störmer, A. C. Gossard Two-Dimensional Magnetotransport in the Extreme Quantum Limit Phys. Rev. Lett. 48, 1559 (1982). DOI:10.1103/PhysRevLett.48.1559
5. ↑ ^{1 2} Ando T., Fowler A. B. and Stern F. Electronic properties of two-dimensional systems Rev. Mod. Phys. 54, 437 (1982).
6. ↑ Л. Д. Ландау, Е. М. Лифшиц «Теоретическая физика», в 10 т, т. 3 «Квантовая механика (нерелятивистская теория)», М., Физматлит, 2002, 808 с., ISBN 5-9221-0057-2 (т. 3), гл. 15 «Движение в магнитном поле», п. 112 «Движение в однородном магнитном поле», c. 554—559;
7. ↑ Askerov, B. M. (англ.)русск.. Electron Transport Phenomena in Semiconductors, 5-е изд (англ.). — Singapore: World Scientific, 1994. — P. 416.
8. ↑ В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупрводники», п 4.7 «Квантовый эффект Холла», пп 4.7.4 «Целочисленный квантовый эффект Холла», с. 249—253;
9. ↑ R. B. Laughlin, Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations Phys. Rev. Lett. 50, 1395 (1983) DOI:10.1103/PhysRevLett.50.1395
10. ↑ Нобелевские лауреаты по физике за 1998 год
11. ↑ В. К. Воронов, А. В. Подоплелов «Современная физика», учебное пособие, М., КомКнига, 2005, 512 с., ISBN 5-484-00058-0, гл. 4 «Полупроводники», п 4.7 «Квантовый эффект Холла», пп 4.7.5 «Дробный квантовый эффект Холла», с. 253—259;

Литература[править | править код]

Что такое эффект Холла и где он применим?

Американский ученый Эдвин Холл в 1879 году обнаружил, что в помещенном в магнитное поле  проводнике возникает разность потенциалов в направлении, перпендикулярном току I и вектору магнитной индукции В. Данный эффект возник вследствие воздействия силы Лоренца на заряды, движущиеся в этом проводнике.

На рисунке ниже изображена тонкая пластина, пронизываемая магнитным полем с индукцией В, направленным перпендикулярно чертежу, причем линии индукции направлены от зрителя и уходят за чертеж (показаны крестиком):

За направление тока I принимают направление движения положительных зарядов, для которых направление вектора скорости V и тока I совпадают (рисунок а)). У зарядов отрицательных векторы тока и скорости направлены в противоположные стороны (рисунок б)).  Применив правило левой руки легко убедиться в том, что сила Лоренца в обоих случаях будет направлена к верхней (на рисунке) грани пластины.

Эффект Холла наблюдается у полупроводников и металлов. У полупроводников n – типа, а также у металлов, где носителями зарядов являются электроны, на верхней части пластины будет накапливаться избыточный отрицательный заряд, а нижняя грань будет испытывать недостаток электронов и зарядится положительно, как показано на рисунке ниже (а)):

Результатом этого становится возникновение разницы потенциалов между верхней и нижней гранями проводника U_н.

У полупроводников p – типа, носителями заряда которых являются положительно заряженные дырки, верхняя грань (рисунок выше) приобретает в магнитном поле положительный заряд, а нижняя – отрицательный (рисунок б)). При исследовании распределения зарядов можно определить характер проводимости (электронный или дырочный) полупроводника. Также в процессе изучения эффекта Холла было обнаружено, что некоторые металлы обладают смешанной электронно – дырочной проводимостью. У таких металлов, из — за того, что дырки обладают большей подвижностью, распределение зарядов между верхней и нижней гранями будет такое же, как и у полупроводников p – типа.

Поскольку вектор тока I перпендикулярен скорости V перемещения зарядов и магнитному полю В, то выражение для сила Лоренца будет иметь вид:

Заряды, которые скапливаются на нижней и верхней гранях пластины, создают электрическое поле напряженностью Е, которое будет воздействовать на заряды с силой:

Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, эти две силы уравновешивают друг друга, то есть F_л = F_эл, поэтому:

Из формулы плотности тока:

Где: q – заряд частицы, n – количество частиц на единицу объема, V – скорость их движения.

Найдем скорость:

Подставим это выражение в формулу (1):

Разность потенциалов между нижней и верхней гранью с расстоянием между ними d, будет равно:

Коэффициент пропорциональности в этой формуле:

Так же его еще называют постоянной Холла. Уравнение (3) примет вид:

Можно сделать вывод, что разность потенциалов между гранями проводника прямо пропорциональна толщине проводящей пластины d, магнитной индукции В и плотности тока j.

Для любопытных видео о датчиках Холла:

Понятие и применение эффекта Холла

Добавлено 21 декабря 2015 в 08:00

Сохранить или поделиться

Эффект Холла был обнаружен Эдвином Холлом в 1879 году, но прошло много лет, прежде чем технологическое развитие позволило интегральным схемам в полной мере воспользоваться этим явлением. Сегодня микросхемы датчика Холла предлагают удобный способ для достижения точных измерений тока, которые обеспечивают электрическую изоляцию между путем измеряемого тока и измерительной цепью.

От Лоренца к Холлу

Эффект Холла является продолжением силы Лоренца, которая описывает силу, действующую на заряженные частицы – такие как электрон – движущиеся в магнитном поле. Если магнитное поле направлено перпендикулярно направлению движения электронов, на электрон действует сила, которая перпендикулярна и направлению движения, и направлению магнитного поля.

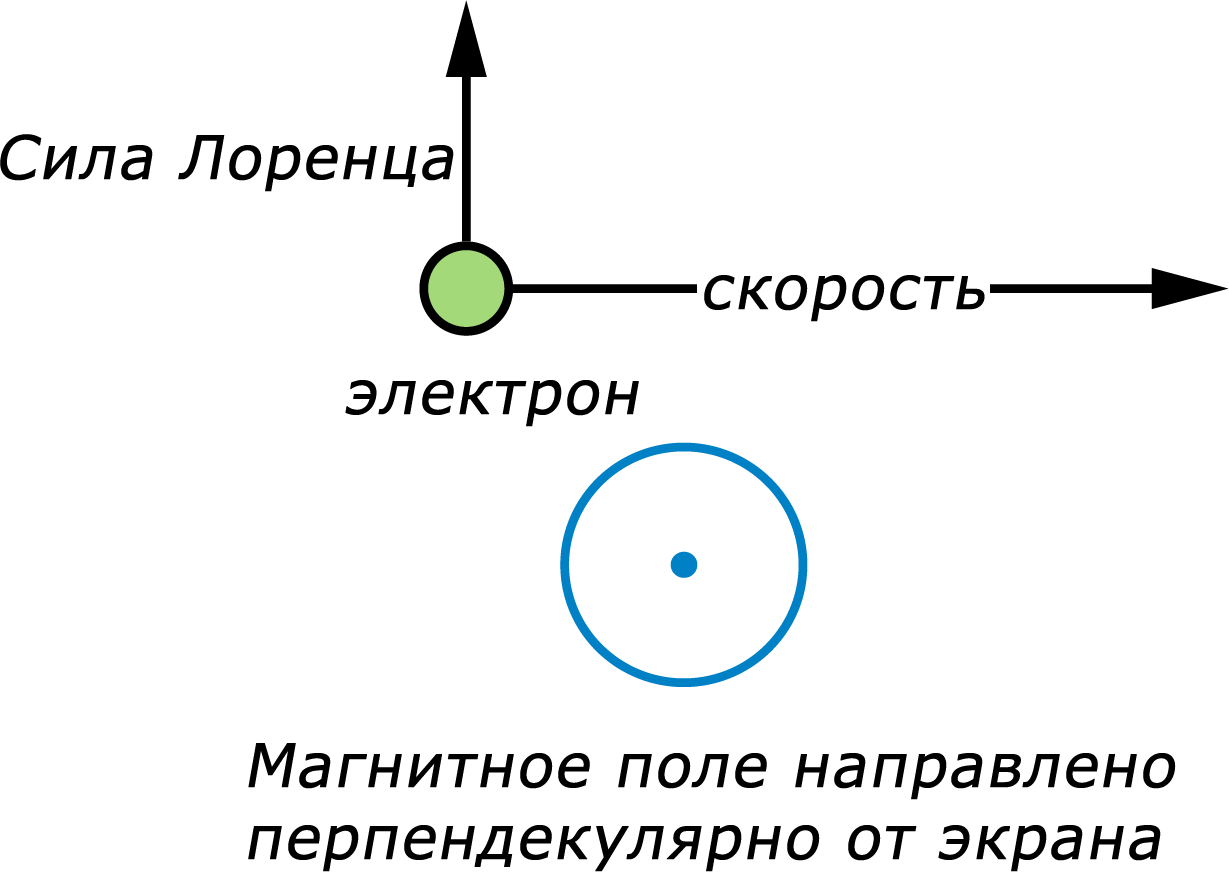
Эффект Холла относится к ситуации, в которой сила Лоренца действует на электроны, движущиеся в проводнике, так что разница потенциалов – или другими словами, напряжение – возникает между двумя сторонами проводника.

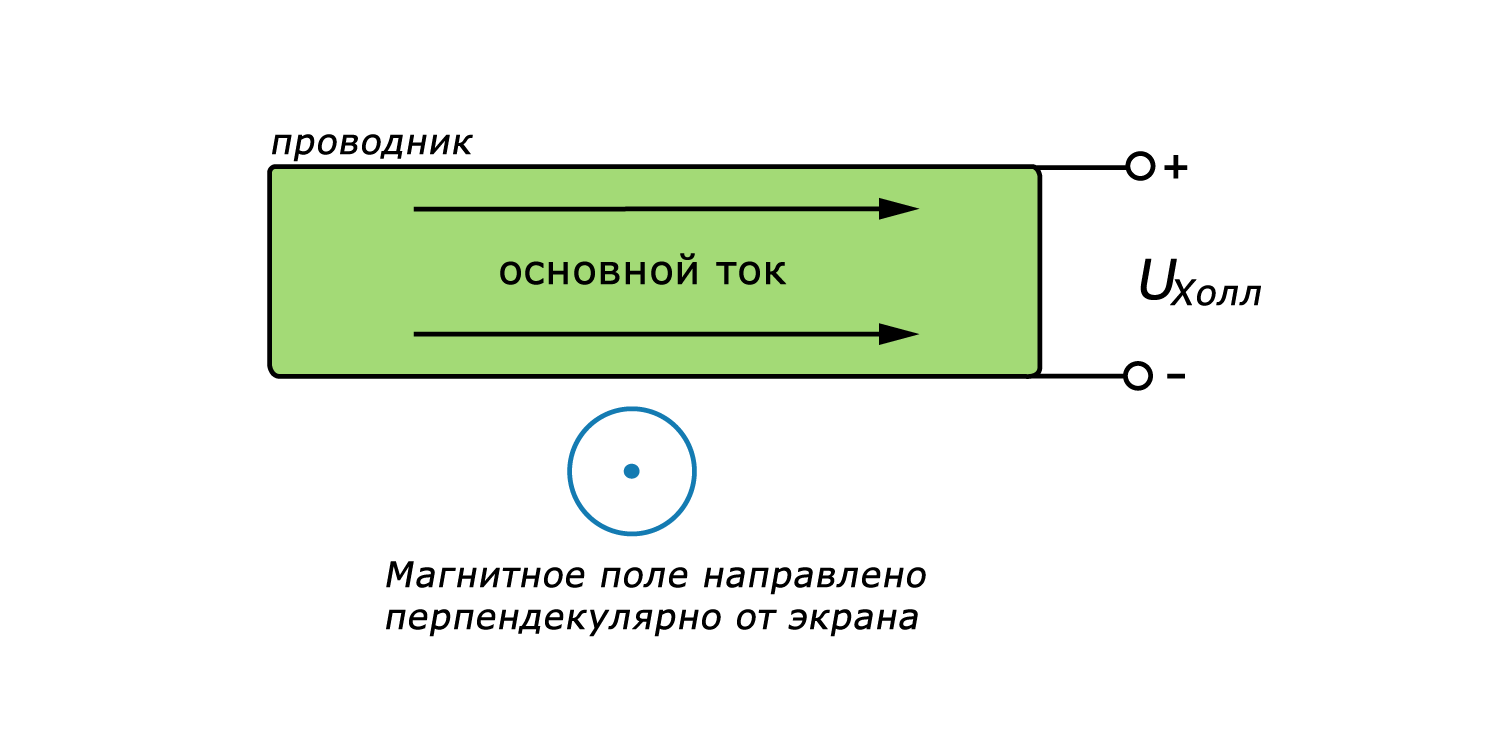
Следует отметить, что стрелки на втором рисунке показывают направления протекания обычного тока, а это означает, что электроны двигаются в противоположном направлении. Направление силы Лоренца определяется правилом правой руки, учитывающим направление движения электрона относительно магнитного поля. На первом рисунке электрон движется вправо, а сила Лоренца направлена вверх. На втором рисунке электроны движутся влево, а сила Лоренца направлена вниз, и, таким образом, отрицательный заряд накапливается на нижней стороне проводника. Результатом является разность потенциалом, которая возникает между верхней и нижней кромками проводника, с верхним краем более положительным по сравнению с нижним. Эта разность потенциалов называется напряжением Холла:

\[U_{Холл}=-\frac{IB}{eρt}\]

Эта формула, которая применяется к токопроводящей пластине, говорит нам, что напряжение Холла зависит от величины тока (I), протекающего через проводник, от магнитной индукции (B), от элементарного заряда электрона (e), количества электронов в единице объема (ρ) и от толщины пластины (t).

Использование эффекта Холла

Напряжения, генерируемые с помощью эффекта Холла малы по отношению к воздействиям шума, смещения и температуры, которые, как правило, влияют на схему, и, таким образом, реальные датчики на основе эффекта Холла не были широко распространены до появления полупроводниковой технологии, позволившей создание компонентов с высокой степенью интеграции, которые включали в себя и элемент Холла, и дополнительную схему, необходимую для усиления напряжения Холла. Тем не менее, датчики на основе эффекта Холла ограничены в своей способности измерять небольшие токи. Например, чувствительность ACS712 от Allegro MicroSystems составляет 185 мВ/А. Это означает, что ток 10 мА создаст выходное напряжение только 1,85 мВ. Это напряжение может быть приемлемым, если у схемы низкий уровень шума, но, если в цепь протекания тока включить резистор 2 Ом, в результате можно получить напряжение 20 мВ, что значительно лучше.

Эффект Холла используется в различных датчиках; устройства, основанные на относительно простой связи между током, магнитным полем и напряжением, могут использоваться для измерения положения, скорости и напряженности магнитного поля. В данной статье мы сосредоточим внимание на устройствах, которые измеряют ток через напряжение Холла, генерируемое, когда магнитное поле, создаваемое измеряемым током, концентрируется в элементе датчика Холла.

Достоинства и недостатки

Характеристики у разных датчиков тока на основе эффекта Холла сильно отличаются, поэтому трудно суммировать достоинства и недостатки использования эффекта Холла относительно другого распространенного способа измерения тока; а именно, вставки прецизионного резистора в цепь протекания тока и измерения появившегося на нем падения напряжения с помощью дифференциального усилителя. В целом, датчики Холла ценятся за «невлияние» и обеспечение электрической изоляции между цепью протекания тока и измерительной цепью. Эти устройства рассматриваются как не оказывающие влияния потому, что в цепь протекания тока не вставляется какого-либо существенного сопротивления, и, таким образом, схема при проведении измерений ведет себя так же, как если бы датчика не было вовсе. Дополнительным преимуществом является то, что датчиком рассеивается минимальная мощность; это особенно важно при измерении больших токов.

Что касается точности, доступные в настоящее время датчики Холла могут достичь минимальной ошибки в 1%. Хорошо продуманный датчик на основе резистора может дать лучший результат, но одного процента, как правило, хватает при работе с большими токами/напряжениями, где и подходит использование датчиков Холла.

Недостатки датчиков Холла включают в себя ограниченный диапазон частот и высокую стоимость. ACS712 работает до 80 кГц, а диапазон Melexis MLX91208, который позиционируется, как «широкополосный», ограничивается верхней границей 250 кГц. Резистивный датчик тока с высокоскоростным усилителем, с другой стороны, может хорошо работать и мегагерцовом диапазоне. Кроме того, как обсуждалось выше, эффект Холла по своей природе имеет ограничение в отношении измерения малых токов.

Изоляция

Одно из главных преимуществ датчиков Холла заключается в электрической изоляции, которую в контексте проектирования схем и систем называют гальванической развязкой. Принцип гальванической развязки используется всякий раз, когда проект требует, чтобы две схемы связывались таким способом, который предотвращает любую возможность протекания между ними электрического тока. Простой пример, когда цифровой сигнал передается через оптоизолятор, который преобразует импульсы напряжения в импульсы света и таким образом передает данные оптическим способом, а не электрическим. Одной из основных причин для реализации гальванической развязки является предотвращение проблем, связанных с земляными контурами:

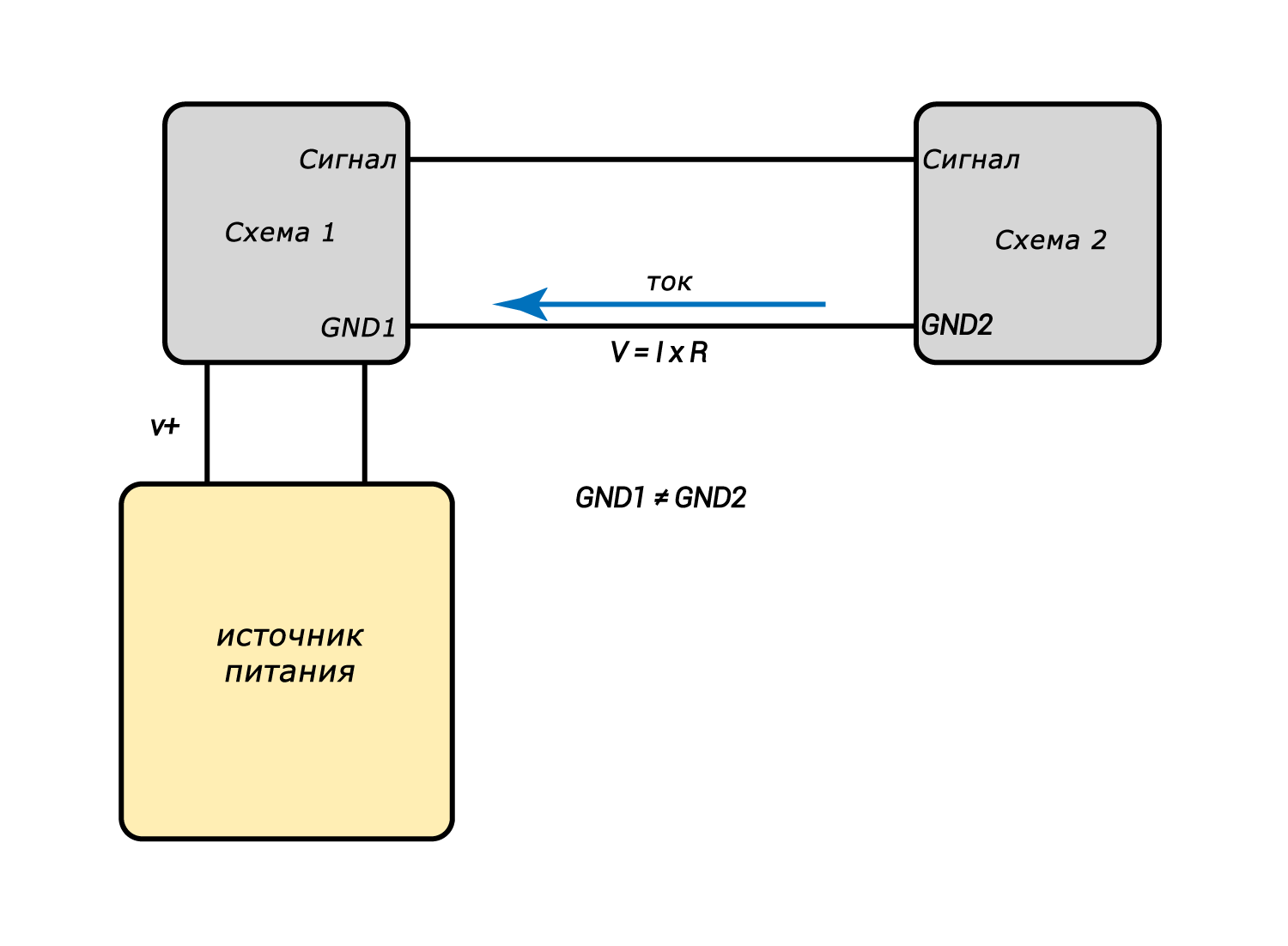
Основные принципы проектирования схем предполагают, что взаимосвязанные компоненты совместно используют общую точку земли, на которой предполагается 0 В. В реальной жизни, однако, «земля» состоит из проводников, имеющих ненулевое сопротивление, и эти проводники служат в качестве обратного пути протекания тока от схемы назад к источнику питания. Закон Ома напоминает нам, что ток и сопротивление дадут напряжение, и это падение напряжения в обратном пути означает, что «земля» в одной части схемы не точно такая же по потенциалу, как «земля» в другой части схемы. Эта разница в потенциалах земли может привести к проблемам, начиная от незначительных до катастрофических.

Для предотвращения протекания постоянного тока между двумя схемами используется гальваническая развязка, позволяющая успешно общаться схемам с различными потенциалами земли. Это особенно актуально для измерения токов: низковольтный датчик и обрабатывающая цепь могут понадобиться для контроля больших, изменяющихся в больших пределах токов, например, в цепи привода двигателя. Эти большие, быстро изменяющиеся токи приведут к значительным колебаниям напряжения в цепи обратного пути протекания тока. Датчик Холла позволяет системе контролировать ток привода и защитить схему высокоточного датчика от этих вредных колебаний земли.

Синфазное напряжение

Другое важное применение датчиков Холла заключается в измерении токов при работе с высокими напряжениями. В схеме резистивного датчика тока дифференциальный усилитель измеряет разницу между напряжениями на одной стороне резистора и на другой. Проблема возникает, когда эти напряжения велики по сравнению с потенциалом земли:

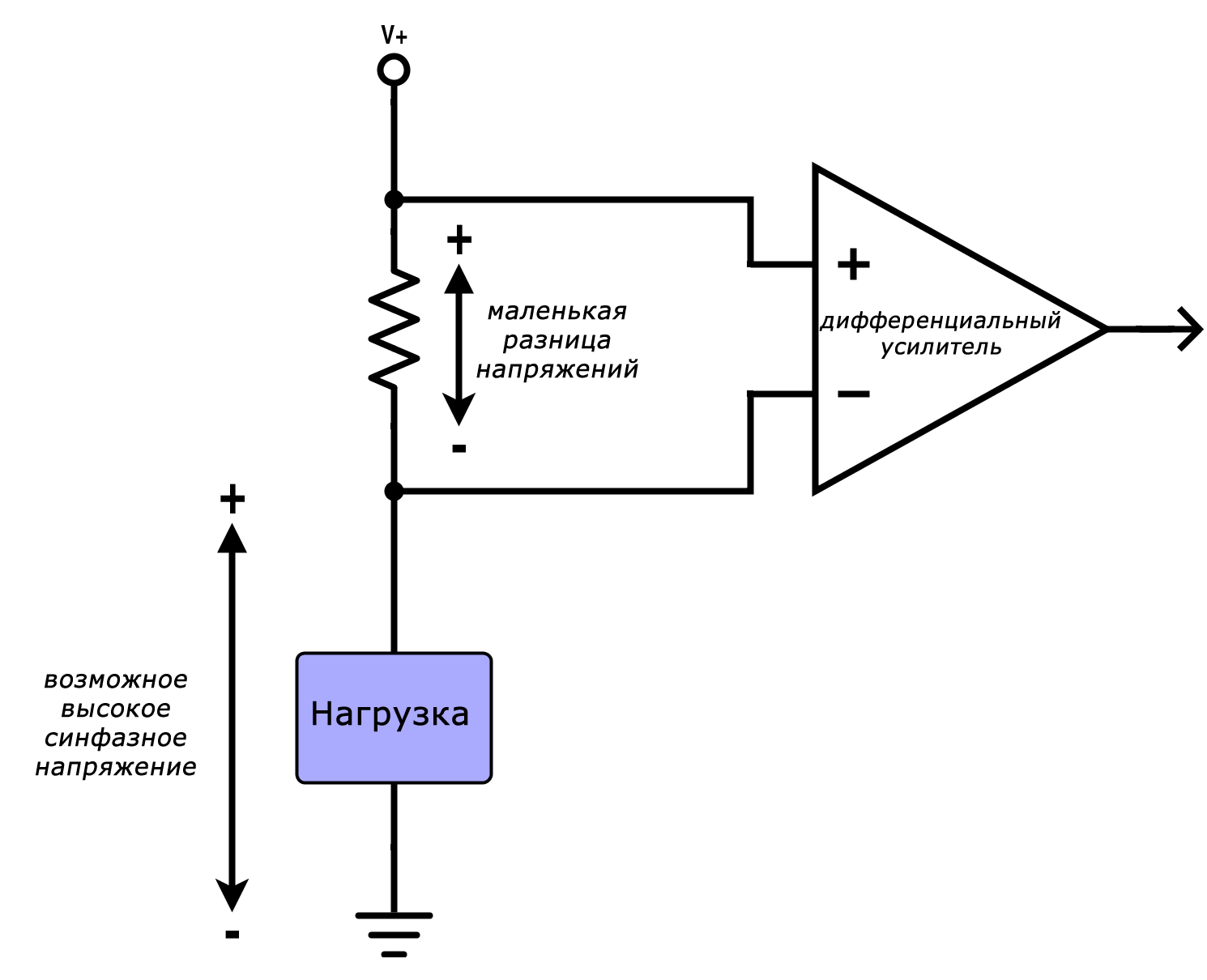
Реальные усилители имеют ограниченный «диапазон синфазности», что означает, что устройство не будет функционировать должным образом, разница между входными напряжениями мала, и очень велика разница между ними и землей. Диапазоны синфазных входных напряжений токоизмерительных усилителей, как правило, не выходят за пределы 80 или 100 В. С другой стороны, датчики Холла могут преобразовать ток в напряжение без связи с потенциалом земли в измеряемой цепи. Следовательно, пока напряжение не достаточно велико, чтобы вызвать физическое повреждение, синфазное напряжение не влияет на работу датчика Холла.

Оригинал статьи

Теги

Гальваническая развязкаДатчикДатчик токаДатчик ХоллаЗемляная петляИзмерениеИзмерение токаМагнитное полеЭлектрический токЭффект Холла

Сохранить или поделиться

29. Эффект Холла и его применение.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 годув тонких пластинках золота.

Впростейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле  течёт электрический ток под действием напряжённости . Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов не скомпенсирует магнитную составляющую силы Лоренца:

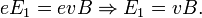
Скорость электронов 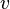 можно выразить через плотность тока:

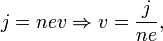
где 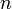— концентрация носителей заряда. Тогда

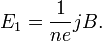
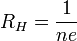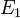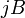Коэффициент  пропорциональности между  и  называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак 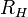, что объясняется в полуклассической и квантовой теориях твёрдого тела.

Аномальный эффект Холла

Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.

Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах с намагниченностью^[2].

Квантовый эффект Холла

Основная статья: Квантовый эффект Холла

В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.

Спиновый эффект Холла

Основная статья: Спиновый эффект Холла

В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.