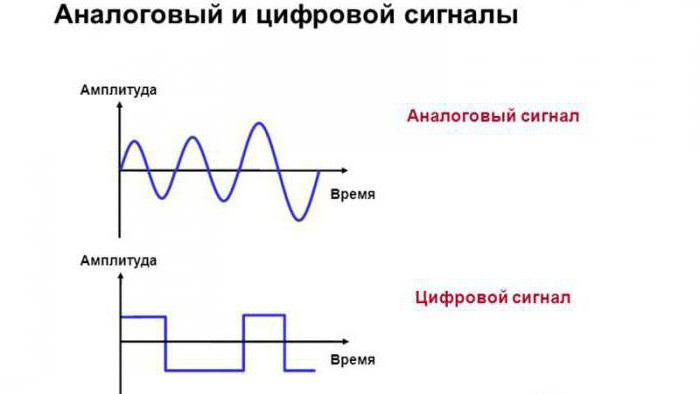
Аналоговые и дискретные сигналы примеры

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Страница проекта на GitHub.

Содержание

Вводные понятия

Сигнал называют аналоговым, если он определен на непрерывной оси времени , и в каждый момент может принимать произвольные значения. Аналоговый сигнал может быть представлен непрерывной, или кусочно-непрерывной функции переменной . Пример аналогового сигнала показан на рисунке 1.

Если сигнал принимает произвольные значения только в фиксированные моменты времени , — целое число, то такой сигнал называется дискретным. Наиболее широкое распространение получили дискретные сигналы, определенные на равноотстоящей сетке , где — интервал дискретизации. При этом в моменты дискретизации дискретный сигнал может принимать произвольные значения. Если значения дискретного сигнала также берутся на фиксированной сетке значений, и при этом сами значения могут быть представлены числом конечной разрядности в одной из систем счисления, то такой дискретный сигнал называется цифровым . Часто говорят, что цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Примеры дискретного и цифрового сигналов также показаны на рисунке 1. Тонкая разница между дискретными и цифровыми сигналами дает возможность их отождествлять практически во всех прикладных задачах. Аналоговый сигнал может быть описан функцией времени, в то время как дискретный и цифровой сигналы могут быть заданы вектором отсчетов :

Указанный преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов. Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.

Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).

Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

В данном параграфе мы рассмотрим способ выборки дискретных значений аналогового сигнала. Структурная схема устройства дискретизации показана на рисунке 2. Данное устройство называется аналого-цифровой преобразователь (АЦП), потому что оно преобразует аналоговый сигнал в набор оценок дискретных значений , где — целое число, взятых через равноотстоящие промежутки времени .

Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).

На входе АЦП имеется аналоговый сигнал . Генератор импульсов формирует равноотстоящие стробирующие импульсы , которые управляют ключом, в результате чего на вход усилителя подаются котроткие выборки сигнала длительности длительности , взятые через интервал дискретизации .

Оценка дискретного сигнала может быть представлена в виде

Интегрируя на каждом интервале длительности стробирующего импульса получим оценку значения сигнала в момент времени . При конечной величине мы можем говорить об оценке значения сигнала в момент времени с некоторой погрешностью, ввиду изменения сигнала на интервале . Поэтому мы используем шапочку над обозначением , чтобы подчеркнуть приближенную оценку.

При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :

В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.

Размерность дискретного сигнала

Пусть исходный аналоговый сигнал описывает изменение напряжения во времени и имеет размерность вольт . Вспомним, что дельта-функция Дирака имеет размерность, обратную размерности ее аргумента. Тогда решетчатая функция , согласно (4) имеет размерность , а размерность дискретного сигнала (5) будет .

Заметим, что значения дискретного сигнала, полученные из (6) как результат интегрирования дискретного сигнала в окрестности момента времени , будут иметь размерность исходного сигнала .

Преобразование Фурье решетчатой функции

В данном разделе мы проанализируем спектральную плотность решетчатой функции . Для начала рассмотрим как периодический сигнал. Тогда можно представить в виде разложения в ряд Фурье:

Тогда (7) с учетом (8):

Выражение (10) представляет как бесконечную сумму комплексных экспонент.

Рассмотрим теперь преобразование Фурье решетчатой функции:

Поменяем операции интегрирования и суммирования и применим фильтрующее свойство дельта-функции:

Выражение (12) также представляет собой бесконечную сумму комплексных экспонент. Учтем, что и получим:

Таким образом, спектральная плотность решетчатой функции представляет собой также решетчатую функцию.

Период повторения дельта-функций в частотной области равен , при этом дельта-функции масштабируются в раз, как это показно на рисунке 5.

Заметим, что умножение на в частотной области изменяет размерность спектральной плотности , в результате чего спектральная плотность переходит в безразмерный спектр (что не удивительно, потому что исходная решетчатая функция — периодическая).

Спектральная плотность дискретного сигнала

Пусть дан аналоговый сигнал , спектральная плотность которого равна . В данном параграфе мы рассмотрим процесс равноотстоящей дискретизации сигнала в частотной области.

Преобразование Фурье дискретного сигнала (5) равно:

Применим свойство преобразования Фурье произведения сигналов, тогда представляет собой свертку спектральной плотности решетчатой функции и спектральной плотности исходного сигнала :

Уравнение (17) задает спектральную плотность дискретного сигнала как бесконечную сумму масштабированных копий спектральной плотности , отстоящих друг от друга на рад/с по частоте, как это показано на рисунке 6.

Заметим, что мы не накладываем никаких ограничений ни на интервал дискретизации , ни на сигнал , ни на спектральную плотность . Вне зависимости от частоты дискретизации рад/с, и формы , спектральная плотность дискретного сигнала всегда будет представлять собой сумму масштабированных копий , отстоящих друг от друга на величину частоты дискретизации рад/с.

Размерность спектра дискретного сигнала

Проанализируем выражение (17) на предмет размерности , в предположении, что исходный аналоговый сигнал имеет размерность :

Если аналоговый сигнал описывает изменения напряжения во времени и измеряется в единицах вольт, то при дискретизации аналогового сигнала, получим дискретные отсчеты, также измеряемые в вольт, и спектр дискретного сигнала также будет измеряться в единицах вольт. Тогда функцию мы можем назвать спектром, а не спектральной плотностью.

Главный вывод: преобразование Фурье дискретного сигнала не изменяет размерности дискретных отсчетов сигнала, в отличии от преобразования Фурье аналогового сигнала, которое возвращает спектральную плотность .

Выводы

В данном разделе мы ввели понятие дискретного и цифрового сигналов. Мы опеределили, что дискретный сигнал может быть представлен как результат произведения решетчатой функции и аналогового сигнала.

Были детально рассмотрены свойства решетчатой функции и показано, что спектральная плотность решетчатой функции также представляет собой масштабированную по амплитуде решетчатую функцию.

В результате свойств решетчатой функци получили, что спектральная плотность дискретного сигнала представляется бесконечной суммой копий спектральных плотностей исходного сигнала, отставленных дург от друка на величину равную частоте дискретизации.

Каждый день люди сталкиваются с использованием электронных приборов. Без них невозможна современная жизнь. Ведь речь идет о телевизоре, радио, компьютере, телефоне, мультиварке и прочем. Раньше, еще несколько лет назад, никто не задумывался о том, какой сигнал используется в каждом работоспособном приборе. Сейчас же слова «аналоговый», «цифровой», «дискретный» уже давно на слуху. Некоторые виды сигналов из перечисленных являются качественными и надежными.

Цифровая передача стала использоваться намного позже, чем аналоговая. Это связано с тем, что такой сигнал намного проще обслуживать, да и техника на тот момент не была настолько усовершенствована.

С понятием «дискретность» сталкивается каждый человек постоянно. Если переводить это слово с латинского языка, то означать оно будет «прерывистость». Углубляясь далеко в науку, можно сказать, что дискретный сигнал представляет собой метод передачи информации, который подразумевает изменение во времени среды-переносчика. Последняя принимает любое значение из всех возможных. Сейчас дискретность уходит на второй план, после того, как было принято решение производить системы на чипе. Они являются целостными, а все компоненты тесно взаимодействуют друг с другом. В дискретности же все с точностью наоборот – каждая деталь завершена и связана с другими за счет специальных линий связи.

Сигнал

Сигнал представляет собой специальный код, который передается в пространство одной или несколькими системами. Эта формулировка является общей.

В сфере информации и связи сигналом назван специальный носитель каких-либо данных, который используется для передачи сообщений. Он может быть создан, но не принят, последнее условие не обязательно. Если же сигнал является сообщением, то его «ловля» считается необходимой.

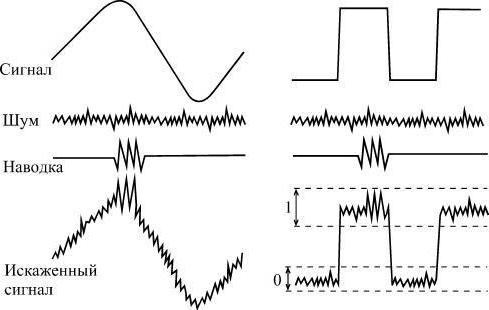
Описываемый код передачи данных задается математической функцией. Она характеризует все возможные изменения параметров. В радиотехнической теории эта модель считается базовой. В ней же аналогом сигнала был назван шум. Он представляет собой функцию времени, которая свободно взаимодействует с переданным кодом и искажает его.

В статье охарактеризованы виды сигналов: дискретный, аналоговый и цифровой. Также коротко дана основная теория по описываемой теме.

Виды сигналов

Существует несколько типов классификации имеющихся сигналов. Рассмотрим, какие бывают виды.

1. По физической среде носителя данных разделяют электрический сигнал, оптический, акустический и электромагнитный. Имеется еще несколько видов, однако они малоизвестны.
2. По способу задания сигналы делятся на регулярные и нерегулярные. Первые представляют собой детерминированные методы передачи данных, которые задаются аналитической функцией. Случайные же формулируются за счет теории вероятности, а также они принимают любые значения в различные промежутки времени.
3. В зависимости от функций, которые описывают все параметры сигнала, методы передачи данных могут быть аналоговыми, дискретными, цифровыми (способ, который является квантованным по уровню). Они используются для обеспечения работы многих электрических приборов.

Теперь читателю известны все виды передачи сигналов. Разобраться в них не составит труда любому человеку, главное — немного подумать и вспомнить школьный курс физики.

Для чего обрабатывается сигнал?

Сигнал обрабатывается с целью передачи и получения информации, которая в нем зашифрована. Как только она будет извлечена, ее можно использовать различными способами. В отдельных ситуациях ее переформатируют.

Существует и другая причина обработки всех сигналов. Она заключается в небольшом сжатии частот (чтобы не повредить информацию). После этого ее форматируют и передают на медленных скоростях.

В аналоговом и цифровом сигналах используются особенные методы. В частности, фильтрация, свертка, корреляция. Они необходимы для восстановления сигнала, если он поврежден или имеет шум.

Создание и формирование

Зачастую для формирования сигналов необходим аналого-цифровой (АЦП) и цифро-аналоговый (ЦАП) преобразователи. Чаще всего они оба используются лишь в ситуации с применением DSP-технологий. В остальных случаях подойдет только использование ЦАП.

При создании физических аналоговых кодов с дальнейшим применением цифровых методов полагаются на полученную информацию, которая передается со специальных приборов.

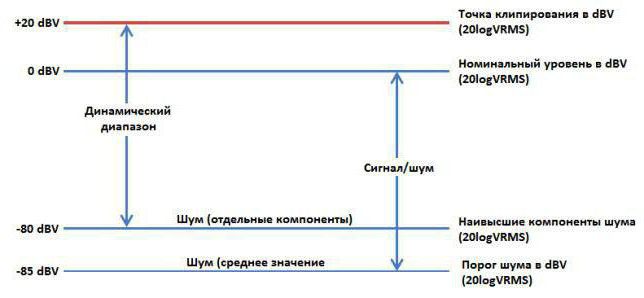
Динамический диапазон

Диапазон сигнала вычисляется разностью большего и меньшего уровня громкости, которые выражены в децибелах. Он полностью зависит от произведения и особенностей исполнения. Речь идет как о музыкальных треках, так и об обычных диалогах между людьми. Если брать, например, диктора, который читает новости, то его динамический диапазон колеблется в районе 25-30 дБ. А во время чтения какого-либо произведения он может вырастать до 50 дБ.

Аналоговый сигнал

Аналоговый сигнал является непрерывным во времени способом передачи данных. Недостатком его можно назвать присутствие шума, который иногда приводит к полной потере информации. Очень часто возникают такие ситуации, что невозможно определить, где в коде важные данные, а где обычные искажения.

Именно из-за этого цифровая обработка сигналов приобрела большую популярность и постепенно вытесняет аналоговую.

Цифровой сигнал

Цифровой сигнал является особым потоком данных, он описывается за счет дискретных функций. Его амплитуда может принять определенное значение из уже заданных. Если аналоговый сигнал способен поступать с огромным количеством шумов, то цифровой отфильтровывает большую часть полученных помех.

Помимо этого, такой вид передачи данных переносит информацию без лишней смысловой нагрузки. Через один физический канал может быть отправлено сразу несколько кодов.

Виды цифрового сигнала не существуют, так как он выделяется как отдельный и самостоятельный метод передачи данных. Он представляет собой двоичный поток. В наше время такой сигнал считается самым популярным. Это связано с простотой использования.

Применение цифрового сигнала

Чем же отличается цифровой электрический сигнал от других? Тем, что он способен совершать в ретрансляторе полную регенерацию. Когда в оборудование связи поступает сигнал, имеющий малейшие помехи, он сразу же меняет свою форму на цифровую. Это позволяет, например, телевышке снова сформировать сигнал, но уже без шумового эффекта.

В том случае, если код поступает уже с большими искажениями, то, к сожалению, восстановлению он не подлежит. Если брать в сравнении аналоговую связь, то в аналогичной ситуации ретранслятор может извлечь часть данных, затрачивая много энергии.

Обсуждая сотовую связь разных форматов, при сильном искажении на цифровой линии разговаривать практически невозможно, так как не слышны слова или целые фразы. Аналоговая связь в таком случае более действенна, ведь можно продолжать вести диалог.

Именно из-за подобных неполадок цифровой сигнал ретрансляторы формируют очень часто для того, чтобы сократить разрыв линии связи.

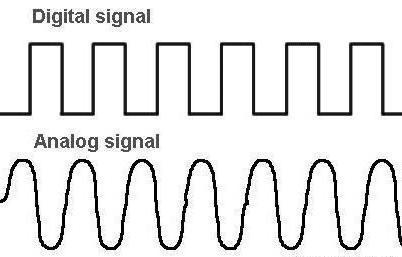
Дискретный сигнал

Сейчас каждый человек пользуется мобильным телефоном или какой-то «звонилкой» на своем компьютере. Одна из задач приборов или программного обеспечения – это передача сигнала, в данном случае голосового потока. Для переноса непрерывной волны необходим канал, который имел бы пропускную способность высшего уровня. Именно поэтому было предпринято решение использовать дискретный сигнал. Он создает не саму волну, а ее цифровой вид. Почему же? Потому что передача идет от техники (например, телефона или компьютера). В чем плюсы такого вида переноса информации? С его помощью уменьшается общее количество передаваемых данных, а также легче организуется пакетная отправка.

Понятие «дискретизация» уже давно стабильно используется в работе вычислительной техники. Благодаря такому сигналу передается не непрерывная информация, которая полностью закодирована специальными символами и буквами, а данные, собранные в особенные блоки. Они являются отдельными и законченными частицами. Такой метод кодировки уже давно отодвинулся на второй план, однако не исчез полностью. С помощью него можно легко передавать небольшие куски информации.

Сравнение цифрового и аналогового сигналов

Покупая технику, вряд ли кто-то думает о том, какие виды сигналов использованы в том или другом приборе, а об их среде и природе уж тем более. Но иногда все же приходится разбираться с понятиями.

Уже давно стало ясно, что аналоговые технологии теряют спрос, ведь их использование нерационально. Взамен приходит цифровая связь. Нужно понимать, о чем идет речь и от чего отказывается человечество.

Если говорить коротко, то аналоговый сигнал – способ передачи информации, который подразумевает описание данных непрерывными функциями времени. По сути, говоря конкретно, амплитуда колебаний может быть равна любому значению, находящемуся в определенных границах.

Цифровая обработка сигналов описывается дискретными функциями времени. Иначе говоря, амплитуда колебаний этого метода равна строго заданным значениям.

Переходя от теории к практике, надо сказать о том, что аналоговому сигналу характерны помехи. С цифровым же таких проблем нет, потому что он успешно их «сглаживает». За счет новых технологий такой метод передачи данных способен своими силами без вмешательства ученого восстановить всю исходную информацию.

Говоря о телевидении, можно уже с уверенностью сказать: аналоговая передача давно изжила себя. Большинство потребителей переходят на цифровой сигнал. Минус последнего заключается в том, что если аналоговую передачу способен принимать любой прибор, то более современный способ – только специальная техника. Хоть и спрос на устаревший метод уже давно упал, все же такие виды сигналов до сих пор не способны полностью уйти из повседневной жизни.

Сигнал информационный — физический процесс, имеющий для человека или технического устройства информационноезначение. Он может быть непрерывным (аналоговым) или дискретным

Термин “ «сигнал» очень часто отождествляют с понятиями “данные” (data) и “информация” (information). Действительно, эти понятия взаимосвязаны и не существуют одно без другого, но относятся к разным категориям.

Сигнал— это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко — полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.

Передается информация в виде сигналов. Сигнал есть физический процесс, несущий в себе информацию. Сигнал может быть звуковым, световым, в виде почтового отправления и др

Сигнал является материальным носителем информации, которая передается от источника к потребителю. Он может быть дискретным и непрерывным (аналоговым)

Аналоговый сигнал— сигнал данных, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений.

Аналоговые сигналы описываются непрерывными функциями времени, поэтому аналоговый сигнал иногда называют непрерывным сигналом . Аналоговым сигналам противопоставляются дискретные (квантованные, цифровые).

Примеры непрерывных пространств и соответствующих физических величин: (прямая: электрическое напряжение; окружность: положение ротора, колеса, шестерни, стрелки аналоговых часов, или фаза несущего сигнала; отрезок: положение поршня, рычага управления, жидкостного термометра или электрический сигнал , ограниченный по амплитуде различные многомерные пространства: цвет, квадратурно-модулированный сигнал .)

Свойства аналоговых сигналов в значительной мере являются противоположностью свойств квантованных или цифровых сигналов .

Отсутствие чётко отличимых друг от друга дискретных уровней сигнала приводит к невозможности применить для его описания понятие информации в том виде, как она понимается в цифровых технологиях. Содержащееся в одном отсчёте «количество информации» будет ограничено лишь динамическим диапазоном средства измерения.

Отсутствие избыточности. Из непрерывности пространства значений следует, что любая помеха, внесенная в сигнал , неотличима от самого сигнала и, следовательно, исходная амплитуда не может быть восстановлена. В действительности фильтрация возможна, например, частотными методами, если известна какая-либо дополнительная информация о свойствах этого сигнала (в частности, полоса частот).

Аналоговые сигналы часто используют для представления непрерывно изменяющихся физических величин. Например, аналоговый электрический сигнал , снимаемый с термопары, несет информацию об изменении температуры, сигнал с микрофона — о быстрых изменениях давления в звуковой волне, и т.п.

Дискретный сигналслагается из счетного множества (т.е. такого множества, элементы которого можно пересчитать) элементов (говорят – информационных элементов). Например, дискретным является сигнал “кирпич”. Он состоит из следующих двух элементов (это синтаксическая характеристика данного сигнала): красного круга и белого прямоугольника внутри круга, расположенного горизонтально по центру. Именно в виде дискретного сигнала представлена та информация, которую сейчас осваивает читатель. Можно выделить следующие ее элементы: разделы (например, “Информация”), подразделы (например, “Свойства”), абзацы, предложения, отдельные фразы, слова и отдельные знаки (буквы, цифры, знаки препинания и т.д.). Этот пример показывает, что в зависимости от прагматики сигнала можно выделять разные информационные элементы. В самом деле, для лица, изучающего информатику по данному тексту, важны более крупные информационные элементы, такие как разделы, подразделы, отдельные абзацы. Они позволяют ему легче ориентироваться в структуре материала, лучше его усваивать и готовиться к экзамену. Для того, кто готовил данный методический материал, помимо указанных информационных элементов, важны также и более мелкие, например, отдельные предложения, с помощью которых излагается та или иная мысль и которые реализуют тот или иной способ доступности материала. Набор самых “мелких” элементов дискретного сигнала называется алфавитом, а сам дискретный сигнал называют также сообщением.

Дискретизация – это преобразование непрерывного сигнала в дискретный (цифровой).

Разница между дискретным и непрерывным представлением информации хорошо видна на примере часов. В электронных часах с цифровым циферблатом информация представляется дискретно – цифрами, каждая из которых четко отличается друг от друга. В механических часах со стрелочным циферблатом информация представляется непрерывно – положениями двух стрелок, причем два разных положения стрелки не всегда четко отличимы (особенно если на циферблате нет минутных делений).

Непрерывный сигнал– отражается некоторой физической величиной, изменяющейся в заданном интервале времени, например, тембром или силой звука. В виде непрерывного сигнала представлена настоящая информация для тех студентов – потребителей, которые посещают лекции по информатике и через звуковые волны (иначе говоря, голос лектора), носящие непрерывный характер, воспринимают материал.

Как мы увидим в дальнейшем, дискретный сигнал лучше поддается преобразованиям, поэтому имеет преимущества перед непрерывным. В то же время, в технических системах и в реальных процессах преобладает непрерывный сигнал. Это вынуждает разрабатывать способы преобразования непрерывного сигнала в дискретный.

Для преобразования непрерывного сигнала в дискретный используется процедура, которая называется квантованием.

Цифровой сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.

Дискретный цифровой сигнал сложнее передавать на большие расстояния, чем аналоговый сигнал , поэтому его предварительно модулируют на стороне передатчика, и демодулируют на стороне приёмника информации. Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надёжность передачи информации.

Замечание. Следует иметь в виду, что реальный цифровой сигнал по своей физической природе является аналоговым . Из-за шумов и изменения параметров линий передачи он имеет флуктуации по амплитуде, фазе/частоте (джиттер), поляризации. Но этот аналоговый сигнал (импульсный и дискретный ) наделяется свойствами числа. В результате для его обработки становится возможным использование численных методов (компьютерная обработка).

8 Формы представления сигналов. Аналоговые, дискретные, цифровые сигналы.

Выделяют следующие типы сигналов, которым соответствуют определенные формы их математического описания.

Аналоговый сигнал(analog signal) является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения аргументов. Источниками аналоговых сигналов, как правило, являются физические процессы и явления, непрерывные в динамике своего развития во времени, в пространстве или по любой другой независимой переменной, при этом регистрируемый сигнал подобен (“аналогичен”) порождающему его процессу. Пример математической записи сигнала:

.

Графическое отображение данного сигнала приведено на рисунке 2.12. При этом как сама функция, так и ее аргументы, могут принимать любые значения в пределах некоторых интервалов . Если интервалы значений сигнала или его независимых переменных не ограничиваются, то по умолчанию они принимаются равными от -до +. Множество возможных значений сигнала образует континуум — непрерывное пространство, в котором любая сигнальная точка может быть определена с точностью до бесконечности. Примеры сигналов, аналоговых по своей природе — изменение напряженности электрического, магнитного, электромагнитного поля во времени и в пространстве.

Рисунок 2.12 — Аналоговый сигнал

Дискретный сигнал(discrete signal) по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента. По множеству своих значений он является конечным (счетным) и описывается дискретной последовательностью отсчетов (samples), где,— интервал между отсчетами (интервал или шаг дискретизации, sample time),n= 0, 1, 2,…,N. Величина, обратная шагу дискретизации:, называется частотой дискретизации (sampling frequency). Если дискретный сигнал получен дискретизацией (sampling) аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам.

Пример дискретизации аналогового сигнала, приведенного на рисунке 2.12, представлен на рисунке 2.13. При = const (равномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначениемy(n). В технической литературе в обозначениях дискретизированных функций иногда оставляют прежние индексы аргументов аналоговых функций, заключая последние в квадратные скобки — y[t].

Рисунок 2.13 — Дискретный сигнал

При неравномерной дискретизации сигнала обозначения дискретных последовательностей (в текстовых описаниях) обычно заключаются в фигурные скобки — , а значения отсчетов приводятся в виде таблиц с указанием значений координат. Для числовых последовательностей (равномерных и неравномерных) применяется и следующее числовое описание:. Пример дискретного сигнала – показания прибора фиксируемые оператором через минуту.

Цифровой сигнал(digital signal) квантован по своим значениям и дискретен по аргументу. Он описывается квантованной решетчатой функцией, где— функция квантования с числом уровней квантования, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например — логарифмическим. Задается цифровой сигнал, как правило, в виде дискретного ряда (discrete series) числовых данных — числового массива по последовательным значениям аргумента при= cons, но в общем случае сигнал может задаваться и в виде таблицы для произвольных значений аргумента.

По существу, цифровой сигнал по своим значениям (отсчетам) является формализованной разновидностью дискретного сигнала при округлении отсчетов последнего до определенного количества цифр, как это показано на рисунке 2.14. Цифровой сигнал конечен по множеству своих значений. Процесс преобразования бесконечных по значениям аналоговых отсчетов в конечное число цифровых значений называется квантованием по уровню, а возникающие при квантовании ошибки округления отсчетов (отбрасываемые значения) – шумами (noise) или ошибками (error) квантования (quantization).

Рисунок 2.14 — Цифровой сигнал

1.3 Сигналы непрерывные и дискретные. Преобразование сигналов.

Информация (сообщения и сигналы) может существовать в двух формах: непрерывной и дискретной.

В большинстве случаев информация о протекании того или иного физического процесса вырабатывается соответствующими датчиками в виде сигналов, непрерывно изменяющихся во времени. Такой сигнал можно представить в виде непрерывной функции Х(t) непрерывного аргументаt– функции, которая может принимать любые вещественные значения в интервале (X_min,X_max) для любых значений аргументаtв интервале (0, Т) (рис. 1.10а). Множество значений непрерывной функции бесконечно.

Дискретные сообщения и сигналы состоят из конечного множества элементов, поступающих последовательно во времени. Набор элементов (символов) составляет алфавит источника дискретной информации. Обычно элементами дискретных сигналов являются последовательности чисел.

Для передачи информации по каналу связи и ее дальнейшей обработки средствами вычислительной техники непрерывный сигнал преобразуют в дискретный. Это преобразование осуществляется с помощью специальных устройств – преобразователей непрерывных сигналов и может быть выполнено дискретизацией во времени, квантованием по уровню или одновременно дискретизацией во времени и квантованием по уровню. При этом соответственно возможны три разновидности сигналов.

Дискретизация во временисостоит в преобразовании непрерывного сигнала Х(t) непрерывного аргументаt(рис. 1.10а) в непрерывный сигнал Х(t_i) дискретного аргументаt_iс шагом дискретизации ∆t(рис. 1.10б). Сигнала Х(t_i) может принимать любые значения в интервале (X_min,X_max), но лишь на дискретном множестве значений аргументаt_i(t₁,t₂, …,t_к) в интервале (0, Т). Какой бы малый шаг дискретизации не выбирался, множество значений дискретной функции будет конечно (ограничено). Примером такого сигнала может быть последовательность импульсов, модулированных по амплитуде. Рассмотренная дискретизации является равномерной, т.к. длительность шага дискретизации ∆t_i=constна всем интервале (0, Т). Дискретизация может быть и неравномерной, если длительность шага ∆t_iразлична (∆t_i=var). Методы изменения шага ∆t_iмогут быть адаптивными, когда он изменяется в зависимости от текущего изменения параметров сигнала, и программируемыми, когда он изменяется в соответствии с заранее установленной программой или оператором, на основе анализа поступающей информации. Очевидно, что каждый вид дискретизации имеет свои преимущества и недостатки. Все же в основном, применяется равномерная дискретизация, так как алгоритмы и аппаратура для ее реализации существенно проще. Однако очевидно, что при этом в случае медленно изменяющихся сигналов возможны «лишние» отсчеты, т.е. избыточность информации.

Квантование по уровнюсостоит в преобразовании непрерывных значений сигнала Х(t_i) в дискретные значения. При этом образуется дискретный сигнал непрерывного аргумента; соседние значения сигнала различаются на элементарную величину ∆Х – квант (рис. 1.10в). Значения, которые может принимать сигнал Х(t), образуют дискретный ряд заранее заданных чисел Х₁, Х₂,…Х_кили уровней 1, 2, 3, 4 и т.д.; значение аргументаtможет быть любым в интервале (0,Т). Примером такого сигнала может быть сигнал на выходе проволочного потенциометра, выходное напряжение которого квантуется за счет скачков сопротивления при перемещении движка с витка на виток. Можно отметить, что квантование по уровню может быть и неравномерным, если ∆Х=var. В основном, используется равномерное квантование — ∆Х=const.

С

Преобразование непрерывного сигнала в дискретный

овместное применение операции дискретизации во времени и квантования по уровнюпозволяет преобразовать непрерывный сигнал Х(t) в дискретный по координатам Х иt(рис. 1.10г). При этом образуется дискретный сигнал дискретного аргумента. Значения сигнала Х(t) и аргументаtобразуют дискретные ряды чисел Х₁, Х₂, …Х_киt₁,t₂, …t_к, заполняющие интервалы (Х_min,Х_max) и (0,Т) соответственно.

Первые две из рассмотренных разновидностей принадлежат дискретно-непрерывным сигналам, а третья – дискретному сигналу. Последний называется также цифровым, так как дискретные значения сигнала обычно представляются в цифровой форме.

Рассмотрим некоторые вопросы, связанные с точностью представления непрерывных сигналов Х(t) в результате дискретизации во времени и квантования по уровню.

В результате дискретизации во времени исходный непрерывный сигнал Х(t) представляется конечной последовательностью отдельных значений Х(t_i), измеренных с шагом дискретизации ∆t=t_i-t_i-1. По значениям Х(t_i) можно восстановить исходный сигнал Х(t) с некоторой погрешностью. Функцию Х(t), полученную в результате восстановления (интерполяции) по значениям Х(t_i), называют воспроизводящей. При дискретизации возникает вопрос о точности преобразования, которая очевидно зависит от частоты отсчетов функцииf_k=1/∆t_i, т.е. от выбранного шага дискретизации ∆t_i. С одной стороны, очевидно, что с уменьшением (увеличением) ∆t_iточность преобразования будет расти (уменьшаться) за счет увеличения (уменьшения) количества отсчетов. С другой стороны, очевидно, что нет смысла стремиться всегда брать отсчеты как можно чаще, независимо от вида сигнала Х(t), так как в случае медленно изменяющегося сигнала Х(t) два соседних значения Х(t_i) и Х(t_i+1) могут быть настолько связаны (коррелированны) между собой, что по одному из них Х(t_i) можно прогнозировать другое Х(t_i+1), т.е. никакой новой информации о сигнале при его последующем восстановлении по отсчетам это не дает. Проблема обеспечении точности дискретизации может быть сформулирована следующим образом: с каким максимальным интервалом необходимо брать отсчеты значений сигнала Х(t_i), чтобы не пропустить существенных его изменений или, другими словами, какое минимальное количество отсчетов необходимо брать для обеспечения заданной точности воспроизведения сигнала Х(t). От этого, в конечном счете, зависит количество информации, которую надо хранить и преобразовывать в вычислительном устройстве.

Возможны различные пути решения указанной проблемы.

В общем виде задача о представлении некоторого сигнала, являющегося непрерывной функцией времени, в виде конечного числа значений, взятых для дискретных значений времени, решена В.А. Котельниковым. В двух теоремах В.А. Котельников применительно к системе передачи сообщений по линии связи определил, как следует выбрать частоту дискретизации, обеспечивающую по полученным дискретным данным последующее воспроизведение исходного сигнала с заданной точностью.

Теорема 1. Любую функцию Х(t), имеющую спектр частот от 0 доf_m, можно представить суммой функцииsinx/x, т.е. рядом:

, (1.51)

где K– целое число,

– отсчеты мгновенных значений функции Х(t) с шагом дискретизации ∆t,

ω_m= 2πf_m,f_m– максимальная частота в спектре частот сигнала Х(t), Гц

ω_m– круговая частота.

Из этой теоремы может быть сделан и обратный вывод: любая функция, представленная рядом Котельникова (1.51), имеет спектр, состоящий из частот от 0 до f_m.

Теорема 2. Любая функция Х(t), содержащая частоты от 0 доf_m, полностью определяется дискретными значениями этой функции, следующими друг за другом с частотой 2f_m, т.е. через интервалсек. Таким образом, передачу непрерывного сигнала Х(t) с ограниченным спектром частот, поступающего от какого-либо датчика, можно свести к передаче последовательности дискретных чисел – значений этого сигнала, взятых через интервал времени 1/2f_m; число этих значений равно 2f_m. Через полученные значения ординат, при обработке результатов измерений, можно провести единственным способом воспроизводящую непрерывную функцию. Поэтому, проще говоря, нет смысла брать отсчеты чаще, чем интервал 1/2f_m, так как никакой новой информации о функции при ее последующем восстановлении по отсчетам это не дает. Следует подчеркнуть, что сказанное справедливо только в том случае, если в получаемой информации действительно отсутствует частоты вышеf_m.

Теоремы В.А. Котельникова, являющиеся основой современной теории передачи сообщений, очень удобны для исследования всевозможных линий связи, вследствие того, что для этих линий известны частотные характеристики, а спектр передаваемых сигналов ограничен. Другое дело – реальные сигналы, имеющие конечную длительность Т. Для их точного представления, в отличие от моделей сигналов с ограниченным спектром (1.51), необходим спектр, который простирался бы от нуля до бесконечности. Теоретически, чтобы избежать погрешности дискретизации, для такого спектра требуется бесконечно большая частота взятия отсчетов. Практически выбирают такую частоту дискретизации, при которой погрешность не превышает заданной величины В этой связи теорему 2 В.А. Котельникова можно рассматривать как приближенную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют как 2f_mk, т.е. интервал между отсчетами

(1.52)

где f_m– максимальная допустимая частота в спектре сигнала Х(t)

k– коэффициент запаса (обычно). Так как безграничный частотный спектр заменяется ограниченным, вне которого спектральная плотность принимается равной нулю, то погрешность дискретизации будет определяться соотношением составляющих, лежащих внутри спектра и вне его.

Другой, практически легко реализуемый путь определения оптимального интервала дискретизации ∆tнепрерывного сигнала Х(t) заключается в построении автокорреляционной функции сигнала и нахождении интервала корреляции τ_к .Дискретные отсчеты, взятые через интервал ∆t=τ_к, будут независимыми и информативными; для их обработки могут быть использованы методы математической статистики.

В случае, когда непрерывный сигнал Х(t) представлен своими дискретными значениями, полученными при равномерной или неравномерной дискретизации, он может быть заменен некоторой приближающей (аппроксимирующей) зависимостью. В общем случае исходный сигнал может быть аппроксимирован специальной функцией или полиномом, график которого проходит через известные дискретные значения. Наиболее часто используются степенные алгебраические полиномы, но так как обычно исходный сигнал задается в графическом или табличном, а не в аналитическом виде, то проведение аппроксимации полиномами с порядком выше первого затруднительно. При аппроксимации полиномом первого порядка все точки кривой, соответствующие дискретным моментам времени, соединяются отрезками прямых (кусочно-линейная аппроксимация). Алгебраические полиномы удобны для программирования и обработки с помощью вычислительной техники

При квантовании исходного сигнала по уровню возникает погрешность квантования. Так как в процессе преобразования значение сигнала Х(t) обычно отображается ближайшим уровнем квантования Х_m, то все значения, кроме кратныхХ, представляются с некоторой погрешностью, максимальное значение которой равно 0,5.

В заключение этого параграфа отметим, что дискретизация и квантование находят широкое применение в преобразователях информации, используемых для связи вычислительных устройств с реальными объектами.

26 вопросов и ответов. Теория электрических цепей. Курс лекций

Можно воспользоваться обратным z-преобразованием (подобно тому как мы пользуемся обратным преобразованием Лапласа):

,

где интегрирование ведется по замкнутому контуру в z-плоскости.

Другой способ заключается в том, чтобы разложить функцию в степенной ряд по степеням . Тогда коэффициенты при степенях будут, в соответствии с формулой (13), отсчетами дискретного сигнала .

Пример 10.1. Найдем дискретный сигнал , которому соответствует z-преобразование .

Воспользуемся разложением функции в ряд .

Для заданного z-преобразования , поэтому запишем z-преобразование в виде

.

Сравнивая полученное выражение с общей формулой z-преобразования , записываем последовательность

{1; 0,5; 0,25; 0,125; …}.

Общий член этой последовательности .

Пример 10.2. Найдем отсчеты дискретного сигнала по его z-преобразованию

.

Для разложения функции в степенной ряд по степеням выполним деление числа 5 на многочлен . В результате получим частное . Отсчеты дискретного сигнала равны

и т.д.

Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе , не слишком сложные.

Более эффективным способом нахождения по известному является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.

Пример 10.3. Найдем общий член дискретного сигнала , которому соответствует z-изображение, заданное в примере 10.2

.

Функция имеет полюсы в точках и , или, что то же, в точках и .

Разложим на сумму простых дробей:

. (16)

Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления реактивных двухполюсников при синтезе их по схеме Фостера:

Подобно тому, как формула (15) представляет сумму ряда (14), простые дроби в (16) являются суммами рядов

и .

Поскольку z-преобразование – это линейная операция, то последовательность состоит из суммы двух последовательностей:

.

После выполнения операции возведения в степень n получим отсчеты дискретного сигнала

и т.д.

Самоконтроль

1. Какие способы используются для нахождения дискретного сигнала по его z-преобразованию?

2. Запишите общий член последовательности , имеющей z-преобразование .

3. Запишите общий член последовательности , имеющей z-преобразование . Найдите значения , и этой последовательности.

15. Энергия дискретного сигнала. Цифровая обработка сигналов

Категория: Цифровая обработка сигналов

В качестве энергии W_x дискретного сигнала x(nT) применяется мера:

Энергию можно вычислить и в частотной области, применяя равенство Парсеваля:

– спектр сигнала x(nT).

– спектр инверсного сигнала x(-nT).

X(jω) · X^*(jω) = X²(ω) = S_x(jω) – энергетический спектр сигнала x(nT).

Энергетическому спектру S_x(jω) соответствует во временной области корреляционная функция S_x(nT) сигнала x(nT).

В соответствии с определением энергетического спектра корреляционная функция определяется сверткой сигнала с инверсной копией.

– формула корреляции сигнала x(nT).

Согласно формуле корреляции в точке:

n = 0

Если S_x(jω) – спектр непрерывного сигнала S_x(nT), то S_x(jmω₁) – спектр периодической дискретной последовательности S_x(nT).

Периодическая дискретная последовательность S_x(nT) определяется через свой спектр по формуле обратного ДПФ.

При n = 0

– равенство Парсеваля для периодической дискретной последовательности.

1.3. СПЕКТР ДИСКРЕТНОГО СИГНАЛА

8

Рис. 1.4. Эквивалентная схема дискретизации сигнала по времени

В математике дискретные сигналы относятся к классу так называемых

решетчатых функций или временных рядов.

Спектральную плотность дискретного сигнала X(jω ), для упрощения называемую в дальнейшем спектром, можно найти, дискретизировав по времени преобразование Фурье соответствующего ему аналогового сигнала

∞
X a ( jω ) = ∫ x( t )e− jω t dt . Заменив	t	на nТд, интеграл	на сумму и dt на Тд,
− ∞
получим	∑∞
X ( jω ) = Tд		x( nTд )e− jω nTд .	(1.2)
	n=	−∞

С другой стороны, он может быть найден и прямым преобразованием Фурье дискретного сигнала, представленного функцией непрерывного времени (1.1):

X д ( jω ) = ∫ xд ( t )e− jω t dt =	∑∞	∫ x( t )δ	( t− nTд )e− jω	t dt = ∑∞	x( nTд )e− jω nTд 1.3)
∞		∞
− ∞	n= −∞	− ∞		n=	−∞

(при выводе использовано фильтрующее свойство δ -функции [1]). Выражения (1.2) и (1.3) отличаются только масштабным (и размерным)

множителем Тд, который при односкоростной обработке обычно опускают.

д ) nTд

9

В силу периодичности комплексной экспоненты e− jω nTд = e− j(ω + kω

спектр дискретного сигнала в отличие от аналогового периодичен по частоте с периодом ω д: Х(jω ) = X[j(ω + kω д)], k = 0, ± 1, ± 2,… (рис.1.5).

Периодизация спектра обусловлена дискретизацией сигнала по времени.

Справедливо и обратное утверждение о периодичности сигналов с дискретным по частоте (или линейчатым) спектром. Оба эти свойства отвечают фундаментальному положению о взаимосвязи дискретизации и периодизации сигналов во временной и частотной области [1].

Определяют спектр дискретного сигнала в основной полосе частот

(0 ± ω д/2).

1.4. СВЯЗЬ МЕЖДУ СПЕКТРАМИ ДИСКРЕТНОГО И АНАЛОГОВОГО СИГНАЛОВ. ЯВЛЕНИЕ НАЛОЖЕНИЯ СПЕКТРОВ

Связь между спектрами дискретного и аналогового сигналов получается на основе определения дискретного сигнала (1.1), в котором дискретизирующая функция fδ (t) представляется или заменяется

аппроксимирующим ее рядом Фурье fδ ( t ) = ∑∞					Ck e jkω дt :
хд(t) = x( t ) ∑∞				k = −∞
				Ck e jkω дt .				(1.4)
			k = −∞
		1	nTд	+ Tд / 2		1	e− jkω дnTд =	1
Коэффициенты ряда Ck =				∫δ ( t − nTд )e− jkω	дt dt =				,
	Tд nT
				− T / 2		Tд		Tд
			д	д

как и следовало ожидать, соответствуют равномерному дискретному (или линейчатому) спектру этой периодической функции. Такой спектр может быть описан также непрерывным преобразованием Фурье с помощью частотной дискретизирующей функции

Fδ (jω ) =

1

∑∞

δ (ω − kω д).

Tд k =

−∞

Преобразование Фурье (1.4) при Сk =1/ Тд приводит к выражению

1

∞

∞

jkω

t

− jω

t

1

∞

Хд(jω ) =

∑

−∫∞

x( t )e

д

e

dt =

∑ X a [ j(ω − kω

д )].

(1.5)

Tд k = −∞

Tд k = −∞

Этот же результат дает свертка спектра аналогового сигнала и частотной дискретизирующей функции, соответствующая произведению (1.1) во временной области:

10

Хд(jω ) =

1

∞

X a (jϑ ) Fδ [j(ω −ϑ )]dϑ =

1

∑∞

∞

X a (jϑ )δ (ω − kω д− ϑ )dϑ =

2π −

∫∞

− ∫∞

Tд k = −∞

=

1

∑∞

X a [j(ω − kω д)].

T

−∞

д k =

Из (1.5) следует, что спектр дискретного сигнала с точностью до

постоянного множителя равен сумме спектров аналогового сигнала

Ха(jω ), смещенных по частоте на kω д. Перенос спектра Ха(jω ) на частоты kω д вызван умножением аналогового сигнала на множество комплексных

экспонент e jkω дt , являющихся гармониками дискретизирующей функции fδ (t) (см. (1.4) и рис. 1.4). Он физически объясняет явление размножения или периодизации спектров при дискретизации, которое математически обосновано в 1.3.

Выражение (1.5) может быть проиллюстрировано для различных случаев дискретизации аналоговых сигналов с ограниченным (финитным) и неограниченным спектрами, которые во временной области имеют соответственно бесконечную и конечную длительности.

Первый случай соответствует аналоговому сигналу с финитным спектром, ограниченным максимальной частотой ω m , отвечающей условию: ω m ≤ ω д/2. При этом условии (рис.1.5) спектр дискретного сигнала в основной полосе частот ± ω д/2 (при ω ≤ ω д/2) точно совпадает (до постоянного

множителя Тд) со спектром аналогового сигнала: ТдХд(jω ) = Ха(jω ).
Дискретизация не сопровождается здесь искажениями. Условие ω m ≤ ω д/2 или
ω д ≥ 2ω	m отвечает теореме отсчетов Котельникова. В этом случае возможно
точное	восстановление аналогового сигнала по его дискретным

выборкам с помощью		идеального ФНЧ с		прямоугольной частотной
характеристикой Пω	( jω	), равной Тд при ω	≤	ω д/2 и равной нулю при
	m

ω > ω д/2 (рис. 1.5).

11

Tд Xд(jω )

Пω m (jω )

Xа(jω )

-ω д	-ω	m		0		ω	m	ω д	ω
	-ω	д/2				ω	д/2
				Основная	полоса

Рис. 1.5. Спектральные преобразования при дискретизации аналогового сигнала с финитным спектром в случае ω д ≥ 2ω m

Сигнал на выходе ФНЧ соответствует обратному преобразованию Фурье

	депериодизированного спектра дискретного сигнала Пω							m (jω	)Хд(jω ):
			ω	д / 2	= ∑∞		sin[ω	д ( t −	nTд ) / 2]
	x(t)=	Tд		∫ Пω m (jω ) Хд(jω ) e jω t dω		x (nTд)				. (1.6)
		2π − ω					ω д ( t − nTд ) / 2 )
				д / 2	n=−∞

Выражение (1.6) является разложением аналогового сигнала x(t) в ряд по базисным интерполирующим функциям sinx/x с весовыми коэффициентами x(nTд) (ряд Котельникова), в соответствии с которым и осуществляется его восстановление [1].

Восстановление аналогового сигнала может быть представлено также сверткой дискретного сигнала хд(t) с импульсной характеристикой идеального ФНЧ h(t), связанной обратным преобразованием Фурье с его частотной характеристикой:

			ω	д / 2
	h(t) =	Tд		∫ Пω m (jω ) e jω t dω		= (sin ω дt/2)/(ω	дt/2).	(1.7)
		2π − ω
				д	/ 2
						∞
	Подстановка (1.7) в интеграл свертки х(t) =						и его вычисление
						∫ x д(τ )h(t − τ )dτ
						− ∞

приводят к интерполяционному ряду (1.6).

12

Частота, определяемая как ω д/2 = ω m, носит известное по зарубежной литературе название частоты Найквиста.

Во втором случае, когда сигнал с финитным спектром дискретизируется

с частотой ω д < 2ω m (рис.1.6,					а) спектр дискретного сигнала в основной
полосе	частот	ω	≤ ω д/2		отличается	от	спектра	аналогового
сигнала:
TдХд(jω ) ≠	Ха(jω ). Периодизация спектра Ха(jω ) здесь приводит к перекрытию
и суммированию			его	с	соседними	смещенными		по	частоте
спектрами Ха[j(ω		−	kω д)]	(на рис.1.6, а k		= ± 1). Это явление называют

наложением спектров при дискретизации. Связанные с ним погрешности дискретизации также называют погрешностями или искажениями наложения. При наложении невозможно точное восстановление аналогового сигнала по его дискретным выборкам.

					Tд Xд(jω	)
					Пω m (jω	)
						Xа(jω	)
-ω д	-ω m -ω 1	-ω′ 1		0	ω′ 1 ω 1 ω m		ω д	ω
	-ω	д/2	Основная полоса			ω д/2

Рис. 1.6 а. Спектральные преобразования при дискретизации аналогового сигнала с финитным спектром в случае ω д < 2ω m

Третий случай соответствует сигналу x(t) конечной длительности Tс с неограниченным по частоте, но затухающим спектром. Такой сигнал можно представить произведением соответствующего ему сигнала бесконечной длительности x∞ (t) и прямоугольной весовой функции ПТс(t) конечной длины Tс: x(t) = x∞ (t)ПТс(t) (так называемый временной фильтр [4]). В частотной области это соответствует свертке спектра Xa∞ (jω ) сигнала x∞ (t) с частотной

характеристикой ПТс(jω ) = sin(ω Tс/2)/(ω Tс/2) весовой функции	Xa(jω ) =
= Xa∞ (jω ) ПТс(jω ), которая и приводит к размыванию по частоте	спектра

сигнала конечной длительности. Это относится, в частности, и к простому гармоническому колебанию, спектр которого при конечной длине сигнала

13

является теоретически бесконечным. Наложение спектров в данном случае (рис.1.6, б) имеет место при любом значении частоты дискретизации, но уровни смещенных по частоте спектров, перекрывающиеся в основной полосе, уменьшаются с ростом частоты дискретизации.

				Tд Xд(jω		)
	Пω m (jω		)	Xa(jω			)
-ω д	-ω m		0		ω m		ω д	ω
-ω	д/2	Основная полоса			ω		д/2

Рис. 1.6 б. Спектральные преобразования при дискретизации аналогового сигнала конечной длительности

Восстановленный с помощью идеального ФНЧ или интерполяционного

!	N − 1		sin[ω д ( t − nTд ) / 2	]
	∑	x (nTд)			отличается по
ряда Котельникова сигнал x(t) =			ω д ( t − nTд ) / 2 )
	n= o

форме от сигнала x(t) и имеет бесконечную длительность. Частота дискретизации сигнала конечной длительности fд = 2fm и число его отсчетов или выборок N = fдTc = 2fmTc, называемое базой сигнала x(t) [1], связываются в данном случае с некоторой частотой его спектра fm, условно принимаемой за максимальную. Она является граничной частотой финитного спектра аппроксимирующего сигнала x!(t) , совпадающего со спектром дискретного

сигнала х(nTд) в основной полосе частот ± fд/2.

С наложением спектров при дискретизации реальных сигналов связано также явление подмены или маскирования частот, в результате которого частотный состав дискретного сигнала в основной полосе частот ± fд/2 может отличаться от состава частот аналогового сигнала в той же полосе частот. Это обусловлено тем, что высокочастотные составляющие сигнала, а также внешние шумы или помехи с частотами ω вч >ω д/2 при дискретизации трансформируются или преобразуются в основную полосу частот дискретного сигнала, создавая помехи наложения на частотах ω ’вч = |ω вч−

14

kω д| ≤ ω д/2. В общем случае такие частотные составляющие либо отсутствуют во входном сигнале, либо накладываются на существующие, искажая исходный спектр. Например, частота ω 1 на рис.1.6, а преобразуется в частоту ω ’1= ω д − ω 1. Говорят, что она подменяет частоту ω ’1 или маскируется под частоту ω ’1, которой во входном сигнале могло и не быть. График преобразования частот аналогового сигнала fАС и дискретного сигнала fДС показан на рис. 1.7.

f Д	fдс
2
f1′
					fАС
0	f Д / 2	f Д	f1	3 f Д / 2	2 f Д

Рис. 1.7. График преобразования частот при дискретизации сигнала

Другой наглядный способ анализа преобразования частот (подмены частот) [35] при дискретизации дает также диаграмма рис. 1.8.

fВЧ

3 f Д

5 f Д / 2

2 f Д

3 f Д / 2

f Д

f Д / 2

fВ’Ч

Рис. 1.8. Диаграмма подмены частот при дискретизации сигнала

Ослабить уровень помех наложения	можно, только ограничив
полосу частот дискретизируемого сигнала,	приведя ее в соответствие с

частотой дискретизации сигнала. В этом и заключается роль аналогового

15

ФНЧ на входе	системы ЦОС, как и его название −
противомаскировочный.

1.5. ОПРЕДЕЛЕНИЕ И ОЦЕНКА МЕТОДИЧЕСКОЙ ПОГРЕШНОСТИ, ВЫЗЫВАЕМОЙ ДИСКРЕТИЗАЦИЕЙ СИГНАЛА ПО ВРЕМЕНИ

Как показано выше, дискретизация сигналов с неограниченным по

частоте спектром, как и сигналов с финитным, но	не отвечающим
условию	∆ x(t) = x(t) −	x(t),
ω д ≤ ω m/2 , сопровождается методической погрешностью
	!

равной разности восстановленного и исходного аналоговых сигналов. Количественно погрешность оценивают предельным значением ∆ x(t) max

или интегральным (среднеквадратичным). Последнее определяют в виде корня квадратного из отношения энергий разностного сигнала (ошибки) Е[∆ x(t)] и исходного Е[x(t)]:

ε

= {Е[∆

x(t)]/Е[x(t)]}1/2,

∞

1

∞

2

где Е[∆ x(t)] =

∫ ∆ x2( t )dt =

∫

X a ( jω ) − X

д ( jω

)Пω д/2 ( jω )

dω ,

2π

−

∞

− ∞

∞

1

∞

2dω .

Е[x(t)] =

∫ x2( t )dt =

∫

X а( jω )

(1.8)

2π

−

∞

− ∞

Двум способам выражения энергии сигналов в (1.8) соответствуют временной и спектральный способы оценки относительной среднеквадратичной погрешности дискретизации, причем спектральный способ оценки во многих случаях оказывается эффективнее [3].

В качестве примера в соответствии с (1.8) рассчитаны погрешности дискретизации прямоугольного импульса длительностью Ти= NTд при различных значениях N = Ти/Tд = Ти fд . Результаты расчета, выполненного с

помощью программы MathCad (рис. 1.9, а) характеризуют зависимость погрешности от частоты дискретизации fд = N/Ти = N∆ fгл/2, где ∆ fгл = 2/Ти –

ширина главного лепестка спектральной плотности прямоугольного импульса. На рис. 1.9, б показан также график восстановленного сигнала x!(t) , вычисленного в моменты времени t = 0,1TД l, l = 0, 1, 2,… для случая N

=16 или fд = 16/Ти .

Опорядке погрешности дискретизации сигналов конечной длительности Tc можно судить также по соотношению [4]: ε = 1/(fmTc). При fд = 2fm и

Tc = NTд оно принимает вид: ε = 2/N. Например, при N = 100 ε = 2%.