Т. Применения силы Лоренца — PhysBook
Использование силы Лоренца. Масс-спектрограф
Действие, оказываемое магнитным полем на движущиеся заряженные частицы, очень широко используют в технике.
Например, отклонение электронного пучка в кинескопах телевизоров осуществляют с помощью магнитного поля, которое создают специальными катушками. В ряде электронных приборов магнитное поле используется для фокусировки пучков заряженных частиц.
В созданных в настоящее время экспериментальных установках для осуществления управляемой термоядерной реакции действие магнитного поля на плазму используют для скручивания ее в шнур, не касающийся стенок рабочей камеры. Движение заряженных частиц по окружности в однородном магнитном поле и независимость периода такого движения от скорости частицы используют в циклических ускорителях заряженных частиц — циклотронах.
Действие силы Лоренца используют и в приборах, называемых масс-спектрографами, которые предназначены для разделения заряженных частиц по их удельным зарядам.
Схема простейшего масс-спектрографа показана на рисунке 1.
Рис. 1
В камере 1, из которой откачан воздух, находится источник ионов 3. Камера помещена в однородное магнитное поле, в каждой точке которого индукция \(~\vec B\) перпендикулярна плоскости чертежа и направлена к нам (на рисунке 1 это поле обозначено кружочками). Между электродами А ч В приложено ускоряющее напряжение, под действием которого ионы, вылетающие из источника, разгоняются и с некоторой скоростью попадают в магнитное поле перпендикулярно линиям индукции. Двигаясь в магнитном поле по дуге окружности, ионы попадают на фотопластинку 2, что позволяет определить радиус R этой дуги. Зная индукцию магнитного поля В и скорость υ ионов, по формуле
можно определить удельный заряд ионов. А если заряд иона известен, можно вычислить его массу.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 328.
Применение силы лоренца. Применение сил Ампера и Лоренца в науке и технике. Амперметр, телеграф, электромагниты, масс-анализаторы
Наряду с силой Ампера, кулоновского взаимодействия, электромагнитными полями в физике часто встречается понятие сила Лоренца. Это явление является одним из основополагающих в электротехнике и электронике, на ряду с , и прочими. Она воздействует на заряды, которые двигаются в магнитном поле. В этой статье мы кратко и понятно рассмотрим, что такое сила Лоренца и где она применяется.
Определение
Когда электроны движутся по проводнику – вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и двигать его – возникнет ЭДС электромагнитной индукции. Если через проводник, который находится в магнитном поле, протекает ток – на него действует сила Ампера.
Её величина зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она вычисляются по формуле:
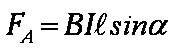
Рассматриваемая сила отчасти похожа на ту, что рассмотрена выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула имеет вид:
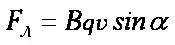
Важно! Сила Лоренца (Fл) действует на электрон, движущийся в магнитном поле, а на проводник – Ампера.
Из двух формул видно, что и в первом и во втором случае, чем ближе синус угла aльфа к 90 градусам, тем большее воздействие оказывает на проводник или заряд Fа или Fл соответственно.
Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое происходит воздействие со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Fл не совершает работы. Соответственно изменяется именно направление скорости движения заряженной частицы, а не её величина.
Что касается единицы измерения силы Лоренца, как и в случае с другими силами в физике используется такая величина как Ньютон. Её составляющие:
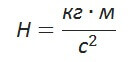
Как направлена сила Лоренца
Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости. Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции.

При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.
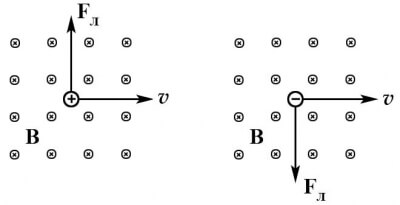
Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц. Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.
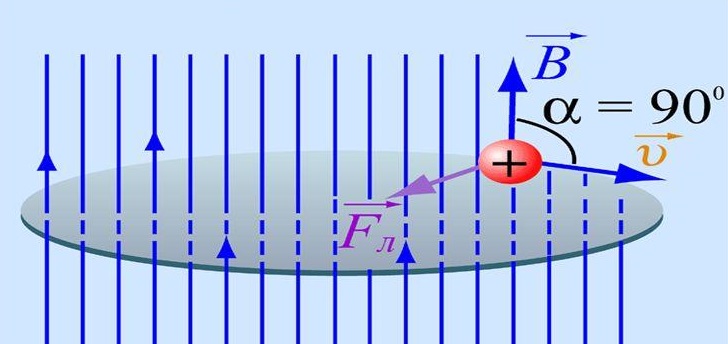
Применение
Из всех сфер, где используется сила Лоренца, одной из масштабнейших является движение частиц в магнитном поле земли. Если рассмотреть нашу планету как большой магнит, то частицы, которые находятся около северного магнитного полюсов, совершают ускоренное движение по спирали. В результате этого происходит их столкновение с атомами из верхних слоев атмосферы, и мы видим северное сияние.
Тем не менее, есть и другие случаи, где применяется это явление. Например:
- Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор испо
Урок физики: Применение силы Лоренца.
Урок 7. Применение силы Лоренца
Цель: показать практическую значимость силы Лоренца.
Ход урока
I. Организационный момент
II. Повторение изученного
— Какую силу называют силой Лоренца?
— Чему равна сила Лоренца?
— Что такое электрическое поле?
— Какое поле называют однородным?
— В каком случае электрическое поле разгоняет заряженную частицу, а в каком тормозит?
— Что такое магнитное поле?
— Как определить направление магнитной силы Лоренца?
— Как движется частица в магнитном поле в разных случаях?
III. Выполнение лабораторной работы
Лабораторная работа
Цели: ознакомление с устройством электронно-лучевой трубки осциллографа, использование знаний о силе Лоренца для определения скорости движения заряда.
Оборудование: подковообразный магнит с рассчитанным модулем В магнитной индукции, линейка, осциллограф (электроннолучевая трубка).
Ход работы
1. Установите след электронного луча (светящуюся точку) в центре экрана, вращая ручки вертикального и горизонтального смещения луча осциллографа. Осторожно прижмите подкову магнита к экрану и измерьте линейкой смещение луча по Y.
2. Зарисуйте положение магнита относительно экрана, начальное и конечное положение луча на экране. Укажите направление линий магнитной индукции между полюсами магнита. Определите направление движения электронов.
3. Радиус кривизны найдите по формуле:
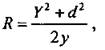
где R — радиус кривизны; d — толщина слоя, где действует магнитное поле; у — смещение.
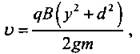
где q и m — табличные данные.
4. Если известно напряжение между ускоряющими электродами осциллографа, то можно провести оценку:

IV. Изучение нового материала
Рассмотрим некоторые из многочисленных применений силы Лоренца, которые встречаются в науке и технике.
1. Управление электронным пучком.
Как видно из лабораторной работы, с помощью магнитных полей можно изменить направление движения электронов. Впервые управлять электронными лучами научился Дж.-Дж. Томсон.
2. Определение скорости движения частиц.
3. Действие магнитного поля на движущиеся заряженные частицы используется для преобразования кинетической энергии плазменной струи в электрическую (МГД-генераторы) (магнитогидродинамики).
Поток плазмы направляется в поперечное магнитное поле, которое действует на движущиеся заряженные частицы  направленное перпендикулярно к скорости их движения. В результате положительные ионы отклоняются вверх, а электроны и отрицательные ионы — вниз.
направленное перпендикулярно к скорости их движения. В результате положительные ионы отклоняются вверх, а электроны и отрицательные ионы — вниз.
Верхний катод электризуется положительно, а нижний — отрицательно, их выводы являются полюсами генератора. Между электродами ток течет снизу вверх. Происходит уменьшение скорости струи и ее кинетической энергии. На МГД-генераторе кинетическая энергия плазменной струи преобразовывается непосредственно в электрическую энергию.
Совместное использование на тепловых электростанциях гидродинамического метода преобразования энергии и обычных паротурбинных установок позволяет значительно повысить экономическую эффективность электростанций.
4. Определение знака заряда движущейся частицы.
5. Магнитные ловушки.
6. Определение удельного заряда и массы частиц.
7. Ускорители заряженных частиц.
8. Электронный микроскоп.
V. Закрепление изученного материала
— Каким методом можно определить скорость заряженных частиц?
— Как с помощью магнитного поля можно узнать заряжена ли частица?
— Опишите принцип действия циклотрона.
VI. Подведение итогов урока
Домашнее задание
П. 6; упр. № 1 (3 : 4).
Дополнительный материал
Полярные сияния
Одним из красивейших оптических явлений природы является полярное сияние.
В большинстве случаев полярные сияния имеют зеленый или сине-зеленый оттенок с изредка появляющимися пятнами или каймой розового или красного цвета.
Полярные сияния наблюдают в двух основных формах — в виде лент и в виде облакоподобных пятен. Когда сияние интенсивно, оно приобретает форму лент. Теряя интенсивность, оно превращается в пятна. Однако многие ленты исчезают, не успев разбиться на пятна. Ленты как бы висят в темном пространстве неба, напоминая гигантский занавес или драпировку, тянущуюся обычно с востока на запад на тысячи километров. Высота этого занавеса составляет несколько сотен километров, толщина не превышает нескольких сотен метров, причем он так нежен и прозрачен, что сквозь него видны звезды. Нижний край занавеса довольно резко и отчетливо очерчен и часто подкрашен в красный или розоватый цвет, напоминающий кайму занавеса, верхний — постепенно теряется в высоте и это создает особенно эффектное впечатление глубины пространства.
Различают четыре типа полярных сияний:
— Однородная дуга — светящаяся полоса имеет наиболее простую, спокойную форму. Она более яркая снизу и постепенно исчезает кверху на фоне свечения неба.
— Лучистая дуга — лента становится несколько более активной и подвижной, она образует мелкие складки и струйки.
— Лучистая полоса — с ростом активности более крупные складки накладываются на мелкие.
При повышении активности складки или петли расширяются до огромных размеров, нижний край ленты ярко сияет розовым свечением. Когда активность спадает, складки исчезают и лента возвращается к однородной форме. Это наводит на мысль, что однородная структура является основной формой полярного сияния, а складки связаны с возрастанием активности.
Часто возникают сияния иного вида. Они захватывают весь полярный район и оказываются очень интенсивными. Происходят они во время увеличения солнечной активности. Эти сияния представляются в виде беловато-зеленой шапки. Такие сияния называют шквалами.
По яркости сияния разделяют на четыре класса, отличающиеся друг от друга на один порядок (то есть в 10 раз). К первому классу относятся сияния еле заметные и приблизительно равные по яркости Млечному Пути, сияния же четвертого класса освещают Землю так ярко, как полная Луна.
Надо отметить, что возникшее сияние распространяется на запад со скоростью 1 км/с. Верхние слои атмосферы в области вспышек сияний разогреваются и устремляются вверх, что сказалось на усиленном торможении искусственных спутников Земли, проходящих эти зоны.
Во время сияний в атмосфере Земли возникают вихревые электрические токи, захватывающие большие области. Они возбуждают дополнительные неустойчивые магнитные поля, так называемые магнитные бури. Во время сияний атмосфера излучает рентгеновские лучи, которые, по-видимому, являются результатом торможения электронов в атмосфере.
Интенсивные вспышки сияния часто сопровождаются звуками, напоминающими шум, треск. Полярные сияния вызывают сильные изменения в ионосфере, что в свою очередь влияет на условия радиосвязи. В большинстве случаев радиосвязь значительно ухудшается. Возникают сильные помехи, а иногда полная потеря приема.
Как возникают полярные сияния. Земля представляет собой огромный магнит, южный полюс которого находится вблизи северного географического полюса, а северный — вблизи южного. Силовые линии магнитного поля Земли, называемые геомагнитными линиями, выходят из области, прилегающей к северному магнитному полюсу Земли, охватывают земной шар и входят в него в области южного магнитного полюса, образуя тороидальную решетку вокруг Земли.
Долго считалось, что расположение магнитных силовых линий симметрично относительно земной оси. Теперь выяснилось, что так называемый «солнечный ветер» — поток протонов и электронов, излучаемых Солнцем, налетая на геомагнитную оболочку Земли с высоты около 20000 км, оттягивает ее назад, в сторону от Солнца, образуя у Земли своеобразный магнитный «хвост».
Электрон или протон, попавшие в магнитное поле Земли, движутся по спирали, как бы навиваясь на геомагнитную линию. Электроны и протоны, попавшие из солнечного ветра в магнитное поле Земли, разделяются на две части. Часть из них вдоль магнитных силовых линий сразу стекает в полярные области Земли; другие попадают внутрь тероида и движутся внутри него, вдоль замкнутой кривой ABC. Эти протоны и электроны в конце концов по геомагнитным линиям также стекают в область полюсов, где возникает их увеличенная концентрация. Протоны и электроны производят ионизацию и возбуждение атомов и молекул газов. Для этого они имеют достаточно энергии, так как протоны прилетают на Землю с энергиями 10000- 20000 эВ (1 эВ = 1,6 ·10 Дж), а электроны с энергиями 10-20 эВ. Для ионизации же атомов нужно: для водорода — 13,56 эВ, для кислорода — 13,56 эВ, для азота — 124,47 эВ, а для возбуждения еще меньше.
Возбужденные атомы газов отдают обратно полученную энергию в виде света, наподобие того, как это происходит в трубках с разреженным газом при пропускании через них токов.
Спектральное исследование показывает, что зеленое и красное свечение принадлежит возбужденным атомам кислорода, инфракрасное и фиолетовое — ионизованным молекулам азота. Некоторые линии излучения кислорода и азота образуются на высоте 110 км, а красное свечение кислорода — на высоте 200-400 км. Другим слабым источником красного света являются атомы водорода, образовавшиеся в верхних слоях атмосферы из протонов, прилетевших с Солнца. Захватив электрон, такой протон превращается в возбужденный атом водорода и излучает красный свет.
Вспышки сияний происходят обычно через день-два после вспышек на Солнце. Это подтверждает связь между этими явлениями. Исследование при помощи ракет показало, что в местах большей интенсивности сияний имеется более значительная ионизация газов электронами.
В последнее время ученые установили, что полярные сияния более интенсивны у берегов океанов и морей.
Но научное объяснение всех явлений, связанных с полярными сияниями, встречает ряд трудностей. Например, неизвестен точно механизм ускорения частиц до указанных энергий, не вполне ясны их траектории в околоземном пространстве, не все сходится количественно в энергетическом балансе ионизации и возбуждения частиц, не вполне ясен механизм образования свечения различных видов, неясно происхождение звуков.
Разработка урока на тему «Применение силы Лоренца»
Применение силы Лоренца
Цель: показать практическую значимость силы Лоренца.
Ход урока
L Организационный момент
II. Повторение изученного
— Какую силу называют силой Лоренца?
— Чему равна сила Лоренца?
— Что такое электрическое поле?
— Какое поле называют однородным?
— В каком случае электрическое поле разгоняет заряженную частицу, а в каком тормозит?
— Что такое магнитное поле?
Как определить направление магнитной силы Лоренца?
— Как движется частица в магнитном поле в разных случаях?
III. Выполнение лабораторной работы
Лабораторная работа
Цели: ознакомление с устройством электронно-лучевой трубки осциллографа, использование знаний о силе Лоренца для определения скорости движения заряда.
Оборудование: подковообразный магнит с рассчитанным модулем В магнитной индукции, линейка, осциллограф (электроннолучевая трубка). .^- —’
Ход работы
1. Установите след электронного луча (светящуюся точку) в центре экрана, вращая ручки вертикального и горизонтального смещения луча осциллографа. Осторожно прижмите подкову магнита к экрану и измерьте линейкой смещение луча по У.
2. Зарисуйте положение магнита относительно экрана, начальное и конечное положение луча на экране. Укажите направление линий
магнитной индукции между полюсами магнита. Определите направление движения электронов.
3. Радиус кривизны найдите по формуле:
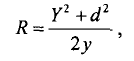
где R — радиус кривизны; d — толщина слоя, где действует магнитное поле; у — смещение.
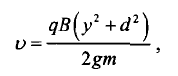
где цулт- табличные данные.
4. Если известно напряжение между ускоряющими электродами осциллографа, то можно провести оценку:
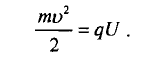
IV. Изучение нового материала
Рассмотрим некоторые из многочисленных применений силы Лоренца, которые встречаются в науке и технике.
1. Управление электронным пучком.
Как видно из лабораторной работы, с помощью магнитных полей можно изменить направление движения электронов. Впервые управлять электронными лучами научился Дж.-Дж. Томсон.
2. Определение скорости движения частиц.
3. Действие магнитного поля на движущиеся заряженные частицы используется для преобразования кинетической энергии плазменной струи в электрическую (МГД-генераторы) (магнитогидродинамики).
Поток плазмы направляется в поперечное магдаггное поле, которое действует на движущиеся заряженные частицы Fn =Bq—v, направленное перпендикулярно к скорости их движения. В результате положительные ионы отклоняются вверх, а электроны и отрицательные ионы — вниз.
Верхний катод электризуется положительно, а нижний — отрицательно, их выводы являются полюсами генератора. Между электродами ток течет снизу вверх. Происходит уменьшение скорости струи и ее кинетической энергии. На МГД-генераторе кинетическая энергия плазменной струи преобразовывается непосредственно в электрическую энергию.
Совместное использование на тепловых электростанциях гидродинамического метода преобразования энергии и обычных паротурбинных установок позволяет значительно повысить экономическую эффективность электростанций.
4. Определение знака заряда движущейся частицы.
5. Магнитные ловушки.
6. Определение удельного заряда и массы частиц.
7. Ускорители заряженных частиц.
8. Электронный микроскоп.
V. Закрепление изученного материала
— Каким методом можно определить скорость заряженных частиц?
— Как с помощью магнитного поля можно узнать заряжена ли частица?
— Опишите принцип действия щпслотрона.
VI. Подведение итогов урока
Домашнее задание п. 6; упр. №1(3:4).
Сила Лоренца — это… Что такое Сила Лоренца?
Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Уравнение (единицы СИ)
Заряженная частица
Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:
где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .Для непрерывного распределения заряда, сила Лоренца принимает вид:
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- , где — 4-сила, q — заряд частицы, — тензор электромагнитного поля, — 4-скорость.
Частные случаи
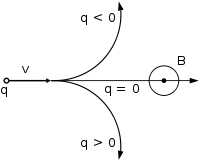 Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :
Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :
Применение силы Лоренца
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеВ электроприборах
Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.
В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
Другие применения
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
См. также
Сила Лоренца
Известно, что на
каждый элемент тока 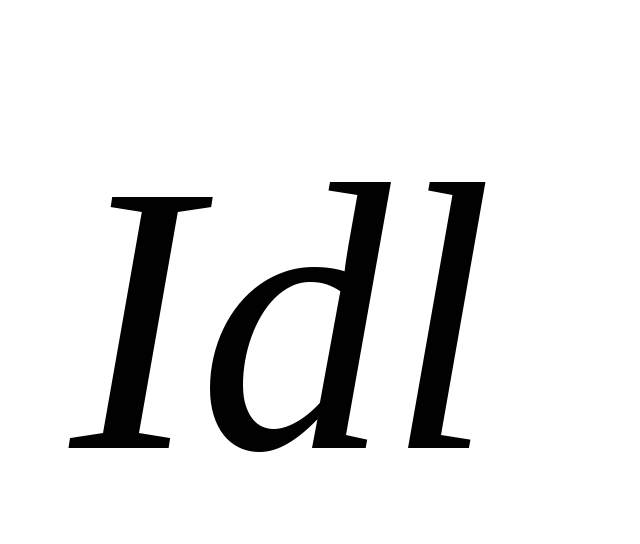 в магнитном поле действует сила Ампера:
в магнитном поле действует сила Ампера:
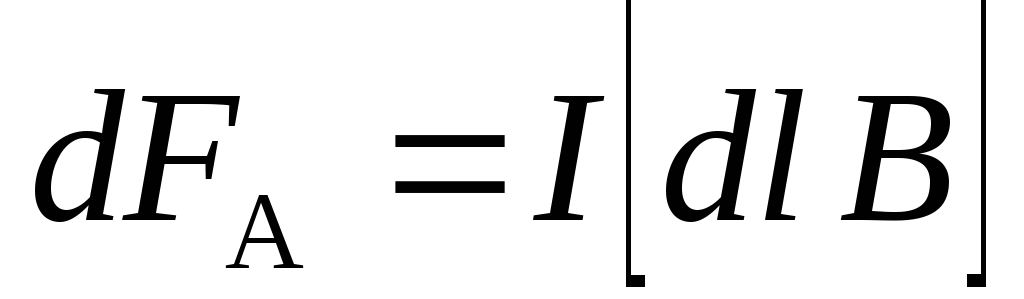 . (9.9)
. (9.9)
Если поместить в магнитное поле проводник
без тока, то никакой силы мы не обнаружим.
Это означает, что магнитное поле «не
чувствует» неподвижные заряды. Но стоит
им придти в направленное движение, в
проводнике появляется ток и на проводник
начинает действовать сила (9.9). Можно
предположить, что магнитное поле
действует на каждый отдельный носитель
заряда, направленно движущийся в
проводнике, а сила Ампера — интегральный
результат сложения всех этих сил. Тогда
силу, действующую в магнитном поле на
движущийся заряд, можно вычислить,
разделив силу Ампера на число носителей
заряда dN, движущихся
со скоростью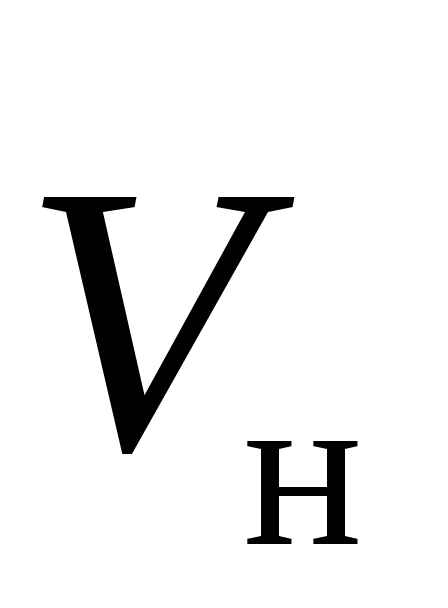 на элементе проводникаdl:
на элементе проводникаdl:
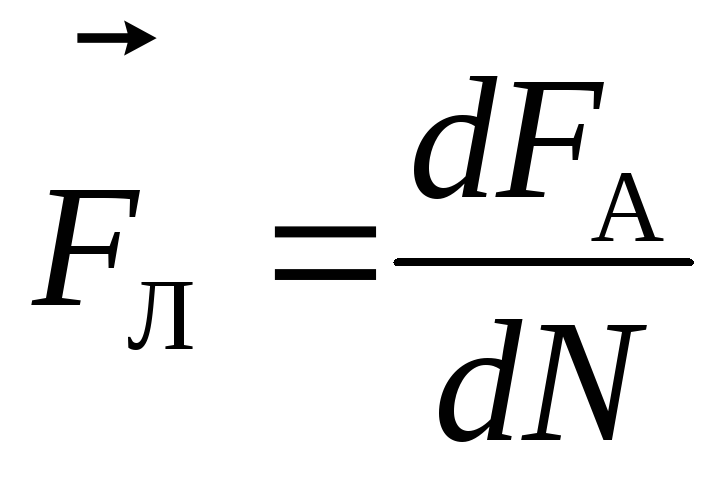 .
.
Здесь dN=nSdl— число носителей заряда. Вспомнив, чтоI=iS, а плотность токаi=nqVн, представим (9.8) в таком виде:
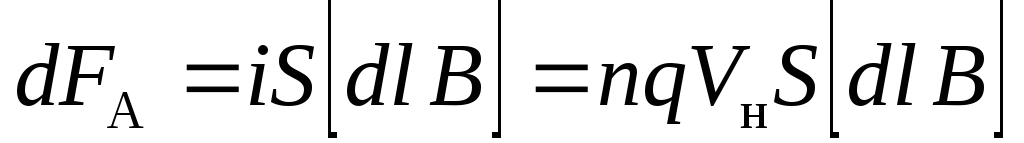 . (9.10)
. (9.10)
По определению, вектор  совпадает по направлению с векторами
плотности тока
совпадает по направлению с векторами
плотности тока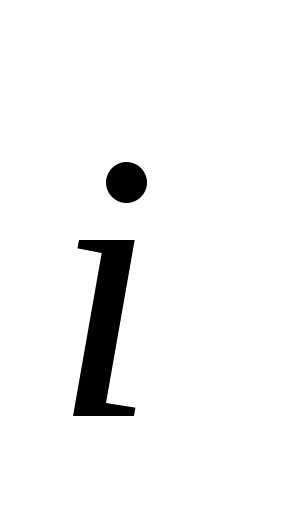 и скорости направленного движения
и скорости направленного движения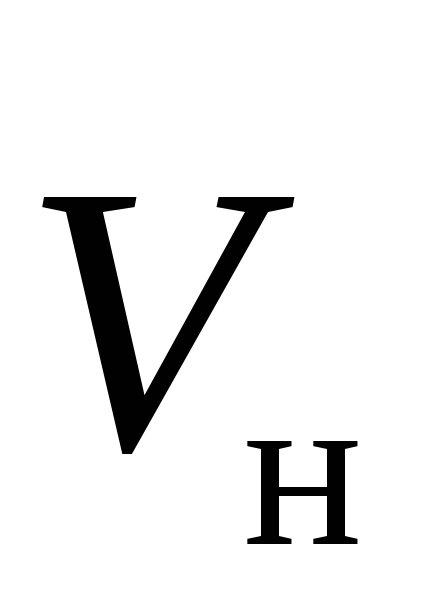 .
Поэтому (9.10) можно переписать ещё и так:
.
Поэтому (9.10) можно переписать ещё и так:
 .
.
Теперь, разделив эту силу на число
носителей заряда dN,
получим силу Лоренца — силу, действующую
на зарядq, движущийся
со скоростью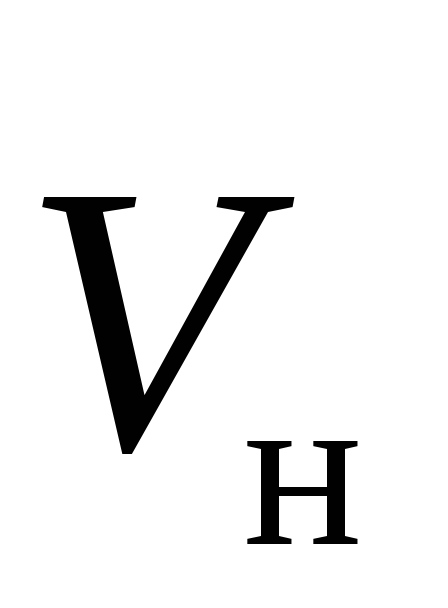 в магнитном поле
в магнитном поле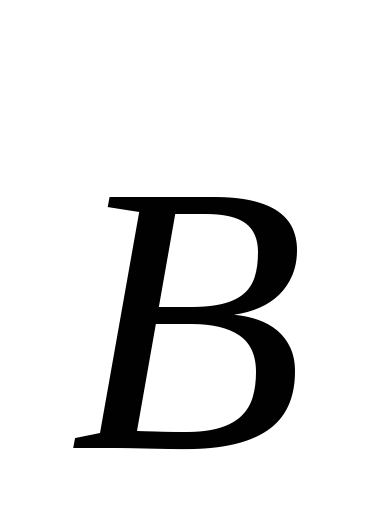 :
:
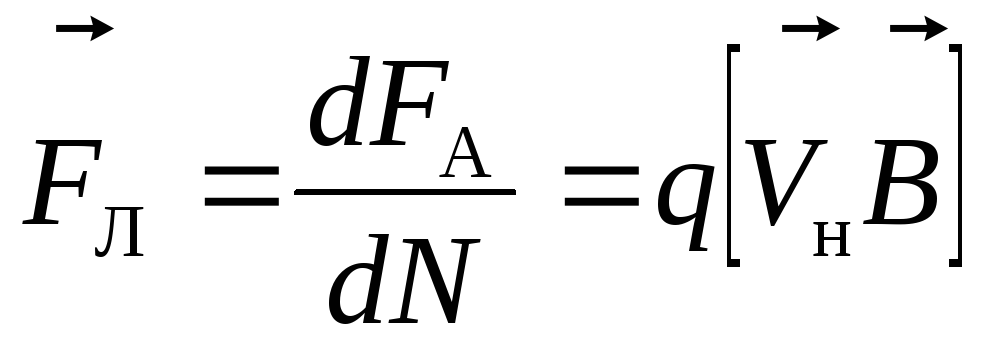 . (9.11)
. (9.11)
Сила Лоренца пропорциональна заряду
движущейся частицы q,
её скоростиVни величине индукции магнитного поляB.
Кроме того, эта сила зависит от угламежду векторами и
и (рис. 9.2.):
(рис. 9.2.):
FЛ=qVнBsin.

Рис. 9.2.
В любом случае сила Лоренца перпендикулярна
и вектору  и скорости движения частицы
и скорости движения частицы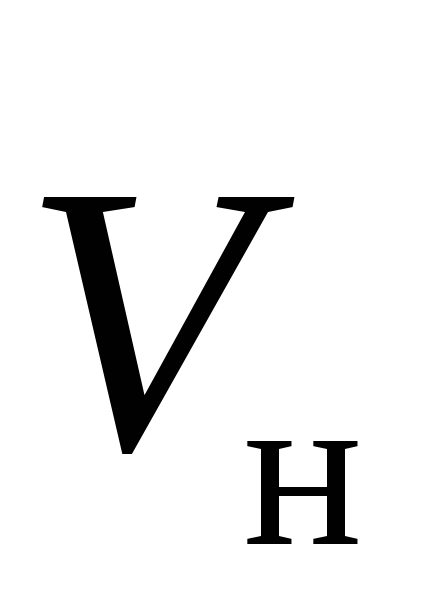 .
Последний результат представляет особый
интерес. Если
.
Последний результат представляет особый
интерес. Если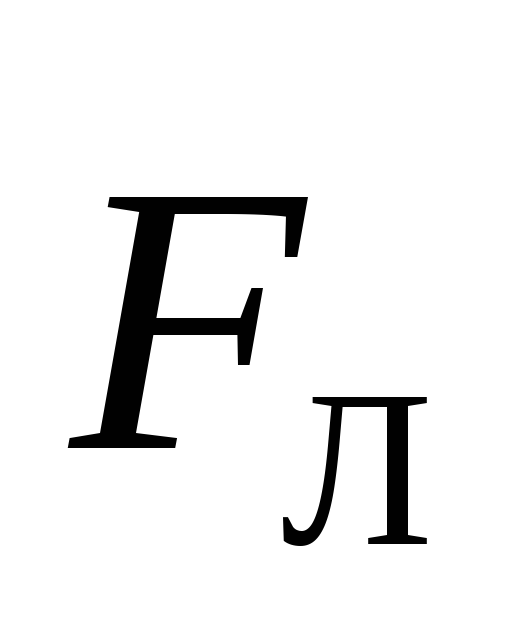
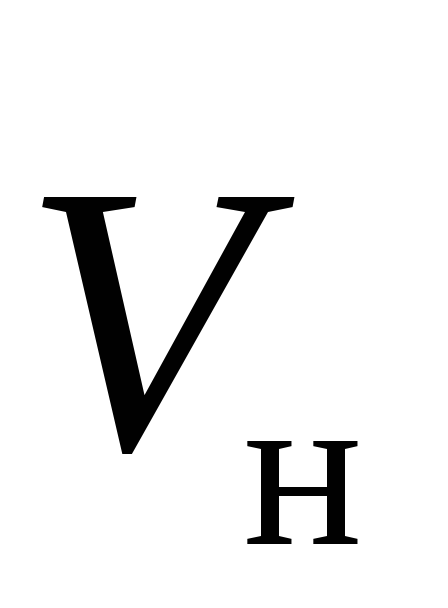 ,
то работа такой силы всегда равна нулю:
,
то работа такой силы всегда равна нулю:
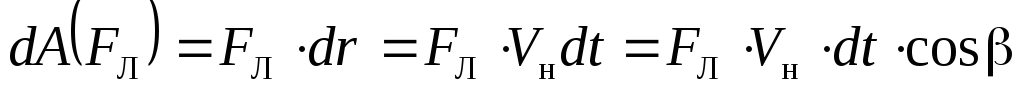 =0.
=0.
Здесь =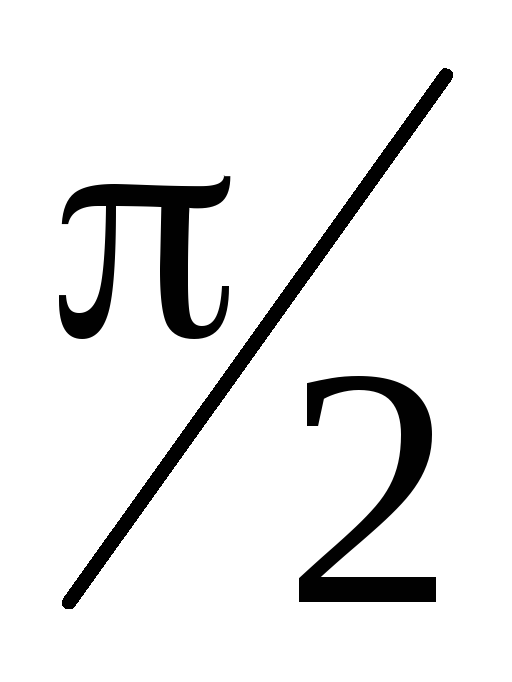 — угол между векторами
— угол между векторами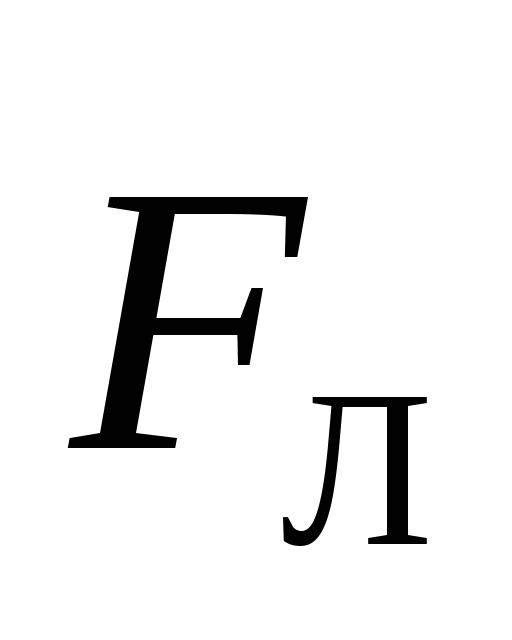 и
и ;
следовательно,cos= 0 и работа
;
следовательно,cos= 0 и работа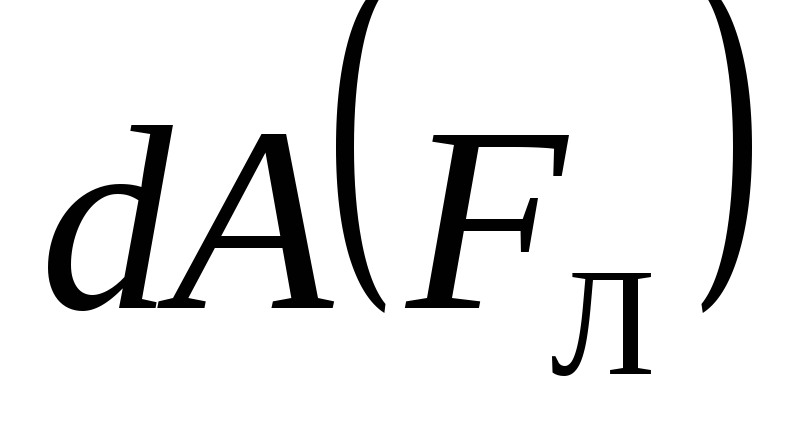 =
0. Это тот случай, когда есть сила, есть
перемещение точки её приложения, но
работа отсутствует, благодаря особой
взаимной ориентации этих двух векторов.
Действие такой силы не может привести
к изменению величины скорости частицы
и её кинетической энергии. Действительно,
согласно теореме о кинетической энергии,
её изменение равно работе силы:
=
0. Это тот случай, когда есть сила, есть
перемещение точки её приложения, но
работа отсутствует, благодаря особой
взаимной ориентации этих двух векторов.
Действие такой силы не может привести
к изменению величины скорости частицы
и её кинетической энергии. Действительно,
согласно теореме о кинетической энергии,
её изменение равно работе силы:
dкин=dA.
Но если работа не производится, то и кинетическая энергия не меняется. Неизменность кинетической энергии означает постоянство скорости частицы.
Если заряженная частица движется со
скоростью  одновременно в двух полях: и в магнитном
и в электростатическом, то сила,
действующая на неё — сила Лоренца —
будет в этом случае складываться из
двух сил (опять принцип суперпозиции —
теперь сил!):
одновременно в двух полях: и в магнитном
и в электростатическом, то сила,
действующая на неё — сила Лоренца —
будет в этом случае складываться из
двух сил (опять принцип суперпозиции —
теперь сил!):
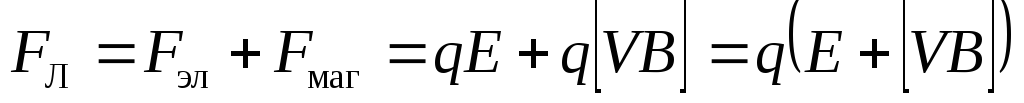 . (9.12)
. (9.12)
Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.
Вычислив магнитное поле прямолинейного тока (8.7), мы обнаружили, что силовые линии этого поля — замкнутые окружности, охватывающие проводник с током (рис. 9.3.). Это поле можно «увидеть», разместив вокруг проводника небольшие магнитные стрелки (рис. 9.4.). Они укажут направление магнитных силовых линий в различных точках пространства.
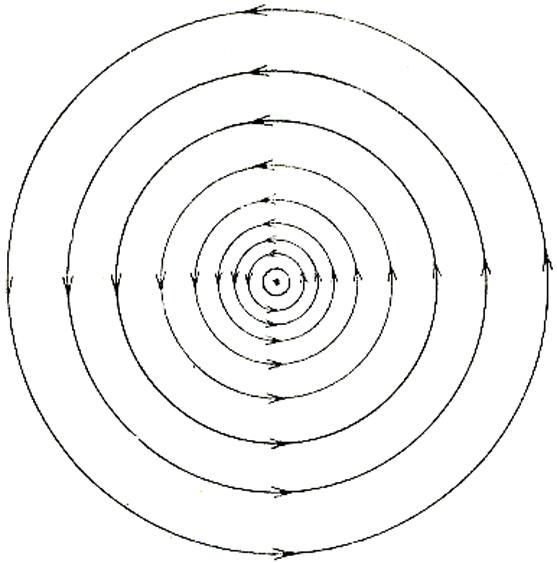
Рис. 9.3.
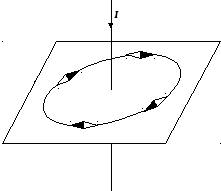
Рис. 9.4.
Ограниченное число магнитных стрелок можно заменить железными опилками. Каждый такой кусочек металла будет представлять собой магнитную микрострелку, которая будет ориентироваться вдоль магнитных силовых линий поля. На рис. 9.5. представлены магнитные поля кругового тока и катушки с током (соленоида), полученные с помощью таких опилок. Опилки насыпают на лист картона, пронизанный проводником с током. При постукивании по картону опилки распределяются вдоль магнитных силовых линий.

Рис. 9.5.
Присмотревшись к рисункам 9.4. и 9.5., легко обнаружить, что замкнуты не только силовые линии магнитного поля прямолинейного тока, но и силовые линии магнитных полей кругового тока и соленоида.
Можно показать, что замкнутость силовых линий магнитного поля — особенность любых магнитных полей. Здесь уместно напомнить, что силовые линии электростатического поля разомкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных. Замкнутость магнитных силовых линий приобретает принципиальное значение: из этого свойства следует вывод, что в природе нет магнитных зарядов. Электрические заряды существуют в природе. Они и являются источниками потенциальных электростатических полей. Магнитных зарядов в природе нет. Как же создаются тогда магнитные поля? Их источниками являются электрические токи. В отличие от электростатических полей, магнитные поля не потенциальные.Они называются вихревыми или соленоидальными.
Теперь обратимся к теореме Гаусса для магнитного поля. В этой теореме рассматривается поток вектора магнитной индукции через произвольную замкнутую поверхность:
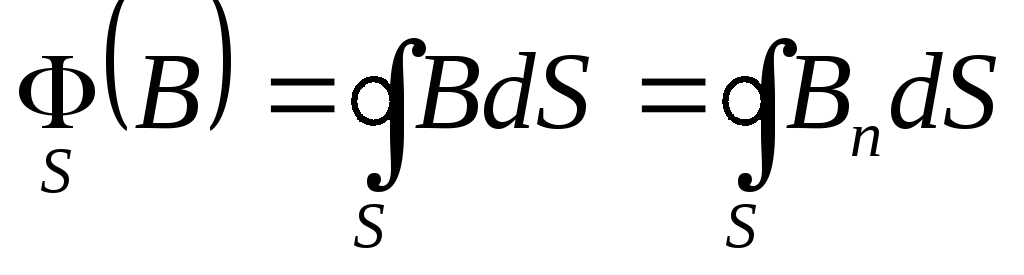 . (9.13)
. (9.13)
На рис. 9.6. замкнутая гауссова поверхность выбрана в магнитном поле прямолинейного тока.

Рис. 9.6.
Если густота магнитных силовых линий соответствует величине вектора магнитной индукции в выбранной точке пространства, то интеграл (9.12) — есть алгебраическая сумма числа силовых линий входящих (–) и покидающих (+) замкнутую поверхность. Учитывая соленоидальность магнитного поля, то есть замкнутость его силовых линий, придём к выводу: число входящих и выходящих силовых линий одинаково и их сумма всегда равна нулю:
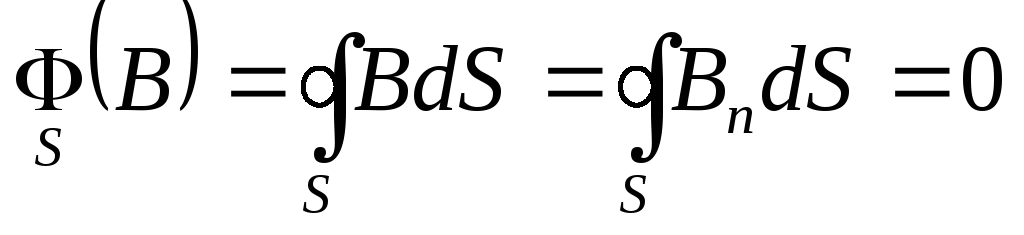 . (9.14)
. (9.14)
Полученное выражение (9.13) — математическая запись теоремы Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Иными словами, эта теорема утверждает: в природе нет магнитных зарядов.
Напомним, что совсем по-другому заканчивается теорема Гаусса для электростатического поля:
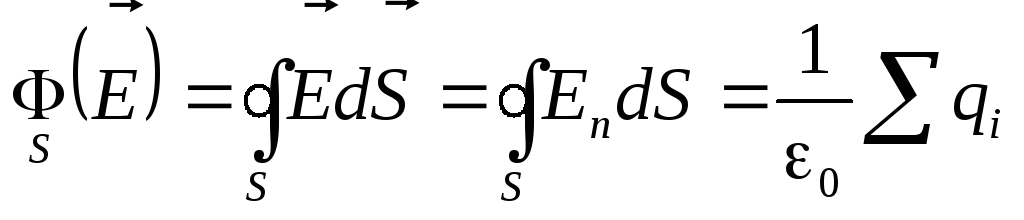 .
.
Поток вектора напряжённости электростатического поля через любую замкнутую поверхность пропорционален величине заряда,заключённого внутри этой поверхности.
Это означает, что электрические заряды — реальность природы, а вот магнитных зарядов в природе нет.
Теорема о циркуляции магнитного поля
Теперь займёмся вычислением циркуляции
вектора магнитной индукции 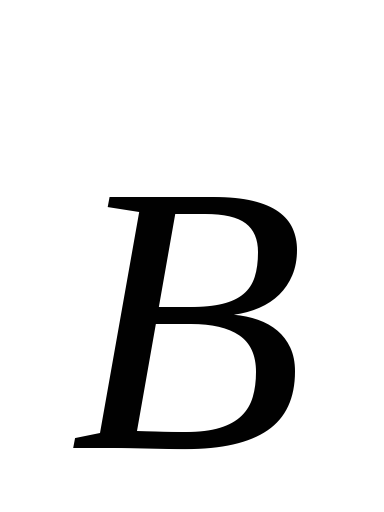 по замкнутому контуру. Начнём с простого
контура. Пусть для начала контур совпадает
с силовой линией магнитного поля
прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
по замкнутому контуру. Начнём с простого
контура. Пусть для начала контур совпадает
с силовой линией магнитного поля
прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
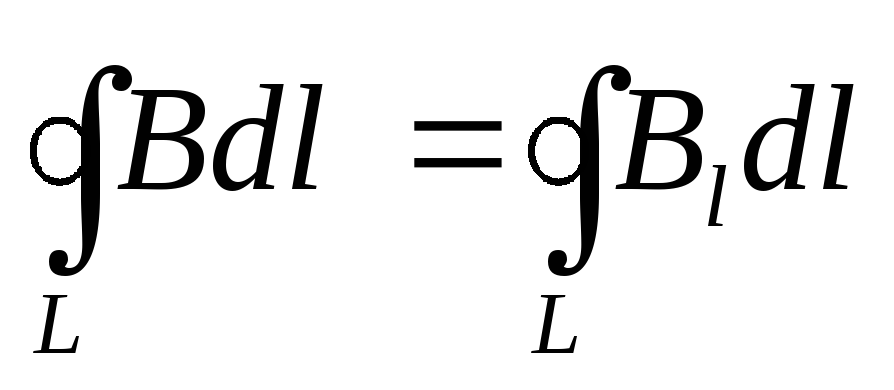 .
.

Рис. 9.7.
Обратим внимание на то, что модуль вектора магнитной индукции в нашем случае одинаков во всех точках силовой линии и, следовательно, контура L:
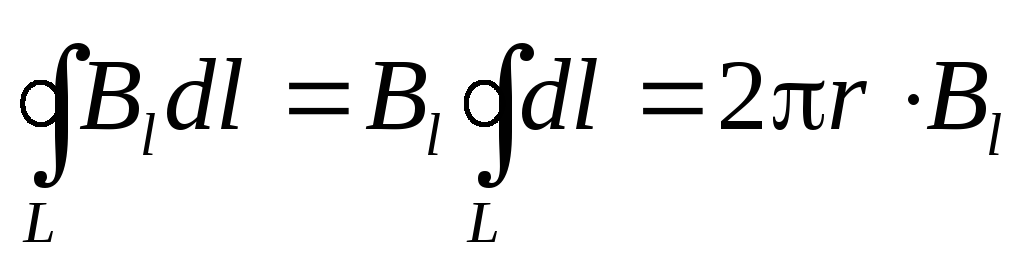 . (9.15)
. (9.15)
Согласно (9.8), 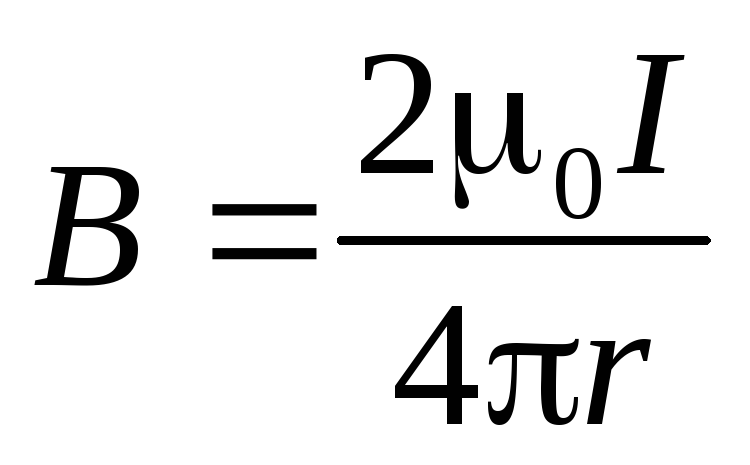 .
Поэтому циркуляцию вектора
.
Поэтому циркуляцию вектора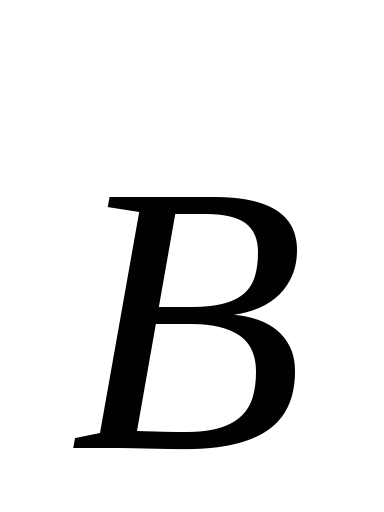 (9.15) можно записать так:
(9.15) можно записать так:
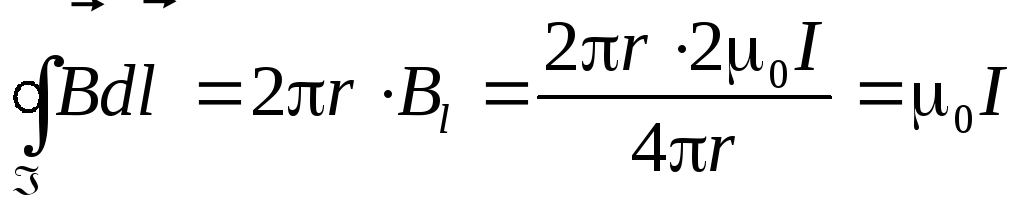 .
.
Вывод. В рассмотренном частном случае циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна току, охватываемому этим контуром.
Усложним задачу.
Выберем теперь почти произвольный
контур L в магнитном поле прямолинейного тока I.
Контур по-прежнему охватывает ток и
лежит в плоскости, перпендикулярной
проводнику с током (рис. 9.8.). Циркуляция  на участке контура
на участке контура равна:
равна:
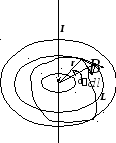
Рис. 9.8.
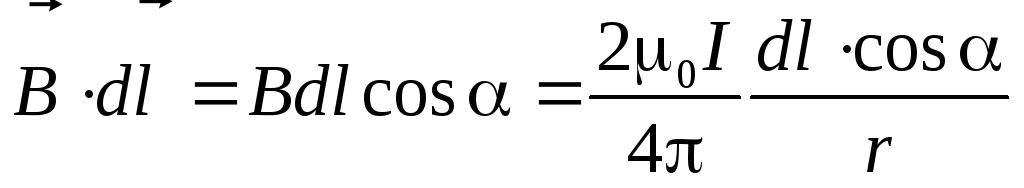
Здесь 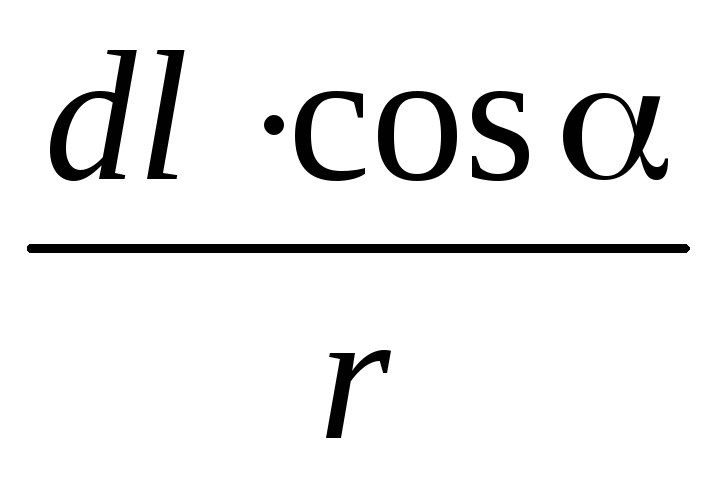 =d,
поэтому циркуляцию по всему замкнутому
контуруLможно записать
так:
=d,
поэтому циркуляцию по всему замкнутому
контуруLможно записать
так:
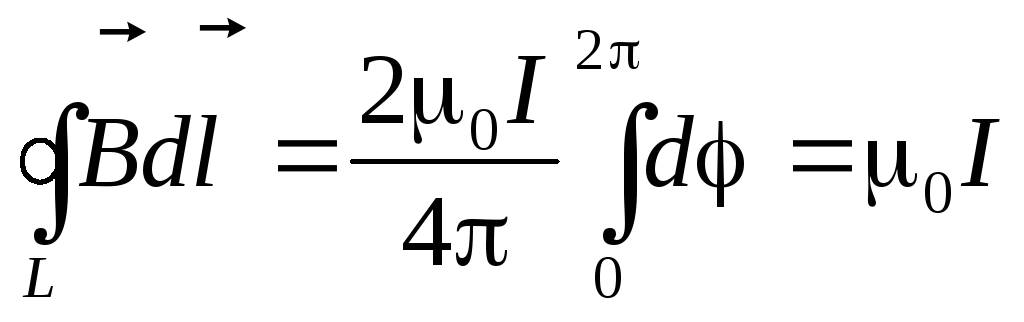 .
.
Мы вновь пришли к прежнему результату: циркуляция магнитного поля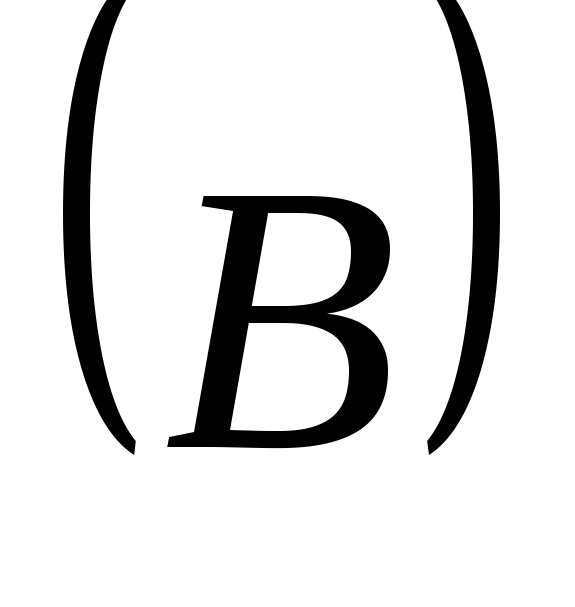 по замкнутому контуру пропорциональна
току, охватываемому этим контуром.
по замкнутому контуру пропорциональна
току, охватываемому этим контуром.
Что произойдёт, если контур не охватывает ток (рис. 9.9.)?
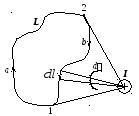
Рис. 9.9.
Циркуляция на участке  по-прежнему будет равна:
по-прежнему будет равна:
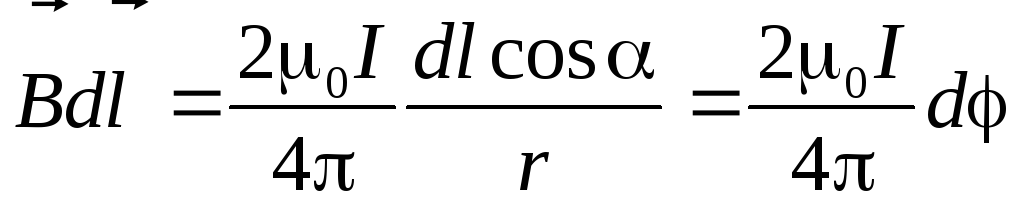 .
.
При обходе такого контура на участке 1-а-2 угол будет расти от нуля, а на участке 2-b-1 — уменьшаться до нуля. Поэтому циркуляция в этом случае окажется равно нулю:
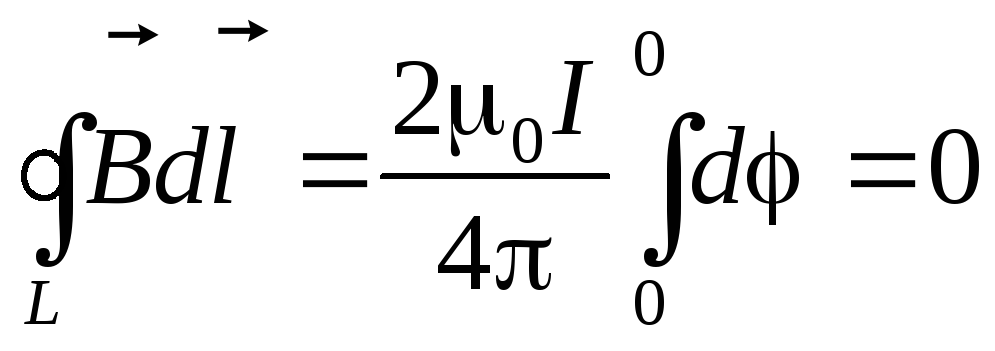 .
.
Сделаем ещё одно важное замечание.
Циркуляция вектора  — скалярная величина. Она может быть
положительной и отрицательной.
— скалярная величина. Она может быть
положительной и отрицательной.
Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна (рис. 9.10.b).
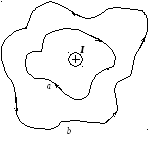
Рис. 9.10.
Если магнитное поле создаётся не одним, а несколькими токами, то циркуляция такого поля по замкнутому контуру будет пропорциональна алгебраической сумме токов, охватываемыхэтим контуром:
 . (9.16)
. (9.16)
Для случая, представленного на рис. 9.11.:
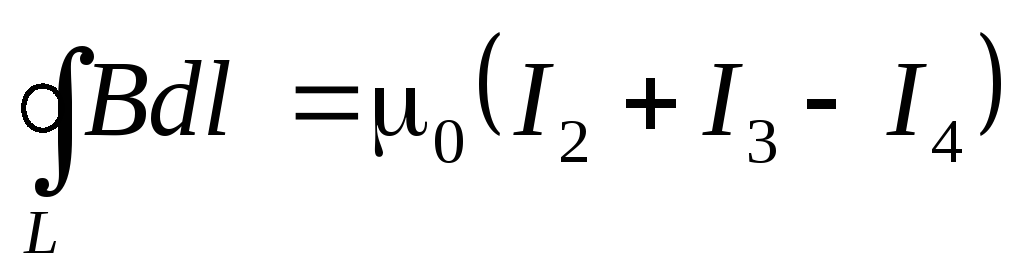 .
.
При выбранном направлении обхода контура (по часовой стрелке — на рис. 9.11.) знак тока определяется правилом буравчика. Токи I1иI5не вошли в сумму токов, так как они оказались вне замкнутого контура.
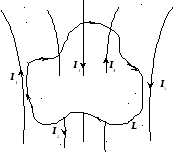
Рис. 9.11.
Подводя итог, сформулируем теорему о циркуляции магнитного поля: циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, охватываемых этим контуром.
Здесь заканчивается важный этап нашей работы: мы записали последнее уравнение системы уравнений Максвелла для электро- и магнитостатики. Вот эти уравнения:
| (I) |
| (III) |
| (II) |
| (IV) |
Система включает два уравнения потока (IиIII) и два уравнения циркуляции (IIиIV) для электростатических и магнитных полей.
Повторим физическое содержание этих уравнений:
I — | источником электростатического поля являются электрические заряды; |
II — | электростатическое поле потенциально; |
III — | в природе отсутствуют магнитные заряды; |
IV — | источником магнитного поля является электрический ток. |
Сила Лоренца — это… Что такое Сила Лоренца?
Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:
Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом[2].
Макроскопическим проявлением силы Лоренца является сила Ампера.
Уравнение (единицы СИ)
Заряженная частица
Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:
где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:
где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.
Непрерывное распределение заряда
Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .Для непрерывного распределения заряда, сила Лоренца принимает вид:
где dF — сила, действующая на маленький элемент dq.
Ковариантная запись
4-сила выражается через вектор 4-скорости частицы по формуле
- , где — 4-сила, q — заряд частицы, — тензор электромагнитного поля, — 4-скорость.
Частные случаи
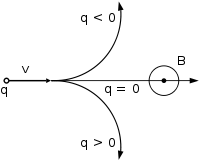 Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)
Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:
Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :
Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :
Применение силы Лоренца
Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллонеВ электроприборах
Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.
В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.
В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
Другие применения
Примечания
- ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
- ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.




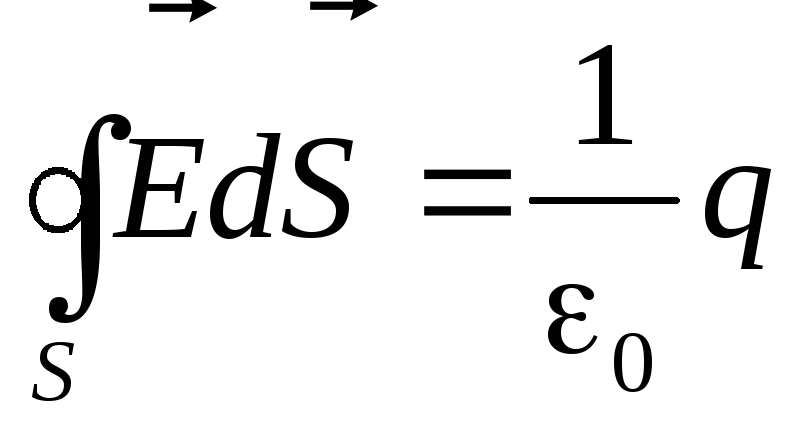 ,
, ,
,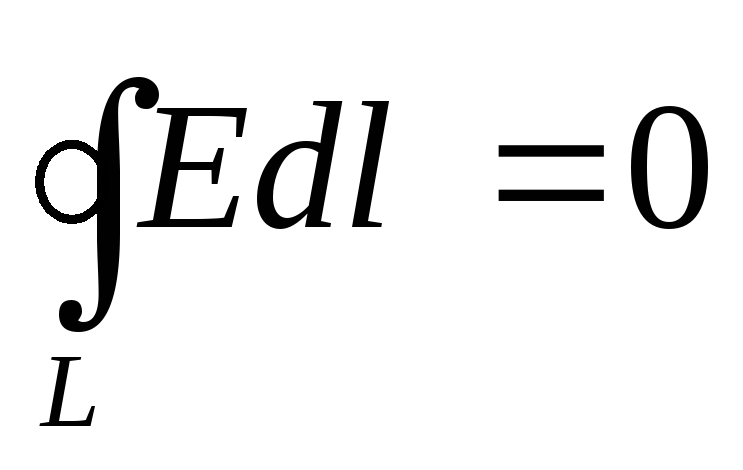 ,
,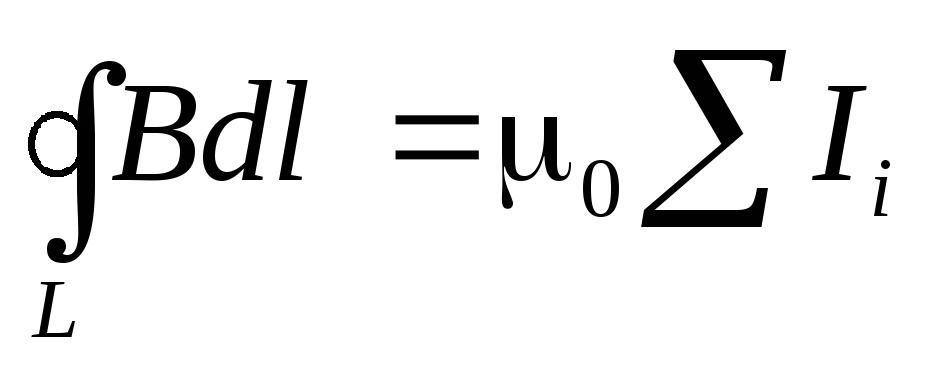 .
.