При каком условии резонансные свойства колебательной системы проявляются отчетливо?
Гипермаркет знаний>>Физика и астрономия>>Физика 11 класс>> Воздействие резонанса и борьба с ним
§ 26 ВОЗДЕЙСТВИЕ РЕЗОНАНСА И БОРЬБА С НИМ
Если колебательная система находится под действием внешней периодической силы, то может наступить резонанс и связанное с ним резкое увеличение амплитуды колебаний.
Любое упругое тело, будь то мост, станина машины, ее вал, корпус корабля, представляет собой колебательную систему и характеризуется собственными частотами колебаний. При работе двигателей нередко возникают периодические усилия, связанные с движением частей двигателя (например, поршней) или с недостаточно точной центровкой их вращающихся деталей (например, валов). Если частота этих периодических усилий совпадает с частотой свободных колебаний системы, то возникает резонанс. Амплитуда колебаний может возрасти настолько, что возможна поломка машин, хотя напряжение в материале и не превышает предела прочности при статических нагрузках. Дело в том, что железо, сталь и другие материалы при переменных нагрузках со временем теряют прочность, после чего внезапно разрушаются.
При переходе через мост воинским частям запрещается идти в ногу. Строевой шаг приводит к периодическому воздействию на мост. Если случайно частота этого воздействия совпадет с собственной частотой колебаний моста, то он может разрушиться.
С важными применениями резонанса мы ознакомимся в дальнейшем.
1. Два маятника представляют собой шарики одинакового радиуса, подвешенные на нитях равной длины. Массы шариков различны. Колебания какого из маятников прекратятся быстрее: легкого или тяжелого!
2. Приходилось ли вам наблюдать явление резонанса дома или на улице!
3. Для того чтобы удержать открытую дверь в вестибюле метро (дверь открывается в обе стороны и возвращается в положение равновесия пружинами), нужно приложить к ручке двери силу около 50 Н. Можно ли открыть дверь, приложив к ручке силу 0,005 Н! (Трением в петлях двери пренебречь.)
4. При каком условии резонансные свойства колебательной системы проявляются отчетливо!
Итак, мы ознакомились с механическими колебаниями. Обратим внимание на одну общую для всех колебаний особенность, отличающую их от других видов механического движения.
Как правило, при рассмотрении механического движения тела (например, движения космического корабля или планеты под действием сил всемирного тяготения) нужно бывает определить положение тела и его скорости в любой момент времени. Но при изучении периодических колебательных процессов особый интерес представляют общие признаки, характеризующие повторяемость в движении, а не положение и скорость колеблющегося тела в любой момент времени. Важно знать амплитуду, период и фазу колебаний, т. е. величины, характеризующие процесс в целом. При вынужденных колебаниях надо знать отношение частоты вынуждающей силы ю и частоты свободных колебаний . Именно оно определяет амплитуду и фазу колебаний.
Видео по физике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
конспект урока
опорный каркас
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Резонанс в цепи переменного тока — Электромагнитные колебания и волны — ЭЛЕКТРОДИНАМИКА — ВСЕ УРОКИ ФИЗИКИ 11 КЛАСС АКАДЕМИЧЕСКИЙ УРОВЕНЬ — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике
2-й семестр
ЭЛЕКТРОДИНАМИКА
4. Электромагнитные колебания и волны
УРОК 7/49
Тема. Резонанс в цепи переменного тока
Цель урока: выяснить условия возникновения резонанса в электрических цепях.
Тип урока: урок изучения нового материала.
ПЛАН УРОКА
Контроль знаний |
5 мин. |
1. Резистор в цепи переменного тока. 2. Конденсатор в цепи переменного тока. 3. Катушка индуктивности в цепи переменного тока. 4. Закон Ома для цепи переменного тока. |
Демонстрации |
3 мин. |
Резонанс напряжений в цепи переменного тока. |
Изучение нового материала |
25 мин. |
1. Условия возникновения резонанса в электрической цепи. 2. Использование резонанса. |
Закрепление изученного материала |
12 мин. |
1. Качественные вопросы. 2. Учимся решать задачи. |
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
1. Условия возникновения резонанса в электрической цепи
В идеальном колебательном контуре могут существовать свободные электромагнитные колебания, собственная частота которых определяется по формуле Томсона:
Соединим колебательную систему с источником переменного напряжения — генератором. ЭДС генератора будет создавать в контуре переменный электрический ток, частота которого совпадает с частотой изменения ЭДС, т.е. в контуре возникнут вынужденные электромагнитные колебания.
Если изменять емкость конденсатора или индуктивность катушки, изменяя тем самым собственную частоту колебаний контура, то можно заметить, что:
1) во время приближения собственной частоты контура к частоте изменения внешней ЭДС амплитуда вынужденных колебаний силы тока будет увеличиваться;
2) чем больше активное сопротивление контура, тем слабее выраженный всплеск амплитуды колебаний силы тока.
Характер зависимости силы тока от частоты при постоянном значении напряжения U можно предсказать на основе анализа закона Ома для цепи переменного тока:
Амплитуда силы тока будет максимальной за минимального полного сопротивления. Сопротивление R не зависит от частоты, а минимальное значение квадрата разности ωL и 1/ωC равна нулю. Поэтому максимальная амплитуда силы тока возникает, если:
Это равенство справедливо, если частота вынужденных колебаний совпадает с частотой собственных колебаний в контуре:
Резонанс напряжений заключается в резком увеличении амплитудного значения силы тока Imax при условии, что частота v0 переменного напряжения совпадает с частотой v0 собственных колебаний в контуре из катушки и конденсатора.
На рисунке показана зависимость Imax(v) при разных значениях активного сопротивления цепи. Резонанс является «острым» (то есть график функции Imax(v) имеет узкий высокий максимум) за малых значений активного сопротивления. А когда активное сопротивление очень большой, то резонанс вообще не наблюдают.
2. Использование резонанса
Явление электрического резонанса широко используют в радиотехнике: в схемах настройки радиоприемников, усилителей, генераторов высокочастотных колебаний. Например, радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот. Но только в случае резонансных колебаний силы тока в контуре будут значительными. Настройка контура на нужную частоту ю0 обычно осуществляется путем изменения емкости конденсатора.
На явлении резонанса основана работа многих измерительных приборов (например, резонансный волномер).
В некоторых случаях резонанс в электрической цепи может нанести значительный ущерб. Если круг не рассчитано на работу в условиях резонанса, то возникновение резонанса приведет к аварии. Чрезмерно высокие токи могут перегреть провода. Высокие напряжения приведут к пробою изоляции.
ВОПРОС К УЧАЩИМСЯ В ХОДЕ ИЗЛОЖЕНИЯ НОВОГО МАТЕРИАЛА
Первый уровень
1. Когда наблюдается резонанс в механических колебательных системах?
2. При каких условиях в цепи переменного тока наступает резонанс?
3. При каком условии резонансные свойства контура выражены наиболее четко?
Второй уровень
1. Чему равна разность фаз между колебаниями силы тока и напряжения во время резонанса?
2. Может ли амплитуда силы тока во время резонанса в колебательном контуре активного сопротивления R превысить силу постоянного тока в цепи такого же активного сопротивления и постоянного напряжения, равный амплитуде переменного напряжения?
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
1). Качественные вопросы
1. Лампа накаливания, конденсатор и катушка индуктивности соединены последовательно и подключены к источнику переменного напряжения. Когда в цепь последовательно включают еще одну катушку, яркость свечения лампы резко увеличивается. В случае последовательного подключения третьей катушки яркость свечения лампы становится такой, как вначале. Объясните явление. Как связаны между собой частота v переменного тока, емкость C конденсатора и индуктивность L каждой из трех одинаковых катушек?
Указание. то есть при включении в круг двух катушек наблюдается резонанс.
2. Можно установить режим резонанса в цепи переменного тока, не изменяя индуктивности и электроемкости в кругу. Как это сделать?
2). Учимся решать задачи
1. В сеть переменного напряжения 50 Гц включены последовательно лампочка, конденсатор емкостью 40 мкФ и катушка, в которую медленно вводят сердечник. Индуктивность катушки без сердечника равна 125 мГн, а если сердечник ввести полностью — 2 Гн. Опишите, как будет изменяться накал лампочки мере ввода в катушку сердечника.
Решения. Сила тока будет максимальной за резонанса, когда
По мере ввода сердечника индуктивность катушки сначала будет приближаться к этому значению, а потом становиться все меньше. Следовательно, накал лампы будет сначала расти, достигнув во время резонанса максимума, а затем убывать.
2. В круг включена последовательно катушка индуктивностью 50 мГн и конденсатор електроємністю 20 мкФ. Какой частоты переменный ток нужно создать в этом кругу, чтобы наступил резонанс напряжений?
3. Показанное на рисунке круг подключен к выходу генератора переменного напряжения, частоту которого плавно изменяют (действующее значение напряжения остается неизменным). За частот v1 = 200 Гц и v2 = 3,2 кГц сила тока в цепи одинакова. При которой частоты сила тока в цепи максимальна?
ЧТО МЫ УЗНАЛИ НА УРОКЕ
• Резонанс напряжений заключается в резком увеличении амплитудного значения силы тока Imax при условии, что частота v переменного напряжения совпадает с частотой v0 собственных колебаний в контуре из катушки и конденсатора:
Домашнее задание
Подр-1: § 31; подр-2: § 16 (п. 2).
Резонанс в цепи переменного тока — Электромагнитные колебания и волны — ЭЛЕКТРОДИНАМИКА — ВСЕ УРОКИ ФИЗИКИ 11 КЛАСС АКАДЕМИЧЕСКИЙ УРОВЕНЬ — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике
2-й семестр
ЭЛЕКТРОДИНАМИКА
4. Электромагнитные колебания и волны
УРОК 7/49
Тема. Резонанс в цепи переменного тока
Цель урока: выяснить условия возникновения резонанса в электрических цепях.
Тип урока: урок изучения нового материала.
ПЛАН УРОКА
Контроль знаний | 5 мин. | 1. Резистор в цепи переменного тока. 2. Конденсатор в цепи переменного тока. 3. Катушка индуктивности в цепи переменного тока. 4. Закон Ома для цепи переменного тока. |
Демонстрации | 3 мин. | Резонанс напряжений в цепи переменного тока. |
Изучение нового материала | 25 мин. | 1. Условия возникновения резонанса в электрической цепи. 2. Использование резонанса. |
Закрепление изученного материала | 12 мин. | 1. Качественные вопросы. 2. Учимся решать задачи. |
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
1. Условия возникновения резонанса в электрической цепи
В идеальном колебательном контуре могут существовать свободные электромагнитные колебания, собственная частота которых определяется по формуле Томсона:
Соединим колебательную систему с источником переменного напряжения — генератором. ЭДС генератора будет создавать в контуре переменный электрический ток, частота которого будет совпадать с частотой изменения ЭДС, то в контуре возникнут вынужденные электромагнитные колебания.
Если изменять емкость конденсатора или индуктивность катушки, изменяя тем самым собственную частоту колебаний контура, то можно заметить, что:
1) во время приближения собственной частоты контура к частоте изменения внешней ЭДС амплитуда вынужденных колебаний силы тока будет увеличиваться;
2) чем больше активное сопротивление контура, тем слабее выражен всплеск амплитуды колебаний силы тока.
Характер зависимости силы тока от частоты при постоянном значении напряжения U можно предсказать на основе анализа закона Ома для цепи переменного тока:
Амплитуда силы тока будет максимальной за минимального полного сопротивления. Сопротивление R не зависит от частоты, а минимальное значение квадрата разности ωL и 1/ωC равна нулю. Поэтому максимальная амплитуда силы тока возникает, если:
Это равенство справедливо, если частота вынужденных колебаний совпадает с частотой собственных колебаний в контуре:
Резонанс напряжений заключается в резком увеличении амплитудного значения силы тока Imax при условии, что частота v0 переменного напряжения совпадает с частотой v0 собственных колебаний в контуре из катушки и конденсатора.
На рисунке показана зависимость Imax(v) при разных значениях активного сопротивления цепи. Резонанс является «острым» (то есть график функции Imax(v) имеет узкий высокий максимум) при малых значениях активного сопротивления. А когда активное сопротивление очень велико, то резонанс вообще не наблюдают.
2. Использование резонанса
Явление электрического резонанса широко используется в радиотехнике: в схемах настройки радиоприемников, усилителей, генераторов высокочастотных колебаний. Например, радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот. Но только в случае резонансных колебаний силы тока в контуре будут значительными. Настройка контура на нужную частоту ю0 обычно осуществляется путем изменения емкости конденсатора.
На явлении резонанса основана работа многих измерительных приборов (например, резонансный волномер).
В некоторых случаях резонанс в электрической цепи может нанести значительный ущерб. Если круг не рассчитан на работу в условиях резонанса, то возникновение резонанса приведет к аварии. Чрезмерно высокие токи могут перегреть провода. Высокие напряжения приведут к пробою изоляции.
ВОПРОСЫ К УЧАЩИМСЯ В ХОДЕ ИЗЛОЖЕНИЯ НОВОГО МАТЕРИАЛА
Первый уровень
1. Когда наблюдается резонанс в механических колебательных системах?
2. При каких условиях в цепи переменного тока наступает резонанс?
3. При каком условии резонансные свойства контура выражены наиболее отчетливо?
Второй уровень
1. Чему равна разность фаз между колебаниями силы тока и напряжения во время резонанса?
2. Может ли амплитуда силы тока во время резонанса в колебательном контуре активного сопротивления R превысить силу постоянного тока в цепи такого же активного сопротивления и постоянного напряжения, равный амплитуде переменного напряжения?
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
1). Качественные вопросы
1. Лампа накаливания, конденсатор и катушка индуктивности соединены последовательно и подключены к источнику переменного напряжения. Когда в цепь последовательно включают еще одну катушку, яркость свечения лампы резко увеличивается. В случае последовательного подключения третьей катушки яркость свечения лампы становится такой, как сначала. Объясните явление. Как связаны между собой частота v переменного тока, емкость C конденсатора и индуктивность L каждой из трех одинаковых катушек?
Указание. то есть при включении в цепь двух катушек наблюдается резонанс.
2. Можно установить режим резонанса в цепи переменного тока, не изменяя индуктивности и электроемкости в кругу. Как это сделать?
2). Учимся решать задачи
1. В сеть переменного напряжения 50 Гц включены последовательно лампочка, конденсатор емкостью 40 мкФ и катушка, в которую медленно вводят сердечник. Индуктивность катушки без сердечника равна 125 мГн, а если сердечник ввести полностью — 2 Гн. Опишите, как будет изменяться накал лампочки по мере введения в катушку сердечника.
Решения. Сила тока будет максимальной за резонанса, когда
По мере введения сердечника индуктивность катушки сначала будет приближаться к этому значению, а потом становиться все меньше. Следовательно, накал лампы будет сначала расти, достигнув во время резонанса максимума, а затем убывать.
2. В круг включена последовательно катушка индуктивностью 50 мГн и конденсатор електроємністю 20 мкФ. Какой частоты переменный ток нужно создать в этом кругу, чтобы наступил резонанс напряжений?
3. Показанное на рисунке круг подключен к выходу генератора переменного напряжения, частоту которого плавно изменяют (действующее значение напряжения остается неизменным). За частот v1 = 200 Гц и v2 = 3,2 кГц сила тока в цепи одинакова. При которой частоты сила тока в цепи максимальна?
ЧТО МЫ УЗНАЛИ НА УРОКЕ
• Резонанс напряжений заключается в резком увеличении амплитудного значения силы тока Imax при условии, что частота v переменного напряжения совпадает с частотой v0 собственных колебаний в контуре из катушки и конденсатора:
Домашнее задание
Подр-1: § 31; подр-2: § 16 (п. 2).
«Конденсатор и катушка индуктивности в цепи переменного тока. Резонанс в электрической цепи».
Физический диктант
Учени__ 11 __ класса «__»__________ 20__г.
§22, 23 «Конденсатор и катушка индуктивности в цепи переменного тока. Резонанс в электрической цепи»
Вариант I
Вопросы.
Как различаются по фазе колебания напряжения на конденсаторе.
Какую величину называют ёмкостным сопротивлением?
Что называют резонансом в электрическом контуре?
Запишите формулу полного сопротивления цепи.
Чему равна амплитуда установившихся колебаний?
Ответы:
1._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
2._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
3._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
4._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
5._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
Физический диктант
Учени__ 11 __ класса «__»__________ 20__г.
§22, 23 «Конденсатор и катушка индуктивности в цепи переменного тока. Резонанс в электрической цепи»
Вариант II
Вопросы.
Как различаются по фазе колебания напряжения на катушке.
Какую величину называют индуктивным сопротивлением?
Чему равна удельная работа вихревого поля.
При каком условии резонансные свойства контура выражены наиболее отчетливо?
Запишите формулу ЭДС источника в любой момент времени.
Ответы:
1._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
2._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
3._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
4._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
5._______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________.
«Исследование параллельного резонансного контура»
Цель:изучить основные свойства, временные и частотные характеристики параллельного колебательного контура, суть понятия резонанса токов и условия его возникновения.
Краткие теоретические сведения
Параллельным колебательным контуром называется электрическая цепь, в которой индуктивности и емкости распределены по двум параллельным ветвям, подключенным параллельно к источнику энергии. Принципиальные схемы контуров любого вида можно заменить схемами замещения двух видов (показаны на рис. 28 а и б).
а). б). |
Рис. 28 – Схемы параллельных колебательных контуров
Рассмотрим схему, представленную на рис. 28б. Комплексная функция входного сопротивления для нее:
Zвх(jω)= (R + jωL)(1/jωС) / [R + jωL+ 1/(jωC)]. | (23) |
На частотах, близких к резонансной (ω ≈ ωо), и больших добротностях контура (Q >>1) справедливо неравенство R<<ω0L.
Тогда с учетом (17)-(18) комплексная функция входного сопротивления
Zвх(jω) = R0e /(1+jξ). | (24) |
На частоте резонанса входное сопротивление параллельного резонансного контура имеет чисто резистивный характер. Резонансное сопротивление параллельного контура R0e в Q2 раз превышает сопротивление потерь последовательного колебательного контура:
R0e = L/(RC) = ρ2/R = ρQ = RQ2. | (25) |
Частотная характеристика полного входного сопротивления
Zвх(ω) = R0e / √(1+ξ2), | (26) |
а фазо-частотная характеристика
φ(ω) = – arctg ξ. | (27) |
Резонанс в параллельном контуре наблюдается на частоте, при которой реактивная составляющая входного сопротивления равна нулю и комплексное сопротивление вещественно. В (24) это будет при ξ =0, т.е. на резонансной частоте последовательного контура (16). Выражение (24) верно при R<<ω0L . Более точное выражение для резонансной частоты можно получить, приравнивая нулю правую часть (23):
ω0п = ω0 √ 1 – 1/Q2 . | (27) |
Из (27) следует, что резонансная частота параллельного контура при учете сопротивления потерь меньше резонансной частоты последовательного контура.
Передаточная функция параллельного контура по току равна
КI (jω) = ỈC / Ỉ1 = jωCZвх(ω) = j Q ω /[ω0(1 + jξ)]. | (28) |
Т. к. ŮC = Ů1 , передаточная функция по напряжению КU (jω)=1. В параллельном колебательном контуре на резонансной частоте ток в контуре IС в Q раз больше входного тока (т.е. в параллельном контуре наблюдается резонанс токов).
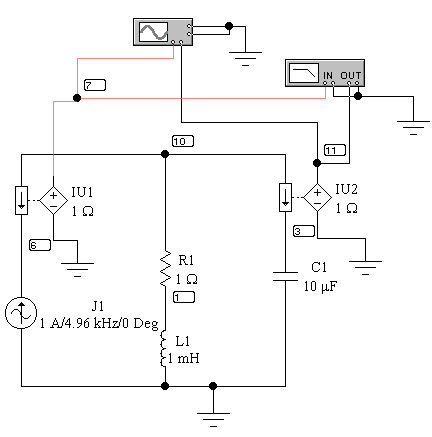
Задание. Собрать схему, представленную на рис. 29. Изменяя значения R, С и L, снять амплитудно-частотные и фазо-частотные характеристики параллельного контура. Изучить влияние параметров контура на его характеристики – резонансную частоту, добротность, полосу частот.
Порядок выполнения.
Как отмечалось выше, в параллельном колебательном контуре наблюдается резонанс токов, поэтому на контур подается сигнал с источника тока J1(коэффициент передачи по напряжению равен 1). Для измерения токов можно воспользоваться источниками напряжения, управляемыми током (IU1 и IU2 на рис. 29). Напряжение на выходе этих элементов пропорционально токам, протекающих в первичной цепи этих источников. Коэффициент передачи этих источников равен отношению выходного напряжения к току в первичной цепи и имеет размерность Ом. В данном примере этот коэффициент равен 1В/1А=1 Ом. Таким образом, сигналы, подаваемые на вход измерительных приборов (осциллографа и плоттера), будут пропорциональны токам, протекающим во входной цепи и через емкость соответственно.
На плоттере удобно наблюдать и измерять АЧХ и ФЧХ. С помощью осциллографа можно наблюдать соотношение между входным и выходным сигналом (сигналы пропорциональны токам!). Для этих исследований необходимо изменять частоту источника тока J1.
|
Рис. 29 – Схема измерения параметров параллельного колебательного контура
Способы измерения с помощью опций меню Analysis и измерителя АЧХ и ФЧХ подробно изложены в работе 6.
Используя описанные методики, измерить и занести в таблицу 13 параметры амплитудно-частотной и фазо-частотной характеристик параллельного контура для следующих значений элементов:
А). R=0,1 Ом, С=1 мкФ и L=1, 2 …..10 мГн;
Б). R=0,1 Ом, L= 1 мГн и С=1, 2……10 мкФ;
В).L= 1 мГн, С=1 мкФ и R =1, 2 …….10 Ом.
По результатам измерений построить амплитудно-частотные и фазо-частотные характеристики, а также годографы комплексной передаточной функции параллельного резонансного контура.
Построить зависимости характеристик контура – резонансной частоты, добротности, полосы частот – от значений R, L и C.
Табл.13
f1,Гц | f2,Гц | fn,Гц | ωo | Q | |||
R=….. L=….. C=….. | Кu | ||||||
φ,град |
Контрольные вопросы:
Как определяются токи в цепи синусоидального тока с параллельным соединением резистора, индуктивности и ёмкости. Запишите закон Ома в комплексной форме.
Что такое треугольник проводимостей? Как его построить?
Какую цепь называют параллельным колебательным контуром?
При каком условии в параллельном колебательном контуре наступает резонанс? Почему резонанс в такой цепи называют резонансом токов?
Как определяется резонансная частота?
Что называют характеристическим сопротивлением контура и добротностью контура?
Изменением каких величин в параллельном колебательном контуре можно достичь резонанса токов?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 8