Магнитное поле. Индукция магнитного поля

Как вы уже знаете, между заряженными телами или частицами, кроме гравитационного взаимодействия, существует ещё и электромагнитное. Если заряды покоятся относительно определённой инерциальной системы отсчёта, то электромагнитное взаимодействие между ними называют электростатическим. А силы, действующие между неподвижными зарядами, определяются законом Кулона.

Однако при движении электрически заряженных частиц проявляется вторая составляющая электромагнитного взаимодействия, а именно, магнитное взаимодействие. Поговорим о нём подробнее.

Итак, изучая электрический ток мы с вами познакомились с его основными действиями. К числу самых очевидных принадлежат: тепловое, химическое и магнитное действие тока.

Напомним, что тепловое действие тока проявляется в том, что среда, в которой протекает ток, нагревается.

Химическое действие тока проявляется, как правило, при его протекании через растворы и расплавы электролитов.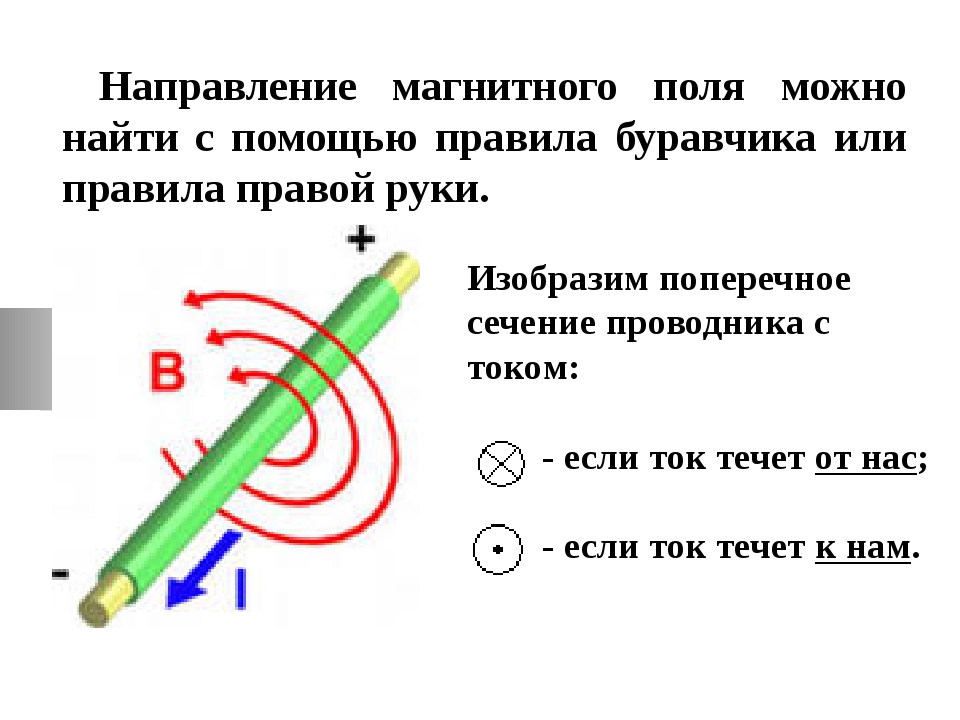

А единственное действие тока, которое проявляется у всех без исключения проводников — это магнитное.

Теперь давайте выясним, как связаны между собой электричество и магнетизм? Для этого проделаем такой опыт.  Поднесём к магнитной стрелке наэлектризованную стеклянную палочку. Как видим, стрелка останется неподвижной.

Взаимодействия нет. Не будет взаимодействия, если к стрелке поднести отрицательно заряженную эбонитовую палочку. Можно ли на основании этих опытов говорить об отсутствии всякой связи магнетизма и электричества? Конечно, нет. Между магнетизмом и электричеством существует теснейшая связь, что можно подтвердить опытом, который провёл в 1820 году датский физик Ханс Кристиан Эрстед. Установка состоит из магнитной стрелки, укреплённой на острие, и проводника, соединённого с источником тока. До включения тока стрелка располагается в магнитном поле Земли, ориентируясь с севера на юг. Замкнув цепь, мы увидим, как магнитная стрелка начнёт поворачиваться, пока не установится перпендикулярно проводнику с током.

Разомкнём цепь — стрелка возвращается в своё исходное положение. Если изменить направление тока в проводнике на противоположное, то, замкнув цепь, мы увидим, как стрелка опять поворачивается и устанавливается перпендикулярно к проводнику, но уже в противоположном направлении.

Таким образом, можно говорить о том, что магнитная стрелка взаимодействует с проводником с током. Следовательно, вокруг проводника с током существует магнитное поле, которое и совершает работу по повороту магнитной стрелки.

Опыт Эрстеда вызвал необычайный интерес у физиков того времени. Раньше электрические и магнитные явления рассматривались как совершенно независимые. Открытие же Эрстеда обнаружило взаимосвязь между ними.

Таким образом, на основании проведённых опытов, мы с вами можем сделать очень важный вывод: неподвижные электрические заряды порождают только электрическое поле, которое не действует на магнитную стрелку. Вокруг же движущихся зарядов, то есть электрического тока, существует как электрическое, так и магнитное поле.

Согласно представлениям классической электродинамики магнитное поле — особая форма материи, созданная движущимися (относительно определённой инерциальной системы отсчёта) электрическими зарядами или переменными электрическими полями.

Опыты показывают, что магнитное поле возникает при движении любых электрических зарядов. А взаимодействие между ними осуществляется посредством магнитного поля, которое действует с некоторыми силами на любые другие движущиеся в данном магнитном поле электрические заряды. Таким образом,

о существовании магнитного поля можно судить по наличию силы, действующей на электрический заряд, движущийся относительно выбранной инерциальной системы отсчёта.

Силы, действующие со стороны магнитного поля на находящиеся в нём проводники с током или движущиеся заряды, в дальнейшем будем называть магнитными силами.

Поскольку магнитное поле проводника с током действует с определённой силой на магнит (в опыте Эрстеда — на магнитную стрелку), то естественно предположить, что со стороны магнитного поля магнита на проводник с током должна действовать сила.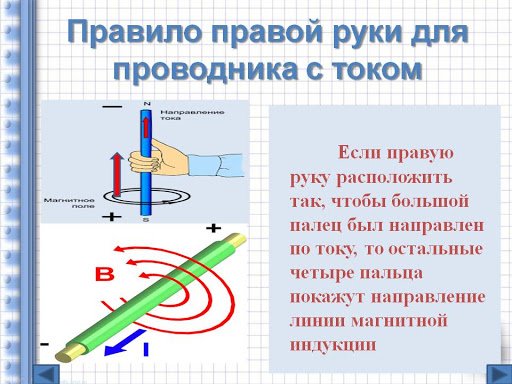

Проверим это предположение на опыте.

При разомкнутой цепи действия со стороны магнитного поля дугообразного магнита на гибкий проводник не наблюдается. Однако при замыкании цепи проводник приходит в движение: он либо втягивается в пространство между полюсами дугообразного магнита, либо выталкивается из него при обратном расположении полюсов магнита или при изменении направления тока в цепи.

Но действие магнитного поля на проводник с током не всегда проявляется в притяжении или отталкивании. Например, если подвесить на некотором расстоянии от проводника на тонких и гибких подводящих проводах маленькую рамку, то при пропускании по проводнику и рамке электрического тока рамка повернётся и расположится так, что окажется в одной плоскости с проводником с током.

Если же рамку с током поместить между полюсами дугообразного магнита, то она повернётся в магнитном поле так, чтобы её плоскость была перпендикулярна прямой, соединяющей полюсы магнита.

Изучая электростатику, мы узнали, что распределение поля в пространстве можно сделать «видимым», пользуясь представлениями о линиях напряжённости. Магнитные поля также можно изображать графически в виде магнитных линий. Для описания магнитного поля введём его основную характеристику, аналогичную напряжённости электростатического поля. Такой характеристикой служит

векторная физическая величина — индукция магнитного поля (или магнитная индукция), являющаяся силовой характеристикой магнитного поля.

Для определения направления индукции магнитного поля используют ориентирующее действие магнитного поля на магнитную стрелку или рамку с током. Направление от южного полюса к северному полюсу магнитной стрелки, свободно устанавливающейся в магнитном поле, принимают за направление магнитной индукции.

Это направление совпадает с направлением положительной нормали к замкнутому контуру с током. Положительная нормаль направлена в ту сторону, куда перемещается буравчик (с правой нарезкой), если вращать его по направлению тока в рамке.

Вектор магнитной индукции в центре рамки совпадает по направлению с положительной нормалью.

Изучим магнитное поле прямого проводника с током. Для этого сквозь лист картона, на котором установлены магнитные стрелки, пропустим проводник, соединённый с источником тока. При замыкании электрической цепи стрелки расположатся вдоль линий магнитного поля. Если же изменить направление тока в проводнике, то все стрелки повернутся на 180^о.

Однако использование магнитных стрелок не всегда рационально. Поэтому для определения направление вектора магнитной индукции прямого проводника с током пользуются

правилом буравчика: если поворачивать головку винта так, чтобы поступательное движение острия винта происходило вдоль тока в проводнике, то направление вращения головки указывает направление линий магнитной индукции поля прямого проводника с током.

Линией индукции магнитного поля называют воображаемую линию в пространстве, касательная к которой совпадает с направлением индукции магнитного поля в каждой точке поля.

Исследование различных магнитных полей показало, что линии магнитной индукции в отличие от линий напряжённости электростатическое поля являются замкнутыми линиями.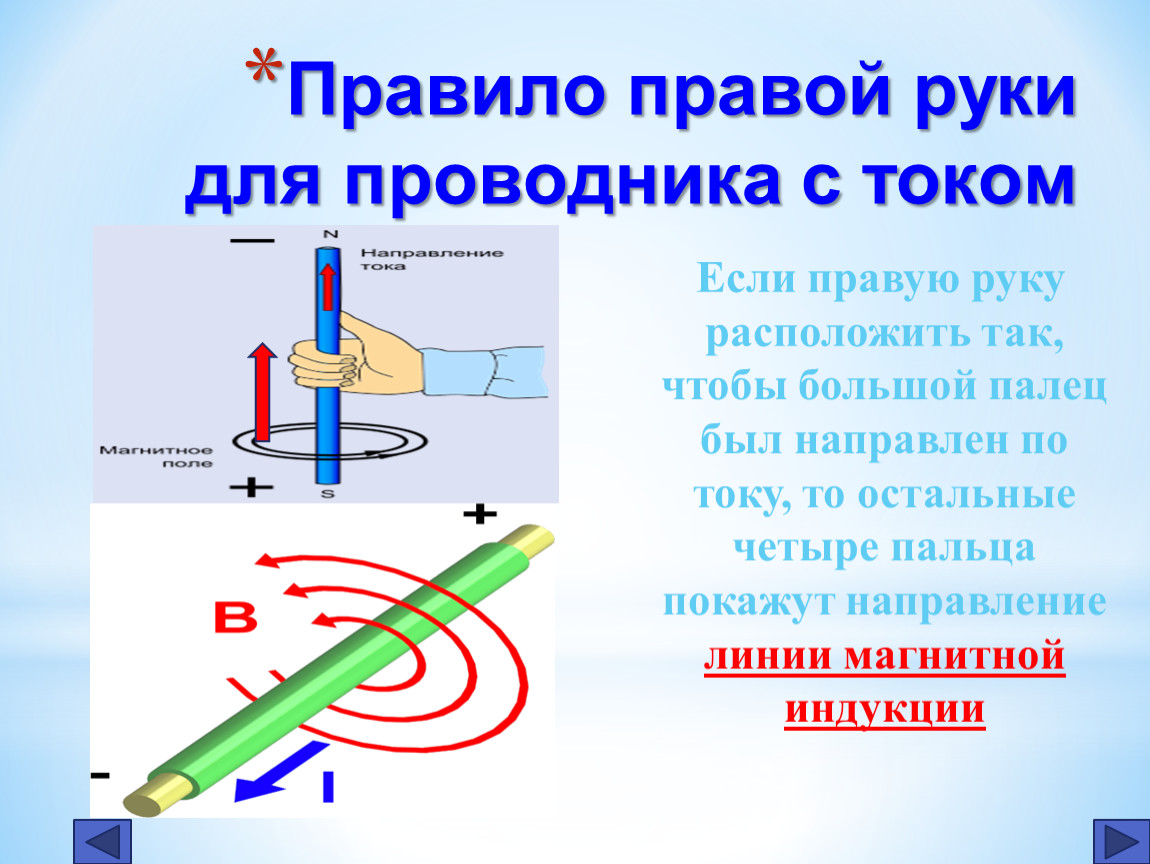

Это характерно для любых магнитных полей. Поля, обладающие таким свойством, называют вихревыми.

Замкнутость линий магнитной индукции свидетельствует о том, что магнитных зарядов, подобных электрическим в природе нет. Источником магнитного поля являются движущиеся заряды и переменные электрические поля.

Хотя современные научные представления предсказывают существование частицы с магнитным зарядом — магнитные монополи. Магнитный монополь можно представлять как отдельно взятый полюс длинного и тонкого постоянного магнита. Однако у всех известных магнитов всегда два полюса, то есть он является диполем. Если разрезать магнит на две части, то у каждой его части по-прежнему будет два полюса. Поэтому магнитные монополи пока экспериментально не наблюдали.

Очевидно, что через любую точку в магнитном поле можно провести только одну линию индукции. Поскольку индукция магнитного поля в любой точке пространства имеет определённое направление, то и направление линии индукции в каждой точке этого поля может быть только единственным.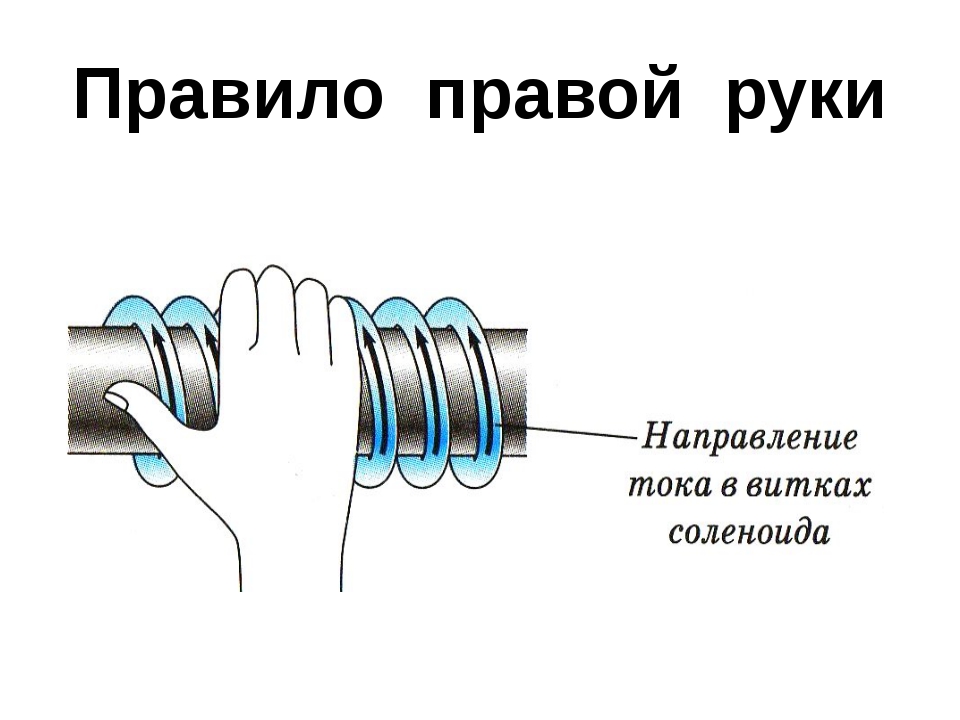 Это означает, что линии магнитной индукции, так же, как и линии напряжённости электрического поля, не пересекаются.

Определить направление линий индукции магнитного поля прямолинейного проводника с током можно также с помощью

правила правой руки: если мысленно обхватить проводник правой рукой так, чтобы большой палец указывал направление тока, то остальные пальцы окажутся согнуты в направлении линий магнитной индукции.

На практике часто приходится иметь дело с магнитными полями электрических токов, проходящих по соленоидам. Напомним, что соленоид — это цилиндрическая катушка, на которую виток к витку намотан провод.

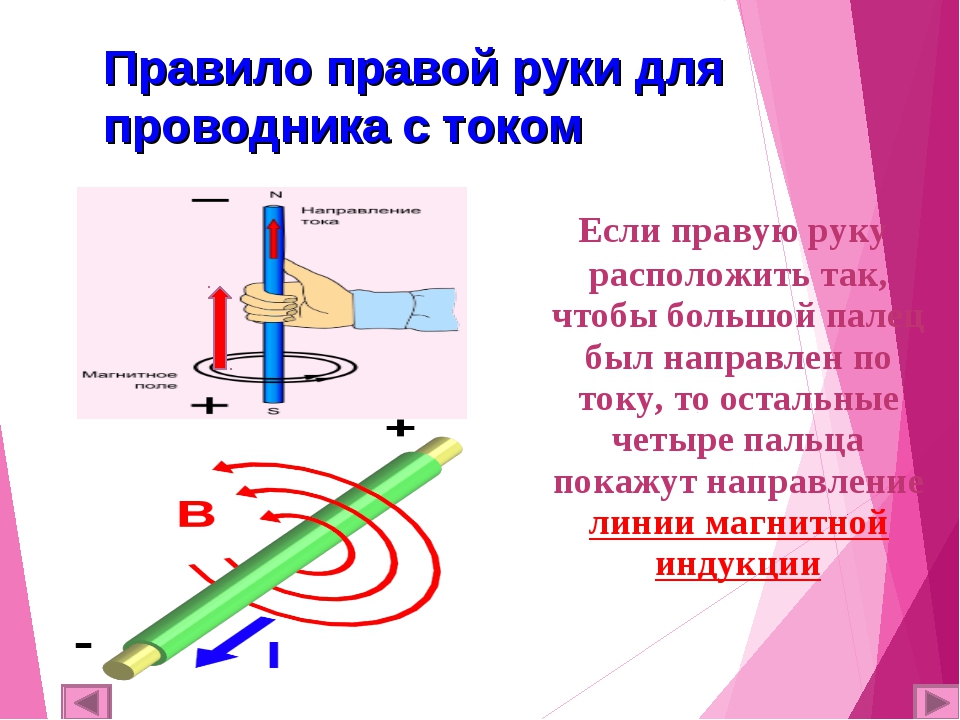
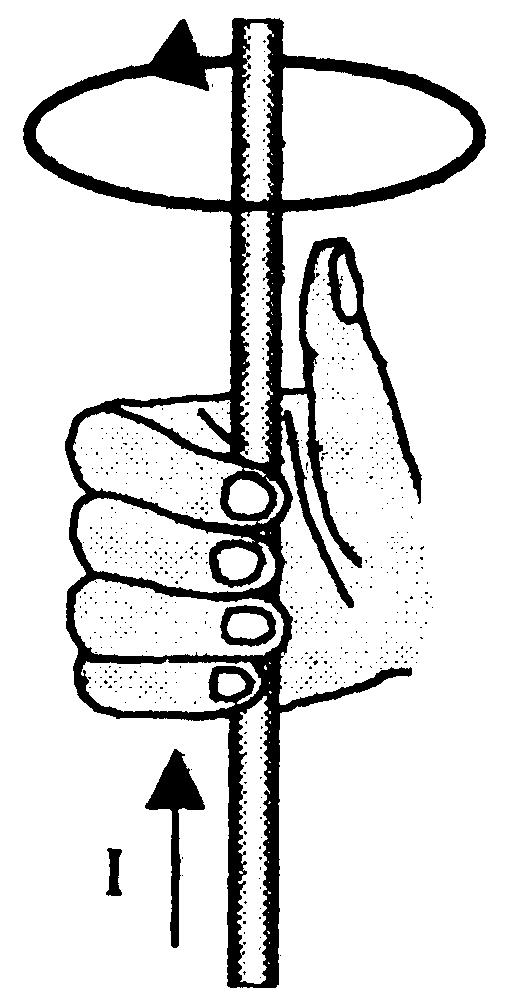
Для определения направления магнитного поля внутри соленоида можно использовать правило правой руки: если ладонью правой руки обхватить катушку с током так, чтобы четыре пальца расположились по направлению тока, то отставленный большой палец укажет направление магнитного поля внутри катушки.

Если длина соленоида много больше его диаметра, то внутри центральной части соленоида линии индукции магнитного поля практически параллельны и направлены вдоль его оси. Магнитное поле, индукция которого во всех точках одинакова, называют однородным. Линии индукции такого поля параллельны. Очевидно, что в противном случае поле называют неоднородным.

Таким образом, для определения направления магнитной индукции можно воспользоваться любым из правил, сформулированных нами ранее. Причём, пользуясь правилом буравчика, надо помнить, что направление тока — это направление упорядоченного движения положительных зарядов.

Вспомним ещё один важный момент. Для графического обозначения направления тока в проводнике, перпендикулярного плоскости чертежа, пользуются следующим приёмом. Если ток направлен от нас за чертёж, то его обозначают крестиком, если наоборот, то есть из-за чертежа к нам, — то точкой.

Мысленно это можно представить следующим образом: каждый крестик — это как бы видимое нами хвостовое оперение летящей от нас стрелы, а точка — остриё стрелы, летящей к нам.

ЦОР физика — медиаматериалы 11 класс — ЦОР

ЦОР физика — медиаматериалы 11 класс

Подробности

Обновлено 31. 07.2021 17:03

Просмотров: 2709

Основы электродинамики

Опыт Эрстеда ………. смотреть
Опыт Эрстеда (2) ………. смотреть
Опыты Эрстеда ………. смотреть
Магнитная стрелка, её ориентация в магнитном поле ………. смотреть
Опыт с прямым проводником ………. смотреть
Определение формы и направления силовых линий магнитного поля прямолинейного проводника с током ………. смотреть
Магнитное поле полосового магнита ………. смотреть
Магнитное поле дугообразного магнита ………. смотреть
Постоянные магниты. Их взаимодействие ………. смотреть
Магнитное поле катушки с током ………. смотреть
Магнитное поле соленоида ………. смотреть
Опыт с электромагнитом ………. смотреть
Электромагнитное реле ………. смотреть
Магнитный сепаратор ………. смотреть
Поезд на магнитной подушке . ……… смотреть
Опыты, доказывающие существование магнитного поля ………. смотреть
Опыты с компасом ………. смотреть
Опыты с компасом ………. смотреть
Опыты по наблюдению магнитного поля ………. смотреть
Картины магнитных полей, созданных разными магнитами ………. смотреть
Однородное магнитное поле ………. смотреть
Правило буравчика ………. смотреть
Действие магнитного поля на проводник с током ………. смотреть
Действие магнитного поля на проводник с током ………. смотреть
Магнитная и географическая оси Земли ………. смотреть
Магнитные аномалии и магнитные бури ………. смотреть
Намагничивание ферромагнетиков ………. смотреть
Действие магнитного поля на проводник с током ………. смотреть
Ориентирующее действие магнитного поля ………. смотреть
Вектор магнитной индукции .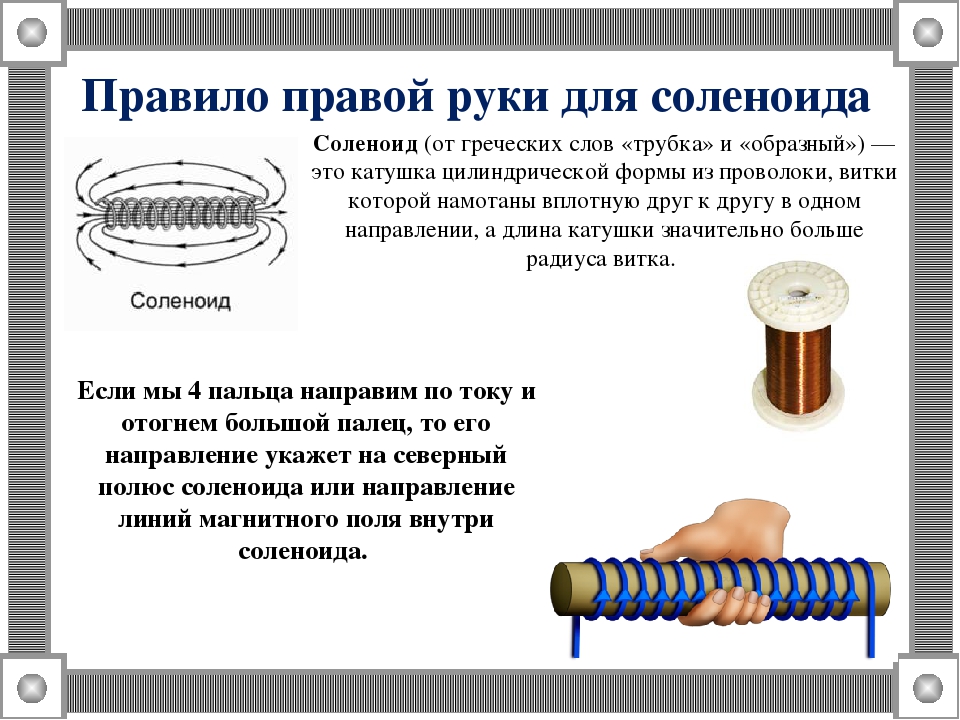 ……… смотреть
Вектор магнитной индукции в центре кругового тока ………. смотреть
Модуль вектора магнитной индукции ………. смотреть
Правило правой руки ………. смотреть
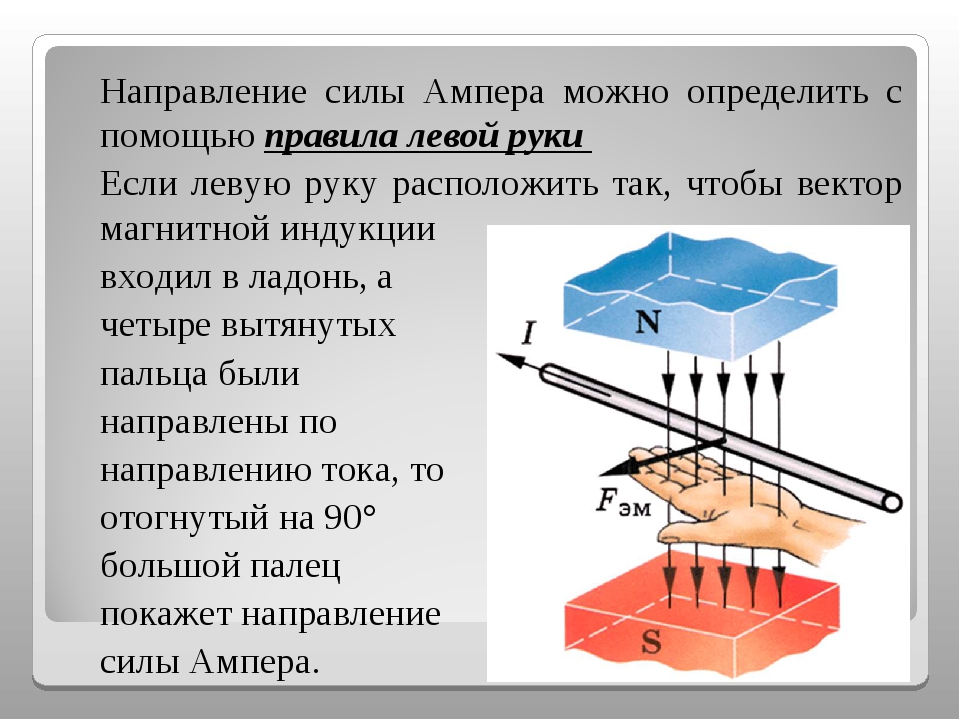
Правило левой руки (1) ………. смотреть
Правило левой руки (2) ………. смотреть
Магнитный поток ………. смотреть
Опыт Ампера ………. смотреть
Действие магнитного поля на проводник с током ………. смотреть
Взаимодействие параллельных проводников с током ………. смотреть
Ориентирующее действие магнитного поля ………. смотреть
Линии магнитной индукции ………. смотреть
Сила Ампера ………. смотреть
Сила Лоренца ………. смотреть
Использование силы Лоренца ………. смотреть
Сила Ампера и правило левой руки ………. смотреть
Закон Ампера, рамка с током в магнитном поле ……….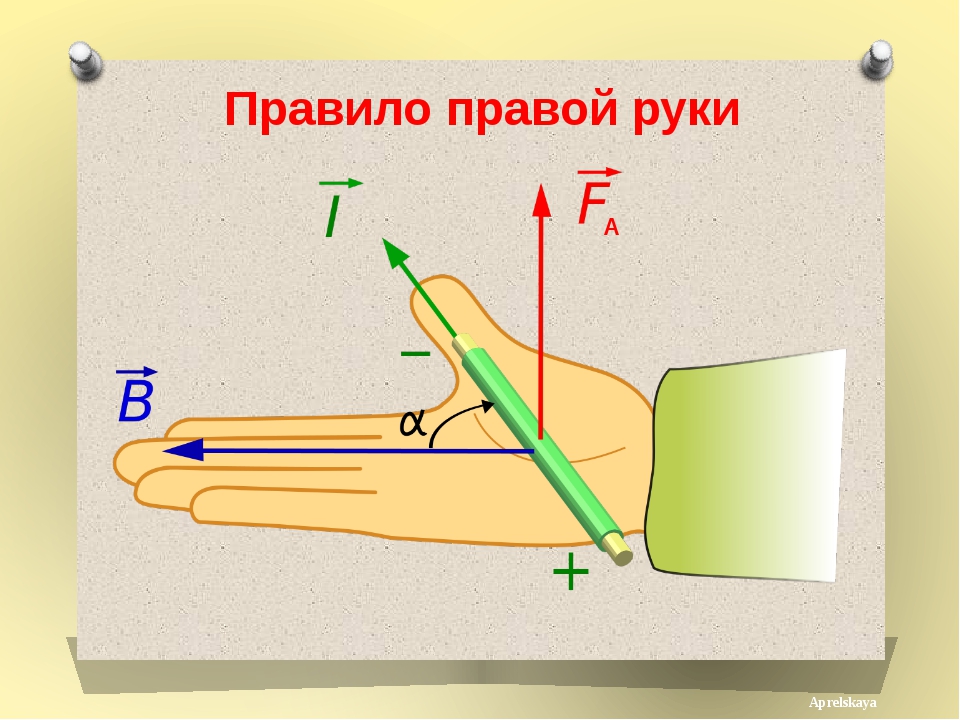 смотреть
Правило левой руки для частицы ………. смотреть
Движение заряженной частицы в однородном магнитном поле ………. смотреть
Магнитный поток ………. смотреть
Опыт Фарадея. Явление электромагнитной индукции ………. смотреть
Явление электромагнитной индукции ………. смотреть
Опыты Фарадея (1) ………. смотреть
Опыты Фарадея (2) ………. смотреть
Опыты Фарадея с электромагнитом ………. смотреть
Опыты Фарадея: взаимодействие соленоида и магнита ………. смотреть
Опыты Фарадея с постоянным магнитом ………. смотреть
Опыты Фарадея: появление индукционного тока при включении-выключении тока во вторичной катушке ………. смотреть
Опыты Фарадея. Взаимодействие соленоида и магнита ………. смотреть
Закон электромагнитной индукции ………. смотреть
ЭДС индукции в движущихся проводниках ..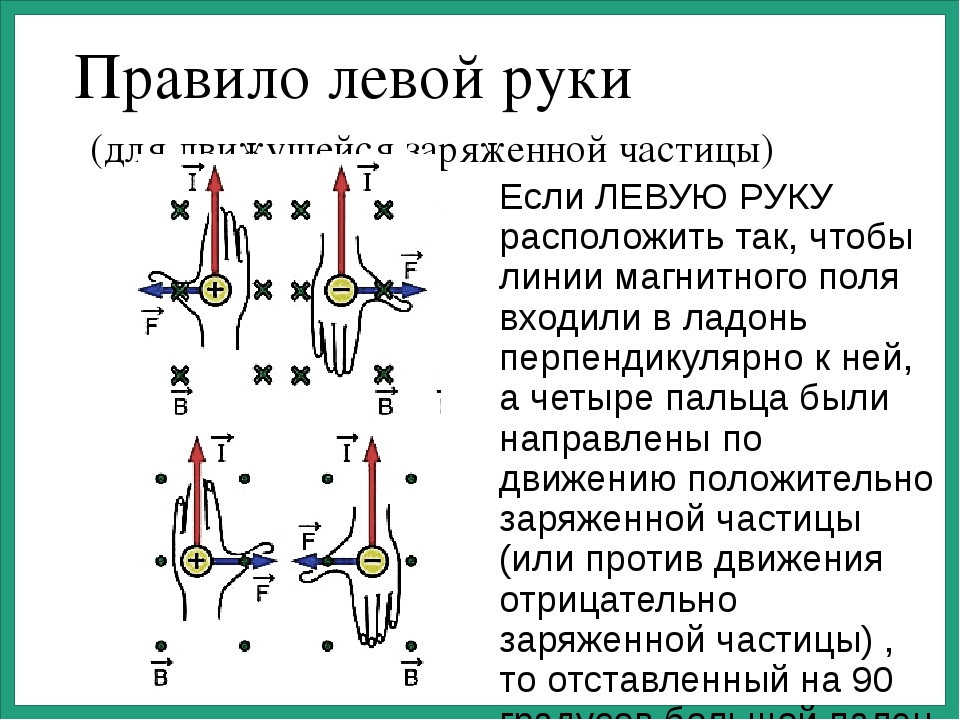 …….. смотреть
Принцип действия электродвигателя ………. смотреть
Коллекторный электродвигатель ………. смотреть
Электродвигатели в технике ………. смотреть
Генератор постоянного тока ………. смотреть
Опыт с разрезанным и сплошным кольцами ………. смотреть
Взаимодействие кольца с постоянным магнитом ………. смотреть
Правило Ленца ………. смотреть
Правило Ленца ………. смотреть
Правило Ленца. Физика ………. смотреть
Правило Ленца ………. смотреть
Правило Ленца ………. смотреть
Вихревые токи ………. смотреть
Индукционный ток в проводниках, движущихся в магнитном поле ………. смотреть
Самоиндукция ………. смотреть
Явление самоиндукции ………. смотреть
Явление самоиндукции ………. смотреть
Индуктивность ………. смотреть

Колебания и волны

Механические колебания

Механические колебания.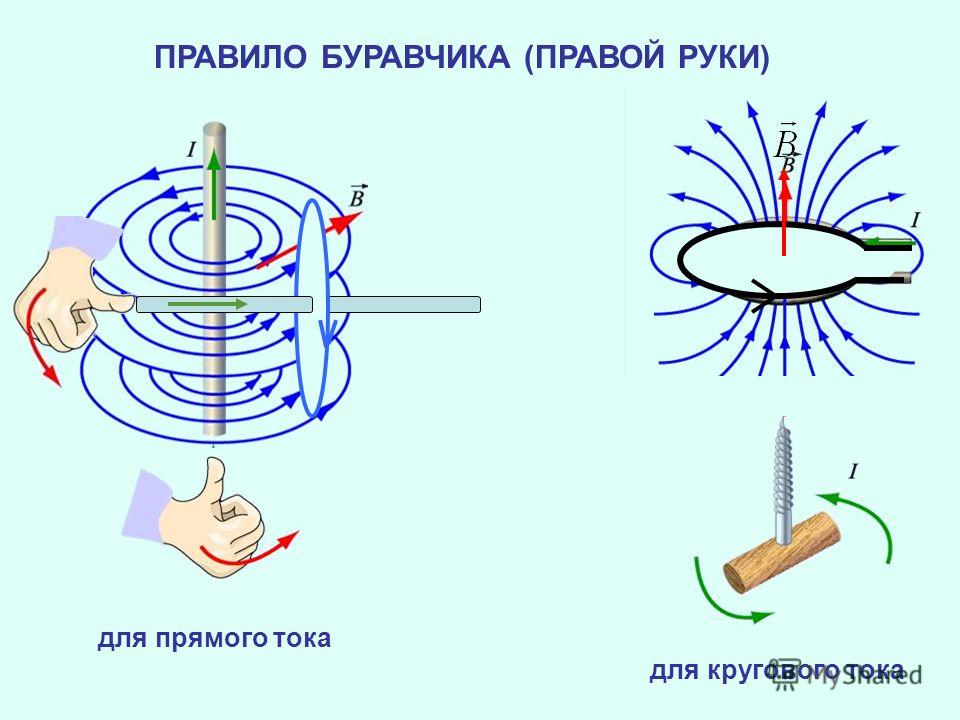 Характеристики механического колебания ………. смотреть
Отклонение маятника ………. смотреть
Колебания шарика под действием силы упругости ………. смотреть
Пружинный маятник ………. смотреть
Колебания пружинного маятника ………. смотреть
Колебания математического маятника ………. смотреть
Условия существования свободных колебаний (вертик. пружина) ………. смотреть
Характеристики колебаний ………. смотреть
Математический маятник ………. смотреть
Математический маятник ………. смотреть
Математический маятник (смещение, амплитуда) ………. смотреть
Математический маятник (сила) ………. смотреть
Математическая модель гармонического колебания ………. смотреть
Гармонические колебания ………. смотреть
Частота и период гармонических колебаний ………. смотреть
Период колебаний математического маятника и опыт с магнитом .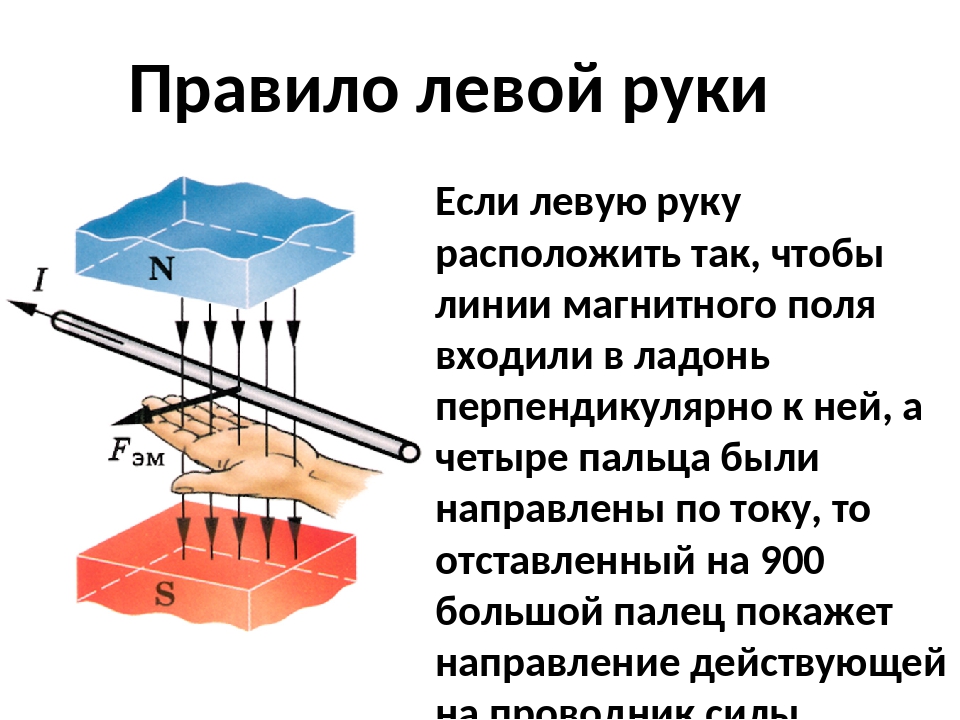 ……… смотреть
Колебания шарика под действием силы упругости ………. смотреть
Пружинный маятник ………. смотреть
Период колебаний пружинного маятника ………. смотреть
Затухающие колебания ………. смотреть
Свободные и вынужденные колебания ………. смотреть
Примеры незатухающих колебаний ………. смотреть
Явление механического резонанса ………. смотреть
Графическое представление колебаний ………. смотреть
Уравнение гармонических колебаний ………. смотреть
Энергетика колебаний ………. смотреть
Превращение энергии при свободных колебаниях ………. смотреть
Определение мгновенного значения скорости колебательного движения ………. смотреть
Определение мгновенного значения ускорения колебательного движения ………. смотреть

Электромагнитные колебания

Колебательный контур . ……… смотреть
Принцип работы колебательного контура ………. смотреть
Зависимость заряда конденсатора и силы тока от времени ………. смотреть
Графическое представление колебаний. Уравнение колебаний ………. смотреть
Электромагнитные колебания ………. смотреть
Свободные колебания ………. смотреть
Свободные колебания – затухающие ………. смотреть
Свободные электромагнитные колебания ………. смотреть
Вынужденные электромагнитные колебания. Принцип получения переменного тока ………. смотреть
Исследование электромагнитных колебаний в колебательном контуре с помощью осциллографа ………. смотреть
Изменение электрического и магнитного полей в колебательном контуре ………. смотреть
Аналогия между механическими и электромагнитными колебаниями ………. смотреть
Вынужденные колебания, резонанс ………. смотреть
Переменный ток . ……… смотреть
Переменный ток, действующее значение силы тока и напряжения ………. смотреть
Конденсатор в цепи переменного тока ………. смотреть
Конденсатор в цепи переменного тока ………. смотреть
Индуктивность в цепи переменного тока ………. смотреть
Катушка индуктивности в цепи переменного тока ………. смотреть
Активная нагрузка в цепи переменного тока ………. смотреть
Закон Ома для цепи переменного тока ………. смотреть

Производство, передача и использование электрической энергии

Трансформатор ………. смотреть
Устройство трансформатора ………. смотреть
Коэффициент трансформации ………. смотреть
Связь силы тока и числа витков ………. смотреть
Напряжения на первичной и вторичной обмотках трансформатора ………. смотреть
Снижение потерь энергии при передаче ее на большие расстояния . ……… смотреть
ЛЭП — линии электропередач ………. смотреть
Тепловые электростанции. Принцип работы ………. смотреть
Гидроэлектростанция. Как она работает? ………. смотреть

Механические волны

Механические волны. Виды волн ………. смотреть
Продольные и поперечные волны ………. смотреть
Поперечные волны (мех) ………. смотреть
Продольные волны (мехх) ………. смотреть
Продольная волна в пружине ………. смотреть
Отражение от преграды звуковой волны ………. смотреть
Поперечная волна в шнуре ………. смотреть
Волновое движение ………. смотреть
Определение длины поперечной и продольной волны ………. смотреть
Длина волны. Скорость волны ………. смотреть
Длина и скорость волны ………. смотреть
Направление вектора скорости волны ………. смотреть
Звук. Источник звука ………. смотреть
Скорость звука ………. смотреть
Зависимость высоты звука от частоты колебания источника ………. смотреть
Зависимость громкости звука от амплитуды колебания ………. смотреть
Звуковые волны в различных средах ………. смотреть
Опыт с волновой ванной ………. смотреть
Закон отражения механических волн ………. смотреть
Стоячая волна (мех) ………. смотреть
Стоячая волна в трубе ………. смотреть
Звуковые волны в различных средах ………. смотреть
Два способа передачи воздействия ………. смотреть
Интерференция волн ………. смотреть
Интерференция ………. смотреть
Интерференционная картина ………. смотреть
Дифракция ………. смотреть
Дифракция волн (1 — мех) ………. смотреть
Дифракция волн (2 — мех) ………. смотреть

Электромагнитные волны

Электромагнитые волны .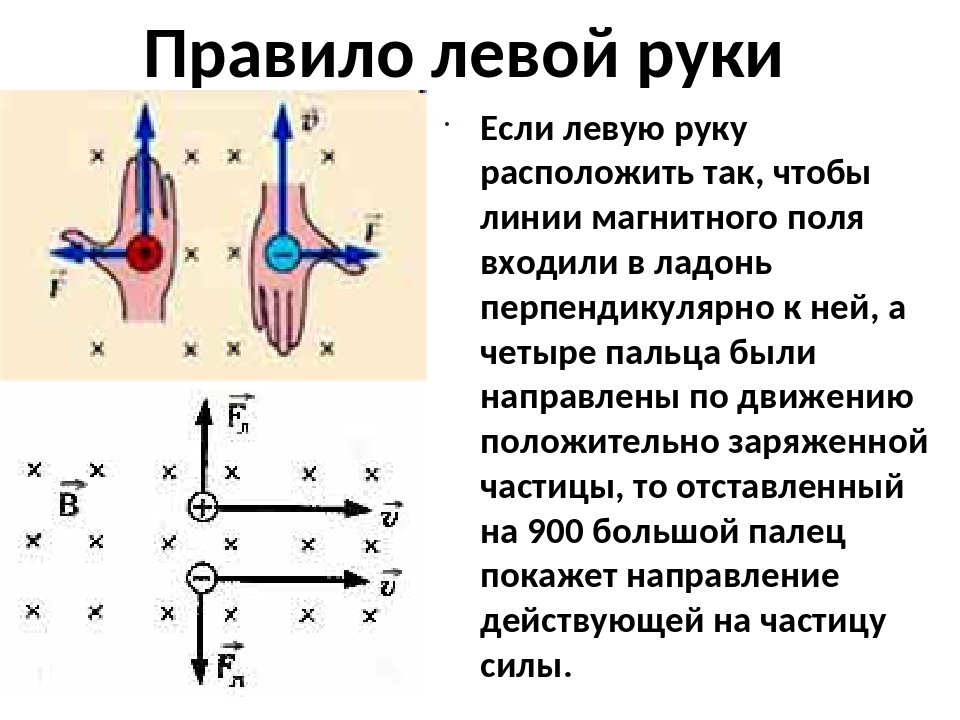 ……… смотреть
Вибратор Герца ………. смотреть
Скорость электромагнитной волны ………. смотреть
Регистрация электромагнитной волны вибратором Герца ………. смотреть
Опыты Герца ………. смотреть
Прямолинейное распространение электромагнитной волны ………. смотреть
Отражение электромагнитной волны ………. смотреть
Измерение скорости света. Опыт Рёмера ………. смотреть
Преломление электромагнитной волны ………. смотреть
Направление вектора скорости волны (эл-маг) ………. смотреть
Свойства электромагнитных волн ………. смотреть
Интерференция электромагнитной волны ………. смотреть
Дифракция электромагнитной волны ………. смотреть
Свойства электромагнитных волн ………. смотреть
Свойства электромагнитных волн в разных диапазонах ………. смотреть
Преобразование колебательного контура в антенну . ……… смотреть
Принцип радиосвязи ………. смотреть
Амплитудная модуляция ………. смотреть
Детектирование ………. смотреть

Оптика

Геометрическая и волновая оптика

Основные законы геометрической оптики ………. смотреть
Образование тени и полутени ………. смотреть
Распространение света в однородных оптических средах ………. смотреть
Опыт Олафа Рёмара. Измерение скорости света ………. смотреть
Опыт Физо. Измерение скорости света ………. смотреть
Опыт Майкельсона. Измерение скорости света ………. смотреть
Закон отражения света (волн.) ………. смотреть
Закон отражения света ………. смотреть
Закон отражения ………. смотреть
Зеркальное и рассеянное отражение света ………. смотреть
Явление полного отражения света ………. смотреть
Изображение предмета в плоском зеркале . ……… смотреть
Построение изображения в плоском зеркале и его характеристика ………. смотреть
Закон отражения, плоское зеркало, построение изображения ………. смотреть
Линзы. Основные понятия ………. смотреть
Собирающая линза. Рассеивающая линза ………. смотреть
Постоение изображений в линзах ………. смотреть
Построение изображения в собирающей линзе (1) ………. смотреть
Построение изображения в собирающей линзе (2) ………. смотреть
Построение изображения предмета в собирающей линзе ………. смотреть
Мнимое изображение предмета в собирающей линзе ………. смотреть
Формула тонкой линзы – ошибка ………. смотреть
Сферические линзы ………. смотреть
Основные линии и точки сферического зеркала ………. смотреть
Применение вогнутых зеркал ………. смотреть
Построение изображения в сферическом зеркале . ……… смотреть
Рассеивающая линза ………. смотреть
Построение изображения в рассеивающей линзе ………. смотреть
Двояковыпуклая тонкая линза ………. смотреть
Собирающая линза ………. смотреть
Построение изображения в собирающей линзе ………. смотреть
Ход лучей в лупе ………. смотреть
Преломление света ………. смотреть
Закон преломления света ………. смотреть
Вывод закона преломления света ………. смотреть
Преломление света на границе раздела двух сред ………. смотреть
Изменение направления распространения света призмой ………. смотреть
Поворотная призма. Уголковый отражатель. Перископ ………. смотреть
Волоконная оптика ………. смотреть

Оборотная призма. Световоды ………. смотреть
Дисперсия света ………. смотреть
Дисперсия света (2) ………. смотреть
Разложение света .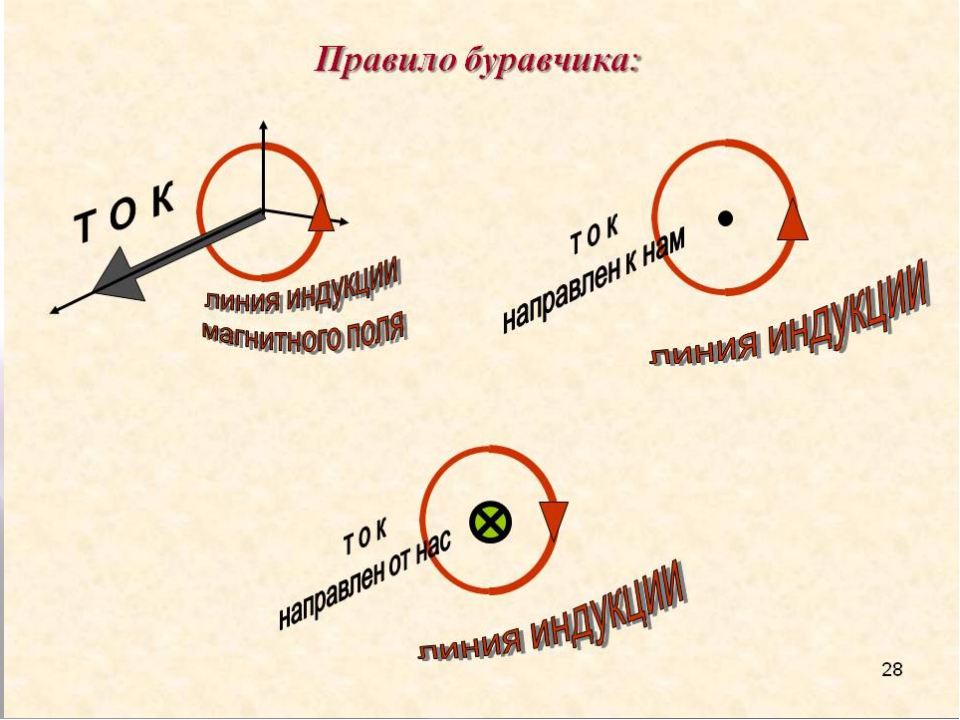 ……… смотреть
Разложение белого света в спектр ………. смотреть

Интерференция света ………. смотреть
Интерференция света при отражении от металлического зеркала ………. смотреть
Интерференция света. Опыт с бипризмой Френеля ………. смотреть
Цвета тонких пленок ………. смотреть
Интерференция света на тонкой пленке ………. смотреть
Интерференционная картина ………. смотреть
Кольца Ньютона в проходящем и отраженном свете ………. смотреть
Сложение волн ………. смотреть
Дифракция света. Волновая оптика ………. смотреть
Дифракционная решётка ………. смотреть
Дифракционная решетка, главные максимумы ………. смотреть
Сложение волн ………. смотреть
Дифракция света на тонкой нити и щели ………. смотреть
Дифракция на нити, щели и круглом отверстии ………. смотреть
Дифракционная решетка одномерная . ……… смотреть
Дифракционная решетка, главные максимумы ………. смотреть
Поперечность световых волн. Поляризяция света. Опыты с турмалином ………. смотреть
Механическая модель волны. Поляризация ………. смотреть
Поляризация света. Поворот плоскости поляризации при деформации ………. смотреть

Элементы теории относительности

Относительность расстояний. Объяснение Эйнштейна ………. смотреть
Относительность одновременности ………. смотреть
Измерение собственного времени наблюдателем, движущимся вместе со световыми часами ………. смотреть
Измерение времени неподвижным наблюдателем ………. смотреть
Взаимопревращение вещества и поля ………. смотреть

Излучение и спектры

Спектр испускания ………. смотреть
Линейчатый спектр испускания ………. смотреть
Сплошной спектр испускания .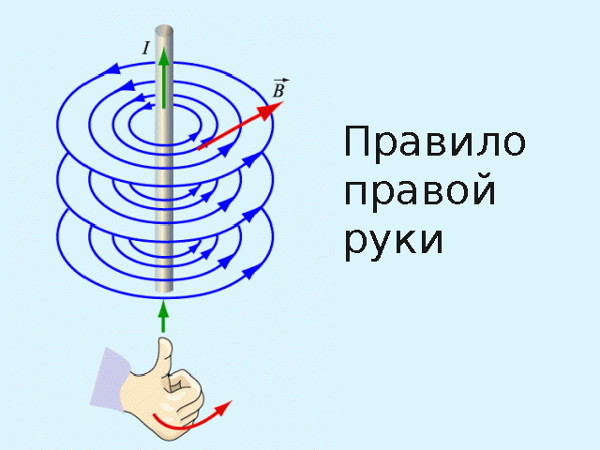 ………смотреть

Квантовая физика

Световые кванты

Корпускулярно-волновой дуализм ………. смотреть
Корпускулярно-волновой дуализм (2) ………. смотреть
Гипотезы Эйнштейна и Планка ………. смотреть
Фотоэффект ………. смотреть
Наблюдение фотоэффекта ………. смотреть
Фотоэффект. Опыты и законы ………. смотреть
Опыт Герца по фотоэффекту ………. смотреть
Давление света (2) ………. смотреть
Давление света ………. смотреть
Давление света ………. смотреть

Атомная физика

Модель атома Томсона ………. смотреть
Модель атома Томсона ………. смотреть
Модель атома Резерфорда ………. смотреть
Опыты Резерфорда. Планетарная модель атома ………. смотреть
Опыт Резерфорда ………. смотреть
Постулаты Бора ………. смотреть
Теоретическое следствие теории Бора . ………смотреть
Доказательство постулатов Бора. Опыты Франка и Герца ………. смотреть
Лазеры. Вынужденное излучение ……….смотреть
Принцип действия лазера ………. смотреть
Устройство и принцип действия лазера ………. смотреть
Создание вынужденного излучения ………. смотреть

Физика атомного ядра

Медоты регистрации элементарных частиц. Наблюдение следов заряженных частиц ………. смотреть
Камера Вильсона ………. смотреть
Радиоактивность (три вида) ………. смотреть
Состав радиоактивного излучения ………. смотреть
Нуклоны: протон и нейтрон ………. смотреть
Протонно-нейтронная модель ядра ………. смотреть
Открытие протона ………. смотреть
Открытие нейтрона ………. смотреть
Изотопы, массовое число ………. смотреть
Альфа-распад ………. смотреть
Бета-распад . ……… смотреть
Период полураспада, закон радиоактивного распада ………. смотреть
Механизмы ядерных реакций ………. смотреть
Короткодействие ядерных сил ………. смотреть
Энергия связи ядра ………. смотреть
Ядерная реакция с азотом и альфа-частицей ………. смотреть
Ядерная реакция с литием и протоном ………. смотреть
Ядерная реакция с алюминием и нейтроном ………. смотреть
Законы сохранения зарядового и массового чисел ………. смотреть
Дефект массы ………. смотреть
Расчет энергетического выхода ядерной реакции ………. смотреть
Механизм деления ядер ………. смотреть
Деление ядер урана ………. смотреть
Цепная реакция деления ядер урана ………. смотреть
Реакция деления ядер урана ………. смотреть
Цепная реакция деления ………. смотреть
Замедлители нейтронов .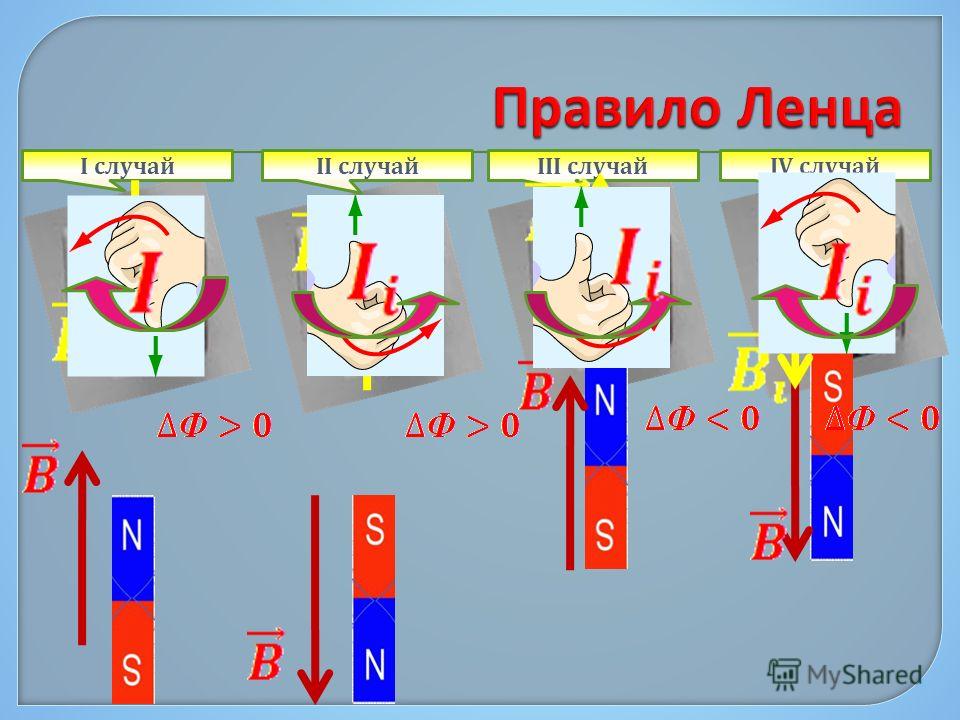 ……… смотреть
Критическая масса, ядерный реактор ………. смотреть
Схема энергетической установки с ядерным реактором ………. смотреть
Атомные электростанции ………. смотреть
Термоядерные реакции ………. смотреть
Действия радиоактивных излучений на живые организмы ………. смотреть
Проникающая способность. Виды радиоактивного излучения ………. смотреть
Счетчик Гейгера ………. смотреть
Применение радиоактивного излучения ………. смотреть

Элементарные частицы

Элементарные частицы ………. смотреть
Античастицы ………. смотреть

Календарно-тематическое планирование по физике 11 класс профильное обучение к учебнику Мякишева

Календарно-тематическое планирование учебного материала по физике в 11 классе (профильный уровень)

(5 часов в неделю, всего 170 часов)

Составлено на основании Программы для общеобразовательных учреждений «Физика 7-11кл.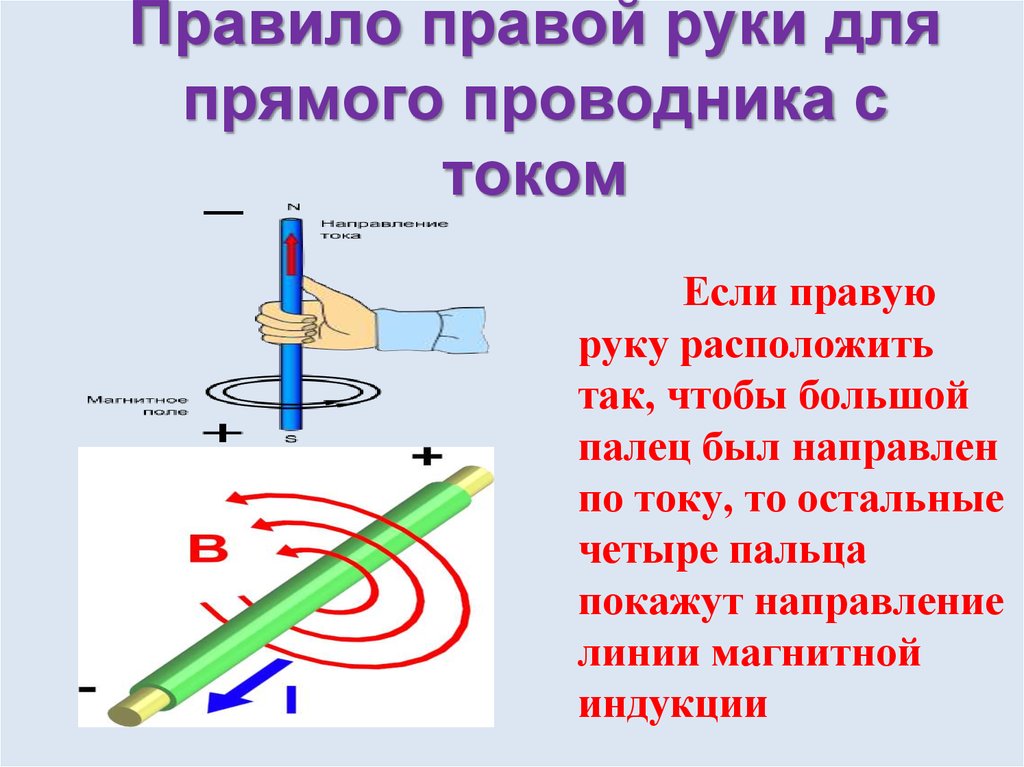 Астрономия-11кл», рекомендованной Департаментом образовательных программ и стандартов общего образования МО РФ. М.;Дрофа.2010г.

Автор программы Г.Я.Мякишев.

Учебник «Физика -11». Г.Я.Мякишев, Б.Б.Буховцев ( М.: Просвещение, 2010)

№

Раздел и тема раздела

Требования к уровню

подготовки учащихся

Коли-чество часов

Сроки

проведения

Особые

формы

контроля

I. Основы электродинамики (продолжение)

24

Магнитное поле

12

1.

1.Стационарное магнитное поле

Знать:

понятия

магнитное поле, характеристики МП., свойства

законы и правила:

Ампера, Лоренца, Буравчика, левой руки для тока, левой руки для скорости частицы в МП.

Формулы:

Fa=IBlsinа, Fл=qBvsinа

применять: правило буравчика для определения направления силы тока и линий индукции магнитного поля, правило левой руки для определения направления силы Ампера и силы Лоренца, тока и скорости частиц в МП.

2.

2.Решение задач на правило буравчика

3.

3.Сила Ампера

4.

4.Л.р.№1 «Наблюдение действия магнитного поля на ток»

Л.р. №1 «Наблю-дение действия магнитного поля на ток»

5.

5.Сила Лоренца

6.

6.Решение задач по теме «Сила Лоренца»

7.

7.Магнитные свойства вещества

8.

8.Обобщающе-повторительное занятие по теме «Магнитное поле»

9.

9.Зачет по теме «Магнитное поле»

решать задачи:

на движение и равновесие заряженных частиц в магнитном поле;

производить расчеты:

силы Ампера и силы Лоренца, заряда, массы, скорости, энергии частиц, находящихся в магнитном поле.

Зачет

10.

10.Контрольная работа по теме «Магнитное поле»

Контрольная работа по теме «Магнитное поле»

11.

11.Коррекция знаний по теме «Магнитное поле»

12.

12. Резерв

Электромагнитная индукция

12

13.

1. Явление электромагнитной индукции

Знать:

понятия: индукция МП, магнитный поток, магнитная проницаемость, электромагнитная индукция, самоиндукция; индуктивность, электромагнитное поле;

законы и правила: ЭМИ, правой руки для ЭДС индукции; правило Ленца

Формулы: ЭДС, магнитный поток

Уметь:

применять

правило правой руки по определению направления ЭДС индукции;

решать задачи:

на расчет ЭДС индукции, индуктивности, магнитного потока, работы магнитного поля;

14.

2. Индукционное (вихревое) электрическое поле

15.

3.Направление индукционного тока.

Правило Ленца

16.

4. Решение задач на применение правила Ленца

17.

5. Л.р. « Изучение явления электромагнитной индукции»

Л.р. №2 «Изуче-ние явления электромагнитной индукции»

18.

6. Закон электромагнитной индукции

19.

7.Решение задач на закон электромагнитной индукции

20.

8. Вихревые токи и их использование в технике

21.

9. Явление самоиндукции. Индуктивность

22.

10. Обобщающе-повторительное занятие по теме «Электромагнитная индукция».

Зачет

23.

11. Контрольная работа по теме «Электромагнитная индукция»

К.р. по теме «Электромагнит-ная индукция»

24.

12. .Коррекция знаний по теме «Электромагнитная индукция»

II. Колебания и волны

31

Механические колебания

Знать:

понятия:

свободные и вынужденные колебания; гармонические колебания, превращение энергии при гармонических колебаниях, резонанс.

Формулы: уравнение движения маятника, уравнение гармонических колебаний, энергии, периода колебаний.

устройство и принцип действия: математический и пружинный маятник, ухо, автоколебательная система,

читать и строить графики:

колебаний х=х(t).

рассчитывать: амплитуду, период, частоту, массу маятника, жесткость пружины, используя формулу ускорения свободного падения и длины маятника.

число колебаний, время колебаний, период колебаний, ускорение свободного падения с помощью м.м., длину маятника.

Знать: понятия: электромагнитные колебания, колебательный контур, переменный ток, резонанс, трансформатор, волна, электромагнитная волна;

 формулы: Уравнение свободных электромагнитных колебаний, сопротивления в цепи переменного тока

устройство и принцип действия: конденсатор, колебательный контур, радиоприемник, радиолокатор, радиотелескоп; 

читать и строить графики волн;

 рассчитывать:   скорость распространения волны, параметры колебательного контура.

измерять:скорость распространения волны

7

25.

1.Свободные и вынужденные механические колебания

26.

2. Динамика колебательного движения. Уравнение движения маятника.

27.

3.Гармонические колебания

28.

4.Решение задач с использованием характеристик пружинного и математического маятников.

29.

5.Л.р. №3.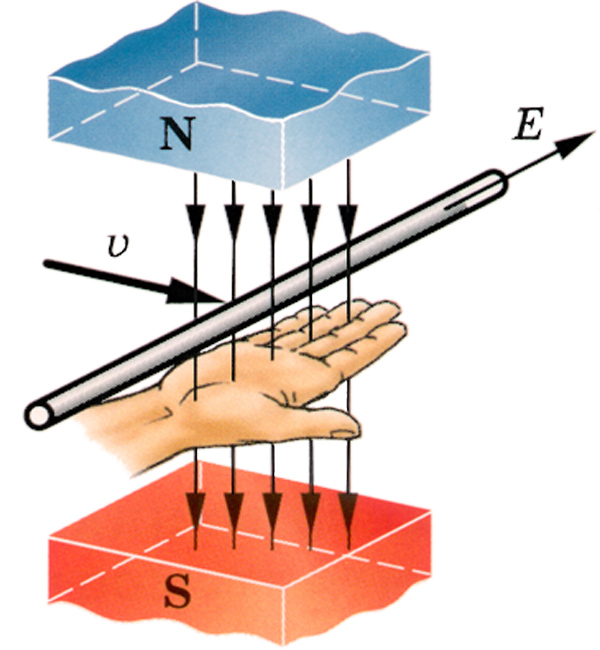 »Определение ускорения свободного падения при помощи маятника»

Л.р. №3 «Опреде-ление ускорения свободного паде-ния при помощи маятника»

30.

6. Превращение энергии при гармонических колебаниях.

31.

7.Вынужденные колебания. Резонанс

Самостоятельная работа

Электромагнитные колебания

11

32.

1. Свободные и вынужденные электромагнитные колебания

33.

2. Аналогия между механическими и электрическими колебаниями

34.

3.Уравнение свободных электромагнитных колебаний в закрытом контуре

35.

4.Решение задач по теме «Электромагнитные колебания»

36.

5.Переменный электрический ток

37.

6.Сопротивления в цепи переменного тока

38.

7. Сопротивления в цепи переменного тока

39.

8. Решение задач на различные виды сопротивлений в цепи переменного тока

40.

9. Решение задач на различные виды сопротивлений в цепи переменного тока

Самостоятельная работа

41.

10.Резонанс в электрической цепи

42.

11. Электрические автоколебания. Генератор на транзисторе.

Производство, передача и использование электрической энергии

2

43.

1. Трансформаторы.

44.

2. Производство, передача и использование электрической энергии

Урок-семинар

Механические волны

4

45.

1. Волна. Свойства волны. Основные характеристики

46.

2. Волна. Свойства волны. Основные характеристики

47.

3.Звуковые волны

48.

4. Решение задач на свойства волн

Самостоятельная работа

Электромагнитные волны

7

49.

1.Опыты Герца

50

2. Изобретение радио А.С. Поповым. Принципы радиосвязи

51.

3. Современные средства связи

Урок-конференция

52.

4. Современные средства связи

53.

5.Обобщающе-повторительное занятие по теме «Колебания и волны»

54.

6.Зачёт по теме «Колебания и волны»

Зачет

55.

7..Контрольная работа по теме «Колебания и волны»

К.р. по теме «Колебания и волны»

III. Оптика

Знать: понятия: свет, корпускулярно-волновой дуализм, отражение и преломление света, полное отражение, зеркала, линзы, фокусное расстояние, оптическая сила, линейное увеличение, интерференция, дифракция, поляризация и дисперсия света,

законы: принцип Гюйгенса, законы отражения и преломления света, полного отражения, принцип постоянства скорости света в вакууме, формула тонкой линзы; практическое применение: интерферо-метр, просветление оптики, дифракционная решетка, поляроиды;

Уметь: строить: изображение предмета в зеркалах и линзах, системе «линза-зеркало», чертить ход  лучей при отражении, преломлении и полном отражении света;

вычислять: фокусное расстояние, оптическая сила, линейное увеличение линзы, расстояние от объекта до линзы, расстояние от линзы до изображения; условие max и min интерференции и дифракции, период решетки, длину волны света;

пользоваться: дифракционной решеткой для определения длины световой волны, стеклянной призмой для определения показателя преломления света.

Знать : понятия:

относительность движения, тело отсчета, система отсчета, относительность одновременности, относительность расстояний, релятивистская динамика,

законы:

постулаты теории относительности, релятивистский закон сложения скоростей, зависимость массы и энергии от скорости, формула Эйнштейна;

Уметь: решать задачи:

на применение основных следствий СТО: определение возраста космонавтов, продолжительности процесса в ПСО, определение собственных размеров тел, на определение массы и энергии  тела, движущегося со   с.

Знать: понятия: источник света, излучение, тепловое излучение, электролюминесценция, катодолюминесценция, хемилюминесценция, фотолюминесценция, спектр, непрерывный, линейчатый, полосатый спектры, спектр излучения и поглощения, спектральный анализ, спектроскоп, ИК и УФ излучение

 устройство и принцип действия:

спектроскоп, спектрограф, рентгеновская трубка, приборы ночного видения.

Уметь: объяснить: природу и характерные отличия  спектров излучения и спектров поглощения, назначение спектрального анализа в технике; пользоваться:

спектроскопом . ..

Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.

«Взаимодействие токов. Магнитное поле, его характеристики». 11-й класс

Цель урока:

• дать учащимся представление о магнитном поле;
• сформировать представления учащихся о магнитном поле и его свойствах.

Демонстрации:

1. Опыт Эрстеда, движения проводника с током в магнитном поле;
2. Силовых линий магнитного поля постоянного магнита, магнитного поля прямого тока.

Оборудование:

• источник питания;
• ключ;
• переменный резистор;
• амперметр;
• катушка на подставке;
• компас;
• соединительные провода.

ХОД УРОКА

I. Актуализация знаний

1. Знакомство с учениками, с классом.
2. Знакомство с учебником, правилами и требованиями учителя.
3. Запись учениками школьных принадлежностей для урока физики.

а) учебник;
б) тетрадь 48 л.;
в) тетрадь для лабораторных и практических работ – 12-18 л.;
г) тетрадь для контрольных работ – 12-18 л.;
д) микрокалькулятор
е) линейка, карандаш, ластик, треугольник, транспортир, ручка (синяя и чёрная).

II. Правила техники безопасности в кабинете физики и на уроках физики, при выполнении демонстраций, практических и лабораторных работ.

а) ИОТ – 6;
б) ИОТ – 7;
в) ИОТ – 8;
г) журнал по технике безопасности на уроках физики (роспись учащихся об ознакомлении с правилами по ТБ).

 III. Изучение нового материала.

Неподвижные электрические заряды создают вокруг себя электрическое поле.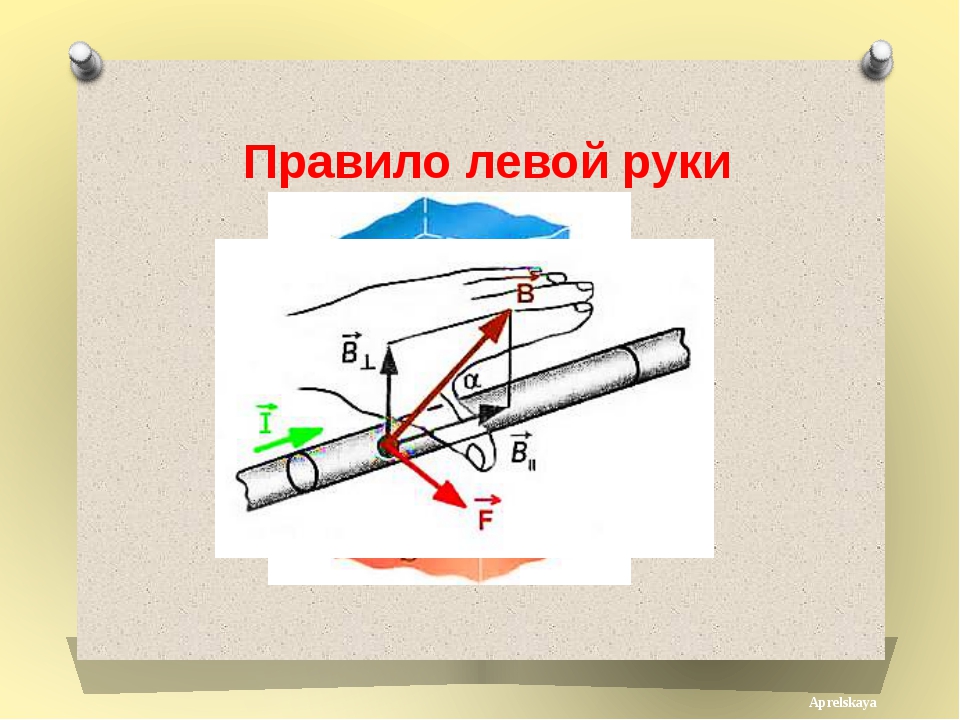 Движущиеся заряды создают магнитное поле.
Вокруг любого магнита существует магнитное поле.
В 1820 году Эрстед обнаружил, что магнитное поле порождается электрическим током (демонстрация опыта Эрстеда).
В 1820 году Ампер предложил, что «магнитные свойства постоянных магнитов обусловлены множеством круговых токов, циркулирующих внутри молекул этих тел».

Свойства магнитного поля.

1. Магнитное поле порождается только движущимися зарядами, в частности электрическим током.

• В отличие от электрического поля магнитное поле обнаруживается по его действию на движущиеся заряды (заряженные тела).
• Магнитное поле материально, т.к. оно действует на тело, следовательно обладает энергией.
• Магнитное поле обнаруживается по действию на магнитную стрелку.

Опыт Ампера

Пропускаем ток по параллельным проводникам. Гибкие проводники укрепляются вертикально, затем присоединяем их к источнику тока. Ничего не наблюдаем. Но если замкнуть концы проводников проволокой, в проводниках возникнут токи противоположного направления. Проводники начнут отталкиваться друг от друга.

В случае токов одного направления проводники притягиваются. Это взаимодействие между проводниками с током, т.е. взаимодействие между движущимися электрическими зарядами, называют магнитным. Силы, с которыми проводники с током действуют друг на друга, называют магнитными силами.

Изобретение компаса

В 12 веке в Европе стал известен компас как прибор, с помощью которого можно определить направление частей света.
Применение (12 в.) в морских путешествиях для определения курса корабля в открытом море.
Магнит имеет два полюса: северный и южный, одноимённые полюсы отталкиваются, разноимённые – притягиваются.

Эксперимент 1

Расположим перед катушкой компас. Замкнём цепь и будем наблюдать за поведением компаса.
Вывод: вокруг проводника с током существует (возникает) магнитное поле.

Эксперимент 2

Расположим перед катушкой компас так, чтобы расстояние между ними было около 12 см. замкнём электрическую цепь. В данном случае отклонения стрелки не наблюдается. При приближении катушки к компасу на расстоянии 8 см, наблюдается отклонение стрелки (300). Уменьшая расстояние, видим увеличение угла отклонения стрелки. Чем дальше от проводника с током, тем слабее магнитное поле.

Магнитное поле можно изобразить графически при помощи линий, касательные к которым в каждой точке совпадают с направление вектора магнитной индукции.
Линии магнитной индукции не пересекаются. При изображении магнитного поля с помощью линий магнитной индукции эти линии наносятся так, чтобы их густота в любом месте поля была пропорциональна значению модуля магнитной индукции.
Характерной особенностью линий магнитной индукции является их замкнутость. Магнитное поле   вихревое.

Правило правого винта: Если вы когда-нибудь закручивали винт или шуруп, то вы наверняка знаете, в какую сторону он закручивается, а в какую выкручивается. Люди унифицировали направление закручивая винтов и шурупов. Это значит, что все шурупы и винты во всем мире закручиваются в одну сторону. То есть, если вы купите некий прибор в другой стране, то в случае его ремонта или сборки вам не потребуются винты с нарезкой в иную сторону, такие, каких не купишь в вашей стране. Нарезка всех винтов в мире совпадает. Это правило нарушают лишь в некоторых особых случаях, когда от нарезки зависит вращение некой части устройства. Но для таких случаев делают специальные детали. Это простое, но гениальное решение избавило от множества потенциальных проблем.

«Правило буравчика», направление тока и линий его магнитного поля

Оказывается, что это правило применимо не только в механике к закручиванию винтов. Если мы имеем проводник с током, то это правило помогает нам определить направление линий магнитного поля, образованного этим током. Только это правило в данном случае носит название «правила буравчика». Правило буравчика звучит следующим образом:
Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Буравчик это винт или шуруп, который мы ввинчиваем. Направление ручки буравчика это направление вращения нашей руки. Если ток движется от нас, то и шуруп движется от нас, то есть мы его ввинчиваем, так как мы условились считать их направления совпадающими.
Тогда направление вращения нашей руки в процессе ввинчивания это направление магнитных линий. Они будут направлены по часовой стрелке.
В случае противоположного направления электрического тока, линии магнитного поля будут направлены, соответственно, против часовой стрелки. Таким же было бы направление руки в процессе выкручивая винта или направление ручки буравчика в случае его движения к нам.
А как определить направление тока, если мы знаем направление магнитных линий? Очень просто. По тому же правилу. Только изначально бы берем за известный факт не направление движения буравчика, а направление вращения его ручки.

Правило правой руки

В случае, когда мы имеем дело с магнитным полем катушки с током или соленоида, картина будет более сложной. Поэтому для простого нахождения направления линий магнитного поля в таком случае существует правило правой руки. Оно гласит:

Если обхватить соленоид ладонью правой руки, направив четыре пальца по направлению тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Открытие электромагнетизма:

В XVIII в. электричество и магнетизм считались хотя и похожими, но все же имеющими различную природу явлениями. Правда, были известны некоторые факты, указывающие на существование как будто бы связи между магнетизмом и электричеством, например намагничение железных предметов в результате ударов молнии. Больше того, Франклину удалось как будто бы намагнитить кусок железа с помощью разряда лейденской банки. Все-таки известные факты не позволяли уверенно утверждать, что между электрическими и магнитными явлениями существует связь.

Такую связь впервые обнаружил датский физик Ханс Кристиан Эрстед в 1820 г. Он открыл действие электрического тока на магнитную стрелку.

Интересна история этого открытия. Идею о связи между электрическими и магнитными явлениями Эрстед высказал еще в первом десятилетии XIX в. Он полагал, что в явлениях природы, несмотря на все их многообразие, имеется единство, что все они связаны между собой.

Руководствуясь этой идеей, он поставил перед собой задачу выяснить на опыте, в чем эта связь проявляется.

Эрстед открыл, что если над проводником, направленным вдоль земного меридиана, поместить магнитную стрелку, которая показывает на север, и по проводнику пропустить электрический ток, то стрелка отклоняется на некоторый угол.

После того как Эрстед опубликовал свое открытие, многие физики занялись исследованием этого нового явления. Французские ученые Био и Савар постарались установить закон действия тока на магнитную стрелку, т. е. определить, как и от чего зависит сила, действующая на магнитную стрелку, когда она помещена около электрического тока. Они установили, что сила, действующая на магнитный полюс (на конец длинного магнита) со стороны прямолинейного проводника с током, направлена перпендикулярно к кратчайшему расстоянию от полюса до проводника и модуль ее обратно пропорционален этому расстоянию.

Познакомившись с работой Био и Савара, Лаплас заметил, что для расчета «магнитной» силы, т. е., говоря современным языком, напряженности магнитного поля, полезно рассматривать действие очень малых отрезков проводника с током на магнитный полюс. Из измерений Био и Савара следовало, что если ввести понятие элемента проводника ∆l, то сила ∆F, действующая со стороны этого элемента на полюс магнита, будет пропорциональна ∆F ~ (∆lr2)sinθ –, где ∆l – элемент проводника, θ – угол, образованный этим элементом и прямой, проведенной из элемента ∆l в точку, в которой определяется сила, а r – кратчайшее расстояние от магнитного полюса до линии, являющейся продолжением элемента проводника.
После того как было введено понятие силы тока и напряженности магнитного поля, этот закон стали записывать так:

где ∆H – напряженность магнитного поля, I – сила тока, а k – коэффициент, зависящий от выбора единиц, в которых измеряются эти величины. В международной системе единиц СИ этот коэффициент равен 1/4π.

Новый важнейший шаг в исследовании электромагнетизма был сделан французским ученым Андре Мари Ампером в 1820г.
Раздумывая над открытием Эрстеда, Ампер пришел к совершенно новым идеям. Он предположил, что магнитные явления вызываются взаимодействием электрических токов. Каждый магнит представляет собой систему замкнутых электрических токов, плоскости которых перпендикулярны оси магнита. Взаимодействие магнитов, их притяжение и отталкивание объясняются притяжением и отталкиванием, существующими между токами. 3емной магнетизм также обусловлен электрическими токами, которые протекают в земном шаре.

IV. Закрепление изученного материала.

1. Какие взаимодействия называются магнитными.
2. Основные свойства магнитного поля.
3. Опишите опыт Эрстеда, что доказывает опыт Эрстеда?
4. Правило правого винта.
5. От чего зависит магнитная индукция поля внутри вытянутой катушки?

V. Домашнее задание.

§ 1,2  учебника Мякишев Г. Я., Буховцев Б. Б.    Физика – 11 (базовый и профильный уровни),– М.: Просвещение, 2010 г.

Правило большого пальца правой руки гласит: A Если мы придерживаемся класса 11 по физике, CBSE

Подсказка: Проводник с током создает линии магнитного поля вокруг проводника. Чтобы узнать направление магнитных силовых линий или силовых линий магнитного поля, существует правило, называемое правилом правой руки и большого пальца. С помощью правила большого пальца правой руки вы можете увидеть форму магнитного поля, создаваемого проводником с током.

Полный пошаговый ответ :
В 1820 году Эрстед показал, что проводник с током создает вокруг себя магнитные поля.то есть, если вы поместите компас рядом с проводником с током, он покажет некоторое отклонение. Напряженность магнитного поля в любой точке вблизи проводника с током можно определить по закону Био-Савара.
Закон Био-Савара гласит, что направление магнитного поля в любой точке рядом с проводником с током будет перпендикулярно плоскости, содержащей проводник, и вектору положения точки относительно провода. Но если вы возьмете прямой провод с током, который проходит через картон перпендикулярно, и положите немного железной пыли, пыль переставит их в концентрические круги.Это показывает, что силовые линии магнитного поля вокруг провода имеют форму концентрических кругов. Направление магнитных силовых линий вокруг провода определяется правилом большого пальца правой руки.
Правило большого пальца правой руки гласит: «Если вы представите, что держите токопроводящий провод в правой руке с большим пальцем, указывающим в направлении потока электрического тока, то направление, в котором изгибаются ваши пальцы, дает направление силовых линий магнитное поле ».

Итак, правильный вариант — вариант Б.

Дополнительная информация: Есть еще одно правило, чтобы знать направление силовых линий магнитного поля токоведущего проводника. Это правило Максвелла для пробки. В нем говорится, что если правый винт для пробки поместить вдоль проводника, по которому проходит ток, ось которого совпадает с направлением тока, так что, если пробка скручена, она перемещается вперед в направлении тока. Направление, в котором поворачивается конец ручки, определяет направление силовых линий.

Примечание : обратите внимание, что вам не нужно держать токоведущий провод, чтобы узнать направление силовых линий магнитного поля. Вы должны представить, что держите провод, чтобы узнать магнитное поле. Прикосновение к токоведущему проводу очень опасно. Также вы должны указать большим пальцем в направлении тока, чтобы завиток давал направление силовых линий магнитного поля.

Правила магнетизма для правой руки 11 класс Физика Power Point

Это Power Point на 3 правила магнетизма правой руки.Он также включает магнитные поля вокруг прямых проводов, силовые линии магнитного поля, магнитную силу, закон Ампера, параллельные провода, силу магнитной силы, Fm = BIL и определение направления тока и ЭДС. Он объясняет тему с помощью слов, диаграмм и гифок. Содержание подходит для курса физики 11 класса. Power Point состоит из 19 слайдов и включает в себя примеры решенных задач по теме.

Меня зовут Даррин Мэтьюсон, я доктор органической химии. Я преподаю физику и химию более 15 лет.Мои студенты нашли эти Power Points очень полезными для понимания физики и химии во время онлайн-уроков и личного обучения. Учащиеся находят полностью решенные типовые задачи чрезвычайно полезными для укрепления своих математических навыков и навыков решения проблем. Многочисленные гифки и диаграммы чрезвычайно эффективны, помогая учителям объяснять и разъяснять концепции, представленные в Power Points.

У меня есть более 140 очков Power Point на продажу в моем магазине, 40 пакетов рабочих листов, 100 тестовых пакетов, 100 пакетов с множественным выбором и 70 пакетов с короткими ответами.У меня есть Power Points, тесты, викторины, вопросы с несколькими вариантами ответов, вопросы с короткими ответами и рабочие листы по каждой теме, охваченной естественными науками 10 класса, химией 11 класса, физикой 11 класса и химией 12 класса!

Все публикуемые мной PowerPoint, рабочие листы, викторины и тесты правильно отформатированы и готовы к печати. Проверены на ошибки и опечатки!

Чтобы оценить мою работу, ознакомьтесь с моими 8 БЕСПЛАТНЫМИ ПРОДУКТАМИ, включая Power Points, викторины и тесты!
https: // www.tes.com/teaching-resource/resource-12555615 (Power Point)
https://www.tes.com/teaching-resource/resource-12545047 (тест по органической химии)
https://www.tes.com / Teaching-resource / resource-12545057 (физический тест на равномерное движение и векторы)
https://www.tes.com/teaching-resource/resource-12545034 (викторина по именованию соединений)
https://www.tes.com/ обучающий-ресурс / ресурс-12545028 (тест по стехиометрии)
https://www.tes.com/teaching-resource/resource-12544990 (наименование алканов в Power Point)
https: // www.tes.com/teaching-resource/resource-12544998 (ограничение стехиометрии реагентов Power Point)
https://www.tes.com/teaching-resource/resource-12545007 (функция клеток и использование микроскопа Power Point)

Правило правой руки по физике: определение и практика — видео и стенограмма урока

Правило правой руки # 1

Давайте посмотрим на наше первое правило правой руки. Его лучше всего использовать для определения направления магнитной силы, предполагая, что вы знаете направление тока и направление магнитного поля.Итак, вот как это работает. Возьми свою правую руку. Укажите пальцами в направлении магнитного поля. Теперь, поскольку ток и магнитное поле перпендикулярны, сделайте большой палец перпендикулярным пальцам. По сути, вы должны выглядеть так, как будто собираетесь пожать чью-то руку. Как только ваши пальцы встали на свои места, вы создали плоскую плоскость. Это твоя ладонь. Теперь, если вы представите прямую линию, выходящую из вашей ладони перпендикулярно плоскости, которую вы создали, это направление магнитной силы .Для людей, которые не умеют воображать невидимые линии, согните указательный палец в суставе, чтобы создать перпендикулярную линию, выходящую из плоскости.

Видите, как легко это было? Технически, мы могли бы вычислить направление различных сил с помощью довольно сложных уравнений, но большинство людей согласятся, что проще просто поднять руку. Магнитные силы и электрические токи на самом деле не то, что мы можем увидеть, поэтому это отличный способ визуализировать направление сил, когда пальцы представляют направление магнитного поля, большой палец представляет направление тока, а магнитный сила, распространяющаяся наружу перпендикулярно ладони.

Правило правой руки №2

Это первое правило правой руки является наиболее распространенным, но на самом деле есть другой способ использовать тот же принцип для определения направления магнитного поля вокруг токоведущего провода. По этому проводу проходит электрический ток и создается магнитное поле, но как узнать, в какую сторону вращается это поле? Легкий. Возьмите правую руку и укажите большим пальцем в направлении течения. Теперь оберните пальцы полукругом вокруг проволоки.В качестве примечания: в зависимости от того, насколько хорошо изолирован провод, вы можете не захотеть к нему прикасаться. Просто говорю. Теперь, когда вы это сделали, направление ваших пальцев указывает направление магнитного поля. Обычно магнитное поле вращается против часовой стрелки перпендикулярно направлению тока. Вы продемонстрировали это правой рукой.

Стоит отметить, что это работает только с положительным электрическим зарядом. Магнитное поле ведет себя иначе при отрицательном заряде.Но с помощью всего лишь этого простого инструмента мы снова обошли некоторые очень сложные уравнения и определили направление невидимой силы.

Краткое содержание урока

В мире вокруг нас магнитное поле, магнитные силы и электрические токи ведут себя и взаимодействуют определенным образом, что является удачным для нас, поскольку позволяет нам изобретать небольшие уловки для определения этих направлений. Правила для правой руки — это простые устройства для определения направления магнитной силы, тока или магнитного поля, используя только вашу правую руку.

Первое правило правой руки используется для определения направления магнитной силы . Поскольку магнитная сила, магнитное поле и ток перпендикулярны друг другу, если ваши пальцы указывают в направлении магнитного поля, а большой палец перпендикулярен пальцам, представляющим направление тока, тогда магнитная сила распространяется. наружу перпендикулярно ладони.

Второе правило правой руки , используемое для определения направления магнитного поля , аналогично.Если большой палец указывает в направлении тока, а пальцы образуют полукруг, они указывают направление вращения магнитного поля. Это намного проще, чем пытаться определить это с помощью длинных уравнений. Итак, как вы думаете, природа предпочитает одну руку другой? Верно.

8 января — Принцип двигателя

Смотрите это:

Вчера мы заговорили о соленоидах. Сегодня мы продолжили с еще несколькими заметками:

Как увеличить силу магнитного поля в соленоиде?

— увеличить текущий

— увеличить количество петель на

— диаметр петель уменьшить на

— замена сердечника соленоида

(вставлен в ферромагнитный материал)

Применение соленоидов

— динамики

— колокольчики

— подъемники

— замки

— МРТ

Вот насколько мощным может быть магнитное поле МРТ:

Принцип двигателя

Когда проводник с током находится во внешнем (перпендикулярном) магнитном поле, он испытывает перпендикулярную силу.

Эта сила задается правилом правой руки.

— пальцы указывают в сторону Б.

— большой палец указывает в сторону I.

— ладонь указывает в направлении F.

Вот два взгляда на правило правой руки.

Вот как это может выглядеть в реальной жизни:

Величина этой силы:

F = BIL

B = величина магнитного поля (тесла)

I = ток (Амперы)

L = длина проводника (метры)

F = сила (Ньютоны)

Используя этот принцип, мы можем строить двигатели!

Вот самые простые двигатели, которые вы можете построить:

Задача: Два параллельных провода отводят ток от страницы.В каком направлении сила?

Домашнее задание:

Не отставайте от плана объекта и попробуйте обратную сторону листа, который я раздал вчера.

Hc Verma II для класса 11 по естествознанию Глава 35

Страница № 248:

Ответ:

Согласно правилу большого пальца правой руки, если большой палец нашей правой руки указывает в направлении протекающего тока, то сгибание пальцев будет указывать направление магнитного поля, возникающего из-за этого, и наоборот.Рассмотрим случай, когда электрический ток течет по проводу с севера на юг.
Согласно правилу большого пальца правой руки,
(a) для любой точки на востоке провода, магнитное поле будет выходить из плоскости бумаги
(b) для точки на западе провода, т.е. магнитное поле войдет в плоскость бумаги
(c) для любой точки вертикально над проводом, магнитное поле будет справа налево
(d) для любой точки вертикально под проводом, магнитное поле будет слева направо

Страница № 248:

Ответ:

Магнитное поле, создаваемое длинным прямым проводом, определяется выражением
B = μoi2πd∵Скорость света, c = 1μoεo⇒μo = 1c2εo⇒B = i2πc2εod
(в терминах ε ₀ , c , i и d )

Страница № 248:

Ответ:

Согласно правилу большого пальца правой руки, если мы согнем пальцы правой руки в направлении протекания тока, то большой палец будет указывать в направлении создаваемого им магнитного поля, и наоборот.Следовательно, в этом случае поле в центре удаляется от нас.

Страница № 248:

Ответ:

В законе Ампера ∮B → .dl → = μoi, i — это полный ток, пересекающий область, ограниченную замкнутой кривой. Магнитное поле B в левой части является результирующим полем из-за всех существующих токов.

Страница № 248:

Ответ:

Магнитное поле из-за длинного соленоида определяется как B = µ ₀ ni , , где n — количество петель на единицу длины.Итак, если мы добавим больше петель на концах соленоида, произойдет увеличение количества петель и увеличение длины, из-за чего соотношение n останется неизменным, что приведет к незначительному эффекту на поле внутри соленоида.

Страница № 248:

Ответ:

Закон Ампера действует для некруглого контура. Однако он должен иметь некоторое распределение заряда в замкнутой области, чтобы иметь постоянное электрическое поле в этой области и ненулевое магнитное поле.Даже если заданная петля не имеет своего собственного распределения заряда, но имеет электрическое влияние некоторого другого распределения заряда, она может иметь некоторое постоянное магнитное поле (∮B → .dl → = μoienclosed).

Страница № 248:

Ответ:

Магнитная сила, действующая на провод, по которому проходит электрический ток i , равна F → = i. (L → × B →), где l — длина провода, а B — магнитное поле, действующее на него.Если равномерно заряженное кольцо начинает вращаться вокруг прямого провода, то, согласно правилу большого пальца правой руки, магнитное поле из-за кольца на прямом проводе с током, размещенном на его оси, будет параллельно ему. Таким образом, перекрестное произведение будет
(l → × B →) = 0⇒F → = 0
Следовательно, на провод не будет действовать магнитная сила.

Страница № 248:

Ответ:

Магнитная сила, действующая на провод, по которому проходит электрический ток i , равна F → = i.(l → × B →), где l — длина провода, а B — действующее на него магнитное поле. Предположим, у нас есть один провод в горизонтальном направлении (фиксированный), а другой провод в вертикальном направлении (свободный для движения). Если горизонтальный провод, по которому проходит ток справа налево, удерживается фиксированным перпендикулярно вертикальному проводу, который может свободно перемещаться, верхняя часть свободного провода будет стремиться двигаться в левом направлении, а нижняя часть провода будет стремиться двигаться в правильном направлении, согласно правилу левой руки Флеминга, поскольку магнитное поле, действующее на провод из-за закрепленного провода, будет указывать на плоскость бумаги над проводом и выходить из бумаги под горизонтальным проводом и током будет течь вверх по свободному проводу.Таким образом, свободный провод будет стремиться стать параллельным фиксированному проводу, чтобы испытать максимальную силу притяжения.

Страница № 248:

Ответ:

Два пучка протонов, идущие в одном направлении, отталкиваются друг от друга, поскольку они подобны зарядам, а мы знаем, что подобные заряды отталкивают друг друга.
Когда заряд находится в движении, с ним связано магнитное поле. Два провода, по которым проходят токи в одном направлении, создают свои поля (действующие друг на друга) в противоположных направлениях, поэтому результирующая магнитная сила, действующая на них, является притягивающей.Из-за магнитной силы эти два провода притягиваются друг к другу.
Но когда заряд находится в состоянии покоя, с ним связано только электрическое поле, и он не создает никаких магнитных полей. Таким образом, в состоянии покоя он отталкивает подобный заряд, воздействуя на него электрическим током.
Движущийся заряд может создавать как электрическое, так и магнитное поле.
Сила притяжения между двумя токоведущими проводами возникает из-за магнитного поля, а сила отталкивания возникает из-за электрического поля.

Страница № 248:

Ответ:

Мы можем получить магнитное поле из-за прямого, длинного провода, используя закон Ампера, указав ток, протекающий в проводе, не акцентируя внимание на источнике тока в проводе.Чтобы применить закон Ампера, нам нужно, чтобы в проводе протекал постоянный ток, независимо от его источника.

Страница № 248:

Ответ:

Соединительные провода, по которым проходят токи в противоположных направлениях, скручиваются вместе при использовании электрических приборов. Если провод скручен, то результирующие поля от последовательных скручиваний имеют противоположные направления. Таким образом, совокупный эффект на длинной длине провода примерно равен нулю.

Пусть в любой точке между двумя проводами B ₁ и B ₂ будет магнитное поле, создаваемое проводом 1 и проводом 2 соответственно.

Из диаграммы мы можем видеть, что чистое магнитное поле из-за первого витка попадает в бумагу, а из-за второго скрученного витка выходит за пределы плоскости бумаги, поэтому эти поля будут компенсировать друг друга. Следовательно, если провод скручен, то результирующие поля от последовательных скручиваний будут в противоположных направлениях. Таким образом, совокупный эффект на длинной длине провода примерно равен нулю.

Страница № 248:

Ответ:

Магнитное поле не может делать никакой работы и, следовательно, никогда не может ускорять или замедлять частицу.
Рассмотрим 2 провода, по которым ток идет вверх.
Магнитное поле из-за тока в проводе 1 создает магнитное поле из плоскости бумаги в месте расположения провода 2. Из-за этого магнитного поля на провод 2 действует сила. Электрон провода 2, движущийся вниз, движется по круговым путям из-за этой магнитной силы.Поскольку эти электроны не могут выйти из провода, поэтому при описании кругового пути они ударяются о края провода и передают импульс проводу. Из-за этого изменения количества движения проволока начинает двигаться и приобретает кинетическую энергию.

Страница № 248:

Ответ:

(c) вверх

Вертикальный провод проводит ток в направлении вверх, поэтому создаваемое магнитное поле будет направлено против часовой стрелки (согласно правилу большого пальца правой руки).Поскольку электронный луч направляется горизонтально к проводу, направление тока будет горизонтально от провода (направление обычного тока противоположно направлению отрицательного заряда). Согласно правилу левой руки Флеминга, сила будет действовать в направлении вверх, отклоняя луч в том же направлении.

Страница № 248:

Ответ:

(c) не будет оказывать никакого воздействия на круговую петлю.

Магнитная сила на проводе, по которому проходит электрический ток i , задается как F → = i.(l → × B →), где l — длина провода, а B — действующее на него магнитное поле. Если прямой провод с током расположен вдоль оси круговой петли, по которой проходит ток, то, согласно правилу большого пальца правой руки, магнитное поле из-за провода на токопроводящей петле будет вдоль ее окружности, которая содержит текущий элемент i dl →.
Таким образом, перекрестное произведение будет
(l → × B →) = 0⇒F → = 0
Таким образом, прямой провод не будет оказывать никакого усилия на петлю.

Страница № 248:

Ответ:

(a) в сторону протонного пучка
Протонный пучок идет с севера на юг, поэтому направление тока из-за пучка также будет с севера на юг. Кроме того, электронный луч идет с юга на север, поэтому направление тока из-за луча также будет с севера на юг. Направление обычного тока — вдоль направления потока положительного заряда и противоположно направлению потока отрицательного заряда.Магнитное поле, создаваемое ими, войдет в плоскость бумаги на западе и выйдет из плоскости бумаги на востоке, согласно правилу большого пальца правой руки. Поскольку оба луча имеют токи в одном направлении, они будут прикладывать равные и противоположные силы друг к другу и, следовательно, будут притягиваться друг к другу. Таким образом, электронный пучок будет отклонен навстречу протонному пучку.

Страница № 248:

Ответ:

(d) направлен на запад как в A, так и в B.
Согласно правилу большого пальца правой руки, если мы согнем пальцы правой руки в направлении течения, то растяжение большого пальца покажет направление движения. магнитное поле создается за счет этого, и наоборот.
Пусть север-юг проходит по оси x, а восток-запад — по оси y. Круглый провод находится в плоскости xz. Тогда точка A будет лежать на положительной оси y, а точка B — на отрицательной оси y. Если смотреть из точки B, ток течет против часовой стрелки, поэтому магнитное поле будет указывать справа налево. Следовательно, магнитное поле из-за петли будет направлено на запад как в точках A, так и в B.

Страница № 248:

Ответ:

(b) двигаться по направлению к проводу

Сила, действующая на провод на единицу длины, несущая ток i ₂ из-за проводящего ток провода i ₁ , расположенного на расстоянии d задается
F = μoi1i22πd
Итак, силы на единицу длины, действующие на стороны AB и CD , следующие:
FAB = μoi1i22πd (По направлению к проводу) FCD = μoi1i22π (d + a) (Вдали от провода)
Здесь, F _AB > F _CD , потому что сила обратно пропорциональна расстоянию от провода, а провод AB ближе к проводу, по которому проходит ток i _1.
Силы на единицу длины, действующие на стороны BC и DA , будут равны и противоположны, поскольку они одинаково удалены от провода, по которому проходит ток i ₁ , с током i ₂ течет в обратном направлении.
∴ F _BC = -F _DA
Now,
Чистая сила:
F = FAB + FBC + FCD + FDA⇒F = μoi1i22πd + FBC-μoi1i22FBC (d + a) -a ⇒F = μoi1i22π1d-1d + a⇒F = μoi1i2a2πd (d + a)

(По направлению к проводу)
Следовательно, петля будет двигаться к проводу.

Страница № 248:

Ответ:

(d) ноль

Сила, действующая на заряженную частицу q , движущуюся со скоростью v в магнитном поле B , определяется как
F → = q (v → × B →)
Поскольку заряд движется вдоль магнитной силовой линии векторы скорости и магнитного поля будут указывать в одном направлении, создавая перекрестное произведение.
(v → × B →) = 0⇒F → = 0
Итак, магнитная сила, действующая на частицу, будет равна нулю.

Страница № 248:

Ответ:

(c) оба из них

Из-за наличия заряда частица создает электрическое поле. Кроме того, из-за его движения, то есть потока заряда или тока, возникает магнитное поле.

Страница № 249:

Ответ:

(c) кинетическая энергия

Когда частица массой m , несущая заряд q , проецируется со скоростью v в плоскости, перпендикулярной однородному магнитному полю B , поле стремится отклонить частицу в круговой путь радиусом r .
∴mv2r = qvB⇒r = mvqBNow, Площадь, A = πr2⇒A = πmvqB2⇒A = kv2 Здесь, k = πmqB2
Кинетическая энергия частицы, E = 12mv2
Следовательно, ограниченная площадь пропорциональна кинетической энергии.

Страница № 249:

Ответ:

(c) R12R22
Частицы X и Y с соответствующими массами м ₁ и м ₂ несут заряд q , описывая круговые пути с соответствующими радиусами R _{1 9018 R 2 так, что
R1 = m1v1qBR2 = m2v2qB
Поскольку обе частицы ускоряются через одинаковую разность потенциалов, обе будут иметь одинаковую кинетическую энергию.
∴12m1v12 = 12m2v22∵R1 = m1v1qB⇒v1 = R1qBm1And, R2 = m2v2qB ⇒v2 = R2qBm2∴m1R1qBm12 = m2R2qBm22⇒m1m2 = R12R22}

Страница № 249:

Ответ:

(b) в сторону 40 A

Согласно правилу левой руки Флеминга, если указательный и средний пальцы нашей левой руки указывают на магнитное поле, действующее на провод, и ток, текущий в проводе, соответственно, тогда большой палец будет указывать в направлении, в котором будет действовать сила (сохраняя все три перпендикулярно).Направление силы можно определить с помощью правила левой руки Флеминга.

На рисунке пунктирным кружком показаны линии магнитного поля, образованные обоими проводами.
Магнитное поле в любой точке среднего провода будет действовать по касательной к линиям магнитного поля в этой точке.
Следовательно, на провод будет воздействовать магнитное поле, направленное в сторону провода 40 A.
Из-за AB сила будет направлена ​​вправо, а из-за CD сила, действующая на провод, будет направлена. Таким образом, обе силы складываются, чтобы получить результирующую силу, которая будет направлена ​​вправо, то есть по направлению к токоведущему проводу на 40 А.

Страница № 249:

Ответ:

(c) 2

Магнитное поле из-за протекающего с током длинного прямого провода в точке a определяется как
B = μoi2πa
Когда оба провода проходят токи i ₁ и i ₂ в одном направлении, они создают магнитные поля в противоположных направлениях в любой точке между проводами.
B ‘= μoi12πa-μoi22πa = 10 мкТл .. (1)
Здесь a — это расстояние от средней точки до обоих проводов.
Когда оба провода переносят токи в противоположных направлениях, они создают поля в одном направлении в средней точке двух проводов.
B » = μoi12πa + μoi22πa = 30 μT .. (2)
При решении уравнений (1) и (2) получаем
i1-i2 = 10i1 + i2 = 30⇒i1 = 20, i2 = 10⇒i1i2 = 21 = 2

Страница № 249:

Ответ:

(a) μoi2πr
Магнитное поле не будет зависеть от движения наблюдателя, потому что скорость, с которой движется наблюдатель, сравнима со скоростью дрейфа электрона, которая очень мала по сравнению со скоростью потока тока с одного конца провод к другому концу.Таким образом, им можно пренебречь, и, следовательно, магнитное поле из-за провода относительно наблюдателя будет
B = μoi2πr

μ0i2πr

Страница № 249:

Ответ:

(a) μ0i4πdl → × r → r3
(b) -μ0i4πr → × dl → r3

Магнитное поле в начале координат из-за токового элемента i dl →, помещенного в позицию r →, определяется как
дБ → = μo4πir → × dl → r3
Согласно свойству кросс-произведения,
A → × B → = -B → × A → ⇒dB → = -μo4πir → × dl → r3

Страница № 249:

Ответ:

(а) x , y имеют одинаковые размеры.
(b) y , z имеют одинаковые размеры.
(c) z , x имеют одинаковые размеры.

Сила Лоренца:
qvB = qE⇒ Размеры x = [v] = EB = [LT-1]
y = 1μoεo = 4πμo × 14πεo = 9 × 10910-7 = 3 × 108 = c⇒ Размеры y = [c] = [LT-1]
Постоянная времени цепи RC = RC , поэтому размерно [ RC] = [T]
⇒z = lRC ⇒ [z] = [LT-1]
Следовательно, x , y и z имеют одинаковые размеры.

Страница № 249:

Ответ:

(b) направления магнитных полей одинаковы
(c) величины магнитных полей равны
(d) поле в одной точке противоположно полю в другой точке.
Рассмотрим токоведущий провод, лежащий вдоль оси x.
В любых двух точках на оси z, которые находятся на равном расстоянии от провода, одна над проводом и одна под ним, величина магнитного поля будет одинаковой, а их направления будут противоположными друг другу.
В любых двух точках на оси z, которые находятся на разном расстоянии от провода, одна над проводом, а другая также над проводом, величина магнитного поля будет разной, и их направления будут одинаковыми.

Страница № 249:

Ответ:

(b) минимум на оси провода
(c) максимум на поверхности провода

Длинный прямой провод с радиусом R проводит ток i , который равномерно распределен по его поперечному сечению.Согласно закону Ампера,
∮B → .dl → = μoiinsideAt surface, B × 2πR = μoi⇒Bsurface = μoi2πRInside, B × 2πr = μoi ‘для r Здесь i ^, — ток, заключенный в внутри проволоки протянута петля ампериана.
B _внутри будет пропорционально расстоянию от оси.
На оси
B = 0
Магнитные поля из точек на поперечном сечении будут указывать в противоположных направлениях и нейтрализовать друг друга в центре.
Снаружи, B × 2πr = μoi⇒Boutside = μoi2πr, r> R
Следовательно, величина магнитного поля максимальна на поверхности провода и минимальна на оси провода.

Страница № 249:

Ответ:

(b) постоянно внутри трубки
(c) равно нулю на оси

Полая трубка проводит однородный электрический ток по всей своей длине, поэтому ток, заключенный внутри трубки, равен нулю.
Согласно закону Ампера,
∮B →.dl → = μoiinside Внутри трубки ∮B → .dl → = 0, r

Магнитные поля от точек на круговой поверхности будут указывать в противоположных направлениях и нейтрализовать друг друга.
Снаружи трубки, B × 2πr = μoi⇒Boutside = μoi2πr, r> R

Страница № 249:

Ответ:

(a) снаружи кабеля
(b) внутри внутреннего проводника
Согласно закону Ампера, в коаксиальном прямом кабеле проходят токи i во внутреннем проводнике и — i (одинаково в противоположном направлении) в внешний проводник.
Внутри внутреннего проводника
∮B → .dl → = μoiinside∮B → .dl → = 0⇒Bl = 0⇒B = 0
Между двумя проводниками
∮B → .dl → = μoi⇒B = μoi2πr
За пределами внешнего проводника
∮B → .dl → = μo (ii) ⇒B = 0
Следовательно, магнитное поле вне кабеля равно нулю.

Страница № 249:

Ответ:

(b) Магнитное поле на оси проводника равно нулю.
(c) Электрическое поле вблизи проводника равно нулю.
Поскольку ток течет по проводнику, он распространяется только по поверхности проводника, а не в объеме цилиндрического проводника. Это эквивалентно распределению заряда на цилиндрическом листе, для которого электрическое поле внутри проводящего цилиндрического листа всегда равно нулю.
Магнитные поля в любой точке внутри проводящего цилиндра пропорциональны расстоянию от оси цилиндра.
На оси r = 0. Это означает, что поле на оси будет нулевым.

Страница № 249:

Ответ:

Используя соотношение F → = qv⇀ × B →, получаем
B = Fqv = FItv
единиц
силы ( F ) = N
Ток ( I ) = A
Время ( T ) = с
Скорость ( v ) = м / с
⇒B = N / Am
Теперь, используя соотношение B = μ0i2πr, получаем
⇒μ0 = B2πri = NA-m × mA⇒μ0 = N / A2

Страница № 249:

Ответ:

Дано:
Величина тока, I = 10 A
Расстояние между острием и проводом, d = 1 м

Дано магнитное поле B → в точке (1 м, 0, 0) на
B = μ0i2πd = 4π × 10-7 × 102π × 1⇒B = 2 × 10-6 T
(По оси + ve y по правилу большого пальца правой руки)

Страница № 250:

Ответ:

Дано:
Величина тока, I = 10 А
Диаметр проволоки, d = 1.6 × 10 ⁻³ м
∴ Радиус провода = 0,8 × 10 ⁻³ м

Напряженность магнитного поля определяется как
B = μ0i2πr
= 2 × 10-7 × 200,8 × 10-3 = 5 мТ

Страница № 250:

Ответ:

Дано:
Величина тока, I = 100 A
Отделение дороги от провода, d = 8 м
Таким образом, магнитное поле определяется как
B = μ0i2πd = 2 × 10-7 × 1008 = 2.5 мТ

Страница № 250:

Ответ:

Дано:
Однородное магнитное поле, B ₀ = 1.0 × 10 ⁻⁵ T (вертикально вверх)
Отделение острия от провода, d = 2 см = 0,02 м
Магнитное поле из-за к проводу дается
Bw = μ0i2πd = 4π × 10-7 × 1 2π × 0,02⇒Bw = 1 × 10-5 T

Теперь,
Чистое магнитное поле в точке P:
B _P = B _{w + B 0 = 2 × 10 ⁻⁵ T
Чистое магнитное поле в точке Q:
B Q = B w 0 B 0 = 0}

Страница № 250:

Ответ:

(a) Поскольку рассматриваемый провод проводит ток, он также создает вокруг себя магнитное поле.А для длинного прямого провода оно будет максимальным в средней точке, называемой P.
Теперь,
Магнитное поле, создаваемое токоведущим проводом = μoi2πr
Чистое магнитное поле = B + μ0i2πr

(b) Магнитное поле B = 0
при r <μ0i2πB
Очевидно,
B = 0
при r = μ0i2πB
Но когда r> μ0i2πB,
Чистое магнитное поле = B-μ0i2πr

Страница № 250:

Ответ:

Дано:
Однородное магнитное поле, B ₀ = 4.0 × 10 ⁻⁴ T
Величина тока, I = 30 A
Отделение острия от провода, d = 0,02 м
Таким образом, магнитное поле, создаваемое током в проводе, равно
B = μ0I2πd

= 2 × 10-7 × 300,02 = 3 × 10-4 T

B ₀ перпендикулярно B (как показано на рисунке).
∴ Результирующее магнитное поле
Bnet = B2 + B02 = (4 × 10-4) 2+ (3 × 10-4) 2 = 5 × 10-4 Тл

Страница № 250:

Ответ:

Дано:
Однородное магнитное поле, B ₀ = <sup>2.0 × 10 −3 Тл (с юга на север)
Чтобы сделать результирующее магнитное поле равным нулю, магнитное поле, создаваемое проводом, должно иметь ту же величину, что и B ₀ , и в направлении с севера на юг .
Вышеупомянутое условие будет выполнено, когда требуемая точка будет размещена на западе от реки. провод.
Пусть расстояние от точки до провода будет d.

Магнитное поле из-за тока в проводе определяется как
B = μ0I2πd</sup>

Из вопроса, B = B ₀ .
⇒2,0 × 10-3 = μ0I2πd
⇒2,0 × 10-3 = 2 × 10-7 × 10d⇒d = 10-3 м = 1 мм

Страница № 250:

Ответ:

Для точки A ₁ ,
Величина тока в проводах, I = 10 A
Разделение точки A _{1 от провода с левой стороны, d = 2 см
Разделение точки A 1 от провода с правой стороны, d ‘= 6 см}

На рисунке
красная и синяя стрелки обозначают направление магнитного поля, создаваемого проводом, отмеченным красным и синим соответственно.
P (отмечен красным) обозначает провод, несущий ток в плоскости, входящей в бумагу.
Q (отмечен синим) обозначает провод, по которому проходит ток в плоскости, выходящей из бумаги.
Также из рисунка видно, что
PA4 = QA4 ∠ A4A3P = ∠A4A3Q = 90 ° ⇒∠ A4PA3 = ∠ A4QA3 = 45 ° ⇒∠ PA4A3 = ∠ QA4A3 = 45 ° ⇒∠ PA4Q = 90 °
Магнитное поле при A ₁ из-за тока в проводах определяется выражением
B = μ0I2πd-μ0I2πd ‘… (1)

⇒B = 2 × 10-7 × 102 × 10-2-2 × 10-7 × 106 × 10-2 = 1-13 × 10-4 = 0.67 × 10-4 Тл

Аналогично, мы получаем магнитное поле в A ₂ , используя уравнение. (1).
B = 2 × 10-7 × 101 × 10-2 + ​​2 × 10-7 × 103 × 10-2 = 83 × 10-4 T = 2,67 × 10-4 T

Теперь,
Магнитное поле на A ₃ :
B = 2 × 10-7 × 102 × 10-2 + ​​2 × 10-7 × 102 × 10-2 = 2 × 10-4 Тл

Магнитное поле на A ₄ :
Разделение точек A _{4 от проволоки с левой стороны, d = 22 + 22 = 22 см
Отделение точки A 4 от проволоки с правой стороны, d ‘= 22 + 22 = 22 см
Таким образом, магнитное поле в точке A 4 , обусловленное током в проводах, равно
B = 2 × 10-7 × 1022 × 10-22 + 2 × 10-7 × 1022 × 10-22 = 1 × 10-4 т}

Страница № 250:

Ответ:

Дано:
Величина токов, I _{1 = I 2 = 10 A
Отделение точки от проводов, d = 2 см
Таким образом, магнитное поле из-за тока в провод обозначен как
B1 = B2 = μ0I2πd}

На рисунке пунктирным кружком показаны силовые линии магнитного поля, создаваемые проводом с током, размещенным в плоскости, перпендикулярной плоскости бумаги.
Из рисунка видно, что ∆PI1I2 — равносторонний треугольник.
∠I1PI2 = 60 °
Угол между магнитными полями из-за тока в проводе, θ = 60 °
∴ Требуемое магнитное поле при P
Bnet = B12 + B22 + 2B1B2cosθ
= 2 × 10-7 × 102 × 10-22 + 2 × 10-7 × 102 × 10-22 + 2 × 10-7 × 102 × 10-2 + ​​2 × 10-7 × 102 × 10-2cos60 °
= (10-4) + (10 -4) 2 + 2 (10-4) (10-4) × 12 = 3 × 10-4 T = 1,732 × 10-4 T

Страница № 250:

Ответ:

Дано:
Величина тока, I = 5 A
Расстояние между острием и проводом, d = 1 м
Таким образом, величина магнитного поля, создаваемого током в проводах, определяется как
B1 = B2 = μ0I2πd

(a) В точке (1 м, 1 м) магнитные поля, создаваемые проводами, одинаковы по величине, но противоположны по направлению.
Следовательно, чистое магнитное поле равно нулю.

(b) В точке (-1 м, 1 м) магнитные поля из-за проводов направлены вверх.
⇒Bnet = B1 + B2 = 2 × 10-7 × 51 + 2 × 10-7 × 51
= 2 × 10 ⁻⁶ T (По оси z )

(c) В точке ( −1 м, −1 м) магнитные поля, создаваемые проводами, одинаковы по величине, но противоположны по направлению.
Следовательно, чистое магнитное поле равно нулю.

(d) В точке (1 м, -1 м) магнитные поля из-за проводов направлены вверх.
⇒Bnet = B1 + B2 = 2 × 10-7 × 51 + 2 × 10-7 × 51
= 2 × 10 ⁻⁶ T (по отрицательной оси z )

Страница № 250:

Ответ:

Дано:

Пусть горизонтальные провода, расположенные внизу и вверху, обозначены как W ₁ и W ₂ соответственно.
Пусть вертикальные провода, помещенные справа и слева в точку P, обозначены как W ₃ и W ₄ соответственно.
Величина тока, I = 5 A
(a) Рассмотрим точку P.
Магнитные поля от проводов W ₁ и W _{2 одинаковы по величине, но противоположны по направлению.
Магнитные поля из-за проводов W 3 и W 4 одинаковы по величине, но противоположны по направлению.
Следовательно, чистое магнитное поле равно нулю.
Чистое магнитное поле в точке P из-за этих четырех проводов = 0}

(b) Рассмотрим точку Q ₁ .
Из-за проволоки W ₁ расстояние между точкой Q _{1 и проволокой ( d ) составляет 7,5 см.
Итак, магнитное поле из-за тока в проводе определяется как
BW1 = μ0I2πd
= 4 × 10 ^{−5 T (в направлении вверх)}}

Из-за провода W ₂ , разделение точек Q _{1 из проволоки ( d ) 2,5 см.
Итак, магнитное поле из-за тока в проводе определяется как
BW2 = 43 × 10-5 Тл (в направлении вверх)}

Из-за провода W ₃ , отделение точки Q _{1 от провода ( d ) равно 7.5 см.
Итак, магнитное поле из-за тока в проводе определяется как
B W 3 = 4 × 10 ⁻⁵ T (в направлении вверх)}

Из-за провода W ₄ , разделение точки Q _{1 из проволоки ( d ) 2,5 см.
Итак, магнитное поле из-за тока в проводе определяется как
BW4 = 43 × 10-5 Тл (в направлении вверх)}

∴ Чистое магнитное поле в точке Q ₁
BQ1 = 4 + 43 + 4 + 43 × 10-5 = 323 × 10-5 = 1.06 × 10-4 T (в направлении вверх)

В точке Q ₂ ,
Магнитное поле из-за провода W ₁ :
B _{W 1 = 4 × 10 ⁻⁵ T (в направлении вверх)
Магнитное поле из-за провода W 2 :
BW2 = 43 × 10-5 Тл (в направлении вверх)
Магнитное поле из-за провода W 3 :
BW3 = 43 × 10-5 T (в направлении вниз)
Магнитное поле из-за провода W 4 :
BW4 = 4 × 10-5 Тл (в направлении вниз)}

∴ Чистое магнитное поле в точке Q _{2 ,
BQ2 = 0}
Аналогично, в точке Q ₃ магнитное поле равно 1.1 × 10 ^{−4 Тл (в направлении вниз) и в точке Q ₄ магнитное поле равно нулю.}

Страница № 250:

Ответ:

Как показано на рисунке, точки P, Q, R и S лежат на окружности радиуса d .
Пусть провода будут называться W ₁ и W ₂ .

Теперь,
В точке P магнитное поле из-за провода W ₁ определяется как
B ₁ = 0
В точке P магнитное поле из-за провода W ₂ определяется как
B2 = μ0i4πd (перпендикулярно плоскости в наружном направлении)
⇒Bnet = μ0i4πd (перпендикулярно плоскости наружу)

В точке Q магнитное поле, создаваемое проводом W ₁ , равно
B1 = μ0i4πd (Перпендикулярно плоскости внутрь)
В точке Q магнитное поле, создаваемое проводом W ₂ , равно
B ₂ = 0
⇒Bnet = μ0i4πd (Перпендикулярно плоскости внутрь)

В точке R магнитное поле, создаваемое проводом W ₁ , определяется как
B ₁ = 0
В точке R магнитное поле, создаваемое проводом W ₂ , определяется как
B2 = μ0i4πd (Перпендикулярно плоскости внутрь)
⇒Bnet = μ0i4πd (Перпендикулярно к плоскости внутрь)

В точке S магнитное поле, создаваемое проводом W ₁ , определяется как
B1 = μ0i4πd (перпендикулярно плоскости наружу)
В точке S магнитное поле, создаваемое проводом W ₂ определяется как
B ₂ = 0
⇒Bnet = μ0i4πd (перпендикулярно плоскости наружу)
Следовательно, величина магнитного поля в точках P, Q, R и S равна μ0i4πd .

Страница № 250:

Ответ:

Пусть AB — провод длиной x со средней точкой О.
Дано:
Величина тока = i
Расстояние между точкой и проводом = d

Теперь,
Магнитное поле на серединном перпендикуляре определяется выражением
B = μ0i4πd (sinθ + sinθ)
B = μ0i4πd2xx2 + 4d2
Итак, если d >> x (без учета x ), то
B = μ0i4πd2x2d⇒B∝1d2, если d << x (без учета d ), тогда
B = μ0i4πd2xx⇒B∝1d

Страница № 250:

Ответ:

Пусть AB — провод длиной 10 см, а P — требуемая точка.
Дано:
Величина тока, i = 10 A
Углы между точками A и B и точкой P равны θ1 = 30 ° и θ2 = 30 ° соответственно.
∴ Отделение острия от провода, d = 32a = 32 × 10 = 53 см

Таким образом, магнитное поле из-за тока в проводе определяется как
B = μ0i4πd (sinθ1 + sinθ2) = 10- 7 × 1053 × 10-212 + 12 = 11,54 × 10-6 т

Страница № 250:

Ответ:

Дано:
Величина тока = i
Отделение точки от провода = d

Таким образом, магнитное поле из-за тока в длинном проводе определяется как
B1 = μ0i2πd
Также магнитное поле поле из-за участка длиной l на серединном перпендикуляре определяется выражением
B2 = μ0i4πd2ll2 + 4d2

⇒μ0i l4πd2dl2d2 + 4 Без учета очень малого l2d2, получаем B2 = μ0i l4πd2 × 224 = 2μ0i l4πd2 × 224 = 2μ0i l4πd2 × 224 = 2μ0 1 > B ₂
Согласно вопросу
B1-B2B1 = 1100⇒B2 = 0.99 B1⇒2μ0il4πd2 = 0,99 × μ0i2πd⇒dl = 1,4141,98 = 0,71

Страница № 250:

Ответ:

Пусть токи в проводах ABC и ADC равны i ₁ и i ₂ соответственно.
Сопротивления в проводах ABC и ADC равны r и 2 r соответственно.

∴ i1i2 = 21⇒ i1-2i2 = 0 … 1
And,
i1 + i2 = i … 2
Используя (1) и (2), получаем
i1 = 2i3 и i2 = i3
Углы между точками A и D и точкой O равны θ1 = 45 ° и θ2 = 45 ° соответственно.
Отделение точки от провода, d = a /2
Итак,
Магнитное поле из-за тока в проводе AD определяется как
B = μ0i24πd (sinθ1 + sinθ2) ⇒B = μ0i34πa2 (sin45 + sin45)
Магнитное поле в центре, создаваемое проводным АЦП, определяется выражением
B ‘= 2B = μ04πi3aa2 × 4 × 2 = 2μ0i3πa
(Перпендикулярно плоскости наружу)

Магнитное поле в центре, создаваемое проводом ABC, равно задается формулой
B » = μ4π2i3aa2 × 4 × 2 = 22μ0i3πa
(перпендикулярно плоскости внутрь)
∴Bnet = B ‘- B’ = 2μ0i3πa
(перпендикулярно плоскости внутрь)

Страница № 250:

Ответ:

Б при P из-за AD = μ04π.i2.4d2.aa2a22 + a42 + a2a22 + 3a42along •
μ0i4πaa2a22 + a42 + a2a22 + 3a42along •

B в точке P из-за AC = μ04π.i2.169a2.a.23a43a42 + a22
= 4μa22a2a2 + a22
= 4μa22a2 + a P из-за AB = μ04π.i2.169a2.a.23a43a42 + a22along •
B в P из-за BC = μ04π.i2.4a2.a.a2a22 + a42 + a2a22 + 3a42 вдоль •
= μ0i2πaa2a22 + a42 + a2a22 + 3a42along⊗
Итак, чистое магнитное поле в точке P.
B = 4μ0iπaa4a22 + a42-4μ0i9πa3a4a22 + 3a42 = 4μ0iπa14114 + 116-4μ0i9πa.34114 + 916
= 4μ0i4πa15-Вдоль
-000
= 4μ0i4πa45-μ139139πa = 9π0139a = 4μ0i4πa45-μ139139πa = 4μ0i4πa45-μ139139πa = 9π0139πa = 9π0139a = 9π0139πa = 9π0139π 1313 по •

Страница № 251:

Ответ:

Цепь ABCD может рассматриваться как цепь с двумя параллельными сопротивлениями: одно вдоль ветви AB, а другое — вдоль ветви ADC.

Так как стороны шлейфа идентичны, их сопротивления тоже одинаковы.

Пусть сопротивление каждой стороны будет r .

Сопротивление ветви AB = r

Сопротивление ветви ADC = 3 r

Ток в ответвлениях рассчитывается как:

iAB = i × 3r3r + r = 3i4

iADC = i × r3r + r = i4
Поскольку ток идет по пути с наименьшим сопротивлением, поэтому

Ток в ветви AB = 3i4
Ток в ветви ADC = i4
В центре контура:

Магнитное поле из-за проводов AD, DC и CB будет в плоскости бумаги согласно правилу большого пальца правой руки.
Магнитное поле из-за провода AB будет вне плоскости бумаги в соответствии с правилом большого пальца правой руки.
Чистое магнитное поле в центре = B _AD + B _DC + B _CB — B _AB , которое будет вне плоскости бумаги.
As, перпендикулярное расстояние центра от каждого провода будет равно a2, а угол между угловыми точками каждой стороны в центре равен 45 °.
BAD = μ0 (i4) 4π (a2) (sin45 ° + sin45 °) = μ0i8πaBAD = BDC = BCBBAD + BDC + BCB = B, = 3μ0i8πaBAB = μ0 (3i4) 4π (a2) (sin45 ° + sin45 °) = 3μ0i8πaBnet = B, — BAB = 0

Страница № 251:

Ответ:

Пропустить ток 2 I в цепь.
Поскольку провод однородный, ток будет равномерно разделен в точке A (как показано на рисунке).

Итак,
Магнитное поле в точке P из-за провода AB = B (скажем)
(перпендикулярно плоскости во внешнем направлении)

Магнитное поле в точке P из-за провода BD = B ‘ (скажем)
( Перпендикулярно плоскости в наружном направлении)

Магнитное поле в P из-за провода AC = Магнитное поле в P из-за провода AB = B
(Перпендикулярно плоскости во внутреннем направлении)

Магнитное поле в P из-за провода CD = Магнитное поле в точке P из-за провода BD = B ‘
(перпендикулярно плоскости внутрь)

∴ Чистое магнитное поле при P = B + B’ — B — B ‘ = 0

Страница № 251:

Ответ:

Пусть ABC — равносторонний треугольник со стороной l /3 и центром M.
(a)
В ∆AOB, AO = l32-I62 = l19-136 = l4-136 = l112∴MO = 13 × l112 = l63
Углы между точками B и C с центром M равны θ1 = 60 ° и θ2 = 60 ° соответственно.
Отделение точки от провода, d = MO = l63
Таким образом, магнитное поле из-за тока в проводе BC определяется как
B = μ0i4πd (sin θ1 + sin θ2) ⇒B = μ0i4πl63 (sin 60 + sin 60)
⇒B = μ0i4πl63 × 3
Итак,
Чистое магнитное поле при M = Магнитное поле из-за провода BC + Магнитное поле из-за провода CA + Магнитное поле из-за провода AB
Поскольку все провода одинаковые,
Bnet = 3B = 27μ0iπl
Он перпендикулярен плоскости во внешнем направлении, если ток направлен против часовой стрелки, и перпендикулярно плоскости во внутреннем направлении, если ток идет по часовой стрелке.

(b)
Углы между точками B и C с центром M равны θ1 = 45 ° и θ2 = 45 ° соответственно.
Отделение точки от провода, d = l /8
Таким образом, магнитное поле, создаваемое током в проводе BC, определяется как
B = μ0i4πd (sin θ1 + sin θ2) ⇒B = μ0i4πl8 (sin 45 + sin 45) = 22μ0iπl
Поскольку все провода одинаковые,
Чистое магнитное поле при M = 4 × Магнитное поле, создаваемое проводом BC
⇒Bnet = 4B = 82μ0iπl

Страница № 251:

Ответ:

Пусть CAB — провод, образующий угол α, P — точка на биссектрисе этого угла, расположенная на расстоянии x от вершины A, а d — перпендикулярное расстояние между AC и AB от P.

На рисунке
sin α2 = dx
d = xsin α2
Углы между точками A и C и точкой P равны θ1 = 90-α2 и θ2 = 90 ° соответственно.
Отделение точки от провода, d = xsin α2
Таким образом, магнитное поле из-за тока в проводе переменного тока определяется как
B = μ0i4πd (sin θ1 + sin θ2) = μ0i4πxsin α2sin 90-α2 + sin 90
μ0i4πxsin α2cos α2 + 1 = μ0i2cos2 α44πx2sin α4cos α4 = μ0icot α44πx
Теперь магнитное поле, создаваемое проводами AC и AB, равно
Bnet = 2B = μ0icot α42πx

Страница № 251:

Ответ:

Пусть углы, образованные точками A и B с точкой O, равны θ1 и θ2 соответственно.
А,
θ1 = θ2 = θ
Отделение точки от проволоки, d = b /2

In ∆AOM, AO = b22 + l22 = 12b2 + l2
And,
sin θ = l2121b2 + l2 = lb2 + l2
Таким образом, магнитное поле из-за тока в проводе AB определяется выражением
B = μ0i4πd (sin θ1 + sin θ2) ⇒B = μ0i4πd × 2sin θ
⇒B = μ0i4πb2 × 2ll2 + b2 = μ0iπbll2 + b2
Точно так же магнитное поле, вызванное током в проводе BC, определяется как
B ‘= μ0iπlbl2 + b2
Итак,
Магнитное поле из-за тока в проводе CD = Магнитное поле из-за тока в проводе AB = B
And,
Магнитное поле, создаваемое током в проводе DA = Магнитное поле, создаваемое током в проводе BC = B ‘

∴Bnet = 2B + B’ = 2μ0iπbll2 + b2 + μ0iπlbl2 + b2 = 2μ0iπl2 + b2lb + bl = 2μ0ib2 + l2πbl

Страница № 251:

Ответ:

(a)
Используя рисунок,
Для правильного многоугольника из n сторон, угол в центре равен 2πntanθ = l2x⇒x = l2tanθ с учетом того, что угол будет малым l2 = πrn Используя закон Био-Савара для одной стороны B = μ04πidlsinθx2 ⇒B = μ04πi (sinθ + sinθ) x2 = μ0i2tanθ2sinθ4πl Подставляем значение r⇒B = μ0i2ntanπn2sinπn4π2πr Подставляем значение lFor n-сторонний многоугольник B ‘= nB⇒B’ = μ0in2tanπnsinπn2π2r 9, когда окружность с радиусом r
и магнитным полем станет
B = μ0i2r

Страница № 251:

Ответ:

Применяя закон напряжения Кирхгофа, мы видим, что ток в цепи равен нулю.
Чистый ток в цепи = 0
Поскольку магнитное поле
всегда пропорционально току, протекающему в цепи, следовательно,
Чистое магнитное поле в точке P = 0
Поле в точке P не зависит от значений сопротивлений в цепи .

Страница № 251:

Ответ:

Дано:
Величина тока в обоих проводах, i ₁ = i ₂ = 20 A
Сила, действующая на 0.1 м второго провода, F = 2,0 × 10 ⁻⁵ Н
∴ Сила на единицу длины = 2 × 10-50,1 = 2,0 × 10 ⁻⁴ Н / м
Теперь,
Пусть расстояние между два провода должны быть d .
Таким образом, сила на единицу длины равна
Fl = μ0i1i22πd⇒2,0 × 10-4 = 2 × 10-7 × 20 × 20d⇒d = 0,4 м = 40 см

Страница № 251:

Ответ:

Пусть провода W ₁ , W ₂ и W ₃ расположены, как показано на рисунке.

Дано:
Величина тока в каждом проводе, i _{1 = i 2 = i 3 = 10 A
Магнитная сила на единицу длины на проводе из-за параллельный токоведущий провод определяется как
Fl = μ0i1i22πd
Итак, для провода W 1 ,
Fl = провод Flby W2 + провод Flby W3 = μ0 × 10 × 102π × 5 × 10-2 + ​​μ0 × 10 × 102π × 10 × 10-2 = 2 × 10-7 × 1025 × 10-2 + ​​2 × 10-7 × 102 10 × 10-2 = 4 × 10-4 + 2 × 10-4 = 6 × 10-4 Н}

Для проволоки W ₂ ,
Fl = Fl по проводам W1-Fl по проводам W3 = μ0 × 10 × 102π × 5 × 10-2-μ0 × 10 × 102π × 5 × 10-2 = 0

Для проволока W ₃ ,
Fl = Fl по проводам W1 + Fl по проводам W2 = μ0 × 10 × 102π × 5 × 10-2 + ​​μ0 × 10 × 102π × 10 × 10-2
= 6 × 10 ⁻⁴ N

Страница № 251:

Ответ:

Пусть третий провод W ₃ , имеющий ток и в направлении вверх, расположен на расстоянии x см от провода на 10 А.

Магнитная сила на единицу длины на проводе, создаваемая параллельным проводом с током, определяется как
Fl = μ0i1i22πd
Согласно вопросу, провод W _{3 не испытывает магнитной силы.
∴ Fl из-за провода W1 = Fl из-за провода W2
⇒μ010i2πx = μ040i2π (10-x) ⇒10-x = 4x⇒x = 2 см
Таким образом, провод W 3 расположен на расстоянии 2 см от 10 A текущий провод.}

Страница № 251:

Ответ:

Поскольку провода AB, CD и EF имеют одинаковое сопротивление, ток (30 А) распределяется в них поровну, то есть по 10 А на каждый провод.

Магнитная сила на единицу длины на проводе, создаваемая параллельным проводом с током, определяется как
Fl = μ0i1i22πd
∴ Магнитная сила на единицу длины AB = Сила из-за тока в CD + Сила из-за тока в EF
Fl = μ0 × 10 × 102π × 1 × 10-2 + ​​μ0 × 10 × 102π × 2 × 10-2 = 2 × 10-7 × 10210-2 + ​​2 × 10-7 × 1022 × 10-2 = 2 × 10-3 + 10-3 = 3 × 10-3 Н / м
Аналогично,
Магнитная сила на единицу длины CD = Сила из-за тока в AB — Сила из-за тока в EF
∵ Сила на CD из-за тока в AB = сила тока в EF
∴ Магнитная сила на единицу длины CD = 0

Страница № 251:

Ответ:

Дано:
Величина тока, i ₁ = 10 A
Расстояние между двумя проводами, d = 5 мм
Линейная массовая плотность второго провода, λ = 1.0 × 10 ⁻⁴ кгм ⁻¹
Теперь
Пусть i <sub>2 будет током во втором проводе в противоположном направлении.
Таким образом, магнитная сила на единицу длины на проводе из-за параллельного токоведущего провода определяется как
Fml = μ0i1i22πd (вверх)
Кроме того,
Вес второго провода, Вт = мг
Вес на единичная длина второго провода, Wl = λg (вниз)

Теперь по вопросу
Fml = Wl⇒μ0i1i22πd = λg
⇒2 × 10-7 × 50 × i25 × 10-3 = 1 × 10-4 × 9.8⇒i2 = 9,8 × 10-720 × 10-7 = 0,49 А</sub>

Страница № 251:

Ответ:

Дано:
Ток в контуре, i ₁ = 6 A
Ток в проводе, i ₂ = 10 A

Теперь рассмотрим элемент на PQ шириной dx на расстоянии х из проволоки.

Сила, действующая на элемент, определяется как
dF = μ0i1i22πxdx
Сила, действующая на деталь PQ, определяется как
FPQ = μ0i1i22π∫13dxx = 2 × 10-7 × 6 × 10 [lnx] 13 = 120 × 10-7ln3 NS Аналогично , FRS = μ0i1i22π∫31dxx = 120 × 10-7ln 13 = -120 × 10-7ln3 N
Обе силы равны по величине, но противоположны по направлению.

(b) Напряженность магнитного поля, создаваемого проводом на SP, определяется как
B = μ0i22πr

Сила на части SP определяется как
FSP = i1Bl = μ0i1i22πlr = μ0i1i22π21
(Справа)

Сила на части RQ составляет определяется как
FRQ = i1Bl = μ0i1i22πlr = μ0i1i22π23
(Влево)

Таким образом, результирующая сила на петле определяется как
Fnet = FSP-FRQ = μ0i1i22π21-23 = 2 × 10-7 × 6 × 10 × 43 = 16 × 10-6 N
(вправо)

Страница № 251:

Ответ:

Дано:
No.витков, n = 1
Величина тока, i = 5,00 A
Теперь пусть радиус петли равен r .
Таким образом, магнитное поле в центре из-за тока в петле определяется выражением
B = μ0i2r
⇒0,2 × 10-3 = 4π × 10-7 × 52r⇒r = 1,57 × 10-2 м = 1,57 см.

Страница № 251:

Ответ:

Дано:
Число витков, n = 100
Радиус петли, r = 5 см = 0.05 м
Напряженность магнитного поля, B = 6.0 × 10 ⁻⁵ T
Теперь пусть величина тока будет i.
Используя B = μ0ni2r, получаем 6,0 × 10-7 = 4π × 10-7 × 102 × i2 × 0,05⇒i = 60 × 10-74π × 10-7 × 102 = 4,777 × 10-2≈48 мА.

Страница № 251:

Ответ:

Дано:
Частота электрона = 3 × 10 ⁵
Время, затрачиваемое электроном на один оборот, T = 1 Частота
Ток в круге, i = qt
Радиус петли, r = 0.5 A ° = 0,5 × 10-10 м
Таким образом, магнитное поле в центре из-за тока в контуре определяется выражением
B = μ0I2r
= 4π × 10-7 × qT2 × 0,5 × 10-10 = 4π × 10-7 × 1,6 × 10-192 × 0,5 × 10-10 × 3 × 105 = 6 × 10-10 т

Страница № 251:

Ответ:

Поскольку центр петли, то есть точка O, лежит на одной линии двух длинных прямых проводов, магнитное поле в точке O, создаваемое каждым прямым проводом, равно нулю.

Поскольку провода ABC и ADC идентичны, ток равномерно распределяется на две части в точке A.Итак, магнитное поле, создаваемое ABC и ADC в точке O, равны по величине, но противоположны по направлениям. (как показано на рисунке).
∴ Чистое магнитное поле при O = 0

Страница № 252:

Ответ:

Число витков: n ₁ = 50 и n ₂ = 100
Величина токов: i ₁ = i ₂ = 2 A
Радиусы шлейфов: r ₁ = 5 см и r ₂ = 10 см
(a) В том же смысле:

Напряженность магнитного поля в центре определяется как
B = μ0n1i12r1 + μ0n2i22r2 = 4π × 10- 7 × 50 × 22 × 5 × 10-2 + ​​4π × 10-7 × 100 × 22 × 10 × 10-2 = 4π × 10-4 + 4π × 10-4 = 2 × 4π × 10-6 = 8π × 10-3 Тл

(b) В противоположном смысле:
Напряженность магнитного поля в центре определяется как

B = μ0n1i12r1-μ0n2i22r2 = 4π × 10-7 × 50 × 22 × 5 × 10-2-4π × 10-7 × 100 × 22 × 10 × 10-2 = 0

Страница № 252:

Ответ:

Дано:
No.витков: n ₁ = 50 и n ₂ = 100
Величина токов: i ₁ = i ₂ = 2 A
Радиусы контуров: r ₁ = 5 см и r ₂ = 10 см
(a) В том же смысле:

Напряженность магнитного поля в центре из-за C ₁ определяется как
B1 = μ0n1i12r1 = 4π × 10 -7 × 50 × 22 × 5 × 10-2 = 4π × 10-4 T
(В плоскости бумаги в направлении вверх)

Напряженность магнитного поля в центре из-за C ₂ определяется как
B2 = μ0n2i22r2 = 4π × 10-7 × 100 × 22 × 10 × 10-2 = 4π × 10-4 T

(В плоскости бумаги в направлении вверх)

В этом случае магнитные поля из-за C ₁ и C ₂ в центре расположены в одном направлении.
Таким образом, чистое магнитное поле определяется выражением
Bnet = B1 + B2 = (4π × 10-4) + (4π × 10-4) = 8π × 10-4 T = 25,12 мТл
(b) Когда направление ток в двух катушках противоположен друг другу, тогда магнитные поля также будут указывать в противоположных направлениях, как показано на рисунке. Следовательно, чистое магнитное поле будет получено вычитанием двух магнитных полей.

Bnet = B1-B2 = (4π × 10-4) — (4π × 10-4) = 0

Страница № 252:

Ответ:

Дано:
Величина тока в контуре, I = 10 A
Радиус контура, r = 20 см = 20 × 10 ⁻² м
Таким образом, напряженность магнитного поля в центре дана на
B = μ0I2r
Теперь
Скорость электрона, v = 2 × 10 ⁶ м / с
Угол между скоростью и напряженностью магнитного поля, θ = 30 °
Таким образом, магнитная сила на электроне равно
F = evBsin θ = 1.6 × 10-19 × 2 × 106 × μ0i2Rsin 30 ° = 1,6 × 10-19 × 2 × 106 × 4π × 10-7 × 102 × 20 × 10-2 × 12 = 16π × 10-19 N

Страница № 252:

Ответ:

Дано:
Для внешнего контура
Величина тока = I
Радиус контура = R
Таким образом, магнитное поле в центре из-за большего контура определяется выражением
B = μ0I2R
Пусть A — это площадь меньшего контура, и пусть ток i проходит через него.
Теперь,
Угол между вектором площади меньшего контура и магнитным полем из-за большего контура = 90 °
Таким образом, требуемый крутящий момент определяется как
Γ = i (A → × B →)
= iAB sin 90 °
= iπr2μ0I2R = μ0πr2Ii2R

Страница № 252:

Ответ:

Дано:
Для внешнего контура
Величина тока = I
Радиус контура = R
Таким образом, магнитное поле в центре из-за большего контура определяется выражением
B = μ0I2R
Пусть A — это площадь меньшего контура, и пусть ток i проходит через него.
Теперь,
Угол между вектором площади меньшего контура и магнитным полем из-за большего контура = 30 °
Таким образом, крутящий момент на меньшем контуре определяется как
Γ = i (A → × B →)
= iAB sin 30 °
= iπr2μ0I4R = μ0πr2Ii4R
Если меньшая петля зафиксирована в своем положении, тогда
Крутящий момент из-за магнитного поля = Момент из-за внешней силы на его периферии
⇒Fr = μ0πr2Ii4R⇒irR = μ0πI
Это минимальная величина силы для уравновешивания данного состояния.

Страница № 252:

Ответ:

Дано:
Величина тока, I = 5 A
Радиус полукруглого провода, r = 10 см
∴ Требуемое магнитное поле в центре кривизны
B = 12 × μ0i2r = 10-7 × 510 × 10-2 = 5π × 10-6 = 1,6 × 10-5 Т

Страница № 252:

Ответ:

Дано:
Величина тока, I = 6 A
Радиус полукруглой проволоки, r = 10 см
Угол, расположенный в центре, θ = 120 ° = 2π3
∴ Требуемый магнитный поле в центре кривизны
B = μ0i2rθ2π = 4 × 10-7 × 52 × 10 × 10-2 × 2π3 × 2π = 4π × 10-6 = 1.26 × 10-5 т

Страница № 252:

Ответ:

Дано:
Величина тока = i
Радиус петли = r
Магнитное поле, создаваемое петлей в ее центре, B l = μ0i2r
Пусть прямой провод, по которому проходит ток 4 i , помещается в расстояние x от центра так, чтобы магнитные поля контура и провода были равны по величине, но в противоположном направлении на O.

Магнитное поле из-за провода в центре петли, Bw = μ04i2πx
Согласно вопросу
Bl = Bw⇒μ0i2r = μ04i2πx⇒ x = 8r2π = 4rπ
Это означает, что провод размещен на 4rπ от центра петли (как показано на рисунке).

Страница № 252:

Ответ:

Число витков, n = 200
Радиус катушки, r = 10 см
Ток в катушке, i = 2A
(a) Пусть магнитное поле в центре катушки равно B .
Поскольку соотношение для магнитного поля в центре круглой катушки определяется выражением
B = nμ0i2r = 200 × 4π × 10-7 × 22 × 10 × 10-2 = 2,51 × 10-3 = 12,56 мТл
(b) Поскольку магнитное поле в любой точке P (скажем) на оси круглой катушки задается соотношением
BP = nμ0ir22 (x2 + r2) 32
, где x — расстояние от точки до центра катушки.
По вопросу
12Bcentre = BP⇒12nμ0i2r = nμ0ir22 (x2 + r2) 32⇒ (x2 + r2) 32 = 2r3⇒ (x2 + r2) = 41 / 3r2⇒x2 + r2 = 1,58r2⇒x = 0,766 r ⇒x = ± 7,66 см
Магнитное поле упадет до половины своего значения в центре, если расстояние этой точки от центра катушки вдоль оси катушки равно 7.66 см.

Страница № 252:

Ответ:

Дано:
Величина тока, I = 5,0 A
Радиус петли, r = 4,0 см

(a) Напряженность магнитного поля B в точке O на расстоянии x на осевая линия равна
B = μ02ir2 (x2 + r2) 3/2
= 4π × 10-7 × 5 × 16 × 10-42 [(9 × 16) × 10-4] 3/2 = 4π × 80 × 10-112 × 125 × 10-6 = 4,019 × 10-5 Тл (в направлении вниз)

(б) Напряженность магнитного поля B в точке O ‘на расстоянии x на осевой линии равна задается формулой
B = μ02ir2 (x2 + r2) 3/2
= 4π × 10-7 × 5 × 16 × 10-42 [(9 × 16) × 10-4] 3/2 = 4π × 80 × 10- 112 × 125 × 10-6 = 4.019 × 10-5 Т (по направлению вниз)

Страница № 252:

Ответ:

Дано:
Величина зарядов, q = 3,14 × 10 ⁻⁶ C
Радиус кольца, r = 20 см = 20 × 10-2 м
Угловая скорость кольца, ω = 60 рад / с
Время на 1 оборот = 2π60
∴Ток, i = qt = 3,14 × 10-6 × 602π = 30 × 10-6 A
На рисунке E ₁ и E ₂ обозначает электрическое поле в точке на оси на расстоянии 5.00 см от центра за счет небольших элементов 1 и 2 кольца соответственно.
E — это результирующее электрическое поле всего кольца в точке на оси на расстоянии 5,00 см от центра.
Электрическое поле в точке на оси на расстоянии x от центра определяется выражением
E = xq4πε0 (x2 + r2) 32

Магнитное поле в точке на оси на расстоянии x от центра. центр равен
B = μ02ir2 (x2 + r2) 3 / 2EB = xq4πε0 (x2 + r2) 32μ02ir2 (x2 + r2) 3/2 = 9 × 109 × 3.14 × 10-6 × 2 × (20,6) 3 × 10-625 × 10-4 × 4π × 10-14 × 12 = 9 × 3,14 × 2 × (20,6) 325 × 4π × 12 = 1,88 × 1015 м / с

Страница № 252:

Ответ:

(a) Магнитное поле внутри любой проводящей трубки всегда равно нулю.
∴ Магнитное поле внутри трубки на расстоянии r /2 от поверхности = 0

(b) Пусть точка вне трубки с расстоянием r2 будет P.

∴ Чистое расстояние от центра, r ‘= r + r2 = 3r2
Рассмотрим петлю Ампера, как показано на рисунке.
Длина петли, l = 2π × 32r = 3πr
Ток, заключенный в петле = i
Применяя закон Ампера, получаем
∫B.dl = μ0i⇒B × 3πr = μ0i⇒B = μ0i3πr

Страница № 252:

Ответ:

а) Магнитное поле внутри любой проводящей трубки всегда равно нулю.
∴ Магнитное поле внутри трубки равно нулю.

(b) Пусть точка вне трубы на расстоянии b будет P.
Рассмотрим петлю Ампера, как показано на рисунке.
Длина петли, l = 2π × b = 2πb
Ток, заключенный в петле = i
Применяя закон Ампера, получаем
∫B.dl = μ0i⇒B × 2πb = μ0i⇒B = μ0i2πb

Страница № 252:

Ответ:

Дано:
Величина тока = i
Радиус провода = b

Для точки на расстоянии a от оси,
Вложенный ток, i ‘= iπb2 × πa2
По цепи Ампера закон,
∮Б.dl = μ0i ‘
Для данных условий
B × 2πa = μ0iπb2 × πa2⇒B = μ0ia2πb2

Страница № 252:

Ответ:

Дано:
Величина тока, i = 5 A
Радиус провода, b = 10 см = 10 × 10-2 м
Для точки на расстоянии a от оси,
Ток заключено, i ‘= iπb2 × πa2
По закону Ампера,
∮B.dl = μ0i’
Для данных условий
B × 2πa = μ0iπb2 × πa2⇒B = μ0ia2πb2… 1
(a) a = 2 см = 2 × 10-2 м
Опять же, используя круговой закон, получаем
B = 4π × 10-7 × 5 × 2 × 10-22π × 10-2 = 2 × 10-6 T = 2 мкТл

( б) Положив a = 10 см = 10 × 10-2 м в (1), мы получим
B = 10 мкТл

(в) Используя круговой закон, получим
B.dl = μ0iB = μ0i2πa = 2 × 10-7 × 520 × 10-2 = 5 × 10-6 T = 5 мкТл

Страница № 252:

Ответ:

Половина петли PQRS находится в области магнитного поля, а половина — в области нулевого магнитного поля.

Рассмотрим токоведущий провод круглого сечения, благодаря которому в данной области создается однородное магнитное поле.

Возьмем точку A внутри цикла PQRS в области, где B = 0

Согласно закону Ампера,
B.dl = μ0i

Если есть ток, заключенный в петлю PQRS, то магнитное поле B не может быть 0.

Тогда как мы приняли магнитное поле в точке A равным нулю.

Таким образом, такое поле невозможно.

Страница № 252:

Ответ:

В точке P,
Ток, i = 0
∴ Магнитное поле B = 0
В точке Q ,
Применяя закон Ампера, получаем
B.dl = μ0i⇒ B.dl = μ0kdl⇒ B = μ0k
В точке R,
Ток, i = 0
∴ B = 0

Страница № 252:

Ответ:

Дано:
Заряд = q
Масса = м
Радиус = r
Мы знаем, что радиус, описываемый заряженной частицей в магнитном поле, определяется как
r = mvqB
Используя закон Ампера B .dl = μ0i⇒ B.dl = μ0kdl⇒ B = μ0k
⇒v = Bqrm = μ0kqrm

Страница № 252:

Ответ:

Дано:
Величина тока, i = 5 A
Напряженность магнитного поля, B = 3.14 × 10 ⁻² T
Мы знаем, что магнитное поле внутри длинного соленоида, имеющего n витков на единицу длины, определяется выражением
B = μ0ni 3,14 × 10-2 = 4π × 10-7 × n × 5. ⇒n = 10-220 × 10-7 = 5 × 103 = 5000 витков / м

Страница № 252:

Ответ:

Дано:
Радиус проволоки, r = 0,5 мм
Ширина каждого витка, = диаметр проволоки, 2 r = 1 мм = 1 × 10 ⁻³ м
∴ Общее количество витков в 1 м соленоид
n = 11 × 10-3 = 103 Величина тока, i = 5 A. Используя B = μ0ni, получаем B = 4π × 10-7 × 103 × 5B = 2π × 10-3 T

Страница № 252:

Ответ:

Дано:
Сопротивление на единицу длины провода, Rl = 0.01 Ом / м
Радиус провода, r = 1,0 см = 0,01 м
Общее кол-во витков, N = 400
Напряженность магнитного поля, B = 1.0 × 10 ^{−2 T
Теперь,
Пусть E будет ЭДС батареи, а R ₀ будет общей сопротивление провода.
∴i = ER0 = E0.01 × 2πr × 400 = E0.01 × 2 × π × 0.01 × 400}

Магнитное поле около центра соленоида равно
B = μ0ni = 1 × 10-2 = 4π × 10-7 × 40020 × 10-2 × E2π × 4 × 10-2⇒E = 10-2 × 20 × 10-2 × 2 × 10-210-7 × 4 × 102 = 1 В

Страница № 253:

Ответ:

(a) Дано:
Ток в контуре или круговой ток = indx
Радиус контура с круговым током = r
Расстояние центра соленоида от кругового тока = l2-x
Магнитное поле при центр из-за круговой петли,
B = μ02ir2 (x2 + r2) 3/2
B = ∫dB = ∫01μ0a2nidx4πa2 + (l-2x) 23/2 = ∫01μ0nia2dx4πa31 + l-2xa23 / 2 = μ0ni4πa∫01dx1 + l-2xa23 / 2 = μ0ni4πa.4πa1 + 2al = μ0ni1 + 2al2
(б) Когда a >> l ,
B = μ0ni2a

Страница № 253:

Ответ:

Дано:
Величина тока в соленоиде, i = 2 А
Частота электрона, f = 1 × 108 об / с
Масса электрона, m = 9,1 × 10-31 кг
Заряд электрона , q = 1,6 × 10-19 C
Мы знаем, что магнитное поле внутри соленоида определяется выражением
B = µ ₀ ni
Если частица совершает равномерное круговое движение внутри магнитного поля, частота частицы равна
f = qB2πm⇒B = 2πmfq⇒ μ0ni = 2πmfq [Используя (1)] ⇒n = 2πmfμ0qi = 2π × 9.1 × 10-31 × 1 × 1084π × 10-7 × 1,6 × 10-19 × 2 = 1420 витков / м

Страница № 253:

Ответ:

Дано:
Величина тока в соленоиде = i
Число витков на единицу длины = n
Когда частица проецируется перпендикулярно магнитному полю, она описывает круговой путь.
И чтобы частица (проецируемая из точки на оси в направлении, перпендикулярном оси) не ударялась о соленоид, максимальный радиус этой круговой траектории должен составлять r /2.

∴ Радиус круга = r2

Мы знаем,
Центростремительная сила = Магнитная сила
мВ2r = qVB⇒V = qBrm = qμ0nir2m

Страница № 253:

Ответ:

Дано:
Число витков на единицу длины соленоида = n
(a) Поскольку чистое магнитное поле около центра соленоида равно 0,
∴B → пластина = B → соленоид Используя закон Гуасса для пластины, получаемBplate × 2l = μ0i = μ0klBplate = μ0k2… 1

Для соленоида
Bsolenoid = μ0ni… (2)

Из (1) и (2) получаем
i = k2n

(b) Подставляя значение n в (2), получаем
B → соленоид = μ0k2
Теперь , B → пластина и B → соленоид перпендикулярны друг другу.
Таким образом, чистое магнитное поле около центра соленоида определяется выражением
Bnet = μ0k22 + μ0k22 = μ0k2

Страница № 253:

Ответ:

Дано:
Емкость, C = 100 мкФ
Напряжение, V = 20 В
Заряд, накопленный в конденсаторе, Q = CV
= 100 × 10-6 × 20 = 2 × 10-3 C
Принято, что потенциал разница на конденсаторе падает до 90% от максимального значения.
Таким образом,
В ‘=

× 20 = 18 В Новый заряд, Q’ = CV ‘= 1,8 × 10-3 CNow, Ток, i = Q-Q’t⇒i = (2-1,8) × 10-32 = 2 × 10-42⇒i = 1 × 10-4 A

Число витков на метр, n = 4000
Таким образом, среднее магнитное поле в центре соленоида равно
B = μ0ni = 4π × 10-7 × 4000 × 10-4 = 16π × 10-8 Т

Просмотреть решения NCERT для всех глав класса 11

Правило большого пальца правой руки в уроке физики 12

Загрузите лучшее приложение для подготовки к экзаменам в Индии

класс 9-10, JEE и NEET

Скачать приложение eSaral Правило большого пальца правой руки в физике гласит, что: чтобы определить направление магнитной силы на положительный движущийся заряд, ƒ, направьте большой палец правой руки в направлении v, пальцы в направлении B и перпендикулярно ладони указывает в сторону F.

Правило большого пальца правой руки:

Если мы возьмем проводник на ладони правой руки так, чтобы большой палец указывал в направлении потока тока, то направление, в котором изгибаются пальцы, дает направление силовых линий магнитного поля. Для тока, протекающего по проводнику в направлении, показанном на рис. (a) или (b) оба правила предсказывают, что силовые линии магнитного поля будут направлены против часовой стрелки, если смотреть сверху.

Магнитное поле, создаваемое прямым проводником с током, имеет круговую симметрию.Магнитные силовые линии представляют собой концентрические окружности с проводником с током, проходящим через их общий центр. Плоскость магнитных силовых линий перпендикулярна длине проводника.

Также читают:

Закон Био Савара

Щелкните здесь, чтобы просмотреть видеоуроки по магнитному эффекту тока класса 12

О eSaral В eSaral мы предлагаем полную платформу для подготовки к IIT-JEE и NEET. Основная миссия eSaral — предоставить образование каждому учащемуся в Индии путем устранения географических и экономических факторов, поскольку прогресс и развитие страны зависят от доступности качественного образования для всех и каждого.Благодаря сочетанию образования и технологий команда eSaral сделала обучение индивидуальным и адаптируемым для всех.

Чтобы получить бесплатные видеолекции и полные учебные материалы, загрузите приложение eSaral.

Загрузите лучшее приложение для подготовки к экзаменам в Индии

класс 9-10, JEE и NEET

Скачать приложение eSaral

Уроки по физике

Видео Описание / ссылка	Номер	Марка
Графики Движение
Положение-время (d-t) Графики
	Гр-1	11
	Гр-2	11
	Gr-3	11
Скорость-время (v-t) Графики
	Gr-4	11
	Гр-5	11
	Gr-6	11
	Gr-7	11
Время разгона (a-t) Графики
	Gr-8	11
Сводка Графики
	Гр-9	11
Использование Один график для рисования других
	Гр-10	11
	Gr-11	11
Математический Операции
	Conv-1	11 и 12
Движение Уравнения кинематики
Кинематика постоянная скорость и постоянная скорость
Определения положения, расстояния, перемещения	Кин-1	11 и 12
Как для расчета скорости и скорости	Кин-2	11 и 12
Кинематика формулы ускорения с объектами, движущимися вперед и назад
	Кин-3	11 и 12
	Кин-4	11 и 12
Образец проблема, которая очень часто встречается на тестах.Объект ускоряется и позже притормаживает.	Кин-5	11 и 12
	Кин-6	11 и 12
	Кин-7	11 и 12
Образец проблема, когда Супермен мчится, чтобы догнать пулю	Кин-8	11 и 12
Объекты брошенный вверх или вниз
	Кин-9	11 и 12
Образец проблема с падением одного мяча и брошенным вторым 1 с позже.	Кин-10	11 и 12
Образец проблема, когда Супермен должен поймать падающего студента	Кин-11	11 и 12
Это это очень сложная задача с двумя поднятыми стрелами.	Кин-12	11 и 12
Объекты движение по кривой или окружности
	Кин-13	11 и 12
Это пример задачи использует кинематические уравнения для решения ускорения и перемещение на колесе обозрения.	Кин-14	11 и 12
	Кин-15	11 и 12
Векторы
Введение в Векторы
	Вект-1	11 и 12
	Вект-2	11
	Вект-3	11 и 12
Вектор Компоненты
Как разбить вектор на составляющие и как вычислить составляющие	Вект-4	11 и 12
Образцы разбиения векторов на составляющие	Вект-5	11 и 12
	Вект-6	11 и 12
	Вект-7	11 и 12
	Вект-8	11 и 12
	Вект-9	11 и 12
Сложение / Вычитание Векторы с компонентами (алгебраический метод)
	Вект-10	12
	Вект-11	11 и 12
	Вект-12	11 и 12
Родственник Скорость
Простой Прямоугольные задачи
	RelV-1	11 и 12
	РелВ-2	11 и 12
Подробнее Комплексные проблемы
	RelV-3	12
	RelV-4	12
	RelV-5	12
	RelV-6	12
	RelV-7	12
Ньютона Законы и схемы свободного тела
Введение первого и второго закона Ньютона
	Тритон-1	11 и 12
	Тритон-2	11 и 12
	Тритон-3	11 и 12
	Ньют-4	11 и 12
	Ньют-5	11 и 12
	Ньют-6	11 и 12
Простой Задачи второго закона Ньютона (без диаграмм свободного тела)
А пример проблемы с тянущим автомобилем.Используется трение, и проблема видоизменена во второй половине ролика.	Тритон-7	11 и 12
А в этом примере задачи пуля проходит через блок.	Тритон-8	11 и 12
Иногда вы не можете использовать уравнения x и y для решения проблемы.Это показывает как добавить силы к объекту под разными углами при взгляде сверху.	Ньют-9	12
Бесплатно Основы схемы тела
Бесплатно Диаграммы кузова с указанием сил	FBD-1
	FBD-2	11 и 12
	FBD-3	11 и 12
	FBD-4	11 и 12
	FBD-5	11 и 12
	FBD-6	11 и 12
	FBD-7	11 и 12
	FBD-8	11 и 12
	FBD-9	11 и 12
Лифт Проблемы
	Элев-1	11 и 12
	Элев-2	11 и 12
Это Пример задачи охватывает все, что вам нужно знать о лифте.	Элев-3	11 и 12
Это В примере задачи лифт движется вверх и вниз вместе с человеком стоя на весах	Элев-4	11 и 12
Трение И законы Ньютона Проблемы с трением
Введение к коэффициент трения и принцип трения	Fric-1	11 и 12
Как работы статического и кинетического трения	Fric-2	11 и 12
Статический и проблема кинетического трения, показывающая разницу между два	Fric-3	11 и 12
А проблема трения с коробкой и сила, давящая на нее	Fric-4	11 и 12
Fn не% $ #! равно Fg (простая версия)	Fric-5	11 и 12
Это Пример задачи включает в себя 2 коробки, которые тянутся с трением и сила под углом.	Fric-6	12
Это это 1 из 2 сложных примеров задач, использующих штабелированные блоки, трение и схемы свободного тела	Fric-7	12
Это это 2 из 2 сложных примеров задач, использующих штабелированные блоки, трение и схемы свободного тела	Fric-8	12
Силы под углом на ящиках
	F / Ang-1	11 и 12
	F / Ang-2	11 и 12
	F / Ang-3	11 и 12
	F / Ang-4	11 и 12
Наклоны Ramps Hill Acceleration
Как для рисования FBD объекта на склоне или холме	Inc-1	12
Проблема скольжения по склону, холму или пандусу с трением	Inc-2	12
	Inc-3	12
	Inc-4	12
	Inc-5	11 и 12
Ньютона Третий закон
	Тритон (3) -1	11 и 12
	Тритон (3) -2	11 и 12
	Тритон (3) -3	11 и 12
Типичный Задача 2-го и 3-го закона Ньютона с вертолетом, поднимающим машину.	Тритон (3) -4	12
	Тритон (3) -5	12
	Тритон (3) -6	12
Это проблема с образцом — это более сложная версия вытягиваемых ящиков и включает милых пингвинов	Тритон (3) -7	12
Шкив Системы
Простой Шкивы
	Pull-1	12
	Pull-2	12
	Pull-3	12
	Pull-4	12
	Pull-5	12
	Pull-6	12
Подробнее расширенный взгляд на эту проблему	Pull-7	12
Комплекс Системы с несколькими шкивами
	Pull-8	12
	Pull-9	12
Центростремительный (Круговое) движение
Центростремительный Разгон
An объяснение того, что такое центростремительное ускорение	ac-1	12
А центростремительный Пример ускорения при повороте автомобиля	ac-2	12
Центростремительный Усилие
	Fc-1	12
	Fc-2	12
	Fc-3	12
	Fc-4	12
	Fc-5	12
	Fc-6	12
	Fc-7	12
	Fc-8	12
	Fc-9	12
	Fc-10	12
Снаряд Движение
Уроки
	Проект-1	12
	Проект-2	12
	Проект-3	12
	Проект-4	12
Простой способ решить проблему с снарядом, но он работает, только если объект приземляется на том же уровне, на котором был произведен выстрел.	Проект-5	12
Как для расчета максимальной высоты снаряда	ПРОЖ-6	12
Образец Проблемы
Это проблема связана с тем, что самолет роняет объект.	ПРОЖ-7	12
Барт Симпсон пытается перепрыгнуть ущелье, и самая сложная часть — найти скорость	Проект-8	12
Как для расчета угла выстрела снаряда.	ПРОЖ-9	12
Столкновения Использование импульса и энергии
Импульс
Объекты врезаться друг в друга по прямой
	Col-1	12
	Col-2	12
Объекты врезаться друг в друга под углом
	Col-3	12
	Col-4	12
Энергетика в столкновениях
	Col-5	12
	Col-6	12
	Col-7	12
	Col-8	12
	Col-9	12
Энергия, Мощность и эффективность
Работа, Сохранение кинетической и гравитационной энергии
	NRG-1	11 и 12
	NRG-2	11 и 12
	NRG-3	11 и 12
	NRG-4	11 и 12
	NRG-5	11 и 12
Комплекс проблема американских горок.Найдите высоту, необходимую для петли	NRG-6
эластичный (Весна) Энергия
	NRG-7	12
	NRG-8	12
	NRG-9	12
Мощность и энергетика
	POW-1	11
Эффективность и энергетика
	EFF-1	11
	ЭФФ-2	11
	EFF-3	11
Планетарный Механика и гравитация
Ньютона Универсальный закон всемирного тяготения
	Грав-1	11 и 12
	Grav-2	11 и 12
Кеплер и Ньютон
	ПМеч-1	12
	ПМеч-2	12
	ПМеч-3	12
Использование Уравнения энергии для объектов, выведенных на орбиту
	ПМеч-4	12
	ПМеч-5	12
	ПМеч-6	12
Кинетический энергии, когда спутник находится на орбите, и его скорость в орбита	ПМеч-7	12
Электроэнергия
Фомулас и простые расчеты
An введение в самые распространенные формулы	ЭЛЕК-1	11
Как использовать формулу Q = Ne	ЭЛЕК-2	11
Как использовать формулу V = E / Q	Elec-3	11
Как использовать формулу I = Q / t	Elec-4	11
Как использовать формулу R = V / I	Elec-5	11
Как длина, площадь и сопротивление материала воздействию	Elec-6	11
Как использовать формулу R = удельное сопротивление * L / A	Elec-7	11
Как использовать 3 формулы мощности	Elec-8	11
Использование тариф энергии для расчета стоимости электроэнергии	Elec-9	11
Электрический Цепи: последовательные и параллельные
Чертеж схемы и 4 части	Elec-10	11
Установка в вольтах и ​​амперметрах в цепи	Elec-11	11
Как для расчета тока в электрической цепи	Elec-12	11
Как для расчета напряжения в электрической цепи	Elec-13	11
Как для расчета сопротивления в электрической цепи	ЭЛЕК-14	11
Простой пример решения схемы	Elec-15	11
Подробнее сложный пример решения схемы	Elec-16	11
Электромагнетизм
Левый и правила для правой руки
Как найти магнитное поле вокруг провода	EM-1	11
Как найти северный конец электромагнита	EM-2	11
Как найти направление силы двигателя	EM-3	11
Как для расчета силы двигателя	EM-4	11
Генераторы и трансформаторы
Как найти направление, в котором будет течь электричество	EM-5	11
Как найти направление, в котором будет течь электричество	EM-6	11
Как для простых расчетов трансформатора	EM-7	11
Как для расчета нескольких трансформаторов	EM-8	11
Как для расчета трансформатора, если КПД не 100%	EM-9	11
Волны (Свет и звук)
Недвижимость всех типов волн
	Волна-1	11 и 12
	Волна-2	11 и 12
	Волна-3	11 и 12
	Волна-4	11 и 12
	Волна-5	11 и 12
	Волна-6	11 и 12
	Волна-7	11 и 12
	Волна-8	11 и 12
	Волна-9	11 и 12
	Волна-10	11 и 12
Звук Волны
	Волна-11	11 и 12
	Волна-12	11 и 12
	Волна-13	11 и 12
	Волна-14	11 и 12
	Волна-15	11 и 12
	Волна-16	12
Волны в 2 размерах (интерференция)
	Волна-17	12
	Волна-18	12
	Волна-19	12
	Волна-20	12
	Волна-21	12
Оптика
Преломление света
	Опц-1	10
	Опт-2	10
	Опт-3	10
изогнутый Зеркала
	Опц-4	10
	Опц-5	10
	Опт-6	10
	Опт-7	10
Линзы
	Opt-8	10
	Опт-9	10
	Опт-10	10
	Опт-11	10
	Опт-12	10
	Опт-13	10
	Опт-14	10
Графики используя Excel : Снимки экрана видео-уроки НЕ наши учебные уроки
	GrEx-1	11 И 12
	GrEx-2	11 И 12
Действительно Потрясающие веселые видео
Физика Обещание: несколько вещей, которые сводят нас с ума, учителя физики.
1 Миллион просмотров Видео с благодарностью: Кажется, так давно мы достигли 1 миллион просмотров. Спасибо за вашу поддержку
Видео классной деятельности
Наука Ярмарки
г. Другие видео и материалы Каруаны-Дингли
г Каруана-Дингли получает премию Toronto Urban Hero Eductional Award !! Щелкните, чтобы увидеть статью newpapaer.
г Каруана-Дингли получает статью в газету для своей коллекции
г Каруана-Дингли разговаривает с Алексом Лифсоном из Rush !!
г Каруана-Дингли во время завтрака по телевидению демонстрирует граммофоны
г Каруана-Дингли о старинном охотнике, демонстрирующем граммофоны
г Каруана-Дингли играет на гитаре в своем акустическом дуэте
г Каруана-Дингли играет песню, которую он написал со своей рок-группой
г. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт