Урок 3. магнитная индукция. действие магнитного поля на проводник с током и движущуюся заряженную частицу — Физика — 11 класс
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» — правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.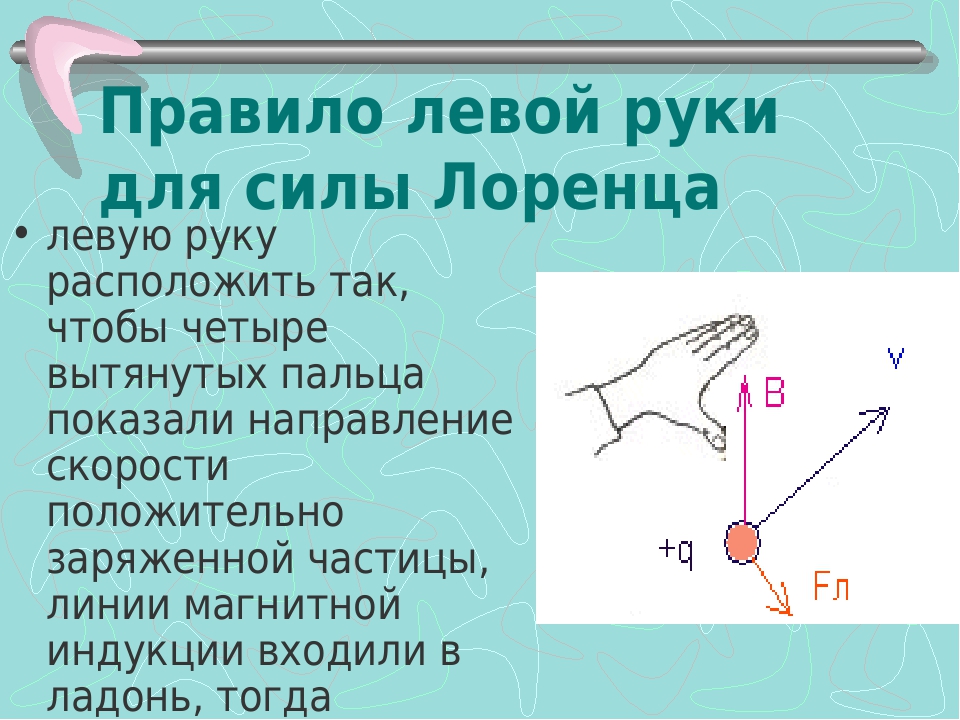
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б.,. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. — М: Дрофа, 2009. – С.109 — 112
Основное содержание урока
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
F_max ~ I; F ~ Δl.
Тогда, зависимость силы от этих двух величин выглядит следующим образом
Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:
Единицей измерения магнитной индукции является 1 тесла (Тл).
1Тл = 1Н/(1А∙1м).
Закон Ампера:
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:
где α – угол между вектором B и направлением тока.
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 900 большой палец покажет направление силы Ампера.
Сила Ампера — сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:
– заряд частицы;
– скорость частицы;
B – модуль магнитной индукции;
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 900 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.
Согласно 2-му закону Ньютона
Отсюда
Время, за которое частица делает полный оборот (период обращения), равно:
Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
Варианты ответов:
1. вправо →;
2. влево ←;
3. вниз ↓;
4. вверх ↑.
— точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 900 большой палец покажет направление силы Ампера, т. е. она направлена влево.
Правильный вариант:
2. влево ←.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл.
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10—¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
2. Дано:
l = 40cм = 0,4 м,
I = 10 A,
F =8 мН = 0,008 Н.
Найти: B
Решение:
Запишем формулу модуля магнитной индукции:
Делаем расчёт:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Ответ: 2 мTл.
3. Дано:
l = 50 cм = 0,5 м,
I = 10 A,
B = 0,l5 Tл.
Найти: F
Решение:
Запишем формулу силы Ампера:
Делаем расчёт:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Ответ: 750 мН.
4. Дано:
B = 0,0l Tл,
r = l0 cм = 0,l м.
Найти: v
Решение:
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:
Отсюда следует:
Делаем расчёт:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
5. Дано:
B = l,8 Tл,
F = 3,6·l0⁻¹² Н,
α = 90°.
Найти:
Решение:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,
Делаем расчёт:
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
6. Дано:
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
q₀ = l,6·l0⁻ˡ⁹ Кл,
Найти: Т
Решение:
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:
Делаем расчёт:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
Ответ: T ≈ ll нс.
Правило левой руки
Проводник с током в магнитном поле. Магнитная индукция.
Если проводник, по которому проходит электрический ток, внести в магнитное поле, то в результате взаимодействия магнитного поля и проводника с током проводник будет перемещаться в ту или иную сторону.
Направление перемещения проводника зависит от направления тока в нем и от направления магнитных линий поля.
Допустим, что в магнитном поле магнита NS находится проводник, расположенный перпендикулярно плоскости рисунка; по проводнику протекает ток в направлении от нас за плоскость рисунка.
Ток, идущий от плоскости рисунка к наблюдателю, обозначается условно точкой, а ток, направляющийся за плоскость рисунка от наблюдателя,— крестом.
Движение проводника с током в магнитном поле
1 — магнитное поле полюсов и тока проводника,
2 — результирующее магнитное поле.
Всегда всё уходящее на изображениях обозначается крестом,
а направленное на смотрящего — точкой.
Под действием тока вокруг проводника образуется свое магнитное поле рис.1.
Применяя правило буравчика, легко убедиться, что в рассматриваемом нами случае направление магнитных линий этого поля совпадает с направлением движения часовой стрелки.
При взаимодействии магнитного поля магнита и поля, созданного током, образуется результирующее магнитное поле, изображенное на рис.2.
Густота магнитных линий результирующего поля с обеих сторон проводника различна. Справа от проводника магнитные поля, имея одинаковое направление, складываются, а слева, будучи направленными встречно, частично взаимно уничтожаются.
Следовательно, на проводник будет действовать сила, большая справа и меньшая слева. Под действием большей силы проводник будет перемещаться по направлению силы F.
Перемена направления тока в проводнике изменит направление магнитных линий вокруг него, вследствие чего изменится и направление перемещения проводника.
Для определения направления движения проводника в магнитном поле можно пользоваться правилом левой руки, которое формулируется следующим образом:
Если расположить левую руку так, чтобы магнитные линии пронизывали ладонь, а вытянутые четыре пальца указывали направление тока в проводнике, то отогнутый большой палец укажет направление движения проводника.
Сила, действующая на проводник с током в магнитном поле, зависит как от тока в проводнике, так и от интенсивности магнитного поля.
Основной величиной, характеризующей интенсивность магнитного поля, является магнитная индукция В. Единицей измерения магнитной индукции является тесла (Тл=Вс/м2).
О магнитной индукции можно судить по силе действия магнитного поля на проводник с током, помещенный в это поле. Если на проводник длиной 1 м и с током 1 А, расположенный перпендикулярно магнитным линиям в равномерном магнитном поле, действует сила в 1 Н (ньютон), то магнитная индукция такого поля равна 1 Тл (тесла).
Магнитная индукция является векторной величиной, ее направление совпадает с направлением магнитных линий, причем в каждой точке поля вектор магнитной индукции направлен по касательной к магнитной линии.
Сила F, действующая на проводник с током в магнитном поле, пропорциональна магнитной индукции В, току в проводнике I и длине проводника l, т. е.
F=BIl.
Эта формула верна лишь в том случае, когда проводник с током расположен перпендикулярно магнитным линиям равномерного магнитного поля.
Если проводник с током находится в магнитном поле под каким-либо углом а по отношению к магнитным линиям, то сила равна:
F=BIl sin a.
Если проводник расположить вдоль магнитных линий, то сила F станет равной нулю, так как а=0.
(Подробно и доходчиво в видеокурсе «В мир электричества — как в первый раз!»)
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Магнитное поле. Вектор магнитной индукции. Правило буравчика. Закон Ампера и сила Ампера. Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||
1.4. Сила Лоренца. Правило левой руки для определения направления силы Лоренца
Силу,
действующую на движущуюся заряженную
частицу со стороны магнитного поля,
называют силой
Лоренца. Опытным путём установлено, что сила,
действующая в магнитном поле на заряд
,
перпендикулярна векторами,
а ее модуль определяется формулой:
Опытным путём установлено, что сила,
действующая в магнитном поле на заряд
,
перпендикулярна векторами,
а ее модуль определяется формулой:
,
где – угол между векторами и.
Направление силы Лоренца определяется правилом левой руки (рис. 6):
если вытянутые пальцы расположить по направлению скорости положительного заряда, а силовые линии магнитного поля будут входить в ладонь, то отогнутый большой палец укажет направление силы , действующей на заряд со стороны магнитного поля.
Для отрицательного заряда направление следует изменить на противоположное.
Рис. 6. Правило левой руки для определения направления силы Лоренца.
1.5. Сила Ампера. Правило левой руки для определения направления силы Ампера
Экспериментально
установлено, что на проводник с током,
находящийся в магнитном поле, действует
сила, получившая название силы Ампера
(см. п. 1.3.). Направление силы Ампера (рис.
4) определяется правилом
левой руки (см. п. 1.3).
п. 1.3.). Направление силы Ампера (рис.
4) определяется правилом
левой руки (см. п. 1.3).
Модуль силы Ампера вычисляется по формуле
,
где – сила тока в проводнике,- индукция магнитного поля,- длина проводника,- угол между направлением тока и вектором.
1.6. Магнитный поток
Магнитным потоком сквозь замкнутый контур называется скалярная физическая величина, равная произведению модуля вектора на площадьконтура и на косинус угламежду вектором и нормалью к контуру (рис. 7):
Рис. 7. К понятию магнитного потока
Магнитный поток наглядно можно истолковать как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью .
Единицей магнитного потока является вебер .
Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
1
Вб =1
Тл·м2.
2. Электромагнитная индукция
2.1. Явление электромагнитной индукции
В 1831г. Фарадей обнаружил физическое явление, получившее название явления электромагнитной индукции (ЭМИ), заключающееся в том, что при изменении магнитного потока, пронизывающего контур, в нем возникает электрический ток. Полученный Фарадеем ток называется индукционным.
Индукционный ток можно получить, например, если постоянный магнит вдвигать внутрь катушки, к которой присоединен гальванометр (рис. 8, а). Если магнит вынимать из катушки, возникает ток противоположного направления (рис. 8, б).
Индукционный ток возникает и в том случае, когда магнит неподвижен, а движется катушка (вверх или вниз), т.е. важна лишь относительность движения.
Но
не при всяком движении возникает
индукционный ток. При вращении магнита
вокруг его вертикальной оси тока нет,
т.к. в этом случае магнитный поток сквозь
катушку не изменяется (рис.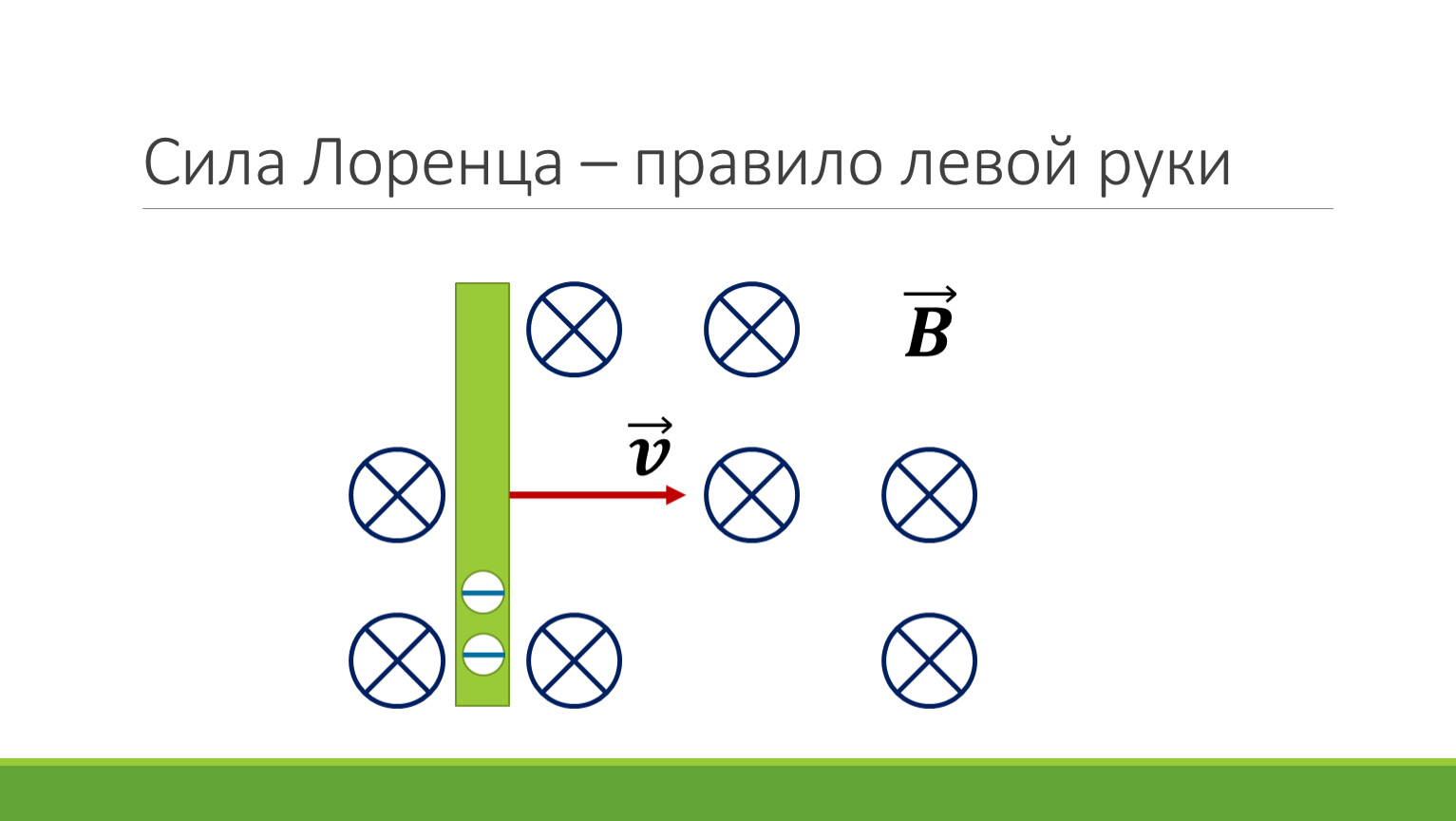 8, в), в то
время как в предыдущих опытах магнитный
поток меняется: в первом опыте он растет,
а во втором – уменьшается (рис. 8, а, б).
8, в), в то
время как в предыдущих опытах магнитный
поток меняется: в первом опыте он растет,
а во втором – уменьшается (рис. 8, а, б).
Направление индукционного тока подчиняется правилу Ленца:
возникающий в замкнутом контуре индукционный ток всегда направлен так, чтобы создаваемое им магнитное поле противодействовало причине, его вызывающей.
Индукционный ток препятствует внешнему потоку при его увеличении и поддерживает внешний поток при его убывании.
Рис. 8. Явление электромагнитной индукции
Ниже на левом рисунке (рис. 9) индукция внешнего магнитного поля , направленного «от нас» (+) растет (>0), на правом – убывает (<0). Видно, чтоиндукционный ток направлен так, что его собственное магнитное поле препятствует изменению внешнего магнитного потока, вызвавшего этот ток.
Рис. 9. К определению направления индукционного
тока
9. К определению направления индукционного
тока
Физика 11 класс
Правило правой руки. Сила Лоренца.
Вводные замечания
Правило правой руки обычно применяется школьниками для того, чтобы определить куда будет отклоняться заряженная частица, движущаяся в магнитном поле.
Сила, которая отклоняет такие частицы, называется силой Лоренца
Величина силы Лоренца вычисляется в школе по формуле
F = q ⋅ v ⨯ B
B — вектор магнитной индукции
v — скорость движения частицы
q — заряд частицы
⨯ — это векторное произведение.
После умножения заряда на скорость и индукцию мы получаем силу Лоренца. Её величину
можно посчитать на калькуляторе просто перемножив остальные величины друг на друга.
Любая сила — это вектор, следовательно, у силы есть не только величина, но и направление.
Направление любого векторного произведения можно легко найти зная направления множителей.
Для этого и нужно правило правой руки.
И как Вы могли догадаться, оно может применяться не только к силе Лоренца, но и к любым другим векторным произведениям.
Необходимые знания
Прежде чем знакомиться с правилом правой руки, нужно усвоить как определяется направление электрического тока.
Электроны и отрицательно заряженные ионы движутся от катода к аноду.Протоны, дырки и положительно заряженные ионы движутся в обратном направлении — от анода к катоду.
За направление электрического тока принято направление противоположное тому,
в котором движутся электроны.
Направление, в котором частица отклонится от первоначальной траектории под действием магнитного поля зависит от заряда частицы.
Направление силы Лоренца
Направление силы Лоренца обозначено коричневой стрелкой. Сама сила обозначена как F. Синим цветом обозначена траектория движения отрицательно заряженных частиц при условии, что:
- Отрицательно заряженная частица изначально летела слева направо
- Вектор индукции магнитного поля направлен из экрана
Красным цветом обозначена траектория движения положительно заряженной частицы при выполнении тех же условий.
Прямой чёрной линией обозначается движение частицы не имеющей
заряда. На неё магнитное поле не действует и она как двигалась слева направо так и
двигается.
Поляризация света
Консервативные и диссипативные силы
Вспомним известный с седьмого класса материал о том, что такое путь и что такое перемещение.
Теперь перейдём непосредственно к типам сил
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
Генденштейн. Дик. Физика 11 класс
Физика. 11 класс. Л. Э. Генденштейн, Ю. И. Дик
М.: 2012 — 272 с. Учебник — базовый уровень
Для подготовки к ЕГЭ обязательно пригодится самая основная теория,
которую лучше всего взать в привычном школьном учебнике. Предлагаю учебник Генденштена — один из лучших учебников базового уровня
по физике.
Предлагаю учебник Генденштена — один из лучших учебников базового уровня
по физике.
В учебнике изложены основы электродинамики, оптики, атомной физики и астрофизики. Четкая структура учебника облегчает понимание учебного материала.
Приведено много примеров проявления и применения физических законов в окружающей жизни, сведений из истории физических открытий, дано иллюстрированное описание физических опытов. Приведены примеры решения ключевых задач
ОГЛАВЛЕНИЕ
К учителю и ученику
Предисловие
ЭЛЕКТРОДИНАМИКА
Глава 1. ЗАКОНЫ ПОСТОЯННОГО ТОКА
§ 1. Электрический ток
1. Источники постоянного тока
2. Сила тока
3. Действия электрического тока
§ 2. Закон Ома для участка цепи
1. Сопротивление и закон Ома для участка цепи
2. Природа электрического сопротивления
3. Сверхпроводимость
§ 3. Последовательное и параллельное соединение проводников
1. Последовательное соединение
2. Параллельное соединение
Параллельное соединение
3. Измерения силы тока и напряжения
§ 4. Работа и мощность постоянного тока
1. Работа тока и закон Джоуля—Ленца
2. Мощность тока
§ 5. Закон Ома для полной цепи
1. Источник тока
2. Закон Ома для полной цепи
3. Передача энергии в электрической цепи
Глава 2. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
§ 6. Взаимодействие магнитов и токов
1. Взаимодействие магнитов
2. Взаимодействие проводников с токами и магнитов
3. Взаимодействие проводников с токами
4. Связь между электрическим и магнитным взаимодействиями
§ 7. Магнитное поле
1. Магнитное поле
2. Магнитная индукция
3. Сила Ампера и сила Лоренца
4. Линии магнитной индукции
Глава 3. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
§ 8. Электромагнитная индукция
1. Явление электромагнитной индукции
2. Закон электромагнитной индукции
§ 9. Правило Ленца. Индуктивность. Энергия магнитного поля
1. Правило Ленца
2. Явление самоиндукции
3. Энергия магнитного поля
§ 10. Производство, передача и потребление электроэнергии
Производство, передача и потребление электроэнергии
1. Производство электроэнергии
2. Передача и потребление электроэнергии
§ 11. Электромагнитные волны
1. Теория Максвелла
2. Электромагнитные волны
§ 12. Передача информации с помощью электромагнитных волн
1. Изобретение радио и принципы радиосвязи
2. Генерирование и излучение радиоволн
3. Передача и прием радиоволн
Глава 4. ОПТИКА
§ 13. Природа света. Законы геометрической оптики
1. Развитие представлений о природе света
2. Прямолинейное распространение света
3. Отражение света
4. Преломление света
§ 14. Линзы
1. От стеклянного шара до микроскопа
2. Виды линз и основные элементы линзы
3. Построение изображений в линзах
§ 15. Глаз и оптические приборы
1. Глаз
2. Оптические приборы
§ 16. Световые волны
1. Интерференция света
2. Дифракция света
3. Соотношение между волновой и геометрической оптикой
§ 17. Цвет
1. Дисперсия света
2. Как глаз различает цвета
Как глаз различает цвета
3. Окраска предметов
4. Невидимые лучи
КВАНТОВАЯ ФИЗИКА
Глава 5. КВАНТЫ И АТОМЫ
§ 18. Кванты света — фотоны
1. Равновесное тепловое излучение
2. «Ультрафиолетовая катастрофа»
3. Гипотеза Планка
§ 19. Фотоэффект
1. Законы фотоэффекта
2. Теория фотоэффекта
3. Применение фотоэффекта
§ 20. Строение атома
1. Опыт Резерфорда
2. Планетарная модель атома
3. Постулаты Бора
§ 21. Атомные спектры
1. Спектры излучения и поглощения
2. Энергетические уровни
§ 22. Лазеры
1. Применение лазеров
2. Спонтанное и вынужденное излучение
3. Принцип действия лазера
§ 23. Квантовая механика
1. Корпускулярно-волновой дуализм
2. Вероятностный характер атомных процессов
3. Соответствие между классической и квантовой механикой
Глава 6. АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
§ 24. Атомное ядро
1. Строение атомного ядра
2. Ядерные силы
§ 25. Радиоактивность
1. Открытие радиоактивности
2. Радиоактивные превращения
Радиоактивные превращения
§ 26. Ядерные реакции и энергия связи ядер
1. Ядерные реакции
2. Энергия связи атомных ядер
3. Реакции синтеза и деления ядер
§ 27. Ядерная энергетика
1. Ядерный реактор
2. Перспективы и проблемы ядерной энергетики
3. Влияние радиации на живые организмы
§ 28. Мир элементарных частиц
1. Открытие новых частиц
2. Классификация элементарных частиц
3. Фундаментальные частицы и фундаментальные взаимодействия
СТРОЕНИЕ И ЭВОЛЮЦИЯ ВСЕЛЕННОЙ
Глава 7. СОЛНЕЧНАЯ СИСТЕМА
§ 29. Размеры Солнечной системы
1. Земля и Луна
2. Орбиты планет
3. Размеры Солнца и планет
§ 30. Солнце
1. Источник энергии Солнца
2. Строение Солнца
§ 31. Природа тел Солнечной системы
1. Планеты земной группы
2. Планеты-гиганты
3. Малые тела Солнечной системы
4. Происхождение Солнечной системы
Глава 8. ЗВЕЗДЫ, ГАЛАКТИКИ, ВСЕЛЕННАЯ
§ 32. Разнообразие звезд
1. Расстояния до звезд
2. Светимость и температура звезд
§ 33. Судьбы звезд
Судьбы звезд
1. «Звезда-гостья» и «звезда Тихо Браге»
2. От газового облака до белого карлика
3. Эволюция звезд разной массы
§ 34. Галактики
1. Наша Галактика — Млечный Путь
2. Другие галактики
§ 35. Происхождение и эволюция Вселенной
1. Расширение Вселенной
2. Большой Взрыв
3. Будущее Вселенной
Лабораторные работы
Предметно-именной указатель
Магнитная сила Лоренца. Формула. Электрон. Индукция магнитного поля. Правило руки буравчика
Как уже было сказано ранее, магнитное поле действует на движущийся заряд. В ряде экспериментов было показано, что при влёте в магнитное поле заряженной частицы, её траектория искривляется (т.е. отклоняется от прямой). Вследствие знания второго закона Ньютона и наличия центростремительного ускорения (т.к. тело движется по кривой), такое движение объясняется наличием силы — силы Лоренца.
Значение модуля этой силы:
(1)Рис. 1. Сила Лоренца
Направление силы Лоренца — перпендикуляр к касательной траектории (т. е. перпендикуляр к скорости в данный момент). Однако в плоскости рисунка возможны два направления для перпендикуляра. Какое из них выбрать — вопрос заряда и правила левой руки. Пусть положительный заряд
е. перпендикуляр к скорости в данный момент). Однако в плоскости рисунка возможны два направления для перпендикуляра. Какое из них выбрать — вопрос заряда и правила левой руки. Пусть положительный заряд
В случае, если движущийся заряд будет отрицательным, направление силы изменяется на противоположное.
Правило левой руки для силы Лоренца: ориентируем руку так, чтобы линии магнитной индукции входили в ладонь. Четыре пальца руки сонаправляем с вектором скорости частицы, тогда противопоставленный большой палец указывает на направление силы Лоренца для положительно заряженной частицы. Направление силы Лоренца для отрицательно заряженной частицы противоположно.
Задачи на силу Лоренца можно условно разделить на два типа:
- направление скорости перпендикулярна линиям магнитной индукции (тогда задача сводится к записи второго закона Ньютона и плану решения задач по динамике) и фактически рисунка 1,
- направление скорости составляет угол с линиями магнитной индукции. Тогда заряженное тело будет двигаться по спирали (рис. 2).
Рис. 2. Сила Лоренца (Спираль)
Для решения второго типа задач рассматривается логика движения тела, брошенного под углом к горизонту. Т.е. мысленно разделяем движение на две оси (вдоль и перпендикулярно полю) и анализируем движение: одно — движение по окружности, второе — прямолинейное.
Вывод: задачи на силу Лоренца (1) практически идентичны друг другу. Обычно решаются через второй закон Ньютона и определение центростремительного ускорения. Надо чётко различать задачи, в которых частица движется в магнитном поле перпендикулярно линиям магнитной индукции (тогда тело движется по окружности) или влетает в поле под углом к линиям магнитной индукции (тогда частица движется по винтовой траектории).
Поделиться ссылкой:
Билет 11.Сила Лоренца. Правило левой руки — КиберПедия
Сила Лоренца
— сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
где q — заряд частицы;
V — скорость заряда;
B — индукции магнитного поля;
a — угол между вектором скорости заряда и вектором магнитной индукции.
Направление силы Лоренца определяется по правилу левой руки:
Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца
.
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).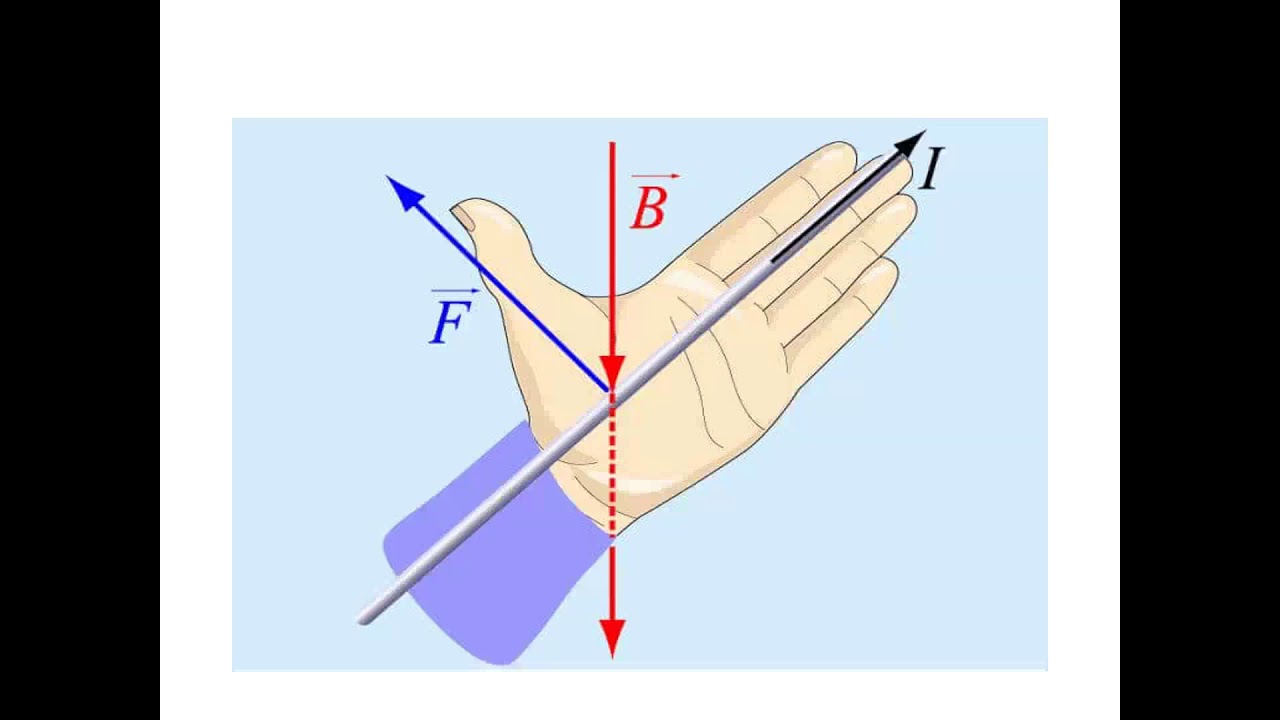
Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.
Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной
и создает центростремительное ускорение равное
В этом случае частица движется по окружности.
.
Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение
тогда радиус окружности
а период обращения заряда в магнитном поле
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.
Билет 12.ЭДС индукции в движущихся проводниках.
Прямолинейный проводник АВ движется в магнитном поле с индукцией В по проводящим шинам, которые замкнуты на гальванометр.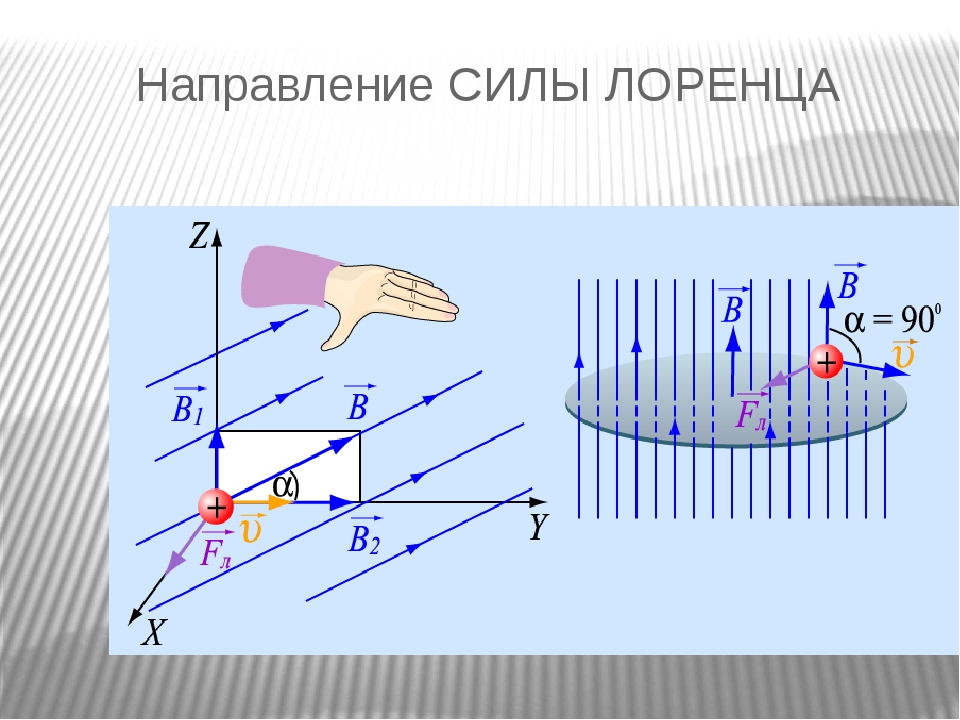
На электрические заряды, перемещающиеся вместе с проводником в магнитном поле, действует
сила Лоренца:
Fл = /q/vB sin a
q – заряд (Кл)
V – скорость (м/с)
B – магнитная индукция (Тл)
Её направление можно определить по правилу левой руки.
Под действием силы Лоренца внутри проводника происходит распределение положительных и отрицательных зарядов вдоль всей длины проводника l.
Сила Лоренца является в данном случае сторонней силой, и в проводнике возникает ЭДС индукции, а на концах проводника АВ возникает разность потенциалов.
Причина возникновения ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца на свободные заряды.
ЗАДАНИЕ.
1. При каком направлении движения контура в магнитном поле в контуре будет возникать индукционный ток?
2. Укажите направление индукционного тока в контуре при введении его в однородное магнитное поле.
3. Как изменится магнитный поток в рамке, если рамку повернуть на 90 градусов из положения 1 в положение 2 ?
4. Будет ли возникать индукционный ток в проводниках, если они движутся так, как показано на рисунке?
5. Определить направление индукционного тока в проводнике АБ, движущемся в однородном магнитном поле.
6. Указать правильное направление индукционного тока в контурах.
Электромагнетизм
— Объясняет ли закон силы Лоренца правило мотора левой руки Флемингса и правило динамо правой руки?
Да, уравнение $ F = qv \ times B $ действительно учитывает направления трех компонентов. Взгляните на это изображение с https://en.wikipedia.org/wiki/Cross_product
Для нашей формулы $ F = qv \ times B $, $ v $ обозначен буквой «a» на диаграмме, а $ B $ — меткой «b» на диаграмме. Допустим, a указывает на восток, b указывает на север, а a $ \ times $ b указывает вверх. Затем вы можете проверить с помощью любого ручного правила, которое захотите, что протон, движущийся на восток через магнитное поле, указывающее на север, будет испытывать восходящую силу. Та же диаграмма работает для электрона (или любого отрицательного заряда в целом). Для электрона мы берем точно такое же перекрестное произведение, но $ q $ будет отрицательным, поэтому, взяв перекрестное произведение, мы умножаем вектор на -1. Если вы умножите вектор, указывающий вверх, на -1, вектор будет указывать в противоположном направлении (вниз). Это можно увидеть по фиолетовой стрелке, указывающей вниз на диаграмме. Вы можете убедиться сами, что электрон, направляющийся на восток в магнитном поле, направленном на север, будет испытывать нисходящую силу.
Та же диаграмма работает для электрона (или любого отрицательного заряда в целом). Для электрона мы берем точно такое же перекрестное произведение, но $ q $ будет отрицательным, поэтому, взяв перекрестное произведение, мы умножаем вектор на -1. Если вы умножите вектор, указывающий вверх, на -1, вектор будет указывать в противоположном направлении (вниз). Это можно увидеть по фиолетовой стрелке, указывающей вниз на диаграмме. Вы можете убедиться сами, что электрон, направляющийся на восток в магнитном поле, направленном на север, будет испытывать нисходящую силу.
Однако, если вы используете это, чтобы помочь себе запомнить, это может не помочь, поскольку нет очевидной причины, почему кросс-произведение создает вектор в этом направлении. Фактически, у перекрестного произведения есть собственное правило, объясняющее, в какую сторону указывает вектор результата.
Лично я нахожу обычные правила для рук довольно запутанными, потому что я никогда не могу вспомнить, какая сила действует на какой палец и т. Д. Мой учитель физики в старшей школе научил меня трюку, который я люблю использовать. Первая часть — решить, что правая рука положительна, а левая — отрицательна.Это легко запомнить, потому что большинство людей предпочитают правую руку (положительный опыт), а не левую (негативный опыт). Вторая часть — представить, что вы толкаете дверь ладонью ладони на двери.
Д. Мой учитель физики в старшей школе научил меня трюку, который я люблю использовать. Первая часть — решить, что правая рука положительна, а левая — отрицательна.Это легко запомнить, потому что большинство людей предпочитают правую руку (положительный опыт), а не левую (негативный опыт). Вторая часть — представить, что вы толкаете дверь ладонью ладони на двери.
Как на этом изображении
Теперь эти три компонента легко запомнить следующим образом. Очевидно, что сила направлена в направлении силы, которую вы прикладываете. Магнитные поля всегда представлены несколькими линиями, поэтому направление магнитного поля — это ваши 4 пальца.Наконец, последний из них (скорость) отображается большим пальцем.
Если вы повернете руку ладонью вверх, вы увидите, что она соответствует первому изображению. Тогда вы можете использовать левую руку для электрона.
Что касается «правила двигателя» и «правила динамо», я полагаю, вы имеете в виду силу, которую испытывает провод, по которому проходит ток, в магнитном поле, и ток, индуцируемый в проводе, когда он перемещается через магнитное поле. И то, и другое можно найти с помощью силы Лоренца, думая о том, что происходит с одним электроном, а затем понимая, что все электроны испытывают силу в одном направлении, поэтому вы можете просто сложить ее.
И то, и другое можно найти с помощью силы Лоренца, думая о том, что происходит с одним электроном, а затем понимая, что все электроны испытывают силу в одном направлении, поэтому вы можете просто сложить ее.
. Почему в электромагнетизме природа предпочитает правило правой руки правилу левой?
Классический электромагнетизм совершенно инвариантен к четности; он по своей сути не левша или правша. Это правда, что вам нужно использовать правило правой руки, чтобы найти магнитное поле, но вам нужно использовать его снова , , чтобы найти магнитную силу. Поскольку вы всегда используете его дважды, чтобы получить любую непосредственно наблюдаемую величину, знак минус, который вы выбрали бы при использовании правила левой руки, отменяется.
Если сформулировать все в терминах сил, то электростатика и магнитостатика сводятся к тому, что (1) одинаковые заряды отталкиваются и (2) параллельные токи притягиваются. Это явно не зависит от каких-либо соглашений о ручке. (Кстати, относительный знак здесь происходит от относительного знака между временем и пространством в теории относительности.)
(Кстати, относительный знак здесь происходит от относительного знака между временем и пространством в теории относительности.)
Здесь скрывается более глубокая математика. Напомним, что векторное произведение двух векторов определяется как вектор, указывающий перпендикулярно параллелограмму, образованному двумя векторами, с той же длиной, что и площадь параллелограмма.В трех измерениях есть два направления, перпендикулярных каждому параллелограмму, поэтому нам нужно правило правой руки, чтобы выбрать одно. В более высоких измерениях это определение вообще не работает, потому что существует бесконечно много направлений, перпендикулярных каждой плоскости.
Следовательно, магнитное поле в общих размерах нельзя рассматривать как вектор . Вместо этого лучше просто сказать, что — это сам параллелограмм — это плоскость и площадь в каждой точке, а не направление и длина, как вектор.Магнитная сила просто заставляет частицы вращаться в плоскости поля. Текущий $ \ mathbf {J} $ в начале координат создает магнитное поле в $ \ mathbf {r} $ в плоскости, охватываемой $ \ mathbf {r} $ и $ \ mathbf {J} $.
Текущий $ \ mathbf {J} $ в начале координат создает магнитное поле в $ \ mathbf {r} $ в плоскости, охватываемой $ \ mathbf {r} $ и $ \ mathbf {J} $.
Формально эти элементы площади называются дифференциальными формами ранга $ 2 $. Они слишком сложны для начального курса, поэтому вместо этого мы используем правило правой руки для преобразования площади в вектор, вводя произвольный выбор. Но всю физику можно записать явно симметричным образом, потому что явления действительно симметричны.
электромагнетизм — правило правой и левой руки Флеминга
Очень жаль, что физика магнетизма обременена несколькими разными * правилами рук, и что они используют разные руки. Разберем их:
Флеминг
левый — линейкадает вам направление силы, действующей на ток, если вы знаете магнитное поле.
Источник изображения
Это правило применяется к двигателям , т.е.е. устройства, которые используют токи в магнитном поле для создания движения. Это основано на силе Лоренца,
$$
\ mathbf F = q \ mathbf v \ times \ mathbf B,
$$
в котором ток идет со скоростью заряда, а индуцированное движение идет вдоль направления силы. Вот почему это правило совпадает с правилом левой руки, используемым в перекрестных произведениях в целом.
Это основано на силе Лоренца,
$$
\ mathbf F = q \ mathbf v \ times \ mathbf B,
$$
в котором ток идет со скоростью заряда, а индуцированное движение идет вдоль направления силы. Вот почему это правило совпадает с правилом левой руки, используемым в перекрестных произведениях в целом.
Флеминг
правая -линейкагораздо реже используется в физике (хотя я не могу говорить о том, как работают инженеры).Это относится к генераторам , то есть устройствам, которые используют движение в магнитном поле для генерации токов. Это опять же основано на перекрестном произведении силы Лоренца, за исключением того, что теперь скорость заряда определяется движением объекта, а сила вдоль провода — это то, что устанавливает ток. Это означает, что вы поменяли местами средний палец на большой в соответствии с правилом левой руки Флеминга, что вы можете сделать, сохраняя (расплывчатые) назначения на «движение» и «текущую» и меняя руки.
Источник изображения
Мне очень не нравится это соглашение, и я бы посоветовал вам забыть о нем все, кроме того факта, что он существует и его следует избегать. 3}
$$
Опять же, это перекрестное произведение, которое определяет направление поля, и вы должны сами убедиться, что оно работает, как показано на рисунке.
3}
$$
Опять же, это перекрестное произведение, которое определяет направление поля, и вы должны сами убедиться, что оно работает, как показано на рисунке.
Как видите, правила совсем другие. Поэтому крайне важно, чтобы, если вы хотите использовать их в качестве мнемоники, вы правильно усвоили, какой из них применяется, и что вы применяете их правильно. (Нет смысла учить, какой рукой использовать, если вы, например, поменяете местами указательный и средний пальцы.)
Однако самое важное, что нужно усвоить, — это закон силы Лоренца, который основан на правиле левой руки и руки (заряд-время-ток на среднем пальце, поле на указательном, сила на большом пальце), обозначенное перекрестное произведение.Это, по сути, безотказно, если вы применяете его правильно, и меньше подвержено путанице с другими правилами.
Электромагнетизм— Объясняет ли закон силы Лоренца правило мотора левой руки Флемингса и правило динамо правой руки?
Да, уравнение $ F = qv \ times B $ действительно учитывает направления трех компонентов. Взгляните на это изображение с https://en.wikipedia.org/wiki/Cross_product
Взгляните на это изображение с https://en.wikipedia.org/wiki/Cross_product
Для нашей формулы $ F = qv \ times B $, $ v $ обозначен буквой «a» на диаграмме, а $ B $ — меткой «b» на диаграмме.Допустим, a указывает на восток, b указывает на север, а a $ \ times $ b указывает вверх. Затем вы можете проверить с помощью любого ручного правила, которое захотите, что протон, движущийся на восток через магнитное поле, указывающее на север, будет испытывать восходящую силу. Та же диаграмма работает для электрона (или любого отрицательного заряда в целом). Для электрона мы берем точно такое же перекрестное произведение, но $ q $ будет отрицательным, поэтому, взяв перекрестное произведение, мы умножаем вектор на -1. Если вы умножите вектор, указывающий вверх, на -1, вектор будет указывать в противоположном направлении (вниз).Это можно увидеть по фиолетовой стрелке, указывающей вниз на диаграмме. Вы можете убедиться сами, что электрон, направляющийся на восток в магнитном поле, направленном на север, будет испытывать нисходящую силу.
Однако, если вы используете это, чтобы помочь себе запомнить, это может не помочь, поскольку нет очевидной причины, почему кросс-произведение создает вектор в этом направлении. Фактически, у перекрестного произведения есть собственное правило, объясняющее, в какую сторону указывает вектор результата.
Лично я нахожу обычные правила рук довольно запутанными, потому что я никогда не могу вспомнить, какая сила действует на какой палец и т.Мой учитель физики в старшей школе научил меня трюку, который я люблю использовать. Первая часть — решить, что правая рука положительна, а левая — отрицательна. Это легко запомнить, потому что большинство людей предпочитают правую руку (положительный опыт), а не левую (негативный опыт). Вторая часть — представить, что вы толкаете дверь ладонью ладони на двери.
Как на этом изображении
Теперь эти три компонента легко запомнить следующим образом.Очевидно, что сила направлена в направлении силы, которую вы прикладываете. Магнитные поля всегда представлены несколькими линиями, поэтому направление магнитного поля — это ваши 4 пальца. Наконец, последний из них (скорость) отображается большим пальцем.
Если вы повернете руку ладонью вверх, вы увидите, что она соответствует первому изображению. Тогда вы можете использовать левую руку для электрона.
Что касается «правила двигателя» и «правила динамо», я полагаю, вы имеете в виду силу, которую испытывает провод, по которому проходит ток, в магнитном поле, и ток, индуцируемый в проводе, когда он перемещается через магнитное поле.И то, и другое можно найти с помощью силы Лоренца, думая о том, что происходит с одним электроном, а затем понимая, что все электроны испытывают силу в одном направлении, поэтому вы можете просто сложить ее.
Магнитная сила на движущемся электрическом заряде
Величина магнитной силы
Магнитная сила, действующая на заряженную частицу q, движущуюся в магнитном поле B со скоростью v (под углом θ к B), равна [latex] \ text {F} = \ text {qvBsin} (\ theta) [/ latex].
Цели обучения
Основные выводы
Ключевые моменты
- Магнитные поля действуют на движущиеся заряженные частицы.
- Направление магнитной силы [латекс] \ text {F} [/ latex] перпендикулярно плоскости, образованной [латексом] \ text {v} [/ latex] и [латексом] \ text {B} [ / латекс], как определено правилом правой руки.
- Единица СИ для величины напряженности магнитного поля называется тесла (Тл), что эквивалентно одному Ньютону на амперметр.Иногда вместо этого используется меньшая единица измерения Гаусс (10 -4 Тл).
- Когда выражение для магнитной силы комбинируется с выражением для электрической силы, комбинированное выражение известно как сила Лоренца.
Ключевые термины
- Кулоновская сила : электростатическая сила между двумя зарядами, как описано законом Кулона
- магнитное поле : Состояние в пространстве вокруг магнита или электрического тока, в котором существует обнаруживаемая магнитная сила и где присутствуют два магнитных полюса.
- тесла : В Международной системе единиц — производная единица плотности магнитного потока или магнитной индукции. Символ: T
Величина магнитной силы
Как один магнит притягивает другой? Ответ основан на том факте, что весь магнетизм основан на токе, потоке заряда. Магнитные поля действуют на движущиеся заряды , и поэтому они действуют на другие магниты, у всех из которых есть движущиеся заряды.
Магнитная сила, действующая на движущийся заряд, — одна из самых фундаментальных известных.Магнитная сила так же важна, как электростатическая или кулоновская сила. Однако магнитная сила более сложна как по количеству влияющих на нее факторов, так и по ее направлению, чем относительно простая кулоновская сила. Величина магнитной силы [латекс] \ text {F} [/ latex] на заряд [латекс] \ text {q} [/ latex], движущийся со скоростью [латекс] \ text {v} [/ latex] в напряженность магнитного поля [латекс] \ text {B} [/ latex] определяется выражением:
[латекс] \ text {F} = \ text {qvBsin} (\ theta) [/ latex]
, где θ — угол между направлениями [латекс] \ text {v} [/ latex] и [latex] \ text {B} [/ latex].Эта формула используется для определения магнитной силы [латекс] \ text {B} [/ latex] в терминах силы, действующей на заряженную частицу, движущуюся в магнитном поле. Единица СИ для величины напряженности магнитного поля называется тесла (Тл) в честь гениального и эксцентричного изобретателя Николы Тесла (1856–1943), внесшего большой вклад в наше понимание магнитных полей и их практического применения. Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем [latex] \ text {F} = \ text {qvBsin} (\ theta) [/ latex] для [latex] \ text {B} [/ latex] :
[латекс] \ text {B} = \ frac {\ text {F}} {\ text {qvsin} (\ theta)} [/ latex]
Поскольку sin θ безразмерен, тесла составляет
[латекс] 1 \ text {T} = \ frac {1 \ text {N}} {\ text {C} * \ text {m} / \ text {s}} = \ frac {1 \ text {N} } {\ text {A} * \ text {m}} [/ latex]
Иногда используется еще одна меньшая единица измерения, называемая гауссом (G), где 1 G = 10 −4 T.Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл или более. Магнитное поле Земли на ее поверхности составляет всего около 5 × 10 −5 Тл, или 0,5 Гс.
Направление магнитной силы [латекс] \ text {F} [/ latex] перпендикулярно плоскости, образованной [латексом] \ text {v} [/ latex] и [латексом] \ text {B} [ / латекс], как определено правилом правой руки, которое проиллюстрировано на рисунке 1. В нем говорится, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении [латекса ] \ text {v} [/ latex], пальцы в направлении [latex] \ text {B} [/ latex], а перпендикуляр к ладони указывает в направлении [latex] \ text {F} [ /латекс].Один из способов запомнить это — это одна скорость, и поэтому большой палец представляет ее. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, в котором вы толкаете ладонью. Сила, действующая на отрицательный заряд, прямо противоположна силе, действующей на положительный заряд.
Правило правой руки : Магнитные поля действуют на движущиеся заряды. Эта сила — одна из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и соответствует правилу правой руки –1 (RHR-1), как показано.Величина силы пропорциональна q, v, B и синусу угла между v и B.
Направление магнитной силы: Правило правой руки
Правило правой руки используется для определения направления магнитной силы на положительный заряд.
Цели обучения
Примените правило правой руки, чтобы определить направление магнитной силы на заряд
Основные выводы
Ключевые моменты
- При рассмотрении движения заряженной частицы в магнитном поле релевантными векторами являются магнитное поле B, скорость частицы v и магнитная сила, действующая на частицу F.Все эти векторы перпендикулярны друг другу.
- Правило правой руки гласит, что для определения направления магнитной силы на положительный движущийся заряд большой палец правой руки должен указывать в направлении v, пальцы в направлении B, а сила (F) равна направлен перпендикулярно ладони правой руки.
- Направление силы F, действующей на отрицательный заряд, противоположно указанному выше (направлено от тыльной стороны руки).
Ключевые термины
- Правило правой руки : Направление угловой скорости ω и углового момента L, на которое указывает большой палец правой руки, когда вы сгибаете пальцы в направлении вращения.
Направление магнитной силы: правило правой руки
До сих пор мы описывали величину магнитной силы, действующей на движущийся электрический заряд, но не направление. Магнитное поле является векторным полем, поэтому приложенная сила будет ориентирована в определенном направлении. Есть умный способ определить это направление, используя не что иное, как вашу правую руку. Направление магнитной силы F перпендикулярно плоскости, образованной v и B , как определено правилом правой руки, которое проиллюстрировано на рисунке выше.Правило правой руки гласит, что: чтобы определить направление магнитной силы на положительный движущийся заряд, ƒ, направьте большой палец правой руки в направлении v , пальцы в направлении B и перпендикулярно ладони указывает в направлении F .
Правило правой руки : Магнитные поля действуют на движущиеся заряды. Эта сила — одна из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и соответствует правилу правой руки –1 (RHR-1), как показано.Величина силы пропорциональна q, v, B и синусу угла между v и B.
Один из способов запомнить это — наличие одной скорости, представленной соответственно большим пальцем. Есть много линий поля, обозначенных пальцами соответственно. Сила направлена в том направлении, в котором вы толкаете ладонью. Сила, действующая на отрицательный заряд, прямо противоположна силе, действующей на положительный заряд. Поскольку сила всегда перпендикулярна вектору скорости, чистое магнитное поле не будет ускорять заряженную частицу в одном направлении, но будет производить круговое или спиральное движение (концепция, более подробно исследуемая в будущих разделах).Важно отметить, что магнитное поле не оказывает силы на статический электрический заряд. Эти два наблюдения соответствуют правилу, согласно которому магнитные поля не действуют, , , .
Что такое сила Лоренца? — Новости о хранении энергии, батареях, изменении климата и окружающей среде
Сила Лоренца — это закон физики, в частности, электромагнетизма, который описывает силовое взаимодействие между магнитными полями двух заряженных частиц.Он был назван в честь Хендрика Лоренца, голландского физика 1800-х годов, который проявлял большой интерес к науке об электромагнетизме.
Сила Лоренца лучше всего описывается уравнением
F = q (E + v x B)
, где B — напряженность магнитного поля, E — электрическое поле, q — заряд частицы и v — скорость частицы. В качестве единицы измерения он выражается в «Ньютонах».
Согласно этому уравнению, если частица с зарядом q движется (через другое магнитное поле) со скоростью v в присутствии электрического поля E и магнитного поля B , то она будет испытывать реактивную сила. Эта реактивная сила известна как сила Лоренца .
Уравнение силы Лоренца фактически было получено из знаменитого уравнения Максвелла. Есть варианты этого основного уравнения силы Лоренца.Другие уравнения, которые можно найти в других учебниках, описывают магнитную силу на проводе с током, электродвижущую силу в проволочной петле, движущейся через магнитное поле, и силу, действующую на заряженную частицу, которая может двигаться со скоростью, близкой к скорости света. .
Другой интересный факт, обнаруженный уравнением силы Лоренца, — это направление магнитного поля, движения электронов и самой силы Лоренца. Это широко известно как «Правила рук», которые легко понять на этих фотографиях.
Когда заряд движущейся частицы отрицательный, используется правило левой руки .
Правило левой руки
Когда заряд движущейся частицы положительный, используется правило правой руки .
Правило правой руки
Источник изображений: CK-12 Website
В наших предыдущих двух экспериментах на тему «Как сделать электромагнит?» и «Как магнитное всасывание работает на дверных звонках», мы поняли, как возникает электромагнетизм.Когда электрический ток наводится на провод, атомы начинают становиться движущимися зарядами (положительными или отрицательными в зависимости от протекания тока), которые действуют как маленькие магниты, указывающие в разных направлениях. Реактивная сила (или сила Лоренца) является результатом эффекта намагничивания, когда движущийся заряд приближается к другому магнитному полю. Правила для рук (слева или справа) разъясняют истинное направление магнитного поля, когда движущийся заряд является положительным или отрицательным.
Чтобы получить дополнительную научную информацию о силе Лоренца, посмотрите это видео, демонстрирующее правила рук в очень творческой установке.
магнитное действие электрического тока
Статьи по теме:
Что такое электромагнетизм?
Джеймс Клерк Максвелл (1831 — 1879)
Как сделать электромагнит?
Как работает магнитное всасывание на дверных звонках
Правило для правой руки — wikidoc
Левая ориентация показана слева, а правая — справа.Главный редактор: C. Майкл Гибсон, M.S., M.D. [1]
В математике и физике правило правой руки является общей мнемоникой для понимания условных обозначений для векторов в 3 измерениях. Он был изобретен британским физиком Амброузом Флемингом в начале 1900-х годов. [1]
При выборе трех векторов, которые должны быть перпендикулярны друг другу, есть два различных решения, поэтому, выражая эту идею в математике, нужно удалить неоднозначность того, какое решение имеется в виду.
Есть вариации мнемоники в зависимости от контекста, но все вариации связаны с одной идеей выбора соглашения.
Направление, связанное с упорядоченной парой направлений
Одна форма правила правой руки используется в ситуациях, когда упорядоченная операция должна выполняться над двумя векторами a и b , результатом которого является вектор c , перпендикулярный обоим векторам a и б . Самый распространенный пример — векторное векторное произведение.Правило правой руки требует следующей процедуры выбора одного из двух направлений.
- a → × b → = c → {\ displaystyle {\ vec {a}} \ times {\ vec {b}} = {\ vec {c}}}
- Удерживайте большой, указательный и средний пальцы под прямым углом друг к другу. Убедитесь, что большой и указательный пальцы имеют L-образную форму или форму пистолета. Средний палец — это направление c , когда большой палец представляет a , а указательный палец — b .
Направление вращения
Вектор, назначенный повороту.Другая форма правила правой руки используется в ситуациях, когда вектор должен быть назначен вращению на тела, магнитного поля или жидкости. В качестве альтернативы, когда вращение задается вектором, и необходимо понимать, каким образом происходит вращение, применимо правило правой руки.
В этой форме пальцы правой руки согнуты, чтобы соответствовать кривизне и направлению движения или магнитного поля. Большой палец указывает направление вектора.
Приложения
Первая форма правила используется для определения направления векторного произведения двух векторов. Это приводит к широкому использованию в физике, где бы ни встречалось перекрестное произведение. Список физических величин, направления которых связаны правилом правой руки, приведен ниже. (Некоторые из них только косвенно связаны с перекрестными произведениями и используют вторую форму.)
Правило левой руки Флеминга — это правило для определения направления тяги в проводнике, по которому проходит ток в магнитном поле.
Левша
В определенных ситуациях может быть полезно использовать противоположное соглашение, когда один из векторов перевернут, и поэтому создается левосторонняя триада вместо правосторонней триады.
Пример такой ситуации для материалов для левшей. Обычно для электромагнитной волны электрическое и магнитное поля, а также направление распространения волны подчиняются правилу правой руки. Однако левосторонние материалы обладают особыми свойствами — отрицательным показателем преломления.Это делает направление распространения в противоположном направлении.
Перевод Де Граафа правила левой руки Флеминга, в котором используются сила тяги, поля и тока, а также правила правой руки, является правилом ФБР. Правило ФБР изменяет тягу на F (сила Лоренца), B (направление магнитного поля) и I (ток). Правило ФБР легко запоминается гражданами США из-за общеизвестной аббревиатуры Федерального бюро расследований.
Симметрия
| Вектор | Правая | Правая | Правая | Левый | Левый | левый |
|---|---|---|---|---|---|---|
| a, x или I | Большой палец | Пальцы или ладонь | Первая или Индекс | Большой палец | Пальцы или ладонь | Первая или Индекс |
| b, y или B | Первая или Индекс | Большой палец | Пальцы или ладонь | Пальцы или ладонь | Первая или Индекс | Большой палец |
| c, z или F | Пальцы или ладонь | Первая или Индекс | Большой палец | Первая или Индекс | Большой палец | Пальцы или ладони |
См. Также
Шаблон: Commons2
Внешние ссылки
cs: Pravidlo pravé ruky de: Drei-Finger-Regel это: Regola della mano destra он: כלל יד ימין nl: Rechterhandregel sv: Högerhandsregeln
Шаблон: WikiDoc Sources
Шаблон: Jb1
.



 Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля
Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля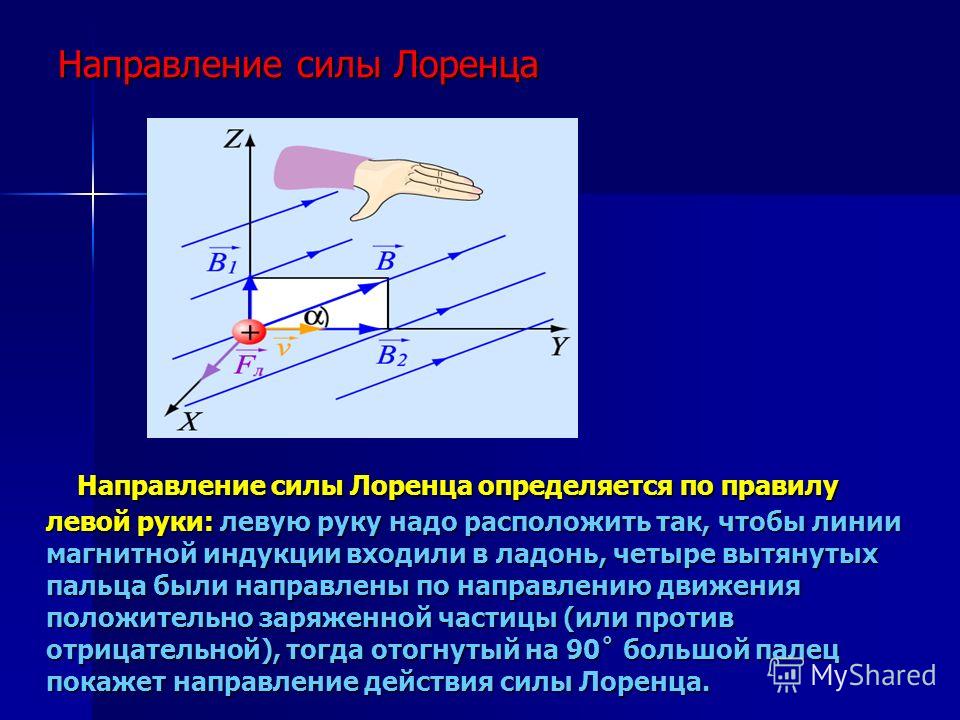 Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный
Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный

 Введите свой запрос:
Введите свой запрос: