Правило Ленца для электромагнитной индукции

Содержание:

Электромагнитная индукция:

Неоценимая заслуга в изучении явления электромагнитной индукции принадлежит известному английскому физику М. Фарадею — непревзойденному мастеру проведения физического эксперимента.

Фарадей Майкл (1791-1867) — выдающийся английский физик, основоположник учения об электромагнитном поле, один из основателей электрохимии, исследователь взаимодействия вещества и магнитного поля.

Обнаружение в 1820 г. датским физиком X. Эрстедом связи магнитного поля с электрическим током положило начало фундаментальным исследованиям открытого явления. Обладая широким научным кругозором, выдающийся физик и исследователь М. Фарадей предусмотрел возможность обратной связи магнитного поля и электрического тока, когда появление магнитного поля приводит к возникновению электрического тока.

В результате длительных научных поисков он в 1821 г. получил первые положительные результаты: добился того, что в замкнутых проводниках, находящихся в переменном магнитном поле, возникал электрический ток. Явление получило название электромагнитной индукции, а ток, возникающий в проводниках, назвали индукционным.

Явление возникновения электрического тока в замкнутом проводнике, который расположен в переменном магнитов ном поле, называется электромагнитной индукцией.

Опишем основные опыты М. Фарадея, которые можно повторить и на школьном оборудовании.

C клеммами гальванометра соединим длинный проводник, пасть которого укреплена в штативе.

Постоянный подковообразный магнит сначала будем приближать к проводнику, а потом удалять от него (рис. 2.26). При этом увидим, что стрелка гальванометра будет отклоняться сначала в одну сторону, потом в противоположную.

Изменим условия опыта. Укрепим теперь подковообразный магнит в лапках штатива, а проводник, присоединенный к клеммам гальванометра, будем вводить в между полюсное пространство и выводить из него (рис. 2.27). Стрелка гальванометра также будет отклоняться сначала в одну, а потом в противоположную сторону.

Pиc. 227. Опыт с движущимся проводником

Видоизменим опыт. Одну из катушек присоединим к клеммам гальванометра, а вторую включим в электрическую цепь, состоящую из источника постоянного тока и выключатели. Замкнув цепь второй катушки, будем приближать ее к первой катушке (рис. 2.28). Отклонение стрелки гальванометра засвидетельствует появление тока в цепи первой катушки. Направление этого тока изменится, если вторую катушку удалять от первой. При неподвижных катушках ток будет отсутствовать.

Рис. 228. Опыт с движущейся катушкой с током

Разместив вторую катушку неподвижно на первой, начнем замыкать и размыкать цепь второй катушки (рис. 2.29). Когда цепь будет замыкаться, стрелка гальванометра отклонится в одну сторону. При размыкании стрелка отклонится в противоположную сторону.

Pиc. 229. Замыкание и размыкание цепи второй катушки

Изменим условия последнего опыта. Включим в цепь второй катушки реостат и снова замкнем цепь. Когда стрелка остановится на нулевом делении, начнем изменять силу тока, перемещая ползунок реостата (рис. 2.30).

Рис. 230. Сила тока в катушке изменяется с помощью реостата

При увеличении силы тока в цепи первой катушки стрелка гальванометра будет отклоняться в одну сторону. При уменьшении силы тока отклонение стрелки будет противоположным.

После этого, не изменяя положения катушек и не разрывая цепи второй катушки, введем в катушки стальной стержень (рис. 2.31). Стрелка и в этом случае отклонится от положения равновесия и возвратится в начальное положение. Во время вынимания стержня из катушки заметим, что стрелка гальванометра отклоняется в противоположную сторону.

Pиc. 231. Опыт, когда движется стальной стержень

Электрический ток, возникающий в замкнутом проводнике в изменяющемся магнитном поле, называют индукционным.

Результаты всех опытов свидетельствуют, что при любом изменении магнитного поля или движении замкнутого проводника в магнитном поле возникает электрический ток.

Его направление зависит от характера изменения магнитного поля: при увеличении магнитной индукции ток имеет одно направление, при уменьшении — противоположное.

На практике направление тока в проводнике, который возникает вследствие электромагнитной индукции, определяют по правилу правой руки (рис. 2.32): если правую руку разместить в поле так, чтобы линии магнитной индукции входили в ладонь, а отставленный большой палец показывал направление движения проводника, то вытянутые пальцы руки покажут направление тока в проводнике.

Рис. 2.32 Правило правой руки

Чтобы ток в проводниках протекал длительное время, необходимо, чтобы все это время существовала разность потенциалов. А это возможно при непрерывном движении проводника. При этом будет происходить разделе ние в проводнике положительно и отрицательно заряженных частиц под действием силы Лоренца, которая имеет неэлектростатическое происхождение. Это приводит к возникновению ЭДС индукции.

Определим способ рассчета ЭДС, для случая, когда прямой проводник, который является частью электрической цепи, равномерно движется в магнитном поле. Вызванное силой Лоренца движение заряженных частиц образует электрический ток, а в это время на него в магнитном поле будет действовать сила Ампера (рис. 2.33):

где В — модуль вектора магнитной индукции; I — сила тока в проводнике; l длина проводника; — угол между направлением тока в проводнике и вектором магнитной индукции.

Возникающий ток в проводнике всегда будет иметь направление, при котором сила Ампера «тормозит» движение проводника. Чтобы проводник двигался равномерно (условие существования электрического тока), к нему нужно приложить силу, которая по модулю равна силе Ампера, а по направлению противоположна:


Рис. 2.33. К объяснению ЭДС индукции

Если за определенное время △t проводник сместится па △s, то работа будет равна

Таким образом,

Приняв во внимание, что по определению сила тока равна  а ЭДС равна . И произведя определенные математические преобразования, получим

Таким образом, для случая, когда проводник движется равномерно в однородном магнитном поле, значение ЭДС индукции зависит от магнитной индукции поля, длины
прямого проводника и скорости его движения в магнитном поле, учитывая значение угла между  и .

Правило Ленца

Правило установлено известным русским физиком Э.Х. Ленцем как обобщение многочисленных опытов по определению направления индукционного тока. C этой целью Э.Х. Ленц исследовал взаимодействие замкнутого проводника и переменного магнитного поля, которое вызвало индукционный ток в этом проводнике.

Чтобы лучше понять сущность этого правила, рассмотрим опыт.
На легком горизонтальном рычаге, который имеет вертикальную ось вращения, находятся два легких металлических кольца, одно из которых сплошное, я второе разрезано (рис. 2.35). Рычаг посажен на тонкое стальное острие так, чтобы трение было минимальным.
 

Pиc. 235. Прибор для демонстрации правила Ленца

Введем в сплошное кольцо катушку с ферромагнитным сердечником (электромагнитом), включенным в электрическую цепь из источника тока и выключателя (рис. 2.36).

Рис. 236. К правилу Ленца

В момент .замыкания цепи кольцо, как бы отталкиваясь от катушки, сместится на определенное расстояние и развернет рычаг на некоторый угол.

В момент появления тока в электромагните электропроводное кольцо, находящееся возле полюса электромагнита, всегда — притягивается к нему.

Если опыт повторить, изменив направление тока в катушке, то будем наблюдать тот же эффект. Таким образом, определяющим в данном случае является не направление магнитной индукции, а характер изменения магнитной индукции.

Если опыт попытаться пронести с разрезанным кольцом, то подобного эффекта наблюдать не сможем. Это свидетельствует, что отталкивание кольца связано с индукционным током, который возникает в сплошном кольце.

При размыкании цепи питания электромагнита проводящее кольцо будет двигаться от него.

Чтобы разобраться в дальнейших рассуждениях, необходимо вспомнить, что параллельные проводники, в которых ток проходит в одном направлении, притягиваются, а в противоположных отталкиваются. Таким образом, если кольцо отталкивается от катушки, то в нем индуцируется ток, противоположный току в катушке по направлению.

Взаимно противоположными будут и магнитные индукции полей этих токов.

Обобщив результаты опытов, можно сделать выводы, к которым пришел Э.Х. Ленц: магнитное поле индукционного тока всегда противодействует изменениям, которые вызвали этот так.

Правило Ленца: индукционный ток в замкнутом проводнике имеет такое направление, что его магнитное поле компенсирует изменение магнитного поля, которое вызвало этот ток.

Магнитный поток

Электромагнитную индукцию можно наблюдать в двух случаях: когда проводник движется в однородном магнитном поле или неподвижный проводник находится и магнитном поле, магнитная индукция которого изменяется со временем. Нa практике, как правило, случается так, что одновременно изменяется магнитная индукция и положение проводника в магнитном поле. Примером может быть движение проводника в неоднородном магнитном поле. Так как в этом случае расчеты сложнее» для их упрощения ввели физическую величину, которая одновременно зависит и от индукции магнитного поля, и от параметров движения проводника. Эта величина получила название магнитного потока.

Представим себе проводник в виде замкнутого кольца, которое находится в магнитном поле (рис. 2.38-а). Приведем кольцо в движение так, чтобы оно двигалось в плоскости, перпендикулярной к линиям магнитного поля. При этом количество линий индукции магнитного поля, которые проходят через него, будет уменьшаться, и в кольце возникнет индукционный ток (рис. 2.38-б).

Pис. 238. Движение кольца в магнитом поле

Если теперь кольцо проводника поместить в магнитное поле, индукция которого изменяется, то количество линий магнитной индукции, которые проходят через контур, также будет изменяться и в проводнике возникнет индукционный ток (рис.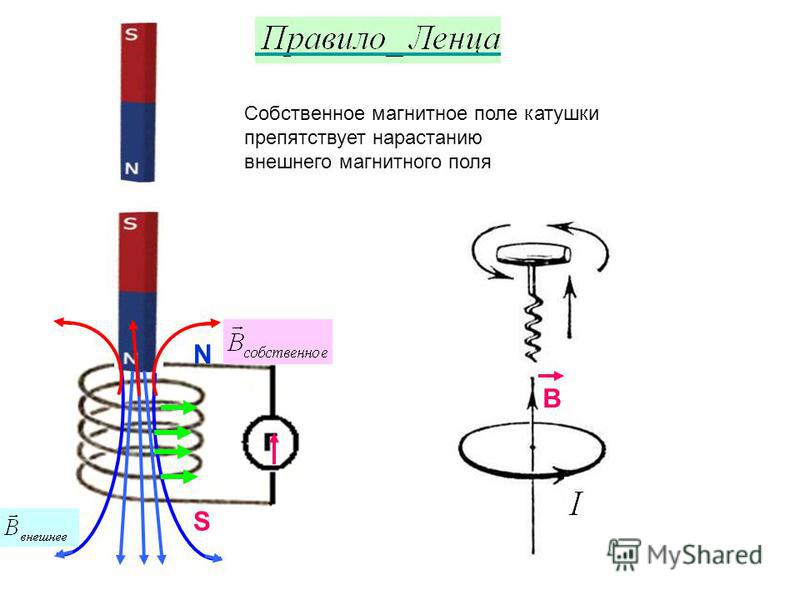 2.39).

Pиc. 239. Изменение магнитного потока через кольцо

Оба описанных случая можно объяснить проще, если для каждого их них учитывать произведение площади кольца на значение магнитной индукции магнитного поля. Именно это произведение изменялось в обоих случаях. Фактически это произведение характеризовало поток линий магнитной индукции, которые пронизывают контур определенной площади, или просто — магнитный поток.

Магнитный поток Ф зависит не только от модуля магнитной индукции и площади контура, но и от угла, который образуют нормаль с плоскостью контура и вектором магнитной индукции поля (рис. 2.40). Поэтому в общем виде значении магнитного потока записывается как

где Ф — магнитный поток; В — модуль магнитной индукции поля; — угол между нормалью к плоскости контура и вектором магнитной индукции.

Величина, которая описывает магнитное поле и равна произведению магнитной индукции на площадь замкнутого контура и косинус угла (между вектором магнитной индукции и нормалью к контуру), называется магнитным потоком, или потоком магнитной индукции.

Анализ формулы показывает, что минимальное значение магнитного потока (Ф = 0) будет тогда, когда = 90º, т. е. плоскость контура параллельна линиям магнитного поля. Если = 0, то магнитный поток при всех равных условиях будет максимальным (Ф = BS).

Магнитный поток — скалярная величина. В СИ магнитный поток измеряется в веберах (Вб), на честь известного немецкого физика В. Вебера.

Если магнитная индукция магнитного поля 1 Тл, а площадь контура, сквозь который проходит магнитный поток, 1 м², то магнитный поток равен 1 веберу (1 Вб):
1 Вб = 1 Тл • 1 м².

Любые изменения магнитного поля или площади контура вызывают явление электромагнитной индукции.

Вебер Вильгельм Эдуард (1804-1881) — немецкий физик, основные работы посвящены электромагнетизму, работал также над проблемами акустики, теплоты, молекулярной физики, земного магнетизма.

Таким образом, любое изменение магнитного потока обусловливает возникновение электрического тока в замкнутом проводящем контуре. C учетом закона Ома для полной цепи последний вывод можно записать так: любое, изменение. магнитного потока приводит к возникновению ЭДС индукции.

Закон электромагнитной индукции

Проанализировав результаты экспериментальных исследований электромагнитной индукции, можно найти общую формулу для выражения особенностей этого явления, которые отражают сущность закона электромагнитной индукции: при изменении магнитного потоки в замкнутых проводниках возникает электрический ток, вызванный ЭДС индукции, которая пропорциональна скорости изменения магнитного потока:

 или 
где электродвижущая сила индукции; -скорость изменения магнитного потока Ф; k — коэффициент пропорциональности.

Закон электромагнитной индукции: электродвижущая сила индукции пропорциональна скорости изменения магнитного потока.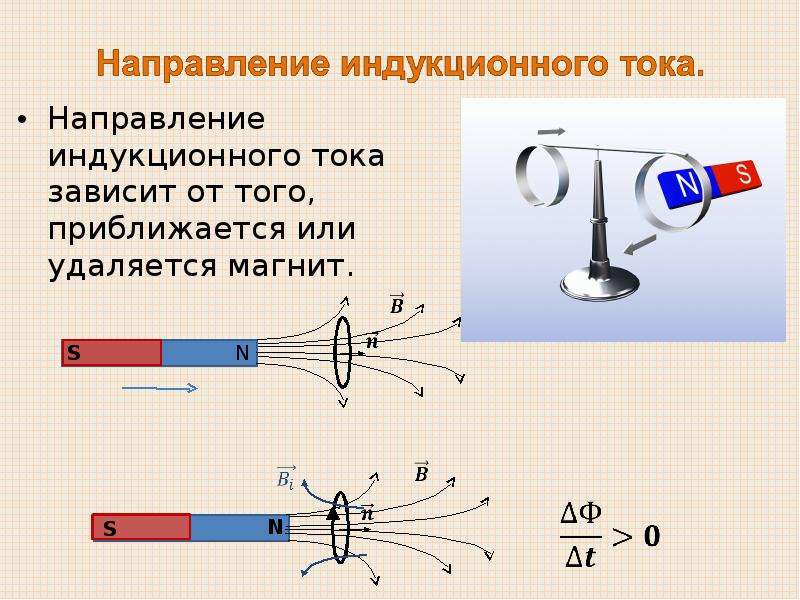

При использовании единиц СИ коэффициент k = 1. Приняв во внимание, что индукционный ток противодействует изменению магнитного потока (правило Ленца), окончательно имеем:

Так как согласно закону Ома  то можно записать его для случая электромагнитной индукции в виде , где  — сопротивление контура, а r=0.

Заряд, который проходит в контуре вследствие электромагнитной индукции: Q = I∆t.

Учитывая, что заряд скалярная величина, а знак минус можно опустить, получим:

Пример решения задачи №1

Магнитный поток, пронизывающий катушку, которая состоит из 75 витков, равен 4,8 ∙ 10^-3 Вб. На протяжении какого времени исчезнет этот поток, если в катушке индуцируется ЭДС индукции 0,74 В?

Дано: Φl= 4,8 • 103 Вб, Ф2 = 0, N= 75, = 0,74 В.	Решение ЭДС индукции возникает в катушке потому, что магнитный поток, пронизывающий ее, изменяется на △Φ = Φ2 — Φl. 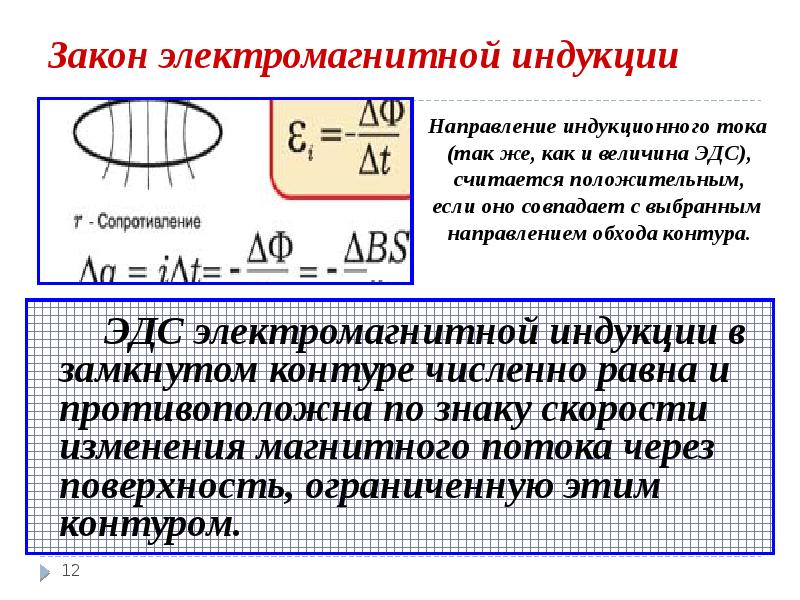В каждом витке катушки при этом будет возникать ЭДС индукции в соответствии с законом ΔΦ электромагнитной индeкции:
∆t — ?

Общая ЭДС будет в N раз больше: . Отсюда:    .
Подставив значения физических величин, получим

Ответ: ток исчезнет через 0,48 с.

Электродинамический микрофон

Одним из примеров практического применения явления электромагнитной индукции является электродинамический микрофон. C помощью этого прибора звуковые колебания превращаются в колебания электрического тока, которые усиливаются при помощи специальных электронных усилителей и используются в быту, научных исследованиях, производстве.

Микрофоны превращают звуковые колебания в электрические.

Обязательной частью электродинамического микрофона является постоянный магнит, изготовленный в виде кольца (рис. 2.41).

К одному из полюсов магнита приклеен цилиндрический стержень 1 из мягкого ферромагнетика (железа).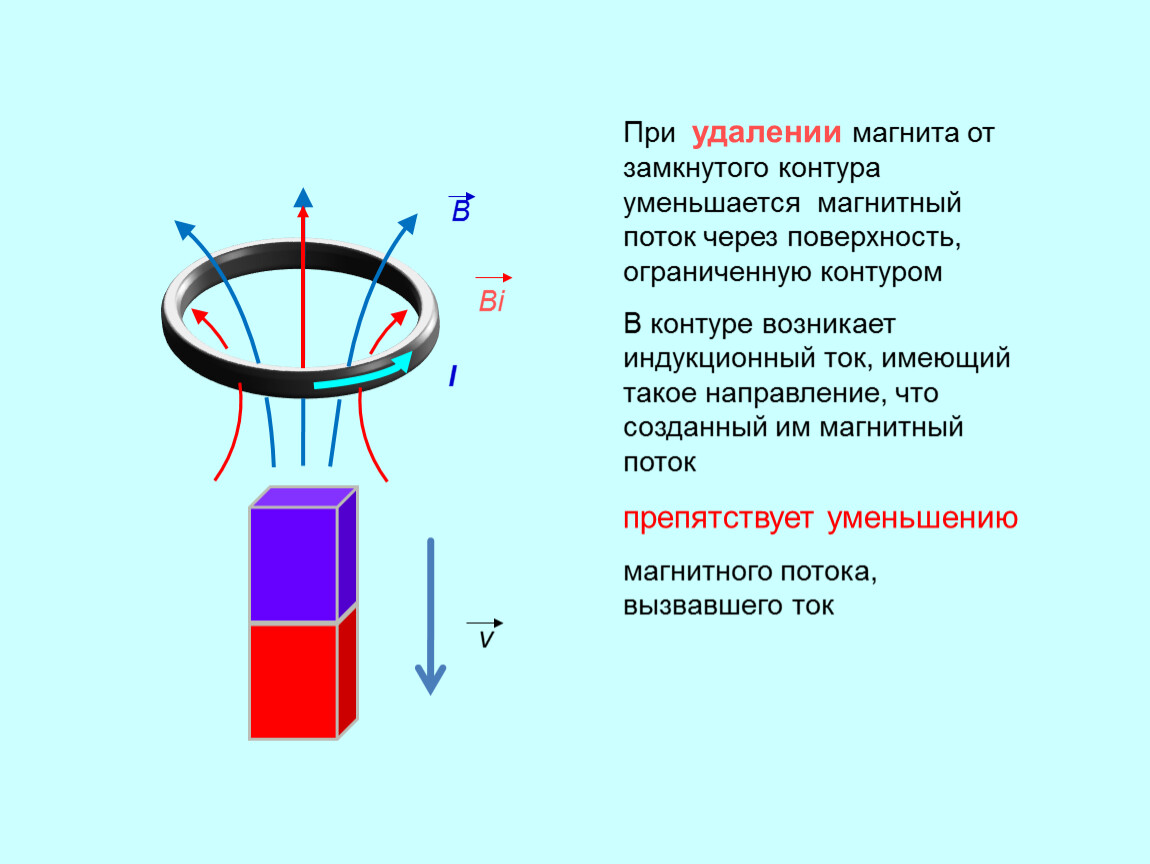 К другому — ферромагнитная пластина 2 из такого же ферромагнетика. В центре этой пластины находится круглое отверстие, которое охватывает стержень. Диаметр отверстия несколько больше диаметра стержня, поэтому между стержнем и пластиной образуется узкая щель 5, в которой сосредоточен весь магнитный поток магнита.

На стержне находится мембрана 3, которая колеблется под действием звуковых волн. К нижней части мембраны приклеена небольшая катушка 4 с некоторым количеством витков изолированного провода. Катушка помещена в кольцевую щель
между полюсами постоянного магнита.

В электродинамическом микрофоне катушка находится в магнитном поле.

Концы катушки соединены гибкими проводниками со специальными клеммами. Если на мембрану микрофона попадают звуковые волны, то она начинает колебаться вместе с катушкой. При колебании катушки магнитный поток, пронизывающий ее, изменяется и в ней индуцируется ЭДС индукции.

В движущейся катушке, находящейся в магнитном поле, возникает ЭДС индукции.

Если катушка включена в цепь электронного усилителя, то электрические колебания усиливаются и могут быть или записаны на магнитный либо оптический диск, или сразу
воспроизведены громкоговорителем.

Принцип действия электродинамического микрофона используется в различных датчиках для изучения и контроля колебательных процессов.

Самоиндукция

Каждый проводник, в котором существует электрический ток, создает «собственное» магнитное поле. Это поле образуется сразу же, как только в проводнике начинает про ходить электрический ток. Если индукция магнитного поля перед замыканием цепи была равна нулю, то через некоторое время после замыкания она будет иметь максимальное значение B, соответствующее силе тока в проводнике. Таким образом, момент возникновения электрического тока можно читать моментом начала изменения магнитного потока. А любое изменение магнитного потока, по закону электромагнитной индукции, порождает вихревое электрическое поле, способствующее появлению ЭДС индукции во всех проводниках,находящихся в магнитном поле.

Явление самоиндукции выявил Д. Генри в 1832 г.

Не может быть исключения и для проводника, который является «источником» этого поля. Вихревое поле создает и в нем ЭДС индукции , которую назвали ЭДС самоиндукции.

Наличие ЭДС самоиндукции можно подтвердить опытом. Для этого составим электрическую цепь из источника тока, выключателя и электрической лампочки (рис. 2.43). При
замыкании цепи лампочка зажигается практически мгновенно. Если же в цепь включить катушку с железным сердечником, то максимальная яркость свечения лампочки устанавливается постепенно (рис. 2.44).

Pиc. 2.43. Лампочка загорается сразу после замыкания цепи

Рис 2.44 В цепи с катушкой лампочка загорается постепенно

Это является свидетельством того, что ток в цепи увеличивается во мгновенно, а на протяжении некоторого времени. Посмотрев на графики рисунков 2.45 и 2.46, можно сказать, что в цепи, где находится катушка из 100 витков, ток нарастает быстрее, чем в цепи, в которой находится катушка из 1000 витков. На прохождение тока н цепи существенно влияет также ферромагнитный сердечник в катушке (рис. 2.47).

Pиc. 2.45. График силы тока при замыкании цепи с катушкой из 100 витков	Рис. 2.46. График силы тока при замыкании цепи с катушкой из 1000 витков
Рис. 2.47. График силы тока при замыкании цепи с катушкой (сердечником)

Поскольку ЭДC самоиндукции противодействует ЭДС источники тока, то можно сделать вывод, что ЭДС самоиндукции зависит от характеристик катушки или проводника, включенного в электрическую цепь.

А магнитный поток, создаваемый катушкой или проводником, будет пропорционален силе тока в них: Ф ~ I. Если внести коэффициент пропорциональности, то можно получить более точное соотношение и новую формулу: Ф = L ∙ I. Здесь коэффициент пропорциональности L учитывает электромагнитные свойства катушки (проводника) и называется индуктивностью. Индуктивность определяется формой и размерами проводника, а также магнитными свойствами среды.

Физическую величину, которая характеризует электромагнитные свойства катушки или проводника, называют индуктивностью.

Если при изменении силы тока в проводнике на 1 А за 1 с в нем индуцируется ЭДС самоиндукции 1 В, то этот проводник имеет индуктивность 1 Гн.

В СИ индуктивность измеряют в генри (Гн) в честь известного американского физика Д. Генри.

Единица 1 генри имеет довольно большой размер, поэтому применяют, как правило, долевые единицы:

• 1 миллигенри = 1 мГн = 10^-3 Гн;
• 1 микрогенри = 1 мкГн = 10^-6 Гн.

Если в любом проводнике изменяется электрический ток, то это приводит к изменению магнитного потока ΔΦ — LΔI, которое вызывает ЭДС самоиндукции:

Явление самоиндукции наблюдается также при размыкании цепи c током. Составим цепь из источника тока, выключателя, катушки и лампочки. Лампу накаливания, сопротивление которой значительно меньше сопротивления катушки, включим параллельно катушке (рис. 2.48). Если замкнуть цепь, то накаливание волоска лампочки будет происходить постепенно, как
бы с задержкой. Если после полного загорания лампы разомкнуть ключ, то она ярко вспыхнет. Это будет проявлением самоиндукции. В результате размыкания цепи возникнет ЭДС самоиндукции, которая поддержит ток в цепи лампочки и катушки.

Рис. 2.48. Схема электрической цепи для наблюдения явления самоиндукции при размыкании

Пример решения задачи №2

Определить индуктивность катушки, если сила тока в ней изменяется на 50 А за 1 с и при этом появляется ЭДС самоиндукции 0,08 В.

Дано: ΔI = 50 А, Δt— 1 с, = 0,08 В.	Решение По закону ЭДС самоиндукции Отсюда  Подставив значения физических величин,  получим
L— ?

Ответ: индуктивность катушки 1,6 мГн.

Энергия магнитного поля

Самоиндукция подтверждает действие закона сохранения и превращения энергии в электромагнитных явлениях.

Как известно, вследствие явления самоиндукции при замыкании цепи возникает ЭДС самоиндукции . Если же сила тока не изменяется, ЭДС самоиндукции не возникает. Такое положение в электрической цепи обусловлено тем, что за счет энергии источника тока выполняется работа по компенсации ЭДС самоиндукции. Это аналогично случаю, когда для сообщения скорости неподвижному телу необходимо выполнить определенную работу по преодолению инерции.

Любые изменения силы тока в катушке вызовут появление ЭДС индукции и приведут к выполнению работы источником тока для компенсации ее действия. Эта работа равна энергии магнитного поля катушки или проводника.

Для компенсации ЭДС самоиндукции источник тока выполнит работу по перемещению заряженных частиц, общий заряд которых равен Q. Приняв во внимание, что, и то, что , получим значение выполненной работы для явления самоиндукции:

ЭДС самоиндукции зависит от индуктивности проводника и скорости изменения силы тока в нем.

При этом сила тока в цепи изменяется от пуля до I_max которое равно I₀. По определению Q=IΔt.

Поскольку при замыкании цепи сила тока не имеет постоянного значения, то для упрощения расчетов будем считать,что сила тока линейно изменяется на протяжении всего времени. Тогда сила тока
Таким образом,

Изменение силы тока ΔI за интервал времени Δt равно I₀.

Работа, выполненная источником тока, равна энергии магнитного поля катушки с током:

Энергия магнитного поля катушки с током пропорциональна индуктивности катушки и квадрату силы тока в ней.

Направление индукционного тока. Правило Ленца. Явление самоиндукции. Физика, 9 класс: уроки, тесты, задания.

1.	Правило для определения направления индукционного тока Сложность: лёгкое	1,5
2.	Определение полюса магнитного поля тока в кольце Сложность: лёгкое	1
3.	Формула для определения энергии магнитного поля Сложность: лёгкое	1
4.	Самоиндукция в цепи Сложность: среднее	2
5.	Способы изменения индуктивности катушки Сложность: среднее	2
6.	Энергия магнитного поля Сложность: среднее	2
7.	Расчёт силы тока Сложность: сложное	3
8.	Применение правила Ленца Сложность: сложное	3
9.	Проявление самоиндукции Сложность: сложное	4

Правило Ленца

Правило Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда противодействует тому изменению магнитного потока, которым он вызван.

Закон Фарадея: ЭДС индукции равна скорости изменения магнитного потока через поверхность, ограни­ченную контуром.

Знак минус в формуле отражает правило Ленца.

В 1833 году Ленц опытным путем доказал утверждение, которое называется правилом Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

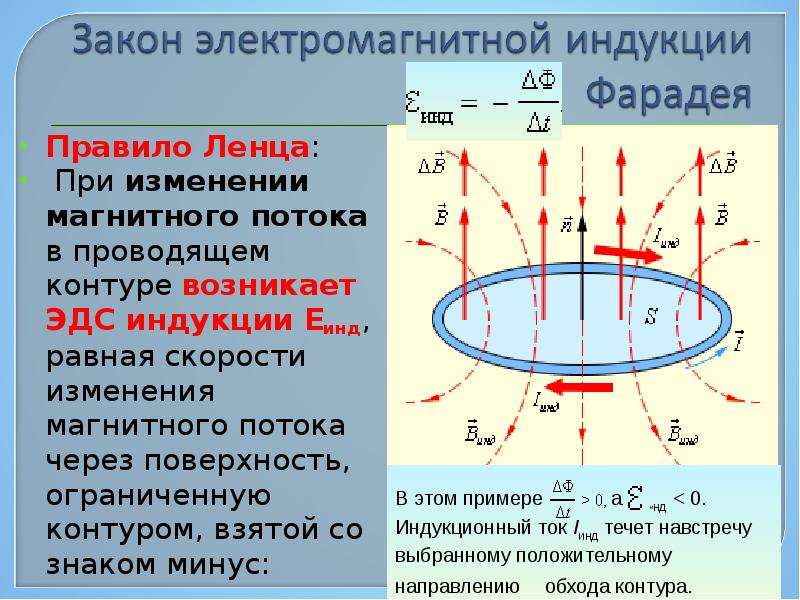
При возрастании магнитного потока Ф>0, а ε_инд<0, т.е. ЭДС индукции вызывает ток такого направления, при котором его маг­нитное поле уменьшает магнитный поток через контур.

При уменьшении магнитного потока Ф<0, а ε_инд>0, т.е. магнитное поле индукционного тока увеличивает убывающий магнитный поток через контур.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии: если магнитное поле через контур увеличивается, то ток в контуре направлен так, что его магнитное поле направлено против внешнего, а если внешнее магнитное поле через контур уменьшается, то ток направлен так, что его магнитное поле поддерживает это убывающее магнитное поле.

ЭДС индукции зависит от разных причин. Если вдвигать в катушку один раз сильный магнит, а в другой — слабый, то показания прибора в первом случае будут более высокими. Они будут более высокими и в том случае, когда магнит движется быстро. В каждом из проведённых в этой работе опыте направление индукционного тока определяется правилом Ленца. Порядок определения направления индукционного тока показан на рисунке.

На рисунке синим цветом обозначены силовые линии магнитного поля постоянного магнита и линии магнитного поля индукционного тока. Силовые линии магнитного поля всегда направлены от N к S – от северного полюса к южному полюсу магнита.

По правилу Ленца индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока. Поэтому в катушке направление силовых линий магнитного поля противоположно силовым линиям постоянного магнита, ведь магнит движется в сторону катушки. Направление тока находим по правилу буравчика: если буравчик (с правой нарезкой) ввинчивать так, чтобы его поступательное движение совпало с направлением линий индукции в катушке, тогда направление вращения рукоятки буравчика совпадает с направлением индукционного тока.

Поэтому ток через миллиамперметр течёт слева направо, как показано на рисунке красной стрелкой. В случае, когда магнит отодвигается от катушки, силовые линии магнитного поля индукционного тока будут совпадать по направлению с силовыми линиями постоянного магнита, и ток будет течь справа налево.

Лестницы. Входная группа. Материалы. Двери. Замки. Дизайн

Правило ленца позволяет определить направление. Правило Ленца. Определение, пример опыта

Правило Ленца необходимо для определения направления тока, который возникает в результате электромагнитной индукции. И звучит оно так: ток, который возникает в замкнутом проводнике под действием электромагнитной индукции, имеет такое направление, что созданный им поток магнитной индукции компенсирует тот поток, который его вызвал.

Проще говоря, индукционный ток всегда имеет такое направление, чтобы препятствовать потоку его вызвавшему.

Проведем такой эксперимент. Возьмем замкнутый контур, состоящий из проводника. В этот контур не будет включен никакой источник тока, и он будет иметь форму соленоида. К этому соленоиду будет подключён гальванометр. Далее в этот соленоид будем вводить постоянный магнит, повернутый северным полюсом. Вследствие этого начнет, увеличивается магнитный поток пронизывающий соленоид и, следовательно, в нем возникнет индуцированный ток. Направление этого тока укажет стрелка гальванометра.

Рисунок 1 — Введение постоянного магнита в солиноид

Этот самый индуцированный ток вызовет появление магнитного поля вокруг соленоида. Поле будет сходно с полем постоянного магнита. Но направлено оно будет навстречу вводимому магниту. То есть северный полюс индуцированного поля будет направлен в сторону северного полюса постоянного магнита.

Рисунок 2 — Возникновение индуцированного поля

Исходя из того что поля направлены встречно то есть между ними возникнут силы отталкивания то ток наведенный в контуре соленоида будет иметь такое направление чтобы противодействовать введению постоянного магнита в контур.
Теперь начнем удалять постоянный магнит от контура. Стрелка гальванометра повернется в другую сторону. Таким образом, станет понятно, что ток в контуре изменил свое направление. И поле, порожденное индуцированным током, будет стремиться сохранить убывающий магнитный поток.

Рисунок 3 — Удаление постоянного магнита от солиноида

В данном опыте не обязательно перемещать магнит. Его можно вращать относительно оси, которая разделяет магнитные полюса. Также можно перемещать либо вращать соленоид. В качестве постоянного магнита можно использовать другой соленоид, к которому подключён источник тока.

В 1834 году русский академик Э. Х. Ленц, известный своими многочисленными исследованиями в области электромагнитных явлений, дал универсальное правило для определения направления индуктированной электродвижущей силы (ЭДС) в проводнике. Это правило, известное как , может быть сформулировано так:

Направление индуктированной ЭДС всегда таково, что вызванный ею ток и его имеют такое направление, что стремятся препятствовать причине, порождающей эту индуктированную ЭДС.

Справедливость формулировки правила Ленца подтверждается следующими опытами:

Рисунок 1. Противодействие проводника с индуктированным током своему движению

1. Если расположить так, как показано на рисунке 1, то при движении вниз проводник будет пересекать это магнитное поле. Тогда в проводнике индуктируется ЭДС, направление которой можно определить по . В нашем случае направление индуктированной ЭДС, а стало быть и тока будет «к нам». Посмотрим теперь, как будет вести себя наш проводник с током в магнитном поле. Из предыдущих статей нам известно, что проводник с током из магнитного поля будет выталкиваться. Направление выталкивания определяется по правилу левой руки. В нашем случае сила выталкивания направлена вверх. Таким образом, индуктированный ток, взаимодействуя с магнитным полем, мешает движению проводника, то есть противодействует причине, которая его вызвала.

2. Для опыта соберем цепь, показанную на рисунке 2. Опуская в катушку (северным полюсом вниз), заметим отклонение стрелки гальванометра. Опыт показывает, что направление индуктированного тока в катушке будет такое, как показано стрелками на рисунке 2, а . Пусть ему соответствует отклонение стрелки влево от среднего нулевого положения. Следовательно, катушка как бы превратилась в и указанное направление тока создает наверху ее северный полюс, а внизу — южный. Так как одноименные полюса магнита и соленоида будут отталкиваться, то индуктированный ток в катушке будет мешать движению постоянного магнита, то есть будет противодействовать причине, которая его вызвала.

Рисунок 2. Противодействие соленоида движению магнита:
а — вниз, б — вверх

Если мы будем вынимать постоянный магнит из катушки, то стрелка гальванометра отклонится вправо (рисунок 2, б ). Этому отклонению стрелки гальванометра, как показывает опыт, соответствует направление индуктированного тока, показанное стрелками на рисунке 2, б , и противоположное направлению тока на рисунке 2, а .

Определяя полюса катушки по «правилу буравчика», найдем, что южный полюс будет теперь наверху катушки, а северный внизу. Разноименные полюса магнита и соленоида, притягиваясь, будут тормозить движение магнита. Значит, индуктированный ток опять будет противодействовать причине, которая его вызвала.

Рисунок 3. Возникновение индуктированного тока II : а — в момент замыкания цепи I , б — в момент размыкания цепи

3. Замыкая цепь I (рисунок 3, а ), пропустим ток по проводнику АБ . Направление тока показано на рисунке стрелками. Магнитное поле проводника АБ , созданное появившимся током, распространяясь во все стороны, будет пересекать проводник ВГ , и в цепи II возникает индуктированная ЭДС. Поскольку цепь II замкнута на гальванометр, в ней появится ток. Гальванометр в этом случае включен также, как и в предыдущем опыте.

Стрелка гальванометра, отклонившись влево, покажет, что ток через прибор идет сверху вниз. Сравнивая направление токов в проводниках АБ и ВГ, мы видим, что токи их направлены в разные стороны.

Как мы уже знаем, проводники, токи в которых направлены в разные стороны, один от другого. Поэтому проводник ВГ с индуктированным током будет стремиться оттолкнуться от проводника АБ (так же, как и проводник АБ от ВГ ), устранить влияние поля проводника АБ и тем самым препятствовать причине, вызвавшей индуктированный ток.

Индуктированный ток в цепи II будет проходить непродолжительное время. Как только проводника АБ установится, прекратится пересечение проводника ВГ магнитным полем проводника АБ , ток в цепи II пропадет.

При размыкании цепи I исчезающий ток вызовет уменьшение магнитного поля, индукционные линии которого, пересекая проводник ВГ , создадут в нем индуктированный ток того же направления, что и в проводнике АБ (рисунок 3, б ).

Нам известно, что проводники, в которых ток идет в одном направлении, один к другому. Поэтому проводник ВГ будет стремиться протянуться к проводнику АБ , чтобы поддержать его убывающее магнитное поле.

4. Для следующего примера возьмем катушку, имеющую круглый сердечник, набранный из нарубленной стальной проволоки, на который свободно надето легкое алюминиевое кольцо (рисунок 4). В момент замыкания цепи по обмотке катушки начинает проходить , создающий магнитное поле, индукционные линии которого, пересекая алюминиевое кольцо, индуктируют в нем ток. В момент включения катушки в алюминиевом кольце возникает индуктированный ток, направленный обратно току в витках катушки. Проводники имеющие разное направление индукционного тока отталкиваются. Поэтому в момент включения катушки алюминиевое кольцо подскакивает вверх.

Нам теперь известно, что при всяком изменении во времени магнитного потока, пронизывающего контур, в нем появляется индуктированная ЭДС, определяемая равенством:

Выражение в данной формуле представляет собою среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени Δt , тем меньше вышеуказанная ЭДС отличается от ее действительного значения в данный момент времени. Знак минус, стоящий перед выражением , показывает направление индуктированной ЭДС, то есть учитывает правило Ленца.

При увеличении магнитного потока выражение будет положительным, а ЭДС — отрицательной. В этом и заключается правило Ленца: ЭДС и созданный ею ток противодействуют причине, которая их вызвала .

При равномерном изменении во времени магнитного потока выражение будет постоянно. Тогда абсолютное значение ЭДС в проводнике будет равно:

Размерность магнитного потока будет:

[Ф] = [e × t ] = В × сек или вебер.

Если мы имеем не один проводник, а катушку, состоящую из w витков, то величина индуктированной ЭДС будет:

Произведение числа витков катушки на сцепленный с ними магнитный поток называется потокосцеплением катушки и обозначается буквой ψ. Поэтому закон можно записать и в другой форме:

Электромагнитная индукция — это физическое явление, состоящее в возникновении в замкнутом контуре электрического тока при изменении потока магнитной индукции через поверхность, ограниченную этим контуром.

2. Изменение каких физических величин может привести к изменению магнитного потока?

К изменению магнитного потока может привести изменение с течением времени площади поверхности, которая ограничена контуром; модуля вектора магнитной индукции; угла, который образуют вектор индукции с вектором площади этой поверхности.

3. В каком случае направление индукционного тока считается положительным, а в каком — отрицательным?

Если выбранное направление обхода контура совпадает с направлением индукционного тока, то оно считается положительным. Если выбранное направление обхода контура противоположно направлению индукционного тока, то оно считается отрицательным.

4. Сформулируйте закон электромагнитной индукции. Запишите его математическое выражение.

ЭДС электромагнитной индукции в замкнутом контуре равна по модулю и противоположна по знаку скорости изменения магнитного потока через поверхность, которая ограничена этим контуром.

5. Сформулируйте правило Ленца. Приведите примеры его применения

Индукционный ток, возникающий в контуре, своим магнитным полем противодействует изменению магнитного потока, вызвавшего этот ток. Например, при увеличении магнитного потока через контур магнитный поток индукционного тока будет отрицательным, а результирующий поток, равный их сумме, уменьшится. А при уменьшении магнитного потока через контур магнитный поток индукционного тока будет поддерживать результирующий поток, не давая ему резко убывать.

Правило или закон Ленца получил своё имя в честь физика немецкого происхождения, жившего и преподававшего в России, Эмилия Ленца. Его правило подчиняется третьему закону Ньютона (на каждое действие существует равное противодействие) и закону сохранения энергии (в замкнутой системе энергия не может ни возникать, ни исчезать, поэтому сумма всех энергий в ней остаётся постоянной величиной).

В основании правила Ленца лежит выведенный Фарадеем закон электромагнитной индукции. Необходимо вспомнить, что по нему воздействующее на катушку стороннее переменное магнитное поле, вызывает в ней ЭДС.

Перемещение постоянного магнита к катушке или удаление его от неё изменяет магнитный поток, пронизывающий контур катушки. Величина ЭДС, наведённой в контуре, прямо пропорциональна скорости изменения магнитного потока.

В ситуациях а) и с), когда магнит приближают к катушке или удаляют от неё, в катушке начинают направленное движение электроны (индуцируется ток). В ситуации b) магнит неподвижен, следовательно, можно говорить, что магнитное поле постоянно и в катушке отсутствует ток.

Как узнать, куда направлен индуцированный ток?

Эмилий Ленц сформулировал простое правило (закон), которое объясняет направление индуцированного в катушке тока:

Индукционный ток протекает так, чтобы противодействовать своим магнитным полем изменяющемуся потоку внешнего магнитного поля, которым он вызван.

Объяснение правила Ленца

Для понимания закона Ленца, обратим внимание на две экспериментальных ситуации.

Магнит приближается к катушке

Северный полюс магнита стремятся приблизить к катушке. Магнитный поток, пронизывающий витки катушки, возрастает. Ток, появляющийся в катушке, создаёт вокруг неё магнитное поле. Оно по правилу Ленца выступает против увеличения магнитного потока через катушку. Такая ситуация возможна лишь тогда, когда ближайшая к магниту сторона катушки приобретает полярность северного полюса. Зная полярность, можно легко определить направление индукционного тока, применяя правило правой руки. Ток течёт в направлении против часовой стрелки.

Магнит удаляется от катушки

Когда северный полюс магнита удаляется от катушки, магнитный поток, пронизывающий катушку, уменьшается. В катушке возникает ток по закону Фарадея. Этот ток создаёт собственное магнитное поле. По правилу Ленца, это магнитное поле будет противодействовать уменьшению магнитного потока через катушку. Это возможно лишь в том случае, если на ближайшей к магниту стороне катушки существует южный магнитный полюс. Противоположные полюса притягиваются. Нам известна полярность катушки. Применим правило правой руки и определим направление тока в катушке. В этой ситуации он течёт по часовой стрелке.

Урок на тему «Явление электромагнитной индукции. Правило Ленца. Закон электромагнитной индукции»

Цели урока:

• обучающие: изучить явление электромагнитной индукции и условия его возникновения; показать причинно-следственные связи при наблюдении явления электромагнитной индукции; раскрыть сущность явления при постановке опытов, изучить правило Ленца (правила для определения направления индукционного тока), разъяснить закон электромагнитной индукции.
• развивающие: развивать логическое мышление и внимание, умение анализировать, сопоставлять полученные результаты, делать соответствующие выводы, представлять результаты проделанной работы, развивать общую культуру речи, навыки групповой работы.
• воспитательные: вызвать заинтересованность к изучаемой теме с точки зрения получаемой профессии, способствовать самостоятельному получению знаний.

Тип урока: изучение нового материала

Методы обучения: Метод проблемного изложения, частично-поисковый.

Формы организации познавательной деятельности:

• Групповая
• Фронтальная

Оборудование: электронная доска, презентация, мультимедийный курс Физика: полный курс.7-11 классы (под ред. В. Акопяна), полосовой магнит, соединительные провода, гальванометр, миллиамперметр, катушки, источник тока, ключ, проволочные мотки, магнит дугообразный, прибор для демонстрации правила Ленца.

План урока

Этапы урока	Время, мин	Приемы и методы
Создание проблемной ситуации, исторические сведения	8 мин	Создание проблемной ситуации преподавателем. Демонстрации, подводящие к цели урока. Беседа.
Изучение нового материала в ходе экспериментальной работы в группах (явление ЭМИ, правило Ленца)	2 мин	Эксперимент. Наблюдение. Выделение главного. Формулировка выводов.
Изучение нового материала (правила определения направления индукционного тока, закон электромагнитной индукции).	20 мин	Беседа. Ответы на вопросы.
Подведение итогов. Домашнее задание.	5 мин	Выделение главного. Оценивание (взаимооценивание) “Цепочка”.

Ход урока

1. Создание проблемной ситуации (дальняя перспектива)

Здравствуйте, ребята! На слайде (Слайд 1) презентации изображены опоры ЛЭП в разных странах: в Финляндии, например в виде оленей. Но опоры не меняют содержание: все ЛЭП предназначены для передачи электрического тока на большие расстояния, и все ЛЭПы – высоковольтные.

Почему все линии электропередачи высоковольтные?

(Ответы обучающихся, как правило — “Течет ток высокого напряжения”).

Зачем повышают напряжение? (Слайд 2). Посмотрите на схему передачи электроэнергии: трансформатор повышает и без того высокое напряжение, а в быту, в осветительной сети необходимо всего 220В! Так зачем повышают напряжение? (Ответы обучающихся)

Пока мы вели с вами беседу через проволочный моток протекал электрический ток.

Демонстрация 1: Проволочный моток закреплен в лапке штатива, по нему пропускают электрический ток.

Какое действие электрического тока можно заметить?

(Ответы обучающихся, как правило — “Проводник, по которому течет ток нагревается. Это тепловое действие тока”).

Молодцы, верно! Ток, текущий по ЛЭП, нагревает линию (провод) происходит потеря энергии: часть электрической энергии превращается в тепловую. Потери тепловой энергии необходимо минимизировать. (Слайд 3) Давайте вспомним закон Джоуля-Ленца: уменьшить тепловые потери можно уменьшив, например, силу тока. Прибор, который уменьшает силу тока и одновременно с этим повышает напряжение во столько же раз (и наоборот), практически без потери мощности был изобретен в 1878 году русским ученым П.Н. Яблочковым и был назван трансформатором.

Давайте подведем небольшой итог: чтобы уменьшить тепловые потери при передаче электроэнергии на большие расстояния необходимо понизить силу тока, а эту роль выполнит повышающий трансформатор, но одновременно с этим он во столько же раз повысит напряжение. Вот почему все линии электропередач высоковольтные.

2. Создание проблемной ситуации (ближняя перспектива)

Но на каком принципе построена работа трансформатора?

(Обучающиеся затрудняются с ответом)

Его работа основана на явлении электромагнитной индукции, которое было открыто Майклом Фарадеем в 1831 году и является величайшим открытием ХIХ века. (Слайд 4)

На этом явлении построен принцип работы индукционных печей (ОМД, сталеплавильное производство) и лагов, индукционных варочных панелей (Технолог), металлодетекторов, трансформаторов(Сварщик) и генераторов переменного тока(Техническое обслуживание электрического и электромеханического оборудования). Ваша будущая профессия (специальность) неразрывно связана с этим явлением: без электрического тока вырабатываемого генераторами на ЭС невозможна работа станков (Станочник), электромагнитов (Машинист крана), электрических печей и плит (Технолог) и т.д.

Демонстрация 2. Моток закреплен в лапке штатива, по нему пропускают электрический ток, подносят магнит.

Какое действие электрического тока можно заметить?

(Ответы обучающихся, как правило — “Магнитное. Если по проводнику течет ток, то вокруг проводника возникает магнитное поле”). Молодцы!

Верно. Если электрический ток порождает собой магнитное поле, то не может ли в свою очередь, магнитное поле породить электрический ток?

В 1821 году этим вопросом был озадачен Майкл Фарадей. “Превратить магнетизм в электричество” было написано у него в дневнике. Через 10 лет, 29 августа 1831 года эта задача была решена.

Запишите тему урока. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. ПРАВИЛО ЛЕНЦА. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ.

Давайте экспериментально установим, при каких условиях магнитное поле может породить электрический ток в проводнике (контуре).

(Обучающиеся выполняют экспериментальные задания по группам).

• 1 группа: Приложение 1
• 2 группа: Приложение 2
• 3 группа: Приложение 3

Подведем итоги работы наших групп:

1 группа (Ответы обучающихся). (Слайд 5) (ответы обучающихся 1 группы дополняются ответами обучающихся из других групп)

Вывод: В проводящем замкнутом контуре возникает электрический ток, если контур находится в переменном магнитном поле или движется в постоянном во времени поле так, что число линий магнитной индукции, пронизывающих контур, меняется.

Из истории вопроса: Почти одновременно с Фарадеем получить электрический ток в катушке с помощью магнита пытался швейцарский физик Колладон. При работе он пользовался гальванометром, легкая магнитная стрелка которого помещалась внутри катушки прибора. Чтобы магнит не оказывал непосредственного влияния на стрелку, концы катушки, куда вводили магнит, были выведены в соседнюю комнату и там присоединены к гальванометру. Вставив магнит в катушку, Колладон шел в соседнюю комнату и с огорчением убеждался, что гальванометр не показывал тока. Стоило бы ему все время находится рядом с гальванометром, а кого-нибудь попросить заняться магнитом, замечательное открытие было бы сделано. Но этого не случилось. Покоящийся относительно катушки магнит не вызывает в ней тока.

Введем понятие магнитного потока. (Слайд 6)

Магнитный поток — физическая величина, равная произведению модуля вектора магнитной индукции B на площадь S косинус угла ? между векторами и

Ф = В S cos

 1 Вб = 1 Тл*1м²

Магнитный поток в 1 Вебер создается магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции.

Ток, возникающий в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называют индукционным током.

2 группа (Ответы обучающихся).

Вывод: Величина индукционного тока зависит (Слайд 7)

• сила индукционного тока зависит не от скорости изменения магнитной индукции, а от скорости изменения потока магнитной индукции (от скорости изменения магнитного потока)
• от числа витков в контуре

Общий вывод работы 1 и 2 группы:

Явление возникновения индукционного тока в замкнутом контуре при изменении магнитного потока, пронизывающего контур, называют явлением электромагнитной индукции.

3 группа (Ответы обучающихся). (Слайд 8). Правило Ленца.

Исследуя явление электромагнитной индукции, Э. X. Ленц в 1833 г. установил общее правило для определения направления индукционного тока:

Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым был вызван.

Направление индукционного тока.

Правило правой руки

Если правую руку расположить так, чтобы вектор B входил в ладонь, а отогнутый на 90^о большой палец был направлен по движению проводника, то четыре пальца руки укажут направление индукционного тока проводнике.

При объяснении материала можно использовать мультимедийный курс Физика: полный курс.7-11 классы (под ред. В.Акопяна) (урок “Явление электромагнитной индукции”)

1. Определить направление линий индукции внешнего поля.
2. Определить, увеличивается или уменьшается магнитный поток через контур (если магнит вдвигается в кольцо, то Ф>0, если выдвигается, то Ф<0).
3. Определить направление линий индукции магнитного поля В’, созданного индукционным током (если Ф>0, то линии В и В’ направлены в противоположные стороны; если Ф<0, то линии В и В’ сонаправлены).
4. Пользуясь правилом буравчика (правой руки), определить направление индукционного тока.

Закон электромагнитной индукции

Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сторонних сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока, через поверхность, ограниченную контуром, в последнем появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции.

Так как

~ и =, то

= — для 1 витка

= * N- для N витков

В соответствии с правилом Ленца:

= — *N — для N витков

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

Ребята, сегодня мы познакомились с явлением электромагнитной индукции (ЭМИ). Работа многих приборов основана на этом явлении, особенную роль следует отвести генераторам переменного тока, в которых механическая энергия превращается в электрическую. Без электрического тока жизнь современного человека представить практически невозможно, так же как и Вашу будущую работу: индукционные варочные панели – Технолог, индукционные печи — ОМД, трансформатор – Сварщик и т.д.

Подведем итог урока, ответим на вопросы:

Вопросы:

1. В чем заключается явление электромагнитной индукции?

2. Что называют магнитным потоком?

3. Как связана работа станочника (машиниста крана, машиниста локомотива и т. д.) с явлением ЭМИ?

4. Почему закон электромагнитной индукции формулируется для ЭДС, а не для силы тока? Сформулируйте закон ЭМИ.

5. Почему в законе электромагнитной индукции стоит знак “минус”?

6. Как определить направление индукционного тока?

Сегодня мы плодотворно работали, проводили опыты, ребята оцените работу каждой группы: работу своей группы и работу студентов в других группах.

(Обсуждение, диалог обучающихся)

3. Домашнее задание:

8-11, конспект, стр. 27 (привести примеры возникновения индукционного тока, используя две катушки на общем сердечнике), подготовить сообщения (Металлодетекторы, поезд на магнитной подушке, индукционные печи, индукционные варочные панели).

Цепочка:

Как обычно, выходим из класса по “цепочке” (необходимо назвать физическую величину и единицы измерения физической величины).

---

Приложение 1

Опыт	Вывод
Внесите постоянный магнит в катушку, оставьте его в состоянии покоя. Наблюдается ли возникновение тока?
Осуществляйте движение постоянного магнита относительно катушки. Наблюдается ли возникновение тока?
При внесении и вынесении постоянного магнита из катушки изменялось ли направление возникающего тока?
Осуществляйте движение катушки относительно лежащего неподвижно постоянного магнита, лежащего неподвижно. Наблюдается ли возникновение тока?

Приложение 2

Опыт	Вывод
Осуществляйте движение постоянного магнита внутри катушки: а) медленно б) быстро Наблюдается ли возникновение тока? Что можно сказать о величине тока?
Подключите катушку с бльшим числом витков. Изменилась ли сила возникающего тока?
Осуществите движение проволочного мотка между полюсами подковообразного магнита: а) перпендикулярно силовым линиям магнитного поля б) вдоль силовых линий магнитного поля В каком случае сила возникающего тока больше?

Приложение 3

Опыт	Вывод
Внесите постоянный магнит северным полюсом в разомкнутое кольцо. Что удается пронаблюдать?
Внесите постоянный магнит южным полюсом в разомкнутое кольцо. Что удается пронаблюдать?
Поднести постоянный магнит к замкнутому кольцу. Что удается пронаблюдать? Медленно удаляйте магнит от кольца. Что удается пронаблюдать?

Закон Ленца — определение, формула и пример

Что такое закон Ленца?

Закон Ленца, названный в честь физика Эмиля Ленца, был сформулирован в 1834 году. Он гласит, что направление тока, индуцируемого в проводнике изменяющимся магнитным полем, таково, что магнитное поле, создаваемое индуцированным током, противодействует начальному изменяющемуся магнитному полю.

Когда ток индуцируется магнитным полем, то магнитное поле, создаваемое индуцированным током, создает свое магнитное поле.Таким образом, этому магнитному полю будет противостоять создавшее его магнитное поле.

Закон Ленца основан на законе индукции Фарадея, который гласит, что изменяющееся магнитное поле индуцирует ток в проводнике, тогда как закон Ленца сообщает нам направление индуцированного тока, которое противодействует начальному изменяющемуся магнитному полю, создавшему его. Следовательно, это обозначено в формуле закона Фарадея отрицательным знаком.

\ [\ epsilon = — \ frac {d \ Phi_ {B}} {dt} \]

Магнитное поле можно изменить, изменив его силу, либо перемещая магнит по направлению к катушке или от нее, либо перемещая катушка находится в магнитном поле или вне его.

Следовательно, мы можем сказать, что величина электромагнитного поля, индуцированного в цепи, пропорциональна скорости изменения магнитного потока.

\ [\ varepsilon \ propto \ frac {d \ Phi} {dt} \].

Формула закона Ленца:

Согласно закону Ленца, когда электромагнитное поле генерируется изменением магнитного потока, полярность индуцированного электромагнитного поля создает индуцированный ток, магнитное поле которого противодействует начальному изменяющемуся магнитному полю, создавшему его.

Формула закона Ленца показана ниже:

\ [\ epsilon = — N \ frac {\ partial \ Phi_ {B}} {\ partial t} \]

Где,

ε = индуцированная ЭДС

δΦB = изменение магнитного потока

N = количество витков в катушке

Применения закона Ленца:

Применения закона Ленца включают:

1. Когда источник электромагнитного поля подключается к катушке индуктивности, ток начинает течь через него. Обратное электромагнитное поле будет противодействовать этому увеличению тока через катушку индуктивности.Чтобы установить ток, внешний источник электромагнитного поля должен проделать некоторую работу для преодоления этого противостояния.

2. Закон Ленца используется в электромагнитных тормозах и индукционных варочных панелях.

3. Применяется также для электрогенераторов, генераторов переменного тока.

4. Вихретоковые весы

5. Металлодетекторы

6. Вихретоковые динамометры

7. Тормозные системы на поезде

8. Считыватели карт

9. Микрофоны

Lenz Law Experiment4 Чтобы найти направление наведенной электродвижущей силы и тока, воспользуемся законом Ленца.Ниже приведены некоторые эксперименты.

(изображение будет загружено в ближайшее время)

Первый эксперимент:

В первом эксперименте, когда ток в катушке протекает в цепи, создаются силовые линии магнитного поля. По мере того, как ток, протекающий через катушку, увеличивается, магнитный поток увеличивается. Направление потока индуцированного тока должно быть таким, чтобы оно было противоположным при увеличении магнитного потока.

Второй эксперимент:

Во втором эксперименте, когда катушка с током намотана на железный стержень с левым концом, ведущим себя как N-полюс, и перемещается к катушке S, возникает индуцированный ток.

Третий эксперимент:

В третьем эксперименте катушка притягивается к магнитному потоку, связанная катушка продолжает уменьшаться, что означает, что площадь катушки внутри магнитного поля уменьшается.

Согласно закону Ленца, катушка движется противоположно, когда индуцированный ток прикладывается в том же направлении.

Чтобы произвести ток, магнит в петле прикладывает силу. Чтобы противодействовать изменению, сила тока на магните должна быть приложена.

Закон Ленца | Brilliant Math & Science Wiki

Обычным экспериментом, демонстрирующим закон Ленца, является эксперимент с «каплей магнита». В этом эксперименте магнит (часто мощный, неодимовый) опускают через проводящую трубку, часто сделанную из меди. Изменяющийся магнитный поток при падении магнита индуцирует в трубке ток, который создает магнитное поле, противоположное магнитному полю постоянного магнита. Поскольку одинаковые полюса магнита отталкиваются, а индуцированное магнитное поле кажется одинаковым полюсом на обоих концах магнита, на постоянный магнит действует магнитная сила, которая замедляет его падение из-за силы тяжести.

Мощный магнит, упавший в медную трубку, заставил левитировать в трубке по закону Ленца; здесь короткая медная трубка многократно вращается, чтобы удерживать магнит в подвешенном состоянии [2].

Постоянный магнит массы MMM выходит из состояния покоя в середине длинной медной трубки с сопротивлением RRR и площадью поперечного сечения AAA, как указано выше. Сделайте приближение, что сила магнитного поля постоянного магнита падает, как в подсказке 1 ниже, с заменой III на некоторую постоянную I0I_0I0.{3/2}}. B = 2 (ρ2 + z2) 3 / 2μ0 Iρ.

, где zzz — расстояние по оси контура, а III — ток в контуре.

Совет 2: Сила между двумя магнитными дипольными моментами равна

.

F = ∣∇ (m⃗⋅B⃗) ∣F = | \ nabla (\ vec {m} \ cdot \ vec {B}) | F = ∣∇ (m⋅B) ∣

, где поле BBB обусловлено одним дипольным моментом, а m = IAm = IAm = IA — другим дипольным моментом, где III — эффективный ток, а AAA — площадь поперечного сечения, рассматривающая второй диполь как токовую петлю.{5/2}}. I (t) = 2R (A + πr (t) 2) 5 / 23μ0 I0 r (t) v (t) A π2.

Ниже падающего магнита магнитный поток со временем увеличивается. Таким образом, направление тока создает магнитное поле, противоположное полю постоянного магнита, которое проявляется как сила отталкивания. Над падающим магнитом магнитный поток составляет , со временем уменьшаясь на . Таким образом, направление тока создает магнитное поле в том же направлении, что и постоянный магнит, которое проявляет себя как сила притяжения.{5}} .F = AI (t) ∣∇ (B (t) ∣ = 2R (A + πr (t) 2) 5 / 23μ0 I0 r (t) v (t) A3 / 2π2 (2 (A / π + r (t) 2) 5 / 23μ0 I0 A / π r (t)) = 4R (A + πr (t) 2) 59μ02 I02 r (t) 2v (t) A2π4. {3/2}} v (t) \ end {выровнен} Ftotal = 2∫0∞ 4R (A + πr (t) 2) 59μ02 I02 r (t) 2v (t) A2π4 dr = 2R9μ02 I02 v (t) A2π4 ∫0∞ ( A + πr (t) 2) 5r (t) 2 dr = 2R9μ02 I02 v (t) A2π4 (256π A7 / 25) = 512RA3 / 245μ02 I02 π3 / 2 v (t)

Форма силы — вязкая демпфирующая сила, пропорциональная скорости, что является хорошей проверкой справедливости приведенного выше обсуждения.2} {2M} .v (t) ≈κMg (Mκt −2M2κ2t2) = gt − 2Mκgt2.

Это обеспечивает небольшую отрицательную коррекцию на ранних этапах обычного линейного роста скорости gtgtgt, как и ожидалось.

В ходе этого вычисления было сделано много приближений: приближение магнитного диполя как токовой петли, приближение длины трубки и малого поперечного сечения, так что краевые эффекты незначительны, и предположение, что взаимодействие магнита с каждым токовым кольцом можно хорошо смоделировать диполь-дипольное взаимодействие.Тем не менее, полученное выше аналитическое выражение очень хорошо отражает качественное поведение физического сценария. Если поперечное сечение трубки широкое или сопротивление велико, индуцированный ток невелик и затухание происходит очень медленно с более высокой конечной скоростью. Если I0I_0I0 велик, постоянный магнит очень силен, вызывая сильный эффект демпфирования, совместимый с небольшой конечной скоростью и высокой скоростью демпфирования, обнаруженными выше.

Тот же эффект наблюдается в сканерах МРТ, которые похожи на трубки с гораздо более мощными магнитными полями.Ниже закон Ленца демонстрируется на примере медленного движения алюминиевого стержня в магнитном поле МРТ:

Мощное магнитное поле МРТ индуцирует магнитное поле от алюминиевого стержня, которое вызывает силу, действующую против силы тяжести. Полоса падает, в реальном времени [3].

Магнетизм — Закон индукции Фарадея

Магнетизм — Закон индукции Фарадея — Физика 299

« Перестань говорить Богу, что делать с его кубиками. «

Нильс Бор

• До сих пор мы рассматривали электричество и магнетизм как почти отдельные предметы. Теперь мы начинаем обсуждать явления, которые показать, что электричество и магнетизм неразрывно связаны, отсюда термин электромагнетизм . Первое из этих свойств известен как закон Фарадея Индукция .

Формально, время независимое электрические и магнитные свойства можно описать, рассматривая электричество и магнетизм как в значительной степени отдельные явления. Однако, когда зависимость от времени становится частью «уравнения» мы обнаруживаем, что электрические и магнитные свойства становятся неразрывно связаны — электромагнетизм.

• Этот закон удобно записать в терминах магнитного потока, который определяется так же, как электрический поток.

где S — поверхность, по которой идет поток. оценен.

Для постоянного B, перпендикулярно поверхности, Φ _B = BA, где A — площадь поверхности S.

Магнитный поток Φ _B составляет важно, что у него есть собственная единица Вебера — 1 Вебер = 1 т.м ² . В первые дни электромагнетизм было принято измерять магнитное ( B ) поле по Веберу / м ² .

• В терминах закона индукции магнитного потока Фарадея предоставлено,

Индуцированная электродвижущая сила ( ЭДС ) в цепи равна скорости изменения магнитного поток через цепь.

ЭДС не сила, скорее его можно рассматривать как индуцированное напряжение в замкнутом контуре.

Фарадея экспериментально определил свой закон в изложенной выше форме.

---

• Один из самых простых способов изменить магнитный поток через цепь — перемещать постоянный (стержневой) магнит к цепи или от нее, как показано на диаграммы ниже.

(а) Магнитный поток проходит по цепи, но не меняется со временем, поэтому нет индуцированной ЭДС и, следовательно, нет индуцированной Текущий.

(б) Поток через контур увеличивается с увеличением время, вызывающее наведенную ЭДС и ток.

(c) По мере того, как магнит движется быстрее, скорость изменение потока со временем увеличивается, вызывая большее ЭДС и ток.

(d) Когда магнит удаляется от цепи поток уменьшается со временем, поэтому индуцированная ЭДС и ток поменяны местами.

---

• Причина изменения магнитного потока (поля) не ограничивается постоянными магнитами. В магнитное поле из-за второй цепи может производить аналогичный эффект, как описано в примерах ниже.
  

На диаграмме справа ток в левой цепи постоянный, но поток через другую цепь увеличивается как две цепи становятся ближе.

В положении слева оба контура стационарные. Течение в левая цепь изначально равна нулю, но быстро увеличивается до постоянного значения, когда переключатель находится в закрыто.Когда ток достигает своего финала (постоянное) значение потока через правую цепь увеличивается со временем, таким образом, по формуле Фарадея Закон, вызывающий кратковременный импульс индуцированного ток во второй цепи. Когда выключатель разомкнут поток в правой цепи быстро уменьшается, вызывая короткий индуцированный ток импульс в обратном направлении.

---

Мне сказали, что у меня кровь группы А, но это был Тип О.

Доктор К. Л. Дэвис
Физический факультет
Университет Луисвилля
электронная почта : [email protected]

Закон Ленца: объяснение, уравнения и примеры

Мы знаем, что электромагнитная индукция подчиняется двум фундаментальным законам — закону Фарадея и закону Ленца. Закон Фарадея устанавливает связь между наведенной ЭДС (ε) и величиной магнитного потока (dφ / dt) в проводящей катушке из N витков.Формула закона Ленца дается выражением:

.

ε = — N dφ / dt

Однако это уравнение ничего не говорит о сохранении энергии. Закон Ленца может объяснить сохранение энергии и отрицательный знак в уравнении закона Фарадея.

Что такое Закон Ленца

Закон Ленца гласит, что

«Полярность наведенной ЭДС такова, что она противодействует изменению магнитного потока, создавшему ее».

Когда магнитное поле индуцирует ток в проводящей катушке, индуцированный ток создает свое магнитное поле, противоположное индуцирующему магнитному полю.Другими словами, индуцированный ток всегда будет противодействовать движению, которое его изначально запустило. Закон Ленца важен, поскольку он может определять направление индуцированного тока и магнитного поля, индуцированного током.

Изменение магнитного потока вокруг проводящей катушки может быть вызвано несколькими причинами:

• Изменение напряженности магнитного поля
• Переместите магнит к катушке или от нее
• Переместите катушку в магнитное поле или из него
• Поверните катушку относительно магнита

Закон Ленца

Закон Ленца назван в честь немецкого физика Генриха Фридриха Ленца после того, как он вывел его в 1834 году.

Закон Ленца и сохранение энергии

Чтобы подчиняться закону сохранения энергии, направление тока, индуцируемого по закону Ленца, должно создавать магнитное поле, которое противодействует магнитному полю, которое его в первую очередь создало. Направление этого индуцированного магнитного поля определяется правилом правой руки .

Предположим, что ток не противодействует магнитному полю магнита. Тогда индуцированное магнитное поле будет в том же направлении, что и индуцирующее магнитное поле.Эти два магнитных поля суммируются и создают большее магнитное поле. Это большее магнитное поле вызовет в катушке еще один ток, в два раза превышающий первоначальный ток. Этот индуцированный ток создаст другое магнитное поле, и процесс будет продолжаться. Таким образом, возникнет бесконечный цикл индуцированных токов и магнитных полей, нарушающих закон сохранения энергии. Следовательно, закон Ленца является следствием принципа сохранения энергии.

Применение закона Ленца

Закон Ленца может применяться к следующим устройствам:

• Индуктор
• Электрогенераторы
• Электромагнитное торможение
• Индукционная посуда
• Вихретоковые компенсаторы
• Вихретоковые динамометры
• Микрофоны
• Картридеры

Примеры проблем и решений

П.1. Рассчитайте величину наведенной ЭДС, когда магнит вдавливается в катушку. Приведена следующая информация: одноконтурная катушка имеет радиус 5 см, а среднее значение комплексной составляющей магнитного поля B cos θ увеличивается с 0,1 Тл до 0,5 Тл за 0,2 с.

Soln. Дан,

N = 1

r = 5 см = 0,05 м

A = πr ² = π (0,05 м) ² = 0,0079 м ²

Δt = 0,2 с

(B cos θ) _{начальный} = 0.1 т

(B cos θ) _{конечный} = 0,5 T

ΔB = (B cos θ) _{конечный} — (B cos θ) _{начальный} = 0,5 T — 0,1 T = 0,4 T

Из закона Фарадея,

| ε | = N Δφ / Δt

или, | ε | = N A Δ (B cos θ) / Δt

или, | ε | = 1 x 0,0079 м ² x 0,4 T / 0,2 с = 0,016 Tm ² / с = 16 мВ

П.2. Круглая катушка с 450 витками и радиусом 8 см размещена на столе горизонтально.Медленно включается однородное магнитное поле, направленное прямо на провод и перпендикулярное его поверхности, так что напряженность магнитного поля может быть выражена как функция времени как B (t) = 0,01 (Ts ^-2 ) xt. ² . (А) Какова полная ЭДС в катушке как функция времени? (B) В каком направлении течет ток?

Soln. Дан,

B (t) = 0,01 (Ts ^-2 ) x t ²

N = 450

r = 8 см = 0.08 м

A = πr ² = π (0,08 м) ² = 0,02 м ²

Из закона Фарадея,

ε = — N dφ / dt

или, ε = — 450 x d (BA) / dt

или, ε = — 450 x 0,02 м ² x d (0,01 (Ts ^-2 ) x t ² ) / dt

или, ε = — 0,09 x 2t Tm ² / с ²

или, ε = — 0,18т Т / с

(B) Ток будет направлен по часовой стрелке сверху.

Последнее обновление статьи: четверг, 30 сентября 2021 г.

Уравнения Максвелла: Закон Фарадея

Третье уравнение Максвелла

На этой странице мы объясним значение третьего уравнения Максвелла, Закон Фарадея , который дан в уравнении [1]:

		[Уравнение 1]

Фарадей был ученым, экспериментировавшим с цепями и магнитными катушками еще в 1830-е гг.Схема его эксперимента, которая привела к закону Фарде, показана на рисунке 1:

Рисунок 1. Экспериментальная установка для Фарадея.

Сам эксперимент несколько прост. Когда аккумулятор отключен, у нас нет электрического тока, протекающего по проводу. Следовательно, нет магнитного поток, индуцированный внутри Железа (Магнитного Ядра). Железо похоже на шоссе для Магнитные поля — они очень легко проходят через магнитный материал. Итак, цель сердечника состоит в том, чтобы создать путь для потока Магнитного потока.

Когда переключатель замкнут, электрический ток будет течь внутри провода. прикреплен к аккумулятору. Когда этот ток течет, он имеет связанный магнитный поле (или магнитный поток) с ним. Когда проволока наматывается на левую сторону магнитный сердечник (как показано на рисунке 1), магнитное поле (магнитный поток) индуцируется внутри ядра. Этот поток движется по сердцевине. Итак, магнитный поток произведенная проводной катушкой слева существует внутри проводной катушки справа, который подключен к амперметру.

Теперь происходит забавная вещь, которую заметил Фарадей. Когда он замкнул выключатель, тогда ток начнет течь, и амперметр подскочит в одну сторону (скажем, измерение +10 ампер с другой стороны). Но это было очень кратко, и ток на правая катушка пошла бы в ноль. Когда переключатель был открыт, измеренный ток будет скачок на другую сторону (скажем, будет измерено -10 ампер), а затем измеренный ток на правой стороне снова будет равен нулю.

Фарадей понял, что происходит.Когда переключатель был первоначально изменен от открытого к закрытому магнитный поток внутри магнитопровода увеличивался от нуля до некоторого максимального числа (которое было постоянным значением в зависимости от времени). Когда поток увеличивался, на противоположной стороне существовал наведенный ток. боковая сторона.

Точно так же, когда переключатель был открыт, магнитный поток в сердечнике уменьшился бы. от его постоянного значения до нуля. Следовательно, уменьшающийся поток в пределах сердечник индуцировал противоположный ток на правой стороне.

Фарадей выяснил, что изменяющийся Магнитный поток внутри контура (или замкнутого контура провода) создавал наведенную ЭДС или напряжение в цепи. Он написал это как:

		[Уравнение 2]

В уравнении [2] — магнитный поток внутри цепи, а ЭДС — это электродвижущая сила, которая в основном источник напряжения. Уравнение [2] говорит, что индуцированное напряжение в цепи противоположна скорости изменения магнитного потока во времени.Для получения дополнительной информации о производных финансовых инструментах см. страница частных производных.

Уравнение [2] известно как Закон Ленца . Ленц был тем парнем, который понял минус подписать. Мы знаем, что электрический ток порождает магнитное поле, но благодаря Фаради мы также знаем, что магнитное поле внутри петли порождает электрическому току. Вселенная любит симметрию, и уравнения Максвелла много этого.

Вывод закона Фарадея

Теперь у нас есть экспериментальный результат уравнения [2], как нам выйти из этого привести к стандартной форме закона Фарде в уравнении [1]? Ну, я рад вы спрашивали.Представим простой цикл с изменяющимся во времени полем B внутри:

Рис. 1. Проволочная петля с плотностью магнитного потока B (t) внутри нее.

Мы знаем, что скорость изменения полного магнитного потока равна противоположной ЭДС , или электрическая сила внутри провода. Полный магнитный поток представляет собой просто интеграл (или сумму) поля B по площади, ограниченной проводом:

		[Уравнение 3]

Чтобы найти общее ЭДС , индуцированное по всей цепи, мы суммируем по длине провода EMF создавалось в каждой точке.Это известно как линейный интеграл. Это записывается как:

		[Уравнение 4]

Напомним, что Электрическое поле напрямую связано с силой электрических зарядов. Напряжение также определяется как сумма (интеграл) электрического поля на пути. [напомним, что электрическое поле измеряется в вольт / метр]. Следовательно, E-поле есть фактически пространственная производная напряжения (E-поле равно скорости изменения напряжения по отношению к расстоянию).Эти факты резюмируются следующим образом:

		[Уравнение 5]

Следовательно, уравнения [4] и [5] говорят нам, что дифференциальная величина ЭДС в любой точке цепи ( dEMF в [4]) равна E поле в этом месте. Следовательно:

		[Уравнение 6]

Теперь некий математик по имени Стокс выяснил, что интегрирование (усреднение) поля вокруг петли в точности эквивалентно интегрированию завиток поля внутри петля.Это должно быть для вас чем-то вроде интуитивной истины: завиток — это мера вращения поля, поэтому ротор векторного поля внутри поверхность должна быть связана с интегралом поля вокруг петли, которая охватывает поверхность. Если это не имеет смысла, подумайте об этом больше или просто примите следующее как правда (потому что это правда — не только для полей E , но и для любого поля):

		[Уравнение 7]

Теперь мы почти у цели.Если мы заменим закон уравнения Фарде [2] на термины, которые мы нашли в уравнении [3] и уравнении [7], то получаем:

		[Уравнение 8]

В уравнении [8] отметим, что если у нас есть два интеграла по поверхностям, а поверхности могут быть какими бы они ни были, тогда интегрируемые величины также должны быть таким же. И вот так мы получили закон Фарадея в окончательной форме: внесены в список уравнений Максвелла!

Толкование закона Фарде

Закон Фарадея показывает, что изменяющееся магнитное поле внутри петли порождает на индуцированный ток, который возникает из-за силы или напряжения в этой цепи.Тогда мы можем сказать следующее о законе Фардея:

Электрический ток вызывает магнитные поля. Магнитные поля вокруг цепь порождает электрический ток.

Магнитное поле, изменяющееся во времени, вызывает циркуляцию электрического поля. вокруг него.

Циркулирующее электронное поле во времени вызывает изменение магнитного поля во времени.

Закон Фардея очень силен, поскольку он показывает, насколько Вселенная любит симметрию. Если ток вызывает магнитное поле, то магнитное поле может вызвать электрическому току.А изменяющееся E-поле в космосе порождает изменяющееся B-поле. во время. И когда мы перейдем к окончательному из уравнений Максвелла, Ампера Закон, мы увидим еще больше этой симметрии!

---

Уравнения Максвелла

Эта страница закона индукции Фарде защищена авторским правом, в частности все отношения с уравнениями Максвелла. Авторские права www.maxwells-equations.com, 2012.

Государственный закон Ленца и кратко объясните.

Вопрос:

Изложите закон Ленца и кратко объясните.

Закон Фарадея

Закон Фарадея — одно из уравнений электромагнетизма Максвелла. Он связывает существование электрического поля с изменением во времени магнитного потока через поверхность. Закон Фарадея в его целостной форме устанавливает:

{eq} \ varepsilon_ {ind} = \ displaystyle \ oint_ {C} \ vec {E} \ cdot d \ vec {l} = — \ dfrac {d \ Phi_B} {dt} {/ eq},

, где {eq} \ Phi_B = \ displaystyle \ int_S \ vec {B} \ cdot d \ vec {S} {/ eq} — магнитный поток через поверхность {eq} S {/ eq} и {eq} C {/ eq} — это путь, охватывающий поверхность.Фарадей экспериментально продемонстрировал этот закон, замыкая круг возможных источников возникновения электрического поля: электрические заряды и изменяющиеся во времени магнитные поля .

Ответ и пояснение: 1

В краткой форме закон Лена гласит:

Направление любого эффекта магнитной индукции таково, что оно противостоит причине, которая его порождает .

Закон Ленца — это просто другой взгляд на условные обозначения знаков, используемый в законе Фарадея, хотя и очень полезный, обеспечивающий глубокое понимание физического явления индукции.

Чтобы исправить идеи, давайте рассмотрим проводящую петлю с постоянной площадью {eq} A {/ eq} и перпендикулярное переменное магнитное поле. Магнитный поток через петлю равен,

{eq} \ Phi_m = B (t) A {/ экв}.

Изменение магнитного потока во времени составляет,

{eq} \ dfrac {d \ Phi} {dt} = A \ dfrac {дБ (t)} {dt} {/ экв}.

Если магнитное поле растет, увеличивается и магнитный поток. Это наше дело. В результате в контуре появляется наведенная ЭДС, создающая ток, который противодействует увеличению магнитного потока.Индуцированный ток создает индуцированное магнитное поле, которое уменьшает поток через петлю. ЭДС, ток и индуцированное поле — все это эффекты. Этот результат можно распространить на любую ситуацию, когда магнитный поток изменяется во времени.

закон Ленца | Что такое, история, формула, приложения, пример, кто это предложил

Физика

Закон Ленца , также называемый законом Ленца-Фарадея, используется в электромагнетизме и позволяет определять направление индуцированного тока. Это можно сформулировать следующим образом: изменение состояния электромагнитной системы вызывает явление, эффекты которого имеют тенденцию противодействовать этому изменению . Генрих Фридрих Ленц, физик немецкого происхождения, в 1834 году предположил, что индуцированные напряжения будут противодействовать чувству изменения, создаваемому магнитным потоком, который их производит, с целью создания закона, по которому рассматривается сохранение электрической энергии.

Что такое закон Ленца?

Закон Ленца связан с электромагнитной областью , поскольку его подход основан на соотношении изменений или напряжений, вызванных изменениями свойств магнитного потока, из которых эти изменения представлены в направлении, противоположном потоку, который их производит.В честь своего создателя закон Ленца носит его фамилию. Физик Генрих Ленц сформулировал его в начале 19 века с целью сохранения энергии.

О законе Ленца

Цель закона Ленца — предсказать направление электродвижущей силы, генерируемой в электрической цепи. Это происходит из-за того, что генерируемая электродвижущая сила (или направление тока) такова, что ее магнитные последствия противодействуют или отталкивают изменение потока магнитного поля, в котором оно создается.

Этот магнитный поток нарастает по спирали, и обнаруживается электрический ток, который может генерировать магнитное поле с отрицательным магнитным потоком, которое постепенно уменьшается с увеличением первоначального провисания.

Кто предложил закон Ленца?

Закон Ленца так назвал тот, кто его создал, Генрих Фридрих Ленц , физик немецкого происхождения, изучавший химию и физику . Этот ученый сначала сосредотачивается на изучении климатических условий, до 1831 года, когда он решает сосредоточиться на изучении электромагнетизма, внося наиболее значительный вклад за всю свою карьеру: «Чувство токов или наведенной электродвижущей силы таково, что оно всегда в противоположность причине, которая его порождает, то есть изменению потока ».

Таким образом, это завершает теорию, представленную Фарадеем, в одной из наиболее важных ассоциаций с развитием физики.

История

Генрих Фридрих Ленц на протяжении своей карьеры посвятил себя области физики и химии, став профессором, а затем ректором Университета и Академии наук города Санкт-Петербурга. Вначале он изучал эффект Пельтье , проводимость металлов и изменение электрического сопротивления в зависимости от температуры.Ленц изучает электропроводность , а затем он обнаруживает, что представляет собой эффект Джоуля в настоящее время, добиваясь на его основе изучения независимости электрических колебаний , в обмене опытом и выводами, которые позволяют ему хорошо сформулировать -известен закон Ленца 1834 г. . Таким образом, Ленц вносит свой вклад в важный прогресс в электромагнетизме, позволяя определять смысл и направление изменения потоков энергии.

Формула

Закон Ленца математически выражается следующим образом:

• E означает ЭДС (электродвижущая сила).
• N — количество спиралей.
• ∆ϕ представлен на веберах и представляет поток магнитной индукции.
• ∆t представляет время, выраженное в секундах.

Следует отметить, что знак — указывает на то, что полярность напряжения такова, что оно противодействует причине, вызвавшей его.

Применение Закона Ленца

Генераторы переменного тока — это устройства, вырабатывающие переменные электрические токи, отсюда и их название.Они состоят из двух основных элементов: ротора, который заставляет все вращаться, и статора, который окружает предыдущий и вращается вокруг своей оси. Эти генераторы переменного тока вырабатывают переменный ток с целью использования в двигателях, вырабатывающих, в свою очередь, механическую энергию, начиная с электрической энергии; с помощью только соединения щеток генератора переменного тока с другим генератором.