Уравнения кирхгофа онлайн калькулятор
Построение и преобразование схемы к двухконтурной
| Шифр студента:12 | |||
| Номер ветви | Начало-конец | Сопротивление | Источники |
| ЭДС | Тока |
Построим схему соединений ветвей цепи по заданным точкам.
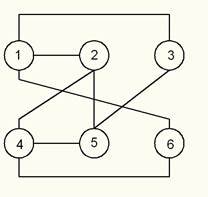
Рис 1.1.1 – Схема соединения ветвей
Развернем схему ветвей, для составления принципиальной схемы:
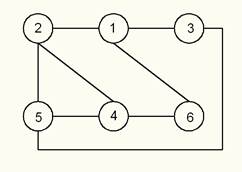
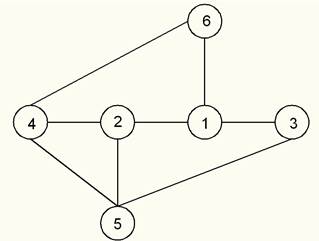
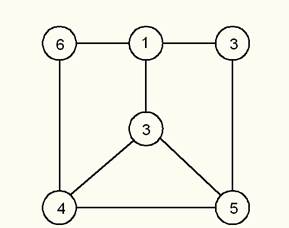
Рис 1.1.2 – Принципиальная схема (а, б, в)
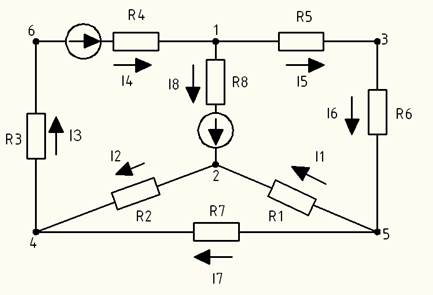
Рис 1.1.3 – Принципиальная схема с обозначенными ЭДС
Упростим схему, заменив последовательно соединённые резисторы R6 и R5 резистором R65, резисторы R4 и R3 сопротивлением R43 (Рис 1.1.4).
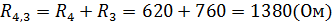
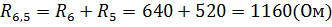
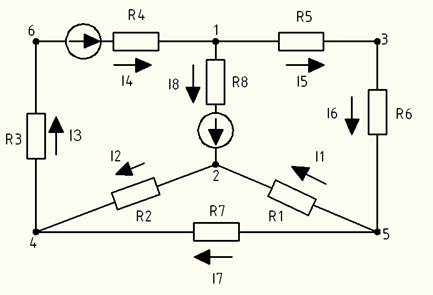
Рис 1.1.4 – Упрощенная схема
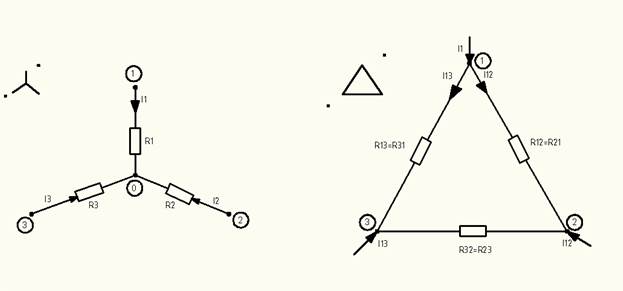
Рис 1.1.5 – Преобразование звезда – треугольник
Преобразуем участок цепи соединённый в треугольник в эквивалентное соединение звездой:
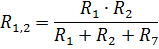
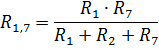
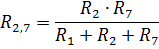
Подставим числовые значения:
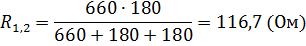
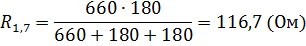
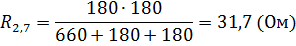
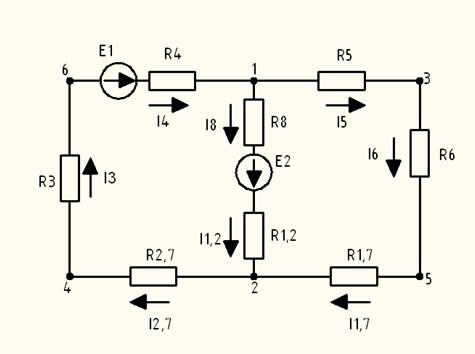
Рис 1.1.6 – Схема после преобразования звезды в треугольник
Метод свертывания
Постепенно упрощая схему преобразуем ее к двухконтурной. Преобразуем участок цепи соединённый в треугольник в эквивалентное соединение звездой:
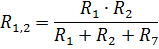
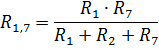
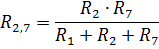
Подставим числовые значения:
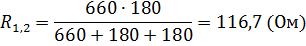
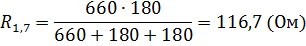
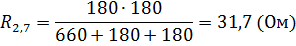
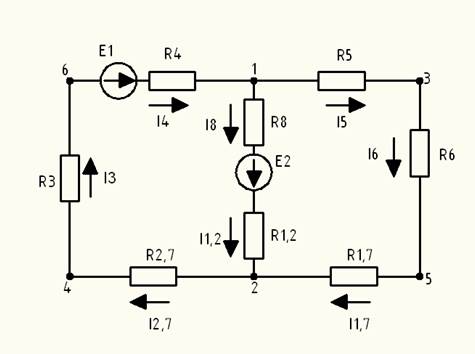
Рис 1.2.1 – Схема после преобразования треугольник-звезда
Перечертим схему, обозначим направление движения контурных токов.
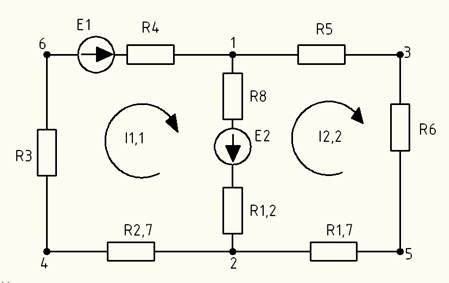
Рис 1.2.2 – Контурные токи на схеме
Заменим последовательно подключенные резисторы на им эквивалентные.
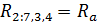
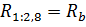
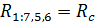
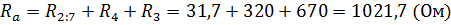
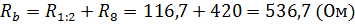
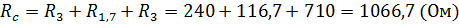
С 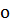 ставим систему уравнений
ставим систему уравнений
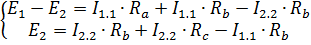
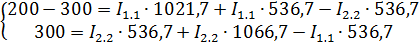
Теперь можем составить уравнения для нахождения токов I1.1 и I2.2
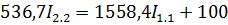
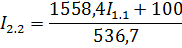
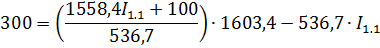
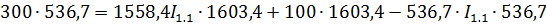
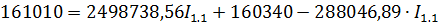
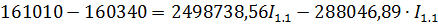
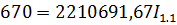
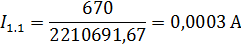
Решим систему методом подстановки, вычислим I2.2;
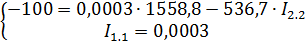
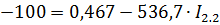
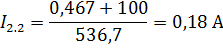
Т.к. через Rc проходит 2 тока направленные противоположно друг другу I1.1 и I2.2, то I8=I1.1-I2.2
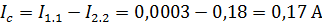
Составим уравнения для нахождения оставшихся токов:
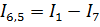
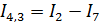
Р 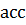 читываем проводимость каждой ветви по формуле единица разделить на сумму всех сопротивлений ветви и определяем напряжение между двумя узлами, в эту формулу Е входит со знаком “плюс” если она направлена к узлу А, и со знаком “минус”, если от узла.
читываем проводимость каждой ветви по формуле единица разделить на сумму всех сопротивлений ветви и определяем напряжение между двумя узлами, в эту формулу Е входит со знаком “плюс” если она направлена к узлу А, и со знаком “минус”, если от узла.
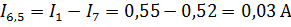
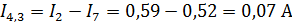
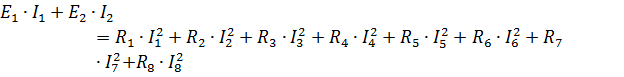
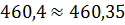
Расчет электрической цепи методом уравнений Кирхгофа.
Первое правило Кирхгофа: В узлах электрической схемы алгебраическая сумма токов всегда равна 0. Ток, втекающий в узел считается положительным со знаком “ +”, а ток вытекающий из узла со знаком “ -”.
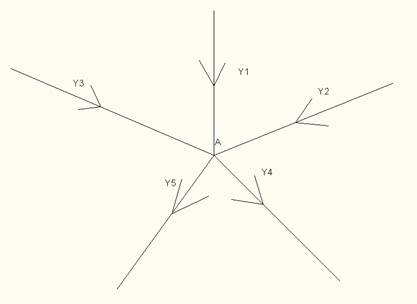
Рис 1.3.1 – Алгебраическая сумма токов в узле
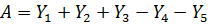
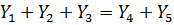
Сумма токов втекающих в узел равна сумме токов вытекающих из узла. Для проверки правильности расчета электрической цепи используют уравнения баланса мощностей. Мощность, отдаваемая источником тока равна сумме мощностей всех потребителей электрической цепи.
Второе правило Кирхгофа: Алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех элементах цепи в замкнутом контуре.
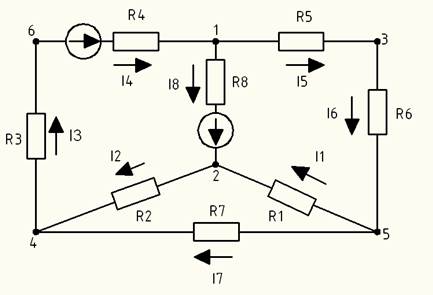
Рис 1.3.2 – Исходная схема
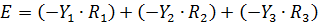
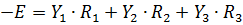
Для расчета электрической цепи содержащей несколько источников ЭДС составляют систему уравнений, используя первое и второе правило Кирхгофа.
у- количество узлов в схеме.
По первому правилу Кирхгофа составляем (у-1) – уравнений
с – количество ветвей в цепи.
По второму правилу Кирхгофа составляем с-(у-1) – уравнений.
1. Нарисуем нашу схему, расставив направление токов в ветвях.
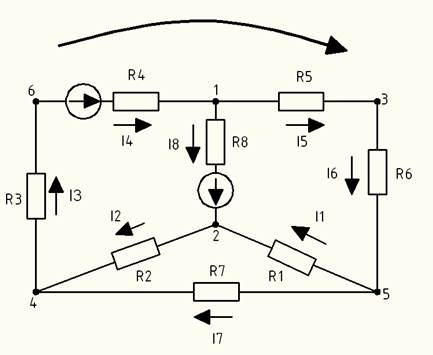
Рис 1.3.3 – Расчетная схема с обозначенными токами
2. По первому правилу Кирхгофа составим уравнения для узлов АВС, так как схема имеет 4 узла, то по формуле “y-1”, где у – количество узлов, мы составим 3 уравнения.
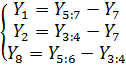
3. Схема состоит из четырех замкнутых контуров. Для решения задачи достаточно составить 3 уравнения по второму правилу Кирхгофа.
Выбираем обход по контуру по часовой стрелке.
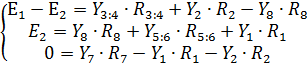
4. Преобразуем и упростим наши уравнения
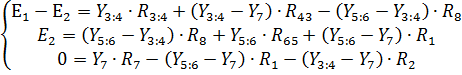
5. Подставим числовые значения в полученные уравнения.
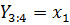
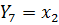
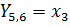
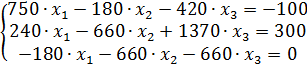
6. У нас получилось 3 неизвестных во всех 3 уравнениях. Для того чтобы решить данную систему мы воспользуемся методом решения матриц.
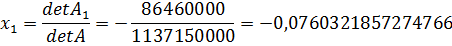
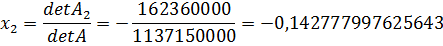
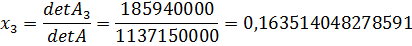
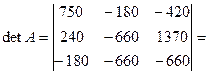
Из элементов столбца 3 вычитаем соответствующие элементы столбца 2.
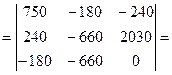
Разлагаем определитель по элементам третьей строки.
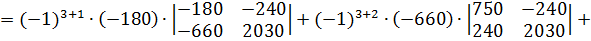
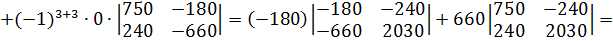
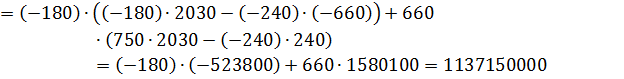
Найдем det A1:
Определитель det A1 получается из определителя det A путем замены первого столбца коэффициентов столбцом из свободных членов.

К элементам строки 2 прибавляем соответствующие элементы строки 1, умноженные на 3.
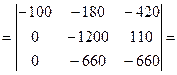
Разложим определитель по элементам первого столбца.
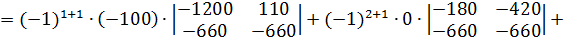
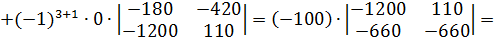
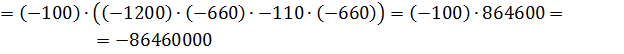
Найдем det A2:
Определитель det A2 получается из определителя det A путем замены второго столбца коэффициентов столбцом из свободных членов.
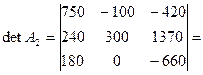
К элементам строки 2 прибавляем соответствующие элементы строки 1, умноженные на 3.
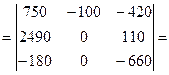
Разложим определитель по элементам второго столбца.
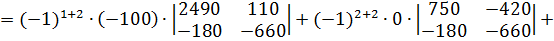
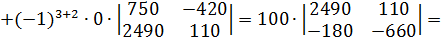
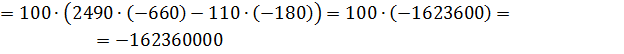
Найдем det A3:
Определитель det A3 получается из определителя det A путем замены третьего столбца коэффициентов столбцом из свободных членов.
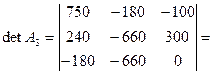
К элементам строки 2 прибавляем соответствующие элементы строки 1, умноженные на 3.
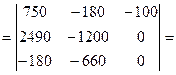
Разложим определитель по элементам третьего столбца.
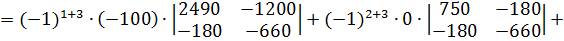
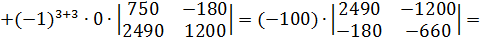
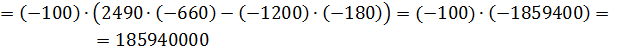
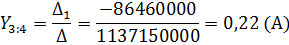
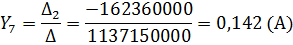
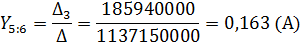
7. Найдя значения 3 переменных, по первому закону Кирхгофа найдем токи на наших сопротивлениях.
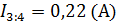
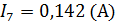
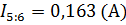
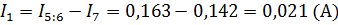
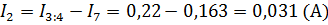
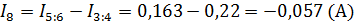
8. Расчетные значения величины токов, полученные данным методом, соответствуют значениям полученным предыдущими методами.
Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системы линейных уравнений c l неизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.)
Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными.
Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:
Выбирают положительные направления токов в ветвях электрической цепи.
Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.
Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.
Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.
Решают систему из (l-m) линейных уравнений любым удобным способом.
На рисунке изображена схема сложной электрической цепи, содержащей 4 узла и 6 ветвей (k=4, l=6). Для расчета цепи необходимо составить систему из 6 линейных уравнений. Предварительно выберем направления токов в каждой из ветвей. По первому закону Кирхгофа составляем 3 уравнения (k-1=4-1=3), например для узлов A, B и C. Вместо любого из этих узлов для составления уравнения можно взять узел D, на результат расчетов это не повлияет. Оставшиеся 3 уравнения (l-k+1-m=6-4+1-0=3) придется составлять по второму закону Кирхгофа ()
Подставляем известные значения
Решаем получившуюся систему.
Получаем ответы в матричном виде.
12. Метод контурных токов.
В данном методе расчета полагают, что в каждом контуре протекает свой контурный ток. Контурные токи и принимают за неизвестные, находят их, и уже затем через контурные токи определяют токи в ветвях. Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, количество неизвестных можно существенно сократить, включая источники в разные контура. В таких схемах применение этого метода наиболее рационально. Число неизвестных в данном методе равно количеству уравнений, которые необходимо было бы составить по второму закону Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока.
Алгоритм расчета цепи методом контурных токов.
Определяем общее число ветвей p*
Определяем число ветвей с источниками тока pит.
Определяем число ветвей с неизвестными токами p*-pит
Определяем число контуров, необходимое и достаточное для определения всех неизвестных токов m= p*-(q-1).
Произвольно наносим на схему номера и направления неизвестных токов.
Обозначаем на схеме контура и выбираем направления их обхода. Необходимо, чтобы каждая ветвь входила хотя бы в один из обозначаемых контуров. При этом ветви с источниками тока обязательно включаем, но каждую в свой контур. Токи данных контуров считаем известными и равными токам источников – таким образом, число неизвестных сокращается.
Записываем выражения для токов в ветвях через контурные токи. Контурные токи в ветвях, не являющихся смежными, и будут истинными токами. Для ветвей, входящих в несколько контуров (смежных ветвей) истинный ток будет являться суммой либо разностью контурных токов данных контуров. При этом те контурные токи, которые совпадают по направлению с током в ветви, берем со знаком плюс, а те, направления которых противоположны – со знаком минус. Определяем собственные сопротивления контуров как сумму всех сопротивлений, входящих в контур (только для контуров без источников тока). Эти сопротивления обозначаются двойным повторяющимся индексом: и т.д.
Определяем сопротивления смежных ветвей и их знаки: плюс – если контурные токи сонаправлены в данной ветви, и минус, если их направления встречны. Эти сопротивления обозначаются двойным индексом, цифры которого указывают номера смежных контуров и т.д.
Аналогично определяем сопротивления ветвей, являющихся смежными с контурами, содержащими источники тока.
Определяем суммарную ЭДС контура (также обозначается двойным повторяющимся индексом — и т.д.). Это алгебраическая сумма ЭДС, входящих в данный контур, причем со знаком плюс берут те ЭДС, направления которых совпадают с выбранным направлением обхода, и наоборот, со знаком минус те, что направлены встречно.
Записываем систему уравнений по форме, приведенной ниже:
Решаем данную систему относительно контурных токов.
Определяем токи в ветвях, подставляя контурные токи в выражения п. 7
Найти токи в схеме рис. 35 с применением метода контурных токов.
Дано:
1.2.1.1. Топология цепи.
Определяем общее число ветвей: p*=5
Определяем число ветвей с источниками тока: pит=1.
Определяем число ветвей с неизвестными токами: p*- pит=4.Количество узлов – 3
Определяем необходимое и достаточное число контуров: 3
Произвольно наносим на схему номера и направления неизвестных токов (рис. 36)
Определяем собственные сопротивления контуров (для контуров без источников тока):
Определяем сопротивления смежных ветвей и их знаки:
Аналогично определяем сопротивления ветвей, являющихся смежными с контуром, содержащим источник тока:
Определяем суммарную ЭДС контуров:
Записываем систему уравнений по форме:
Если произвести подстановку сопротивлений, то видно, что данная система полностью совпала с системой, полученной в п. 7:
Решаем данную систему относительно контурных токов:
Определяем токи в ветвях, подставляя контурные токи в выражения п. 7
В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.
Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.
Здесь ток I1— ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I 3 в левую часть выражения (1), тем самым получим:
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Расчеты электрических цепей с помощью законов Кирхгофа.
Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.
Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E1=12 в и E2=5 в , с внутренним сопротивлением источников r1=r2=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.
Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:
так как I1 и I 2 втекают в узел А , а ток I вытекает из него.
Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.
Для внешнего контура:
Для внутреннего левого контура:
Итак, у нас получилась система их трех уравнений с тремя неизвестными:
Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:
12 = 0,1I1 +2I.
Далее из первого и второго уравнения выразим ток I2
12 = 0,1I1 + 2I.
Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:
12 = 0,1I1 + 2I.
Выражаем из первого уравнения значение I
I = 2I1– 70;
И подставляем его значение во второе уравнение
Решаем полученное уравнение
12 = 0,1I1 + 4I1 – 140.
12 + 140= 4,1I1
Теперь в выражение I = 2I1– 70 подставим значение
I1=37,073 (А) и получим:
I = 2*37,073 – 70 = 4,146 А
Ну, а согласно первому закона Кирхгофа ток I2=I — I1
I2=4,146 — 37,073 = -32,927
Знак «минус» для тока I2 означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I 2 вытекает из узла А .
Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.
Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.
 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Для закрепления результатата предлагаю посмотреть подготовленное мной видео:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Второй закон Кирхгофа — третий кит электротехники
 Удивительно не то, как просто всё рассчитывается, когда знаешь два понятных всем правила расчёта — первый и второй Законы Кирхгофа, а то, как гениально это было придумано.
Удивительно не то, как просто всё рассчитывается, когда знаешь два понятных всем правила расчёта — первый и второй Законы Кирхгофа, а то, как гениально это было придумано.
Ведь не было тогда бытовой электрической сети. Куда просто вкрутил лампочку, нажал выключатель, и всё — заработало напряжение, побежал ток, разогрелась спираль лампочки и засиял свет. Вот она, понятная работа электричества. Её нам сейчас ничуть не труднее осознать, чем бурчание воды в отоплении или гудение воздуха в инструменте трубача.
Закон Ома — первый кит электротехники
А когда Георг Симон Ом, изучая гальванические, как тогда называли, цепи, вывел своё простейшее соотношение, этого понять не мог никто, кроме немногих посвящённых. Просто потому, что обыденный мозг тогда сразу упирался в нечто невообразимое, а значит, непреодолимое: что это за течение такое, ток частиц, которых не то что пощупать, но и представить нельзя ввиду абсолютно исчезающей малости. Да ещё «текущих» в металле, твёрдом предмете. Уж не то, что попытаться составлять какие-либо точные формулы.
Теперь это соотношение кажется простым и ясным, как удар молнии. Видимо, он сумел почувствовать это явление — электрическое напряжение. Если цепь разомкнута, то тока ещё никакого нет, ничего не нагревается и не пузырится (как вода под током), а напряжение вот оно — попробуй, тронь! Видимо, как-то сумел гений потрогать и попробовать.
Собственно, вся любая электрическая цепь и описана законом Ома. Источник, дающий напряжение и нагрузка, подставляющая напряжению своё тело, отчего получается электрический ток. Соотношение простейшее — чем больше напряжение, тем больше ток. А конкретно каким он получится, определяет пропускная способность нагрузки, G, или проводимость.
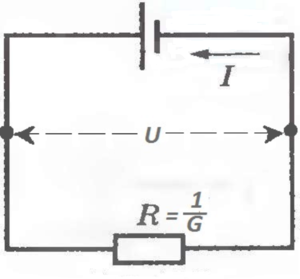 I=U*G
I=U*G
Удобнее и нагляднее оказалось вместо проводимости пользоваться понятием сопротивления, R, величиной обратной проводимости (R=1/G).
И обозначения на первой электросхеме самые простейшие: прямоугольничек — нагрузка, две линии поперёк тока — батарейка.
Самая первая электрическая схема
Видимо, и подключали поначалу что-то одно к чему-то одному. Но вот и эта схема «под напором реальности» усложняется. Во-первых, сама батарейка имеет сопротивление.
Как это изобразить, вот так? 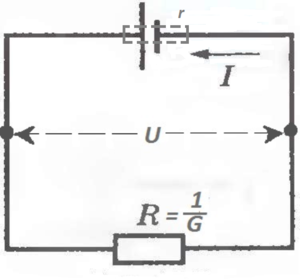
Некрасиво.
Лучше располагать рядом так:
Есть искушение поставить этот прямоугольничек на другую сторону, рядом с нагрузкой, а нельзя, всё-таки батарейка и её внутреннее сопротивление — одно нераздельное физическое устройство.
Чтобы видеть действие тока, лучше в качестве нагрузки
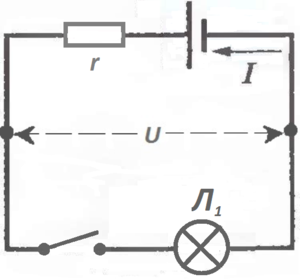
Мы получили последовательную цепочку.
Ток во всех её частях обязан быть одним и тем же, то есть одинаковый везде.
Это логично, и если включить выключатель, лампочка сразу загорится.
При этом никто и не задумывается, что если у нас через лампочку течёт ток всего в один ампер, то это значит, что каждую секунду через неё пробегает:
6 квинтиллионов 241 квадриллион 509 триллионов 125 миллиардов 493 миллиона 690 тысяч с небольшим электронов.
И все они вышли из небольшой батареечки и в неё же и вернутся с другой стороны.
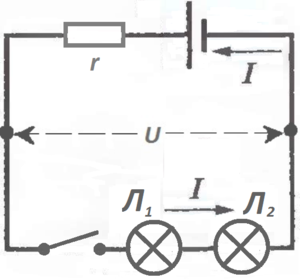
Если поставить вместо одной лампочки две одинаковых, то они загорятся вполнакала, то есть ток I, протекающей последовательно из батарейки через выключатель сначала в лампочку Л1, потом в лампочку Л2 и снова в батарейку, станет меньше, чем был, когда стояла одна лампочка.
Это значит, что сопротивление стало больше: было R у одной лампочки, стало R+R, то есть 2R.
Токи и напряжения в сети
Точную величину тока можно подсчитать, если применить закон Ома ко всей нашей цепи, общее сопротивление которой есть сумма сопротивлений всех её нагрузок.
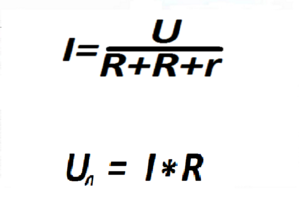
(1) А если оставить в формуле сопротивление только одной лампочки, то, зная, что ток у нас везде один и тот же, можно вычислить напряжение Uл конкретно для этого потребителя, лампочки.
Это напряжение, которое падает именно на нашу лампочку, так и называется «падение напряжения». Оно примерно вдвое меньше нашего напряжения питания U. Примерно — потому что в формуле (1) среди сопротивлений есть ещё небольшой довесок в виде
А теперь взглянем на нашу цепь как на единый контур, который можно обходить по часовой или против часовой стрелки. Ток наш идёт, как нарисовано, против часовой стрелки. Двинемся по этому направлению с любого места и пройдём всё, складываем падения напряжения на всех попадающихся по дороге приборах.
Для токов — узлы, для напряжений — контуры
Получится:
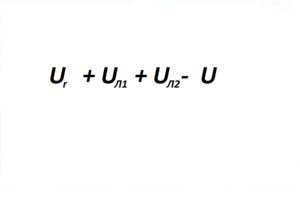
Последним напряжением добавлено то, которое вырабатывается батареей, только со знаком минус, так как оно работает не на потребление, а наоборот, вырабатывается и поставляется в сеть нашей героической батареей. И что у нас получилось?
Правило Кирхгофа для напряжений (2й закон)
А получилось ровно 0. Потому что вся энергия от батареи потребляется лампочками + внутреннее сопротивление батареи. И понятно, это есть высшая справедливость природы. То есть второй закон Кирхгофа в действии.
И вдруг у нас случился… прорыв.
Правило Кирхгофа для токов (1й закон)
К нам в двух точках — А и B — подключились неизвестные, скорее всего, инопланетяне.
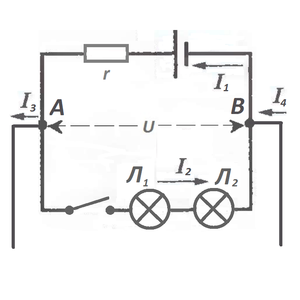
И начали качать от нас энергию. И теперь мы знаем, что ток I3 и ток I4 — не наши, они инопланетянские. И наша схема может быть безнадёжно испорчена.
Но!
А обойдём ка мы контур снова. Может быть, не всё ещё потеряно. И вот:
Ur=I1*r
Uл1=I2*R=Uл2
И, наконец:
U=Uг+Uл1+Uл2.
Потому что I1=I2+I3. И I1=I2+I4.
То есть сколько току вытекло в качестве тока I3 в точке А, столько его и вернулось к нам в точке B в виде тока I4. Высшая справедливость всё-таки восторжествовала. А помогло нам при этом здравое рассуждение, о том, что в любой точке цепи, где электрическая сеть разветвляется, общее количество тока, вытекающего из узла, то есть этой точки, равно количеству тока, втекающего в этот узел. Поэтому смело рисуем схему, зная, что нам помог уже первый, а не второй закон Кирхгофа:
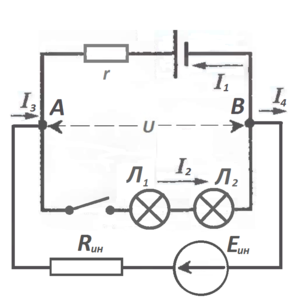 Почему-то оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки загорелись полным накалом.
Почему-то оказалось, что токи I3 и I4 оказались точно равными -I1, и значит… наши лампочки загорелись полным накалом.
Ох уж эти выдумки инопланетянские! С нашей стороны осталось только в схеме поставить стрелочки токов (и ЭДС у источника ЭДС Eин)
Расчёт цепи по законам Кирхгофа интуитивно понятен — правила позволяют рассчитывать электрические цепи, то есть определять все неизвестные параметры — токи, напряжения — любой, сколь угодно замысловатой цепи.
Применение законов Кирхгофа для расчёта сложных цепей
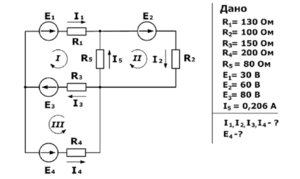
Цепь состоит из ветвей, соединяющихся в узлах. Ветвь — это несколько последовательно соединённых электрических приборов. В узлах могут соединяться три и более ветвей. Это значит, что через узел проходят токи, выходящие из ветвей, которые в нём соединяются.
Ну и теперь, вооружившись проверенными нами базовыми законами электротехники, решим пример, зная, что всё и для любой электрической цепи решаемо.
Смело решаем задачу.
Путь таков:
- Составляются уравнения для токов в узлах — работает первый закон Кирхгофа. Составляются уравнения для падений напряжений по всем независимым контурам — дело второго закона Кирхгофа.
- Уравнения сводятся в систему и решаются методами математики для системы из N линейных уравнений с N неизвестными.
- Делается проверка решения другим способом, например, подсчётом общей мощности сети
Составляем уравнения для токов, втекающих/вытекающих в узлы. Узлов сего три, значит, уравнений будет 3-1, то есть два.
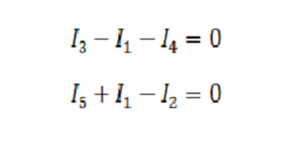
Теперь составляем уравнения для контуров и падений напряжения в них. Контуров у нас независимых три (в которых в каждом есть хотя бы одна ветвь, не встречающаяся в других).
Вот и получается три уравнения по второму закону Кирхгофа: Собрав все пять уравнений вместе, получаем систему из пяти уравнений с пятью неизвестными.
Остальное — дело королевы наук, то есть математики. Такие системы она щёлкает не глядя.
И получаются вполне похожие на правду ответы:
А мы знаем, хорош тот ответ, который поддаётся проверке.
Сделаем-ка мы расчёт мощности, выделяемой на всех устройствах данной схемы при полученной нами картине токов и напряжений двумя способами, пользуясь немного разными определениями для мощности:
- мощность как произведение тока на напряжение
- мощность, как квадрат силы тока, умноженный на сопротивление
Как видим, всё у нас правильно, задача нашего непростого примера решена.
Первое правило Кирхгофа, теория и примеры
При решении задачи нахождения силы токов в участках сложной цепи постоянного тока при известных сопротивлениях участков цепи и заданных электродвижущих силах (ЭДС) часто применяют правила Кирхгофа. Всего их два. Правила Кирхгофа не являются самостоятельными законами. Они всего лишь следствия закона сохранения заряда (первое правило) и закона Ома (второе правило). При любой сложности цепи можно провести все расчеты параметров сети, применяя закон Ома и закон сохранения заряда. Правила Кирхгофа используют для того, чтобы упростить процедуру написания системы линейных уравнений, в которые входят искомые токи.
Формулировка первого правила Кирхгофа
Для формулировки первого правила Кирхгофа определим, что считается узлом цепи. Узел разветвленной цепи -это точка цепи, в которой сходятся три или больше проводников с токами.
Для верной записи формулы первого правила Кирхгофа необходимо принимать во внимание направления течения токов. Следует помнить, что токи, входящие в узел и токи, выходящие из него, записываются в уравнения с разными знаками. Если в задаче направления токов не заданы, то их выбирают произвольно. Если в ходе решения задачи выясняется, что полученный ток имеет знак минус, то это означает, что истинное направление тока является противоположным. При решении задачи, следует решить, какие токи считать положительными, например, выходящие из узла, и тогда все токи в этой задаче записывать в соответствующих уравнениях со знаком плюс.
Математическая запись первого правила Кирхгофа:
Формула (1) значит, что сумма токов с учетом знаков в каждом узле цепи постоянного тока равна нулю.
Обычно для наглядности и простоты при составлении уравнений на схемах указывают направления течения, выбирая их произвольно.
Первое правило Кирхгофа иначе называют правилом узлов.
Это правило следствие закона сохранения электрического заряда. Сумма токов (с учетом их знаков), которая сходится в узле — это заряд, проходящий через данный узел в единицу времени. Если токи в узле не зависят от времени, то их сумма должна быть равна нулю, в противном случае, потенциал узла будет изменяться со временем, соответственно токи будут переменными. Если ток в цепи постоянный, то в цепи не может быть точек, которые бы накапливали заряд. Иначе токи будут изменяться во времени.
Используя только одно первое правило Кирхгофа не получится составить полную систему независимых уравнений, которых было бы достаточно для решения задачи нахождения всех сил токов, которые текут во всех сопротивлениях цепи при известных ЭДС и сопротивлениях. Для написания дополнительных уравнений используют второе правило Кирхгофа.
Примеры решения задач
|
Закон токов Кирхгофа |
Закон напряжений Кирхгофа |
Алгебраическая сумма токов в любой точке любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком) ΣIi = I1+I2+ …+In = 0 Иными словами, сколько тока втекает в точку цепи ( на практике используют узел — см. выше), столько из нее и вытекает (из узла и вытекает). Сколько дает уравнений: Если цепь содержит p узлов, то она описывается p-1 независимыми уравнениями токов относительно узлов. Удобно считать входящие токи положительными, а выходящие отрицательными. |
Алгебраическая сумма падений напряжений по любому ЗАМКНУТОМУ контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю. (Если направление тока совпадает с направлением обхода контура, перепад напряжения считается положительным, в противном случае — отрицательным). если в замкнутом контуре k штук ЭДС и n проводников , то: E1+E2+ …+Ek = U1+U2+ …+Un = I1R1+I2R2+ …+InRn Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Сколько дает уравнений: Если цепь содержит n ветвей, из которых k содержат источники тока (ЭДС) и p узлов , то она описывается n-k-(p-1) независимыми уравнениями напряжений относительно узлов. ( т.е. на практике в расчетах опираются на узлы, а не на что попало) |



