Магнитное поле электрического тока. Правило буравчика

Вы уже знаете, что вокруг проводника с током существует магнитное поле. Исследуем это поле с помощью железных опилок. Для этого проводник пропустим через лист картона перпендикулярно его поверхности, насыплем на картон железные опилки и пустим через проводник электрический ток. В магнитном поле проводника опилки намагнитятся и воссоздадут картину линий магнитной индукции магнитного поля прямого проводника с током — концентрические круги, охватывающих проводник. А как определить направление магнитных линий?

Знакомимся с правилом буравчика

Расположим рядом с проводником несколько магнитных стрелок и пустим в проводнике ток — стрелки повернутся в магнитном поле проводника. Северный полюс каждой стрелки укажет направление вектора индукции магнитного поля в данной точке, а следовательно, и направление магнитных линий этого поля.

С изменением направления тока в проводнике изменится и ориентация магнитных стрелок. Это означает, что направление магнитных линий зависит от направления тока в проводнике.

Понятно, что определять направление линий магнитной индукции с помощью магнитной стрелки неудобно, поэтому используют правило буравчика: если вкручивать буравчик по направлению тока в проводнике, то направление вращения ручки буравчика укажет направление линий магнитного поля тока.

Или иначе:

Если направить большой палец правой руки по направлению тока в проводнике, то четыре согнутых пальца укажут направление линий магнитного поля тока.

Выясняем, от чего зависит модуль индукции магнитного поля проводника с током

Вспомните: магнитное действие проводника с током первым обнаружил Г. Эрстед в 1820 г. А вот почему это открытие не было сделано раньше? Дело в том, что с увеличением расстояния от проводника магнитная индукция созданного им магнитного поля значительно уменьшается. Итак, если магнитная стрелка расположена не вблизи проводника с током, магнитное действие тока почти незаметно.

Магнитная индукция зависит от силы тока: с увеличением силы тока в проводнике магнитная индукция созданного им магнитного поля увеличивается.

Изучаем магнитное поле катушки с током

Смотайте изолированный провод в катушку и пустим в нем ток. Если теперь вокруг катушки разместить магнитные стрелки, то к одному торцу катушки стрелки вернутся северным полюсом, а ко второму — южным. Итак, вокруг катушки с током существует магнитное поле.

Как и полосовой магнит, катушка с током имеет два полюса — южный и северный. Полюса катушки расположены на ее торцах, и их легко определить с помощью правой руки: Если четыре согнутые пальцы правой руки направить по направлению тока в катушке, то отогнутый на 90 ° большой палец укажет направление на северный полюс катушки, то есть направление вектора магнитной индукции внутри катушки.

Сопоставив магнитные линии постоянного полосового магнита и магнитные линии катушки с током, увидим их удивительное сходство. Отметим: магнитная стрелка, подвешенная катушка с током и подвешен полосовой магнит ориентируются в магнитном поле Земли одинаково.

Подводим итоги

Вокруг проводника с током существует магнитное поле. Магнитная индукция поля, созданного током, уменьшается с увеличением расстояния от проводника и увеличивается с увеличением силы тока в проводнике.

Направление линий магнитной индукции магнитного поля проводника с током можно определить с помощью магнитных стрелок или с помощью правила буравчика.

Катушка с током, как и постоянный магнит, имеет два полюса. Их можно определить с помощью правой руки: если четыре согнутых пальцы правой руки направить по направлению тока в катушке, то отогнутый на 90 ° большой палец укажет направление на ее северный полюс.

Характеристики магнитного поля — fiziku5.ru

Магнитное поле – одна из двух сторон электромагнитного поля, характеризующаяся воздействием на электрически заряженную частицу с силой, пропорциональной заряду частицы и её скорости.

В проводнике с током и вокруг него возникает магнитное поле. Оно может возникать не только вокруг проводников с током, но и при движении любых заряженных частиц и тел, а также при изменении электрического поля.

Свойства магнитного поля:

— оказывает силовое воздействие на движущиеся в нем заряженные тела и на неподвижные проводники с электрическим током;

— способно намагничивать ферромагнитные тела;

— возбуждать ЭДС в проводниках, которые перемещаются в магнитном поле.

Характеристики магнитного поля:

— магнитная индукция В = ;

— магнитный поток Ф = В · S;

— абсолютная магнитная проницаемость

μа = μ0 · μr;

— относительная магнитная проницаемость μr;

— магнитная постоянная μ0

— напряжённость магнитного поля Н = .

Правило буравчика (для прямолинейного проводника): если поступательное движение буравчика совпадает с направлением тока в проводе, то вращение рукоятки буравчика укажет направление магнитных силовых линий.

Правило буравчика для катушки с током: если рукоятку буравчика вращать по направлению тока в витках, то его поступательное движение совпадёт с направлением магнитных линий внутри катушки.

Правило правой руки

(для определения направления ЭДС индукции): если ладонь правой руки нужно расположить так, чтобы магнитные линии входили в неё, а отогнутый под прямым углом большой палец указывал направление движения проводника, то выпрямленные четыре пальца руки укажут направление индуцированной ЭДС.

Правило левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в неё, а четыре выпрямленных пальца совпадали с направлением тока, то отогнутый под прямым углом большой палец укажет направление силы.

10

2. Данные всех приборов и машин занесите в таблицу 1.

I. Снятие характеристики холостого хода

3. После проверки схемы преподавателем, включите схему. Плавно изменяя ток возбуждения Iвозб, с помощью реостата Rрег снять показания амперметра и вольтметра. Данные замеров занесите в таблицу 2.

Таблица 2

№ опыта	Iвозб, А	Евосх, В	Енисх, В
1
2
3
4
5
6
7
8

4. По данным опыта постойте характеристики холостого хода:

 

Е, В

 

Iвозб, А

II. Снятие внешней характеристики

5. Включить двигатель и с помощью реостата Rрег установить на зажимах генератора номинальное напряжение Uн, согласно заданию преподавателя. Плавно увеличивая ток нагрузки Iн, включая поочерёдно соответствующие тумблеры снять показания амперметров и вольтметра. Данные замеров занесите в таблицу 3.

Таблица 3

№ опыта	U, В	Iнагр, А	Iвозб, А
1
2
3

35

В любой машине чётко выделяются подвижная (ротор) и неподвижная (статор) части. Часть машины, в которой индуцируется электродвижущая сила (ротор), называют якорем, а часть машины, в которой создаётся магнитное поле возбуждения (статор) – индуктором.

Работа электрической машины характеризуется взаимодействием двух направленных навстречу друг другу вращающих моментов, один из которых создаётся механическими, а другой – электромагнитными силами. Кроме того, работа двигателя и генератора характеризуется взаимодействием напряжения сети и ЭДС, возникающей в обмотке якоря.

Различают генераторы независимого возбуждения и генераторы с самовозбуждением.

В генераторах независимого возбуждения основной магнитный поток создаётся либо постоянным магнитом, либо электромагнитом (обмоткой возбуждения), питаемым от источника постоянного тока.

В генераторах с самовозбуждением питание обмотки главных полюсов осуществляется напряжением самого генератора. При этом отпадает необходимость в отдельном источнике энергии. В зависимости от схемы включения обмотки возбуждения различают генераторы параллельного, последовательного и смешанного возбуждения.

Основные характеристики генераторов:

·  холостого хода – зависимость ЭДС генератора от тока возбуждения при постоянной частоте вращения якоря и отключённой нагрузке Е = f (Iв);

·  внешняя характеристика – зависимость нагрузки на зажимах генератора от тока нагрузки при постоянной частоте вращения и постоянном сопротивлении цепи возбуждения U = f (I);

·  регулировочная характеристика – зависимость тока возбуждения от тока нагрузки при постоянных частоте вращения и напряжении на зажимах генератора Iв = f (I).

Порядок выполнения работы:

1. Соберите электрическую схему, показанную на рисунке 1.

Рисунок 1.

34

Оборудование:

1. Аккумуляторная батарея

2. Гальванометр

3. Реостат

4. Полосовой постоянный магнит

5. Индукционная катушка с сердечником

Порядок выполнения работы:

I. Проверка законов электромагнитной индукции

1. Вводя в катушку постоянный электромагнит, как показано на рисунке 1, замерьте отклонения стрелки гальванометра и запишите результаты измерений.

Рисунок 1

·  Рис. а) — __________________________________________________________________________________________________________________________________________________________________________________________________________________

·  Рис. б) — __________________________________________________________________________________________________________________________________________________________________________________________________________________

·  Рис. в) — __________________________________________________________________________________________________________________________________________________________________________________________________________________

·  Рис. г) — __________________________________________________________________________________________________________________________________________________________________________________________________________________

11

II. Изучение явления самоиндукции

2. Изучите явление самоиндукции, используя две индукционных катушки, как показано на рисунке 2. Запишите результаты наблюдений.

Рисунок 2

·  Рис. а) — ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

·  Рис. б) — ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

28. Магнитное поле. Магнитная индукция. Принцип суперпозиции. Закон Био-Савара-Лапласа. Правило буравчика.

Магнитное поле — особый вид материи, оно порождается проводником с током. Магнитная индукция основная силовая характеристика магн.поля.

Принцип суперпозиции для магнитного поля. Индукция магнитного поля, одновременно создаваемого в некоторой точке пространства несколькими источниками, равна сумме векторов индукций магнитных полей, которые создавались бы в этой же точке каждым из источников по отдельности

З-н Био Савара-Лапласа Правило Буравчика – если Буравчик ввинчивать по направлению тока в проводнике то направление движения рукоятки совпадёт с направлением в-ра магнитной индукции.

29. Расчет магнитного поля прямолинейного проводника с током. Расчет магнитного по­ля кругового проводника с током.

Индукция магнитного поля прямолин. проводн. ,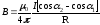

Индукция магнитного поля на оси кругового проводника с током.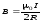

30. Закон Ампера. Взаимодействие двух проводников с током. Единица силы тока — Ампер.

(сила, действующая со стороны магнитного поля на элемент с током) .

Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную 210^–7 Н на каждый метр длины

31. Магнитный момент витка с током. Магнитное поле движ-я электрического заряда.

Магнитным полем наз одна из форм проявления электромагнитного поля. Магнитное поле дейсвует только на движущиеся электрически заряженные частицы и тела, на проводники с током и на частицы и тела, обладающие магнитными моментами

32. Закон полного тока для магнитного поля в вакууме. Магнитное поле внутри соленои­да и тороида.

Циркуляция в-ра магн. индукции по проводн замкн. контура угла = произ-ю магнитн пост на алгебраич сумму токов, пронизыв контур.

соленоида и тороида

33. Действие магнитного поля на движущийся электрический заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле.

Магнитн поле оказ воздейств не только на пров-ки и на свободн эл заряды движ в этом поле.

Сила Лоренца (сила, действующая со стороны магнитного поля на движущийся заряд) .

Правило левой руки.

Если расположить ладонь так чтобы в нее вход силовые линии поля, а 4 пальца – по направлению скор полож заряда (против в-ра скорости для отриц зарядов) Большой палец пакажет направл силы Л.

Зависит от угла. 1)Вдоль а=0 F=0 2)Перпенд. a=п/2 3)п>a>0 Движ по спирали

34. Эффект Холла. Мгд-генератор. Масс-спектрограф. Циклотрон.

Возникновен эл тока в пров-ке /полупр с током помещ в магн поле, в-р индукц перп в-ру пл-ти тока

. МГД-генератор Находит применение в методе преобр внутр энерг ионизир газа в электр энергию

спектром масс частиц наз совокупность значений их масс. Весьма точно измеряют массы и относительные концентрации различных изотопов химических элементоа.

Для ускорения протонов, дейтронов и других более тяжелых частиц применяются резонансные циклические ускорители, в которых частица многократно проходит через переменное электр поле, каждый раз увеличивая свою скорость.Простейшим резонанс цикличес ускорителем – циклотрон.

Правило буравчика для определения направления магнитного поля

Далеко не все явления в нашей жизни мы можем увидеть, хотя используем их постоянно. Например, электрический ток и магнитное поле. Если к току, как к явлению, мы более-менее привыкли, с магнитными полями не очень легко разобраться. О том, что это такое и как правило буравчика позволяет определить его направление и поговорим.

Содержание статьи

Что такое магнитное поле

Все, наверное, знают что такое постоянные магниты — они «липнут» к железу и некоторым другим материалам. Если приблизить два магнита, то они будут притягиваться или отталкиваться — в зависимости от того, как мы их повернем друг относительно друга. Почему и за счет чего так происходит? За счет того, что вокруг магнитов создается магнитное поле. Оно возникает при движении заряженных частиц. Например, вокруг провода, по которому протекает электрический ток, есть магнитное поле. Оно слабое, но оно есть.

Магнитное поле нельзя увидеть, но можно ощутить

Постоянные магниты

Как же тогда с магнитами? Откуда в них магнитное поле, ведь в них нет направленного движения частиц? Все просто. В них магнитное поле создается зарядами частиц. Как известно, любой материал состоит из положительно и отрицательно заряженных частиц. В некоторых материалах частицы можно расположить так, чтобы положительные были сконцентрированы с одной стороны, отрицательные — с другой. Эти «две стороны» называют полюсами магнита. Отрицательный — северный, обозначается латинской буквой N и закрашивается обычно синим цветом, положительный называют «южный» и обозначается S, закрашивается в красный цвет.

Постоянные магниты и их виды

Причем, стоит помнить, что однополюсных магнитов не бывает. Всегда есть два полюса. Если есть у вас большой магнит, его можно распилить пополам. И вы получите два магнита меньшего размера с двумя полюсами. Если распилите их — получите еще более мелкие двухполюсные магнитики.

Постоянные магниты можно сделать далеко не из всех материалов. Для этих целей подходят всего три вещества: железо (Fe), никель (Ni) и кобальт (Co). Если их выдержать в магнитном поле, частицы «рассортируются» по полюсам, материал станет магнитом. Но не все будут долго сохранять эти свойства. По способности удерживать магнитные свойства, материалы разделают на магнитомягкие и магнитотвердые материалы. Первые быстро намагничиваются, но и быстро теряют свои свойства. К таким относится железо (не обработанное). Магнитотвердый материал — например, сталь — в магнитном поле надо выдерживать долго. Зато после «выдержки» он становится магнитом на значительный промежуток времени. Можете поэкспериментировать со стальными скрепками.

Что такое магнитное поле

Приближая магниты друг к другу, на некотором расстоянии вы начнете ощущать, как они притягиваются или отталкиваются. Чем ближе подносите, тем сильнее они взаимодействуют. Все потому, что вокруг них существует магнитное поле. И чем ближе к магниту, тем поле сильнее.  Причем выглядит это поле как округлые линии, которые выходят из северного полюса и «заходят» в южный.

Магнитное поле можно представить в виде линий

Почему так решили? А потому что можно эти линии увидеть «вживую». Для этого надо провести эксперимент. На лист фанеры положить магнит, насыпать вокруг мелких металлических опилок и лист фанеры немного потрусить. Металлические опилки расположатся именно так, как показано на рисунке ниже справа. Обратите внимание — чем ближе к магниту, тем опилок больше, чем дальше — тем меньше. Это потому что магнитное поле ослабевает по мере удаления.

Экспериментальное подтверждение: смотрим на магнитное поле и на взаимодействие полюсов

Опилки помогут понять и правила притяжения или отталкивания полюсов. На левом рисунке мы видим что происходит, если приблизить два противоположных полюса. Они притягиваются. Причем когда процесс завершится, картинка будет один в один как та, что справа. Как видите, они даже немного похожи.

Если поднести поближе два одноименных полюса — юг-юг или север-север — они будут отталкиваться. Это демонстрирует средний рисунок. И чем ближе их подносите, тем сильнее будет ощущаться противодействие.

Правило буравчика для магнитных полей

Речь шла о постоянных магнитах. У них все всегда понятно: где какой полюс и куда направлены линии магнитного поля — от северного полюса к южному. Но магнитное поле возникает и вокруг проводников, по которым течет ток. Просто оно слабое, так что даже если поднести два участка, по которым течет ток, особого притяжения или отталкивания мы не ощутим. Чтобы создать сильное электромагнитное поле, проводник накручивают вокруг какого-то сердечника. Это изделие называют соленоидом. Когда по нему течет ток, создается ощутимое магнитное поле. Но как направлены линии магнитного поля в электромагнитах? Где у них северный, где южный полюс? Вот это и выясняют с помощью правила буравчика.

Буравчик можно себе представить как обычный штопор с ручкой-перекладиной и витками, накрученными вправо. Чтобы закручивать такой штопор, ручку надо вращать вправо — по часовой стрелке. При этом острие штопора/буравчика продвигается вниз. Чтобы выкручивать его, надо рукоятку вращать влево — против часовой стрелки. Острие при этом движется вверх.

Правило буравчика для магнитного поля

С движением острия буравчика и направлением вращения рукоятки и связано определение направление магнитного поля. Вот как звучит правило буравчика (еще называют правило винта):

Если направление движения острия буравчика (винта) совпадает с направлением движения тока, то движение рукоятки буравчика укажет направление линий магнитного поля.

С ровными проводниками все просто. Представляете, вкручивать или выкручивать надо буравчик, получаете направление силовых линий. Если по условиям задачи есть только направление линий магнитного поля, при помощи правила буравчика можно установить направление тока. Для этого мысленно представляем, что ручка штопора крутится в указанном направлении. В зависимости от этого, определяем куда движется острие, а, значит, и куда течет ток.

Правило правой руки

Не всегда и не у всех с буравчиком «складывается». Некоторым людям сложно представить, как будет двигаться винт. В этом случае можно попробовать одну из его вариаций: правило правой руки. Для кого-то оно проще и наглядней. Вот как определять направление магнитного поля по правилу правой руки.

Если отогнуть большой палец правой руки и направить его в сторону течения тока, согнутые вокруг проводника пальцы, покажут направление движения магнитного поля.

Правило буравчика в другой интерпретации: правой руки для проводника (иллюстрация)

Внимание! Во время применения правила прикасаться к проводнику не надо. Все операции надо проделывать в собственном воображении, или на солидном расстоянии от реального проводника тока.

Правило правой руки для соленоида

Чем хорош этот вариант, так это тем что его легко применить и для соленоида. Направляем большой палец в том направлении, куда течет ток, и по остальным определяем направление магнитного поля. Все просто. С буравчиком так не получится.

По правилу правой руки определять также можно направление тока по имеющимся линиям магнитного поля. Пальцы располагаем вдоль этих линий, повернув их по движению. Отогнутый на 90° большой палец покажет направление тока.

Магнитное поле кругового тока

Французские ученые Ж. Био и Ф. Савар изучали магнитные поля, создаваемые постоянными токами разной формы. Результаты их работы обобщил известный математик и физик П. Лаплас.

Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока

Закон Био-Савара–Лапласа описывает порождение магнитного поля током $I$ на элементе проводника длиной $dl$ в некоторой точке пространства ($\mu$ — магнитная проницаемость вещества в котором локализовано поле):

$d\vec{B}=\frac{\mu_{0}\mu }{4\pi }\frac{I\left[ d\vec{l}\vec{r}\right]}{r^{3}}\left( 1 \right)$

где $d \vec l ⃗$ — вектор, длина которого равна длине элемента проводника $dl$, направленный по току; $\vec r$ – радиус-вектор, который проведен от элемента $dl$ в точку, в которой исследуется магнитное поле. Поскольку в правой части формулы (1) находится векторное произведение, очевидно, что индукция элементарного магнитного поля будет направлена перпендикулярно плоскости, в которой находятся векторы $\vec r$ и $\vec l$ и при этом является касательной к силовой линии поля.

Величину вектора $\vec{dB}$ из выражения (1) найдем как:

$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl\sin \alpha }{r^{2}}\left( 2 \right)$.

где $ \alpha $– угол между векторами $\vec r$ и $\vec l$ .

Конкретное направление $\vec{dB}$ находят по правилу буравчика (правилу правой руки):

Если правый винт вращать так, что его поступательное движение будет совпадать с направлением течения тока в избранном элементе, то вращение его головки укажет направление $\vec{dB}$.

Магнитные поля подчиняются принципу суперпозиции:

Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:

$\vec{B}=\sum\limits_{i=1}^N \vec{B}_{i} \left( 3 \right). $

Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:

$\vec{B}=\int {d\vec{B}_{i}} \left( 4 \right).$

Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:

1. Выделить на проводнике с током элементарный отрезок $dl$.
2. Записать для исследуемой точки поля закон Био – Савара – Лапласа.
3. Определить направление элементарного поля $\vec{dB}$ в избранной точке.
4. Воспользоваться принципом суперпозиции для магнитных полей (учесть, что суммируются векторы).

Магнитное поле кругового тока в его центре

Рисунок 1. Магнитное поле кругового тока в его центре. Автор24 — интернет-биржа студенческих работ

Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.

Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:

$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl_{1}\sin \alpha }{r^{2}}\left( 5\right).$

Из рис.1 мы видим:

1. что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
2. элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $\vec r$.

Учитывая сказанное выражение (5) представим в виде:

$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl_{1}}{R^{2}}\left( 6 \right)$.

Обезличивая витки с током, положим далее $dl_1=dl$.

Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:

$B=\oint\limits_L {dB=} \frac{\mu_{0}\mu }{4\pi}\frac{I}{R^{2}}\oint\limits_L {dl} =\frac{\mu_{0}\mu }{4\pi}\frac{I}{R^{2}}2\pi R\to$

$B=\mu_{0}\mu \frac{I}{2R}\left( 7 \right)$.

Замечание 1

$L=2πR$ — длина окружности витка.

Индукция магнитного поля кругового тока на его оси

Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка — $R$ (рис.2).

Рисунок 2. Индукция магнитного поля кругового тока на его оси. Автор24 — интернет-биржа студенческих работ

Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:

• $\vec{r}=\vec{R}+\vec{h}$,

• $d\vec{l}\times \vec{r}=d\vec{l}\times \vec{R}+d\vec{l}\times \vec{h}(9).$

Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:

$\vec{B}=\oint\limits_L {dB=}$$\frac{\mu \mu_{0}}{4\pi }I\oint\limits_L \frac{d\vec{l}\times\vec{r}}{r^{3}} $ $=\frac{\mu \mu_{0}}{4\pi }\frac{I}{r^{3}}\left( \oint\limits_L{d\vec{l}\times \vec{R}+} \oint\limits_L {d\vec{l}\times \vec{h}}\right)\left( 10 \right).$

В выражении (10) при записи интеграла, мы учли, что величина вектора $\vec{r}$ не изменяется. Кроме этого вектор $\vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:

$\oint\limits_L {d\vec{l}\times \vec{h}} =(\oint\limits_L {d\vec{l})\times\vec{h}} =0\, \left( 11 \right),$

так как ( $\oint\limits_L {d\vec{l})=0.}$

Вычислим интеграл: $\oint\limits_L {d\vec{l}\times \vec{R}.}$ Введем единичный вектор ($\vec n$), нормальный к плоскости витка с током.

$\oint\limits_L {d\vec{l}\times \vec{R}=\oint\limits_L {\vec{n}Rdl=\vec{n}R}} \oint\limits_L {dl=\vec{n}R} 2\pi R=2\pi R^{2}\vec{n}\left( 12 \right)$.

Подставляем результаты интегрирования из (12) в (10), имеем:

$\vec{B}=\frac{\mu \mu_{0}}{4\pi }\frac{I}{r^{3}}2\pi R^{2}\vec{n}=\frac{\mu\mu_{0}I}{2}\frac{R^{2}}{\left( R^{2}+h^{2}\right)^{\frac{3}{2}}}\vec{n}\left( 13 \right)$

где при записи окончательного результата мы учли, что:

$r^{3}=\left( R^{2}+h^{2} \right)^{\frac{3}{2}}$.

Кольца Гельмгольца

Кольцами Гельмгольца считают пару проводников в виде колец одного радиуса, расположенных в параллельных плоскостях (рис.3) на одной оси. Расстояние между плоскостями колец равно их радиусу.

Рисунок 3. Кольца Гельмгольца. Автор24 — интернет-биржа студенческих работ

Рассмотрим магнитное поле на оси этих колец.

Декартову систему координат разместим так, что ее начало совпадает с центром нижнего кольца с током. Ось Z нашей системы будет направлена по оси колец (рис.3).

Запишем индукцию магнитного поля в точке с координатой $z$ на оси колец. Используем формулу (13):

$B_{z}=\frac{\mu \mu_{0}I}{2}R^{2}\left[ \frac{1}{\left( R^{2}+z^{2}\right)^{\frac{3}{2}}}+\frac{1}{\left[ \left( z-d \right)^{2}+R^{2}\right]^{\frac{3}{2}}} \right]\left( 14\right)$.

Исследуем полученное поле. Считается, что магнитное поле на оси колец Гельмгольца на посередине между ними является однородным.

Неоднородность в первом приближении характеризуют первой производной:

$\frac{\partial B_{z}}{\partial z}=\frac{3\mu \mu_{0}I}{2}R^{2}\left[\frac{-z}{\left( R^{2}+z^{2} \right)^{\frac{5}{2}}}+\frac{z-d}{\left[ \left(z-d \right)^{2}+R^{2} \right]^{\frac{5}{2}}} \right]\left( 15 \right)$.

Если $z=\frac{d}{2}\quad$ , подставим в (15), имеем:

$\frac{\partial B_{z}}{\partial z}=0.$

Найдем $\frac{\partial^{2}B_{z}}{\partial z^{2}}:$

$\frac{\partial^{2}B_{z}}{\partial z^{2}}=\frac{3\mu \mu_{0}I}{2}R^{2}\left( \frac{5z^{2}}{\left( R^{2}+z^{2}\right)^{\frac{7}{2}}}-\frac{1}{\left( R^{2}+z^{2}\right)^{\frac{5}{2}}}+\frac{5\left( z-d \right)^{2}}{\left[ \left( z-d \right)^{2}+R^{2} \right]^{\frac{7}{2}}}-\frac{1}{\left[ \left( z-d\right)^{2}+R^{2} \right]^{\frac{5}{2}}} \right)\left( 16 \right)$

По условию для колец Гельмгольца, имеем: $d=R.$

На середине их общей оси ($z=\frac{d}{2})$, получаем:

$\frac{\partial^{2}B_{z}}{\partial z^{2}}=0\, \left( 17 \right)$.

Равенство нулю второй производной от $B_z$ по координате $z$, показывает, что в на середине оси колец магнитное поле является однородным с высокой степенью точности.

Правило буравчика: особенности и приёмы

Правило буравчика – упрощенная наглядная демонстрация при помощи одной руки правильного умножения двух векторов. Геометрия школьного курса подразумевает осведомленность учеников о скалярном произведении. В физике часто встречается векторное.

Понятие вектора

Полагаем, нет смысла истолковывать правило буравчика при отсутствии знания определения вектора. Требуется открыть бутылку – знание о правильных действиях поможет. Вектором называют математическую абстракцию, не существующую реально, выказывающую указанные признаки:

1. Направленный отрезок, обозначаемый стрелкой.
2. Точкой начала послужит точка действия силы, описываемой вектором.
3. Длина вектора равна модулю силы, поля, прочих описываемых величин.

Не всегда затрагивают силу. Векторами описывается поле. Простейший пример показывают школьникам преподаватели физики. Подразумеваем линии напряженности магнитного поля. Вдоль обычно рисуются векторы по касательной. В иллюстрациях действия на проводник с током увидите прямые линии.

Правило буравчика

Векторные величины часто лишены места приложения, центры действия выбираются по договоренности. Момент силы исходит из оси плеча. Требуется для упрощения сложения. Допустим, на рычаги различной длины действуют неодинаковые силы, приложенные к плечам с общей осью. Простым сложением, вычитанием моментов найдем результат.

Векторы помогают решить многие обыденные задачи и, хотя выступают математическими абстракциями, действуют реально. На основе ряда закономерностей возможно вести предсказание будущего поведения объекта наравне со скалярными величинами: поголовье популяции, температура окружающей среды. Экологов интересуют направления, скорость перелета птиц. Перемещение является векторной величиной.

Правило буравчика помогает найти векторное произведение векторов. Это не тавтология. Просто результатом действия окажется тоже вектор. Правило буравчика описывает направление, куда станет указывать стрелка. Что касается модуля, нужно применять формулы. Правило буравчика – упрощенная чисто качественная абстракция сложной математической операции.

Аналитическая геометрия в пространстве

Каждому известна задачка: стоя на одном берегу реки, определить ширину русла. Кажется уму непостижимым, решается в два счета методами простейшей геометрии, которую изучают школьники. Проделаем ряд несложных действий:

1. Засечь на противоположном берегу видный ориентир, воображаемую точку: ствол дерева, устье ручейка, впадающего в поток.
2. Под прямым углом линии противоположного берега сделать засечку на этой стороне русла.
3. Найти место, с которого ориентир виден под углом 45 градусов к берегу.
4. Ширина реки равна удалению конечной точки от засечки.

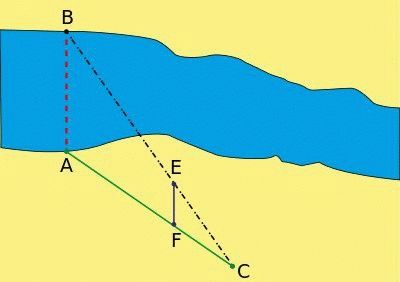
Определение ширины реки методом подобия треугольников

Используем тангенс угла. Не обязательно равен 45 градусов. Нужна большая точность – угол лучше брать острым. Просто тангенс 45 градусов равен единице, решение задачки упрощается.

Аналогичным образом удается найти ответы на животрепещущие вопросы. Даже в микромире, управляемом электронами. Можно однозначно сказать одно: непосвященному правило буравчика, векторное произведение векторов представляются скучными, занудными. Удобный инструмент, помогающий в понимании многих процессов. Большинству будет интересным принцип работы электрического двигателя (безотносительно к конструкции). Легко может быть объяснен использованием правила левой руки.

Во многих отраслях науке бок-о-бок идут два правила: левой, правой руки. Векторное произведение иногда может описываться так или эдак. Звучит расплывчато, предлагаем немедленно рассмотреть пример:

• Допустим, движется электрон. Отрицательно заряженная частица бороздит постоянное магнитное поле. Очевидно, траектория окажется изогнута благодаря силе Лоренца. скептики возразят, по утверждениям некоторых ученых электрон не частица, а скорее, суперпозиция полей. Но принцип неопределенности Гейзенберга рассмотрим в другой раз. Итак, электрон движется:

Расположив правую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление полета частицы, отогнутый на 90 градусов в сторону большой палец вытянется в направлении действия силы. Правило правой руки, являющееся иным выражением правила буравчика. Слова-синонимы. Звучит по-разному, по сути – одно.

Правило левой руки

• Приведем фразу Википедии, отдающую странностью. При отражении в зеркале правая тройка векторов становится левой, тогда нужно применять правило левой руки вместо правой. Летел электрон в одну сторону, по методикам, принятым в физике, ток движется в противоположном направлении. Словно отразился в зеркале, поэтому сила Лоренца определяется уже правилом левой руки:

Если расположить левую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление течения электрического тока, отогнутый на 90 градусов в сторону большой палец вытянется, указывая вектор действия силы.

Видите, ситуации похожие, правила просты. Как запомнить, которое применять? Главный принцип неопределенности физики. Векторное произведение вычисляется во многих случаях, причем правило применяется одно.

Какое правило применить

Слова синонимы: рука, винт, буравчик

Вначале разберем слова-синонимы, многие начали спрашивать себя: если тут повествование должно затрагивать буравчик, почему текст постоянно касается рук. Введем понятие правой тройки, правой системы координат. Итого, 5 слов-синонимов.

Потребовалось выяснить векторное произведение векторов, оказалось: в школе это не проходят. Проясним ситуацию любознательным школьникам.

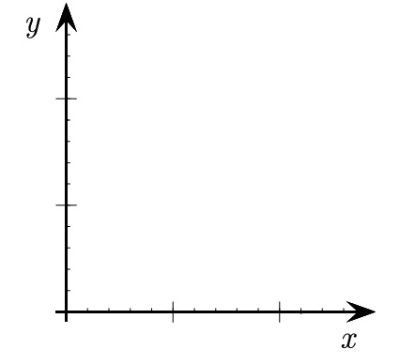
Декартова система координат

Школьные графики на доске рисуют в декартовой системе координат Х-Y. Горизонтальная ось (положительная часть) направлена вправо – надеемся, вертикальная – указывает вверх. Делаем один шаг, получая правую тройку. Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.

В Википедии написано: допустимо брать левые тройки, правые, вычисляя векторное произведение, несогласны. Усманов в этом плане категоричен. С разрешения Александра Евгеньевича приведем точное определение: векторным произведением векторов называют вектор, удовлетворяющий трем условиям:

1. Модуль произведения равен произведению модулей исходных векторов на синус угла меж ними.
2. Вектор результата перпендикулярен исходным (вдвоем образуют плоскость).
3. Тройка векторов (по порядку упоминания контекстом) правая.

Правую тройку знаем. Итак, если ось Х – первый вектор, Y – второй, Z будет результатом. Почему назвали правой тройкой? По-видимому, связано с винтами, буравчиками. Если закручивать воображаемый буравчик по кратчайшей траектории первый вектор-второй вектор, поступательное движение оси режущего инструмента станет происходить в направлении результирующего вектора:

1. Правило буравчика применяется к произведению двух векторов.
2. Правило буравчика качественно указывает направление результирующего вектора этого действия. Количественно длина находится выражением, упомянутым (произведение модулей векторов на синус угла меж ними).

Теперь каждому понятно: сила Лоренца находится согласно правилу буравчика с левосторонней резьбой. Векторы собраны левой тройкой, если взаимно ортогональны (перпендикулярны один другому), образуется левая система координат. На доске ось Z смотрела бы в направлении взгляда (от аудитории за стену).

Простые приемы запоминания правил буравчика

Люди забывают, что силу Лоренца проще определять правилом буравчика с левосторонней резьбой. Желающий понять принцип действия электрического двигателя должен как дважды два щелкать подобные орешки. В зависимости от конструкции число катушек ротора бывает значительным, либо схема вырождается, становясь беличьей клеткой. Ищущим знания помогает правило Лоренца, описывающее магнитное поле, где движутся медные проводники.

Для запоминания представим физику процесса. Допустим, движется электрон в поле. Применяется правило правой руки для нахождения направления действия силы. Доказано: частица несет отрицательный заряд. Направление действия силы на проводник находится правилом левой руки, вспоминаем: физики совершенно с левых ресурсов взяли, что электрический ток течет в направлении противоположном тому, куда направились электроны. И это неправильно. Поэтому приходится применять правило левой руки.

Не всегда следует идти такими дебрями. Казалось бы, правила больше запутывают, не совсем так. Правило правой руки часто применяется для вычисления угловой скорости, которая является геометрическим произведением ускорения на радиус: V = ω х r. Многим поможет визуальная память:

1. Вектор радиуса круговой траектории направлен из центра к окружности.
2. Если вектор ускорения направлен вверх, тело движется против часовой стрелки.

Посмотрите, здесь опять действует правило правой руки: если расположить ладонь так, чтобы вектор ускорения входил перпендикулярно в ладонь, персты вытянуть по направлению радиуса, отогнутый на 90 градусов большой палец укажет направление движения объекта. Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.

Аналогичным образом определяется момент силы. Исходит перпендикулярно из оси плеча, совпадает направлением с угловым ускорением на рисунке, описанном выше. Многие спросят: зачем нужно? Почему момент силы не скалярная величина? Зачем направление? В сложных системах непросто проследить взаимодействия. Если много осей, сил, помогает векторное сложение моментов. Можно значительно упростить вычисления.

Правило буравчика кратко и понятно

Тем, кому в школе плохо давалась физика, правило буравчика и сегодня — самая настоящая «терра инкогнита». Особенно если попытаться найти определение известного закона в Сети: поисковые системы тут же выдадут множество мудрёных научных объяснений со сложными схемами. Однако вполне возможно кратко и понятно объяснить, в чём же оно состоит.

В чём состоит правило буравчика

Буравчик — инструмента для сверления отверстий

Оно звучит так: в случаях, когда направление буравчика совпадает с направлением тока в проводнике во время поступательных движений, то одновременно идентичным ему будет и направление вращения ручки буравчика.

В поисках направления

Чтобы разобраться, придётся всё-таки вспомнить школьные уроки. На них учителя физики рассказывали нам о том, что электроток — это движение элементарных частиц, которые при этом несут свой заряд по проводящему материалу. Благодаря источнику движение частиц в проводнике — направленное. Движение, как известно, жизнь, а потому вокруг проводника возникает не что иное, как магнитное поле, и оно тоже вращается. Но как?

Ответ даёт именно это правило (без использования каких-либо специальных инструментов), и результат оказывается весьма ценным, ведь в зависимости от направления магнитного поля парочка проводников начинает действовать по совершенно разным сценариям: либо отталкиваться друг от друга, либо, напротив, устремляться навстречу.

Использование

Самый простой способ определения пути движений линий магнитного поля — применение правила буравчика

Представить это можно и так — на примере собственной правой руки и самого обычного провода. Провод кладём в руку. Четыре пальца крепко сжимаем в кулак. Большой палец указывает вверх — наподобие жеста, которым мы демонстрируем, что нам что-то нравится. В данной «раскладке» большой палец чётко укажет направление движения тока, тогда как остальные четыре — путь движений линий магнитного поля.

Правило вполне применимо в жизни. Физикам оно необходимо для того, чтобы определить направление магнитного поля тока, рассчитать механическое вращение скорости, вектор магнитной индукции и момент сил.

Кстати, о том, что правило применимо к самым разным ситуациям говорит и то, что существует сразу несколько его толкований — в зависимости от рассматриваемого каждого конкретного случая.