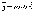2.7. Правила Кирхгофа
Простые электрические цепи достаточно легко рассчитываются с применением законов Ома и законов последовательного и параллельного соединения проводов. Более сложные разветвленные электрические цепи удобнее рассчитывать при помощи правил Кирхгофа.
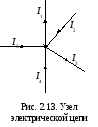
Рассмотрим произвольную разветвленную цепь, на отдельных участках которой включены источники тока с известными характеристиками. Точка цепи, в которой сходится более двух проводов (рис. 2.13), называется узлом.
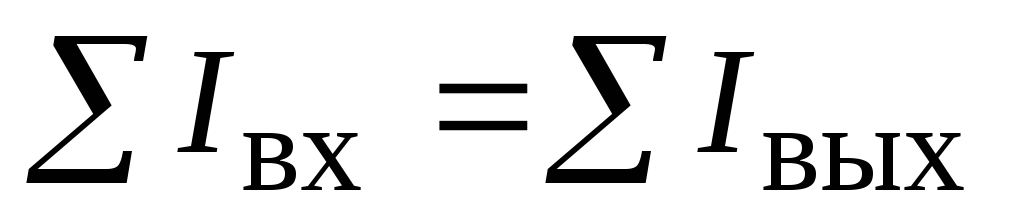 .
(2.19)
.
(2.19)
Эквивалентная формулировка первого
правила Кирхгофа: алгебраическая сумма
токов, сходящихся в узле, равна нулю 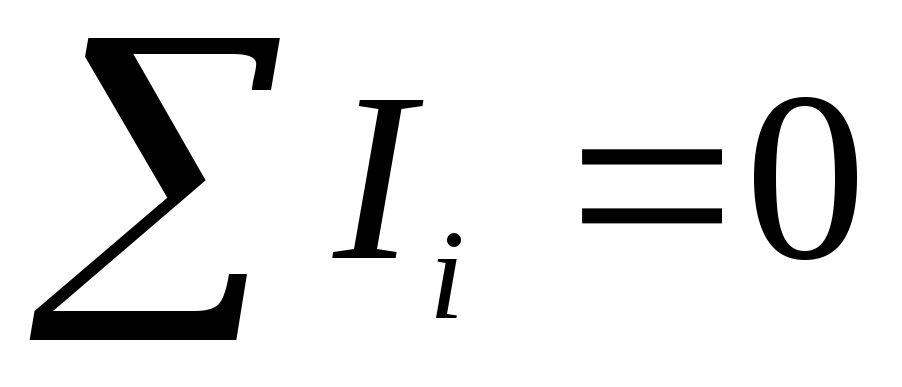 .
При этом втекающим и вытекающим из узла
токам приписываются противоположные
знаки. В нашем случае (рис. 2.13):
.
При этом втекающим и вытекающим из узла
токам приписываются противоположные
знаки. В нашем случае (рис. 2.13):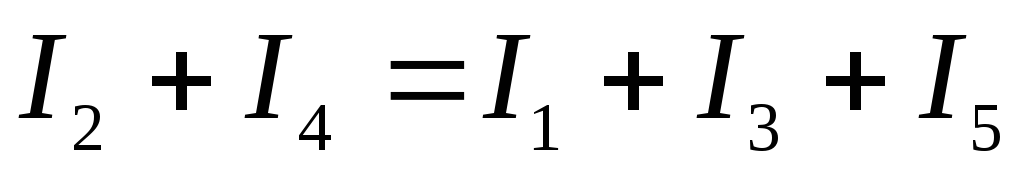 .
.
Первое правило Кирхгофа, по сути, является следствием закона сохранения заряда. Оно также отражает тот факт, что при постоянном токе в узле не происходит нарастающее во времени накопление заряда того или иного знака. Для этого нужно, чтобы количество заряда, втекающее в узел в единицу времени, было равно количеству заряда, вытекающего из него.
Второе правило Кирхгофа. В произвольном замкнутом контуре алгебраическая сумма ЭДС, действующих в этом контуре, рана сумме падений напряжений на отдельных участках этого контура:
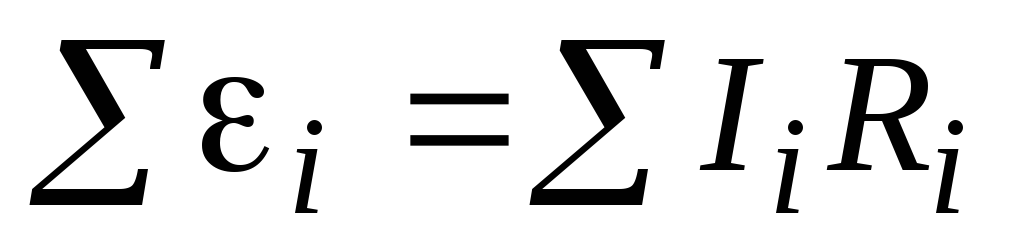 (2.20)
(2.20)
Некоторые слагаемые в (2.20) как слева, так и справа могут быть отрицательными. При решении конкретных задач токи на отдельных участках первоначально расставляются произвольным образом. Затем произвольным образом выбирается положительное направление обхода замкнутого контура (по часовой или против часовой стрелки). Если ток течет вдоль положительного направления, его берут со знаком «+», если против положительного направления – со знаком «». Если ЭДС действует вдоль положительного направления, т.е. при обходе контура источник проходится от клеммы «» к клемме «+», то значение ЭДС берется со знаком «+», и наоборот. Если в результате расчета сила тока получится отрицательной, то значит, мы не угадали направление тока на данном участке и его просто следует изменить на противоположное. Сама же величина тока, независимо от того, как мы расставим токи в начале решения задачи, получится правильной.
Для доказательства второго правила Кирхгофа рассмотрим произвольный замкнутый контур в цепи, который в общем случае может включать в себя внешние сопротивления и ЭДС на каждом участке (от узла до узла). Положительным будем считать направление по часовой стрелке. Пусть для определенности наш контур включает три участка (рис. 2.14). Направление токов расставим произвольно. Применим закон Ома (2.18) к каждому из трех неоднородных участков цепи. Для первого участка 2-1 работа электрического поля положительна, а работа источника (он заряжается) отрицательна, поэтому:
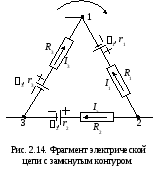

На втором участке цепи 2-3 также работа электрического поля положительна, а работа источника отрицательна, поэтому:
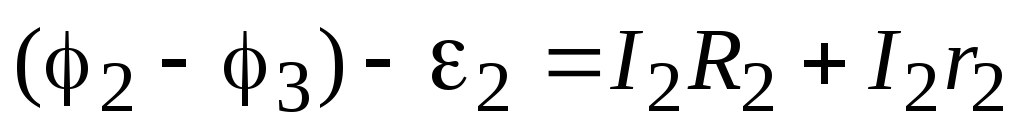 .
.
На третьем участке цепи 3-1 работа источника положительна, поэтому:
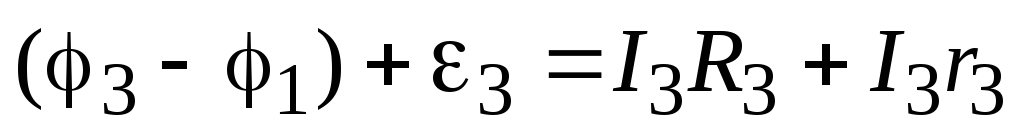 .
.
Сложим правые и левые части трех последних уравнений, предварительно домножив первое уравнение на «1». Тогда все потенциалы сократятся, в результате получим:
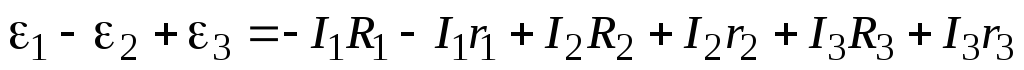
Последнее
уравнение совпадает с формулировкой
второго правила Кирхгофа (2.20) с учетом
всех замечаний, сделанных по поводу
знаков токов и ЭДС (выражения типа 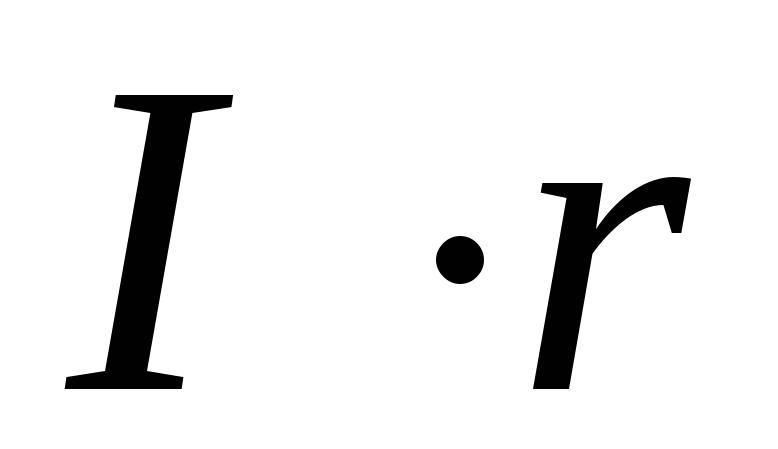 можно формально рассматривать как
падения напряжений на внутренних
сопротивлениях).
можно формально рассматривать как
падения напряжений на внутренних
сопротивлениях).
Отметим, что второе правило Кирхгофа, являясь следствием закона Ома для неоднородного участка цепи, по сути дела является следствием закона сохранения энергии.
Правила
Кирхгофа применимы и в том случае, когда
в цепь включены неомические, т.е. не
подчиняющиеся закону Ома (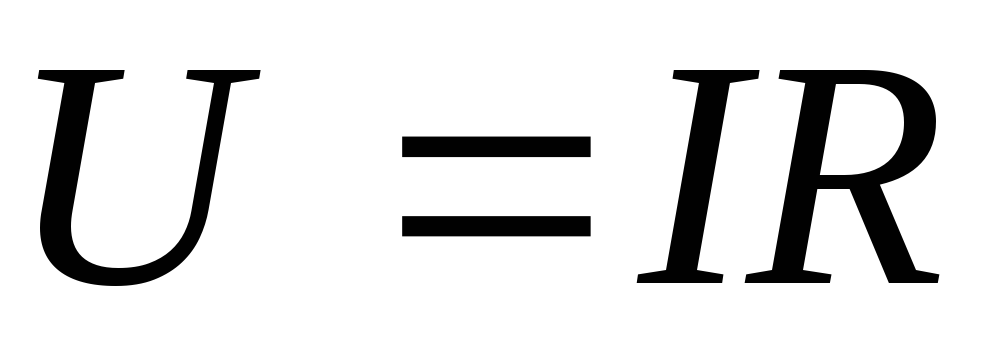
 ,
а
,
а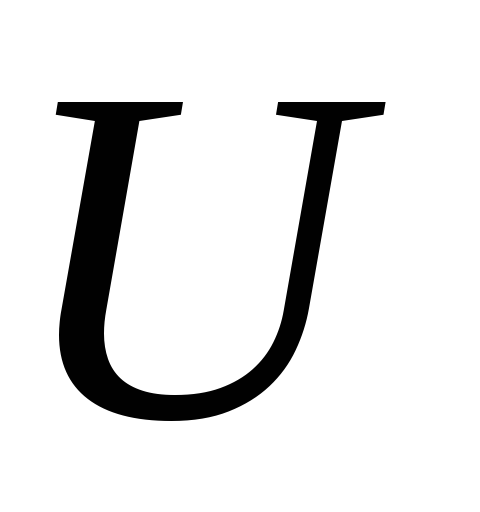 .
Второе правило Кирхгофа при этом имеет
вид:
.
Второе правило Кирхгофа при этом имеет
вид: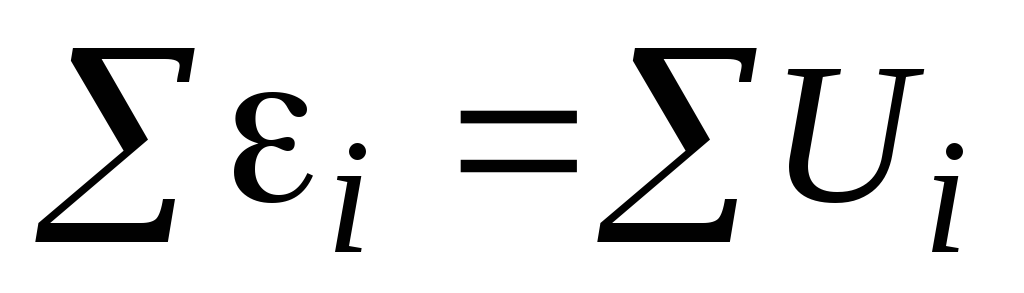 .
.
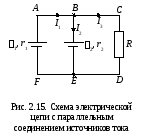
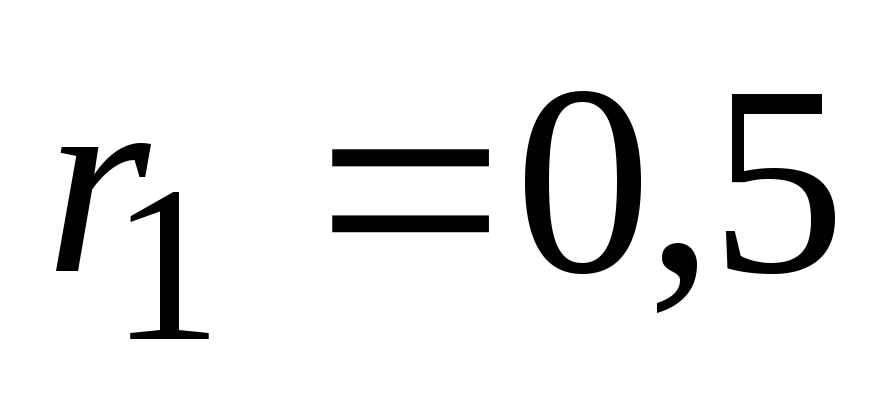 Ом,2=12
В,
Ом,2=12
В, 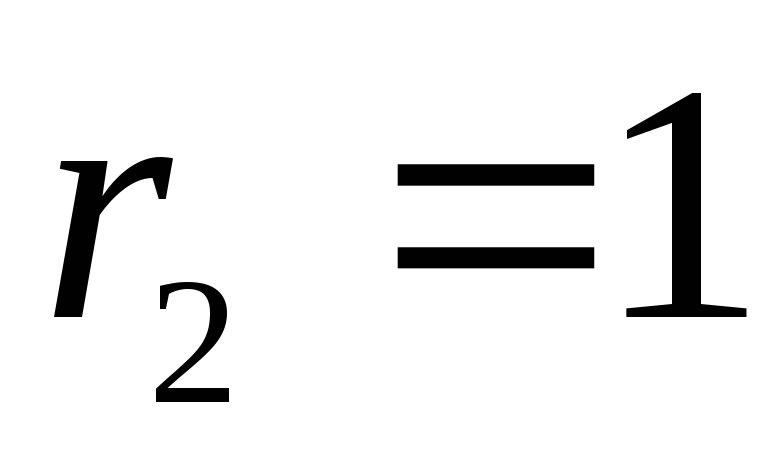 Ом,
Ом,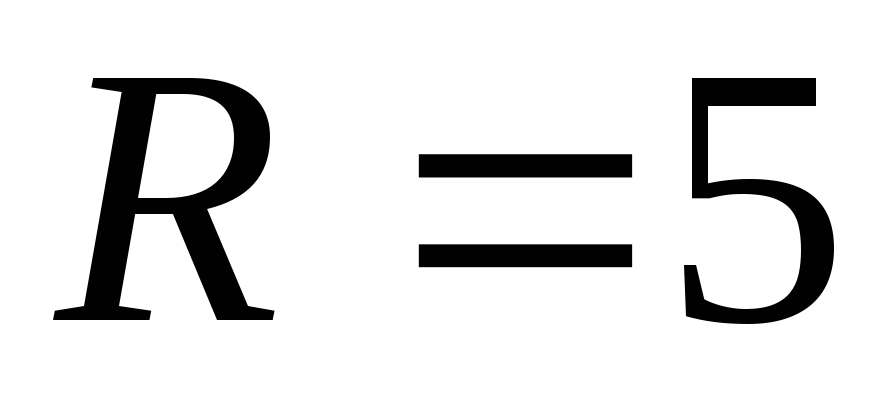 Ом. Определить токи во всех ветвях.
Ом. Определить токи во всех ветвях.Решение. Произвольно расставим токи во всех ветвях (рис. 2.15).
В цепи имеется два узла: В и Е. Запишем первое правило Кирхгофа для узла В (для узла Е получится то же самое уравнение):
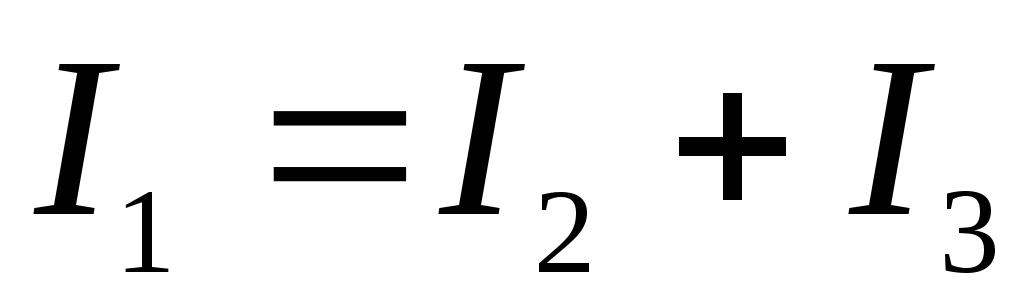 .
.
Так как в задаче три неизвестных тока, необходимо три уравнения. Для этого достаточно рассмотреть какие-либо два замкнутых контура цепи и записать для них второе правило Кирхгофа.
Контур АВЕFA: 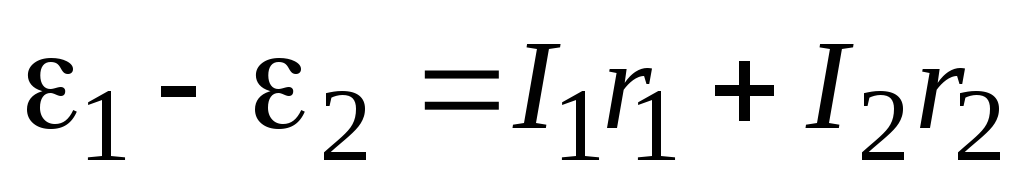
Контур АВСDEFA:  .
.
Отметим, что положительное направление обхода контуров задает последовательность букв, которыми они обозначены. Например, в контуре АВЕFA положительное направление обхода – по часовой стрелке. Напомним, что ЭДС первого источника взята со знаком «+», так как при движении вдоль контура по часовой стрелке он проходится от клеммы «» к клемме «+». ЭДС второго источника взята со знаком минус, так как при движении по часовой стрелке он проходится от клеммы «+» к клемме «». В правой части уравнения оба тока взяты знаком «+», поскольку они текут вдоль положительного направления обхода — по часовой стрелке. Такие же правила использованы и для контура
Перед решением полученной систему из трех уравнений удобно подставить в них известные величины:
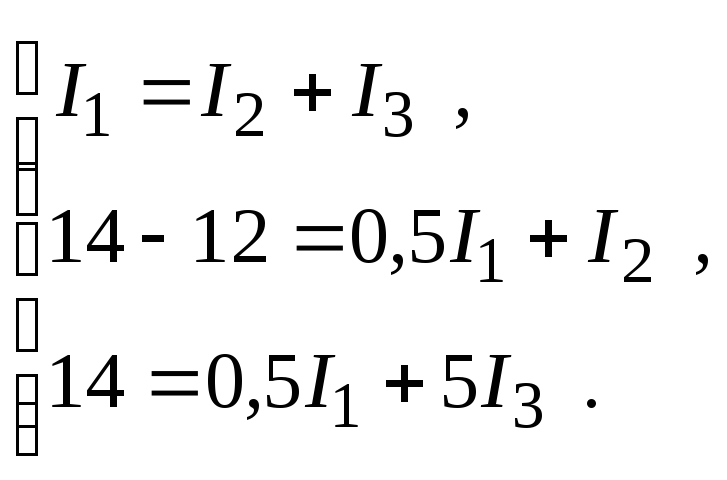
В
результате решения системы получаем
ответ: 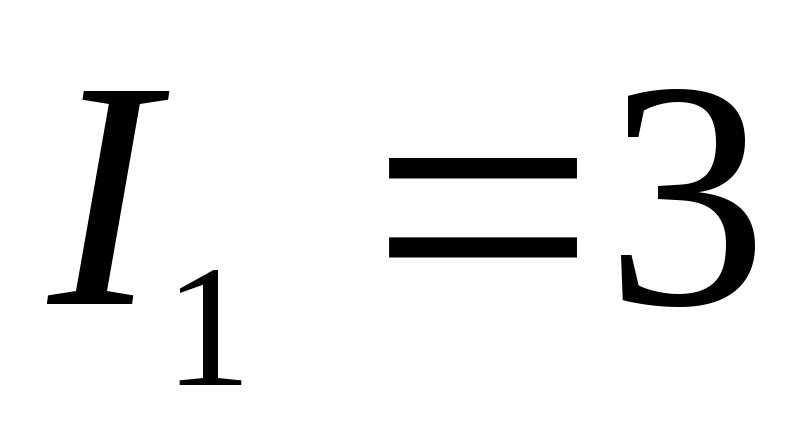 А,
А,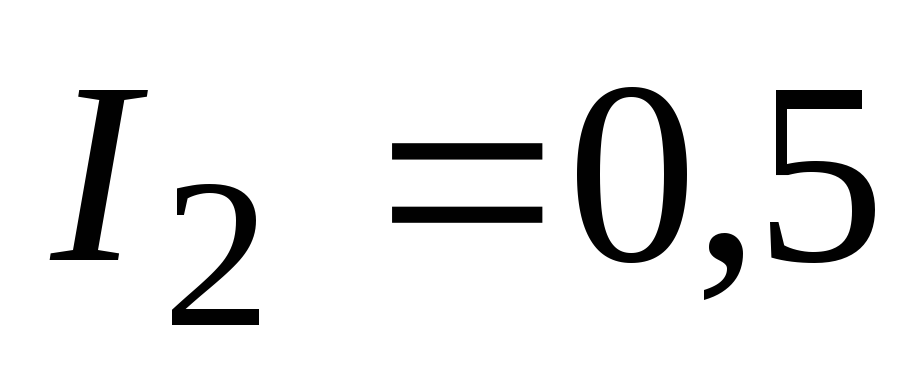 А,
А,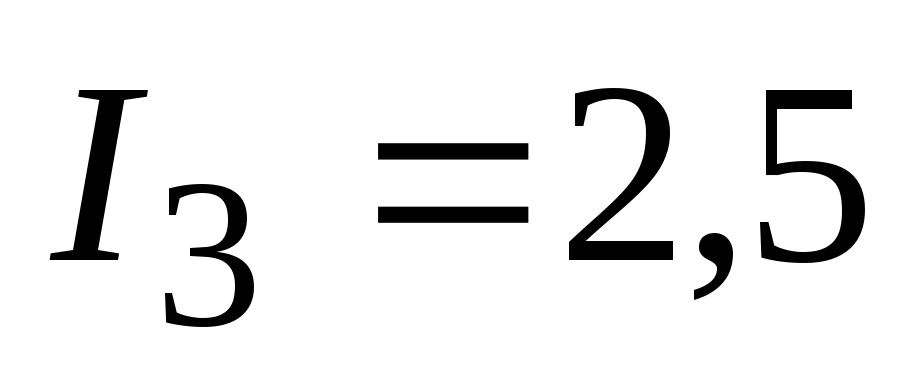 А.
Так как все токи получились положительными,
их направления были случайно указаны
верно.
А.
Так как все токи получились положительными,
их направления были случайно указаны
верно.
Анализируя
полученный результат, можно сделать
вывод, что первый источник питает не
только нагрузку 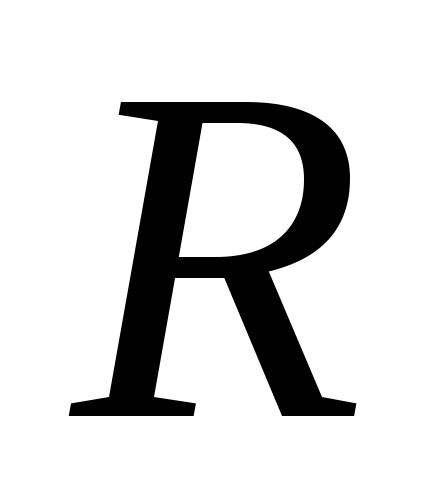 ,
но и заряжает второй источник. Второй
источник играет роль «паразита». Однако
такая схема все-таки иногда используется
на практике. Например, в системах
электрического питания автомобилей
роль первого источника играет генератор
постоянного тока, а роль второго –
аккумулятор. Если на питание нагрузки
расходуются небольшие токи (общее
сопротивление внешней цепи велико), то
генератор не только питает нагрузку,
но и еще подзаряжает аккумулятор. При
увеличении тока, потребляемого нагрузкой,
направление тока
,
но и заряжает второй источник. Второй
источник играет роль «паразита». Однако
такая схема все-таки иногда используется
на практике. Например, в системах
электрического питания автомобилей
роль первого источника играет генератор
постоянного тока, а роль второго –
аккумулятор. Если на питание нагрузки
расходуются небольшие токи (общее
сопротивление внешней цепи велико), то
генератор не только питает нагрузку,
но и еще подзаряжает аккумулятор. При
увеличении тока, потребляемого нагрузкой,
направление тока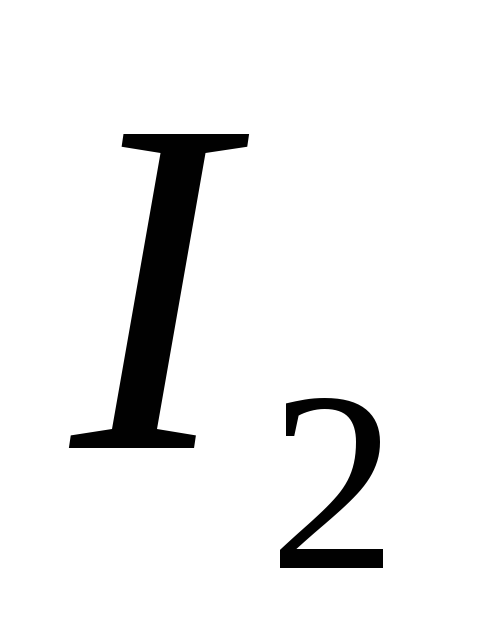
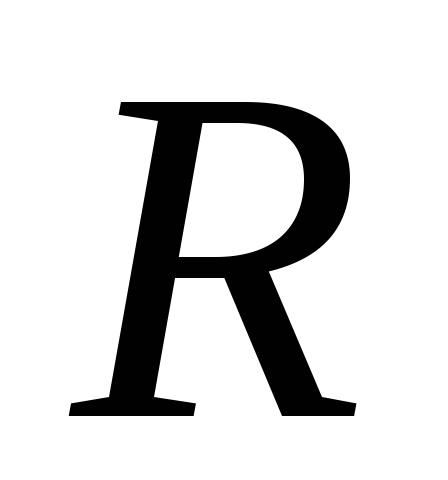 (рис. 2.15) параллельно подключена еще
точно такая же нагрузка. Тогда сопротивление
внешней цепи становится равным
(рис. 2.15) параллельно подключена еще
точно такая же нагрузка. Тогда сопротивление
внешней цепи становится равным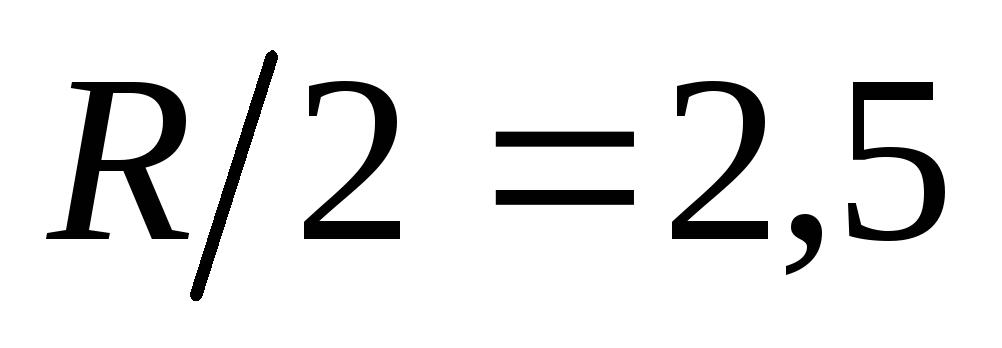 Ом. Третье уравнение системы изменится,
и решение становится другим:
Ом. Третье уравнение системы изменится,
и решение становится другим: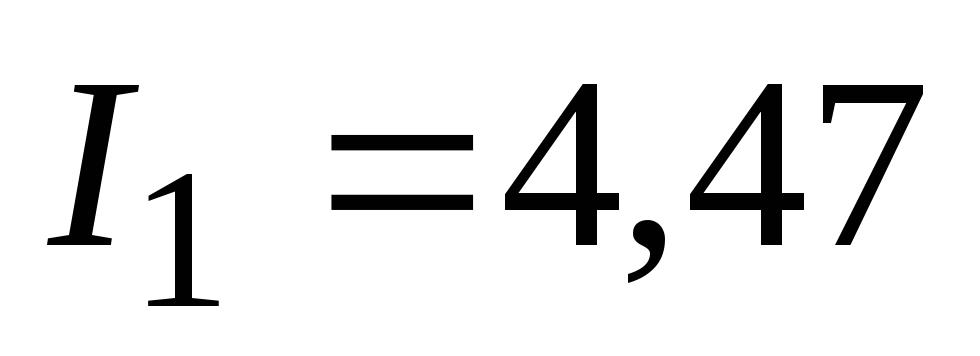 А,
А,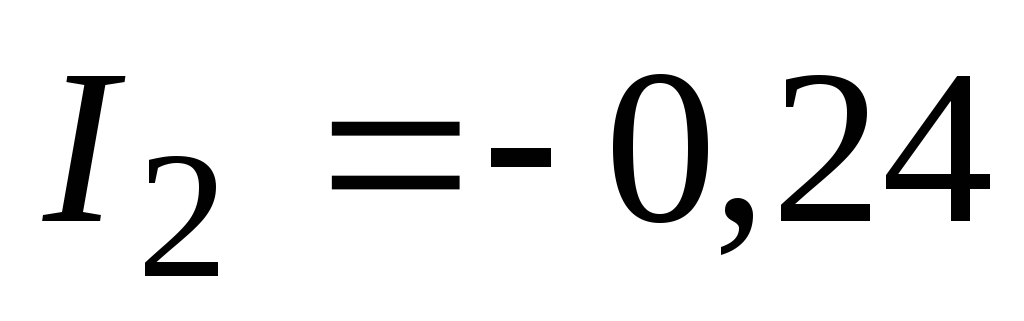 А,
А,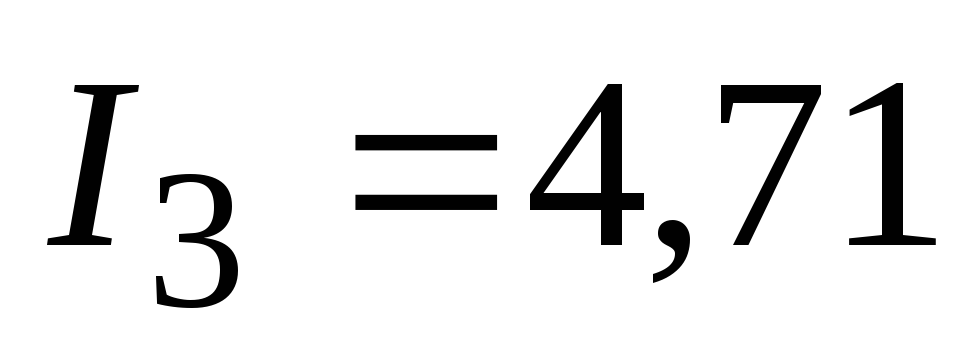 А.
Отрицательное значение второго тока и
свидетельствует о том, что он теперь
направлен в сторону, противоположную
указанной на рис. 2.15, т.е. разряжается.
А.
Отрицательное значение второго тока и
свидетельствует о том, что он теперь
направлен в сторону, противоположную
указанной на рис. 2.15, т.е. разряжается.Правила Кирхгофа — Википедия
Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает.i2 + i3 = i1 + i4
Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.
- ∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}
- для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Видео по теме
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.
- Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
Пример
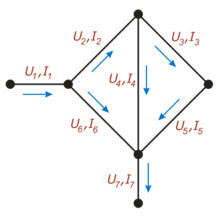
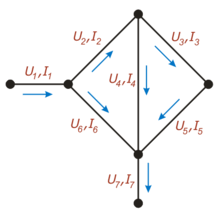 На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)
На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)Количество узлов: 3.
p−1=2{\displaystyle p-1=2}
Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.
m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}
Количество контуров: 2.
Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:
- {I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
- {U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}
Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
- Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
Электричество и магнетизм
Приведем пример расчета токов в разветвленной цепи (рис. 4.25).
Рис. 4.25. Пример разветвленной цепи
Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I1, участок b–d с током I2 и участок b–c–d с током I3 (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике?
Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным. В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25).
Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла b, куда входит ток I2 и выходят токи I1 и I3
|
(4.45) |
Шаг третий. Нам осталось написать уравнения (в нашем случае — два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.
Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока, I1 и I2, направления которых совпадают с выбранным направлением обхода. ЭДС также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как
|
(4.46) |
В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока I1 и I3, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых войдет в уравнения со знаком плюс, а — со знаком минус. Уравнение для этого замкнутого пути имеет вид
|
(4.47) |
Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I3 через I1 из уравнения (4.47)
|
(4.48) |
I2 через I1 с помощью уравнения (4.46)
|
(4.49) |
и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное I1, которое находится без труда
|
(4.50) |
Подставляя это выражение в (4.48), (4.49), находим соответственно токи I2, I3
|
(4.51) |
физическое обоснование, формулировка, правила знаков; применение для расчета линейных электрических цепей, баланс мощностей.
Правила Кирхгофа— соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Определения
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
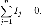
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для
постоянных напряжений 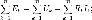
для
переменных напряжений 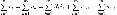
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Баланс мощности – система показателей, характеризующая соответствие суммы значений нагрузок потребителей энергосистемы (ОЭС) и необходимой резервной мощности величине располагаемой мощности энергосистемы.
23. Классическая теория проводимости: природа носителей тока в металлах; постулаты теории, дифференциальная форма законов Ома и Джоуля-Ленца.
Основные положения этой теории сводятся к следующим:
1). Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.
2). Поведение электронов подобно поведению молекул идеального газа (электронный газ).
3). При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.
4). При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.
При
включении электрического поля на
хаотическое движение электронов
накладывается упорядоченное движение (называемое иногда «дрейфовым»), происходящее с некоторой средней
скоростью  ;
возникает направленное движение
электронов –электрический
ток.
Плотность тока определяется по формуле
;
возникает направленное движение
электронов –электрический
ток.
Плотность тока определяется по формуле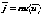 .
.
Оценки
показывают, что при максимально допустимой
плотности тока в металлах j = 107 А/м2 и концентрации носителей 1028 –
1029м-3,
. Таким образом, даже при очень больших
плотностях тока средняя скорость
упорядоченного движения электронов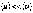 .
.
закона Ома в дифференциальной форме.
Здесь 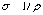 –удельная
электропроводность.
–удельная
электропроводность.
Размерность
σ – [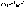 ].
].
Плотность
тока можно выразить через заряд электрона е,
количество зарядов n и дрейфовую скорость 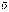 :
:
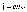 .
.
Обозначим 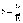 ,
тогда
,
тогда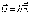 ;
;
|
|
Теперь,
если удельную электропроводность σ
выразить через е, n и b: 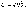 то
вновь получим выражениезакона
Ома в дифференциальной форме:
то
вновь получим выражениезакона
Ома в дифференциальной форме: 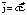
24. Собственная и примесная проводимость полупроводников: механизмы электронной и дырочной проводимости, донорные и акцепторные примеси, зависимость концентрации носителей тока от температуры. Терморезисторы.
Терморезистор — полупроводниковый резистор, в котором используется зависимость электрического сопротивления полупроводникового материала от температуры[1]. Для терморезистора характерны большой температурный коэффициент сопротивления (ТКС) (в десятки раз превышающий этот коэффициент у металлов), простота устройства, способность работать в различных климатических условиях при значительных механических нагрузках, стабильность характеристик во времени. Терморезистор был изобретён Самюэлем Рубеном (SamuelRuben) в 1930 году. Различают терморезисторы с отрицательным (термисторы) и положительным (позисторы) ТКС. Их ещё называют NTC-термисторы и PTC-термисторы соответственно. У позисторов с ростом температуры растет и сопротивление, а у термисторов —- наоборот: при увеличении температуры сопротивление падает.
Режим работы терморезисторов зависит от того, на каком участке статической вольт-амперной характеристики (ВАХ) выбрана рабочая точка. В свою очередь ВАХ зависит как от конструкции, размеров и основных параметров терморезистора, так и от температуры, теплопроводности окружающей среды, тепловой связи между терморезистором и средой
Виды проводимости полупроводников
Полупроводниковые материалы имеют твердую кристаллическую структуру и по своему удельному сопротивлению, ) занимают промежуточную область между проводниками электрического тока, ) и диэлектриками.
Донорные примеси — атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию электронов. Донорными примесями являются химические элементы, внедренные в полупроводник с меньшей, чем у примеси, валентностью.
Акцепторные примеси — атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию дырок. Акцепторными примесями являются химические элементы, внедренные в полупроводник с большей, чем у примеси, валентностью.
Правила Кирхгофа — Википедия
Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает.i2 + i3 = i1 + i4
Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.
- ∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}
- для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.
- Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
Пример
На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)Количество узлов: 3.
p−1=2{\displaystyle p-1=2}
Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.
m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}
Количество контуров: 2.
Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:
- {I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
- {U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}
Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
- Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
Правила Кирхгофа — Википедия. Что такое Правила Кирхгофа
Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает.i2 + i3 = i1 + i4
Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.
- ∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}
- для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.
- Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
Пример
 На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)
На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)Количество узлов: 3.
p−1=2{\displaystyle p-1=2}
Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.
m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}
Количество контуров: 2.
Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:
- {I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
- {U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}
Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
- Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
Правила Кирхгофа — это… Что такое Правила Кирхгофа?
Правила Кирхгофа (часто, в литературе, называются не совсем корректно Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Формулировка правил
Определения
Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U1, I1 есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Термин замкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
- для постоянных напряжений
- для переменных напряжений
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
- Пример
 На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)Например, для приведённой на рисунке цепи, в соответствии с первым правилом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.
Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.
В соответствии со вторым правилом, справедливы соотношения:
Снова, полученная система уравнений, полностью описывает анализируемую цепь и её решение определяет все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.
Особенности составления уравнений для расчёта токов и напряжений
Если цепь содержит узлов, то она описывается уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.
Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений.
- Правила Кирхгофа, записанные для узлов или контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
- Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
- положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
- Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
- При записи линейно независимых уравнений по второму правилу Кирхгофа, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
- В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение, в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.
Примечания
Литература
- Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
- Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.