Правила (законы) Кирхгофа простыми словами: формулировки и расчеты

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Первое правило Кирхгофа

Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.

Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.

На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.

Рис. 1. Схема контура

Ток I₁ входит в узел A, образованный ветвями контура. На схеме электрический  заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I₁ = I₂ + I₃.

На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i

1, i₂, i₃, i₄ то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i₁ + i₂ + i₃ + i₄ = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Рис. 2. Абстрактный узел

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.

Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.

Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».

Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.

Второе правило Киргхофа

Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.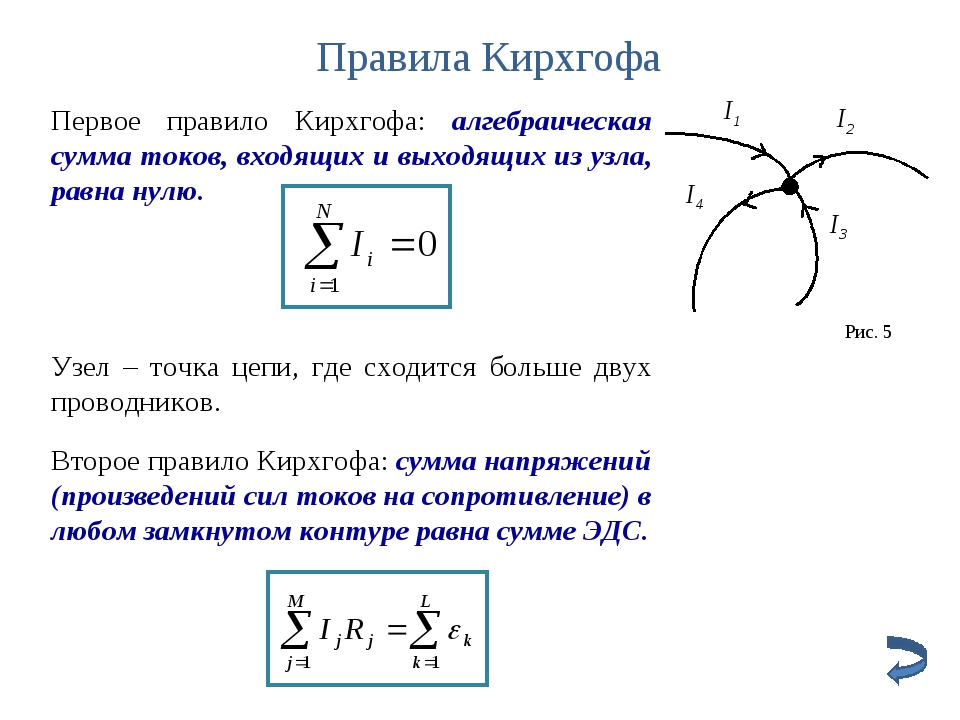

Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.

При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Рис. 4. Иллюстрация второго правила Кирхгофа

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.

Формулировки уравнений общего характера:

, где где L_k и C_k – это индуктивности и ёмкости, соответственно.

Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

Рис. 4. Магнитные контуры цепей

В частности: ∑Ф=0.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Примеры расчета цепей

Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i₁, i₂, i₃, i₄. Из них –  два входящие ( i₂, i₃) и два исходящие из узла (i₁, i₄). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.

Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i₁ + i₂ + i₃ – i₄ = 0.

На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.

Рассмотрим алгоритм решения на примере рис. 5.

Рис. 5. Пример для расчёта

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:

1. 1 и 2.
2. 1 и 3.
3. 2 и 3.

Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I₁ +  I₂ –  I₃ = 0.

Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом

а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.

Пишем уравнения:

• I₁R₁ +  I₃ R₃ = E₁;
• I₂R₂ +  I₃R₃ = E₂.

Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:

1. I₁ = 1,36 (значения в миллиамперах).
2. I₂ = 2,19 мА.;
3. I₃ = 3,55 мА.

Потенциал узла а равен: U_a = I₃*R₃ = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:

E₁ – E₂ + I₁R₁+ I₂R₂ = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).

Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.

Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.

Электричество и магнетизм

Приведем пример расчета токов в разветвленной цепи (рис.

4.25).

Рис. 4.25. Пример разветвленной цепи 

Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I₁, участок b–d с током I₂ и участок b–c–d с током I₃ (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (

n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике? 

Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным. В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25). 

Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла b, куда входит ток I₂ и выходят токи I₁ и I₃

(4.45)

Шаг третий. Нам осталось написать уравнения (в нашем случае — два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.

Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока, I₁ и I₂, направления которых совпадают с выбранным направлением обхода. ЭДС также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как

(4.46)

В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока I₁ и I₃, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых  войдет в уравнения со знаком плюс, а  — со знаком минус. Уравнение для этого замкнутого пути имеет вид

(4.47)

 

Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I₃ через I₁ из уравнения (4.47)

(4.48)

I₂ через I₁ с помощью уравнения (4. 46)

(4.49)

и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное I₁, которое находится без труда

(4.50)

Подставляя это выражение в (4.48), (4.49), находим соответственно токи I₂, I₃

(4.51)

Второе правило Кирхгофа, теория и примеры

Второе правило Кирхгофа – это один из приемов, который применяют для упрощения расчетов параметров сложных разветвленных цепей постоянного тока. Электрические цепи постоянного тока могут иметь в своем составе большое число сопротивлений, источников тока, множество замкнутых контуров и узлов. Параметры цепи постоянного тока любой сложности можно вычислить, если применять законы Ома и законы сохранения заряда. Правила Кирхгофа являются следствиями вышеназванных законов, с их помощью можно значительно упростить процедуру написания уравнений, связывающих силы тока, сопротивления и электродвижущие силы (ЭДС) для рассматриваемой цепи.

Первое правило Кирхгофа называют правилом узлов. Оно предназначено для написания уравнения для токов, которые сходятся в узле цепи.

Второе правило Кирхгофа относится к замкнутым контурам, которые выделяют в разветвленной цепи. Это правило еще называют правилом контуров.

Формулировка второго правила Кирхгофа

Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В виде формулы второй закон Кирхгофа записывают как:

   

Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа — это следствие закона Ома.

Количество независимых уравнений, получаемых при использовании правил Кирхгофа

Применяя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже рассмотренных контуров. Число независимых контуров () равно:

   

где – число ветвей в цепи; – количество узлов.

Количество независимых уравнений, которые дадут первое и второе правила Кирхгофа равно ():

   

Вывод: количество независимых уравнений, полученных с использованием обоих правил Кирхгофа равно числу разных токов в рассматриваемой цепи.

Примеры решения задач

§ 18. Правила Кирхгофа — ЗФТШ, МФТИ

Соединения резисторов и источников в сложных цепях не всегда можно свести к совокупности последовательного и параллельного их соединений. Для расчётов сложных цепей удобно применять правила Кирхгофа.

Узлом электрической цепи будем называть точку, где сходятся не менее трёх проводников. Токи, подходящие к узлу, будем считать положительными, а выходящие из узла – отрицательными. Узел – это не обкладки конденсатора, где может происходить существенное накопление заряда. Отсюда следует первое правило Кирхгофа: 

алгебраическая сумма токов в узле равна нулю.

Участок цепи между двумя узлами называется ветвью. Возьмём в сложной цепи произвольный замкнутый контур, состоящий из отдельных ветвей. Выберем направление обхода контура по часовой стрелке или против. ЭДС в каждой ветви контура будем считать положительной, если направление её действия совпадает с выбранным направлением обхода контура, а в противном случае – отрицательной. Падение напряжения (произведение тока на сопротивление) в любой ветви контура будем считать положительным, если направление тока в этой ветви совпадает с направлением обхода контура, в противном случае – отрицательным. Записав для каждой ветви контура уравнение закона Ома для участка цепи, содержащего ЭДС, и сложив все уравнения, получим второе правило Кирхгофа:

в произвольном замкнутом контуре любой электрической цепи сумма падений напряжений во всех ветвях контура равна алгебраической сумме ЭДС во всех ветвях контура.

Оба правила Кирхгофа справедливы не только для постоянных во времени значений всех величин, входящих в соответствующие уравнения, но и для их мгновенных значений.

При составлении уравнений по правилам Кирхгофа нужно придерживаться следующих рекомендаций. Если в цепи содержится nn узлов, то по первому правилу Кирхгофа можно составить только n–1n–1 независимых уравнений. При составлении уравнений по второму правилу Кирхгофа надо следить, чтобы в каждом новом контуре была хотя бы одна ранее не использованная ветвь. Отступление от этих рекомендаций приводит к появлению уравнений, являющихся следствием системы ранее составленных уравнений. В процессе решения такой «переполненной» системы может возникнуть тождество 0=00=0, что приводит в замешательство решающего из-за «исчезновения» неизвестных системы.

Рис. 18.1

В схеме на рис. 18.1 E1=4,2{\mathcal E}_1=4,2 B, E2=3,8{\mathcal E}_2=3,8 B, R1=R2=10R_1=R_2=10 Ом, R3=45R_3=45 Ом. Найти силу и направление тока во всех участках цепи. Считать, что внутренние сопротивления источников вошли в R1R_1, и R2R_2.

Зададим направления токов произвольно, например так, как показано на рис. 18.1.
Для нахождения трёх неизвестных токов надо составить три независимых уравнения. В схеме n=2n=2 узла. По первому правилу Кирхгофа составляем n-1=1n-1=1 уравнение. Для узла `C`:

I1-I2+I3=0I_1-I_2+I_3=0.

Недостающие два уравнения составляем по второму правилу Кирхгофа для контуров `ABCA` и `ABCDA`: 

I1R1-I3R3=E1I_1R_1-I_3R_3={\mathcal E}_1, I1R1+I2R2=E1-E2I_1R_1+I_2R_2={\mathcal E}_1-{\mathcal E}_2.

Решение системы полученных трёх уравнений в общем виде трудоёмко и даёт громоздкие выражения для токов. Систему удобно решать, подставив в неё значения ЭДС и сопротивлений: 

I1-I2+I3=0I_1-I_2+I_3=0, 10I1-45I2=4,210I_1-45I_2=4,2, 10I1+10I2=0,410I_1+10I_2=0,4.

Решая систему последний трёх уравнений, находим:

I1=0,06I_1=0,06 A, I2=-0,02I_2=-0,02 A, I3=-0,08I_3=-0,08 A.

Отрицательные значения токов I2I_2 и I3I_3 говорят о том, что истинные направления этих токов противоположны указанным на рис. 18.1.

Уравнения Кирхгофа для электрических цепей

Расчет сложных (разветвленных) сетей постоянного тока заключается в отыскании по заданным сопротивлениям участков цепи и приложенных к ним ЭДС сил токов в каждом участке. Для решения этой группы задач применяют правила (иногда в литературе их называют законами, что не корректно) Кирхгофа.

Сформулируем правила (уравнения) Кирхгофа. Но прежде, определим, что узлом в разветвленной цепи называют точку (на рисунке это точка А), в которой имеется более двух возможных направлений тока (рис. 1). В узле сходится более двух проводников.

рис. 1

Первое правило (уравнение) Кирхгофа

Первое правило Кирхгофа (правило узлов): алгебраическая сумма токов сходящихся в узле, равна нулю:

   

где n- количество проводников, сходящихся в узле. Надо отметить, что положительными считают токи, подходящие к узлу, отрицательными – токи, отходящие от него. Если рассмотреть рис.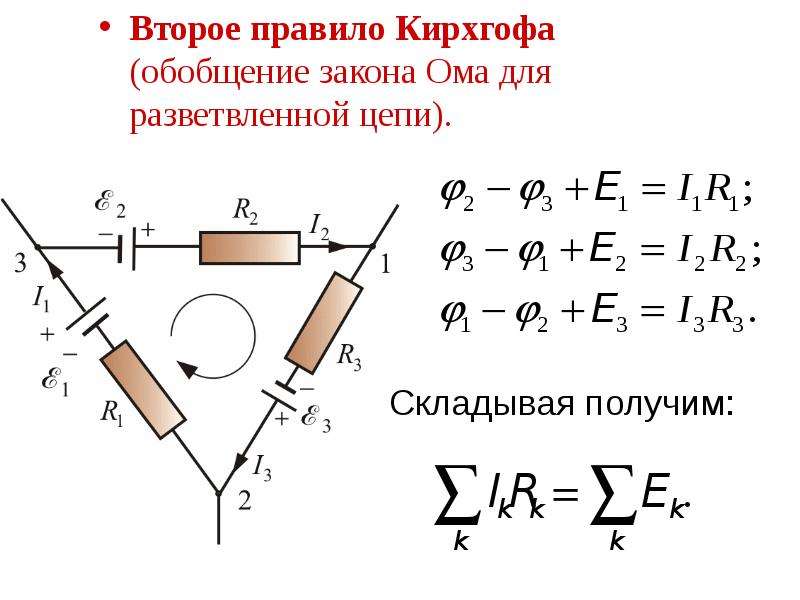 1, то , а остальные токи отрицательные.

Второе правило (уравнение) Кирхгофа

Второе правило Кирхгофа (правило контуров): в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме приложенных в нем ЭДС :

   

При использовании второго правила Кирхгофа выбирают определенное направление обхода контура. Токи , совпадающие по направлению с направлением обхода, считают положительными. ЭДС источников тока считают положительными, если они создают токи, направленные в сторону обхода контура.

Таким образом, порядок расчёта цепи постоянного тока с использованием правил Кирхгофа следующий:

1. произвольным образом выбираем направления токов во всех участках цепи;
2. для m узлов цепи записываем m-1 независимых уравнений правила узлов;
3. выделяем произвольные замкнутые контуры так, чтобы каждый новый контур содержал хотя бы один участок цепи, не входящий в уже рассмотренные контуры. В разветвленной цепи, состоящей из p ветвей (участков цепи между соседними узлами) и m узлов, число независимых уравнений правила контуров равно p-m+1.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

1.2 Правила Кирхгофа — Законы постоянного тока

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рисунок 1.1) Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.

Рисунок 1.1
Узел электрической цепи. I1, I2 > 0; I3,I4 < 0

В узлах цепи постоянного тока не может происходить накопление зарядов.

Первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + … + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называютсямконтурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

Рисунок 1.2
Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.3.

Рисунок 1.3.
«Правила знаков»

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I1R1 = Δφbc – 1.

Для участка da: I2R2 = Δφda – 2.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:

I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2.

Аналогично, для контура adef можно записать:

– I2R2 + I3R3 = 2 + 3.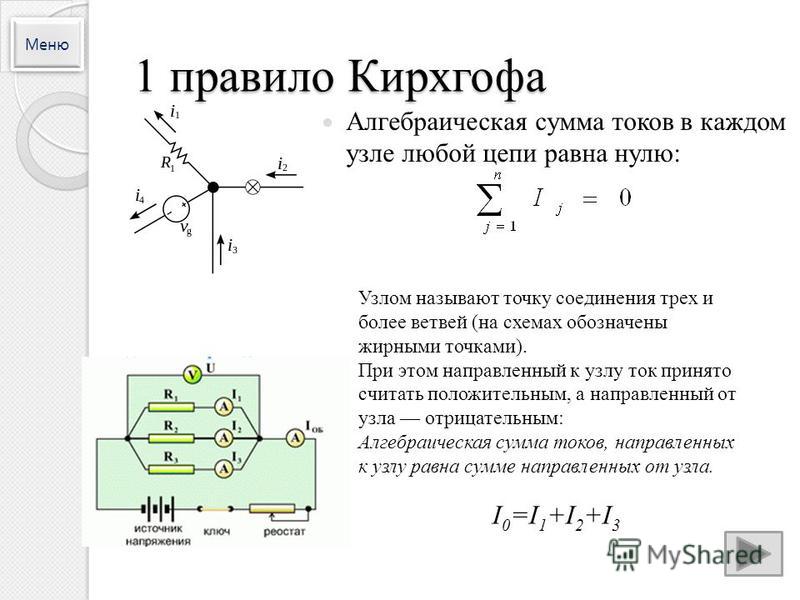

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:

I1R1 + I2R2 = – 1 – 2,

– I2R2 + I3R3 = 2 + 3,

– I1 + I2 + I3 = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

Модель. Цепи постоянного тока

Модель. Конденсаторы в цепях постоянного тока

4.4. Разветвленные цепи. Правила Кирхгофа

Расчет разветвленных цепей значительно упрощается, если пользоваться правилами, сформулированными немецким физиком Г. Р. Кирхгофом. Этих правил два.

Первое из них относится к узлам цепи. Узлом называется точка, в которой сходится более чем два проводника (рис. 4.4). Ток, текущий к узлу, считается положительным, текущий от узла имеет противоположный знак. Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю:

.

Это правило вытекает из уравнения непрерывности, т. е., в конечном счете, из закона сохранения заряда. Число уравнений, составленных по первому правилу Кирхгофа, должно быть на одно меньше, чем число узлов в исследуемой цепи.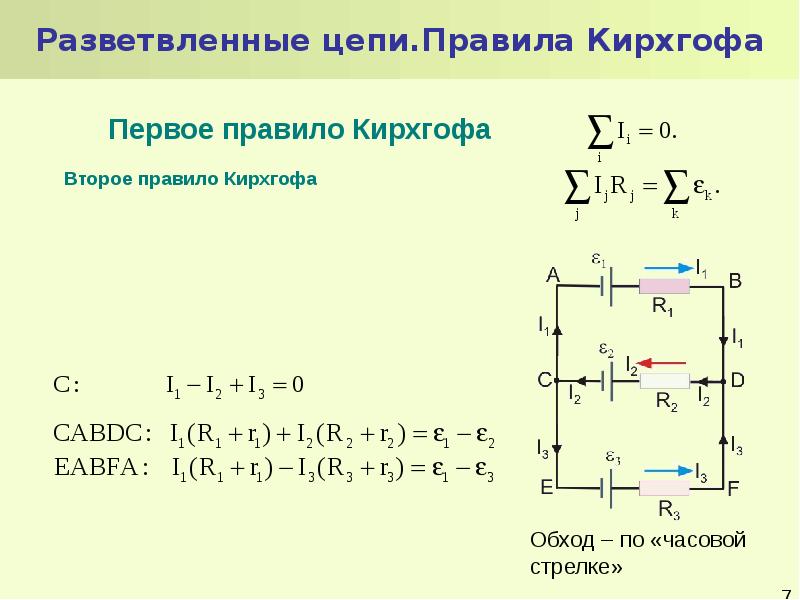 Этим обеспечивается линейная независимость получаемых уравнений.

Второе правило относится к любому выделенному в разветвленной цепи замкнутому контуру (например, 1-3-2) (см. рис. 4.5). Зададим направление обхода, изобразив его стрелкой. Применим к каждому из неразветвленных участков контура закон Ома:

; .

При сложении этих выражений получается одно из уравнений

; ,

которое выражает второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре.

Подобные уравнения могут быть составлены для всех замкнутых контуров, существующих в данной разветвленной цепи, однако их число должно быть ограничено уравнениями для независимых контуров, в которых встречается хотя бы один ток, не входящий в остальные.

При составлении уравнений согласно второму правилу Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода.

Например, ток нужно считать положительным, он течет по направлению обхода. ЭДС также нужно приписать знак «плюс», так как она действует в направлении обхода. Току и ЭДС приписывается знак «минус».

На практике, при решении задач, при составлении уравнений направления токов выбирают произвольно и в соответствии с этим применяют правило знаков.

Действительное направление токов определится решением задачи: если какой-либо ток окажется положительным, то его направление выбрано правильно, если отрицательным, то в действительности он течет противоположно выбранному направлению.

Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, равно числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы ЭДС и сопротивления, то могут быть вычислены все токи.

---

Вопросы

1) На чем основаны правила Кирхгофа
2) Сколько независимых уравнений необходимо составить при использовании первого правила Кирхгофа
3) Сколько независимых уравнений, составленных по второму правилу Кирхгофа, необходимо, для вычисления токов в цепи

Правил Кирхгофа

Правил Кирхгофа
Далее: Конденсаторы в цепях постоянного тока Up: Электрический ток Предыдущий: резисторов последовательно и Теперь мы знаем почти все, что нам нужно знать об ЭДС и резисторах. Тем не мение, было бы удобно, если бы мы могли обобщить наши знания в ряд удобных правил, которые затем можно использовать для анализа любой цепи постоянного тока. По сути, это то, что сделал немецкий физик Густав Кирхгоф в 1845 году. когда он предложил два простых правила для работы с цепями постоянного тока.

Первое правило Кирхгофа применяется к точкам соединения в цепях постоянного тока ( т. Е. , точки соединения трех или более проводов). Правило соединения:

Сумма всех токов, поступающих в любую точку соединения, равна сумма всех токов, выходящих из этой точки соединения.

Это правило легко понять. Как мы уже отмечали, если это правило не были удовлетворены, то в точках стыковки накапливались бы заряды, нарушая наши фундаментальное установившееся предположение.

Второе правило Кирхгофа применяется к петлям в цепях постоянного тока.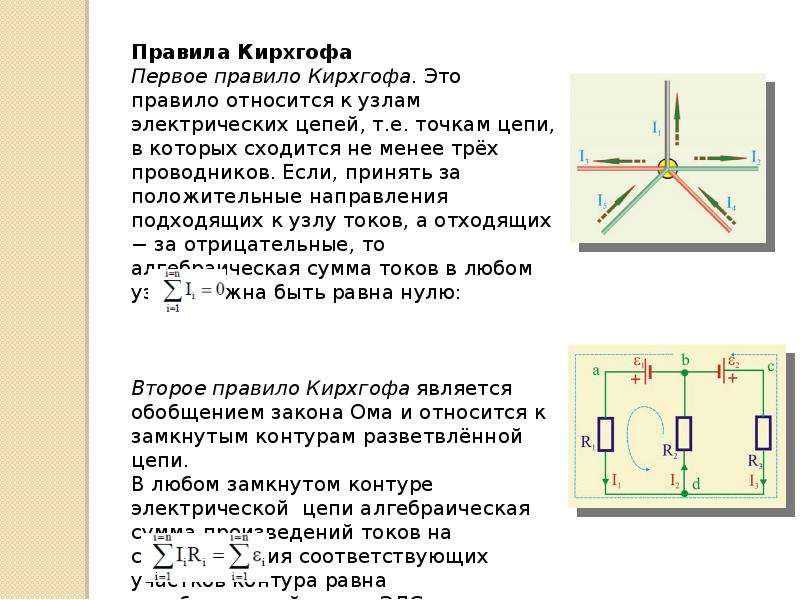 Правило цикла:

Алгебраическая сумма изменений электрического потенциала, встречающихся в полный обход любого замкнутого контура равен нулю.

Это правило тоже легко понять. Мы уже видели (в разделе 5) что нулевая чистая работа сделана в медленном перемещении заряда по некоторому замкнутому контуру в электростатическом поле. Поскольку проделанная работа равна произведению заряда и разницы по электрическому потенциалу между начальной и конечной точками из цикла следует, что эта разница должна быть равна нулю.Таким образом, если мы применим это результат к частному случаю петли в цепи постоянного тока, мы сразу приходим ко второму правилу Кирхгофа. При использовании этого правила мы сначала выбираем замкнутый контур в цепи постоянного тока, который мы анализируем. Затем мы решаем, собираемся ли мы пройти через это петля по часовой стрелке или против часовой стрелки (выбор произвольный). Если пересечь источник ЭДС в направлении увеличения потенциала тогда изменение потенциала есть. Однако, если ЭДС проходит в противоположном направлении, то изменение потенциала будет.Если резистор, несущий ток, проходит в направлении тока, то изменение потенциал есть. Наконец, если резистор проходит в в противоположном направлении, то изменение потенциала равно.

Токи, протекающие по общей цепи постоянного тока, всегда можно найти, применив Первое правило Кирхгофа для всех узловых точек, Второе правило Кирхгофа для всех петель, а затем решение Полученные таким образом совместные алгебраические уравнения. Эта процедура работает независимо от сложности рассматриваемой схемы ( e.грамм. , Кирхгофа правила используются в полупроводниковой промышленности для анализа невероятно сложные схемы, вытравленные на поверхности кремниевых пластин, которые используются для построить центральные процессоры компьютеров).

---

Далее: Конденсаторы в цепях постоянного тока Up: Электрический ток Предыдущий: резисторов последовательно и

Ричард Фицпатрик 2007-07-14

Когда использовать законы Кирхгофа

Когда использовать законы Кирхгофа

Когда использовать законы Кирхгофа

Вот три типичных принципиальные схемы, которые, возможно, потребуется решить (например,грамм. учитывая сопротивление всех резисторов и напряжений всех батарей, найдите все токов).

Рисунок слева можно легко решить с помощью правила добавления сопротивлений параллельно и последовательно. Резисторы R ₃ , R ₄ и R ₅ можно рассматривать, как если бы они были одним резистором сопротивления R ₃₄₅ .Это эффективное сопротивление можно добавить параллельно с R ₂ дать еще одно эффективное сопротивление R ₂₃₄₅ . Наконец, это эффективное сопротивление может быть добавлено последовательно с R ₁ для расчета чистого сопротивления R = R ₁ + R ₂₃₄₅ видел аккумулятор. Это значение R можно использовать для вычисления тока, производимого аккумулятор. Ток от батареи весь течет через R ₁ , поэтому падение напряжения на R ₁ можно вычислить по закону Ома. Поскольку напряжение аккумулятора известно, вы можете затем вычислите падение напряжения на R ₂ . Теперь применяя закон Ома к R ₂ сообщает вам ток через него; и т.п.Таким образом вы в конечном итоге выясните токи и падения напряжения. везде в цепи.

Середина и правые фигуры не могут быть решены такой простой (?) стратегией. Вместо, вы должны записать законы Кирхгофа и решить уравнения.

Для В качестве примера рассмотрим правую фигуру. Дайте имена неизвестные токи i 1 , i 2 и i 3 через 3 резистора (выбирая направления ad lib). Эти неизвестные токи можно найти, решив 3 уравнения:

1. Первый уравнение описывает текущее сохранение в узле.
2. Второй уравнение выражает требование, чтобы потери напряжения отмените прирост напряжения для петли слева.
3. Третий уравнение выражает то же самое для петли справа.Обратите внимание, что если сделать цикл против часовой стрелки, один идет против тока через R ₃ и знак этого термина поэтому напротив нормального.

Вы также можете написать уравнение для третьего контура, которое определяется перемещением по внешней стороне схемы. Это уравнение было бы немного сложнее потому что в нем задействованы обе батареи; но это не нужно, так как это будет просто линейной комбинацией уравнения. 2 и уравнение. 3 выше.

---

Примеры Законы Кирхгофа индекс Список лекций

Законы тока и напряжения Кирхгофа

Законы Кирхгофа действуют как лучший инструмент для методов анализа цепей. Работа Георга Ома (закон Ома) легла в основу создания Закона Кирхгофа (KCL) и Закона о напряжении Кирхгофа (KVL) Густавом Робертом Кирхгофом в 1845 году. Цель этого поста — дать лучшее понимание законов Кирхгофа о токе и напряжении. , его применение, преимущества и ограничения.

Законы Кирхгофа

Законы Кирхгофа — это два уравнения, которые касаются сохранения энергии и заряда применительно к электрическим цепям. Они очень важны при анализе замкнутых и сложных электрических цепей, таких как мостовые или Т-сети, в которых вычисление напряжений или токов, циркулирующих в цепи, становится затруднительным, используя только закон Ома.

Рис. 1 — Введение в Первый и Второй законы Кирхгофа

Законы тока и напряжения Кирхгофа

Законы тока и напряжения Кирхгофа можно разделить на два отдельных закона, т.е.д .:

• Текущий закон Кирхгофа (KCL) или Первый закон
• Закон напряжения Кирхгофа (KVL) или Второй закон

Текущий закон Кирхгофа (KCL) или Первый закон :

Первый закон из законов Кирхгофа является Текущий закон Кирхгофа. В нем говорится, что «Полный ток или заряд, входящий в соединение или узел, в точности равен току, выходящему из узла, поскольку в узле не происходит потери заряда». Это также можно сформулировать как сумму токов в сети проводников, встречающихся в узле, равной нулю.

Рис. 2 — Визуальное представление закона тока Кирхгофа

Из приведенного выше рисунка мы можем сделать вывод, что сумма токов, входящих и выходящих из узла, равна нулю (0). Ток, текущий по направлению к соединению, считается положительным, а ток, текущий от узла или соединения, считается отрицательным.

Другими словами, KCL можно определить как алгебраическую сумму всех токов, входящих и выходящих из узла, которые должны быть равны нулю, то есть I _в + I _{на выходе} = 0.

Закон Кирхгофа о напряжении (KVL) или Второй закон :

Второй закон Кирхгофа — это Закон Кирхгофа о напряжении. В нем говорится, что в любой сети с замкнутым контуром сумма значений ЭДС в любом замкнутом контуре равна сумме падений потенциала в этом контуре.

Рис. 3 — Визуальное представление закона Кирхгофа о напряжении

Другими словами, это также можно сказать как «Общее напряжение вокруг контура равно сумме всех падений напряжения в одном контуре». , что равно нулю.

Применение законов Кирхгофа

В число приложений входят:

• Их можно использовать для анализа любой электрической цепи.
• Расчет тока и напряжения сложных цепей.

Преимущества законов Кирхгофа

Преимущества:

• Легко вычислить неизвестные токи и напряжения.
• Упрощение и анализ сложных схем с обратной связью становится управляемым.

Ограничения законов Кирхгофа

Ограничение обоих законов Кирхгофа состоит в том, что они работают в предположении, что в замкнутом контуре нет флуктуирующего магнитного поля. Могут быть индуцированы электрические поля и ЭДС, что приводит к нарушению правила петли Кирхгофа в присутствии переменного магнитного поля.

  Читайте также:  Серия  Схема - Принцип работы, характеристики, применение, преимущества   Что такое параллельная схема - Как сделать, характеристики, применение   Вольтметр - Принцип работы, чувствительность к напряжению, типы и применения  

Кирхгофа Закон: определение и применение — видео и стенограмма урока

Законы Кирхгофа

Названы в честь их создателя, Густава Кирхгофа, Законы Кирхгофа могут помочь вам понять ток и напряжение в цепи, а также могут быть использованы для анализа сложных цепей, которые нельзя свести к одному эквивалентному сопротивлению, используя то, что вы уже знаю про последовательные и параллельные резисторы.

Закон Кирхгофа говорит, что сумма токов, входящих в переход, должна равняться сумме токов, выходящих из перехода. Ток в цепи никогда не расходуется, поэтому имеет смысл, что весь ток, который идет в переход, также должен возвращаться.

Закон петли Кирхгофа гласит, что сумма изменений напряжения вокруг и замкнутого контура в цепи всегда должна быть равна нулю. Это означает, что если вы сложите напряжение на каждом элементе схемы по всему контуру, вы получите ноль.

Пример проблемы

Давайте посмотрим, как использовать два закона Кирхгофа для анализа сложной схемы, подобной той, что сейчас на вашем экране:

Первым шагом является определение количества ветвей в цепи и определение переменной тока для каждой ветви. Вам нужно найти только один ток в каждой ветви, потому что каждая точка в ветви будет иметь точно такое же количество тока; но разные ветви могут иметь разные токи.

В этой схеме вы можете видеть, что у нас есть три ветви, и мы пометили три тока и определили их направление. Итак, как мы узнали направление тока в каждой ветви? Мы этого не сделали! В большинстве случаев в такой сложной цепи, как эта, вы не сможете определить, в каком направлении будет течь ток в ветви цепи, просто взглянув на нее.

Ничего страшного! Вам просто нужно выбрать направление и убедиться, что все ваши расчеты с ним согласуются.Если вы выбрали неправильное направление, при вычислении тока оно будет отрицательным. Это позволит вам узнать, что ток на самом деле идет в противоположном направлении от того, как вы предсказывали.

Теперь вы можете использовать закон соединений, чтобы написать первое уравнение, которое мы будем использовать для анализа этой схемы.

Следующим шагом является маркировка всех батарей и резисторов, чтобы вы знали направление напряжения на каждом из них. Отметьте батареи, посмотрев, какая сторона длиннее на принципиальной схеме. Условно, длинная сторона батареи на принципиальной схеме является положительной стороной, а короткая сторона — отрицательной стороной.

Мы маркируем резисторы в зависимости от направления, в котором через них проходит ток. Ток должен проходить через каждый резистор с ПОЛОЖИТЕЛЬНОГО на ОТРИЦАТЕЛЬНЫЙ. Сторона резистора, через которую ток проходит первой, должна быть обозначена положительной, а сторона, с которой он выходит, должна быть обозначена отрицательной.

Теперь мы готовы применить закон цикла. Прежде чем вы сможете написать какие-либо уравнения, вы должны сначала идентифицировать петли. Опять же, не имеет значения, в каком направлении вы рисуете петли, потому что закон петли Кирхгофа говорит нам, что сумма напряжений вокруг любого замкнутого контура равна нулю.

В этой задаче выберем эти две петли и обозначим их S1 и S2:

Начните с начала каждой петли и складывайте все напряжения, пока не вернетесь туда, откуда начали. Помните, что напряжение на резисторе можно найти с помощью закона Ома , который равен V = IR.

Используйте положительные и отрицательные знаки, которыми вы пометили батареи и резисторы, чтобы определить, нужно ли вам прибавлять или вычитать напряжение на каждом элементе схемы.

Если ваш контур переходит от отрицательного к положительному при перемещении по элементу схемы, вы прибавите напряжение к общему значению. Если при перемещении по элементу схемы оно меняется от положительного к отрицательному, вы ВЫЧИТАЕТЕ напряжение из общего значения.

Для двух циклов, показанных выше, вы должны получить следующие два уравнения закона цикла, которые вы сейчас видите на своем экране:

Теперь мы использовали законы Кирхгофа, чтобы получить три уравнения: одно из закона соединений и два из закона петли. Мы можем решить их как одновременную систему уравнений, чтобы найти ток в каждой ветви. Вы должны получить три тока:

Резюме урока

Давайте рассмотрим то, что мы узнали. Помните, что ток — это поток электронов по цепи, а напряжение — это разность электрических потенциалов между двумя точками в цепи. Законы Кирхгофа используются, чтобы помочь нам понять, как ток и напряжение работают в цепи. Их также можно использовать для анализа сложных схем, которые нельзя свести к одному эквивалентному сопротивлению, используя то, что вы уже знаете о последовательных и параллельных резисторах.

Кирхгоф изобрел два основных закона.

1. Закон Кирхгофа говорит, что сумма токов, входящих в переход, должна равняться сумме токов, выходящих из перехода.
2. Закон петли Кирхгофа гласит, что сумма изменений напряжения вокруг и замкнутого контура в цепи всегда должна быть равна нулю.

Теперь вы должны лучше понимать сложные схемы.

Правила Кирхгофа

Электрические цепи обычно состоят из ряда резисторов и ячеек, соединенных между собой иногда сложным образом.Выведенных нами ранее формул для последовательной и параллельной комбинации резисторов не всегда достаточно для определения всех токов и разностей потенциалов в цепи. Прежде чем понять эти законы, мы сначала определим несколько терминов.

1. Электрическая сеть : Термин «электрическая сеть» используется для обозначения сложной системы электрических проводников.
2. Соединение : Любая точка в электрической цепи, где два или более проводника соединены вместе, является соединением.
3. Петля или сетка : Любой замкнутый проводящий путь в электрической сети называется петлей или сеткой.
4. Филиал : Ветвь — это любая часть сети, которая находится между двумя узлами.

Первый закон Кирхгофа или правило соединения:

В электрической цепи алгебраическая сумма токов на любом соединении равна нулю. Или сумма токов, входящих в переход, равна сумме токов, выходящих из этого перехода.

Математически этот закон может быть выражен как

Знаковое соглашение для применения правила перехода:

1. Ток, текущий в сторону перехода, считается положительным.
2. Текущие от перехода токи считаются отрицательными.

Рис . В соединении а ток на выходе составляет I ₁ + I ₂ , а ток на входе составляет I ₃ . Правило соединения гласит: I ₃ = I ₁ + I ₂ . В точке h входящий ток составляет I ₁ . Есть только один ток, выходящий из h, и по правилу соединения он также будет I ₁ . Для циклов «ahdcba» и «ahdefga» правила цикла дают –30I ₁ — 41 I ₃ + 45 = 0 и –30I ₁ + 21 I ₂ — 80 = 0.

Второй закон Кирхгофа или правило петли:

В любом замкнутом контуре сети алгебраическая сумма зарядов в потенциале должна быть равна нулю. Или алгебраическая сумма ЭДС в любых контурах цепи равна сумме произведений токов и сопротивления в ней.

Математически правило цикла может быть выражено как

Соглашение о знаках для применения правила цикла:

1. В качестве направления обхода мы можем принять любое направление (по часовой стрелке или против часовой стрелки).
2. ЭДС ячейки считается положительной, если направление прохождения от ее отрицательной клеммы к положительной (через электролит).

Отчет лаборатории 8 Правила Кирхгофа PHYS 1434 — ЛАБОРАТОРИЯ ТЕХНОЛОГИЧЕСКОГО КОЛЛЕДЖА НЬЮ-ЙОРКА 6: Удельное сопротивление

Текст предварительного просмотра

ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ НЬЮ-ЙОРКА

LAB 6: Удельное сопротивление

Цель:

В этом лабораторном эксперименте мы узнаем о текущем правиле Кирхгофа.Мы сравните наш измеренный ток с расчетным с помощью KCL, чтобы увидеть их сходство, чтобы доказать, что наша стимуляция верна.

Данные и схема

• Во-первых, мы строим схему с использованием трех резисторов: 5 Ом, 20 Ом и усилитель; 50 Ом и 2 батареи: 6 В и усилитель; 12 В. Конец каждой петли сверху соединяется положительной стороной батареи. Мы поменяли батарейки, чтобы убедиться, что резистор 5 Ом и К положительному полюсу батарей подключены 50 Ом. Затем наблюдаем текущее поток через контур, как показано на рисунке 1:

Рисунок 1

• Во-вторых, мы начинаем измерять ток вокруг каждого резистора с помощью 3 амперметров, добавляя их в нашу схему, как показано на рисунке 2.

Расчет:

• В-третьих, как было предложено в видео, мы заменили одну из батарей и сделали Резистор 5 Ом подключается к минусовой клемме аккумулятора.

Рисунок 3

Для рисунка 3 I 1 = 0.49A, I 2 = 0,18 A & amp; I 3 = 0,31 А. Ток для всех резисторов равен течет в одном направлении и не приближается к среднему резистору, в отличие от первого схема. И ток по всей цепи изменился и сильно отличается от нашего расчетные значения для тока.

Заключение:

В заключение, в сегодняшней лаборатории мы узнали о том, как ток течет через параллельная схема с 3 резисторами. Самое важное, что мы узнали, — это правильно измерять ток от нашей стимуляции, мы должны были убедиться, что наши ЭДС (батареи) были подключены к резисторы с их положительных сторон на каждом конце. Мы смогли сопоставить наши текущие измерения от нашей стимуляции с нашими расчетами. Что показывает нашу стимуляцию был успешным с точки зрения правил Кирхгофа.

Самый быстрый словарь в мире: Vocabulary.com

Законы Кирхгофа (физика) два закона, управляющие электрическими сетями, в которых протекают устойчивые токи: сумма всех токов в точке равна нулю, а сумма приростов и падений напряжения вокруг любого замкнутая цепь нулевая

Borago officinalis европейское однолетнее волосистое растение с голубыми цветками, долгое время использовавшееся в фитотерапии и употреблявшееся в сыром виде, как салатная зелень, или приготовленное как шпинат

Galega officinalis высокий кустистый европейский многолетник, выращиваемый из-за его перистой листвы и тонких колосьев синих цветов; иногда используется в медицинских целях

Gorgonocephalus корзиночные звезды

75″>

грузовое судно судно, предназначенное для перевозки грузов

Закон Грешема (экономика): принцип, согласно которому, когда в обращении находятся два вида денег с одинаковой номинальной стоимостью, более ценные деньги будут накапливаться, а деньги с более низкой внутренней стоимостью будут циркулировать более свободно до тех пор, пока не появятся более ценные деньги. из обращения; плохие деньги вытесняют хорошие; приписывается сэру Томасу Грешэму

Veronica officinalis обыкновенный опушенный европейский многолетник с бледно-голубыми или сиреневыми цветками в пазушных кистях

Quercus phellos, средне-крупный лиственный дуб на востоке США, с длинными ланцетными листьями и мягкой прочной древесиной

47″>

Кирхгоф Немецкий физик, который вместе с Бунзеном был пионером в спектральном анализе и сформулировал два закона, регулирующих электрические сети (1824-1887)

Мелководная акула Carcharias taurus с острыми зазубренными зубами, обитающая по обе стороны Атлантики; иногда опасно для пловцов

Корсаковское психозное слабоумие, наблюдаемое на последних стадиях тяжелого хронического алкоголизма; включает потерю памяти о недавних событиях, хотя долговременная память не повреждена

Sarcophilus Тасманский дьявол

без признаков, без явных или индивидуальных характеристик

8″>

Джорджо Вазари Итальянский художник и историк искусства (1511–1574)

салат от шеф-повара Комбинированный салат, приготовленный по специальности шеф-повара

Церковь Саентологии — новая религия, основанная Л.Роном Хаббардом в 1955 году, для которого характерна вера в способность человеческого духа очиститься от прошлых болезненных переживаний посредством самопознания и духовного удовлетворения

Перевозка торговых судов, осуществляемая судами, принадлежащими одной стране или отрасли

Пурпура при болезни Верльгофа, связанная со снижением количества тромбоцитов в циркулирующей крови, которое может быть результатом множества факторов