Потенциал электростатического поля. Разность потенциалов

На прошлом уроке мы с вами говорили о том, что на помещённый в электростатическое поле пробный заряд, будет действовать сила, под действием которой заряд способен перемещаться вдоль линии напряжённости поля. Иными словами, электростатическое поле способно совершать работу, значение которой пропорционально величине переносимого заряда и зависит только от того, из какой и в какую точку поля заряд переносится:

При этом на замкнутой траектории работа сил электростатического поля равна нулю.

Напомним, что если работа сил поля не зависит от формы траектории и на замкнутой траектории равна нулю, то такое поле называется потенциальными. Следовательно, точечный заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем, значение которой определяют относительно произвольно выбираемой нулевой точки (чаще всего, это бесконечно удалённая точка поля).

В нулевой точке потенциальную энергию заряда в поле принимают равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершили бы силы поля при перемещении данного заряда из указанной точки поля в нулевую точку:

Из этого определения следует, что величина потенциальной энергии заряда в электростатическом поле пропорционально значению этого заряда:

Иными словами, если мы будем вносить в одну и туже точку электростатического поля пробные заряды, значения которых будут отличаться в два, три, четыре и так далее раз, то потенциальные энергии этих зарядов будут отличаться во столько же раз.

Однако, отношение потенциальной энергии пробного заряда в поле к значению этого заряда для данной точки поля остаётся неизменным:

Отношение потенциальной энергии пробного заряда, помещённого в данную точку поля, к величине этого заряда, называется потенциалом электростатического поля в данной точке пространства:

Обозначать потенциал мы будем греческой буквой «Фи» (φ).

Вы уже знаете, что силовой характеристикой электрического поля является напряжённость. Потенциал же характеризует энергетическое состояние поля в данной точке пространства.

Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, то потенциал поля в данной точке численно равен работе, совершаемой при перемещении пробного заряда из данной точки поля в бесконечность (то есть в нулевую точку):

Найдём формулу, по которой можно рассчитать потенциал электростатического поля, создаваемого точечным зарядом, на некотором расстоянии от него. Для этого запишем формулу для определения работы электростатического поля:

Здесь r — это расстояние от создающего поле заряда до исследуемой точки поля. А модуль напряжённости поля прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости:

Перепишем формулу для потенциала поля с учётом наших рассуждений.

После упрощения, получим формулу, по которой можно рассчитать потенциал электростатического поля точечного заряда на заданном расстоянии от него. Из формулы видно, что знак заряда-источника поля определяет знак потенциала этого поля.

По этой же формуле можно рассчитывать и потенциал поля, создаваемого равномерно заряженной проводящей сферой в точках, находящихся вне сферы. Для точек же, находящихся на поверхности и внутри сферы, в знаменателе формулы «Эр малое» заменяется на радиус сферы:

Если электростатическое поле создаётся системой зарядов, то имеет место принцип суперпозиции: потенциал такого поля в любой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом системы в отдельности:

Зная потенциал поля в данной точке, можно рассчитать потенциальную энергию заряда, помещённого в эту точку:

На прошлом уроке мы с вами отмечали тот факт, что работа сил электростатического поля по перемещению электрического заряда из начальной точки в конечную равна изменению потенциальной энергии, взятому с обратным знаком:

Давайте выразим потенциальную энергию через потенциалы поля в соответствующих точках:

Подставим значения потенциальных энергий в формулу для работы.

Как видно из полученной формулы, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек.

А теперь давайте разделим выражение для работы на величину переносимого заряда q₀:

Скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда, называется разностью потенциалов.

Как и изменение потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки.

Из определения следует, что единицей разности потенциалов в СИ является Дж/Кл. Эта единица называется вольтом, в честь итальянского учёного Алессандро Джузеппе Антонио Анастасио Джероламо Умберто Вольта.

1 В — это разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа 1 Дж.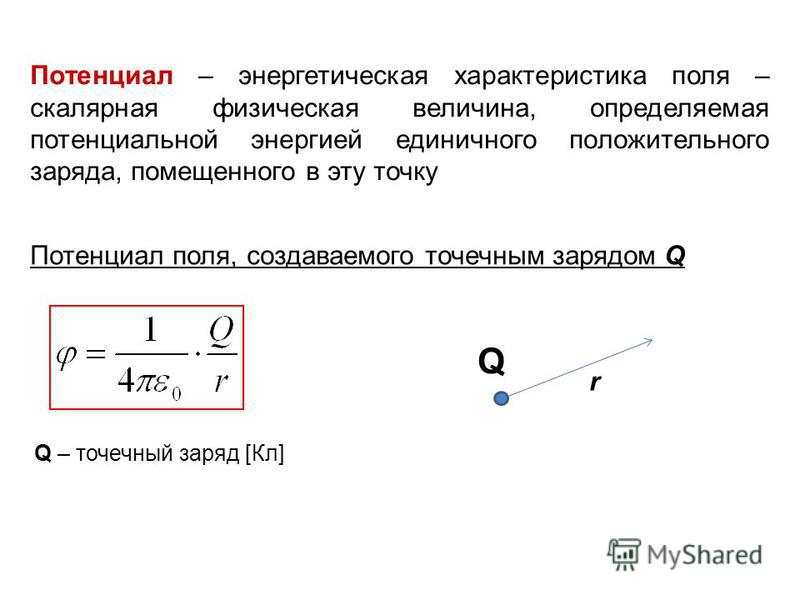

Как вы, наверное, догадались, разность потенциалов очень часто называют напряжением.

То есть напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.

Для закрепления нового материала, решим с вами несколько задач. Задача 1. В центре проводящей сферы с равномерно распределённым положительным зарядом в 45 нКл находится металлический шарик с отрицательным зарядом, модуль которого равен 17 нКл. Определите потенциал электростатического поля в точке, находящейся вне сферы на расстоянии 30 м от её центра.

Задача 2. Электрон влетает в однородное электростатическое поле по направлению силовой линии. Определите потенциал точки поля, в которой электрон поменяет направление движения, если в точке поля с потенциалом 1 В его скорость равнялась 300 км/с.

Электростатический (кулоновский) потенциал. Потенциал поля точечного заряженного тела (№1) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Особенности электрического взаимодей­ствия имеют много общего с гравитацион­ными. В частности, работа силы тяжести и работа электрической силы выражаются по­добными зависимостями.

Для силы тяготения:

A = mg(h₁ — h₂) = -(mgh₁ — mgh₂).

Для электрической силы:

A = qE(l₁ — l₂) = -(qEl₂ — qEl₁).

Из этого можно сделать вывод, что ра­бота электрической силы равна изменению потенциальной энергии тела, взятой с про­тивоположным знаком. То есть заряженное тело в однородном электрическом поле име­ет

потенциальную энергию

W_p = qEl.

Заряженное тело в электроста­тическом поле имеет потен­циальную энергию.

Потенциальная энергия заряженного те­ла определяется как электрическими харак­теристиками тела (его заряд), так и харак­теристиками выбранной точки электричес­кого поля — напряженность и координата. Изменение одной из трех характеристик ве­дет к изменению потенциальной энергии

тела в целом.

Значение потенциальной энер­гии заряженного тела зависит от его заряда, напряженности электрического поля и коорди­наты.

Исследуем одну из точек электрического поля с целью определения ее энергети­ческих характеристик. Для этого проведем несколько мысленных экспериментов с то­чечным заряженным телом.

Пусть точечное тело имеет заряд q₁ и находится в поле напряженностью E̅ на расстоянии l от источника поля. Его потен­циальная энергия будет равна

W_p1 = q₁El.

Увеличим значение заряда в 2 раза. Его потенциальная энергия будет

W_p2 = 2q₁El.

Таким образом, потенциальная энергия тела увеличится в 2 раза. Любые изменения заряда тела ведут к соответствующему из­менению его потенциальной энергии. Но в каждом случае отношение потенциальной энергии заряженного тела к его электри­ческому заряду в данной точке поля будет оставаться постоянным

W_p / q = φ.

Величина φ называется потенциалом точ­ки поля. Если в полученное соотношение подставить значение потенциальной энергии W_p, то получим

φ = qEl / q = El.

В значении потенциала отсутствуют ха­рактеристики тела, в том числе и его заряд. Поэтому можно считать справедливым ут­верждение, что потенциал является харак­теристикой электрического поля.

Физическая величина, которая является эне­ргетической характеристикой электрическо­го поля и равна отношению потенциальной энергии заряженного тела в электрическом поле к его заряду, называется потенциалом.

φ = W_p / q,

где W_p — потенциальная энергия заряжен­ного тела; q — заряд тела.

При измерении потенциала пользуются единицей, которая называется вольтом (В). Единица названа в честь итальянского уче­ного Алессандро Вольта.

Алессандро Вольта (1745 — 1825) — италь­янский физик и физиолог, один из ос­нователей учения об электрическом то­ке. Изобрел смоляной электрофор, чувст­вительный электроскоп с конденсато­ром, первый химический источник элект­рического тока, проводил широкие ис­следования электрических возбужде­ний мышц и нервов.

В соответствии с определением

1 В = 1 Дж / 1 Кл.

Применяются также кратные и дольные единицы потенциала:

1 милливольт = 1 мВ = 10^-3 В;

1 микровольт = 1 мкВ = 10^-6 В;

1 киловольт = 1 кВ = 10³ В;

1 мегавольт = 1 MB = 10⁶ В.

Все вышеизложенные соображения каса­ются однородного поля, напряженность ко­торого не зависит от координаты точки на­блюдения.

Но их можно распространить и на другие случаи, в частности на электрическое поле точечного заряженного тела. Оно неодно­родно, напряженность изменяется от точки к точке вдоль силовых линий по закону

E = (1 / 4πε₀) • (q / r²).

Воспользуемся определением потенциала точки электрического поля:

φ = El = (1 / 4πε₀) • (q • l / r²)

Учитывая, что l = r, получим

φ = (1 / 4πε₀) • (q / r).

Потенциал поля точечного заряженного тела уменьшается обратно пропорционально расстоянию.

Потенциал не имеет направле­ния.

Потенциал является скалярной величи­ной и не имеет направления. Поэтому мож­но говорить, что вокруг точечного заряжен­ного тела существует бесконечно большое множество точек, в которых потенциалы будут одинаковы. Все они будут лежать на сферической поверхности радиуса r с цент­ром в источнике поля. Такую поверхность называют эквипотенциальной. Материал с сайта http://worldofschool.ru

Рис. 4.60. Потенциал является аддитивной величиной

На понятие потенциала распространяет­ся принцип суперпозиции. Потенциал точ­ки, в которой действуют поля нескольких электрически заряженных тел, равняется алгебраической сумме потенциалов каждого из них (рис. 4.60). При этом считается, что потенциал поля отрицательно заряженного тела отрицательный.

φ_A = φ₁ + φ₂ — φ₃.

В общем случае

φ = φ₁ + φ₂ + φ₃ + … + φ_n.

Для измерения потенциала можно исполь­зовать электрометр, который в этом случае называют электростатическим вольтметром. Если внешний металлический корпус со­единить с поверхностью Земли, потенциал которой условно считается равным нулю, то электрометром можно измерять потенциал тела, соединенного с его стержнем.

На этой странице материал по темам:

• Урок физики. потенциальная энергия заряженного тела. потенциал

• Как определяется потенциал точечного заряженного тела

• Кулоновский потенциальная энергия

• Як визначається потенціал точкового зарядженого тіла?

Вопросы по этому материалу:

• Почему заряженное тело в электрическом поле имеет потен­циальную энергию?

• От чего зависит потенциальная энергия заряженного тела в электрическом поле?

• Какое свойство поля характеризует потенциал?

• Как определяется потенциал поля точечного заряженного тела?

• Какие единицы измерения потенциала?

• Каким прибором можно измерять потенциал?

• Как применяется принцип суперпозиции к потенциалу?

Химический потенциал — Физическая энциклопедия

ХИМИЧЕСКИЙ ПОТЕНЦИАЛ -термодинамич. функция состояния ,определяющая изменение потенциалов термодинамических при изменении числа частиц в системе и необходимая для описания свойств открытых систем (с перем. числом частиц).

X. п. m_i i-го компонента многокомпонентной системы равен частной производной от любого из термодинамич. потенциалов по кол-ву (числу частиц) этого компонента при пост. значениях остальных термодинамич. переменных, определяющих данный термодинамич. потенциал, напр. m_i = (дF/дN_i)_T,V,N (F-свободная энергия, Т-темп-ра, V-объём, ji). Т. о., в системах с перем. числом частиц в выражение для дифференциала, напр. dF, следует добавить величину :

где р — давление, S-энтропия. Наиб. просто X. п. связан с термодинамич. потенциалом G (см. Гиббса энергия): . Для однокомпонентной системы X. п. m = G/N,

т. е. представляет собой энергию Гиббса, отнесённую к одной частице. Вследствие аддитивности G, кроме давления и темп-ры, X. п. зависит только от концентраций отд. компонентов, но не от числа частиц в каждом компоненте. В простейшем случае идеальных газов m_i зависит только от концентрации i-го компонента:

где -полное число частиц, m^~_i-X. п. чистого i-го

компонента. Часто величины m_i удобно использовать в качестве независимых термодинамич. переменных вместо N_i. В переменных Т, V, m_i состояние системы характеризует термодинамич. потенциал

X. п. является термодинамич. параметром в большом каноническом распределении Гиббса для систем с перем. числом частиц. В качестве нормировочной постоянной X. п. входит в распределения Больцмана, Бозе — Эйнштейна и Ферми — Дирака для частиц идеальных газов (см. Статистическая физика ).В системах, к к-рым применима статистика Больцмана или Бозе — Эйнштейна, X. п. всегда отрицателен. Для ферми-газа X. п. при нулевой темп-ре положителен и определяет граничную ферми-энергию (см. Ферми-поверхность)и вырождения температуру. Если

полное число частиц в системе не фиксировано, а должно определяться из условия термодинамич. равновесия, как, напр., для фононов в твёрдом теле или для фотонов в случае равновесного теплового излучения, то равновесие характеризуется равенством нулю X. п.

Понятие X. п. позволяет сформулировать условия равновесия термодинамического. Одно из условий состоит в том, что X. п. любого компонента одинаков в разл. фазах и в разных местах одной фазы. Это обусловлено возможностью перераспределения частиц, приводящего к выравниванию X. п. Для систем в пространственно неоднородном внеш. поле равновесие означает, что

где m_i⁰ — X. п. в отсутствие поля, U_i(r)-потенц. энергия частиц i-го компонента во внеш. поле. Для газа в поле тяжести это условие приводит к барометрич. ф-ле для плотности газа. В случае заряж. частиц в электрич. поле (напр., в полупроводниках) величину m_i наз. э л е к т р о х им и ч е с к и м п о т е н ц и а л о м, оставляя название X. п. за m_i⁰. Равенство значений X. п. для частиц одного компонента, находящихся в разных фазах, определяет условия равновесия при фазовых переходах (Гиббса правило фаз)и хим. реакциях (закон действующих масс), ионизационное равновесие, свойства растворов (законы Вант-Гоффа, Генри, Рауля) и т. д. Если для частиц одного из компонентов переход из одной части системы в другую невозможен, то для этого компонента условия постоянства X. п. нарушаются и в системе возникает осмотическое давление (см. Осмос).

X. п. был введён Дж. У. Гиббсом (J. W. Gibbs) в 1875 при рассмотрении хим. равновесия в многокомпонентных системах, отсюда его название. Численно X. п. выражается в единицах энергии на единицу массы (Дж/кг), или на единицу кол-ва вещества (Дж/моль), или на 1 частицу.

Лит. см. при ст. Термодинамика. А. Э. Мейерович.

      Предметный указатель      >>   

Физико-техническая школа «Потенциал» :: Петрозаводский государственный университет

В дни школьных каникул прошли мероприятия в рамках физико-технической школы «Потенциал», организованной Физико-техническим институтом и Институтом математики и информационных технологий ПетрГУ совместно с Центром развития образования при поддержке отдела профориентационной работы.

Физико-техническая школа «Потенциал» была создана в целях повышения значимости физических и технических знаний и поиска эффективных форм работы с обучающимися. В этом году ее участниками стали около 50 человек из школ города Петрозаводска. Как и в предыдущие годы Школа работала на протяжении трех дней.

Начало занятий состоялись в стенах Физико-технического института. Участников поприветствовали заместитель директора Центра развития образования О.С.Серёдкина и И.В. Иванов, они пожелали ребятам удачи и успехов.

Путешествие в интересный мир науки ребята начали с лекции доцента кафедры физики твердого тела Т.А. Екимовой «Что мы знаем о кристаллах?». Ребята узнали, что такое кристаллы, какими они бывают и как их можно исследовать. Далее школьники приняли участие в астрономической интеллектуальной игре «Через тернии к звездам», которую провела для них доцент кафедры электроэнергетики и энергообеспечения предприятий Н.С. Скорикова.

После перерыва участники Школы отправились в Институт математики и информационных технологий, где доцент кафедры теории и методики обучения математике и информационно-коммуникационным технологиям в образовании Т. В. Бежану рассказала об Олимпиадных задачах по геометрии.

Второй день Школы ребята провели в научной лаборатории «Физики наноструктурированных оксидных пленок и покрытий». Заведующая лабораторией  профессор Н.М. Яковлева, а также сотрудники К.В. Степанова, А.Н. Кокатев и С.Г. Васильев  провели лекционно-практические занятия на тему: «Нанотехнологии здесь и сейчас». Во время занятий учащиеся узнали о том, что такое нанотехнологии и наноматериалы, как их можно исследовать  и каковы перспективы их использования в повседневной жизни. Познакомились с научными направлениями, реализуемыми в лаборатории, узнали о том, что такое наноструктурированные анодные оксидные пленки.

Финальный день работы школы начался в Институте математики и информационных технологий с занятия старшего преподавателя кафедры прикладной математики и кибернетики Ю.А. Дорофеевой «Игровые задачи».

После чего ребята отправились в Физико-технический институт. Участники Школы вместе со старшим преподавателем кафедры общей физики Е. М. Тетелевой обсудили свойства бумаги – как сделать ее более прочной, как пройти через открытку и многое другое. Сотрудник кафедры физики твердого тела О.В. Спирин продемонстрировал ребятам настоящий физический фейерверк – ребята смогли пронаблюдать различные лазерные установки и даже прикоснуться к молнии. В завершении доцент кафедры общей физики О. В. Сергеева, вместе со своими помощниками – студентами физико-технического института — продемонстрировали участникам школы увлекательные эксперименты. Ребята узнали, что такое гироскоп, какими свойствами обладают жидкости, и можно ли забить гвоздь в доску, которая лежит на неньютоновской жидкости.

 Мероприятие прошло в рамках реализации Программы развития опорного университета.

 

Электростатика. Потенциал электростатического поля. Напряжение. (Лекция 2.2)

Кафедра физики
Лекция 2_2
ЭЛЕКТРОСТАТИКА
ПЛАН ЛЕКЦИИ
1. Потенциал электростатического поля. Напряжение.
2. Электродвижущая сила.
3. Вычисление потенциалов электростатических полей :
— Потенциал поля бесконечной заряженной плоскости
— Потенциал поля двух разноименно заряженных плоскостей
— Потенциал поля бесконечного заряженного цилиндра
— Потенциал поля объемно-заряженного шара
Общая физика. «Электростатика»
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
F
E
— напряженность
qпр
Wp
— потенциал
qпр
Кафедра физики
основные характеристики
электростатического поля
Напряженность — силовая характеристика поля
Потенциал — это энергетическая характеристика поля, т.к. он
определяет потенциальную энергию зарядов по отношению к полю.
Связь между напряженностью и потенциалом выражается формулой
E qrad
ex
ey
e z
y
z
x
Общая физика. «Электростатика»
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Электростатическое поле является одномерным, если
характеристики поля зависят лишь от одной координаты.
Поля сферической, цилиндрической и плоской симметрий –
одномерные поля. В полях сферической и цилиндрической
симметрий характеристики зависят от радиальной координаты r,
центра или оси симметрии. Для этого
которая отсчитывается от
случая формула связи E и выглядит следующим образом:
d 0
E r
r
dr
0
r — единичный вектор, характеризующий направление
Формула используется при расчете электрических полей для
нахождения напряженности E r по известному потенциалу r .
Общая физика. «Электростатика»
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Обратная задача – определить связь с E.
В скалярной форме связь и E выглядит как d E r dr.
Тогда
d E r dr
r
r
r
r0
r0
r r0 E r r dr
r
или
Пусть
r0 0
r0
r0
Тогда
r E r r dr
r
Эта формула используется для определения потенциала
известной напряженности E r r .
Общая физика. «Электростатика»
r по
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Электрическое напряжение.
Рассмотрим в поле вектора E произвольную кривую l, соединяющую
точки 1 и 2, и зададим на ней положительное направление
2
малые
Разобьем кривую 1 – 2 на
El
векторные элементы dl
и
составим для каждого элемента
скалярное произведение E , dl
dl
E
1
Проинтегрируем это произведение вдоль всей кривой l
E,dl El dl U
l
l
Этот интеграл называют криволинейным интегралом
вектора
кривой l или напряжением поля вектора E вдоль кривой l
Общая физика. «Электростатика»
E вдоль
Кафедра физики
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Электрическое напряжение.
2
El
2
dl
1
E
l
E,dl El dl U
l
Напряжение поля вектора E вдоль кривой l
показывает, в какой мере вектор E
dl кривой l.
проецируется на элементы
Поскольку вектор E
имеет смысл силы,
действующей на единичный положительный
заряд, то интеграл выражает работу поля по перемещению
такого заряда вдоль кривой l.
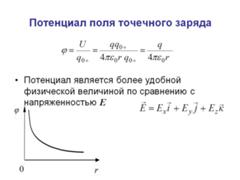
Работа сил поля над зарядом q равна произведению величины заряда
на разность потенциалов в начальной и конечной точках: A12 q 1 2
1
Тогда, обозначив точки 1, 2 на кривой 1 и 2 , для единичного
положительного заряда можно записать интеграл в виде
U
Общая физика. «Электростатика»
l
E, dl 1 2
Кафедра физики
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
U 1 2 Отсюда следует, что
Электрическое напряжение.
Электрическое напряжение вдоль кривой не зависит от
формы кривой и определяется только положениями
начальной и конечной точек
2
l 21
Если кривая замкнутая, то интеграл, имеет
название – циркуляция векторного поля
(циркуляция вектора напряженности) по
контуру
Рассмотрим замкнутый контур L l12 l 21
2
l12
1
1
L
Запишем для контура L
E, dl E, dl E, dl ( 1 2 ) ( 2 1 ) 0
Общая физика. «Электростатика»
l12
l21
ПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Электрическое напряжение.
Запишем определение:
Циркуляция вектора напряженности электростатического поля по
контуру называется электродвижущей силой это контура (ЭДС)
Исходя из этого определения, полученное соотношение для замкнутого
контура
E , dl 0
L
можно сформулировать в виде нового определения
В электростатическом поле ЭДС замкнутого контура равна нулю
Общая физика. «Электростатика»
Кафедра физики
Расчет потенциалов электростатических полей.
1. Поле бесконечной однородно заряженной плоскости
Пусть поверхностная плотность положительного заряда во всех
точках плоскости одинакова и равна
1
E
2
E
Электростатическое поле можно
изобразить графически не только
силовыми линиями, но и с помощью
эквипотенциальных поверхностей.
Эквипотенциальной поверхностью
называется геометрическое место
точек с одинаковым потенциалом.
Эквипотенциальные поверхности поля бесконечной однородно
заряженной плоскости представляют собой плоскости, параллельные
носителю заряда
Кафедра физики
Расчет потенциалов электростатических полей.
1. Поле бесконечной однородно заряженной плоскости
1
2
E
E
1
Поскольку
,
E
2 0
2
Найдем разность потенциалов между
точками 1 — 2, которые соответствуют
потенциалам поля 1 и 2 . Пусть эти
точки расположены на расстоянии x1
и. x 2 от заряженной плоскости.
Для однородного поля с плоской
симметрией связь между E и .
выражается формулой
x2
x2
x1
x1
2 1 E x x dx E dx E x1 x 2
окончательно получим:
x1 x2
2 1
2 0
Кафедра физики
Расчет потенциалов электростатических полей.
2. Поле двух разноименно заряженных плоскостей.
E
1
d
2
Две параллельные бесконечные плоскости
заряжены разноименно с одинаковой по
величине поверхностной плотностью
Поле сосредоточено между плоскостями и
однородно. В области между плоскостями
E
0
Вне плоскостей
Формула связи между
После интегрирования получим
Подставим в формулу выражение
для E , получим окончательно
иE
:
E 0
d Edx
d
d
0
0
1 2 Edx E dx Ed
d
1 2
0
Кафедра физики
Расчет потенциалов электростатических полей.
2. Поле двух разноименно заряженных плоскостей.
E
1
d
2
Подставим в формулу выражение
для E , получим окончательно
d
1 2
0
Кафедра физики
Расчет потенциалов электростатических полей.
3. Поле бесконечного заряженного цилиндра
Поле создается бесконечной положительно
заряженной цилиндрической поверхностью
Напряженность поля в каждой точке
направлена
вдоль
радиальной
прямой,
перпендикулярной к оси цилиндра
Определим разность потенциалов между
точками r1 и r2 .
1
E r
2 0 r
r R
r dr
r2
1 2 E r dr
ln
r
2 0 r r 2 0 r1
r2
2
1
1
r2
1 2
ln
2 0 r1
E
E
1
2
r1
r2
Кафедра физики
Расчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
Рассмотрим область пространства, представляющую собой шар
радиусом R с объемной плотностью заряда .
Найдем потенциал электрического поля
внутри и вне шара.
0 r R
— поле внутри шара
R
1
q
E r
r
3
4 0 R
q
4 0 r
3 0
r R
— поле вне шара
E r
E r
r
2
E r
R3
3 0 r 2
Кафедра физики
Расчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
Определим r по известной величине E r . Уравнение связи для
одномерного поля со сферической симметрией выглядит так:
r
R
r0
r E r r dr
r
Интегрирование проведем по радиальной
прямой r, соединяющей центр шара с точкой,
удаленной в бесконечность
— поле внутри шара 0 r R
Для определения r внутри шара интегрирование
проведем через две области с разными формулами
напряженности.
Кафедра физики
Расчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R 3 dr
r
rdr
2
3 0 r
3 0 R r
R
R
Вычислим интегралы:
R
dr
3
r
( rdr R 2 )
3εε0
r
R
r
ρ
Первый интеграл:
R
1 2 2
rdr R r
2
r
Второй интеграл:
dr
1
3 1
3 1
R
R R
R2
2
R
r R
r
R
3
Кафедра физики
Расчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R
В итоге получим
r
1 2
2 R 2 ρ 3 R 2 1 r 2 ρ 3 R 2 1 r 2
R
r
3εε
3εε0 2
2 3εε0 2
3
0 2
ρ
Окончательно
2 1 2
r
R r
2εε0
3
ρ
Кафедра физики
Расчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R
— поле вне шара
r R
Для внешней области интегрируем по той же линии
от r r R до .
r Er r dr
r
ρ R3
dr
3εε0 r r 2
Такой интеграл мы рассмотрели выше —
В итоге для внешней области шара получим
r
dr
1
r2 r
r
ρ R3
3εε0 r
Кафедра физики
Расчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R
Таким образом, потенциал поля
объемнозаряженного шара определяется выражениями:
ρ R3
r
0 r R
3εε0 r
r
2 1 2
R r
2εε0
3
ρ
r R
Проверим правильность выражений
При r R потенциал должен быть одинаковым независимо от формулы.
2 1 2
ρ
R
R2
R R
2εε0
3
3εε0
ρ
R
ρ R3
3εε0 R
ρ
3εε0
R2

биоэлектричества | биология | Britannica

биоэлектричество , электрические потенциалы и токи, производимые или возникающие внутри живых организмов. Биоэлектрические потенциалы генерируются множеством биологических процессов и обычно имеют силу от одного до нескольких сотен милливольт. Однако у электрического угря генерируются токи в один ампер при напряжении от 600 до 1000 вольт. Далее следует краткое рассмотрение биоэлектричества. Для полного лечения см. электричество: Биоэлектрические эффекты.

Биоэлектрические эффекты были известны в древности по активности таких электрических рыб, как нильский сом и электрический угорь. Эксперименты Луиджи Гальвани и Алессандро Вольта в 18 веке о связи между электричеством и сокращением мышц у лягушек и других животных сыграли важную роль в развитии наук физики и физиологии. В наше время измерение биоэлектрических потенциалов стало обычной практикой в ​​клинической медицине. Например, электрические эффекты, возникающие в активных клетках сердца и мозга, обычно отслеживаются и анализируются в диагностических целях.

Британская викторина

Biology Bonanza

Что означает слово «миграция»? Сколько комплектов ножек у креветки? От ядовитой рыбы до биоразнообразия — узнайте больше об изучении живых существ в этой викторине.

Биоэлектрические потенциалы идентичны потенциалам, создаваемым такими устройствами, как батареи или генераторы.Однако почти во всех случаях биоэлектрический ток состоит из потока ионов (, т. Е. электрически заряженных атомов или молекул), тогда как электрический ток, используемый для освещения, связи или питания, представляет собой движение электронов. Если два раствора с разными концентрациями иона разделены мембраной, которая блокирует поток ионов между ними, дисбаланс концентраций вызывает разность электрических потенциалов между растворами. В большинстве растворов ионы с заданным электрическим зарядом сопровождаются ионами противоположного заряда, так что сам раствор не имеет суммарного заряда.Если два раствора с разной концентрацией разделены мембраной, которая пропускает один вид иона, но не пропускает другой, концентрации иона, который может пройти, будут стремиться к выравниванию за счет диффузии, создавая равные и противоположные суммарные заряды в двух растворах. В живых клетках два решения находятся внутри и вне клетки. Клеточная мембрана, отделяющая внутреннюю часть от внешней, является полупроницаемой, позволяя одним ионам проходить сквозь них, блокируя другие. В частности, мембраны нервных и мышечных клеток слегка проницаемы для положительных ионов калия, которые диффундируют наружу, оставляя чистый отрицательный заряд в клетке.

Биоэлектрический потенциал через клеточную мембрану обычно составляет около 50 милливольт; этот потенциал известен как потенциал покоя. Все клетки используют свои биоэлектрические потенциалы для помощи или контроля метаболических процессов, но некоторые клетки специально используют биоэлектрические потенциалы и токи для различных физиологических функций. Примеры такого использования можно найти в нервных и мышечных клетках. Информация передается с помощью электрических импульсов (называемых потенциалами действия), проходящих по нервным волокнам.Подобные импульсы в мышечных клетках сопровождают сокращение мышц. В нервных и мышечных клетках химическая или электрохимическая стимуляция приводит к временным изменениям проницаемости клеточных мембран, позволяя электрическому потенциалу между внутренней и внешней частью разряжаться в виде тока, который распространяется по нервным волокнам или активирует сократительный механизм мышечных волокон. Транспорт ионов натрия участвует в производстве потенциалов действия. Среди других клеток, в которых специализированные функции зависят от поддержания биоэлектрических потенциалов, находятся рецепторные клетки, чувствительные к свету, звуку и прикосновению, а также многие клетки, которые секретируют гормоны или другие вещества.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Различные рыбы, как морские, так и пресноводные, развили особые органы, способные генерировать значительные электрические разряды, в то время как у других есть ткани, которые могут ощущать слабые электрические поля в воде. У более чем 200 видов рыб биоэлектрический орган участвует в самообороне или охоте. Торпеда, или электрический скат, и электрический угорь имеют особенно мощные электрические органы, которые они, по-видимому, используют для обездвиживания или убийства добычи.Электрический угорь имеет три пары электрических органов; они составляют большую часть массы тела и около четырех пятых общей длины рыбы. Считается, что эта рыба способна произвести достаточно мощный электрический шок, чтобы оглушить человека. Электрические лучи имеют два больших дискообразных электрических органа, по одному на каждой стороне тела, которые вносят свой вклад в дискообразную форму тела.

Электрический сом в Африке, рыба-нож в Латинской Америке и звездочеты, вероятно, используют свои биоэлектрические органы в качестве органов чувств при обнаружении других рыб.

Основным элементом биоэлектрического органа является уплощенная ячейка, называемая гальваническим налетом. Большое количество гальванических пластинок расположены последовательно и параллельно для повышения напряжения и токоподъемности электрического органа. Рыбы производят внезапный разряд электричества, синхронизируя нервные импульсы, которые активируют отдельные гальванические образования, тем самым обеспечивая одновременное действие всего массива.

Учебник по физике: электрический потенциал

В предыдущем разделе Урока 1 было рассмотрено, что движение положительного тестового заряда в электрическом поле сопровождается изменениями потенциальной энергии. Гравитационная аналогия использовалась для объяснения причин взаимосвязи между местоположением и потенциальной энергией. Перемещение положительного пробного заряда против направления электрического поля похоже на перемещение массы вверх в пределах гравитационного поля Земли. Оба движения были бы подобны , идущему против природы , и потребовали бы работы внешней силы. Эта работа, в свою очередь, увеличит потенциальную энергию объекта. С другой стороны, движение положительного пробного заряда в направлении электрического поля будет похоже на падение массы в гравитационном поле Земли.Оба движения были бы похожи на , идущие по природе , и происходили бы без необходимости работы внешней силы. Это движение приведет к потере потенциальной энергии. Потенциальная энергия — это запасенная энергия положения объекта, и она связана с расположением объекта в поле. В этом разделе Урока 1 мы познакомимся с концепцией электрического потенциала и свяжем это понятие с потенциальной энергией положительного тестового заряда в различных местах в пределах электрического поля.

Возвращение к гравитационной аналогии

Вокруг Земли существует гравитационное поле, которое оказывает гравитационное влияние на все массы, находящиеся в окружающем ее пространстве. Перемещение объекта вверх против гравитационного поля увеличивает его гравитационную потенциальную энергию. Объект, движущийся вниз в пределах гравитационного поля, потерял бы потенциальную гравитационную энергию. Когда гравитационная потенциальная энергия была введена в Блоке 5 Физического Класса, она была определена как энергия, запасенная в объекте из-за его вертикального положения над Землей.Количество гравитационной потенциальной энергии, хранящейся в объекте, зависело от количества массы, которым обладал объект, и величины высоты, на которую он был поднят. Гравитационная потенциальная энергия зависела от массы объекта и его высоты. У объекта с удвоенной массой будет вдвое больше потенциальной энергии, а у объекта с удвоенной высотой будет вдвое больше потенциальной энергии. Обычно высокие позиции называют локациями с высоким потенциалом энергии. Взгляд на диаграмму справа показывает ошибочность такого утверждения.Обратите внимание, что груз весом 1 кг, удерживаемый на высоте 2 метра, имеет такую ​​же потенциальную энергию, как и масса весом 2 кг, удерживаемая на высоте 1 метр. Потенциальная энергия зависит не только от местоположения; это также зависит от массы. В этом смысле потенциальная гравитационная энергия зависит как минимум от двух типов величин:

1) Масса — свойство объекта, испытывающего гравитационное поле, и

2) Высота — положение в гравитационном поле

Таким образом, неправильно называть высокие позиции в гравитационном поле Земли позициями с высокой потенциальной энергией.Но есть ли какое-то количество, которое можно было бы использовать для оценки таких высот как имеющих большой потенциал обеспечения больших количеств потенциальной энергии массам, которые там находятся? Да! Хотя это не обсуждается во время блока по гравитационной потенциальной энергии, можно было бы ввести величину, известную как гравитационный потенциал — потенциальная энергия на килограмм. Гравитационный потенциал — это величина, которую можно использовать для оценки различных мест на поверхности Земли с точки зрения того, какой потенциальной энергией будет обладать каждый килограмм массы, когда он будет помещен туда.Величина гравитационного потенциала определяется как ПЭ / масса. Поскольку числитель и знаменатель PE / масса пропорциональны массе объекта, выражение становится независимым от массы. Гравитационный потенциал — это величина, зависящая от местоположения, которая не зависит от массы объекта, испытывающего поле. Гравитационный потенциал описывает эффекты гравитационного поля на объекты, которые находятся в различных местах внутри него.

Если гравитационный потенциал — это средство оценки различных мест внутри гравитационного поля с точки зрения количества потенциальной энергии на единицу массы, тогда концепция электрического потенциала должна иметь аналогичное значение.Рассмотрим электрическое поле, создаваемое положительно заряженным генератором Ван де Граафа. Направление электрического поля находится в том направлении, в котором будет проталкиваться положительный испытательный заряд; в этом случае направление направлено наружу от сферы Ван де Граафа. Потребуется работа, чтобы переместить положительный испытательный заряд к сфере против электрического поля. Количество силы, задействованной при выполнении работы, зависит от количества перемещаемого заряда (согласно закону электрической силы Кулона).Чем больше заряд на испытательном заряде, тем больше сила отталкивания и тем больше работы, которая должна быть проделана с ним, чтобы переместить его на такое же расстояние. Если два объекта с разным зарядом — один из которых в два раза больше заряда другого — перемещаются на одинаковое расстояние в электрическое поле, то объект с двойным зарядом потребует вдвое большей силы и, следовательно, в два раза больше работы. Эта работа изменит потенциальную энергию на величину, равную количеству проделанной работы. Таким образом, электрическая потенциальная энергия зависит от количества заряда на объекте, испытывающем поле, и от местоположения внутри поля. Так же, как и потенциальная гравитационная энергия, электрическая потенциальная энергия зависит как минимум от двух типов величин:

1) Электрический заряд — свойство объекта, испытывающего электрическое поле, и

2) Расстояние от источника — местоположение в пределах электрического поля

В то время как электрическая потенциальная энергия зависит от заряда объекта, испытывающего электрическое поле, электрический потенциал зависит исключительно от местоположения.Электрический потенциал — это потенциальная энергия на заряд.

Понятие электрического потенциала используется для выражения эффекта электрического поля источника с точки зрения местоположения внутри электрического поля. Пробный заряд с удвоенным количеством заряда будет обладать удвоенной потенциальной энергией в данном месте; тем не менее, его электрический потенциал в этом месте будет таким же, как и у любого другого испытательного заряда. Положительный тестовый заряд будет иметь высокий электрический потенциал, когда он удерживается рядом с положительным зарядом источника, и с более низким электрическим потенциалом, когда он находится дальше. В этом смысле электрический потенциал становится просто свойством местоположения внутри электрического поля. Предположим, что электрический потенциал в данном месте составляет 12 джоулей на кулон, тогда это электрический потенциал заряженного объекта в 1 или 2 кулона. Утверждение, что электрический потенциал в данном месте составляет 12 джоулей на кулон, будет означать, что 2-кулоновский объект будет обладать 24 джоулями потенциальной энергии в этом месте, а объект 0,5 кулонов будет испытывать 6 джоулей потенциальной энергии в этом месте.

Электрический потенциал в цепях

Когда мы начнем обсуждать электрические цепи, мы заметим, что электрическая цепь с батарейным питанием имеет места с высоким и низким потенциалом. Заряд, движущийся по проводам цепи, будет сталкиваться с изменениями электрического потенциала при прохождении по цепи. В электрохимических элементах батареи между двумя выводами создается электрическое поле, направленное от положительного вывода к отрицательному. Таким образом, перемещение положительного тестового заряда через ячейки от отрицательного вывода к положительному потребует работы, таким образом увеличивая потенциальную энергию каждого кулоновского заряда, который движется по этому пути. Это соответствует движению положительного заряда против электрического поля. По этой причине положительный вывод описывается как вывод с высоким потенциалом. Подобные рассуждения привели бы к заключению, что движение положительного заряда по проводам от положительного вывода к отрицательному будет происходить естественным образом.Такое движение положительного испытательного заряда должно происходить в направлении электрического поля и не требует работы. Заряд будет терять потенциальную энергию при движении через внешнюю цепь от положительного вывода к отрицательному. Отрицательная клемма описывается как клемма с низким потенциалом. Это назначение высокого и низкого потенциала клеммам электрохимической ячейки предполагает традиционное соглашение о том, что электрические поля основаны на направлении движения положительных тестовых зарядов.

В определенном смысле электрическая цепь — это не что иное, как система преобразования энергии. В электрохимических элементах электрической цепи с батарейным питанием химическая энергия используется для работы с положительным испытательным зарядом, чтобы переместить его с клеммы с низким потенциалом на клемму с высоким потенциалом. Химическая энергия преобразуется в электрическую потенциальную энергию во внутренней цепи (то есть в батарее). Попав на клемму с высоким потенциалом, положительный тестовый заряд будет перемещаться по внешней цепи и воздействовать на лампочку, двигатель или катушки нагревателя, преобразовывая свою электрическую потенциальную энергию в полезные формы, для которых схема была разработана.Положительный тестовый заряд возвращается к отрицательному выводу с низкой энергией и низким потенциалом, готовый к повторению цикла (или, лучше сказать, цепи ) снова и снова.

Проверьте свое понимание

1. Величина электрического потенциала определяется как величина _____.

а. электрическая потенциальная энергия

г. сила, действующая на заряд

г.потенциальная энергия на заряд

г. усилие на заряд

2. Заполните следующую запись:

Когда над положительным испытательным зарядом выполняется работа с помощью внешней силы по перемещению его из одного места в другое, потенциальная энергия _________ (увеличивается, уменьшается) и электрический потенциал _________ (увеличивается, уменьшается).

3.На следующих диаграммах показано электрическое поле (представленное стрелками) и две точки, обозначенные A и B, расположенные внутри электрического поля. Положительный тестовый заряд показан в точке A. Для каждой диаграммы укажите, нужно ли проделать работу над зарядом, чтобы переместить его из точки A в точку B. Наконец, укажите точку (A или B) с наибольшей электрической потенциальной энергией и наибольший электрический потенциал.

7: Электрический потенциал — Physics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Без заголовков

В этой главе мы исследуем взаимосвязь между напряжением и электрической энергией и начнем исследовать некоторые из многих приложений электричества.

• 7.1: Введение к электрическому потенциалу

  Два термина, обычно используемых для описания электричества, — это его энергия и напряжение, которые, как мы показываем в этой главе, напрямую связаны с потенциальной энергией в системе. Мы знаем, например, что большое количество электроэнергии может храниться в батареях, передаваться по стране токами по линиям электропередач и может прыгать из облаков, чтобы взорвать сок деревьев. Аналогичным образом на молекулярном уровне ионы пересекают клеточные мембраны и передают информацию.

• 7.2: Электрическая потенциальная энергия

  Когда свободный положительный заряд q ускоряется электрическим полем, ему придается кинетическая энергия (рисунок). Этот процесс аналогичен ускорению объекта гравитационным полем, как если бы заряд спускался с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую, хотя, конечно, источники сил очень разные.

• 7.3: Электрический потенциал и разность потенциалов

  Электрический потенциал — это потенциальная энергия на единицу заряда. Разность потенциалов между точками A и B, VB-VA, то есть изменение потенциала заряда q, перемещенного от A к B, равна изменению потенциальной энергии, деленному на заряд. Разность потенциалов обычно называется напряжением и обозначается символом ΔV.

• 7.4: Расчет электрического потенциала

  Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи.Кроме того, сферическое распределение заряда (например, заряд на металлической сфере) создает внешние электрические поля точно так же, как точечный заряд. Таким образом, нам необходимо рассмотреть электрический потенциал из-за точечного заряда.

• 7.5: Определение поля по потенциалу

  В некоторых системах мы можем вычислить потенциал путем интегрирования по электрическому полю. Как вы, возможно, уже подозреваете, это означает, что мы можем вычислить электрическое поле, взяв производные от потенциала, хотя переход от скалярной к векторной величине привносит некоторые интересные морщины.Нам часто требуется E для расчета силы в системе; поскольку часто проще вычислить потенциал напрямую, существуют системы, в которых полезно вычислить V, а затем получить E.

• 7.6: Эквипотенциальные поверхности и проводники

  Мы можем представить электрические потенциалы графически, точно так же, как мы рисовали картинки, чтобы проиллюстрировать электрические поля. Это неудивительно, поскольку эти два понятия связаны. Мы используем стрелки, чтобы обозначить величину и направление электрического поля, и мы используем зеленые линии, чтобы обозначить места, где электрический потенциал постоянен.Они называются эквипотенциальными поверхностями в трех измерениях или эквипотенциальными линиями в двух измерениях.

• 7.7: Применение электростатики

  Исследование электростатики оказалось полезным во многих областях. Этот модуль охватывает лишь некоторые из множества применений электростатики.

• 7.A: Электрический потенциал (ответ)

• 7.E: Электрический потенциал (упражнения)

• 7.S: Электрический потенциал (Сводка)

Гравитационный потенциал | IOPSpark

Гравитационная потенциальная энергия

Энергия и теплофизика

Гравитационный потенциал

Глоссарий Определение для 16-19

Описание

Гравитационный потенциал в точке в гравитационном поле — это работа, совершаемая на единицу массы, которая должна быть совершена некоторой внешней приложенной силой, чтобы привести массивный объект в эту точку из некоторого определенного положения с нулевым потенциалом, обычно бесконечность .Это гравитационная разность потенциалов между выбранной точкой и положением нулевого потенциала.

Гравитационный потенциал часто обозначается символом V .

Если поле возникает из-за изолированного массивного точечного объекта (или любого объекта конечного размера), то принято определять нулевой потенциал на бесконечном расстоянии от объекта; потенциал везде отрицательный, потому что сила гравитации всегда притягивает.

Гравитационный потенциал также определяется как гравитационная потенциальная энергия на единицу массы относительно определенного положения нулевой потенциальной энергии.Эти два определения эквивалентны.

Обсуждение

Существует сильное сходство между гравитационным потенциалом и электростатическим потенциалом. В обоих случаях основные силы зависят от расстояния r взаимодействующих объектов как 1 r ² , и в обоих случаях изменение потенциала определяется через работу, выполняемую при изменении расстояния между объектами. взаимодействующие объекты. Разница заключается в природе силы: заряды могут быть положительными или отрицательными, поэтому электростатическое взаимодействие может быть притягивающим или отталкивающим.Сила притяжения всегда притягательна.

Блок СИ

Дж кг ^-1

Выражается в базовых единицах СИ

м ² с ^-2

Другая часто используемая единица (и)

нет

Математические выражения

• Поднятие объекта на высоту Δ h у поверхности Земли приводит к изменению гравитационного потенциала
  Δ V = г Δ h
где g — гравитационное поле у ​​поверхности Земли, а Δ h намного меньше радиуса Земли.
• В более общем смысле
  Δ V = G M R — G M R + Δ h = G M R Δ h R

  0 h + Δ23 h
  , где M и R — соответственно масса и радиус Земли, а G — универсальная гравитационная постоянная.

Связанные записи

• Гравитационное поле
• Потенциальная энергия

В контексте

Разница в гравитационном потенциале между уровнем моря и вершиной Эвереста составляет около 8.7 × 10 ⁴ Дж кг ^–1 . Если альпинист массой 100 кг путешествует с уровня моря на вершину Эвереста, гравитационная потенциальная энергия системы Земля-альпинист увеличивается примерно на 8,7 × 10 ⁶ J.

Модель потенциала в физике высоких энергий

Модель потенциала, которая рассматривает один или несколько членов взаимодействия для физической системы, используется в различных рамках для исследования систем частиц и систем высоких энергий.Это включает применение в обыкновенных волновых уравнениях квантовой механики к их различным обобщениям. Несмотря на свои ограничения, этот подход с самого начала дал нам надежную основу. В некоторых случаях мы знаем, что взаимодействия игрушечной модели, такие как Кулон или Юкава, должны быть изменены, чтобы учесть наблюдаемые экспериментальные данные. Предмет также тесно связан с взаимодействием квантовой механики с теориями, которые происходят из физики высоких энергий, и использовался для изучения многих сложных тем, которые выходят за рамки наших нынешних экспериментальных возможностей.

Этот специальный выпуск предназначен для рассмотрения различных экспериментальных и теоретических аспектов потенциальной модели, или, как вариант, подхода волновых уравнений, связанных с физикой частиц и высоких энергий.

Я хочу посвятить свой вклад в этот специальный выпуск моему профессору доктору Масуду Вахаби-Могхадаму в его 67-летие.

Потенциальные темы включают, но не ограничиваются следующим:

• Линейные волновые уравнения, включая Дирака, Кляйн-Гордона, Даффина-Кеммера-Петяу, Прока и Рита-Швингер
• Волновые уравнения и спектроскопия частиц
• Волновые уравнения, моды распада и состояния рассеяния
• Зависящие от времени гамильтонианы в кварк-глюонной плазме и других родственных полях
• Волновые уравнения в пространстве-времени космических струн и связанные аспекты, включая флуктуации светового конуса
• Волновые уравнения в некоммутативном пространстве и фазовом пространстве
• Уравнение Дирака и темная материя
• Уравнение Дирака и физика нейтрино
• Монополи
• Переходы с нейтрино в рамках DKP
• Волновые уравнения в искривленном пространстве-времени
• Модифицированные волновые уравнения в соответствии с обобщенным принципом неопределенности
• Нелинейные волновые уравнения и солитоны
• Функциональное уравнение Шредингера
• Синус-G Модель Ордона
• Связанные аспекты математической физики, включая алгебры Ли
• Интегрируемые и суперинтегрируемые системы в физике высоких энергий

Электрический потенциал — Физика Видео от Brightstorm

Поговорим об электрическом потенциале.Электрический потенциал — это еще одна величина, которую очень очень полезно определять, и она как бы проходит по тем же линиям электрического поля. Итак, если я перемещаю заряд через электрическое поле, это требует работы, и это потому, что электрическое поле будет прикладывать силы к электрическому заряду. Итак, электрическая сила — это консервативная сила, и это означает, что любую работу, которую она совершает, можно выразить в терминах функции потенциальной энергии. Работа равняется отрицательному изменению потенциальной энергии.

Теперь, как и в случае с электрическими полями, я хочу относиться ко всем тестовым зарядам одинаково.Я хочу лечить их всех одновременно и не хочу смотреть на них всех по отдельности. Итак, мы собираемся определить электрический потенциал как электрическую потенциальную энергию, деленную на тестовый заряд. И это в точности то же самое, что мы сделали для электрического поля. Электрическое поле — это электрическая сила, разделенная на испытательный заряд. Хорошо, функция электрического потенциала расскажет нам, сколько положительного заряда было бы лучше в одном месте, чем в другом. Итак, как мы понимаем из простой механики, всякий раз, когда потенциальная энергия высока, это означает, что объект на самом деле не хочет там находиться.Поэтому всякий раз, когда электрический потенциал высок, это означает, что положительный заряд не хочет присутствовать. Лучше бы там, где электрический потенциал низкий. Итак, отрицательный заряд скорее будет там, где электрический потенциал высок. И предпочел бы не быть там, где электрический потенциал низкий. Хорошо.

Единицей электрического потенциала является вольт, и это точно такой же вольт, который вы хорошо знаете по батареям. Итак, вольт, один вольт, равен одному джоуля на кулон. Таким образом, он говорит нам, сколько энергии требуется для того, чтобы заряд находился в определенном месте на один кулон заряда.Так что, если у меня есть электрический потенциал в три вольта или что-то еще, мне потребовалось бы вдвое больше энергии, чтобы поместить туда двойной заряд. Джоули на кулон. Хорошо? Хорошо.

Итак, мы знаем из закона Кулона, что электрический потенциал, связанный с большим зарядом, капиталом q, будет kq больше r, и это в точности то же самое, что вы помните из гравитации, где электрическая, извините, где гравитационная потенциальная энергия gmm больше r. Тогда как сила была gmm больше r в квадрате.Так что это то же самое. Закон Кулона говорит нам, что kqq больше r в квадрате, но потенциальная энергия энергии чуть больше r. А затем, когда я делю на другой заряд, я получаю kq больше r. И это указывает на то, что когда вы близки к положительному заряду, электрический потенциал высок. Это положительно. Когда вы близки к отрицательному заряду, электрический потенциал отрицательный. Так что это самое простое из возможных и, конечно же, имеет смысл. Если я попытаюсь получить положительный тестовый заряд, близкий к положительному большому заряду, это будет стоить энергии.Он не хочет быть рядом с этим положительным зарядом. Это означает, что электрический потенциал должен увеличиться, и это именно то, что нам говорит закон Кулона.

Хорошо. Приведем пример. Итак, предположим, что у меня есть аккумулятор с разностью потенциалов 3 вольта. И я хочу знать, сколько мне будет стоить энергии, чтобы взять 2 микрокулоны заряда и переместить его с отрицательной стороны на положительную сторону батареи. Конечно, это будет стоить мне энергии, потому что эти 2 микрокулоны положительны.Это означает, что он хочет быть на отрицательной стороне. Он хочет быть рядом со всем отрицательным зарядом, потому что ему это нравится. Он не хочет быть положительным. Итак, я хочу знать, сколько энергии на это потребуется. Ну, блин. Энергия равна заряду, умноженному на напряжение. Заряд составляет 2 микрокулоны, заметьте, мы все делаем в единицах СИ. Напряжение равно 3 вольтам, и поэтому, когда мы умножим, мы получим 6 умножить на 10 до -6, а затем получим кулоны, умноженные на вольты, то есть джоули. Таким образом, мне потребуется 6 микроджоулей энергии, чтобы переместить этот заряд с отрицательной стороны на положительную.Хорошо.

А теперь проведем качественный анализ. И мы собираемся внести некоторые электрические поля, когда мы тоже это сделаем. Я думаю, что это отличное упражнение, которое просто помогает нам понять, что происходит с электрическим потенциалом и электрическими полями. И я хочу просто провести здесь несколько линий, чтобы разделить их. У меня есть 3 разных примера. Хорошо. Итак, у меня есть 2 положительных заряда и 3 точки a, b и c. И я хочу знать по каждому из этих трех пунктов, я не хочу точно знать, каков потенциал.Я не хочу точно знать, что такое электрическое поле. Я просто хочу знать, является ли электрический потенциал положительным, отрицательным или нулевым. А в каком направлении указывает электрическое поле? Хорошо.

Итак, давайте продолжим первый пример. Положительный, положительный, и я прямо здесь понял свою точку зрения. Хорошо. Давайте сначала рассмотрим электрический потенциал. Таким образом, a близко к 2 положительным зарядам. Каждый из этих положительных зарядов вносит положительный электрический потенциал. И тогда [IB] электрический потенциал положительный.Хорошо. А что насчет электрического поля?

Ну, я должен об этом подумать. Этот положительный заряд хочет сместить любой положительный заряд вправо. Этот положительный заряд хочет сместить любой положительный заряд влево. Тот же заряд, такое же расстояние, они отменяют. Итак, электрическое поле в точке a равно нулю. Он вообще не указывает ни в каком направлении. Хорошо. Сделаем б.

Опять же в точке b электрический потенциал должен быть положительным, потому что вклад вносят только положительные элементы. Итак, у нас есть положительный электрический потенциал.А что насчет электрического поля? Что ж, в данном случае этот положительный заряд всех отталкивает. Этот позитивный заряд всех отталкивает. И когда я складываю эти два вектора вместе, это входит в мои предыдущие вычисления, но электрическое поле будет указывать прямо вверх. Хорошо. Сделаем пункт c. Очевидно, снова электрический потенциал положительный. В этом случае оба положительных заряда сдвигаются влево, а это означает, что электрическое поле влево.Хорошо, отлично. Сделаем второй пример. Вот этот прямо здесь.

Теперь у меня есть положительный заряд и отрицательный заряд. Итак, давайте посмотрим на точку а. Что ж, в точке а одинаковое расстояние от положительного и отрицательного. Так что вы думаете об электрическом потенциале? Ну, будет ноль. Итак, v = 0. Хорошо. Посмотрим на электрическое поле. Положительный заряд требует, чтобы любой тестовый заряд в точке a переместился вправо, отрицательный заряд хочет, чтобы любой тестовый заряд в точке a переместился вправо.Так что ты думаешь? Он будет справа. Хорошо? Сделаем пункт б.

Теперь для точки b это такое же расстояние от положительного, как и от отрицательного. А это снова означает, что электрический потенциал будет равен нулю. Хорошо. А что насчет электрического поля? Что ж, положительный заряд хочет, чтобы тестовый заряд двигался вот так. Отрицательный заряд хочет, чтобы тестовый заряд двигался таким образом. Когда я складываю эти два вектора вместе, электрическое поле находится прямо справа. Хорошо. А как насчет пункта c?

Точка c ближе к положительному заряду, чем к отрицательному.Так что положительного заряда больше, он сильнее. Более важен электрический потенциал в точке c. А это значит, что положительный. Хорошо. Теперь займемся электрическим полем. В точке c положительный заряд сдвигается влево. Отрицательный заряд тянет вправо. Итак, электрическое поле будет нулевым? Что ж, давайте подумаем. Положительный заряд ближе, значит, выигрывает. Итак, мы идем. Хорошо. Электрическое поле слева. Хорошо. Теперь займемся этим последним.

Вот у меня 4 заряда.Положительный, отрицательный, отрицательный, положительный. Хорошо. Итак, давайте посмотрим на файл. Электрический потенциал. Ну, точка а находится на одинаковом расстоянии от двух положительных зарядов и на таком же расстоянии от двух отрицательных зарядов. Итак, электрический потенциал исчезнет. Будет ноль, хорошо? А что насчет электрического поля? Что ж, здесь происходит то, что у меня есть отрицательный заряд, который вот так тянет. У меня есть этот положительный заряд, который вот так толкает, но затем у меня есть этот положительный заряд, который нейтрализует его, и у меня есть отрицательный заряд, который равен [IB]. Это означает, что электрическое поле также нуль.Эта ситуация называется квадропольным моментом. Там, где у нас есть электрический потенциал и электрическое поле, оба равны нулю. Хорошо. А как насчет пункта б?

Ну, точка b находится на таком же расстоянии от этого положительного заряда, как и от этого. Что касается электрического потенциала, эти ребята даже не имеют значения. Хорошо? А как насчет здесь и здесь? Ну и опять такое же расстояние. Итак, электрический потенциал снова равен нулю. А что насчет электрического поля? Ну что ж, посмотрим. Электрическое поле здесь тянется к отрицательному.Электрическое поле здесь отталкивается от [IB], поэтому они согласны друг с другом. Теперь эти парни собираются сделать прямо противоположное, но они еще дальше. Таким образом, они не смогут полностью отменить этот вклад, и электрическое поле будет указывать в том направлении, вправо. А как насчет пункта c? В точке c вы снова можете убедиться, что электрический потенциал будет равен нулю, а электрическое поле снова будет справа.

Хорошо. Итак, это электрический потенциал.

— Потенциальная энергия

Потенциальная энергия — это способность выполнять работу или накопленная энергия. Есть разные виды потенциальная энергия. Например:

• Химический потенциал Энергия — например, бензин, аккумуляторы
• Электрический Потенциал Энергия — например, напряжение
• Упругий потенциал Энергия — например, пружины
• Гравитационная потенциальная энергия — например, работа, сделанная кем-либо или против сила тяжести.

Нашим символом потенциальной энергии будет полиэтилен. Иногда вы увидите символ U используется для потенциальной энергии. Нижний индекс будет обозначать тип. Например, потенциальная энергия гравитации будет равна PE _г или U _г . Потенциальная энергия всегда относительно другой потенциальной поверхности. Например, гравитационная потенциальная энергия может быть выбрана для высоты над землей, над столом или в любой нижней точке, которую мы назовем h = 0.Для наших обсуждений здесь мы поговорим о двух формах механического Потенциальная энергия: гравитационная потенциальная энергия и упругая потенциальная энергия.

Гравитационная потенциальная энергия — это энергия, доступная объекту за счет положение объекта относительно заданной точки (высота над поверхностью). Это энергия, доступная ему, если гравитация воздействует на объект. Напомним, что Work = Ф · д . Поскольку сила, необходимая для подъема объекта с постоянной скоростью, равна его весу, мг и расстояние — это высота объекта, мы говорим, что гравитационная потенциальная энергия, PE _g или U _g = mgh.

Пример: что такое PE _г коробки 5 кг, установленной на полка 2 метра над полом? Сверху ПЭ _г = mgh =

(5 кг) (9,8 м / с ² ) (2 м) = 98 Джоули.

Еще один пример того, как вычисляется гравитационная потенциальная энергия. относительно заданного положения:

Упругая потенциальная энергия — это энергия, доступная в упругом устройстве, таком как пружина, резинка, супербол или эластичный шнур. Для начала нам нужно знать закон Гука: расстояние, на которое смещается пружина, пропорционально силе, приложенной к пружине, или

F _p = — к х,

, где k — жесткость пружины (в Н / м), а x — смещение пружина в метрах.Сила отрицательная, потому что возвращающая сила всегда будет противоположной направлению смещения пружины. Чтобы вычислить жесткость пружины, мы выполняем закон Гука Экспериментируйте. Как только мы узнаем жесткость пружины k, мы сможем найти упругая потенциальная энергия прямо.