потенциал — Викисловарь

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	потенциа́л	потенциа́лы
Р.	потенциа́ла	потенциа́лов
Д.	потенциа́лу	потенциа́лам
В.	потенциа́л	потенциа́лы
Тв.	потенциа́лом	потенциа́лами
Пр.	потенциа́ле	потенциа́лах

по-тен-ци-а́л

Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).

Корень: -потенциал-. ^{[Тихонов, 1996]}

Произношение[править]

Семантические свойства[править]

Значение[править]

1. физ. величина, характеризующая запас энергии тела, находящегося в данной точке поля ^{[≈ 1][≠ 1][▲ 1][▼ 1]} ◆ Отсутствует пример употребления (см. рекомендации).
2. перен. совокупность всех имеющихся возможностей, средств в какой-либо области, сфере ^{[≈ 2][≠ 2][▲ 2][▼ 2]} ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы

Антонимы

Гиперонимы

Гипонимы

Родственные слова[править]

Этимология[править]

Происходит от лат. potentialis «мощный», далее из potentia «сила, мощь», далее из potēns «могущий», part. praes. act. от posse «мочь, быть в состоянии» из прил. potis «могущественный, могу́щий» + esse «быть», восходит к праиндоевр. *es- «быть».

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Библиография[править]

Потенциалы — это… Что такое Потенциалы?

потенциалы — В линейном программировании дополнительные переменные, включаемые в формулировку транспортной задачи при ее решении специальным методом, который так и называется метод потенциалов. [http://slovar lopatnikov.ru/] Тематики экономика EN potentials …   Справочник технического переводчика

ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ — энергетич. характеристики эл. магн. поля, к рые вводят для описания поля наряду с силовыми хар ками напряжённостью электрич. поля Е и магн. индукцией В. В электростатике векторное электрич. поле можно характеризовать одной скалярной ф цией… …   Физическая энциклопедия

ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕСКИЕ — определённые функции объёма (V), давления (р), темп ры (Т), энтропии (S), числа ч ц системы (N) и др. макроскопич. параметров (xi), характеризующих состояние термодинамической системы. К П. т. относятся: внутренняя энергия U=U(S, V, N, xi),… …   Физическая энциклопедия

Потенциалы Лиенара — Вихерта — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм …   Википедия

ПОТЕНЦИАЛЫ ЗАПАЗДЫВАЮЩИЕ — решения уравнений для потенциалов переменного электромагнитного поля, учитывающие конечную скорость распространения электромагнитного взаимодействия. Изменения плотности зарядов и токов сказываются на изменении потенциалов через промежуток… …   Большой Энциклопедический словарь

ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕСКИЕ — функции объема, давления, температуры, энтропии, числа частиц и других независимых макроскопических параметров, характеризующих состояние термодинамической системы. К потенциалам термодинамическим относятся внутренняя энергия, энтальпия, изохорно …   Большой Энциклопедический словарь

Потенциалы электромагнитного поля — Потенциалы электромагнитного поля  термин, под которым в обычной трехмерной формулировке электродинамики понимаются cкалярный потенциал и векторный потенциал , через которые выражаются напряженность электрического поля и вектор магнитной… …   Википедия

ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ — (скалярный и векторный) характеристики электромагнитного поля, через которые выражаются напряженности электрических и магнитных полей …   Большой Энциклопедический словарь

Потенциалы термодинамические — Термодинамические потенциалы Статья является частью серии «Термодинамика». Внутренняя энергия Энтальпия Свободная энергия Гельмгольца Энергия Гиббса Большой термодинамический потенциал (Ω) Разделы …   Википедия

Потенциалы электромагнитного поля —         величины, характеризующие электромагнитное поле. В электростатике векторное электрическое поле можно характеризовать одной скалярной функцией потенциалом электростатическим (См. Потенциал электростатический). В общем случае для описания… …   Большая советская энциклопедия

Биопотенциал — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июня 2018; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июня 2018; проверки требуют 2 правки.

Биопотенциал (биоэлектрический потенциал, устар. биоток) — энергетическая характеристика взаимодействия зарядов, находящихся в исследуемой живой ткани, например, в различных областях мозга, в клетках и других структурах.

Измеряется не абсолютный потенциал, а разность потенциалов между двумя точками ткани, отражающая её биоэлектрическую активность, характер метаболических процессов. Биопотенциал используют для получения информации о состоянии и функционировании различных органов.

Разность потенциалов между возбуждённой и невозбуждённой частями отдельных клеток всегда характеризуется тем, что потенциал возбуждённой части клетки меньше потенциала невозбуждённой части. Для ткани разность потенциалов определяется совокупностью потенциалов отдельных клеток.

Разность электрических потенциалов в одних случаях играет очень важную роль для жизнедеятельности организма (Электрический скат), а в других — побочную, являясь следствием биохимических превращений.

Потенциал действия и потенциал покоя[править | править код]

Потенциалом действия называют потенциал, возникающий при возбуждении ткани. Обычно он быстро достигает своего максимума (за ~0,1—10 миллисекунд), а затем более медленно (миллисекунды — секунды) снижается до нуля.

Потенциал покоя — потенциал, существующей между средой, в которой находится клетка, и её содержимым.

Потенциал повреждения — потенциал между повреждённой и не повреждённой частями ткани. Повреждённая часть ткани получает отрицательный потенциал по отношению к неповреждённой.

Напряжение, создаваемое мышечной или нервной тканью, меньше напряжения, создаваемого отдельным волокном, вследствие шунтирующего действия внеклеточных жидкостей или соединительных оболочек. При регистрации биопотенциалов между электродами, отводящими потенциал, обычно находится не одно волокно, а целая система мышечных или нервных волокон. Измеряемая величина ЭДС при этом остается примерно той же, что и у одиночного волокна, но сопротивление источника ЭДС (сопротивление ткани) уменьшается. Так, сопротивление одного сантиметра одиночного нервного волокна составляет несколько десятков МОм, а сопротивление одного сантиметра нервного ствола — десятки кОм.

Регистрация потенциалов действия производится наружными электродами (двухполюсное отведение и соответствующей ему двухфазный потенциал действия).

Медицинская диагностика[править | править код]

Электростимуляторы[править | править код]

Наглядные проявления биопотенциалов в природе[править | править код]

У некоторых животных в организме существуют специализированные клетки, способные создавать, для защиты или нападения, высокий потенциал. Образуемая в этом случае ЭДС может достигать нескольких сотен вольт:

Потенциал действия — это… Что такое Потенциал действия?

Потенциа́л де́йствия — волна возбуждения, перемещающаяся по мембране живой клетки в процессе передачи нервного сигнала. По сути своей представляет электрический разряд — быстрое кратковременное изменение потенциала на небольшом участке мембраны возбудимой клетки (нейрона, мышечного волокна или железистой клетки), в результате которого наружная поверхность этого участка становится отрицательно заряженной по отношению к соседним участкам мембраны, тогда как его внутренняя поверхность становится положительно заряженной по отношению к соседним участкам мембраны. Потенциал действия является физической основой нервного или мышечного импульса, играющего сигнальную (регуляторную) роль.

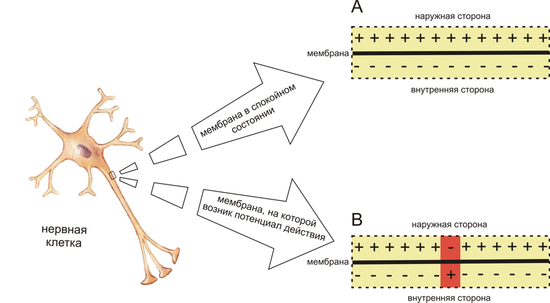Рис. 1. Схема распределения зарядов по разные стороны мембраны возбудимой клетки в спокойном состоянии (

A) и при возникновении потенциала действия (B) (см. объяснения в тексте).

Потенциалы действия могут различаться по своим параметрам в зависимости от типа клетки и даже на различных участках мембраны одной и той же клетки. Наиболее характерный пример различий: потенциал действия сердечной мышцы и потенциал действия большинства нейронов. Тем не менее, в основе любого потенциала действия лежат следующие явления:

1. Мембрана живой клетки поляризована — её внутренняя поверхность заряжена отрицательно по отношению к внешней благодаря тому, что в растворе возле её внешней поверхности находится бо́льшее количество положительно заряженных частиц (катионов), а возле внутренней поверхности — бо́льшее количество отрицательно заряженных частиц (анионов).
2. Мембрана обладает избирательной проницаемостью — её проницаемость для различных частиц (атомов или молекул) зависит от их размеров, электрического заряда и химических свойств.
3. Мембрана возбудимой клетки способна быстро менять свою проницаемостъ для определённого вида катионов, вызывая переход положительного заряда с внешней стороны на внутреннюю (Рис.1).

Первые два свойства характерны для всех живых клеток. Третье же является особенностью клеток возбудимых тканей и причиной, по которой их мембраны способны генерировать и проводить потенциалы действия.

Фазы потенциала действия

1. Предспайк — процесс медленной деполяризации мембраны до критического уровня деполяризации (местное возбуждение, локальный ответ).
2. Пиковый потенциал, или спайк, состоящий из восходящей части (деполяризация мембраны) и нисходящей части (реполяризация мембраны).
3. Отрицательный следовой потенциал — от критического уровня деполяризации до исходного уровня поляризации мембраны (следовая деполяризация).
4. Положительный следовой потенциал — увеличение мембранного потенциала и постепенное возвращение его к исходной величине (следовая гиперполяризация).

Общие положения

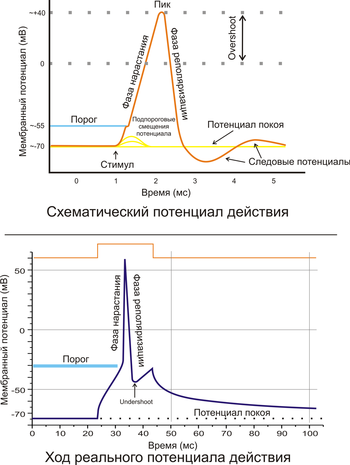Рис. 2. A. Схематичное изображение идеализированного потенциала действия. B. Реальный потенциал действия пирамидного нейрона гиппокампа крысы. Форма реального потенциала действия обычно отличается от идеализированной.

Поляризация мембраны живой клетки обусловлена отличием ионного состава с её внутренней и наружной стороны. Когда клетка находится в спокойном (невозбуждённом) состоянии, ионы по разные стороны мембраны создают относительно стабильную разность потенциалов, называемую потенциалом покоя. Если ввести внутрь живой клетки электрод и измерить мембранный потенциал покоя, он будет иметь отрицательное значение (порядка −70 — −90 мВ). Это объясняется тем, что суммарный заряд на внутренней стороне мембраны существенно меньше, чем на внешней, хотя с обеих сторон содержатся и катионы, и анионы. Снаружи — на порядок больше ионов натрия, кальция и хлора, внутри — ионов калия и отрицательно заряженных белковых молекул, аминокислот, органических кислот, фосфатов, сульфатов. Надо понимать, что речь идёт именно о заряде поверхности мембраны — в целом среда и внутри, и снаружи клетки заряжена нейтрально.

Потенциал мембраны может изменяться под действием различных стимулов. Искусственным стимулом может служить электрический ток, подаваемый на внешнюю или внутреннюю сторону мембраны через электрод. В естественных условиях стимулом часто служит химический сигнал от соседних клеток, поступающий через синапс или путём диффузной передачи через межклеточную среду. Смещение мембранного потенциала может происходить в отрицательную (гиперполяризация) или положительную (деполяризация) сторону.

В нервной ткани потенциал действия, как правило, возникает при деполяризации — если деполяризация мембраны нейрона достигает некоторого порогового уровня или превышает его, клетка возбуждается, и от её тела к аксонам и дендритам распространяется волна электрического сигнала. (В реальных условиях на теле нейрона обычно возникают постсинаптические потенциалы, которые сильно отличаются от потенциала действия по своей природе — например, они не подчиняются принципу «всё или ничего». Эти потенциалы преобразуются в потенциал действия на особом участке мембраны — аксонном холмике, так что потенциал действия не распространяется на дендриты).

Рис. 3. Простейшая схема, демонстрирующая мембрану с двумя натриевыми каналами в открытом и закрытом состоянии, соответственно

Это обусловлено тем, что на мембране клетки находятся ионные каналы — белковые молекулы, образующие в мембране поры, через которые ионы могут проходить с внутренней стороны мембраны на наружную и наоборот. Большинство каналов ионоспецифичны — натриевый канал пропускает практически только ионы натрия и не пропускает другие (это явление называют селективностью). Мембрана клеток возбудимых тканей (нервной и мышечной) содержит большое количество потенциал-зависимых ионных каналов, способных быстро реагировать на смещение мембранного потенциала. Деполяризация мембраны в первую очередь вызывает открытие потенциал-зависимых натриевых каналов. Когда одновременно открывается достаточно много натриевых каналов, положительно заряженные ионы натрия устремляются через них на внутреннюю сторону мембраны. Движущая сила в данном случае обеспечивается градиентом концентрации (с внешней стороны мембраны находится намного больше положительно заряженных ионов натрия, чем внутри клетки) и отрицательным зарядом внутренней стороны мембраны (см. Рис. 2). Поток ионов натрия вызывает ещё бо́льшее и очень быстрое изменение мембранного потенциала, которое и называют потенциалом действия (в специальной литературе обозначается ПД).

Согласно закону «всё-или-ничего» мембрана клетки возбудимой ткани либо не отвечает на стимул совсем, либо отвечает с максимально возможной для неё на данный момент силой. То есть, если стимул слишком слаб и порог не достигнут, потенциал действия не возникает совсем; в то же время, пороговый стимул вызовет потенциал действия такой же амплитуды, как и стимул, превышающий пороговый. Это отнюдь не означает, что амплитуда потенциала действия всегда одинакова — один и тот же участок мембраны, находясь в разных состояниях, может генерировать потенциалы действия разной амплитуды.

После возбуждения нейрон на некоторое время оказывается в состоянии абсолютной рефрактерности, когда никакие сигналы не могут его возбудить снова, затем входит в фазу относительной рефрактерности, когда его могут возбудить исключительно сильные сигналы (при этом амплитуда ПД будет ниже, чем обычно). Рефрактерный период возникает из-за инактивации быстрого натриевого тока, то есть инактивации натриевых каналов (см. ниже).

Распространение потенциала действия

Распространение потенциала действия по немиелинизированным волокнам

По немиелинизированному волокну ПД распространяется непрерывно. Проведение нервного импульса начинается с распространением электрического поля. Возникший ПД за счет электрического поля способен деполяризовать мембрану соседнего участка до критического уровня, в результате чего на соседнем участке генерируются новые ПД. Сами ПД не перемещаются, они исчезают там же, где возникают. Главную роль в возникновении нового ПД играет предыдущий.

Если внутриклеточным электродом раздражать аксон посередине, то ПД будет распространяться в обоих направлениях. Обычно же ПД распространяется по аксону в одном направлении (от тела нейрона к нервным окончаниям), хотя деполяризация мембраны происходит по обе стороны от участка, где в данный момент возник ПД. Одностороннее проведение ПД обеспечивается свойствами натриевых каналов — после открывания они на некоторое время инактивируются и не могут открыться ни при каких значениях мембранного потенциала (свойство рефрактерности). Поэтому на ближнем к телу клетки участке, где до этого уже «прошел» ПД, он не возникает.

При прочих равных условиях распространение ПД по аксону происходит тем быстрее, чем больше диаметр волокна. По гигантским аксонам кальмара ПД может распространяться почти с такой же скоростью, как и по миелинизированным волокнам позвоночных (около 100 м/c).

Распространение потенциала действия по миелинизированным волокнам

По миелинизированному волокну ПД распространяется скачкообразно (сальтаторное проведение). Для миелинизированных волокон характерна концентрация потенциалзависимых ионных каналов только в областях перехватов Ранвье; здесь их плотность в 100 раз больше, чем в мембранах безмиелиновых волокон. В области миелиновых муфт потенциалзависимых каналов почти нет. ПД, возникший в одном перехвате Ранвье, за счет электрического поля деполяризует мембрану соседних перехватов до критического уровня, что приводит к возникновению в них новых ПД, то есть возбуждение переходит скачкообразно, от одного перехвата к другому. В случае повреждения одного перехвата Ранвье ПД возбуждает 2-й, 3-ий, 4-й и даже 5-й, поскольку электроизоляция, создаваемая миелиновыми муфтами, уменьшает рассеивание электрического поля. Это увеличивает скорость распространения ПД по миелинизированным волокнам по сравнению с немиелинизированными. Кроме того, миелинизированные волокна толще, а электрическое сопротивление более толстых волокон меньше, что тоже увеличивает скорость проведения импульса по миелинизированным волокнам. Другим преимуществом сальтаторного проведения является его экономичность в энергетическом плане, так как возбуждаются только перехваты Ранвье, площадь которых меньше 1 % мембраны, и, следовательно, необходимо значительно меньше энергии для восстановления трансмембранных градиентов Na⁺ и K⁺, расходующихся в результате возникновения ПД, что может иметь значение при высокой частоте разрядов, идущих по нервному волокну.

Чтобы представить, насколько эффективно может быть увеличена скорость проведения за счёт миелиновой оболочки, достаточно сравнить скорость распространения импульса по немиелинизированным и миелинизированным участкам нервной системы человека. При диаметре волокна около 2 µм и отсутствии миелиновой оболочки скорость проведения будет составлять ~1 м/с, а при наличии даже слабой миелинизации при том же диаметре волокна — 15—20 м/с. В волокнах большего диаметра, обладающих толстой миелинововой оболочкой, скорость проведения может достигать 120 м/с.

Скорость распространения потенциала действия по мембране отдельно взятого нервного волокна отнюдь не является постоянной величиной — в зависимости от различных условий, эта скорость может очень значительно уменьшаться и, соответственно, увеличиваться, возвращаясь к некоему исходному уровню.

Активные свойства мембраны

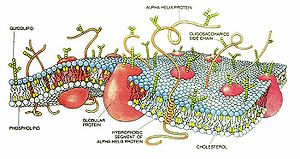Схема строения мембраны клетки.

Активные свойства мембраны, обеспечивающие возникновение потенциала действия, основываются главным образом на поведении потенциалзависимых натриевых (Na⁺) и калиевых (K⁺) каналов. Начальная фаза ПД формируется входящим натриевым током, позже открываются калиевые каналы и выходящий K⁺-ток возвращает потенциал мембраны к исходному уровню. Исходную концентрацию ионов затем восстанавливает натрий-калиевый насос.

По ходу ПД каналы переходят из состояния в состояние: у Na⁺ каналов основных состояний три — закрытое, открытое и инактивированное (в реальности дело сложнее, но этих трёх достаточно для описания), у K⁺ каналов два — закрытое и открытое.

Поведение каналов, участвующих в формировании ПД, описывается через проводимость и высчиляется через коэффициенты переноса (трансфера).

Коэффициенты переноса были выведены Ходжкиным и Хаксли.^[1][2]

Проводимость для калия G_K на единицу площади [S/cm²]

Проводимость для натрия G_Na на единицу площади [S/cm²]

рассчитывается сложнее, поскольку, как уже было сказано, у потенциал-зависимых Na+ каналов, помимо закрытого/открытого состояний, переход между которыми описывается параметром , есть ещё инактивированное/не-инактивированное состояния, переход между которыми описывается через параметр

См. также

Литература

1. ↑ Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117: 500—544. PMID 12991237 free full text (англ.)
2. ↑ J.Malmivuo, R.Plonsey. Bioelectromagnetism. Oxford University Press. New York, Oxford. 1995.free full text (англ.)

Вызванный потенциал — Википедия

Вызванный потенциал (сокр. ВП) — электрическая реакция органов (в основном мозга) на внешний раздражитель или на выполнение умственной (когнитивной) задачи. Наиболее широко используемыми раздражителями являются визуальные для регистрации зрительных ВП, звуковые для регистрации аудиторных ВП и электрические для регистрации соматосенсорных ВП. Запись ВП производится при помощи электроэнцефалографических электродов, расположенных на поверхности головы. Термин психофизиологии^[1].

Метод вызванных потенциалов применяется для исследования функции сенсорных систем мозга (соматосенсорной — соматосенсорная система , зрительной — зрительная система, аудиторной — слуховая сенсорная система) и систем мозга ответственных за когнитивные процессы. В основе метода лежит регистрация биоэлектрических реакций мозга в ответ на внешнее раздражение (в случае сенсорных ВП) и при выполнении когнитивной задачи (в случае когнитивных ВП). В зависимости от времени появления (латентности) вызванного ответа после предъявления стимула ВП принято разделять на коротко-латентные (до 50 миллисекунд), средне-латентные (50-100 мс) и длинно-латентные (свыше 100 мс). Особой разновидностью ВП являются моторные вызванные потенциалы, которые регистрируются с мышц конечностей в ответ на транскраниальное электрическое или магнитное раздражение моторной зоны коры (Транскраниальная магнитная стимуляция). Моторные ВП позволяют производить оценку функции кортико-спинальных (моторных) систем мозга.

Поскольку амплитуда ВП (5-15 мкВ) гораздо меньше амплитуды ЭЭГ в состоянии бодрствования (20-70 мкВ), то для выделения ВП проводят усреднение сигнала: стимул предъявляется несколько раз, после чего компьютер суммирует отрезки ЭЭГ, которые следуют сразу после предъявления стимула. В результате постоянные компоненты ВП суммируются и выделяются, а «случайные» компоненты ЭЭГ, наложившиеся на запись во время регистрации ВП, нивелируются.^[2][3][4] Следует отметить, что соотношение сигнал/шум при выделении ВП из ЭЭГ находится в прямой зависимости от квадратного корня из количества поданных стимулов. Например, если средняя амплитуда ЭЭГ при записи ВП составляет 50 мкВ, то после 25 поданных сигналов уровень шума уменьшится до 50/25=10{\displaystyle 50/{\sqrt {25}}=10} мкВ, после 50 поданных сигналов — до значения около 7 мкВ, после 100 — до 5 мкВ и т. д. Так как при получении когнитивных ВП зачастую используются несколько различных типов сигналов, то для четкого выделения ВП на конкретный тип стимула следует учитывать не общее количество поданных сигналов, а количество поданных сигналов этого типа. Рекомендуется для выделения компонентов с высокой амплитудой подавать 50-60 стимулов, со средней амплитудой — 200—300, с низкой — более 500^[5].

Кроме электроэнцефалографии, для регистрации ВП используют также магнитоэнцефалографию (МЭГ)^[6].

Различают зрительные ВП (ЗВП), аудиторные ВП (АВП), соматосенсорные ВП (СВП), связанные с событиями ВП (ССВП), когнитивные ВП (КВП), которые являются частным случаем ССВП и моторные ВП (МВП).

Характеристиками вызванных потенциалов являются латентный период (латентность), амплитуда (или площадь), полярность (негативная/позитивная) и форма.

Для диагностических целей наибольшее применение получили коротколатентные аудиторные, соматосенсорные, зрительные и моторные ВП. Например, стволовые АВП (Brainstem auditory evoked potentials) используются в качестве стандартного нейрофизиологического теста для исследования поражений ствола мозга и объективной оценки нарушений слуха. Соматосенсорные и моторные ВП позволяют выявить и оценить степень нарушения функции проводящих путей спинного мозга. Зрительные ВП имеют важное значение в диагностике рассеянного склероза.

В научной практике, ВП первоначально выступали как основа для анализа реакций мозга на внешние стимулы, в дальнейшем стали использоваться и для анализа внутренне обусловленных нервных процессов. На основании данных, полученных с помощью этого метода, строятся гипотезы относительно восприятия, внимания, интеллекта, функциональной асимметрии мозга и индивидуальной психофизиологической дифференциации. В частности, могут быть зафиксированы биоэлектрические колебания, связанные с активностью двигательной коры (моторный потенциал), с окончанием движения, с состоянием намерения произвести какое-либо действие (Е-волна), пропуска ожидаемого стимула. Форма, амплитуда и латентный период колебаний длинно-латентных вызванных потенциалов обусловлены местом локализации регистрирующего электрода, модальностью и интенсивностью стимула, состоянием и специфическими особенностями индивида.

Поскольку отдельные компоненты или комплексы компонентов ВП оказались весьма чувствительны к определенным видам психической деятельности, возникли специальные методики выделения тех или иных компонентов, а также методики анализа психических функций при помощи данных выделенных компонентов.

Наиболее значимые техники и виды ССВП:

У человека фиксируются, как правило, от поверхности головы при помощи специальных технических устройств. Виды:

• первичные ответы, возникающие в первые 100 мс. после предъявления стимула,
• вторичные, более поздние.

потенциалы, связанные с событием

Теория потенциала — Википедия

Теория потенциала — раздел математики и математической физики, посвящённый изучению свойств дифференциальных уравнений в частных производных в областях с достаточно гладкой границей посредством введения специальных видов интегралов, зависящих от определённых параметров, называемых потенциалами.

Абстрактная теория потенциала — обобщение теории потенциала на абстрактные топологические пространства^[1]; в качестве основного абстрактной теории используется понятие гармонического пространства — произвольного топологического пространства, снабжённого пучком непрерывных вещественных функций, обладающих (зафиксированными аксиоматически) свойствами, характерными для гармонических функций^[1].

Изначально возникла как часть небесной механики, изучающая свойства сил притяжения, действующих согласно закону всемирного тяготения. Основной вклад в создание и первоначальное развитие теории внесли Ньютон, Лагранж, Лежандр, Лаплас. В частности, Лагранж показал, что поле сил тяготения является потенциальным.

Начиная с Гаусса метод потенциалов начал применяться также для задач электростатики и магнетизма, в качестве потенциалов стали рассматриваться «массы» (заряды, намагниченность) произвольного знака. В рамках развития теории в XIX веке выделились основные краевые задачи: задача Дирихле, задача Неймана, задача Робена, задача о выметании масс, значительный вклад в изучение основных краевых задач в конце XIX века внесли Ляпунов и Стеклов.

Результаты теории существенно обобщены в начале XX века с использованием аппарата теории меры и обобщённых функций. Впоследствии в теории потенциалов задействованы аналитические, гармонические и субгармонические функции, инструментарий теорией вероятностей.

В 1950-е годы на основе методов топологии и функционального анализа разработана аксиоматическая абстрактная теория потенциалов.

Логарифмические потенциалы (двумерные потенциалы)[править | править код]

Потенциал площади[править | править код]

На плоскости объёмным логарифмическим потенциалом (или потенциалом площади) называется интеграл вида

V(M)=∫Dρ(Q)ln⁡1RQMdσQ{\displaystyle V(M)=\int \limits _{D}\rho (Q)\ln {\frac {1}{R_{QM}}}d\sigma _{Q}}.

Если плотность ρ(M){\displaystyle \rho (M)} непрерывна вместе со своими первыми производными, то объёмный потенциал является классическим решением уравнения Пуассона:

ΔV=−2πρ{\displaystyle {\Delta }V=-{2\pi \rho }}

Логарифмический потенциал простого слоя[править | править код]

В двумерном случае потенциалом простого слоя называется интеграл:

V(M)=∫Cμ(P)ln⁡1RMPdlP{\displaystyle V(M)=\int \limits _{C}\mu (P)\ln {\frac {1}{R_{MP}}}dl_{P}},

где C{\displaystyle C} — некоторая кривая.

Логарифмический потенциал двойного слоя[править | править код]

Потенциалом двойного слоя на плоскости называется интеграл:

W(M)=−∫Cν(P)∂∂nPln⁡1RMPdlP{\displaystyle W(M)=-\int \limits _{C}\nu (P){\frac {\partial }{\partial n_{P}}}\ln {\frac {1}{R_{MP}}}dl_{P}},

где nP{\displaystyle \mathbf {n} _{P}} — внешняя нормаль к кривой C{\displaystyle C} в точке P{\displaystyle P}. В случае незамкнутой кривой направление внешней нормали выбирается произвольно.

Трёхмерные потенциалы[править | править код]

Объёмный потенциал[править | править код]

Пусть в ограниченной области D{\displaystyle D} задана функция ρ(M){\displaystyle \rho (M)}, интеграл

V(M)=∫Dρ(Q)RQMdV{\displaystyle V(M)=\int \limits _{D}{\frac {\rho (Q)}{R_{QM}}}dV}

называется объёмным потенциалом.

Функция 1RQM{\displaystyle {\frac {1}{R_{QM}}}} представляет собой, определённый во всех точках M≠Q{\displaystyle M\neq Q} потенциал единичного точечного заряда, сосредоточенного в точке Q{\displaystyle Q}. Если в области D{\displaystyle D} непрерывно распределён заряд с объёмной плотностью ρ(M){\displaystyle \rho (M)}, то в силу принципа суперпозиции естественно предполагать, что потенциал, создаваемый данным распределением объёмного заряда, выражается вышеприведённым интегралом. Функция ρ(M){\displaystyle \rho (M)} называется плотностью потенциала.

Если плотность ρ(M){\displaystyle \rho (M)} непрерывна вместе со своими первыми производными, то объёмный потенциал является классическим решением уравнения Пуассона:

ΔV=−4πρ{\displaystyle {\Delta }V=-{4\pi \rho }}

Поверхностные потенциалы[править | править код]

Потенциал простого слоя[править | править код]

Потенциалом простого слоя в трёхмерном случае называется интеграл

V(M)=∫Sμ(P)dSPRMP,{\displaystyle V(M)=\int \limits _{S}\mu (P){\frac {dS_{P}}{R_{MP}}},}

где S{\displaystyle S} — некоторая поверхность, μ(P){\displaystyle \mu (P)} — функция заданная на поверхности S{\displaystyle S}, она называется плотностью потенциала простого слоя.

Свойства:

1. ΔV(M)=0,∀M∉S.{\displaystyle \Delta V(M)=0,\forall M\notin S.}
2. V=O(1r),r→∞.{\displaystyle V=O\left({\frac {1}{r}}\right),r\rightarrow \infty .}
3. V∈C(R3){\displaystyle V\in C(\mathbb {R} ^{3})}, если S{\displaystyle S} — гладкая поверхность, плотность μ(Q){\displaystyle \mu (Q)} — ограничена и непрерывна.
4. Пусть S{\displaystyle S} — замкнутая поверхность Ляпунова, ограничивающая область D{\displaystyle D}, P0∈S{\displaystyle P_{0}\in S}, ne(P){\displaystyle \mathbf {n} _{e}(P)} — внешняя нормаль к поверхности S{\displaystyle S} в точке P∈S{\displaystyle P\in S}. Тогда разрыв потенциала при переходе через поверхность S{\displaystyle S} определяется следующими формулами:

limM∈DM→P0,(∂V∂ne)(M)=(∂V∂ne)(P0)+2πμ(P0),{\displaystyle \lim _{\stackrel {M\rightarrow P_{0},}{M\in D}}\left({\frac {\partial V}{\partial n_{e}}}\right)(M)=\left({\frac {\partial V}{\partial n_{e}}}\right)(P_{0})+2\pi \mu (P_{0}),}

limM∉D∪SM→P0,(∂V∂ne)(M)=(∂V∂ne)(P0)−2πμ(P0),{\displaystyle \lim _{\stackrel {M\rightarrow P_{0},}{M\notin D\cup S}}\left({\frac {\partial V}{\partial n_{e}}}\right)(M)=\left({\frac {\partial V}{\partial n_{e}}}\right)(P_{0})-2\pi \mu (P_{0}),}

limM∈DM→P0,(∂V∂ne)(M)−limM∉D∪SM→P0,(∂V∂ne)(M)=4πμ(P0).{\displaystyle \lim _{\stackrel {M\rightarrow P_{0},}{M\in D}}\left({\frac {\partial V}{\partial n_{e}}}\right)(M)-\lim _{\stackrel {M\rightarrow P_{0},}{M\notin D\cup S}}\left({\frac {\partial V}{\partial n_{e}}}\right)(M)=4\pi \mu (P_{0}).}

Потенциал двойного слоя[править | править код]

Потенциалом двойного слоя в трёхмерном случае называется интеграл:

W(M)=−∫Sν(P)∂∂nP1RMPdSP,{\displaystyle W(M)=-\int \limits _{S}\nu (P){\frac {\partial }{\partial n_{P}}}{\frac {1}{R_{MP}}}dS_{P},}

где S{\displaystyle S} — двусторонняя поверхность, nP{\displaystyle \mathbf {n} _{P}} — внешняя нормаль к поверхности S{\displaystyle S} в точке P{\displaystyle P} (в том случае, когда поверхность S{\displaystyle S} незамкнута, внешняя нормаль выбирается произвольно), ν(P){\displaystyle \nu (P)} — функция, заданная на поверхности S{\displaystyle S}, она называется плотностью потенциала двойного слоя.

Выражение для потенциала двойного слоя также может быть переписано в виде:

W(M)=∫Sν(P)cos⁡φRMP2dSP,{\displaystyle W(M)=\int \limits _{S}\nu (P){\frac {\cos \varphi }{R_{MP}^{2}}}dS_{P},}

где φ{\displaystyle \varphi } — угол между внутренней нормалью к поверхности S{\displaystyle S} в точке P{\displaystyle P} и вектором PM{\displaystyle \mathbf {PM} }.

Свойства:

1. ΔW(M)=0,∀M∉S.{\displaystyle \Delta W(M)=0,\forall M\notin S.}
2. W=O(1r2),r→∞.{\displaystyle W=O\left({\frac {1}{r^{2}}}\right),r\rightarrow \infty .}
3. Пусть S{\displaystyle S} — поверхность Ляпунова. Потенциал двойного слоя с непрерывной и ограниченной плотностью |ν(P)|≤C{\displaystyle |\nu (P)|\leq C} на поверхности S{\displaystyle S} существует, то есть является сходящимся несобственным интегралом при M∈S{\displaystyle M\in S}.
4. Пусть S{\displaystyle S} — замкнутая поверхность Ляпунова, ограничивающая область D{\displaystyle D}, P0∈S{\displaystyle P_{0}\in S}. Тогда разрыв потенциала двойного слоя при переходе через поверхность S{\displaystyle S} определяется следующими формулами:

limM∈DM→P0,W(M)=W(P0)+2πν(P0),{\displaystyle \lim _{\stackrel {M\rightarrow P_{0},}{M\in D}}W(M)=W(P_{0})+2\pi \nu (P_{0}),}

limM∉D∪SM→P0,W(M)=W(P0)−2πν(P0),{\displaystyle \lim _{\stackrel {M\rightarrow P_{0},}{M\notin D\cup S}}W(M)=W(P_{0})-2\pi \nu (P_{0}),}

limM∈DM→P0,W(M)−limM∉D∪SM→P0,W(M)=4πν(P0).{\displaystyle \lim _{\stackrel {M\rightarrow P_{0},}{M\in D}}W(M)-\lim _{\stackrel {M\rightarrow P_{0},}{M\notin D\cup S}}W(M)=4\pi \nu (P_{0}).}

• Потенциала теория — статья из Математической энциклопедии. А. И. Прилепко, Е. Д. Соломенцев
• Свешников А. Г., Боголюбов А. Н., Кравцов В. В. Глава V. Уравнения эллиптического типа. Краевые задачи для уравнения Лапласа. // Лекции по математической физике. — 2-е изд., испр. и доп. — М.: Изд-во МГУ; Наука, 2004. — С. 203. — 416 с. — ISBN 5-211-04899-7.
• Тихонов А. Н., Самарский А. А. Глава IV. Уравнения эллиптического типа. // Уравнения математической физики. — 7-е изд. — М.: Изд-во МГУ; Наука, 2004. — С. 348. — 798 с. — ISBN 5-211-04843-1.
• Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.

потенциалы — это… Что такое потенциалы?

Потенциалы — [potentials], в линейном программировании дополнительные переменные, включаемые в формулировку транспортной задачи при ее решении специальным методом, который так и называется метод потенциалов …   Экономико-математический словарь

потенциалы — В линейном программировании дополнительные переменные, включаемые в формулировку транспортной задачи при ее решении специальным методом, который так и называется метод потенциалов. [http://slovar lopatnikov.ru/] Тематики экономика EN potentials …   Справочник технического переводчика

ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ — энергетич. характеристики эл. магн. поля, к рые вводят для описания поля наряду с силовыми хар ками напряжённостью электрич. поля Е и магн. индукцией В. В электростатике векторное электрич. поле можно характеризовать одной скалярной ф цией… …   Физическая энциклопедия

ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕСКИЕ — определённые функции объёма (V), давления (р), темп ры (Т), энтропии (S), числа ч ц системы (N) и др. макроскопич. параметров (xi), характеризующих состояние термодинамической системы. К П. т. относятся: внутренняя энергия U=U(S, V, N, xi),… …   Физическая энциклопедия

Потенциалы Лиенара — Вихерта — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм …   Википедия

ПОТЕНЦИАЛЫ ЗАПАЗДЫВАЮЩИЕ — решения уравнений для потенциалов переменного электромагнитного поля, учитывающие конечную скорость распространения электромагнитного взаимодействия. Изменения плотности зарядов и токов сказываются на изменении потенциалов через промежуток… …   Большой Энциклопедический словарь

ПОТЕНЦИАЛЫ ТЕРМОДИНАМИЧЕСКИЕ — функции объема, давления, температуры, энтропии, числа частиц и других независимых макроскопических параметров, характеризующих состояние термодинамической системы. К потенциалам термодинамическим относятся внутренняя энергия, энтальпия, изохорно …   Большой Энциклопедический словарь

Потенциалы электромагнитного поля — Потенциалы электромагнитного поля  термин, под которым в обычной трехмерной формулировке электродинамики понимаются cкалярный потенциал и векторный потенциал , через которые выражаются напряженность электрического поля и вектор магнитной… …   Википедия

ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ — (скалярный и векторный) характеристики электромагнитного поля, через которые выражаются напряженности электрических и магнитных полей …   Большой Энциклопедический словарь

Потенциалы термодинамические — Термодинамические потенциалы Статья является частью серии «Термодинамика». Внутренняя энергия Энтальпия Свободная энергия Гельмгольца Энергия Гиббса Большой термодинамический потенциал (Ω) Разделы …   Википедия

Потенциалы электромагнитного поля —         величины, характеризующие электромагнитное поле. В электростатике векторное электрическое поле можно характеризовать одной скалярной функцией потенциалом электростатическим (См. Потенциал электростатический). В общем случае для описания… …   Большая советская энциклопедия