Потенциал поля точечного заряда.
Подставим в соотношение для определения потенциала выражение для напряженности электрического поля точечного заряда:
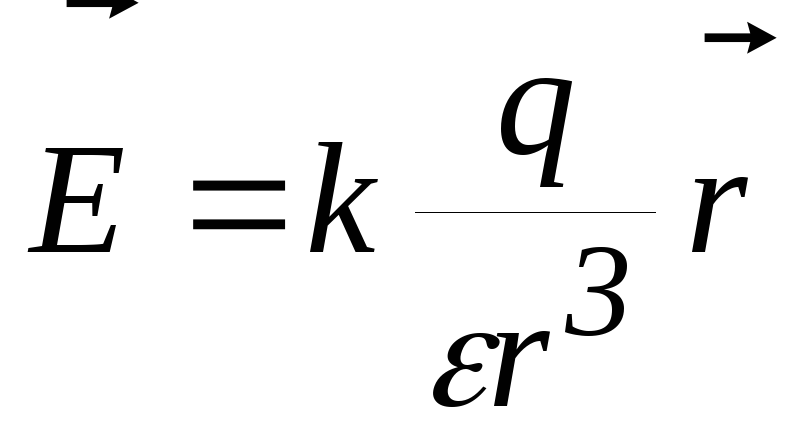 .
.
При интегрировании учтем, что 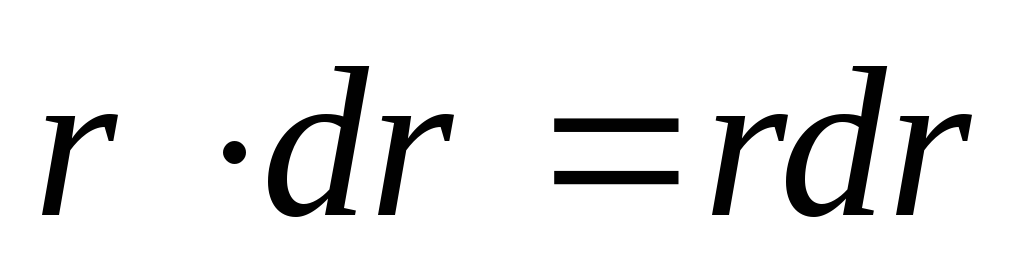 .
.
После интегрирования получаем:
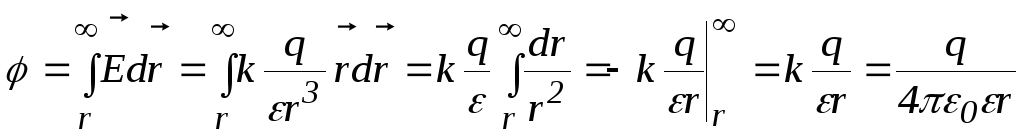 .
.
Потенциал точечного заряда пропорционален величине заряда и убывает обратно пропорционально расстоянию, стремясь на бесконечности к нулю.
Потенциал поля системы зарядов.
Пусть система состоит из 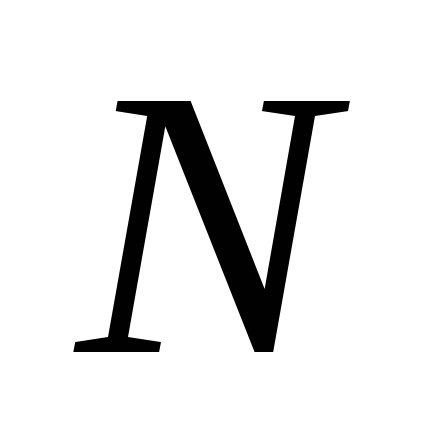 неподвижных точечных зарядов
неподвижных точечных зарядов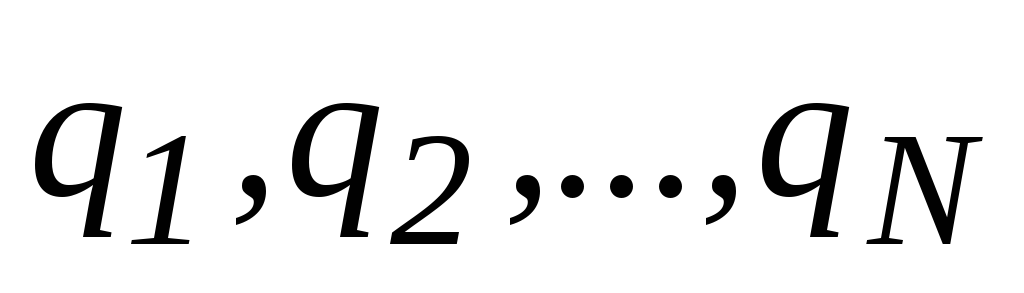
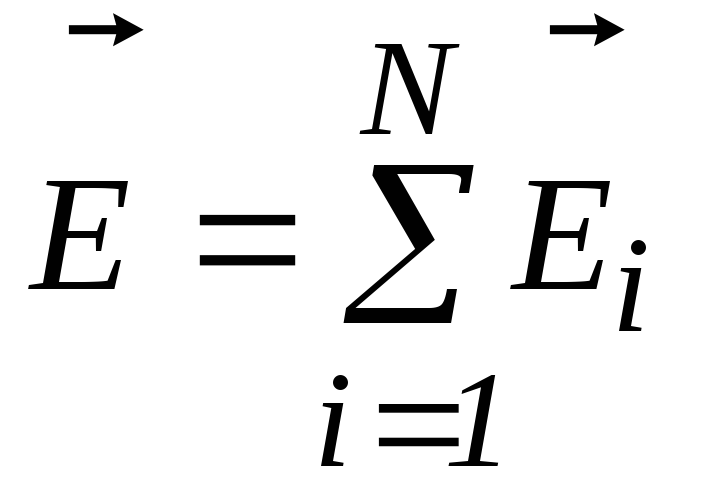 ,
где
,
где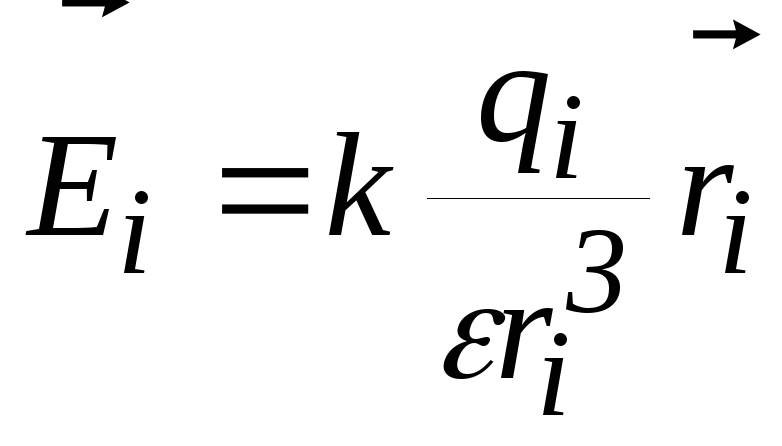 —
напряженность поля
—
напряженность поля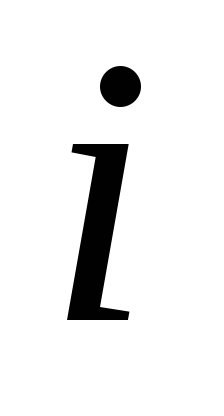 -го
точечного заряда в исследуемой точке,
находящейся на расстоянии
-го
точечного заряда в исследуемой точке,
находящейся на расстоянии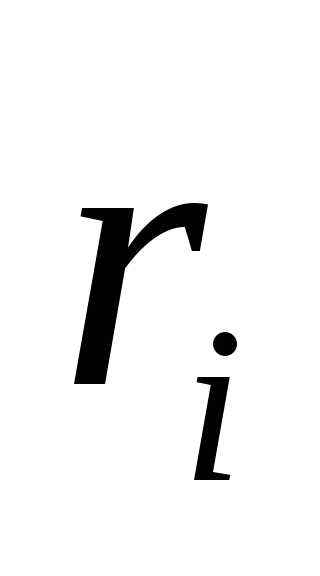 от заряда
от заряда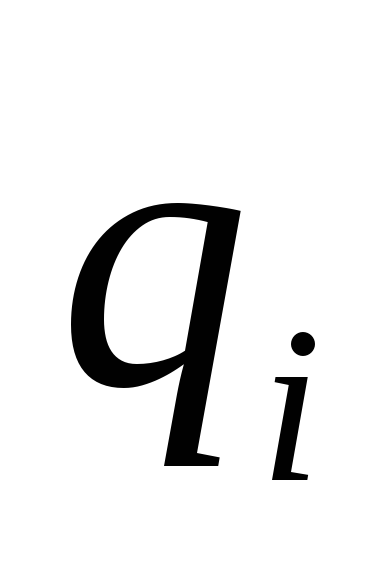 .
. ,
получим:
,
получим: 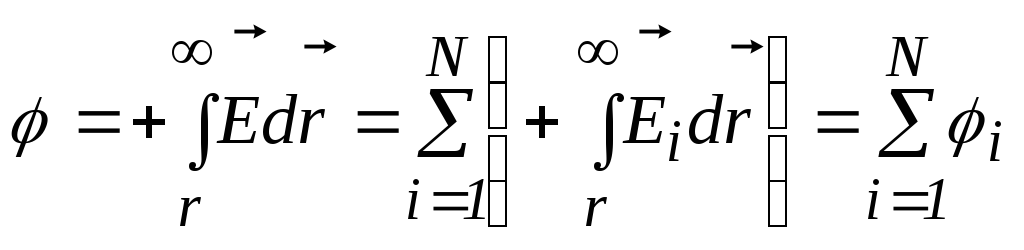 ,
,
где 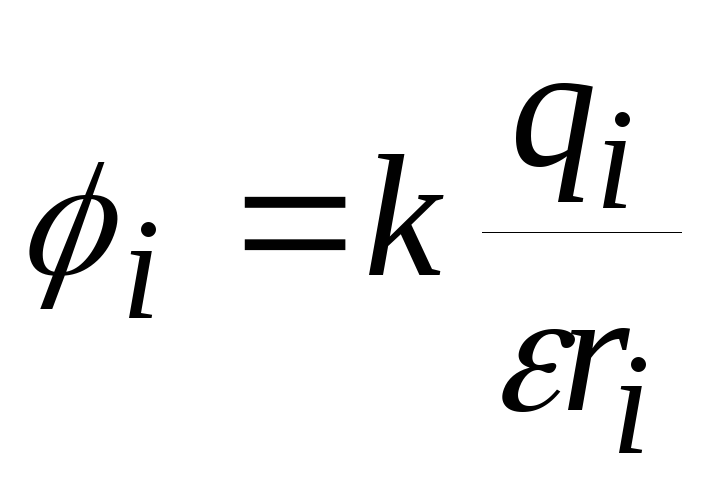 —
потенциал поля
—
потенциал поля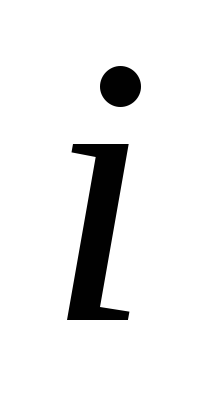 -го
точечного заряда в исследуемой точке.
-го
точечного заряда в исследуемой точке.
Таким образом, потенциал системы точечных зарядов в любой точке пространства равен алгебраической сумме потенциалов, создаваемых всеми точечными зарядами в этой точке.
Если заряды непрерывно распределены по объему, то сумму следует заменить объемным интегралом:
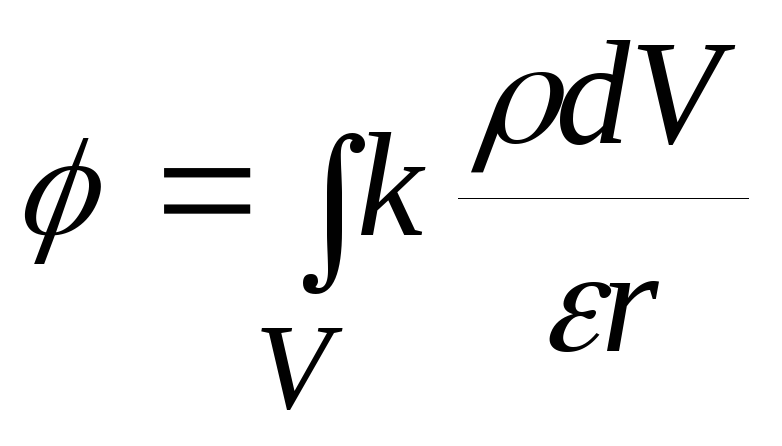 ,
,
где интегрирование проводится по объему,
где 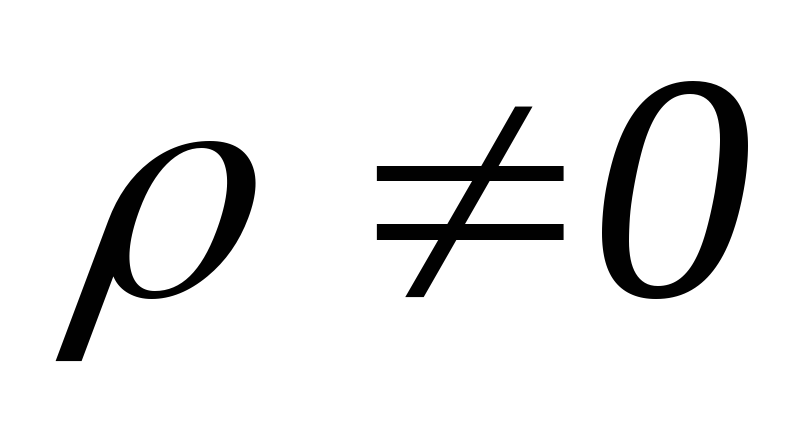 .
.
Аналогичные выражения получаются при поверхностном и линейном распределении зарядов:
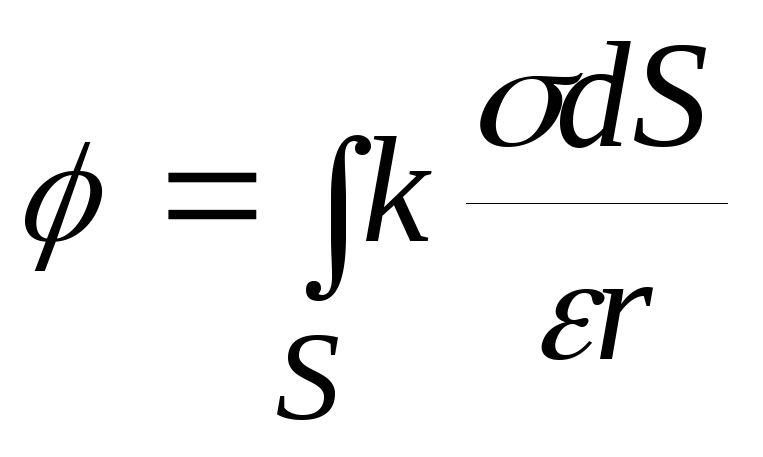 ,
,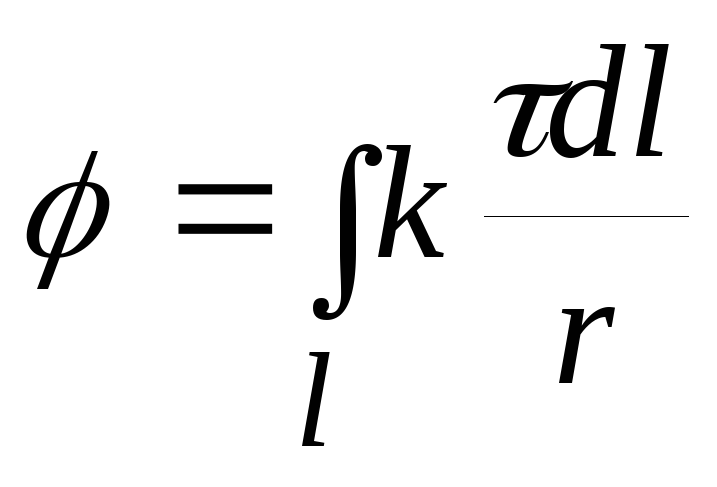 .
.
Рассмотрим ряд примеров расчета потенциала и разности потенциалов, которые понадобятся нам в дальнейшем изложении.
Потенциал поля точечного диполя.
Согласно
принципу суперпозиции, учитывая, что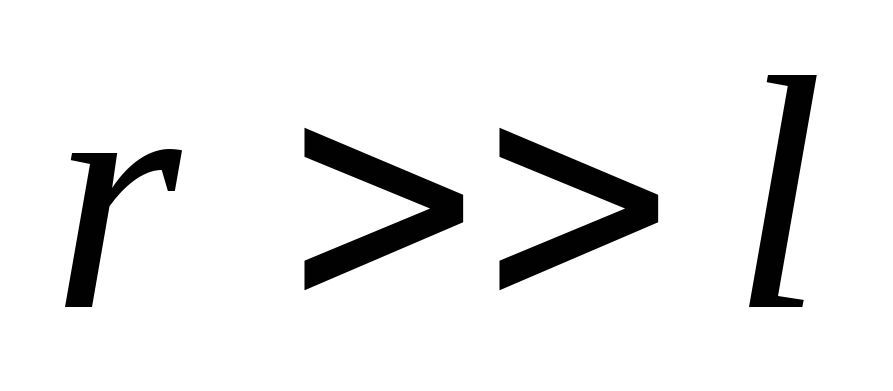 :
:
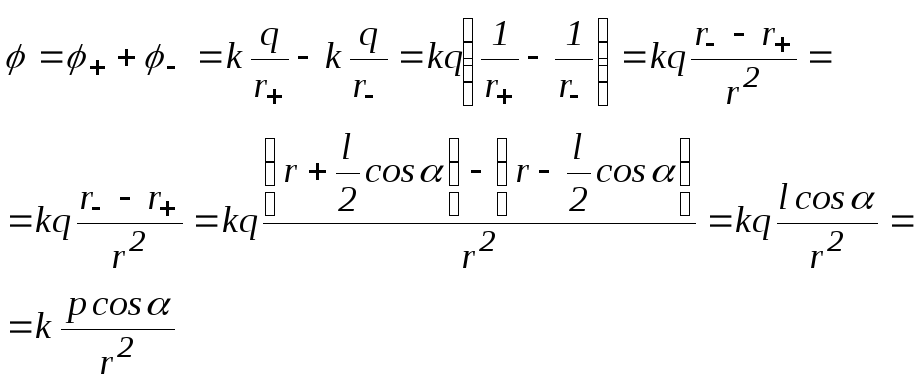 Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда
Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда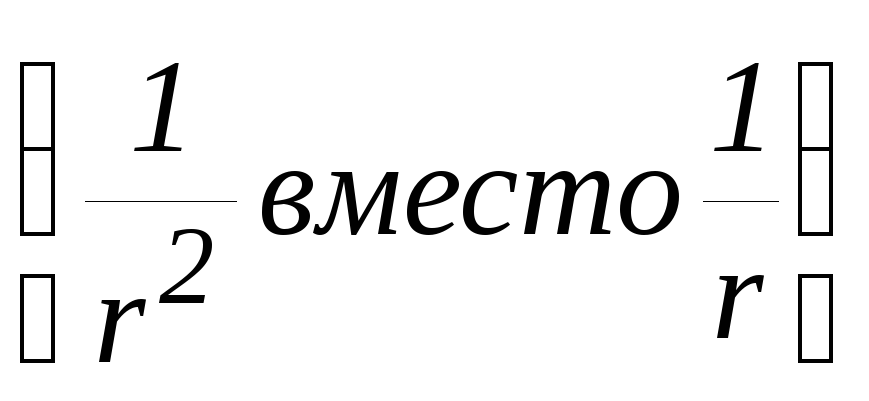
Потенциал поля в точках на оси заряженного кольца.
Для расчета 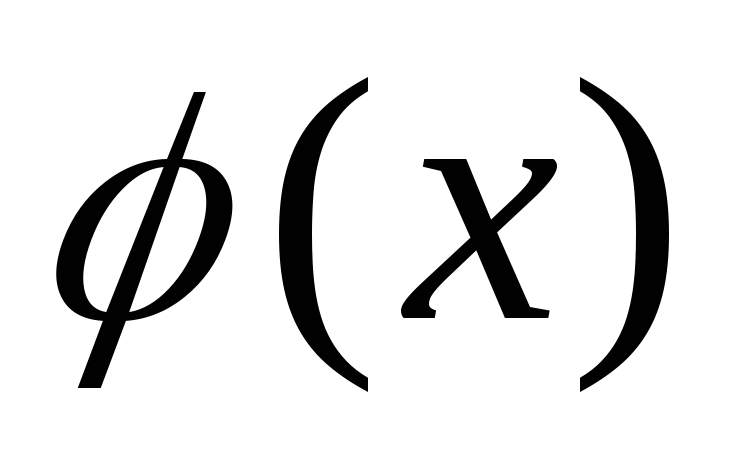 воспользуемся
линейным интегралом:
воспользуемся
линейным интегралом:
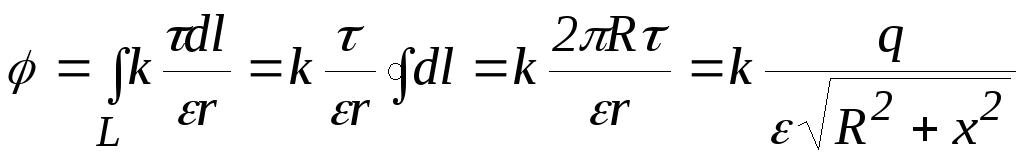
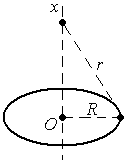 ,
,
где 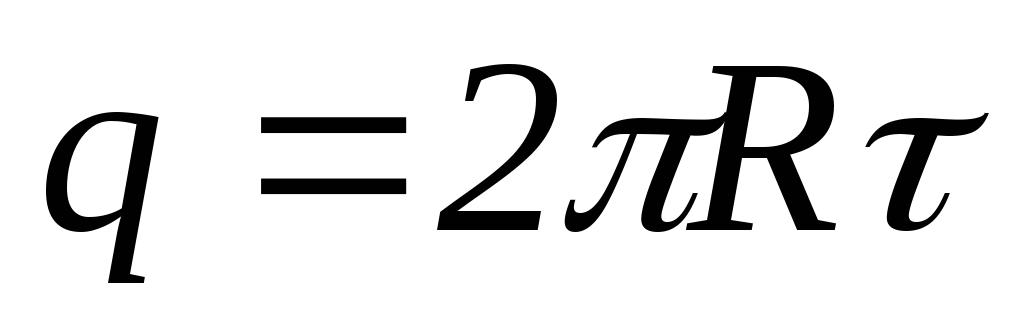

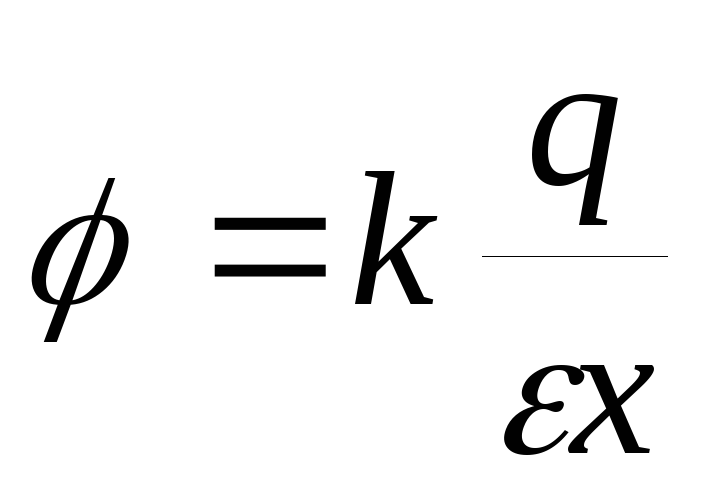
— потенциал кольца убывает как потенциал поля точечного заряда.
В центре кольца (x= 0) потенциал равен:
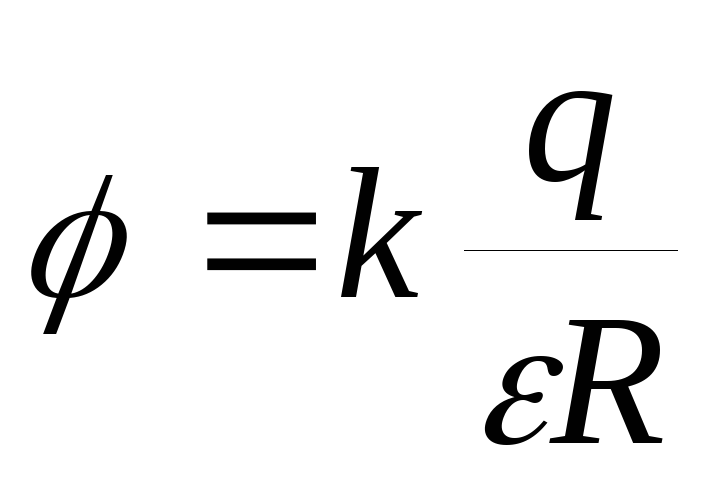 .
.
Потенциал в точках на оси равномерно заряженного круга
 .
.
Д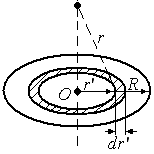
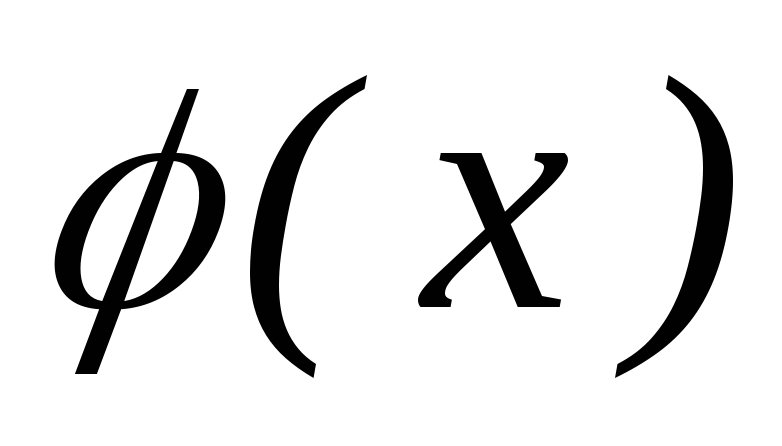 следует
воспользоваться поверхностным интегралом:
следует
воспользоваться поверхностным интегралом: 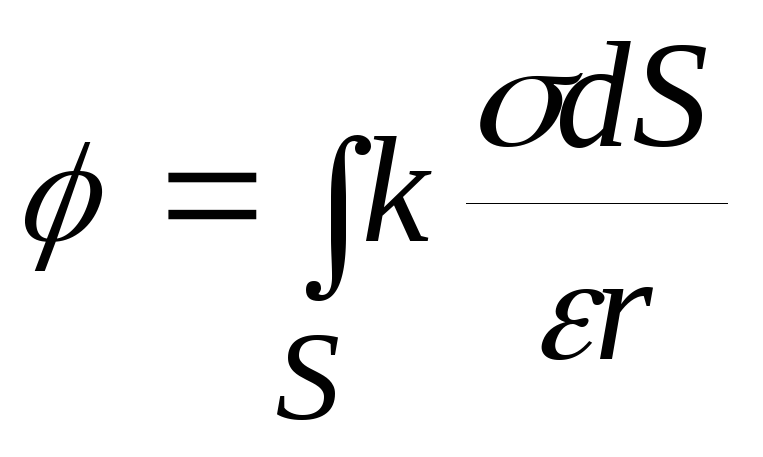 .
.
Представим круг как систему колец с
радиусами 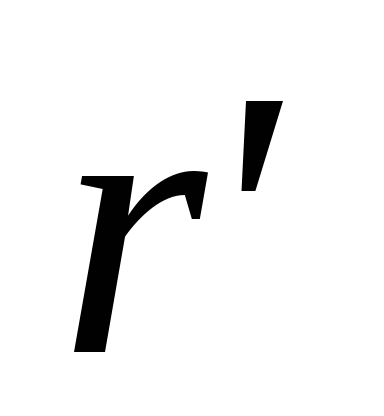 ,
тогда
,
тогда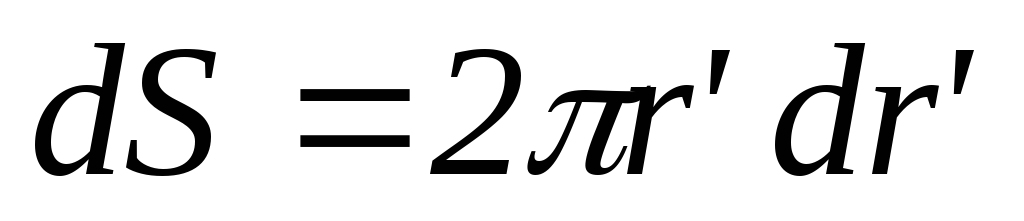 ,
,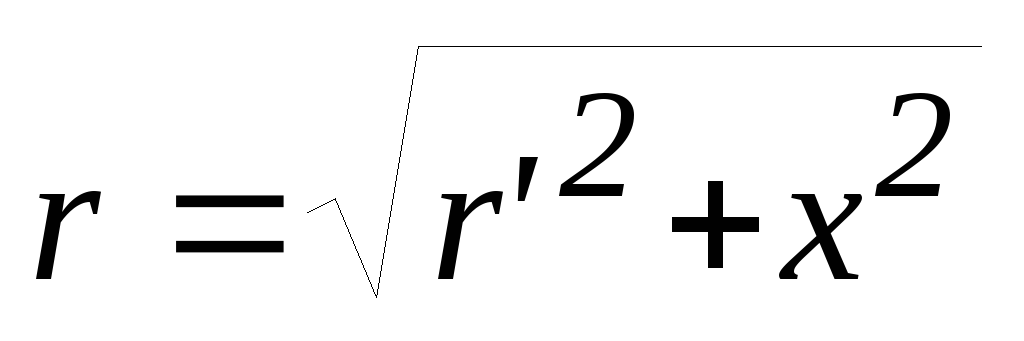 ,
,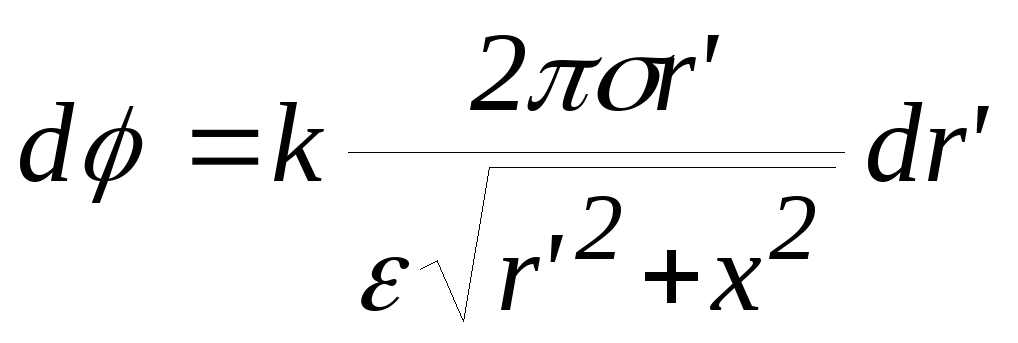
Для  получим:
получим:
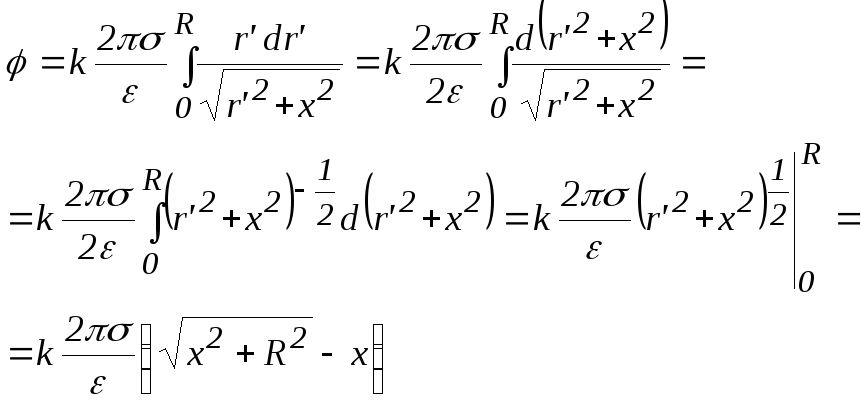 .
.
Для точек достаточно удаленных от круга 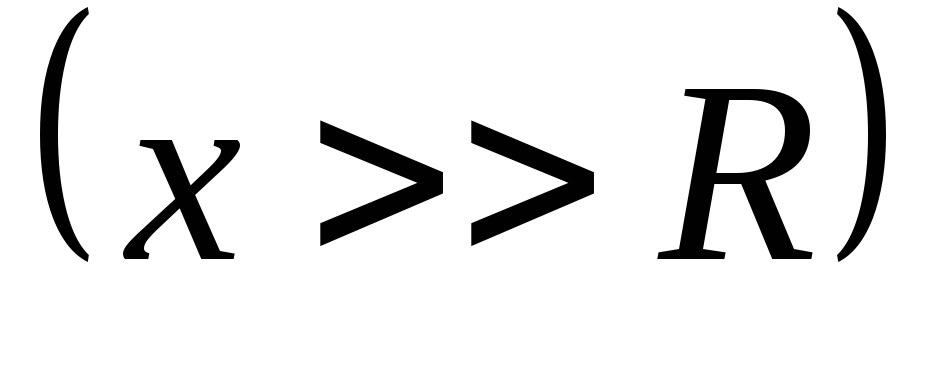 :
:
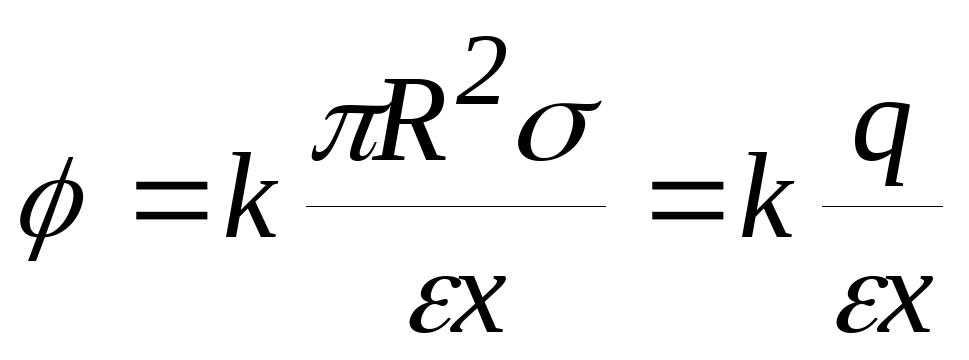 .
.
Получите самостоятельно этот результат.
Потенциал поля объемно заряженного шара

Для простоты расчетов примем 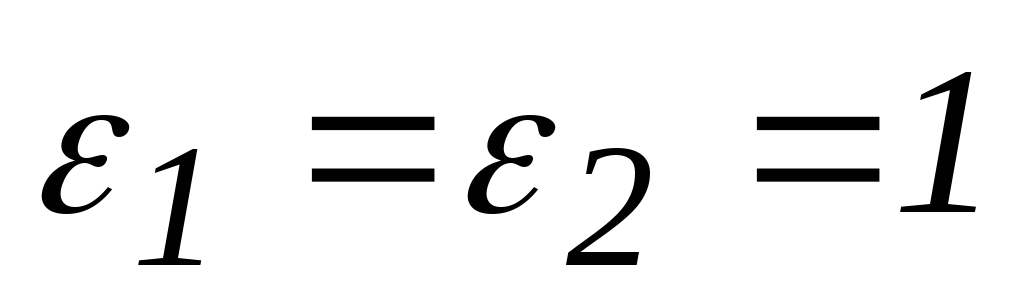 .
.
Зависимость 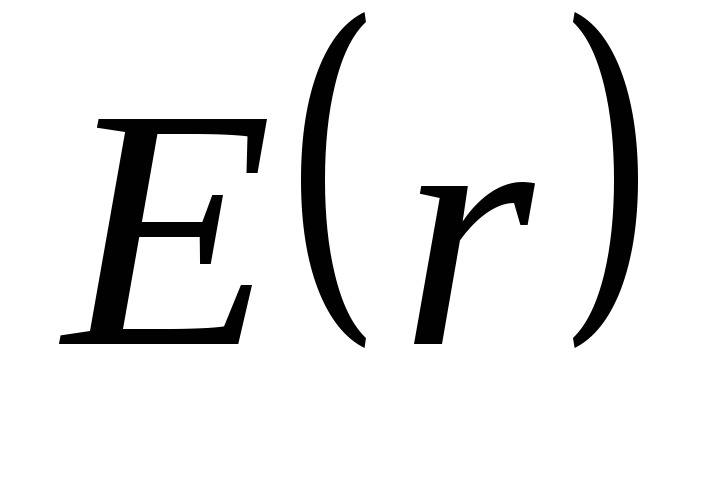 для этого случая представлена на рисунке.
Потенциал точек внутри шара
для этого случая представлена на рисунке.
Потенциал точек внутри шара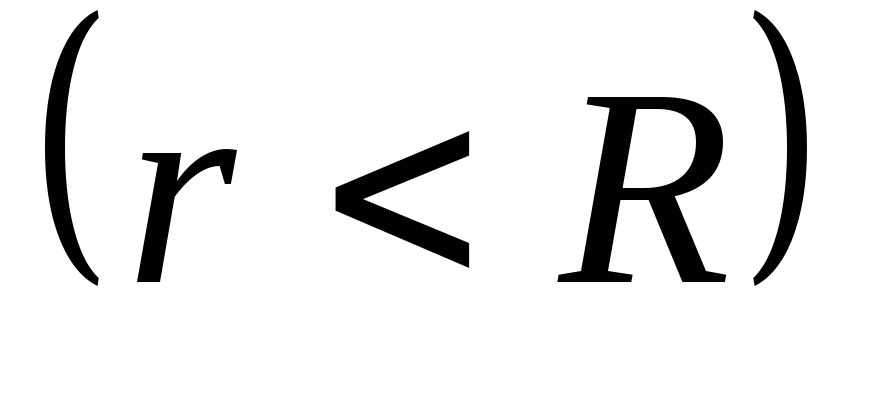 равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
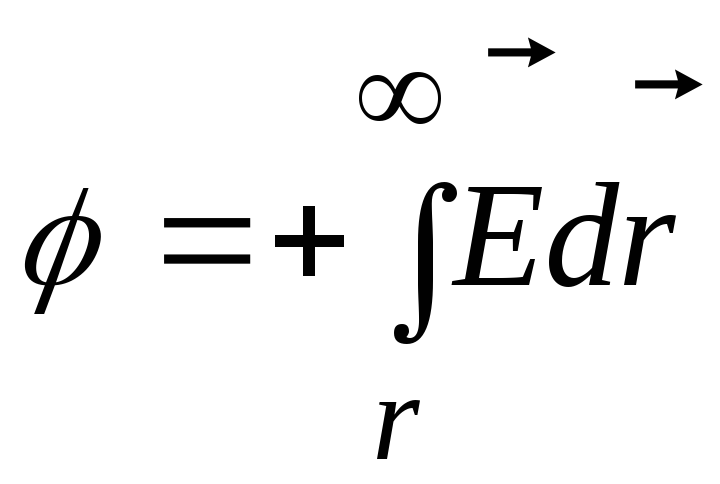 ,
,
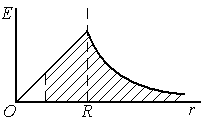 ак
как потенциал равен работе по перемещению
единичного положительного из данной
точки в бесконечность, где потенциал
принят равным нулю.
ак
как потенциал равен работе по перемещению
единичного положительного из данной
точки в бесконечность, где потенциал
принят равным нулю.Учитывая зависимость:

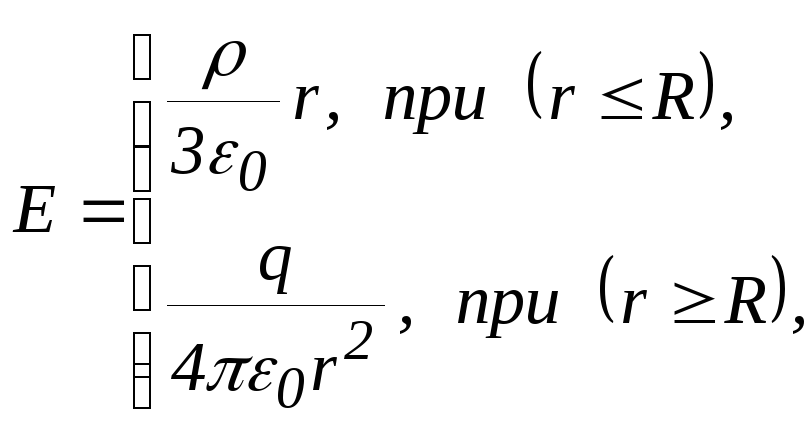
где 
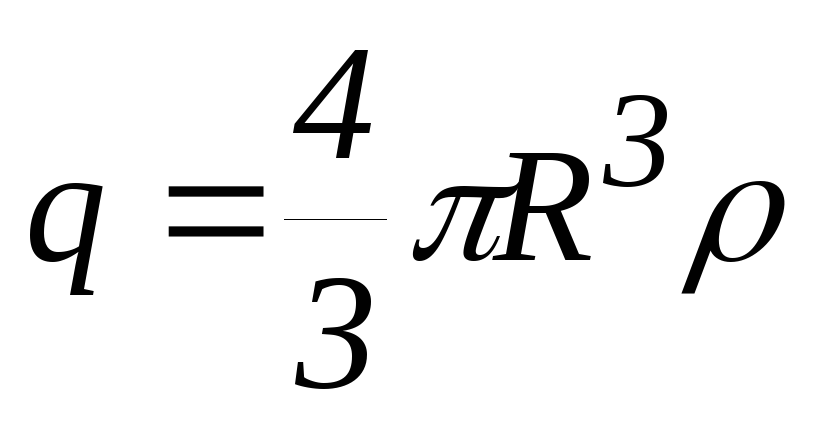 ,
получаем для точек внутри шара:
,
получаем для точек внутри шара:
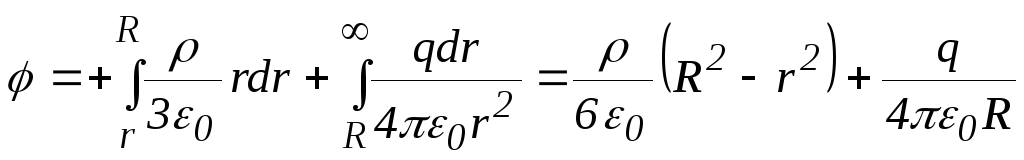
Д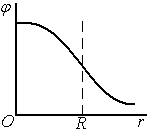 ля
точек вне шара
ля
точек вне шара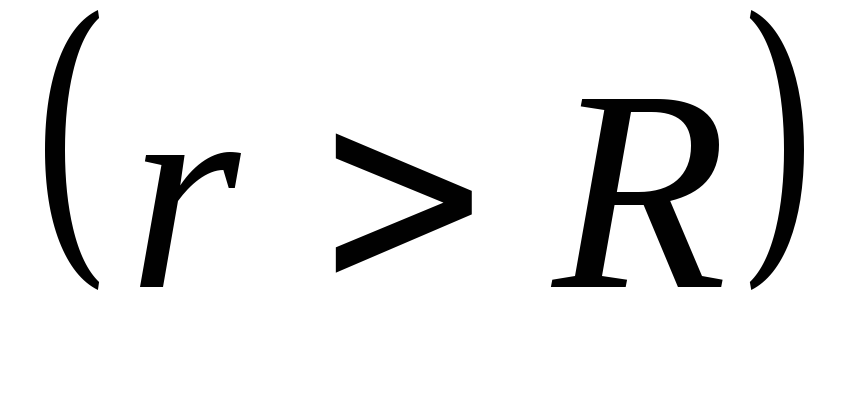 потенциал убывает с расстоянием как
поле точечного заряда:
потенциал убывает с расстоянием как
поле точечного заряда:
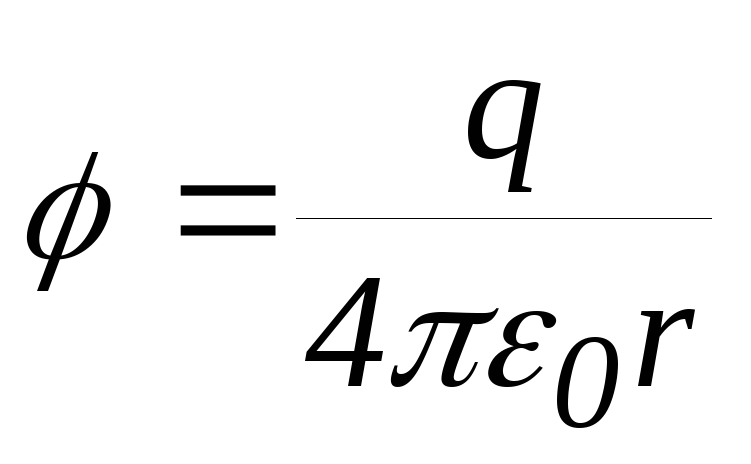 .
.
Зависимость 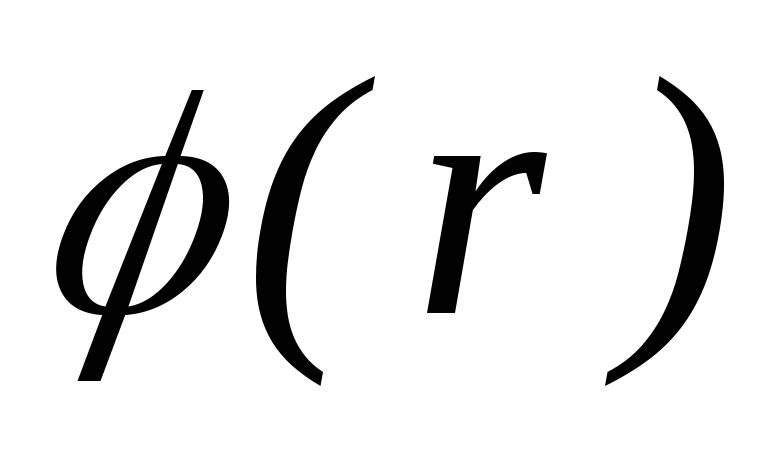 представлена на рисунке, где
представлена на рисунке, где
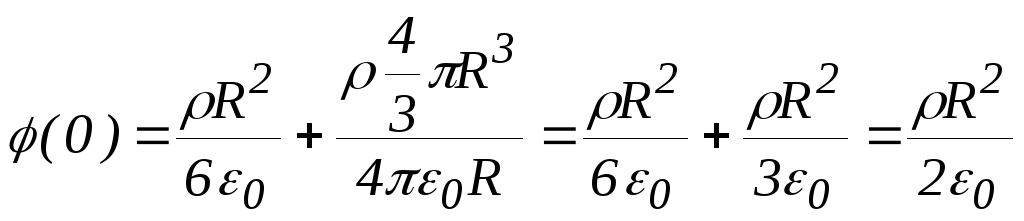 ,
,
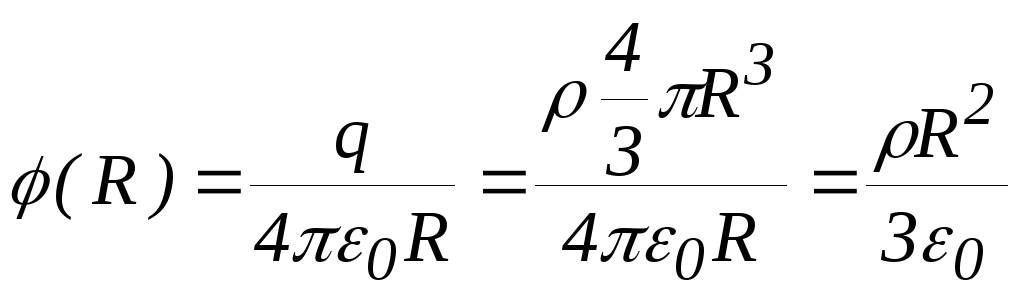 .
.Разность потенциалов двух точек поля заряженной сферы
 .
.
Для точек вне сферы в однородном диэлектрике
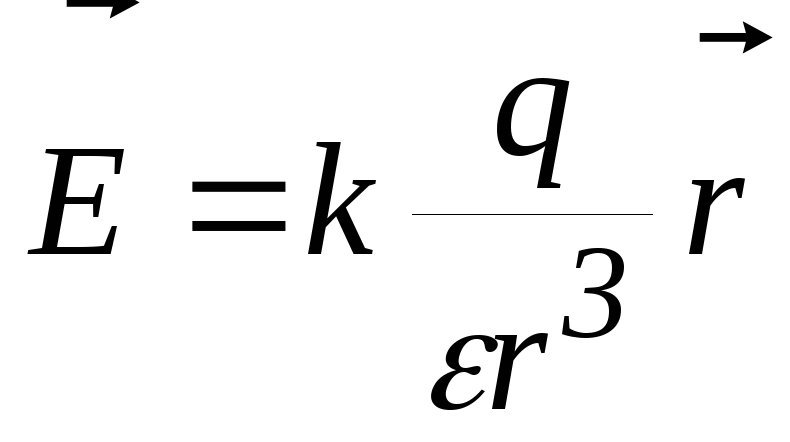
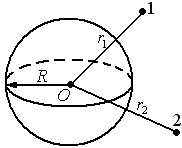 .
.
Найдем разность потенциалов:
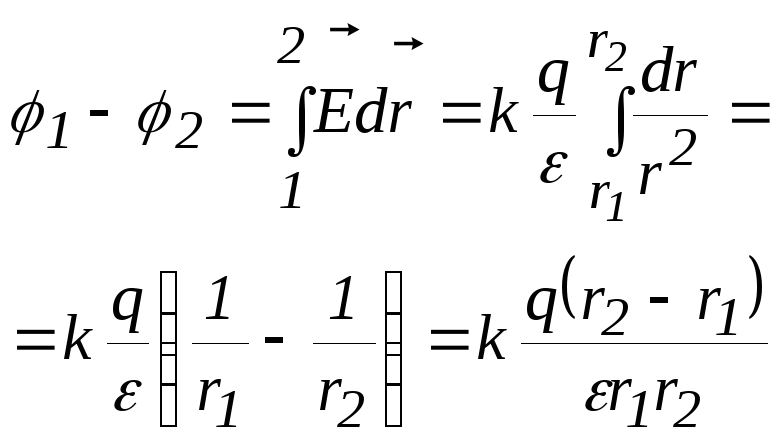
П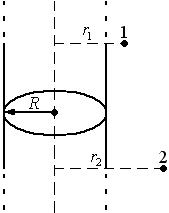 ри
интегрировании учтено, что
ри
интегрировании учтено, что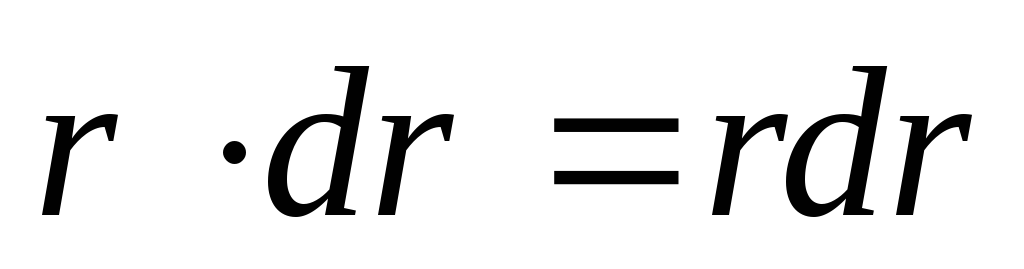 ,
где
,
где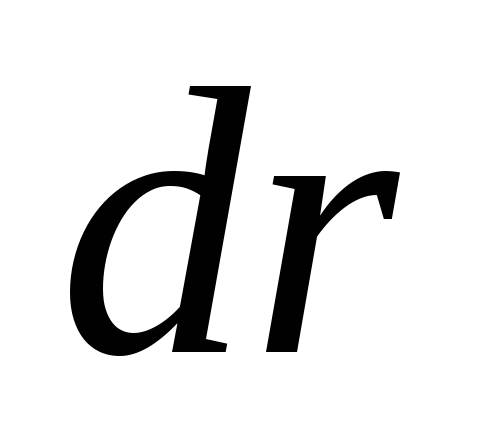 – приращение модуля радиус-вектора
– приращение модуля радиус-вектора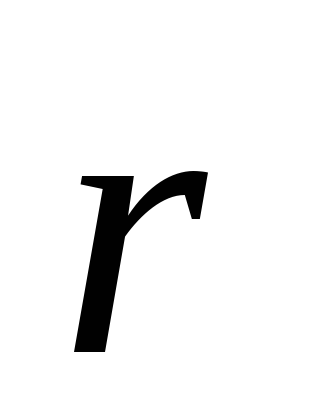 .
.
Разность потенциалов двух точек поля заряженного цилиндра
 .
.
Для точек вне цилиндра 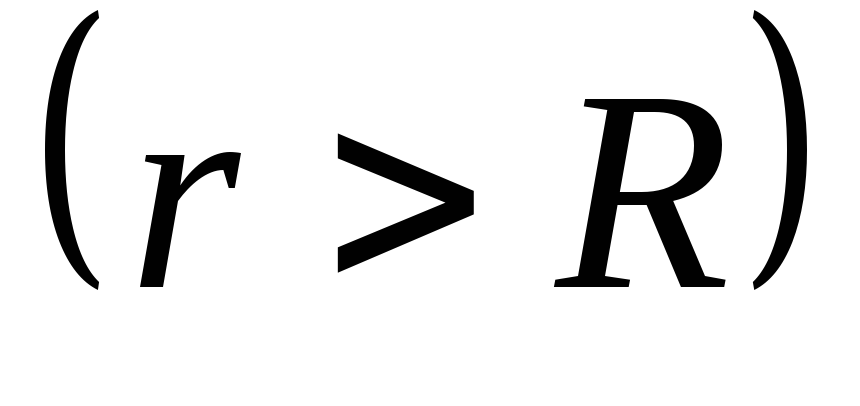 в однородном диэлектрике:
в однородном диэлектрике:
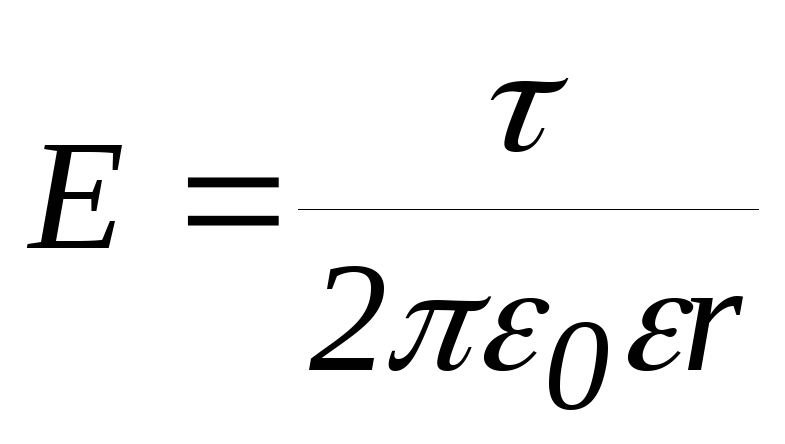 ,
,
где 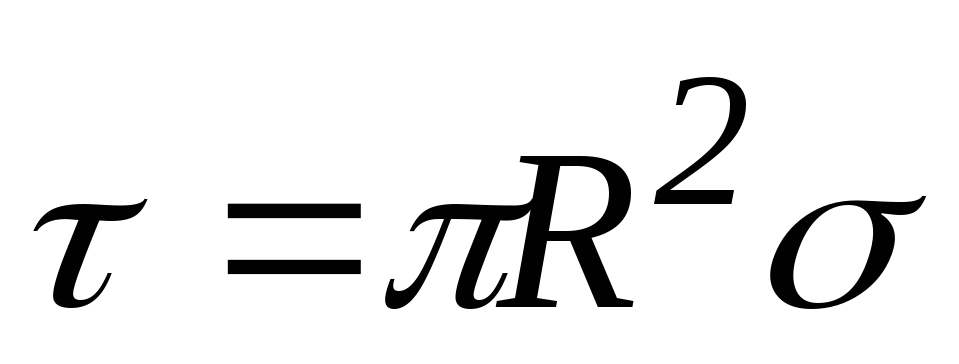 .
.
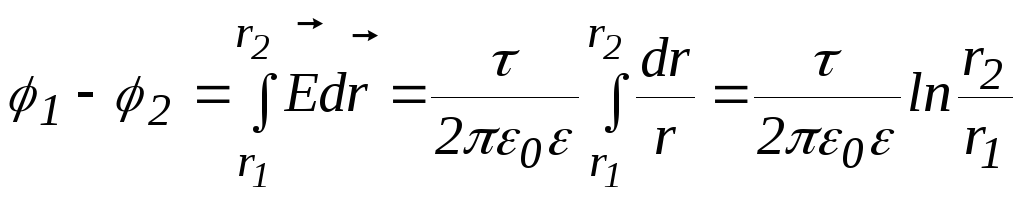 .
.
Лекция 5.
Потенциал поля точечного заряда.
Подставим в соотношение для определения потенциала выражение для напряженности электрического поля точечного заряда:
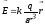 .
.
При интегрировании учтем, что 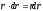 .
.
После интегрирования получаем:
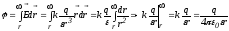 .
.
Потенциал точечного заряда пропорционален величине заряда и убывает обратно пропорционально расстоянию, стремясь на бесконечности к нулю.
Потенциал поля системы зарядов.
Пусть система состоит из 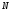 неподвижных точечных зарядов
неподвижных точечных зарядов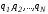 .
Согласно принципу суперпозиции в любой
точке поля напряженность равна
.
Согласно принципу суперпозиции в любой
точке поля напряженность равна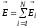 ,
где
,
где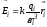 —
напряженность поля
—
напряженность поля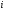 -го
точечного заряда в исследуемой точке,
находящейся на расстоянии
-го
точечного заряда в исследуемой точке,
находящейся на расстоянии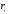 от заряда
от заряда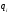 .
.
Подставив в соотношение для определения
потенциала значение 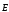 ,
получим:
,
получим:
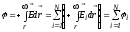 ,
,
где 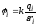 —
потенциал поля
—
потенциал поля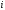 -го
точечного заряда в исследуемой точке.
-го
точечного заряда в исследуемой точке.
Таким образом, потенциал системы точечных зарядов в любой точке пространства равен алгебраической сумме потенциалов, создаваемых всеми точечными зарядами в этой точке.
Если заряды непрерывно распределены по объему, то сумму следует заменить объемным интегралом:
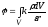 ,
,
где
интегрирование проводится по объему,
где 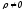 .
.
Аналогичные выражения получаются при поверхностном и линейном распределении зарядов:
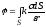 ,
,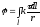 .
.
Таким образом, зная распределение зарядов, в принципе можно найти потенциал и разность потенциалов поля любой системы зарядов.
Рассмотрим ряд примеров расчета потенциала и разности потенциалов, которые понадобятся нам в дальнейшем изложении.
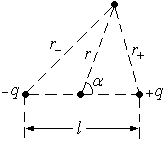
Потенциал поля точечного диполя.
Согласно
принципу суперпозиции, учитывая, что 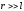 :
:
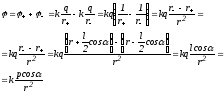 Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда
Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда .
.
Потенциал поля в точках на оси заряженного кольца.
Для
расчета 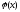 воспользуемся
линейным интегралом:
воспользуемся
линейным интегралом:
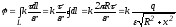 ,
,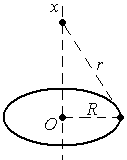
где 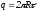 —
заряд кольца. Для всех
—
заряд кольца. Для всех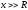
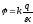
— потенциал кольца убывает как потенциал поля точечного заряда.
В центре кольца (x= 0) потенциал равен:
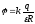 .
.
Потенциал в точках на оси равномерно заряженного круга
 .
.
Для расчёта 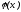 следует
воспользоваться поверхностным интегралом:
следует
воспользоваться поверхностным интегралом: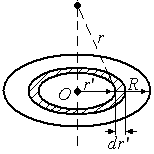
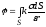 .
.
Представим круг как систему колец с
радиусами 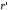 ,
тогда
,
тогда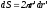 ,
,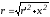 ,
,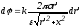 .
.
Для 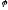 получим:
получим:
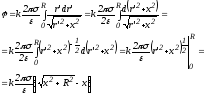 .
.
Для
точек достаточно удаленных от круга 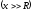 :
:
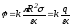 .
.
Получите самостоятельно этот результат.
Потенциал поля объемно заряженного шара
 .
.
Для простоты расчетов примем 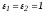 .
.
Зависимость 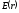 для этого случая представлена на рисунке.
Потенциал точек внутри шара
для этого случая представлена на рисунке.
Потенциал точек внутри шара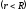 равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
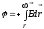 ,
,
так
как потенциал равен работе по перемещению
единичного положительного из данной
точки в бесконечность, где потенциал
принят равным нулю.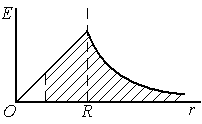
Учитывая зависимость:

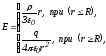
где 
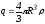 ,
получаем для точек внутри шара:
,
получаем для точек внутри шара:
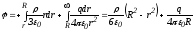 .
.
Для
точек вне шара 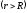 потенциал убывает с расстоянием как
поле точечного заряда:
потенциал убывает с расстоянием как
поле точечного заряда: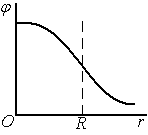
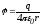 .
.
Зависимость 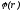 представлена на рисунке, где
представлена на рисунке, где
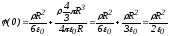 ,
,
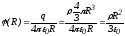 .
.
Разность потенциалов двух точек поля заряженной сферы
 .
.
Для точек вне сферы 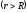 в однородном диэлектрике
в однородном диэлектрике
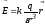 .
.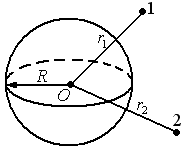
Найдем разность потенциалов:
 .
.
При интегрировании учтено, что 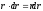 ,
где
,
где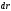 – приращение модуля радиус-вектора
– приращение модуля радиус-вектора .
.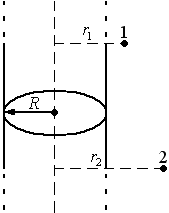
Разность потенциалов двух точек поля заряженного цилиндра
 .
.
Для точек вне цилиндра 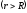 в однородном диэлектрике:
в однородном диэлектрике:
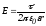 ,
,
где 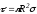 .
.
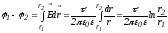 .
.
Лекция 5.
Потенциал поля точечного заряда
Обратимся
теперь к сферическому (точечному) заряду.
Выше показано, что напряжённость
электрического поля, созданного
равномерно распределённым по сфере
зарядом Q,
не зависит от радиуса сферы. Представим,
что на некотором расстоянии r от
центра сферы находится пробный заряд q.
Напряжённость поля в точке, где находится
заряд, 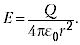
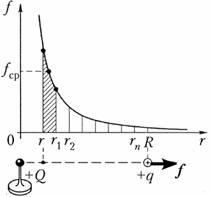
На
рисунке изображён график зависимости
силы электростатического взаимодействия
между точечными зарядами от расстояния
между ними. Чтобы найти работу
электрического поля при перемещении
пробного заряда q с
расстояния r до
расстоянияR,
разобьём этот промежуток
точками r1, r2,…, rп на
равные отрезки. Средняя сила, действующая
на заряд q в
пределах отрезка [rr1],
равна 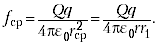
Работа этой силы на этом участке:
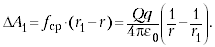
Аналогичные выражения для работы получатся для всех других участков. Поэтому полная работа:
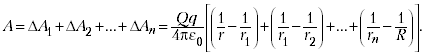
Одинаковые слагаемые с противоположными знаками уничтожаются, и окончательно получаем:
– работа
поля над зарядом 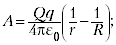
– разность
потенциалов 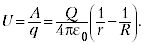
Теперь, чтобы найти потенциал точки поля относительно бесконечности, устремляем R к бесконечности и окончательно получаем:
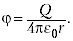 (6.2)
(6.2)
Итак, потенциал поля точечного заряда обратно пропорционален расстоянию до заряда.
24. Потенциальная энергия заряда в поле системы зарядов. Принцип суперпозиции для потенциалов. Принцип суперпозиции для потенциалов
Любое
как угодно сложное электростатическое
поле можно представить в виде суперпозиции
полей точечных зарядов. Каждое такое
поле в выбранной точке имеет определённый
потенциал. Поскольку потенциал является
скалярной величиной, результирующий
потенциал поля всех точечных зарядов
есть алгебраическая сумма
потенциалов 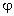 1,
1, 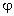 2,
2, 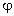 3,
… полей отдельных зарядов:
3,
… полей отдельных зарядов: 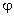 =
= 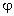 1 +
1 + 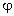 2 +
2 + 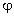 3 +
… Это соотношение является прямым
следствием принципа суперпозиции
электрических полей.
3 +
… Это соотношение является прямым
следствием принципа суперпозиции
электрических полей.
Потенциальная энергия заряда в электрическом поле. Продолжим сравнение гравитационного взаимодействия тел и электростатического взаимодействия зарядов. Тело массой mв поле тяжести Земли обладает потенциальной энергией. Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком:
A = —(Wp2 — Wp1) = mgh.
(Здесь и далее мы будем обозначать энергию буквой W.) Точно так же, как тело массой m в поле силы тяжести обладает потенциальной энергией, пропорциональной массе тела, электрический заряд в электростатическом поле обладает потенциальной энергией Wp, пропорциональной заряду q. Работа сил электростатического поля А равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:
A = —(Wp2 — Wp1) . (40.1)
25. Разность потенциалов. Эквипотенциальные поверхности
Эквипотенциальная поверхность – поверхность, каждая точка которой имеет одинаковый потенциал.
Как следует из связи работы и потенциалов:
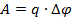
при
переносе заряда вдоль эквипотенциальных
поверхностей электрическое поле работы
не совершает, так как 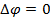 .
.
Работа при ненулевой силе равна нулю только в том случае, если вектор силы перпендикулярен вектору перемещения. Из этого следует, что линии напряженности перпендикулярны эквипотенциальным поверхностям. Примерами эквипотенциальных поверхностей служат сферы для поля точечного заряда и параллельные плоскости для однородных полей (рис. 3).
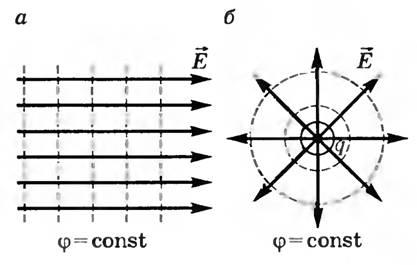
Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к модулю этого заряда: U = φ1 — φ2 = -Δφ = A / q, A = -(Wп2 — Wп1) = -q(φ2 — φ1) = -qΔφ
Разность потенциалов измеряется в вольтах (В = Дж / Кл) Связь между напряжённостью электростатического поля и разностью потенциалов: Ex = Δφ / Δx Напряжённость электростатического поля направлена в сторону убывания потенциала. Измеряется в вольтах, делённых на метры (В / м)
FTF 3 semestr.ISAEV / 4
Потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Работа в электрическом поле.
Так как сила, действующая в электрическом поле на точечный заряд Q Равна
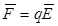 (6.1)
(6.1)
То при
перемещении заряда Q на
расстояние 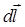 Эта
сила совершает работу:
Эта
сила совершает работу:
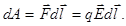 (6.2)
(6.2)
При перемещении заряда из точки 1 в точку 2 по траектории работа равна:
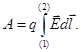 (6.3)
(6.3)
Потенциальность кулоновского поля.
Поле, созданное кулоновскими зарядами, потенциально. Поле сил называется потенциальным, если при перемещении в этом поле работа зависит лишь от начального и конечного положения точек (тела) пути и не зависит от формы пути — траектории. Вторым эквивалентным определением потенциальности поля является условие равенства нулю работы при перемещении в нем по любому замкнутому контуру.
На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Из
сказанного следует, что 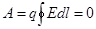 ,
тогда условие потенциальности
электрического поля
,
тогда условие потенциальности
электрического поля
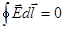 (6.4)
(6.4)
(6.4) – интегральная формулировка потенциальности электрического поля.
Дифференциальная формулировка потенциальности поля.
Если воспользоваться формулой Стокса
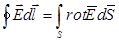 ,
то из (6.4) следует дифференциальная
формулировка потенциальности поля:
,
то из (6.4) следует дифференциальная
формулировка потенциальности поля:
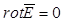 (6.5)
(6.5)
Непосредственной проверкой можно убедиться, что
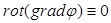 .
(6.6)
.
(6.6)
Тогда сопоставляя (6.6) и (6.5) можно записать:
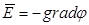 ,
(6.7)
,
(6.7)
где 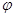 —
некоторая скалярная функция, которая
называется потенциалом. Знак «-» выбран
для того, чтобы вектор напряженности Е был
направлен в сторону убывания
—
некоторая скалярная функция, которая
называется потенциалом. Знак «-» выбран
для того, чтобы вектор напряженности Е был
направлен в сторону убывания 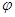 .
Скалярная функция
.
Скалярная функция 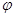 называется
скалярным потенциалом электрического
поля.
называется
скалярным потенциалом электрического
поля.
Если
напряженность поля можно измерить
экспериментально, то потенциал 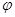 не
имеет определенного числового значения
и бессмысленно говорить об экспериментальном
определении его значения. Потенциал
определен с точностью до некоторого
постоянного значения.
не
имеет определенного числового значения
и бессмысленно говорить об экспериментальном
определении его значения. Потенциал
определен с точностью до некоторого
постоянного значения.
Для того, чтобы не было неоднозначности, используют процедуру нормировки потенциала. При решении пространственных задач за ноль принимают потенциал бесконечно удаленной точки. А при решении задач, связанных с изучением электрических полей вблизи поверхности Земли, за ноль принимают потенциал Земли.
Выражение работы через потенциал.
Если заряд перемещается между точками (1) и (2), то
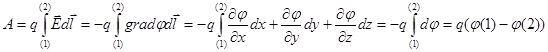 (6.8)
(6.8)
Если
сопоставить (6.8) и (6.3), то 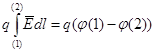 ,
откуда следует
,
откуда следует
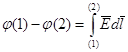 (6.9)
(6.9)
Таким образом, с помощью (6.9) можно вычислить разность потенциалов между двумя точками поля.
Потенциал поля точечного заряда.
Будем
нормировать потенциал на нуль в
бесконечности. Считая, что в формуле
(6.9) точка (2) находится в бесконечности,
полагаем 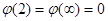 и
получаем выражение для потенциала в
точке (1):
и
получаем выражение для потенциала в
точке (1):
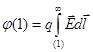 .
(6.10)
.
(6.10)
Воспользовавшись выражением для напряженности поля точечного заряда получим:
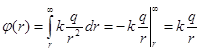 .
(6.11)
.
(6.11)
Соотношение (6.11) определяет потенциал поля, создаваемого точечным зарядом.
Потенциал поля системы точечных зарядов.
Если имеется система из точечных зарядов, то потенциал поля в некоторой точке А равен
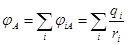 .
(6.12)
.
(6.12)
В случае,
когда заряд распределен непрерывно с
объемной плотностью 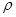 =
=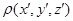 ,
потенциал в некоторой точке (x, y, z) поля:
,
потенциал в некоторой точке (x, y, z) поля:
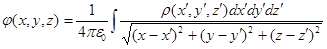 (6.13)
(6.13) 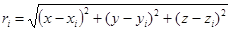 —
расстояние от точечного заряда
—
расстояние от точечного заряда 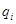 находящегося
в точке
находящегося
в точке 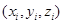 до
точки
до
точки 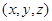 где
вычисляется потенциал.
где
вычисляется потенциал.
Если
заряд распределен по поверхности, то
потенциал определяется формулой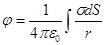 ,
(6.14)
,
(6.14)
где R –расстояние между элементом площадки DS и точкой, где
Вычисляется потенциал.
Бесконечность потенциала поля точечного заряда.
Из (6.14)
следует, что при 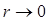 потенциал
потенциал 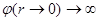 .
Это связано с тем, что точечный заряд
формально имеет бесконечную объемную
плотность, поскольку его объем равен
нулю. Именно бесконечная
объемная плотность заряда и обуславливает
обращение в бесконечность потенциала.
.
Это связано с тем, что точечный заряд
формально имеет бесконечную объемную
плотность, поскольку его объем равен
нулю. Именно бесконечная
объемная плотность заряда и обуславливает
обращение в бесконечность потенциала.
При непрерывном распределении заряда с конечной плотностью потенциал нигде не обращается в бесконечность, т. е. потенциал функция конечная.
Конечность потенциала при непрерывном распределении заряда с конечной плотностью.
При
непрерывном распределении заряда с
конечной плотностью потенциал нигде
не обращается в бесконечность. В этом
можно убедиться при вычислении потенциала
по формуле (6.13). Причем точку (X,Y,Z) за
начало координат(X=Y=Z=0) и
будем вести расчет в сферической системе
координат. Элемент объема в ней выражается
формулой 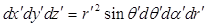 ,
где
,
где 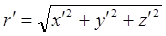 .
Тогда [см. (6.13)]
.
Тогда [см. (6.13)]
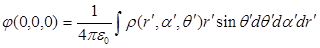 .
.
Следовательно, Если 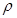 Конечно,
то и потенциал
Конечно,
то и потенциал 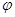 конечен, Что
и требовалось доказать.
конечен, Что
и требовалось доказать.
Непрерывность потенциала.
Производная
от потенциала по декартовой координате
дает соответствующую компоненту
напряженности электрического поля.
Ясно, что напряженность не может быть
бесконечной, значит, производные по
координатам от потенциала должны быть
конечными. А это означает, что потенциал
является непрерывной функцией. Таким
образом, потенциал 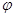 является
непрерывной и конечной функцией с
конечными производными по координатам.
Эти условия важны при решении
дифференциальных уравнений для
является
непрерывной и конечной функцией с
конечными производными по координатам.
Эти условия важны при решении
дифференциальных уравнений для 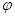 .
.
Обязательные вопросы по физике
1. Напряженность электростатического поля
Силовой характеристикой поля, создаваемого зарядом q, является отношение силы, действующей на заряд, к величине этого заряда называемое напряженностью электростатического поля.
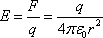
2. Напряженность поля точечного заряда
Обозначим: q — заряд, создающий поле,
q0 — заряд, помещенный в поле (внешний заряд).
Закон
Кулона: 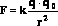 .
Напряженность поля:
.
Напряженность поля: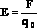 .
.
Тогда
напряженность поля точечного заряда: 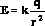
3. Линейная, поверхностная, объемная плотность заряда

4. Дипольный момент
Электрический дипольный момент — векторная физическая величина, характеризующая, наряду с суммарным зарядом, электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
Дипольный момент, электрический, величина, характеризующая электрические свойства системы заряженных частиц. Дипольный момент р электро-нейтральной системы, состоящей из n заряженных частиц, равен:
p = Σni=1eivi, где ei—заряд i-той частицы, vi; — её радиус-вектор
5. Теорема Гаусса для электростатического поля в вакууме
Теорема: Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.
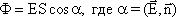
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
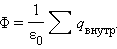
6. Циркуляция вектора напряженности электростатического поля
Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L.
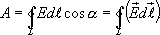
Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.
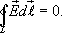
7. Потенциал электростатического поля
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду:
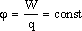
— энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.
В СИ потенциал измеряется в вольтах.
8. Потенциал поля точечного заряда
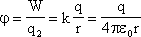
9. Разность потенциалов
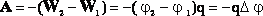
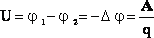
Напряжение — разность значений потенциала в начальной и конечной точках траектории.
Напряжение численнао равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля.
Разность потенциалов (напряжение) не зависит от выбора системы координат. Измеряется в вольтах.
10. Связь напряженности и потенциала
Напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d)
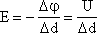
А) Вектор напряженности направлен в сторону уменьшения потенциала.
Б) Электрическое поле существует, если существует разность потенциалов.
В)
Единица напряженности: 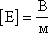
11. Поле равномерно заряженной плоскости
Если заряд распределён по поверхности, удобно пользоваться понятием поверхностной плотности заряда. Выделим на плоской поверхности малый участок площадью ΔS; пусть его заряд Δq. Тогда поверхностная плотность заряда равна σ =Δq/ΔS. Если заряд распределён равномерно, то σ =q/S.
12. Поле двух параллельных равномерно заряженных плоскостей
Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и −σ. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности.
На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E = 0
В
области между плоскостями E+ + E— (E+ и E— определяются по формуле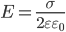 ),
поэтому результирующая напряженность:
),
поэтому результирующая напряженность: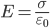 .
.
Таким образом, результирующая напряженность поля в области между плоскостями описывается этой формулой, а вне объема, ограниченного плоскостями, равна нулю.
1.4.Потенциал. Потенциальная энергия заряда в электростатическом поле
Работа
сил электрического поля, созданного
зарядом  ,
по перемещению заряда
,
по перемещению заряда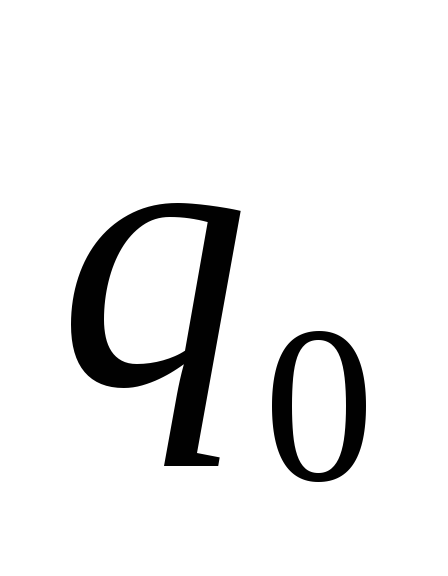 из точки 1 в точку 2 равна:
из точки 1 в точку 2 равна:
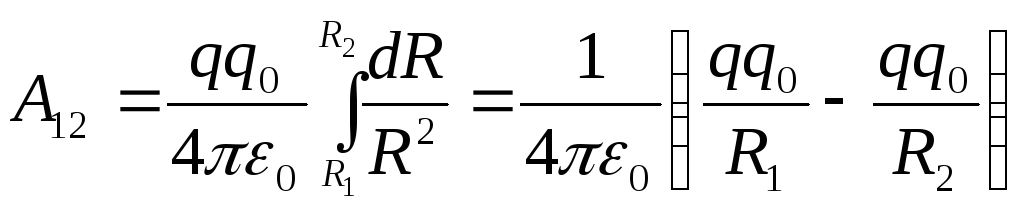 .
.
Работа сил консервативного поля равна убыли потенциальной энергии:
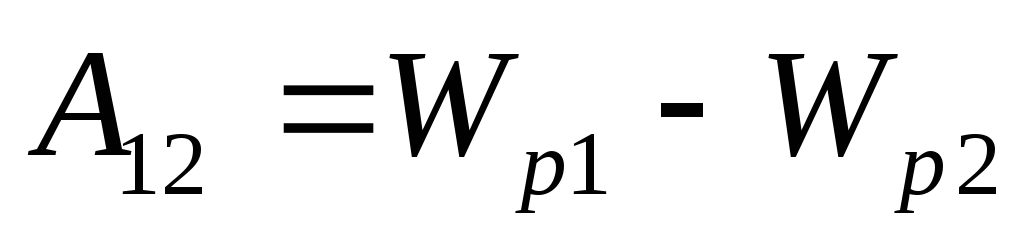 ,
,
тогда
потенциальная энергия заряда 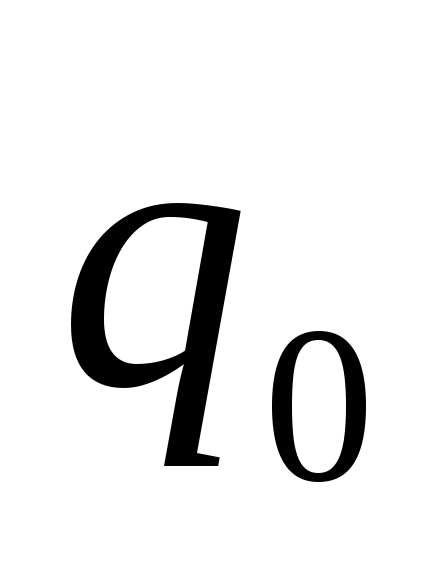 в поле заряда
в поле заряда равна:
равна:
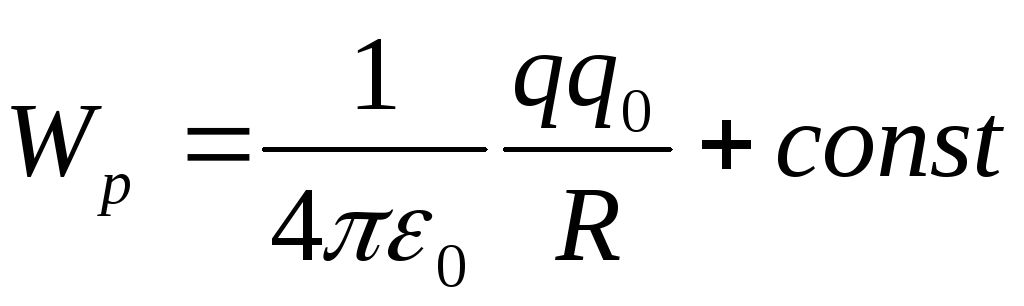 .
.
Значение
константы выбирается таким, чтобы при
удалении заряда на бесконечность (то
есть при 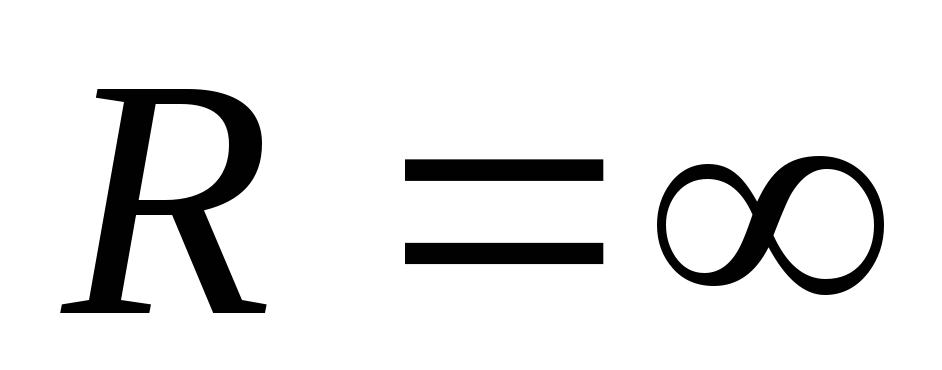 )
потенциальная энергия обратилась бы в
ноль, поэтому
)
потенциальная энергия обратилась бы в
ноль, поэтому
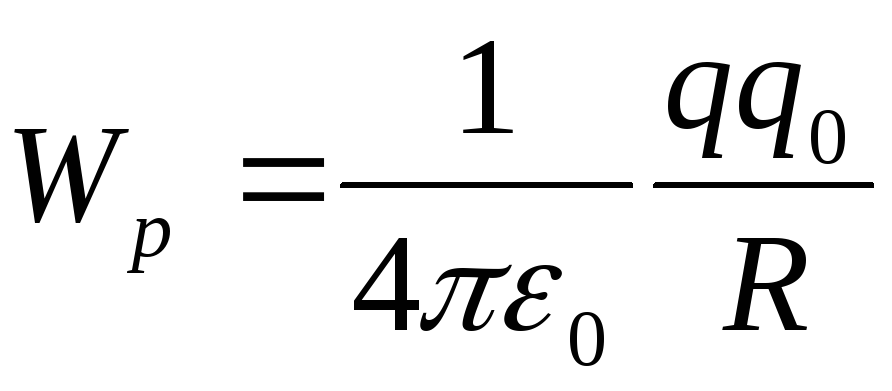 .
.
Ясно,
что разные пробные заряды 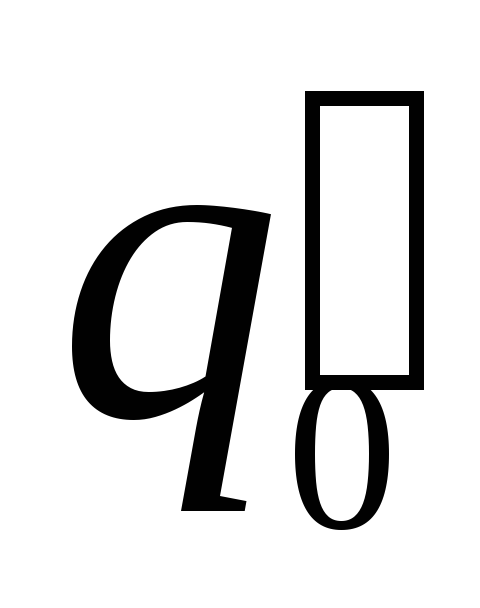 и
и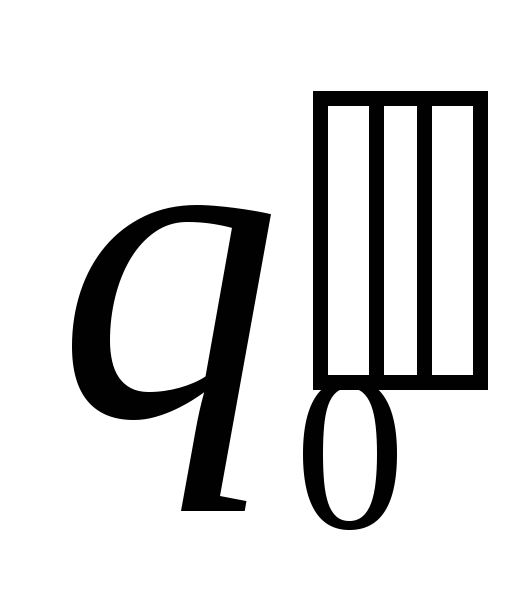 в одной и той же точке поля будут обладать
разной потенциальной энергией
в одной и той же точке поля будут обладать
разной потенциальной энергией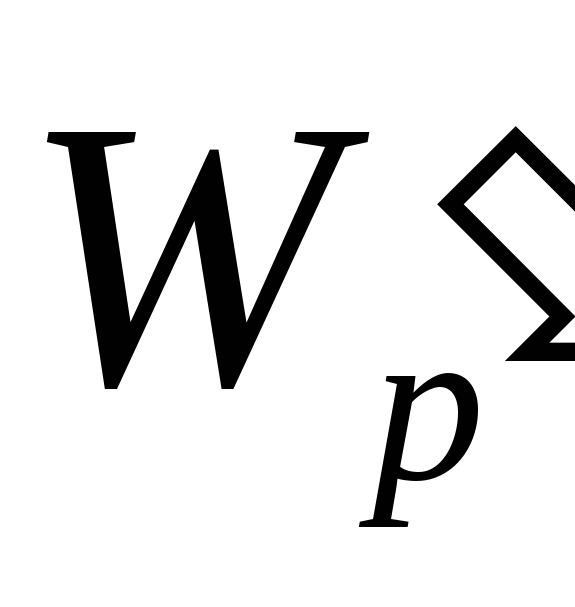 и
и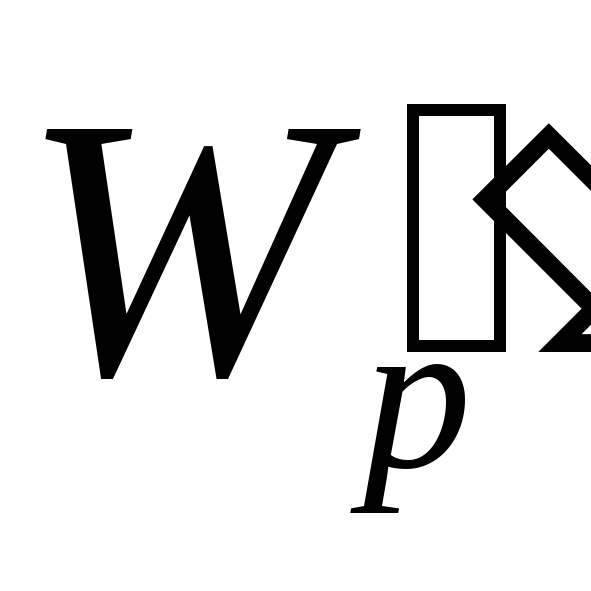 .
Однако отношение
.
Однако отношение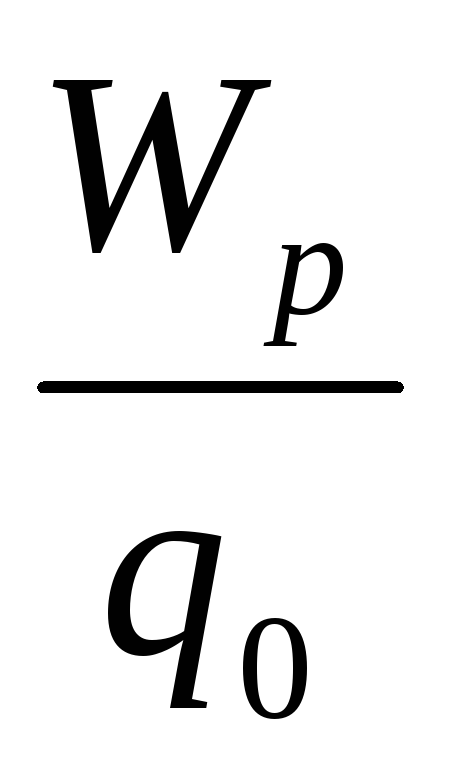 для всех пробных зарядов будет одинаково.
Величина
для всех пробных зарядов будет одинаково.
Величина
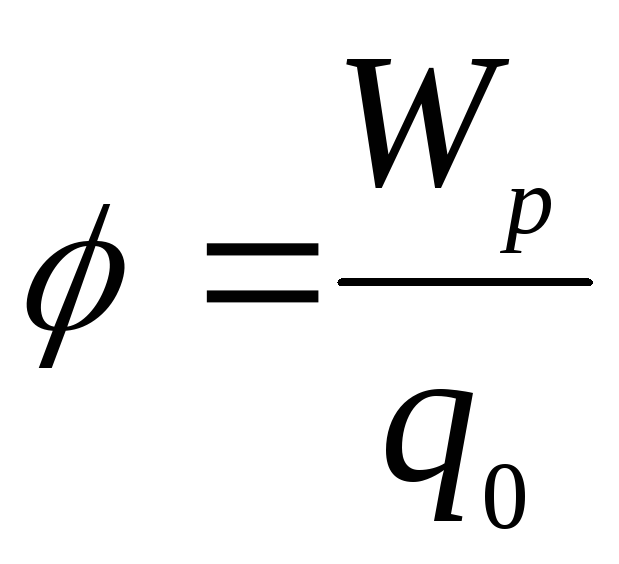
называется потенциалом электрического поля и является его энергетической характеристикой. Потенциал поля точечного заряда равен
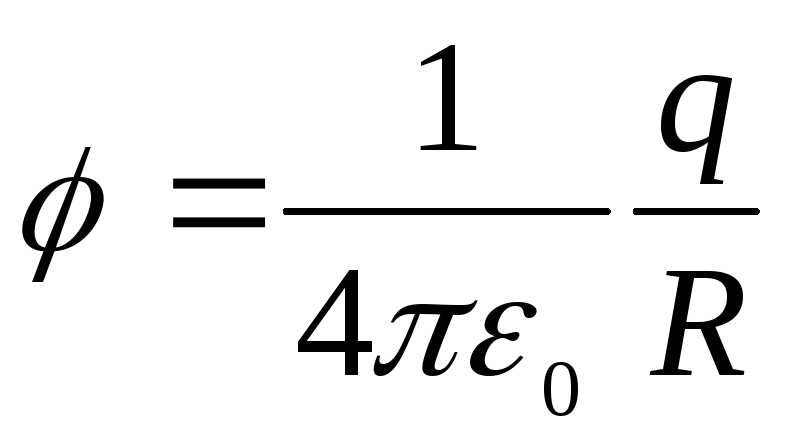 .
.
Если
поле создается системой 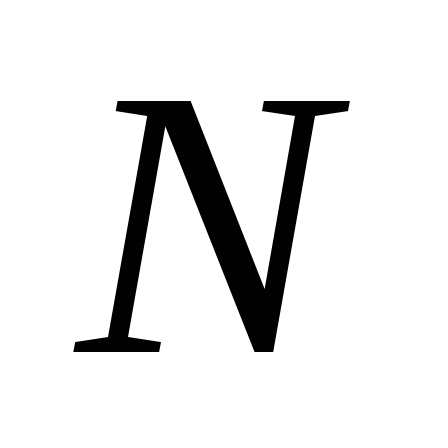 точечных зарядов, то
точечных зарядов, то
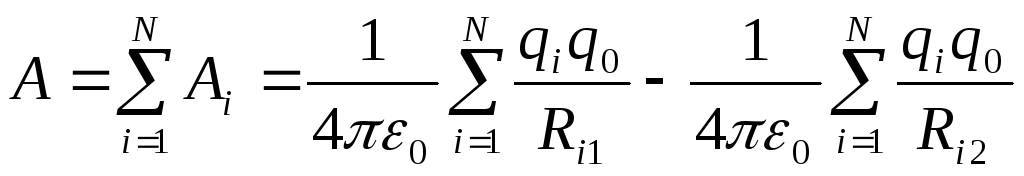 ,
,
где 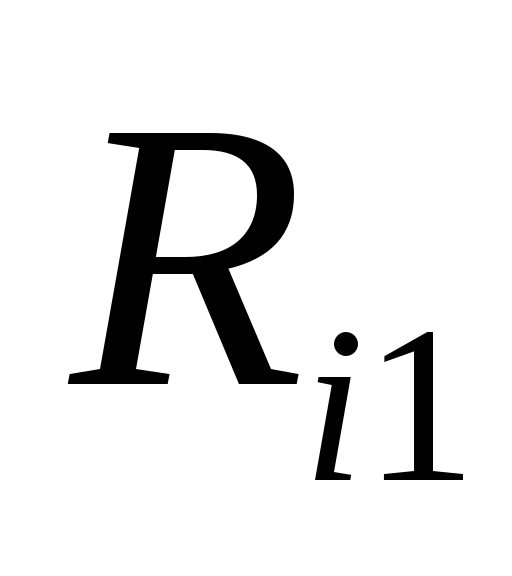 — расстояние от заряда
— расстояние от заряда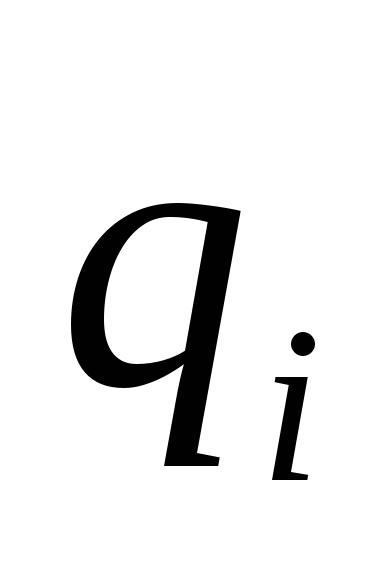 до начального положения заряда
до начального положения заряда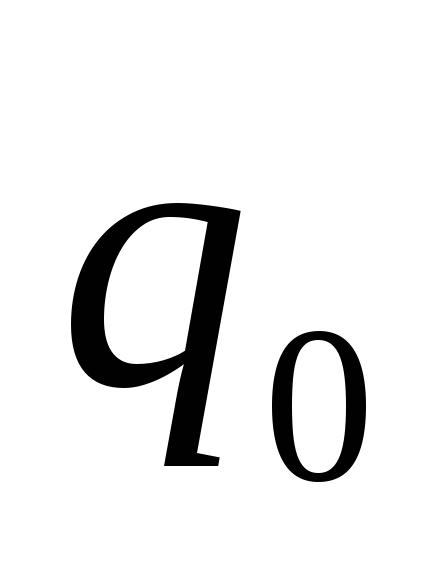 ,
,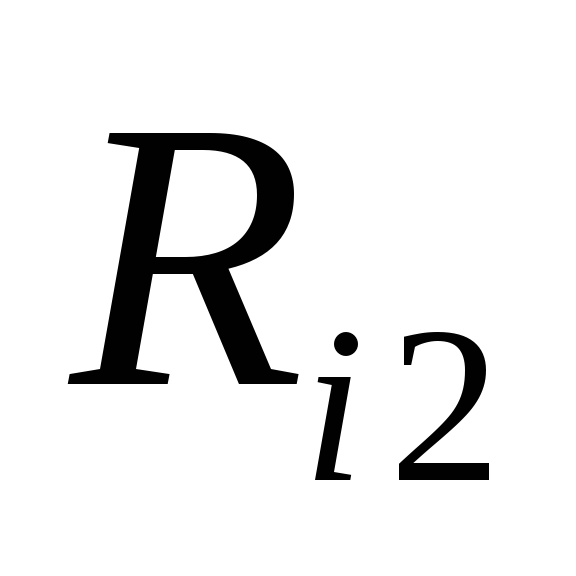 — расстояние от заряда
— расстояние от заряда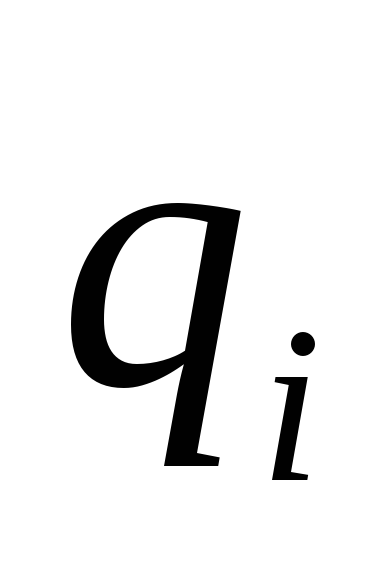 до конечного положения заряда
до конечного положения заряда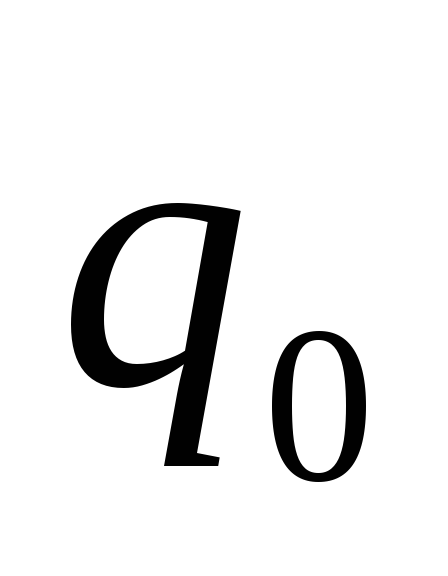 (заряд
(заряд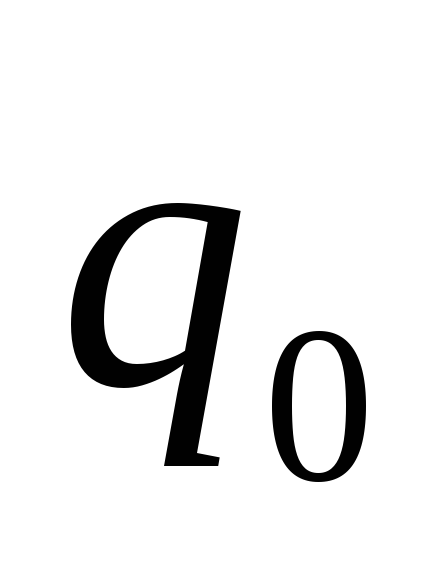 перемещается силами поля).
перемещается силами поля).
Тогда
потенциальная энергия заряда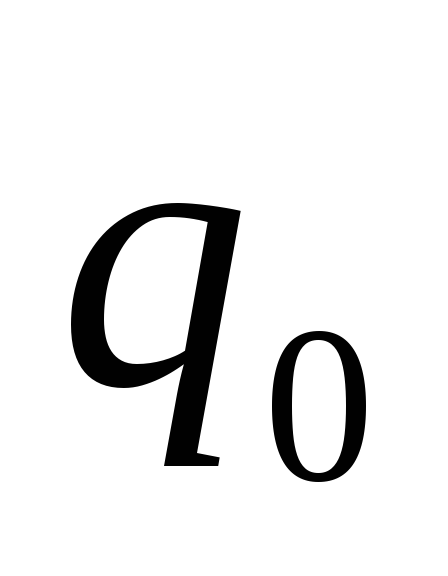 в поле системы зарядов:
в поле системы зарядов:
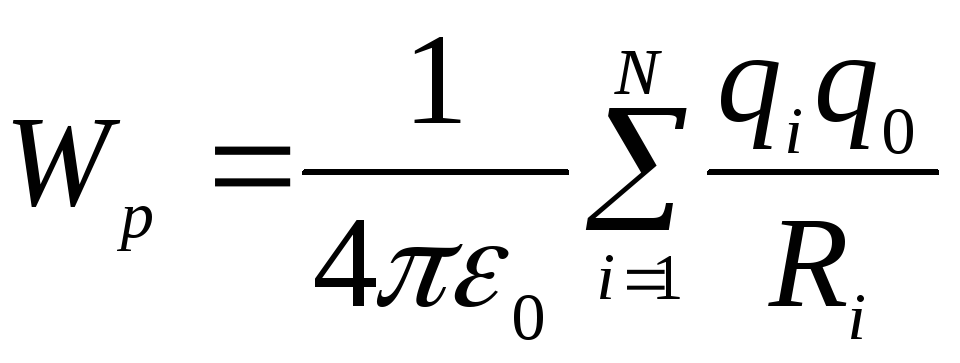 ,
,
а потенциал
потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Зная
потенциал, можно найти потенциальную
энергию заряда 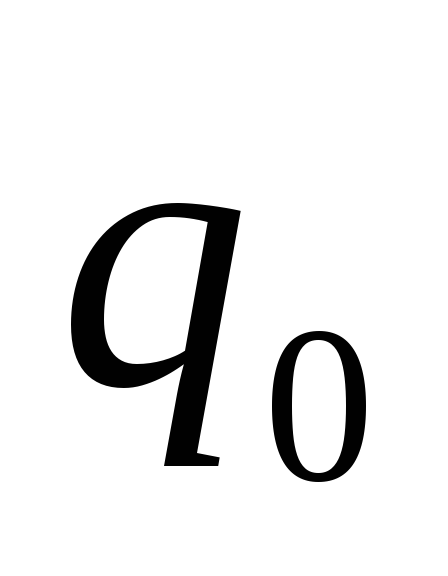 в электрическом поле:
в электрическом поле:
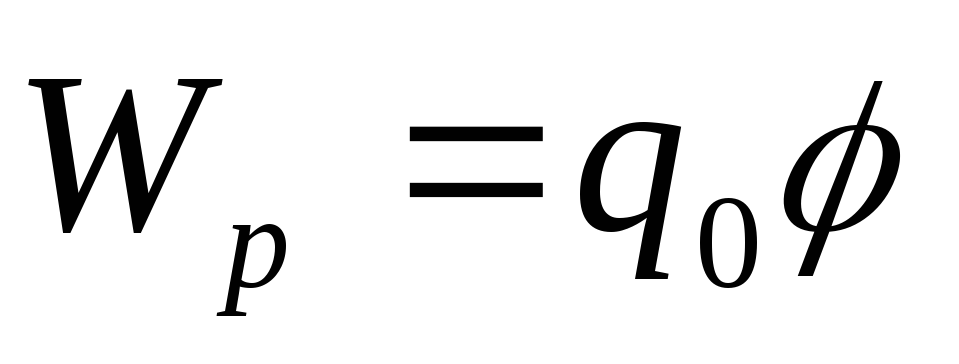 .
.
Работа поля над зарядом:
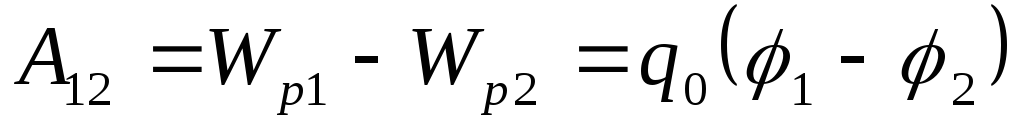
— работа равна убыли потенциала, умноженной на заряд.
Если заряд удаляется из точки на бесконечность, то работа сил поля равна
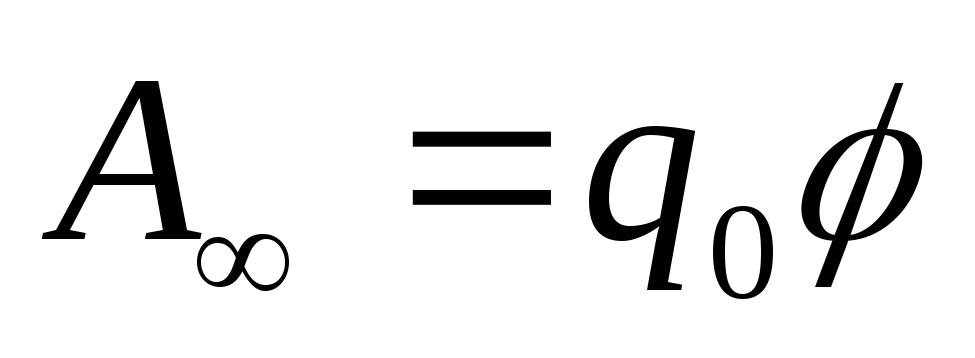
следовательно,
потенциал численно равен отношению
работы, которую совершают силы поля над
положительным зарядом при удалении его
из данной точки на бесконечность, к
величине этого заряда. Потенциал
измеряется в вольтах: 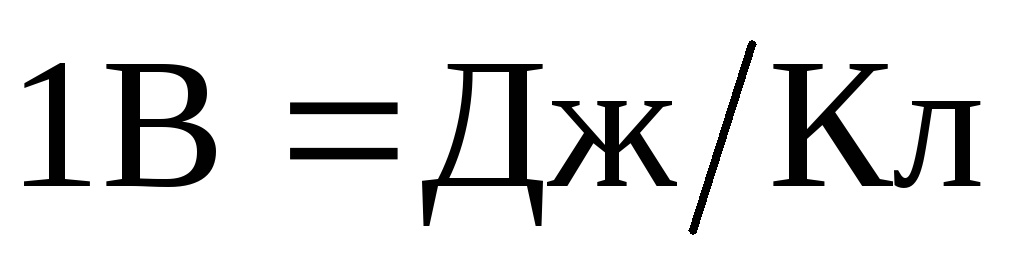 .
.
1.5.Связь между напряженностью и потенциалом
Электрическое
поле можно описывать либо с помощью
векторной величины  (силовая характеристика), либо с помощью
скаляра
(силовая характеристика), либо с помощью
скаляра (энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
(энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
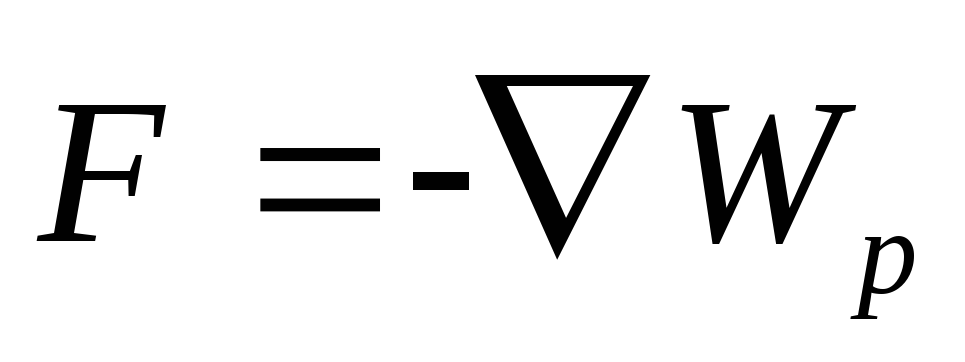 ,
,
где  — оператор Набла,
— оператор Набла,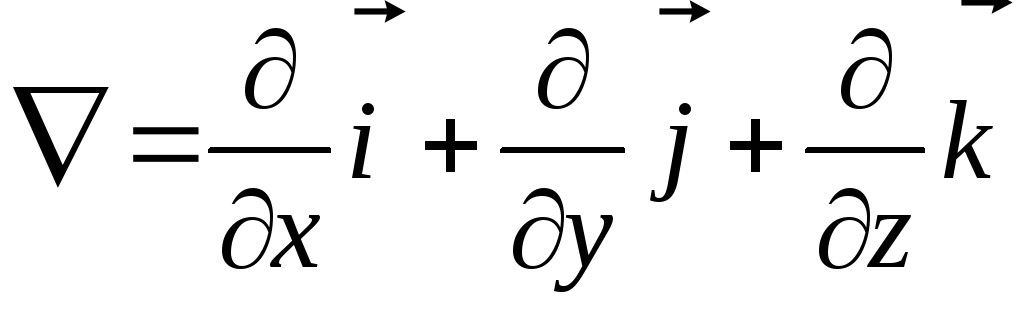 .
.
Для
заряженной частицы в электрическом
поле: 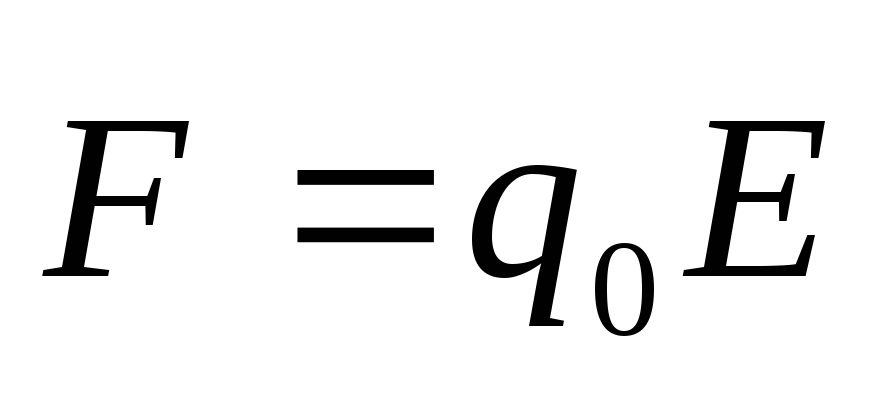 ,
,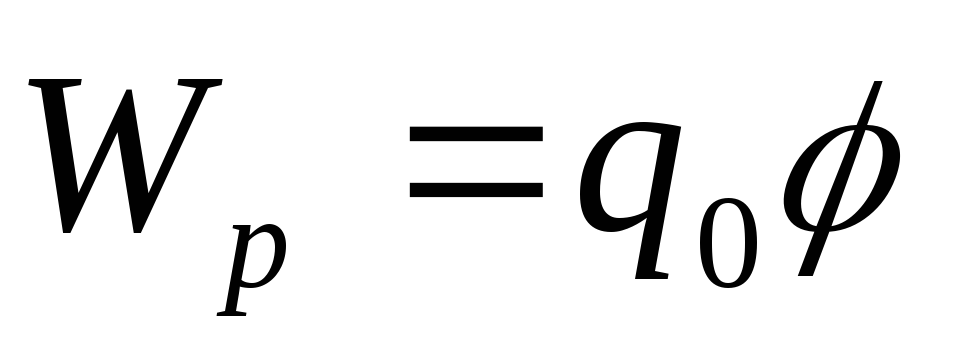 ,
тогда
,
тогда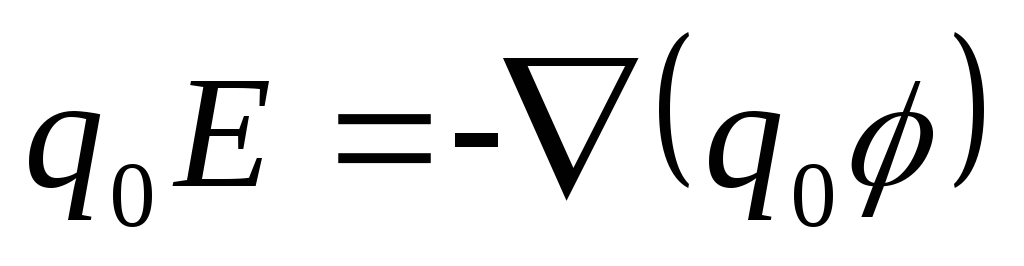 ,
,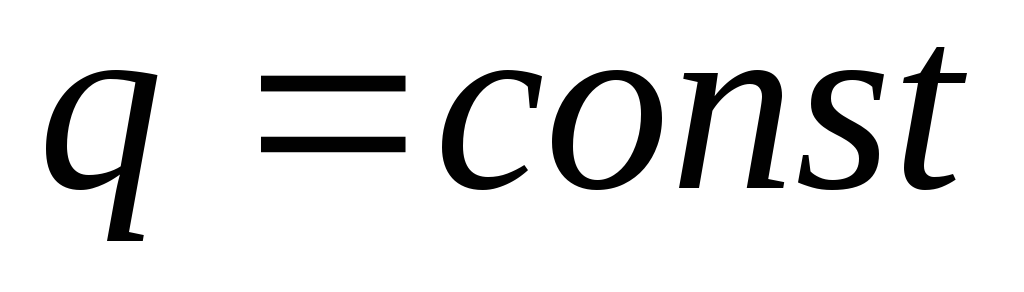 ,
тогда
,
тогда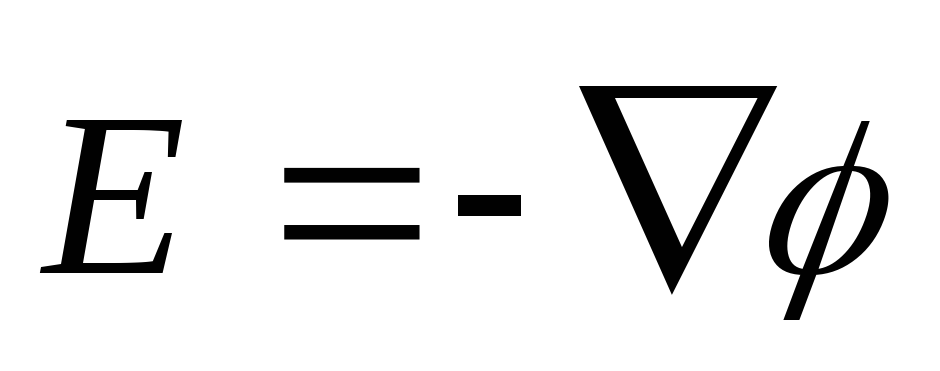 — связь напряженности и потенциала, или
— связь напряженности и потенциала, или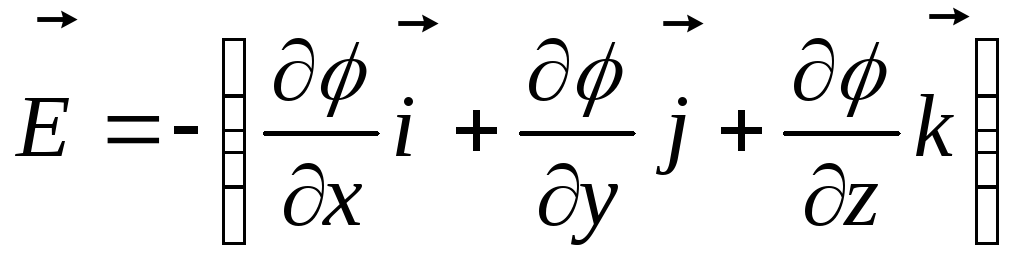 ,
или
,
или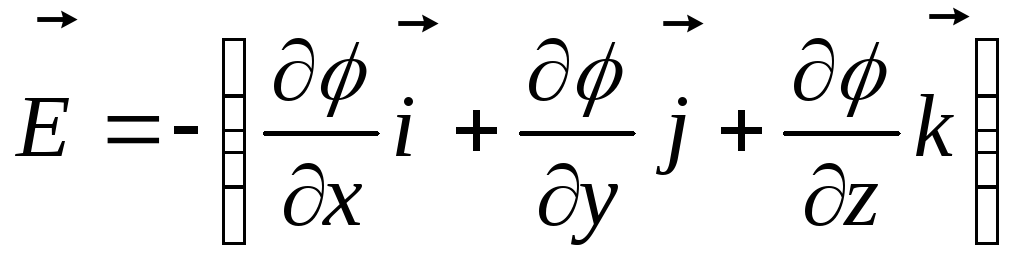 ,
или
,
или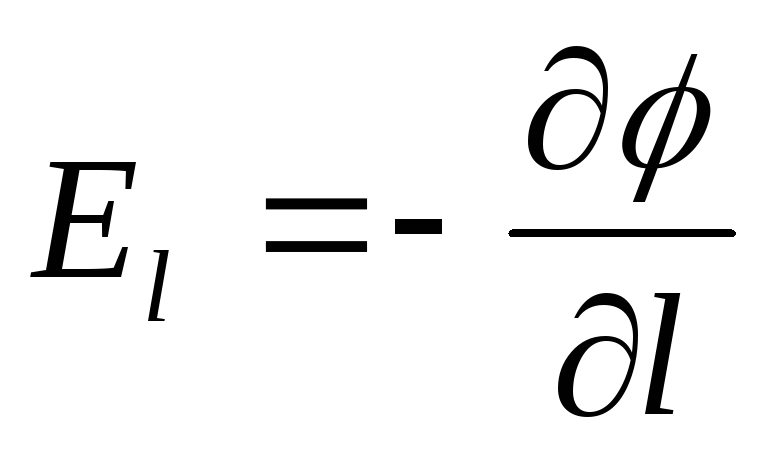 — проекция
вектора
— проекция
вектора  на произвольное направление
на произвольное направление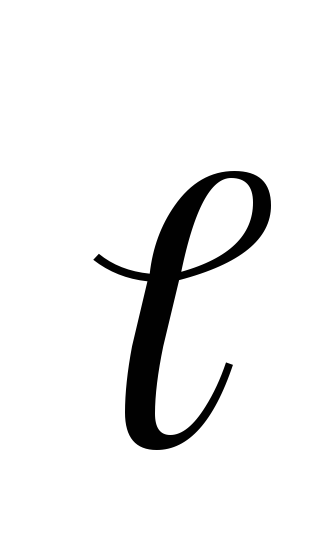 равна скорости убывания потенциала
равна скорости убывания потенциала вдоль направления
вдоль направления 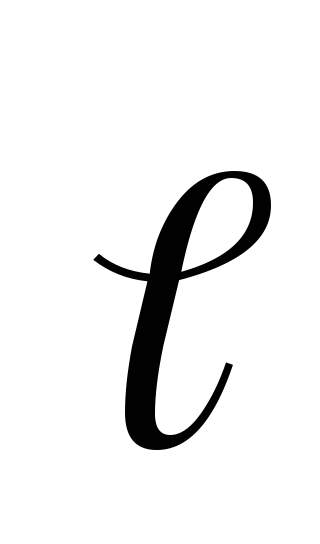 ,или
,или 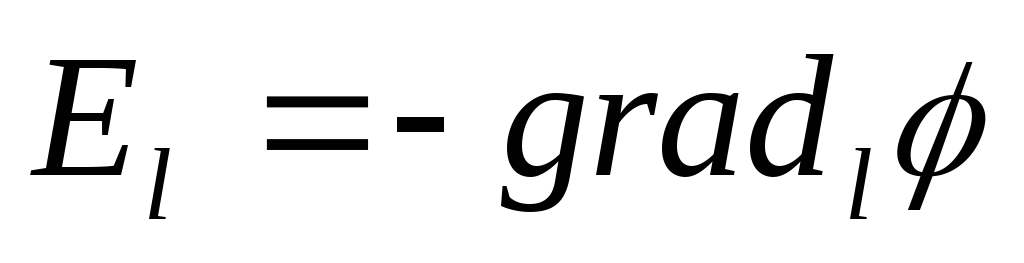 .
.
Так как градиент потенциала направлен в сторону его возрастания, а численная величина градиента является мерой быстроты этого возрастания, то можно сказать, что напряженность электрического поля есть мера быстроты спадания потенциала, или, просто, что она равна спаду потенциала.
Вернемся к
определению работы поля: 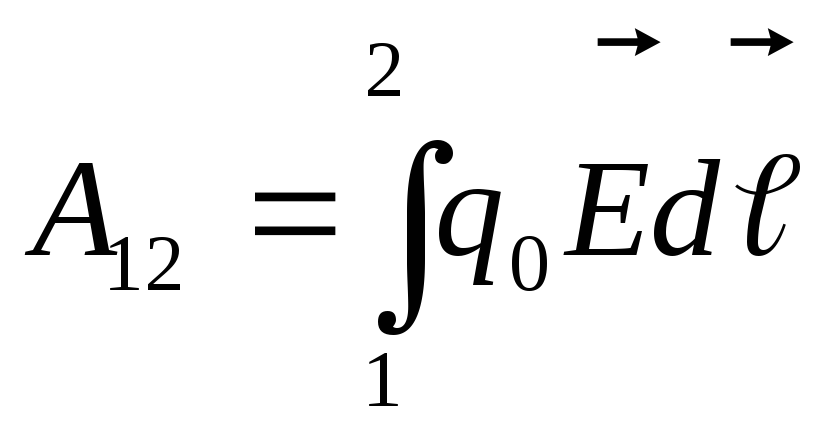 ,
,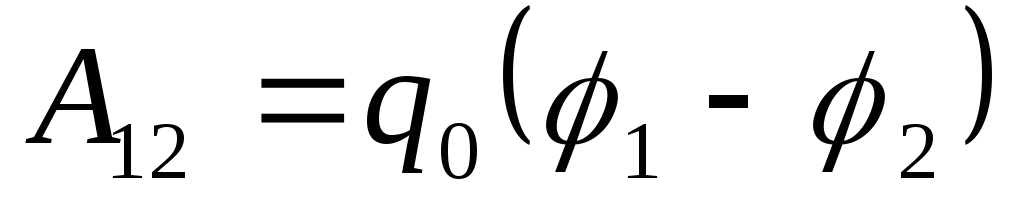 ,
отсюда циркуляция вектора
,
отсюда циркуляция вектора  на
участке 1=2
равна
на
участке 1=2
равна 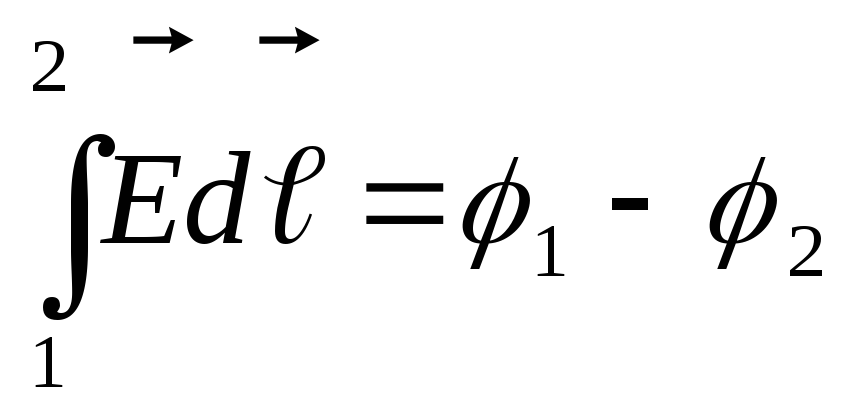 .
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
.
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
Для
обхода по замкнутому контуру: 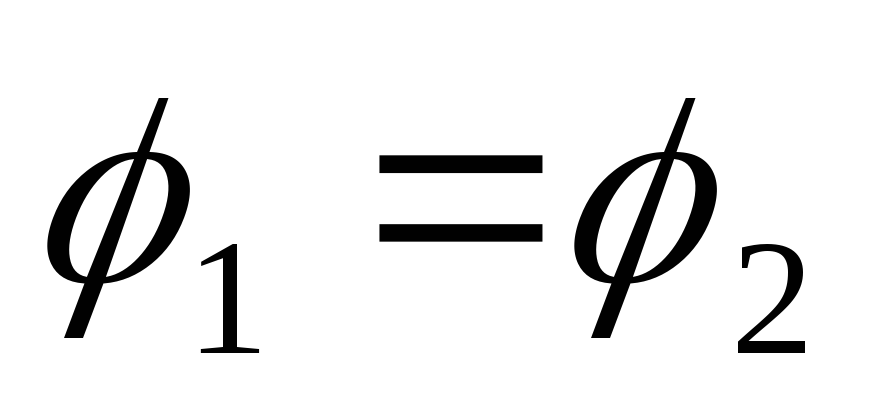 и
и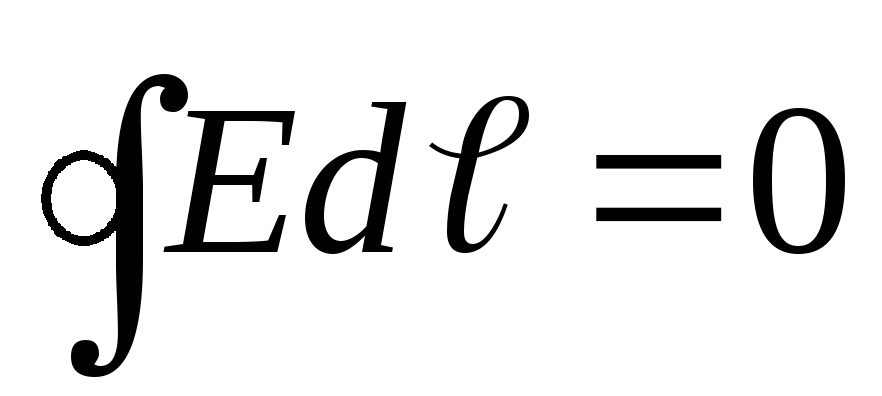 — пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
— пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
1.6. Эквипотенциальные поверхности
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью:
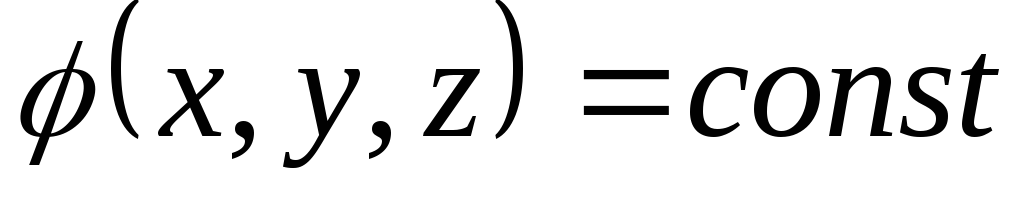
— уравнение эквипотенциальной поверхности.
При
перемещении по эквипотенциальной
поверхности на отрезок 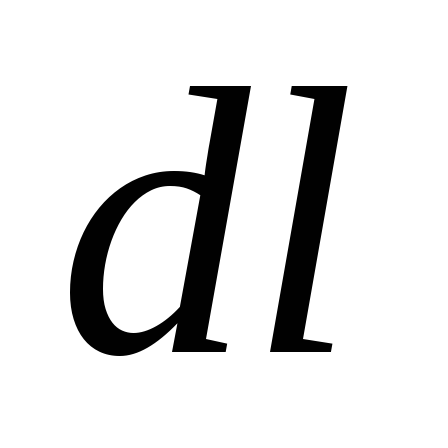 потенциал не изменяется
потенциал не изменяется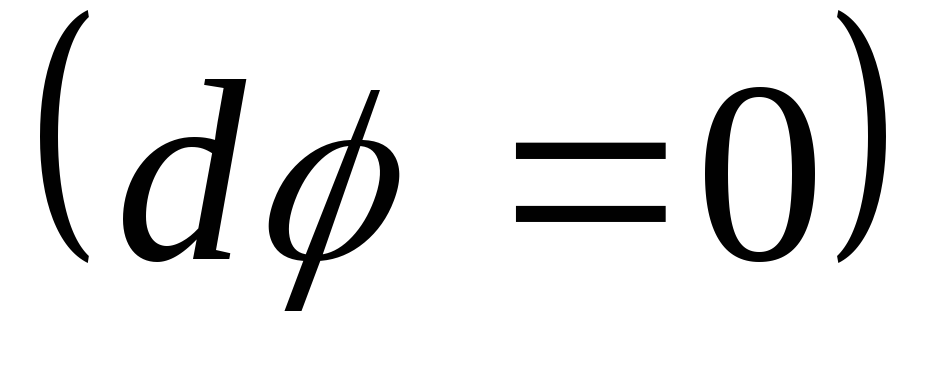 .
Таким образом, касательная к поверхности
составляющая вектора
.
Таким образом, касательная к поверхности
составляющая вектора равна нулю. Тогда вектор
равна нулю. Тогда вектор направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
 Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше
Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше ,
тем больше
,
тем больше .
.
Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.
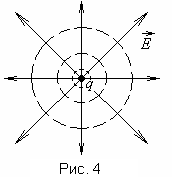
Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.4)
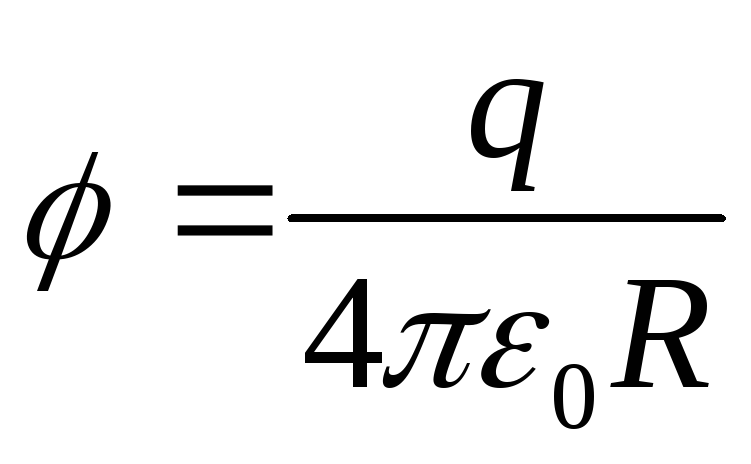 .
.
Таким
образом, эквипотенциальная поверхность
этого заряда будет сферой радиуса 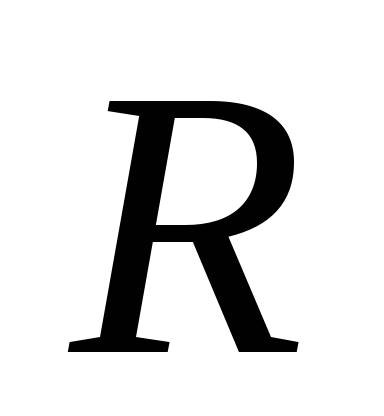 с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он 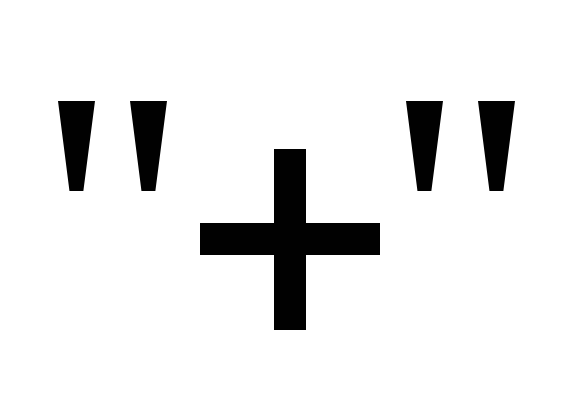 ,
или сходятся к заряду, если он “-”. То
есть вектор
,
или сходятся к заряду, если он “-”. То
есть вектор перпендикулярен эквипотенциальным
поверхностям.
перпендикулярен эквипотенциальным
поверхностям.
6. Работа сил электростатического поля в случае двух точечных зарядов. Потенциал. Потенциал поля, создаваемого системой точечных зарядов.
Работа
сил электростатического поля. Для точечных зарядов сила, действующая
на заряд 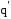 ,
направлена вдоль линии, соединяющей
зарядыq
и
,
направлена вдоль линии, соединяющей
зарядыq
и 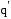 ,
т.е. по радиус-вектору
,
т.е. по радиус-вектору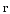 (зарядq
находится в начале координат) (см. рис.
3.1).
(зарядq
находится в начале координат) (см. рис.
3.1).
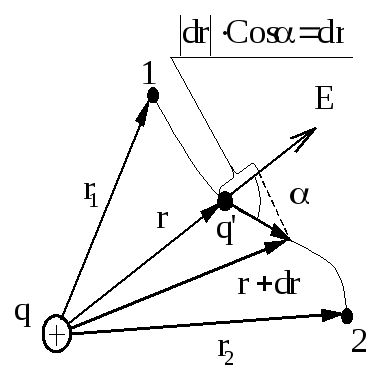
Рис. 3.1
Вектор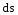 бесконечно малого перемещения заряда
бесконечно малого перемещения заряда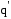 совпадает,
при таком выборе системы координат, с
вектором
совпадает,
при таком выборе системы координат, с
вектором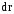 – бесконечно
малым приращением радиус-вектора
– бесконечно
малым приращением радиус-вектора 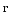 заряда
заряда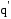 .
Значитds
– модуль бесконечно малого перемещения
– равен модулю вектора
.
Значитds
– модуль бесконечно малого перемещения
– равен модулю вектора 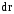 ,т. е.
,т. е.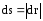 .Из рисунка видно, что
.Из рисунка видно, что 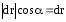 , здесь dr – бесконечно малое приращение длины вектора
, здесь dr – бесконечно малое приращение длины вектора 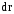 .
.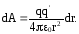
Работа на всем пути, от точки 1 до точки 2, равна:
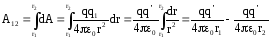 .
.
Потенциал.
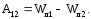
потенциальная энергия взаимодействия двух точечных зарядов в вакууме дается следующей формулой:
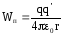 . (3.3)
. (3.3)
Из
формулы (3.3) видно, что потенциальную
энергию взаимодействия двух точечных
зарядов можно представить как произведение
величины второго заряда 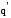 на
функцию,
зависящую от величины первого заряда
q
и расстояния до точки, в которой находится
второй заряд:
на
функцию,
зависящую от величины первого заряда
q
и расстояния до точки, в которой находится
второй заряд:
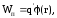
где 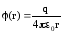 – потенциал электростатического поля
точечного заряда
– потенциал электростатического поля
точечного заряда
В
общем случае электростатический
потенциал
поля, создаваемого произвольным
распределением зарядов равен, по
определению,
отношению потенциальной энергии 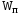 пробного заряда
пробного заряда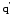 в
электростатическом поле к величине
этого пробного заряда:
в
электростатическом поле к величине
этого пробного заряда:
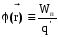 . (3.5)
. (3.5)
Единица потенциала в системе СИ – вольт (В):
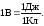
Зная 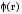 – потенциал электростатического поля в
любой точке пространства, легко найти
потенциальную энергию
– потенциал электростатического поля в
любой точке пространства, легко найти
потенциальную энергию 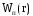 любого точечного зарядаq,
помещенного в данную точку пространства:
любого точечного зарядаq,
помещенного в данную точку пространства:
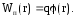 (3.6)
(3.6)
Следовательно, работу электростатического поля по перемещению электрического заряда можно выразить, используя (3.2) и (3.6), следующим образом:
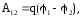 (3.7)
(3.7)
здесь 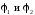 – потенциалы поля в точках, между которыми
переместился заряд.
– потенциалы поля в точках, между которыми
переместился заряд.
Потенциал поля, создаваемого системой точечных зарядов.
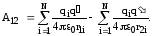
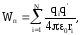
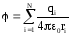
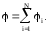 —
Формула выражает принцип
суперпозиции для потенциала электростатического
поля: потенциал
поля системы зарядов равен алгебраической сумме
потенциалов, создаваемых каждым из
зарядов в отдельности.
—
Формула выражает принцип
суперпозиции для потенциала электростатического
поля: потенциал
поля системы зарядов равен алгебраической сумме
потенциалов, создаваемых каждым из
зарядов в отдельности.
7.Циркуляция вектора напряженности электрического поля. Связь между напряжённостью электростатического поля и потенциалом.
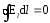 , (3.14)
, (3.14)
кружок
у знака интеграла в (3.14) обозначает, что
интеграл берется по замкнутому контуру.
Интеграл вида (3.14) по замкнутому контуру
называют циркуляцией вектора 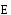 .
Следовательно, циркуляция
вектора
.
Следовательно, циркуляция
вектора 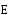 электростатического
поля, вычисленная
по любому замкнутому контуру, равна нулю. Это
общее свойство всех полей консервативных
сил (потенциальных полей).
электростатического
поля, вычисленная
по любому замкнутому контуру, равна нулю. Это
общее свойство всех полей консервативных
сил (потенциальных полей).
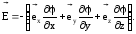 (3.17)
(3.17)
Если ввести следующее обозначение:
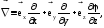 (3.18)
(3.18)
то формула (3.17) запишется в компактном виде:
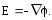 (3.19)
(3.19)
Введенный
нами математический объект 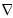 называетсяоператором
градиента и формула (3.19) читается так: «вектор
называетсяоператором
градиента и формула (3.19) читается так: «вектор 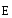 равен минус градиент».
равен минус градиент».
8.Эквипотенциальные поверхности, их связь с силовыми линиями.
Из самого названия следует, что эквипотенциальные поверхности – это поверхности равного потенциала. Следовательно, уравнение эквипотенциальной поверхности имеет вид:
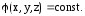
Форма эквипотенциальных поверхностей связана с формой силовых линий: эквипотенциальные поверхности расположены так, что в каждой точке пространства силовая линия и эквипотенциальная поверхность взаимно перпендикулярны.
Если условиться проводить эквипотенциальные поверхности так, чтобы разность потенциалов между двумя соседними поверхностями была одинакова, то по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля.
Если рассечь эквипотенциальную поверхность плоскостью, то в сечении получаются линии равного потенциала, эквипотенциальные линии.




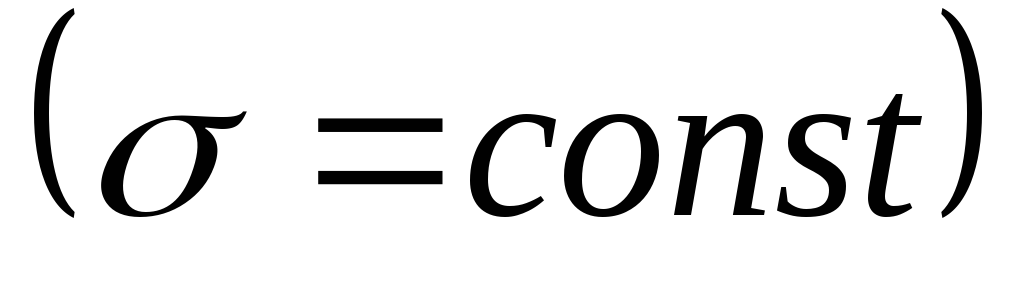 .
.
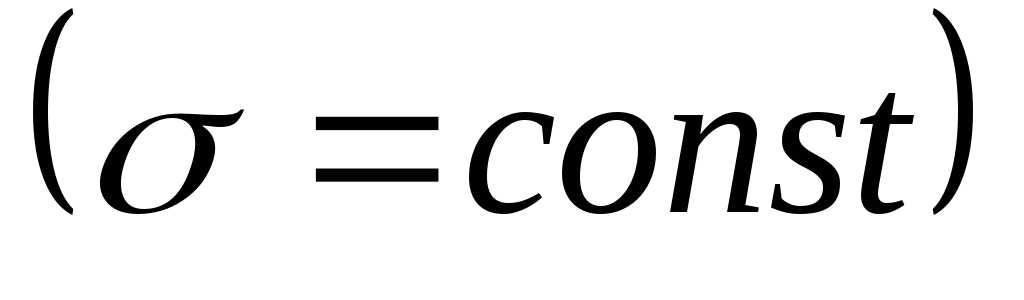 .
. .
. .
. .
. .
. .
.