Потенциал поля точечного заряда
Оглавление
Введение
1. Теоретические сведения
1.1 Электрическе поле
1.2 Поле точечного заряда
1.3 Распределение зарядов
1.4 Потенциал
1.5 Потенциал поля точечного заряда
1.6 Потенциал поля системы зарядов
1.7 Связь между потенциалом и напряженностью поля
1.8 Эквипотенциальные поверхности
2. Средства среды MathCAD
2.1 ДЛЯ РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2.2 Простейшиевычисления в среде MathCad
3. Анализ распределения потенциала с использованием компьютерной программы Mathcad
Заключение
Список использованной литературы
Введение
Электростатика — раздел электродинамики, изучающий взаимодействие неподвижных электрических зарядов. В повседневной жизни человек постоянно сталкивается с примерами электростатического взаимодействия тел. Рамки электростатического влияния охватывают каждый атом, как на земле, так и за её пределами, включая, как и простую расческу, так и земной шар. Однако в общеобразовательных учебных заведениях, зачастую рассматриваются лишь теоретические аспекты электростатики, и опускается реальное применение, да никто об этом особо и не задумывается, а ведь оно на использовании её законов видно чуть ли не на каждом шагу: к примеру на свойстве металлических проводников экранировать пространство от внешних полей основано его применение для электростатической защиты хоть в той же медицине (аппаратура, пациенты, обслуживающий персонал, окруженные проводящей металлической сеткой, не испытывают воздействия внешних электрических полей, что необходимо как для безопасности больного да врача, так и для предотвращения искажений при снятии, например электрокардиограммы). Поэтому исследование электростатических полей является актуальным и на сегодняшний день.
Теоретические сведения
Электрическое поле
Согласно современным представлениям взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд
Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный», заряд испытывает действие силы.
Опыт показывает, что сила F, действующая на неподвижный точечный пробный заряд q, всегда может быть представлена как
F= qE (1.1)
где вектор Е называют напряженностью электрического поля в данной точке. Вектор Е, как видно из (1.1), можно определить как силу, действующую на единичный положительный неподвижный заряд. Здесь предполагается, что пробный заряд
Поле точечного заряда.
Поле точечного заряда
Из опыта (закон Кулона) непосредственно следует, что напряженность поля неподвижного точечного заряда q на расстоянии r от него можно представить как

Где 
 -электрическая постоянная, ε — электрическая проводимость среды,
-электрическая постоянная, ε — электрическая проводимость среды, 
 — орт радиуса-вектора г, проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Формула (1.2) записана в СИ. Здесь коэффициент
— орт радиуса-вектора г, проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Формула (1.2) записана в СИ. Здесь коэффициент

заряд qвыражается в кулонах (Кл), напряженность поля ε — в вольтах на метр (В/м). В зависимости от знака заряда
По существу формула (1.2) выражает не что иное, как закон Кулона, но в «полевой» форме. Весьма важно, что напряженность Е поля точечного заряда обратно пропорциональна квадрату расстояния г.
Вся совокупность экспериментальных фактов показывает, что этот закон справедлив для расстояний от 10~ 13 см до нескольких километров, и пока нет никаких оснований ожидать, что этот закон не выполняется и при больших расстояниях.
Заметим еще, что в поле, создаваемом неподвижным точечным зарядом, сила, действующая на пробный заряд, не зависит от того, покоится пробный заряд или движется. Это относится и к системе не подвижных зарядов.
Распределение зарядов
Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру (электроны, ядра), и считать, что они «размазаны» определенным образом в пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. Это позволяет значительно упрощать расчеты, не внося сколько-нибудь значительной ошибки.
При переходе к непрерывному распределению вводят понятие о плотности зарядов — объемной ρ, поверхностной σ и линейной λ

где dq — заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dl.
С учетом этих распределений формула (1.3) может быть представлена в другой форме. Например, если заряд распределен по объему, то надо заменить qiна dq = pdV и сумму на интеграл, тогда

где интегрирование проводится по всему пространству, в котором ρ отлично от нуля. Таким образом, зная распределение зарядов, мы можем полностью решить задачу о нахождении напряженности электрического поля по формуле (1.3), если распределение дискретно, или по формуле (1.5) и аналогично ей, если распределение непрерывно. В общем случае расчет сопряжен со значительными трудностями. Действительно, для нахождения вектора Е надо вычислить сначала его проекции Е
Потенциал
До сих пор мы рассматривали описание электрического поля с помощью вектора Е. Существует, однако, и другой адекватный способ описания — с помощью потенциала φ (заметим сразу, что оба эти способа однозначно соответствуют друг другу). Как мы увидим, второй способ обладает рядом существенных преимуществ.
Тот факт, что линейный интеграл

представляющий собой работу сил поля при перемещении единичного положительного заряда из точки 1 в точку 2, не зависит от пути между этими точками (из механики известно, что любое стационарное поле центральных сил, является консервативным, то есть работа сил этого поля не зависит от пути, а зависит только от положения начальной и конечной точки), позволяет утверждать, что в электрическом поле существует некоторая скалярная функция координат φ (r), убыль которой

где φ1 и φ2 — значения функции φ в точках 1 и 2. Так определенная величина φ (r) называется потенциалом поля. Из сопоставления выражения (1.7) с выражением для работы сил потенциального поля (которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал — это величина, численно равная потенциальной энергии единичногоположительного заряда в данной точке поля.
Потенциалу какой-либо произвольной точки Ополя можно условно приписать любое значение φ0. Тогда потенциалы всех других точек поля определяются согласно (1.7) однозначно. Если изменить φ0 на некоторую величину Δφ, то на такую же величину изменятся и потенциалы во всех других точках поля.
Таким образом, потенциал φ определяется с точностью до произвольной аддитивной постоянной. Значение этой постоянной не играет роли, так как все электрические явления зависят только от напряженности электрического поля. Последняя же определяется, как мы увидим, не самим потенциалом в данной точке поля, а разностью потенциалов в соседних точках поля.
Единицей потенциала является вольт (В).
График X-Y
 |
Полярный график
 |
График Поверхностей
 |
Линии Уровня
 |
Заключение
Справившись с поставленной задачей, мы можем по имеющимся рисункам судить о поле, создаваемым точечным зарядом. По густоте линий равного потенциала можно судить о наибольшей напряженности вокруг заряженного тела. Итак, такая картина напоминает изображение линий равного потенциала и силовых линий поля точечного заряда. В результате выполнения работы была создана компьютерная программа в среде программирования MathCad, которая является самой оптимальной программой для реализации поставленной задачи. Созданная программа позволяет решить задачу как рассчитать потенциал электрического поля создаваемого зарядом q.
Список использованной литературы
1. Иродов И.У. Основные законы электромагнетизма-2е изд., стереотип. — М. Высш. шк. М.: Наука. Гл. ред. физ. — мат. лит., 1991-289 с.
2. Клюбин В.В. Курс общей физики: учеб. пособие. ч.3. Электростатика. Постоянный ток. СПб.: СПбГМТУ, 2005 — . — В надзаг.: С. — Петерб. гос. мор. техн. ун-т. — 2006. — 217 с
3. Смайт В. Электростатика и электродинамика. М. — издательство иностранной лин-ры. 1954 — 605 с.
Оглавление
Введение
1. Теоретические сведения
1.1 Электрическе поле
1.2 Поле точечного заряда
1.3 Распределение зарядов
1.4 Потенциал
1.5 Потенциал поля точечного заряда
1.6 Потенциал поля системы зарядов
1.7 Связь между потенциалом и напряженностью поля
1.8 Эквипотенциальные поверхности
2. Средства среды MathCAD
2.1 ДЛЯ РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2.2 Простейшиевычисления в среде MathCad
3. Анализ распределения потенциала с использованием компьютерной программы Mathcad
Заключение
Список использованной литературы
Введение
Электростатика — раздел электродинамики, изучающий взаимодействие неподвижных электрических зарядов. В повседневной жизни человек постоянно сталкивается с примерами электростатического взаимодействия тел. Рамки электростатического влияния охватывают каждый атом, как на земле, так и за её пределами, включая, как и простую расческу, так и земной шар. Однако в общеобразовательных учебных заведениях, зачастую рассматриваются лишь теоретические аспекты электростатики, и опускается реальное применение, да никто об этом особо и не задумывается, а ведь оно на использовании её законов видно чуть ли не на каждом шагу: к примеру на свойстве металлических проводников экранировать пространство от внешних полей основано его применение для электростатической защиты хоть в той же медицине (аппаратура, пациенты, обслуживающий персонал, окруженные проводящей металлической сеткой, не испытывают воздействия внешних электрических полей, что необходимо как для безопасности больного да врача, так и для предотвращения искажений при снятии, например электрокардиограммы). Поэтому исследование электростатических полей является актуальным и на сегодняшний день.
Теоретические сведения
Электрическое поле
Согласно современным представлениям взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд q изменяет определенным образом свойства окружающего его пространства — создает электрическое поле.
Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный», заряд испытывает действие силы.
Опыт показывает, что сила F, действующая на неподвижный точечный пробный заряд q, всегда может быть представлена как
F= qE (1.1)
где вектор Е называют напряженностью электрического поля в данной точке. Вектор Е, как видно из (1.1), можно определить как силу, действующую на единичный положительный неподвижный заряд. Здесь предполагается, что пробный заряд q’ должен быть достаточно малым, чтобы его внесение не вызвало заметного искажения интересующего нас поля (вследствие возможного перераспределения создающих поле зарядов).
Поле точечного заряда.
Поле точечного заряда
Из опыта (закон Кулона) непосредственно следует, что напряженность поля неподвижного точечного заряда q на расстоянии r от него можно представить как

Где 
 -электрическая постоянная, ε — электрическая проводимость среды,
-электрическая постоянная, ε — электрическая проводимость среды, 
 — орт радиуса-вектора г, проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Формула (1.2) записана в СИ. Здесь коэффициент
— орт радиуса-вектора г, проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Формула (1.2) записана в СИ. Здесь коэффициент

заряд qвыражается в кулонах (Кл), напряженность поля ε — в вольтах на метр (В/м). В зависимости от знака заряда q вектор Е направлен так же, как и r, или противоположно ему.
По существу формула (1.2) выражает не что иное, как закон Кулона, но в «полевой» форме. Весьма важно, что напряженность Е поля точечного заряда обратно пропорциональна квадрату расстояния г.
Вся совокупность экспериментальных фактов показывает, что этот закон справедлив для расстояний от 10~ 13 см до нескольких километров, и пока нет никаких оснований ожидать, что этот закон не выполняется и при больших расстояниях.
Заметим еще, что в поле, создаваемом неподвижным точечным зарядом, сила, действующая на пробный заряд, не зависит от того, покоится пробный заряд или движется. Это относится и к системе не подвижных зарядов.
Распределение зарядов
Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру (электроны, ядра), и считать, что они «размазаны» определенным образом в пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. Это позволяет значительно упрощать расчеты, не внося сколько-нибудь значительной ошибки.
При переходе к непрерывному распределению вводят понятие о плотности зарядов — объемной ρ, поверхностной σ и линейной λ. По определению

где dq — заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dl.
С учетом этих распределений формула (1.3) может быть представлена в другой форме. Например, если заряд распределен по объему, то надо заменить qiна dq = pdV и сумму на интеграл, тогда

где интегрирование проводится по всему пространству, в котором ρ отлично от нуля. Таким образом, зная распределение зарядов, мы можем полностью решить задачу о нахождении напряженности электрического поля по формуле (1.3), если распределение дискретно, или по формуле (1.5) и аналогично ей, если распределение непрерывно. В общем случае расчет сопряжен со значительными трудностями. Действительно, для нахождения вектора Е надо вычислить сначала его проекции Еx, Еy, Еz, а это по существу три интеграла типа (1.5). И только в тех случаях, когда система зарядов обладает той или иной симметрией, задача, как правило, значительно облегчается.
Потенциал
До сих пор мы рассматривали описание электрического поля с помощью вектора Е. Существует, однако, и другой адекватный способ описания — с помощью потенциала φ (заметим сразу, что оба эти способа однозначно соответствуют друг другу). Как мы увидим, второй способ обладает рядом существенных преимуществ.
Тот факт, что линейный интеграл

представляющий собой работу сил поля при перемещении единичного положительного заряда из точки 1 в точку 2, не зависит от пути между этими точками (из механики известно, что любое стационарное поле центральных сил, является консервативным, то есть работа сил этого поля не зависит от пути, а зависит только от положения начальной и конечной точки), позволяет утверждать, что в электрическом поле существует некоторая скалярная функция координат φ (r), убыль которой

где φ1 и φ2 — значения функции φ в точках 1 и 2. Так определенная величина φ (r) называется потенциалом поля. Из сопоставления выражения (1.7) с выражением для работы сил потенциального поля (которая равна убыли потенциальной энергии частицы в поле) можно сказать, что потенциал — это величина, численно равная потенциальной энергии единичногоположительного заряда в данной точке поля.
Потенциалу какой-либо произвольной точки Ополя можно условно приписать любое значение φ0. Тогда потенциалы всех других точек поля определяются согласно (1.7) однозначно. Если изменить φ0 на некоторую величину Δφ, то на такую же величину изменятся и потенциалы во всех других точках поля.
Таким образом, потенциал φ определяется с точностью до произвольной аддитивной постоянной. Значение этой постоянной не играет роли, так как все электрические явления зависят только от напряженности электрического поля. Последняя же определяется, как мы увидим, не самим потенциалом в данной точке поля, а разностью потенциалов в соседних точках поля.
Единицей потенциала является вольт (В).
Потенциал поля точечного заряда
Формула (1.7) содержит не только определение потенциала φ, но и способ нахождения этой функции. Для этого достаточно вычислить интеграл 
 по любому пути между двумя точками и представить затем полученный результат в виде убыли некоторой функции, которая и есть ср (г). Можно поступить и проще. Воспользуемся тем, что формула (1.23) справедлива не только для конечных перемещений, но и для элементарных dl. Тогда согласно этой формуле элементарная убыль потенциала на этом перемещении есть
по любому пути между двумя точками и представить затем полученный результат в виде убыли некоторой функции, которая и есть ср (г). Можно поступить и проще. Воспользуемся тем, что формула (1.23) справедлива не только для конечных перемещений, но и для элементарных dl. Тогда согласно этой формуле элементарная убыль потенциала на этом перемещении есть

электростатическое поле заряженное тело
Другими словами, если известно поле Е (г), то для нахождения φ надо представить Еdl (путем соответствующих преобразований) как убыль некоторой функции. Эта функция и есть φ.
Найдем таким способом потенциал поля неподвижного точечного заряда:

где учтено, что 
 dl = l (dl) r, ибо проекция вектора dl на вектор
dl = l (dl) r, ибо проекция вектора dl на вектор 
 , а значит, и на r равна приращению модуля вектора r, т.е. dr. Величина, стоящая в круглых скобках под знаком дифференциала, и есть φ (r). Так как присутствующая здесь аддитивная константа никакой физической роли не играет, ее обычно опускают, стремясь выражение для φ сделать проще. Таким образом, потенциал поля точечного заряда
, а значит, и на r равна приращению модуля вектора r, т.е. dr. Величина, стоящая в круглых скобках под знаком дифференциала, и есть φ (r). Так как присутствующая здесь аддитивная константа никакой физической роли не играет, ее обычно опускают, стремясь выражение для φ сделать проще. Таким образом, потенциал поля точечного заряда

Отсутствие в этом выражении аддитивной константы означает, что мы условно полагаем потенциал на бесконечности (r→∞) равным нулю.
Потенциал поля точечного заряда.
Подставим в соотношение для определения потенциала выражение для напряженности электрического поля точечного заряда:
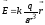 .
.
При интегрировании учтем, что 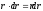 .
.
После интегрирования получаем:
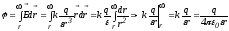 .
.
Потенциал точечного заряда пропорционален величине заряда и убывает обратно пропорционально расстоянию, стремясь на бесконечности к нулю.
Потенциал поля системы зарядов.
Пусть система состоит из 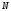 неподвижных точечных зарядов
неподвижных точечных зарядов .
Согласно принципу суперпозиции в любой
точке поля напряженность равна
.
Согласно принципу суперпозиции в любой
точке поля напряженность равна ,
где
,
где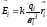 —
напряженность поля
—
напряженность поля -го
точечного заряда в исследуемой точке,
находящейся на расстоянии
-го
точечного заряда в исследуемой точке,
находящейся на расстоянии от заряда
от заряда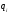 .
.
Подставив в соотношение для определения
потенциала значение 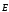 ,
получим:
,
получим:
 ,
,
где  —
потенциал поля
—
потенциал поля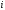 -го
точечного заряда в исследуемой точке.
-го
точечного заряда в исследуемой точке.
Таким образом, потенциал системы точечных зарядов в любой точке пространства равен алгебраической сумме потенциалов, создаваемых всеми точечными зарядами в этой точке.
Если заряды непрерывно распределены по объему, то сумму следует заменить объемным интегралом:
 ,
,
где
интегрирование проводится по объему,
где 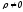 .
.
Аналогичные выражения получаются при поверхностном и линейном распределении зарядов:
 ,
, .
.
Таким образом, зная распределение зарядов, в принципе можно найти потенциал и разность потенциалов поля любой системы зарядов.
Рассмотрим ряд примеров расчета потенциала и разности потенциалов, которые понадобятся нам в дальнейшем изложении.
Потенциал поля точечного диполя.
Согласно
принципу суперпозиции, учитывая, что  :
:
 Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда
Потенциал
поля диполя зависит от его электрического
моментаpи убывает с
расстоянием быстрее, чем потенциал поля
точечного заряда .
.
Потенциал поля в точках на оси заряженного кольца.
Для
расчета 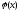 воспользуемся
линейным интегралом:
воспользуемся
линейным интегралом:
 ,
,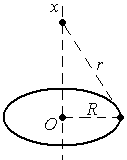
где  —
заряд кольца. Для всех
—
заряд кольца. Для всех

— потенциал кольца убывает как потенциал поля точечного заряда.
В центре кольца (x= 0) потенциал равен:
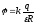 .
.
Потенциал в точках на оси равномерно заряженного круга
 .
.
Для расчёта  следует
воспользоваться поверхностным интегралом:
следует
воспользоваться поверхностным интегралом:
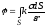 .
.
Представим круг как систему колец с
радиусами 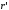 ,
тогда
,
тогда ,
,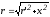 ,
,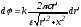 .
.
Для 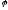 получим:
получим:
 .
.
Для
точек достаточно удаленных от круга  :
:
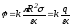 .
.
Получите самостоятельно этот результат.
Потенциал поля объемно заряженного шара
 .
.
Для простоты расчетов примем  .
.
Зависимость  для этого случая представлена на рисунке.
Потенциал точек внутри шара
для этого случая представлена на рисунке.
Потенциал точек внутри шара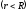 равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
равен заштрихованной площади, согласно
геометрическому смыслу интеграла:
 ,
,
так
как потенциал равен работе по перемещению
единичного положительного из данной
точки в бесконечность, где потенциал
принят равным нулю.
Учитывая зависимость:


где 
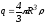 ,
получаем для точек внутри шара:
,
получаем для точек внутри шара:
 .
.
Для
точек вне шара  потенциал убывает с расстоянием как
поле точечного заряда:
потенциал убывает с расстоянием как
поле точечного заряда: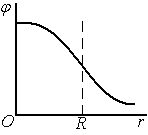
 .
.
Зависимость  представлена на рисунке, где
представлена на рисунке, где
 ,
,
 .
.
Разность потенциалов двух точек поля заряженной сферы
 .
.
Для точек вне сферы 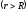 в однородном диэлектрике
в однородном диэлектрике
 .
.
Найдем разность потенциалов:
 .
.
При интегрировании учтено, что  ,
где
,
где – приращение модуля радиус-вектора
– приращение модуля радиус-вектора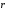 .
.
Разность потенциалов двух точек поля заряженного цилиндра
 .
.
Для точек вне цилиндра  в однородном диэлектрике:
в однородном диэлектрике:
 ,
,
где  .
.
 .
.
Лекция 5.
38.Энергетическая характеристика электростатического поля — потенциал. Потенциал поля точечного заряда и системы зарядов. Связь между напряженностью электрического поля и потенциалом.
Энергетическая характеристика электростатического поля — потенциал
потенциа́л— скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда.
потенциал
равен отношению потенциальной энергии
взаимодействия заряда с полем к величине
этого заряда: 
Напряжённость
электри́ческого по́ля — векторная
физическая величина, характеризующая
электрическое поле в данной точке и
численно равная отношению силы
действующей на пробный заряд, помещенный
в данную точку поля, к величине этого
заряда q: 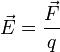
Для установления связи между силовой характеристикой электрического поля — напряжённостью и его энергетической характеристикой — потенциаломрассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA = — dWп = — q d, где d — изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат
Ex dx + Ey dy + Ez dz = -d(фи)
где
Ex, Ey, Ez — проекции вектора напряженности
на оси системы координат. Поскольку
выражение (1.8) представляет собой полный
дифференциал, то для проекций вектора
напряженности имеем 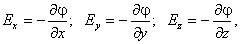
откуда
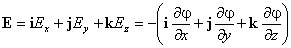
Стоящее в скобках выражение является градиентом потенциала j, т. е.
E = — grad = -Ñ.
Напряжённость
в какой-либо точке электрического поля
равна градиенту потенциала в этой точке,
взятому с обратным знаком. Знак «минус»
указывает, что напряженность E направлена
в сторону убывания потенциала. Рассмотрим
электрическое поле, создаваемое
положительным точечным зарядом q (рис.
1.6). Потенциал поля в точке М, положение
которой определяется радиус-вектором
r, равен = q / 4pe0er. Направление радиус-вектора
r совпадает с направлением вектора
напряженности E, а градиент потенциала
направлен в противоположную сторону.
Проекция градиента на направление
радиус-вектора 
Проекция
же градиента потенциала на направление
вектора t, перпендикулярного вектору
r, равна 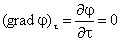
т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const).
В
рассмотренном случае направление
вектора r совпадает с направлением 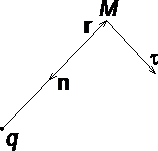
силовых
линий. Обобщая полученный результат,
можно утверждать, что во всех точках
кривой, ортогональной к силовым линиям,
потенциал электрического поля одинаков.
Геометрическим местом точек с одинаковым
потенциалом является эквипотенциальная
поверхность, ортогональная к силовым
линиям. 
При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали — штриховыми.
Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.
1.4.Потенциал. Потенциальная энергия заряда в электростатическом поле
Работа
сил электрического поля, созданного
зарядом  ,
по перемещению заряда
,
по перемещению заряда из точки 1 в точку 2 равна:
из точки 1 в точку 2 равна:
 .
.
Работа сил консервативного поля равна убыли потенциальной энергии:
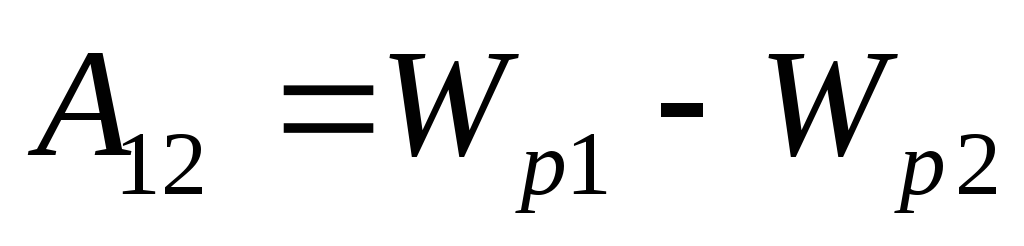 ,
,
тогда
потенциальная энергия заряда  в поле заряда
в поле заряда равна:
равна:
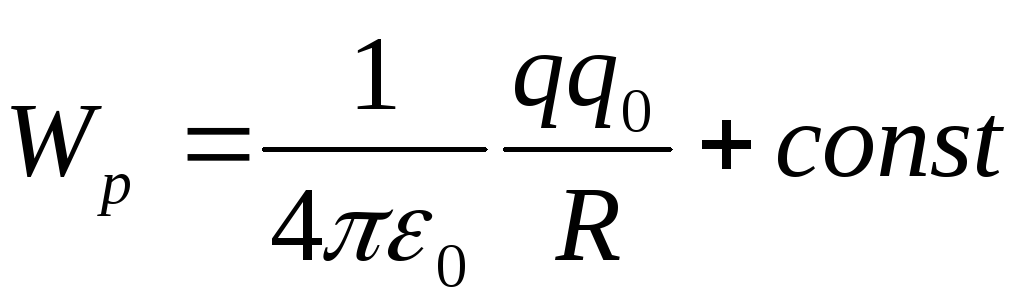 .
.
Значение
константы выбирается таким, чтобы при
удалении заряда на бесконечность (то
есть при  )
потенциальная энергия обратилась бы в
ноль, поэтому
)
потенциальная энергия обратилась бы в
ноль, поэтому
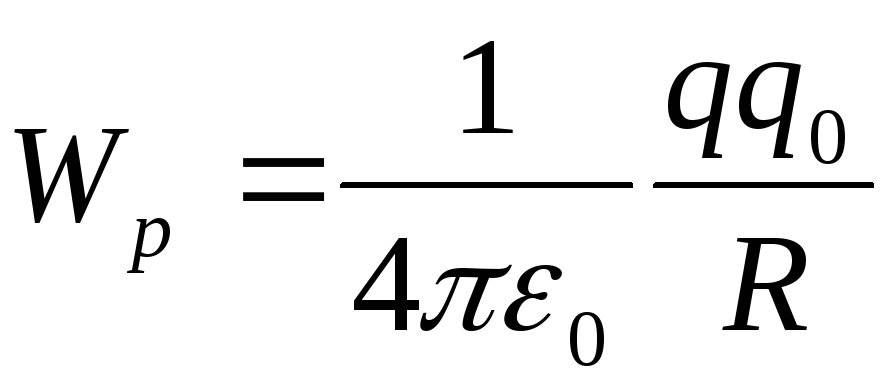 .
.
Ясно,
что разные пробные заряды  и
и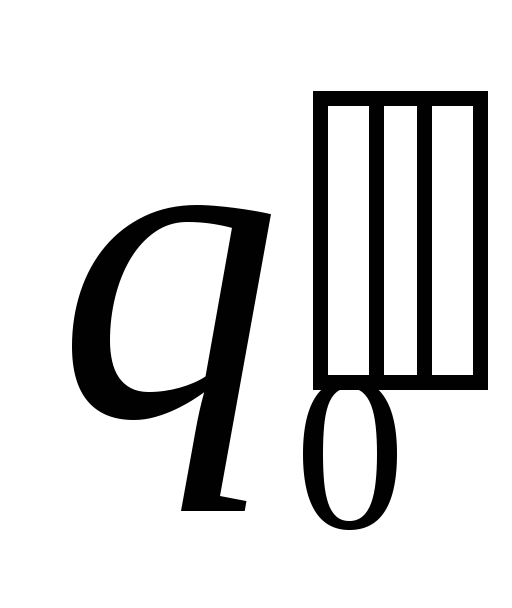 в одной и той же точке поля будут обладать
разной потенциальной энергией
в одной и той же точке поля будут обладать
разной потенциальной энергией и
и .
Однако отношение
.
Однако отношение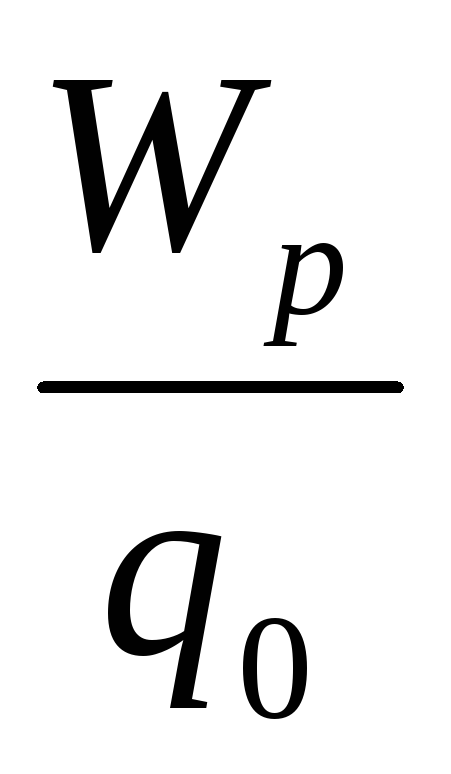 для всех пробных зарядов будет одинаково.
Величина
для всех пробных зарядов будет одинаково.
Величина

называется потенциалом электрического поля и является его энергетической характеристикой. Потенциал поля точечного заряда равен
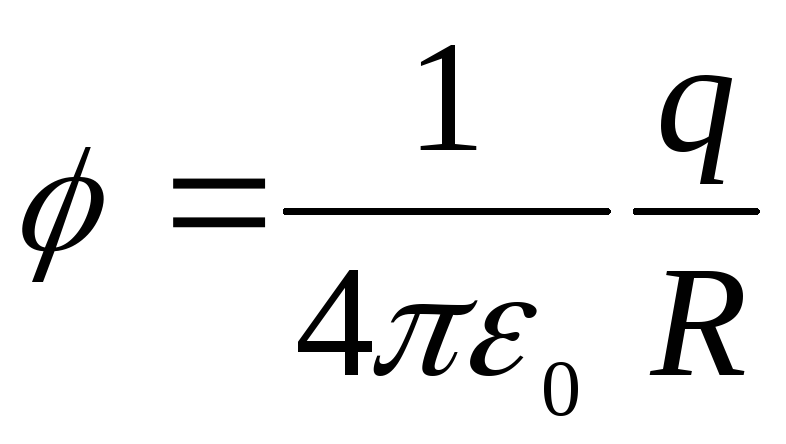 .
.
Если
поле создается системой 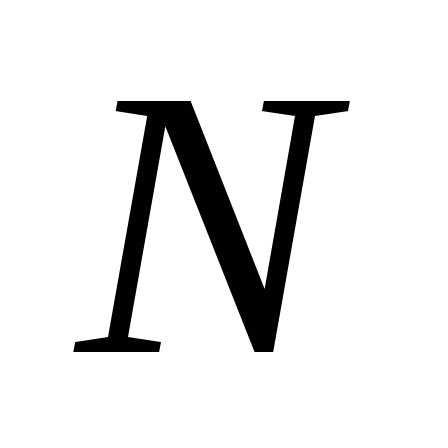 точечных зарядов, то
точечных зарядов, то
 ,
,
где  — расстояние от заряда
— расстояние от заряда до начального положения заряда
до начального положения заряда ,
, — расстояние от заряда
— расстояние от заряда до конечного положения заряда
до конечного положения заряда (заряд
(заряд перемещается силами поля).
перемещается силами поля).
Тогда
потенциальная энергия заряда в поле системы зарядов:
в поле системы зарядов:
 ,
,
а
потенциал 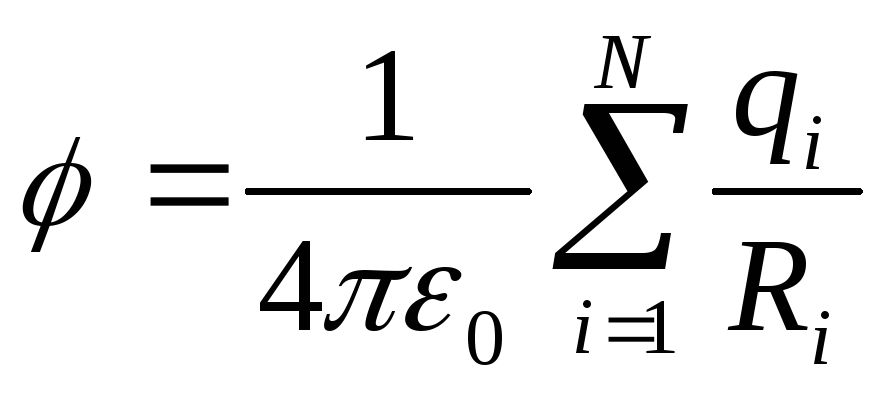
потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Зная
потенциал, можно найти потенциальную
энергию заряда 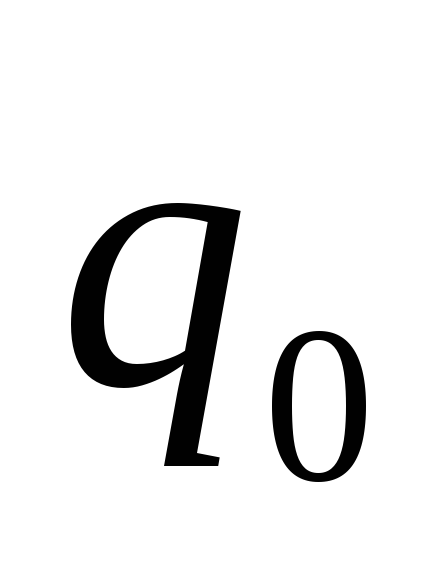 в электрическом поле:
в электрическом поле:
 .
.
Работа поля над зарядом:

— работа равна убыли потенциала, умноженной на заряд.
Если заряд удаляется из точки на бесконечность, то работа сил поля равна
следовательно,
потенциал численно равен отношению
работы, которую совершают силы поля над
положительным зарядом при удалении его
из данной точки на бесконечность, к
величине этого заряда. Потенциал
измеряется в вольтах:  .
.
1.5.Связь между напряженностью и потенциалом
Электрическое
поле можно описывать либо с помощью
векторной величины  (силовая характеристика), либо с помощью
скаляра
(силовая характеристика), либо с помощью
скаляра (энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
(энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
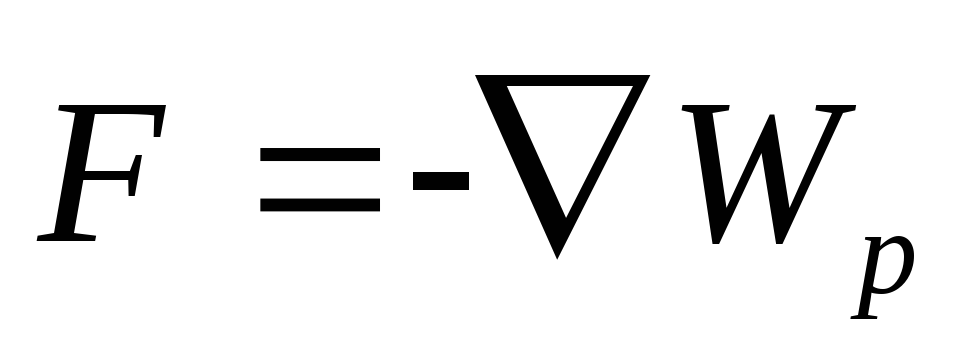 ,
,
где  — оператор Набла,
— оператор Набла, .
.
Для
заряженной частицы в электрическом
поле: 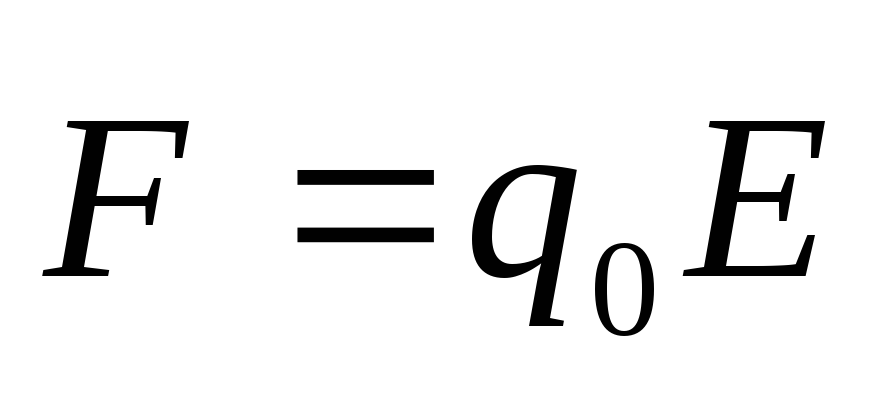 ,
,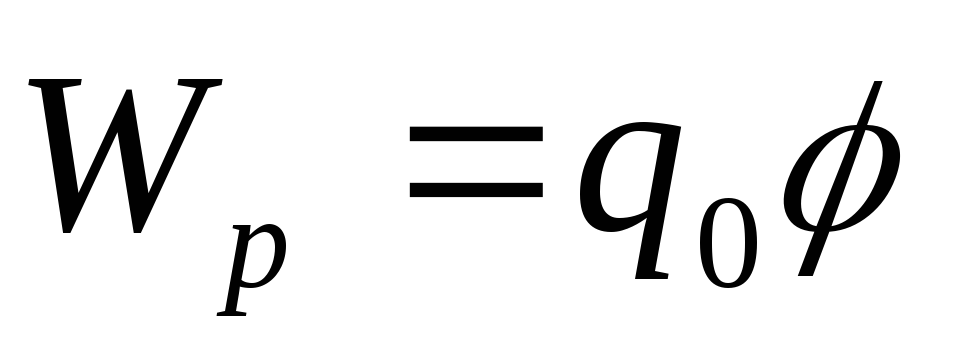 ,
тогда
,
тогда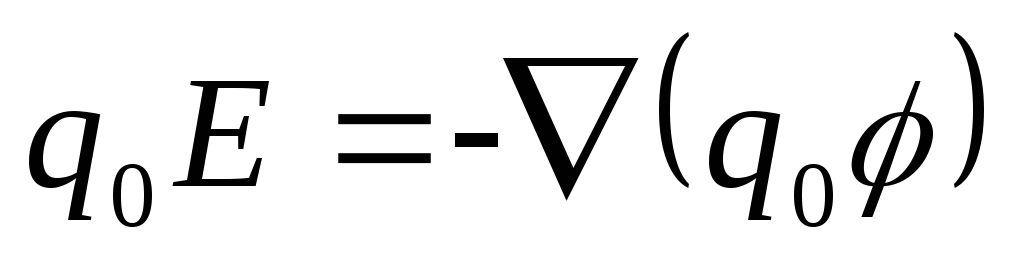 ,
, ,
тогда
,
тогда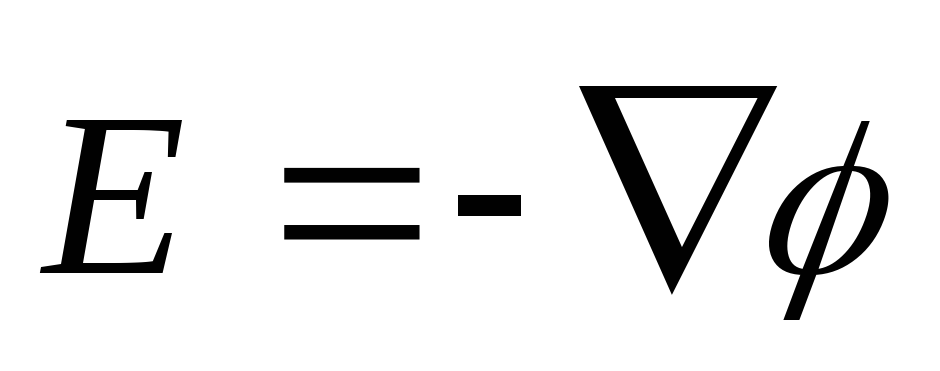 — связь напряженности и потенциала, или
— связь напряженности и потенциала, или ,
или
,
или ,
или
,
или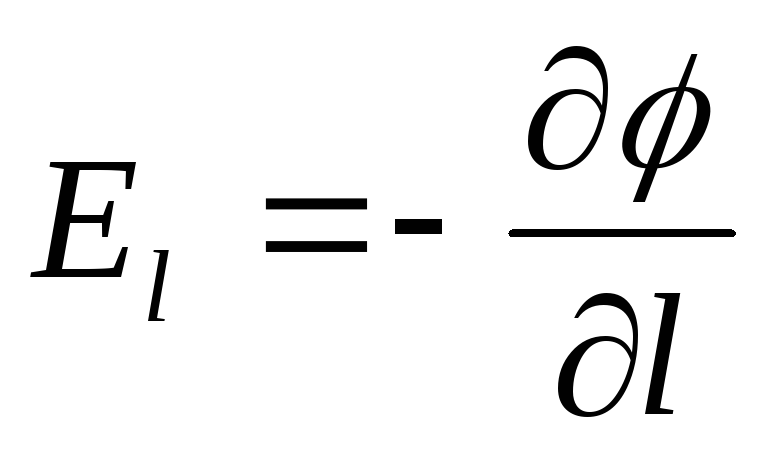 — проекция
вектора
— проекция
вектора  на произвольное направление
на произвольное направление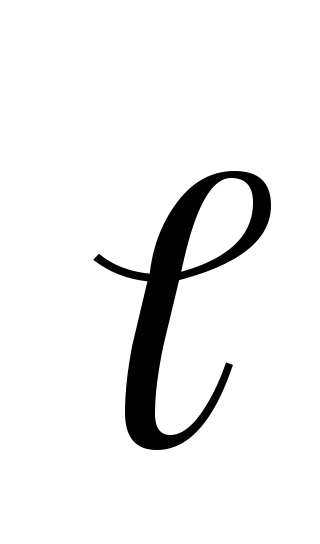 равна скорости убывания потенциала
равна скорости убывания потенциала вдоль направления
вдоль направления 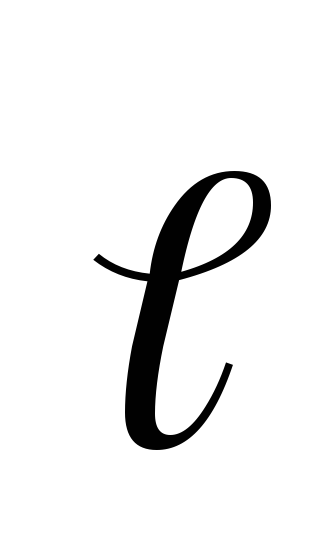 ,или
,или 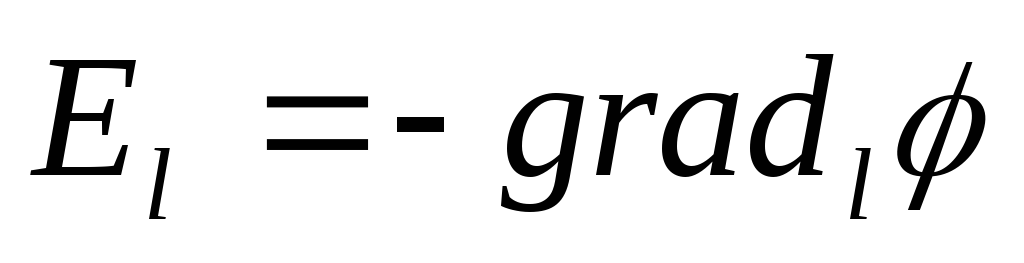 .
.
Так как градиент потенциала направлен в сторону его возрастания, а численная величина градиента является мерой быстроты этого возрастания, то можно сказать, что напряженность электрического поля есть мера быстроты спадания потенциала, или, просто, что она равна спаду потенциала.
Вернемся к
определению работы поля:  ,
, ,
отсюда циркуляция вектора на
участке 1=2
равна
,
отсюда циркуляция вектора на
участке 1=2
равна  .
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
.
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
Для
обхода по замкнутому контуру:  и
и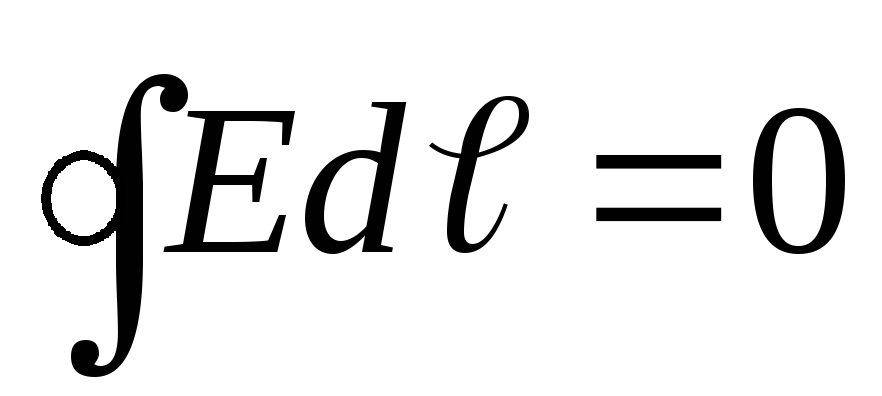 — пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
— пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
1.6. Эквипотенциальные поверхности
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью:
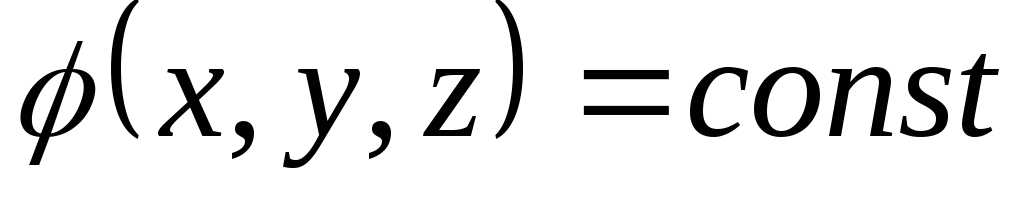
— уравнение эквипотенциальной поверхности.
При
перемещении по эквипотенциальной
поверхности на отрезок  потенциал не изменяется
потенциал не изменяется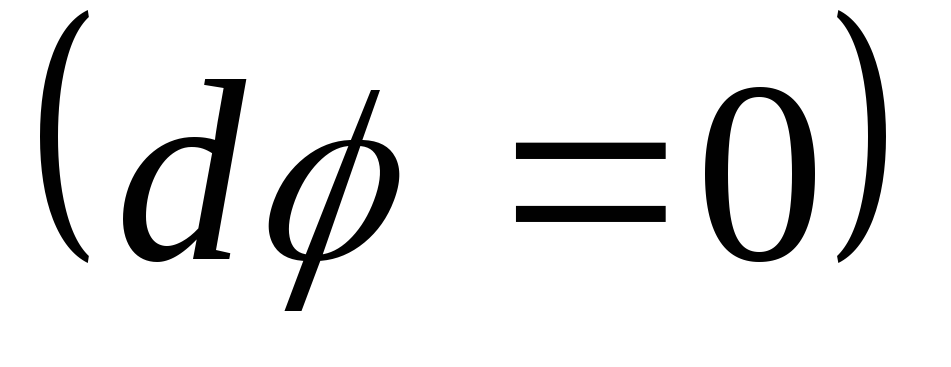 .
Таким образом, касательная к поверхности
составляющая вектора
.
Таким образом, касательная к поверхности
составляющая вектора равна нулю. Тогда вектор
равна нулю. Тогда вектор направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
 Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше
Если
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше ,
тем больше
,
тем больше .
.
Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.
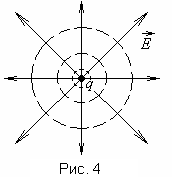
Рассмотрим эквипотенциальную поверхность точечного заряда. Потенциал точечного заряда (рис.1.4)
 .
.
Таким
образом, эквипотенциальная поверхность
этого заряда будет сферой радиуса  с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он  ,
или сходятся к заряду, если он “-”. То
есть вектор
,
или сходятся к заряду, если он “-”. То
есть вектор перпендикулярен эквипотенциальным
поверхностям.
перпендикулярен эквипотенциальным
поверхностям.
13. Характеристики электрического поля точечного заряда (напряжённость, силовые линии, потенциал, эквипотенциальные поверхности).
Электрическое
поле – вид материи, с помощью которого
осуществляется связь и взаимодействие
между телами, имеющими электрический
заряд. Электрическое поле имеет
определённые характеристики. Силовой
характеристикой электрического поля
является напряжённость Е. Это векторная
величина, численно равная силе F,
с которой поле действует на единичный
точечный заряд
q0,
находящийся в этом поле, и направление
которой совпадает с направлением силы,
действующей на положительный заряд.
Е= (Н/Кл). Электрическое поле изображают
системой силовых линий или линий
напряжённости.
(Н/Кл). Электрическое поле изображают
системой силовых линий или линий
напряжённости.

Это воображаемые линии, при построении которых пользуются следующими правилами:
1) Касательная к силовой линии в каждой точке совпадает с вектором напряжённости поля;
2) Силовые линии всегда не замкнуты: они начинаются на поверхности положительно заряженного тела и заканчиваются на поверхности отрицательно заряженного тела, или они могут начинаться или заканчиваться в бесконечности.
3)Силовые линии не пересекаются, т.к. в каждой точке поля вектор напряжённости имеет лишь одно направление;
4) В любой точке поля плотность силовых линий равна модулю напряжённости поля в этой точке.
Энергетической характеристикой электрического поля является его потенциал φ. Потенциал в какой-либо точке элетростатического поля есть скалярная величина, определяемая отношением потенциальной энергии WF единичного положительного заряда q0, помещённого в эту точку к этому заряду:
φ = .
.
По
мере удаления от заряда q,
создающего электрическое поле, его
потенциал убывает. Единицей измерения
потенциала в СИ является вольт (В). На
практике чаще пользуются понятием
разности потенциалов между двумя точками
электрического поля. В электрической
цепи эта разность потенциалов называется
напряжением. Силовая и энергетическая
характеристики связаны между собой.
Напряженность в любой точке однородного
электрического поля численно равна
разности потенциалов, приходящейся на
единицу длины силовой линии ∆l:
Е= .
Поверхность, на которой все точки имеют
равный между собой потенциал, называют
эквипотенциальной поверхностью.
Эквипотенциальные поверхности однородного
поля представляют собой плоскости, а
поля точечного заряда – концентрические
сферы. Одним из свойств эквипотенциальных
поверхностей является то, что в каждой
точке эквипотенциальной поверхности
вектор напряжённости поля перпендикулярен
к ней и направлен в сторону убывания
потенциала.
.
Поверхность, на которой все точки имеют
равный между собой потенциал, называют
эквипотенциальной поверхностью.
Эквипотенциальные поверхности однородного
поля представляют собой плоскости, а
поля точечного заряда – концентрические
сферы. Одним из свойств эквипотенциальных
поверхностей является то, что в каждой
точке эквипотенциальной поверхности
вектор напряжённости поля перпендикулярен
к ней и направлен в сторону убывания
потенциала.

Сплошными линиями обозначены силовые линии, пунктиром сечения эквипотенциальных поверхностей.
14. Диполь. Характеристика поля диполя (распределение силовых линий, дипольный момент, потенциал диполя).

Электрическим диполем называется система двух одинаковых по величине точечных зарядов +q и –q, расстояние l между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Электрические свойства диполя характеризуются электрическим дипольным моментом. Электрический момент диполя равен произведению модуля одного из электрических зарядов диполя на вектор l, проведённый от отрицательного заряда к положительному (также направлен и вектор дипольного момента):
p(вектор) = q(модуль)*l(вектор). Единицей измерения электрического дипольного момента является Кл/*м.
По
принципу сеперпозиции и его следствию
потенциал поля диполя равен сумме
потенциалов полей, создаваемых каждым
из зарядов диполя. Определим потенциал
поля, созданного диполем в некоторой
точке О, удалённой от зарядов диполя
соответственно на расстояния  и
и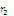 :
:

φ
= 
Если
точка О достаточно удалена от диполя
( ,
, ),
тогда
),
тогда =(приблизительно)
=(приблизительно)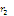 и
и =
(приблизительно)
=
(приблизительно)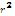 ,
, —
— =l
cos
α, где α – угол между вектором p
и направление от диполя на точку О.
Получаем:
=l
cos
α, где α – угол между вектором p
и направление от диполя на точку О.
Получаем:
φ
= 
В вакууме или идеальном изоляторе электрический диполь может сохраняться сколь угодно долго. Однако в реальной действительности диполь, как правило, находится в проводящей среде, поэтому под действием электрического поля диполя возникает электрический ток, который приводит к нейтрализации диполя.
22 Потенциальная энергия заряда в поле другого заряда
Тело,
находящееся в поле потенциальных сил,
обладает потенциальной энергией, за
счет которой совершается работа силами
поля. Следовательно, работа может быть
представлена как разность значений
потенциальных энергий, которыми обладает
заряд q’ в
точках 1 и 2 поля заряда q 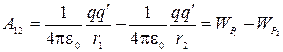 Можно
показать также, что, так как
Можно
показать также, что, так как 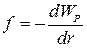 ,
, 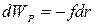
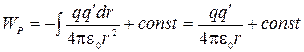 .
Отсюда
для потенциальной энергии заряда
.
Отсюда
для потенциальной энергии заряда 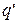 в
поле заряда q получаем:
в
поле заряда q получаем:  (6)
Значение const в
(6) обычно выбирают таким образом, чтобы
при удалении заряда q’ на
бесконечность (
(6)
Значение const в
(6) обычно выбирают таким образом, чтобы
при удалении заряда q’ на
бесконечность ( )
потенциальная энергия обращалась в
нуль. При этом условии получается,
что
)
потенциальная энергия обращалась в
нуль. При этом условии получается,
что 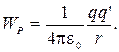 (7)
Будем считать q’ пробным
зарядом. Тогда потенциальная энергия,
которой обладает пробный заряд, зависит
не только от его значения
(7)
Будем считать q’ пробным
зарядом. Тогда потенциальная энергия,
которой обладает пробный заряд, зависит
не только от его значения 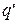 ,
но и от значения q и r,
определяющих поле. Следовательно, эта
энергия может быть использована для
описания поля, подобно тому, как была
использована для этой цели сила,
действующая на пробный заряд.
Разные
пробные заряды
,
но и от значения q и r,
определяющих поле. Следовательно, эта
энергия может быть использована для
описания поля, подобно тому, как была
использована для этой цели сила,
действующая на пробный заряд.
Разные
пробные заряды  ,
,  будут
обладать в одной и той же точке поля
различной энергией
будут
обладать в одной и той же точке поля
различной энергией  ,
, 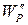 и
т.д. Однако отношение
и
т.д. Однако отношение  будет
для всех зарядов одно и то же.
Величина
будет
для всех зарядов одно и то же.
Величина 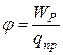 (8)
(8) называется потенциалом поля
в данной точке и используется наряду с
напряженностью поля
называется потенциалом поля
в данной точке и используется наряду с
напряженностью поля 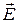 ,
для описания электрических полей.
Как
следует из (8) потенциал
численно равен потенциальной энергии,
которой обладает в данной точке поля
единичный положительный заряд. Таким
образом, для потенциального поля
точечного заряда получаем следующее
выражение:
,
для описания электрических полей.
Как
следует из (8) потенциал
численно равен потенциальной энергии,
которой обладает в данной точке поля
единичный положительный заряд. Таким
образом, для потенциального поля
точечного заряда получаем следующее
выражение:  (9)
Если поле создано системой точечных
зарядов q1, q2,
…, qn,
находящихся на расстояниях
соответственно r1, r2,…, rn до
точки поля, в которой находится заряд
(9)
Если поле создано системой точечных
зарядов q1, q2,
…, qn,
находящихся на расстояниях
соответственно r1, r2,…, rn до
точки поля, в которой находится заряд 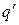 ,
то работа, совершаемая силами этого
поля над зарядом
,
то работа, совершаемая силами этого
поля над зарядом 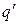 ,
будет равна алгебраической сумме работ
сил, обусловленных каждым из зарядов в
отдельности:
,
будет равна алгебраической сумме работ
сил, обусловленных каждым из зарядов в
отдельности: 
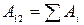 .
Но
каждая из работ
.
Но
каждая из работ  равна:
равна: 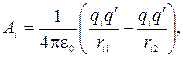 где
где 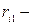 расстояние
от заряда
расстояние
от заряда  до
начального положения
заряда
до
начального положения
заряда 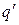 ,
,  расстояние
от заряда
расстояние
от заряда  до
конечного положения
заряда
до
конечного положения
заряда  .
Следовательно:
.
Следовательно:  .
Сопоставляя
это выражение с соотношением
.
Сопоставляя
это выражение с соотношением  ,
получаем для потенциальной энергии
заряда
,
получаем для потенциальной энергии
заряда 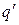 в
поле системы зарядов
выражение:
в
поле системы зарядов
выражение: 
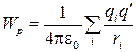 ,
(10)
откуда
,
(10)
откуда 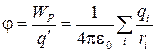 .
(11).
Следовательно, потенциал поля,
создаваемого системой зарядов, равен
алгебраической сумме потенциалов,
создаваемых каждым из зарядов в
отдельности.
Из соотношения
.
(11).
Следовательно, потенциал поля,
создаваемого системой зарядов, равен
алгебраической сумме потенциалов,
создаваемых каждым из зарядов в
отдельности.
Из соотношения 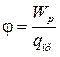 вытекает,
что заряд
вытекает,
что заряд  ,
находящийся в точке поля с потенциалом
,
находящийся в точке поля с потенциалом  ,
обладает потенциальной энергией
,
обладает потенциальной энергией 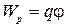 .
Следовательно, работа сил поля над
зарядом
.
Следовательно, работа сил поля над
зарядом  может
быть выражена через разность
потенциалов:
может
быть выражена через разность
потенциалов: 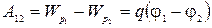 (12)
Таким образом, работа, совершаемая
над зарядом силами
поля,
равна произведению заряда на разность
потенциалов в начальной и конечной
точках. Если заряд
(12)
Таким образом, работа, совершаемая
над зарядом силами
поля,
равна произведению заряда на разность
потенциалов в начальной и конечной
точках. Если заряд  из
точки с потенциалом
из
точки с потенциалом  удаляется
на бесконечность (где по условию потенциал
равен нулю), работа сил поля будет
равна
удаляется
на бесконечность (где по условию потенциал
равен нулю), работа сил поля будет
равна 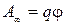 или
или 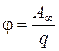 ,
,
23.Потенциал. Потенциал поля точечного заряда.
Потенциал — отношение потенциальной энергии заряда в поле к величине этого заряда:

Потенциал однородного поля равен
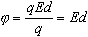
где d — расстояние, отсчитываемое от некоторого нулевого уровня.
Потенциальная
энергия взаимодействия заряда q с
полем равна 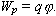 .
.
Потенциал поля точечного заряда
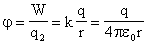
Потенциал. Разность потенциалов. Потенциал поля точечного заряда и системы точечных зарядов.
Энергетической характеристикой поля в данной точке является потенциал. Потенциал численно равен потенциальной энергии, которой обладает в данной точке единичный заряд
 . .
| (10.5.1) |
Потенциал поля точечного заряда Q, находящегося в точке на расстоянии r от него равен
 . .
| (10.5.2) |
Если поле образовано несколькими точечными зарядами, то потенциал результирующего поля
 , ,
| (10.5.3) |
где  — потенциал поля, создаваемого отдельным зарядом.
— потенциал поля, создаваемого отдельным зарядом.
работа сил поля над зарядом может быть представлена через разность потенциалов
 | (10.5.4) |
где Δφ – разность потенциалов между двумя точками электрического поля. Таким образом, потенциал электрического поля численно измеряется работой, совершаемой полем при перемещении единичного положительного пробного заряда по любому пути из данной точки.
В системе Си разность потенциалов измеряется в вольтах (В).
Для графического изображения распределения потенциала в электростатическом поле пользуются системой так называемых поверхностей равного потенциала (Эквипотенциальных поверхностей). Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.
На рисунке 10.9. пунктиром изображены силовые линии, сплошными линиями — сечения эквипотенциальных поверхностей для: положительного точечного заряда (а), диполя (б), двух одноименных зарядов (в), заряженного металлического проводника сложной конфигурации (г).
 |
Для точечного заряда эквипотенциальные поверхности -концентрические сферы. С другой стороны, линии напряженности — радиальные прямые. Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Во всех случаях вектор Е перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала.
Связь между энергетической и силовой характеристикой
Определим работу по перемещению заряда из точки с потенциалом φ1 в точку с потенциалом φ2:

Формула (10.6.1.) выражает зависимость силовой и энергетической характеристик электростатического поля.
С учетом проекций на оси координат уравнение (10.6.1.) примет вид:

Знак «-» в формуле (10.6.1.) показывает, что вектор напряженности электрического поля численно равен градиенту потенциала, но направлен в противоположную сторону, т.е. в сторону падения потенциала.




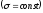 .
. .
.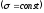 .
.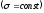 .
.