Электрический потенциал — Electric potential
Электрический потенциал (также называемый потенциал поля электрического , падение потенциала или электростатический потенциал ) является количество работы , необходимые для перемещения единицы положительного заряда от опорной точки к определенной точке внутри области , не вызывая ускорение. Как правило, опорная точка является Землей или точка на бесконечности , хотя любая точка вне влияния заряда электрического поля может быть использована.
Согласно классической электростатики , электрический потенциал является скалярной величиной обозначим через V или иногда φ , равна электрической потенциальной энергии любого заряженной частицы в любом месте (измеряется в джоулях ) , деленную на заряд этой частицы (измеряется в кулонах ). Разделив из заряда на частицу фактор получается , что является свойством самого электрического поля.
Эта величина может быть вычислена в любом статическом (стационарна) или динамический (изменения со временем) электрическое полем в определенный момент времени в единицах джоулей на кулоны ( JC
В электродинамике , когда нестационарные поля присутствуют, то электрическое поле не может быть выражена только в терминах скалярного потенциала . Вместо этого, электрическое поле может быть выражено в терминах как скалярного электрического потенциала и магнитного векторного потенциала . Электрический потенциал и магнитный векторный потенциал вместе образуют четыре вектора , так что эти два вида потенциала смешивает в соответствии с преобразованиями Лоренца .
Вступление
Классическая механика исследует такие понятия, как сила , энергия , потенциальная и т.д. Сила и потенциальная энергия непосредственно связаны. Чистая сила , действующая на любой объект приведет к его ускорению . Как объект движется в направлении , в котором сила ускоряет его, его потенциальная энергия уменьшается: гравитационный потенциал энергии пушечного ядра на вершине холма больше , чем у основания холма. Как она катится вниз по склону его потенциал уменьшается энергии, переводится в движение, кинетическая энергия.
Можно определить потенциал некоторых силовых полей , так что потенциальная энергия объекта в этой области зависит только от положения объекта по отношению к полю. Два таких силовых полей являются гравитационное поле и электрическое поле (в отсутствие изменяющихся во времени магнитных полей). Такие поля должны воздействовать на объекты из — за внутренние свойства объекта (например, массы или заряды) и положение объекта.
Объекты могут обладать свойством известный как электрический заряд и электрическое поле оказывает силовое воздействие на заряженные объекты. Если заряженный объект имеет положительный заряд сила будет в направлении вектора электрического поля в этой точке , а если заряд отрицателен сила будет находиться в противоположном направлении. Величина силы определяется количеством заряда , умноженной на величину вектора электрического поля.
электростатика

Электрический потенциал в точке г в статическом электрическом поле Е определяется линией интегральной
ВЕзнак равно-∫СЕ⋅dℓ{\ Displaystyle V _ {\ mathbf {E}} = — \ Int _ {C}, \ mathbf {E} \ CDOT \ mathrm {d} {\ boldsymbol {\ ell_p}} \,}
где С представляет собой произвольный путь , соединяющий точку с нулевым потенциалом к
Езнак равно-∇ВЕ,{\ Displaystyle \ mathbf {E} = -. \ Mathbf {\ набла} V _ {\ mathbf {E}} \,}
Тогда, по закону Гаусса , потенциал удовлетворяет уравнению Пуассона :
- ∇⋅Езнак равно∇⋅(-∇ВЕ)знак равно-∇2ВЕзнак равноρ/ε0,{\ Displaystyle \ mathbf {\ наб} \ CDOT \ mathbf {Е} = \ mathbf {\ наб} \ CDOT \ влево (- \ mathbf {\ набла} V _ {\ mathbf {E}} \ справа) = — \ набла ^ {2} V _ {\ mathbf {E}} = \ Rho / \ varepsilon _ {0}, \,}
где ρ представляет общую плотность заряда ( в том числе связанного заряда ) и ∇ · обозначает дивергенцию .
Понятие электрического потенциала тесно связана с потенциальной энергией . Пробный заряд Q имеет электрическую потенциальную энергию U Е , данную
- UЕзнак равноQВ,{\ Displaystyle U _ {\ mathbf {E}} = д \, В. \,}
Потенциальная энергия и, следовательно, также электрический потенциал только определена с точностью до аддитивной константы: нужно произвольно выбрать положение, в котором потенциальная энергия и электрический потенциал равен нуль.
Эти уравнения не могут быть использованы , если завиток ∇ × E ≠ 0 , то есть, в случае неконсервативного электрического поля (вызванное изменяющимся магнитным полем , см уравнений Максвелла ). Обобщение электрического потенциала в данном случае описано ниже.
Электрический потенциал из-за точечный заряд
 Электрический потенциал , создаваемый зарядом Q является V = Q / (4πε о г ). Различные значения Q будут делать различные значения электрического потенциала V ( как показано на рисунке).
Электрический потенциал , создаваемый зарядом Q является V = Q / (4πε о г ). Различные значения Q будут делать различные значения электрического потенциала V ( как показано на рисунке).Электрический потенциал , возникающий из точечного заряда Q , на расстоянии г от заряда наблюдается быть
- ВЕзнак равно14πε0Qр,{\ Displaystyle V _ {\ mathbf {E}} = {\ гидроразрыва {1} {4 \ р \ varepsilon _ {0}}} {\ гидроразрыва {Q} {г}}, \,}
где ε 0 является диэлектрическая проницаемость вакуума . известен как потенциал Кулона . ВЕ{\ Displaystyle V _ {\ mathbf {E}}}
Электрический потенциал для системы точечных зарядов равен сумме индивидуальных потенциалов точечных зарядов. Это обстоятельство упрощает расчеты существенно, так как добавление потенциала (скалярных) полей намного проще, чем добавление электрического (вектор) полей.
Приведенное выше уравнение для электрического потенциала (и всех уравнений , используемых здесь) в формах , требуемых единицами СИ . В некоторой другой (менее распространенной) системе единиц, такие как CGS-Gaussian , многие из этих уравнений будут изменены.
Обобщение электродинамики
При изменяющемся во время магнитных полей присутствуют (что справедливо , когда есть изменяющийся во время электрических полей , и наоборот), это не невозможно описать электрическое поле просто в терминах скалярного потенциала V , поскольку электрическое поле больше не консервативное : это путь в зависимости от , потому что ( закон электромагнитной индукции Фарадея ). ∫СЕ⋅dℓ{\ Displaystyle \ TextStyle \ Int _ {C}, \ mathbf {E} \ CDOT \ mathrm {d} {\ boldsymbol {\ ell_p}}}∇×Е≠0{\ Displaystyle \ mathbf {\ Nabla} \ раз \ mathbf {E} \ NEQ \ mathbf {0}}
Вместо этого, все еще можно определить скалярный потенциал, также включая магнитные векторный потенциал A . В частности, определяются для удовлетворения:
- Взнак равно∇×A,{\ Displaystyle \ mathbf {B} = \ mathbf {\ Nabla} \ раз \ mathbf {A}, \,}
где В представляет собой магнитное поле . Поскольку дивергенция магнитного поля всегда равна нулю из — за отсутствия магнитных монополей , такой всегда можно найти. Учитывая это, количество
- Fзнак равноЕ+∂A∂T{\ Displaystyle \ mathbf {F} = \ mathbf {Е} + {\ гидроразрыва {\ парциальное \ mathbf {A}} {\ парциальное т}}}
является консервативным полем по закону Фарадея, и , следовательно , можно написать
- Езнак равно-∇В-∂A∂T,{\ Displaystyle \ mathbf {E} = — \ mathbf {\ набла} В — {\ гидроразрыва {\ парциальное \ mathbf {A}} {\ парциальное т}}, \,}
где V обозначает скалярный потенциал , определяемый консервативным поле F .
Электростатический потенциал просто частный случай этого определения , где не зависит от времени. С другой стороны, для изменяющихся во времени полей,
- -∫aбЕ⋅dℓ≠В(б)-В(a),{\ Displaystyle — \ Int _ {а} ^ {Ь} \ mathbf {E} \ CDOT \ mathrm {d} {\ boldsymbol {\ ell_p}} \ NEQ V _ {(б)} — V _ {(а)}, \}
в отличие от электростатики.
Единицы
Производные единицы СИ электрического потенциала является вольтой (в честь Алессандро Вольта ), поэтому разница в электрическом потенциале между двумя точками известна как напряжение . Старые единицы редко используются сегодня. Варианты сантиметровых грамм второй системы единиц включают в себя ряд различных устройств для электрического потенциала, в том числе abvolt и statvolt .
Гальвани потенциал по сравнению с электрохимическим потенциалом
Внутри металлов (и других твердых тел и жидкостей), энергия электрона зависит не только от электрического потенциала, но и конкретной атомной среды , что он находится. Когда вольтметр подключен между двумя различными типами металла, он измеряет не разность электрических потенциалов, но вместо того, чтобы разность потенциалов с поправкой на различные атомные среды. Количество измеряется с помощью вольтметра, называется электрохимическим потенциалом или уровень Ферми , в то время как чистый нескорректированные электрический потенциал V иногда называют Гальвани потенциал . Термины «напряжение» и «электрический потенциал» немного неоднозначные в том, что на практике, они могут относиться к любому из них в различных контекстах. φ{\ Displaystyle \ Phi}
Смотрите также
Рекомендации
дальнейшее чтение
- Politzer P, Truhlář DG (1981). Химические применения атомных и молекулярных электростатических потенциалах: Реактивность, структура, рассеяние и энергетики органических, неорганических и биологических систем . Boston, MA: Springer США. ISBN 978-1-4757-9634-6 .
- Сен К, Мюррей JS (1996). Молекулярные электростатические Потенциалы: понятия и приложение . Амстердам: Elsevier. ISBN 978-0-444-82353-3 .
- Griffiths DJ (1998). Введение в электродинамике (третий. Ред.). Prentice Hall. ISBN 0-13-805326-X .
- Джексон JD (1999). Классическая электродинамика (третья. Ред.). США: John Wiley & Sons, Inc. ISBN 978-0-471-30932-1 .
- Вангснесса РК (1986). Электромагнитные поля (второе., Перераб, иллюстрированное изд.). Wiley. ISBN 978-0-471-81186-2 .
Электродный потенциал — это… Что такое Электродный потенциал?
- Электродный потенциал
- разность электрических потенциалов между Электродом и находящимся с ним в контакте электролитом (См. Электролиты) (чаще всего между металлом и раствором электролита). Возникновение Э. п. обусловливается переносом заряженных частиц через границу раздела фаз, специфической адсорбцией ионов, а при наличии полярных молекул (в том числе молекул растворителя) — ориентационной адсорбцией их. Величина Э. п. в неравновесном состоянии зависит как от природы и состава контактирующих фаз, так и от кинетических закономерностей электродных реакций на границе раздела фаз.
Равновесное значение скачка потенциалов на границе раздела электрод/раствор определяется исключительно особенностями электродной реакции и не зависит от природы электрода и адсорбции на нём поверхностно-активных веществ. Эту абсолютную разность потенциалов между точками, находящимися в двух разных фазах, нельзя измерить экспериментально или рассчитать теоретически. Практическое значение имеют относительные Э. п., обычно называемые просто Э. п., представляющие собой разность Э. п. рассматриваемого электрода и электрода сравнения — чаще всего нормального водородного электрода (См. Водородный электрод), Э. п. которого условно принимается равным нулю.
При электрохимическом равновесии на электроде величина Э. п. (E) может быть выражена через изменение гиббсовой энергии (См. Гиббсова энергия) (ΔG) реакции: Е = —ΔG/zF, где z — число электронов, участвующих в электрохимическом процессе, F — Фарадея число. Э. п. в этом случае зависит от активности (а) участвующих в реакции веществ (потенциалопределяющих веществ). Для электродов Me/Men+Е = E0 + (RT/zF) ln aMen+, где R — газовая постоянная, Т — температура, E0 — Нормальный потенциал. Для окислительно-восстановительных систем с инертным электродом, у которых все компоненты электрохимической реакции находятся в растворе, Э. п. (Окислительно-восстановительный потенциал) определяется активностями как окисленной (aok), так и восстановленной (ав) форм вещества:

,
где ν — стехиометрический коэффициент.
В случае, когда на электроде возможно одновременное протекание более одной электродной реакции, используется понятие стационарного Э. п. При пропускании электрического тока измеренный Э. п. будет отличаться от равновесного на величину поляризации (см. Поляризация электрохимическая).В. В. Городецкий.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Электродные процессы
- Электродоменная печь
Смотреть что такое «Электродный потенциал» в других словарях:
ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ — разность электрических потенциалов (напряжений) между электродом и находящимся с ним в контакте электролитом. Появление Э. п. вызвано образованием у поверхности электрода двойного электрического слоя. На практике используют значения так… … Большая политехническая энциклопедия
ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ — в электрохимии разность электрических потенциалов на границе фаз электрод электролит. На практике пользуются значениями т. н. относительного электродного потенциала, равного разности электродного потенциала, данного электрода и электрода… … Большой Энциклопедический словарь
ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ — ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ, мера способности электрода вступать в реакцию. Электрод из элемента М, помещенный в раствор его ионов (М+), представляет собой ПОЛУЭЛЕМЕНТ. Теоретически в ходе реакций типа ММ++е между электродом и раствором всегда… … Научно-технический энциклопедический словарь
Электродный потенциал — мера способности электрода вступать в реакцию. Между электродом и раствором всегда образуется разность потенциалов. Стандартные потенциалы электродов определяют относительно водородного электрода при определенных величинах температуры,… … Официальная терминология
электродный потенциал — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN electrode potentialelectrolytic potentialelectropolarization… … Справочник технического переводчика
электродный потенциал — [electrode potential] разность электрических потенциалов между электродами и находящимся с ним в контакте электролитом (чаще всего между металлом и раствором электролита). Практическое значение имеют относительные электродные потенциалы,… … Энциклопедический словарь по металлургии
электродный потенциал — 3.8 электродный потенциал: Мера способности электрода вступать в реакцию. Между электродом и раствором всегда образуется разность потенциалов. Стандартные потенциалы электродов определяют относительно водородного электрода при определенных… … Словарь-справочник терминов нормативно-технической документации
Электродный потенциал — У этого термина существуют и другие значения, см. Потенциал. Электродный потенциал разность электрических потенциалов между электродом и находящимся с ним в контакте электролитом (чаще всего между металлом и раствором электролита). Возникновение… … Википедия
Электродный потенциал — Electrode potential Электродный потенциал. Потенциал электрода в электролизе измеренный относительно электрода сравнения. В электродный потенциал не входят потери противодействия потенциалу, как в растворе, так и внешней цепи. Он представляет… … Словарь металлургических терминов
электродный потенциал — elektrodo potencialas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas potencialų skirtumu, susidarančiu tarp joninės terpės (elektrolito tirpalo ar lydalo) ir į ją įdėto elektrodo. atitikmenys: angl. electrode… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электродный потенциал — elektrodo potencialas statusas T sritis Standartizacija ir metrologija apibrėžtis Elektrodo potencialas kito kūno arba terpės, kurioje jis yra, atžvilgiu. atitikmenys: angl. electrode potential vok. Elektrodenpotential, n rus. потенциал электрода … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Электродный потенциал — это… Что такое Электродный потенциал?
У этого термина существуют и другие значения, см. Потенциал.Электро́дный потенциа́л — разность электрических потенциалов между электродом и находящимся с ним в контакте электролитом (чаще всего между металлом и раствором электролита).
Возникновение электродного потенциала обусловлено переносом заряженных частиц через границу раздела фаз, специфической адсорбцией ионов, а при наличии полярных молекул (в том числе молекул растворителя) — ориентационной адсорбцией их. Величина электродного потенциала в неравновесном состоянии зависит как от природы и состава контактирующих фаз, так и от кинетических закономерностей электродных реакций на границе раздела фаз.
Равновесное значение скачка потенциалов на границе раздела электрод/раствор определяется исключительно особенностями электродной реакции и не зависит от природы электрода и адсорбции на нём поверхностно-активных веществ. Эту абсолютную разность потенциалов между точками, находящимися в двух разных фазах, нельзя измерить экспериментально или рассчитать теоретически.
Измерение потенциалов
Практическое значение имеют относительные электродные потенциалы, обычно называемые просто электродные потенциалы, представляющие собой разность электродных потенциалов рассматриваемого электрода и электрода сравнения — чаще всего нормального водородного электрода, электродный потенциал которого условно принимается равным нулю (для водных систем).
Способы устранения омической составляющей при измерении
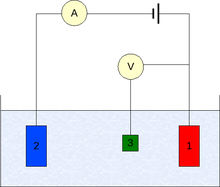 Трёхэлектродная схема
Трёхэлектродная схема- Компенсационная схема
- Трёхэлектродная схема
См. также
Электромагнитный потенциал — это… Что такое Электромагнитный потенциал?
У этого термина существуют и другие значения, см. Потенциал.В современной физике электромагни́тный потенциа́л обычно означает четырехмерный потенциал электромагнитного поля, являющийся 4-вектором (1-формой). Именно в связи с векторным (4-векторным) характером электромагнитного потенциала электромагнитное поле относится к классу векторных полей в том смысле, который употребляется в современной физике по отношению к фундаментальным бозонным полям (например, гравитационное поле является в этом смысле не векторным, а тензорным полем).
- Обозначается электромагнитный потенциал чаще всего или , что подразумевает величину с индексом, имеющую четыре компоненты или , причём индексом 0 как правило обозначается временная компонента, а индексами 1, 2, 3 — три пространственных. В этой статье мы будем придерживаться первого обозначения.
- В современной литературе могут использоваться более абстрактные обозначения.
В любой определенной инерциальной системе отсчета электромагнитный потенциал распадается[1] на скалярный (в трехмерном пространстве) потенциал и трехмерный векторный потенциал ; эти потенциалы и — и есть те скалярный и векторный потенциалы, которые используются в традиционной трехмерной формулировке электродинамики. В случае, когда электромагнитное поле не зависит от времени (или быстротой его изменения в конкретной задаче можно пренебречь), то есть в случае (приближении) электростатики и магнитостатики, напряженность электрического поля выражается через ф, называемый в этом случае электростатическим потенциалом, а напряженность магнитного поля (магнитная индукция)[2] — только через векторный потенциал. Однако в общем случае (когда поля меняются со временем) в выражение для электрического поля входит также и векторный потенциал, тогда как магнитное — всегда выражается лишь через векторный (нулевая компонента электромагнитного потенциала в это выражение не входит).
Связь напряжённостей с электромагнитным потенциалом в общем случае такова в традиционных трехмерных векторных обозначениях[3]:
где — напряженность электрического поля, — магнитная индукция (или — что в случае вакуума в сущности то же самое — напряженность магнитного поля), — оператор набла, причём — градиент скалярного потенциала, а — ротор векторного потенциала.
В несколько более современной четырехмерной формулировке эти же соотношения можно записать как выражение тензора электромагнитного поля через 4-вектор электромагнитного потенциала:
где — тензор электромагнитного поля, компоненты которого представляют собой компоненты .
Приведенное выражение является обобщением выражения ротора для случая четырехмерного векторного поля.
При переходе от одной инерциальной системы отсчета к другой, компоненты преобразуются, как это свойственно компонентам 4-вектора, посредством преобразований Лоренца.
Физический смысл
Физический смысл четырехмерного электромагнитного потенциала можно прояснить, заметив, что этот потенциал при взаимодействии с заряженной частицей[4] (с электрическим зарядом q) дает добавку в фазу ее квантовой волны вероятности:
- ,
или, иначе говоря, вклад в действие (формула отличается от записанной выше только отсутствием множителя , а в системе единиц, где — просто совпадает с ней).
Физический смысл электрического и магнитного потенциалов в более простом частном случае электростатики и магнитостатики, а также единицы измерения этих потенциалов обсуждаются в статьях Электростатический потенциал и Векторный потенциал электромагнитного поля.
Примечания
- ↑ В данной записи использовано ковариантное представление электромагнитного потенциала в сигнатуре лоренцевой метрики (+—), используемое и в других формулах статьи. Контравариантное представление отличается от ковариантного в лоренцевой метрике (такой сигнатуры) лишь знаком трёх пространственных компонент. В представлении с мнимой временной компонентой (в формально евклидовой метрике) электромагнитный потенциал всегда записывается в одинаковом виде: .
- ↑ В этой статье мы рассматриваем лишь поля в вакууме, поэтому напряженность магнитного поля и магнитная индукция в сущности не различаются (правда, в некоторых системах единиц, например, в СИ, они имеют разную размерность, но даже в таких единицах в вакууме отличаются друг от друга лишь постоянным множителем).
- ↑ В зависимости от используемой системы физических единиц, в эти формулы, а также в формулы, связывающие четырехмерный электромагнитный потенциал с трехмерными векторным потенциалом и скалярным потенциалом, могут входить различные размерные постоянный коэффициенты; мы для простоты приводим формулы в системе единиц, где скорость света равна единице, и все скорости безразмерны.
- ↑ Имеется в виду точечная частица без магнитного момента.
См. также
Электронные потенциалы и электродвижущие силы
При решении задач этого раздела см. табл. 8,
Если металлическую пластинку опустить в воду, то катионы металла на ее поверхности гидратируются полярными молекулами воды и переходят в жидкость. При этом электроны, в избытке остающиеся в металле, заряжают его поверхностный слой отрицательно. Возникает электростатическое притяжение между перешедшими в жидкость гидратированными катионами и поверхностью металла. В результате этого в системе устанавливается подвижное равновесие:
Me
+ mH2O
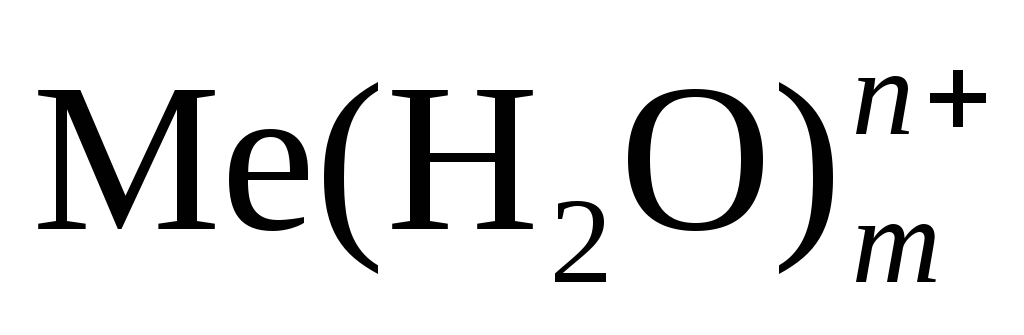 + ne–
+ ne–
в растворе на металле
где п – число электронов, принимающих участие в процессе. На границе металл – жидкость возникает двойной электрический слой, характеризующийся определенным скачком потенциала – электродным потенциалом. Абсолютные значения электродных потенциалов измерить не удается. Электродные потенциалы зависят от ряда факторов (природы металла, концентрации, температуры и др.). Поэтому обычно определяют относительные электродные потенциалы в определенных условиях – так называемые стандартные электродные потенциалы (Е°).
Стандартным электродным потенциалом металла называют его электродный потенциал, возникающий при погружении металла в раствор собственного иона с концентрацией (или активностью), равной 1 моль/л, измеренный по сравнению со стандартным водородным электродом, потенциал которого при 25°С условно принимается равным нулю (Е° = 0; DG° = 0).
Располагая металлы в ряд по мере возрастания их t стандартных электродных потенциалов (E°), получаем так называемый ряд напряжений.
Положение того или иного металла в ряду напряжений характеризует его восстановительную способность, а также окислительные свойства его ионов в водных растворах при стандартных условиях. Чем меньше значение E°, тем большими восстановительными способностями обладает данный металл в виде простого вещества, и тем меньшие окислительные способности проявляют его ионы, и наоборот. Электродные потенциалы измеряют в приборах, которые получили название гальванических элементов. Окислительно-восстановительная реакция, которая характеризует работу гальванического элемента, протекает в направлении, в котором ЭДС элемента имеет положительное значение. В этом случае DG° < 0, так как DG° = = – nFE°.
Пример 1. Стандартный электродный потенциал никеля больше, чем кобальта (табл. 8) . Изменится ли это соотношение, если измерить потенциал никеля в растворе его ионов с концентрацией 0,001 моль/л, а потенциалы кобальта – в растворе с концентрацией 0,1 моль/л?
Таблица 8.
Стандартные электродные потенциалы (e°) некоторых металлов (ряд напряжений)
Электрод | E°, В | Электрод | E°, В |
Li+/Li | -3,045 | Cd2+/Cd | -0,403 |
Rb+/Rb | -2,925 | Co2+/Co | -0,277 |
K+/K | -2,924 | Ni2+/Ni | -0,25 |
Cs+/Cs | -2,923 | Sn2+/Sn | -0,136 |
Ba2+/Ba | -2,90 | Pb2+/Pb | -0,127 |
Ca2+/Ca | -2,87 | Fe3+/Fe | -0,037 |
Na+/Na | -2,714 | 2H+/H2 | -0,000 |
Mg2+/Mg | -2,37 | Sb3+/Sb | +0,20 |
Al3+/Al | -1,70 | Bi3+/Bi | +0,215 |
Ti2+/Ti | -1,603 | Cu2+/Cu | +0,34 |
Zr4+/Zr | -1,58 | Cu+/Cu | +0,52 |
Mn2+/Mn | -1,18 | Hg2+2/2Hg | +0,79 |
V2+/V | -1,18 | Ag+/Ag | +0,80 |
Cr2+/Cr | -0,913 | Hg2+/Hg | +0,85 |
Zn2+/Zn | -0,763 | Pt2+/Pt | +1,19 |
Cr3+/Cr | -0,74 | Au3+/Au | +1,50 |
Fe2+/Fe | -0,44 | Au+/Au | +1,70 |
Решение. Электродный потенциал метала (E) зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:
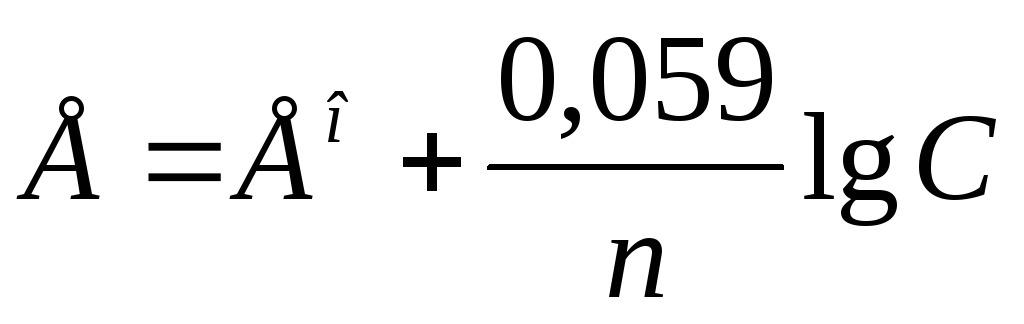 ,
,
где E° – стандартный электродный потенциал; n – число электронов, принимающих участие в процессе; С – концентрация (при точных вычислениях – активность) гидратированных ионов металла в растворе, моль/л; E° для никеля и кобальта соответственно равны -0,25 и -0,277 В. Определим электродные потенциалы этих металлов при данных в условии концентрациях:
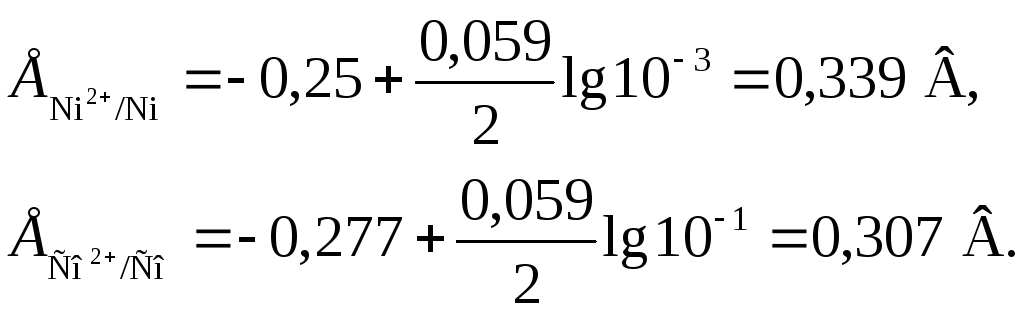
Таким образом, при изменившейся концентрации потенциал кобальта стал больше потенциала никеля.
Пример 2. Магниевую пластинку опустили в раствор его соли. При этом электродный потенциал магния оказался равен -2,41 В. Вычислите концентрацию ионов магния (в моль/л).
Решение. Подобные задачи также решаются на основании уравнения Нернста (см. пример 1):
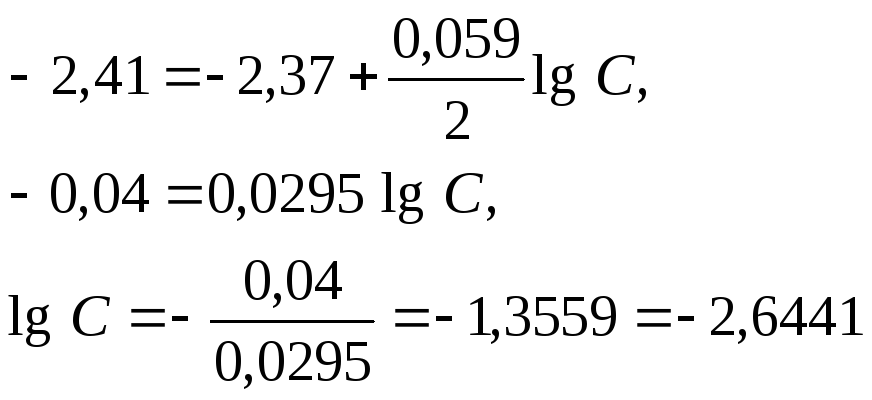
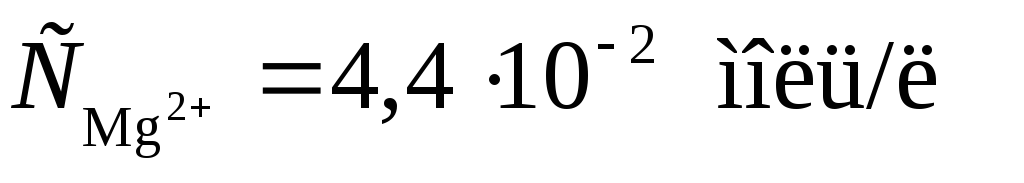 .
.
Пример 3. Составьте схему гальванического элемента, в котором электродами являются магниевая и цинковая пластинки, опущенные в растворы их ионов с активной концентрацией 1 моль/л. Какой металл является анодом, какой катодом? Напишите уравнение окислительно-восстановительной реакции, протекающей в этом гальваническом элементе, и вычислите его ЭДС.
Решение. Схема данного гальванического элемента
(–) Mg |Mg2+| |Zn2+| Zn (+)
Вертикальная линейка обозначает поверхность раздела между металлом и раствором, а две линейки – границу раздела двух жидких фаз – пористую перегородку (или соединительную трубку, заполненную раствором электролита). Магний имеет меньший потенциал (–2,37 в) и является анодом, на котором протекает окислительный процесс:
Mg0 – 2e– = Mg2+ (1)
Цинк, потенциал которого -0,763 В, – катод, т.е. электрод, на котором протекает восстановительный процесс:
Zn2++2е– = Zn0 (2)
Уравнение окислительно-восстановительной реакции, характеризующее работу данного гальванического элемента, можно получить, сложив электронные уравнения анодного (1) и катодного (2) процессов:
Mg + Zn2+ = Mg2+ + Zn
Для определения ЭДС гальванического элемента из потенциала катода следует вычесть потенциал анода. Так как концентрация ионов в растворе равна 1 моль/л, то ЭДС элемента равна разности стандартных потенциалов двух его электродов:
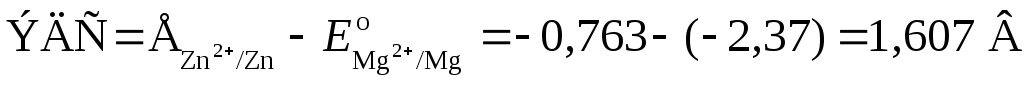 .
.




