Т. Потенциал — PhysBook
Потенциал
Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система «заряд — электростатическое поле» обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:
\(~A_{12} = -(W_{p2} — W_{p1}) = W_{p1} — W_{p2} . \qquad (1)\)Если Wp2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда q0 равна работе, которая была бы совершена при перемещении заряда q0 из данной точки в точку с нулевой энергией.
Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q (рис. 2).
Рис. 2
Будем помещать в точку Μ этого поля различные пробные положительные заряды
Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).
Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд, помещенный в эту точку, к значению заряда.
Потенциал — это энергетическая характеристика поля в отличие от напряженности поля, являющейся силовой характеристикой поля.
Необходимо отметить, что потенциальная энергия заряда в данной точке поля, а значит, и потенциал зависят от выбора нулевой точки. Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.
Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал можно определить только с точностью до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.
В технике принято считать нулевой точкой любую заземленную точку, т.е. соединенную проводником с землей. В физике за начало отсчета потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если нулевая точка выбрана, то потенциальная энергия (соответственно и потенциал в данной точке) заряда
На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой
\(~\varphi = \frac{q}{4 \pi \varepsilon_0 \varepsilon r} .\)При указанном выше выборе нулевой точки потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:
еслиПо этой формуле можно рассчитывать потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R в точках, находящихся на поверхности сферы и вне ее. Внутри сферы потенциал такой же, как и на поверхности, т.е.
\(~\varphi = \frac{q}{4 \pi \varepsilon_0 \varepsilon R}\) при r ≤ R и \(~\varphi = \frac{q}{4 \pi \varepsilon_0 \varepsilon r}\) при r > R .Если электростатическое поле создается системой зарядов, то имеет место принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности
Зная потенциал φ поля в данной точке, можно рассчитать потенциальную энергию заряда q0 помещенного в эту точку: Wp1 = q0φ. Если положить, что Wp2 = 0, то из уравнения (1) будем иметь
\(~A_{1\infty} = W_{p1} = q_0 \varphi_1 .\)Потенциальная энергия заряда q0 в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q0 из данной точки в нулевую. Из последней формулы имеем
\(~\varphi_1 = \frac{A_{1\infty}}{q_0} .\)Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в нулевую (в бесконечность).
Потенциальная энергия заряда q0 помещенного в электростатическое поле точечного заряда q на расстоянии r от него,
\(~W_p = \frac{qq_0}{4 \pi \varepsilon_0 \varepsilon r} .\)Если q и q0 — одноименные заряды, то Wp > 0, если q и q0 — разные по знаку заряды, то Wp < 0.
Отметим еще раз, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение Wp выбрано ее значение при r = ∞.
Если электростатическое поле образовано системой n точечных электрических зарядов, то потенциальная энергия системы определяется по формуле
\(~W = \frac 12 \sum_{i=1}^n q_i \varphi_i ,\)где φi — потенциал поля, созданного всеми зарядами, кроме заряда qi, в той точке поля, где находится заряд qi.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 229-231.
ПОТЕНЦИАЛ (в физике) — это… Что такое ПОТЕНЦИАЛ (в физике)?
- ПОТЕНЦИАЛ (в физике)
- ПОТЕНЦИАЛ (в физике) ПОТЕНЦИА́Л (потенциальная функция), понятие, характеризующее широкий класс физических силовых полей (электрических, гравитационных и т. п.) и вообще поля физических величин, представляемых векторами (поле скоростей жидкости и т. п.). В общем случае потенциал векторного поля a(x,y,z) — такая скалярная функция u(x,y,z), что a=grad u (см. Градиент (см. ГРАДИЕНТ)).
Энциклопедический словарь. 2009.
- ПОТЕМКИН Петр Петрович
- ПОТЕНЦИАЛ (источники, возможности)
Смотреть что такое «ПОТЕНЦИАЛ (в физике)» в других словарях:
Потенциал Юкавы — модельный потенциал для описания сильного взаимодействия между адронами. Энергия взаимодействия между адронами, выраженная через потенциал Юкавы, выглядит где g константа, задающая интенсивность ядерного взаимодействия, k постоянная с… … Википедия
Потенциал (средства) — Потенциал (от лат. potentia сила), в широком смысле средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой либо задачи; … Большая советская энциклопедия
ПОТЕНЦИАЛ — (потенциальная функция) (от лат. potentia сила), хар ка векторных полей, к к рым относятся мн. силовые поля (эл. магн., гравитационное), а также поле скоростей в жидкости и т. п. Если П. векторного поля а(r) скалярная ф ция j(r), такая, что… … Физическая энциклопедия
потенциал — 1. В физике величина, характеризующая в данной точке силовое поле электрическое, магнитное, гравитационное и пр. Соответственно различаются потенциал электрический, магнитный и пр. 2. Совокупность наличных средств, возможностей в некоей области,… … Большая психологическая энциклопедия
Потенциал — Содержание 1 Биология 2 Математика 3 Физика и химия 4 Лингвистика … Википедия
Потенциал (журнал) — У этого термина существуют и другие значения, см. Потенциал … Википедия
Потенциал — I Потенциал (от лат. potentia сила) в широком смысле средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой… … Большая советская энциклопедия
ПОТЕНЦИАЛ — потенциальная функция, одна из характеристик векторного поля. Скалярный потенциал скалярная функция v(M).такая, что a=gradv(M).во всех точках области задания поля а (М).(иногда, напр, в физике, П. наз. величину, противоположную по знаку). Если… … Математическая энциклопедия
Потенциал — в широком смысле средства, запасы, источники, имеющиеся в наличии, а также средства, которые могут быть мобилизованы, приведены в действие, использованы для достижения определенной цели, решения какой либо задачи; возможности отдельного лица,… … Краткий словарь оперативно-тактических и общевоенных терминов
ПОТЕНЦИАЛ — (от лат. potentia сила) в физике понятие, характеризующее физ. силовые поля (электрич., магн., гравитац.) и вообще поля векторных физ величин (напр., поле скоростей в жидкости). П. представляет собой вспомогат. скалярную или векторную функцию, т … Большой энциклопедический политехнический словарь
Книги
- Статистическая физика сложных систем. От фракталов до скейлинг-поведения. Выпуск 57, Абаимов С.Г.. Многообразие происходящих в природе явлений, на первый взгляд, не подчиняется каким-то унифицированным принципам, и каждое явление требует введения своих законовописания поведения. Однако… Подробнее Купить за 1225 грн (только Украина)
- Статистическая физика сложных систем. От фракталов до скейлинг-поведения, С. Г. Абаимов. Многообразие происходящих в природе явлений, на первый взгляд, не подчиняется каким-то унифицированным принципам, и каждое явление требует введения своих законовописания поведения. Однако… Подробнее Купить за 1039 руб
- Статистическая физика сложных систем. От фракталов до скейлинг-поведения. Выпуск № 57, Абаимов С.Г.. Многообразие происходящих в природе явлений, на первый взгляд, не подчиняется каким-то унифицированным принципам, и каждое явление требует введения своих законовописания поведения. Однако… Подробнее Купить за 947 руб
Потенциал электрического поля
Электростатическое поле точечного заряда – центральное, поэтому оно потенциально. В силу принципа суперпозиции потенциально любое электростатическое поле.
Потенциальная энергия заряда в электростатическом поле (Wp) – физическая величина, равная работе электростатического поля при перемещении заряда из его положения на нулевой уровень. Как правило, в электростатике принимается, что нулевой уровень находится на бесконечности.
Работа перемещения заряда в электростатическом поле равна изменению потенциальной энергии заряда, взятому с противоположным знаком: A = – (Wp2 – Wp1).
Потенциал электростатического поля (j) – физическая величина, равная отношению потенциальной энергии заряда в поле к его значению.
Потенциал – величина скалярная. За его единицу в системе СИ принимается вольт (1 В = 1 Дж/Кл).
Принцип суперпозиции для потенциала. Потенциал электростатического поля, одновременно создаваемого в некоторой точке пространства несколькими зарядами, равна сумме потенциалов электростатических полей, которые создавались бы в этой же точке каждым из зарядов по отдельности
Эквипотенциальная поверхность – поверхность, во всех точках которой потенциал имеет одинаковые значения. Для поля точечного заряда эквипотенциальными поверхностями являются сферы с центром в точке расположения заряда.
Работа
электрического поля на криволинейном
участке траектории
.
Циркуляция электростатического поля
на замкнутой траектории  .
Потенциал электростатического поля
точечного заряда
.
Потенциал электростатического поля
точечного заряда 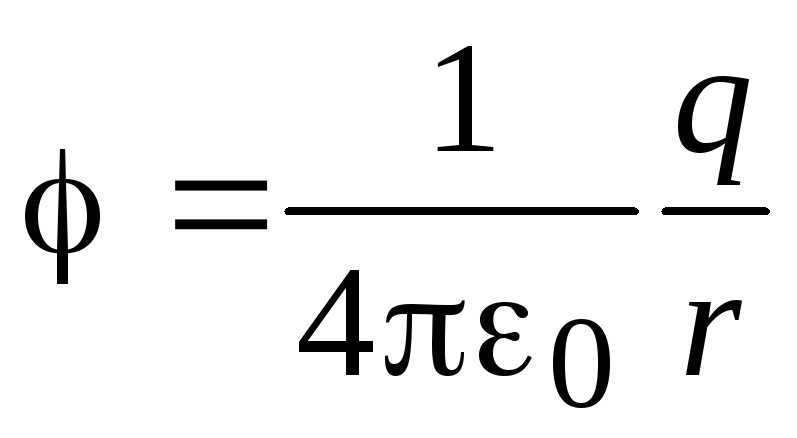
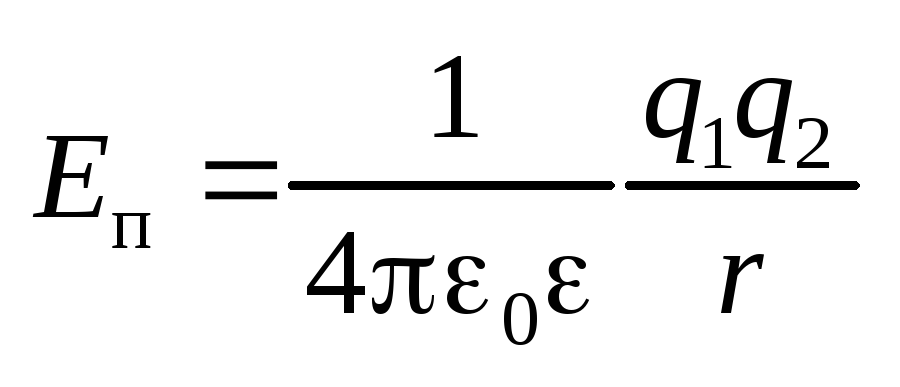 .
Потенциал электростатического поля
(определение)
.
Потенциал электростатического поля
(определение) 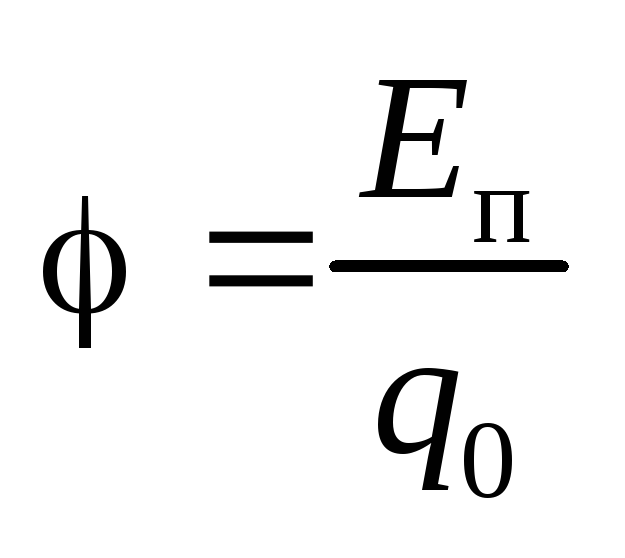 .
Связь работы электростатического поля
с разностью потенциалов
.
Связь работы электростатического поля
с разностью потенциалов 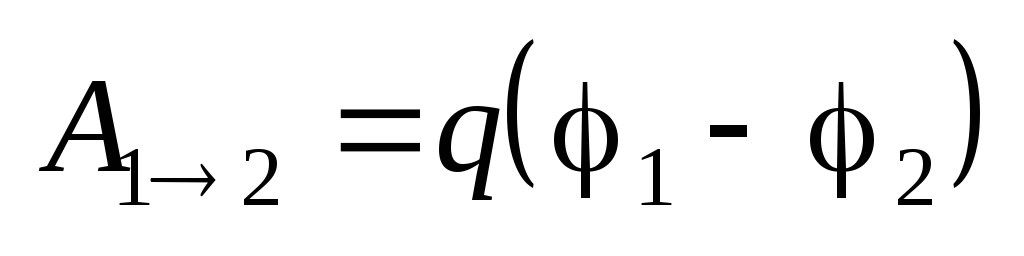 .
Выражение потенциала поля через работу
пробного заряда
.
Выражение потенциала поля через работу
пробного заряда 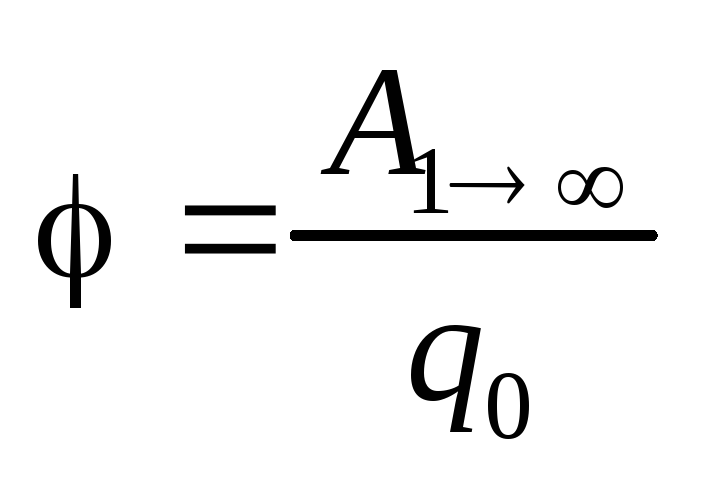
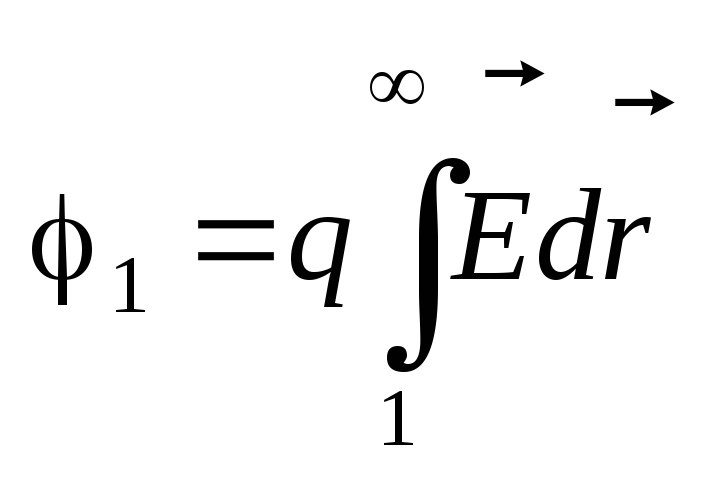 .
Расчет напряженности поля по распределению
потенциала
.
Расчет напряженности поля по распределению
потенциала 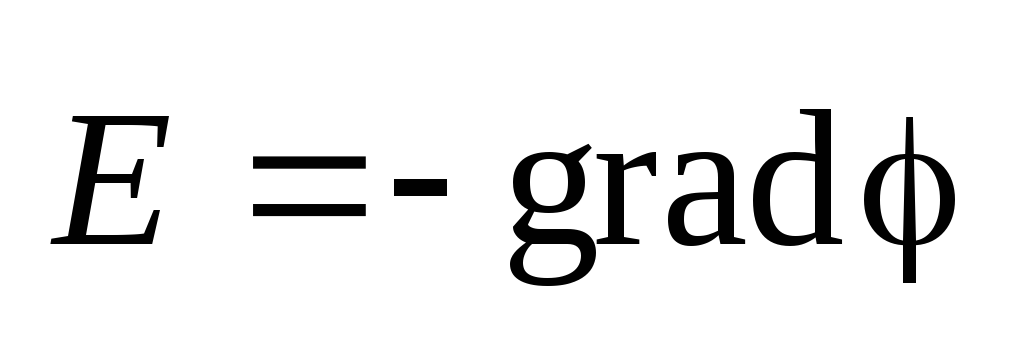 .
Связь между напряжением и напряженностью
для однородного поля
.
Связь между напряжением и напряженностью
для однородного поля 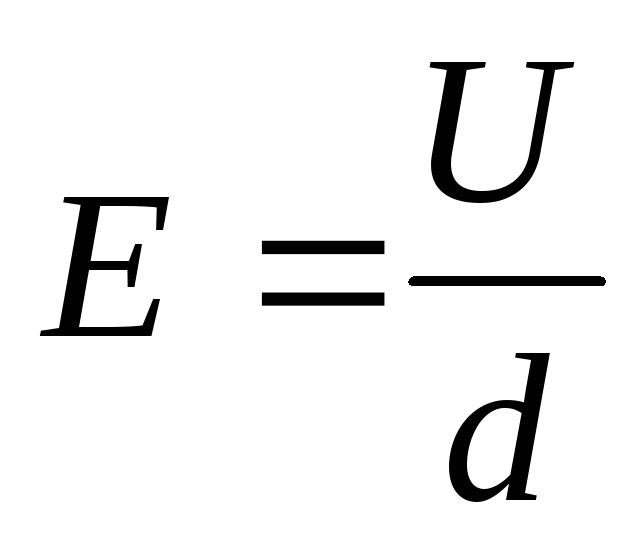 .
Дипольный момент электрического диполя
.
Дипольный момент электрического диполя  .
Момент сил, действующих на электрический
диполь в электрическом поле
.
Момент сил, действующих на электрический
диполь в электрическом поле 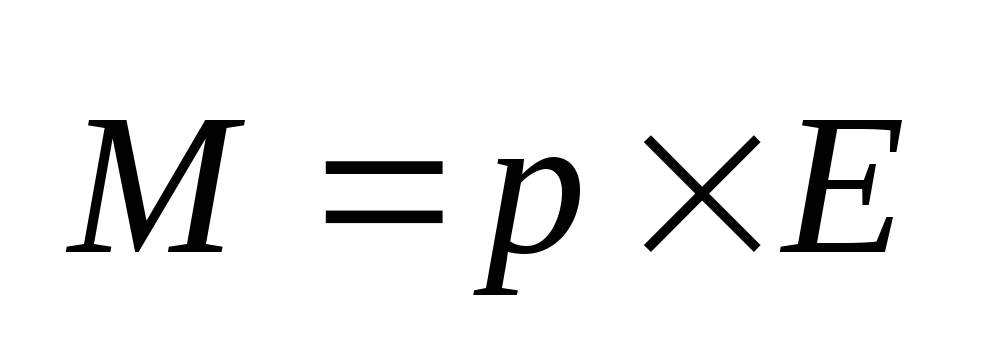
 .
Потенциальная энергия электрического
диполя во внешнем электрическом поле
.
Потенциальная энергия электрического
диполя во внешнем электрическом поле 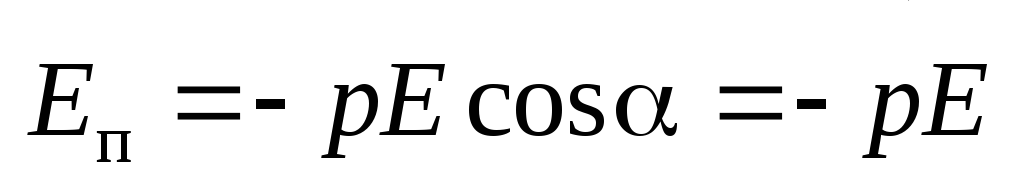 .
.Проводник в электростатическом поле
Проводники – вещества, в которых имеются свободные заряды, способные перемещаться под действием электрического поля.
Электростатическая индукция – явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле.
Свободные заряды в проводнике, находящемся во внешнем электростатическом поле, перераспределяются так, что создаваемое ими собственное поле компенсирует внешнее, в результате чего напряженность результирующего поля в проводнике становится равной нулю. На этом явлении основана
Конденсатор – устройство для накопления значительных по величине разноименных электрических зарядов. Конденсатор состоит из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Электроемкость конденсатора – физическая величина, равная отношению заряда одной из пластин конденсатора (по модулю) к напряжению между его обкладками.
Свойства
электростатического поля внутри
проводника 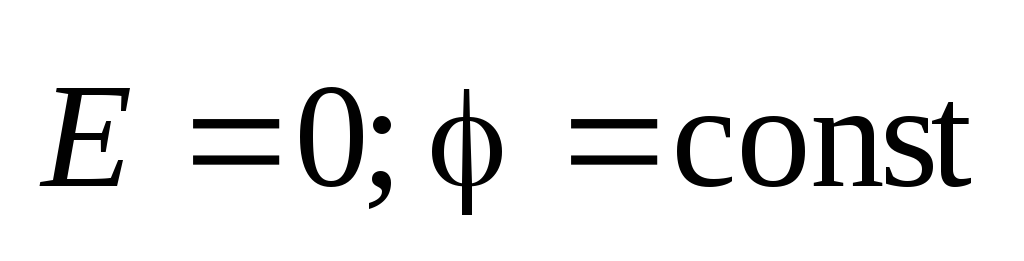 .
Свойства электростатического поля вне
проводника около его поверхности
.
Свойства электростатического поля вне
проводника около его поверхности 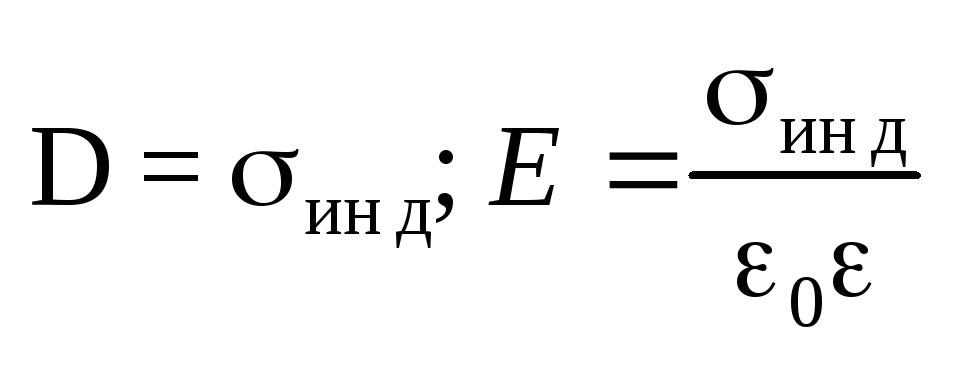 .
Электроемкость уединенного проводника
(определение)
.
Электроемкость уединенного проводника
(определение) 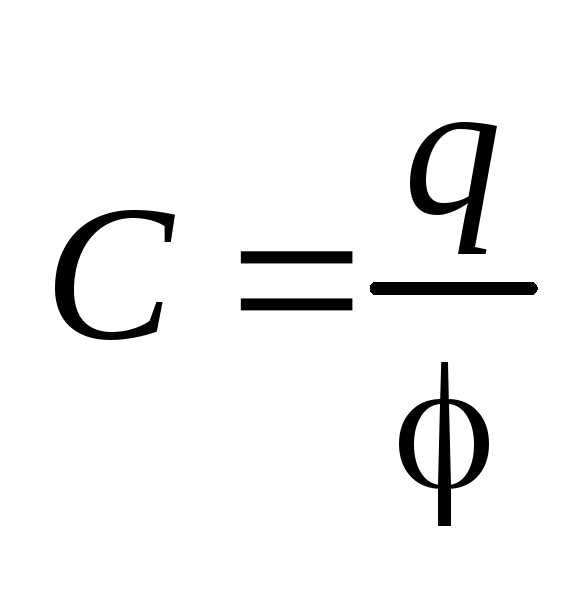 .
Электроемкость шара
.
Электроемкость шара  .
Электроемкость конденсатора (определение)
.
Электроемкость конденсатора (определение) 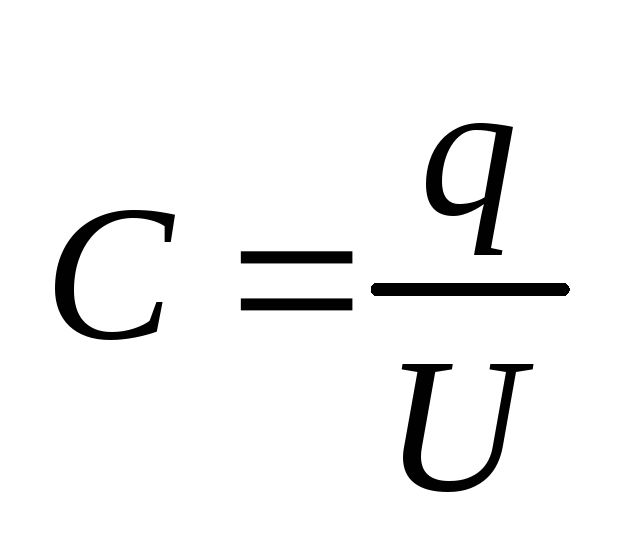
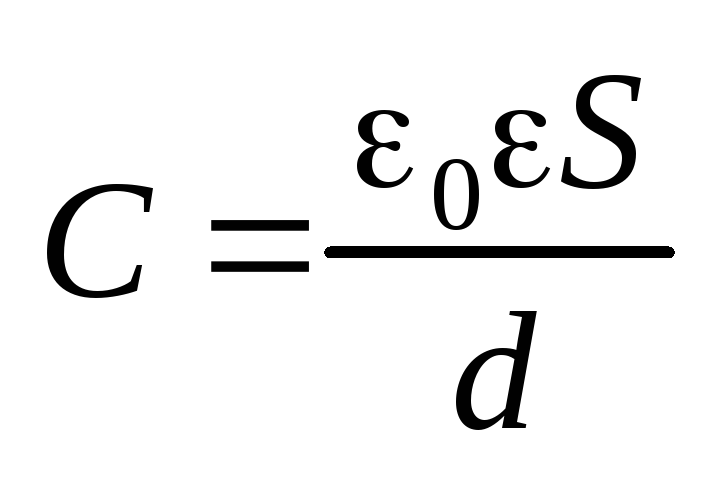 .
Электроемкость цилиндрического
конденсатора
.
Электроемкость цилиндрического
конденсатора 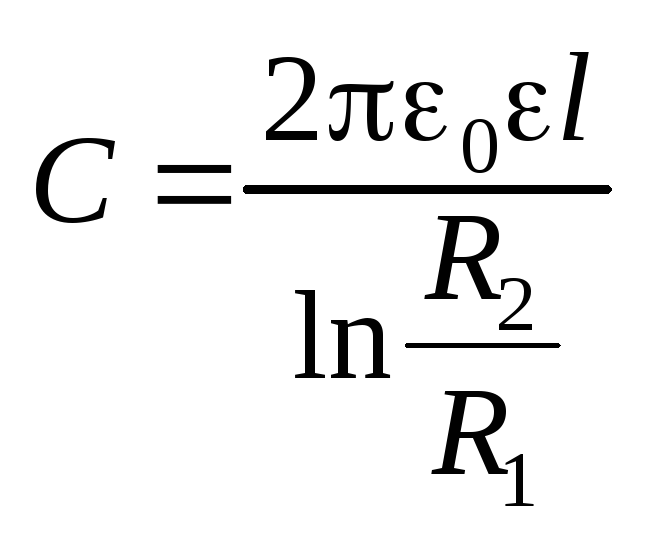 .
Электроемкость сферического конденсатора
.
Электроемкость сферического конденсатора 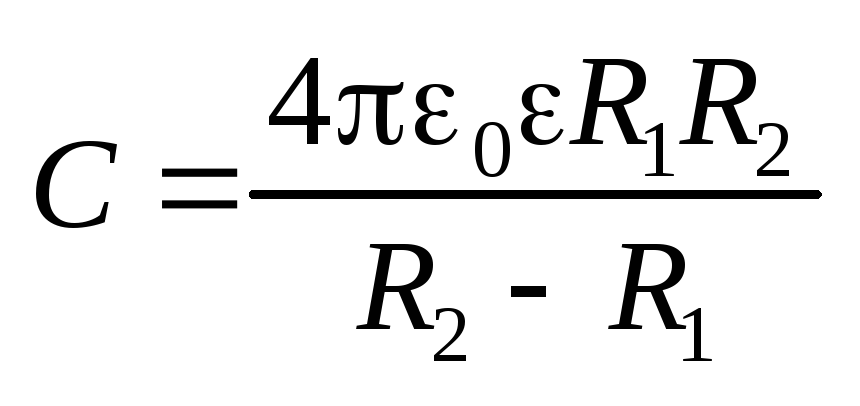 .
Электроемкость параллельно соединенных
конденсаторов
.
Электроемкость параллельно соединенных
конденсаторов 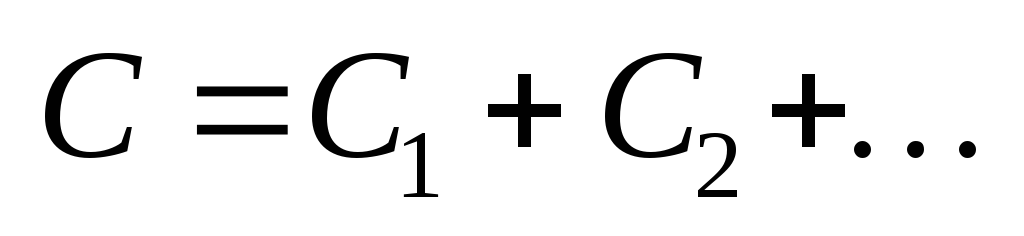 .
Электроемкость последовательно
соединенных конденсаторов
.
Электроемкость последовательно
соединенных конденсаторов 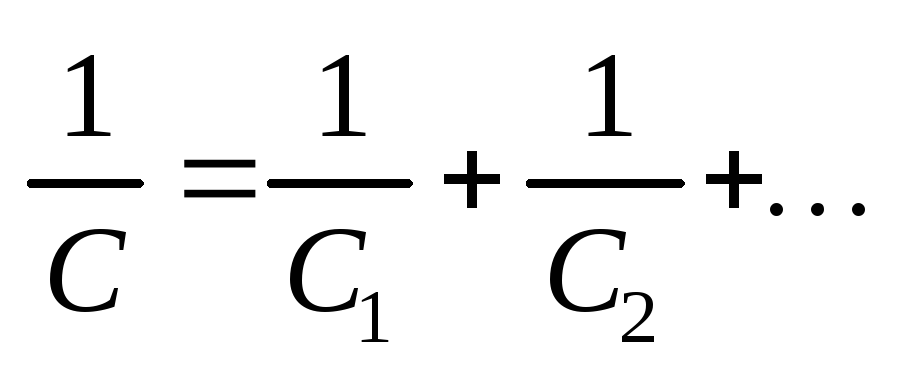 .
Потенциальная энергия системы
электрических зарядов
.
Потенциальная энергия системы
электрических зарядов 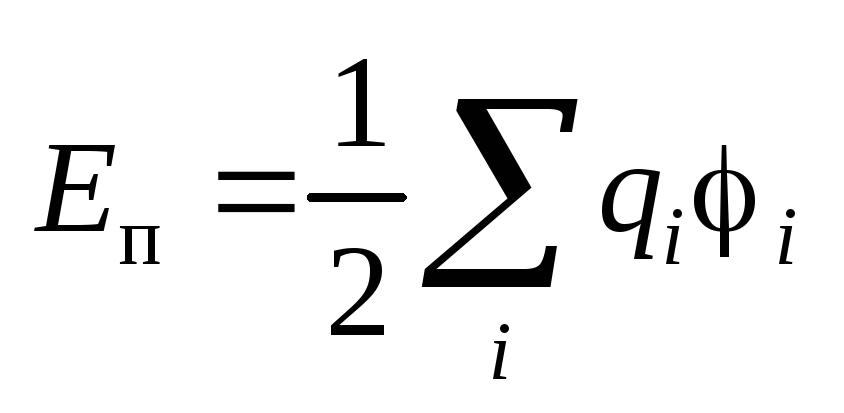 .
Потенциальная энергия уединенного
проводника
.
Потенциальная энергия уединенного
проводника 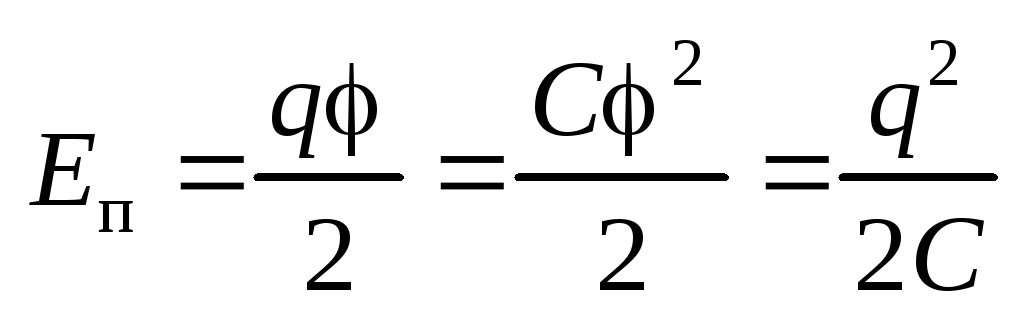 .
Потенциальная энергия конденсатора
.
Потенциальная энергия конденсатора 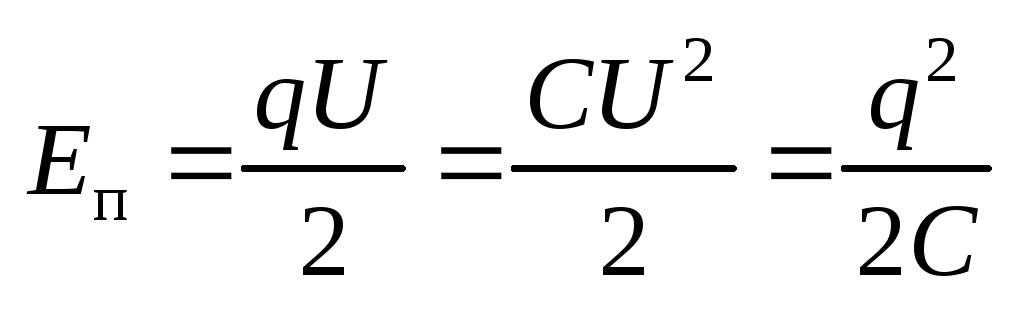 .
Объемная плотность энергии электрического
поля
.
Объемная плотность энергии электрического
поля 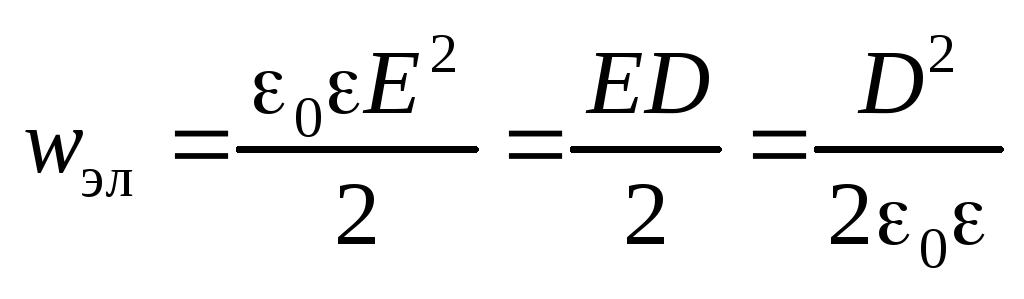 .
Условия на границе раздела двух
диэлектриков
.
Условия на границе раздела двух
диэлектриков 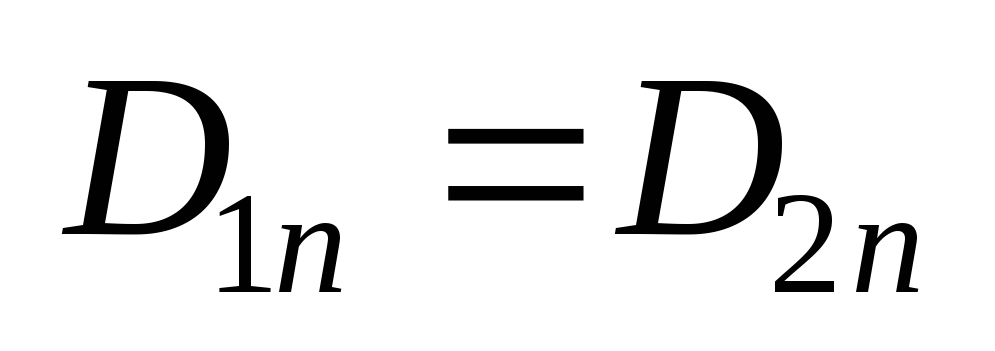 ;
; 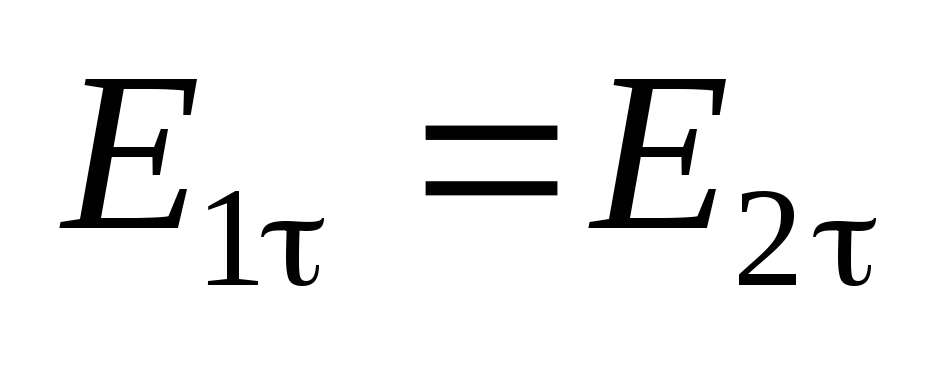 .
.
|
|
|
Плоский конденсатор | Параллельное соединение | Последовательное соединение |
Понятие потенциала — fiziku5.ru
то есть мы видим, что в рассматриваемом случае это действительно так (вектор отсчитывается от источника).
Мы так подробно обсуждаю центральность поля точечного заряда, потому что центральное поле обладает замечательным свойством: оно потенциально. Определение потенциальности в отношении силового поля давалось в механике, там где шла речь о потенциальной энергии. Сейчас, опираясь на уже полученные знания, нам будет легко обобщить понятие потенциальности на любые (не обязательно силовые) векторные поля.
Определение: контурный интеграл векторного поля по замкнутому контуру L:
называется циркуляцией. Форма контура значения не имеет.
Потенциальным называется векторное поле, циркуляция которого по любому замкнутому контуру равна 0.
Легко доказать (уже доказывалось в лекциях по механике), что центральное поле обладает этим свойством.
следовательно,
Для дальнейшего важно понимать, что циркуляция не зависит от начала отсчёта. То есть если начало отсчёта векторов положения сместить из центра поля, циркуляция по данному замкнутому контуру по-прежнему будет равна 0. Это обстоятельство позволяет доказать, что электростатическое поле произвольной системы зарядов потенциально. Если поле создано не одним точечным зарядом, то согласно принципу суперпозиции
,
поскольку мы получили сумму циркуляций, каждая из которых равна 0. Начало отсчёта векторов положения произвольно (может находиться за пределами расположения системы зарядов).
§14.2. Понятие потенциала
Если векторное поле — силовое, то физический смысл скалярного произведения — элементарная работа dА силового поля на перемещении материальной точки, чьё силовое поле мы рассматриваем. В механике доказывалось, то работа потенциального силового поля на перемещении (рис.14.2)
Рис.14.2
выражается через сброс энергии положения или потенциальной энергии материальной точки в её силовом поле:
.
Как Вы помните, потенциальная энергия определялась через отрицательную работу сил поля от некой точки пространства O, произвольно избранной в качестве начала отсчёта потенциальной энергии (W(О)=0).
,
где В — произвольная точка пространства, заполненного полем. При этом контур L, по которому материальная точка движется в потенциальном поле от точки О до точки В (то есть по которому производится интегрирование), может быть любым. В механике потенциальную энергию, как и любую другую энергию, принято обозначать буквой Е. В электромагнетизме энергия обозначается буквой W, поскольку Е «занята» на обозначении электрической напряжённости.
В случае поля электростатических сил, то есть сил, действующих со стороны зарядов-источников на пробный заряд q, его потенциальная энергия в этом поле
Дадим определение: потенциал в данной точке пространства , заполненного электростатическим полем, совпадает с потенциальной энергией , которую имел бы в этом поле точечный единичный положительный пробный заряд, если его поместить в данную точку. «Идеология» этого определения та же, что и в определении напряжённости. То есть слово «совпадает» связано с тем, что потенциал − это характеристика поля самого по себе, а потенциальная энергия пробного заряда в поле характеризует и поле, и пробный заряд. Иными словами,
Потенциальная энергия единичного положительного пробного заряда
.
Тогда по определению потенциала
.
Эта формула позволяет определить потенциал поля в любой точке пространства по известному полю напряжённости. Здесь точка О выбрана началом отсчёта потенциала (j(О)=0). Значит, потенциальная энергия пробного заряда в поле источников имеет вид:
Отсюда можно получить физическую размерность потенциала: . Потенциал в СИ измеряется в вольтах.
Работа сил поля на перемещении пробного заряда определяется по закону изменения его потенциальной энергии:
Þ ,
где − сброс потенциала или напряжение.
Из формулы связи потенциала и напряжённости следует формула разности потенциалов:
и выражение элементарного изменения или дифференциала потенциала:
.
§14.3. Связь между векторным полем напряжённости и скалярным полем потенциала
Очевидно, что распределение в пространстве потенциала данного электростатического поля с точки зрения математики представляет скалярное поле . Оказывается, последняя формула предыдущего параграфа указывает на то, что векторное поле напряжённости однозначно определяется заданием скалярного поля потенциала . Значит, данное электростатическое поле одинаково успешно может быть представлено как векторным полем , так и скалярным полем . Покажем это.
Используя координатное представление скалярного произведения в декартовых координатах, перепишем выражение элементарного изменения потенциала:
.
С другой стороны, поскольку , то дифференциал j в соответствие с правилами дифференцирования функции многих переменных
.
Сравнивая эти два равенства, приходим к выводу, что
Значит, действительно, задание скалярного поля определяет все его частные производные, а это, оказывается, определяет проекции вектора на координатные оси, что, очевидно, однозначно определяет вектор . Таким образом, поле напряжённости получается в результате процедуры трехмерного дифференцирования поля потенциала. Эта математическая процедура называется градиентом.
В математике процедуру или совокупность действий по преобразованию функции называют оператором. Градиент является многомерным дифференциальным оператором. В трёхмерном случае (случай функции 3-х переменных) градиент обозначается и выражается так:
.
Электромагнитный потенциал — Википедия
У этого термина существуют и другие значения, см. Потенциал.В современной физике электромагни́тный потенциа́л обычно означает четырёхмерный потенциал электромагнитного поля, являющийся 4-вектором (1-формой). Именно в связи с векторным (4-векторным) характером электромагнитного потенциала электромагнитное поле относится к классу векторных полей в том смысле, который употребляется в современной физике по отношению к фундаментальным бозонным полям (например, гравитационное поле является в этом смысле не векторным, а тензорным полем).
- Обозначается электромагнитный потенциал чаще всего Ai{\displaystyle A_{i}} или φi{\displaystyle \varphi _{i}}, что подразумевает величину с индексом, имеющую четыре компоненты A0,A1,A2,A3{\displaystyle A_{0},A_{1},A_{2},A_{3}} или φ0,φ1,φ2,φ3{\displaystyle \varphi _{0},\varphi _{1},\varphi _{2},\varphi _{3}}, причём индексом 0 как правило обозначается временная компонента, а индексами 1, 2, 3 — три пространственных. В данной статье мы будем придерживаться первого обозначения.
- В современной литературе могут использоваться более абстрактные обозначения.
В любой определенной инерциальной системе отсчета электромагнитный потенциал (A0, A1, A2, A3){\displaystyle (A_{0},\ A_{1},\ A_{2},\ A_{3})} распадается[1]на скалярный (в трёхмерном пространстве) потенциал φ≡A0{\displaystyle \varphi \equiv A_{0}} и трехмерный векторный потенциал A→≡(Ax,Ay,Az)≡(−A1,−A2,−A3){\displaystyle {\vec {A}}\equiv (A_{x},A_{y},A_{z})\equiv (-A_{1},-A_{2},-A_{3})}; эти потенциалы φ {\displaystyle \varphi \ } и A→{\displaystyle {\vec {A}}} — и есть те скалярный и векторный потенциалы, которые используются в традиционной трехмерной формулировке электродинамики. В случае, когда электромагнитное поле не зависит от времени (или быстротой его изменения в конкретной задаче можно пренебречь), то есть в случае (приближении) электростатики и магнитостатики, напряженность электрического поля выражается через φ{\displaystyle \varphi }, называемый в этом случае электростатическим потенциалом, а напряженность магнитного поля (магнитная индукция)[2] — только через векторный потенциал. Однако в общем случае (когда поля меняются со временем) в выражение для электрического поля входит также и векторный потенциал, тогда как магнитное — всегда выражается лишь через векторный (нулевая компонента электромагнитного потенциала в это выражение не входит).
Связь напряжённостей с электромагнитным потенциалом в общем случае такова в традиционных трехмерных векторных обозначениях[3]:
- E→=−∇φ−∂A→∂t,{\displaystyle {\vec {E}}=-\nabla \varphi -{\frac {\partial {\vec {A}}}{\partial t}},}
- B→=∇×A→,{\displaystyle {\vec {B}}=\nabla \times {\vec {A}},}
где E→{\displaystyle {\vec {E}}} — напряженность электрического поля, B→{\displaystyle {\vec {B}}} — магнитная индукция (или — что в случае вакуума в сущности то же самое — напряженность магнитного поля), ∇{\displaystyle \nabla } — оператор набла, причём ∇φ≡gradφ{\displaystyle \nabla \varphi \equiv \mathrm {grad} \,\varphi } — градиент скалярного потенциала, а ∇×A→≡rotA→{\displaystyle \nabla \times {\vec {A}}\equiv \mathrm {rot} \,{\vec {A}}} — ротор векторного потенциала.
В несколько более современной четырехмерной формулировке эти же соотношения можно записать как выражение тензора электромагнитного поля через 4-вектор электромагнитного потенциала:
- Fμν=∂μAν−∂νAμ,{\displaystyle F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu },}
где Fμν{\displaystyle F_{\mu \nu }} — тензор электромагнитного поля, компоненты которого представляют собой компоненты Ex,Ey,Ez,Bx,By,Bz{\displaystyle E_{x},E_{y},E_{z},B_{x},B_{y},B_{z}}.
Приведенное выражение является обобщением выражения ротора для случая четырехмерного векторного поля.
При переходе от одной инерциальной системы отсчета к другой, компоненты A0,A1,A2,A3{\displaystyle A_{0},A_{1},A_{2},A_{3}} преобразуются, как это свойственно компонентам 4-вектора, посредством преобразований Лоренца.
Физический смысл четырехмерного электромагнитного потенциала можно прояснить, заметив, что при взаимодействии заряженной частицы [4] (с электрическим зарядом q) с электромагнитным полем этот потенциал дает добавку в фазу φ{\displaystyle \varphi } волновой функции частицы:
- Δφ=−1ℏ∫qAidxi=−1ℏ∫qAiuidτ{\displaystyle \Delta \varphi =-{\frac {1}{\hbar }}\int qA_{i}dx^{i}=-{\frac {1}{\hbar }}\int qA_{i}u^{i}d\tau },
или, иначе говоря, вклад в действие (формула отличается от записанной выше только отсутствием множителя 1/ℏ{\displaystyle 1/\hbar }, а в системе единиц, где ℏ=1{\displaystyle \hbar =1} — просто совпадает с ней). Изменение фазы волновой функции частицы проявляется в сдвиге полос при наблюдении интерференции заряженных частиц (см., например, эффект Ааронова-Бома).
Физический смысл электрического и магнитного потенциалов в более простом частном случае электростатики и магнитостатики, а также единицы измерения этих потенциалов обсуждаются в статьях Электростатический потенциал и Векторный потенциал электромагнитного поля.
- ↑ В данной записи использовано ковариантное представление электромагнитного потенциала в сигнатуре лоренцевой метрики (+−−−), используемое и в других формулах статьи. Контравариантное представление Ai≡(A0, A1, A2,A3)=(φ, Ax, Ay, Az){\displaystyle A^{i}\equiv (A^{0},\ A^{1},\ A^{2},A^{3})=(\varphi ,\ A_{x},\ A_{y},\ A_{z})} отличается от ковариантного в лоренцевой метрике (такой сигнатуры) лишь знаком трёх пространственных компонент. В представлении с мнимой временной компонентой (в формально евклидовой метрике) электромагнитный потенциал всегда записывается в одинаковом виде: (i φ, Ax, Ay, Az){\displaystyle (i\ \varphi ,\ A_{x},\ A_{y},\ A_{z})}.
- ↑ В статье статье рассматривается лишь поля в вакууме, поэтому напряженность магнитного поля и магнитная индукция в сущности не различаются (правда, в некоторых системах единиц, например, в СИ, они имеют разную размерность, но даже в таких единицах в вакууме отличаются друг от друга лишь постоянным множителем).
- ↑ В зависимости от используемой системы физических единиц, в эти формулы, а также в формулы, связывающие четырехмерный электромагнитный потенциал с трехмерными векторным потенциалом и скалярным потенциалом, могут входить различные размерные постоянный коэффициенты; мы для простоты приводим формулы в системе единиц, где скорость света равна единице, и все скорости безразмерны.
- ↑ Имеется в виду точечная частица без магнитного момента.
Векторный потенциал электромагнитного поля — Википедия
Ве́кторный потенциа́л электромагни́тного по́ля (вектор-потенциал, магнитный потенциал) — в электродинамике, векторный потенциал, ротор которого равен магнитной индукции:
- B=rotA=∇×A.{\displaystyle \mathbf {B} =\operatorname {rot} \mathbf {A} =\nabla \times \mathbf {A} .}
Вектор-потенциал является пространственной компонентой 4-вектора электромагнитного потенциала.
Одним из способов записи уравнений Максвелла является формулировка в терминах векторного и скалярного потенциалов.
При этом уравнение divB=0{\displaystyle \operatorname {div} \mathbf {B} =0} удовлетворяется автоматически.
Подстановка выражения для A{\displaystyle \mathbf {A} } в
- rotE=−∂B∂t{\displaystyle \operatorname {rot} \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
приводит к уравнению
- rot(E+∂A∂t)=0,{\displaystyle \operatorname {rot} \left(\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}\right)=0,}
согласно которому, так же как и в электростатике вводится скалярный потенциал. Однако теперь в E{\displaystyle \mathbf {E} } вносят вклад и скалярный и векторный потенциал:
- E=−gradφ−∂A∂t.{\displaystyle \mathbf {E} =-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}.}
Из уравнения rotH=j+∂D∂t{\displaystyle \operatorname {rot} \mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}} следует
- rotrotA=μ0j+ε0μ0∂∂t(−gradφ−∂A∂t).{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\mu _{0}\mathbf {j} +\varepsilon _{0}\mu _{0}{\frac {\partial }{\partial t}}\left(-\operatorname {grad} \;\varphi -{\frac {\partial \mathbf {A} }{\partial t}}\right).}
Используя равенство rotrotA=graddivA−∇2A{\displaystyle \operatorname {rot} \;\operatorname {rot} \mathbf {A} =\operatorname {grad} \;\operatorname {div} \mathbf {A} -\nabla ^{2}\mathbf {A} }, уравнения для векторного и скалярного потенциалов можно записать в виде
- ΔA−grad(divA+1c2∂φ∂t)−1c2∂2A∂t2=−μ0j,{\displaystyle \Delta \mathbf {A} -\operatorname {grad} \left(\operatorname {div} \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}\right)-{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}=-\mu _{0}\mathbf {j} ,}
- Δφ+∂∂tdivA=−ρε0.{\displaystyle \Delta \varphi +{\frac {\partial }{\partial t}}\operatorname {div} \mathbf {A} =-{\frac {\rho }{\varepsilon _{0}}}.}
Вектор-потенциал и магнитный поток[править | править код]
В соответствии с теоремой Стокса, магнитный поток Φ{\displaystyle \Phi } через контур L{\displaystyle L} легко выразить через циркуляцию векторного потенциала A{\displaystyle \mathbf {A} } по этому контуру:
- Φ=∮LA⋅dl.{\displaystyle \Phi =\oint \limits _{L}\mathbf {A} \cdot \mathbf {dl} .}
Легко убедиться, что преобразования
- A→A+∇ψ,{\displaystyle \mathbf {A} \rightarrow \mathbf {A} +\nabla \psi ,}
- φ→φ−∂ψ∂t,{\displaystyle \varphi \rightarrow \varphi -{\frac {\partial \psi }{\partial t}},}
где ψ{\displaystyle \psi } — произвольная скалярная функция координат и времени, не изменяют уравнений Максвелла (калибровочная инвариантность, по теореме Нётер ей соответствует закон сохранения электрического заряда). Для удобства решения этих уравнений накладывают дополнительное искусственное условие, называемое калибровкой потенциала. При решении различного класса задач удобнее бывает та или иная калибровка. Широкое распространение получили две — калибровка Кулона и калибровка Лоренца.
Калибровка Кулона[править | править код]
Калибровкой Кулона называют выражение:
- divA=0.{\displaystyle \operatorname {div} \mathbf {A} =0.}
Эта калибровка удобна для рассмотрения магнитостатических задач (с постоянными во времени токами).
Калибровка Лоренца[править | править код]
Калибровкой Лоренца называют условие равенства нулю 4-дивергенции потенциала (в СИ):
- ∇μAμ=divA+1c2∂φ∂t=0.{\displaystyle \nabla _{\mu }A_{\mu }=\operatorname {div} \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \varphi }{\partial t}}=0.}
В этом случае уравнения переписываются в виде даламбертианов:
- ◻A≡ΔA−1c2∂2A∂t2=−μ0j,{\displaystyle \square \mathbf {A} \equiv \Delta \mathbf {A} -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}=-\mu _{0}\mathbf {j} ,}
- ◻φ≡Δφ−1c2∂2φ∂t2=−ρε0.{\displaystyle \square \varphi \equiv \Delta \varphi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\varphi }{\partial t^{2}}}=-{\frac {\rho }{\varepsilon _{0}}}.}
Уравнения, записанные в таком виде, удобнее использовать для решения нестационарных задач.
Физический смысл векторного потенциала[править | править код]
Обычно считается, что векторный потенциал — величина, не имеющая непосредственного физического смысла, вводимая лишь для удобства выкладок. Однако удалось поставить эксперименты, показавшие, что векторный потенциал доступен непосредственному измерению. Подобно тому, как электростатический потенциал связан с понятием энергии, векторный потенциал обнаруживает тесную связь с понятием импульса.
Смещение квантовомеханической фазы[править | править код]
Влияние магнитного поля на движение квантовой частицы приводит к смещению фазы[1][2]:
- ΔφH=eℏc∫S(A,dl),{\displaystyle \Delta \varphi _{H}={\frac {e}{\hbar c}}\int _{S}^{}(\mathbf {A} ,\;d\mathbf {l} ),}
где e{\displaystyle e} — заряд электрона, c{\displaystyle c} — скорость света в вакууме, ℏ{\displaystyle \hbar } — приведенная постоянная Планка, A{\displaystyle \mathbf {A} } — векторный потенциал магнитного поля и dl{\displaystyle d\mathbf {l} } — элемент траектории движения частицы.
При этом смещение фазы возникает и тогда, когда частица проходит по областям, в которых B=0{\displaystyle \mathbf {B} =0}, не равен нулю только A{\displaystyle \mathbf {A} }. Например, это происходит при наблюдении эффекта Ааронова — Бома[3].
Обобщённый импульс[править | править код]
При движении частицы в электромагнитном поле полный импульс P{\displaystyle \mathbf {P} } равен не просто p=mv1−v2/c2{\displaystyle \mathbf {p} ={\frac {m\mathbf {v} }{\sqrt {1-v^{2}/c^{2}}}}}, а p+qA{\displaystyle \mathbf {p} +q\mathbf {A} }. Следовательно, при движении частицы в чисто магнитном поле сохраняется именно эта величина. Налицо аналогия с полной энергией частицы E=T+U=mc21−v2/c2+qφ{\displaystyle E=T+U={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}+q\varphi }, которую можно считать суммой кинетической и потенциальной энергии.
Импульс частицы при быстром отключении магнитного поля[править | править код]
Если заряженная частица находится вблизи источника магнитного поля, которое в определённый момент времени быстро отключают, то она приобретает дополнительный импульс Δp=qA{\displaystyle \Delta \mathbf {p} =q\mathbf {A} } даже в том случае, если B{\displaystyle \mathbf {B} } в точке нахождения частицы было равно нулю (например, с внешней стороны соленоида). В частности, если частица до отключения поля покоилась, то она начинает движение с импульсом, равным qA{\displaystyle q\mathbf {A} }. Таким образом мы получаем возможность непосредственно измерить векторный потенциал в макроскопической системе.
В системе СИ единицей векторного потенциала является вебер на метр (Вб/м, размерность — В·с/м = кг·м·с−2·А−1).
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. — М.: Мир, 1966. — Т. 6. — 344 с.
- ↑ Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. — М.: Мир, 1968. — 382 с.
- ↑ Aharonov, Y. and D. Bohm. Significance of electromagnetic potentials in quantum theory // Phys. Rev.. — 1959. — Т. 115.
Что такое потенциал или что называют потенциалом в физике??.
Заряд электронов вроде
Первое. Потенциал может быть не только у электрического поля, но и у гравитационного (например) . Второе. Сам по себе потенциал мало кому нужен, это величина довольно условная. И определяется как работа, которую надо совершить, чтоб удалить объект из данной точки в бесконечность (где взаимодействие этого объекта — заряда или массы — с источником поля уже можно считать нулевым) . А вот что таки да, ИМЕЕТ значение, — так это РАЗНОСТЬ потенциалов. Потому как именно разность потенциалов между двумя точками и есть та реальная работа, которую надо затратить или можнополучить, когда заряд (или тело) перемещается из одной точки в другую. Во-первых, это то, что можно измерить, потому что не надо отправляться на бесконечность. Обе точки — вот они. Во-вторых, это то, что практически и надо. Это работа, которую надо совершить, чтоб занести рояль на пятый этаж (массу рояля надо умножить на разность потенциалов гравитационного поля между первый и пятым этажами) . Это работа, которую надо совершить, чтоб пропихнуть вот этот заряд через вот эту цепь (величина заряда на разность потенциалов электрического поля на двух концах цепи) . Описание «Потенциал показывает какой потенциальной энергией будет обладать единичный положительный заряд, помещенный в данную точку электрического поля» — НЕВЕРНОЕ описание. Потому что потенциал ВСЕГДА определяется ОТНОСИТЕЛЬНО ЧЕГО-ТО. Относительно другой точки. То есть хотя бы формально (а на самом деле и практически) должно быть указано, относительно какой точки определяется или измеряется потенциал. В формальном определении за эту вторую точку принимается бесконечность. Потому что вот этот единичный положительный заряд, как и гиря в 1 кг, потенциальной энергией обладает не «вообще», а только относительно отсчётного уровня. С гирей это особенно наглядно проявляется — относительно пола у неё одна потенциальная энергия, а относительно первого этажа (напомню, мы уже добрались до пятого) — совсем другая.
Потенциалом называю способность поля (электрического, гравитационного и любого другого потенциального поля) совершать работу. Иногда про человека говорят «У него большой потенциал» имея ввиду что он может многого достичь. Здесь примерно так же…
определение выглядит хитровато, но по смыслу простое. физики подметили, что два важнейших поля, гравитационное и электрическое обладают прекрасным свойством: если мы перетащим тело из точки А в точку Б, работа силы поля получится одинаковой, каким бы мы путем не тащили тело. Работа зависит только от выбора этих точек. ну попросту, для гравитации у земли, она совершает работу только в зависимости от разности высот точек. Упал кирпич к крыши — работа mgh. Подняли назад — -mgh. Каким путем он падал или как его поднимали — по прямой на веревке или несли зигзагами по лестнице — неважно. так давайте примем какую-от точку за ноль, например — поверхность земли, а лучше — уровень моря, тогда в каждой точке мы можем посчитать работу для перемещения тела с поверхности в эту точку. Это и есть потенциал. точки с одинаковым потенциалом около земли — просто лежат на одинаковой высоте от уровня моря. естественно, мы вольны выбрать и другой уровень за ноль. Например, решая задачу с тележкой на столе — взять за ноль уровень стола. астрономы вообще за ноль берут бесконечность, так у них формулы получаются короче. использовать потенциалы часто удобнее, чем считать каждый раз силы, сила — 3-хмерный вектор, а потенциал — одно число. А если надо, через потенциал легко получается вектор силы.
Потенциал — локальная характеристика любого поля, обладающего потенциальностью. Это значит, что работа, совершаемая любым объектом в этом и только этом поле по ЛЮБОМУ замкнутому пути равна нулю… Определяется как отношение энергии пробного элемента в данной точке к величине пробного элемента (массы, заряда и т. д)
Если Вы понимаете, что такое потенциальная энергия, то подкину Вам такую мысль. Заметьте, что в терминах «потенциал» и «потенциальная энергия» много общего. Только вот потенциальная энергия зависит как от положения тела в пространстве, так и от характерик тела (например, массы или заряда), а потенциал в точке от характеристик пробного тела не зависит, он зависит только от того, где эта точка находится. Поделите потенциальную энергию тела в точке на нужную характеристику тела (чтоб от нее избавиться), получите потенциал в точке. Умножьте потенциал в точке на нужную характеристику тела, получится потенциальная энергия тела в точке. Ну и да, раз уж речь об этом… Потенциальную энергию и потенциал имеет смысл считать относительно чего-то одинакового в обоих случаях (например, относительно точки на земной поверхности, если говорите о потенциальной энергии/потенциале тела на какой-то высоте).