3.4. Порядок построения векторных диаграмм напряжений и токов
3.4.1. Схема звезда с нейтральным проводом
1. Выберите масштабы отдельно по току и напряжению.
2. Проведите координатную сетку. При построении диаграмм трехфазных приемников, для удобства построения ось действительных величин +1 располагают вертикально.
3. В выбранном масштабе постройте векторы фазных напряжений
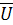 ax,
ax, by,
by,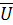 cz , в соответствии с уравнениями 3.1.
cz , в соответствии с уравнениями 3.1.
4.
Постройте векторы линейных напряжений 
 bc,
bc,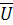 ca в соответствии с уравнениями 3.4.
ca в соответствии с уравнениями 3.4.
Разность двух векторов равна вектору, направленному из конца второго вектора в конец первого.
Правильно построенные векторы линейных напряжений образуют равносторонний треугольник линейных напряжений.
5.
В выбранном масштабе постройте векторы
фазных токов 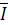
 by,
by,  cz,
совпадающими по фазе с соответствующими
векторами фазных напряжений
cz,
совпадающими по фазе с соответствующими
векторами фазных напряжений
6.
Постройте вектор тока в нейтральном
проводе  N путем сложения векторов фазных токов
по правилу параллелограмма.
N путем сложения векторов фазных токов
по правилу параллелограмма.
Рассмотрим пример.
Пусть
UBCВ
Uax,
В
Uby,
В
Ucz,
В
Iax,
А
А
Icz,
А
IN,
А
240
140
140
140
0
0,3
0,3
0,3

Рис. 3.6. Векторная диаграмма токов и напряжений приемника, включенного звездой с нейтральным проводом
3.4.2. Схема звезда без нейтрального провода
1. Диаграмму стройте в том же масштабе, что и в предыдущем случае.
2.
Постройте треугольник линейных напряжений  ab,
ab,  bc,
bc,  ca
ca
3. Найдите центр звезды несимметричных фазных напряжений, для чего:
• из вершины А треугольника линейных напряжений проведите дугу радиусом Uax;
• из вершины В треугольника линейных напряжений проведите дугу радиусом Uby;
• из вершины С треугольника линейных напряжений проведите дугу радиусом Ucz;
• точка пересечения дуг есть центр звезды напряжений.
4. Постройте векторы фазных напряжений, соединив центр звезды с вершинами треугольника.
 ax,
ax,  by, cz строятся, как описано выше.
by, cz строятся, как описано выше.Рассмотрим пример.
Пусть
UBCВ
Uax,
Uby,
В
Ucz,
В
Iax,
А
Iby,
А
Icz,
А
240
208
120
0
0,3
0,3

Рис. 3.7. Векторная диаграмма токов и напряжений приемника, включенного звездой без нейтрального провода
3.4.3. Схема треугольник
1.
Постройте звезду фазных напряжений,
так же как это делали для приемника,
включенного звездой с нейтральным
проводом. Она же будет звездой линейных
напряжений 
 bc,
bc, 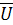 ca,
т.к. в схеме треугольник фазные и линейные
напряжения равны.
ca,
т.к. в схеме треугольник фазные и линейные
напряжения равны.
2.
Постройте векторы фазных токов  ax,
ax, 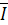 by,,
by,, 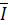
 ax, by,
ax, by,  cz.
cz.
3.
Постройте векторы линейных токов  A,
A, 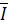 B,
B, 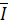 C в соответствии с уравнением 3.7.
C в соответствии с уравнением 3.7.
Рассмотрим пример.
Пусть
IA,
A
Iax,
A
Iby,
A
A
UBC,
В
Uax,
В
Uby,
В
Ucz,
В
0,55
0
0,55
0,55
240
240
240
240

Рис. 3.8. Векторная диаграмма токов и напряжений приемника, включенного треугольником
Указания по построению векторных диаграмм
Построение векторных диаграмм
для всех пунктов программы лабораторной работы начинается
с построения с
соблюдением масштаба напряжений (1 см
= 20 В) симметричной трехлучевой звезды векторов
фазных напряжений приемника,
соединенного треугольником, которые
одновременно являются линейными
напряжениями генератора (питающей
трехпроводной сети):  .
.
Вначале рассмотрим построение векторной диаграммы напряжений и токов для случая симметричной нагрузки (рис. 16).
П оскольку
симметричный режим характеризуется
равенством величин фазных токовIab = Ibc = Ica = IФ и равенством углов сдвига φab = φbc = φca = 0 (активная нагрузка – резисторы), то
задавшись масштабом тока (1 см = 0,25 А),
можно определить длину IФ векторов фазных токов и построить их
совпадающими со «своими» фазными
напряжениями (рис. 16). Ранее было показано
(рис. 8), что векторы линейных токов
оскольку
симметричный режим характеризуется
равенством величин фазных токовIab = Ibc = Ica = IФ и равенством углов сдвига φab = φbc = φca = 0 (активная нагрузка – резисторы), то
задавшись масштабом тока (1 см = 0,25 А),
можно определить длину IФ векторов фазных токов и построить их
совпадающими со «своими» фазными
напряжениями (рис. 16). Ранее было показано
(рис. 8), что векторы линейных токов 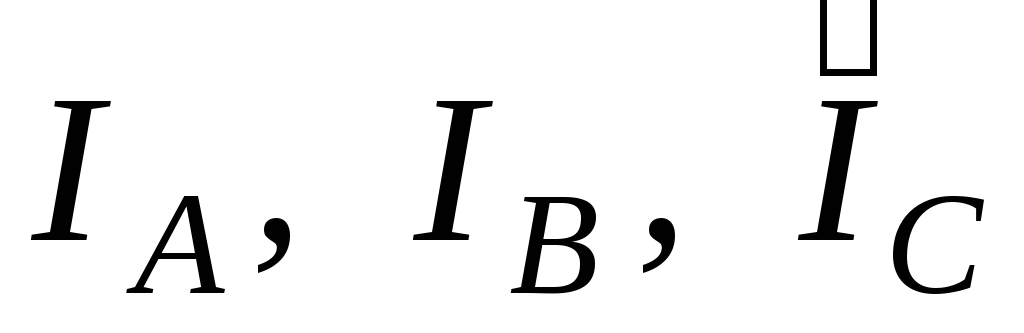 могут быть изображены в виде сторон
векторного треугольника, вершинами
которого являются концы векторов фазных
токов, если они построены в виде
трехлучевой звезды векторов.
могут быть изображены в виде сторон
векторного треугольника, вершинами
которого являются концы векторов фазных
токов, если они построены в виде
трехлучевой звезды векторов.
Так как режим
симметричный, то векторы
фазных токов  (рис. 16)образуют
симметричную звезду векторов, а векторный
треугольник со сторонами
(рис. 16)образуют
симметричную звезду векторов, а векторный
треугольник со сторонами  является
равносторонним.
является
равносторонним.
В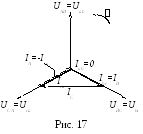 екторная
диаграмма при обрыве одной фазы строится в том же порядке: изображается
симметричная звезда векторов фазных
напряжений, а затем строятся векторы
фазных токов
екторная
диаграмма при обрыве одной фазы строится в том же порядке: изображается
симметричная звезда векторов фазных
напряжений, а затем строятся векторы
фазных токов  и
и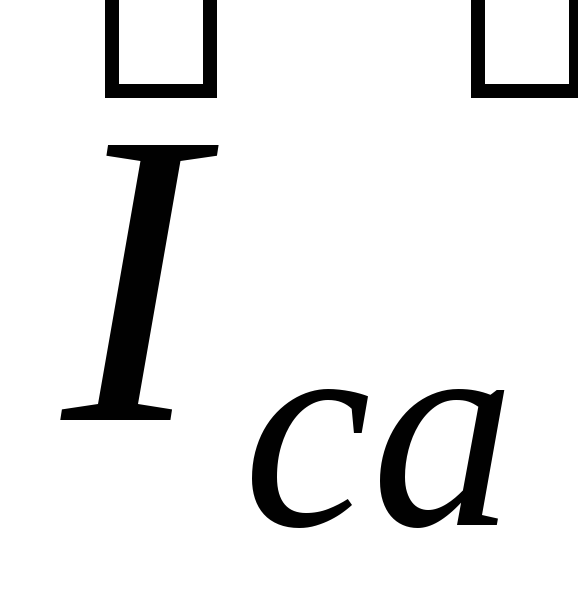 ,
посколькуIab = 0, а величины токов Ibc и Ica сохраняются (рис. 17). C
учетом равенства нулю тока Iab система равенств (6) принимает вид:
,
посколькуIab = 0, а величины токов Ibc и Ica сохраняются (рис. 17). C
учетом равенства нулю тока Iab система равенств (6) принимает вид:

Таблица 2
Таблица измерений и вычислений
Нагрузка | Измеряются | Вычисляются | ||||||||||||||||
Iab | Ibc | Ica | IA | IB | IC | UAB | UBC | UCA | P1 | P2 | ∑P | Pab | Pbc | Pca | ∑P | Q | S | |
ампер | вольт | ватт | ватт | вар | ВА | |||||||||||||
Симметричная | ||||||||||||||||||
Обрыв (разгрузка) одной фазы | ||||||||||||||||||
Обрыв двух фаз | ||||||||||||||||||
Обрыв линейного провода В | ||||||||||||||||||
Несимметричная | ||||||||||||||||||
Равномерная | ||||||||||||||||||

В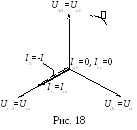 екторная
диаграмма при обрыве двух фаз (рис.18) строится
с учетом того, что Iab = 0, Ibc = 0 и остается неизменным ток Iса в фазе с–а.
Сделав соответствующие уточнения в
системе
уравнений для линейных токов (6), получим:
екторная
диаграмма при обрыве двух фаз (рис.18) строится
с учетом того, что Iab = 0, Ibc = 0 и остается неизменным ток Iса в фазе с–а.
Сделав соответствующие уточнения в
системе
уравнений для линейных токов (6), получим:

Таким образом один линейный ток IВ равен нулю, а два других равны по величине фазному току оставшейся включенной фазе с–а.
В рассмотренных режимах разгрузки одной и двух фаз приемника наглядно проявляется независимость работы фаз треугольника.
В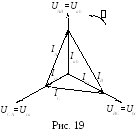 екторная
диаграмма при несимметричной нагрузке
всех трех фаз приемника (рис. 19). Порядок построения, как и в
предыдущих режимах, сохраняется: вначале
строится симметричная
звезда векторов фазных напряжений
екторная
диаграмма при несимметричной нагрузке
всех трех фаз приемника (рис. 19). Порядок построения, как и в
предыдущих режимах, сохраняется: вначале
строится симметричная
звезда векторов фазных напряжений  ,
а звезда векторов фазных токов
,
а звезда векторов фазных токов  оказывается несимметричной, поскольку
длины векторов (в масштабе токов) не
равны друг другу Iab Ibc Ica.
Очевидно несимметричной будет и система
векторов линейных токов
оказывается несимметричной, поскольку
длины векторов (в масштабе токов) не
равны друг другу Iab Ibc Ica.
Очевидно несимметричной будет и система
векторов линейных токов  ,
показанных на диаграмме (рис. 19) в виде
сторон векторного треугольника, стороны
которого не равны друг другу IA IB IC.
,
показанных на диаграмме (рис. 19) в виде
сторон векторного треугольника, стороны
которого не равны друг другу IA IB IC.
Векторная диаграмма при равномерной нагрузке отличается от предыдущих тем, что в одной из фаз приемника (фазе с–z) векторы тока и напряжения не совпадают друг с другом, а ток Ica опережает напряжение на 90° (φca = –90°). Это объясняется тем, что в фазу с–z вместо резисторов включен реактивный элемент – конденсатор с емкостью С (рис. 15).
Построение
диаграммы начинается с изображения
звезды векторов фазных напряжений (рис.
20). Затем строятся одинаковые по длине
векторы фазных токов: в фазах a–x и b–y совпадающими со своими фазными
напряжениями, а вектор тока 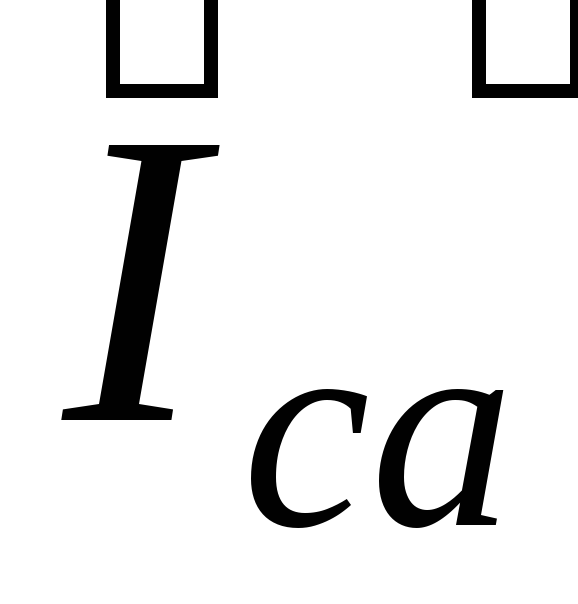 изображается опережающим фазное
напряжение
изображается опережающим фазное
напряжение на 90°. Как видно из диаграммы (рис. 20)
векторы фазных токов
на 90°. Как видно из диаграммы (рис. 20)
векторы фазных токов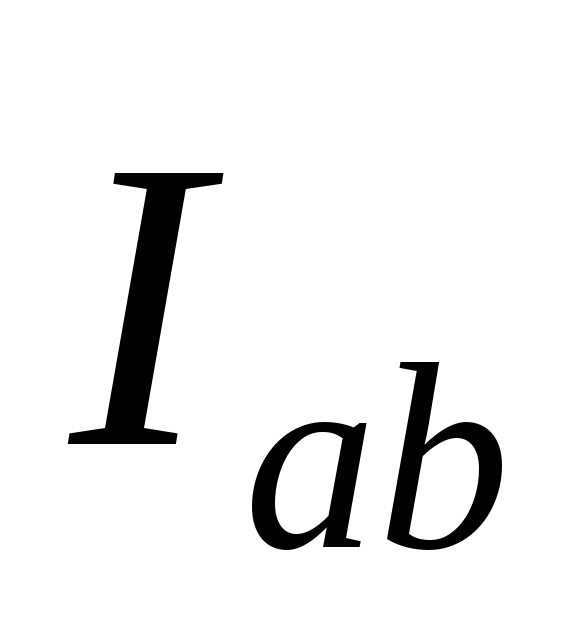 ,
,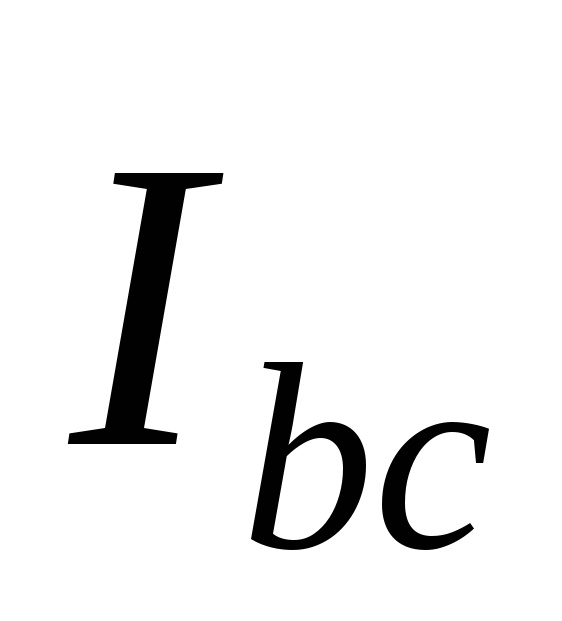 ,
, одинаковые по величине, образуютнесимметричную
звезду векторов.
одинаковые по величине, образуютнесимметричную
звезду векторов.
Н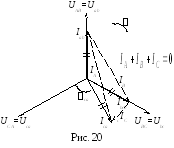 есимметричной
оказывается и система трех векторов
линейных токов
есимметричной
оказывается и система трех векторов
линейных токов ,
показанных пунктиром в виде сторон
векторного треугольника, вершинами
которого являются концы векторов фазных
токов (рис. 20).
,
показанных пунктиром в виде сторон
векторного треугольника, вершинами
которого являются концы векторов фазных
токов (рис. 20).
Это свидетельствует о том, что равномерная нагрузка при одинаковых величинах фазных токов является частным случаем несимметричной.
Следует обратить
внимание (рис. 20), что один из линейных
токов IC меньше фазного (при симметричной нагрузке  ).
).
Векторная диаграмма при обрыве линейного провода B–b представляет собой векторную диаграмму однофазной цепи (рис. 21б). Данный режим осуществляется размыканием выключателя К3 (схема на рис. 15) при замкнутых ключах К1 и К2, причем до этого приемник, соединенный треугольником, представлял собой симметричную активную нагрузку: rab = rbc = rca = r , где r – активное сопротивление одной фазы.
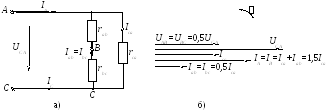
Рис. 21
Получилась по существу уже не трехфазная, а однофазная цепь с двумя параллельными ветвями (рис. 21а), включенная на однофазное напряжение UCA (соответствующее линейное напряжение трехфазного источника питания). Поэтому она должна рассчитываться и анализироваться с использованием методов расчета однофазных цепей.
Активные
сопротивления двух параллельных ветвей,
включенных между электрическими узлами A и С однофазной цепи (рис. 21а) соответственно
равны rab + rbc = 2r и rca = r . Токи в параллельных ветвях: 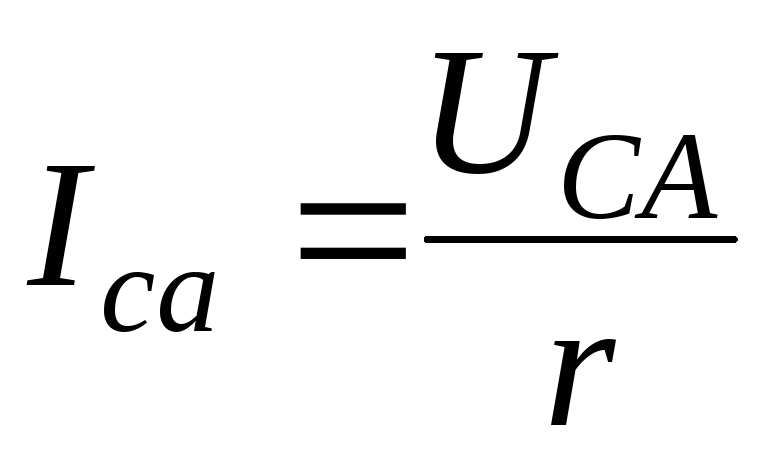 ,
,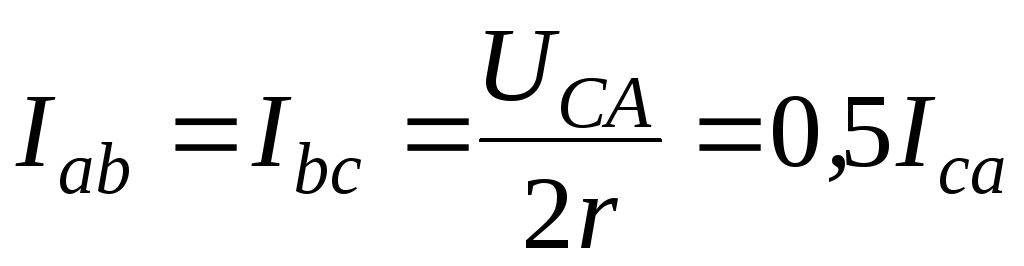 ;
ток в неразветвленной цепиIA = IC = Ica + Iab = 1,5Ica.
Напряжение на входе цепи UCA =UAB + UBC,
откуда UAB = UBC = 0,5UCA.
;
ток в неразветвленной цепиIA = IC = Ica + Iab = 1,5Ica.
Напряжение на входе цепи UCA =UAB + UBC,
откуда UAB = UBC = 0,5UCA.
Поскольку в рассматриваемой однофазной цепи включены только резисторы, то векторы напряжений и токов на всех участках цепи совпадает по фазе. На рисунке 21б показаны векторные диаграммы для всех ветвей, построенные с учетом соответствующих масштабов и полученных выше соотношений для напряжений и токов однофазной цепи.
Расчетные формулы для заполнения раздела таблицы измерений и вычислений (табл. 2) «Вычисления».
Активные мощности фаз:
 .
.
Суммарная активная мощность цепи:

при чисто активной нагрузке φab = φbc = φca = 0 (cos0 = 1).
Реактивная мощность каждой фазы вычисляется по формуле:
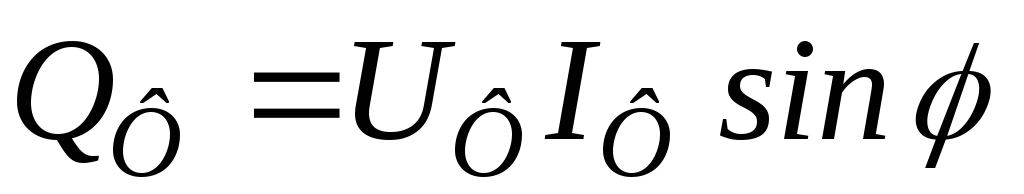 (при φ = 0 sinφ = 0),
(при φ = 0 sinφ = 0),
а полная (кажущаяся) мощность
 или
или 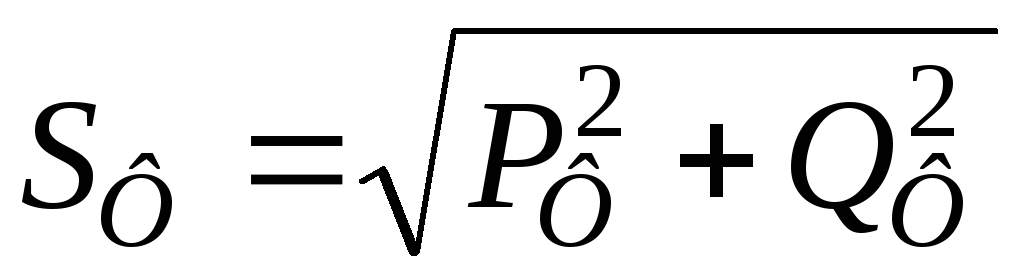 (из треугольника мощностей).
(из треугольника мощностей).
Контрольные вопросы
Как соединить фазы приемника треугольником?
Что называется фазными и линейными токами и напряжениями, и как соотносятся фазные и линейные величины при соединении треугольником?
Какая разница между симметричной и равномерной нагрузкой?
При каких условиях соединение треугольником обеспечивает независимую работу фаз приемника?
В чем преимущества и недостаток схемы двух ваттметров, применяемой при измерении активной мощности в трехпроводных трехфазных цепях?
12.Объяснить построение векторных диаграмм для всех режимов.
Ответ:
Выбрать масштаб для напряжений и токов.
Построить топографическую векторную диаграмму линейных напряжений в виде равностороннего треугольника.
Из каждой вершины треугольника циркулем провести засечки, радиусы которых в масштабе соответственно равны напряжениям. Точку их пересечения и соединить с вершинами треугольника, получив векторы фазных напряжений.
Построить векторы фазных токов, учитывая характер нагрузки каждой фазы приемника: при активной нагрузке — ток и напряжение совпадают по фазе, при индуктивной — ток отстает по фазе от напряжения на 90°, при емкостной — ток опережает напряжение на 90°.
Построить вектор тока в нейтральном проводе по уравнению
 и
определить его величину, измерив длину
вектора и учтя масштабный коэффициент.
и
определить его величину, измерив длину
вектора и учтя масштабный коэффициент.
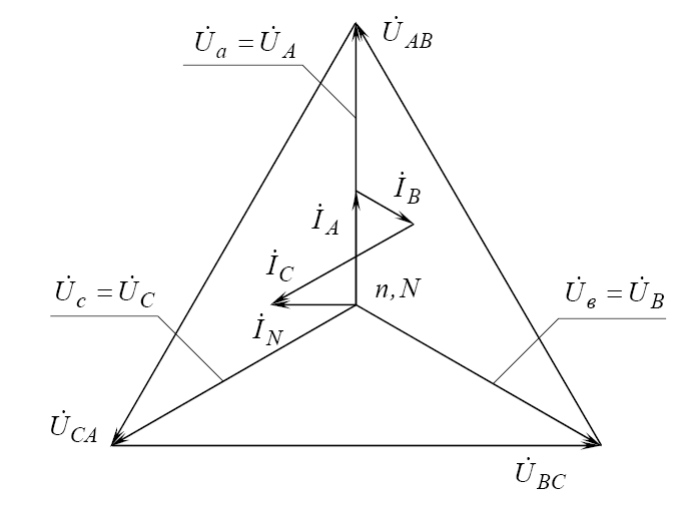 .
.
Рис.11. Векторная диаграмма напряжений и токов несимметричного приемника с нейтральным проводом
Список литературы
ГОСТ 19880-74 Электротехника. Основные понятия. Термины и определения. M.: Издательство стандартов, 1974
ГОСТ 2.710-81 ЕСКД. Обозначения буквенно-цифренные в электрических схемах.
И. И. Иванов , Г. И. Соловьев, В. С. Радоник. Электротехника Издательство «Лань»; 2005-496c.
В. В. Бережных, И. П. Макарьева Электрические цепи. Электротехника. Методические указания к выполнению лабораторных работ ; Иркутск 2001-36с
Касаткин А. С., Немцов М. В. Электротехника M.:Высшая школа 1999-524с.
Стандарт организации ИрНИТУ — СТО 005-2015
16
Построение в заданном масштабе векторной диаграммы напряжений, отложив горизонтально вектор тока, страница 7
Начертить схему цепи. Определить фазное напряжение 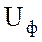 ; фазные
; фазные 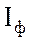 и
линейные
и
линейные 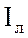 токи; активную мощность
токи; активную мощность 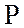 всех трех фаз.
всех трех фаз.
Построить в масштабе 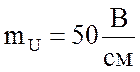 ,
, 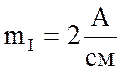 векторную диаграмму напряжений и токов;
графически (из векторной диаграммы) определить ток в нейтральном (нулевом)
проводе
векторную диаграмму напряжений и токов;
графически (из векторной диаграммы) определить ток в нейтральном (нулевом)
проводе 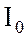 .
.
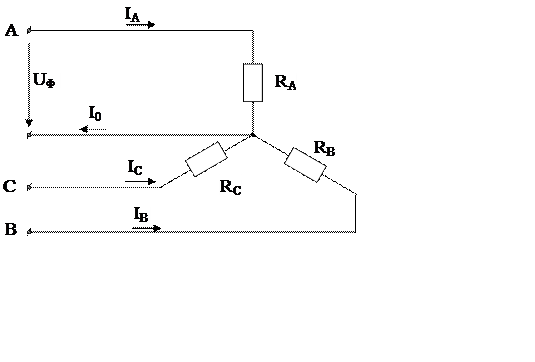 Дано:
Дано:
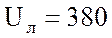 В;
В;
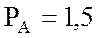 кВт;
кВт;
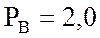 кВт;
кВт;
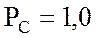 кВт;
кВт;
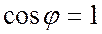 ;
;
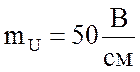 ;
;
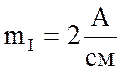 .
.
 Найти:
Найти: 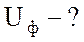 ;
;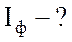 ;
; 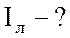 ;
; 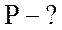 .
.
Решение.
1. Найду фазное напряжение:
Поскольку задана равномерная однородная нагрузка фаз, то доже при отсутствии нулевого провода фазные напряжения равны.
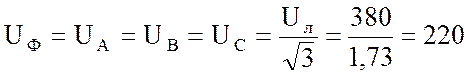 В.
В.
2. Рассчитаю фазные токи (они же линейные):
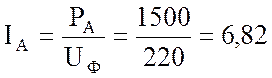 А;
А;
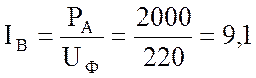 А;
А;
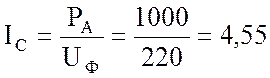 А.
А.
3. Определяю активную мощность трех фаз:
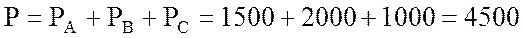 Вт.
Вт.
4. Строю векторную диаграмму:
Длины векторов фазных напряжений в масштабе 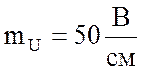 будут
равны:
будут
равны:
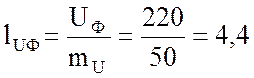 см.
см.
Длины векторов фазных токов в масштабе 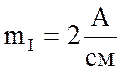 будут
равны:
будут
равны:
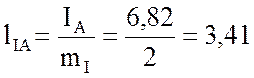 см;
см; 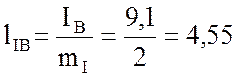 см;
см; 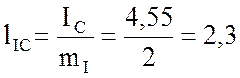 см
см
Вначале откладываем векторы фазных напряжений. Вектор 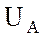 откладывается вертикально вверх,
вектор
откладывается вертикально вверх,
вектор 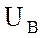 отстает от вектора
отстает от вектора 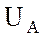 на 120º, а вектор
на 120º, а вектор 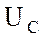 в свою очередь отстает от вектора
в свою очередь отстает от вектора 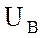 на 120º. Соединив концы векторов
фазных напряжений, получим треугольник линейных напряжений
на 120º. Соединив концы векторов
фазных напряжений, получим треугольник линейных напряжений 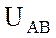 ,
, 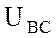 ,
, 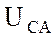 . Векторы фазных токов совпадают с
векторами соответствующих фазных напряжений, так как нагрузка фаз активная..
. Векторы фазных токов совпадают с
векторами соответствующих фазных напряжений, так как нагрузка фаз активная..

5. Нахожу
вектор тока в нейтральном (нулевом) проводе. Он согласно первому закину
Кирхгофа равен сумме векторов фазных токов, т.е. 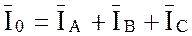 .Выполню
сложение векторов на векторной диаграмме. Величину тока
.Выполню
сложение векторов на векторной диаграмме. Величину тока 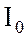 нахожу,
измерив длину его вектора и пользуясь масштабом:
нахожу,
измерив длину его вектора и пользуясь масштабом: 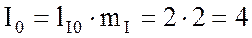 А.
А.
Ответ: фазное напряжение 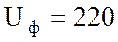 В;
ток фазы А он же линейный
В;
ток фазы А он же линейный 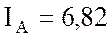 А, ток фазы В он
же линейный
А, ток фазы В он
же линейный 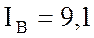 А; ток фазы С он же линейный
А; ток фазы С он же линейный 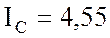 А; активную мощность всех трех фазах
А; активную мощность всех трех фазах 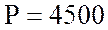 В, ток в нейтральном (нулевом)
проводе
В, ток в нейтральном (нулевом)
проводе 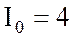 А.
А.
Контрольная работа №4.
Задача 5.
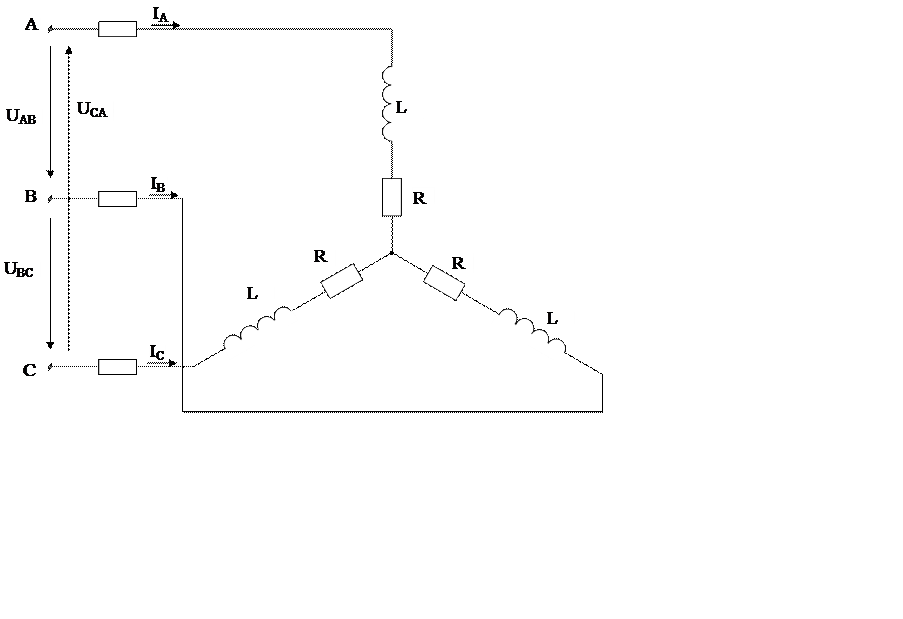
В трехфазную
сеть напряжением 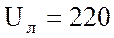 В включен двигатель,
потребляющий мощность
В включен двигатель,
потребляющий мощность 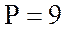 кВт. Обмотка двигателя
соединена звездой. Линейный ток двигателя
кВт. Обмотка двигателя
соединена звездой. Линейный ток двигателя 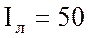 А.
Начертить схему цепи. Определить фазное напряжение
А.
Начертить схему цепи. Определить фазное напряжение 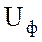 ;
полное
;
полное 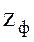 , активное
, активное 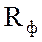 и
индуктивное
и
индуктивное 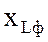 сопротивления фазы; коэффициент
мощности
сопротивления фазы; коэффициент
мощности 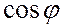 ; полную
; полную 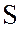 и
реактивную
и
реактивную  мощности двигателя. Построить в
масштабе
мощности двигателя. Построить в
масштабе 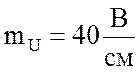 ,
, 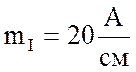 векторную
диаграмму напряжений и токов.
векторную
диаграмму напряжений и токов.
 Дано:
Дано:
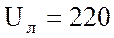 В;
В;
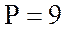 кВт;
кВт;
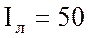 А;
А;
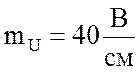 ;
;
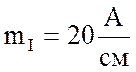 ..
..
 Найти:
Найти: 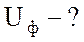 ;
; 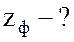 ;
;
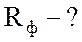 ;
; 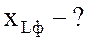 ;
; 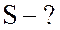 ;
; 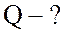 .
.
Решение.
1. 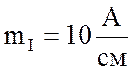
 Найду фазное
напряжение:
Найду фазное
напряжение:
Поскольку задана равномерная однородная нагрузка фаз, то доже при отсутствии нулевого провода фазные напряжения равны.
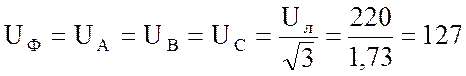 В.
В.
2. Рассчитаю фазные токи, они равны линейным:
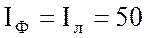 А.
А.
3. Найду полное сопротивление каждой фазы:
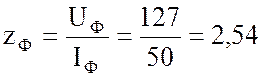 Ом.
Ом.
4. Определю коэффициент мощности фазы (а так как нагрузка фаз равномерная и однородная, то и всего потребителя)
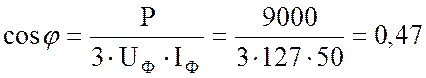 ;
;
следовательно, 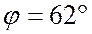 ;
; 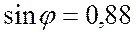 .
.
5. Рассчитаю активное сопротивление фазы:
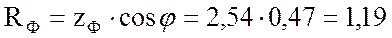 Ом
Ом
6. Рассчитаю реактивное сопротивление фазы:
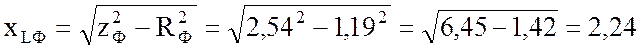 Ом
Ом
7. Определяю мощности трехфазных потребителей:
полная:  ВА;
ВА;
реактивная: 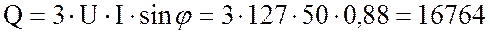 вар.
вар.
8. Строю векторную диаграмму:
Длины векторов фазных напряжений в масштабе  будут
равны:
будут
равны: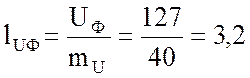 см.
см.
Длины векторов фазных токов в масштабе 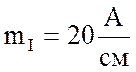 будут
равны:
будут
равны: 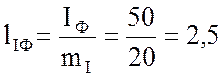 см.
см.
Вначале откладываем векторы фазных напряжений. Вектор 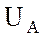 откладывается вертикально вверх,
вектор
откладывается вертикально вверх,
вектор 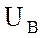 отстает от вектора
отстает от вектора 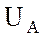 на 120º, а вектор
на 120º, а вектор 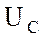 в свою очередь отстает от вектора
в свою очередь отстает от вектора 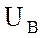 на 120º. Соединив концы векторов
фазных напряжений, получим треугольник линейных напряжений
на 120º. Соединив концы векторов
фазных напряжений, получим треугольник линейных напряжений 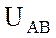 ,
, 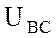 ,
, 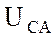 . Поскольку нагрузка фаз
активно-индуктивная, то векторы фазных токов
. Поскольку нагрузка фаз
активно-индуктивная, то векторы фазных токов 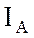 ,
, 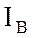 ,
, 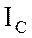 будут
отставать от векторов фазных напряжений
будут
отставать от векторов фазных напряжений 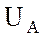 ,
, 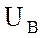 ,
, 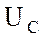 на
угол
на
угол 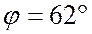 (
(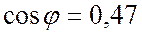 ).
).
Ответ: фазное
напряжение 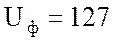 В; фазные токи
В; фазные токи 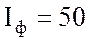 А; полное сопротивление фазы
А; полное сопротивление фазы 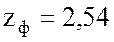 Ом; активное
сопротивление фазы
Ом; активное
сопротивление фазы 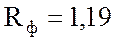 Ом и индуктивное сопротивление
фазы
Ом и индуктивное сопротивление
фазы 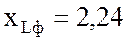 Ом; полную мощность
Ом; полную мощность 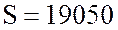 ВА, реактивную мощность
ВА, реактивную мощность 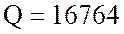 вар.
вар.
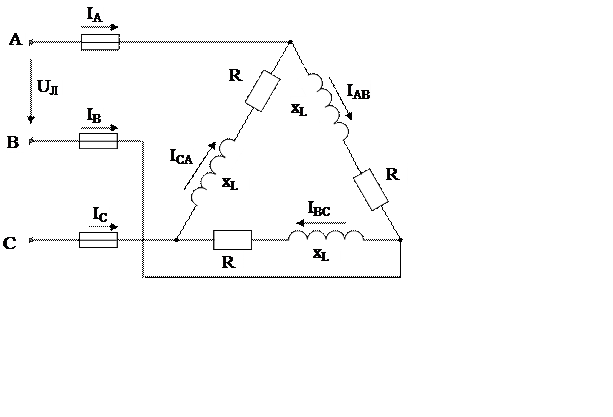
Задача 6.
В трехфазную сеть напряжением 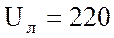 В
включен треугольником потребитель мощностью
В
включен треугольником потребитель мощностью 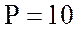 кВт
при
кВт
при 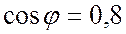 .
.
Начертить схему цепи. Определить фазное напряжение 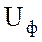 ; фазный
; фазный 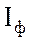 и
линейный
и
линейный 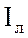 ток потребителя; полную
ток потребителя; полную 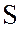 и реактивную
и реактивную  мощности
потребителя.
мощности
потребителя.
 Построить в масштабе
Построить в масштабе 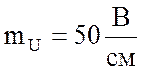 ,
, 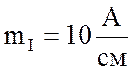 векторную диаграмму напряжений и
токов.
векторную диаграмму напряжений и
токов.
 Дано:
Дано:
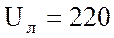 В;
В;
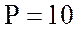 кВт;
кВт;
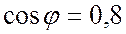 ;
;
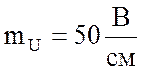 ;
;
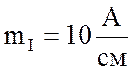 ..
..
 Найти:
Найти: 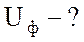 ;
; 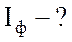 ;
;
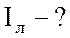 ;
; 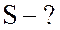 ;
; 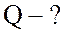 .
.
Решение.
1. При соединении треугольником фазное напряжение равно линейному, то есть:
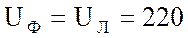 В.
В.
2. Из формулы мощности нахожу фазный ток потребителя:
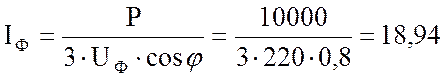 А.
А.
3. Рассчитываю линейный ток:
Так как нагрузка равномерная, то
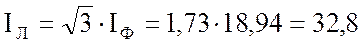 А.
А.
4. Нахожу полную мощность приемника
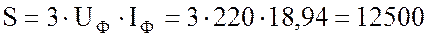 ВА.
ВА.
5. Рассчитываю реактивная мощность приемника:
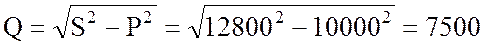 вар.
вар.
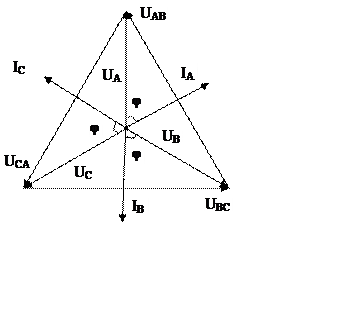
6. Строю векторную диаграмму.
Длина векторов фазных (линейных) напряжений
в масштабе 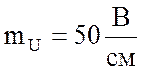 будут равны:
будут равны:
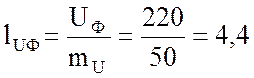 см.
см.
Длина векторов фазных токов в масштабе 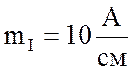 будут равны:
будут равны:
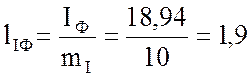 см;
см;
При
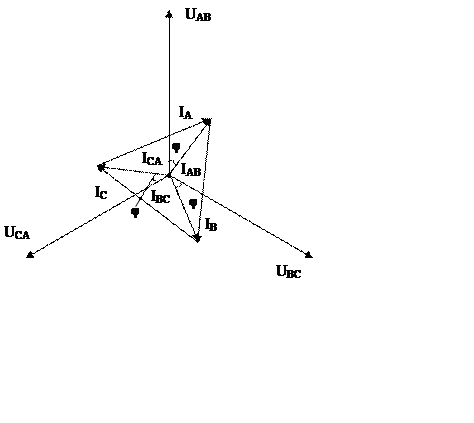
построении векторной диаграммы вначале откладываю три вектора линейных (фазных)
напряжений со сдвигом относительно друг друга на 120º. Векторы фазных токов
отстают от векторов фазных напряжений на угол 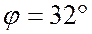 (
(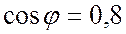 ), нагрузка активно индуктивная.
Соединив концы векторов фазных токов, получу треугольник линейных токов; при
этом векторы линейных токов являются разностью векторов соответствующих фазных
токов:
), нагрузка активно индуктивная.
Соединив концы векторов фазных токов, получу треугольник линейных токов; при
этом векторы линейных токов являются разностью векторов соответствующих фазных
токов:
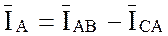 ;
; 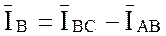 ;
; 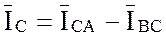
Ответ: фазное напряжение 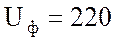 В; фазный ток потребителя
В; фазный ток потребителя 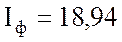 А; линейный ток потребителя
А; линейный ток потребителя 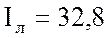 А; полная мощность потребителя
А; полная мощность потребителя 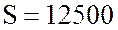 ВА; и реактивная мощность
потребителя
ВА; и реактивная мощность
потребителя 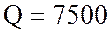 вар.
вар.
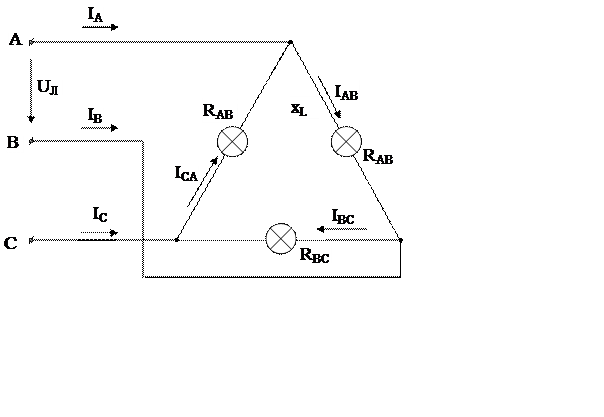
Задача 7.
В трехфазную сеть с линейным напряжением 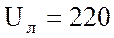 В включены треугольником три разные
группы ламп. Мощность ламп в фазах составляет:
В включены треугольником три разные
группы ламп. Мощность ламп в фазах составляет: 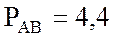 кВт,
кВт, 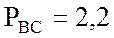 кВт,
кВт, 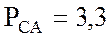 кВт.
кВт.
Начертить схему цепи. Определить фазное напряжение 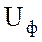 ; фазные токи
; фазные токи 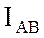 ,
, 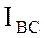 ,
, 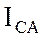 и
мощность
и
мощность 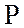 , потребляемую всеми лампами.
, потребляемую всеми лампами.
Построить в масштабе 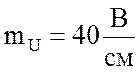 ,
, 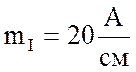 векторную диаграмму напряжений и
токов. Пользуясь масштабом, найти по векторной диаграмме значения токов в
линейных проводах
векторную диаграмму напряжений и
токов. Пользуясь масштабом, найти по векторной диаграмме значения токов в
линейных проводах 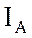 ,
, 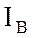 ,
, 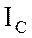 .
.
 Дано:
Дано:
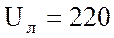 В;
В;
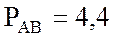 кВт;
кВт;
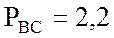 кВт;
кВт;
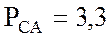 кВт;
кВт;
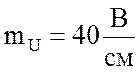 ;
;
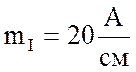 .
.
 Найти:
Найти: 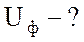 ;
; 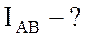 ;
;
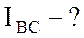 ;
; 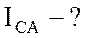 ;
; 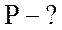 ;
; 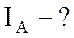 ;
;
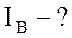 ;
; 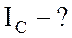 .
.
Решение.
1. При соединении треугольником фазное напряжение равно линейному, то есть:
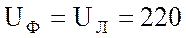 В.
В.
2. Определяю фазные токи:
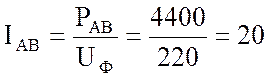 А;
А;
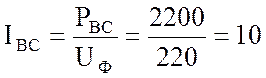 А;
А;
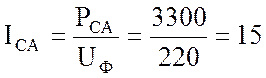 А.
А.
3. Нахожу активную мощность всех ламп:
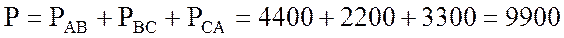 Вт.
Вт.
4. Строю векторную диаграмму.
Длина векторов фазных (линейных) напряжений
в масштабе 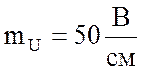 будут равны:
будут равны:
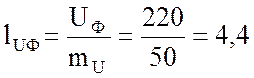 см.
см.
Длина векторов фазных токов в масштабе 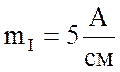 будут равны:
будут равны:
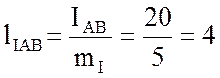 см;
см; 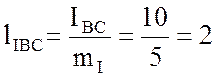 см;
см; 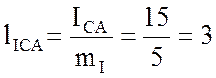 см
см
При построении векторной диаграммы вначале откладываю три вектора линейных (фазных) напряжений со сдвигом относительно друг друга на 120º. Векторы фазных токов совпадают с векторами фазных напряжений, так как нагрузка фаз – активная. Векторы линейных токов, равные разности векторов составляющих фазных токов получу соединив концы векторов фазных токов:
Построение в заданном масштабе векторной диаграммы напряжений, отложив горизонтально вектор тока, страница 3
4. Рассчитываю силу тока в цепи:
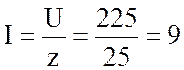 А.
А.
5. Рассчитываю падения напряжений на активном и емкостном сопротивлениях:
на активном 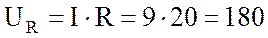 В;
В;
на реактивном 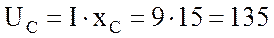 В.
В.
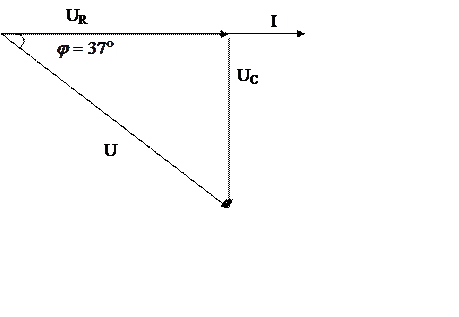
6. Построю векторную диаграмму.
Построение векторной диаграммы начну с вектора тока 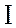 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 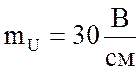 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
 см;
см;
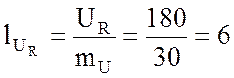 см;
см;
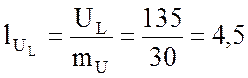 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 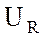 ;
на конце вектора
;
на конце вектора 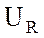 перпендикулярно вектору
тока строю отстающий ток на
перпендикулярно вектору
тока строю отстающий ток на 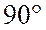 вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 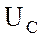 .
.
Замыкающий вектор, равный сумме векторов 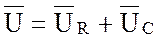 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 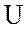 отстает от вектора
отстает от вектора 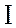 на угол
на угол  .
.
Ответ: сопротивление конденсатора 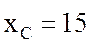 Ом, полное сопротивление цепи
Ом, полное сопротивление цепи 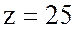 Ом, коэффициент мощности
Ом, коэффициент мощности 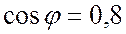 , угол
, угол 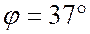 ,
ток в цепи
,
ток в цепи 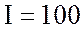 А, падение напряжения на активном
сопротивлении
А, падение напряжения на активном
сопротивлении 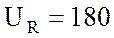 В, а на емкостном
сопротивлении
В, а на емкостном
сопротивлении 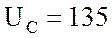 В
В
Задача 8.
Последовательно соединены
резистор с сопротивлением 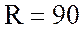 Ом и конденсатор,
имеющий сопротивление
Ом и конденсатор,
имеющий сопротивление 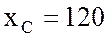 Ом. По цепи проходит ток
Ом. По цепи проходит ток 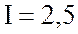 А. Частота напряжения питающей сети
А. Частота напряжения питающей сети 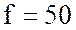 Гц.
Гц.
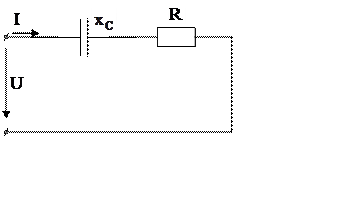
Начертить схему цепи.
Определить полное сопротивление цепи 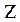 , коэффициент
мощности
, коэффициент
мощности 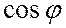 , угол
, угол 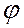 ,
подведенное напряжение
,
подведенное напряжение 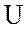 , падения напряжения
, падения напряжения 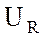 и
и 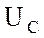 на
активном и емкостном сопротивлениях, емкость конденсатора С.
на
активном и емкостном сопротивлениях, емкость конденсатора С.
Построить в масштабе 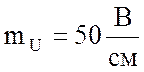 векторную диаграмму напряжений,
отложив горизонтально вектор тока.
векторную диаграмму напряжений,
отложив горизонтально вектор тока.
 Дано:
Дано:
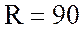 Ом;
Ом;
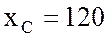 Ом;
Ом;
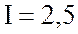 А;
А;
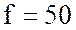 Гц
Гц
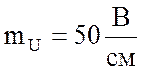
 Найти:
Найти: 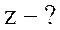 ;
; 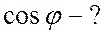 ;
;
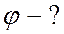 ;
; 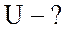 ;
; 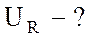 ;
; 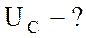 ;
;
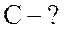 .
.
Решение.
1. Найду полное сопротивление цепи:
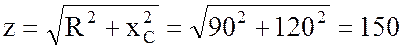 Ом.
Ом.
2. Нахожу коэффициент мощности и угол 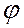 :
:
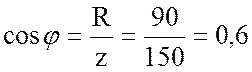 ;
;
 ;
;
3. Рассчитываю падение напряжения цепи:
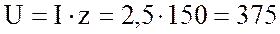 В.
В.
4. Рассчитываю падения напряжений на активном и емкостном сопротивлениях:
на активном 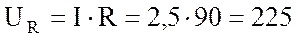 В;
В;
на реактивном 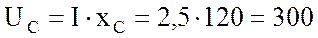 В.
В.
5. Найду емкость конденсатора:
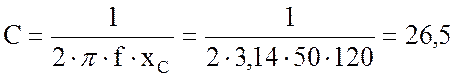 мкФ
мкФ
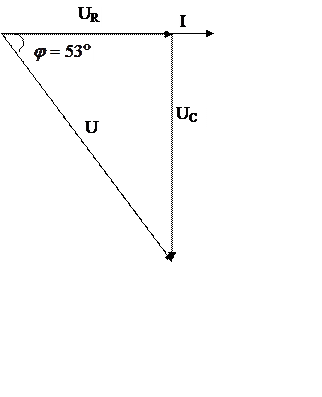
6. Построю векторную диаграмму.
Построение векторной диаграммы начну с вектора тока 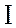 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 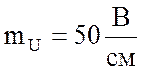 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
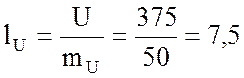 см;
см;
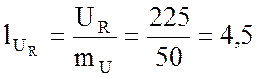 см;
см;
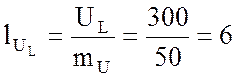 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 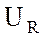 ;
на конце вектора
;
на конце вектора 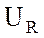 перпендикулярно вектору
тока строю отстающий ток на
перпендикулярно вектору
тока строю отстающий ток на 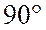 вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 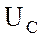 .
.
Замыкающий вектор, равный сумме векторов 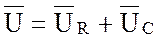 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 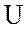 отстает от вектора
отстает от вектора 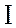 на угол
на угол 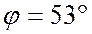 .
.
Ответ: полное сопротивление цепи 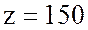 Ом, коэффициент мощности
Ом, коэффициент мощности 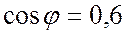 , угол
, угол 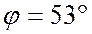 ,
ток в цепи
,
ток в цепи 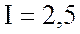 А, падение напряжения на активном
сопротивлении
А, падение напряжения на активном
сопротивлении 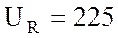 В, а на емкостном
сопротивлении
В, а на емкостном
сопротивлении 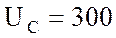 В
В
Задача 9.
К переменному напряжению 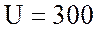 В частотой
В частотой 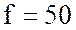 Гц
подключены последовательно соединенные резистор и конденсатор. По цепи проходит
ток
Гц
подключены последовательно соединенные резистор и конденсатор. По цепи проходит
ток 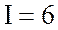 А, при этом на резисторе возникает
падение напряжения
А, при этом на резисторе возникает
падение напряжения 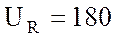 В.
В.
Начертить схему цепи.
Определить полное сопротивление цепи 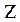 , сопротивление
резистора
, сопротивление
резистора 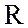 , сопротивление конденсатора
, сопротивление конденсатора 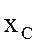 и емкость
и емкость 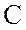 конденсатора,
коэффициент мощности
конденсатора,
коэффициент мощности 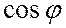 , угол
, угол 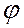 , падение напряжения
, падение напряжения 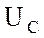 на емкостном сопротивлении.
на емкостном сопротивлении.
Построить в масштабе 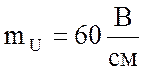 векторную диаграмму напряжений,
отложив горизонтально вектор тока.
векторную диаграмму напряжений,
отложив горизонтально вектор тока.
 Дано:
Дано:
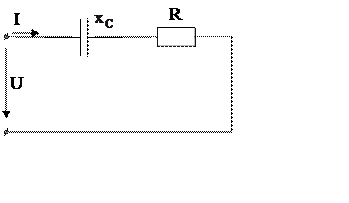
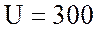 В;
В;
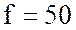 Гц;
Гц;
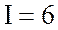 А;
А;
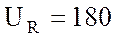 В;
В;
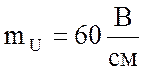 .
.
 Найти:
Найти: 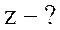 ;
; 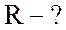 ;
; 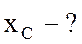 ;
;
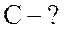
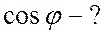 ;
; 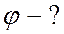 ;
; 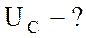 .
.
Решение.
1. Найду полное сопротивление цепи:
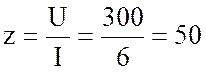 Ом.
Ом.
2. Найду активное сопротивление цепи:
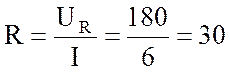 Ом.
Ом.
3. Нахожу сопротивление конденсатора:
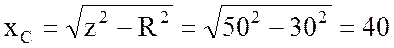 Ом
Ом
4. Найду емкость конденсатора:
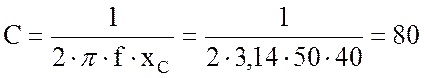 мкФ
мкФ
5. Нахожу коэффициент мощности и угол 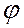 :
:
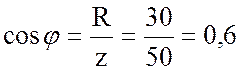 ;
;
 ;
;
6. Рассчитываю падение напряжения на емкостном сопротивлении:
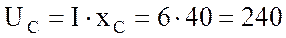 В.
В.
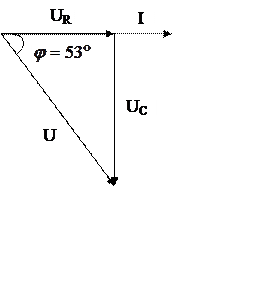
7. Построю векторную диаграмму.
Построение векторной диаграммы начну с вектора тока 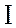 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 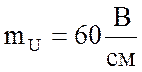 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
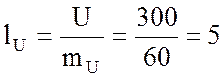 см;
см;
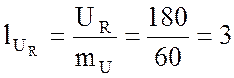 см;
см;
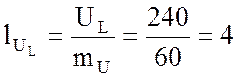 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 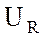 ;
на конце вектора
;
на конце вектора 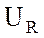 перпендикулярно вектору
тока строю отстающий ток на
перпендикулярно вектору
тока строю отстающий ток на 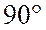 вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 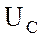 .
.
Замыкающий вектор, равный сумме векторов 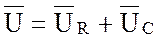 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 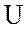 отстает от вектора
отстает от вектора 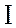 на угол
на угол 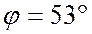 .
.
Ответ: полное сопротивление цепи 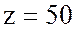 Ом, сопротивление резистора
Ом, сопротивление резистора 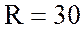 Ом, сопротивление конденсатора
Ом, сопротивление конденсатора 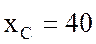 Ом, емкость конденсатора
Ом, емкость конденсатора 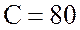 мкФ; коэффициент мощности
мкФ; коэффициент мощности 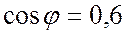 , угол
, угол 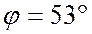 ,
напряжение на емкостном сопротивлении
,
напряжение на емкостном сопротивлении 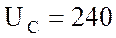 В
В
Задача 10.
Последовательно соединены
резистор и конденсатор. Цепь подключена к переменному напряжению частотой 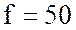 Гц. Известны падение напряжений на
активном
Гц. Известны падение напряжений на
активном 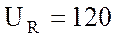 В и емкостном
В и емкостном 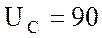 В сопротивлениях, а также
сопротивление резистора
В сопротивлениях, а также
сопротивление резистора 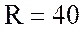 Ом.
Ом.
Начертить схему цепи.
Определить напряжение на зажимах цепи 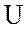 ,
ток в цепи
,
ток в цепи 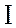 , емкостное сопротивление
, емкостное сопротивление 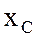 и емкость
и емкость 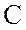 конденсатора,
полное сопротивление цепи
конденсатора,
полное сопротивление цепи 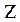 , коэффициент
мощности
, коэффициент
мощности 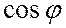 и угол
и угол 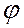
Построить в масштабе 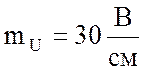 векторную диаграмму напряжений,
отложив горизонтально вектор тока.
векторную диаграмму напряжений,
отложив горизонтально вектор тока.
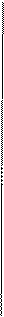 Дано:
Дано:

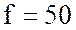 Гц;
Гц;
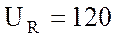 В;
В;
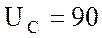 В;
В;
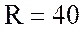 Ом;
Ом;
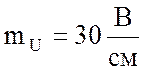 .
.
 Найти:
Найти: 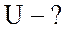 ;
; 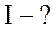 ;
; 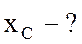 ;
;
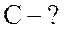 ;
; 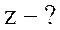 ;
; 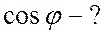 ;
;
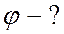 ;
; 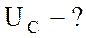 .
.
Решение.
1. Определяю напряжение на зажимах:
 В.
В.
2. Определяю ток в цепи:
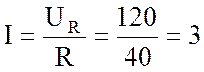 А
А
3. Нахожу сопротивление конденсатора:
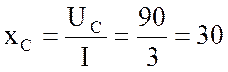 Ом
Ом
4. Найду емкость конденсатора:
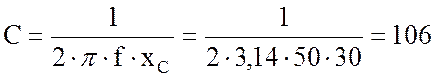 мкФ
мкФ
5. Найду полное сопротивление цепи:
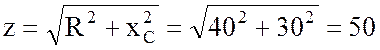 Ом.
Ом.
6. Нахожу коэффициент мощности и угол 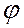 :
:
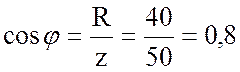 ;
;
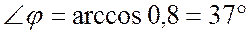 ;
;
7. Построю векторную диаграмму.
Построение векторной диаграммы начну с вектора тока 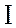 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 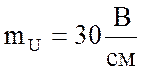 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
 см;
см;
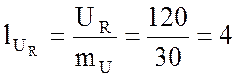 см;
см;
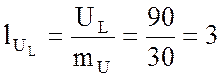 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 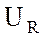 ;
на конце вектора
;
на конце вектора 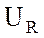 перпендикулярно вектору
тока строю отстающий ток на
перпендикулярно вектору
тока строю отстающий ток на 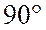 вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 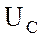 .
.
Замыкающий вектор, равный сумме векторов 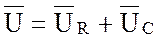 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 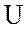 отстает от вектора
отстает от вектора 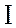 на угол
на угол  .
.

Ответ: напряжение на зажимах цепи 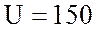 В, ток в цепи
В, ток в цепи 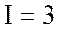 А, емкостное сопротивление
конденсатора
А, емкостное сопротивление
конденсатора 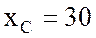 Ом, емкость конденсатора
Ом, емкость конденсатора 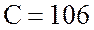 мкФ, полное сопротивление цепи
мкФ, полное сопротивление цепи 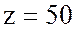 Ом, коэффициент мощности
Ом, коэффициент мощности 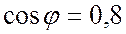 , угол
, угол  .
.




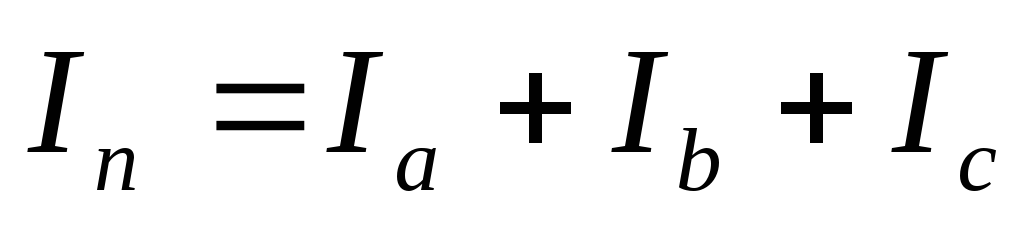 и
определить его величину, измерив длину
вектора и учтя масштабный коэффициент.
и
определить его величину, измерив длину
вектора и учтя масштабный коэффициент.