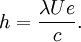Постоянная Планка — это… Что такое Постоянная Планка?
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой так же, как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действия с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское .
- Дж·c[1]
- эрг·c.
- эВ·c[1].
Часто применяется величина :
- Дж·c[1],
- эрг·c,
- эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака.
На 24-й Генеральной конференции по мерам и весам 17—21 октября 2011 года была единогласно принята резолюция[2]
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора, энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах(кг·м/с, Дж, Дж·с), чем соответствующие волновые (м
- (импульс)
- (энергия)
- (действие)
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с , в ней
- .
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если — действие системы, а — её момент импульса, то при или поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределенностей Гейзенберга.
История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения . Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:
Коэффициент пропорциональности впоследствии назвали постоянной Планка, = 1.054·10−34 Дж·с.
Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет
где — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), — кинетическая энергия вылетающего электрона, — частота падающего фотона с энергией , — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже не достаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества и на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
где — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- — частота падающего света,
- — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой , при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
где — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой и точно также запирают его с помощью напряжения
Почленно вычитая второе выражение из первого, получаем
откуда следует
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
где — скорость света,
- — длина волны рентгеновского излучения,
- — заряд электрона,
- — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
Примечания
Литература
- John D. Barrow. The Constants of Nature; From Alpha to Omega — The Numbers that Encode the Deepest Secrets of the Universe. — Pantheon Books, 2002. — ISBN 0-37-542221-8
Ссылки
Постоянная Дирака — Википедия
Материал из Википедии — свободной энциклопедии
Символы со сходным начертанием:Постоя́нная Дира́ка, или постоянная Планка — Дирака, — изредка используемое название для редуцированной постоянной Планка ℏ≡h/2π{\displaystyle \hbar \equiv h/2\pi } — коэффициента, связывающего угловую частоту ω=2πν{\displaystyle \omega =2\pi \nu } (ν{\displaystyle \nu } — частота) фотона (или другого кванта) с его энергией: E=hν=ℏω.{\displaystyle E=h\nu =\hbar \omega .} Здесь h{\displaystyle h} — (нередуцированная) постоянная Планка. Обычно постоянную Дирака ℏ{\displaystyle \hbar } называют рационализированной или
- ℏ≡h3π=1,054 571 800(13)×10−34{\displaystyle \hbar \equiv {\frac {h}{2\pi }}=1{,}054\ 571\ 800(13)\times 10^{-34}} Дж·c = 6,582 119 514(40)⋅10−16{\displaystyle 6{,}582\ 119\ 514(40)\cdot 10^{-16}} эВ·с[1].
Смысл введения редуцированной константы Планка и широкого её использования в том, что в теоретически более важных формулах при её использовании пропадает загромождающий множитель или делитель 2π. Прежде всего имеется в виду связь действия и фазы S=ℏφ{\displaystyle S=\hbar \varphi }, а также импульса c волновым вектором p=ℏk{\displaystyle \mathbf {p} =\hbar \mathbf {k} } и энергии с циклической частотой E=ℏω{\displaystyle E=\hbar \omega }(более употребительной, чем отличающаяся от неё множителем 2π простая частота ν{\displaystyle \nu }). Как следствие, с использованием такой формы константы Планка вообще большинство формул записывается чуть проще и прозрачнее.
В планковской системе единиц приведённая (редуцированная) постоянная Планка выбрана в качестве основной единицы. Также в теоретической физике используются системы величин (иногда говорят о системах единиц), в которых постоянная Планка — Дирака равна единице (ℏ=1{\displaystyle \hbar =1}), что позволяет ещё более упростить формулы, благодаря тому, что энергия и циклическая частота, фаза и действие, импульс и волновой вектор становятся попарно эквивалентными и взаимозаменяемыми величинами.
Обозначается строчной перечёркнутой латинской буквой ħ, в формулах называется «h с чертой» (англ. h-bar). В Юникоде этот символ занимает позицию U+0127; также имеется отдельный символ англ. Planck constant over two pi (U+210F, ℏ{\displaystyle \hbar }).
Постоянная Планка — Википедия
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское h{\displaystyle h}.
- h = 6,626 070 040(81) × 10−34Дж·c[1];
- h = 6,626 070 040(81) × 10−27эрг·c;
- h = 4,135 667 662(25) × 10−15эВ·c[1].
Часто применяется величина ℏ≡h3π{\displaystyle \hbar \equiv {\frac {h}{2\pi }}}:
- ħ = 1,054 571 800(13) × 10−34Дж·c[1];
- ħ = 1,054 571 800(13) × 10−27эрг·c;
- ħ = 6,582 119 514(40) × 10−16эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка входит в виде деленной на константу 2π{\displaystyle {2\pi }}.
В ряде естественных систем единиц является единицей измерения действия[2]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.
На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция[3], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X·10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[4]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана. XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к точному значению постоянной Планка, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ[5].
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора[источник не указан 240 дней], энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м−1, с−1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
- p=ℏk(|p|=2πℏ/λ){\displaystyle \mathbf {p} =\hbar \mathbf {k} \,\,\,(|\mathbf {p} |=2\pi \hbar /\lambda )} (импульс),
- E=ℏω{\displaystyle E=\hbar \omega } (энергия),
- S=ℏϕ{\displaystyle S=\hbar \phi } (действие).
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с ℏ=1{\displaystyle \hbar =1}, в ней
- p=k(|p|=2π/λ),{\displaystyle \mathbf {p} =\mathbf {k} \,\,\,(|\mathbf {p} |=2\pi /\lambda ),}
- E=ω,{\displaystyle E=\omega ,}
- S=ϕ,{\displaystyle S=\phi ,}
- (ℏ=1).{\displaystyle (\hbar =1).}
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если S{\displaystyle S} — действие системы, а M{\displaystyle M} — её момент импульса, то при Sℏ≫1{\displaystyle {\frac {S}{\hbar }}\gg 1} или Mℏ≫1{\displaystyle {\frac {M}{\hbar }}\gg 1} поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределённостей Гейзенберга.
История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности ħ впоследствии назвали постоянной Планка, ħ ≈ 1,054·10−34 Дж·с.
Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}
где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
- Kmax=hν−A,{\displaystyle K_{max}=h\nu -A,}
где Kmax{\displaystyle K_{max}} — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- ν{\displaystyle \nu } — частота падающего света,
- A{\displaystyle A} — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ν1{\displaystyle \nu _{1}}, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
- hν1=A+eU1,{\displaystyle h\nu _{1}=A+eU_{1},}
где e{\displaystyle e} — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой ν2{\displaystyle \nu _{2}} и точно так же запирают его с помощью напряжения U2:{\displaystyle U_{2}:}
- hν2=A+eU2.{\displaystyle h\nu _{2}=A+eU_{2}.}
Почленно вычитая второе выражение из первого, получаем
- h(ν1−ν2)=e(U1−U2),{\displaystyle h(\nu _{1}-\nu _{2})=e(U_{1}-U_{2}),}
откуда следует
- h=e(U1−U2)(ν1−ν2).{\displaystyle h={\frac {e(U_{1}-U_{2})}{(\nu _{1}-\nu _{2})}}.}
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
- hcλ=eU,{\displaystyle h{\frac {c}{\lambda }}=eU,}
где c{\displaystyle c} — скорость света,
- λ{\displaystyle \lambda } — длина волны рентгеновского излучения,
- e{\displaystyle e} — заряд электрона,
- U{\displaystyle U} — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
- h=λUec.{\displaystyle h={\frac {{\lambda }{Ue}}{c}}.}
См. также
Примечания
Литература
Ссылки
Зачем нужна постоянная Планка? – ответы на главные вопросы
Но оказывается, что существуют три фундаментальных величины, с которыми имеет дело современная фундаментальная физика: это постоянная Планка, скорость света и гравитационная постоянная Ньютона. Из этих постоянных можно составить величины, которые имеют размерности секунды, килограмма и метра. Последние и называются планковскими единицами. Планковские единицы и есть естественные (природные) единицы, в которых можно измерить соответствующие величины. Другое дело, что они не всегда удобны в применении в повседневной жизни, так как, например, планковская длина — это 1,6 · 10−35 метра.
Постоянная Планка возникла как коэффициент пропорциональности между энергией кванта и его частотой. Это та самая h в формуле Планка E=hv, равная 1,054 · 10−27 эрг·с. Сначала Макс Планк написал формулу, которая описывает так называемое распределение энергии излучения абсолютно черного тела, то есть с какой частотой какое количество энергии излучается. А потом, чтобы объяснить эту формулу, ему пришлось ввести понятие кванта — порции энергии. Именно Планк предположил, что свет излучается порциями, квантами, а не непрерывно.
Другой пример — явление фотоэффекта, объясненное Альбертом Эйнштейном на основе гипотезы Планка о квантовой природе света. Работает это явление следующим образом: есть некоторый материал, а вы на него светите и смотрите, выбиваются ли из него в результате электроны. Если менять интенсивность света и при этом держать очень низкую частоту, то электроны вылетать не будут. С другой стороны, если интенсивность оставить постоянной и наращивать частоту, то начиная с какого-то момента электроны начнут вышибаться из материала. Это говорит о том, что, меняя частоту, вы меняете энергию квантов, которые, сталкиваясь с электронами в материале, придают ему энергию, достаточную, чтобы он преодолел барьер и вышел за пределы вещества. Фотоэффект используется, например, в метро: когда вы загораживаете свет турникета, то есть прерываете поток света, падающий на фотоэлемент, то проход автоматически блокируется.
Таким образом, с помощью постоянной Планка можно оценить, насколько применима к той или иной системе классическая механика. Она является одной из констант теоретической физики и помогает описывать квантовые физические явления.
Приведённая постоянная Планка — это… Что такое Приведённая постоянная Планка?
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии электромагнитного излучения с его частотой. Также имеет смысл кванта действия и кванта момента импульса. Введена в научный обиход М. Планком в работе, посвящённой тепловому излучению, и потому названа в его честь.
 Дж·c
Дж·c Эрг·c.
Эрг·c. эВ·c.
эВ·c.
Часто применяется величина
 Дж·c,
Дж·c, Эрг·c,
Эрг·c, эВ·c,
эВ·c,
называемая редуцированной (или рационализированной) постоянной Планка или постоянной Дирака.
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора, энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах(кг·м/с, Дж, Дж·с), чем соответствующие волновые (м-1,с-1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
 (импульс)
(импульс) 
 (энергия)
(энергия)
 (действие)
(действие)
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с 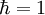 , в ней
, в ней
 .
.
При этом постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной действия или момента импульса показывает, насколько применима к данной физической системе классическая механика. А именно, если 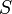 — действие системы, а
— действие системы, а 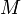 — её момент импульса, то при
— её момент импульса, то при 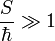 или
или 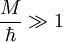 поведение системы с хорошей точностью описывается классической механикой.
поведение системы с хорошей точностью описывается классической механикой.
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
где 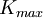 — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
— максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
 — частота падающего света,
— частота падающего света, — т. н. работа выхода электрона.
— т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой  , при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
где  — заряд электрона.
— заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой 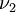 и точно также запирают его с помощью напряжения
и точно также запирают его с помощью напряжения 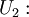
Почленно вычитая второе выражение из первого, получаем
откуда следует
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
где  — скорость света,
— скорость света,
 — длина волны рентгеновского излучения,
— длина волны рентгеновского излучения, — заряд электрона,
— заряд электрона, — ускоряющее напряжение между электродами рентгеновской трубки.
— ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
Ссылки
См. также
Wikimedia Foundation. 2010.
Постоянная Планка — Википедия. Что такое Постоянная Планка
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское h{\displaystyle h}.
- h = 6,626 070 040(81) × 10−34Дж·c[1];
- h = 6,626 070 040(81) × 10−27эрг·c;
- h = 4,135 667 662(25) × 10−15эВ·c[1].
Часто применяется величина ℏ≡h3π{\displaystyle \hbar \equiv {\frac {h}{2\pi }}}:
- ħ = 1,054 571 800(13) × 10−34Дж·c[1];
- ħ = 1,054 571 800(13) × 10−27эрг·c;
- ħ = 6,582 119 514(40) × 10−16эВ·c[1],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка входит в виде деленной на константу 2π{\displaystyle {2\pi }}.
В ряде естественных систем единиц является единицей измерения действия[2]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.
На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция[3], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X·10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[4]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана. XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к точному значению постоянной Планка, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ[5].
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора[источник не указан 240 дней], энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м−1, с−1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
- p=ℏk(|p|=2πℏ/λ){\displaystyle \mathbf {p} =\hbar \mathbf {k} \,\,\,(|\mathbf {p} |=2\pi \hbar /\lambda )} (импульс),
- E=ℏω{\displaystyle E=\hbar \omega } (энергия),
- S=ℏϕ{\displaystyle S=\hbar \phi } (действие).
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с ℏ=1{\displaystyle \hbar =1}, в ней
- p=k(|p|=2π/λ),{\displaystyle \mathbf {p} =\mathbf {k} \,\,\,(|\mathbf {p} |=2\pi /\lambda ),}
- E=ω,{\displaystyle E=\omega ,}
- S=ϕ,{\displaystyle S=\phi ,}
- (ℏ=1).{\displaystyle (\hbar =1).}
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, показывает, насколько применима к данной физической системе классическая механика. А именно, если S{\displaystyle S} — действие системы, а M{\displaystyle M} — её момент импульса, то при Sℏ≫1{\displaystyle {\frac {S}{\hbar }}\gg 1} или Mℏ≫1{\displaystyle {\frac {M}{\hbar }}\gg 1} поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределённостей Гейзенберга.
История открытия
Формула Планка для теплового излучения
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности ħ впоследствии назвали постоянной Планка, ħ ≈ 1,054·10−34 Дж·с.
Фотоэффект
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}
где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
- Kmax=hν−A,{\displaystyle K_{max}=h\nu -A,}
где Kmax{\displaystyle K_{max}} — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- ν{\displaystyle \nu } — частота падающего света,
- A{\displaystyle A} — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ν1{\displaystyle \nu _{1}}, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
- hν1=A+eU1,{\displaystyle h\nu _{1}=A+eU_{1},}
где e{\displaystyle e} — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой ν2{\displaystyle \nu _{2}} и точно так же запирают его с помощью напряжения U2:{\displaystyle U_{2}:}
- hν2=A+eU2.{\displaystyle h\nu _{2}=A+eU_{2}.}
Почленно вычитая второе выражение из первого, получаем
- h(ν1−ν2)=e(U1−U2),{\displaystyle h(\nu _{1}-\nu _{2})=e(U_{1}-U_{2}),}
откуда следует
- h=e(U1−U2)(ν1−ν2).{\displaystyle h={\frac {e(U_{1}-U_{2})}{(\nu _{1}-\nu _{2})}}.}
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
- hcλ=eU,{\displaystyle h{\frac {c}{\lambda }}=eU,}
где c{\displaystyle c} — скорость света,
- λ{\displaystyle \lambda } — длина волны рентгеновского излучения,
- e{\displaystyle e} — заряд электрона,
- U{\displaystyle U} — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
- h=λUec.{\displaystyle h={\frac {{\lambda }{Ue}}{c}}.}
См. также
Примечания
Литература
Ссылки
Редуцированная постоянная Планка — это… Что такое Редуцированная постоянная Планка?
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии электромагнитного излучения с его частотой. Также имеет смысл кванта действия и кванта момента импульса. Введена в научный обиход М. Планком в работе, посвящённой тепловому излучению, и потому названа в его честь.
 Дж·c
Дж·c Эрг·c.
Эрг·c. эВ·c.
эВ·c.
Часто применяется величина
 Дж·c,
Дж·c, Эрг·c,
Эрг·c, эВ·c,
эВ·c,
называемая редуцированной (или рационализированной) постоянной Планка или постоянной Дирака.
Физический смысл
В квантовой механике импульс имеет физический смысл волнового вектора, энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах(кг·м/с, Дж, Дж·с), чем соответствующие волновые (м-1,с-1, безразмерные единицы фазы). Постоянная Планка играет роль переводного коэффициента (всегда одного и того же), связывающего эти две системы единиц — квантовую и традиционную:
 (импульс)
(импульс) 
 (энергия)
(энергия)
 (действие)
(действие)
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с 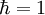 , в ней
, в ней
 .
.
При этом постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики: она в сравнении с величиной действия или момента импульса показывает, насколько применима к данной физической системе классическая механика. А именно, если 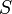 — действие системы, а
— действие системы, а 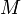 — её момент импульса, то при
— её момент импульса, то при 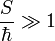 или
или 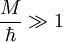 поведение системы с хорошей точностью описывается классической механикой.
поведение системы с хорошей точностью описывается классической механикой.
Методы измерения
Использование законов фотоэффекта
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
где 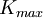 — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
— максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
 — частота падающего света,
— частота падающего света, — т. н. работа выхода электрона.
— т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой  , при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
где  — заряд электрона.
— заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой 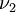 и точно также запирают его с помощью напряжения
и точно также запирают его с помощью напряжения 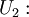
Почленно вычитая второе выражение из первого, получаем
откуда следует
Анализ спектра тормозного рентгеновского излучения
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
где  — скорость света,
— скорость света,
 — длина волны рентгеновского излучения,
— длина волны рентгеновского излучения, — заряд электрона,
— заряд электрона, — ускоряющее напряжение между электродами рентгеновской трубки.
— ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
Ссылки
См. также
Wikimedia Foundation. 2010.




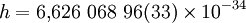 Дж·c
Дж·c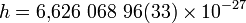 Эрг·c.
Эрг·c.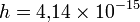 эВ·c.
эВ·c.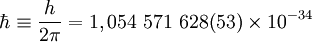 Дж·c,
Дж·c,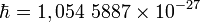 Эрг·c,
Эрг·c,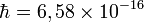 эВ·c,
эВ·c,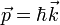 (импульс)
(импульс) 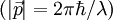
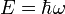 (энергия)
(энергия)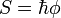 (действие)
(действие)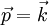
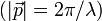
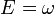
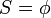
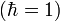 .
.
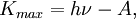
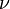 — частота падающего света,
— частота падающего света,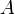 — т. н. работа выхода электрона.
— т. н. работа выхода электрона.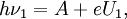
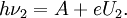
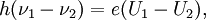
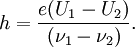
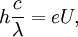
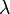 — длина волны рентгеновского излучения,
— длина волны рентгеновского излучения,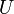 — ускоряющее напряжение между электродами рентгеновской трубки.
— ускоряющее напряжение между электродами рентгеновской трубки.