электрическая постоянная — это… Что такое электрическая постоянная?



электрическая постоянная

электри́ческая постоя́нная коэффициент пропорциональности ε₀ в законе Кулона , определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q₁ и q₂; ε₀ = (μ₀c²)^-1Ф/м = 8,854187817·10^-12Ф/м, где μ₀ — магнитная постоянная. Электрическая постоянная называется также диэлектрической проницаемостью вакуума.

* * *

ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ ЭЛЕКТРИ́ЧЕСКАЯ ПОСТОЯ́ННАЯ, коэффициент пропорциональности e_о в законе Кулона
определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q₁ и q₂; e_о = (m_о c²)^-1 Ф/м = 8,854187817·10^-12 Ф/м, где m_о — магнитная постоянная (см. МАГНИТНАЯ ПОСТОЯННАЯ). Электрическая постоянная называется также диэлектрической проницаемостью вакуума.

Энциклопедический словарь. 2009.

• электрическая подстанция
• электрическая прочность

Смотреть что такое «электрическая постоянная» в других словарях:

• ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (e0) (по старой терминологии диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур ний в рационализованной форме, в соответствии с к рой образованы электрич. и магн. ед …   Физическая энциклопедия

• ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — коэффициент пропорциональности ?о в законе Кулона определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ?о = (?оc2) 1 Ф/м = 8,854187817.10 12 Ф/м, где ?о магнитная постоянная.… …   Большой Энциклопедический словарь

• электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м …   Справочник технического переводчика

• ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) …   Большая политехническая энциклопедия

• электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… …   Политехнический терминологический толковый словарь

• Электрическая постоянная — 14. Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник …   Словарь-справочник терминов нормативно-технической документации

• Электрическая постоянная — (ранее также носила название диэлектрической постоянной)  физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона …   Википедия

• электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… …   Automatikos terminų žodynas

• электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… …   Fizikos terminų žodynas

Электрическая постоянная | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Электрическая постоянная — определяет напряжённость электрического поля в вакууме

Электрическая постоянная называется также диэлектрической проницаемостью вакуума. Используется в Законе Кулона.

В системе Си электрическая постоянная имеет размерность фарад на метр . В системе СГС (Гауссовской) принимают равной единице.

В отличии от диэлектрической проницаемости, электрическая зависит только от выбора системы единиц.

В формуле мы использовали :

— Электрическая постоянная

— Магнитная постоянная

— Скорость света

— Сила Кулона

— Электрический заряд тела

— Расстояние между зарядами

— Диэлектрическая проницаемость среды

Электрическая постоянная Википедия

Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)

[1].

Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума^[2]. Измеряется в фарадах, делённых на метр.

Определение

По определению в СИ электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением^[1]

ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}

Численное значение

В Международной системе единиц

До изменения СИ 2018—2019 годов

Поскольку в СИ для магнитной постоянной было справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м, то для электрической постоянной выполнялось соотношение

ε0=14πc2⋅107{\displaystyle \varepsilon _{0}={\frac {1}{4\pi c^{2}}}\cdot 10^{7}}м/Гн,^[3]

также являвшееся точным.

Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение ε0{\displaystyle \varepsilon _{0}} в СИ:

ε0=14π⋅ 2997924582×10−7{\displaystyle \varepsilon _{0}={\frac {1}{4\pi \cdot \ 299792458^{2}\times 10^{-7}}}} Ф/м ≈ 8,85418781762039 · 10⁻¹² Ф·м⁻¹.

Или, выражая то же через основные единицы СИ,

ε₀ ≈ 8,85418781762039 · 10⁻¹² м⁻³·кг⁻¹·с⁴·А².

После изменений СИ 2018—2019 годов

С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение электрической постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение электрической постоянной, рекомендованное CODATA^[4]:

ε₀ = 8,8541878128(13)· 10⁻¹² м⁻³·кг⁻¹·с⁴·А², или Ф·м⁻¹.

В системе СГС

В системе СГС электрическая постоянная как коэффициент, связывающий напряжённость и индукцию электрического поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС электрическая постоянная имеет разную размерность и значение. Конкретно, Гауссова система единиц и система СГСЭ построены так, что электрическая постоянная безразмерна и равна 1, а в системе СГСМ она равна ε₀ = 1/c² ≈ 1,11265005605362 · 10⁻²¹ с²·см⁻².

Некоторые уравнения электродинамики в СИ

В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:

D=ε0 E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}

Она также входит в запись закона Кулона (тоже в вакууме):

F12=14πε0⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}

При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.

См. также

Примечания

Электрическая постоянная — Википедия. Что такое Электрическая постоянная

Электри́ческая постоя́нная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)^[1].

Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума^[2]. Измеряется в фарадах, делённых на метр.

Определение

По определению электрическая постоянная ε0{\displaystyle \varepsilon _{0}} связана со скоростью света c{\displaystyle c} и магнитной постоянной μ0{\displaystyle \mu _{0}} соотношением^[1]

ε0=1μ0c2.{\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}.}

Поскольку в СИ для магнитной постоянной справедливо точное равенство μ0=4π × 10−7 {\displaystyle \mu _{0}=4\pi \ \times \ 10^{-7}\ }Гн/м, то для электрической постоянной выполняется соотношение

ε0=14πc2×107{\displaystyle \varepsilon _{0}={\frac {1}{4\pi c^{2}}}\times 10^{7}}м/Гн,^[3]

также являющееся точным.

Численное значение

Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение ε0{\displaystyle \varepsilon _{0}} в СИ:

ε0=14π× 2997924582×10−7{\displaystyle \varepsilon _{0}={\frac {1}{4\pi \times \ 299792458^{2}\times 10^{-7}}}} Ф/м ≈8,85418781762039×10−12{\displaystyle \approx 8,85418781762039\times 10^{-12}} Ф·м⁻¹.

Или, выражая то же через основные единицы СИ,

ε0≈8,85418781762039×10−12{\displaystyle \varepsilon _{0}\approx 8,85418781762039\times 10^{-12}} м⁻³·кг⁻¹·с⁴·А².

В системе СГСМ μ0=1{\displaystyle \mu _{0}=1} и потому ε0=1c2≈1,11265005605362×10−21{\displaystyle \varepsilon _{0}={\frac {1}{c^{2}}}\approx 1,11265005605362\times 10^{-21}} с²·см⁻².

Некоторые уравнения электродинамики в СИ

В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D{\displaystyle \mathbf {D} } и вектор напряжённости электрического поля E{\displaystyle \mathbf {E} }:

D=ε0 E.{\displaystyle \mathbf {D} =\varepsilon _{0}\ \mathbf {E} .}

Она также входит в запись закона Кулона (тоже в вакууме):

F12=14πε0⋅q1q2r122r12r12.{\displaystyle \mathbf {F} _{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}q_{2}}{r_{12}^{2}}}{\frac {\mathbf {r} _{12}}{r_{12}}}.}

При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.

Предполагаемое переопределение

В 2011 году XXIV Генеральная конференция по мерам и весам (ГКМВ) приняла резолюцию^[4], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить несколько основных единиц, включая ампер, таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов.

Предполагается, что в СИ величине элементарного электрического заряда e будет приписано точное значение, равное 1,602 17X·10⁻¹⁹Кл^[5], а новое определение ампера будет основано на этом точном значении элементарного заряда, выраженного в c·А.

Следствием такого подхода к определению ампера станет изменение статуса электрической постоянной: после предполагаемого переопределения ампера значение электрической постоянной будет равно 14π× 2997924582× 10−7{\displaystyle {\frac {1}{4\pi \times \ 299792458^{2}\times \ 10^{-7}}}} Ф/м, но это значение приобретёт погрешность (неопределённость) и в дальнейшем будет определяться экспериментально^[4].

См. также

Примечания

электрическая постоянная — это… Что такое электрическая постоянная?



электрическая постоянная

электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты

Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к потоку вектора напряженности электрического поля сквозь эту поверхность в пустоте.

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• поляризация
• диэлектрическая проницаемость пустоты

Смотреть что такое «электрическая постоянная» в других словарях:

• ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (e0) (по старой терминологии диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур ний в рационализованной форме, в соответствии с к рой образованы электрич. и магн. ед …   Физическая энциклопедия

• ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — коэффициент пропорциональности ?о в законе Кулона определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ?о = (?оc2) 1 Ф/м = 8,854187817.10 12 Ф/м, где ?о магнитная постоянная.… …   Большой Энциклопедический словарь

• электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м …   Справочник технического переводчика

• ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) …   Большая политехническая энциклопедия

• Электрическая постоянная — 14. Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник …   Словарь-справочник терминов нормативно-технической документации

• электрическая постоянная — коэффициент пропорциональности ε0 в законе Кулона , определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ε0 = (μ0c2) 1Ф/м = 8,854187817·10 12Ф/м, где μ0  магнитная постоянная …   Энциклопедический словарь

• Электрическая постоянная — (ранее также носила название диэлектрической постоянной)  физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона …   Википедия

• электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… …   Automatikos terminų žodynas

• электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… …   Fizikos terminų žodynas

Термоэлектронная эмиссия — Википедия

Термоэлектро́нная эми́ссия (эффе́кт Ричардсо́на, эффект Эдисо́на) — явление выхода электронов из твёрдого тела, металла или карбидов или боридов переходных металлов в свободное пространство, обычно в вакуум или разрежённый газ при нагреве его до высокой температуры. Заметная эмиссия электронов наблюдается при нагреве чистых металлов только до температур свыше 900 К.

Впервые об этом явлении сообщил Эдмонд Беккерель в 1853 году^[1][2].

Явление было вновь открыто в 1873 году Фредериком Гатри^[en] в Великобритании^[3]. Во время работы с заряженными телами Гатри обнаружил, что раскаленный железный шар теряет свой заряд если он заряжен отрицательно, но положительно заряженный шар заряд не теряет^[4].

Также это явление изучали Иоганн Гитторф (1869—1883)^[5], Ойген Гольдштейн (1885)^[6], Юлиус Эльстер^[en] и Ганс Гейтель^[en] (1882—1889)^[7].

Эффект был вновь открыт Томасом Эдисоном 13 февраля 1880 года. В своих опытах Эдисон пытался выяснить причину преждевременного перегорания нитей накала и образования темного налёта на стекле колбы с её внутренней стороны вблизи положительного электрода нити в создаваемой им лампе накаливания. Эдисон производил опыты с несколькими экспериментальными вакууммированными лампами накаливания с дополнительной металлической пластиной или листочком фольги внутри колбы, электрически изолированной от нити накаливания и имеющей дополнительный электрический вывод сквозь стекло колбы. В этих опытах Эдисон обнаружил, что если эта пластина имела положительный потенциал относительно нити накала, то через вакуум протекал заметный ток и ток отсутствовал, если потенциал пластины был отрицательный относительно нити накала, причем ток наблюдался только в том случае, если нить накала была достаточно сильно разогрета.

Это явление теперь объясняется испусканием электронов, которые являются отрицательно заряженными частицами, нагретыми телами. В описываемое время электрон ещё не был открыт, его открыл Джозеф Томсон в 1897 году и термин «электрон» не использовался при обсуждении экспериментов до открытия электрона.

Эдисон также обнаружил, что ток от нагретой нити быстро увеличивался с ростом напряжения накала и подал заявку на патент 15 ноября 1883 года на устройство для регулирования напряжения с использованием эффекта (патент США 307 031), считается, что это первый патент США на электронное устройство^[8].

Несколько экземпляров ламп накаливания с демонстрацией эффекта Эдисон представил на Международной электрической выставке в Филадельфии в сентябре 1884 года. Британский ученый Уильям Прис, посетивший выставку забрал с собой несколько таких ламп для изучения явления. После их изучения он подготовил в 1885 году доклад, в котором назвал термоэлектронную эмиссию «эффектом Эдисона»^[9][10].

Затем британский физик Джон Амброз Флеминг, работавший в британской компании «Wireless Telegraphy», обнаружил, что эффект Эдисона может использоваться для детектирования радиоволн. Флеминг продолжил разработку двухэлектродной вакуумной лампы, теперь известной как электровакуумный диод, на которую получил патент 16 ноября 1904 года^[11].

Для выхода электрона из металла во внешнее пространство ему необходимо придать некоторую энергию, называемую работой выхода электрона — преодолеть потенциальный барьер.

Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. При комнатной температуре доля таких электронов очень мала и ток термоэлектронной эмиссии неизмеримо мал. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода быстро растёт, и явление термоэлектронной эмиссии становится заметным.

Исследование закономерностей термоэлектронной эмиссии можно наблюдать с помощью простейшей двухэлектродной лампы — вакуумного диода, представляющего собой баллон из которого откачан газ, с размещёнными внутри него двумя электродами: катодом и анодом. В простейшем случае катодом может служить проволока из тугоплавкого металла (например, вольфрама), накаливаемая электрическим током. Анод чаще всего выполняют в виде полого металлического цилиндра, окружающего катод. Если между анодом и катодом приложить напряжение, то, при горячем катоде и подаче на анод положительного относительно катода напряжения, через промежуток между анодом и катодом начинает протекать ток. Если на анод подавать отрицательное относительно катода напряжение, то ток прекращается, как бы сильно катод ни нагревали. Из этого опыта следует, что нагретый катод испускает отрицательные частицы — электроны.

Если поддерживать температуру накалённого катода постоянной и построить зависимость анодного тока от анодного напряжения — вольт-амперную характеристику вакуумного диода, то оказывается, что она нелинейна, то есть для вакуумного диода закон Ома не выполняется.

Зависимость термоэлектронного тока от анодного напряжения в области малых положительных значений описывается законом трёх вторых (установлен русским физиком С. А. Богуславским и американским физиком И. Ленгмюром):

I=BU3/2{\displaystyle I=BU^{3/2}},

где B{\displaystyle B} — коэффициент, зависящий от формы и размеров электродов, а также их взаимного расположения.

При увеличении анодного напряжения ток возрастает до некоторого максимального значения, называемого током насыщения и далее не увеличивается при последующем повышении напряжения на аноде. При этом практически все электроны, покидающие катод, поглощаются анодом, поэтому дальнейшее увеличение напряжённости поля между анодом и катодом не может привести к увеличению тока. Следовательно, плотность тока насыщения характеризует эмиссионную способность материала катода.

Термоэлектронный диод также может использоваться для преобразования разности температур в электроэнергию напрямую, без движущихся частей — термоэлектронный преобразователь, разновидность теплового двигателя.

Формула Ричардсона для плотности тока насыщения[править | править код]

Формула, первоначально полученная Ричардсоном на основе классической электронной теории металлов, а затем уточнённая русско-американским учёным С. Дэшманом (англ.) на основе квантовой теории, называется уравнением Ричардсона — Дешмана.

Плотность тока насыщения определяется формулой Ричардсона — Дешмана, выведенной теоретически на основе квантовой статистики^[12]:

j=(1−hRi)A⋅T2⋅e−We/kT{\displaystyle j=(1-{\mathcal {h}}_{R{\mathcal {i}}})A\cdot T^{2}\cdot e^{-W_{e}/kT}},

где hRi{\displaystyle {\mathcal {h}}_{R{\mathcal {i}}}} — усреднённое по спектру термоэлектронов значение коэффициента отталкивания электронов от потенциального барьера;

A{\displaystyle A} — термоэлектрическая постоянная, равная 120,4[AK2cm2];{\displaystyle 120,4{\Big [}{\cfrac {A}{K^{2}cm^{2}}}{\Big ]};} в модели свободных электронов А. Зоммерфельда A0=4πmk2eh4=1,20173×106Am−2K−2;{\displaystyle A_{0}={4\pi mk^{2}e \over h^{3}}=1,20173\times 10^{6}\,\mathrm {A\,m^{-2}\,K^{-2}} ;}

We{\displaystyle W_{e}} — работа выхода электронов из катода;

k{\displaystyle k} — постоянная Больцмана;

e{\displaystyle e} и m{\displaystyle m} — заряд и масса электрона;

h{\displaystyle h} — постоянная Планка;

T{\displaystyle T} — абсолютная температура.

Для практического применения эту формулу также записывают в виде^[13]:

j=a⋅T2⋅e−b/kT{\displaystyle j=a\cdot T^{2}\cdot e^{-b/kT}},

где a, b{\displaystyle a,\ b} — постоянные для данного материала катода параметры, определяемые из опыта.

Уменьшение работы выхода приводит к быстрому увеличению плотности тока насыщения. Поэтому практически катоды из чистых металлов применяются редко и используют оксидные катоды (например, никель, покрытый тонким слоем оксидов щёлочноземельных металлов), работа выхода электронов у которых мала (1—1,5 эВ).

Эффект Шоттки при термоэлектронной эмиссии[править | править код]

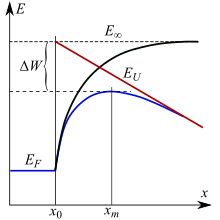Вид электростатического потенциала вблизи отрицательно заряженного электрода и снижение работы выхода за счёт эффекта Шоттки. Чёрная линия — потенциал без наложения внешнего поля; красная линия — потенциал EU{\displaystyle E_{U}} от внешнего поля; синяя линия — потенциал электрона с одновременным учётом работы выхода и внешнего поля; xm{\displaystyle x_{m}} — расстояние от электрода с максимумом потенциала.

При наложении внешнего электростатического поля, силовые линии которого направлены к эмиттирующему электроду (катоду), то есть этот электрод имеет отрицательный потенциал относительно анода, наблюдается снижение работы выхода электронов из катода. Это явление называется эффектом Шоттки, получившее название в честь Вальтера Шоттки, рассмотревшему это явление. Приблизительное объяснение эффекта приведено на рисунке. Внешнее электрическое поле EU{\displaystyle E_{U}} понижает работу выхода на величину ΔW{\displaystyle \Delta W}. Электроны в металле имеют энергию равную энергии уровня Ферми EF{\displaystyle E_{F}}, а электроны на бесконечном удалении от поверхности имеют энергию E∞{\displaystyle E_{\infty }}. Разность этих энергий — это работа выхода Ee{\displaystyle E_{e}}. Сумма сил притяжения к катоду и от внешнего поля имеет локальный максимум на расстоянии xm{\displaystyle x_{m}} от катода, причём этот максимум имеет энергию ниже энергии выхода, что увеличивает термоэлектронную эмиссию. Эмиссия электронов, которая происходит в результате совместного действия эффекта Шоттки и термоэлектронной эмиссии часто называется «эмиссией Шоттки». Формулу для плотности тока термоэлектронной эмиссии с учётом эффекта Шоттки можно получить простой модификацией формулы Ричардсона, подставив в неё вместо We{\displaystyle W_{e}} энергию We−ΔW{\displaystyle W_{e}-\Delta W}^[14][15]:

J(F, T, W)=AGT2e−(We−ΔW)kT.{\displaystyle J(F,\ T,\ W)=A_{\mathrm {G} }T^{2}e^{-(W_{e}-\Delta W) \over kT}.}

Величина уменьшения работы выхода ΔW{\displaystyle \Delta W}за счёт эффекта Шоттки даётся формулой:

ΔW=q3E4πε0,{\displaystyle \Delta W={\sqrt {q^{3}E \over 4\pi \varepsilon _{0}}},}

где q{\displaystyle q} — элементарный заряд;

E{\displaystyle E} — напряжённость электрического поля;

ε0{\displaystyle \varepsilon _{0}} — диэлектрическая постоянная вакуума.

Эта формула даёт хорошее согласие с опытом при напряжённости электрического поля до примерно 10⁸ В/м. Для напряженности электрического поля выше 10⁸ В/м становится существенно туннелирование электронов через потенциальный барьер, так называемое туннелирование Фаулера — Нордхайма и при этом туннельный ток начинает вносить значительный вклад в общий ток эмиссии. В этом режиме эффекты усиленной полем термоэлектронной и туннельной эмиссии могут быть описаны уравнением Мерфи — Гуда^[16]. В ещё более сильных полях туннелирование Фаулера — Нордхайма становится доминирующим механизмом электронной эмиссии, при этом катод работает в так называемом режиме «холодной электронной эмиссии» или «автоэлектронной эмиссии».

Термоэлектронная эмиссия также может усиливаться от других формам возбуждения поверхности катода, например, при облучении светом^[17]. Так, возбужденные атомы цезия в парах в термоэмиссионных преобразователях образуют активные центры Cs^—Ридберга^[en], которые приводят к уменьшению работы выхода с 1,5 эВ до 1,0—0,7 эВ. Эти центры имеют большое время жизни и работа выхода остается низкой, что существенно повышает эффективность термоэмиссионного преобразователя^[18].

На явлении термоэлектронной эмиссии основана работа всех вакуумных электронных приборов и электронно-лучевых приборов, электронно-лучевой технологии, электронных микроскопах, термоэмиссионных преобразователей энергии.

1. ↑ Paxton, William THERMIONIC ELECTRONEMISSION PROPERTIES OF NITROGEN-INCORPORATED POLYCRYSTALLINE DIAMOND FILMS (неопр.). Дата обращения 22 ноября 2016. Архивировано 23 ноября 2016 года.
2. ↑ Thermionic power converter (неопр.). Encyclopedia Britannica. Дата обращения 22 ноября 2016. Архивировано 23 ноября 2016 года.
3. ↑ См. например:
4. ↑ Richardson O. W. Thermionic Emission from Hot Bodies (неопр.). — Wexford College Press, 2003. — С. 196. — ISBN 978-1-929148-10-3.
5. ↑ См. например:
6. ↑ E. Goldstein (1885) «Ueber electrische Leitung in Vacuum» Архивировано 13 января 2018 года. (On electric conduction in vacuum) Annalen der Physik und Chemie, 3rd series, 24 : 79—92.
7. ↑ См. например:
   • Elster and Geitel (1882) «Ueber die Electricität der Flamme» (On the electricity of flames), Annalen der Physik und Chemie, 3rd series, 16 : 193—222.
   • Elster and Geitel (1883) «Ueber Electricitätserregung beim Contact von Gasen und glühenden Körpern» (On the generation of electricity by the contact of gases and incandescent bodies), Annalen der Physik und Chemie, 3rd series, 19 : 588—624.
   • Elster and Geitel (1885) «Ueber die unipolare Leitung erhitzter Gase» (On the unipolar conductivity of heated gases») Annalen der Physik und Chemie, 3rd series, 26: 1—9.
   • Elster and Geitel (1887) «Ueber die Electrisirung der Gase durch glühende Körper» (On the electrification of gases by incandescent bodies») Annalen der Physik und Chemie, 3rd series, 31 : 109—127.
   • Elster and Geitel (1889) «Ueber die Electricitätserregung beim Contact verdünnter Gase mit galvanisch glühenden Drähten» (On the generation of electricity by contact of rarefied gas with electrically heated wires) Annalen der Physik und Chemie, 3rd series, 37 : 315—329.
8. ↑ Edison, Thomas A., «Electrical indicator», US 307031, published November 15, 1883, issued October 21, 1884
9. ↑ Preece, William Henry. On a peculiar behaviour of glow lamps when raised to high incandescence (англ.) // Proceedings of the Royal Society of London : journal. — 1885. — Vol. 38, no. 235—238. — P. 219—230. — DOI:10.1098/rspl.1884.0093. Архивировано 26 июня 2014 года. Preece coins the term the «Edison effect» on page 229.
10. ↑ Josephson M. Edison (неопр.). — McGraw-Hill Education, 1959. — ISBN 978-0-07-033046-7.
11. ↑ См. например:
    • Provisional specification for a thermionic valve was lodged on November 16, 1904. In this document, Fleming coined the British term «valve» for what in North America is called a «vacuum tube»: «The means I employ for this purpose consists in the insertion in the circuit of the alternating current of an appliance which permits only the passage of electric current in one direction and constitutes therefore an electrical valve».
    • Fleming, John Ambrose, «Improvements in instruments for detecting and measuring alternating electric currents», GB 190424850, published August 15, 1905, issued September 21, 1905
    • Fleming, John Ambrose, «Instrument for converting alternating electric currents into continuous currents», US 803684, published April 29, 1905, issued November 7, 1905
12. ↑ Фридрихов С. А., Мовнин С. М. Глава 10. Физические основы эмиссионной электроники // Физические основы электронной техники. — М.: Высшая школа, 1982. — С. 434—435. — 608 с.
13. ↑ Зиновьев В. А. Краткий технический справочник. Том 1. — М.-Л. Техтеориздат, 1949. — c. 183
14. ↑ Kiziroglou M. E.; Li X.; Zhukov A. A.; De Groot P. A. J.; De Groot C. H. Thermionic field emission at electrodeposited Ni-Si Schottky barriers (англ.) // Solid-State Electronics : journal. — 2008. — Vol. 52, no. 7. — P. 1032—1038. — DOI:10.1016/j.sse.2008.03.002. — Bibcode: 2008SSEle..52.1032K.
15. ↑ Orloff, J. Schottky emission // Handbook of Charged Particle Optics (неопр.). — 2nd. — CRC Press, 2008. — С. 5—6. — ISBN 978-1-4200-4554-3.
16. ↑ Murphy E. L.; Good G. H. Thermionic Emission, Field Emission, and the Transition Region (англ.) // Physical Review : journal. — 1956. — Vol. 102, no. 6. — P. 1464—1473. — DOI:10.1103/PhysRev.102.1464. — Bibcode: 1956PhRv..102.1464M.
17. ↑ Mal’Shukov A. G.; Chao K. A. Opto-Thermionic Refrigeration in Semiconductor Heterostructures (англ.) // Physical Review Letters : journal. — 2001. — Vol. 86, no. 24. — P. 5570—5573. — DOI:10.1103/PhysRevLett.86.5570. — Bibcode: 2001PhRvL..86.5570M. — PMID 11415303.
18. ↑ Svensson R.; Holmlid L. Very low work function surfaces from condensed excited states: Rydber matter of cesium (англ.) // Surface Science : journal. — 1992. — Vol. 269/270. — P. 695—699. — DOI:10.1016/0039-6028(92)91335-9. — Bibcode: 1992SurSc.269..695S.

• Херинг К., Никольс М. Термоэлектронная эмиссия. — М.: Издательство иностранной литературы, 1950. — 196 с.