Резонанс в последовательном и параллельном LC контуре. » Хабстаб

Чтобы понять причину возникновения резонанса необходимо разобраться как течёт ток через конденсатор и катушку индуктивности.
При протекании тока через катушку индуктивности напряжение опережает ток. Давайте рассмотрим этот процесс подробнее, когда напряжение на концах катушки максимально, ток через катушку не течет, по мере уменьшения напряжения, ток увеличивается и когда напряжение на концах катушки равно нулю, ток через катушку максимален. Далее, напряжение уменьшается и достигает минимума, ток при этом равен нулю. Из этого можно сделать вывод, что ток через катушку максимален, когда напряжение на её концах равно нулю и ток равен нулю, когда напряжение на её концах максимально. Таким образом, если сопоставить графики изменения напряжения и тока , создаётся впечатление, что напряжение опережает ток на 90 градусов. Это можно увидеть на рисунке ниже.

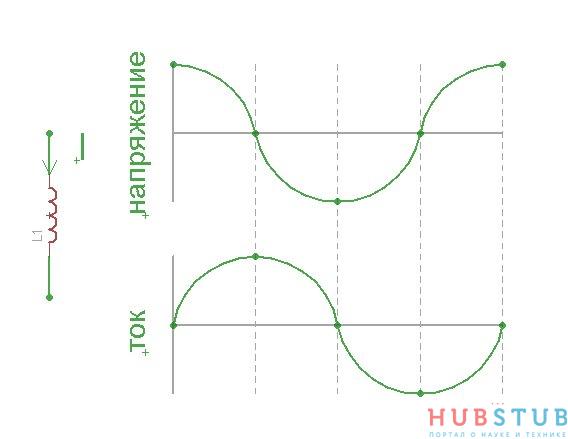
Совсем противоположно катушке индуктивности ведет себя конденсатор. Когда напряжение на концах конденсатора равно нулю, ток через него максимален, по мере зарядки конденсатора ток через него уменьшается, это связано с тем, что разность потенциалов между конденсатором и источником напряжения уменьшается, а чем меньше разность потенциалов, тем меньше ток. Когда конденсатор полностью заряжен ток через него не течет так, как нет разности потенциалов. Напряжение начинает уменьшаться и становится равно нулю, при этом ток максимален только течет в другом направлении, далее напряжение достигает минимума и ток через конденсатор снова не течет. Делаем вывод, что ток через конденсатор максимальный когда напряжение на его обкладках равно нулю и ток равен нулю когда напряжение на конденсаторе минимально. Если сопоставить графики изменения тока и напряжение, создается впечатление, что ток опережает напряжение на 90 градусов. Это можно увидеть на рисунке ниже.

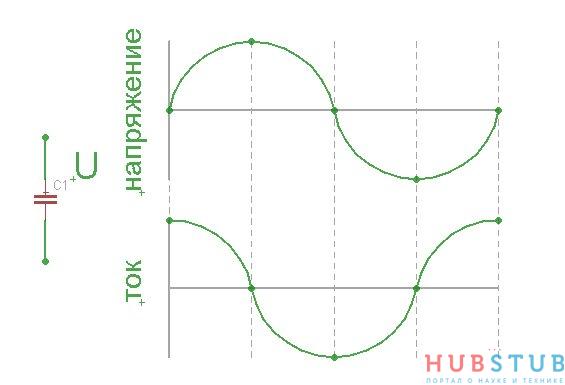
На резонансной частоте для контура, состоящего из конденсатора и катушки индуктивности, неважно параллельный он или последовательный, их сопротивления равны и сдвиг фаз между напряжением и током равен нулю. Ведь действительно если подумать, то в конденсаторе ток опережает напряжение на 90 градусов, то есть +90 градусов, а в катушке индуктивности ток отстает от напряжения на 90 градусов, то есть -90 градусов и если сложить их получится нуль. Для пары, конденсатор и катушка индуктивности параллельный и последовательный резонанс возникают на одной и той же частоте.

Давайте рассмотрим резонанс в последовательном колебательном контуре.

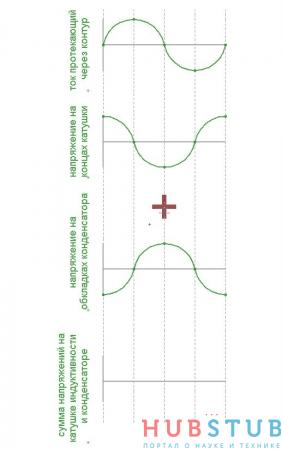
На верхнем графике изображена зависимость тока от времени, протекающего через контур, ниже два графика это напряжения, на конденсаторе и катушке, самый нижний это сумма напряжений на катушке и конденсаторе. Видно, что суммарное напряжение на конденсаторе и катушке индуктивности равно нулю, также говорят, что сопротивление последовательного колебательного контура на резонансной частоте стремится к нулю.
Давайте соберем простую схему, изображенную на рисунке.

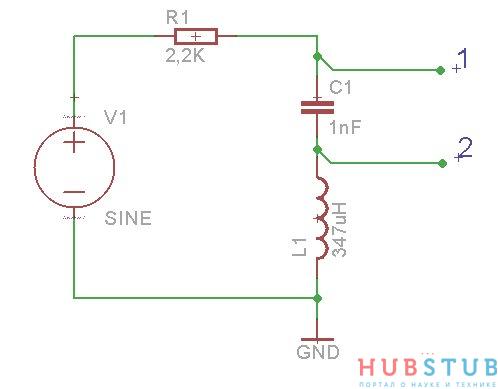
Сопротивление резистора должно быть больше выходного сопротивления генератора, то есть больше 50 Ohm, я взял первый попавшийся.
Расчетная резонансная частота такого контура 270 KHz, но так как номиналы имеют определенный допуск, который обычно указывается в процентах, придется ее подобрать. Подбирать будем исходя из того, что сопротивления катушки индуктивности и конденсатора на резонансной частоте равны, а так как они соединены последовательно, то равны и падения напряжений. Первый канал показывает напряжение на контуре, второй канал напряжение на катушке, канал Math показывает разность между первым и вторым каналом, а по сути напряжение на конденсаторе. Причина по которой, я не подключил щуп осциллографа параллельно конденсатору, будет подробно описана в следующей статье. Если кратко, то есть правило подключать земляной крокодил только к земле, если осциллограф и исследуемая схема питаются от бытовой сети и имеют заземление. Делается это, для того чтобы не спалить исследуемую схему и осциллограф.


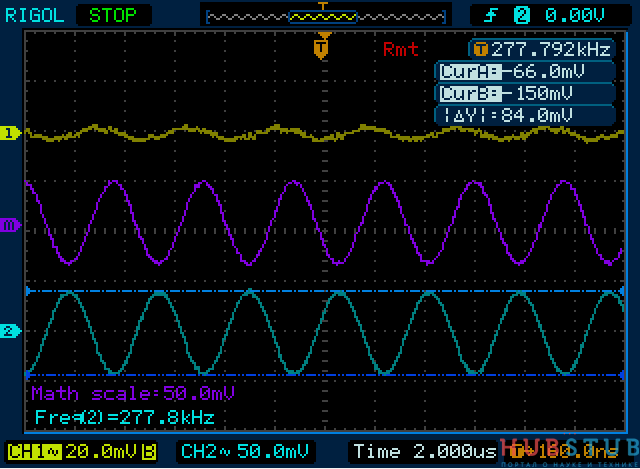
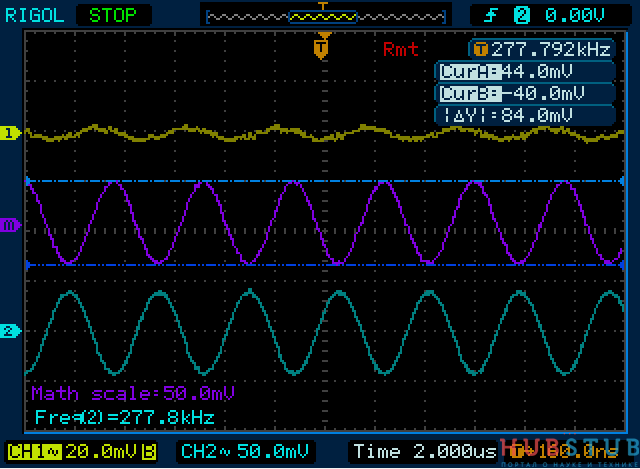
На осциллограммах видно, что на резонансной частоте падение напряжения на катушке и конденсаторе равны и противоположны по знаку, а суммарное падение напряжения на контуре стремится к нулю. В последовательном колебательном контуре на резонансной частоте напряжение на катушке и конденсаторе выше чем на генераторе. Давайте увеличим частоту и посмотри что изменится.

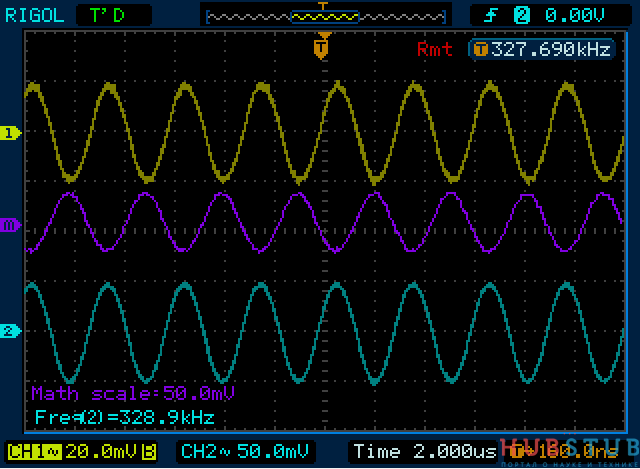
Видим, что напряжение на катушке увеличилось потому, что увеличилось её сопротивление, так как оно прямо пропорционально зависит от частоты. Напряжение на конденсаторе уменьшилось потому, что его сопротивление с ростом частоты уменьшается. Теперь уменьшим частоту.

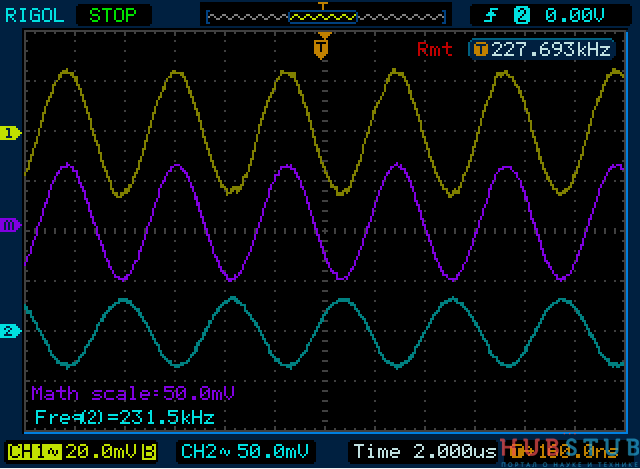
Видим, что напряжение на конденсаторе увеличилось, а на катушке уменьшилось, также надо отметить, что разность фаз между сигналами равна 180 градусам.

Давайте теперь рассмотрим резонанс в параллельном контуре, ситуация аналогичная с последовательным контуром, только в последовательном мы рассматривали напряжения, а в параллельном будем рассматривать токи.

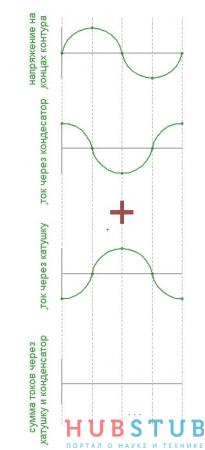
Видим, что токи сдвинуты относительно друг друга на 180 градусов, а их сумма равна нулю, то есть ток через контур не течет, а его сопротивление стремится к бесконечности. Параллельный колебательный контур используют как полосно-заграждающий фильтр, радиолюбители называют его фильтр- пробка. Он не пропускает напряжение частота которого равна его резонансной частоте. Давайте соберем простую схему, изображенную на картинке ниже и посмотрим как будет изменяться напряжение на концах контура в зависимости от частоты.

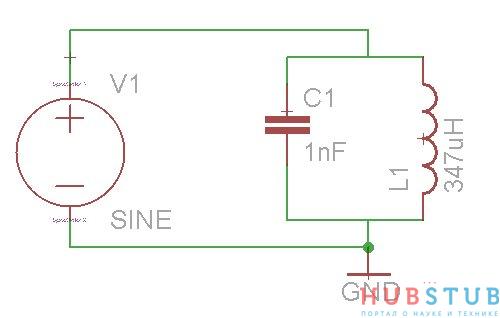
Так как конденсатор и индуктивность те же, что и в прошлом эксперименте резонансная частота контура та же.

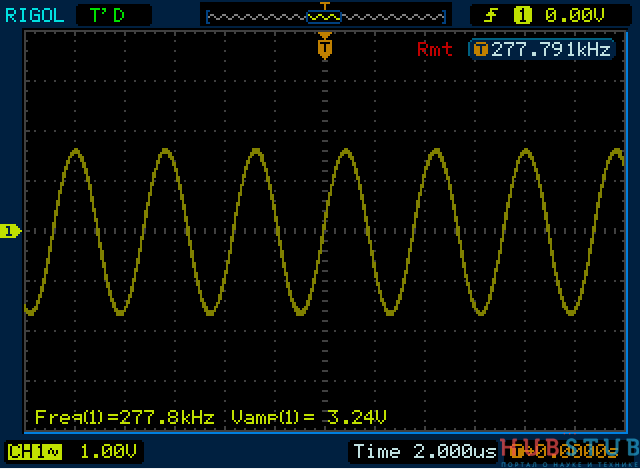
На резонансной частоте сопротивление контура стремится к бесконечности, следовательно и напряжение будет максимально. Давайте уменьшим частоту.

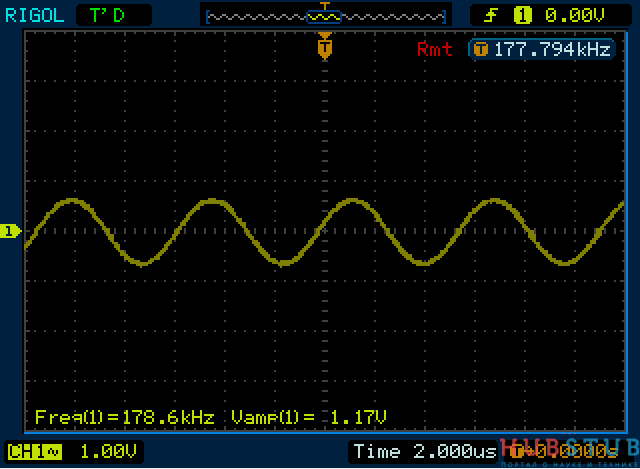
Видим, что напряжение на контуре уменьшилось, произошло это потому, что сопротивление катушки уменьшилось и она зашунтировала конденсатор.
Теперь давайте увеличим частоту.

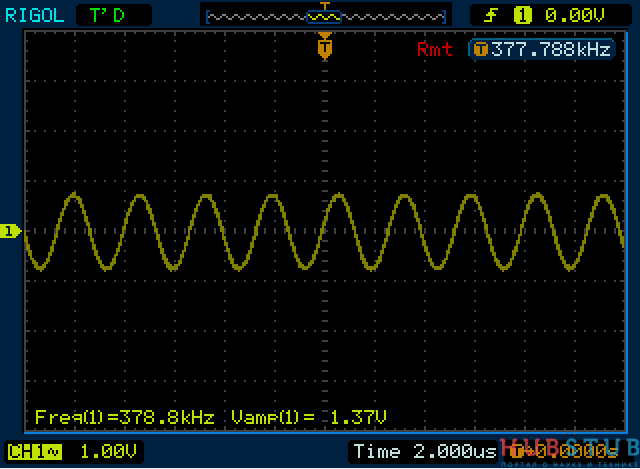
С ростом частоты сопротивление конденсатора уменьшилось и он зашунтировал катушку.
Пожалуй, это всё, что хотелось рассказать про резонанс.

5. Резонанс в последовательно параллельных цепях | 6. Резонанс | Часть2

5. Резонанс в последовательно параллельных цепях

Резонанс в последовательно параллельных цепях

В простых реактивных схемах с небольшим сопротивлением или отсутствием такового, на резонансной частоте проявляются эффекты радикального изменения импеданса. Импеданс параллельной LC цепи (колебательного контура) в состоянии резонанса достигает бесконечного значения. Импеданс последовательной LC цепи в состоянии резонанса достигает нулевого значения. Формула расчета резонансной частоты, как вы помните, имеет следующий вид:

 

 

Однако, как только в большинство LC цепей вводятся значимые значения сопротивлений, этот простой расчет резонанса становится недействительным. Мы с вами рассмотрим несколько LC цепей, с включенными в их состав резисторами, используя прежние значения емкости и индуктивности: 10 мкФ и 100 мГн соответственно. Согласно приведенной выше формуле, резонансная частота этих цепей должна быть равна 159,155 Гц. Давайте при помощи ниже приведенных SPICE анализов посмотрим, в каких точках значения тока будут иметь максимальные или минимальные значения:

 

 

resonant circuit  
v1 1 0 ac 1 sin 
с1 1 0 10u      
r1 1 2 100      
l1 2 0 100m     
.ac lin 20 100 400      
.plot ac i(v1)  
.end    

 

 

Как видите, ток достигает своего минимального значения на частоте 136,8 Гц (вместо рассчитанной по формуле частоты 159,2 Гц).

 

 

Фиктивный резистор в ветвь с катушкой индуктивности мы включили для того, чтобы предотвратить прямую связь «катушка индуктивности — источник напряжения», которую так не может терпеть SPICE. Этот резистор должен иметь очень низкое значение для минимального воздействия на поведение схемы.

 

resonant circuit  
v1 1 0 ac 1 sin 
r1 1 2 100      
c1 2 0 10u      
rbogus 1 3 1e-12
l1 3 0 100m     
.ac lin 20 100 400      
.plot ac i(v1)  
.end   

 

Минимальный ток будет на частоте близкой к 180 Гц вместо 159,2 Гц!

 

 

Теперь давайте переключим наше внимание на последовательные LC цепи. Здесь мы поэкспериментируем с подключением значимых сопротивлений параллельно катушке индуктивности или конденсатору (помимо этих сопротивлений нам нужно последовательно с катушкой индуктивности и конденсатором включить резистор (R1) сопротивлением 1 Ом, который будет ограничивать общий ток при резонансе). Если мы подключим резистор (R2) сопротивлением 100 Ом параллельно катушке индуктивности, то результат будет следующим:

 

 

resonant circuit  
v1 1 0 ac 1 sin 
r1 1 2 1
c1 2 3 10u      
l1 3 0 100m     
r2 3 0 100      
.ac lin 20 100 400      
.plot ac i(v1)  
.end    

 

Максимальный ток будет на частоте близкой к 178,9 Гц вместо 159,2 Гц!

 

 

И наконец, рассмотрим последовательную LC цепь, в которой сопротивление включено параллельно с  конденсатором:

 

 

resonant circuit  
v1 1 0 ac 1 sin 
r1 1 2 1
c1 2 3 10u      
r2 2 3 100      
l1 3 0 100m     
.ac lin 20 100 200      
.plot ac i(v1)  
.end   

 

Максимальный ток будет на частоте 136,8 Гц вместо 159,2 Гц!

 

 

Способность добавочного сопротивления смещать точку, в которой импеданс LC цепи достигает максимума или минимума, называется антирезонансом. Разобрав вышеприведенные примеры вы наверное заметили как сопротивление влияет на резонансную частоту схемы:

Параллельная LC цепь (колебательный контур):

• R последовательно с L: резонансная частота смещается вниз
• R последовательно с C: резонансная частота смещается вверх

Последовательная LC цепь:

• R параллельно с L: резонансная частота смещается вверх
• R параллельно с C: резонансная частота смещается вниз

Все вышесказанное показывает нам взаимодополняющую природу конденсаторов и катушек индуктивности: последовательное соединение сопротивления с одним из этих компонентов (например с конденсатором) создает эффект антирезонанса, эквивалентный параллельному соединению этого же сопротивления с другим компонентом (катушкой индуктивности). Если вы еще внимательнее посмотрите на SPICE примеры, то увидите, что частоты смещаются на одинаковую величину, а графики представляют собой зеркальное отображение друг друга.

Антирезонанс — это эффект, о котором должны знать все проектировщики резонансных схем. Уравнения для определения «смещения» антирезонанса довольно сложны, и не будут рассматриваться в рамках данной статьи. Для начинающих радиолюбителей изложенного материала вполне достаточно, чтобы понять, что такой эффект существует и каковы его последствия.

Дополнительное сопротивление может возникнуть практически во всех LC цепях. Если при производстве конденсаторов существует возможность минимизировать паразитные сопротивления, то практически все катушки индуктивности имеют значимые величины таких сопротивлений благодаря длинным проводам, используемым при их изготовлении. Более того, благодаря скин-эффекту сопротивление провода будет увеличиваться вместе с увеличением частоты. Таким образом, катушки индуктивности обладают не просто сопротивлением, а частотно-зависимым сопротивлением.

Помимо борьбы с сопротивлением проводов, мы также должны бороться с потерями в железных сердечниках катушек индуктивности (которые проявляются в виде дополнительных сопротивлений в цепи). Нам известно, что железо является проводником как электричества, так и магнитного потока. Исходя из этого можно прийти к выводу, что изменение магнитного потока, произведенное прохождением переменного тока через катушку индуктивности, индуцирует электрические токи в самом сердечнике (вихревые токи). Этот эффект можно минимизировать путем применения пластинчатых сердечников, высококачественных материалов и правильными расчетами самих сердечников. Полностью устранить данный эффект практически невозможно.

Заметным исключением из правила смещения резонансной частоты при добавлении значимого сопротивления являются схемы с последовательным включением резистора, катушки индуктивности и конденсатора («RLC»). До тех пор, пока все компоненты будут соединены последовательно друг с другом, резонансная частота не будет зависеть от сопротивления.

 

 

series rlc circuit 
v1 1 0 ac 1 sin 
r1 1 2 100      
c1 2 3 10u      
l1 3 0 100m     
.ac lin 20 100 200      
.plot ac i(v1)  
.end    

 

Максимальный ток на частоте 159,2 Гц!

 

 

Обратите внимание, что пиковое значение тока на этом графике не изменилось по сравнению с рассмотренной в одной из предыдущих статей последовательной LC цепью (с символическим сопротивлением 1 Ом), хотя величина сопротивления теперь в 100 раз больше. Единственной вещью, которая подверглась изменению, является «острота» кривой. Очевидно, эта цепь резонирует не так сильно, как цепь с меньшим последовательным сопротивлением (как говорят, она «менее избирательна»), но, по крайней мере, она обладает той же самой собственной частотой.

Стоит отметить, что антирезонанс создает эффект демпфирования (успокоения) колебаний в таких LC цепях, как колебательные контуры. В начале этого раздела мы с вами видели, как подключенные друг к другу конденсатор и катушка индуктивности действуют подобно маятнику. Если при раскачивании маятника происходит превращение кинетической энергии (движение) в потенциальную (высота), то в электрической цепи происходит передача энергии от конденсатора к катушке индуктивности и обратно посредством чередующихся форм тока (кинетическое движение электронов) и напряжения (потенциал электрической энергии). В идеальном колебательном контуре (с нулевым сопротивлением) такие колебания будут продолжаться вечно, точно так же как лишенный трения маятник будет вечно раскачиваться на своей резонансной частоте. Но, в реальном мире такие электрические цепи и механизмы найти практически невозможно. Потери энергии через сопротивление (или потери в сердечнике катушки индуктивности и т.п) приводят к тому, что амплитуда колебаний постепенно снижается, и в конце концов сходит на нет. Если в колебательном контуре будут достаточно большие потери энергии, то он вообще не будет резонировать.

Демпфирующее свойство антирезонанса рассмотрено нами не только ради праздного любопытства. Оно весьма эффективно может использоваться для устранения нежелательных колебаний в цепях, содержащих паразитные индуктивности или емкости (а ими обладают практически все цепи). В качестве примера давайте рассмотрим следующую L/R цепь:

 

 

Идея этой схемы проста: она «заряжает» катушку индуктивности, когда выключатель замкнут. Скорость зарядки катушки устанавливается отношением L/R, представляющим собой постоянную времени цепи (измеряемую в секундах). Однако, если вы сами соберете такую схему, то столкнетесь с неожиданными колебаниями напряжения на катушке индуктивности при замкнутом выключателе (см. рисунок ниже). Почему это происходит? Как мы можем иметь резонансное колебание в цепи, в которой нет конденсатора, а есть только катушка индуктивности, резистор и батарея?

 

 

Все катушки индуктивности обладают определенной величиной паразитной емкости. Эта емкость возникает между отдельными витками катушки, между витками и сердечником, витками и экраном, витками и другими элементами конструкции. Кроме того, паразитную емкость может создать размещение дорожек на печатных платах. Устранить полностью такую емкость практически невозможно. Если паразитная емкость приводит к появлению ненужного резонанса (нежелательным колебаниям переменного напряжения), то на помощь может прийти дополнительное сопротивление. Высокая величина сопротивления R  вызовет состояние антирезонанса, рассеивая достаточно энергии, чтобы помешать индуктивности и паразитной емкости поддерживать колебания в течении длительного времени.

Интересно, что принцип применения сопротивления для устранения нежелательного резонанса очень часто используется при проектировании механических систем, где любой движущийся объект (обладающий определенной массой) является потенциальным резонатором. Одним из таких примеров являются амортизаторы в автомобиле. Без амортизаторов автомобиль будет долго прыгать на резонирующей частоте после любой неровности на дороге. Роль амортизаторов заключается во введении антирезонирущего эффекта путем гидравлического рассеивания энергии (точно так же, как резистор рассеивает энергию электрически).

Резонанс

Последовательный резонанс

Рассмотрим цепь (последовательный резонансный контур) на рис. 6.1, где резистор R включен последовательное катушкой индуктивности L и конденсатором С. Резистор R может быть реальным резистором или может представлять активное сопротивление катушки индуктивности. Величина сопротивления этого резистора не зависит от частоты, т. е. сохраняет постоянное значение при всех частотах. Реактивные сопротивления катушки индуктивности и конденсатора, напротив, являются частотно-зависимыми. При увеличении частоты, начиная от 0 Гц, реактивное сопротивление катушки индуктивности возрастает, а реактивное сопротивление конденсатора уменьшается. При достижении некоторой частоты f0 реактивные сопротивления ХL и ХC обоих элементов сравниваются. Говорят, что схема находится в резонансе и f0 – резонансная частота.
На резонансной частоте противофазные реактивные сопротивления ХL и ХC компенсируют друг друга, в результате чего импеданс, или полное сопротивление, цепи становится чисто резистивным Z = R. Это минимум полного сопротивления Z, поэтому па резонансной частоте электрический ток в цепи достигает своего максимального значения, что иллюстрирует АЧХ на рис. 6.2. Поскольку последовательный резонансный контур характеризуется максимальным значением тока в резонансе, его называют также схемой отбора тока.

                                    

Рис. 6.1. Последовательный резонансный Рис. 6.2. АЧХ последовательного
контур. резонансного контура.

       Рис. 6.3. Параллельный резонансный контур.   Рис. 6.4. АЧХ параллельного резонансного контура.

 

Параллельный резонанс

Резонанс может быть получен также при параллельном соединении катушки индуктивности и конденсатора (рис. 6.3). При одном конкретном значении частоты, определяемом номиналами элементов L и С, реактивное сопротивление катушки индуктивности компенсирует реактивное сопротивление конденсатора, в результате чего достигается резонанс. Полное сопротивление цепи на резонансной частоте теперь максимально, поэтому напряжение также достигает своего максимального значения. Данная схема называется схемой режекции. АЧХ или частотная зависимость импенданса для этой схемы показана на рис. 6.4.
Как для последовательного, так и для параллельного резонанса резонансная частота определяется выражением:

 

Полагая L = 10 мГн и C = 1 мкФ, получаем f0 = 1,59 кГц.
Заметим, что резонансная частота не зависит от сопротивления резистора в схеме.

 

Полоса пропускания и избирательность

Резонансные цепи используются главным образом в качестве частотно-избирательных цепей из-за селективности их АЧХ. Обычно используются параллельные частотно-избирательные цепи, поскольку они характеризуются высоким импедансом и, следовательно, большим выходным напряжением.

Рис. 6.5. АЧХ частотно-избирательной цепи

(∆f – ширина полосы про¬пускания).

Рис. 6.6. Влияние шунтирования на АЧХ частотно-избирательной це-пи.
1 – без шунтирующего резисто¬ра;
2 – с шунтирующим резистором.

АЧХ частотно-избирательной цепи показана на рис. 6.5. Ширина полосы пропускания определяется между точками по уровню 3 дБ, как показано на рисунке. Избирательность (селективность) такой цепи – это мера ее способности подавлять соседние частоты в пользу выделения требуемой частоты настройки. Цепь с более высокой избирательностью имеет более узкую полосу пропускания по сравнению с менее избирательной цепью, имеющей более широкую полосу пропускания. Избирательность Цепи задается параметром Q, который называется добротностью и определяется как

Таким образом, чем выше избирательность схемы, тем выше ее добротность, и наоборот.

 

Демпфирование

В тех применениях, где требуется широкая полоса пропускания, например в ТВ-приемниках, нужны низкодобротные частотно-избирательные цепи. Низкую добротность можно получить путем шунтирования параллельного контура резистором Д, как показано на рис. 6.6(а). Резистор оказывает так называемый демпфирующий эффект на АЧХ частотно-избирательной цепи, уменьшая селективность последней (рис. 6.6(б)).

 

Затухающие колебания

Рассмотрим резонансный контур, настроенный на частоту 1 кГц. Поскольку этот контур подавляет все другие частоты, то единственным сигналом, который можно снять с его выводов, является синусоидальный сигнал с частотой 1 кГц. Такой выходной сигнал может быть получен путем подачи в контур энергии переменного тока, в результате чего воз-никают синусоидальные колебания. Эта энергия может подаваться в виде гармонического сигнала резонансной частоты или в виде сигнала сложной формы, имеющего гармонику на резонансной частоте.

 

На рис. 6.7 показан резонансный контур, настроенный на частоту 3,3 кГц, который возбуждается периодическим сигналом в виде меандра с частотой 1 кГц. В контуре возникают незатухающие колебания на частоте третьей гармоники возбуждающего сигнала (т. е. на частоте 3,3 кГц). На рис. 6.8 показан тот же самый контур, но возбуждаемый ступенькой напряжения при замыкании ключа S. Сигнал ступенчатой формы содержит бесконечное число гармоник, что обеспечивает возбуждение колебаний в контуре на его резонансной частоте 3,3 кГц.

Рис. 6.7. Резонансный контур, генерирующий колебания на третьей гармонике возбуждающего сигнала.

Рис. 6.8. Затухающие колебания в резонансном контуре, возбуждаемые сигналом ступенчатой формы.

Однако эти колебания демпфируются, т. е. затухают, так как энергия, переданная в контур при ступенчатом изменении напряжения, постепенно теряется за счет малых потерь в катушке индуктивности и конденсаторе, а также из-за наличия сопротивления соединительных проводов и т. п. Через некоторое время колебания полностью прекращаются. Аналогичные затухающие колебания в резонансном контуре можно также получить путем размыкания ключа S.
Колебания, возбуждаемые в резонансном контуре, обязательно будут затухающими, если среднее по времени количество электрической энергии, передаваемой в этот контур, недостаточно для компенсации указанных выше потерь в контуре.

Добавить комментарий

физический смысл и применение, формулы и способы расчета

Физическое явление параллельного резонанса широко применяется в радиоэлектронике. Для построения колебательных контуров, состоящих из активного и реактивного сопротивлений, следует собрать цепь из сопротивления, емкости, а также индуктивности. Для этого необходимо разобраться в назначении резонанса, нахождении сопротивления радиокомпонентов, его основном применении в радиотехнике, а также условии его возникновения.

Общие сведения

Электрическим сопротивлением проводника является свойство проводить электрический ток. Для построения и расчета колебательного контура необходимо знать способы нахождения активного и реактивного сопротивлений. Сопротивление для цепей, питающихся от переменного тока (ЦПТ), бывает следующих видов: активное, реактивное и полное.

Активным сопротивлением ® является обыкновенный резистор. Реактивное состоит из следующих типов нагрузки: индуктивное и емкостное. Индуктивное (Xl) — сопротивление катушки индуктивности в цепи переменного тока, а емкостное (Xc) определяется наличием емкости в цепи (конденсатора).

При сложении активного и реактивного сопротивлений получается полное сопротивление участка электрической цепи, которое обозначается литерой Z.

Активное сопротивление

Активным сопротивлением в ЦПТ называется наличие любой нереактивной нагрузки. Его можно рассчитать следующими способами: при помощи измерения величины сопротивления и расчетным методом. Для измерения R применяется прибор, который называется омметром. Омметр входит в состав комбинированных приборов измерения электрических величин, которые называются мультиметрами. Он подключается параллельно нагрузке, причем для проведения измерений следует выключить электрическую цепь, поскольку наличие тока приведет прибор к выходу из строя.

Существует еще один способ, который является расчетным, однако он требует знаний в области физики. При вычислении величины R следует произвести измерения силы тока и напряжения, а точнее, их амплитудных значений (Uм и Iм соответственно). Это возможно сделать при помощи соответствующих приборов.

Для измерения величины напряжения применяется вольтметр, а силу тока можно измерить при помощи амперметра. Кроме того, эти приборы измеряют только действующие значения напряжения (Uд) и силы тока (Iд). Для расчета амплитудных значений следует воспользоваться следующими формулами:

1. Uм = Uд * sqrt (2).
2. Iм = Iд * sqrt (2).

​Для расчета R, которое можно найти, используя закон Ома для участка цепи (Iм = Uм / R): R = Uм / Iм. Воспользовавшись соотношениями зависимостей амплитудных значений от действующих, возможно рассчитать R: R = Uд * sqrt (2) / Iд * sqrt (2) = Uд / Iд. На практике применяют способ измерения сопротивления омметром.

Другие виды нагрузок

При наличии в ЦПТ катушки индуктивности возникает Xl, которую необходимо только рассчитывать. Индуктивное сопротивление рассчитывается по формуле, для которой необходимы циклическая частота (w) и индуктивность катушки (L): Xl = w * L.

Циклическая частота рассчитывается по следующей формуле, для которой необходимо только знать частоту переменного тока (f) и число ПИ (3,1416): w = 2 * 3,1416 * f. Индуктивность катушки рассчитывается, исходя из значений диаметра катушки (D в мм), числа витков (n) и длины намотки (l): L = (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l). Если подставить в формулу расчета индуктивного сопротивления все соотношения, то получается: Xl = 2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l).

Если в ЦПТ присутствует конденсатор с емкостью C, то добавляется еще и емкостное сопротивление — Xl, которое рассчитывается по следующей формуле: Xc = 1 / (w * C) = 1 / (2 * 3,1416 * f * C). Полное сопротивление в ЦПТ обозначается литерой Z и рассчитывается по формуле: Z = sqrt [sqr® +sqr (Xс — Xl)]. Если подставить в формулу полного сопротивления соотношения, по которым находятся R, Xl и Xc, то получается следующая формула: Z = sqrt [sqr (Uд / Iд) +sqr ((1 / (2 * 3,1416 * f * C)) — (2 * 3,1416 * f * (sqr (D/10) * sqr (n)) / (4,5 * D + 10 * l))]. Для упрощения вычисления можно рассчитать отдельно значения R, Xc и Xl.

Понятие о резонансе

Резонанс в цепи переменного тока происходит при образовании резонансной частоты, при которой некоторые сопротивления компенсируют друг друга. Основными признаками резонанса являются:

1. Совпадения по фазе U и I в цепи.
2. Значение активного и полного сопротивлений совпадают: Z = R.
3. Сила тока является максимальной.
4. Падение величины U на R равно U, которое приложено к контуру LC.
5. Выполняется равенство падений U на индуктивности и емкости, а также противоположность по фазе и больше приложенного напряжения: Ul > U, Ul = I * Xl = I * Xc и U = I * R.

В последнем случае коэффициент усиления по напряжению рассчитываются следующим способом: Ku = Ul / U = sqrt (L/C) / R = p / R. Этот коэффициент называется добротностью контура и обозначается литерой Q. Волновое сопротивление контура обозначается p, которое вычисляется по формуле: p = sqrt (L/C).

Резонанс в ЦПТ бывает двух видов: последовательный и параллельный. Для последовательного резонанса условием является минимальное сопротивление и нулевая фаза. В основном он применяется в схемах с реактивными составляющими L и C. При параллельном типе резонанса происходит равенство емкостных и индуктивных сопротивлений, которые компенсируют друг друга. Этот тип соединения должен постоянно быть равен расчетной величине. Он получил широкое применение, благодаря резкому минимуму импеданса. Импеданс — полное сопротивление в цепи переменного тока, который обозначается Z.

Контур является схемой, в которой подключены параллельно или последовательно следующие элементы: резистор, катушка индуктивности и конденсатор.

Эта схема образует осциллятор для тока с гармонической составляющей. Наличие сопротивления в схеме приводит к затуханию и уменьшает резонансную пиковую частоту.

Во всей силовой радиоэлектронике применяются колебательные контуры. Примером его является силовой трансформатор. Кроме того, контур используется для настройки телевизоров, согласования антенн. Возможно применение в качестве полосового и режекторного фильтров, которые применяются в датчиках для распределения низких и высоких частот. Эффект резонанса применяется и в медицине при микротоковой терапии, и при проведении биорезонансной диагностики.

Случаи для тока и напряжения

В радиоэлектронике применяется резонанс напряжений и токов. Они отличаются друг от друга и применяются в определенных случаях. Резонанс напряжений возникает при последовательном соединении в RLC-цепи (схема 1):

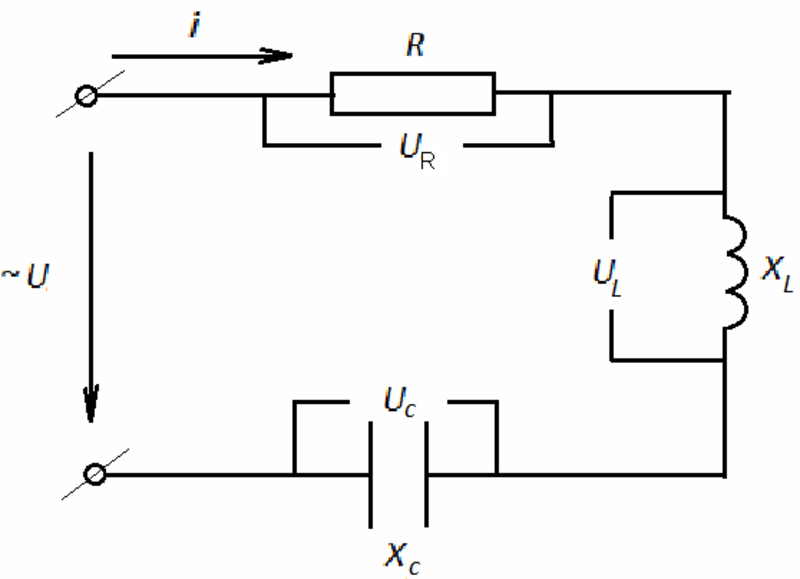
Схема 1 — Последовательное соединение элементов.

Основным условием возникновения резонанса является равенство частот источника питания и колебательного контура. Кроме того, Xc = Xl, они являются противоположными величинами (по знаку) и равны 0. Напряжения Uc и Ul противоположны по фазам и компенсируют друг друга, следовательно, Z = R. В результате этого происходит увеличение тока, так как при уменьшении сопротивления по закону Ома происходит увеличение I. Вырастает не только I, но и значения U на элементах схемы. При резонансе значения напряжений на конденсаторе и катушке индуктивности могут быть больше относительно напряжения источника питания.

При увеличении частоты значение Xl увеличивается, а Xc — уменьшается. При равенстве частот резонансной и источника питания значение Z будет уменьшаться. Резонансная частота находится по формуле: w = sqrt (1 / (L * C)). Резонанс в ЦПТ зависит от следующих величин: частоты источника питания — f, параметров L и C. Обмен электрической энергией осуществляется между катушкой и конденсатором через источник питания.

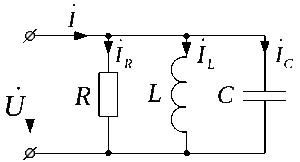
Резонанс токов в цепи переменного тока возникает при параллельном включении активных и реактивных нагрузок. На схеме 2 изображен контур с параллельным соединением:

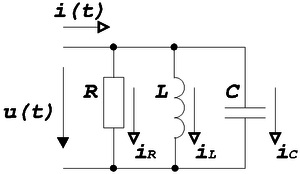
Схема 2 — Параллельное соединение в RLC-контуре.

В этом случае резонанс возникает при равенстве частот источника питания и резонансной, а также равенства проводимостей конденсатора (Bc) и катушки (Bl). Проводимость — величина, обратная сопротивлению. При увеличении частоты источника питания происходит рост полного сопротивления, при котором ток уменьшается. В результате этого, ток уменьшается и равняется активной составляющей. Для определения резонансной частоты следует воспользоваться алгоритмом нахождения этой величины:

1. Удельные проводимости для резистора, катушки индуктивности и конденсатора: G = 1 / R, Bl = 1 / (w * L) и Bc = w * C соответственно.
2. 1 / (w * L) = w * C.
3. Резонансная частота вычисляется по формуле: w = sqrt (1 / (L * C)).

Явление резонанса может привести к выходу из строя элементов схемы, приборов или устройств. Для того чтобы избежать этого, необходимо производить точные расчеты колебательных контуров.

Расчет параллельного контура

Необходимо сделать параллельный контур, частота резонанса которого равна 1,5 МГц. Для его изготовления нужно осуществить расчет, исходя из которого возможно будет его изготовить. Рассчитывать контур следует точно, поскольку любая неточность может привести к негативным последствиям. Основной задачей является расчет нужных индуктивности катушки и емкости конденсатора. Расчет осуществляется по следующему алгоритму:

1. Вычислить необходимую индуктивность в мкГн при заданной емкости и частоте: L = sqr (159,12 / f) / C.
2. Рассчитать количество витков (n) и диаметр каркаса (d в мм) катушки: n = 32 * sqrt (L / d).

Пусть С = 2000 пФ, тогда L = sqr (159,12 / 2) / 2000 = 5,6 мкГн. Количество витков для катушки с d = 3 мм: n = 32 * sqr (5,6 / 3) = 112.

Этот метод является приближенным, поскольку не учитывается межвитковое пространство катушки. Радиолюбители часто применяют уже готовые катушки, имеющие длину 15 мм с диаметром d = 3 мм. Вычислить можно, используя другую формулу: n = 8,5 * sqrt (L) = 8,5 * 2,3664 = 21.

Таким образом, явление резонанса применяется при построении различной радиоаппаратуры и требует выполнения верных расчетов, поскольку даже при незначительных ошибках могут выйти из строя дорогостоящие детали.

42. Определение резонанса, понятие последовательного и параллельного колебательных контуров.

Последовательный колебательный контур – это цепь, составленная из последовательно соединенных индуктивности и ёмкости.(рис1)рис 1

R – это эквивалентное («виртуальное») активное сопротивление контура, характеризующее потери в реактивных элементах. При этом сами L и C, можно представить как идеальные без потерь.

È – синусоидальный источник, напряжение которого описывается уравнением È = Èmejωt , где ω– это конечно не число витков катушки, а круговая частота: ω = 2πƒ. Тогда ток в цепи: Ì = È / Ζ, где Ζ – полное комплексное сопротивление цепи, которое, как известно, для последовательной цепи определяется как сумма сопротивлений всех ее элементов

Ζ = R + (jωL + 1 / jωC) = R + jωX

Или, что тоже самое:

Ζ = ¦Ζ¦ejφ, где ¦Ζ¦ = √R2 + X2, φ = arctg(X / R), X = ωL — (1 / ωC)

Параллельным колебательным контуром называется цепь, составленная из катушки индуктивности и конденсатора, подключенных параллельно выходным зажимам источника. R_L и R_C – это внутренние сопротивления потерь конденсатора и катушки, представленные в виде «виртуальных» элементов. R_i – это внутреннее сопротивление источника.

43.Условие и способы получения резонанса. Резонансная частота

Явление резонанса. Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника ? может оказаться равной угловой частоте ?0, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний ?0, возникающих в какой-либо физической системе, с частотой вынужденных колебаний ?, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?0, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

44. Резонанс в последовательном колебательном контуре. Добротность, векторная диаграмма. Характеристическое сопротивление, затухание контура.

Резонанс напряжений – явление, при котором цепь содержащая активные и реактивные сопротивления, будет только активное сопротивление (XL — XC = 0). При этом ток в цепи совпадает по фазе с напряжением. Условие возникновение резонанса напряжений – равенство нулю реактивного сопротивления.

— характеристическое сопротивление контура.

Таким образом: – резонансная частота

-резонансная для парралельного

При резонансе напряжений ток максимален, так как сопротивление минимально, а

Добротностью контура называется отношение модуля реактивной составляющей напряжения в цепи к модулю входного напряжения в момент резонанса.

Полосу частот вблизи резонанса, на границах которой ток снижается до величины принято называтьполосой пропускания резонансного тока.

Чем больше добротность, тем острее кривая и уже полоса пропускания

13.Резонанс в электрических цепях. Резонансы в последовательном и параллельном контурах (определение, условие, следствия, характеристики).

Последовательное соединение:

Z=√(R²+(X_L—Xc)²)

Между катушкой и конденсатором происходит обмен энергиями, при котором мгновенное значение ЭДС самоиндукции катушки e и напряжение конденсатора uс в любой момент времени направлены на встречу друг к другу. Так в момент времени, когда конденсатор заряжается, возрастающее напряжение конденсатора uc направлено противоположно току (мешая зарядке), и ток уменьшается (при полной зарядке конденсатора он станет равным нулю). Уменьшение тока вызывает ЭДС самоиндукции eL в катушке, которая стремится по закону Ленца, увеличить ток. В результате uc и eL направлены навстречу друг другу и энергия магнитного поля катушки посредством ЭДС eL преобразуется в энергию конденсатора. При разрядке конденсатора все происходит наоборот.

За счет емкости можно уменьшить реактивное сопротивление цепи X=X_L—Xc , что увеличит ток, а значит и падение напряжения U_L=IX_L

В зависимости от соотношений XL и Xc возможны три режима работы цепи:

а) напряжение цепи опережает ток по фазе на угол (который считают положительным) и цепь в целом имеет активно-индуктивный характер;

б) напряжение в цепи отстает по фазе от тока на угол (который считаю отрицательным) и цепь в целом имеет активно-емкостной характер;

в) напряжение т ток цепи совпадают по фазе, характер цепи в цело чисто активный.

Последний режим называется резонансом напряжений, при котором U_L=Uc , X_L=Xc ; настроить цепь в резонанс напряжений можно путем изменения X_L или Xc, т.е. изменяя С, L или f.

Реактивное сопротивление цепи при резонансе напряжений X=X_L — Xc=0. поэтому ток максимальный т.к. Iрез=U/√(R²+(X_L—Xc)²), и f=1/(2π√LC). Явление резонанса в электрических цепях нашло широкое применение в электротехнике, радиотехнике и электронике. Так, в радиотехнике резонанс – почти единственный путь, позволяющий отделить сигналы нужной радиостанции от остальных сигналов. резонансное реле – в системах автоматического управления. Однако при определенных условиях резонансные явления в электрических цепях могут оказаться вредоносными, способными разрушить электроустановку(пробой электроизоляции установки).

Параллельное соединение:

При расчетах реактивный ток индуктивного характера берется со знаком «плюс», а емкостного характера – со знаком «минус», так как катушка и конденсатор обмениваются энергиями.

Анализируя векторную диаграмму, можно сделать вывод о роли конденсатора в схеме цепи. Если емкость конденсатора подобрать так чтобы Ip=Ir. В этом случае источник выдает в цепь только активную мощность. Реактивную мощность катушка получит от конденсатора за счет обмена энергиями, и ток цепи совпадает по фазе с напряжением. Такой режим цепи называется резонансом токов. Настроить цепь на резонанс можно изменением индуктивности, емкости или частоты. Из диаграммы видно, что при резонансе токов ток цепи минимальный. Таким образом, подключая конденсатор параллельно катушке, можно значительно уменьшить ток, потребляемый катушкой от источника.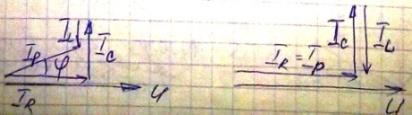

параллельный резонанс — это… Что такое параллельный резонанс?



параллельный резонанс

резонанс токов; отрасл. параллельный резонанс

Явление резонанса в электрической цепи, содержащей параллельно соединенные участки, имеющие индуктивный и емкостный характер.

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• резонанс токов
• резонанс

Смотреть что такое «параллельный резонанс» в других словарях:

• параллельный резонанс — srovių rezonansas statusas T sritis automatika atitikmenys: angl. antiresonance; current resonance; parallel resonance vok. Parallelresonanz, f; Stromresonanz, f rus. параллельный резонанс, m; резонанс токов, m pranc. antirésonance, f; résonance… …   Automatikos terminų žodynas

• параллельный резонанс — lygiagretusis rezonansas statusas T sritis fizika atitikmenys: angl. parallel resonance vok. Parallelresonanz, f rus. параллельный резонанс, m pranc. résonance parallèle, f …   Fizikos terminų žodynas

• ПАРАЛЛЕЛЬНЫЙ РЕЗОНАНС — то же. что резонанс токов …   Большой энциклопедический политехнический словарь

• последовательно-параллельный резонанс — многократный резонанс — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы многократный резонанс EN multiple… …   Справочник технического переводчика

• РЕЗОНАНС ТОКОВ — параллельный резонанс, резонанс в электрич. цепи из катушки индуктивности и конденсатора, соединённых параллельно относительно источника перем. тока. При Р. т. алгебр, сумма реактивных проводимостей ветвей равна нулю и общий ток цепи совпадает по …   Большой энциклопедический политехнический словарь

• резонанс токов — резонанс токов; отрасл. параллельный резонанс Явление резонанса в электрической цепи, содержащей параллельно соединенные участки, имеющие индуктивный и емкостный характер …   Политехнический терминологический толковый словарь

• резонанс токов — srovių rezonansas statusas T sritis automatika atitikmenys: angl. antiresonance; current resonance; parallel resonance vok. Parallelresonanz, f; Stromresonanz, f rus. параллельный резонанс, m; резонанс токов, m pranc. antirésonance, f; résonance… …   Automatikos terminų žodynas

• РЕЗОНАНС — (франц. resonance, от лат. resono звучу в ответ, откликаюсь), относительно большой селективный (избирательный) отклик колебательной системы (осциллятора) на периодич. воздействие с частотой, близкой к частоте её собств. колебаний. При Р.… …   Физическая энциклопедия

• Резонанс — (франц. resonance, от лат. resono звучу в ответ, откликаюсь)         явление резкого возрастания амплитуды вынужденных колебаний (См. Вынужденные колебания) в какой либо колебательной системе (См. Колебательные системы), наступающее при… …   Большая советская энциклопедия

• Parallelresonanz — srovių rezonansas statusas T sritis automatika atitikmenys: angl. antiresonance; current resonance; parallel resonance vok. Parallelresonanz, f; Stromresonanz, f rus. параллельный резонанс, m; резонанс токов, m pranc. antirésonance, f; résonance… …   Automatikos terminų žodynas