Соединение резисторов — Основы электроники

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.

Рисунок 1. Соединение резисторов.

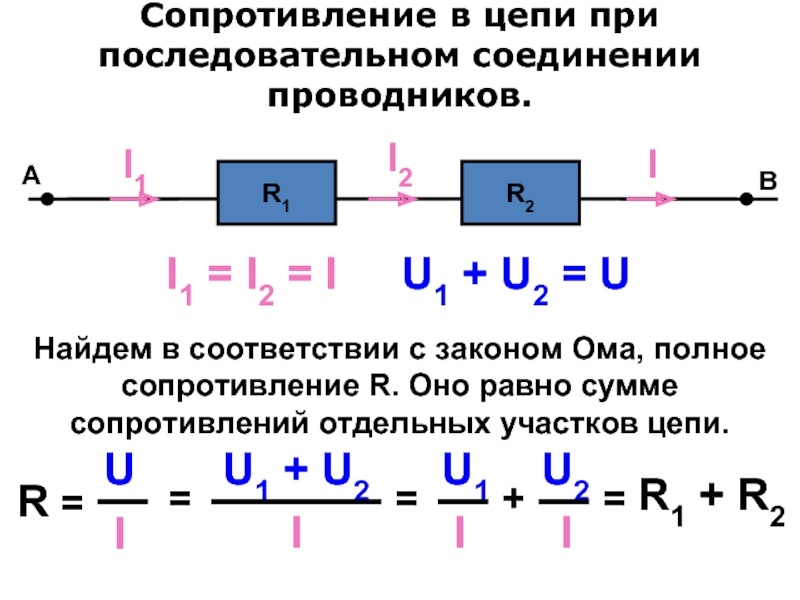
Последовательное соединение резисторов

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).

Рисунок 2. Последовательное соединение резисторов.

То есть при последовательном соединении резисторы подключатся друг за другом.

При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:

Rобщ = R1 + R2 + R3+…+ Rn.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).

Рисунок 3. Параллельное соединение резисторов.

При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:

1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn

Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:

Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.

Смешанное соединение резисторов

Смешанное соединение резисторов

является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.

Рисунок 4. Смешанное соединение резисторов.

На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.

2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.

Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.

Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R

_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.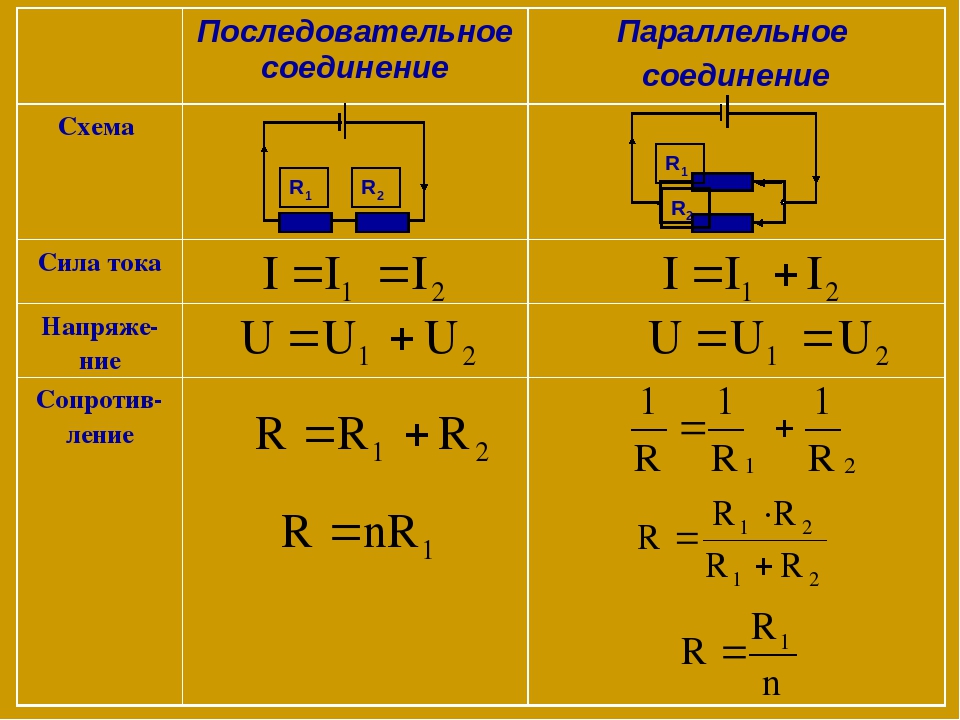

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R

_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.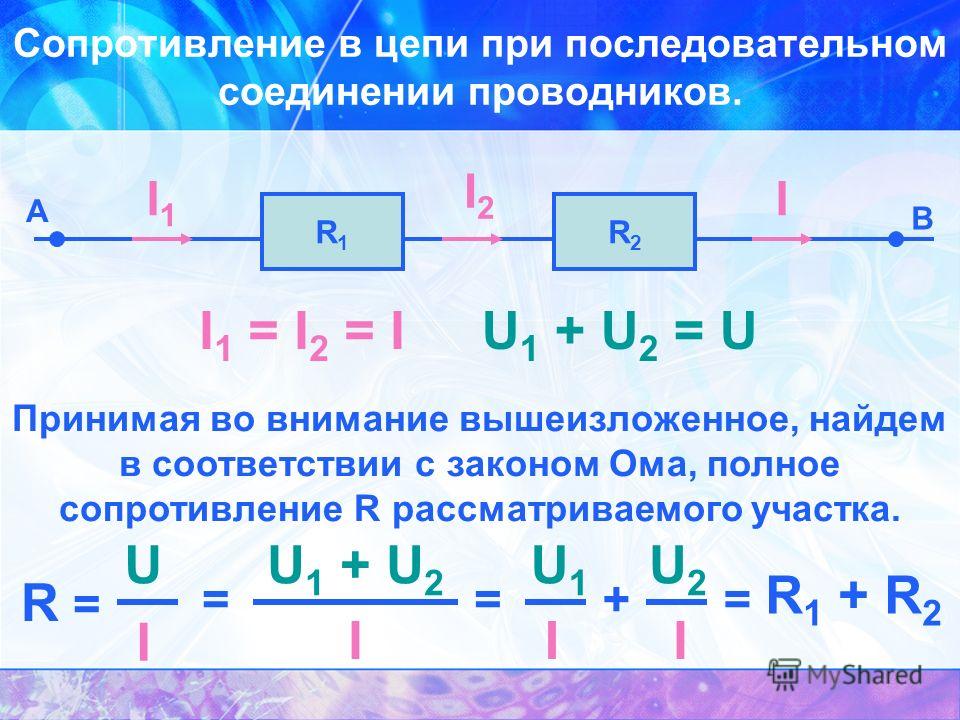

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R

_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

• Цепь разбивают на участки с только пареллельным или только последовательным соединением.
• Вычисляют общее сопротивление для каждого отдельного участка.
• Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

• Если резисторы соединяются последоватеьно — складывать.
• Если резисторы соединяются параллельно — использовать условное обозначение «||».
• Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле:
R = R1 + R2.
Это справедливо и для большего количества соединённых последовательно резисторов:
R = R1 + R2 + R3 + R4 + … + Rn.

 

Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление

большее, чем у любого резистора из этой цепи.

При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.

Параллельное соединение резисторов (формула)

Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.

Расчет параллельного сопротивления

Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:

 

Сопротивление из двух резисторов:	R =	R1 × R2
		R1 + R2

Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:

Сопротивление параллельных резисторов

1	=	1	+	1	+	1	+ . ..
R		R1		R2		R3

Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее.

Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.

Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Например: десять резисторов номиналом 1 КОм и мощностью 1 Вт каждый, соединённые параллельно будут иметь общее сопротивление 100 Ом и мощность 10 Вт.
При последовательном соединении мощность резисторов также складывается. Т.е. в том же примере, но при последовательном соединении, общее сопротивление будет равно 10 КОм и мощность 10 Вт.

Соединение резисторов. Типы соединений и формулы расчёта общего сопротивления резисторов.

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь.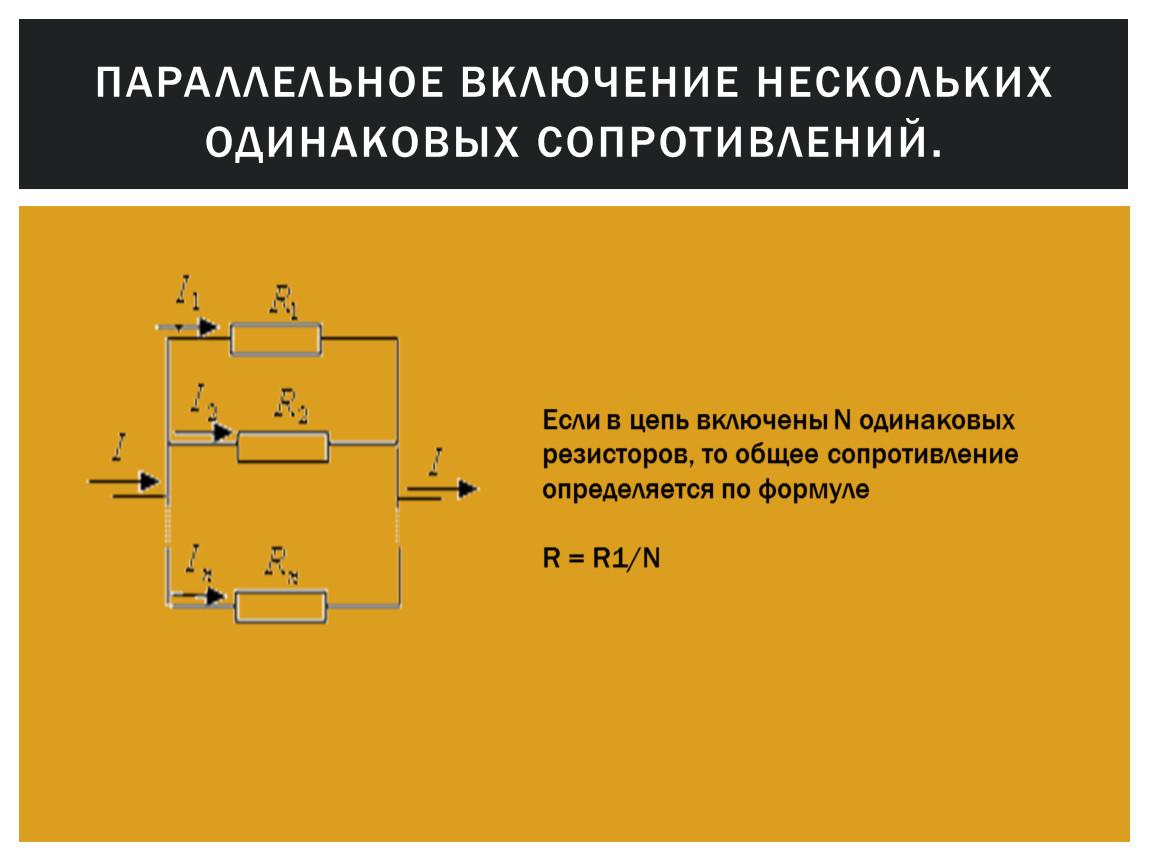 Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Что это значит?

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

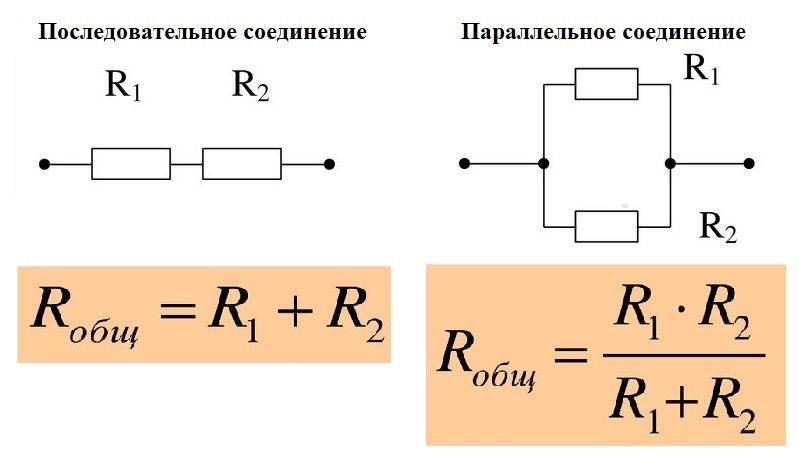
Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала.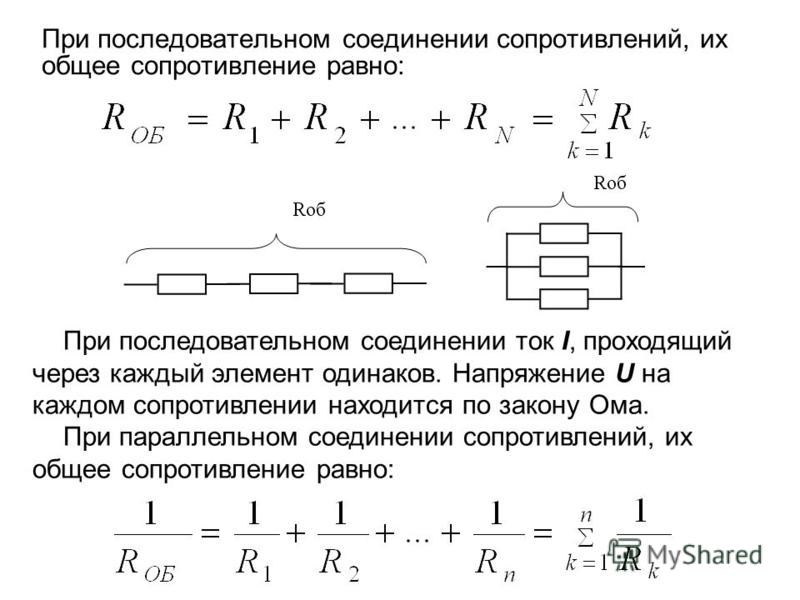 Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.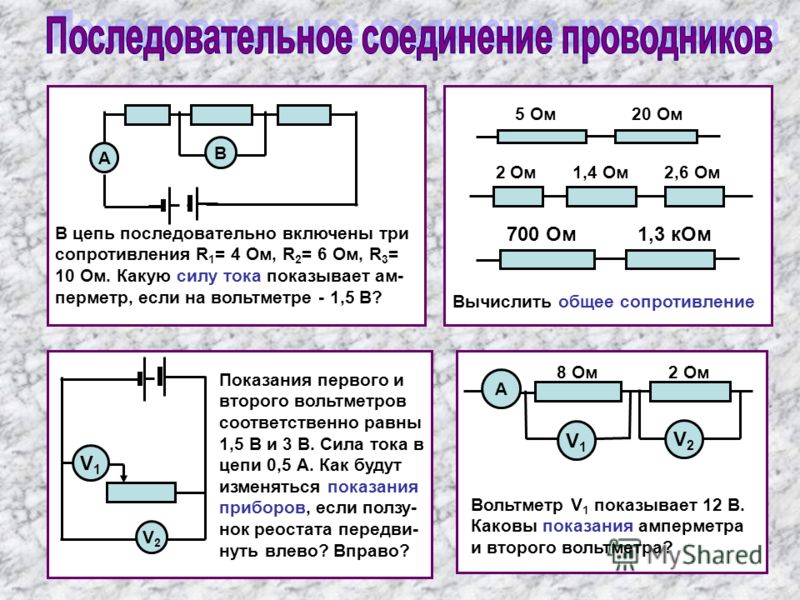

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

 

О параллельном соединении резисторов: расчет подключения, определение мощности

Достаточно большое количество радиолюбителей занимается сборкой, модернизацией и ремонтом разнообразных схем; для кого-то это работа, а для кого-то просто увлечение или хобби. В любом случае необходимо иметь представление о процессах, происходящих в схеме, физических свойствах самих элементов цепи и особенностях взаимодействия элементов между собой.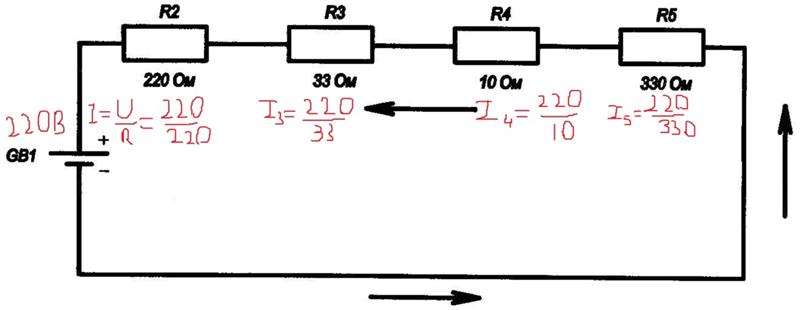

Диагностика электронных схем

Компоненты электронных схем

Все множество компонентов и элементов делится на две основные группы:

1. Активные элементы, особенностью которых является возможность усиливать проходящий по ним сигнал. К такой группе, в первую очередь, относятся транзисторы и построенные на их основе схемы;
2. Пассивные элементы, которые не предназначены для усиления сигнала. Элементами, которые относятся к этой группе, являются резисторы, конденсаторы, катушки индуктивности, диоды и остальные аналоги данных компонентов.

Наиболее простым элементом по своим характеристикам и свойствам является резистор. Основное назначение резисторов заключается в ограничении величины тока, проходящего по нему. Все существующие резисторы подразделяются на два вида:

• Постоянные – шунты, имеющие постоянное значение электрического сопротивления;
• Переменные – шунты, сопротивление между контактами которого меняется механическим путем;

Центральными характеристиками резисторов являются:

• Сила рассеивания, которая представляет собой максимальную мощность тока, выдерживаемую шунтом долгое время и рассеиваемую в виде тепла при постоянных характеристиках самого шунта;
• Параметр точности представляет собой максимальное отступление от величины реального сопротивления в течение эксплуатации шунта;
• Умение компонента противодействовать прохождению электротока в электрической цепи называется сопротивлением. Соответственно, с повышением сопротивления нарастает противостояние прохождению электротока.

Соединение резисторов

В радиотехнике встречается ряд конфигураций по состыковке компонентов в целом и шунтов в частности. Совмещение шунтов подразделяется на такие виды:

• Набор параллельных резисторов;
• Последовательное подключение шунтов;
• Смешанное соединение резисторов.

Сопряжение резисторов

Последовательное соединение резисторов

Последовательным сопряжением компонентов называют такое сплочение нескольких шунтов, при котором каждый одиночный шунт подключается к следующему единичному шунту только в одной точке. Поскольку при последовательном включении по шунтам протекает одинаковый электрический ток, сталкивающийся постоянно с новой преградой в виде последующего сопротивления, то суммарное противодействие возрастает и равно сложению сопротивлений. Согласно картинке выше, при последовательном соединении суммарное последовательное сопротивление равно:

Rобщ=R1+R2, где:

• Rобщ – суммарное противостояние цепи;
• R1 – противодействие первого шунта;
• R2 – противодействие второго шунта

Последовательное сопряжение шунтов

Напряжение при последовательном соединении компонентов понижается на любом отдельном элементе, опираясь на закон Ома, суммарное напряжение такого участка необходимо складывать. Соответственно, результирующий показатель напряжения возможно найти по выражению:

Uобщ=UR1+UR2, где:

• Uобщ – суммарное напряжение участка;
• UR1 – разность потенциалов на первом шунте;
• UR2 – разность потенциалов на втором шунте.

Поскольку проходящий по компонентам электроток неизменный, то справедливо равенство:

Iобщ=IR1=IR2, где:

• Iобщ – суммарная сила тока;
• IR1 – электроток первого шунта;
• IR2 – электроток второго шунта.

Дополнительная информация. При последовательной состыковке компонентов варьирование сопротивления любого элемента из этого участка влечет за собой как изменение сопротивления всего участка, так и изменение силы электротока этого участка.

Параллельное сопряжение резисторов

Параллельное соединение резисторов представляет собой такое соединение элементов, при котором резисторы подключаются друг к другу обоими выводами.

Дополнительная информация. В радиоэлектронике параллельные резисторы могут использоваться с целью снижения суммарного противодействия электротоку. Также мощность при параллельном стыковании компонентов возрастает сравнительно с каждым отдельным элементом.

При параллельном соединении шунтов через каждый единичный элемент потечет свой ток, и значение силы электротока будет обратно пропорционально сопротивлению компонента. Поскольку суммарная проводимость параллельного соединения возрастает, а общая сопротивляемость электротоку убывает, то, согласно закону Ома, общее сопротивление при параллельном соединении равняется:

• Gобщ =1/Rобщ =1/R1+1/R2+1/R3;
• Rобщ =1/Gобщ =R1R2R3/R1R2+R2R3+R1R3, где Gобщ – общая проводимость цепи.

Напряжение при параллельном соединении компонентов равняется разности потенциалов на каждом из компонентов:

Uобщ=UR1=UR2=UR3.

Направление токов в параллельной цепи

Калькулятор поможет определить суммарную силу тока цепи при параллельном совмещении, соответствующую сумме токов через каждый шунт:

Iобщ=IR1+IR2+IR3.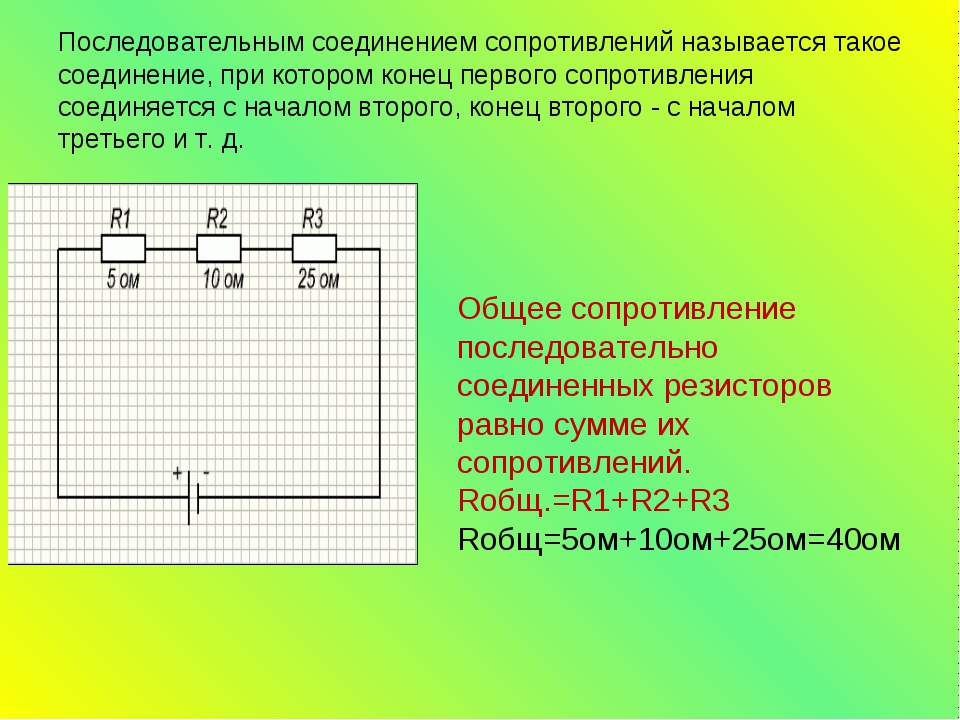

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой последовательное и параллельное соединение резисторов одновременно. Для определения суммарного противодействия цепи с разнотипной состыковкой шунтов требуется придерживаться последовательного алгоритма:

1. Схематически разделить цепь на отдельные участки, включающие в себя последовательное и параллельное соединение сопротивлений;
2. Рассчитать суммарный импеданс всех разделенных областей;
3. Представить первоначальную схему в виде сопротивлений, имеющих некоторую величину эквивалентного сопротивления;
4. Находите суммарное противодействие упрощенной схемы.

Понимание, что такое последовательное и параллельное соединение проводников, и поведения электрических характеристик при таком соединении позволит без особого труда проводить расчет, конструировать устройства различных конфигураций с требуемыми значениями параметров. Появится возможность упрощать и модернизировать схемы, вносить дополнительно какие-либо новшества в цепь.

Видео

Оцените статью:

Последовательное и параллельное соединение резисторов.

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

I = I_1 = I_2

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

U = U_1 + U_2

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

U_1 = I_1R_1 = IR_1

U_2 = I_2R_2 = IR_2

Тогда для вычисления общего напряжения можно будет использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжение также справедлив закон Ома:

U = IR_0

Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

R_0 = R_1 + R_2

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например для следующей цепи:

Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном  соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

R_0 = nR

В данной формуле n равно количеству элементов цепи. С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.

Параллельное соединение резисторов.

При параллельном соединении напряжения на проводниках равны:

U_1 = U_2 = U

А для токов справедливо следующее выражение:

I = I_1 + I_2

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = \frac{U_1}{R_1} = \frac{U}{R_1}

I_2 = \frac{U_2}{R_2} = \frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = \frac{U}{R_1} + \frac{U}{R_2} = U\medspace (\frac{1}{R1} + \frac{1}{R2})

А по закону Ома ток:

I = \frac{U}{R_0}

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = \frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

\frac{1}{R_0} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} + \frac{1}{R_5} + \frac{1}{R_6}

Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = \frac{R1\cdot R2}{R1 + R2} = 1

Теперь у нас образовались две группы последовательно соединенных резисторов:

Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5

R_{4-5} = R_4 + R_5 = 24

Как видите, схема стала уже совсем простой 🙂 Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5}  одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}\enspace = \frac{R_{1-2-3}\medspace\cdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = \frac{5\cdot24}{5 + 24} = 4. 14

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}\medspace +\medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов!

Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!

§ 11. Последовательное, параллельное и смешанное соединения резисторов (приемников электрической энергии)

Последовательное, параллельное и смешанное соединения резисторов.

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др. ), можно рассматривать как некоторые элементы, имеющие определенное сопротивление.

Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение резисторов.

Рис. 25. Схемы последовательного соединения приемников

При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25. Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:

E = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃) = IR_эк (19)

где R_эк = R₁ + R₂ + R₃.

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов. Так как напряжения на отдельных участках цепи согласно закону Ома: U₁=IR₁; U₂ = IR₂, U₃ = IR_з и в данном случае E = U, то для рассматриваемой цепи:

U = U₁ + U₂ +U₃ (20)

Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.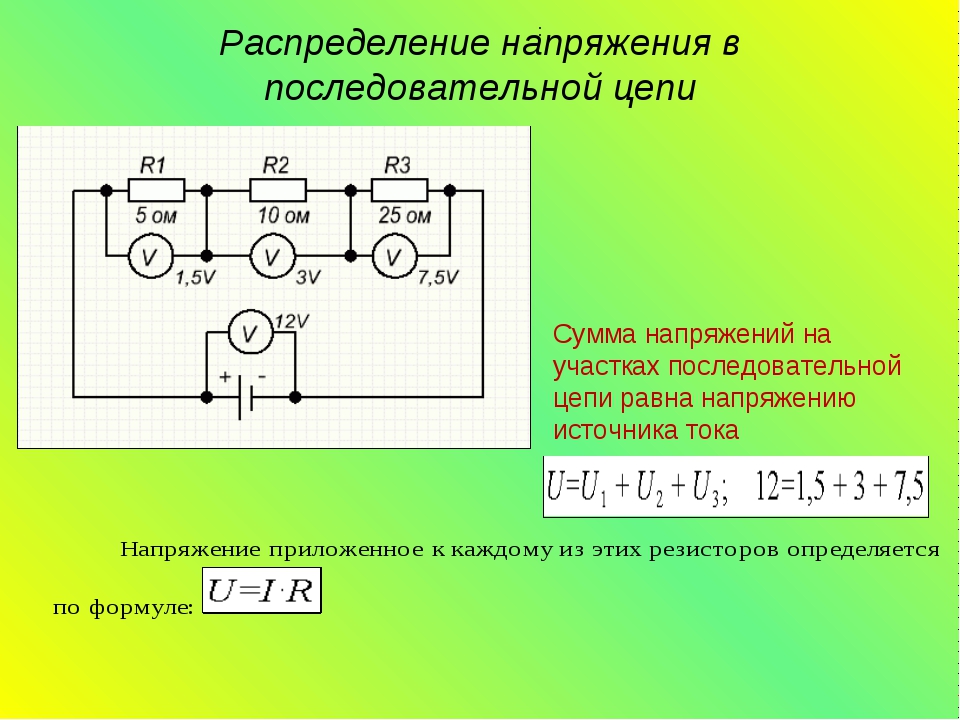
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:

U₁ : U₂ : U₃ = R₁ : R₂ : R₃ (21)

т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.

В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:

U1 = U/n. (22)

При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток.

Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.

Параллельное соединение резисторов.

При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а).

Рис. 26. Схемы параллельного соединения приемников

Заменяя лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или:

I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой:

1/R_эк = 1/R₁ + 1/R₂ + 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.

Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях:

I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.

Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи:

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах:

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.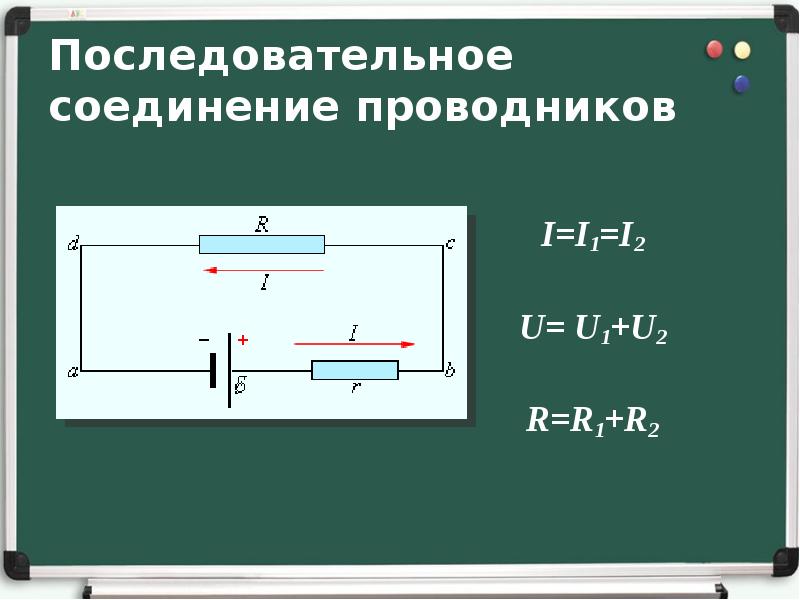 е.:

R_эк = R1 / n (27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.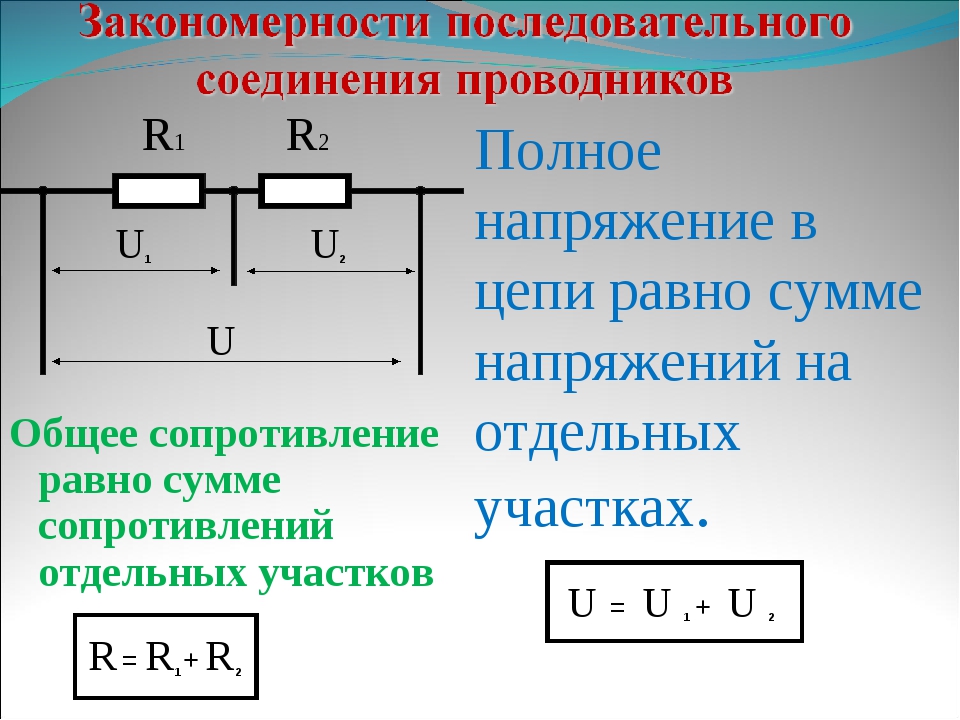

Смешанное соединение резисторов.

Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно.

Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

Рис. 27. Схемы смешанного соединения приемников

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую.

Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле:

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R_эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Последовательное соединение резисторов

— Codrey Electronics

Когда несколько резисторов подключены таким образом, что конец первого резистора подключен к началу второго резистора, а конец второго — к третьему резистору и так далее. Мы говорим, что резисторов в последовательном соединении .

Как вы знаете, резисторы — это электронные компоненты, используемые для управления напряжением и током в цепи. Но, правильно настроив его значение, мы можем использовать его для управления током или напряжением в цепях и приложениях.Отдельные резисторы могут быть соединены вместе последовательно или параллельно для получения номинального резистора, эквивалентное сопротивление которого представляет собой математическую комбинацию отдельных подключенных резисторов. Все типы комбинаций резисторов могут быть преобразованы в эквивалентные резисторы, независимо от того, насколько сложна эта комбинация, потому что все резисторы подчиняются одному и тому же правилу, то есть закону Ом .

Что такое закон Ома?

Закон

Ома определяет, что в любой электрической цепи ток, проходящий через компоненты, прямо пропорционален разности потенциалов, приложенной к компонентам.Закон Ома существует в трех формах. Это V = IR, I = V / R и R = V / I.

Где R — сопротивление, I — ток, протекающий в цепи, V — напряжение. Основываясь на этих трех параметрах (ток, напряжение и сопротивление), согласно закону Ома, ток изменяется непосредственно с приложенным напряжением и изменяется обратно пропорционально сопротивлению.

Резисторы в последовательной цепи

Комбинация цепей резисторов серии t организована в виде гирляндной цепи. Здесь ток остается постоянным во всей цепи.Как только ток передается на один резистор, он никуда не идет, кроме как прямо к месту назначения, то есть к отрицательной клемме батареи.

Резистор в последовательной цепи

Поскольку ток здесь остается постоянным, ток одинаков на всех резисторах.

Следовательно, общий ток (i) в последовательной цепи = i ₁ + i ₂ + i ₃

Когда мы говорим о напряжении, оно делится на каждом резисторе в соответствии с номиналом резисторов. Но сложение всего отдельного напряжения приведет к общему напряжению в цепи.

В = В ₁ + В ₂ + В ₃

Теперь, согласно закону Ома,

В = ИК

∴ iR = iR ₁ + iR ₂ + iR ₃ + iR ₄

Резисторы, подключенные последовательно (а)

Следовательно, эквивалентное сопротивление указанной выше цепи (а) будет

.

R = ₁ + ₂ + R ₃ + ₄

∴ R = 1 Ом + 3 Ом + 4 Ом + 5 Ом = 13 Ом

Резистор серии

как делитель напряжения

Резистор серии

как делитель напряжения

Все напряжение делится на различные падения напряжения на каждом резисторе как V1, V2, V3 и V4 и рассчитывается как

В ₁ (Напряжение на резисторе R ₁ ) = iR ₁ = 1 X 1 = 1 В
В ₂ (Напряжение на резисторе R ₂ ) = iR ₂ = 3 X 1 = 3 В
В ₃ (Напряжение на резисторе R ₄ ) = iR ₃ = 4 X 1 = 4 В
В ₄ (Напряжение на резисторе R ₅ ) = iR ₄ = 5 X 1 = 5 В

Общее напряжение — это сумма напряжений на отдельных сопротивлениях.

Следовательно, V = V1 + V2 + V3 + V4 = 1V + 3V + 4V + 5V = 13V

Цепь (а) может быть изменена с помощью одного резистора, включенного последовательно с батареей 1 В.

Полное сопротивление в серии

Таким образом, резисторы действуют при последовательном соединении. Этот тип комбинации широко используется, когда нам нужно большое сопротивление, например 200 Ом, но 200 Ом недоступны на рынке, поэтому мы последовательно подключаем два резистора 100 Ом, чтобы получить требуемый эквивалент резистора.

Уравнение сопротивления серии

Таким образом, эквивалентное сопротивление этих отдельных последовательных резисторов является просто суммой их индивидуального сопротивления. Например, если имеется n резисторов, скажем, R1, R2 и R3, и так далее до R _n. Общее сопротивление последовательно определяется уравнением или формулой ниже.

∴ R _всего = R1 + R2 ± —— +… R _n

Уравнение резистора серии

Что касается батареи, то несколько отдельных сопротивлений равны одному большому сопротивлению.Это сопротивление известно как эквивалентное сопротивление.

Общее сопротивление определяется как = общее напряжение / общий ток. Очевидно, что это алгебраическая сумма отдельных резисторов.

Резистор в последовательных примерах

Чтобы теоретически найти последовательное сопротивление, вот примеры проблем и решения последовательного резистора.

Пример № 1:

Для последовательного подключения резистора соедините один конец вывода резистора R1 с резистором R2, а другой конец R2 с R3.Точно так же вы можете подключить n резисторов последовательно, как показано ниже. Это повысит сопротивление.

Здесь последовательно соединены 3 резистора R1 (1K), R2 (10K) и R3 (20K). Общее сопротивление в цепи определяется суммой сопротивлений.

Следовательно, полное сопротивление (R) = R ₁ + R ₂ + R ₃ +… .. + R _n = 1K + 10K + 20K = 31K

Пример № 2:

Может возникнуть ситуация, когда вы захотите разделить напряжение ровно пополам.Когда два резистора одинакового номинала соединены последовательно, выходное напряжение станет половиной входного напряжения.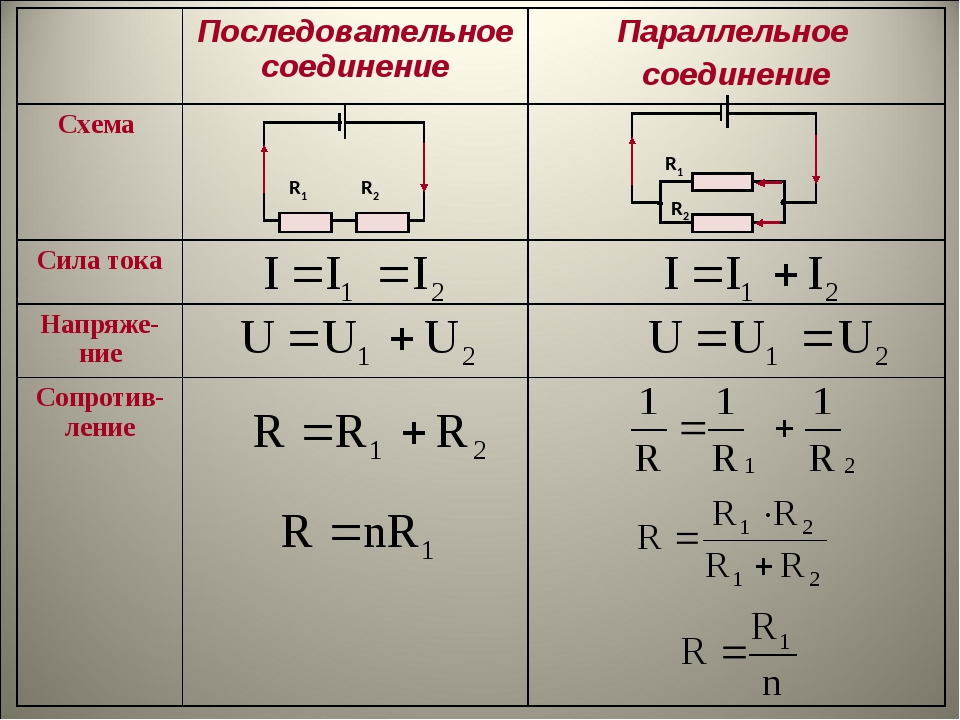 Например, два резистора R1 и R2 одинакового номинала 1K подключаются друг за другом. Входное напряжение составляет 20 В, а выходное напряжение рассчитывается следующим образом.

Здесь нагрузочный резистор (R _L) не рассматривается.

Без подключенного RL

Следовательно, последовательная схема делит напряжение и действует как схема делителя напряжения .

Зависимость тока от последовательного сопротивления

Зависимость тока от сопротивления

Важно соблюдать соотношение между последовательным сопротивлением и током. Как я уже сказал, последовательно включенные резисторы увеличивают сопротивление, но уменьшают ток. Следовательно, соотношение между током и сопротивлением обратное. Здесь по мере увеличения сопротивления ток быстро уменьшается.

Приложения

Некоторые из применений последовательного сопротивления в реальной жизни:

1. Резисторы, включенные последовательно, используются для построения сети делителя напряжения.
2. Используется как термистор (положительный температурный коэффициент) при измерении и контроле температуры.
3. Используется как LDR (светозависимый резистор) для светочувствительных приложений.

Учебное пособие по физике: схемы серии

Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены последовательным соединением, схема называется последовательной схемой .В последовательной цепи каждое устройство подключено таким образом, что существует только один путь, по которому заряд может проходить через внешнюю цепь. Каждый заряд, проходящий через контур внешней цепи, будет последовательно проходить через каждый резистор.

Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов к последовательной цепи приводит к довольно ожидаемому результату — увеличению общего сопротивления.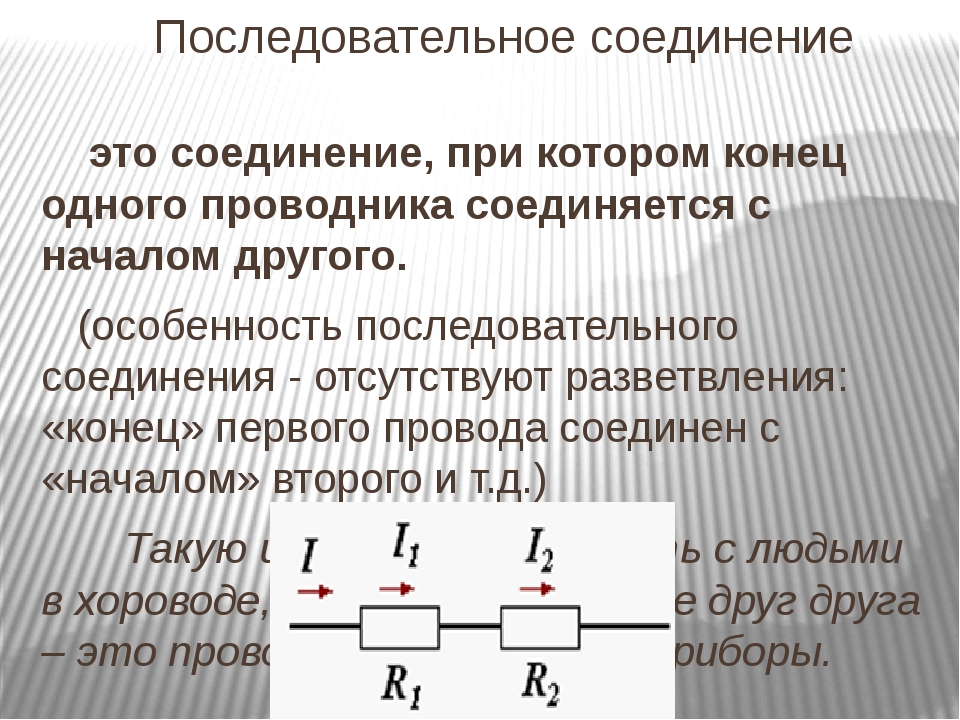 .Поскольку в цепи есть только один путь, каждый заряд встречает сопротивление каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это увеличенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).

Эквивалентное сопротивление и ток

Заряды проходят через внешнюю цепь со скоростью, которая везде одинакова. В одном месте ток не больше, чем в другом.Фактическое количество тока обратно пропорционально общему сопротивлению. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая нагнетает заряд, наличие двух последовательно соединенных резисторов с сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора с сопротивлением 12 Ом. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. А наличие четырех последовательно соединенных резисторов 6 Ом было бы эквивалентно наличию в цепи одного резистора 24 Ом.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в цепи. Для последовательных цепей математическая формула для вычисления эквивалентного сопротивления (R _eq ) составляет

. _экв. = ₁ + ₂ + ₃ +…

, где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, соединенных последовательно.

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Ток в последовательной цепи везде одинаковый.Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами, поэтому в одном месте его меньше по сравнению с другим. Можно представить, что заряды движутся вместе по проводам электрической цепи и везде движутся с одинаковой скоростью. Ток — скорость, с которой течет заряд — везде одинаков. То же самое на первом резисторе, как на последнем резисторе, как в батарее.Математически можно написать

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = …

, где I ₁ , I ₂ и I ₃ — значения тока в отдельных местах расположения резисторов.

Эти значения тока легко вычислить, если известно напряжение батареи и известны отдельные значения сопротивления. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление.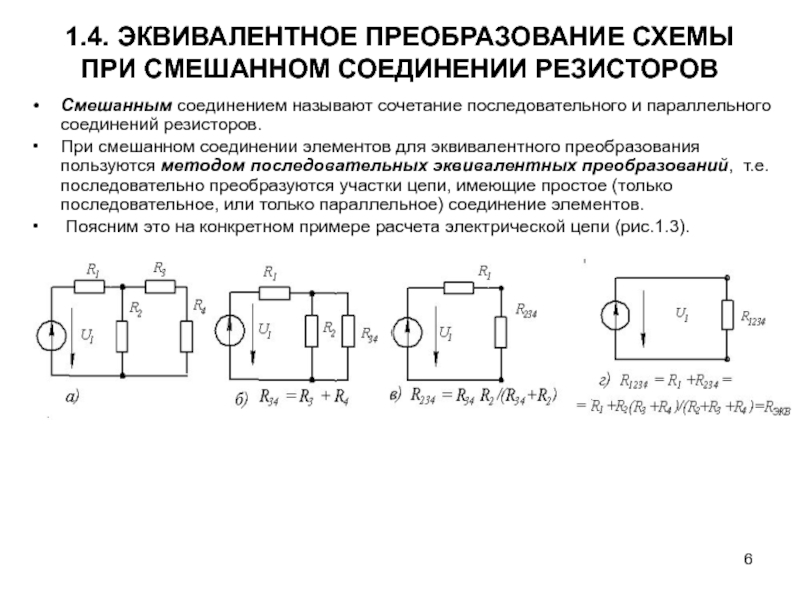 А используя закон Ома (ΔV = I • R), ток в батарее и, следовательно, через каждый резистор можно определить, найдя соотношение напряжения батареи и эквивалентного сопротивления.

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = ΔV _{аккумулятор} / R _eq

Разность электрических потенциалов и падения напряжения

Как обсуждалось в Уроке 1, электрохимический элемент схемы подает энергию на заряд, чтобы перемещать его через элемент и устанавливать разность электрических потенциалов на двух концах внешней цепи.Элемент с напряжением 1,5 В создает разность электрических потенциалов во внешней цепи 1,5 В. Это означает, что электрический потенциал на положительной клемме на 1,5 В больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольт электрического потенциала. Эта потеря электрического потенциала обозначается как падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. Д.).) внутри резисторов или нагрузок. Если электрическая цепь, питаемая элементом на 1,5 В, оснащена более чем одним резистором, то совокупная потеря электрического потенциала составляет 1,5 В. Для каждого резистора существует падение напряжения, но сумма этих падений составляет 1,5 В — то же самое, что и номинальное напряжение источника питания. Это понятие может быть выражено математически следующим уравнением:

ΔV _{аккумулятор} = ΔV ₁ + ΔV ₂ + ΔV ₃ +…

Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B. Предположим, вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам нужно будет использовать приведенное выше уравнение. Батарея обозначается обычным схематическим символом, а рядом с ней указывается ее напряжение. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.

Ранее в Уроке 1 обсуждалось использование диаграммы электрических потенциалов. Диаграмма электрического потенциала — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.

Схема, показанная на схеме выше, питается от источника энергии 12 В.В цепи последовательно соединены три резистора, каждый из которых имеет собственное падение напряжения. Отрицательный знак разности электрических потенциалов просто означает потерю электрического потенциала при прохождении через резистор. Обычный ток направляется через внешнюю цепь от положительной клеммы к отрицательной. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительного вывода, точка A на схеме находится на положительном выводе или выводе с высоким потенциалом.В точке A электрический потенциал 12 вольт, а в точке H (отрицательный вывод) — 0 вольт. Проходя через батарею, заряд приобретает электрический потенциал 12 вольт. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются в три этапа, каждый из которых соответствует прохождению через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда.Поскольку точки A и B разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через свой первый резистор, он теряет 3 В электрического потенциала и падает до 9 В в точке C. точка D отделена от точки C простым проводом, она имеет практически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет практически тот же электрический потенциал 2 В, что и E.Наконец, когда заряд проходит через свой последний резистор, он теряет 2 В электрического потенциала и падает до 0 В в точке G. цепь снова. Прирост энергии обеспечивается аккумулятором при перемещении заряда с H на A.

В Уроке 3 закон Ома (ΔV = I • R) был введен как уравнение, которое связывает падение напряжения на резисторе с сопротивлением резистора и током на резисторе.Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсужденными на этой странице, возникает большая идея.

В последовательных цепях резистор с наибольшим сопротивлением имеет наибольшее падение напряжения.

Поскольку в последовательной цепи ток везде одинаковый, значение I ΔV = I • R одинаково на каждом из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) будет изменяться с изменением сопротивления.Где бы сопротивление ни было наибольшим, падение напряжения будет наибольшим у этого резистора. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.

Δ В 1 = I • R 1

Δ В 2 = I • R 2

Δ В 3 = I • R 3

Математический анализ последовательных цепей

Приведенные выше принципы и формулы могут быть использованы для анализа последовательной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в последовательной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока в батарее (I _до ), а также падений напряжения и тока для каждого из трех резисторов.

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

R _экв = R ₁ + R ₂ + R ₃ = 17 Ом + 12 Ом + 11 Ом = 40 Ом

Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома.При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:

I _до = ΔV _{аккумулятор} / R _eq = (60 В) / (40 Ом) = 1,5 А

Значение тока 1,5 А — это ток в месте расположения батареи. В последовательной цепи без точек разветвления ток везде одинаковый.Ток в месте расположения батареи такой же, как ток в каждом месте расположения резистора. Впоследствии 1,5 ампер — это значение I ₁ , I ₂ и I ₃ .

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = 1,5 А

Осталось определить три значения — падение напряжения на каждом отдельном резисторе. Закон Ома снова используется для определения падения напряжения для каждого резистора — это просто произведение тока на каждом резисторе (вычисленное выше как 1.5 ампер) и сопротивление каждого резистора (указано в постановке задачи). Расчеты показаны ниже.

ΔV 1 = I 1 • R 1 ΔV 1 = (1,5 A) • (17 Ом) ΔV 1 = 25,5 В

ΔV 2 = I 2 • R 2 ΔV 2 = (1,5 A) • (12 Ом) ΔV 2 = 18 В

ΔV 3 = I 3 • R 3 ΔV 3 = (1.5 А) • (11 Ом) ΔV 3 = 16,5 В

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма падений напряжения для каждого отдельного резистора равна номинальному напряжению батареи. Другими словами, ΔV _{батареи} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли ΔV _{аккумулятор} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Это 60 В = 25.5 В + 18 В + 16,5 В?

60 В = 60 В?

Да !!

Математический анализ этой последовательной схемы включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом. Здесь необходимо учитывать концепции, согласно которым ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ.В следующей части Урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход сочетания концепций с уравнениями будет не менее важен для этого анализа.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom.Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как захотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение.Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:

а. Два последовательно включенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора сопротивлением 3 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора 5 Ом, включенные последовательно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

2. По мере увеличения количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается прежним) и ток в цепи __________ (увеличивается, уменьшается, остается прежним).

3. Рассмотрим следующие две схемы последовательных цепей. На каждой диаграмме используйте стрелки, чтобы указать направление обычного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.

4. Три одинаковые лампочки подключены к D-ячейке, как показано справа.Какое из следующих утверждений верно?

а. Все три лампочки будут иметь одинаковую яркость.

г. Лампа между X и Y будет самой яркой.

г. Лампа между Y и Z будет самой яркой.

г. Лампочка между Z и батареей будет самой яркой.

5. Три одинаковые лампочки подключены к батарее, как показано справа.Какие настройки можно было бы внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все подходящие варианты.

а. Увеличьте сопротивление одной из лампочек.

г. Увеличьте сопротивление двух лампочек.

г. Уменьшите сопротивление двух лампочек.

г. Увеличьте напряжение аккумулятора.

e. Уменьшите напряжение аккумулятора.

ф. Удалите одну из луковиц.

6. Три одинаковые лампочки подключены к батарее, как показано справа. W, X, Y и Z обозначают места на трассе. Какое из следующих утверждений верно?

а. Разница потенциалов между X и Y больше, чем между Y и Z.

г. Разница потенциалов между X и Y больше, чем между Y и W.

г. Разность потенциалов между Y и Z больше, чем между Y и W.

г. Разность потенциалов между X и Z больше, чем между Z и W.

e. Разность потенциалов между X и W больше, чем на батарее.

ф. Разница потенциалов между X и Y больше, чем между Z и W.

7.Сравните схему X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на единственном резисторе в цепи X.

а. меньше чем

г. больше

г. то же, что

8. Аккумулятор на 12 В, резистор на 12 Ом и лампочка подключаются, как показано на схеме X ниже.Резистор на 6 Ом добавлен к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано. Лампочка появится ____.

а. диммер в контуре X

г. диммер в контуре Y

г. одинаковая яркость в обеих цепях

9. Три резистора включены последовательно. При размещении в цепи с источником питания 12 В.Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток на каждом резисторе.

Как рассчитать резисторы, включенные последовательно и параллельно — Kitronik Ltd

Резисторы серии

Когда резисторы подключаются друг за другом, это называется последовательным соединением.Это показано ниже. Чтобы рассчитать общее общее сопротивление ряда резисторов, подключенных таким образом, вы складываете отдельные сопротивления. Это делается по следующей формуле: Rtotal = R1 + R2 + R3 и так далее. Пример: чтобы рассчитать общее сопротивление для этих трех последовательно соединенных резисторов.

Rtotal = R1 + R2 + R3 = 100 + 82 + 1 Ом = 183 Ом

---

Задача 1:

Рассчитайте общее сопротивление следующего последовательно включенного резистора.

	R Итого	= _______________
		= _______________

	R Итого	= _______________
		= _______________

	R Итого	= _______________
		= _______________

Параллельные резисторы

Когда резисторы подключаются друг к другу (бок о бок), это называется параллельным подключением.Это показано ниже.

Два параллельных резистора

Чтобы рассчитать общее полное сопротивление a двух резисторов, подключенных таким образом, вы можете использовать следующую формулу:

Пример: чтобы рассчитать полное сопротивление для этих двух резисторов, включенных параллельно.

---

Задача 2:

Рассчитайте полное сопротивление следующего резистора, включенного параллельно.

Три или более резистора, включенных параллельно

Для расчета общего общего сопротивления ряда из трех или более резисторов, подключенных таким образом, вы можете использовать следующую формулу: Пример: Чтобы рассчитать общее сопротивление для этих трех резисторов, подключенных параллельно

---

Задача 3:

Рассчитайте полное сопротивление следующего резистора, включенного параллельно.

---

ответов

Задача 1

1 = 1492 Ом 2 = 2242 Ом 3 = 4847 Ом

Задача 2

1 = 5 Ом 2 = 9,57 Ом 3 = 248,12 Ом

Задача 3

1 = 5,95 Ом 2 = 23,76 Ом Загрузите pdf-версию этой страницы здесь. Подробнее об авторе подробнее »

© Kitronik Ltd — Вы можете распечатать эту страницу и ссылку на нее, но не должны копировать страницу или ее часть без предварительного письменного согласия Kitronik.

Резисторы серии

и параллельные [Analog Devices Wiki]

Цель:

Целью этой лабораторной работы является исследование последовательно и параллельно включенных резисторов.

Серия

и параллельные схемы

Простые схемы, состоящие всего из нескольких компонентов, обычно просты для понимания новичками. Но все усложняется, когда в смесь входит большее количество компонентов. Куда идет ток? Что делают узловые напряжения? Можно ли упростить схему и облегчить понимание? Следующая информация должна помочь.

В этой лабораторной работе мы сначала обсудим разницу между последовательными цепями и параллельными цепями, используя цепи, содержащие самые основные компоненты, резисторы и батареи (или источники напряжения), чтобы показать разницу между двумя конфигурациями.

Прежде чем мы углубимся в объяснение, нам нужно определить, что такое узел схемы. Узел в цепи — это не что иное, как электрическое соединение между двумя или более компонентами. Когда схема изображена на схеме, такой как рисунок 1, узлы представлены проводами (линиями) между компонентами.

Рисунок 1, Пример схемы узла

На схеме изображена схема с 4 резисторами и источником напряжения. Также есть четыре уникальных узла.Цветные узлы (линии) Красный соединяет (+) конец источника напряжения с резистором R ₁ , оранжевый соединяет R ₁ и R ₂ вместе, синий соединяет R ₂ с R ₃ и R ₄ и зеленый соединяет (-) конец источника напряжения с R ₃ и R ₄ . Обратите внимание, что мы обычно определяем один узел как общий узел, на который ссылаются все остальные узлы, в данном случае это зеленый наземный узел.

Нам также необходимо понять, как ток течет по цепи.Обычный ток течет от более высокого или более положительного напряжения к более низкому или менее положительному напряжению в цепи. Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением, обычно называемой землей (0 вольт). Используя приведенную выше схему в качестве примера, вот как ток будет течь от положительной клеммы источника напряжения к отрицательной клемме.

Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂ ) ток на входе такой же, как на выходе.В других узлах (в частности, трехсторонний переход между R ₂ , R ₃ и R ₄ ) основной (красный) ток разделяется на два разных: фиолетовый ток, протекающий в R ₃ и оранжевый ток протекает в R ₄ . Также обратите внимание, что токи I _R3 и I _R4 рекомбинируют в зеленый ток. Это подчеркивает ключевое различие между последовательным и параллельным подключением.

Определение цепей серии

Когда резисторы подключаются последовательно (как показано на рисунке 2), вывод одного резистора подключается непосредственно к выводу следующего резистора, без каких-либо других возможных путей, так что весь ток в одном резисторе должен течь в следующий и скоро.

Когда резисторы включены последовательно, они могут быть объединены или собраны вместе как эквивалентный одиночный резистор с сопротивлением, равным сумме последовательных сопротивлений, , то есть ,

Рисунок 2: Последовательные резисторы, R _СЕРИЯ = R ₁ + R ₂ + R ₃ +…

Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.Итак, для приведенной выше последовательной схемы:

Мы знаем, что все резисторы имеют одинаковый ток I _S .

Аналогично для остальных трех резисторов так:

Или за вычетом I _S :

Таким образом, полное эквивалентное сопротивление — это просто сумма их значений.

Определение параллельных цепей

Когда резисторы включены параллельно (как показано на рисунке 3), все их первые выводы соединены вместе, а все их вторые выводы соединены вместе.

Когда резисторы включены параллельно, они могут быть объединены или объединены в один эквивалентный одиночный резистор, значение которого определяется следующим уравнением:

Для двух параллельно подключенных резисторов это упрощает:

Рисунок 3: Параллельные резисторы

Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление. Итак, для вышеуказанной параллельной схемы:

Мы знаем, что все резисторы имеют одинаковое напряжение В _S .

Ток, подаваемый источником напряжения В _S , является суммой токов в резисторах.

Подставляя четыре резистора, получаем:

Или за вычетом V _S :

Преобразуя сопротивление, получаем полное эквивалентное сопротивление:

Эксперименты

Материалы:

Аппаратный модуль ADALM1000
Макетная плата без пайки и перемычки
Резисторы 3–100 Ом
Резисторы 3–470 Ом

Резисторы в серии:

Поместите три резистора 100 Ом последовательно на беспаечную макетную плату, как показано на рисунке 4.Соедините с помощью перемычек, подключите вход CH A к левой стороне первого резистора, а вход CH B — к правой стороне того же резистора.

Рисунок 4, последовательно соединенные резисторы

Запустите прибор ALICE M1K Ohm Meter. Здесь показан экран. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор 50 Ом, который можно использовать для этого. Убедитесь, что выбран параметр Int. Уровень напряжения, который используется для измерения резистора, может быть установлен.Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите Run, и вы должны увидеть что-то подобное с единственным резистором 100 Ом.

Переместите перемычку CH B к правому концу второго резистора, как показано ниже.

Рисунок 5, два резистора последовательно

Омметр должен теперь показать значение для двух последовательно соединенных резисторов или около 200 Ом. Теперь переместите перемычку CH B к правому концу третьего резистора, как показано ниже.

Рисунок 6, три резистора последовательно

Омметр должен теперь показать значение трех последовательно соединенных резисторов или около 300 Ом.

Параллельные резисторы:

Теперь замените резисторы 100 Ом на резисторы 470 Ом, как показано на рисунке 7.

Измерение одного резистора 470 Ом

Омметр должен теперь показать значение одиночного резистора или около 470 Ом. Переместите средний резистор 470 Ом так, чтобы он был параллелен резистору справа, как показано ниже.

Измерение двух резисторов 470 Ом, включенных параллельно

Омметр должен теперь показать значение для двух резисторов 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?

Переместите третий резистор 470 Ом так, чтобы он был параллелен двум другим резисторам справа, как показано ниже.

Измерение трех резисторов 470 Ом, включенных параллельно

Омметр должен теперь показать значение для трех резисторов 470 Ом, включенных параллельно.Соответствует ли измеренное значение формуле для параллельных резисторов?

Поэкспериментируйте с другими комбинациями резисторов и номиналов, чтобы убедиться, что формулы верны для любого номинала резистора.

Комбинированные схемы

Более сложные соединения резисторов обычно представляют собой просто комбинации последовательного и параллельного соединения. Это часто встречается, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Комбинированная схема может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на рисунке 7. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом последовательно или параллельно.

Комбинированные последовательные и параллельные резисторы

R ₂ и R ₃ соединены параллельно друг другу, поэтому мы знаем, что для этих двух резисторов эквивалентное сопротивление будет:

Комбинированное сопротивление R ₂ и R ₃ последовательно с R1, поэтому общее эквивалентное сопротивление будет:

Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.

Для дальнейшего изучения:
Академия Хана — Резисторные схемы
Безграничная физика
Последовательные и параллельные схемы (по физике)

Вернуться к разделу «Введение в работу электротехнической лаборатории» Содержание

Цепи серии

— базовое электричество

Три закона для последовательных цепей

Существует три основных соотношения, касающихся сопротивления, тока и напряжения для всех последовательных цепей.Важно, чтобы вы усвоили три основных закона для последовательных цепей.

Сопротивление

Когда отдельные сопротивления соединяются последовательно, они действуют так же, как одно большое комбинированное сопротивление. Поскольку существует только один путь для протекания тока в последовательной цепи, и поскольку каждый из резисторов находится в линии, чтобы действовать как противодействие этому протеканию тока, общее сопротивление представляет собой комбинированное сопротивление всех резисторов, установленных в линию.

Общее сопротивление последовательной цепи равно сумме всех отдельных сопротивлений в цепи .

Rt = R1 + R2 + R3…

Используя эту формулу, вы обнаружите, что полное сопротивление цепи равно:

RT = 15 Ом + 5 Ом + 20 Ом = 40 Ом

Рисунок 16. Последовательная схема

Текущая

Поскольку существует только один путь для электронного потока в последовательной цепи, ток имеет одинаковую величину в любой точке цепи.

Общий ток в последовательной цепи такой же, как ток через любое сопротивление цепи.

IT = I1 = I2 = I3…

Учитывая 120 В в качестве общего напряжения и определив общее сопротивление цепи как 40 Ом, теперь вы можете применить закон Ома для определения полного тока в этой цепи:

IT = 120 В / 40 Ом = 3 А

Этот общий ток цепи останется неизменным для всех отдельных резисторов цепи.

Напряжение

Прежде чем какой-либо ток будет протекать через сопротивление, должна быть доступна разность потенциалов или напряжение. Когда резисторы соединены последовательно, они должны «делить» общее напряжение источника.

Общее напряжение в последовательной цепи равно сумме всех индивидуальных падений напряжения в цепи.

Когда ток проходит через каждый резистор в последовательной цепи, он устанавливает разность потенциалов на каждом отдельном сопротивлении.Это обычно называется падением напряжения, и его величина прямо пропорциональна величине сопротивления. Чем больше значение сопротивления, тем выше падение напряжения на этом резисторе.

ET = E1 + E2 + E3…

Используя закон Ома, вы можете определить напряжение на каждом резисторе.

3 А × 15 Ом = 45 В

3 А × 5 Ом = 15 В

3 А × 20 Ом = 60 В

Общее напряжение источника равно сумме отдельных падений напряжения:

45 В + 15 В + 60 В = 120 В

Обрыв в последовательной цепи

При появлении обрыва ток в цепи прерывается.Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю. Однако разность потенциалов источника очевидна. Если вольтметр подключен через разрыв, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.

Рисунок 17. Обрыв цепи

Влияние пропадания линии и потери линии

Медь и алюминий используются в качестве проводников, потому что они мало препятствуют прохождению тока.Хотя сопротивлением часто пренебрегают при простом анализе цепей, в практических приложениях может возникнуть необходимость учитывать сопротивление линий.

Line Drop

Рисунок 18. Падение напряжения

Когда ток 10 А протекает через каждую линию с сопротивлением 0,15 Ом, на каждой линии появляется небольшое падение напряжения. Это падение напряжения на линейных проводниках обычно обозначается как линейное падение .

Поскольку есть две линии, общее падение составляет 2 × 1.5 В = 3 В. Напряжение сети на нагрузке (117 В) меньше напряжения источника.

В некоторых ситуациях может потребоваться использование более крупных проводов с меньшим сопротивлением, чтобы падение напряжения в линии не слишком сильно уменьшало напряжение нагрузки.

Потеря линии

Другой термин, связанный с проводниками, — потери в линии. Это потеря мощности, выраженная в ваттах, и связана с рассеянием тепловой энергии, когда ток течет через сопротивление проводов линии.Потери в линии рассчитываются с использованием одного из уравнений мощности.

Используя предыдущий пример:

P = I ² × R

P = (10A) ² × 0,3 Ом

P = 30 Вт

* Помните:

• Падение напряжения в линии выражается в вольтах.
• Потери в линии выражены в ваттах.

Авторство

резисторов, включенных последовательно и параллельно | Комбинации резисторов

Результаты обучения

• Рассчитайте общее сопротивление различных комбинаций резисторов i.е., последовательно, параллельно и последовательно-параллельно.
• Покажите, как резисторы используются в качестве делителей напряжения и тока.
• Рассчитайте сопротивление и значение мощности для последовательного резистора, понижающего напряжение.

Отдельные резисторы могут быть соединены вместе последовательно, параллельно или в комбинации последовательно и параллельно. Это приводит к более сложной схеме, полное сопротивление которой представляет собой комбинацию отдельных резисторов.

Комбинация резисторов серии

Для подключения резисторов серии , они соединяются конец к концу вместе в одну линию, как показано на рисунке Рисунок 1 .Характеристики последовательно соединенных резисторов можно резюмировать следующим образом:

• Общее сопротивление цепи ( R _T ) увеличивается, если дополнительные резисторы подключаются последовательно, и уменьшается, если резисторы удалены.
• Чтобы определить общее сопротивление цепи, просто найдите сумму отдельных сопротивлений нагрузок.
• В этом примере, если резисторы обозначены как R ₁ , R ₂ и R ₃ , то общее сопротивление R _T рассчитывается по формуле

Рисунок 1 Резисторы, подключенные последовательно.

ПРИМЕР 1

Проблема: Три резистора, R ₁ (4 Ом), R ₂ (50 Ом) и R ₃ (75 Ом) подключены последовательно, как показано на Рисунок 2 . Определите значение общего сопротивления комбинированной цепи.

Рисунок 2 Схема для примера 1.

Решение:

Резисторы, соединенные последовательно, используются в качестве делителей напряжения , , как показано на схеме Рисунок 3 .Делители напряжения широко используются в схемах, где один источник напряжения должен обеспечивать несколько разных значений напряжения для разных частей схемы.

Характеристики схемы последовательного делителя напряжения можно резюмировать следующим образом:

• Через каждый резистор проходит одинаковый ток.
• Входное напряжение делится пропорционально между последовательно соединенными резисторами.
• Падение напряжения на резисторе в последовательной цепи прямо пропорционально сопротивлению резистора.
• Чем выше значение сопротивления, тем больше падение напряжения.

Рисунок 3 Схема делителя напряжения .

Для схемы делителя напряжения падение напряжения на каждом резисторе обычно является фактором, который необходимо определить. Падение напряжения на любом резисторе пропорционально отношению его сопротивления к общему сопротивлению цепи.

Формула делителя напряжения позволяет рассчитать падение напряжения на любом из последовательно подключенных резисторов без необходимости сначала рассчитывать значение тока цепи.Заявлено в виде формулы:

ПРИМЕР 2

Резисторы R ₁ (5 кОм), R ₂ (3 кОм) и R ₃ (2 кОм) ) соединены последовательно, образуя делитель напряжения, как показано на Рисунок 4 . Если на схему подается входное напряжение 9 вольт, рассчитайте значение падения напряжения на каждом из резисторов, используя формулу делителя напряжения.

Рисунок 4 Схема для примера 2.

Решение:

ПРИМЕР 3

У вас есть источник на 120 В и вы хотите использовать последовательно понижающий резистор в сочетании с контрольной лампой 6 В при 150 мА для индикации подачи питания ( Рисунок 5 ). Определите значение сопротивления падения серии и требуемую мощность.

Рисунок 5 Цепь для примера 3.

Решение:

Параллельная комбинация резисторов

Резисторы соединены параллельно путем соединения бок о бок как показано на Рисунок 6 .Обратите внимание, что два конца резисторов подключены к одним и тем же двум точкам.

Характеристики параллельно включенных резисторов можно резюмировать следующим образом:

• Общее сопротивление (R _T ) сформированной цепи на меньше , чем сопротивление самого низкого значения сопротивления, присутствующего в любой из ветвей.
• Каждый резистор обеспечивает отдельный параллельный путь для прохождения тока.
• Если у вас есть несколько резисторов одинакового номинала, подключенных параллельно, то общее сопротивление легче всего найти, разделив общее значение сопротивления на количество подключенных резисторов.Для трех резисторов по 150 Ом, включенных параллельно, общее сопротивление составляет

Рисунок 6 Резисторы, подключенные параллельно.

Чтобы найти полное сопротивление двух неравных значений резисторов, соединенных параллельно (очень распространенное использование), используется формула произведения на сумму. Эта формула:

ПРИМЕР 4

Проблема: Резистор 60 Ом подключается параллельно с резистором 40 Ом, как показано на рис. 7 .Определите значение общего комбинированного сопротивления двух компонентов, используя формулу «произведение на сумму».

Рисунок 7 Схема для примера 4.

Решение:

Формула произведения на сумму лучше всего работает для двух резисторов, включенных параллельно. Если параллельно подключено более двух резисторов, использование становится труднее и менее практичным. Для более чем двух резисторов разных номиналов, соединенных параллельно, используется общая формула для полного сопротивления параллельной цепи.Эта формула:

ПРИМЕР 5

Проблема: Три резистора, R ₁ (120 Ом), R ₂ (60 Ом) и R ₃ ( 40 Ом) подключены параллельно, как показано на Рисунок 8 . Определите значение общего сопротивления комбинированной цепи.

Рисунок 8 Цепь для примера 5.

Решение:

Параллельные резистивные цепи можно рассматривать как делители тока , потому что ток разделяется или делится между различными резисторами, как показано на рисунке 9 .

Характеристики схемы параллельного делителя тока можно резюмировать следующим образом:

• Ток, протекающий через каждый резистор ответвления, обратно пропорционален его значению сопротивления.
• Чем меньше значение сопротивления, тем больше ток, и наоборот.
• Резисторы с одинаковым сопротивлением будут пропускать через них одинаковое количество тока.
• Формула, описывающая делитель тока, аналогична формуле для делителя напряжения и может быть выражена следующим образом:

Рисунок 9 Схема делителя тока.

ПРИМЕР 6

Проблема: Резисторы R ₁ R ₂ и R ₃ (2 Ом, 3 Ом и 6 Ом соответственно) подключены параллельно, как показано на Рисунок 10 . Используйте формулу делителя тока, чтобы вычислить значение тока, протекающего через каждый из нагрузочных резисторов, если общий ток, протекающий в цепи, составляет 10 ампер.

Рисунок 10 Схема для примера 6.

Решение:

ПРИМЕР 7

Проблема: При параллельном подключении дополнительных нагрузок общее сопротивление цепи уменьшается. Для схемы, показанной на рис. 11 , определите полное сопротивление цепи при каждом из следующих рабочих условий:

1. Переключатели 1 и 2 замкнуты.
2. Переключатели 1, 2 и 3 замкнуты.

Рисунок 11 Схема для примера 7.

Решение:

Последовательно-параллельная комбинация резисторов

Комбинированные резистивные цепи, также известные как последовательно-параллельные резистивные цепи , объединяют резисторы последовательно с резисторами, включенными параллельно, как показано на рисунке 12 .

Правила, регулирующие эти цепи, такие же, как и правила, разработанные для последовательных и параллельных цепей. Сначала определяется сопротивление совокупного полного сопротивления параллельной части.Затем общее сопротивление параллельной части добавляется к любому последовательному сопротивлению, чтобы найти общее сопротивление последовательно-параллельной комбинированной цепи.

Рисунок 12 Последовательно-параллельное соединение резисторов.

ПРИМЕР 8

Проблема: Резистор 9 Ом, R ₁ , и резистор 60 Ом, R ₂ , подключены параллельно друг другу и последовательно с резистор 40 Ом, R ₃ , как показано на Рисунок 13 .Определите общее сопротивление этой последовательно-параллельной комбинации резисторов.

Рисунок 13 Схема для примера 8.

Решение:

ПРИМЕР 9

Проблема: Показания сопротивления можно использовать для проверки схем на наличие неисправностей. Как определено в предыдущем примере, нормальное полное сопротивление этой последовательно-параллельной схемы , рис. 14, составляет 60 Ом.

1. Найдите новое значение R _T , если резистор R ₁ выйдет из строя разомкнут , в то время как значения сопротивления R ₂ и R ₃ останутся тем же.
2. Аналогичным образом найдите новое значение R _T , если резистор R ₃ будет поврежден закорочен , в то время как значения сопротивления R ₁ и R ₂ остаются такой же.

Рисунок 14 Цепь для примера 9.

Решение:

1. При разомкнутом отказе R ₁ цепь будет состоять из ₃ R последовательно с R ₂ и всего Сопротивление будет:

1. При коротком замыкании R ₃ цепь будет состоять из R ₁ параллельно с R ₂ , а общее сопротивление будет:

Контрольные вопросы

1. Рассчитайте общее сопротивление для каждой из следующих цепей резисторов:
   1. Последовательная цепь: R1 = 40 Ом, R2 = 75 Ом
   2. Параллельная цепь: R1 = 200 Ом, R2 = 200 Ом, R3 = 200 Ом
   3. Последовательная цепь: R1 = 2000 Ом, R2 = 6000 Ом, R3 = 2200 Ом
   4. Параллельная цепь: R1 = 14 Ом, R2 = 32 Ом
   5. Последовательная цепь: R1 = 4700 Ом, R2 = 800 Ом, R3 = 200 Ом
   6. Параллельная цепь: R1 = 60 Ом, R2 = 30 Ом, R3 = 15 Ом
9 0206 Резисторы R ₁ , R ₂ и R ₃ (50 Ом, 30 Ом и 20 Ом соответственно) подключены последовательно через приложенное напряжение 200 В, чтобы сформировать делитель напряжения.Используя формулу делителя напряжения, рассчитайте напряжения E ₁ , E ₂ и E ₃ .
2. Суммарный ток двух параллельно соединенных резисторов составляет 3 А. Сопротивление резистора R ₁ составляет 10 Ом, а сопротивление R ₂ равно 40 Ом. Используя формулу делителя тока, рассчитайте токи I ₁ и I ₂ .
3. Резистор 5 Ом, R ₁ , и резистор 20 Ом, R ₂ , подключены параллельно друг другу и последовательно с резистором 6 Ом, R ₃ .Вычислите полное сопротивление этой последовательно-параллельной цепи.
4. Вам даны три резистора по 100 Ом, которые нужно соединить вместе. Опишите три возможные конфигурации цепей и вычислите их значения общего сопротивления.

Контрольные вопросы — ответы

1. (а) 115 Ом, (б) 66,7 Ом, (в) 10200 Ом, (г) 9,74 Ом, (д) ​​5700 Ом, (е) 8,57 Ом
2. E ₁ = 100 В, E ₂ = 60 В, E ₃ = 40 В
3. I ₁ = 2.4 A, I ₂ = 0,6 A
4. 10 Ом
5. Три резистора по 100 Ом, подключенных последовательно, общее сопротивление 300 Ом. Три резистора по 100 Ом, подключенные параллельно, общее сопротивление 33,3 Ом. Два резистора 100 Ом, подключенные параллельно, а затем последовательно соединенные с резистором 100 Ом, общее сопротивление 150 Ом.

4.1 Последовательные и параллельные резисторы

Последовательные резисторы

Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, в землю, тогда R1.R1. на рисунке 4.2 (a) может быть сопротивлением вала отвертки, R2R2 сопротивлением ее ручки, R3R3 сопротивлением тела человека, и R4R4 сопротивление ее обуви.

На рисунке 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно.Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь на резиновой подошве с высоким сопротивлением. Это могло быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением к прибору, который уменьшал бы рабочий ток.

Рисунок 4.3 Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).

Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе на Рисунке 4.3.

Согласно закону Ома падение напряжения V, V на резисторе при протекании через него тока рассчитывается по формуле V = IR, V = IR, где II равно току в амперах (A), а RR — это сопротивление в Ом Ω.Ω. Другой способ представить это: VV — это напряжение, необходимое для протекания тока II через сопротивление RR

.

Таким образом, падение напряжения на R1R1 равно V1 = IR1, V1 = IR1, что на R2R2 равно V2 = IR2, V2 = IR2, а на R3R3 равно V3 = IR3.V3 = IR3. Сумма этих напряжений равна выходному напряжению источника; то есть

4.1 В = V1 + V2 + V3.V = V1 + V2 + V3.

Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV, PE = qV, где qq — электрический заряд, а VV — напряжение. Таким образом, энергия, подводимая источником, равна qV, qV, а энергия, рассеиваемая резисторами, равна

. 4.2 qV1 + qV2 + qV3. QV1 + qV2 + qV3.

Связи: законы сохранения

Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, qV = qV1 + qV2 + qV3.qV = qV1 + qV2 + qV3. Заряд qq аннулируется, давая V = V1 + V2 + V3, V = V1 + V2 + V3, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)

Теперь подстановка значений отдельных напряжений дает

4,3 В = IR1 + IR2 + IR3 = I (R1 + R2 + R3). V = IR1 + IR2 + IR3 = I (R1 + R2 + R3).

Обратите внимание, что для эквивалентного одиночного последовательного сопротивления Rs, Rs мы имеем

Это означает, что полное или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs = R1 + R2 + R3.Rs = R1 + R2 + R3.

Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление RsRs последовательного соединения равно

4.5 Rs = R1 + R2 + R3 + …, Rs = R1 + R2 + R3 + …,

, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.

Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на рисунке 4.3 составляет 12,0 В и 12,0 В, а сопротивления равны R1 = 1,00 Ом, R1 = 1,00 Ом, R2 = 6,00 Ом, R2 = 6,00 Ом и R3 = 13,0 Ом. R3 = 13,0 Ом. . а) Каково полное сопротивление? (б) Найдите ток.(c) Рассчитайте падение напряжения на каждом резисторе и покажите, что в сумме они равны выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление — это просто сумма отдельных сопротивлений, как указано в уравнении

4,6 Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом. Rs = R1 + R2 + R3 = 1.00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.

Стратегия и решение для (b)

Ток определяется по закону Ома, V = IR.V = IR. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи.

4,7 I = VRs = 12,0 В 20,0 Ом = 0,600 AI = VRs = 12,0 В 20,0 Ом = 0,600 A

Стратегия и решение для (c)

Напряжение — или падение IRIR — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает

. 4.8 V1 = IR1 = (0,600 A) (1,0 Ом) = 0,600 В. V1 = IR1 = (0,600 A) (1,0 Ом) = 0,600 В.

Аналогично

4,9 В2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В V2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В

и

4,10 V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В.

Обсуждение для (c)

Три капли IRIR в сумме дают 12,0 В, 12,0 В, как и предполагалось.

4,11 V1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 VV1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 В

Стратегия и решение для (d)

Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P = IV, P = IV, где PP — электрическая мощность.В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома V = IRV = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как

4,12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт. P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт.

Аналогично

4,13 P2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 WP2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт

и

4,14 P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт.

Обсуждение для (д)

Мощность также можно рассчитать, используя P = IVP = IV или P = V2R, P = V2R, где VV — это падение напряжения на резисторе (а не полное напряжение источника).Будут получены те же значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать P = IV, P = IV, где VV — напряжение источника. Это дает

4,15 P = (0,600 A) (12,0 В) = 7,20 Вт. P = (0,600 A) (12,0 В) = 7,20 Вт.

Обсуждение для (e)

По совпадению обратите внимание, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, что соответствует мощности, выдаваемой источником. То есть

4.16 P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт. P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 Вт.

Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

Основные характеристики резисторов серии

1. Последовательные сопротивления складываются Rs = R1 + R2 + R3 + …. Rs = R1 + R2 + R3 + ….
2. Одинаковый ток протекает последовательно через каждый резистор.
3. Отдельные последовательно включенные резисторы не получают полное напряжение источника, а скорее делят его.

.