Электрическая цепь с последовательным соединением элементов
|
|
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3,
откуда следует
R
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
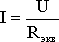 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

Рис. 1.6
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е.

откуда следует, что
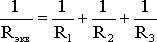 .
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
(1.7)

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв = g1 + g2 + g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IRэкв = I1R1 = I2R2
Отсюда следует, что
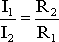 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
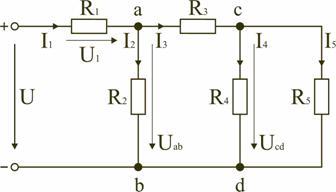
Рис. 1.7
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
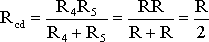
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
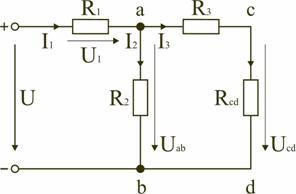
Рис. 1.8
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
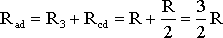 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

Рис. 1.9
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
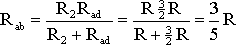 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
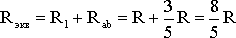
|
|
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока
Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.
Для
получения в линейных цепях синусоидально
изменяющихся токов необходимо, чтобы
э. д. с. также изменялись по синусоидальному
закону. Рассмотрим процесс возникновения
синусоидальной ЭДС. Простейшим генератором
синусоидальной ЭДС может служить
прямоугольная катушка (рамка), равномерно
вращающаяся в однородном магнитном
поле с угловой скоростью
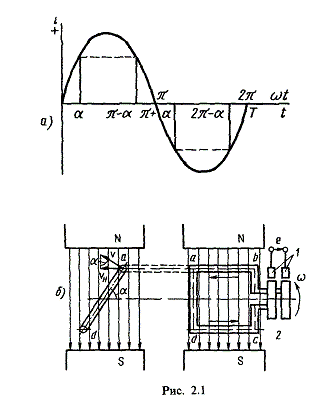
Пронизывающий
катушку магнитный поток во время вращения
катушки abcd наводит (индуцирует) в ней на основании
закона электромагнитной индукции
ЭДС е.
Нагрузку подключают к генератору с
помощью щеток 1,
прижимающихся к двум контактным кольцам 2,
которые, в свою очередь, соединены с
катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени
пропорционально магнитной индукции
e = Blvн (2.1)
где В и l — постоянные величины, a vн — переменная, зависящая от угла α. Выразив скорость vн через линейную скорость катушки v, получим
e = Blv·sinα (2.2)
В
выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая
в катушке, вращающейся в магнитном поле,
является синусоидальной функцией угла
Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. Em = Blv. Поэтому выражение (2.2) можно записать в виде
e = Emsinα (2.3)
Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде
e = Emsinωt (2.4)
где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.
Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.
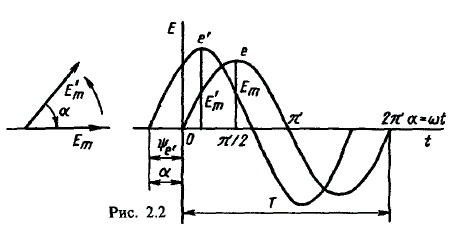
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е’.
Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,
f = Pn / 60
Из рис. 2.2 видно, что ωТ = 2π, откуда
ω = 2π / T = 2πf (2.5)
Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.
Графически изображенные на рис. 2.2 э. д. с. е и е’ можно описать выражениями
e = Emsinωt; e’ = E’msin(ωt + ψe’).
Здесь ωt и ωt + ψe’ — фазы, характеризующие значения э. д. с. e и e’ в заданный момент времени; ψe’ — начальная фаза, определяющая значение э. д. с. е’ при t = 0. Для э. д. с. е начальная фаза равна нулю (ψe = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу — вправо.
Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.
Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.
Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:
u = Umsin(ωt + ψu); i = Imsin(ωt + ψi), (2.6)
причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψu — ψi.
Уравнения (2.6) можно записать иначе:
u = Umsin(ωt + ψi + φ); i = Imsin(ωt + ψu — φ),
поскольку ψu = ψi + φ и ψi = ψu — φ.
Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe),
где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.
Графики мгновенных значений тока и напряжения показаны на рис. 2.3
Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψu > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψi < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ. Сдвиг фаз между напряжением и током
φ = ψu – ψi = ψu – ( — ψi) = ψu + ψi.
Применение аналитической формы для расчёта цепей является громоздкой и неудобной.
На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением
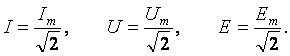
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
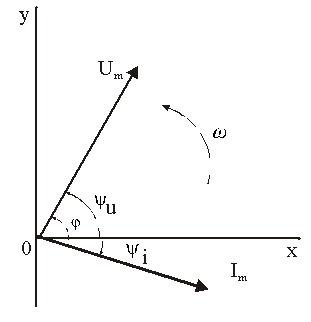 Рис.
2.4
Рис.
2.4
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4
3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
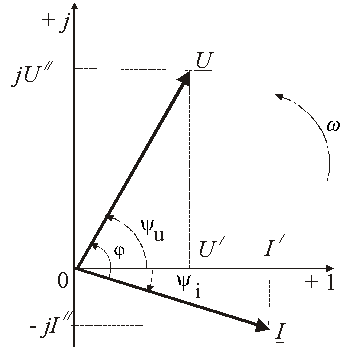 Рис.
2.5
Рис.
2.5
Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:
а). Алгебраической
U = U’+ jU«
I = I’ – jI«,
где U‘, U«, I‘, I» – проекции векторов на оси действительных и мнимых чисел.
б). Показательной

где U, I – модули (длины) векторов; е – основание натурального логарифма;  поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
в). Тригонометрической
U = U·(cosψu + jsinψu)
I = I·(cosψi – jsinψi).
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
еj·ψ = cosψ + jsinψ.
Неразветвлённые электрические цепи
Виды соединения проводников
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.

При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.

При параллельном соединении эквивалентное сопротивление находится как:

В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:


Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R3. Следует понимать, что после преобразования эквивалентное сопротивление R1R2 и резистор R3, соединены последовательно.

Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.

Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.

И находят сопротивления R1, R2 и R3.

Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R3,R4 и R5,R2 соединены между друг другом последовательно, а в парах параллельно.

На этом всё! Примеры расчета сопротивления цепей тут.
Электротехника часть 4. Соединение элементов цепи
Всем доброго времени суток. В прошлой статье я рассмотрел закон Ома, применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса токов, называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и сопротивлениями.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Последовательное соединение приемников энергии
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
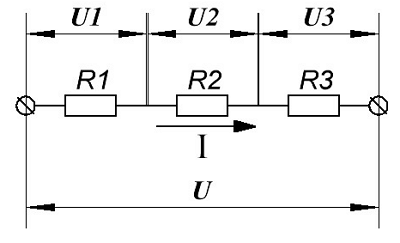

Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с напряжением U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
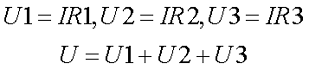
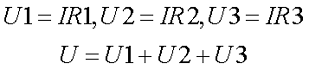
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
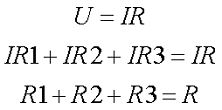
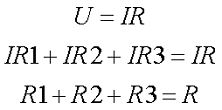
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
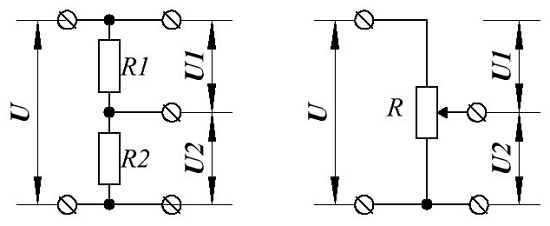

Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Параллельное соединение приемников энергии
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
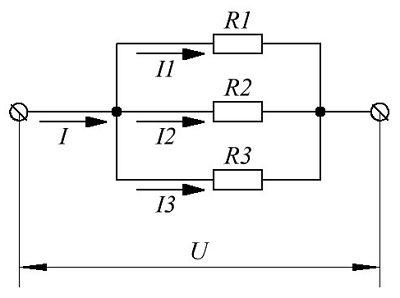

Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
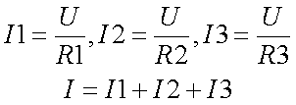
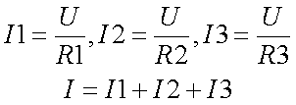
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
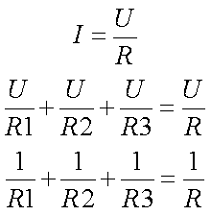
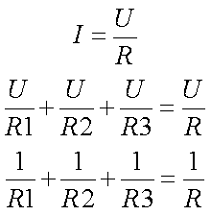
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
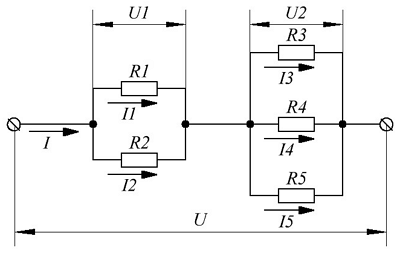

Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
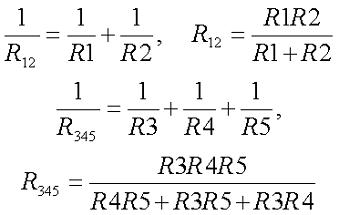
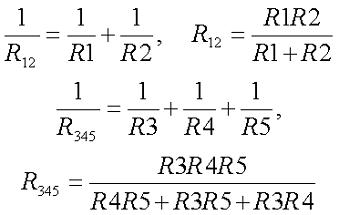
В результате получили цепь из двух последовательных приемников энергии R12R345 эквивалентное сопротивление и ток, протекающий через них, составит
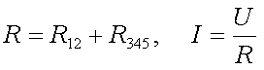
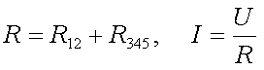
Тогда падение напряжения по участкам составит


Тогда токи, протекающие через каждый приемник энергии, составят
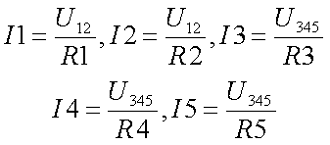
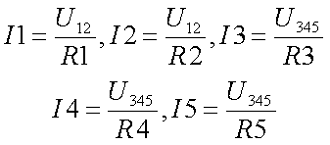
Первый закон Кирхгофа
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
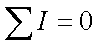
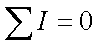
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
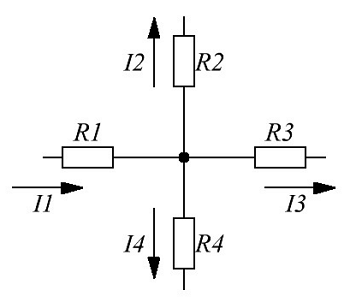

Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
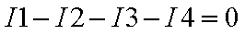
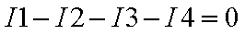
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Второй закон Кирхгофа
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
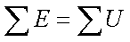
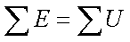
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
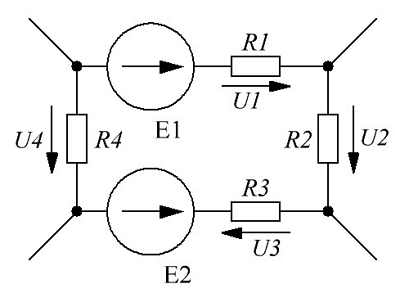

Схема, иллюстрирующая второй закон Кирхгофа.
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
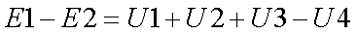
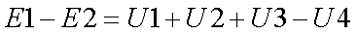
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Цепи постоянного тока Виды соединений приемников Последовательное соединение приемников
Последовательным называется такое соединение, когда во всех включенных элементах ток один и тот же (рис.2.а).
При расчетах цепей часто группа последовательно соединенных сопротивлении заменяется одним сопротивлением, но так, чтобы эта замена не изменила токов и напряжений на остальных участках цепи. Такое соединение называется эквивалентным.
R1 R2 R3
 +
+
+
+
U U1U2 U3I U I RЭКВ
–
а б
Рис.2. Последовательное соединение приёмников
На основании второго закона Кирхгофа можно записать:
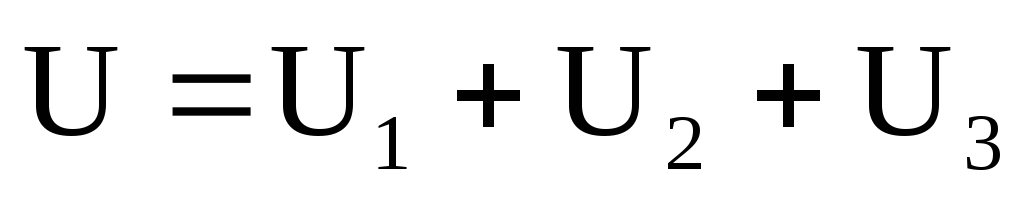 .
.
Применяя закон Ома к каждому сопротивлению и эквивалентному сопротивлению, имеем:
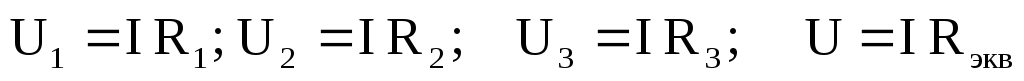 .
.
Тогда  ,
откуда:
,
откуда:
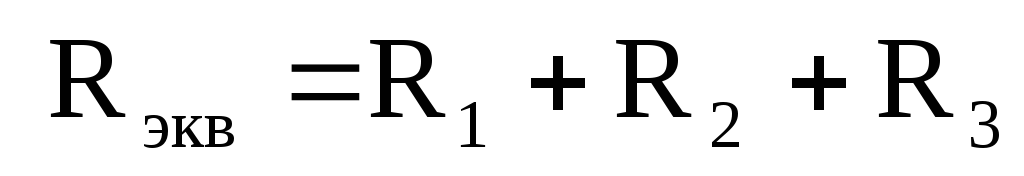 .
.
Когда последовательно соединено n одинаковых сопротивлений R, то
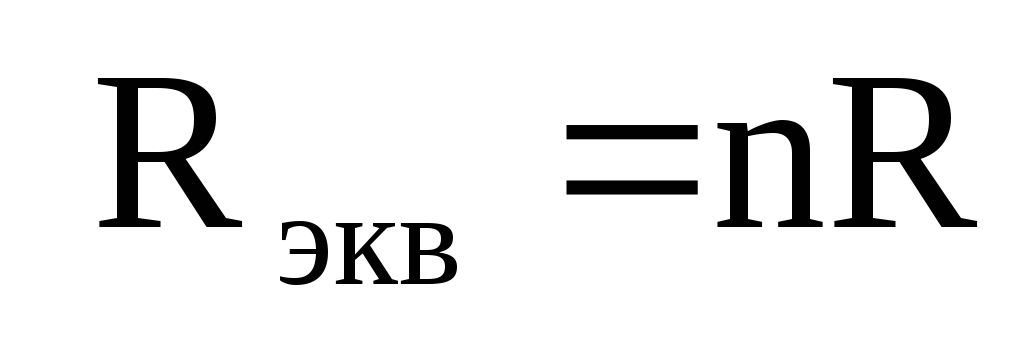 .
.
Ток цепи
 и т.д.
и т.д.
Отсюда следует, что
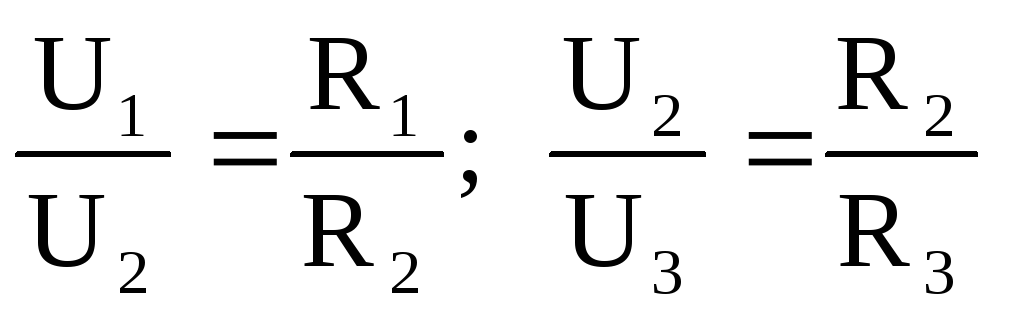 и т.д.
и т.д.
На основании полученных уравнений сделаем основные выводы для последовательной цепи:
ток на всех участках цепи один и тот же;
приложенное к цепи напряжение равно сумме напряжений на отдельных участках;
эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков;
напряжение участков цепи пропорционально их сопротивлениям.
Легко видеть, что режим работы элементов зависит друг от друга, и при выходе из строя одного элемента прекращается работа всех остальных, поэтому последовательное соединение применяется относительно редко.
Последовательное соединение применяется при пуске и регулировании скорости двигателей постоянного тока, когда последовательно с обмоткой якоря и обмоткой возбуждения включают реостаты. Такое соединение используется также в технике электрических измерений, например, для расширения пределов измерения вольтметров последовательно с ними подключают добавочные резисторы.
Параллельное соединение приемников
Параллельным соединением называется такое соединение, когда все приемники присоединены к двум узлам цепи (рис.3.а).
 I
I
I
I
R1 R2 R3
U RЭКВ
I1 I2 I3
а б
Рис.3. Параллельное соединение приёмников
В этом случае все приемники находятся под одним и тем же напряжением U. На основании первого закона Кирхгофа можно записать:
 .
.
Применяя закон Ома к каждому сопротивлению и эквивалентному сопротивлению (рис. 3.б.), имеем
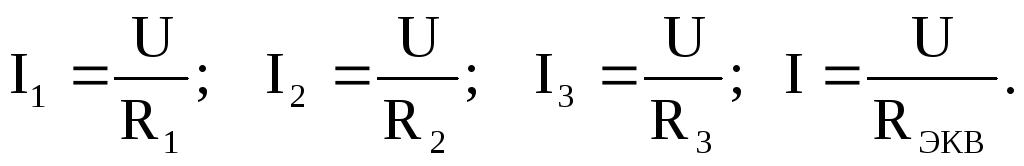
Тогда 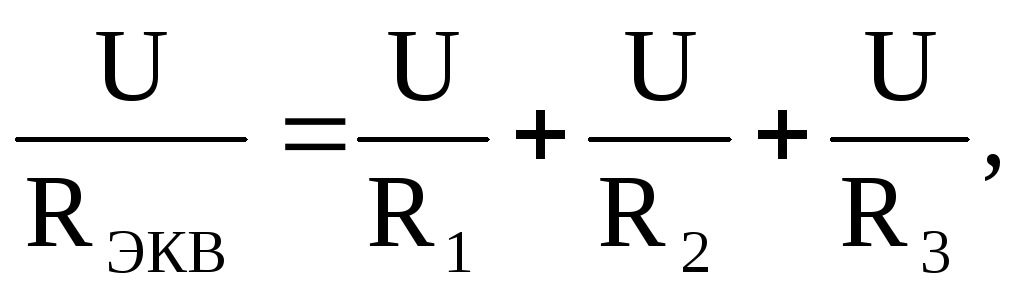 откуда
откуда
 .
.
и ли
ли
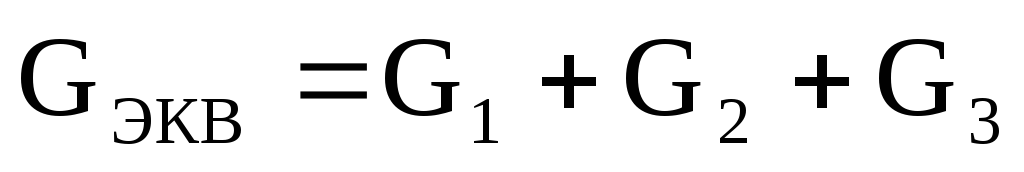 .
.
Если параллельно соединено n одинаковых сопротивлений R, то сопротивление цепи
 .
.
Отсюда следует, что
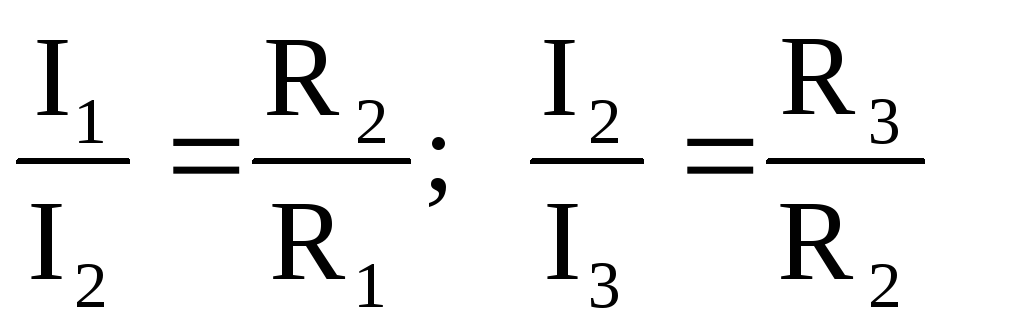 ;
;
 .
.
Особый интерес представляет цепь с двумя параллельно включенными приемниками, имеющими сопротивления R1 и R2. В этом случае
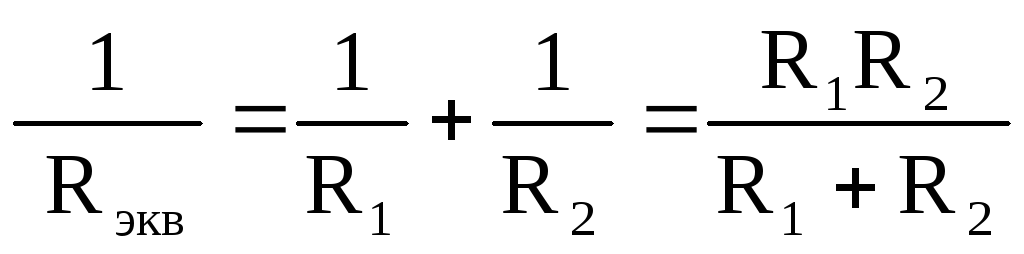 ,
,
откуда  .
.
Эквивалентное сопротивление такой цепи равно произведению сопротивлении, деленному на их сумму.
Токи ветвей этой цепи:
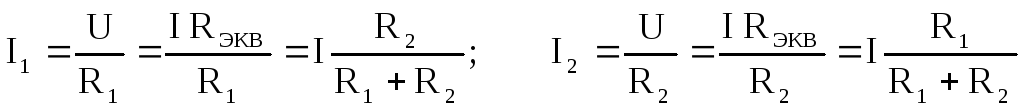 .
.
Ток параллельной ветви равен току в неразветвленной части цепи, умноженному на отношение сопротивления “чужой” ветви к сумме сопротивлений двух ветвей.
На основании полученных уравнений сделаем основные выводы для параллельной цепи:
1) напряжение на всех ветвях одно и тоже;
2) ток в неразветвленной части цепи равен сумме токов отдельных ветвей;
3) эквивалентная проводимость цепи равна сумме проводимостей отдельных ветвей;
4) токи между параллельными ветвями распределяются обратно пропорционально их сопротивлениям.
Следует обратить внимание на то, что эквивалентное сопротивление всегда меньше наименьшего из сопротивлений ветви и при подключении дополнительной ветви эквивалентное сопротивление уменьшается.
Так как режим работы приемников при параллельном их включении не зависит друг от друга, параллельное соединение в электротехнике является основным.
Смешанное соединение приемников
Смешанным называется такое соединение (Рис. 4), при котором в цепи имеются группы параллельно и последовательно включенных приемников.
R2
 R1a б
R1a б
I2
R3
I1
UI3 R4 R5 R6
I4 I5I6
в
рис.4. Смешанное соединение элементов
Предположим, что для цепи рис. 4. известно напряжение U на входе и сопротивления всех резистивных элементов цепи и требуется определить токи и напряжения на всех ее участках.
Порядок расчета:
Производится упрощение схемы путем замены отдельных групп с параллельным соединением элементов эквивалентными элементами. На участке аб содержатся два параллельно соединенных элемента с сопротивлениями R2 и R3. Эквивалентное сопротивление этого участка
 .
.
На участке бв включены параллельно три элемента с сопротивлениями R4, R5, R6.
Эквивалентное сопротивление этого участка можно определить из выражения
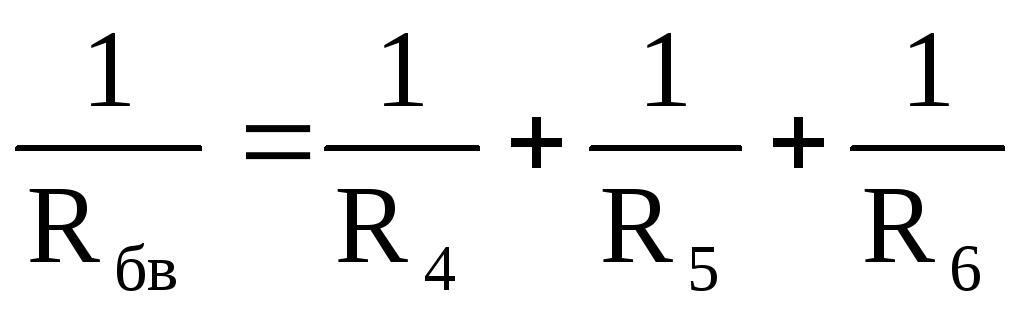 .
.
В результате упрощения исходной схемы получается схема
(рис. 5)с последовательным соединением элементов R1, Rаб, Rбв.
I1 R1 Rаб

 +
+
U1 Uаб
U Uбв Rбв
 –
–
Рис. 5. Схема с последовательным соединением элементов
2. Производится дальнейшее упрощение схемы путем замены последовательно соединенных элементов одним эквивалентным элементом (рис. 6) с сопротивлением
Rэкв =R1 + Rаб + R бс
I
U RЭКВ
Рис. 6. Схема с одним эквивалентным элементом
3. Находится ток цепи
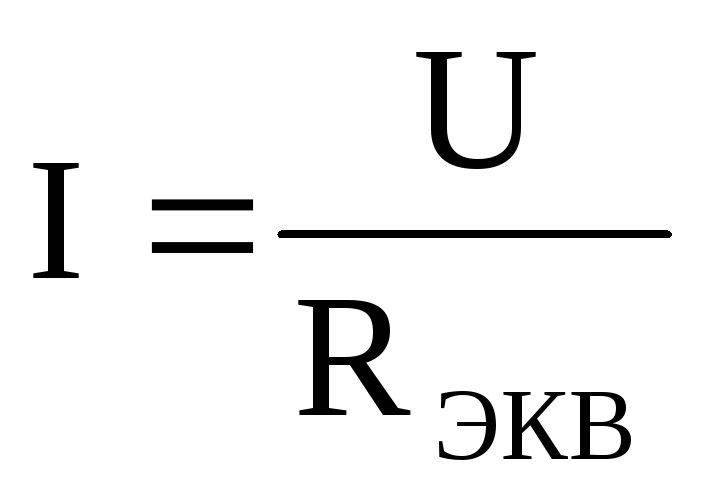 .
.
Ток в неразветвленной части цепи (элемент с сопротивлением R1)

4. Определяются напряжения на всех участках цепи:
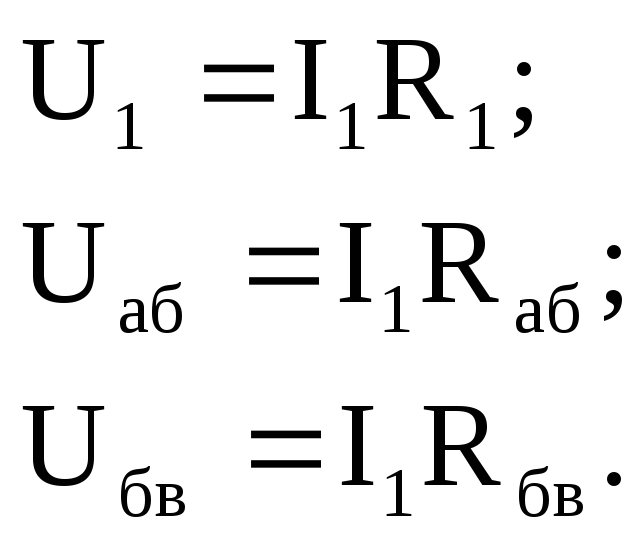
5. Находятся токи всех элементов, соединенных параллельно:
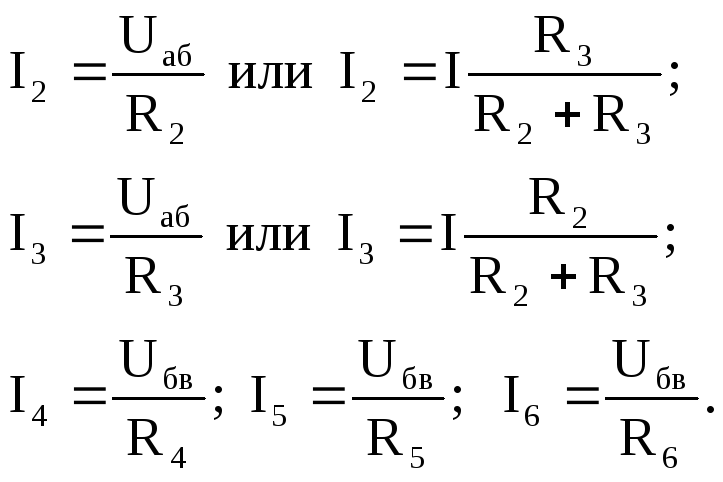
Лабораторная работа 1
Исследование цепи постоянного тока с пассивными элементами
Цель работы: Изучить законы Кирхгофа. Рассмотреть последовательное, параллельное и смешанное соединение токоприемников, исследовать распределение токов, напряжений и мощностей в каждой цепи.
Порядок выполнения работы
Последовательное соединение приемников
Соберите цепь по схеме (рис. 7)
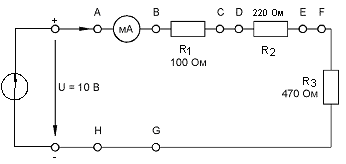
Рис. 7. Последовательное соединение приёмников
Установите напряжение на входе U = 10 B; сопротивления R1 = 100 Ом, R2 = 220 Ом, R3 = 470 Ом. Проведите измерение тока. Заполните табл.1
Таблица 1
Установлено | Измерено | Вычислено | |||
R1 (Ом) | R2 (Ом) | R3 (Ом) | U (В) | I (A) | U1 (В) |
100 | 220 | 470 | |||
Продолжение таблицы 1
Вычислено | ||||||||
U2 (В) | U3 (В) | RЭ (Ом) | Р (Вт) | Р1 (Вт) | P2 (Вт) | Р3 (Вт) | P1+P2+Р3 (Вт) | U1+U2+U3 (В) |
Параллельное соединение приемников
Соберите цепь по схеме (рис.8)
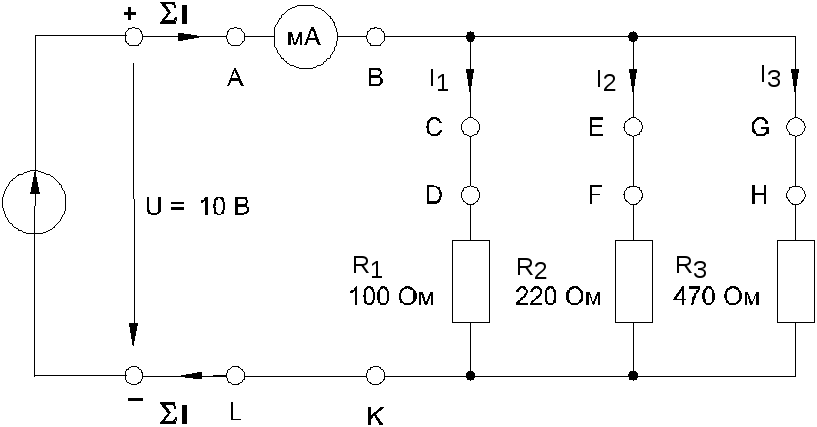
Рис. 8. Параллельное соединение приёмников
Установите напряжение на входе U = 10 B; сопротивления R1 = 100 Ом, R2 = 220 Ом, R3 = 470 Ом. Проведите измерение общего тока. Заполните табл.2
Таблица 2
Установлено | Измерено | ||||
R1 (Ом) | R2 (Ом) | R3 (Ом) | U (В) | I (А) | I1 (А) |
100 | 220 | 470 | |||
Продолжение таблицы 2
Вычислено | ||||||||
I2 (А) | I3 (А) | I1+I2+I3 (А) | RЭ (Ом) | Р (Вт) | Р1 (Вт) | Р2 (Вт) | Р3 (Вт) | P1+P2+Р3 (Вт) |
Последовательное, параллельное и смешанное соединение резисторов.
Контрольная работа № 1
вариант № 10
учащегося (щейся) Кот А.А.
(фамилия, имя, отчество)
1 курса 90-хк группы
специальности технология пищевых производств
Шифр учащегося (щейся) 210
Последовательное, параллельное и смешанное соединение резисторов.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
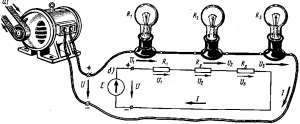
Рис. 1. Схемы последовательного соединения приемников
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 1.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк
где Rэк = R1 + R2 + R3.
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов. Так как напряжения на отдельных участках цепи согласно закону Ома: U1=IR1; U2 = IR2, U3 = IRз
и в данном случае E = U, то для рассматриваемой цепи
U = U1 + U2 +U3
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U1 : U2 : U3 = R1 : R2 : R3
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например n, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в n раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
U1 = U/n.
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 2).
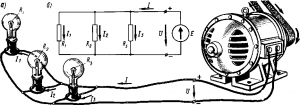
Рис. 2 Схемы параллельного соединения приемников
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа
I = I1+I2+I3, или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/Rэк = 1/R1 + 1/R2 + 1/R3
Вводя в формулу вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:
Gэк = G1+ G2 +G3
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
Rэк=R1R2/(R1+R2)
при трех параллельно включенных резисторах
Rэк=R1R2R3/(R1R2+R2R3+R1R3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
Rэк = R1 / n
Проходящий по каждой ветви ток I1, в этом случае будет в n раз меньше общего тока:
I1 = I / n
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.
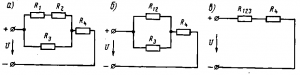
Рис. 3. Схемы смешанного соединения приемников
Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 3, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 3, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис.3, а заменяется эквивалентной схемой рис. 3, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).
При этом схема рис. 3, б заменяется эквивалентной схемой рис. 3, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4
Неразветвленная цепь переменного тока с активным сопротивлением, индуктивностью, емкостью. Полное сопротивление, активная, реактивная, полная мощность, векторная диаграмма тока и напряжений, треугольники сопротивлений и мощностей. Резонанс напряжений.

Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.4).
Рис. 4
В схеме протекает синусоидальный ток
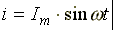
Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,
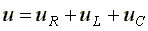 (1)
(1)
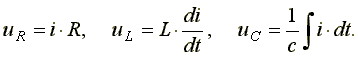
Подставдяем эти формулы в уравнение (1). Получаем:
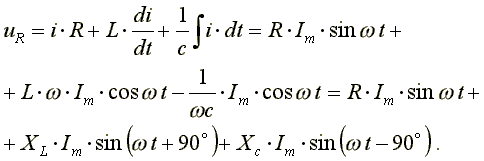
Из выражения (2) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o.
Запишем уравнение (2) в комплексной форме:
 (3)
(3)
Поделим левую и правую части уравнения (3) на √2. Получим уравнение для комплексов действующих значений токов и напряжений
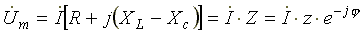 , (4)
, (4)
где 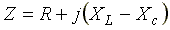 — комплексное сопротивление цепи;
— комплексное сопротивление цепи; 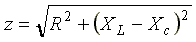 — модуль комплексного сопротивления, или полное сопротивление цепи;
— модуль комплексного сопротивления, или полное сопротивление цепи; 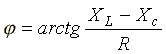 — начальная фаза комплексного сопротивления.
— начальная фаза комплексного сопротивления.
При построении векторных диаграмм цепи рассмотрим три случая.
1. XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис 5).
2. Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.6).
3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.7).
Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.
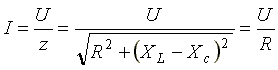
Условие возникновения резонанса: 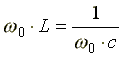 , отсюда резонансная частота равна
, отсюда резонансная частота равна
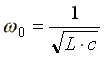 .
.
Из формулы следует, что режима резонанса можно добиться следующими способами:
1. изменением частоты;
2. изменением индуктивности;
3. изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
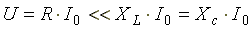 .
.
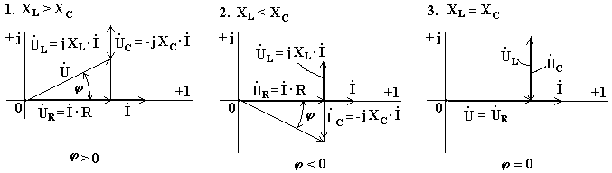
Рис. 5 Рис. 6 Рис. 7
“UL” и “UС” – могут быть выше чем “UОБЩ”.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Решение задач на смешанное соединение проводников.

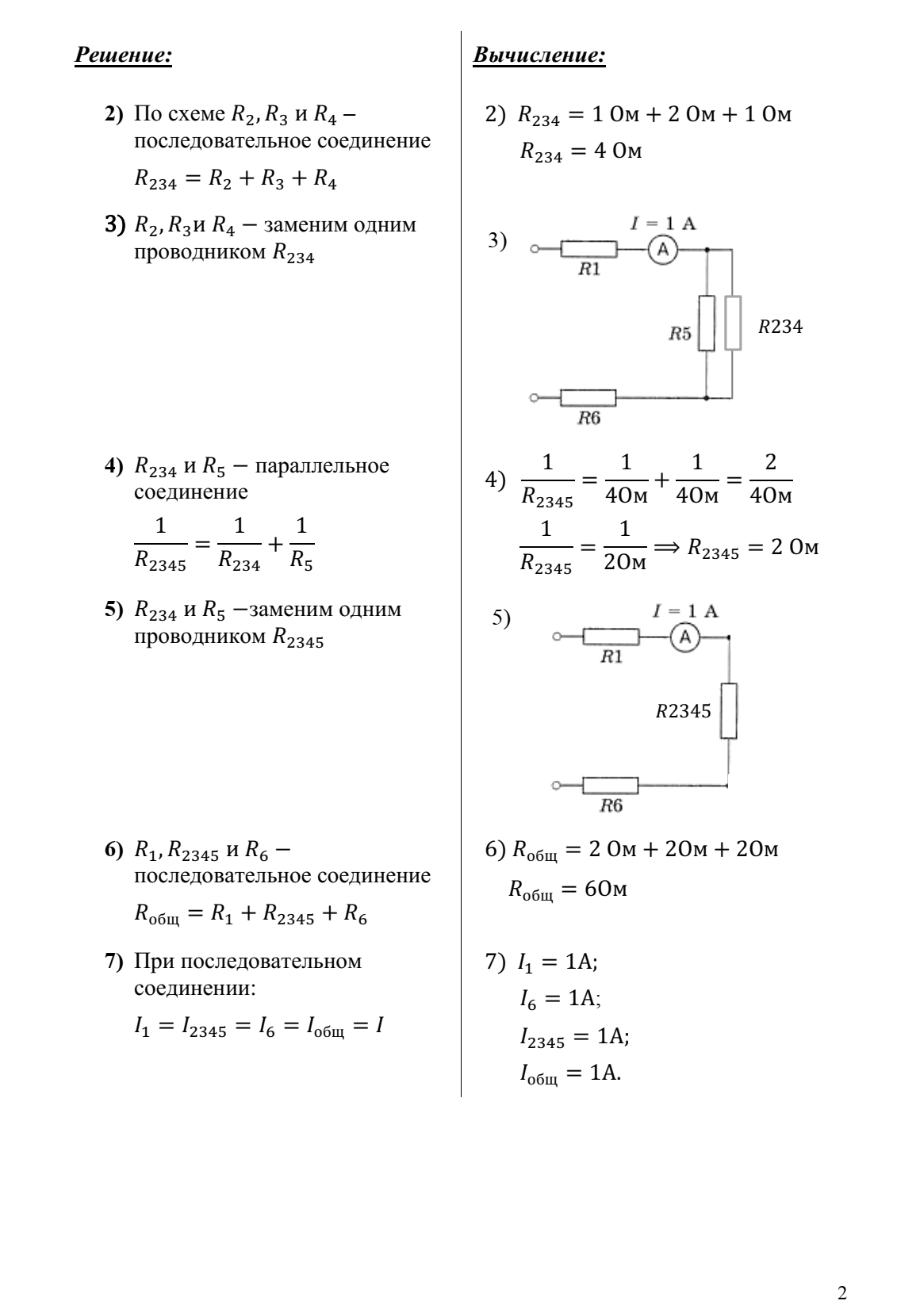
При решении задач на смешанное соединение проводников обычно составляют так называемые эквивалентные схемы, выделяя участки с последовательным и параллельным соединением.
Пример 1.
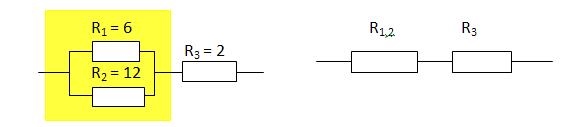
Сопротивление R1,2 заменило выделенный участок цепи, в котором два проводника соединены параллельно.
Тогда мы можем найти сопротивление этого участка с параллельным соединением проводников:
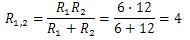
А теперь видно, что проводники R1,2 и R3 соединены последовательно. Общее сопротивление равно R = R1,2 + R3 = 4 + 2 = 6.
Пример 2.
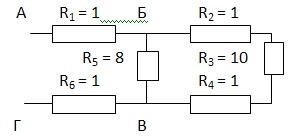
В данном случае нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема разветвляется, а в точке В ветви соединяются. Таким образом, эквивалентные схемы будут иметь вид:
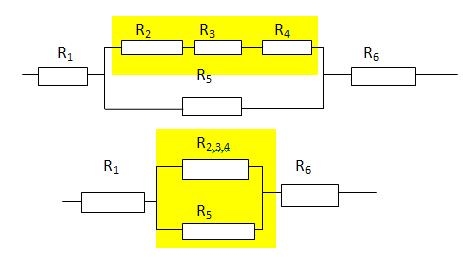
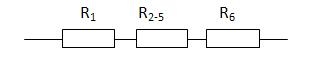
R2, R3 и R4 соединены последовательно. Поэтому R2,3,4 = R2 + R3 + R4 = 1 + 10 + 1 = 12
R2,3,4 и R5 соединены параллельно. Поэтому
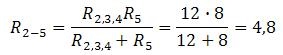
И в последней схеме проводники соединены последовательно. R = R2-5 + R1 + R6 = 1 + 4,8 + 1 = 6,8.
Пример 3. Найти распределение токов и напряжений в цепи.
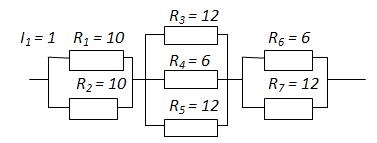
Решение.
Так как известны сила тока и сопротивление на первом участке, то можно найти напряжение на нем: U1 = I1 R1 = 1 ∙ 10 = 10 B.
Первый и второй проводники соединены параллельно. Значит, напряжение на них одинаково, т.е. U1 = U2 = 10 В. Так как первый и второй проводники имеют одинаковое сопротивление, то сила тока на них одинакова: I2 = 1 А. При параллельном соединении I1,2 = I1 + I2 = 2 А.
Участки 1-2, 3-4-5 и 6-7 соединены последовательно между собой, значит I3,4,5 = I6,7 = I1,2 = 2 A.
Найдем общее сопротивление участка 3-4-5:
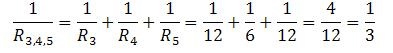
R3,4,5 = 3 Ом. Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно одинаково на всех участках. U3,4,5 = I3,4,5 ∙R3,4,5 = 2 ∙ 3 = 6 В.
U3 = U4 = U5 = 6 В. Зная напряжение на каждом из участков и сопротивление, можно найти силу тока на каждом участке.
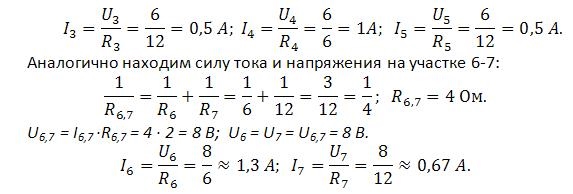




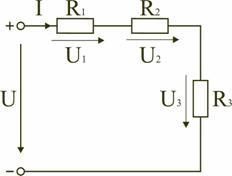 Рис.
1.4
Рис.
1.4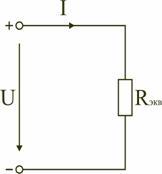 Рис.
1.5
Рис.
1.5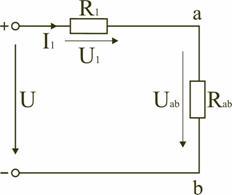 Рис.
1.10
Рис.
1.10 Рис.
1.11
Рис.
1.11