ПОЛНОЕ СОПРОТИВЛЕНИЕ — это… Что такое ПОЛНОЕ СОПРОТИВЛЕНИЕ?
- ПОЛНОЕ СОПРОТИВЛЕНИЕ
- ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: ,где r и x — активное и реактивное сопротивления. Измеряется в омах.
Большой Энциклопедический словарь. 2000.
- ПОЛНОЕ СОБРАНИЕ РУССКИХ ЛЕТОПИСЕЙ
- ПОЛНОЕ ТОВАРИЩЕСТВО
Смотреть что такое «ПОЛНОЕ СОПРОТИВЛЕНИЕ» в других словарях:
Полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи, где r и x активное и реактивное сопротивления.… … Википедия
ПОЛНОЕ СОПРОТИВЛЕНИЕ — (6, м) … Большая политехническая энциклопедия
полное сопротивление КЗ — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN closed end impedance … Справочник технического переводчика
полное сопротивление — pilnutinė varža statusas T sritis automatika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. полное сопротивление, n pranc. impédance, f … Automatikos terminų žodynas
полное сопротивление — pilnutinė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Visuminė elektrinės grandinės varža kintamajai srovei. atitikmenys: angl. apparent resistance; impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полное сопротивление — pilnutinė varža statusas T sritis fizika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное сопротивление, n pranc. impédance, f … Fizikos terminų žodynas
ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрич. цепи току. П. с. синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: Z=U/I = корень из (r2 + х2), где r и х активное и реактивное сопротивления … Естествознание. Энциклопедический словарь
полное сопротивление нулевой последовательности (трехфазной обмотки) — Полное сопротивление обмотки фазы в омах при номинальной частоте между соединенными вместе линейными выводами трехфазной обмотки, соединенной по схеме «звезда» или «зигзаг», и выводом ее нейтрали (МЭС 421 07 04).… … Справочник технического переводчика
46. Полное сопротивление в цепи переменного тока.
Обычно
цепь переменного тока включает в себя
и активное сопротивление, и емкость, и
индуктивность. 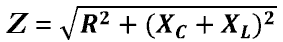 —
полное сопротивление цепи.
—
полное сопротивление цепи.
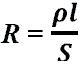 —
активное сопротивление.
—
активное сопротивление. 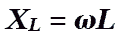 —
индуктивное сопротивление.
—
индуктивное сопротивление. 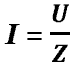 —
полное сопротивление определяет силу
тока в цепи по закону Ома.
—
полное сопротивление определяет силу
тока в цепи по закону Ома. 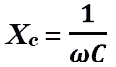
I — действующее значение силы тока (един.измер. А)
U— действующее значение напряжения(един.измер. В)
XL — индуктивное сопротивление(един.измер. Ом)
ω — циклическая частота переменного тока(един.измер. рад/с)
L – индуктивность(ед.из. Гн)
C – емкость (ед.из. Ф)
XC — индуктивное сопротивление (ед.из. Ом)
Z — полное сопротивление (Ом)
R — активное сопротивление (Ом)
ρ — удельное сопротивление проводника (Ом/м)
l — длина проводника (м)
S — площадь сечения проводника (м2
47.Импеданс тканей. Физические основы реографии.
При прохождении через ткани переменного тока, изменяющегося по гармоническому закону
I(t) =I0 cos ωt,
падение напряжения на биологической ткани изменяется по закону
U (t)=Uo⋅cos (ωt+ϕ).
Величиной, определяющей соотношение между напряжением и силой переменного тока, является импеданс — полное электрическое сопротивление цепи переменному току.
На опыте напряжение отстает по фазе от тока (ϕ<0), что характерно для электрических цепей, состоящих из резисторов и конденсаторов.
Для биологического объекта импеданс носит составной (комплексный) характер Z=(R,X). Его активная составляющая R связана, в первую очередь, с проводимостью внутренних жидких сред, являющихся электролитами. Различные процессы в тканях, сопровождающиеся необратимыми потерями энергии, также дают вклад в величину активной составляющей импеданса. Реактивная компонента X определяется емкостными свойствами исследуемой ткани, в частности, емкостью биологических мембран. Кроме того, в емкостную составляющую импеданса дает вклад и область контакта стимулирующих электродов с биологическими тканями.
Абсолютная величина (модуль) электрического импеданса определяется выражением .22XRZ+=
На опыте величина импеданса может быть определена по измерениям амплитудных (или эффективных) значений напряжения Uo и силы тока Io
⏐Z⏐ = Uo/Io (или ⏐Z⏐ = Uэфф/Iэфф).
Фазовый сдвиг ϕ определяет отношение реактивной и активной составляющих импеданса
tg ϕ = X/R.
Значения угла сдвига фаз, полученные при частоте 1 кГц для различных биологических объектов, приведены в таблице 1.
Таблица 1. Угол сдвига фаз (в градусах) для различных видов тканей.
Объект | ϕ , град. |
Кожа человека, лягушки Нерв лягушки Мышцы кролика | -55 -64 -65 |
Составную (комплексную) величину Z принято изображать в виде векторной диаграммы, на которой ось абсцисс — величина активного сопротивления, ось ординат — величина реактивного сопротивления.
Абсолютная величина импеданса ⏐Z⏐ и фазовый сдвиг ϕ являются функциями частоты переменного тока. Зависимость электрического импеданса от частоты носит название
Физические основы реологии.
Величина импеданса тканей зависит от их физиологического состояния, в частности от их кровоснабжения. При кровенаполнении сосудов происходит изменение величины импеданса в такт с работой сердца. По величине изменений импеданса можно судить о состоянии сердечно-сосудистой системы.
Реология — диагностический метод, основанный на регистрации изменения величины импеданса тканей в процессе сердечной деятельности.
Величина импеданса тканей |Z| состоит из двух составляющих |Z| = |Zo| + |z(t)|: постоянной — |Zo| и изменяющейся во времени в соответствии с работой сердца – |z(t)|.
На практике, на исследуемый участок тела накладывают электроды площадью несколько см2 и пропускают переменный ток частотой ≈ 30 − 40 кГц. Выбор частоты определяется несколькими факторами: электробезопасностью, исключением влияния электродов и емкости их контакта с кожей, уменьшением зависимости величины импеданса от механических воздействий на исследуемую ткань. Наполнение сосудов кровью изменяет расстояния между отдельными участками ткани, что должно приводить к изменению ёмкостного сопротивления. Но вклад макроскопических объемов тканей в реактивную составляющую импеданса существенен только в области α- дисперсии. Следовательно, изменения импеданса во времени обусловлены влиянием притока и оттока крови на активную составляющую полного сопротивления.
При прохождении через ткани электрического тока I = Io⋅cos ωt величина напряжения будет изменяться по закону
U = Uο cos (ωt + ϕ) = Io⋅( ⏐Zo⏐ + ⏐z(t)⏐ )⋅cos (ωt +ϕ ).
Электрическими методами выделяют из регистрируемого сигнала составляющую, пропорциональную |z(t)|, содержащую информацию о состоянии кровоснабжения изучаемого участка тканей − реограмму.
Для парных анатомических образований проводят запись реограммы на правой и левой стороне тела.
Полное сопротивление Википедия
Электри́ческий импеда́нс (ко́мплексное электри́ческое сопротивле́ние[1]) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Это понятие и термин ввёл физик и математик О. Хевисайд в 1886 году[2][3].
Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения и является пассивным элементом, поскольку не содержит внутренних источников энергии. Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):
- R=UI.{\displaystyle R={\frac {U}{I}}.}
Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:
- сопротивление идеальной катушки индуктивности стремится к нулю:
- если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:
- U=0;{\displaystyle U=0;}
- R=UI=0I=0;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}
- если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:
- I=0;{\displaystyle I=0;}
- R=UI=U0=∞.{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}
Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:
- напряжение между выводами катушки индуктивности не равно нулю;
- ток, протекающий через конденсатор, не будет равен нулю.
Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.
Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.
Определение
Импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник в установившемся режиме, то есть после завершения переходных процессов. Для линейных пассивных цепей с постоянными параметрами в установившемся режиме импеданс не зависит от времени. Если время t в математическом выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.
| z^(jω)=u^(jω,t)i^(jω,t)=U(ω)ej(ωt+ϕu(ω))I(ω)ej(ωt+ϕi(ω))=U(ω)ejϕu(ω)I(ω)ejϕi(ω)=U^(jω)I^(jω){\displaystyle {\hat {z}}(j\omega )\;={\frac {{\hat {u}}(j\omega ,t)\;}{{\hat {i}}(j\omega ,t)\;}}={\frac {U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}{I(\omega )e^{j(\omega t+\phi _{i}(\omega ))}}}={\frac {U(\omega )e^{j\phi _{u}(\omega )}}{I(\omega )e^{j\phi _{i}(\omega )}}}={\frac {{\hat {U}}(j\omega )\;}{{\hat {I}}(j\omega )\;}}} | (1) |
- Здесь:
Исторически сложилось, что в электротехнике обозначение импеданса, комплексных амплитуд и других комплексных функций частоты записывают как f(jω){\displaystyle f(j\omega )}, а не f(ω){\displaystyle f(\omega )}. Такое обозначение подчёркивает, что используются комплексные представления гармонических функций вида ejωt{\displaystyle e^{j\omega t}}. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: U˙(jω){\displaystyle {\dot {U}}(j\omega )\;} чтобы отличать от соответствующих действительных величин.
Физический смысл
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} можно рассматривать как последовательно соединенные резистор с сопротивлением ℜ(z^(jω)){\displaystyle \Re ({\hat {z}}(j\omega ))} и чисто реактивный элемент с импедансом ℑ(z^(jω)){\displaystyle \Im ({\hat {z}}(j\omega ))}
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.
Ограничения
Понятие импеданса в классической форме применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его параметры не менялись со временем и закончились переходные процессы. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель ejωt{\displaystyle e^{j\omega t}} в (1) не сокращается.
- Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении — для бесконечно малой амплитуды сигнала для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.
Обобщенный импеданс в s-плоскости и преобразование Лапласа
Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:
- Ft(s)=∫0∞fin(t)e−stdt.{\displaystyle F_{t}(s)=\int _{0}^{\infty }f_{in}(t)e^{-st}\,dt.}
Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:
- Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}
| Двухполюсник | Обобщённый импеданс |
|---|---|
| Резистор | R{\displaystyle R\,} |
| Катушка индуктивности | sL{\displaystyle sL\,} |
| Конденсатор | 1sC{\displaystyle {\frac {1}{sC}}\,} |
Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.
Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:
- fF,H(t)=L−1[H(s) Ft(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}[H(s)\ F_{t}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}
- где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.
- Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение
Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:
- HRC(s)=1/sCR+1/sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}
- где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.
Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:
- Uin(t)=U0 h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}
- где U0{\displaystyle U_{0}} — амплитуда ступеньки.
Преобразование Лапласа входного сигнала:
Fin(s)=L[U0 h(t)]=∫0∞e−stU0h(t)dt=U0/s.{\displaystyle F_{in}(s)={\mathcal {L}}[U_{0}\ h(t)]=\int \limits _{0}^{\infty }e^{-st}\,U_{0}\,h(t)\,dt=U_{0}/s.}
- Uout(t)=L−1[HRC(s) Fin(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞est1sT+1⋅U0sds=U0(1−e−t/T).{\displaystyle U_{out}(t)={\mathcal {L}}^{-1}[H_{RC}(s)\ F_{in}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}{\frac {1}{sT+1}}\cdot {\frac {U_{0}}{s}}\,ds=U_{0}(1-e^{-t/T}).}
Таким образом, получен отклик цепи при нулевом начальном условии (UC=0{\displaystyle U_{C}=0} при t=0{\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.
Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.
Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.
Вычисление импеданса
Идеальные элементы
Резистор
Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:
| zR=R{\displaystyle z_{R}=R} | (2) |
Конденсатор
Ток и напряжение для конденсатора связаны соотношением:
| i(t)=CdUdt.{\displaystyle i(t)=C{\frac {dU}{dt}}.} | (3) |
Отсюда следует, что при напряжении
| u^(jω,t)=U(ω)ej(ωt+ϕu(ω)){\displaystyle {\hat {u}}(j\omega ,t)=U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}} | (4) |
ток, текущий через конденсатор, будет равен:
| i^(jω,t)=Cddt(U(ω)ej(ωt+ϕu(ω)))=jωCU(ω)ej(ωt+ϕu(ω)).{\displaystyle {\hat {i}}(j\omega ,t)=C{\frac {d}{dt}}\left(U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}\right)=j\omega CU(\omega )e^{j(\omega t+\phi _{u}(\omega ))}.} | (5) |
После подстановки (4) и (5) в (1) получаем:
| z^C(jω)=1jωC=−jωC.{\displaystyle {\hat {z}}_{C}(j\omega )={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}.} | (6) |
Катушка индуктивности
Аналогичное рассмотрение для катушки индуктивности приводит к результату:
| z^L(jω)=jωL.{\displaystyle {\hat {z}}_{L}(j\omega )\;=j\omega L.} | (7) |
Общий случай
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:
| Z^(jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).} | (8) |
Экспериментальное измерение импеданса
Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.
Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.
В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.
Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.
Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.
Активная и реактивная составляющие импеданса обычно выражают в омах, но могут использоваться связанные с импедансом величины, например, в радиотехнике, линиях передачи, коэффициент стоячей волны или коэффициент отражения имеют бо́льшее удобство.
Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса[5].
Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств[5].
LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.
Применение понятия импеданса
Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал или применять преобразование Лапласа.
См. также
Примечания
Литература
- Бессонов Л. А. Теоретические основы электротехники. — 9-е изд. — М.: Высшая школа, 1996.
- Графов Б. М., Укше Е. А. Электрохимические цепи переменного тока. — М.: Наука, 1983.
Полное сопротивление — это… Что такое Полное сопротивление?
- Полное сопротивление
Полное сопротивление
Полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи, где r и x — активное и реактивное сопротивления. Измеряется в омах.
Wikimedia Foundation. 2010.
- Полное затмение (фильм
- Полномочный представитель Президента Российской Федерации в Межпарламентской ассамблее государств — участников СНГ
Смотреть что такое «Полное сопротивление» в других словарях:
ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: ,где r и x активное и реактивное сопротивления.… … Большой Энциклопедический словарь
полное сопротивление — Параметр пассивного двухполюсника, равный отношению действующего значения электрического напряжения на выводах этого двухполюсника к действующему значению электрического тока через двухполюсник при синусоидальных электрическом напряжении и… … Справочник технического переводчика
ПОЛНОЕ СОПРОТИВЛЕНИЕ — (6, м) … Большая политехническая энциклопедия
полное сопротивление КЗ — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN closed end impedance … Справочник технического переводчика
полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: , где r и х активное и реактивное сопротивления.… … Энциклопедический словарь
полное сопротивление — pilnutinė varža statusas T sritis automatika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. полное сопротивление, n pranc. impédance, f … Automatikos terminų žodynas
полное сопротивление — pilnutinė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Visuminė elektrinės grandinės varža kintamajai srovei. atitikmenys: angl. apparent resistance; impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полное сопротивление — pilnutinė varža statusas T sritis fizika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное сопротивление, n pranc. impédance, f … Fizikos terminų žodynas
ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрич. цепи току. П. с. синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: Z=U/I = корень из (r2 + х2), где r и х активное и реактивное сопротивления … Естествознание. Энциклопедический словарь
полное сопротивление нулевой последовательности (трехфазной обмотки) — Полное сопротивление обмотки фазы в омах при номинальной частоте между соединенными вместе линейными выводами трехфазной обмотки, соединенной по схеме «звезда» или «зигзаг», и выводом ее нейтрали (МЭС 421 07 04).… … Справочник технического переводчика
Полное сопротивление цепи переменного тока при последовательном соединении r, l и c
 .
(2.9)
.
(2.9)
Единицей измерения всех этих сопротивлений служит ом (Ом).
Индуктивное и емкостное сопротивления считаются реактивными. Это значит, что в них, в отличие от активных, не происходит превращение электрической энергии в другие виды энергии. Наличие тока в реактивном элементе объясняется периодическим обменом энергией между таким элементом и сетью.
Произведение мгновенных значений тока и напряжения есть мгновенная мощность цепи переменного тока и в общем случае, при синусоидальных токах и напряжениях, она определяется выражением
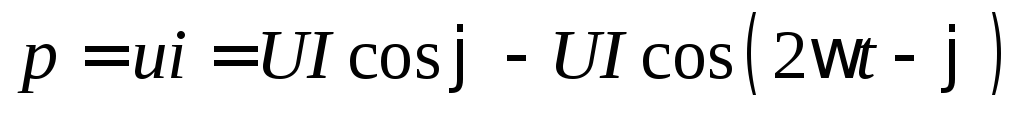 , (2.10)
, (2.10)
где | φ | – | угол сдвига фаз между напряжением и током потребителя. |
Формула для мгновенной мощности состоит из двух составляющих: постоянной, не зависящей от времени UIcosj, и переменной, изменяющейся во времени с двойной частотойUIcos(2wt –j).
Количество электрической энергии, превращающейся в потребителе в другой вид энергии, зависит от средней мощности Pза период переменного тока, которая называется активной мощностью, измеряется в ваттах (Вт) и может быть определена из выражения
 .
(2.11)
.
(2.11)
Сравнивая выражения (2.10) и (2.11), можно отметить, что постоянная составляющая мгновенной мощности равна активной мощности цепи. Измеряется активная мощность с помощью ваттметров.
Для характеристики скорости обмена энергией между реактивными элементами и сетью используется понятие реактивной мощности, под которой подразумевается амплитудное значение мгновенной мощности на этих элементах. Для определения реактивной мощности можно использовать следующие выражения:
 ,
(2.12)
,
(2.12)
где | U, I | – | действующие значения напряжения и тока на участке цепи, для которого рассчитывается реактивная мощность; |
j | – | угол сдвига фаз между напряжением и током на данном участке; | |
xL,xC | – | индуктивное и емкостное сопротивления рассматриваемого участка. |
Единицей измерения реактивной мощности служит вольт-ампер реактивный (вар), а измеряется эта мощность варметрами.
Полная мощность цепи переменного тока
 .
(2.13)
.
(2.13)
Единицей измерения полной мощности служит вольт-ампер (ВА).
Некоторые цепи, несмотря на наличие реактивных элементов, ведут себя по отношению к источнику питания как чисто активное сопротивление. Такое явление в цепи переменного тока называется резонансом. При резонансе напряжение и ток, потребляемый такой цепью, совпадают по фазе, а реактивная мощность всей цепи равна нулю. Основными видами резонанса являются резонанс напряжений при последовательном и резонанс токов при параллельном соединении элементов с индуктивностью и емкостью.
При последовательном соединении катушки индуктивности с индуктивным сопротивлением xL и конденсатора с емкостным сопротивлениемxC резонанс напряжений возникает при равенстве между собой индуктивного и емкостного сопротивлений, xL = xC. Поэтому при данном резонансе полное сопротивление последовательной цепи
 ,
(2.14)
,
(2.14)
где | r | – | активное сопротивление в рассматриваемой ветви, например, сопротивление провода, из которого намотана катушка индуктивности. |
Анализируя выражение (2.14), можно отметить, что полное сопротивление последовательной цепи при резонансе достигает минимального значения, а ток максимален. С увеличением тока повышается напряжение на элементах цепи и при резонансе оно достигает максимума. Особенностью рассматриваемого резонанса является возможность появления перенапряжений на реактивных элементах цепи, когда напряжения на катушке индуктивности и конденсаторе во много раз превышают напряжение источника питания. Такой случай возможен при xL = xC>>r.
При параллельном соединении двух и более ветвей с различным типом реактивного сопротивления может возникать резонанс токов. Условием этого резонанса является равенство индуктивной и емкостной проводимостей ветвей, включённых параллельно, bL =bC.
Для двух ветвей, включённых параллельно, полная проводимость
 ,(2.15)
,(2.15)
где | g1,g2 | – | активные проводимости ветвей, включённых параллельно; |
bL | – | реактивная проводимость ветви с индуктивным характером реактивности; | |
bC | – | реактивная проводимость ветви с емкостным характером реактивности. |
Реактивная проводимость первой ветви, в которой эквивалентная реактивность носит индуктивный характер,
 ,
(2.16)
,
(2.16)
где | xL | – | эквивалентное реактивное сопротивление рассматриваемой ветви; |
r1 | – | эквивалентное активное сопротивление данной ветви. |
Реактивная проводимость второй ветви, в которой эквивалентная реактивность носит емкостной характер,
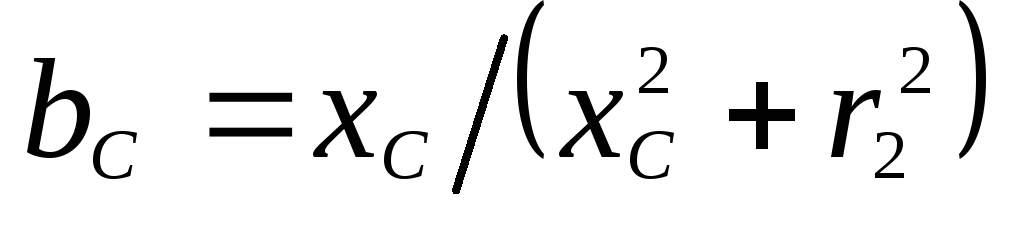 ,
(2.17)
,
(2.17)
где | xС | – | эквивалентное реактивное сопротивление рассматриваемой ветви; |
r2 | – | эквивалентное активное сопротивление данной ветви. | |
Активные проводимости ветвей:
 ,
(2.18)
,
(2.18)
 .
(2.19)
.
(2.19)
В приведённых выше выражениях под эквивалентным реактивным сопротивлением ветви подразумевается разность между индуктивным сопротивлением катушки и емкостным сопротивлением конденсатора, которые включены последовательно в рассматриваемой ветви. Если в ветви индуктивное сопротивление больше емкостного, то её эквивалентное реактивное сопротивление носит индуктивный характер, в противном случае характер эквивалентного реактивного сопротивления меняется на емкостный.
Эквивалентное активное сопротивление ветви равно сумме активных сопротивлений элементов, включённых в неё последовательно.
Для ветвей, в которых включён только один элемент, эквивалентное сопротивление равно соответствующему сопротивлению данного элемента (активному или реактивному).
При резонансе токов полная проводимость цепи равна её активной проводимости, y=g1+g2=g.
Из выражения (2.15) следует, что при резонансе токов полная проводимость разветвлённой цепи минимальна и равна активной проводимости. По этой причине ток, подходящий к участку, на котором возник резонанс токов, становится минимальным. В это же время токи в параллельных ветвях могут достигать больших значений и во много раз превышать ток, подходящий к разветвлённому участку. Возникает такой режим, когдаbL =bC>>g.
Импеданс — это… Что такое Импеданс?
Электри́ческий импеда́нс — комплексное сопротивление двухполюсника для гармонического сигнала. Это понятие ввёл физик и математик О. Хевисайд.
Аналогия с сопротивлением
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения и тока на нём, попытка применения термина электрическое сопротивление к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.
Сопротивление никак не описывает реактивные свойства элементов потому, что оно рассматривается на постоянном токе, то есть на нулевой частоте, когда реактивные свойства не проявляются. В то же время в случае переменного тока свойства реактивных элементов существенно иные: напряжение на катушке индуктивности и ток через конденсатор не равны нулю, однако это поведение сопротивлением уже не описывается[1]. Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некоей стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название электрический импеданс (или просто импеданс). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.
Определение
Импедансом 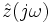 называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит для данного двухполюсника понятие импеданса не применимо.
называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит для данного двухполюсника понятие импеданса не применимо.
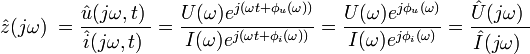 | (1) |
Здесь
- j — мнимая единица;
- ω — циклическая частота;
- U(ω), I(ω) — амплитуды напряжения и тока гармонического сигнала на частоте ω;
- φu(ω), φi(ω) — фазы напряжения и тока гармонического сигнала на частоте ω;
 ,
,  — Комплексные амплитуды напряжения и тока гармонического сигнала на частоте ω;
— Комплексные амплитуды напряжения и тока гармонического сигнала на частоте ω;
Исторически сложилось, что обозначение импеданса, комплексных амплитуд и других комплекснозначных функций частоты записывают как f(jω), а не f(ω). Такое обозначение показывает, что мы имеем дело с комплексными представлениями гармонических функций вида ejωt. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: 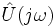 чтобы отличать от соответствующих действительных (некомплексных) величин.
чтобы отличать от соответствующих действительных (некомплексных) величин.
Физический смысл
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом 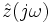 можно рассматривать как последовательно соединенные резистор с сопротивлением
можно рассматривать как последовательно соединенные резистор с сопротивлением 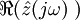 и чисто реактивный элемент с импедансом
и чисто реактивный элемент с импедансом 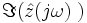
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько ток отстаёт от напряжения.
Ограничения
Понятие импеданса применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель ejωt в (1) не сокращается. Однако, импеданс зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для нее.
Вычисление импеданса
Идеальные элементы
Резистор
Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:
Конденсатор
Ток и напряжение для конденсатора связаны соотношением:
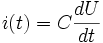 | (3) |
Отсюда следует, что при напряжении
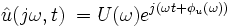 | (4) |
ток, текущий через конденсатор, будет равен:
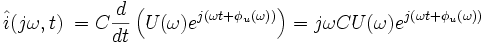 | (5) |
После подстановки (4) и (5) в (1) получаем:
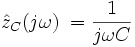 | (6) |
Катушка индуктивности
Аналогичное рассмотрение для катушки индуктивности приводит к результату:
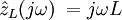 | (7) |
Общий случай
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:
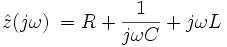 |
Экспериментальное измерение импеданса
Импеданс реальных элементов может быть измерен специальными приборами: измерителем RLC или анализатором импеданса. Эти приборы позволяют производить измерения в широком диапазоне частот и при различных напряжениях смещения.
Применение импеданса
Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал.
См. также
Внешние ссылки
Примечания
- ↑ Потому, что сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Wikimedia Foundation. 2010.
СОПРОТИВЛЕНИЕ ПОЛНОЕ — это… Что такое СОПРОТИВЛЕНИЕ ПОЛНОЕ?
- СОПРОТИВЛЕНИЕ ПОЛНОЕ
электрическое — общее сопротивление электрич. цепи перем. тока, обладающей как активным (омическим) сопротивлением R, так и реактивным (ёмкостным Хс и индуктивным XL) сопротивлением. С. п. определяется векторной суммой отд. составляющих. Модуль С. п. равен

Большой энциклопедический политехнический словарь. 2004.
- СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
- СОПРОТИВЛЕНИЕ РЕАКТИВНОЕ
Смотреть что такое «СОПРОТИВЛЕНИЕ ПОЛНОЕ» в других словарях:
Электрическое сопротивление полное — параметр пассивного двухполюсника, равный отношению действующего значения электрического напряжения на выводах этого двухполюсника к действующему значению электрического тока через двухполюсник при синусоидальных электрическом напряжении и… … Официальная терминология
Полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи, где r и x активное и реактивное сопротивления.… … Википедия
ПОЛНОЕ СОПРОТИВЛЕНИЕ — (6, м) … Большая политехническая энциклопедия
СОПРОТИВЛЕНИЕ — (1) аэродинамическое (лобовое) сила, с которой газ действует на движущееся в нём тело. Оно всегда направлено в сторону, противоположную скорости движения тела, и является одной из составляющих аэродинамической силы; (2) С. гидравлическое… … Большая политехническая энциклопедия
полное сопротивление нулевой последовательности (трехфазной обмотки) — Полное сопротивление обмотки фазы в омах при номинальной частоте между соединенными вместе линейными выводами трехфазной обмотки, соединенной по схеме «звезда» или «зигзаг», и выводом ее нейтрали (МЭС 421 07 04).… … Справочник технического переводчика
полное сопротивление короткого замыкания пары обмоток — Сопротивление, равное Z = R + jХ, Ом, определяемое при номинальной частоте и расчетной температуре между выводами одной из обмоток пары, при замкнутой накоротко другой обмотке этой пары и разомкнутых остальных обмотках при их наличии. Для… … Справочник технического переводчика
полное сопротивление контура — Zs Сумма полных сопротивлений токового контура, включающая в себя полное сопротивление источника тока, полное сопротивление фазного проводника от одного зажима источника тока до точки измерения и полное сопротивление обратного провода (например… … Справочник технического переводчика
полное сопротивление относительно земли — Полное сопротивление (импеданс) между точкой системы или установки, или оборудования и относительной землей на данной частоте. [ГОСТ Р МЭК 60050 195 2005] полное сопротивление относительно земли Полное сопротивление между определенной точкой… … Справочник технического переводчика
полное сопротивление переменного резистора — полное сопротивление Электрическое сопротивление между крайними выводами переменного резистора, измеренное на постоянном токе [ГОСТ 21414 75] Тематики резисторы Синонимы полное сопротивление EN total resistance DE Gesamtwiderstand FR résistance… … Справочник технического переводчика
полное синхронное сопротивление синхронной машины — полное синхронное сопротивление Отношение векторной разности между электродвижущей силой и напряжением на выводах обмотки якоря синхронной машины к току этой обмотки в установившемся режиме. [ГОСТ 27471 87] Тематики машины электрические… … Справочник технического переводчика




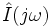 — Комплексные амплитуды напряжения и тока гармонического сигнала на частоте ω;
— Комплексные амплитуды напряжения и тока гармонического сигнала на частоте ω;