§55. Параллельное соединение сопротивлений в цепи переменного тока
Простейшая параллельная цепь. Рассмотрим простейшую цепь, состоящую из параллельно соединенных активного R и реактивного X сопротивлений (рис. 194,а). В данной схеме в качестве
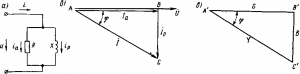 Рис.
194. Схема простейшей параллельной цепи
переменного тока (а), векторная диаграмма
(б) и треугольник проводимостей (в)
Рис.
194. Схема простейшей параллельной цепи
переменного тока (а), векторная диаграмма
(б) и треугольник проводимостей (в)
реактивного принято индуктивное сопротивление, но оно может быть также и емкостным. Для каждой ветви этой схемы можно по закону Ома определить токи Iа и Iр в ветвях и их углы сдвига фаз относительно напряжения, а затем, построив векторную диаграмму (рис. 194,б), найти по правилу сложения векторов ток в неразветвленной части цепи:
? = ?а
При построении векторной диаграммы в качестве исходного вектора используют вектор напряжения ?, а затем под соответствующими углами откладывают векторы токов ?а и ?р. В данном случае ток ?а будет совпадать по фазе с напряжением ?, а ток ?р — отставать от него на угол 90°. Ток I сдвинут относительно напряжения ? на угол ?.
Из треугольника токов ЛВС имеем:
Iа = I cos ?; Iр = I sin ?; I = ?(I2а + I2
Проводимости при переменном токе. Если разделить все стороны треугольника токов ABC на напряжение U, то получим треугольник проводимостей А’В’С’ (рис. 194, в).
При переменном токе существуют три вида проводимостей: активная G, реактивная В и полная Y. Активная проводимость для цепи, содержащей последовательно включенные R, L и С:
G = R / Z2 = R / (R2 + X2)
реактивная проводимость
B
= X / Z2 = X / (R2 + X
Реактивная проводимость в общем случае состоит из двух составляющих: емкостной проводимости BC=XC/Z2 и индуктивной проводимости BL=XL/Z2. При этом В = Вс — BL.
Полная проводимость
Y
= 1/Z = 1/?(R2 + X2) или Y = ?(G2 + B
В цепи переменного тока активная проводимость в общем случае не равна 1/R, она принимает это значение только в том случае, когда в данной параллельной ветви реактивное сопротивление Х = 0. Точно так же и реактивная проводимость в общем случае не равна 1/Х, она принимает это значение только когда в данной параллельной ветви R = 0.
Зная проводимость Y, можно определить ток в цепи:
I = UY
Из треугольника проводимостей А’В’С’ можно определить угол сдвига фаз ? между током I в неразветвленной части цепи и напряжением U:
cos
? = G / Y; sin ? = B / Y; tg ?
Общий случай параллельного соединения сопротивлений. В случае если в каждой ветви включены активное R и реактивное X сопротивления (рис. 195, а), следует по формулам (72) и (73) определить токи I1 и I2 в параллельных ветвях и углы их сдвига фаз ?1 и ?2 относительно напряжения U, а затем, построив векторную диаграмму (рис. 195,б), найти по правилу сложения векторов ток в неразветвленной части цепи ? = ?1+?2 и угол его сдвига фаз ? относительно напряжения U.
Можно также определить эквивалентную активную проводимость всей цепи:
Gэк = G1 + G
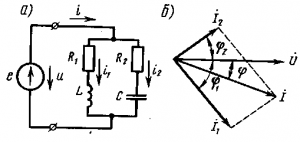 Рис.
195. Схема параллельной цепи переменного
тока, содержащая активное, индуктивное
и емкостное сопротивления (а), и векторная
диаграмма (б)
Рис.
195. Схема параллельной цепи переменного
тока, содержащая активное, индуктивное
и емкостное сопротивления (а), и векторная
диаграмма (б)
эквивалентную реактивную проводимость
Вэк = ВС2 – BL1
полную проводимость всей цепи
Yэк = ?(Gэк2 + Bэк2)
а затем найти ток в неразветвленной части цепи
I = UYэк
В общем случае при определении эквивалентной реактивной проводимости нескольких параллельных ветвей емкостные проводимости ветвей ВС берут со знаком «плюс», а индуктивные BL — со знаком «минус».
Цепь переменного тока при последовательном соединении элементов

i=Imsinωt
При последовательном соединении
элементов ток на всех участках цепи
одинаков. Действующее значение тока 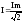
Падение напряжения на каждом элементе цепи можно определить из закона Ома
UR = I R ; UL = I XL = I 2π f L = I ωL; UC = I XC = 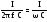
Приложенное напряжение Uравно геометрической сумме падений напряжения на каждом элементе последовательной цепи (IIзакона Кирхгофа).
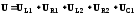 – сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД)
– сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД)Порядок построения ВД:
Строим вектор тока

Относительно вектора тока строим вектор падения напряжения на первом элементе цепи, учитывая величину и направление угла сдвига фаз между током и напряжением.
Из конца этого вектора аналогично строим вектор падения напряжения на следующем элементе цепи и т.д. – в результате получим векторную сумму падений напряжения на всех элементах цепи, т.е. приложенное напряжение


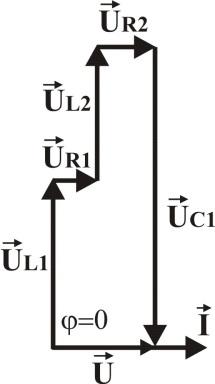
ВД при резонансе напряжений
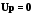
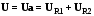
Численное значение приложенного напряжения Uможно определить из ВД
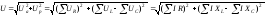
= 
Где: 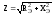 – полное сопротивление цепи
– полное сопротивление цепи
 – эквивалентное активное сопротивление
цепи
– эквивалентное активное сопротивление
цепи
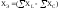 – эквивалентное реактивное
сопротивление цепи
– эквивалентное реактивное
сопротивление цепи
Резонанс в последовательной цепи (резонанс напряжений)
При резонансе напряжений сумма индуктивных напряжений равна сумме емкостных, следовательно, эквивалентное реактивное напряжение
 – условие резонанса напряжений
– условие резонанса напряжений
Следовательно, при резонансе напряжений
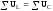

Приложенное напряжение  – равно активному.
– равно активному.
 –
равно сумме активных сопротивлений и
минимально, т.е. всю цепь можно заменить
эквивалентным активным сопротивлениемRЭ.
–
равно сумме активных сопротивлений и
минимально, т.е. всю цепь можно заменить
эквивалентным активным сопротивлениемRЭ. Ток в цепи 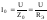 – максимален, и падение напряжения на
отдельных реактивных элементах может
быть больше приложенного напряжения
(см. ВД при резонансе).
– максимален, и падение напряжения на
отдельных реактивных элементах может
быть больше приложенного напряжения
(см. ВД при резонансе).
При резонансе напряжений приложенное напряжение совпадает по фазе с током (φ = 0), т.е. несмотря на наличие реактивных элементов, цепь ведет себя как чисто активный приемник.
Цепь переменного тока при параллельном соединении элементов

При параллельном соединении элементов напряжение на каждой ветви схемы одинаково и равно приложенному. Каждая ветвь схемы представляет из себя последовательное соединение элементов, следовательно, можно для каждой из ветвей найти полное сопротивление Z, токIи угол сдвига фаз φ

Аналогично можно определить Z,Iи φ для остальных ветвей
По Iзакону Кирхгофа ток
в неразветвленной части цепи равен
геометрической сумме токов в ветвях –сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД).
–сумма геометрическая (векторная),
следовательно, необходимо построить
векторную диаграмму (ВД).
Порядок построения ВД:
Строим вектор напряжения

Относительно вектора напряжения строим вектор тока первой ветви
 ,
учитываявеличину и направление угла сдвига фаз между током и напряжением
φ1.
,
учитываявеличину и направление угла сдвига фаз между током и напряжением
φ1.Из конца этого вектора строим вектор тока второй ветви и т.д. – в результате получим векторную сумму токов в ветвях, т.е. ток в неразветвленной части цепи.
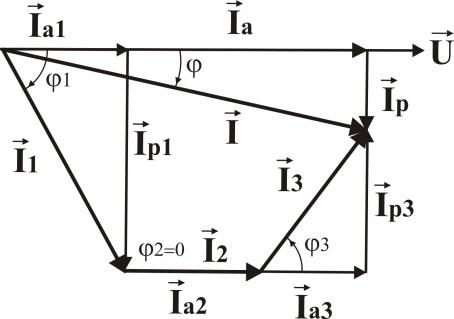

Численное значение полного тока Iможно определить из ВД, если разложить ток каждой ветви на две составляющие
Например, для первой ветви
 – активная составляющая токаI1
– активная составляющая токаI1
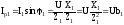 – реактивная составляющая токаI1
– реактивная составляющая токаI1
 – активная проводимость отдельной
ветви
– активная проводимость отдельной
ветви
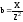 – реактивная проводимость отдельной
ветви
– реактивная проводимость отдельной
ветви
Аналогично можно разложить на составляющие токи всех ветвей
Тогда из ВД, учитывая, что емкостные и индуктивные токи направлены в противоположные стороны, получим
 =
=
= 
Где: 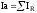 – активная составляющая полного тока
– активная составляющая полного тока
 – реактивная составляющая полного
тока
– реактивная составляющая полного
тока
 – эквивалентная активная проводимость
цепи
– эквивалентная активная проводимость
цепи
 – эквивалентная реактивная проводимость
цепи
– эквивалентная реактивная проводимость
цепи
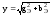 – полная проводимость цепи
– полная проводимость цепи
Резонанс в параллельной цепи (резонанс токов)
При резонансе токов сумма индуктивных токов равна сумме емкостных, следовательно, реактивная составляющая полного тока
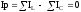 – условие резонанса токов
– условие резонанса токов
Следовательно, при резонансе токов
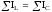

Полный ток (в неразветвленной части
цепи) 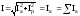 – равен активному, т.е. сумме активных
токов всех ветвей.
– равен активному, т.е. сумме активных
токов всех ветвей.
Полная проводимость цепи  – равно сумме активных проводимостей
всех ветвей и минимальна.
– равно сумме активных проводимостей
всех ветвей и минимальна.
Ток в цепи  – минимален, т.е. параллельная цепь при
резонансе обладает минимальной
проводимостью, т.е. максимальным
сопротивлением.
– минимален, т.е. параллельная цепь при
резонансе обладает минимальной
проводимостью, т.е. максимальным
сопротивлением.
При резонансе токов полный ток совпадает по фазе с приложенным напряжением (φ = 0), т.е. вся цепь имеет чисто активный характер.
Соединение элементов в цепи переменного напряжения и тока
Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Последовательное соединение элементов цепи при переменном напряжении
Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.
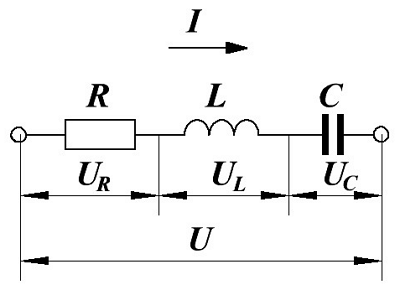

Последовательное соединение элементов цепи.
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах
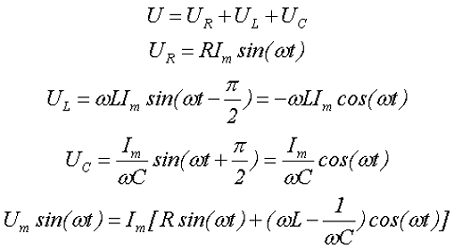
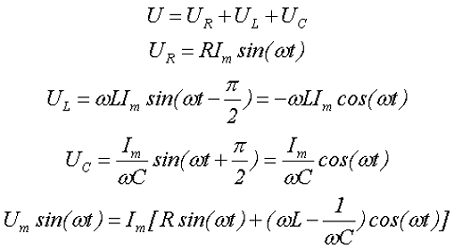
где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Im – амплитудное значение переменного тока.
Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже
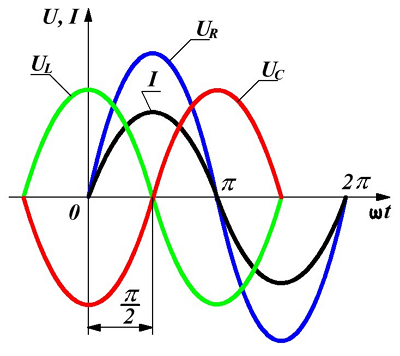

Напряжения и токи при последовательном соединении.
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде
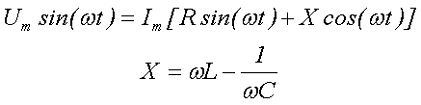
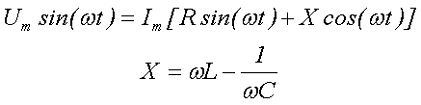
где R – активное сопротивление,
Х – реактивное сопротивление.
Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений
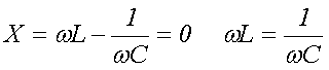
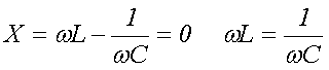
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.
При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение


где Z – полное сопротивление цепи,
ψ – разность фаз между напряжением и током.
Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением
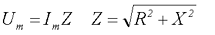
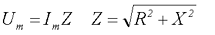
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
Z – полное сопротивление цепи.
Параллельное соединение элементов цепи при переменном напряжении
Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.
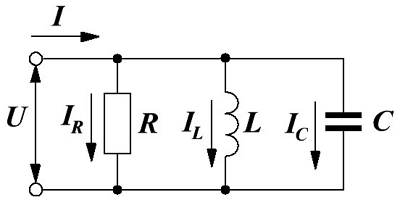

Параллельно соединение элементов цепи.
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи
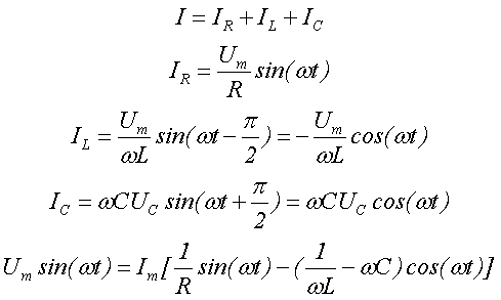
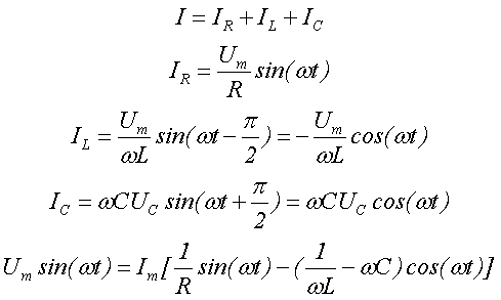
IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
Um – амплитудное значение переменного тока.
Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже
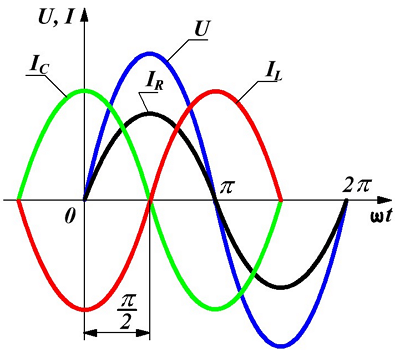

Напряжение и токи при параллельном соединении.
Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
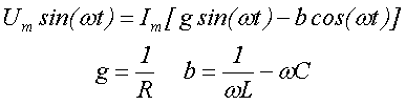
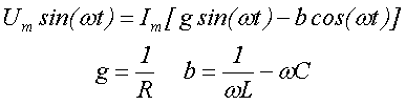
8. Последовательное соединение r, l, c при переменном токе


Рис. 7.
По закону Ома для мгновенного значения напряжения

где  — полное сопротивление цепи раcсчитывается
по формуле
— полное сопротивление цепи раcсчитывается
по формуле
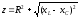
Угол сдвига фаз между приложенным напряжением и током

При последовательном соединении элементов векторную диаграмму удобно начинать строить с вектора общего тока, а затем учитывая II закон Кирхгофа строим вектора напряжений рис.7.
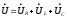
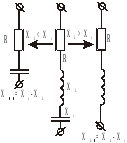
Рис. 8.
При последовательном
соединении 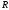 ,
, ,
,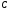 реактивные
сопротивления
реактивные
сопротивления  и
и можно заменить одним эквивалентным,
а характер цепи будет определяться по
величине большего реактивного
сопротивления рис. 8.
можно заменить одним эквивалентным,
а характер цепи будет определяться по
величине большего реактивного
сопротивления рис. 8.
Реактивная мощность
цепи 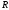 ,
,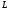 ,
, определяется:
определяется:
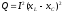
Полная мощность 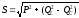
9. Параллельне соединения r и l в цепи переменного тока

Рис. 9.
Мгновенные значения напряжения и тока в неразветвленной цепи
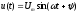

 ,где
,где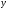 —
полная проводимость цепи
—
полная проводимость цепи

,где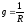 —
активная проводимость
—
активная проводимость
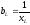 —
реактивная проводимость индуктивности
—
реактивная проводимость индуктивности
Угол сдвига между приложенными напряжением и током
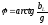
Параллельное соединение r с в цепи переменного тока

Рис. 10.
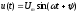
 ,
,
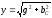 ,
, 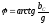
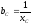 —
реактивная проводимость ёмкости.
—
реактивная проводимость ёмкости.
10. Параллельное соединение r , l , с в цепи переменного тока
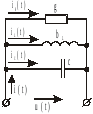
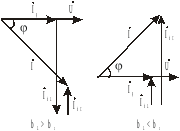
Рис. 11.

,где
Полная проводимость определяется

Угол сдвига между напряжением и током

Для данной схемы соединения векторную диаграмму удобно начинать строить с вектора напряжения, а затем по 1 закону Кирхгофа (рис. 11)
При параллельном
соединении R , L,
С реактивные проводимости 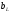 и
и можно заменить одной эквивалентной, а
характер цепи будет определяться по
величине большей реактивной проводимости(рис.12)
можно заменить одной эквивалентной, а
характер цепи будет определяться по
величине большей реактивной проводимости(рис.12)
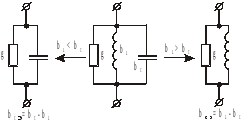
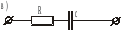
Замена последовательного соединения активных и реактивных сопротивлений в параллельно соединенные активные и реактивные проводимости и обратно: (Рис .13)

 ,
, 
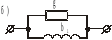
 ,
, 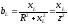
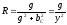 ,
, 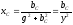

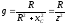 ,
, 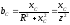
11. Анализ электрической цепи переменного тока методом проводимостей
Для расчетов токов I1,I2,I3 методом проводимостей в цепи (рис.14) необходимо перейти от разветвленной сложной схемы к простейшей последовательной цепи и определить ток в неразветвленном участке цепи I1, а затем в обратном порядке определим токи в параллельных ветвях I2 и I3.
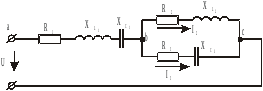
Рис. 14.
Преобразуем
параллельный участок bc в последовательный.
Для этого определим активные проводимости 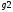 ,
,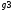 и реактивные
и реактивные и
и (Рис.15)
(Рис.15)

Рис. 15.

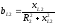

При параллельном соединении участка эквивалентная активная проводимость равна
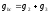
При двух реактивных
проводимостях разного характера,
характер эквивалентный проводимости
будет той, реактивная проводимость
которая больше и будет равна разности
проводимостей. Например,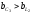 ,
тогда
,
тогда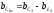
Схема (рис 15) примет такой вид (рис.16)

Рис. 16.
Далее перейдем от
проводимостей и к последовательно
соединенным сопротивлениям  и
и (рис17)
(рис17)
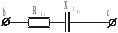
Рис.17.
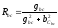

Данная разветвленная схема примет вид последовательно соединенных элементов (рис.18)
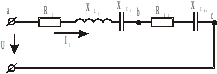
Рис. 18
При последовательном соединении активных сопротивлений эквивалентное активное сопротивление будет равно

а при двух или нескольких соединенных последовательно реактивных сопротивлений, характер эквивалентного сопротивления будет таким, реактивное сопротивление которое больше и будет равна разности сопротивлений.
Например, 
тогда 
Схема рис. 18 примет такой вид (рис. 19) и будет носить активно-емкостной характер
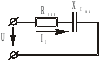
Рис. 19.
Полное сопротивление
цепи 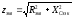
Ток в неразветвленном участке цепи
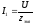 и фаза тока
и фаза тока 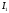

Затем определим
напряжение на участке 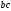
 ,где
,где 
фаза напряжения 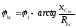
Знак »минус» показывает, что фаза напряжения при активно-
емкостном характере
отстаёт от фазы тока  (Рис.18). После этого можно определить
токи в параллельных ветвях (Рис.14).
(Рис.18). После этого можно определить
токи в параллельных ветвях (Рис.14).
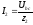 ,где
,где 
фаза тока 
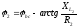
1.4. Параллельное соединения сопротивлений.
При параллельном соединении сопротивлений все они находятся под одним и тем же напряжением, т.е. напряжение между точками А и В, С и D, Е и F равно напряжению U на зажимах цепи (рис 1.5.)
Общий ток I распределяется по ветвям обратно пропорционально сопротивлениям:
I1 =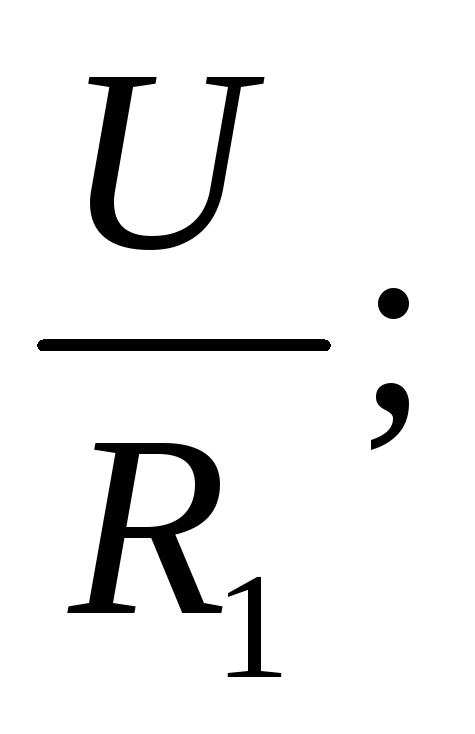 I2 =
I2 = 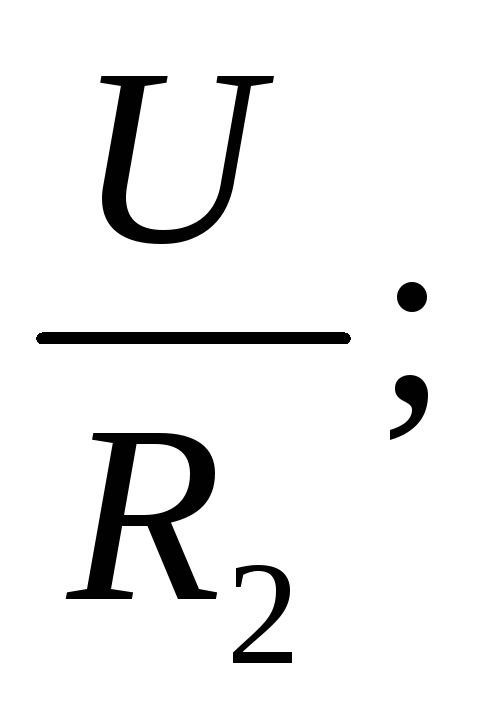 I3=
I3=

Рис. 1.5. Параллельное соединение сопротивлений.
К цепи с параллельным соединением сопротивлений применим первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в любом узле электрической цепи равна нулю, т.е. ∑I=0
Первый закон Кирхгофа можно сформулировать так: сумма токов, притекающих к узлу, равна сумме токов уходящих от узла. Применительно к рассматриваемой схеме для узла А имеем
I = I1 + I2 + I3
Или  (1.7)
(1.7)
где Rэ – эквивалентное сопротивление цепи.
Сокращая все члены уравнения (1.7) на U, получим:
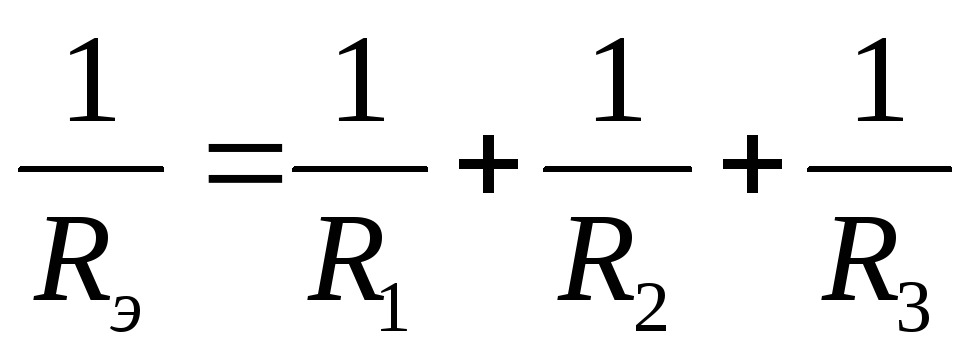 (1.8)
(1.8)
Из уравнения(1.8) получаем выражение для расчета эквивалентного (общего) сопротивления параллельной цепи, состоящей из трех ветвей
Rэ= 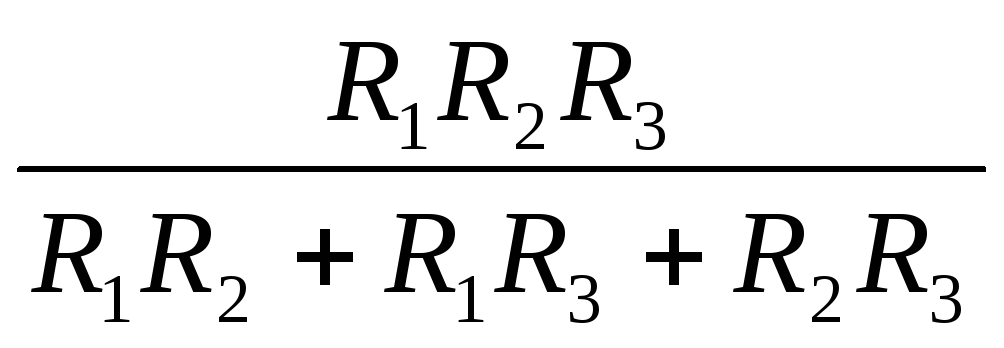 (1.9)
(1.9)
Для цепи из двух ветвей эквивалентное сопротивление рассчитывается по выражению
Rэ = 
Можно показать, что чем больше сопротивлений включаются параллельно друг другу, тем меньше будет величина эквивалентного (общего) сопротивления цепи. Так в случае, если R1 = R2 = R3 = R из выражения (1.9) имеем:
Rэ = 
Величина, обратная сопротивлению, называется электрической проводимостью и измеряется в сименсах:
g = 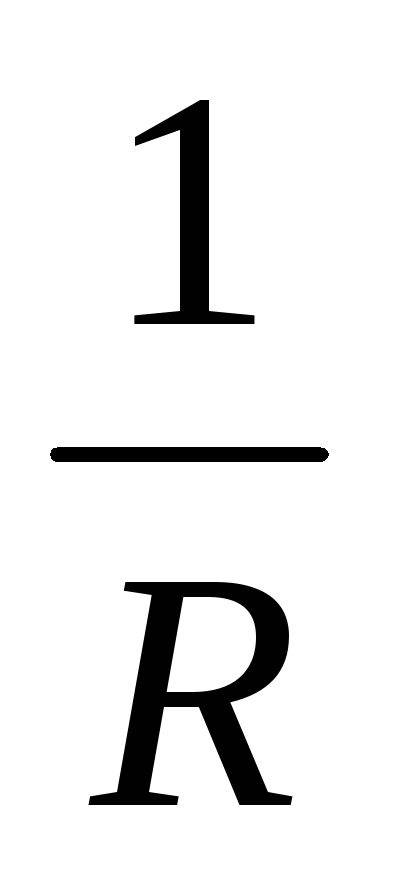 [См] (1.10)
[См] (1.10)
Из выражения (1.8) с учетом (1.10) получаем gэ = g1+ g2+ g3
Таким образом, при параллельном соединении сопротивлений общая проводимость цепи равна сумме проводимостей всех её элементов. Закон Ома для параллельной цепи принимает вид: I=U gэ
К достоинствам параллельного соединения сопротивлений относится возможность обеспечения независимой и автономной работы как генераторов, так и электроприемников. Поэтому на практике разводка электропитания производится таким образом, чтобы все электроприборы подключались к сети параллельно.
1.5. Смешанное соединение сопротивлений.
Рассмотрим электрическую цепь со смешанным соединением сопротивлений (рис. 1.6.)
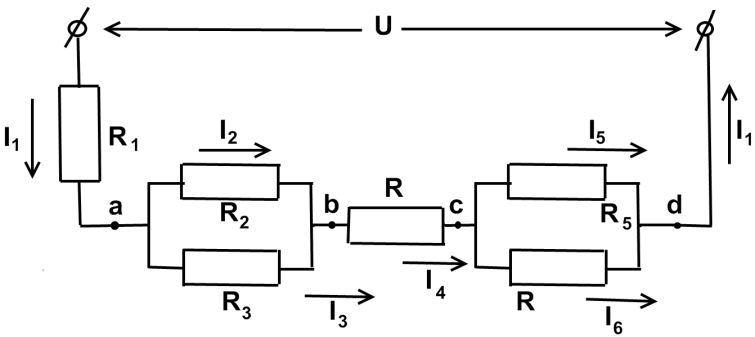
Рис. 1.6. Смешанное соединений сопротивлений.
Для расчета параметров такой цепи упростим схему, заменив группы параллельно соединенных резисторов их эквивалентными сопротивлениями.
Для участка ab:
Rab=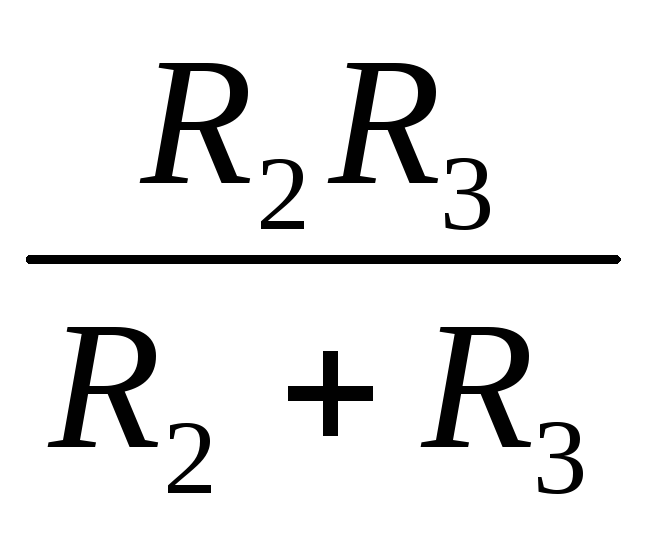 Для
участка cd:
Rcd=
Для
участка cd:
Rcd=
В результате получаем эквивалентную схему замещения представленную на рис. 1.7.
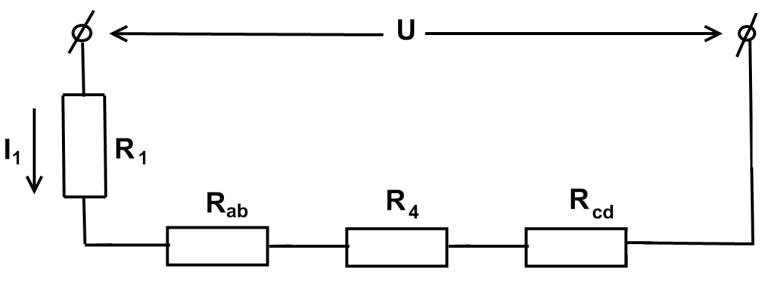
Рис. 1.7. Эквивалентная схема замещения смешанного соединения сопротивлений.
Эквивалентное сопротивление всей цепи равно: Rэ = R1 + Rab + R4+ Rcd
Ток в неразветвленных
участках цепи равен: I
= 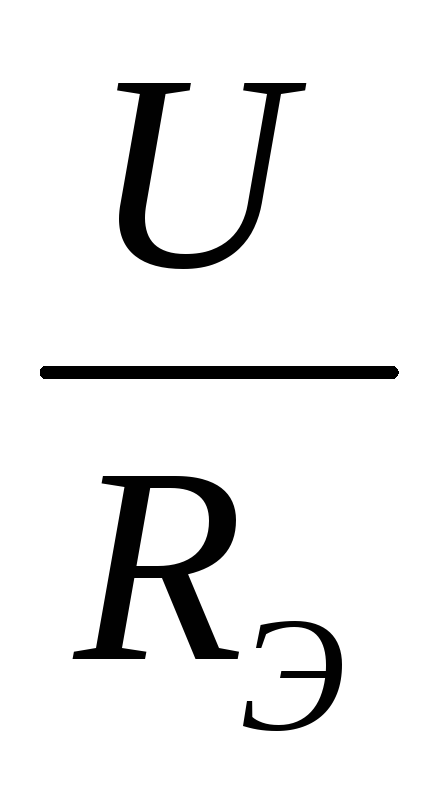
Теперь легко найти напряжения и токи на всех участках цепи:
Uab=IRab; Ucd = IRcd
I1=I;
I2=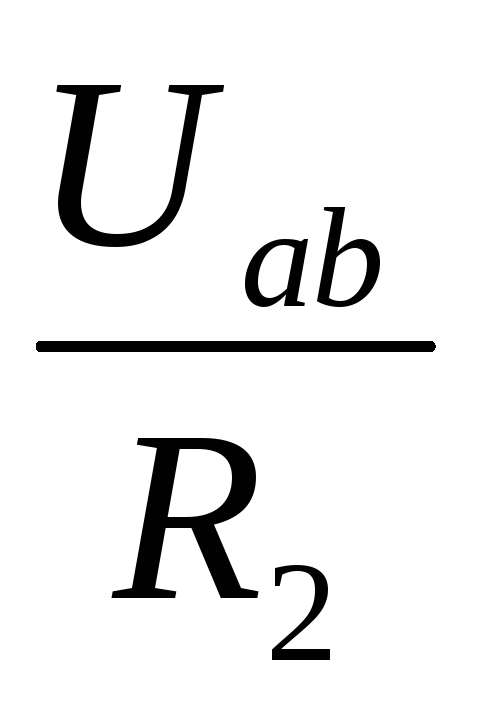 ;
I3 =
;
I3 = 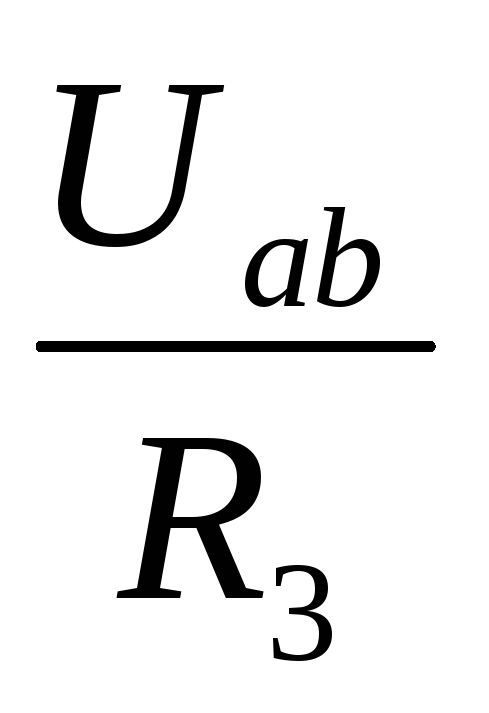 ;
I4=I;
I5 =
;
I4=I;
I5 =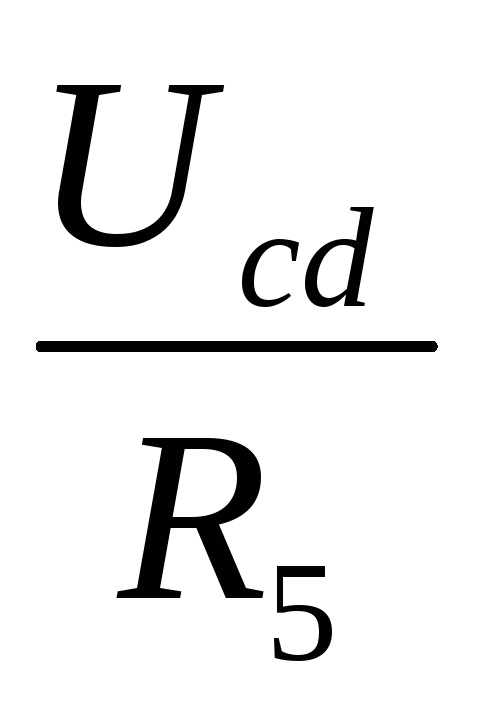 ;
I6 =
;
I6 = 
Цепь переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений
Oпределение: Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.
Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е.  и измеряется в герцах (Гц). Величина
и измеряется в герцах (Гц). Величина  называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду
называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду
 Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом »m» (например, Im). Существует также понятие, действующего значения переменного тока
Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом »m» (например, Im). Существует также понятие, действующего значения переменного тока
Переменный ток можно математически записать в виде:

Рассмотрим цепь с активным, индуктивным и емкостным сопротивлениями, включенными последовательно (рис. 1.3.1).

Для анализа схемы разложим напряжение сети U на три составляющие:
UR — падение напряжения на активном сопротивлении,
UL — падение напряжения на индуктивном сопротивлении,
UC — падение напряжения на емкостном сопротивлении.
Ток в цепи I будет общим для всех элементов:


Следует отметить, что напряжения на отдельных участках цепи не всегда совпадают по фазе с током I.
Так, на активном сопротивлении падение напряжения совпадает по фазе с током, на индуктивном оно опережает по фазе ток на 90° и на емкостном — отстает от него на 90°.
Графически это можно показать на векторной диаграмме (рис. 1.3.2).

Изображенные выше три вектора падения напряжений можно геометрически сложить в один (рис. 1.3.3).

В таком соединении элементов возможны активно-индуктивный или активно-емкостный характеры нагрузки цепи. Следовательно, фазовый сдвиг имеет как положительный, так и отрицательный знак.
Интересным является режим, когда = 0.
В этом случае

Такой режим работы схемы называется резонансом напряжений.
Полное сопротивление при резонансе напряжений имеет минимальное значение:  , и при заданном напряжении U ток I может достигнуть максимального значения.
, и при заданном напряжении U ток I может достигнуть максимального значения.
Из условия  определим резонансную частоту
определим резонансную частоту

Явления резонанса напряжений широко используется в радиотехнике и в отдельных промышленных установках.
Цепь переменного тока с параллельным соединением активного, индуктивного и емкостного сопротивлений
Электрические цепи, в которых электрические величины (токи, напряжения и ЭДС) изменяются с течением времени по периодическому закону, принято называть цепями переменного тока.
Oпределение: Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.
Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е.  и измеряется в герцах (Гц). Величина
и измеряется в герцах (Гц). Величина  называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду
называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду  Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом »m» (например, Im). Существует также понятие, действующего значения переменного тока (I).
Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом »m» (например, Im). Существует также понятие, действующего значения переменного тока (I).
Переменный ток можно математически записать в виде:

Здесь индекс выражает начальную фазу. Если синусоида начинается в точке пересечения осей координат, то = 0, тогда

Начальное значение тока может быть слева или справа от оси ординат. Тогда начальная фаза будет опережающей или отстающей.
Цепь параллельного включения конденсатора и катушки, обладающей активным сопротивлением и индуктивностью (рис. 1.4.1).
 В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь — индуктивная катушка — обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z1 и ток I1определяются по формуле:
В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь — индуктивная катушка — обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z1 и ток I1определяются по формуле:
 , где
, где

Поскольку сопротивление этой ветви комплексное, то ток в ветви отстает по фазе от напряжения на угол  .
.
Покажем это на векторной диаграмме (рис. 1.4.2).

Спроецируем вектор тока I1 на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I1R, а вертикальная — I1L. Количественные значения этих составляющих будут равны:
 где
где

Во вторую ветвь включен конденсатор. Его сопротивление

Этот ток опережает по фазе напряжение на 90°.
Для определения тока I в неразветвленной части цепи воспользуемся формулой:
 <>
<>
Его значение можно получить и графическим путем, сложив векторы I1 и I2(рис.1.4.3)
Угол сдвига между током и напряжением обозначим буквой j.
Здесь возможны различные режимы в работе цепи. При = +90° преобладающим будет емкостный ток, при = -90° — индуктивный. Возможен режим, когда = 0, т.е. ток в неразветвленной части цепи I будет иметь активный характер. Произойдет это в случае, когда I1L = I2, т.е. при равенстве реактивных составляющих тока в ветвях.
Н  а векторной диаграмме это будет выглядеть так (рис. 1.4.4):
а векторной диаграмме это будет выглядеть так (рис. 1.4.4):

Такой режим называется резонансом токов. Также как в случае с резонансом напряжений, он широко применяется в радиотехнике.
Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosj для электроустановок. Известно, что cosjявляется технико-экономическим параметром в работе электроустановок. Определяется он по формуле:
 , где
, где
Р — активная мощность электроустановок, кВт,
S — полная мощность электроустановок, кВт.
На практике cosj определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgj . Далее по таблицам находят и cosj. Чем больше cosj, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosj приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosj, в сравнении с низким. К мероприятиям по повышению cos относятся:
— недопущение холостых ходов электрооборудования,
— полная загрузка электродвигателей, трансформаторов и т.д.
Кроме этого, на cosj, положительно сказывается подключение к сети статических конденсаторов.
17. Трехфазный переменный ток и его получение
Oпределение: Трехфазные электрические цепи представляют собой совокупность трех однофазных цепей переменного тока, сдвинутых по фазе относительно друг друга на 1/3 периода.
Источником трехфазного переменного тока является генератор, на статоре которого расположены три одинаковые обмотки Аx, By, Cz, размещенные под углом 120°.
 При вращении ротора, представляющего собой двухполюсный магнит, в каждой фазной обмотке статора индуктируется ЭДС:
При вращении ротора, представляющего собой двухполюсный магнит, в каждой фазной обмотке статора индуктируется ЭДС:



Графически ЭДС можно изобразить тремя синусоидами, сдвинутыми на 1/3 периода, или тремя векторами, находящимися под углом 120° друг к другу.





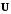

 ,
учитываявеличину и направление угла сдвига фаз между током и напряжением
φ1.
,
учитываявеличину и направление угла сдвига фаз между током и напряжением
φ1.