ПОЛНОЕ СОПРОТИВЛЕНИЕ — это… Что такое ПОЛНОЕ СОПРОТИВЛЕНИЕ?



ПОЛНОЕ СОПРОТИВЛЕНИЕ

ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: ,где r и x — активное и реактивное сопротивления. Измеряется в омах.

Большой Энциклопедический словарь. 2000.

• ПОЛНОЕ СОБРАНИЕ РУССКИХ ЛЕТОПИСЕЙ
• ПОЛНОЕ ТОВАРИЩЕСТВО

Смотреть что такое «ПОЛНОЕ СОПРОТИВЛЕНИЕ» в других словарях:

• Полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи, где r и x активное и реактивное сопротивления.… …   Википедия

• полное сопротивление — Параметр пассивного двухполюсника, равный отношению действующего значения электрического напряжения на выводах этого двухполюсника к действующему значению электрического тока через двухполюсник при синусоидальных электрическом напряжении и… …   Справочник технического переводчика

• ПОЛНОЕ СОПРОТИВЛЕНИЕ — (6, м) …   Большая политехническая энциклопедия

• полное сопротивление КЗ — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN closed end impedance …   Справочник технического переводчика

• полное сопротивление — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: , где r и х  активное и реактивное сопротивления.… …   Энциклопедический словарь

• полное сопротивление — pilnutinė varža statusas T sritis automatika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. полное сопротивление, n pranc. impédance, f …   Automatikos terminų žodynas

• полное сопротивление — pilnutinė varža statusas T sritis Standartizacija ir metrologija apibrėžtis Visuminė elektrinės grandinės varža kintamajai srovei. atitikmenys: angl. apparent resistance; impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• полное сопротивление — pilnutinė varža statusas T sritis fizika atitikmenys: angl. impedance vok. Impedanz, f; Scheinwiderstand, m rus. импеданс, m; полное сопротивление, n pranc. impédance, f …   Fizikos terminų žodynas

• ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрич. цепи току. П. с. синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: Z=U/I = корень из (r2 + х2), где r и х активное и реактивное сопротивления …   Естествознание. Энциклопедический словарь

• полное сопротивление нулевой последовательности (трехфазной обмотки) — Полное сопротивление обмотки фазы в омах при номинальной частоте между соединенными вместе линейными выводами трехфазной обмотки, соединенной по схеме «звезда» или «зигзаг», и выводом ее нейтрали (МЭС 421 07 04).… …   Справочник технического переводчика

общие сведения, зависимость от других величин и формулы расчета

Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.

Физический смысл

Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.

Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.

Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой

R, единицей измерения этой величины является Ом.

Зависимость электропроводимости

R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.

Электрические величины

К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается

е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.

Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).

Геометрические параметры и тип вещества

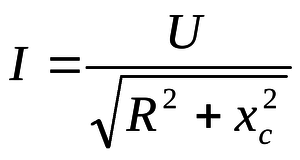Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.

Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.

Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом

, если проводник (П) представляет собой провод цилиндрической формы:

1. Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
2. Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.

П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.

Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:

1. Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат:
   S = sqr(a).
2. Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.

Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:

1. Визуально определить геометрическую фигуру при разрезе П.
2. Найти в справочнике формулу S.
3. Произвести измерения при помощи ШЦ необходимых величин.
4. Подставить в формулу и вычислить S.

Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.

Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.

Температура проводника

Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.

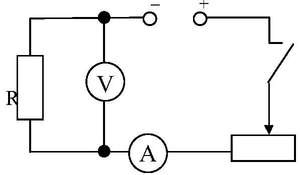
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.

В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:

• для металлов а > 0;
• для электролитов a < 0.

Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.

В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.

Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.

Цепь переменного тока

Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:

• активным;
• индуктивным;
• емкостным;
• полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).

Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.

Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.

При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:

• w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
• C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.

Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:

• геометрии П;
• типа вещества, из которого сделан П;
• температуры;
• деформации различного вида;
• электрических показателей I, U, f, L, C и R.

Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.

Измерение сопротивления

На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.

Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.

Полное сопротивление цепи переменного тока при последовательном соединении r, l и c

. (2.9)

Единицей измерения всех этих сопротивлений служит ом (Ом).

Индуктивное и емкостное сопротивления считаются реактивными. Это значит, что в них, в отличие от активных, не происходит превращение электрической энергии в другие виды энергии. Наличие тока в реактивном элементе объясняется периодическим обменом энергией между таким элементом и сетью.

Произведение мгновенных значений тока и напряжения есть мгновенная мощность цепи переменного тока и в общем случае, при синусоидальных токах и напряжениях, она определяется выражением

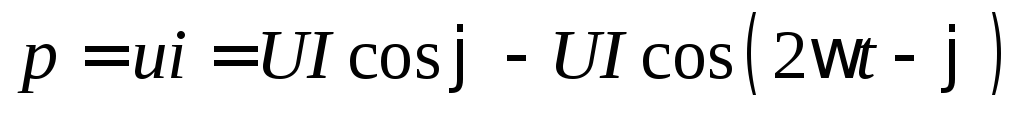, (2.10)

где

φ

–

угол сдвига фаз между напряжением и током потребителя.

Формула для мгновенной мощности состоит из двух составляющих: постоянной, не зависящей от времени UIcosj, и переменной, изменяющейся во времени с двойной частотойUIcos(2wt –j).

Количество электрической энергии, превращающейся в потребителе в другой вид энергии, зависит от средней мощности Pза период переменного тока, которая называется активной мощностью, измеряется в ваттах (Вт) и может быть определена из выражения

. (2.11)

Сравнивая выражения (2.10) и (2.11), можно отметить, что постоянная составляющая мгновенной мощности равна активной мощности цепи. Измеряется активная мощность с помощью ваттметров.

Для характеристики скорости обмена энергией между реактивными элементами и сетью используется понятие реактивной мощности, под которой подразумевается амплитудное значение мгновенной мощности на этих элементах. Для определения реактивной мощности можно использовать следующие выражения:

, (2.12)

где	U, I	–	действующие значения напряжения и тока на участке цепи, для которого рассчитывается реактивная мощность;
	j	–	угол сдвига фаз между напряжением и током на данном участке;
	xL,xC	–	индуктивное и емкостное сопротивления рассматриваемого участка.

Единицей измерения реактивной мощности служит вольт-ампер реактивный (вар), а измеряется эта мощность варметрами.

Полная мощность цепи переменного тока

. (2.13)

Единицей измерения полной мощности служит вольт-ампер (ВА).

Некоторые цепи, несмотря на наличие реактивных элементов, ведут себя по отношению к источнику питания как чисто активное сопротивление. Такое явление в цепи переменного тока называется резонансом. При резонансе напряжение и ток, потребляемый такой цепью, совпадают по фазе, а реактивная мощность всей цепи равна нулю. Основными видами резонанса являются резонанс напряжений при последовательном и резонанс токов при параллельном соединении элементов с индуктивностью и емкостью.

При последовательном соединении катушки индуктивности с индуктивным сопротивлением x_L и конденсатора с емкостным сопротивлениемx_C резонанс напряжений возникает при равенстве между собой индуктивного и емкостного сопротивлений, x_L = x_C. Поэтому при данном резонансе полное сопротивление последовательной цепи

, (2.14)

где

r

–

активное сопротивление в рассматриваемой ветви, например, сопротивление провода, из которого намотана катушка индуктивности.

Анализируя выражение (2.14), можно отметить, что полное сопротивление последовательной цепи при резонансе достигает минимального значения, а ток максимален. С увеличением тока повышается напряжение на элементах цепи и при резонансе оно достигает максимума. Особенностью рассматриваемого резонанса является возможность появления перенапряжений на реактивных элементах цепи, когда напряжения на катушке индуктивности и конденсаторе во много раз превышают напряжение источника питания. Такой случай возможен при x_L = x_C>>r.

При параллельном соединении двух и более ветвей с различным типом реактивного сопротивления может возникать резонанс токов. Условием этого резонанса является равенство индуктивной и емкостной проводимостей ветвей, включённых параллельно, b_L =b_C.

Для двух ветвей, включённых параллельно, полная проводимость

^,(2.15)

где	g1,g2	–	активные проводимости ветвей, включённых параллельно;
	bL	–	реактивная проводимость ветви с индуктивным характером реактивности;
	bC	–	реактивная проводимость ветви с емкостным характером реактивности.

Реактивная проводимость первой ветви, в которой эквивалентная реактивность носит индуктивный характер,

^{, (2.16)}

где	xL	–	эквивалентное реактивное сопротивление рассматриваемой ветви;
	r1	–	эквивалентное активное сопротивление данной ветви.

Реактивная проводимость второй ветви, в которой эквивалентная реактивность носит емкостной характер,

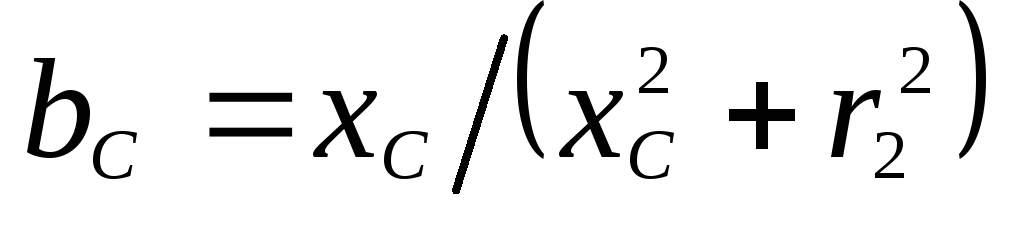^{, (2.17)}

где	xС	–	эквивалентное реактивное сопротивление рассматриваемой ветви;
	r2	–	эквивалентное активное сопротивление данной ветви.

Активные проводимости ветвей:

^{, (2.18)}

^{. (2.19)}

В приведённых выше выражениях под эквивалентным реактивным сопротивлением ветви подразумевается разность между индуктивным сопротивлением катушки и емкостным сопротивлением конденсатора, которые включены последовательно в рассматриваемой ветви. Если в ветви индуктивное сопротивление больше емкостного, то её эквивалентное реактивное сопротивление носит индуктивный характер, в противном случае характер эквивалентного реактивного сопротивления меняется на емкостный.

Эквивалентное активное сопротивление ветви равно сумме активных сопротивлений элементов, включённых в неё последовательно.

Для ветвей, в которых включён только один элемент, эквивалентное сопротивление равно соответствующему сопротивлению данного элемента (активному или реактивному).

При резонансе токов полная проводимость цепи равна её активной проводимости, y=g₁+g₂=g.

Из выражения (2.15) следует, что при резонансе токов полная проводимость разветвлённой цепи минимальна и равна активной проводимости. По этой причине ток, подходящий к участку, на котором возник резонанс токов, становится минимальным. В это же время токи в параллельных ветвях могут достигать больших значений и во много раз превышать ток, подходящий к разветвлённому участку. Возникает такой режим, когдаb_L =b_C>>g.

Формула активного сопротивления переменного тока. Как найти полное сопротивление

Активное сопротивление зависит от материала, сечения и температуры. Активное сопротивление обусловливает тепловые потери проводов и кабелей. Определяется материалом токоведущих проводников и площадью их сечения.

Различают сопротивление проводника постоянному току (омическое) и переменному току (активное). Активное сопротивление больше активного (R а > R ом) из-за поверхностного эффекта. Переменное магнитное поле внутри проводника вызывает противоэлектродвижущую силу, благодаря которой происходит перераспределение тока по сечению проводника. Ток из центральной его части вытесняется к поверхности. Таким образом, ток в центральной части провода меньше, чем у поверхности, то есть сопротивление провода возрастает по сравнению с омическим. Поверхностный эффект резко проявляется при токах высокой частоты, а также в стальных проводах (из-за высокой магнитной проницаемости стали).

Для ЛЭП, выполненных из цветного металла, поверхностный эффект на промышленных частотах незначителен. Следовательно, R а ≈ R ом.

Обычно влиянием колебания температуры на R а проводника в расчётах пренебрегают. Исключение составляют тепловые расчеты проводников. Пересчет величины сопротивления выполняют по формуле:

где R 20 – активное сопротивление при температуре 20 о;

текущее значение температуры.

Активное сопротивление зависит от материала проводника и сечения:

где ρ –удельное сопротивление, Ом мм 2 /км;

l – длина проводника, км;

F – сечение проводника, мм 2 .

Сопротивление одного километра проводника называют погонным сопротивлением:

где удельная проводимость материала проводника, км См/мм 2 .

Для меди γ Cu =53×10 -3 км См/мм2 , для алюминия γ Al =31.7×10 -3 км См/мм2 .

На практике значение r 0 определяют по соответствующим таблицам, где они указаны для t 0 =20 0 С.

Величина активного сопротивления участка сети рассчитывается:

R = r 0 ×l .

Активное сопротивление стальных проводов намного больше омического из-за поверхностного эффекта и наличия дополнительных потерь на гистерезис (перемагничивание) и от вихревых токов в стали:

r 0 = r 0пост + r 0доп,

где r 0пост – омическое сопротивление одного километра провода;

r 0доп – активное сопротивление, которое определяется переменным магнитным полем внутри проводника, r 0доп = r 0поверх.эф + r 0гистер. + r 0вихр.

Изменение активного сопротивления стальных проводников показано на рисунке 4.1.

При малых величинах тока индукция прямо пропорциональна току. Следовательно, r 0 увеличивается. Затем наступает магнитное насыщение: индукция и r 0 практически не изменяются. При дальнейшем увеличении тока r 0 уменьшается из-за снижения магнитной проницаемости стали (m ).

Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.

Формулы

1. Полное сопротивление Z = R или X L или X C (если присутствует что-то одно)
2. Полное сопротивление (последовательное соединение) Z = √(R 2 + X 2) (если присутствуют R и один тип X)
3. Полное сопротивление (последовательное соединение) Z = √(R 2 + (|X L — X C |) 2) (если присутствуют R, X L , X C)
4. Полное сопротивление (любое соединение) = R + jX (j – мнимое число √(-1))
5. Сопротивление R = I / ΔV
6. Индуктивное сопротивление X L = 2πƒL = ωL
7. Емкостное сопротивление X C = 1 / 2πƒL = 1 / ωL

Шаги

Часть 1

Вычисление активного и реактивного сопротивлений

Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:

• Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
• Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.

Сопротивление – это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R. Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете при помощи мультиметра.

• ΔV – это напряжение (разность потенциалов), измеряемое в вольтах (В).
• I – сила тока, измеряемая в амперах (А).
• R – это сопротивление, измеряемое в омах (Ом).

Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:

Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: X L = 2πƒL , где L – индуктивность, измеряемая в генри (Гн).

Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: X C = 1 / 2πƒC . С – это емкость конденсатора, измеряемая в фарадах (Ф).

• Вы можете .
• Эту формулу можно переписать так: X C = 1 / ωL (объяснения см. выше).

Часть 2

Вычисление полного сопротивления

1. Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.

   • Если резисторы соединены последовательно, то полное сопротивление R = R 1 + R 2 + R 3 …
   • Если резисторы соединены параллельно, то полное сопротивление R = 1 / R 1 + 1 / R 2 + 1 / R 3 …

2. Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:

Полное сопротивление Википедия

Электри́ческий импеда́нс (ко́мплексное электри́ческое сопротивле́ние^[1]) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.

Это понятие и термин ввёл физик и математик О. Хевисайд в 1886 году^[2][3].

Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения и является пассивным элементом, поскольку не содержит внутренних источников энергии. Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):

R=UI.{\displaystyle R={\frac {U}{I}}.}

Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:

• сопротивление идеальной катушки индуктивности стремится к нулю:

если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:

U=0;{\displaystyle U=0;}

R=UI=0I=0;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}

если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:

I=0;{\displaystyle I=0;}

R=UI=U0=∞.{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}

Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:

• напряжение между выводами катушки индуктивности не равно нулю;
• ток, протекающий через конденсатор, не будет равен нулю.

Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.

Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.

Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.

Определение

Импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник в установившемся режиме, то есть после завершения переходных процессов. Для линейных пассивных цепей с постоянными параметрами в установившемся режиме импеданс не зависит от времени. Если время t в математическом выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.

z^(jω)=u^(jω,t)i^(jω,t)=U(ω)ej(ωt+ϕu(ω))I(ω)ej(ωt+ϕi(ω))=U(ω)ejϕu(ω)I(ω)ejϕi(ω)=U^(jω)I^(jω){\displaystyle {\hat {z}}(j\omega )\;={\frac {{\hat {u}}(j\omega ,t)\;}{{\hat {i}}(j\omega ,t)\;}}={\frac {U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}{I(\omega )e^{j(\omega t+\phi _{i}(\omega ))}}}={\frac {U(\omega )e^{j\phi _{u}(\omega )}}{I(\omega )e^{j\phi _{i}(\omega )}}}={\frac {{\hat {U}}(j\omega )\;}{{\hat {I}}(j\omega )\;}}}

(1)

Здесь:

Исторически сложилось, что в электротехнике обозначение импеданса, комплексных амплитуд и других комплексных функций частоты записывают как f(jω){\displaystyle f(j\omega )}, а не f(ω){\displaystyle f(\omega )}. Такое обозначение подчёркивает, что используются комплексные представления гармонических функций вида ejωt{\displaystyle e^{j\omega t}}. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: U˙(jω){\displaystyle {\dot {U}}(j\omega )\;} чтобы отличать от соответствующих действительных величин.

Физический смысл

Алгебраическая форма

Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} можно рассматривать как последовательно соединенные резистор с сопротивлением ℜ(z^(jω)){\displaystyle \Re ({\hat {z}}(j\omega ))} и чисто реактивный элемент с импедансом ℑ(z^(jω)){\displaystyle \Im ({\hat {z}}(j\omega ))}

Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.

Тригонометрическая форма

Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.

Ограничения

Понятие импеданса в классической форме применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его параметры не менялись со временем и закончились переходные процессы. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель ejωt{\displaystyle e^{j\omega t}} в (1) не сокращается.

• Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).

Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении — для бесконечно малой амплитуды сигнала для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.

Обобщенный импеданс в s-плоскости и преобразование Лапласа

Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:

Ft(s)=∫0∞fin(t)e−stdt.{\displaystyle F_{t}(s)=\int _{0}^{\infty }f_{in}(t)e^{-st}\,dt.}

Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:

Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}

Двухполюсник	Обобщённый импеданс
Резистор	R{\displaystyle R\,}
Катушка индуктивности	sL{\displaystyle sL\,}
Конденсатор	1sC{\displaystyle {\frac {1}{sC}}\,}

Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.

Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:

fF,H(t)=L−1[H(s) Ft(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}[H(s)\ F_{t}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}

где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.

Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение

Пассивный RС-фильтр нижних частот 1-го порядка

Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:

HRC(s)=1/sCR+1/sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}

где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.

Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:

Uin(t)=U0 h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}

где U0{\displaystyle U_{0}} — амплитуда ступеньки.

Преобразование Лапласа входного сигнала:

Fin(s)=L[U0 h(t)]=∫0∞e−stU0h(t)dt=U0/s.{\displaystyle F_{in}(s)={\mathcal {L}}[U_{0}\ h(t)]=\int \limits _{0}^{\infty }e^{-st}\,U_{0}\,h(t)\,dt=U_{0}/s.}

Uout(t)=L−1[HRC(s) Fin(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞est1sT+1⋅U0sds=U0(1−e−t/T).{\displaystyle U_{out}(t)={\mathcal {L}}^{-1}[H_{RC}(s)\ F_{in}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}{\frac {1}{sT+1}}\cdot {\frac {U_{0}}{s}}\,ds=U_{0}(1-e^{-t/T}).}

Таким образом, получен отклик цепи при нулевом начальном условии (UC=0{\displaystyle U_{C}=0} при t=0{\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.

Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.

Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.

Вычисление импеданса

Идеальные элементы

Резистор

Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:

zR=R{\displaystyle z_{R}=R}

(2)

Конденсатор

Ток и напряжение для конденсатора связаны соотношением:

i(t)=CdUdt.{\displaystyle i(t)=C{\frac {dU}{dt}}.}

(3)

Отсюда следует, что при напряжении

u^(jω,t)=U(ω)ej(ωt+ϕu(ω)){\displaystyle {\hat {u}}(j\omega ,t)=U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}

(4)

ток, текущий через конденсатор, будет равен:

i^(jω,t)=Cddt(U(ω)ej(ωt+ϕu(ω)))=jωCU(ω)ej(ωt+ϕu(ω)).{\displaystyle {\hat {i}}(j\omega ,t)=C{\frac {d}{dt}}\left(U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}\right)=j\omega CU(\omega )e^{j(\omega t+\phi _{u}(\omega ))}.}

(5)

После подстановки (4) и (5) в (1) получаем:

z^C(jω)=1jωC=−jωC.{\displaystyle {\hat {z}}_{C}(j\omega )={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}.}

(6)

Катушка индуктивности

Аналогичное рассмотрение для катушки индуктивности приводит к результату:

z^L(jω)=jωL.{\displaystyle {\hat {z}}_{L}(j\omega )\;=j\omega L.}

(7)

Общий случай

Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:

Z^(jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).}

(8)

Экспериментальное измерение импеданса

Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.

Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.

В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.

Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.

Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.

Активная и реактивная составляющие импеданса обычно выражают в омах, но могут использоваться связанные с импедансом величины, например, в радиотехнике, линиях передачи, коэффициент стоячей волны или коэффициент отражения имеют бо́льшее удобство.

Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса^[5].

Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств^[5].

LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.

Применение понятия импеданса

Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал или применять преобразование Лапласа.

См. также

Примечания

Литература

• Бессонов Л. А. Теоретические основы электротехники. — 9-е изд. — М.: Высшая школа, 1996.
• Графов Б. М., Укше Е. А. Электрохимические цепи переменного тока. — М.: Наука, 1983.

Закон Ома для цепи переменного тока

Введённый нами переменный ток, в любом случае, является током, таким образом, для переменного тока существует закон Ома. Для введения закона воспользуемся классической схемой колебательного LCR-контура (рис. 1). На концах контура извне подаётся переменное ЭДС:

(1)

Рис. 1. Колебательный LCR-контур

В данном случае, его официальное название — закон Ома для последовательной цепи переменного тока.

Формульно:

(2)

Параметр полного сопротивления цепи переменного тока включает в себя сопротивление как пассивных элементов (реостат, лампа, провод и т.д.), так и активных (катушка индуктивности, конденсатор). В общем случае:

(3)

Введённые обозначения:

• индуктивное сопротивление

(4)

• ёмкосное сопротивление

(5)

Вывод: для переменного тока связь между силой тока и ЭДС задаётся соотношением (2). Поиск составляющих — соотношения (3)-(5). В целом, больше в курсе школьной физики задач придумать нельзя.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…