Полная энергия — это… Что такое Полная энергия?
- Полная энергия
Гамильтониа́н (функция Гамильтона) — функция, зависящая от обобщённых координат, импульсов и, возможно, времени, описывающая динамику механической системы в гамильтоновой формулировке классической механики, а также оператор в квантовой механике и квантовой теории поля. В формализме фейнмановского интеграла по траекториям в квантовой механике и квантовой теории поля используется также и классический гамильтониан (функция Гамильтона).
Гамильтониан (если не зависит от времени) выражает полную энергию системы.
Гамильтониан в классической механике
Классический гамильтониан (функция Гамильтона) — участвует в гамильтоновой форме принципа наименьшего (стационарного) действия, канонических уравнениях Гамильтона (одной из возможных форм уравнения движения в классической механике) и уравнении Гамильтона—Якоби, являясь основой гамильтоновой формулировки механики.
Для консервативных систем гамильтониан представляет полную энергию (выраженную как функция координат и импульсов), то есть — в классическом смысле — сумму кинетической и потенциальной энергий системы.
Гамильтониан связан с лагранжианом через преобразование Лежандра.
Гамильтониан в квантовой механике
Гамильтониан в квантовой теории — оператор, соответствующий функции Гамильтона в классической теории. Гамильтониан может быть получен заменой обобщённых координат
 и импульсов
и импульсов 
 , подчиняющиеся перестановочным соотношениям.
, подчиняющиеся перестановочным соотношениям.В соответствии с уравнением Шрёдингера гамильтониан определяет эволюцию квантового состояния со временем.
См. также
Ссылки
Wikimedia Foundation. 2010.
- Полная теория
- Полнодуплексный
Смотреть что такое «Полная энергия» в других словарях:
полная энергия — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN apparent energy … Справочник технического переводчика
полная энергия WT — 3.4 полная энергия WT: Суммарная энергия, затраченная на проникновение бойка в испытуемый образец и пробой образца (рисунки 1 3). В отличие от результатов аналогичных испытаний на пробой с измерительной аппаратурой хрупких пластмасс в виде… … Словарь-справочник терминов нормативно-технической документации
полная энергия — visuminė energija statusas T sritis Standartizacija ir metrologija apibrėžtis Visų sistemos energijos rūšių suma. atitikmenys: angl. total energy vok. Gesamtenergie, f rus. полная энергия, f pranc. énergie totale, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полная энергия — pilnutinė energija statusas T sritis chemija apibrėžtis Laisvosios ir surištosios energijos suma. atitikmenys: angl. total energy rus. полная энергия … Chemijos terminų aiškinamasis žodynas
полная энергия — pilnutinė energija statusas T sritis fizika atitikmenys: angl. total energy vok. Gesamtenergie, f rus. полная энергия, f pranc. énergie totale, f … Fizikos terminų žodynas
полная энергия связи — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN total binding energyTBE … Справочник технического переводчика
полная энергия, распределяемая энергосистемой — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN net electric system energy … Справочник технического переводчика
полная энергия частицы — pilnutinė dalelės energija statusas T sritis radioelektronika atitikmenys: angl. total particle energy vok. Partikelgesamtenergie, f rus. полная энергия частицы, f pranc. énergie totale de particule, f … Radioelektronikos terminų žodynas
удельная полная энергия — Энергия жидкости, равная сумме удельных кинетической энергии, энергии давления и потенциальной энергии … Политехнический терминологический толковый словарь
Книги
- Умные клетки и самоисцеление. Энергия контакта. Эффективный самомассаж (комплект из 3 книг) (количество томов: 3), Капилова Ольга. «Умные клетки и самоисцеление. Сказания высшего» Я»». Ольга Капилова, в прошлом страдающая от множества хронических и сердечно-сосудистых заболеваний, а ныне здоровая и полная сил, на своем… Подробнее Купить за 663 руб
- Тайный язык спящих. Практическое руководство для любящих пар, Томас Эвани. Треть нашей жизни мы проводим в постели. Это сцена, на которой разыгрываются наши драмы; пространство, где формируется наше сознание; место, где раскрываются наши тайные желания и… Подробнее Купить за 222 руб
- Энергия жизни, Ирина Бйорно. Полная книга о секретах жизненной энергии на каждый день: упражнения, диета, секреты каждого дня и, конечно, тайны долголетия. Для того, кто хочет прожить долгую и здоровую жизнь без болезней… Подробнее Купить за 200 руб электронная книга
Энергия покоя | Наука | Fandom
Энергия покоя $ E $, или массовая энергия покоя частицы — её энергия, когда она находится в состоянии покоя относительно данной инерционной системы отсчёта; может немедленно перейти в потенциальную (пассивную) и в кинетическую (активную) энергию, что определяется математической формулой эквивалентности массы и энергии следующим образом:
- $ \ E=m_0 c^2 $,
где $ m_0 $ — масса покоя частицы и $ c $ — скорость света в вакууме.
Эквивалентность массы и энергии выводится из специальной теории относительности (СТО): масса данного тела пропорциональна его кинетической энергии, то есть
- $ dm =\frac {dE_k} {c^2} $,
откуда следует, что энергия и масса эквивалентны. Поэтому, частица, которая остается в состоянии покоя относительно данной инерционной системы отсчёта, имеет определенное количество энергии, когда она имеет массу покоя. Подобно другим видам энергии, энергия покоя может быть преобразована к другим видам энергии в процессе ядерного деления.
В релятивистской механике используются две формулы связи тела, массой $ m $ между его энергией $ E $, скоростью $ v $ и импульсом:
- $ (1) \ \frac {E^2}{c^2}=p^2 + m^2c^2 $
- $ (2) \ \overrightarrow {p}= \frac {E\overrightarrow {v}}{c^2}. $
Очевидно, что подстановка $ \overrightarrow {v}=0 $ в (2), дает $ \overrightarrow {p}=0 $, подставляя последний в (1) получаем выражение для энергии покоя $ E_0 $, равная:
- $ (3) \ E_0=mc^2. $
Такой результат необычен для ньютоновой механики. В самом деле, полная энергия тела, согласно ньютону, складывается из двух: потенциальной $ U $, связанной с полем, и кинетический $ W $, которая связана с движением тела. Понятно, что при отсутсвия поля (т.е. сил, действующих на тело), полная энергия тела равна кинетической. Теперь, если мы свяжем систему отсчета с телом, т.е. скорость последнего будет равна $ \overrightarrow {v}=0 $, то полная энергия будет равна нулю.
Совершенно иной результат получается из СТО. Почему же не удалось обнаружить энергию покоя еще до работ Эйнштейна? Дело в том, что эта энергия никак не проявляет себя в класических уравнениях движения.
Вышеупомянутый результат можно получить, раскладывая выражение для полной энергии
- $ E= \frac{mc^2}{\sqrt{1-v^2/c^2}} $
по степеням $ \frac{v}{c} $:
- $ E \simeq mc^2+ \frac{mv^2}{2} $
Видно, что первый член разложения и есть энергия покоя.
Из уравнения (3), также, следует связь между массой тела и энергией покоя. Можно сказать, что масса — это мера энергии покоя тела $ m=\frac{E_0}{c^2} $, и, очевидно, не зависит от скорости.
Полная энергия колебаний, теория и онлайн калькуляторы
Энергия колебаний пружинного маятника
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника. Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:
\[E=E_k+E_p=const\ \left(1\right).\]Проверим справедливость выражения (1),) непосредственным суммированием выражений для кинетической и потенциальной энергии рассматриваемого маятника.
Уравнение колебаний маятника запишем в виде:
\[x=A{\cos \left({\omega }_0t+\varphi \right)(2)\ },\]где $x$ — смещение груза маятника по оси X. В таком случае изменение кинетической энергии груза, совершающего колебания на напружине равна:
\[E_k=\frac{m}{2}A^2{{\omega }_0}^2{{sin}^2 \left({\omega }_0t+\varphi \right)\left(3\right).\ }\]Потенциальна энергия пружинного маятника равна: потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли:
\[E_p=\frac{kx^2}{2}=\frac{k}{2}A^2{{cos}^2 \left(щ_0t+ц\right)\ }\left(4\right).\]Суммируем правые части выражений (3) и (4), получим:
\[E=\frac{m}{2}A^2{щ_0}^2{{sin}^2 \left(щ_0t+ц\right)+\ }\frac{k}{2}A^2{{cos}^2 \left(щ_0t+ц\right)\ }=\frac{k}{2}A^2=\frac{1}{2}m{\omega }^2_0A^2\left(5\right).\]где ${{\omega }_0}^2=\frac{k}{m}$.
Из формулы (5) мы видим, что неизменная суммарная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=\pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
\[v_x=\pm {\omega }_0A\left(6\right).\]В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $\frac{E}{2}$ находятся в противофазе друг с другом, частота их колебаний равна $2{\omega }_0$.
\[{E_k =\frac{E}{2}\left[1-{\cos 2({\omega }_0t+\varphi )\ }\right]\left(7\right).\ }\] \[E_p=\frac{E}{2}\left[1+{cos 2({\omega }_0t+\varphi )\ }\right]\left(8\right).\]И так, выражения (7) и (8) показывают, что кинетическая и потенциальная энергии колебательной системы совершают гармонические колебания вокруг их общего значения $\frac{E}{2}$ с удвоенной частотой 2${\omega }_0$, тогда как полная энергия системы остается постоянной. Она связана с амплитудой колебаний как:
\[E=\frac{k}{2}A^2.\]Энергия колебательных систем с одной степенью свободы
Все, что сказано для пружинного маятника можно применить , для любых механических колебаний систем с одной степенью свободы. Мгновенное положение такой системы можно определить, используя один параметр, который называют обобщенной координатой ($q$), например, угла поворота или смещения по оси координат. При этом величина $\dot{q}=\frac{dq}{dt}$ называется обобщённой скоростью.
Потенциальная энергия в таких обозначениях примет вид:
\[E_p=\frac{\alpha q^2}{2}\left(9\right),\]кинетическая эн
Энергия связи — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 августа 2016; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 августа 2016; проверки требуют 2 правки.Энергия связи (для данного состояния системы) — разность между энергией состояния, в котором составляющие части системы бесконечно удалены друг от друга и находятся в состоянии активного покоя и полной энергией связанного состояния системы:
- ΔE=∑i=1NEi−E,{\displaystyle \Delta E=\sum _{i=1}^{N}E_{i}-E,}
где ΔE{\displaystyle \Delta E} — энергия связи компонентов в системе из N компонентов (частиц), Ei{\displaystyle E_{i}} — полная энергия i-го компонента в несвязанном состоянии (бесконечно удалённой покоящейся частицы) и E{\displaystyle E} — полная энергия связанной системы.
Для системы, состоящей из бесконечно удалённых покоящихся частиц энергию связи принято считать равной нулю, то есть при образовании связанного состояния энергия выделяется. Энергия связи равна минимальной работе, которую необходимо затратить, чтобы разложить систему на составляющие её частицы. Она характеризует стабильность системы: чем выше энергия связи, тем система стабильнее.
Для валентных электронов (электронов внешних электронных оболочек) нейтральных атомов в основном состоянии энергия связи совпадает с энергией ионизации, для отрицательных ионов — со сродством к электрону.
Энергии химической связи двухатомной молекулы соответствует энергия её термической диссоциации, которая составляет порядка сотен кДж/моль.
Энергия связи адронов атомного ядра определяется в основном сильным взаимодействием. Для большинства ядер она составляет ~8 МэВ на нуклон.
Энергия гармонических колебаний
Кинетическая и потенциальная энергия гармонических колебаний
Кинетическая энергия тела, совершающего гармонические колебания:
Потенциальная энергия тела, совершающего гармонические колебания (под действием квазиупругой силы):
Учитывая, что
можно записать:
Полная энергия гармонических колебаний
Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии:
При свободных колебаниях колебательная система получает энергию только в начальный момент времени, а далее энергия системы, а с ней и амплитуда колебаний не меняются. При движении тела кинетическая и потенциальная энергия переходят друг в друга. Когда отклонение системы от положения равновесия максимально, потенциальная энергия максимальна, а кинетическая равна нулю. При прохождении положения равновесия потенциальная энергия достигает минимума, а кинетическая энергия (а с ней и скорость, импульс тела) максимальна.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Кинетическая энергия | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Кинетическая энергия — скалярная физическая величина, равная половине произведения массы тела на квадрат его скорости.
![Rendered by QuickLaTeX.com \[\LARGE W_k=\frac{m\upsilon ^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-903510ee357d0ffb6790e969240dd5d9_l3.png)
Что бы понять, что же такое кинетическая энергия тела, рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.
Кинетическая-энергия-тела
Как мы знаем, работа постоянной силы вычисляют по формуле
![Rendered by QuickLaTeX.com \[A=FScos\alpha\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b7f11e89f095731ad60414040ced7d92_l3.png)
. Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то
![Rendered by QuickLaTeX.com \[cos\alpha =1\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-79c9bc5a411f2441dc9800271ba8b80b_l3.png)
, и тогда у нас получается, что работа силы равна
![Rendered by QuickLaTeX.com \[А=Fs\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-4ff6eebc0fd47501e8f7b2a42c77fea1_l3.png)
. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения справедлива формула:
![Rendered by QuickLaTeX.com \[\large \upsilon _2^2=\upsilon _1^2+2aS\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f4a6417a29ffbeaacffb47e58533524f_l3.png)
Из это формулы мы выражаем перемещение тела:
![Rendered by QuickLaTeX.com \[\large S=\frac{\upsilon _2^2-\upsilon _1^2}{2a}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-7757b1f76a8fe01e4454fb7caed6f83d_l3.png)
Подставляем найденные значения F и S в формулу работы, и получаем:
![Rendered by QuickLaTeX.com \[\large A=\frac{m\upsilon ^2}{2}-\frac{m\upsilon _1^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-f904f0f3bd35e6c5a859df88947d2867_l3.png)
Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины
![Rendered by QuickLaTeX.com \[\frac{m\upsilon ^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-dd7d19bb870c82f74ab69774ac2ed388_l3.png)
. А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина
![Rendered by QuickLaTeX.com \[\frac{m\upsilon ^2}{2}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-dd7d19bb870c82f74ab69774ac2ed388_l3.png)
представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк.
![Rendered by QuickLaTeX.com \[\large W_k=\frac{m\upsilon ^2}{2} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-44e13af14375c997e0d60df42bf425b1_l3.png)
Если взять выведенную нами формулу работы, то у нас получится
![Rendered by QuickLaTeX.com \[\large A=W_{k2}-W_{k1}=\Delta W_k\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-acb2c752a264932cbe4e1a71f5bdb537_l3.png)
Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела
Так же есть :
Потенциальная энергия :
![Rendered by QuickLaTeX.com \[\large W_p=mgh \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-bb8cf55efe57b360c4712087ecf3fb02_l3.png)
В формуле мы использовали :
![Rendered by QuickLaTeX.com \[W_k\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-fdefdaf99ff1a5468ebee9f4a1013f0b_l3.png)
— Кинетическая энергия
m — Масса тела
![Rendered by QuickLaTeX.com \[ \upsilon\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-61a6a14986c7b1d45a6f39da48f3a43b_l3.png)
— Скорость движения тела
![Rendered by QuickLaTeX.com \[ \upsilon_1\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-3ee646ce78bdfdc2586537a0e204a975_l3.png)
— Начальная скорость тела
![Rendered by QuickLaTeX.com \[ \upsilon_2\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-36adf79a8c949e974e82bd707606d29e_l3.png)
— Конечная скорость тела
A — Работа тела
a — Ускорение тела
F — Сила, действующая на тело
S — Перемещение тела
Кинетическая энергия — урок. Физика, 8 класс.
Энергию, которой обладают только движущиеся тела, называют кинетической энергией.
Если тело находится в состоянии покоя, его кинетическая энергия равна нулю.Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).
Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.
Определяют кинетическую энергию по формуле:
Eкин=m⋅v22.
Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:
m=2⋅Eкинv2 и v=2⋅Eкинm.
С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.
Если масса увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается также в \(2\) раза.
Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной \(2 м/с\).
С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости.
Если скорость увеличивается в \(2\) раза, тогда кинетическая энергия увеличивается в \(4\) раза.
Зависимость кинетической энергии от скорости движения можно отобразить на данном графике, если принять массу тела постоянной и равной \(2 кг\).
Пример:
Автомобиль, масса которого \(1400 кг\), из состояния покоя развивает скорость до значения \(5 м/с\).
Какова кинетическая энергия автомобиля на конечном этапе движения?
Eкин=m⋅v22=1400⋅522=17500Дж.
Источники:
E. Šilters, V. Regusts, A. Cābelis. «Fizika 10 klasei», Lielvārds, 2004, 256 lpp.
(Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.)




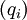 и импульсов
и импульсов 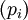
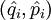 , подчиняющиеся перестановочным соотношениям.
, подчиняющиеся перестановочным соотношениям.