При проектировании трансформаторов исходной является мощность, которая связывает габариты трансформатора с полной мощностью нагрузки:
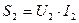 (2.32)
(2.32)
Полная (полезная) мощность многообмоточного трансформатора, есть сумма полных мощностей всех его вторичных обмоток:
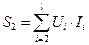 (2.33)
(2.33)
При активной нагрузке мощность активна и равна Р2.
Типовой (габаритной) мощностью трансформатора называют полусумму мощностей всех его обмоток
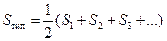 (2.34)
(2.34)
Найдём типовую мощность для двухобмоточного трансформатора.
Полная мощность первичной обмотки 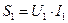 (U1, I1 – действующие значения) – эта мощность определяет габариты обмоток: число витков –входным напряжением, а сечения проводов – действующими токами. Габаритная мощность трансформатора (типовая) определяет реальное сечение сердечника – sс и равна
(U1, I1 – действующие значения) – эта мощность определяет габариты обмоток: число витков –входным напряжением, а сечения проводов – действующими токами. Габаритная мощность трансформатора (типовая) определяет реальное сечение сердечника – sс и равна
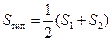 (2.35)
(2.35)
Учитывая, что 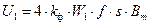
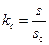 , которую легко измерить. Величина
, которую легко измерить. Величина 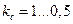 ( зависит от толщины ленты). Для прессованных сердечников
( зависит от толщины ленты). Для прессованных сердечников 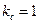
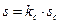 и выражение для напряжения первичной обмотки принимает вид
и выражение для напряжения первичной обмотки принимает вид 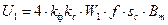 (2.36)
(2.36)
Аналогичное выражение можно записать и для вторичной обмотки, а мощности первичной обмотки и типовая соответственно равны
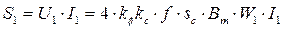
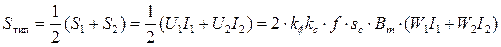 (2.38)
(2.38)
Отношение тока в обмотке к сечению проводника называется плотностью тока и для всех обмоток трансформатора она одинакова.
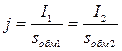 , (2.39)
, (2.39)
где s обм1, sобм2 – площади сечения проводников обмоток.
Заменим токи 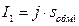
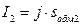 , тогда сумма в скобках в (2.38) равна
, тогда сумма в скобках в (2.38) равна 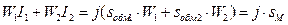 .
.где sм – сечение всех проводников (меди) в окне магнитопровода, как показано на рисунке 2.30.
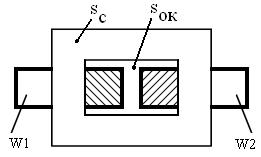
Рисунок 2.30 – К выводу формулы габаритной мощности
Введём коэффициент заполнения окна медью 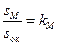
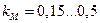 и зависит от толщины изоляции проводов, каркаса, межслойной изоляции, способа намотки и пр. Тогда
и зависит от толщины изоляции проводов, каркаса, межслойной изоляции, способа намотки и пр. Тогда 
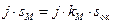 и выражение для типовой мощности принимает окончательный вид
и выражение для типовой мощности принимает окончательный вид 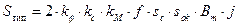
Из выражения (2.40) следует, что типовая мощность определяется произведением 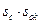 . При увеличении линейного размера трансформатора в m раз, его объём (масса) увеличится в m 3 раз, а мощность возрастёт в m 4 раз. Поэтому, удельные массо-объёмные показатели трансформаторов улучшаются с увеличением габаритной мощности. С этой точки зрения предпочтительны многообмоточные трансформаторы по сравнению с несколькими двухобмоточными.
. При увеличении линейного размера трансформатора в m раз, его объём (масса) увеличится в m 3 раз, а мощность возрастёт в m 4 раз. Поэтому, удельные массо-объёмные показатели трансформаторов улучшаются с увеличением габаритной мощности. С этой точки зрения предпочтительны многообмоточные трансформаторы по сравнению с несколькими двухобмоточными.
При конструировании трансформаторов следует стремиться к увеличению коэффициента заполнения окна магнитопровода обмотками – 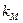
Выражение (2.40) является основой для расчёта трансформатора. Его преобразуют к виду:
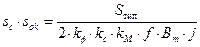 (2.41)
(2.41)
По заданной выходной мощности (Sтип) находят произведение 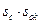
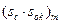 больше или равно найденному из (2.41). Такой сердечник обеспечит требуемую мощность в нагрузке.
больше или равно найденному из (2.41). Такой сердечник обеспечит требуемую мощность в нагрузке.2.5.6 Трёхфазные трансформаторы
Трёхфазные системы были разработаны русским электриком М.О. Доливо-Добровольским (1862 – 1919 гг.). Они широко распространены в энергетике и представляют собой симметричную трёхфазную систему напряжений промышленной частоты, сдвинутых между собой на электрический угол 120 0 . Схематическое изображение источников трёхфазных напряжений (генераторов) показано на рисунке 2.31, где начала фаз обозначены латинскими буквами ABC, а концы фаз буквами XYZ (или условно можно обозначить точками вместо букв ).
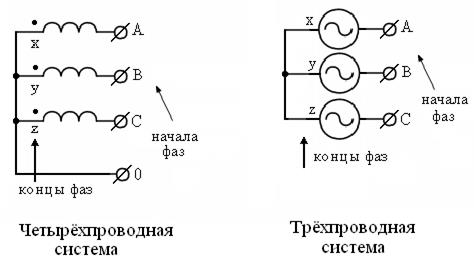
Рисунок 2.31 – Схематическое изображение источников трёхфазных
На рисунке 2.32 показаны временное и векторное представления трёхфазной системы напряжений.
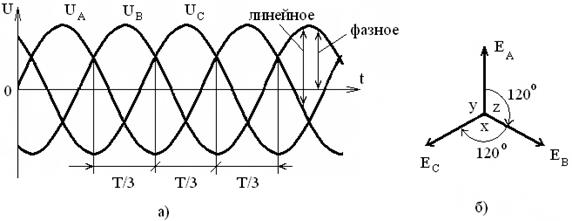
Рисунок 2.32 – Временное (а) и векторное (б) представление трёхфазной
На этом рисунке Т – период, Е – фазная ЭДС. Мгновенные значения фазных ЭДС соответственно равны
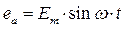
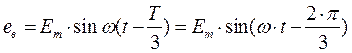 (2.42)
(2.42)
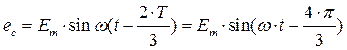
Это симметричная трёхфазная система, в которой в любой момент времени выполняется равенство
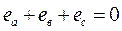
Чередование фаз принято условно положительным по часовой стрелке. Существуют три основные схемы соединения в трёхфазных цепях: звезда, треугольник и зигзаг 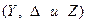 , но наиболее широко известны первые две – звезда и треугольник (говорят соединение в звезду или в треугольник). Рассмотрим их. На рис.2.33 приведена схема соединения источника и нагрузки звездой.
, но наиболее широко известны первые две – звезда и треугольник (говорят соединение в звезду или в треугольник). Рассмотрим их. На рис.2.33 приведена схема соединения источника и нагрузки звездой.
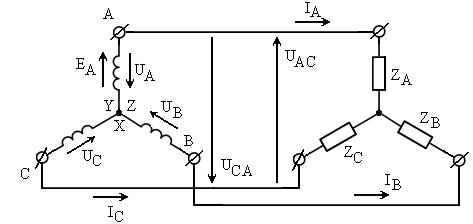
Рисунок 2.33 – Схема соединения источника и нагрузки звездой
На этом рисунке 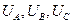 – фазные напряжения. Проводники, идущие от начал фазных обмоток к нагрузке называют линейными проводами (линия). Соответственно напряжения между проводами называют линейными (например, UAC и UCA). Очевидно, что здесь линейный ток равен фазному, а линейное напряжение превышает фазное в корень из трёх раз, поскольку линейное напряжение равно геометрической разности фазных напряжений (см. рис.2.32 ).
– фазные напряжения. Проводники, идущие от начал фазных обмоток к нагрузке называют линейными проводами (линия). Соответственно напряжения между проводами называют линейными (например, UAC и UCA). Очевидно, что здесь линейный ток равен фазному, а линейное напряжение превышает фазное в корень из трёх раз, поскольку линейное напряжение равно геометрической разности фазных напряжений (см. рис.2.32 ).
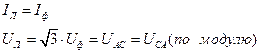 (2.44)
(2.44)
На рис.2.34 приведена схема соединения источника и нагрузки треугольником.
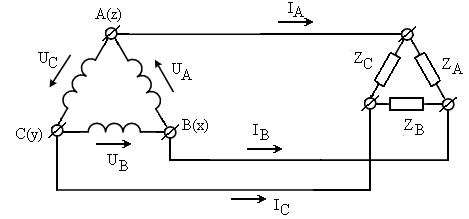
Рисунок 2.34 – Схема соединения источника и нагрузки треугольником
При таком соединении линейные напряжения равны фазным, а линейные токи превышают фазные в корень из трёх раз, поскольку они складываются из фазных.
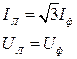 (2.45)
(2.45)
Мощность в трёхфазной цепи не зависит от схемы соединения и складывается из мощностей отдельных фаз.
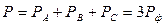 (2.46)
(2.46)
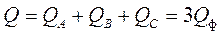 (2.47)
(2.47)
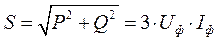 (2.48)
(2.48)
Можно перейти к линейным токам и напряжениям.
Так, при соединении звездой получаем:
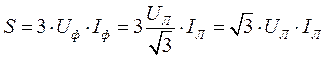 (2.49)
(2.49)
При соединении треугольником:
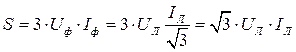 (2.50)
(2.50)
То есть, действительно не зависит от схемы соединения.
Трансформацию трёхфазного напряжения можно осуществлять двумя способами:
– тремя отдельными однофазными трансформаторами, как показано на рисунке 2.35а. Это, так называемый, групповой трансформатор.
– одним трёхфазным трансформатором с общей магнитной системой (рис.2.35б).

Рисунок 2.35 – Условное обозначение группового (а) и трёхфазного (б)
трансформаторов при включении звезда-звезда
Первичные обмотки трансформатора называются обмотками высшего напряжения (ВН) и обозначаются заглавными буквами, а вторичные обмотки называются обмотками низшего напряжения (НН) и обозначаются малыми буквами. Первичные и вторичные обмотки соединяются любым способом.
Соединение в зигзаг применяют, чтобы неравномерную нагрузку вторичных обмоток распределить между фазами первичной сети [1] и для получения требуемых фазовых сдвигов в многопульсных схемах выпрямления. На рис. 2.36 показано соединение обмоток звезда – зигзаг и векторная диаграмма напряжений. Видно, что между напряжениями первичной и вторичной обмоток в одноимённых фазах появился фазовый сдвиг 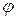 , который можно изменять соотношением витков в частях вторичной обмотки. Если вторичная обмотка разделена на две равные части, то угол
, который можно изменять соотношением витков в частях вторичной обмотки. Если вторичная обмотка разделена на две равные части, то угол 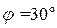 .
.
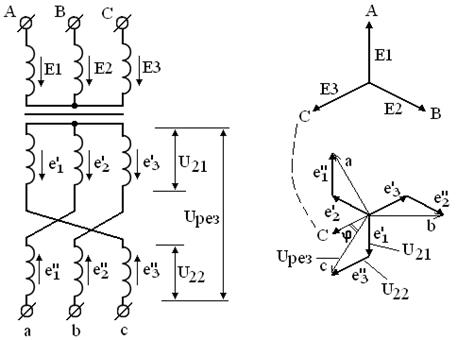
Рисунок 2.36 – Трёхфазный трансформатор при включении звезда-зигзаг
Трёхфазная система напряжений является симметричной, значит и магнитная система трёхфазного трансформатора должна быть симметричной, как показано на рис.2.37а. Изготовить такую магнитную систему очень сложно. Пошли по другому пути. Учитывая, что в трехфазной системе 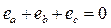 , то и сумма магнитных потоков в центральном стержне
, то и сумма магнитных потоков в центральном стержне 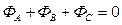 . Необходимость в центральном стержне отпадает и, если сократить ярмо фазы В, то получится плоская, широко известная трёхфазная магнитная система (рис.2.37 б и рис. 2.16 г).
. Необходимость в центральном стержне отпадает и, если сократить ярмо фазы В, то получится плоская, широко известная трёхфазная магнитная система (рис.2.37 б и рис. 2.16 г).
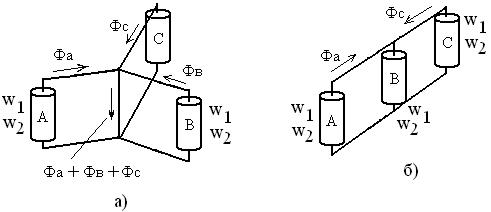
Рисунок 2.37 – Магнитная система трёхфазного
трансформатора: а) симметричная, б) несимметричная
Плоская конструкция магнитной системы высоко технологична и удобна при компоновке (размещению трансформаторов), но она в принципе является несимметричной. Вследствие различия магнитных сопротивлений для разных фаз, намагничивающие токи крайних фаз А и С больше тока средней фазы В. Это приводит к нарушению фазовых углов (они отличаются от 120 градусов). Для уменьшения магнитной асимметрии сечение верхнего и нижнего ярма делают на 10…15% больше чем стержня. Но асимметрия всё равно остаётся.
В настоящее время [10] трёхфазные трансформаторы на мощности единицы киловатт и более изготавливают с симметричной магнитной системой, но такой, как показано на рис. 2.38.
Изготовление ярма сложности не представляет – его наматывают из стальной ленты c помощью оправки. Затем стержни с обмотками и оба ярма стягивают крепежом. Конструкция получилась симметричной и весьма технологичной.
Обмотки низшего напряжения часто соединяют треугольником, так как токи в них в 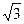 раз меньше чем линейные, а поэтому уменьшается влияние асимметрии фазных нагрузок на первичную сеть.
раз меньше чем линейные, а поэтому уменьшается влияние асимметрии фазных нагрузок на первичную сеть.
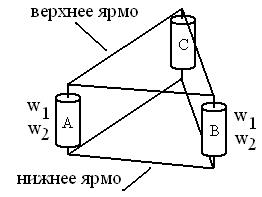
Рисунок 2.38 – Симметричная магнитная система трёхфазного
| | | следующая лекция ==> | |
| Коэффициент полезного действия трансформатора | | | Импульсные трансформаторы |
Дата добавления: 2017-09-19 ; просмотров: 708 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Номинальная мощность.
Номинальной мощностью трансформатора называется мощность, которую он может отдавать длительное время, не перегреваясь свыше допустимой температуры. Нормальный срок службы силового трансформатора должен быть не менее 20 лет. Так как нагрев обмоток зависит от величины протекающего по ним тока, в паспорте трансформ
КПД трансформатора | ООО «НОМЭК»
При работе в трансформаторе возникают потери энергии. Коэффициентом полезного действия трансформатора (КПД) называют отношение отдаваемой мощности Р2 к мощности Р1 поступающей в первичную обмотку:
η = P2/P1 = (U2I2 cos φ2)/(U1I1 cos φ1)
или
η = (Р1 — ΔР)/Р1 = 1 — ΔР/(Р2 + ΔР), (2.49)
где ΔР — суммарные потери в трансформаторе.
Высокие значения КПД трансформаторов не позволяют определять его с достаточной степенью точности путем непосредственного измерения мощностей Р1 и Р2, поэтому его вычисляют косвенным методом по значению потерь мощности.
| Рис. 2.38. Энергетическая диаграмма трансформатора |
Процесс преобразования энергии в трансформаторе характеризует энергетическая диаграмма (рис. 2.38). При передаче энергии из первичной обмотки во вторичную возникают электрические потери мощности в активных сопротивлениях первичной и вторичной обмоток ΔРэл1 и ΔРзл2, а также магнитные потери в стали магнитопровода ΔРм (от вихревых токов и гистерезиса). Поэтому
Р2 = Р1 — ΔРэл1 — ΔРэл2 — ΔРм (2.50)
и формулу (2.49) можно представить в виде
η = |
| = 1 — |
| (2.51) |
Величину Рэм = Р1 — ΔРэл1 — ΔРм, поступающую во вторичную обмотку, называютвнутренней электромагнитной мощностью трансформатора. Она определяет габаритные размеры и массу трансформатора.
Определение потерь мощности. Согласно требованиям ГОСТа потери мощности в трансформаторе определяют по данным опытов холостого хода и короткого замыкания. Получаемый при этом результат имеет высокую точность, так как при указанных опытах трансформатор не отдает мощность нагрузке. Следовательно, вся мощность, поступающая в первичную обмотку, расходуется на компенсацию имеющихся в нем потерь.
При опыте холостого хода ток I0 невелик и электрическими потерями мощности в первичной обмотке можно пренебречь. В то же время магнитный поток практически равен потоку при нагрузке, так как его величина определяется приложенным к трансформатору напряжением. Магнитные потери в стали пропорциональны квадрату значения магнитного потока. Следовательно, с достаточной точностью можно считать, что магнитные потери в стали магнитопровода равны мощности, потребляемой трансформатором при холостом ходе и номинальном первичном напряжении, т. е.
ΔРм ≈ Р0. (2.52)
Для определения суммарных электрических потерь согласно упрощенной схеме замещения (см. рис. 2.33,a) полагают, что 1’2 = 11. При этом
ΔPэл = ΔPэл1 + ΔPэл2 = I12R1 + I’22R2 ≈ I’22 (R1 + R’2) ≈ I’22Rк, (2.53)
или
ΔРэл ≈ β2I’22номRк ≈ β2ΔPэл.ном,(2.54)
где ΔPэл.ном — суммарные электрические потери при номинальной нагрузке.
За расчетную температуру обмоток — условную температуру, к которой должны быть отнесены потери мощности ΔРэл и напряжение ик, принимают: для масляных и сухих трансформаторов с изоляцией классов нагревостойкости А, Е, В (см. § 12.1) температуру 75°С; для трансформаторов с изоляцией классов нагревостойкости F, Н — температуру 115 °С.
Величину ΔРэл.ном ≈ I’22номRк ≈ I12номRк можно с достаточной степенью точности принять равной мощности Рк, потребляемой трансформатором при опыте короткого замыкания, который проводится при номинальном токе нагрузки. При этом магнитные потери в стали ΔРмвесьма малы по сравнению с потерями ΔPэл из-за сильного уменьшения напряжения U1, a следовательно, и магнитного потока трансформатора и ими можно пренебречь. Таким образом,
ΔРэл = β2Pк(2.55)
Полные потери
ΔP = Po + β2Pк (2.56)
Подставляя полученные значения Р в (2.51) и учитывая, что Р2 = U2I2cosφ2 ≈ βSномcosφ2, находим
η = 1 — (β2Pк + P0)/(βSномcosφ2 + β2Pк + P0). | (2.57) |
Эта формула рекомендуется ГОСТом для определения КПД трансформатора. Значения Ро и Рк для силовых трансформаторов приведены в соответствующих стандартах и каталогах.
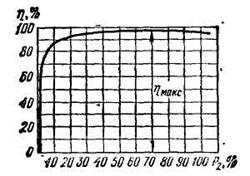
Зависимость КПД от нагрузки. По (2.57) можно построить зависимость КПД от нагрузки (рис. 2.39, а). При β = 0 полезная мощность и КПД равны нулю. С увеличением отдаваемой мощности КПД увеличивается, так как в энергетическом балансе уменьшается удельное значение магнитных потерь в стали, имеющих постоянное значение. При некотором значении βопт кривая КПД достигает максимума, после чего начинает уменьшаться с увеличением нагрузки. Причиной этого является сильное увеличение электрических потерь в обмотках, возрастающих пропорционально квадрату тока, т. е. пропорционально β2, в то время как полезная мощность Р2возрастает только пропорционально β.
Максимальное значение КПД в трансформаторах большой мощности достигает весьма высоких пределов (0,98—0,99).
| Рис. 2.39. Зависимость КПД трансформаторов η от нагрузки β |
Оптимальный коэффициент нагрузки βопт, при котором КПД имеет максимальное значение, можно определить, взяв первую производную dη/dβ по формуле (2.57) и приравняв ее нулю. При этом
β2оптPк = P0 или ΔРэл = ΔРм | (2.58) |
Следовательно, КПД имеет максимум при такой нагрузке, при которой электрические потери в обмотках равны магнит ным потерям в стали. Это условие (равенство постоянных и переменных потерь) приближенно справедливо и для других типов электрических машин. Для серийных силовых трансформаторов
βопт = √P0/Pк ≈ √0,2 ÷ 0,25 ≈ 0,45 ÷ 0,5(2.59)
Указанные значения βопт получены при проектировании трансформаторов на минимум приведенных затрат (на их приобретение и эксплуатацию). Наиболее вероятная нагрузка трансформатора соответствует β = 0,5 ÷ 0,7.
В трансформаторах максимум КПД выражен сравнительно слабо, т. е. он сохраняет высокое значение в довольно широком диапазоне изменения нагрузки (0,4 < β < 1,5). При уменьшении cosφ2 КПД снижается (рис. 2.39,6), так как возрастают токи 12 и I1 при которых трансформатор имеет заданную мощность Р2.
В трансформаторах малой мощности в связи с относительным увеличением потерь КПД существенно меньше, чем в трансформаторах большой мощности. Его значение составляет 0,6—0,8 для трансформаторов, мощность которых менее 50 Вт; при мощности 100-500 Вт КПД равен 0,90-0,92.
Коэффициент полезног действия трансформатора
§ 2.11. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ТРАНСФОРМАТОРА
Энергетическая диаграмма. При работе в трансформаторе возникают потери энергии. Коэффициентом полезного действия трансформатора (КПД) называют отношение отдаваемой мощности Р2 к мощности Р1 поступающей в первичную обмотку:
η = P2/P1 = (U2I2 cos φ2)/(U1I1 cos φ1)
илиη = (Р1 — ΔР)/Р1 = 1 — ΔР/(Р2 + ΔР), (2.49)
где ΔР — суммарные потери в трансформаторе.Высокие значения КПД трансформаторов не позволяют определять его с достаточной степенью точности путем непосредственного измерения мощностей Р1 и Р2, поэтому его вычисляют косвенным методом по значению потерь мощности.
Рис. 2.38. Энергетическая диаграмма трансформатора |
Процесс преобразования энергии в трансформаторе характеризует энергетическая диаграмма (рис. 2.38). При передаче энергии из первичной обмотки во вторичную возникают электрические потери мощности в активных сопротивлениях первичной и вторичной обмоток ΔРэл1 и ΔРзл2, а также магнитные потери в стали магнитопровода ΔРм (от вихревых токов и гистерезиса). Поэтому
Р2 = Р1 — ΔРэл1 — ΔРэл2 — ΔРм (2.50)
и формулу (2.49) можно представить в виде
| η = |
|
= 1 — |
|
(2.51) |
Величину Рэм = Р1 — ΔРэл1 — ΔРм, поступающую во вторичную обмотку, называют внутренней электромагнитной мощностью трансформатора. Она определяет габаритные размеры и массу трансформатора.
Определение потерь мощности. Согласно требованиям ГОСТа потери мощности в трансформаторе определяют по данным опытов холостого хода и короткого замыкания. Получаемый при этом результат имеет высокую точность, так как при указанных опытах трансформатор не отдает мощность нагрузке. Следовательно, вся мощность, поступающая в первичную обмотку, расходуется на компенсацию имеющихся в нем потерь.
При опыте холостого хода ток I0 невелик и электрическими потерями мощности в первичной обмотке можно пренебречь. В то же время магнитный поток практически равен потоку при нагрузке, так как его величина определяется приложенным к трансформатору напряжением. Магнитные потери в стали пропорциональны квадрату значения магнитного потока. Следовательно, с достаточной точностью можно считать, что магнитные потери в стали магнитопровода равны мощности, потребляемой трансформатором при холостом ходе и номинальном первичном напряжении, т. е.
ΔРм ≈ Р0. (2.52)
Для определения суммарных электрических потерь согласно упрощенной схеме замещения (см. рис. 2.33,a) полагают, что 1’2 = 11. При этом
ΔPэл = ΔPэл1 + ΔPэл2 = I12R1 + I’22R2 ≈ I’22 (R1 + R’2) ≈ I‘22Rк, (2.53)
илиΔРэл ≈ β2I’22номRк ≈ β2ΔPэл.ном,(2.54)
где ΔPэл.ном — суммарные электрические потери при номинальной нагрузке.За расчетную температуру обмоток — условную температуру, к которой должны быть отнесены потери мощности ΔРэл и напряжение ик, принимают: для масляных и сухих трансформаторов с изоляцией классов нагревостойкости А, Е, В (см. § 12.1) температуру 75°С; для трансформаторов с изоляцией классов нагревостойкости F, Н — температуру 115 °С.
Величину ΔРэл.ном ≈ I’22номRк ≈ I12номRк можно с достаточной степенью точности принять равной мощности Рк, потребляемой трансформатором при опыте короткого замыкания, который проводится при номинальном токе нагрузки. При этом магнитные потери в стали ΔРм весьма малы по сравнению с потерями ΔPэл из-за сильного уменьшения напряжения U1, a следовательно, и магнитного потока трансформатора и ими можно пренебречь. Таким образом,
ΔРэл = β2Pк(2.55)
Полные потери
ΔP = Po + β2Pк (2.56)
Подставляя полученные значения Р в (2.51) и учитывая, что Р2 = U2I2cosφ2 ≈ βSномcosφ2, находим
| η = 1 — (β2Pк + P0)/(βSномcosφ2 + β2Pк + P0). | (2.57) |
Эта формула рекомендуется ГОСТом для определения КПД трансформатора. Значения Ро и Рк для силовых трансформаторов приведены в соответствующих стандартах и каталогах.
Зависимость КПД от нагрузки. По (2.57) можно построить зависимость КПД от нагрузки (рис. 2.39, а). При β = 0 полезная мощность и КПД равны нулю. С увеличением отдаваемой мощности КПД увеличивается, так как в энергетическом балансе уменьшается удельное значение магнитных потерь в стали, имеющих постоянное значение. При некотором значении βопт кривая КПД достигает максимума, после чего начинает уменьшаться с увеличением нагрузки. Причиной этого является сильное увеличение электрических потерь в обмотках, возрастающих пропорционально квадрату тока, т. е. пропорционально β2, в то время как полезная мощность Р2 возрастает только пропорционально β.
Максимальное значение КПД в трансформаторах большой мощности достигает весьма высоких пределов (0,98—0,99).
Рис. 2.39. Зависимость КПД трансформаторов η от нагрузки β |
| β2оптPк = P0 или ΔРэл = ΔРм | (2.58) |
Следовательно, КПД имеет максимум при такой нагрузке, при которой электрические потери в обмотках равны магнит ным потерям в стали. Это условие (равенство постоянных и переменных потерь) приближенно справедливо и для других типов электрических машин. Для серийных силовых трансформаторов
βопт = √P0/Pк ≈ √0,2 ÷ 0,25 ≈ 0,45 ÷ 0,5(2.59)
Указанные значения βопт получены при проектировании трансформаторов на минимум приведенных затрат (на их приобретение и эксплуатацию). Наиболее вероятная нагрузка трансформатора соответствует β = 0,5 ÷ 0,7.
В трансформаторах максимум КПД выражен сравнительно слабо, т. е. он сохраняет высокое значение в довольно широком диапазоне изменения нагрузки (0,4 < β < 1,5). При уменьшении cosφ2 КПД снижается (рис. 2.39,6), так как возрастают токи 12 и I1 при которых трансформатор имеет заданную мощность Р2.
В трансформаторах малой мощности в связи с относительным увеличением потерь КПД существенно меньше, чем в трансформаторах большой мощности. Его значение составляет 0,6—0,8 для трансформаторов, мощность которых менее 50 Вт; при мощности 100-500 Вт КПД равен 0,90-0,92.
Номинальная мощность.
Номинальной мощностью трансформатора называется мощность, которую он может отдавать длительное время, не перегреваясь свыше допустимой температуры. Нормальный срок службы силового трансформатора должен быть не менее 20 лет. Так как нагрев обмоток зависит от величины протекающего по ним тока, в паспорте трансформатора всегда указывают полную мощность Sном в вольт-амперах или киловольт-амперах.
В зависимости от коэффициента мощности cosφ2, при котором работают потребители, от трансформатора можно получать большую или меньшую полезную мощность. При cosφ2 = l мощность подключенных к нему потребителей может быть равна его номинальной мощности Sном. При cosφ2.
Коэффициент мощности.
Коэффициент мощности cosφ трансформатора определяется характером нагрузки, подключенной к его вторичной цепи. При уменьшении нагрузки начинает сильно сказываться индуктивное сопротивление обмоток трансформатора и коэффициент мощности его снижается. При отсутствии нагрузки (при холостом ходе) трансформатор имеет очень низкий коэффициент мощности, что ухудшает показатели работы источников переменного тока и электрических сетей. В этом случае трансформатор необходимо отключать от сети переменного тока.
Потери мощности и КПД.
При передаче мощности из первичной обмотки трансформатора во вторичную возникают потери мощности как в самих проводах первичной и вторичной обмоток (электрические потери  и
и  или потери в меди), так и в стали магнитопровода (потери в стали
или потери в меди), так и в стали магнитопровода (потери в стали 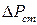 ).
).
При холостом ходе трансформатор не передает электрическую энергию потребителю. Потребляемая им мощность тратится в основном на компенсацию потерь мощности в магнитопроводе от действия вихревых токов и гистерезиса. Эти потери называют потерями в стали 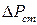 или потерями холостого хода. Чем меньше поперечное сечение магнитопровода, тем больше в нем индукция, а следовательно, и потери холостого хода. Они значительно возрастают также при увеличении напряжения, подводимого к первичной обмотке, свыше номинального значения. При работе мощных трансформаторов потери холостого хода составляют 0,3-0,5% его номинальной мощности. Тем не менее их стремятся максимально уменьшить. Объясняется это тем, что потери в стали не зависят от того, работает ли трансформатор вхолостую или под нагрузкой. А так как общее время работы трансформатора обычно довольно велико, то суммарные годовые потери энергии при холостом ходе составляют значительную величину.
или потерями холостого хода. Чем меньше поперечное сечение магнитопровода, тем больше в нем индукция, а следовательно, и потери холостого хода. Они значительно возрастают также при увеличении напряжения, подводимого к первичной обмотке, свыше номинального значения. При работе мощных трансформаторов потери холостого хода составляют 0,3-0,5% его номинальной мощности. Тем не менее их стремятся максимально уменьшить. Объясняется это тем, что потери в стали не зависят от того, работает ли трансформатор вхолостую или под нагрузкой. А так как общее время работы трансформатора обычно довольно велико, то суммарные годовые потери энергии при холостом ходе составляют значительную величину.
При нагрузке к потерям холостого хода добавляются электрические потери в проводах обмоток 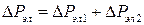 (потери в меди), пропорциональные квадрату нагрузочного тока. Эти потери при номинальном токе примерно равны мощности, потребляемой трансформатором при коротком замыкании, когда на его первичную обмотку подано напряжение Uк. Для мощных трансформаторов ониобычно составляют 0,5-2% номинальной мощности. Уменьшение суммарных потерь достигается соответствующим выбором сечения проводов обмоток трансформатора (снижение электрических потерь в проводах), применением электротехнической стали для изготовления магнитопровода (снижение потерь от перемагничивания) и расслоением магнитопровода на ряд изолированных друг от друга листов (снижение потерь от вихревых токов).
(потери в меди), пропорциональные квадрату нагрузочного тока. Эти потери при номинальном токе примерно равны мощности, потребляемой трансформатором при коротком замыкании, когда на его первичную обмотку подано напряжение Uк. Для мощных трансформаторов ониобычно составляют 0,5-2% номинальной мощности. Уменьшение суммарных потерь достигается соответствующим выбором сечения проводов обмоток трансформатора (снижение электрических потерь в проводах), применением электротехнической стали для изготовления магнитопровода (снижение потерь от перемагничивания) и расслоением магнитопровода на ряд изолированных друг от друга листов (снижение потерь от вихревых токов).
К. п. д трансформатора равен
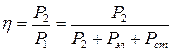
КПД трансформатора сравнительно высок и достигает в трансформаторах большой мощности – 98-99%. В трансформаторах малой мощности КПД может снижаться до 50-70%. При изменении нагрузки КПД трансформатора изменяется, так как меняются полезная мощность и электрические потери. Однако он сохраняет большое значение в довольно широком диапазоне изменения нагрузки (рис. 119,6). При значительных недогрузках КПД понижается, так как полезная мощность уменьшается, а потери в стали остаются неизменными. Понижение КПД вызывается также перегрузками, так как резко возрастают электрические потери (они пропорциональны квадрату тока нагрузки, в то время как полезная мощность – только току в первой степени). Максимальное значение КПД имеет при такой нагрузке, когда электрические потери равны потерям в стали.
При проектировании трансформаторов стремятся, чтобы максимальное значение КПД достигалось при нагрузке 50-75% номинальной; этому соответствует наиболее вероятная средняя нагрузка работающего трансформатора. Такая нагрузка называется экономической.
Полезная мощность — трансформатор
Cтраница 1
Полезная мощность трансформатора составляет 42 кет, а потребляемая 76 ква. [1]
Номинальной полезной мощностью трансформатора называется полная мощность трансформатора на зажимах вторичной обмотки. [2]
Для нахождения полезной мощности трансформатора, определяющей размер и стоимость трансформатора, необходимо знать действующие значения тока и напряжения во вторичной обмотке. Действующее значение напряжения определяется. [3]
При работе трансформатора часть энергии, преобразуемой им, теряется, поэтому полезная мощность трансформатора, отдаваемая им в нагрузку, меньше мощности, потребляемой им из сети источника энергии. Потеря энергии происходит как в магнитопрово-де трансформатора, так и в его обмотках. Обмотки трансформатора нагреваются протекающими по ним токами. [4]
При работе трансформатора часть энергии, преобразуемая им, теряется, поэтому полезная мощность трансформатора, отдаваемая им в нагрузку, меньше мощности, потребляемой им из сети источника энергии. [5]
При работе трансформаторов часть энергии, преобразуемой им, теряется, поэтому полезная мощность трансформатора, отдаваемая им в нагрузку, меньше мощности, потребляемой им из сети источника энергии. Потеря энергии происходит как в магнитопрово-де трансформатора, так и в его обмотках. Обмотки трансформатора нагреваются протекающими по ним токами. [6]
Потери в обмотках Ам определяются показанием ваттметра. При опыте короткого замыкания полезная мощность трансформатора равна нулю, а потери в стали ничтожно малы, так как мал магнитный поток в магнитопроводе. [8]
Потери в обмотках определятся показанием ваттметра. При опыте короткого замыкания полезная мощность трансформатора равна нулю, а потери в стали ничтожно малы, так как мал магнитный поток в сердечнике. [9]
Потери в обмотках Рм определятся показанием ваттметра. При опыте короткого замыкания полезная мощность трансформатора равна нулю, а потери в стали ничтожно малы, так как мал магнитный поток в магнитопроводе. [11]
Страницы: 1
Каждый из нас знает, что такое трансформатор. Он служит для преобразования напряжения в большее или меньшее значение. Когда мы приобретаем трансформатор в специализированных магазинах, как правило, в инструкции к ним имеется полное техническое описание. Вам нет необходимости считать все его параметры и измерять их, так как они все уже подсчитаны и выведены заводом-изготовителем. В инструкции вы сможете найти такие параметры, как мощность трансформатора, входное напряжение, выходное напряжение, количество вторичных обмоток, если их количество превышает одну.

Основные части конструкции трансформатора.
Что делать, если вы приобрели б/у оборудование?
Но если к вам в руки попало уже использовавшееся оборудование и его функциональность вам неизвестна, необходимо самостоятельно рассчитать обмотку трансформатора и его мощность. Но как рассчитать обмотку трансформатора и его мощность хотя бы приблизительно? Стоит отметить, что такой параметр, как мощность трансформатора, очень важный показатель для данного устройства, так как от него будет зависеть, насколько функциональным будет устройство, собранное из него. Чаще всего его используют для создания блоков питания.

Расчет мощностей различных трансформаторов.
В первую очередь следует обозначить, что мощность трансформатора зависит от потребляемого тока и напряжения, которые необходимы для его функционирования. Для того чтобы подсчитать мощность, вам необходимо перемножить эти два показателя: силу потребляемого тока и напряжение питания устройства. Данная формула знакома каждому еще со школьной скамьи, выглядит она следующим образом:
P=Uн*Iн, где
Uн – напряжение питания, измеряется в вольтах, Iн – сила потребляемого тока, измеряется в амперах, P – потребляемая мощность, измеряется в ваттах.
Если у вас имеется трансформатор, который вы бы хотели измерить, то можете делать это прямо сейчас по следующей методике. Для начала необходимо осмотреть сам трансформатор и определиться с его типом и используемыми в нем сердечниками. Всматриваясь в трансформатор, необходимо понять, какой тип сердечника в нем используется. Самым распространенным считается Ш-образный тип сердечника.
Данный сердечник используется в не самых лучших трансформаторах, с точки зрения коэффициента полезного действия, но их вы можете легко найти на прилавках магазинов по продаже электротехники или выкрутить у старой и неисправной техники. Доступность и достаточно низкая цена делают их достаточно популярными среди любителей собрать устройство своими руками. Также можете приобрести тороидальный трансформатор, который иногда называют кольцевым. Он значительно дороже первого и обладает лучшим коэффициентом полезного действия и другими качественными показателями, используется в достаточно мощных и высокотехнологичных устройствах.
Читайте также:
Направляющая для дрели – что это и как использовать.
Правила ремонта болгарки.
О ремонте перфоратора читайте тут.
Вернуться к оглавлению
Самостоятельный расчет обмотки мощности трансформатора

Расчет намотки сварочного трансформатора.
Воспользовавшись книгами по радиотехнике и электронике, мы можем самостоятельно рассчитать обмотку и мощность трансформатора со стандартным Ш-образным сердечником. Для того чтобы рассчитать мощность такого устройства, как трансформатор, необходимо правильно рассчитать сечение магнитопровода. Что касается стандартных трансформаторов с Ш-образным сердечником, размер сечения магнитопровода будет измеряться длиной поставленных пластин, выполненных из специальной электротехнической стали. Итак, для того чтобы определить сечение магнитопровода, необходимо перемножить два таких показателя, как толщина набора пластин и ширина центрального лепестка Ш-образной пластины.
Взяв линейку, мы сможем измерить ширину набора излучаемого трансформатора. Очень важно, что лучше всего все измерения проводить в сантиметрах, как и вычисления. Это сможет исключить появления ошибок в формулах и избавит вас от ненужных вычислений в переводы с сантиметров на метры. Итак, образно возьмем ширину рядов, равную трем сантиметрам.
Дальше необходимо измерить ширину его центрального лепестка. Данная задача может стать проблемной, так как многие трансформаторы могут по своим технологическим особенностям быть закрыты пластиковым каркасом. В таком случае вам будет нельзя, предварительно не видя реальной ширины, сделать какие-либо расчеты, которые хотя бы близко будут походить на реальные. Для того чтобы измерить данный параметр, вам понадобится поискать такие места, где это было бы возможно сделать. В ином случае можно аккуратно разобрать его корпус и измерить данный параметр, но стоит делать это с ювелирной точностью.
Вернуться к оглавлению
Формула расчета мощности

Упрощенный расчет силового трансформатора.
Найдя открытое место или разобрав прибор, вы сможете измерить толщину центрального лепестка. Абстрактно возьмем данный параметр, равный двум сантиметрам. Стоит напомнить, что, примерно рассчитывая мощность, следует как можно точнее проводить измерения. Далее вам необходимо перемножить размер набора магнитопровода, равного трем сантиметрам, и толщину лепестка пластины, равную двум сантиметрам. В итоге мы получаем сечение магнитопровода в шесть квадратных сантиметров. Чтобы делать дальнейший расчет, вам необходимо ознакомиться с такой формулой, как S=1,3*√Pтр, где:
- S – это площадь сечения магнитопровода.
- Pтр – это мощность трансформатора.
- Коэффициент 1,3 является усредненным значением.
Вспомнив формулы из курса математики, мы можем сделать вывод, что, для того чтобы подсчитать мощность, можно сделать следующее преобразование:
〖Ртр=(S/1.33)〗^2
Следующий шаг является подстановкой в данную формулу получившегося значения сечения магнитопровода в 6 квадратных сантиметрах, в итоге получим следующие значение:
〖Ртр=(S/1.33)〗^2=(6/1.33)^2=〖4.51〗^2=20.35 Вт
После всех подсчетов получаем абстрактное значение в 20,35 ватт, которое будет тяжело найти в трансформаторах с Ш-образным сердечником. Реальные значения колеблются в области семи ватт. Данной мощности будет вполне достаточно, чтобы собрать блок питания для аппаратуры, работающей на звуковых частотах и имеющей мощность в пределах от 3 до 5 ватт.
Вернуться к оглавлению
Закрепление пройденного материала расчета мощности
Чтобы закрепить пройденный материал, следует попробовать данный метод на еще одном типе прибора.

Расчет сварочного трансформатора.
Возьмите маломощный трансформатор и попытайтесь рассчитать обмотку трансформатора по уже изученной технологии. Как становится понятно из формулы, мощность трансформатора прямопропорциональна площади его обмотки, из чего можно сделать выводы, что маломощные трансформаторы обладают меньшими размерами. Возьмем одного из таких представителей и измерим размер центрального лепестка. Образно данная цифра будет равна 5 миллиметрам.
Далее, если в данном оборудовании не имеется трудностей с тем, чтобы измерить ширину набора пластин, то вы можете сразу же делать расчеты. Если же вы встретили на своем пути какие-либо препятствия, как описывалось в первом случае, то тогда вам предстоит проделать аналогичные процедуры. После всех действий вы все-таки измерили данный параметр, образно подберем ширину, равную двум сантиметрам. В таком случае вам предстоит перемножить эти две цифры, и получится сечение с размером в один квадратный сантиметр.
Используя формулы для расчета мощности, можно определить, что мощность такого трансформатора составляет 0,56 ватт. Конечно же, как и предполагалось, его мощность достаточно маленькая для каких-либо серьезных устройств. В нем могут находиться две вторичные обмотки с максимальным допустимым значением тока в них в пару десятков миллиампер. Такой трансформатор сможет подойти только для устройств, которые не требуют большого потребления тока.
Если вы действительно хотите сделать правильный расчет, который покажет его реальную мощность, то вам предстоит сделать дополнительные вычисления. Так, например, еще не придумали и, скорее всего, в ближайшее время не смогут найти среду, которая бы передавала электричество без потерь. В любом проводе следует учитывать такой фактор, как потери. Например, если вы делаете подсчет в достаточно массивном трансформаторе, то и, соответственно, потери в нем будут намного больше, чем в трансформаторе с малой обмоткой. Пользуясь данными формулами, вы всегда сможете без труда быстро и правильно выполнить необходимые расчеты по мощности трансформатора.
что это, из каких частей состоит, методика расчета
Понятие полной мощности используется в электротехники для определения фактической нагрузки на элементы сети. Величина полной мощности силового трансформатора является основой для проектирования его конструкции.
Полная мощность превосходит по абсолютной величине активную и зависит от характеристик нагрузки.
Понятие мощности трансформатора
Трансформатор переменного тока не производит электрическую энергию, а лишь преобразовывает ее по величине. Поэтому его мощность полностью зависит от ее величины нагрузки (тока потребления) вторичной цепи. При наличии нескольких потребителей должна учитываться суммарная нагрузка, которая может быть подключена одновременно. Для цепей переменного тока учитывается активный и реактивный характер потребления.

Активная
Данная составляющая часть характеристики определяется как среднее значение мгновенной за определенный период времени. Для цепей синусоидального переменного тока в качестве отрезка времени используется значение периода колебания:
T=1/f,
где f – частота.
Активная часть зависит от характера нагрузки, то есть от сдвига фаз между током и напряжением и определяется по формуле:
P=i∙U∙cosϕ,
где ϕ – угол сдвига фаз.
Активная составляющая устройств переменного тока выражается в Ваттах, как и для цепей постоянного тока.
Реактивная
Реактивная нагрузка отличается от активной тем, что в течение одного периода колебаний напряжения электрическая энергия реально не потребляется, но возвращается назад. В результате того, что к питающему устройству подключены устройства с большой емкостью или индуктивностью (электродвигатели), между током и напряжением возникает сдвиг фаз.
Реактивная составляющая потребления определяется выражением:
Q= i∙U∙sinϕ
Единица измерения – вар (вольт-ампер реактивный).
Полная
Полная мощность трансформатора учитывает всю потребленную и возвращенную энергию и находится из выражения:
S= i∙U
Все составляющие связаны соотношением:
S2=P2+Q2.
Единица измерения – ВА (вольт-ампер).
Полная мощность равняется активной только в случае полностью активной нагрузки.

Номинальная
Номинальная мощность трансформатора учитывает возможность работы конструкции с учетом подключения потребителей разного характера, то есть аналогична полной. При этом гарантируется исправная работа устройства весь заявленный срок службы при оговоренных условиях эксплуатации.
Номинальная мощность, как и полная, учитывает активный и реактивный характер потребления, которое может изменяться во время эксплуатации.
Выражается в вольт-амперах.
Методика расчета мощностей трансформатора
При расчете силового трансформатора питающей подстанции учитывается среднесуточная нагрузка и длительность периода максимальной потребления. При этом должно учитываться соотношение:
Sном≥∑Pмакс
Режим пикового потребления также должен учитывать время воздействия, поскольку при кратковременных всплесках (до 1 часа), устройство будет работать в недогруженном режиме, что экономически не выгодно.
В таких случаях нужно брать в расчет перегрузочную способность конструкции, которая зависит от конструктивных особенностей, температуры окружающего воздуха и условий охлаждения. Это диктуется условиями допустимого нагрева составляющих элементов (обмоток, коммутирующих цепей).
Понятие коэффициента загрузки определяет отношение среднесуточного и максимального потребления электрической энергии. Коэффициент загрузки всегда меньше единицы. Его величина связана с требованиями к надежности электроснабжения. Чем меньше требуемая надежность, тем больше коэффициент может приближаться к единице.
Примеры реальных расчетов
В качестве примера можно выбрать питающую подстанцию жилого района. Нагрузка подстанции является III категории, поэтому коэффициент загрузки допустимо выбирать из большего значения – 0.9-0.95.
Характер потребления тока бытового сектора зависит от времени суток и сезона, но с учетом высокого коэффициента загрузки допустимо учитывать среднее значение потребляемой мощности. Для повышения надежности работы в период максимального потребления рекомендуется использование маслонаполненных трансформаторов, которые отличаются большой перегрузочной способностью в течение длительного периода времени (30% перегрузки в течение 2-х часов).
Эскиз конструкции трансформатора
Конструкция мощного силового трансформатора состоит из нескольких частей:
- Остов.
- Выемная часть.
В состав выемной части входит, собственно сердечник и обмотки с активной частью, которая включает переключатели с приводами, вводы высокого и низкого напряжений, предохранительные устройства.
Остов – основная составляющая конструкции активной части. В состав остова входит магнитная система (сердечник) со всеми обмотками, а также конструктивные элементы для крепления и соединения обмоток и частей магнитной системы.




