2.11. Резонанс в цепях синусоидального тока

2.11. Резонанс в цепях синусоидального тока.

Реактивные сопротивления и проводимость являются частотно-зависимыми величинами. Следовательно, при последовательном или параллельном соединении элементов L и C возможна на какой-то частоте полная компенсация реактивных сопротивлений или проводимостей. Режим, при котором наступает компенсация, называют резонансом. При резонансе входное сопротивление цепи становится активным, входное напряжение совпадает по фазе с входным током, а полная мощность будет активной. Угловая частота, , при которой наступает резонанс, называется резонансной или собственной угловой частотой цепи. Различают две разновидности резонанса: резонанс напряжений и резонанс токов.

2.11.1. Резонанс напряжений.

Может возникнуть в цепи с последовательным соединением L и C, рис. 2.20а.

Для этой цепи запишем:

.

Условие резонанса:

              или             ,

откуда резонансная частота .

Рекомендуемые файлы

Настройку цепи в резонанс, изменение параметров цепи при частотах , отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r, L, C.

На рис. 2.20б,в,г приведены частотные характеристики реактивных сопротивлений  и , суммарного реактивного сопротивления , модуля полного сопротивления , модуля входного тока , а также амплитудно-частотные характеристики напряжений:

,

,

.

По графику  определена резонансная частота , по графику  можно увидеть, что сопротивление цепи при резонансе минимально и равно активному сопротивлению, по графику  — что ток в цепи при резонансе максимален. Графики , ,  имеют ярко выраженный избирательный характер, т.е. имеют максимальные значения на резонансной частоте или вблизи нее. Можно также отметить, что напряжения  и  при резонансе могут превышать значение входного напряжения. Это хорошо иллюстрируется с помощью векторных диаграмм напряжения приведенных на рис. 2.20д,е,ж при частотах ,  и  .Обратите также внимание на значения угла  на этих частотах и сопоставьте эти значения с характером реактивных сопротивлений на соответствующих частотах. Так при частотах  , реактивное сопротивление носит емкостной характер и и т.д.

2.11.2. Резонанс токов.

Возможен в цепях с параллельным соединением L и C элементов, рис. 2.21а.

Рекомендуем посмотреть лекцию «Некоторые аспекты проектного менеджмента».

Для этой цепи запишем уравнение по первому закону Кирхгофа:

Компенсация реактивных проводимостей и реактивных токов:

                     ,

произойдет на резонансной частоте

Для анализа явления резонанса токов построим частотные характеристики реактивных проводимостей рис.2.21б, модуля полной проводимости , рис.2.21в, модуля полного тока , рис. 2.21г. Здесь отмечена резонансная частота, полная проводимость цепи при резонансе минимальна и полный ток минимален. Векторные диаграммы токов, построенные для частот , ,, рис. 2.21д,е,ж, позволяют убедиться, что токи в катушке и конденсаторе могут значительно превышать полный ток.

Колебательные контуры — RadioRadar

Материал предоставлен журналом Радиолюбитель

Последовательный колебательный контур

---

   Как известно, простейшими резонансными (или колебательными) цепями являются последовательный и параллельный колебательные контуры. Рассмотрим цепь, состоящую из последовательно включенных катушки индуктивности и конденсатора (рис. 1). При воздействии на такую цепь переменного (в простейшем случае гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина (амплитуда) которого может быть вычислена согласно закону Ома: I = U/|Х_Σ| , где |Х_Σ| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора. На рис. 2 приведены зависимости реактивных сопротивлений катушки X_L и конденсатора Х_C от круговой частоты ω, а также график зависимости от частоты ω их алгебраической суммы Х_Σ Последний график, по сути, показывает зависимость от частоты общего реактивного сопротивления цепи, изображенной на рис.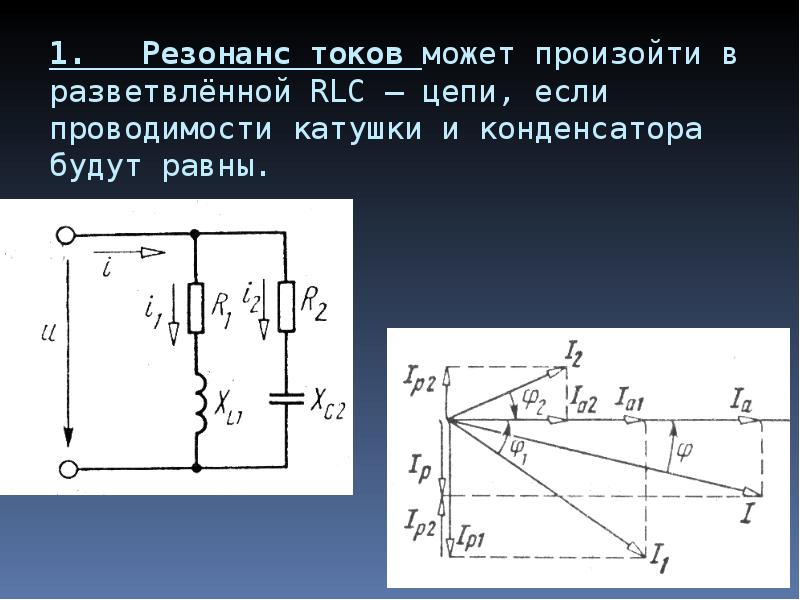 1. Из этого графика видно, что на некоторой частоте ω=ω_р , на которой реактивные сопротивления катушки и конденсатора равны по модулю, общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи, а саму цепь, изображенную на рис. 1, принято называть последовательным колебательным контуром. Также из рис. 2 видно, что на частотах ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах — индуктивный. Что касается самой резонансной частоты, то она может оыть вычислена при помощи известной формулы Томсона: ω_р = 1/√(LC).

Рис. 1
Последовательный колебательный контур

Рис. 2
Зависимости реактивных сопротивлений катушки X_L и конденсатора Х_C от круговой частоты ω

   На рис.3 изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь r, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Модуль полного сопротивления (импеданса) такой цепи определяется следующим образом: |z| = √(r²+|X_Σ|²), где |X_Σ| = ωL-1/ωC. Очевидно, что на резонансной частоте, когда величины реактивных сопротивлений катушки X_L = jωL и конденсатора Х_C= -j/ωС равны по модулю, величина |X_Σ| обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/r. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение U_L=U_C=I|X_L|=I|X_C|.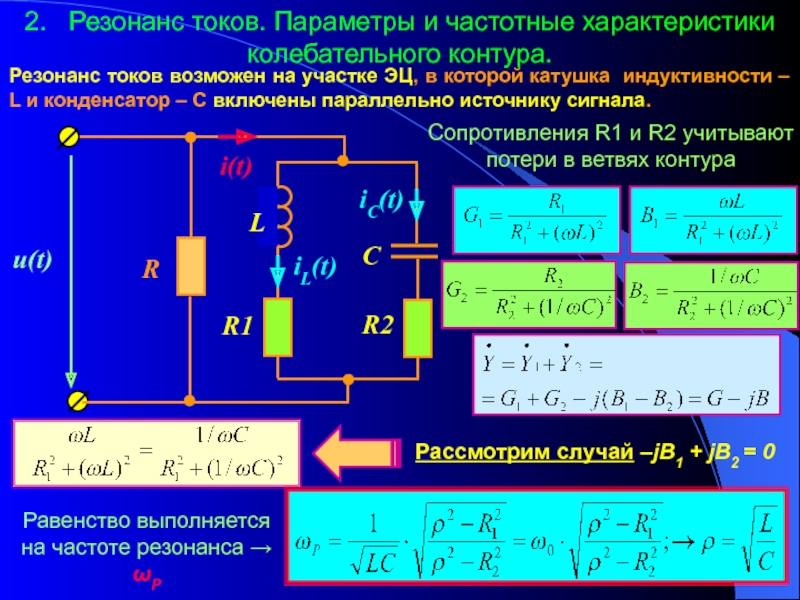 На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы — они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений |X_L| и |X_C| .Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. С учетом приведенной записи для импеданса цепи можно привести часто встречающееся определение резонансной частоты: резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер.

Рис. 3
Эквивалентная схема последовательного резонансного контура

   Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое сопротивление ρ и добротность Q. Характеристическим сопротивлением контура ρ называется величина модуля реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = |Х_L| =|Х_C| при ω =ω_р . В общем случае характеристическое сопротивление может быть вычислено следующим образом: ρ = √(LC). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура — катушкой (энергия магнитного поля) W_L= (LI²)/2 и конденсатором (энергия электрического поля) W_C=(CU²)/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает «качество». Величину, обратную добротности d=1/Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q=ρ/r, где r-сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р=I²r. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.

Рис.4 а

Рис.4 б

Рис. 5 а	Рис. 5 б

   Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ). На рис. 4а и рис. 4б представлены два простейших четырехполюсника, содержащих последовательный колебательный контур. АЧХ этих цепей приведены (показаны сплошными линями) на рис. 5а и рис. 5б соответственно. По вертикальной оси отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному. Для пассивных цепей (не т.е. содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Очевидно, что сопротивление цепи на рис.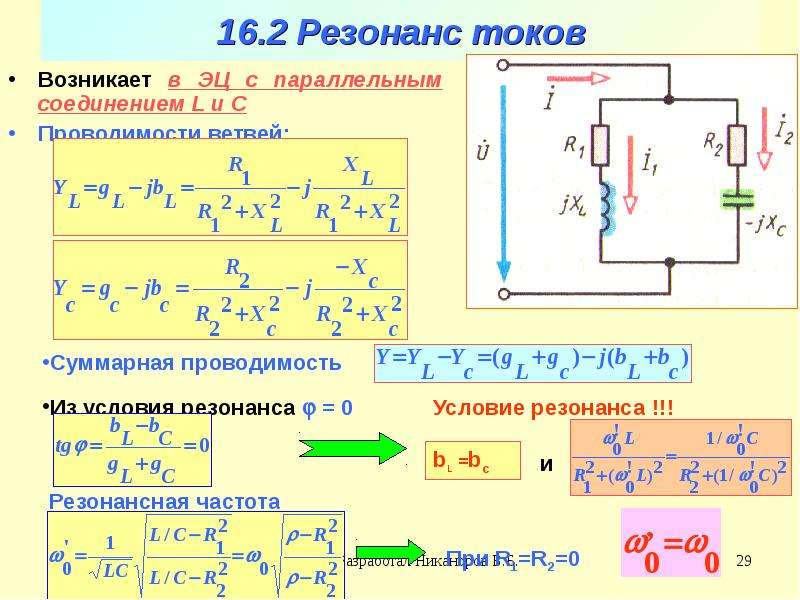 4а переменному току будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля. При резонансе в цепи, изображенной на рис. 4б, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. Чаще всего за полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение — в зависимости от вида цепи) коэффициента передачи относительного его значения на резонансной частоте, не превышает величины 0,707 (3дБ).

   Пунктирными линиями на рис. 5а и рис. 5б показаны АЧХ точно таких же цепей, как на рис. 4а и рис. 4б соответственно, колебательные контуры которых имеют такие же резонансные частоты, как и для случая рассмотренного выше, но обладающие меньшей добротностью (например, катушка индуктивности намотана проводом, обладающим большим сопротивлением постоянному току). Как видно из рис. 5а и рис. 5б, при этом расширяется полоса пропускания цепи и ухудшаются ее селективные (избирательные) свойства. Исходя из этого, при расчете и конструировании колебательных контуров нужно стремиться к повышению их добротности. Однако, в ряде случаев, добротность контура, наоборот, приходится занижать (например, включая последовательно с катушкой индуктивности резистор небольшой величины сопротивления), что позволяет избежать искажений широкополосных сигналов. Хотя, если на практике требуется выделить достаточно широкополосный сигнал, селективные цепи, как правило, строятся не на одиночных колебательных контурах, а на более сложных связанных (многоконтурных) колебательных системах, в т.ч. многозвенных фильтрах.

Параллельный колебательный контур

---

   В различных радиотехнических устройствах наряду с последовательными колебательными контурами часто (даже чаще, чем последовательные) применяют параллельные колебательные контуры На рис. 6 приведена принципиальная схема параллельного колебательного контура Здесь параллельно включены два реактивных элемента с разным характером реактивности Как известно, при параллельном включении элементов складывать их сопротивления нельзя — можно лишь складывать проводимости На рис. 7 приведены графические зависимости реактивных проводимостей катушки индуктивности B_L = j/ωL, конденсатора В_C = -jωC, а также суммарной проводимости В_Σ, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Аналогично, как и для последовательного колебательного контура, имеется некоторая частота, называемая резонансной, на которой реактивные сопротивления (а значит и проводимости) катушки и конденсатора одинаковы. На этой частоте суммарная проводимость параллельного колебательного контура без потерь обращается в нуль. Это значит, что на этой частоте колебательный контур обладает бесконечно большим сопротивлением переменному току. Действительно, если построить зависимость реактивного сопротивления контура от частоты X_Σ=1/B_Σ, эта кривая (рис. 8) в точке ω = ω_р будет иметь разрыв второго рода. Сопротивление реального параллельного колебательного контура (т.е с потерями), разумеется, не равно бесконечности — оно тем меньше, чем больше омическое сопротивление потерь в контуре, т. е уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический смысл понятий добротности, характеристического сопротивления и резонансной частоты колебательного контура, а также их расчетные формулы, справедливы как для последовательного, так и для параллельного колебательного контура.

Рис. 6
Параллельный колебательный контур

Рис. 7
Зависимости реактивных поводимостей катушки и конденсатора и суммарная проводимость этих двух элементов

Рис. 8
Зависимость реактивного сопротивления контура от частоты

   Рассмотрим цепь, состоящую из генератора гармонических колебаний и параллельного колебательного контура. В случае, когда частота колебаний генератора совпадает с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут одинаковыми. В этом случае говорят, что в цепи имеет место резонанс токов. Как и в случае последовательного колебательного контура, реактивности катушки и конденсатора компенсируют друг друга, и сопротивление контура протекающему через него току становится чисто активным (резистивным). Величина этого сопротивления, часто называемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление R_экв=Q·ρ. На частотах, отличных от резонансной, сопротивление контура уменьшается и приобретает реактивный характер (рис. 8) на более низких частотах — индуктивный (поскольку реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких — наоборот, емкостной (т к реактивное сопротивление емкости падает с ростом частоты). В процессе работы контура, дважды за период колебаний, происходит энергетический обмен между катушкой и конденсатором (рис. 9). Энергия поочередно накапливается то в виде энеогии электрического поля заряженного конденсатора, то в виде энергии магнитного поля катушки индуктивности. При этом в контуре протекает собственный контурный ток I_к, превосходящий по величине ток во внешней цепи I в Q раз. В случае идеального контура (без потерь), добротность которого теоретически бесконечна, величина контурного тока также будет бесконечно большой.

Рис. 9
Процесс работы контура

Рис. 10 а	Рис. 10 б

   Рассмотрим, как изменяются коэффициенты передачи четырехполюсников, аналогичных приведенным на рис. 4а и рис. 4б, от частоты, при включении в них не последовательных колебательных контуров, а параллельных. Четырехполюсник, изображенный на рис. 10а, на резонансной частоте контура представляет собой огромное сопротивление току, поэтому при ω=ω_р его коэффициент передачи будет близок к нулю (с учетом омических потерь). На частотах, отличных от резонансной, сопротивление контура будет уменьшатся, а коэффициент передачи четырехполюсника — возрастать. Этот случай соответствует графику АЧХ, приведенному на рассмотренном ранее рис. 5б. Для четырехполюсника, приведенного на рис. 10б, ситуация будет противоположной — на резонансной частоте контур будет представлять собой очень большое сопротивление и практически все входное напряжение поступит на выходные клеммы (т.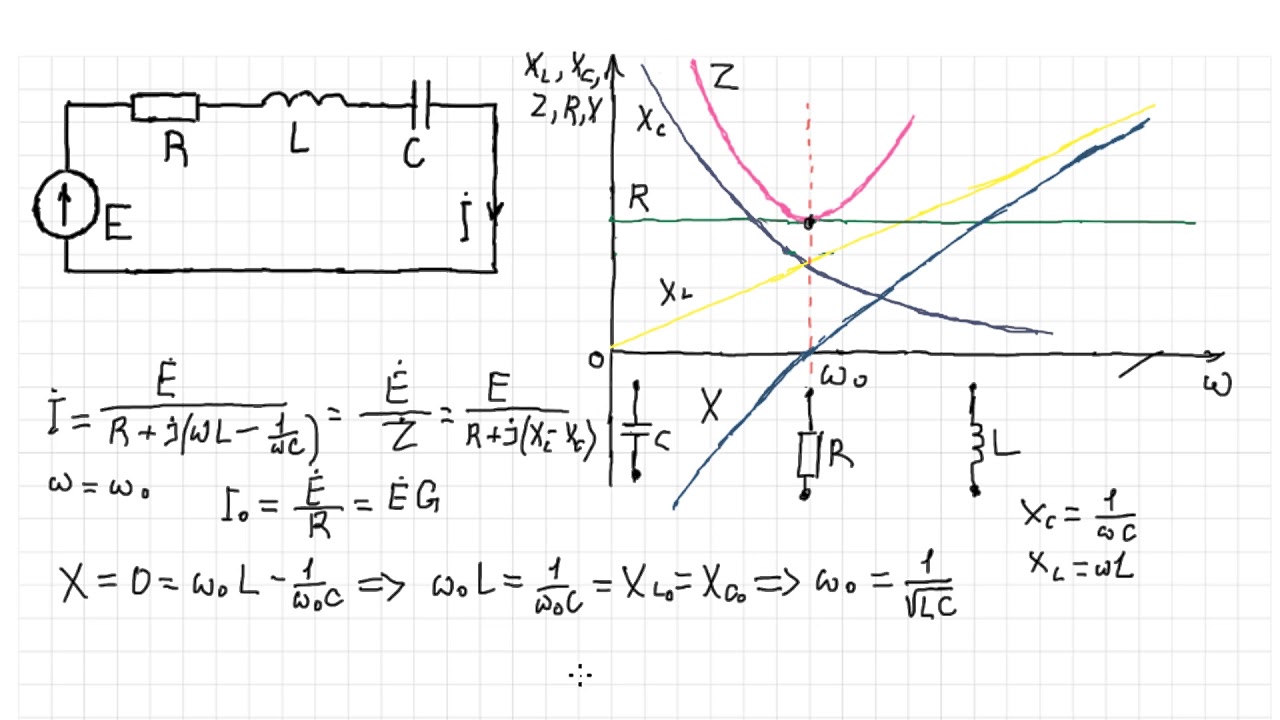 е коэффициент передачи будет максимален и близок к единице). При значительном отличии частоты входного воздействия от резонансной частоты контура, источник сигнала, подключаемый к входным клеммам четырехполюсника, окажется практически закороченном накоротко, а коэффициент передачи будет близок к нулю. АЧХ такого четырехполюсника соответствует изображенной на рис. 5а.

   В заключении настоящего экскурса отметим тот факт, что достаточно часто в реальной радиоэлектронной аппаратуре приходится сталкиваться с необходимостью перестройки колебательных контуров — например, в приемнике, для обеспечения возможности приема радиостанций, работающих на разных частотах В этом случае емкостные элементы контуров выполняются в виде конденсаторов переменной емкости, либо специальных диодов — варикапов, обладающих большой барьерной емкостью, зависящей от приложенного к ней запирающего напряжения В ряде случаев применяют и перестраиваемый катушки индуктивности — вариометры.

Калькулятор импеданса параллельной RLC-цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Калькулятор определяет импеданс и фазовый сдвиг для соединенных параллельно резистора, катушки индуктивности и конденсатора для заданной частоты синусоидального сигнала. Определяется также угловая частота.

Пример. Рассчитать импеданс резистора 300 Ом, катушки индуктивности 100 мГн и конденсатора 10 мкФ на частоте 159 Гц. Калькулятор показывает высокий импеданс около 299,99 Ом. Это почти резонанс. Можно проверить импеданс при почти полном резонансе, если ввести 159,1549 Гц вместо 159 Гц. Цепь в этом случае имеет индуктивный характер и ее индуктивное реактивное сопротивление меньше емкостного. Однако, если ввести чуть большую частоту 159,1550 Гц, характер цепи станет емкостным, индуктивное реактивное сопротивление станет больше емкостного и вы увидите, что фазовый угол, который был чуть больше нуля, станет отрицательным.

Входные данные

Сопротивление, R

миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)

Индуктивность, L

генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)

Емкость, С

фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

Частота, f

герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц)

Выходные данные

Угловая частота ω= рад/с

Емкостное реактивное сопротивление X_C= Ом

Индуктивное реактивное сопротивление X_L= Ом

Полный импеданс RLC |Z_RLC|= Ом

Фазовый сдвигφ = ° = рад

Добротность Q=

Резонансная частота

f₀=   Гц   ω₀=   рад/с

Введите значения сопротивления, емкости, индуктивности и частоты, выберите единицы измерения и нажмите кнопку

Рассчитать. Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.

Для расчетов используются указанные ниже формулы:

Здесь

Z_RLC — импеданс цепи RLC в омах (Ом),

ω = 2πf — угловая частота в рад/с,

f — частота в герцах (Гц),

R сопротивление в омах (Ом),

L — индуктивность в генри (Гн),

C — емкость в фарадах (Ф),

Q добротность параллельной RLC-цепи (безразмерная величина),

ω₀ — резонансная угловая частота в радианах в секунду (рад/с),

f₀ — резонансная частота в герцах (Гц),

φ — фазовый сдвиг между полным напряжением V_T и полным током I_T в градусах (°).

Для расчета введите сопротивление, индуктивность, емкость, частоту и выберите единицы измерения. Импеданс RLC –цепи будет показан в омах, сдвиг фаз в градусах и радианах. Также будут рассчитаны добротность, индуктивное и емкостное реактивные сопротивления и резонансная частота. С помощью ссылки

Вычислить на резонансной частоте можно рассчитать величины при резонансе.

Параллельная цепь RLC состоит из резистора R, катушки индуктивности L и конденсатора C, соединенных параллельно. В англоязычной литературе, а иногда и в неаккуратных русских переводах, можно встретить и иные сочетания этих R, L и C в названии цепи. Как и в идеальной параллельной LC-цепи без сопротивления, в RLC-цепи могут возникать колебания с частотой резонанса, которые, в отличие от LС-цепи, затухают из-за наличия сопротивления.

Слева: график зависимости импеданса

Z_RLC параллельной RLC-цепи от частоты f при различных величинах сопротивления, индуктивности и емкости, причем эти значения выбраны таким образом, что резонансная частота одинаковая на всех графиках.
Справа: график зависимости от частоты f импеданса Z_RLC и сдвига фаз между током и напряжениемφ параллельной RLC-цепи

Резонанс возникает на частоте, при которой импеданс цепи максимален, то есть, при нулевом реактивном сопротивлении цепи. Иными словами, он возникает, если импеданс только резистивный, без реактивной составляющей, то есть его мнимая часть равна нулю. Явление резонанса происходит в том случае, когда реактивные сопротивления катушки индуктивности и конденсатора равны и, поскольку они имеют противоположный знак, они гасят друг друга. Как это происходит — показано ниже на векторной диаграмме.

Калькулятор определяет резонансную частоту RLC-цепи, и можно ввести эту частоту или значение чуть-чуть меньше или чуть-чуть больше резонансной частоты, чтобы посмотреть, как будут себя вести рассчитываемые величины при резонансе и около него.

Калькулятор рассчитывает также добротность Q RLC-цепи — параметр, который используется для характеристики электрических резонансных цепей и устройств, а также механических резонаторов. Чем ниже сопротивление цепи, тем больше потерь и тем выше затухание в RLC-цепях и ниже их добротность. Добротность Q параллельной RLC-цепи рассчитывается по приведенной выше формуле.

Векторная диаграмма параллельной RLC-цепи. 1 —реактивное сопротивление имеет индуктивный характер; 2 — реактивное сопротивление имеет емкостной характер; 3 — импеданс на резонансной частоте определяется только сопротивлением; на резонансной частоте цепь является чисто активной

В параллельной RLC-цепи напряжение на резисторе, конденсаторе и катушке индуктивности одно и то же, однако токи в ветвях цепи различны. На векторной диаграмме показано напряжение V_T

идеального источника напряжения. В связи с наличием сопротивления, на схеме показан горизонтальный вектор тока через резистор в фазе с приложенным напряжением. Вектор тока в индуктивности I_L отстает от вектора напряжения на 90°, поэтому он направлен вниз (–90°). Вектор тока в емкости опережает вектор напряжения на 90°, поэтому он направлен вверх (+90°). Векторная сумма двух векторов, направленных в противоположные стороны, может быть направлена вниз и вверх в зависимости от того, где больше ток: в индуктивности или в емкости. 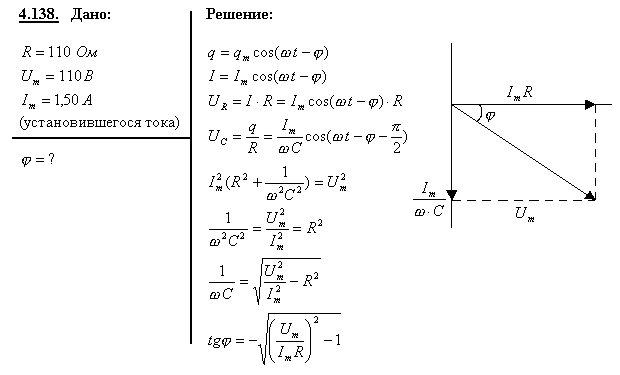Вектор полного тока в цепи I_T определяется по теореме Пифагора.

На частоте резонанса емкостное и индуктивное реактивные сопротивления равны и если мы посмотрим на приведенное выше уравнение для |Z|, мы увидим, что эффективный импеданс будет определяться только величиной сопротивления и будет максимальным. Токи, текущие через катушку индуктивности и конденсатор, равны, так как их реактивные сопротивления тоже равны. Поэтому на резонансной частоте от источника потребляется ток, определяемый лишь резистором. Можно сказать, что для источника напряжения параллельная RLC-цепь при резонансе представляет собой чисто резистивную нагрузку.

В то же время, видно, что при резонансе ток течет между катушкой индуктивности и конденсатором, периодически изменяя направление и постепенно уменьшаясь по амплитуде. Это явление можно сравнить с маятником, который качается с уменьшающейся амплитудой без приложения внешних сил.

Интересно отметить, что в английском языке параллельная RLC цепь часто называется «tank circuit», что в переводе буквально означает «цепь, сохраняющая энергию так же, как сохраняется жидкость в баке». Название объясняется тем, что RLC-цепь хранит энергию в форме электрического и магнитного полей и циркулирующего тока точно так же, как бак хранит жидкость, не выпуская ее. Амплитуда этого циркулирующего тока зависит от импеданса конденсатора и катушки индуктивности. Если индуктивность большая, а емкость маленькая, их реактивные сопротивления будут большими, а ток, соответственно, маленьким. Если же индуктивность невысокая, а емкость высокая, то реактивные сопротивления небольшие и ток будет большим.

Катушки индуктивности без сердечников в высокочастотном модуле телевизионного приемника

Режимы отказа элементов

А что если в этой схеме отказал один из элементов? Нажмите на соответствующую ссылку, чтобы посмотреть соответствующие режимы отказа:

Особые режимы работы цепи

Отказ электролитического конденсатора

Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:

Различные режимы работы на постоянном токе

Короткое замыкание

Обрыв цепи

Чисто емкостная цепь

Цепь при резонансе

Чисто индуктивная цепь

Индуктивная цепь

Примечания

• Нулевая частота в объяснениях поведения этой цепи означает постоянный ток. Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
• При нулевой частоте реактивное сопротивление конденсатора считается нулевым, если его емкость бесконечно большая. Если же емкость конденсатора конечная или нулевая, его реактивное сопротивление бесконечно большое и для источника постоянного напряжения он представляет собой обрыв цепи, иными словами отсутствующий конденсатор.
• При нулевой частоте реактивное сопротивление идеальной катушки индуктивности считается бесконечно большим, если ее индуктивность бесконечно большая. Если же индуктивность катушки конечная или нулевая, ее реактивное сопротивление при нулевой частоте равно нулю и для источника постоянного напряжения она представляет собой короткое замыкание.

Автор статьи: Анатолий Золотков

3.2.6 Простейшие фильтры второго порядка

К простешим фильтрам второго порядка относят цепочки, содержащие две реактивности разного знака: индуктивность и емкость. В зависимости от схемы включения контура к источнику сигнала различают последовательный и параллельный колебательный контуры. В последовательном контуре источник сигнала и элементы контура (обычно это конденсаторы и катушки индуктивности) соединены последовательно. Выходное напряжение чаще снимают с конденсатора (см. рис.12).

Рис. 12

Моделью конденсатора является емкость С, катушку индуктивности обычно представляют последовательным соединением индуктивности L и активного сопротивления , отражающего сопротивление провода катушки постоянному току. На схеме рис.12 источник сигнала представлен источником ЭДС e(t) с внутренним сопротивлением .

В параллельном контуре источник сигнала представляют в виде источника тока, параллельно с которым соединены емкость и катушка индуктивности (рис.13).

Рис. 13

Частотный коэффициент передачи определяется при гармоническом сигнале на входе. Определим собственные параметры контуров (при R_c =0 для источника ЭДС и R_c = для источника тока в режиме холостого хода на выходе).

Для последовательного контура, используя комплексный метод, получаем

.

(1)

Для параллельного контура коэффициентом передачи является сопротивление контура, т.к.

(2)

В обоих случаях знаменатель определяется полным последовательным сопротивлением контура

.

На частоте, называемой резонансной, мнимая часть последовательного сопротивления равна нулю, т.е. , откуда получаем известное соотношение (формула Томпсона) .

Величины определяют волновое или характеристическое сопротивление контура, т.е. сопротивление реактивных элементов на резонансной частоте.

Таким образом, на резонансной частоте .

Отношение волнового сопротивления последовательного контура к сопротивлению потерь катушки называют собственной добротностью контура

.

(3)

Соотношения (1) и (2) с учетом введенных обозначений легко преобразуются к виду

,  ,

(4) (5)

где приближенное равенство справедливо для Q>1.

Коэффициент передачи последовательного контура на резонансной частоте равен добротности, т.е. амплитуда выходного напряжения в Q раз больше амплитуды входного. Собственное сопротивление же последовательного контура на резонансной частоте действительно и равно и увеличивается по модулю с изменением частоты влево или вправо от резонансной.

Коэффициент передачи параллельного контура (а, следовательно, и его полное сопротивление) на резонансной частоте максимальны и равны:

.

С изменением частоты модуль полного сопротивления уменьшается.

При определении характера поведения АЧХ и ФЧХ цепей вблизи резонанса() преобразуем выражение под корнем с учетом следующих обозначений:

,

,

где – абсолютная расстройка частоты сигнала относительно резонансной частоты, — относительная расстройка;

,

(6)

где величина называется обобщенной расстройкой. Тогда вблизи резонанса можно записать

; .

(7) (8)

На частотах, соответствующих = 1, коэффициенты передачи в раз меньше резонансных. При = 1, имеем , где абсолютная расстройка, соответствующая этому случаю. Величина называется полосой пропускания контура как полосового фильтра. Отсюда получают второе определение добротности контура в виде отношения резонансной частоты к полосе частот , определяемой на уровне от максимума.

В области низких частот ()

, .

В области высоких частот ()

, .

Рис. 14

На рис.14 показаны АЧХ и ФЧХ последовательного (а) и параллельного (б) контуров.

На границах полосы пропускания ФЧХ имеет значение от значения ФЧХ на резонансной частоте ().

С увеличением добротности полоса пропускания уменьшается (избирательность увеличивается), наклон ФЧХ в полосе пропускания увеличивается.

Легко показать, что конечные значения сопротивления источника сигнала и нагрузки уменьшают добротность системы, расширяя ее полосу пропускания, т.к. при этом увеличивается последовательное сопротивление контура постоянному току. Так как сопротивление в схеме последовательного контура просто складывается с , то добротность оказывается равной . Для определения влияния и в параллельном контуре заменим последовательную модель катушки индуктивности на параллельную (см. рис.15).

Рис. 15

Величины и выразим из равенства:

.

Преобразуем правую часть в обычную алгебраическую форму комплексного числа, избавившись от комплексности в знаменателе:

.

Вблизи резонансной частоты величина , следовательно

,

(9)

откуда .

Кроме того, при Q>1 можно считать, что , поэтому

,

следовательно, .

Собственная добротность контура в схеме рис.15, б определяется как

.

При учете сопротивлений и общее активное сопротивление контура равно меньше сопротивления , следовательно, добротность меньше собственной добротности контура.

Резонансное сопротивление параллельного контура в этом случае определяется как , и, таким образом, меньше самого меньшего из сопротивлений и . Следовательно, чтобы полностью использовать избирательные свойства контура (заданные полосой ), необходимо на входе использовать источник сигнала с большим выходным сопротивлением , и подключать нагрузку с .

При анализе схем с параллельными контурами можно источник тока с большим заменить источником ЭДС с большим (рис. 16).

Рис. 16

При характеристики такой схемы будут определяться собственными параметрами контура. В этом случае в контур втекает ток . На резонансной частоте

,

Откуда коэффициент передачи на резонансной частоте по напряжению

.

Поведение же АЧХ и ФЧХ этого коэффициента передачи будет аналогично рассмотренному выше поведению АЧХ и ФЧХ сопротивления параллельного контура с добротностью

 .

Сопротивления и можно с помощью формулы (9) пересчитать в последовательные, которые называют вносимыми сопротивлениями:

; ,

откуда ясен смысл уменьшения добротности при и .

При невозможности выполнить эти требования используют так называемое частичное (неполное) включение контура.

Разновидности схем таких контуров приведены на рис.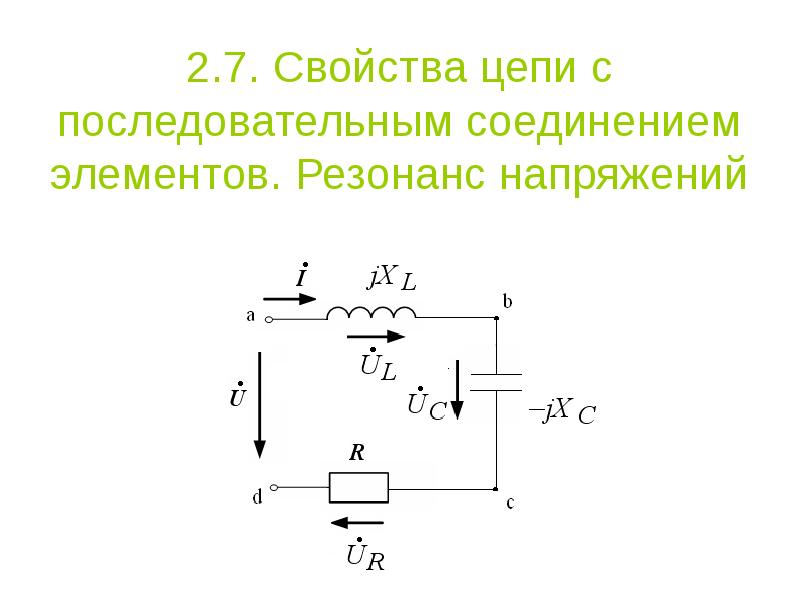 17.

Рис. 17

Схема рис.17,а называется параллельным контуром второго вида, а рис.17,б – параллельным контуром третьего вида. Полное включение, рассмотренное выше, образует контур первого вида.

Коэффициентом включения называют отношение индуктивности (или емкости), к которым подключен источник (или нагрузка), к полной индуктивности (или емкости) контура. Для схемы рис.17,а ; для схемы рис.17,б .

Резонансное сопротивление контуров с неполным включением определяется как . Вносимые сопротивления также уменьшаются в p ² раз. Поэтому полная добротность системы уменьшается меньше, чем при полном включении, а при очень малых практически не уменьшается (правда ценой значительного уменьшения резонансного сопротивления, и, следовательно, выходного напряжения).

На схеме рис.17,в показано подключение источника и нагрузки к контуру так, чтобы ослабить их шунтирующее действие на контур.

Неполное влючение контура используется также для такого согласования с источником и нагрузкой, при котором в нагрузку передается максимальная мощность. Это возможно при выполнении равенств . При этом добротность контура уменьшается в два раза, а полоса вдвое увеличивается.

Одним из недостатков использования схем с неполным включением является дополнительный электротехнический резонанс напряжений, возникающий в ветви, содержащей емкость и индуктивность.

Эти последовательные резонансы происходят на частотах, отличных от резонансной частоты всего контура. Так для схемы рис.17,а , а последовательный резонанс возникает на частоте ; для схемы рис.17,б , а .

Подбирая коэффициенты включения, можно менять частоты последовательных резонансов так, чтобы они не влияли на прохождение сигналов.

[PDF] МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Download МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ. ..

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет)» (МАИ)

ФИЛИАЛ «ВЗЛЕТ» кафедра РЭВС ЛА Нестеров С. В.

ИССЛЕДОВАНИЕ ИЗБИРАТЕЛЬНЫХ СВОЙСТВ КОЛЕБАТЕЛЬНЫХ КОНТУРОВ Методическое указание к лабораторным работам по дисциплине

«ОСНОВЫ ТЕОРИИ ЦЕПЕЙ»

Ахтубинск — 2015

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ Исследование избирательных свойств колебательных контуров производится на установке, блок-схема которой указана на рис 0.1.

Рис.0.1 Блок-схема лабораторной установки. Лабораторная установка состоит из задающего генератора (ГНЧ Г3112), макета, милливольтметра (МВ В3-38В), милливольтметра (МВ В338Б) и магазина сопротивлений (МС). Задающий генератор (ГНЧ Г3-112) является источником синусоидального напряжения или напряжения прямоугольной формы в зависимости от положения ключа на макете. С выхода генератора сигнал заданной амплитуды и частоты подается на вход макета. Лабораторный макет содержит магазины индуктивностей, ёмкостей и резисторов. Для расширения возможностей к макету подключается внешний магазин сопротивлений (МС). Макет предназначен для сборки исследуемой электрической цепи. Сборка цепи, состоящей из сопротивлений Z1, Z2, Z3, R, производится с помощью переключателей. Милливольтметр (МВ В3-38В) предназначен для измерения действующих напряжений на входе и на пассивных элементах исследуемой цепи. Подключение вольтметра к тому или иному участку цепи производится с помощью переключателей, установленных на макете. Милливольтметр (МВ В3-38Б) подключён к задающему генератору (ГНЧ Г3-112) и предназначен для контроля заданного уровня входного напряжения.

1. ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА. Цель работы – исследовать амплитудно-частотные и фазо-частотные характеристики последовательного контура (рис 1.1).

Рис.1.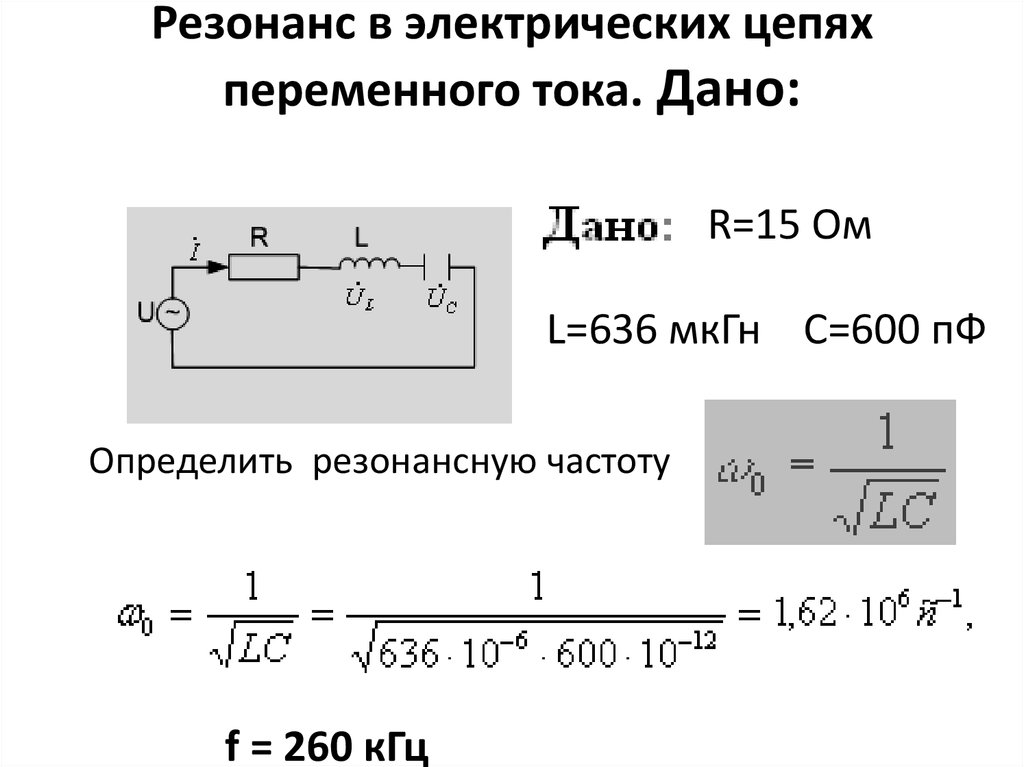 1 Исследуемая схема с последовательным колебательным контуром.

Основные понятия, расчётные формулы и определения Амплитудно-частотной характеристикой (АЧХ) цепи называется частотная зависимость отношения амплитуды гармонического выходного сигнала к амплитуде гармонического входного сигнала. Фазочастотной характеристикой (ФЧХ) называется частотная зависимость разности начальных фаз гармонических выходного и входного сигналов. В электрических цепях, содержащих индуктивные и емкостные элементы, амплитуда тока может резко изменяться, когда частота внешнего воздействия достигает некоторого определённого значения. Это явление называется амплитудным резонансом. В теории цепей под резонансом понимают фазовый резонанс – такой режим работы электрической цепи, при котором реактивная составляющая выходного сигнала равна нулю. Это получается, когда реактивные оставляющие входного сопротивления и проводимости равны нулю. Простейшей цепью, в которой наблюдается явление резонанса, является одиночный колебательный контур, представляющий собой цепь, состоящую из конденсатора С и индуктивной катушки L, соединённых последовательно или параллельно. Последовательный колебательный контур (рис.1.1) представляет собой цепь, содержащую индуктивную катушку L с потерями r, конденсатор C и резистор R, соединённые последовательно с источником сигнала.

При сопротивлении катушки r, много меньшем сопротивления резистора R, схема имеет вид, показанный ниже (рис.1.2).

Рис.1.2 Схема с последовательным колебательным контуром при r

6. Резонансные фильтры | 8. Фильтры | Часть2

6. Резонансные фильтры

Резонансные фильтры

До сих пор мы с вами рассматривали фильтры состоящие либо из конденсаторов, либо из катушек индуктивности, но не из обоих этих компонентов одновременно.  Вы уже знаете, что комбинации L и C, как правило, резонируют, и это свойство можно использовать при проектировании полосовых и полосно-заграждающих фильтрующих схем.

Последовательные LC цепи дают минимальный импеданс в резонансе, в то время как параллельные LC цепи дают максимальный импеданс на резонансной частоте.  Учитывая это, у нас есть две основных стратегии для проектирования либо полосовых, либо полосно-заграждающих (режекторных) фильтров.

Существуют две основные схемы полосовых резонансных фильтров: последовательная LC схема (пропускающая сигнал) и параллельная LC схема (закорачивающая сигнал). Давайте смоделируем и противопоставим эти две схемы:

 

Последовательный полосовой резонансный LC фильтр

Последовательные LC компоненты пропускают в нагрузку сигнал на резонансной частоте, и блокируют сигналы других частот.

 

series resonant bandpass filter
v1 1 0 ac 1 sin 
l1 1 2 1
c1 2 3 1u       
rload 3 0 1k    
.ac lin 20 50 250       
.plot ac v(3)   
.end    

 

Последовательный полосовой резонансный фильтр: пик напряжения находится на резонансной частоте 159.15 Гц. 

Обратите внимание на пару моментов: в полосе пропускания (в диапазоне частот вблизи пика напряжения нагрузки) этого фильтра практически нет затухания сигнала (в отличие от полосовых фильтров, изготовленных только из конденсаторов или катушек индуктивности). Кроме того, поскольку данный фильтр работает по принципу последовательного LC резонанса, резонансная частота которого не зависит от сопротивления цепи, величина нагрузочного резистора не искажает пика частоты. Однако, различные значения нагрузочного резистора будут изменять «крутизну» графика Боде («селективность» фильтра).

Другая схема полосового резонансного фильтра включает в себя колебательный контур (параллельное соединение LC). Она закорачивает сигналы слишком высокой или слишком низкой частоты, и не пропускает их в нагрузку:

 

Параллельный полосовой резонансный фильтр 

 

На резонансной частоте колебательный контур будет иметь высокий импеданс, позволяющий сигналу проходить на нагрузку с минимальным затуханием. На частоте, выше или ниже резонансной, колебательный контур будет обладать низким импедансом, который будет закорачивать большую часть сигнала через последовательный резистор R₁: 

 

parallel resonant bandpass filter            
v1 1 0 ac 1 sin 
r1 1 2 500      
l1 2 0 100m     
c1 2 0 10u      
rload 2 0 1k    
.ac lin 20 50 250       
.plot ac v(2)   
.end    

 

Параллельный полосовой резонансный фильтр: пик напряжения находится на резонансной частоте 159.15 Гц.

 

Аналогично фильтрам верхних и нижних частот, в которых для ослабления нежелательных частот применяются последовательное сопротивление и параллельный «закорачивающий» компонент, данная резонирующая схема не способна доставить полное напряжение источника на нагрузку. При соединении нагрузочного сопротивления с выводами фильтра, на его последовательном сопротивлении всегда будет падать некоторое количество напряжения.

Стоит отметить, что эта схема полосового фильтра очень часто применяется в аналоговых радиоприемниках, она служит для выбора конкретной радиочастоты из множества частот, поступающих от антенны. В большинстве аналоговых радиоприемников вращающийся диск выбора станции приводит в действие переменный конденсатор, расположенный внутри корпуса.

 

При помощи переменного конденсатора радиоприемник настраивается на одну из вещательных станций 

Переменный конденсатор и катушка индуктивности с воздушным сердечником, показанные на фотографии простого приемника, представляют собой основные элементы фильтра, который выделяет сигнал одной радиостанции из множества других.

Последовательные и параллельные резонансные LC контуры можно использовать как для выделения нужной нам частоты из определенного диапазона, так и для блокировки ненужной частоты диапазона, создавая тем самым полосно-заграждающий (режекторный) фильтр. Для реализации вышесказанного существуют две основные стратегии: использование либо последовательного, либо параллельного резонанса. Сначала мы с вами рассмотрим последовательный резонанс:

 

Последовательный резонансный режекторный фильтр

 

Когда последовательный LC контур достигнет резонанса, его очень низкий импеданс закоротит сигнал через резистор R₁ (предотвращая тем самым прохождение этого сигнала к нагрузке).

 

series resonant bandstop filter    
v1 1 0 ac 1 sin 
r1 1 2 500      
l1 2 3 100m     
c1 3 0 10u      
rload 2 0 1k    
.ac lin 20 70 230       
.plot ac v(2)   
.end    

 

 

Последовательный резонансный режекторный фильтр: Частота режекции (заграждения) = резонансной частоте LC (159,15 Гц).

 

Далее мы рассмотрим параллельный резонансный режекторный фильтр:

 

Параллельный резонансный режекторный фильтр

 

Параллельный LC контур на резонансной частоте обладает очень высоким импедансом, который отсекает сигнал от нагрузки. На всех остальных частотах сигнал свободно проходит к нагрузке.

 

parallel resonant bandstop filter  
v1 1 0 ac 1 sin 
l1 1 2 100m     
c1 1 2 10u      
rload 2 0 1k    
.ac lin 20 100 200      
.plot ac v(2)   
.end    

 

Параллельный резонансный режекторный фильтр: Частота режекции (заграждения) = резонансной частоте LC (159,15 Гц)

 

Обратите внимание, что отсутствие последовательного резистора  делает затухания «нужных» сигналов минимальными. С дугой стороны, амплитуда сигнала на частоте режекции очень мала. Можно сказать, что это очень «избирательный» фильтр.

Во всех этих конструкциях резонансных фильтров селективность в значительной степени зависит от «чистоты» используемой индуктивности и емкости. При существовании каких-либо паразитных сопротивлений (особенно это касается катушек индуктивности), уменьшается способность фильтра тонко различать частоты, а также возможно возникновение антирезонансных эффектов, которые будут искажать частоту режекции.

А теперь, небольшое замечание для тех, у кого в данный момент возникли вопросы по проектированию фильтров нижних и верхних частот. После анализа стандартных конструкций RC и LR фильтров нижних и верхних частот, у вас может возникнуть идея, что более эффективные фильтры  можно получить путем объединения емкостных и индуктивных элементов друг с другом:

 

Индуктивно-емкостной фильтр нижних частот

 

Катушки индуктивности в этой схеме должны блокировать любые высокие частоты, а конденсатор должен высокие частоты закорачивать. Их совместная работа должна пропускать к нагрузке только низкие частоты.

На первый взгляд такая стратегия кажется очень хорошей, она позволяет избавиться от последовательного сопротивления. Однако, проницательный читатель поймет, что что любая комбинация конденсаторов и катушек индуктивности в цепи может вызвать резонансные эффекты, происходящие на определенной частоте. Резонанс, как мы уже видели раньше, может вызывать странные вещи. Давайте проведем SPICE анализ вышеприведенной схемы, и посмотрим, что произойдет в широком диапазоне частот:

 

lc lowpass filter  
v1 1 0 ac 1 sin 
l1 1 2 100m     
c1 2 0 1u       
l2 2 3 100m     
rload 3 0 1k    
.ac lin 20 100 1k       
.plot ac v(3)   
.end    

 

Неожиданная реакция L-C фильтра нижних частот.

 

То, что должно было быть фильтром нижних частот, оказалось полосовым фильтром с пиком в районе 526 Гц! Емкость и индуктивность данной фильтрующей схемы достигают резонанса именно на этой частоте, создавая большое падение напряжения на конденсаторе С₁ (это напряжение передается на нагрузку независимо от ослабляющего влияния L₂). Выходное напряжение на нагрузке в данный момент фактически превышает входное напряжение (напряжение источника)! Немного поразмыслив можно прийти к выводу, что если L₁ и С₂ находятся в резонансе, они ложатся тяжелым грузом (благодаря очень низкому импедансу) на источник переменного напряжения. Давайте проведем тот же самый SPICE анализ, только отобразим на графике напряжение С₁ — vm(2), ток источника — I(v1) и напряжение на нагрузке — vm(3):

 

Ток увеличивается при нежелательном резонансе L-C фильтра нижних частот. 

 

Мы видим, что напряжение на С₁ и ток источника максимальны на той же частоте, на которой напряжение нагрузки тоже максимально. Наши ожидания, что данный фильтр будет исполнять функцию простого фильтра нижних частот, не оправдались.

Проблема состоит в том, что L-C фильтр имеет входной и выходной импедансы, которые должны быть согласованы. Импеданс источника напряжения должен соответствовать входному импедансу фильтра, а выходной импеданс фильтра должен быть согласован с «R_{нагрузки}«. Входной и выходной импедансы рассчитываются по следующей формуле:

 

           Z = (L/C)1/2

 

Подставив значения компонентов из вышерассмотренной схемы в данную формулу, мы можем найти импеданс фильтра, и соответствующие ему R_г и R_{нагрузки}:

 

                Для    L= 100 мГн,   C= 1мкФ
           Z = (L/C)1/2=((100 мГн)/(1 мкФ))1/2 = 316 Ом

 

На нижеприведенной схеме мы добавили R_г = 316 Ом к генератору (источнику напряжения), и изменили R_{нагрузки} с 1000 Ом до 316 Ом. Обратите внимание: если нам нужно управлять нагрузкой 1000 Ом, то отношение L / C придется скорректировать так, чтобы оно соответствовало этому сопротивлению.

 

Эта схема соответствует L-C фильтру нижних частот

 

LC matched lowpass filter  
V1 1 0 ac 1 SIN
Rg 1 4 316
L1 4 2 100m
C1 2 0 1.0u
L2 2 3 100m
Rload 3 0 316
.ac lin 20 100 1k       
.plot ac v(3)   
.end    

 

На следующем рисунке показана амплитудно-частотная характеристика L-C фильтра нижних частот, когда импедансы источника и нагрузки соответствуют входным и выходным импедансам фильтра.

 

 

Основным недостатком рассмотренного нами L-C фильтра нижних частот является то, что при изменении величины нагрузки фильтра произойдет значительное изменение напряжения. Особенно этот недостаток нежелателен для L-C фильтров источников питания.

Данный недостаток может быть смягчен при помощи дросселя насыщения. Принцип действия дросселя насыщения основан на изменении магнитной проницаемости ферромагнитных материалов при подмагничивании сердечника постоянным током. При насыщении ферромагнитных материалов увеличивается их магнитное сопро­тивление. Это приводит к уменьшению величины магнитного по­тока, создаваемого ампер-витками переменного тока, а следова­тельно, и к уменьшению э. д. с. самоиндукции, наводимой в этих обмотках. Таким образом, индуктивное сопротивление рабочих обмоток дросселя насыщения при увеличении тока подмагничивания уменьшается. Уменьшение тока в обмотке подмагничивания приводит к увеличению индуктивного сопротивления рабо­чих обмоток.

Несмотря на паразитный резонанс, фильтры нижних частот, составленные из конденсаторов и катушек индуктивности, часто используются на выходе AC/DC источников питания. Они отфильтровывают нежелательное переменное напряжение из постоянного. Возникает резонный вопрос, почему именно эти фильтры находят широкое применение в источниках питания?

Ответ заключается в выборе размеров компонентов фильтра и частот, возникающих в AC/DC преобразователе  (выпрямителе). Роль фильтра в преобразователе напряжения довольно проста, он отделяет постоянное напряжение от небольшого количества относительно высокочастотного переменного напряжения. Катушки индуктивности и конденсаторы фильтра имеют довольно большие значения (несколько Генри для катушек индуктивности и тысячи мкФ для конденсаторов), что делает резонансную частоту фильтра очень, очень низкой. Постоянное напряжение, конечно-же, имеет нулевую частоту, а значит, оно не может заставить LC-цепь резонировать. Пульсирующее напряжение, с другой стороны, является несинусоидальным переменным напряжением, состоящим из основной частоты (которая по крайней мере в два раза превышает частоту исходного переменного напряжения) и множественных гармоник. Для преобразователей напряжения, работающих от бытовой сети переменного тока частотой 50 Гц, самая низкая частота, которую когда-либо будет видеть фильтр, составит 100 Гц, и эта частота намного больше резонирующей точки фильтра. Таким образом, возникновение паразитного резонанса в таком фильтре полностью исключено.

Следующий SPICE анализ рассчитывает выходное напряжение (переменное и постоянное) для рассмотренного выше фильтра. Грубое приближение смешанной частоты на выходе AC/DC преобразователя обеспечивает последовательное соединение источников постоянного и переменного (120 Гц) напряжения.

 

 

ac/dc power supply filter  
v1 1 0 ac 1 sin 
v2 2 1 dc       
l1 2 3 3
c1 3 0 9500u    
l2 3 4 2
rload 4 0 1k    
.dc v2 12 12 1  
.ac lin 1 120 120       
.print dc v(4)  
.print ac v(4)  
.end    

v2            v(4)            
1.200E+01     1.200E+01   DC voltage at load = 12 volts
 
freq          v(4)            
1.200E+02     3.412E-05   AC voltage at load = 34.12 microvolts

 

Как видно из анализа, на нагрузку приходят все 12 вольт постоянного напряжения и только 34,12 микровольт из 1 вольта переменного напряжения. Таким образом, данная конструкция фильтра очень эффективна для применения в источниках питания.

Все, что мы с вами рассмотрели касаемо фильтров нижних частот (использующих конденсаторы и катушки индуктивности), полностью применимо и к фильтрам верхних частот.

Что такое последовательный резонанс? — его эффекты

В последовательной цепи RLC, когда ток схемы находится в фазе с приложенным напряжением, говорят, что цепь находится в последовательном резонансе . Условие резонанса возникает в цепи последовательного RLC, когда индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.

X _L = X _C или (X _L — X _C = 0)

Последовательный резонансный контур может потреблять большой ток и мощность от сети; ее также называют приемной схемой .Цепь последовательного резонанса RLC показана на рисунке ниже:

В резонансе: X _L — X _C = 0 или X _L = X _C

Импеданс будет:

Где Zr — резонансное сопротивление цепи.

Подставив значение X _L — X _C = 0 в уравнение (1), получим:

Zr =

RR

Ток I = V / Zr = V / R

Так как при резонансе противодействием току является только сопротивление (R) цепи.В этом состоянии схема потребляет максимальный ток.

См. Также : Что такое резонансная частота?

Эффекты последовательного резонанса

Следующие эффекты условия последовательного резонанса приведены ниже:

• В условиях резонанса XL = XC полное сопротивление цепи минимально и сводится к сопротивлению цепи. т.е. Zr = R
• В условиях резонанса, поскольку полное сопротивление цепи минимально, ток в цепи максимален.т.е. Ir = V / Zr = V / R
• Поскольку значение резонансного тока Ir является максимальным, следовательно, мощность, потребляемая цепью, также максимальна. т.е. Pr = I ² Rr
• В условиях резонанса ток, потребляемый цепью, очень велик, или мы можем сказать, что ток потребляется максимальным. Следовательно, падение напряжения на индуктивности L ie (V _L = IX _L = I x 2πfrL) и емкость C ie (V _C = IX _C = I x I / 2πfrC) также будут очень большой.

В энергосистеме, в условиях резонанса, чрезмерное напряжение, создаваемое на индуктивном и емкостном компонентах цепи, таких как автоматический выключатель, реакторы и т. Д., Может вызвать повреждение. Таким образом, в энергосистеме избегается состояние последовательного резонанса.

Однако в некоторых электронных устройствах, таких как антенная цепь радио и ТВ-приемника, схема настройки и т. Д. Условие последовательного резонанса используется для увеличения напряжения сигнала и тока на желаемой частоте (fr).

Резонанс серии

• Опишите резонансные цепи серии LCR.
• • Опишите условия последовательного резонанса.
• • Выполните расчеты последовательных цепей LCR, включая реактивное сопротивление, импеданс, напряжения и ток в цепи.

Резонанс серии

возникает, когда реактивные сопротивления равны.

Индуктивное реактивное сопротивление (X _L ) с точки зрения частоты и индуктивности определяется по формуле:

, а емкостное реактивное сопротивление (X _C ) определяется выражением:

Рис. 9.2.1. Электрические свойства последовательной цепи LCR при резонансе.

Индуктивное реактивное сопротивление прямо пропорционально частоте, и его график в зависимости от частоты () представляет собой прямую линию.

Емкостное реактивное сопротивление обратно пропорционально частоте, и его график, построенный против, представляет собой кривую.Эти две величины показаны вместе с R в зависимости от ƒ на рис. 9.2.1. Из этой диаграммы видно, что там, где пересекаются X _C и X _L , они равны, и поэтому график (X _L — X _C ) в этой точке на оси частот должен быть равен нулю.

Электрические свойства последовательной резонансной цепи LCR (рис. 9.2.1)

На рис. 9.2.1a показана последовательная схема LCR, а на рис. 9.2.1b показано, что происходит с реактивными сопротивлениями (X _C и X _L ), сопротивлением (R) и импедансом (Z) в качестве источника питания (V _S ). ) изменяется по частоте от 0 Гц и выше.Сначала цепь ведет себя как конденсатор, полное сопротивление цепи (Z) падает по кривой, очень похожей на X _L — X _C .

На рис. 9.2.1c показана взаимосвязь между напряжениями отдельных компонентов, импедансом цепи (Z) и током питания (I _S ) (который является общим для всех последовательных компонентов).

На определенной частоте ƒ _r можно увидеть, что X _L — X _C упало до нуля, и на линии питания осталось только сопротивление цепи R.Следовательно, ток, протекающий по цепи в этой точке, будет максимальным. Теперь V _C и V _L равны по величине и противоположны по фазе, поэтому полностью компенсируют друг друга. Реактивное сопротивление фактически равно нулю, а цепь полностью резистивна, с Z, равным R. минимум.

По мере того, как частота увеличивается выше этой резонансной частоты ( _r ), импеданс увеличивается, и, поскольку X _L теперь больше из двух реактивных сопротивлений, кривая импеданса начинает следовать за возрастающим значением, больше похожим на линейный график X _Л .

На частотах ниже резонанса схема ведет себя как конденсатор, при резонансе как резистор, а выше ƒ _r схема ведет себя все больше и больше как индуктор, и график X _L — X _C вскоре становится почти прямая линия.

Такое поведение последовательной цепи LCR позволяет сформулировать ряд полезных фактов о последовательной цепи, которые относятся к ее резонансной частоте ƒ _r .

6 Что нужно знать о схемах серии LCR.

• 1. ПРИ РЕЗОНАНСЕ ( _r ) V _C равно, но в противофазе с V _L
• 2 .; ПРИ РЕЗОНАНСЕ ( _r ) Импеданс (Z) минимален и равен СОПРОТИВЛЕНИЮ (R)
• 3. ПРИ РЕЗОНАНСЕ (ƒ _r ) Ток цепи (I _S ) максимально.
• 4. ПРИ РЕЗОНАНСЕ ( _r ) Схема полностью резистивная.
• 5. НИЖЕ РЕЗОНАНСА ( _r ) Схема емкостная.
• 6. ВЫШЕ РЕЗОНАНСА (ƒ _r ) Цепь индуктивная.

Две формулы для последовательного резонанса.

Тот факт, что резонанс возникает, когда X _L = X _C , позволяет построить формулу, которая позволяет рассчитать резонансную частоту (ƒ _r ) контура только по значениям L и C.Наиболее часто используемая в электронике формула для резонансной частоты последовательного контура LCR:

Рис. 9.2.2 Вывод формулы резонанса

Обратите внимание, что в этой формуле нет ссылки на сопротивление (R). Хотя любая цепь, содержащая L, должна иметь хотя бы некоторое сопротивление, наличие небольшого сопротивления в цепи не сильно влияет на частоту , на которой цепь резонирует. Резонансные контуры, разработанные для высоких частот, подвержены влиянию паразитных магнитных полей, индуктивности и емкости в окружающей их среде, поэтому большинство высокочастотных LC-резонансных контуров будут иметь как экранирование, чтобы максимально изолировать их от внешних воздействий, так и регулировку в пределах небольшого диапазон частот, чтобы их можно было точно отрегулировать после сборки в цепи.

Однако, хотя эта формула широко используется на радиочастотах, она часто недостаточно точна на низких частотах, где используются большие индукторы со значительным внутренним сопротивлением. В таком случае необходима более сложная формула, учитывающая также сопротивление. Приведенную ниже формулу можно использовать для расчета низких частот (большое внутреннее сопротивление).

Необходимость тщательной регулировки после сборки схемы часто является решающим фактором для прекращения использования чистых LC-схем во многих приложениях.Во многих случаях они были заменены твердотельными керамическими фильтрами и резонансными кристаллами, не нуждающимися в настройке. Однако иногда может возникнуть проблема с множеством резонансных частот на гармониках (кратных) требуемой частоты с твердотельными фильтрами. Затем может быть включена одна регулируемая настроенная LC-схема, чтобы решить эту проблему.

Расчеты цепи серии

.

В последовательной цепи LCR, особенно при резонансе, происходит много всего, и, следовательно, вычисления часто являются многоступенчатыми.Формулы для многих общих вычислений были описаны в предыдущих модулях этой серии, разница теперь заключается в том, что задача получения соответствующей информации о состоянии цепи зависит от выбора соответствующих формул и их использования в подходящей последовательности.

Например, в приведенной ниже задаче элементы в значениях, показанных красным, являются обязательными, но обратите внимание, что V _C и V _L не могут быть рассчитаны в первую очередь, как значение для _r (и еще одного формула) требуется для расчета реактивного сопротивления.Однако иногда задача упрощается, если вспомнить 6 полезных фактов о последовательном резонансе из серой панели выше. В примере 9.2.2 ниже нет необходимости рассчитывать V _L , потому что при резонансе X _C и X _L равны, и поэтому на них будут развиваться равные напряжения. Обратите внимание, однако, что V _L не то же самое, что полное напряжение, измеренное на L. Напряжение на внутреннем сопротивлении (от 90 ° до V _L ) должно быть включено, и из-за разницы фаз между V _L и напряжение внутреннего сопротивления (VR _L ), общее измеряемое напряжение индуктора V _{L TOT} будет векторной суммой V _L и VR _L

Пример 9.2.2 Расчеты последовательной цепи LCR.

Разработайте каждую из этих формул (карандашом, бумагой и калькулятором), не забывая сначала вычислить части формулы, заключенные в скобки, а затем проверьте свои ответы в Модуле 9.3.

Такая работа во время обучения — хороший способ понять, как работают математические вычисления. В сети, конечно, довольно много калькуляторов LCR, но возьмите совет: ПЕРВЫЙ ПОРАБОТАЙТЕ ЭТО, а затем попробуйте веб-калькулятор (или несколько, поскольку некоторые умнее других), чтобы проверить свой ответ.

Идеальный последовательно-резонансный контур

ИДЕАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНАЯ ЦЕПЬ

Идеальный последовательно-резонансный контур не содержит сопротивления; он состоит только из индуктивность и емкость последовательно друг с другом и с источником напряжения. В этом уважаю, он имеет те же характеристики, что и у изученных вами последовательных цепей ранее. Помните, что ток одинаков во всех частях последовательной цепи, потому что есть только один путь для тока.

Каждая LC-цепь по-разному реагирует на разные входные частоты. В следующих параграфах, мы проанализируем, что происходит внутри цепи последовательного LC, когда применяются частоты в резонансе, ниже резонанса и выше резонанса. L и C значения в цепи — те, которые используются в только что изученной задаче для резонансной частоты. Применяемые частоты — это три входа из рисунка 1-6. Отметим, что резонансный частота каждого из этих компонентов составляет 205 кГц, как указано в задаче.

Рисунок 1-6. — Выход резонансного контура.

Как идеальная цепь последовательного LC откликается на резонансную частоту (205 кГц)

Примечание. Вам даны значения X _L , X _C и f _r , но вы можете применить формулы, чтобы вычислить их. Приведенные значения округлены, чтобы проще анализировать схему.

Во-первых, обратите внимание, что X _L и X _C равны. Это показывает, что схема резонансна приложенной частоте 205 кГц. X _L и X _C являются противоположный эффект; поэтому они вычитаются до нуля. (2580 Ом — 2580 Ом = ноль). резонанс, тогда X = ноль. В нашей теоретически идеальной схеме с нулевым сопротивлением и нулевое реактивное сопротивление, полное сопротивление току (Z) также должно быть нулевым.

Теперь применим закон Ома для переменного тока. схем:

Пусть вас не смущает такое высокое значение тока. Наша идеальная, но невозможная схема не имеет противодействия току. Следовательно, ток будет чрезвычайно высоким. В здесь важно то, что ПРИ РЕЗОНАНСЕ импеданс ОЧЕНЬ НИЗКИЙ, и в результате ток будет сравнительно ВЫСОКИЙ.

Если мы применим закон Ома к индивидуальным реактивным сопротивлениям, мы можем вычислить относительные значения напряжение на каждом реактивном сопротивлении.

Это реактивные напряжения, которые вы изучили ранее. Напряжение на каждом реактивное сопротивление будет сравнительно высоким. Сравнительно высокий ток, умноженный на 2580 Ом, дает высокое напряжение. В любой момент это напряжение будет иметь противоположную полярность, потому что реактивные сопротивления противоположны по действию. E _L + E _C = ноль вольт

ОТДЕЛЬНЫЕ НАПРЯЖЕНИЯ МОГУТ ДОСТИГНУТЬ ДОЛГО ВЫСОКИХ ЗНАЧЕНИЙ.ХОТЯ МАЛЕНЬКАЯ МОЩНОСТЬ ПРИ НАЛИЧИИ НАПРЯЖЕНИЕ НАПРЯЖЕНИЕ РЕАЛЬНО, И ПРИ РАБОТЕ С ЭТИМ НЕОБХОДИМО ПРИНИМАТЬ БЕЗОПАСНОСТЬ.

Подведем итоги наших выводов. В последовательном LC-контуре с резонансной частотой приложено напряжение, существуют следующие условия:

• X _L и X _C равны и вычитаются до нуля.
• Результирующее реактивное сопротивление равно нулю Ом.
• Импеданс (Z) снижается до МИНИМАЛЬНОГО значения.
• При минимальном Z ток МАКСИМАЛЬНЫЙ для данного напряжения.
• Максимальный ток вызывает максимальное падение напряжения на индивидууме. реактивные сопротивления.

Все вышеперечисленное последовательно следует из того факта, что X _L = X _C при резонансная частота.

Как идеальная цепь последовательного LC реагирует на частоту ниже резонанса (100 кГц)

Дано:

Во-первых, обратите внимание, что X _L и X _C больше не равны.X _C — это больше, чем было в резонансе; X _L меньше. Применяя формулы, вы вы узнали, вы знаете, что более низкая частота дает более высокое емкостное реактивное сопротивление и более низкое индуктивное сопротивление. Реактивные сопротивления вычитаются, но не отменяются (X _L — X _C = 1260 — 5300 = 4040 Ом (емкостный)). При входной частоте 100 кГц схема (все еще резонирующий до 205 кГц) имеет чистое реактивное сопротивление 4040 Ом. В нашем теоретически совершенном В цепи полное сопротивление (Z) равно X, или 4040 Ом.

Как и раньше, применим закон Ома к новым условиям.

Падения напряжения на реактивных сопротивлениях следующие:

Таким образом, в цепи последовательного LC с напряжением источника ниже резонансного частота (100 кГц в примере), результирующее реактивное сопротивление (X) и, следовательно, полное сопротивление, выше, чем при резонансе. Кроме того, ток ниже, и напряжение падает на реактивные сопротивления ниже.Все вышеперечисленное следует последовательно в связи с тем, что X _C больше X _L на любой частоте ниже резонансной.

Как идеальная цепь последовательного LC откликается на частоту выше резонанса (300 кГц)

Дано:

Опять же, X _L и X _C не равны. На этот раз X _L — это больше, чем X _C .(Если вы не знаете, почему, примените формулы и просмотрите прошлые несколько страниц.) Результирующее реактивное сопротивление составляет 2000 Ом (X _L — X _C = 3770-1770 = 2000 Ом.) Следовательно, результирующее реактивное сопротивление (X) или полное сопротивление нашего идеальная схема на 300 кГц, составляет 2000 Ом.

Применяя закон Ома, как и раньше:

Таким образом, в цепи последовательного LC с напряжением источника, которое выше резонансного частота (300 кГц в этом примере), импеданс выше, чем при резонансе, ток равен ниже, и падение напряжения на реактивных сопротивлениях меньше.Все вышеперечисленное следует в последовательность из того, что X _L больше, чем X _C на любой частоте выше резонансной частоты.

Сводка отклика идеальной цепи последовательного LC на частоты выше, ниже и в Resonance

Идеальный последовательно-резонансный контур имеет нулевое сопротивление. Импеданс увеличивается для частоты выше и ниже резонансной частоты.Импедансная характеристика получается идеальный последовательно-резонансный контур, потому что результирующее реактивное сопротивление равно нулю Ом при резонанс и ТОЛЬКО при резонансе. Все остальные частоты обеспечивают результирующее реактивное сопротивление. больше нуля.

Нулевое сопротивление при резонансе допускает максимальный ток. Все остальные частоты имеют пониженный ток из-за повышенного импеданса. Напряжение на реактивном сопротивлении равно наибольший при резонансе, потому что падение напряжения прямо пропорционально току.Все различение частот связано с тем, что X _L и X _C полностью противодействовать ТОЛЬКО на резонансной частоте.

Чем типичная схема последовательного LC отличается от идеальной. в этой серии сопротивление всегда присутствует в практических электрических цепях; это невозможно устранить. Таким образом, типичная схема последовательного LC имеет R, а также L и C.

Если наша совершенная (идеальная) схема имеет нулевое сопротивление, а типичная схема имеет «какое-то» сопротивление, то схема с очень маленьким сопротивлением ближе к быть совершенным, чем тот, который имеет большое сопротивление.Перечислим, что происходит в последовательно-резонансный контур из-за наличия сопротивления. Для вас это не новость — просто обзор того, что вы узнали ранее.

В последовательно-резонансном контуре, состоящем в основном из L и C, но содержащего «some» R, верны следующие утверждения:

X _L , X _C и компоненты R присутствуют и могут отображаться на векторная диаграмма, каждая под прямым углом к ​​вектору сопротивления (базовая линия).При резонансе результирующее реактивное сопротивление равно нулю Ом. Таким образом, в резонансе полное сопротивление контура равно только сопротивление (R). Импеданс цепи никогда не может быть меньше R, потому что исходное сопротивление всегда будет присутствовать в цепи. В резонансе практичный Цепь последовательного RLC ВСЕГДА имеет МИНИМАЛЬНОЕ сопротивление. Фактическое значение импеданса составляет сопротивление, присутствующее в цепи (Z = R).

Теперь, если дизайнеры сделают все возможное (а они это сделают), чтобы сохранить значение сопротивления в практической цепи последовательного RLC LOW, тогда мы все еще можем получить довольно высокий ток при резонанс.Сила тока НЕ ​​«бесконечно» высока, как в нашей идеальной схеме, но равна все еще выше, чем на любой другой частоте. Кривая и векторные отношения для Практическая схема представлена ​​на рис. 1-7.

Рисунок 1-7. — Кривые импеданса и тока в резонансном контуре серии RLC.

Обратите внимание, что кривая импеданса не достигает нуля в своей минимальной точке. Векторы выше и ниже резонанса показывают, что фазовый сдвиг контура на этих частотах равен менее 90 градусов из-за сопротивления.

Ширина кривой по горизонтали является мерой того, насколько хорошо схема будет выбирать (различать) одну желаемую частоту. Ширина называется BANDWIDTH, а способность различение частот известно как ИЗБИРАТЕЛЬНОСТЬ. Обе эти характеристики подвержены влиянию сопротивления. Более низкое сопротивление позволяет сужать полосу пропускания, что то же самое как говорится, что схема имеет лучшую селективность. Следовательно, сопротивление — это нежелательная величина. это невозможно исключить, но разработчики схем могут свести к минимуму.

Подробнее о полосе пропускания, селективности и измерении влияния сопротивления в резонансных схемы будут следовать обсуждению параллельного резонанса.

Q.3 Сформулируйте формулу для резонансной частоты.
Q.4 Если значения индуктивности и конденсатора увеличиваются, что происходит с резонансным частота?
Q.5 В «идеальном» резонансном контуре, какова взаимосвязь между импедансом а ток?
Q.6 В цепи последовательного RLC, каково состояние цепи при высоком уровне сопротивление, низкий ток и низкое реактивное напряжение?

Резонанс в цепях серии R-L-C (со схемой)

В этой статье мы обсудим последовательный и параллельный резонанс в цепях R-L-C.

Резонанс определяется инженерными ситуациями, в которых элементы накопления энергии подвергаются форсирующей функции переменной частоты. В частности, резонанс — это термин, используемый для описания установившейся работы схемы или системы на той частоте, для которой результирующий отклик совпадает по временной фазе с функцией источника, несмотря на наличие элементов накопления энергии.

Резонанс не может иметь место, когда присутствует только один тип элемента, накапливающего энергию, e.г., емкостное или пружинное. Должны существовать два типа независимых аккумулирующих энергию элементов, способных обмениваться энергией между собой — например, индуктивность и емкость или масса и пружина. Таким образом, резонанс — это явление, обнаруживаемое в любой системе, включающей два независимых элемента накопления энергии, будь то электрический, механический, пневматический, гидравлический или любой другой.

Если у нас есть цепь переменного тока, имеющая сопротивление R, индуктивность L и емкость C, соединенные последовательно (рис. 6.1), и прикладываем небольшое напряжение V от источника, который может поддерживать величину V постоянной, но может изменять ее частоты, мы обнаруживаем, что величина тока, потребляемого от источника питания, изменяется с изменением частоты источника питания.Будет такое значение частоты, при котором ток будет максимальным. Говорят, что при достижении этого состояния возникает электрический резонанс.

В этой статье мы обсудим это явление (точнее, последовательный резонанс или резонанс напряжения), а также ситуацию, когда на параллельную цепь подается постоянное напряжение переменной частоты. Самая простая параллельная цепь, встречающаяся на практике, представляет собой катушку, имеющую сопротивление R и индуктивность L, включенную параллельно конденсатору C.Резонансное состояние в этом случае называется параллельным резонансом, а иногда и антирезонансным. Последнее название подсказано тем, что при резонансе входной ток в параллельную цепь минимален.

В условиях резонанса такая сеть становится полностью резистивной по своим воздействиям, а напряжение и ток в сети синфазны. Чтобы это произошло, индуктивное реактивное сопротивление и емкостное реактивное сопротивление должны быть уравновешены.

Серия

или резонанс напряжения в цепях R-L-C :

Рассмотрим цепь переменного тока, содержащую сопротивление R, индуктивность L и емкость C, соединенные последовательно, как показано на рис.6.1.

Если для некоторой частоты приложенного напряжения, X _L = X _C по величине, то:

(i) Чистое реактивное сопротивление равно нулю, т.е. X = 0

(ii) Импеданс цепи, Z = R

(iii) Ток, протекающий по цепи, является максимальным и синфазным с приложенным напряжением. Величина тока будет равна

В / Р.

(iv) Падение напряжения на индуктивности равно падению напряжения на емкости и составляет максимум

.

(v) Коэффициент мощности равен единице, а

(vi) Затраченная мощность = VI Вт.

Когда это условие существует, считается, что цепь находится в резонансе, а частота, на которой это происходит, называется резонансной частотой.

Из приведенного выше выражения очевидно, что значение резонансной частоты зависит от параметров двух энергонакопительных элементов.

Фазорные диаграммы для последовательной цепи RLC, показанной на рис. 6.1, на трех разных частотах, т.е. (a) f r (b) f = f _r и (c) f> f _r с L и C сохраняемые постоянными показаны на рис.6.2 (a), (b) и (c) соответственно.

Для любой частоты ниже резонансной частоты f _r индуктивное реактивное сопротивление X _L меньше емкостного реактивного сопротивления X _C , и поэтому схема ведет себя как емкостная цепь. Точно так же для любой частоты выше резонансной индуктивное реактивное сопротивление больше, чем емкостное реактивное сопротивление, и поэтому цепь ведет себя как индуктивная цепь.

Когда частота приложенного напряжения равна резонансной частоте, индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению, падение напряжения на катушке индуктивности по величине равно падению напряжения на конденсаторе, но противоположно по фазе и, следовательно, ток в цепи I находится в фазе с приложенным напряжением i.е., схема ведет себя как резистивная цепь.

Когда цепь находится в резонансе, ток слишком велик и вызывает большое падение напряжения на индуктивности и емкости, которые будут равны по величине, но противоположны по фазе, и каждое из них может быть в несколько раз больше, чем приложенное напряжение. Если бы в цепи не было сопротивления R, такая цепь действовала бы как короткое замыкание на токи с частотой, с которой она резонирует.

Поскольку в этом резонансе напряжение максимальное, он называется резонансом напряжения.Последовательный резонанс также называется цепью акцептора, потому что такая цепь принимает токи на одной конкретной частоте, но отклоняет токи других частот. Такие схемы используются в радиоприемниках.

Графическое представление резонанса в цепи серии R-L-C:

Схема может быть сделана резонансной двумя способами, а именно:

(i) Путем изменения параметров L и C (одного или обоих) при постоянной частоте питания или

(ii) Изменяя частоту подачи / с постоянными параметрами L и C.В нашем исследовании явления последовательного резонанса мы будем поддерживать напряжение, приложенное к цепи, и параметры L и C постоянными, а частоту будем изменять.

Сопротивление цепи R не зависит от частоты питания и, следовательно, остается постоянным. Это было представлено прямой линией, параллельной оси X (или оси частот) на рисунке (рис. 6.3). Индуктивное реактивное сопротивление X _L , равное ωL, увеличивается прямо пропорционально частоте питающей сети и представлено прямой линией, проходящей через начало координат (поскольку X _L считается положительным, поэтому он находится в первом квадранте).Емкостное реактивное сопротивление, равное 1 / ωC, уменьшается обратно пропорционально увеличению частоты и представлено прямоугольной гиперболой, лежащей в четвертом квадранте ниже оси частот (емкостное реактивное сопротивление считается отрицательным).

Чистое реактивное сопротивление — это разница между индуктивным реактивным сопротивлением X _L и емкостным реактивным сопротивлением X _C , и кривая, проведенная между чистым реактивным сопротивлением (X _L ~ X _C ) и частотой будет гиперболой (не прямоугольной). как показано на рис.6.3. Частота, при которой кривая реактивного сопротивления пересекает ось частот, называется резонансной частотой, f _r (или f ₀ ).

Полное сопротивление цепи Z, равное √R ² + (x _L — X _c ) ² , минимально на резонансной частоте f _r .

На частотах ниже резонансной частоты f _r полное сопротивление Z велико и емкостное, поскольку X _C > X _L , а коэффициент мощности является опережающим, а на частотах выше резонансной частоты f _r полное сопротивление Z равно снова большой, но индуктивный, так как X _L > X _C , а коэффициент мощности отстает.Коэффициент мощности имеет максимальное значение, равное единице на резонансной частоте.

Резонансная кривая:

Ток изменяется обратно пропорционально изменению импеданса и, следовательно, он максимален на резонансной частоте, когда импеданс минимален, и уменьшается с изменением частоты по обе стороны от резонансной частоты (поскольку полное сопротивление Z велико), как показано на рис. 6.4.

Кривая, проведенная между током в цепи и частотой приложенного напряжения, называется резонансной кривой, и ее форма зависит от значения сопротивления цепи R, как показано на рисунке. Для меньших значений R резонансная кривая имеет резкий пик, но для больших значений R кривая пологая (рис.6.4).

Избирательность и пропускная способность:

Мы видели, что для цепи с низким сопротивлением резонансная кривая имеет резкий пик, и такая цепь называется резко резонансной или высокоселективной. С другой стороны, цепь с высоким сопротивлением имеет плоскую кривую резонанса и, как говорят, имеет плохую селективность. Селективность различных резонансных контуров сравнивается с точки зрения их ширины полосы частот, которая задается полосами частот, которые лежат между двумя точками по обе стороны от резонансной частоты, где ток в 1 / √2 раз превышает максимальный ток I _max .

Ширина полосы, Δ f = f ₂ — f ₁ … (6.2)

Фактическая потребляемая мощность на частотах f ₁ и f ₂ :

Вот почему частоты f ₁ и f ₂ на границах полосы пропускания называются точками половинной мощности на шкале частот, а соответствующее значение полосы пропускания называется шириной полосы половинной мощности (B _hp ) или полосы пропускания -3 дБ.

Следует отметить следующие моменты относительно точек половинной мощности:

Фактор качества последовательной резонансной цепи:

Q-фактор последовательной цепи R-L-C можно определить любым из следующих способов:

Может быть задано как увеличение напряжения, создаваемое схемой при резонансе.Мы видели, что в резонансе ток в цепи максимален и равен V / R или напряжению питания, V = I _max R.

В случае последовательного резонанса более высокое значение Q-фактора означает не только большее увеличение напряжения, но и более высокую селективность настроечной катушки, поэтому необходимо, чтобы катушка имела высокую индуктивность и низкое сопротивление.

Фактически, добротность последовательного резонансного контура может быть определена как отношение резонансной частоты к ширине полосы:

Ток или параллельный резонанс в цепях R-L-C:

Когда индуктивное реактивное сопротивление и емкостное реактивное сопротивление соединены параллельно, как показано на рис.6.8, могут достигаться условия, при которых будет иметь место резонанс тока (также известный как параллельный или антирезонансный). Рассмотрим практический случай подключения змеевика параллельно конденсатору, как показано на рис. 6.8. Пусть катушка имеет сопротивление R Ом и индуктивность L Генри, а конденсатор — сопротивление R Ом и емкость C фарад.

Считается, что такая цепь находится в электрическом резонансе, когда реактивная (или не имеющая мощности) составляющая линейного тока становится равной нулю. Частота, на которой это происходит, называется резонансной частотой.

Цепь будет в электрическом резонансе, если реактивная составляющая тока ветви RL, I _{R — L} sin ɸ _{R — L} = Реактивная составляющая тока ветви RC, I _{R — C} sin ɸ _{R — c}

Резонансный ток:

Предполагая, что R ₁ = 0, как обычно, на резонансной частоте:

Знаменатель L / CR известен как эффективное или эквивалентное динамическое сопротивление параллельной цепи CR при резонансе.

Важные сведения о токовом или параллельном резонансе :

1. Чистая восприимчивость равна нулю, т.е. 1 / X _C = X _L / X _Z или ω _r C = ω _r L / Z ² или Z = √L / C

2. Допуск равен проводимости.

3. Реактивная составляющая линейного тока равна нулю, следовательно, коэффициент мощности цепи равен единице.

4. Импеданс чисто резистивный, максимальный по величине и равен L / CR.

5. Линейный ток минимален, равен величине V / L / CR и находится в фазе с приложенным напряжением.

6. Частота равна 1 / 2π √1 / LC — R ² / L ² Гц.

Примечание:

Параллельный резонансный контур иногда называют цепью рефлектора, потому что на резонансной частоте линейный ток минимален или почти отклоняется.

Поскольку в параллельных резонансных цепях циркулирующий ток между ветвями во много раз превышает линейный ток, такой тип резонанса иногда называют токовым резонансом.

Индуктивная катушка с индуктивностью L, соединенная параллельно с емкостью C, называется баковой цепью.

Графическое представление тока или параллельного резонанса:

Теперь мы обсудим влияние изменения частоты на сопротивляемость двух параллельных ветвей. Варианты показаны на рис. 6.10.

Индуктивная проводимость, равная 1 / ω L или 1 / 2π f L, уменьшается обратно пропорционально увеличению частоты и представлена ​​прямоугольной гиперболой, лежащей в четвертом квадранте ниже оси частот (индуктивная проводимость считается отрицательной).

Емкостная проводимость, равная ωC или 2π f C, увеличивается прямо пропорционально частоте питающей сети и представлена ​​прямой линией, проходящей через начало координат. Поскольку емкостная восприимчивость считается положительной, значит, она находится в первом квадранте.

Чистая проводимость B — это разность емкостной и индуктивной проводимости, а кривая, проведенная между чистой проводимостью и частотой приложенного напряжения, представляет собой гиперболу (не прямоугольную), как показано на рис.6.10.

Частота, при которой кривая чистой проводимости пересекает ось частот, называется резонансной частотой. В этой точке полное сопротивление максимальное или полное сопротивление минимальное и равно G, следовательно, линейный ток минимален.

Очевидно, что на частоте ниже, чем резонансная, индуктивная проводимость больше, чем емкостная, поэтому цепь является индуктивной, и ток в линии отстает от приложенного напряжения. Но для частот, превышающих резонансную частоту, преобладает емкостная восприимчивость, следовательно, цепь является емкостной, и линейный ток опережает приложенное напряжение.

Если сопротивление относительно низкое, ток значительно упадет на резонансной частоте, а если сопротивление велико, уменьшение тока будет менее выраженным, как показано на рис. 6.11.

Полоса пропускания в случае параллельной резонансной цепи:

Полоса пропускания в случае параллельной цепи определяется так же, как и в случае последовательной цепи. В этом случае также есть верхняя и нижняя точки половинной мощности, где потребляемая мощность составляет половину от резонансной частоты.

На частотах полосы пропускания чистая проводимость B равна проводимости G. Таким образом, на частоте f ₁ чистая проводимость B _L1 — B _C1 = G и на частоте f ₂ , B _C2 — B _L2 = G. Таким образом, проводимость Y = √G ² + B ² = √2 G и фазовый угол ɸ = tan ^-1 1 = 45˚ или π / 4 радиан.

Q-фактор или текущий коэффициент увеличения:

Добротность параллельной цепи определяется как отношение циркулирующего тока к линейному току или как увеличение тока.

[PDF] fig bandwidth — Скачать бесплатно PDF

Скачать фига пропускная способность …

БЛОК 5 РЕЗОНАНСНЫЕ ЦЕПИ Q.1) Определите коэффициент качества и полосу пропускания. Также установите взаимосвязь между ними в последовательном резонансном контуре.

ИЮНЬ 2014, ИЮНЬ 2013, ИЮНЬ 2015

О: Добротность: добротность последовательного резонансного контура — это не что иное, как добротность катушки индуктивности или конденсатора в последовательном резонансном контуре на резонансной частоте. В резонансе реактивное сопротивление катушки индуктивности такое же, как у конденсатора.Следовательно, энергия, запасаемая обоими элементами, будет одинаковой. Добротность последовательного резонансного контура обозначается Q0. В резонансе Q0 определяется как

Таким образом, приведенное выше выражение дает добротность последовательного резонансного контура с точки зрения элементов резонансного контура. Ширина полосы: ширина полосы последовательной цепи RLC определяется как ширина резонансной кривой до частоты, при которой мощность в цепи составляет половину от ее максимального значения. На частоте резонанса максимальный ток I0 определяется выражением

. Этот ток максимален, поскольку импеданс минимален в резонансе.Следовательно, на резонансной частоте мощность в цепи максимальна и определяется выражением P0 = Pmax = (I0) 2 .R Теперь половина максимальной мощности определяется выражением

Таким образом, на частотах, где мощность в цепи равна половине его максимальное значение, ток становится в 1 / √ 2 раза или 0,707 раза от своего максимального значения. Частоты, при которых мощность в цепи составляет половину своего максимального значения, называются частотами половинной мощности. Ширина полосы последовательного резонансного контура показана на рис.

На резонансной частоте мощность в контуре определяется выражением P0 = Pmax = (I0) 2.R На частоте мощность в цепи равна половине, и это определяется как P ’= ½ (I0) 2. R и Аналогичным образом на частоте f2 мощность в цепи равна половине и определяется выражением P ’= ½ (I0) 2. R Таким образом, f1 называется частотой нижней половины мощности, а f2 — частотой верхней половины мощности. В соответствии с определением полосы пропускания, ширина полосы последовательной цепи RLC равна, Полоса пропускания = (f2-f1) Гц Частоты половинной мощности также называются частотами 3 дБ или точками 3 дБ, потому что мощность на этих частотах на 3 дБ меньше, чем что на резонансе.Давайте теперь определим эти частоты 3 дБ и оценим полосу пропускания и выборочно для последовательного резонансного контура. Взаимосвязь между добротностью и шириной полосы. Ток в последовательной цепи RLC определяется уравнением

Таким образом, из приведенного выше уравнения ясно, что на частотах половинной мощности f1 и f2 реактивная часть импеданса последовательной цепи RLC равна резистивная часть импеданса. Мы можем написать

Избирательность резонансного контура определяется как способность контура различать или различать желаемые и нежелательные частоты.Селективность также определяется как отношение резонансной частоты к ширине полосы резонансного контура.

Таким образом, селективность последовательного резонансного контура прямо пропорциональна добротности контура на резонансной частоте. Таким образом, селективность резонансного контура зависит от Q0. Если Q0 очень велико, кривая амплитудной характеристики становится более резкой, эффективно уменьшая полосу пропускания. Если Q0 очень мало, полоса пропускания увеличивается, делая кривую амплитудной характеристики более пологой.

Таким образом, ширина полосы последовательного резонансного контура обратно пропорциональна добротности Q0 контура на резонансной частоте.Q.2) Последовательный резонансный контур с сопротивлением R = 17 Ом. L = 0,1H и C = 50 мкФ имеет приложенное напряжение V = 50 0 ° с переменной частотой. Найдите резонансную частоту, значение частоты

при

, при которой максимальное напряжение возникает на катушке индуктивности, и значение частоты, при которой максимальное напряжение возникает на конденсаторе.

ИЮНЬ 2015, ЯНВАРЬ 2014

Q.3) Покажите, что резонансная частота последовательного резонансного контура равна среднему геометрическому двух частот половинной мощности.

ЯНВ.2015

Таким образом, f1 называется частотой нижней половины мощности, а f2 — частотой верхней половины мощности. В соответствии с определением полосы пропускания, ширина полосы последовательной RCL-цепи равна, Полоса пропускания = (f2-f1) Гц. Частоты половинной мощности также называются частотами 3 дБ или точками 3 дБ, потому что мощность на этих частотах на 3 дБ меньше. чем в резонансе. Давайте теперь определим эти частоты 3 дБ и оценим полосу пропускания и выборочно для последовательного резонансного контура.

Таким образом, из приведенного выше уравнения ясно, что на частотах половинной мощности f1 и f2 реактивная часть импеданса последовательной RCL-цепи равна резистивной части импеданса.Вышеприведенное уравнение является квадратичным по ω, что дает два значения ω как ω1 и ω2, чьи частоты половинной мощности (т.е. f1 и f2) такие, как показано на рис. 20. Мы можем написать

Q.4) В приведенной схеме ниже на фиг. индуктивность 0,1 Гн с добротностью 5 параллельна конденсатору. Определите значение емкости и сопротивления катушки на резонансной частоте 500 рад / сек. ЯНВ.2015

О: Данная схема представляет собой практический параллельный резонансный контур. Антирезонансная частота с точки зрения добротности равна

Q.5) Определите параметры параллельной цепи R-L-C, кривая отклика которых показана на рис. Какие новые значения ωr и ширины полосы при увеличении c в 4 раза? JAN.2013

Q.6) В случае последовательного резонансного контура с изменением частоты получить выражения для i) ωC, при котором максимальное напряжение возникает на C ii) ωL, при котором максимальное напряжение возникает на L, и показать, что ω1> ωC

ЯНВ.2014

Q.7) Выведите выражение для резонансной частоты цепи, показанной на рис.Также покажите, что цепь будет резонировать на всех частотах, если RL = RC = √ L / C

ЯНВАРЬ 2014, ИЮНЬ 2015

Две параллельно соединенные ветви будут создавать резонанс, когда результирующий ток через комбинацию, т.е. фаза с напряжением V, как показано на рис. 10 (b). Условие параллельного резонанса состоит в том, что полное сопротивление параллельной комбинации является чисто резистивным. Условие резонанса может быть получено следующим образом: Полная проводимость ветви, содержащей L и RL, определяется как

, где far — частота резонанса.Значения RL и RC обычно невелики. RL — омическое сопротивление катушки или индуктора, а RC — сопротивление утечки и диэлектрических потерь конденсатора. Оба они неизбежны, но на самом деле оба очень маленькие. Если два сопротивления выбраны так, что мнимый член в уравнении (1) становится равным нулю. Таким образом, реактивное сопротивление равно нулю. Для всех частот схема находится в состоянии единичного коэффициента мощности. При указанном выше условии антирезонанс возможен на всех частотах в цепи.

Резонанс в цепях RLC

Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы. Чтобы изучить резонанс в цепи RLC, как показано ниже, мы можем увидеть, как цепь ведет себя в зависимости от частоты источника управляющего напряжения.

Цепь серии RLC

Последовательная цепь RLC с источником переменного напряжения.2}} $,

, где I _rms и V _rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты $ \ nu $, при этом X _L большое на высоких частотах и ​​X _C большое на низких частотах, определяемое как:

$ X_L = 2 \ pi \ nu L, X_C = \ frac {1} {2 \ pi \ nu C} $.

При некоторой промежуточной частоте $ \ nu_0 $ реактивные сопротивления будут равны и уравновешены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I _{действующее значение} результатов.Мы можем получить выражение для $ \ nu_0 $, взяв X _L = X _C . Подстановка определений X _L и X _C дает:

$ \ nu_0 = \ frac {1} {2 \ pi \ sqrt {LC}} $.

$ \ nu_0 $ — резонансная частота последовательного контура RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. При $ \ nu_0 $ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I _{среднеквадратичное значение} является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.

Приемник в радиостанции — это RLC-цепь, которая лучше всего колеблется на своем $ \ nu_0 $. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик I _rms при $ \ nu_0 = f_0 $.Две кривые относятся к двум разным цепям, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и они не будут такими избирательными, например, в радиоприемнике.

Зависимость тока от частоты

График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.Источник управляющего переменного напряжения имеет фиксированную амплитуду V0.

Учебная серия по электричеству и электронике ВМС (NEETS), модуль 9-1

NEETS Модуль 9 — Введение в генерацию и формирование волн

Страницы i, 1−1, 1-11, 1−21, 1−31, 1−41, 2−1, 2-11, 2−21, 2−31, 3−1, 3-11, 3−21, 3−31, 3−41, 3−51, 4−1, 4-11, 4−21, 4−31, 4−41, 4−51, Индекс

Выбор частоты должен выполняться другим способом.Это придает схеме разные характеристики. Первая из этих характеристик — способность накапливать энергию.

Характеристики Типичная параллельно-резонансная схема

Посмотрите на рисунок 1-11. В этой схеме, как и в других параллельных В цепях индуктивности и конденсатора напряжение одинаково. Токи в компонентах различаются. обратно пропорционально их реактивным сопротивлениям в соответствии с законом Ома.Полный ток, потребляемый схемой, представляет собой вектор сумма двух отдельных составляющих токов. Наконец, эти два тока, IL и IC, выходят на 180 градусов. фазы, потому что эффекты L и C противоположны. В изложенном выше нет ни одного нового для вас факта. Это все на основе того, что вы узнали ранее о параллельных цепях переменного тока, содержащих L и C.

Рисунок 1-11. — Кривые импеданса и тока в параллельном резонансном контуре RLC.

Теперь, в резонансе, X _L все еще равно X _C . Следовательно, I _L должен равняться I _C . Помните, что напряжение такое же; реактивные сопротивления равны; следовательно, согласно закону Ома токи должны быть равным. Но не забывайте, что хотя токи равны, они все равно противоположны. То есть, если текущая течет «вверх» в конденсаторе, течет «вниз» в катушке, и наоборот.Фактически, в то время как один компонент потребляет ток, другой возвращает его источнику. Чистый эффект этого «отдаваться и принимать меры» заключается в том, что нулевой ток выводится из источника в резонансе. Два тока дают полный ток в ноль ампер, потому что они точно равны и противоположны при резонансе.

Замкнутая цепь, к которой приложено напряжение, но имеет нулевой ток, должен иметь БЕСКОНЕЧНЫЙ импеданс (применить закон Ома — любое напряжение, деленное на ноль, дает бесконечность).

1-21

---

К настоящему времени вы знаете, что мы только что проигнорировали сопротивление нашего старого друга из предыдущих обсуждений. В Фактическая схема, в резонансе, токи не будут полностью противодействовать друг другу, потому что каждый компонент будет иметь разное сопротивление. Это сопротивление очень низкое, но все же есть. В результате относительно небольшой ток течет от источника при резонансе вместо нулевого тока.Таким образом, основной Особенностью практической схемы с параллельным LC является то, что при резонансе цепь имеет максимальный импеданс, который дает МИНИМАЛЬНЫЙ ток от источника. Этот ток часто называют линейным током. Об этом свидетельствует пик формы волны для импеданса и впадины для линейного тока, оба

возникают при f _r частота резонанса на рисунке 1-11.

Существует небольшая разница между схемой, генерируемой батареей на рис. 1-8, которая колеблется в резонансном состоянии. (или собственная) частота и схема, которую мы только что обсудили.Равный и противоположный токи в двух компоненты такие же, как токи, которые заряжают и разряжают конденсатор через катушку.

Для при заданном напряжении источника ток, колеблющийся между реактивными частями, будет сильнее в резонансном частота цепи, чем на любой другой частоте. На частотах ниже резонанса емкостной ток будет снижаться; выше резонансной частоты индуктивный ток будет уменьшаться.Следовательно, колеблющийся ток (или циркулирующий ток, как его иногда называют), будучи меньшим из двух реактивных токов, будет максимальным при резонанс.

Если вы помните, основной резонансный контур создавал «затухающую» волну. волна постоянной амплитуды был произведен путем передачи в цепь энергии, которая поддерживала бы ее работу. Для этого энергия должна была быть одинаковой. частота как резонансная частота контура.

Итак, если резонансная частота «синхронизирована» правильно, то все остальные частоты «вне времени» и создают волны, которые имеют тенденцию противодействовать друг другу.Такие частоты не могут производят сильные колебательные токи.

В нашей типовой схеме с параллельным резонансом (LC) линейный ток равен минимальный (потому что сопротивление максимальное). В то же время внутренний колебательный ток в резервуаре составляет максимум. Колебательный ток может быть в несколько сотен раз больше линейного тока при резонансе.

В любом В этом случае этот контур иначе реагирует на резонансную частоту, чем на все остальные частоты.Это делает это эффективный селектор частоты.

Резонанс

И серийный, и Цепи с параллельным LC различают резонансную частоту и все другие частоты путем уравновешивания индуктивное реактивное сопротивление против равного емкостного реактивного сопротивления.

Последовательно эти реактивные сопротивления создают очень низкое сопротивление. Параллельно они создают очень высокий импеданс.Эти характеристики определяют, как и где дизайнеры использовать резонансные контуры. требование низкого импеданса потребует последовательной резонансной цепи. высокоомный Требование потребовало бы, чтобы разработчик использовал параллельный резонансный контур.

Настройка диапазона Частоты

Наши резонансные контуры до сих пор были настроены на одну частоту — резонансную. частота. Это нормально, если требуется только одна частота.Однако на многих разные частоты.

Следовательно, если мы вернемся к нашему исходному приложению, то настройку на другое радиостанции, наши резонансные схемы не практичны. Причина в том, что тюнер для каждой частоты будет требуется, и это непрактично.

1-22

---

Какое практическое решение этой проблемы? Ответ прост.Сделайте либо конденсатор, либо индуктор переменный. Помните, что изменение L или C изменяет резонансную частоту.

Теперь вы знаете, что происходило все эти годы, когда вы «нажимали» кнопку или «вращали» циферблат. Вы меняли L или C в настроенных схемах на величину, необходимую для настройки тюнера на резонанс на желаемой частоте. Нет Независимо от того, насколько сложен блок, если он имеет тюнеры LC, тюнеры подчиняются этим основным законам.

Q-9. Что такое срок сколько раз в секунду энергия контура резервуара накапливается в катушке индуктивности или конденсаторе?

В-10. Какая связь между импедансом и током в цепи с параллельным резонансом? В-11. Когда минимальный линейный ток в цепи с параллельным LC?

РЕЗОНАНСНЫЕ ЦЕПИ КАК ФИЛЬТР Цепи

Принцип последовательного или параллельного резонансного контура находит множество применений в радио, телевидении, связь и различные другие электронные области военно-морского флота.Как вы видели, сделав переменной емкости или индуктивности, можно контролировать частоту, при которой цепь будет резонировать.

дюйм Помимо выбора или настройки станции, резонансные цепи могут отделять токи определенных частот от тех других частот.

Цепи, в которых для этого используются резонансные цепи, называются цепями ФИЛЬТРА.

Если мы сможем выбрать правильные значения резисторов, катушек индуктивности или конденсаторов, сеть ФИЛЬТРОВ или «частота селектор «, который предлагает небольшую оппозицию одной частоте, в то время как блокирование или ослабление другой частоты.сеть фильтров также может быть спроектирована, которая будет «пропускать» полосу частот и «отклонять» все остальные частоты.

Большинство электронных схем требуют использования фильтров в той или иной форме. Ты уже изучал несколько в модулях 6, 7 и 8 NEETS.

Одним из примеров применения фильтра является выпрямительная схема. Как известно, переменное напряжение преобразуется выпрямителем в постоянное.Тем не мение, напряжение постоянного тока не чистое; он все еще пульсирует и колеблется. Другими словами, сигнал все еще имеет переменный ток. составляющая в дополнение к постоянному напряжению. Пропуская сигнал через простые сети фильтров, переменная составляющая уменьшенный. Остающийся DC такой чистый, как того требуют дизайнеры.

Байпасные конденсаторы, которые у вас уже есть изучаемые, являются частью сетей фильтров, которые, по сути, шунтируют или шунтируют нежелательные компоненты переменного тока на землю.

ИДЕЯ «Q»

Несколько раз в этой главе мы обсуждали «идеальный» или теоретический идеальные схемы. В каждом случае вы обнаружили, что сопротивление мешает нашим схемам быть идеальными. Вы также нашли что низкое сопротивление тюнеров было лучше, чем высокое сопротивление. Теперь вы узнаете о факторе, который, по сути, измеряет, насколько близок к совершенству тюнер или компонент тюнера.Этот же фактор влияет на пропускную способность и ИЗБИРАТЕЛЬНОСТЬ. Его можно использовать для расчета напряжения на катушке или конденсаторе в последовательно-резонансной цепи и величина циркулирующего (емкостного) тока в параллельно-резонансном контуре. Этот фактор очень важен

1-23

---

и пригодится дизайнерам. Технические специалисты должны иметь некоторое представление об этом факторе, потому что он влияет на очень многие вещи. Фактор известен как Q.Некоторые говорят, что это символ качества (или достоинств). Чем выше Q, тем лучше схема; чем меньше потери (I ² R), тем ближе схема к идеальной.

Изучив первой части этой главы, вы не должны удивляться, узнав, что сопротивление (R) оказывает большое влияние на это показатель достоинства или качества.

Q Is a Ratio

Q действительно очень просто поймете, если вы вспомните только что рассмотренные принципы настройки схемы.Индуктивность и емкость у всех тюнеры. Сопротивление — это примесь, вызывающая потери. Следовательно, компоненты, обеспечивающие реактивное сопротивление с минимальным сопротивлением «чище» (совершеннее), чем с более высоким сопротивлением. Фактическая мера этого чистота, достоинства или качество должны включать две основные величины, X и R.

Соотношение

делает всю работу за нас. Давайте посмотрим на это и поймем, почему он измеряет качество.

Во-первых, если идеальная схема имеет нулевое сопротивление, то наше отношение должно давать очень высокое значение Q, чтобы отразить высокое качество схемы. Является ли?

Примите любое значение для X и нулевое значение для R.

Затем:

Помните, любое значение, деленное на ноль, равняется бесконечности. Таким образом, наше отношение бесконечно велико для теоретически идеальная схема.

У компонентов с более высоким сопротивлением Q уменьшается. Деление на большее число всегда дает меньшее количество. Таким образом, компоненты более низкого качества дают более низкую добротность. Q, тогда, является прямая и точная мера качества LC-цепи.

Q — это просто соотношение. Это всегда просто число — нет единиц. Чем выше число, тем «лучше» схема. Позже, когда вы перейдете к более практическим схемам, вы может оказаться, что низкий Q может быть желательным для обеспечения определенных характеристик.А пока считайте, что чем выше, тем лучше.

Поскольку конденсаторы имеют гораздо меньшее сопротивление, чем индуктивности, добротность цепи очень часто выражается как добротность катушки или:

Ответ, который вы получите при использовании этой формулы, очень близок к правильному для большинства целей. По сути, Q конденсатор настолько высок, что практически не ограничивает добротность схемы.По этой причине техник может проигнорировать это.

1-24

---

Q катушки

Q — это особенность, встроенная в катушку. Когда катушка при использовании в диапазоне частот, для которого он разработан, Q относительно постоянен. В этом смысле это физическая характеристика.

Индуктивность — это результат физического устройства катушки — количество витков, сердечник, тип обмотки и др.Индуктивность определяет реактивное сопротивление на заданной частоте. Сопротивление заложено в длине, размер и материал проволоки. Следовательно, добротность катушки в основном зависит от физических характеристик.

Значения Q, которые исчисляются сотнями, очень практичны и часто встречаются в типичном оборудовании.

Применение Q

По большей части Q — это забота проектировщиков, а не технических специалистов.Следовательно, шансы, что вам придется вычислить добротность катушки, очень малы. Однако важно знать некоторые отношения цепей, на которые влияет Q.

Q взаимосвязи в последовательных цепях

Q можно использовать для определения «усиления» последовательно-резонансных цепей. Усиление относится к тому факту, что при резонансе падение напряжения на реактивных сопротивлениях больше, чем приложенное напряжение.Помните, когда мы применили закон Ома в последовательно-резонансный контур, он дал нам следующие характеристики:

· Низкое сопротивление, большой ток.

· Сильный ток; высокое напряжение на сравнительно высоких реактивных сопротивлениях.

Это высокое напряжение можно использовать там, где требуется небольшая мощность, например, при возбуждении решетки вакуумной лампы или затвора полевого эффекта транзистор (F.E.T.). Коэффициент усиления правильно спроектированной резонансной цепи может быть таким же большим или большим, чем усиление внутри самого усилителя.Коэффициент усиления является функцией Q, как показано в следующем примере:

E = входное напряжение настроенной цепи

E _L = падение напряжения на катушка в резонансе Q.

Q = добротность катушки.

Тогда:

E _L = EQ

Если бы добротность катушки была 100, то коэффициент усиления был бы 100; то есть напряжение катушки будет в 100 раз входного напряжения в последовательную цепь.

Сопротивление влияет на резонансную кривую ряда схема двумя способами — чем меньше сопротивление, тем выше ток; кроме того, чем ниже сопротивление, тем резче кривая. Поскольку низкое сопротивление вызывает высокое значение Q, эти два факта обычно выражаются как функции от Q. То есть, чем выше Q, тем выше и резче кривая и тем более избирательная схема.

Нижний Q (из-за более высокого сопротивления), тем ниже кривая тока; следовательно, чем шире кривая, тем меньше выборочная схема.Краткое изложение основных характеристик последовательных RLC-цепей в резонансе приведено в Таблица 1-1.

1-25

---

Таблица 1-1. — Основные характеристики цепей RLC серии при резонансе

Взаимосвязи добротности в параллельно-резонансной цепи

Нет усиления напряжения в параллельно-резонансный контур, потому что напряжение одинаково во всех частях параллельного контура.Однако Q помогает дайте нам меру тока, который циркулирует в резервуаре.

1-26

---

Дано:

I _LINE = ток, потребляемый от источника

I _L = ток через катушка (или циркулирующий ток

Q = добротность катушки

Тогда:

I _L = I _LINE Q

Опять же, если бы Q было 100, циркулирующий ток был бы в 100 раз больше, чем линейный ток.Этот может помочь объяснить, почему некоторые размеры проводов в схемах усиления большой мощности очень велики.

The Кривая импеданса параллельно-резонансного контура также зависит от добротности контура аналогично кривая тока последовательной цепи. Q схемы определяет, насколько увеличивается импеданс на параллельная LC-цепь. (Z = Q x X _L )

Чем выше добротность, тем больше импеданс в резонансе и тем резче кривая.Чем ниже добротность, тем ниже сопротивление при резонансе; следовательно, чем шире кривая, тем менее избирательная схема. Основные характеристики цепей с параллельным RLC в резонансе приведены в таблице. 1-2.

1-27

---

Таблица 1-2. — Основные характеристики параллельных цепей RLC при резонансе

Резюме Q

Отношение, которое называется Q, является мерой качества резонансного схемы и компоненты схем.По сути, значение Q является обратной функцией рассеиваемой электрической мощности. через сопротивление цепи. Q — это отношение мощности, накопленной в реактивных компонентах, к мощности, рассеиваемой в сопротивлении. То есть большие потери мощности имеют низкий Q; низкие потери мощности высокие Q.

Разработчики схем обеспечивают правильный Q. Как технический специалист, вы должны знать, что может изменить Q и на какие величины в цепи влияет такое изменение.

1-28

---

Полоса пропускания

Если в цепи Q низкий, коэффициент усиления цепи в резонансе относительно невелик. Схема не четко различать (отклонять нежелательные частоты) между резонансной частотой и частотами на по обе стороны от резонанса, как показано кривой на рисунке 1-12, вид (A). Диапазон частот включен между двумя частотами (426.4 кГц и 483,6 кГц в этом примере), при котором ток падает до 70 процентов его максимальное значение при резонансе называется полосой пропускания цепи.

Рисунок 1-12A. — Полоса пропускания для последовательной цепи с высокой и низкой добротностью. Кривая тока низкой добротности.

Рисунок 1-12B. — Полоса пропускания для последовательной цепи с высокой и низкой добротностью. Кривая тока высокой добротности.

Часто необходимо указать полосу частот, которую будет проходить цепь.Следующий стандарт настроен: предельные частоты — это те частоты по обе стороны от резонанса, при которых кривая падает до точку .707 (приблизительно 70 процентов) от максимального значения. Эта точка называется точкой половинной мощности. Примечание что на рисунке 1-12 последовательно-резонансный контур имеет две точки половинной мощности, одну выше и одну

1-29

---

ниже точки резонансной частоты.Две точки обозначены как верхняя граница частоты (fco) и нижняя граница частоты (f _co ) или просто f ₁ и f ₂ . Диапазон частот между этими двумя точками составляет полосу пропускания. Виды (A) и (B) на рис. 1-12 показывают полосу пропускания для низко- и высокодобротные резонансные контуры. Пропускная способность может быть определена с использованием следующих формул:

Где:

BW = ширина полосы канала в единицах частоты

f _r = резонансная частота

f ₂ = верхняя частота среза

f ₁ = нижняя частота среза частота

Например, применив формулу, мы можем определить полосу пропускания для кривой, показанной на рисунке 1-12, вид (A).

Решение:

BW = f ₂ — f ₁

Полоса пропускания = 483,6 кГц — 426,4 кГц

Полоса пропускания = 57,2 кГц

Если добротность схемы, представленной кривой на рис. 1-12, вид (B), составляет 45,5, что будет пропускная способность?

Решение:

Если Q равно 7,95 для схемы с низкой добротностью, как показано (A) на рисунке 1-12, мы можем проверить наш оригинал. расчет пропускной способности.

1-30

---

–	Материя, энергия и постоянный ток
–	— Переменный ток и трансформаторы
–	Защита, управление и измерение цепей
–	Электропроводники, электромонтажные работы, и схематическое чтение
–	Генераторы и двигатели
–	Электронные излучатели, трубки и источники питания
–	Твердотельные устройства и блоки питания
–	Усилители
–	Цепи генерации и формирования волн
–	Распространение волн, линии передачи и Антенны
–	Принципы СВЧ
–	Принципы модуляции
–	Введение в системы счисления и логические схемы
–	— Введение в микроэлектронику
–	Принципы синхронизаторов, сервоприводов и Гироскопы
–	Введение в испытательное оборудование
–	Принципы радиочастотной связи
–	Принципы работы радаров
–	Справочник техника, мастер-глоссарий
–	Методы и практика испытаний
–	Введение в цифровые компьютеры
–	Магнитная запись
–	Введение в волоконную оптику
Примечание: Обучение электричеству и электронике военно-морского флота Содержимое серии (NEETS) — U. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт