ИЗМЕРИТЕЛЬ СДВИГА ФАЗЫ
Этот простой измеритель сдвига фазы разрабатывался как приставка к компьютеру для снятия фазо-частотных характеристик акустических систем при разработке и настройке разделительных фильтров, но он также может быть использован самостоятельно, так как обладает встроенным отсчетным устройством. Сопряжение с компьютером происходит через звуковую карту. Фазометр выдает переменное напряжение фиксированной частоты с амплитудой пропорциональной фазе измеряемого сигнала. Так как фаза сигнала может иметь различную полярность, а передача сигнала к компьютеру производится на переменном токе, то для получения отрицательных значений приходится сдвигать нуль в область положительных значений. Так, нулевому сдвигу фазы соответствует некоторое определенное значение напряжения которое калибруется перед измерением. Выбирая различные комбинации переключателей расположенных на лицевой панели прибора можно получить на выходе сигналы соответствующие -180, -90, 0, 90 и 180 градусам фазового сдвига.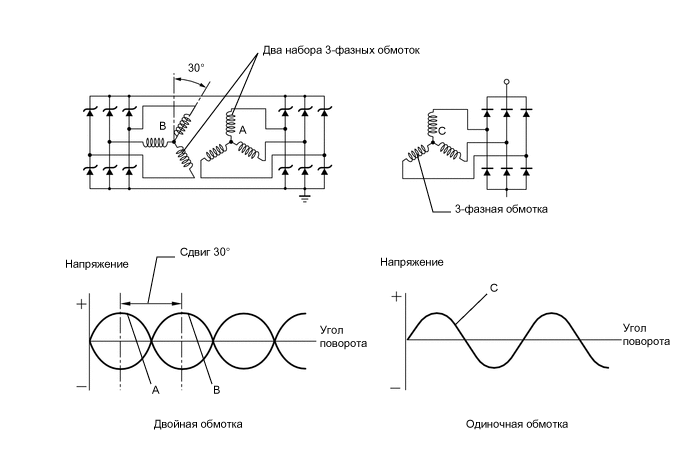
Принцип работы схемы
В виду невысоких требований к точности показаний была применена простая архитектура измерителя. Сигналы обоих каналов преобразовываются в прямоугольные цифровые после чего вычитаются на исключающем ИЛИ. Полученный сигнал имеет скважность пропорциональную модулю фазового сдвига. Для преобразования скважности в амплитуду используется интегрирующая RC цепочка. Напряжение полученное на цепочке измеряется стрелочной головкой по которой можно непосредственно отсчитывать фазу. Для определения полярности сдвига используется D триггер на тактовый вход которого подается опорный сигнал, а на вход данных измеряемый сигнал, в результате в зависимости от того, опережает ли измеряемый сигнал опорный или отстает, триггер переключается в то или иное состояние. В зависимости от состояния триггера изменяется полярность напряжения на выходе интегрирующей цепочки. После чего полученное напряжение модулируется, фильтруется от гармоник и подается на выход.
Сигнал с микрофона подается на чувствительный вход In1, пройдя через усилители на DA1 и DA2 поступает на фильтр верхних частот предназначенный для уменьшения помех. Переменный резистор на выходе DA1 позволяет в небольших пределах регулировать чувствительность микрофонного входа. На вход In2 поступает опорный сигнал.
Переменный резистор на выходе DA1 позволяет в небольших пределах регулировать чувствительность микрофонного входа. На вход In2 поступает опорный сигнал.
С целью получения возможности подключения непосредственно к выходу усилителя установлен переключатель SA1 который уменьшает чувствительность входа. Так как уровень сигнала в этом канале намного выше, используется только буфер на DA4. На выходе буфера стоит такая же цепочка фильтра верхних частот, только тут постоянную времени фильтра можно менять с целью компенсации фазового сдвига в каналах измерения.
Затем сигналы с обоих входов поступают на компараторы с гистерезисом DA3.1. DA3.2. Буферы на DD1.1 и DD1.2 обостряет фронты сигналов с компараторов. Причем DD1.1 инвертирует сигнал который ранее был инвертирован DA2. Полученные цифровые сигналы вычитаются на DD1.3, но подавать этот сигнал на интегрирующую цепочку пока рано ввиду того, что он изменяется от минус питания, до плюс питания, а требуется изменение от земли до плюс питания.
Сигнал со скважностью пропорциональной сдвигу фазы проходит через интегрирующую RC цепочку и аналоговый ключ DD2.1 и подается на измерительную головку. Также этот сигнал подается на буфер DA5 и после на инвертор на DA6. В зависимости от направления сдвига фазы, на фильтр на DA7 через ключи DD2.2 или DD2.3 поступает прямой или инвертированный сигнал.
Управляет ключами триггер DD3.1 который определяет знак фазы. После фильтрации напряжение пропорциональное фазовому сдвигу поступает на модулятор на ключе DD2.4, опорное напряжение которому выдает буфер DA8, а тактовую частоту генератор на триггере DD3.2. Полученный меандр отфильтровывается от гармоник фильтром на DA9. После чего сигнал пройдя через регулятор выходной амплитуды и буфер DA11 поступает на выходной разъем Out.
Узел на DA10 служит для индикации при недостаточном уровни входного сигнала. Недостаточному уровню соответствует свечение светодиода. Также светодиод сигнализирует при отклонении формы входного сигнала от меандра, в этом случаи показания будут ошибочными. Переключатель SA3 служит для калибровки полярности фазы и позволяет выбрать ее положительной, отрицательной или реальной. Переключатель SA2 используется для получения калибровочных сдвигов фазы 90 и 180 градусов.
При установке переключателя в среднее положение, пока заряжается конденсатор, напряжение на выходе соответствует нулевому сдвигу фазы.
Для автономной работы от батареи требуется наличие двухполярного напряжение, положительная часть которого берется непосредственно от батареи, а отрицательная берется от преобразователя на микросхеме DA12. Преобразователь включен по типичной для него схеме и в комментариях не нуждается.
Настройка измерителя фаз
Настройка данного прибора не представляет особых трудностей ввиду практический полной самокалибровки, однако отладка потребует наличие вольтметра и генератора, пусть даже из звуковой карты, в особо тяжелых случаях придется применить осциллограф и разбираться в принципах работы схемы.
Для начала проверяют работу преобразователя напряжения и наличие генерации триггера DD3.2. После чего на оба входа подается сигнал частотой в районе 5-7 килогерц. Вращая подстроечный резистор на выходе DA4 добиваются минимальных показаний показывающего прибора. Затем подают сигнал частотой пару килогерц со сдвигом в 180 градусов. Если такого сигнала под рукой нет, то можно подать сигнал только на вход In1, а вход In2 подключить на выход DA2. Подбирая резистор последовательно с головкой для получения полного отклонения стрелки.
Переключатель SA2 при этом должен быть в среднем положении. Напряжение на входе DA5 не должно быть больше 2 вольт, в противном случаи параллельно головки ставят дополнительные шунты. Переводя переключатель SA2 в положение 90 и 180 градусов вращая соответствующие подстроечники добиваются отклонения стрелки на требуемые значения шкалы. В завершение настройки переключатель SA3 переводят в положение отрицательной фазы и вращая резистор смещения нуля добиваются нулевого выходного напряжения прибора.
Вместо завершения
Так как конструкция изначально задумывалась как проект выходного дня, она была собрана частично навесом, частично на макетных платах, и дабы не шокировать неокрепшие умы начинающих радиолюбителей содержимое коробочки публике показывать не буду.
Работа с прибором довольно интуитивна. Ко входу In1 подключается микрофон, желательно со своим предусилителем, на In2 подается сигнал с усилителя. Выход Out соединяют с микрофонным или линейным входом компьютера. Строить графики фазы можно непосредственно в программах измерения АЧХ при измерении свипом, только выбрать линейный масштаб шкалы по вертикале. Переключателями выбирают сдвиг фазы +180 градусов и изменяя выходное напряжение фазометра добиваются требуемой амплитуды сигнала на графике. Затем перебирая различные положения переключателей калибруют остальные точки шкалы. Ручку чувствительности устанавливают в минимальное положение и увеличивают в случаи зажигания светодиода во время измерения.
Форум по измерениям
Форум по обсуждению материала ИЗМЕРИТЕЛЬ СДВИГА ФАЗЫ
Понятие сдвига фазы в аналоговых цепях
Добавлено 19 июня 2020 в 23:11
Сохранить или поделиться
Рассмотрим, что такое сдвиг фазы, и как это фундаментальное электрическое явление связано с различными конфигурациями схем.
В данной статье рассказывается о сдвиге фазы, о влиянии схемы, вызывающем опережение или отставание напряжения или тока на выходе схемы относительно входа. В частности, нам будет интересно то, как реактивные нагрузки и цепи будут влиять на сдвиг фазы в схеме. Сдвиг фазы может иметь всевозможные последствия, независимо от того, работаете ли вы с генераторами, усилителями, петлями обратной связи, фильтрами и т.п. Например, вы ожидаете, что ваша инвертирующая схема на операционном усилителе будет давать сдвиг фазы на 180°, но вместо этого она возвращает синфазный сигнал и вызывает проблемы с автоколебаниями.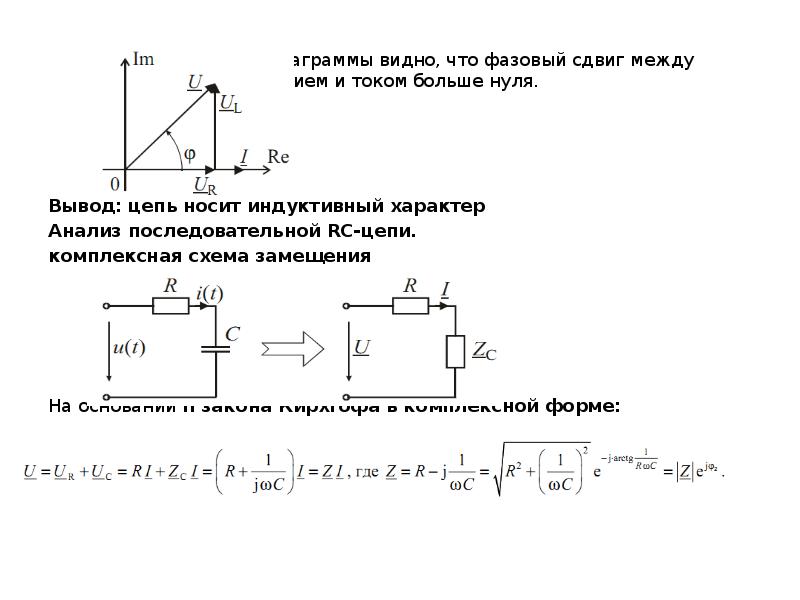
Сдвиг фазы для реактивных нагрузок
Частотно-зависимый сдвиг фазы происходит из-за влияния реактивных компонентов: конденсаторов и катушек индуктивности. Это относительная величина, и поэтому она должна быть задана как разность фаз между двумя точками. В данной статье «сдвиг фазы» будет означать разницу по фазе между выходом и входом. Говорят, что конденсатор вызывает отставание напряжения от тока на 90°, в то время как индуктивность вызывает отставание тока от напряжения на 90°. В векторной форме это обозначается +j или -j в индуктивном и емкостном реактивном сопротивлении соответственно. Но емкость и индуктивность в некоторой степени существуют во всех проводниках. Так почему же они не вызывают сдвиги фаз на 90°?
Так почему же они не вызывают сдвиги фаз на 90°?
Все наши эффекты сдвига фазы будут моделироваться цепями RC и RL. Все схемы могут быть смоделированы как источник с некоторым внутренним сопротивлением, рассматриваемая схема и нагрузка, следующая за схемой. Внутренний импеданс источника также называется его выходным сопротивлением. Я считаю, что проще всего говорить о входном и выходном импедансе и о каскадах, поэтому позвольте мне перефразировать: все схемы могут быть смоделированы как выход одного каскада с некоторым выходным импедансом, питающий следующий каскад, который нагружен входным импедансом следующего каскада. Это важно, потому что это уменьшает сложность цепей до гораздо более простых RLC-цепей, фильтров и делителей напряжения.
Взгляните на следующую схему.
Рисунок 1 – Конденсатор, шунтирующий предыдущий каскад, и нагрузка 10 кОмЭто будет моделировать некоторую цепь источника (например, усилитель) с выходным сопротивлением 50 Ом, который имеет нагрузку 10 кОм и шунтируется конденсатором 10 нФ. Здесь должно быть понятно, что схема, по сути, является RC-фильтром нижних частот, выполненным из R1 и C1. Из базового анализа цепей мы знаем, что сдвиг фазы напряжения в RC-цепи будет изменяться от 0° до -90°, и моделирование подтверждает это.
Здесь должно быть понятно, что схема, по сути, является RC-фильтром нижних частот, выполненным из R1 и C1. Из базового анализа цепей мы знаем, что сдвиг фазы напряжения в RC-цепи будет изменяться от 0° до -90°, и моделирование подтверждает это.
Для низких частот фаза выходного сигнала не зависит от конденсатора. Когда мы доберемся до частоты среза (fср) RC-фильтра, фаза падает до -45°. Для частот выше частоты среза фаза приближается к своему асимптотическому значению -90°.
Эта фазо-частотная характеристика моделирует сдвиг фазы, вызванный любым шунтирующим конденсатором. Шунтирующий конденсатор вызовет сдвиг фазы на резистивной нагрузке между 0° и -90°. Конечно, также важно помнить и об ослаблении.
Аналогичный взгляд на последовательный конденсатор (например, конденсатор емкостной связи по переменному току) показывает типовой эффект подобной схемы.
Рисунок 3 – Схема с последовательным конденсатором. ..Рисунок 4 – … и графики ее амплитудно-частотной и фазо-частотной характеристик
..Рисунок 4 – … и графики ее амплитудно-частотной и фазо-частотной характеристикВ этом случае сдвиг фазы начинается с +90°, а фильтр является фильтром верхних частот. За пределами частоты среза, в конечном итоге, устанавливается значение 0°. Итак, мы видим, что последовательный конденсатор всегда будет вносить сдвиг фазы между +90° и 0°.
Усилитель с общим эмиттером
Имея в распоряжении эту информацию, мы можем применить RC-модель к любой цепи, к какой захотим. Например, этот усилитель с общим эмиттером.
Рисунок 5 – Усилитель с общим эмиттером с сопротивлением обратной связи в цепи эмиттера (смещение не показано)Частотные характеристики данного усилителя будут плоскими примерно до 10 МГц.
Рисунок 6 – Логарифмические амплитудно-частотная и фазо-частотная характеристики усилителя с общим эмиттеромТолько после примерно 10 МГц мы видим изменения сдвига фазы – ниже 180°, что мы и ожидаем, поскольку схема с общим эмиттером представляет собой инвертирующий усилитель. Выходной импеданс усилителя, пренебрегая эффектом Эрли, равен R2 = 3 кОм, что довольно высоко.
Выходной импеданс усилителя, пренебрегая эффектом Эрли, равен R2 = 3 кОм, что довольно высоко.
Теперь мы поставили на выходе шунтирующий конденсатор. Что мы можем ожидать от фазы?
Рисунок 7 – Усилитель с общим эмиттером с шунтирующим конденсатором на выходеИсходя из нашего опыта, мы ожидаем, что частота среза будет составлять 53 Гц, ниже которой сдвиг фазы должен быть 180° (без влияния конденсатора), и выше которой сдвиг фазы будет равен 180° — 90° = 90° (а также большие потери). Моделирование подтверждает наши подозрения:
Рисунок 8 – Графики АЧХ и ФЧХ для усилителя с общим эмиттером с емкостной нагрузкойОбратите внимание, что это эквивалентно тому, если бы фаза изменялась от -180° до -270°. Теперь мы начинаем понимать, что питание емкостной нагрузки может привести к неожиданным изменениям фазы, что может нанести ущерб усилителю с неожиданной обратной связью.
В более распространенном сценарии на выходе используется последовательно включенный конденсатор связи, как показано на следующей схеме.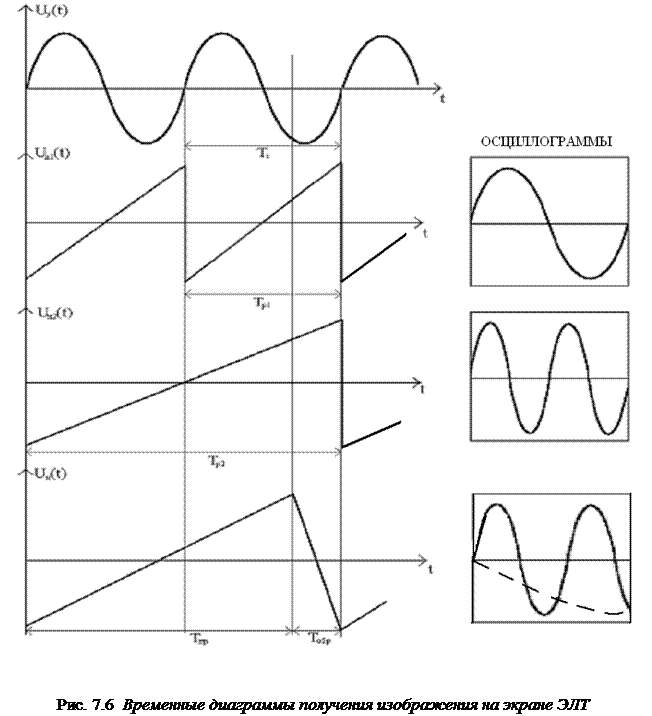
Я изменил номиналы элементов схемы и добавил резистивную нагрузку 100 кОм. Теперь мы имеем фильтр верхних частот, состоящий из C1 и R3, с частотой среза всего 1,6 Гц. Мы ожидаем, что сдвиг фазы будет равен -90° на частотах ниже 1,6 Гц и -180° на частотах выше частоты среза, что подтверждается моделированием.
Рисунок 10 – Графики АЧХ и ФЧХ для усилителя с общим эмиттером с конденсатором связи по переменному токуКонденсатор связи с таким номиналом подошел бы для сигналов звуковой частоты, поскольку область сдвига фазы -90° (и, следовательно, затухания) значительно ниже 10 Гц.
Конечно, такого рода эффекты не ограничиваются конденсаторами. Индуктивности будут оказывать противоположное влияние: шунтирующие катушки индуктивности вызывают сдвиг фазы от 0° (ниже fср) до +90° (значительно выше fср), в то время как последовательно включенные катушки индуктивности вызывают сдвиг фазы от 0° (выше fср) до -90° (ниже fср) , Однако в этом случае необходимо быть осторожным, чтобы не создавать проблемных замыканий на землю, поскольку катушки индуктивности для постоянного тока будут представлять собой короткое замыкание.
Заключение
Мы заложили основу для понимания сдвига фазы в аналоговых схемах. Рассматривая выход схемы как источник с выходным сопротивлением, мы можем эффективно моделировать влияние реактивных нагрузок на фазу схемы. Таким образом, можно моделировать как пассивные, так и активные схемы, что дает нам полезные инструменты для простого анализа и проектирования. В следующей статье мы проверим эти концепции, применив их к схемам на операционных усилителях и к резонансным контурам.
Оригинал статьи:
Теги
Аналоговые цепиЕмкостная связьСдвиг фазыУсилительСохранить или поделиться
Про распространённые кроссоверы I+II и сдвиг фаз на 90 градусов. — Автозвук во всех его проявлениях
1. Почти правильно. Фильтр 1-го порядка крутит фазу на 90 градусов, фильтр 2-го порядка — на 180, но такие значения достигаются только в полосе затухания, где сигнал уже подавлен, а в полосе пропускания фазовый сдвиг любого фильтра стремится к нулю. В области частоты среза фильтра происходит плавный переход фазы от 0 к 90 или 180 градусам (в зависимости от порядка, п*90), на самой частоте среза наклон ФЧХ фильтра будет максимальным, поэтому фазовая рассогласованность ваших излучателей будет наблюдаться в сравнительно узком диапазоне и будет зависеть в числе прочего и от выбора частот среза ФНЧ мидбаса и ФВЧ пищалки.Из теории известно, что кроссовер первого порядка сдвигает фазу на 90 градусов, второго — на 180 градусов и т.
д.
Вопросы:
1. В акустике Focal 165 V1 (VB) стоит кроссовер I+II. Получается, что мидбас и твитер работают не в фазе?
2. Если на г.у. (P88RS) при поканалке этой же акустики имитируется аналогичный кроссовер I+II, г.у. исправляет сдвиг фаз или нет?
3. Если мидбасы обрезаются снизу головным устройством крутизной 18дб, а встроенные фильтры сабвуфера обрезают верха сабвуфера с крутизной 24 дб, стоит ли волноваться о сдвиге фаз между мидбасами и сабвуфером?Спасибо за терпеливые ответы на может быть элементарные вопросы.
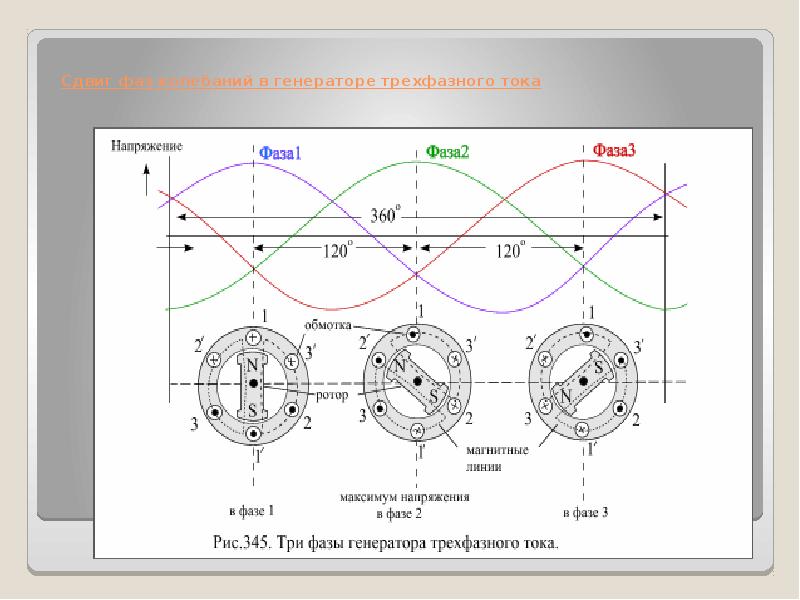 Такая фазовая рассогласованность не страшна, главное не увлекаться фильтрами высоких порядков, при их применении пропорционально увеличивается групповое время задержки (ГВЗ), ухудшается переходная характеристика.
Такая фазовая рассогласованность не страшна, главное не увлекаться фильтрами высоких порядков, при их применении пропорционально увеличивается групповое время задержки (ГВЗ), ухудшается переходная характеристика.2. Нет, не исправляет. Фильтры относятся к числу минимально-фазовых цепей, то есть АЧХ и ФЧХ фильтра жестко взаимосвязаны, более того, ФЧХ фильтра не зависит от способа его реализации, будь он активный или пассивный, аналоговый или цифровой или даже механический.
3. Волноваться или нет — решайте сами, резонансная частота саба в оформлении находится в полосе его основной работы, а на частоте резонанса динамика ФЧХ нелинейна, так что абсолютной фазовой линейности все равно не достичь. Да и не очень-то она нужна, не все ее слышат. А вот в районе раздела саб-мидбас несфазированность более 90 градусов слышат почти все. Тут может помочь плавный фазовращатель на усилителе саба или, на крайний случай, переброс полярности акустических проводов к сабу.
| « НазадФазовые характеристики многополосной акустики 07.01.2014 03:56 Фазовые характеристики многополосных акустических систем
Фазировка многополосной ситемы — очень важный шаг при её настройке. Для кого-то нижеописанное кажется очевидным, а кто-то и понятия не имел о фазировке. Раз уж речь выше зашла о правильном подключении динамиков в многополосной системе в соответствии с подводимой фазой, не лишним будет напомнить о неизбежных фазово-временных задержках, вносимых разделительными фильтрами. То есть тот пассивный фильтр, который стоит перед динамиком, сдвигает фазу проходящего сигнала, поэтому вероятная полярность подводимого к динамику сигнала может меняться, что может потребовать соответственно обратной полярности подключаемого к выходу динамика для восстановления фазы в данной полосе частот. Вариантов решений для точного подгона фаз на частоте стыковки полос очень немного. Есть очень и очень дорогой способ, применяемый в цифровой АС фирмы «Meridian», это применение цифровых же линий задержки. Сколько стоит используемая в схеме обработки звукового сигнала 36-битная разрядность, можете себе представить. Намного более простым способом, который использую я для стыковки двух полос, СЧ и ВЧ, может служить сдвиг динамика одной полосы относительно динамика смежной полосы по глубине от слушателя, так мы можем выставить необходимый фазово-временной сдвиг до полной синфазности и синхронности смежных полос. Реально, сдвиг фаз существует и в пределах полосы частот, воспроизводимой даже одним динамиком, что еще усложняет настройку, и требуется хотя бы правильная стыковка граничных частот (чтобы вращение фаз оставалось хотя бы плавным), то есть, когда на частоте раздела НЧ-СЧ полос диффузор НЧ-динамика начал двигаться вперед, диффузор СЧ-динамика должен одновременно двигаться в эту же сторону. Если он смещается в обратную, то разность фаз равна 180 градусов, и следует поменять полярность динамиков. При смене параметров элементов разделительных фильтров (например для смены частот среза) их фазовые характеристики опять меняются. Почему расчет фильтров — дело вдвойне трудоемкое, так как амплитудные, частотные, фазово-временные характеристики взаимосвязаны, изменение одних затрагивает другие. Утешением может служить разве то, что в массе акустических систем за фазовыми характеристиками на стыке полос при разработке вообще не следили, уделяя внимание лишь АЧХ да характеристической чувствительности, декларируемым в паспорте. Написано 19.07.2000. Игорь Илларионов Источник: http://audio.goldprivacy.com/index.php?button=Button2&articl=0 |
Можно ли сдвинуть фазу одного гармонического ранга, не сдвигая остальную часть искаженного сигнала?
Концептуально, то, что вы предлагаете, похоже, похоже на передачу всего тока ветви сети через систему, которая извлекает определенные гармонические токи и вводит их обратно в сетку с другим фазовым отношением к основному, чтобы отменить исходящие гармоники. в другой ветке. Передача всего тока ветви через любую систему будет менее эффективной, чем какой-либо активный или пассивный фильтр, который будет обрабатывать только одну или несколько конкретных гармоник.
Похожая концепция заключается в том, чтобы основные источники, генерирующие гармоники, изменяли свою стратегию создания формы волны таким образом, чтобы иметь тенденцию подавлять друг друга. Я нашел документ, связанный с этим, но я сделал ошибку, пытаясь спасти его. Я постараюсь найти его снова и опубликовать ссылку позже.
Добавлена справочная информация выше:
Армстронг, Мэтью; Аткинсон, DJ; Джонсон, СМ; Abeyasekera, TD, «Подавление гармоник низкого порядка в системе с несколькими инверторами через сеть с рандомизацией параметров управления», в Power Electronics, IEEE Transactions on, vol.20, no.4, pp.885-892, July 2005 doi: 10.1109 /TPEL.2005.850949 Аннотация: В системах с несколькими инверторами, подключенными к сети, нормально синхронизировать выходной ток каждого инвертора с общим сетевым напряжением. Любые недостатки контроллера тока, которые приводят к гармоникам низкого порядка, также синхронизируются с общим сетевым напряжением. В результате гармоники, создаваемые отдельными преобразователями, показывают высокую степень корреляции и имеют тенденцию быть аддитивными. Каждый контроллер может быть настроен для достижения разного профиля гармоник, так что подавление гармоник может происходить в общей системе, тем самым снижая общий уровень гармонических искажений тока. Тем не менее, связь между инверторами не требуется. В этой статье представлены экспериментальные результаты, демонстрирующие альтернативный подход, который заключается в том, чтобы настроить автоматическую настройку каждого преобразователя с помощью случайного компонента. Это приводит к гармоническому выходному спектру, который изменяется со временем, но не коррелирует с гармоническим спектром любого другого инвертора в системе. Сетевые гармоники от всех инверторов подвергаются определенной степени подавления, и общая система обеспечивает чистое улучшение качества электроэнергии. Ссылка на сайт
Каждый контроллер может быть настроен для достижения разного профиля гармоник, так что подавление гармоник может происходить в общей системе, тем самым снижая общий уровень гармонических искажений тока. Тем не менее, связь между инверторами не требуется. В этой статье представлены экспериментальные результаты, демонстрирующие альтернативный подход, который заключается в том, чтобы настроить автоматическую настройку каждого преобразователя с помощью случайного компонента. Это приводит к гармоническому выходному спектру, который изменяется со временем, но не коррелирует с гармоническим спектром любого другого инвертора в системе. Сетевые гармоники от всех инверторов подвергаются определенной степени подавления, и общая система обеспечивает чистое улучшение качества электроэнергии. Ссылка на сайт
Вот новая статья, написанная некоторыми из тех же авторов, что и ссылка, на которую вы ссылались:
Arghandeh, R .; фон Мейер, A .; Бродвотер Р. «Фазорский подход к оценке гармоник из нескольких распределенных энергетических ресурсов», на общем собрании PES | Конференция и выставка, 2014 IEEE, том, № 1, с. 1-5, 27-31 июля 2014 г.
1-5, 27-31 июля 2014 г.
Вот статья об измерении гармоник, включая информацию о фазе:
Чакир, М .; Камва, я .; Ле Хай, «Расширенные алгоритмы C37.118.1 PMU для совместного отслеживания фундаментальных и гармонических фаз в системах с напряжением питания и микросетями», в разделе «Доставка энергии», «Транзакции IEEE», том 29, № 3, с. 1465-1480. Июнь 2014
Фазировка акустических систем | ldsound.ru
Итак, требуется правильно сфазировать частотные полосы в АС. Для начала все же отмечу, что фильтры на стыке желательно иметь одного порядка – в этом случае фазовые характеристики их идут в целом «параллельно», обеспечивая достаточно стабильное значение электрического рассогласования. В противном же случае оно будет сильно меняться в полосе совместного звучания и говорить об удачной взаимной фазировке по всей полосе уже намного сложнее, ибо всегда найдется участок, где полосы будут «мешать» друг другу.
Предположим, что фильтр рассчитан качественно и взаимное рассогласование достаточно постоянно. У нас есть два варианта фазировки прямая и обратная – в каком-то из вариантов вектора будут скорее складываться, чем вычитаться – именно такая фазировка и будет правильной. Кстати, это и есть главный критерий – при правильной фазировке общая чувствительность АС возрастает.
У нас есть два варианта фазировки прямая и обратная – в каком-то из вариантов вектора будут скорее складываться, чем вычитаться – именно такая фазировка и будет правильной. Кстати, это и есть главный критерий – при правильной фазировке общая чувствительность АС возрастает.
Сама технология:
Начинаем с перехода бас/середина (пусть колонки имеют 3 полосы). Отключаем пищалку (ВЧ) и пробуем варианты. При правильном включении середина звучит лучше, но главный критерий – чувствительность, т.е. «комфортная» громкость в комнате достигается при меньшем значении регулятора громкости на усилителе, причем это, как правило, заметная величина.
Далее подключаем пищалки и фазируем второй переход в целом по этой же схеме. Просто для этого перехода есть еще один критерий, позволяющий при обычном прослушивании сразу сказать, верна ли фазировка. Если фазировка нарушена, то в звуке существует некая «граница» по вертикали – своего рода плоскость. При переходе через эту «плоскость» звук меняется в зависимости «над» или «под».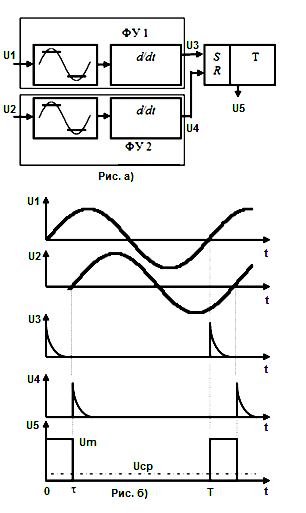 Поскольку неверная фазировка – достаточно распространенная ошибка, то частенько приходится видеть мучения хозяев акустики, которые всячески наклоняют ее назад, пытаясь бороться с указанным эффектом. При правильной фазировке подобная «граница» в звуке, как правило, отсутствует…
Поскольку неверная фазировка – достаточно распространенная ошибка, то частенько приходится видеть мучения хозяев акустики, которые всячески наклоняют ее назад, пытаясь бороться с указанным эффектом. При правильной фазировке подобная «граница» в звуке, как правило, отсутствует…
Ну и еще один весьма интуитивный, но субъективно понятный критерий. Правильно сфазированные колонки звучат так, «как если бы под фальшпанелью был просто один большой динамик» – т.е. воображение вполне может дорисовать «картинку» и образ окажется устойчивым. В случае ошибок фазировки этот образ практически сразу разваливается. При правильной фазировке звук «простой». В случае неверной фазировки его можно описать как «диковинный», иногда в чем-то «эффектный», но никак не «простой». Однако «простота» обычно многого стоит – более качественный усилитель тоже звучит как бы «проще»…
При правильной фазировке звук «открытый», а именно создается впечатление, что фонограмма звучит вне колонок – «висит в воздухе». В случае неправильной фазировки звук, так или иначе, прячется «внутрь» ящика – он может субъективно нравиться своей «эффектностью», но исходить будет как бы «изнутри».
В случае неправильной фазировки звук, так или иначе, прячется «внутрь» ящика – он может субъективно нравиться своей «эффектностью», но исходить будет как бы «изнутри».
Вот, пожалуй, и все критерии + методика. Точнее ушей пока инструмента нет… Кстати, при применении фильтров 2-го порядка фазу на частотном переходе нужно менять – если все полосы выставлены синфазно (а такое имеет место почти всегда), то обычно требуется «перевернуть» полярность на середине (СЧ).
Автор: Владимир Шабунин (iXBT)
Выпрямитель с малым уровнем пульсаций
Источники питания обычно собираются по классической схеме: выпрямитель переменного напряжения, конденсатор фильтра, стабилизатор. Однако в ряде случаев можно обойтись без фильтра, который зачастую и является самым громоздким узлом источника питания. Известно, что конденсатор, включенный в цепь переменного тока, сдвигает его фазу на 90 градусов. Такой фазосдви-гающий конденсатор применяют, например, при подключении трехфазного двигателя к однофазной сети.
Емкостный фильтр сглаживает пульсации выходного напряжения однофазных выпрямителей, создавая приемлемое значение его постоянной составляющей, причем, чем больше емкость конденсаторов фильтра, тем меньше пульсации и, соответственно, больше постоянная составляющая. В трехфазных же выпрямителях, благодаря взаимному перекрытию полуволн напряжения, постоянная составляющая больше, что во многих случаях позволяет обойтись без емкостного фильтра.
Если в однофазном выпрямителе применить фазосдвигающий конденсатор, обеспечивающий взаимное перекрытие полуволн выпрямленного напряжения, во многих случаях при постоянной нагрузке можно обойтись без громоздкого емкостного фильтра или существенно уменьшить его емкость. Схема подобного стабилизированного выпрямителя показана на рис. 6.9.
Трехфазный выпрямитель VD1…VD6 подключен к источнику переменного напряжения через активное (резистор R1) и емкостное (конденсатор С1) сопротивления. Выходное напряжение выпрямителя стабилизирует стабилитрон VD7. Конденсатор (или несколько параллельно включенных конденсаторов для получения необходимой емкости) должен быть рассчитан на работу в цепях переменного тока. Здесь, например, подойдут два параллельно включенных конденсатора К73-17 емкостью по 0,1 мкФ,
Конденсатор (или несколько параллельно включенных конденсаторов для получения необходимой емкости) должен быть рассчитан на работу в цепях переменного тока. Здесь, например, подойдут два параллельно включенных конденсатора К73-17 емкостью по 0,1 мкФ,
Описанный выпрямитель можно применять там, где необходимо уменьшить габариты электронного устройства, поскольку размеры оксидных конденсаторов емкостного фильтра, как правило, больше, чем фазосдвигающего конденсатора сравнительно небольшой емкости. Выигрыш в габаритах особенно заметен в сетевых выпрямителях, когда выпрямляют непосредственно сетевое напряжение без использования понижающего трансформатора.
Еще одно преимущество предложенного варианта состоит в том, что потребляемый ток практически постоянен (в случае постоянной нагрузки), тогда как в выпрямителях с емкостным фильтром в момент включения пусковой ток значительно превышает установившееся значение (вследствие заряда конденсаторов фильтра), что в некоторых случаях крайне нежелательно.
Описанное устройство можно применять и с последовательными стабилизаторами напряжения, имеющими постоянную нагрузку, а также с нагрузкой, не требующей стабилизации напряжения.
Phys 3041 Notes E
Phys 3041 Notes EPhys 3041 Заметки
© 1997 Джонатан Карты. Эти примечания не могут быть распространены или дублированы в какой-либо форме, печатной или электронной, без разрешения. Разрешается устанавливать электронные гипертекстовые ссылки только на эти оригинальные документы.RC фильтры
Мы рассмотрим здесь две простые схемы, в которых последовательно используются резистор и конденсатор. Эти две конфигурации образуют фильтры нижних и верхних частот.В фильтре входное напряжение подается на элемент схемы (здесь последовательная комбинация R-C), а выходное напряжение снимается с некоторой части этого элемента схемы. Фильтр будет создавать измененную версию входного сигнала, и изменения, которые обычно происходят, будут зависеть от частоты входного сигнала.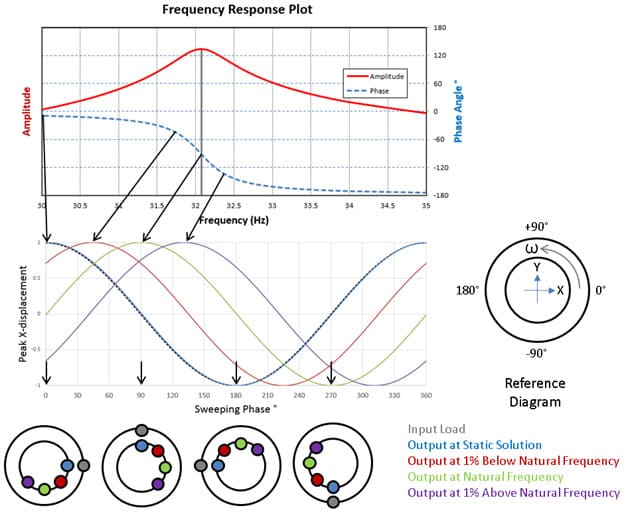 Для наших простых фильтров здесь выходное напряжение меньше входного, и между входным и выходным сигналами будет разность фаз. Эти фильтры представляют собой линейные схемы, в которых синусоидальный входной сигнал воспроизводится как синусоидальный выходной сигнал.
Для наших простых фильтров здесь выходное напряжение меньше входного, и между входным и выходным сигналами будет разность фаз. Эти фильтры представляют собой линейные схемы, в которых синусоидальный входной сигнал воспроизводится как синусоидальный выходной сигнал.Фильтр низких частот
Фильтр нижних частот представляет собой простую последовательную RC-цепь, в которой выходное напряжение принимается как падение напряжения на конденсаторе.Анализ схемы прост. Комбинация RC рассматривается как делитель напряжения. Процедура определения выходного напряжения аналогична анализу резистивного делителя напряжения, за исключением того, что теперь мы должны использовать импеданс конденсатора и провести анализ комплексных напряжений и токов, не забывая брать только действительную часть нашего результаты, когда мы закончим.Процесс прост. Найдите полное последовательное сопротивление комбинации RC. Используйте это, чтобы найти ток, протекающий через комбинацию серии RC. Затем найдите (комплексное) выходное напряжение используя обобщение закона Ома, V = IZ .
 В большинстве подобных ситуаций часто проще вычислить отношение выходного напряжения к входному. V out (t) / V in (t) , что мы будем называть усилением. (Фактически, для этих фильтров коэффициент усиления меньше 1, так что, собственно говоря, сигнал ослабляется.Поскольку позже мы часто будем сталкиваться с таким соотношением в связи с усилителями, мы все равно будем называть это соотношение усилением, хотя это слово обычно предполагает, что выход больше, чем вход.) Это соотношение будет сложным, отражая как изменение в амплитуда и фаза сигнала на выходе. Величина отношения также называется частотной характеристикой фильтра, поскольку обычно она является функцией частоты сигнала.
В большинстве подобных ситуаций часто проще вычислить отношение выходного напряжения к входному. V out (t) / V in (t) , что мы будем называть усилением. (Фактически, для этих фильтров коэффициент усиления меньше 1, так что, собственно говоря, сигнал ослабляется.Поскольку позже мы часто будем сталкиваться с таким соотношением в связи с усилителями, мы все равно будем называть это соотношение усилением, хотя это слово обычно предполагает, что выход больше, чем вход.) Это соотношение будет сложным, отражая как изменение в амплитуда и фаза сигнала на выходе. Величина отношения также называется частотной характеристикой фильтра, поскольку обычно она является функцией частоты сигнала. Коэффициент усиления G можно записать в более удобной форме, но с преобразованием в экспоненциальный формат.Умножьте числитель и знаменатель на iwC , а затем на комплексное сопряжение, 1 — iwRC , полученного знаменателя.
В результате знаменатель становится действительным числом, а числитель остается в стандартной декартовой форме для комплексного числа: x + iy ,
.
 который можно легко преобразовать в экспоненциальный формат:
который можно легко преобразовать в экспоненциальный формат: где фаза равна
.
Выходное напряжение затем легко вычисляется из этого коэффициента усиления и входного напряжения:
Окончательный результат находится, если не забыть взять действительную часть комплексного выходного напряжения: .
Это выявляет два важных аспекта: амплитуда выходного сигнала уменьшается по сравнению с входным, и присутствует фазовый сдвиг, так что выходное напряжение отстает от входного. Амплитуда уменьшается при увеличении частоты, усиление стремится к нулю при увеличении частоты. Сдвиг фазы почти равен нулю на низких частотах, но возрастает, достигая четверти цикла на очень высоких частотах, где амплитуда уже незначительна.Выходное напряжение практически идентично входному напряжению как по амплитуде, так и по фазе для низкочастотных сигналов. Высокочастотные сигналы сильно ослаблены и сдвинуты по фазе. Поэтому схема называется фильтром нижних частот: низкочастотные сигналы практически не затрагиваются, в то время как высокочастотные сигналы ослабляются или отфильтровываются.
 Такое поведение обычно отображается в виде графика зависимости величины усиления (т.е. без какой-либо информации о фазовом сдвиге) от частоты, известного как частотная характеристика.
Такое поведение обычно отображается в виде графика зависимости величины усиления (т.е. без какой-либо информации о фазовом сдвиге) от частоты, известного как частотная характеристика.Грубая разделительная линия между высокими и низкими частотами выбирается установкой безразмерной величины wRC равной 1. Это происходит, когда w = 1 / RC . Изделие RC несет в себе измерения времени и часто называется постоянной времени цепи. Ограничение низких частот происходит для частот, которые удовлетворяют требованиям wRC << 1. Здесь коэффициент усиления практически равен единице, а фазовый сдвиг незначителен. Высокие частоты соответствуют тем, которые удовлетворяют требованиям wRC >> 1 или w >> 1/ RC .Здесь усиление невелико и составляет примерно 1/ wRC , а фазовый сдвиг приближается к запаздыванию 90 o .
Причина опережения фазы в RC-фильтре высоких частот
Переменный ток всегда отстает от напряжения в конденсаторе, независимо от того, используется он последовательно или параллельно. Импеданс (f) всегда определяет ток, протекающий через него, с переменным напряжением на нем.
Импеданс (f) всегда определяет ток, протекающий через него, с переменным напряжением на нем.
Но отношение импеданса как функция частоты определяет как передаточную функцию, так и фазовый сдвиг относительно, скажем, сопротивления, где точка излома составляет 45 градусов, когда R = Zc (f) с запаздывающим током затем приближается к 90 градусов в зависимости от положения крышки. Серия или шунт и, конечно, частота.
Если вы понимаете, это легко визуализировать с помощью фазоров и математики.
Возможно, сложнее интуитивное понимание.
Передаточная функция XY out vs in показана как для HPF, так и для LPF. и передаточная функция каждой части показана XY = VI, где резистор всегда представляет собой линейную линию под 45 градусов для наклона V / I, но конденсаторы всегда с запаздыванием на 90 градусов.
Таким образом, положение Cap определяет, является ли фаза выхода частично опережающей или запаздывающей, когда напряжение на конденсаторе падает почти на 0 выше той же точки останова. Мы интуитивно рассматриваем Caps как короткие замыкания, когда Zc << R, и поэтому при затухании в LPF оно всегда составляет 90 градусов. при высоком f и в HPF он всегда смещен на 0 градусов или наружу = внутрь для наклона перехода в зависимости от масштабов для XY, выглядящих как ~ 45 градусов более или менее, ЕСЛИ они были равными масштабами.
Мы интуитивно рассматриваем Caps как короткие замыкания, когда Zc << R, и поэтому при затухании в LPF оно всегда составляет 90 градусов. при высоком f и в HPF он всегда смещен на 0 градусов или наружу = внутрь для наклона перехода в зависимости от масштабов для XY, выглядящих как ~ 45 градусов более или менее, ЕСЛИ они были равными масштабами.
Итак, вкратце, каждый R и C на графиках XY или Y / X = I / V на графиках Y / X и передаточная функция X / Y = Out / in
Итак, я провел здесь симуляцию.
Несмотря на то, что оба фильтра качаются в замедленном темпе, они должны охватывать почти 3 декады (от 50 Гц до 20 кГц), чтобы показать полный сдвиг фазы на 90 для каждого фильтра, где он смещается наиболее быстро в точке излома f-3 дБ или 0.707 ввода.
Обратите внимание, что только передаточная функция HPF достигает вертикального или 90-градусного фазового сдвига при max f, чтобы соответствовать фазовому сдвигу I / V в конденсаторе, когда он имеет близкое к 0 напряжение.
Таким образом, нагрузка V (R) показывает ток конденсатора I (C), проходящий через нее, на 90 градусов относительно входа X или + 90 градусов. потому что ток крышки ВСЕГДА является запаздывающим током или опережающим напряжением на 90 град.
Обзор .Фильтр нижних частот пропускает низкие частоты и отклоняет высокие
частоты от входного сигнала. И наоборот для фильтра высоких частот. В
простейший из этих фильтров может быть построен всего из двух недорогих электрических
компоненты. В соответствующих частотных диапазонах эти схемы также объединяют
и дифференцировать (соответственно) входной сигнал.Фильтр нижних частотRC-фильтр нижних частот первого порядка — это просто RC-цепочка, проходящая через вход, с выходом через конденсатор.Мы предполагаем, что на выходе цепи не подключен или подключен только к высокому импедансу, так что ток одинаков как в R, так и в C. На этой частоте коэффициент усиления = 1 / √2 = 0,71, как показано на графике. При ω = ω o разность фаз составляет π / 4 радиан или 45, как показано на график φ (ω). Фильтр высоких частот
Применение фильтров и демонстрацииRC и другие фильтры очень широко используются при выборе сигналов (которые являются напряжением компоненты, которые один хочет) и отклонение шума (те, которые не нужны). Низкий проход Фильтр может «сгладить» источник питания постоянного тока: разрешить постоянный ток, но ослабить компоненты переменного тока.И наоборот, фильтр верхних частот может пропускать сигнал в транзистор и из него. каскад усилителя, не пропуская и не влияя на смещение постоянного тока транзистора. Они также может использоваться для сортировки высоких частот от низкочастотных компонентов в чисто Сигнал переменного тока. Конденсаторы часто используются в перекрестных сетях для громкоговорителей,
для подачи высоких частот к «твитеру» (небольшому, легкому динамику) и
низкие частоты на «вуфер» (большой массивный динамик). Включаем звук
примеры здесь в качестве демонстрации. Конденсаторы часто используются в перекрестных сетях для громкоговорителей,
для подачи высоких частот к «твитеру» (небольшому, легкому динамику) и
низкие частоты на «вуфер» (большой массивный динамик). Включаем звук
примеры здесь в качестве демонстрации.
Интегратор
На фотографии вверху страницы изображена треугольная волна на входе RC. интегратор и результирующий результат. Дифференциатор
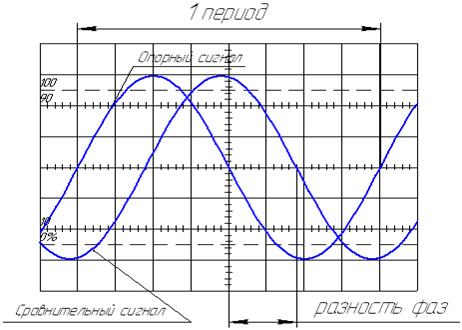 Такие усилители
также может использоваться для сложения, вычитания и умножения напряжений. Аналоговый компьютер
представляет собой комбинацию таких схем и может использоваться для одновременного решения дифференциальных
и интегральные уравнения очень
быстро. Такие усилители
также может использоваться для сложения, вычитания и умножения напряжений. Аналоговый компьютер
представляет собой комбинацию таких схем и может использоваться для одновременного решения дифференциальных
и интегральные уравнения очень
быстро.Вернуться к цепям переменного тока
|
Знакомство с аналоговыми фильтрами
Сотни, если не тысячи различных типов фильтров были разработаны для удовлетворения потребностей различных приложений.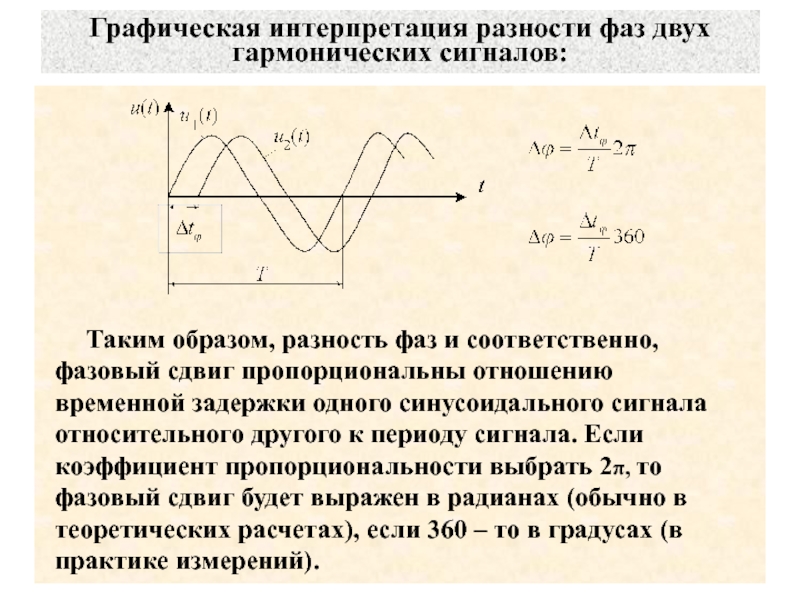 Несмотря на такое разнообразие, многие фильтры можно описать несколькими общими характеристиками. Первым из них является частотный диапазон их полосы пропускания . Полоса пропускания фильтра — это диапазон частот, в котором он будет пропускать входящий сигнал. Частоты сигнала, лежащие вне полосы пропускания, ослабляются. Многие фильтры попадают в одну из следующих категорий отклика в зависимости от общей формы их полосы пропускания.
Несмотря на такое разнообразие, многие фильтры можно описать несколькими общими характеристиками. Первым из них является частотный диапазон их полосы пропускания . Полоса пропускания фильтра — это диапазон частот, в котором он будет пропускать входящий сигнал. Частоты сигнала, лежащие вне полосы пропускания, ослабляются. Многие фильтры попадают в одну из следующих категорий отклика в зависимости от общей формы их полосы пропускания.
Фильтры нижних частот пропускают низкочастотные сигналы, блокируя высокочастотные сигналы.Полоса пропускания колеблется от постоянного тока (0 Гц) до угловой частоты F C .
Фильтры верхних частот пропускают высокочастотные сигналы, блокируя при этом сигналы постоянного тока и низкочастотные сигналы. Полоса пропускания варьируется от угловой частоты (F C ) до бесконечности.
Полосовые фильтры пропускают только сигналы между двумя заданными частотами, блокируя более низкие и высокие сигналы. Полоса пропускания находится между двумя частотами: F L и F H . Сигналы между DC и F L блокируются, как и сигналы от F H до бесконечности.Полоса пропускания этих фильтров часто характеризуется полосой пропускания, симметричной относительно центральной частоты.
Полоса пропускания находится между двумя частотами: F L и F H . Сигналы между DC и F L блокируются, как и сигналы от F H до бесконечности.Полоса пропускания этих фильтров часто характеризуется полосой пропускания, симметричной относительно центральной частоты.
Полосовые фильтры блокируют сигналы, возникающие между двумя заданными частотами, F L и F H . Полоса пропускания делится на низкую сторону (от DC до F L ) и высокую сторону (от F H до бесконечности). По этой причине часто проще указать полосовой фильтр по ширине и центральной частоте его полосы задерживания. Полосовые фильтры также называют режекторными фильтрами, особенно когда полоса заграждения узкая.
На рисунке 1 показано, как каждый из этих фильтров работает с входным сигналом с качающейся частотой.
|
В примерах частота сигнала непрерывно увеличивается от низкой частоты к высокой.Когда частота сигнала находится в пределах полосы пропускания фильтра, фильтр пропускает сигнал. Когда сигнал выходит за пределы полосы пропускания, фильтр начинает ослаблять сигнал.
Обратите внимание, что переход от полосы пропускания к полосе заграждения является постепенным процессом, при котором отклик фильтра непрерывно уменьшается. Хотя вы можете сделать этот переход произвольно резким (за счет сложности фильтра), он никогда не может быть мгновенным, по крайней мере, в фильтрах, физически реализуемых с помощью современных технологий.
Графики Боде и Фаза
Графики Боде описывают поведение фильтра, связывая величину отклика фильтра (усиления) с его частотой. Пример этого типа графика показан на рисунке 2.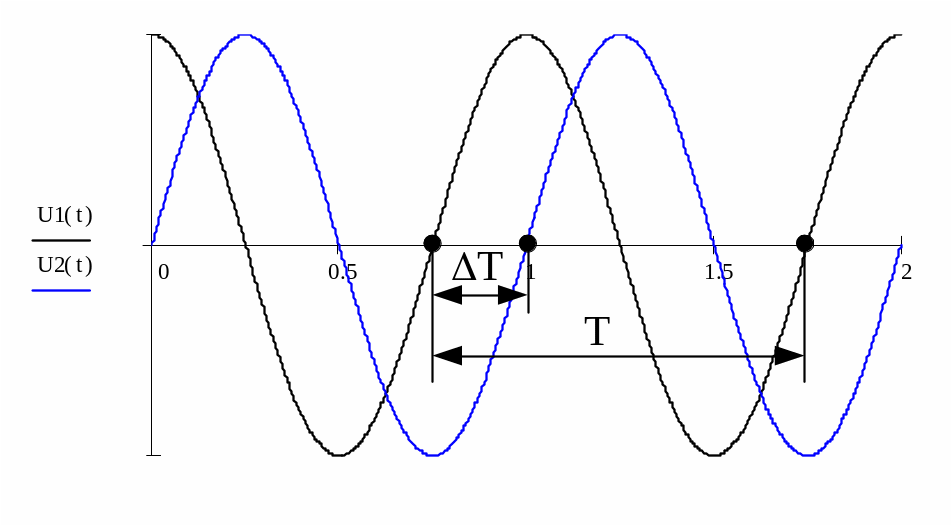
|
Ключевой особенностью этого графика является то, что обе оси имеют логарифмическую шкалу. Горизонтальная ось [s представляет частоту, измеренную в герцах, а вертикальная ось — в децибелах.
Децибелы — это логарифмическая мера мощности, где увеличение на 10 дБ означает 10-кратное увеличение мощности. Поскольку мощность в электрическом сигнале связана с квадратом напряжения, 10-кратное увеличение напряжения сигнала представлено приращением 20 дБ.Преимущество построения кривой отклика фильтра на графике Боде состоит в том, что он обеспечивает простой способ описать отклик фильтра на нескольких десятках частот и на несколько порядков величины. Децибелы усиления фильтра относятся к соотношению между входным и выходным напряжениями:
Децибелы усиления фильтра относятся к соотношению между входным и выходным напряжениями:
| (1) |
Кривая отклика нижних частот на рисунке 2 также иллюстрирует несколько характеристик, общих для многих типов. фильтров.
Угловая частота. Поскольку реальный фильтр постепенно спадает, вы обычно указываете частоту излома как частоту, на которой отклик составляет 1/2 (0,707) отклика в полосе пропускания. Поскольку инженеры-электронщики традиционно описывают относительную мощность сигнала в децибелах, частоту также называют точкой –3 дБ.
Коэффициент затухания. Переход между полосой пропускания и полосой заграждения является непрерывной функцией, а скорость, с которой происходит этот переход, является общим показателем, используемым для выбора фильтра.Обычно вы выражаете коэффициент затухания в децибелах за декаду, где декада — это коэффициент 10 по частоте.
Высокий коэффициент затухания помогает фильтру различать сигналы одинаковой частоты и обычно является желательной характеристикой. Скорость затухания также связана с порядком фильтра. Для фильтра нижних или верхних частот коэффициент затухания будет в –20 раз больше порядка фильтра, в дБ / декаду. Например, фильтр первого порядка будет иметь коэффициент ослабления –20 дБ / декаду, а фильтр четвертого порядка будет иметь коэффициент ослабления, приближающийся к –80 дБ / декаду.
Пульсация полосы пропускания. Для многих типов фильтров характеристика не уменьшается монотонно по мере того, как частота перемещается от центра полосы пропускания к полосе заграждения. Величина отклика может изменяться внутри полосы пропускания, и это изменение называется пульсацией полосы пропускания . Опять же, этот показатель также указывается в децибелах. Пульсации полосы пропускания вызывают усиление частотных составляющих сигнала до разной степени. Это приводит к искажению формы сигнала, проходящего через фильтр.
Помимо воздействия на амплитуду сигнала, фильтр также может вызывать изменения фазы компонентов сигнала. На рисунке 3 показаны амплитудные и фазовые характеристики простого фильтра нижних частот.
|
Если вы пропустите синусоидальные сигналы разных частот через этот фильтр, фильтр не только ослабит более высокую частоту
|
сигналов, но также сдвигает их фазу.
Обратите внимание, что график фазового сдвига описывает сдвиг синусоидальных сигналов. Фазовая характеристика фильтра также важна в случае несинусоидальных сигналов, поскольку фазовые сдвиги искажают формы сигналов. Это связано с тем, что несинусоидальные сигналы можно рассматривать как комбинации синусоидальных сигналов различных частот. Сдвиг фазы этих компонентов относительно друг друга изменит форму всей формы сигнала.
Схемы фильтров 101
Хотя конструкция схем фильтров может потребовать сложного анализа, вы можете развить понимание основных концепций с минимумом математики и теории схем. В качестве отправной точки рассмотрим резистивный делитель напряжения, показанный на рисунке 4. Схема обеспечивает выходное напряжение, которое составляет фиксированную долю входного напряжения. Соотношение между входным и выходным напряжениями определяется следующим образом:
| (2) |
Поскольку характеристики резистора (в идеальном случае) не меняются в зависимости от частоты, соотношение действительно для сигналов постоянного и переменного тока.Однако, если номиналы резисторов зависят от частоты, соотношение выходного и входного напряжения также станет зависимым от частоты.
Если вы рассматриваете сопротивление переменного тока как отношение между напряжением на компоненте и током через него, то индукторы и конденсаторы демонстрируют сопротивление, зависящее от частоты подаваемого сигнала. Однако существует значительная разница между сопротивлением резистора и сопротивлением катушки индуктивности или конденсатора. Для синусоидальных сигналов формы напряжения и тока в резисторе всегда совпадают по фазе.
В случае конденсаторов и катушек индуктивности ток на 90 ° не совпадает по фазе с напряжением. Разница выражается в том, что сопротивление последних устройств обозначается как мнимый , и они представлены с помощью мнимых чисел (j). Термин импеданс обозначает сопротивления, которые имеют мнимые составляющие. Для сигналов переменного тока с частотой f комплексные импедансы резисторов (Z R ), конденсаторов (Z C ) и катушек индуктивности (Z L ) определяются по формуле:
| (3) |
В то время как резистор имеет постоянный импеданс по частоте, импеданс конденсатора уменьшается с увеличением частоты, а сопротивление катушки индуктивности увеличивается.
С помощью инструмента комплексного импеданса вы можете анализировать поведение простых фильтров, основанных на схемах делителя напряжения. Рассмотрим схему, показанную на рисунке 5A, в которой конденсатор заменен на нижний резистор в делителе напряжения.
|
По мере увеличения частоты входного сигнала сопротивление конденсатора будет уменьшаться, что приведет к уменьшению выходного сигнала. Подставив комплексный импеданс конденсатора на R B , вы можете выразить выходное напряжение следующим образом:
| (4) |
Из уравнения 4 вы можете увидеть, что при нулевой частоте ( DC) отношение выходного сигнала к входному равно 1, и оно уменьшается с увеличением частоты.Однако сложное выходное напряжение не более интуитивно понятно, чем комплексный импеданс. Взяв величину уравнения 4 (см. Врезку «Они не называют это сложной математикой ни за что»), вы получите соотношение, которое описывает соотношение между величинами входных и выходных синусоидальных сигналов:
| (5) |
Когда вы устанавливаете f = 1 / 2RC, отклик составляет 1/2 или –3 дБ от отклика постоянного тока. Еще одна особенность этого фильтра — коэффициент затухания.Когда частота увеличивается выше частоты –3 дБ, характеристика становится обратно пропорциональной частоте. Отклик уменьшается в 10 раз на каждое увеличение частоты в 10 раз, что дает коэффициент затухания –20 дБ / декаду. Аналогичный анализ можно провести для различных других простых фильтров, основанных на делении напряжения. Фильтр нижних частот, основанный на катушке индуктивности, показан на рисунке 5B, а два фильтра верхних частот и.е. показаны на рисунках 5D и 5E.
Схемы фильтров операционного усилителя
Вы можете выполнить аналогичный анализ на простых схемах, основанных на реализациях, отличных от делителя напряжения.Например, другой схемой, представляющей общий интерес, является усилитель с обратной связью, построенный на основе операционного усилителя (ОУ). Эта схема (см. Рисунок 6A) обеспечивает коэффициент усиления –R f / R i , предполагая идеальный операционный усилитель с бесконечным усилением.
|
Если вы замените резистор обратной связи R f конденсатором C, как показано на рисунке 6B, результирующее усиление в зависимости от частоты будет:
| (6) |
Коэффициент усиления для этой схемы, как и у фильтра нижних частот, обратно пропорционален частоте, но отличается тем, что увеличивается до бесконечности для сигналов постоянного тока. Кроме того, поскольку усиление мнимое, между входом и выходом всегда существует разность фаз 90 ° (т.е.е., схема всегда будет преобразовывать вход cos (x) в выход sin (x)). С точки зрения временной области схема интегрирует свой вход, и по этой причине она называется интегратором .
Замена входного резистора (Ri) нашего оригинального операционного усилителя на конденсатор приводит к цепи с откликом, пропорциональным увеличению частоты (см. Рисунок 6D). Эта схема берет производную от времени входного сигнала, и по этой причине она называется дифференциатором .
|
Хотя существует ряд приложений, в которых прямолинейные графики Боде интегратора и дифференциатора полезны, вы можете создавать более интересные схемы фильтров, используя последовательно-параллельные схемы резисторов и конденсаторов вокруг операционного усилителя.Один простой пример такой сети показан на рисунке 7. В этой схеме реализован фильтр нижних частот.
Хотя в этом фильтре используется больше компонентов, чем в простом RC-фильтре, он позволяет усилить и отфильтровать сигнал за один этап обработки сигнала. Возможно, что более важно, поскольку выходное сопротивление операционного усилителя невелико, вы можете каскадировать каскады фильтров, не беспокоясь об эффектах нагрузки. В первых представленных схемах фильтров, в которых не используются операционные усилители, любая значительная нагрузка на выходе фильтра может изменить его частотную характеристику и усиление.Фильтры, которые содержат схемы усилителя, такие как тот, который представлен в этом разделе, называются активными фильтрами .
Комбинирование простых фильтров
Поскольку вы можете легко каскадировать только что описанные активные фильтры, вы можете легко предсказать поведение комбинаций этих фильтров и использовать их в качестве строительных блоков для построения более сложных схем. Две из более простых комбинаций — это последовательное соединение и параллельное соединение. Последовательное соединение двух фильтров с передаточными функциями g (f) и h (f) приводит к общей передаточной функции g (f) × h (f).При параллельном подключении выходные сигналы фильтров суммируются, а функции фильтров складывают g (f) + h (f).
Соединяя фильтры нижних и верхних частот через последовательное соединение, вы можете создать полосовой фильтр, если угловая частота устройства нижних частот больше, чем частота фильтра верхних частот (см. Рисунок 9A) .
|
И вы можете использовать параллельное соединение, чтобы сделать полосовой или режекторный фильтр, если угловая частота фильтра нижних частот ниже, чем частота фильтра верхних частот (см. Рис. 9Б). Другие устройства, основанные на последовательной и параллельной конфигурациях, могут использоваться для разработки дополнительных фильтров с более сложными характеристиками.
Одна из очевидных серийных комбинаций — это каскадирование идентичных низкочастотных или высокочастотных секций для получения фильтра с более высокой степенью затухания. Например, можно ожидать, что каскадное соединение двух фильтров нижних частот с коэффициентами затухания –20 дБ / декада приведет к одному с
|
–40 дБ / декада. Хотя окончательный коэффициент затухания действительно приблизится к –40 дБ / декаду, резкость «изгиба» фильтра снизится. Это затрудняет создание более избирательного фильтра путем простого каскадирования идентичных разделов.
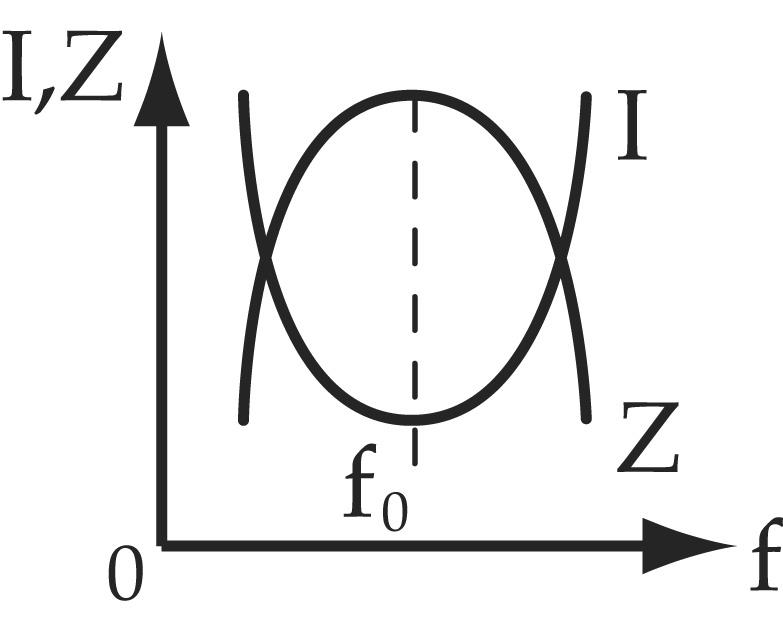
Резонансные цепи
Что делать, если вы замените оба резистора в делителе напряжения конденсаторами и катушками индуктивности? Если вы используете только конденсаторы или только катушки индуктивности, воображаемые компоненты компенсируются, и схема ведет себя как резистивный делитель напряжения, по крайней мере, для сигналов переменного тока.Если вы используете конденсатор для одной ноги и индуктор для другой (см. Рисунок 11A), возникает новое поведение. Если вы подставите мнимые импедансы в уравнение делителя напряжения, вы получите:
| (14) |
Отклик этой схемы полностью реальный, то есть фазового сдвига между входом и выходом нет. Это также фильтр нижних частот, потому что отклик равен единице (1) на постоянном токе и падает до нуля при увеличении частоты.Однако, если вы установите f = 1 / 2LC, знаменатель уравнения отклика станет равным нулю, что означает, что вы получите бесконечное выходное напряжение для конечного входного напряжения. Хотя реальная схема не будет производить бесконечное выходное напряжение, пик все же может быть довольно высоким, с максимальным откликом, возникающим при f = 1 / 2LC. Эта частота называется резонансной частотой контура.
Резонанс — это явление, качественно отличающееся от того, которое может быть получено в схеме пассивного фильтра, состоящей только из резисторов и конденсаторов.Если вы построите график отклика LC-цепи во временной области на ступенчатый вход, вы увидите, что он колеблется или звенит. Резонанс возникает из-за того, что электрическая энергия периодически передается назад и вперед между двумя или более элементами схемы — катушкой индуктивности и конденсатором в приведенном выше случае. Однако энергия в пассивной RC- или RL-цепи течет только в одном направлении, когда цепь движется к установившемуся состоянию. По этой причине эти цепи не колеблются.
Одна полезная особенность цепей LC-фильтров заключается в том, что они имеют более высокие коэффициенты затухания (например,g., –40 дБ / декада), чем RC-фильтры. Это связано с тем, что характеристики схем изменяются со скоростью 1 / f 2 вместо 1 / f. Хотя вы можете получить эту степень затухания путем каскадирования двух RC-фильтров, как обсуждалось выше, резонансный пик LC-цепи позволяет получить более резкий «изгиб» на частоте, на которой фильтр переходит от полосы пропускания к полосе заграждения. Путем включения резистора последовательно с катушкой индуктивности амплитуда пика отклика может быть уменьшена, или затухает, , чтобы контролировать резкость колена.Степень пика в резонансном фильтре может быть определена количественно с помощью показателя, известного как Q фильтра. Для случая RLC-фильтра нижних частот, показанного выше, Q определяется как:
| (18) |
С фильтрами RLC вы также можете получить функции нижних, верхних частот, полосы пропускания и полосы пропускания, переставив элементы схемы. На рисунке 14 показана схема этих фильтров.
|
Возвращение к активным фильтрам
Пассивные фильтры RLC широко используются, поскольку для многих приложений требуются фильтры с высокими коэффициентами затухания и острыми перегибами. К сожалению, для реализации фильтра RLC вам понадобится одна или несколько катушек индуктивности.По сравнению с резисторами и конденсаторами, индукторы имеют тенденцию быть большими, дорогими и имеют плохие допуски. Кроме того, поскольку индукторы генерируют магнитные поля, они могут вызывать нежелательные помехи для других близлежащих компонентов.
|
К счастью, вы можете создавать схемы с резонансом, используя различные топологии схем, состоящие только из резисторов, конденсаторов и усилителей. Один из таких наборов топологий называется , управляемый напряжением источник напряжения (VCVS), фильтры нижних и верхних частот показаны на рисунке 16.
Обе эти схемы обеспечивают фильтры со скоростью затухания –40 дБ / декаду. и более резкие углы, чем каскад из двух фильтров первого порядка.В каждом из них ОУ действует как неинвертирующий усилитель с коэффициентом усиления больше единицы. Коэффициент усиления усилителя определяется по формуле (R 3 + R 4 ) / R 3 .
С интуитивной точки зрения вы можете видеть, что схема, показанная на рисунке 16A, имеет усиление на постоянном токе и спадает при увеличении частоты. Эта схема будет вести себя как фильтр нижних частот. Точно так же, поскольку схема на рисунке 16B имеет свои конденсаторы в пути прохождения сигнала, она будет иметь нулевой отклик при постоянном токе, и отклик будет увеличиваться с увеличением частоты.
И частота среза, и добротность каждого из этих фильтров определяются номиналами конденсаторов (C1 и C2), резисторов (R1 и R2) и коэффициентом усиления усилителя. Для фильтра с максимально плоской полосой пропускания и угловой частотой 1 / 2RC коэффициент усиления усилителя должен быть установлен на 1,586, R 1 = R 2 = R и C 1 = C 2 = C.
|
Недостатком описанных здесь фильтров VCVS является то, что коэффициент усиления полосы пропускания не обязательно равен единице. Когда требуется единичное усиление полосы пропускания, вы можете подключить усилитель как повторитель с единичным усилением. Эта схема называется фильтром Саллена и Кей , и случай нижних частот показан на рисунке 17. Предполагая, что R1 = R2 = R и C1 = C2 = C, угловая частота этого конкретного фильтра определяется выражением f = 1 / 2RC, и коэффициент затухания в цепи также приблизится к –40 дБ / декаду.
Хотя приведенные выше примеры относятся к относительно простым фильтрам второго порядка, их можно использовать в качестве строительных блоков для построения фильтров более высокого порядка и более резких изгибов. Однако теория того, как определять и проектировать эти фильтры более высокого порядка, выходит далеко за рамки данной статьи.
Боковые панели:
|
|
Вызвав макрос проектирования Biquad, вы можете указать частоту излома и Q для желаемого биквада, нажать одну кнопку и получить оптимальный дизайн, перенесенный на экран дизайна PAC-Designer. Моделирование и проверка предложенного проекта могут быть выполнены в среде PAC-Designer за считанные секунды. Когда подходящая конструкция определена, вы можете перенести ее на кремний еще одним щелчком мыши. Общее время, необходимое для перехода от спецификации к рабочему кремнию, может составлять менее пяти минут. Дополнительные макросы проектирования, поставляемые с PAC-Designer, также позволяют аналогичным образом проектировать, оценивать и реализовывать более сложные фильтры более высокого порядка. |
(PDF) Генератор квадратурных сигналов на основе широкополосного фильтра для однофазной синхронизации
СПИСОК ЛИТЕРАТУРЫ
[1] Mai, T .; Hand, M.M .; Болдуин, С.Ф .; Wiser, R.H .; Бринкман, Г.Л .;
Denholm, P .; Arent, D.J .; Porro, G .; Шандор, Д.; Hostick, D.J .; Миллиган,
М .; DeMeo, E.A .; Базилиан М., «Фьючерсы на возобновляемую электроэнергию для
США», IEEE Trans. по устойчивой энергетике, ранний доступ
[2] Collin, A.J .; Hernando-Gil, I .; Acosta, J.L .; Илие, И.-С .; Джокич, С.З.,
«Реализация потенциала интеллектуальных сетей в сетях низкого напряжения. Часть 2:
Microgeneration», ISGT Europe 2011, стр. 1-8, 5-7 декабря 2011 г.
[3] Aparicio, N. ; MacGill, I .; Rivier Abbad, J .; Бельтран, Х., «Сравнение
политики поддержки ветроэнергетики и дизайна рынка электроэнергии в Европе,
в Соединенных Штатах и Австралии», IEEE Trans. на Sust. Энергия, том 3,
№ 4, стр. 809 818, октябрь 2012 г.
[4] Jinwei He; Юн Вэй Ли, «Гибридный подход к управлению напряжением и током
для преобразователей интерфейса DG-Grid с фильтрами LCL» », IEEE Trans.
на Ind. Elec., Том 60, № 5, стр. 1797-1809, май 2013 г.
[5] Руководство по применению IEEE для IEEE Std.1547, Стандарт IEEE для
Соединение распределенных ресурсов с электроэнергетическими системами,
IEEE Std. 1547.2-2008, 2008.
[6] «Руководство IEEE по проектированию, эксплуатации и интеграции распределенных систем
Resource Island с электроэнергетическими системами», IEEE Std
1547.4-2011, стр. 1-54.
[7] Golestan, S .; Монфаред, М .; Freijedo, F.D .; Герреро, Дж. М., «Динамика
Оценка усовершенствованных однофазных структур ФАПЧ», IEEE Trans.на
Ind. Elec., том 60, № 6, стр 2167-2177, июнь 2013 г.
[8] Santos Filho, R.M .; Seixas, P.F .; Cortizo, P.C .; Торрес, Л.А.Б .; Соуза,
A.F., «Сравнение трех однофазных алгоритмов ФАПЧ для приложений ИБП
«, IEEE Trans. on Ind. Elec, vol.55, no.8, pp.2923-2932,
август 2008 г.
[9] Golestan, S .; Монфаред, М .; Freijedo, F.D .; Герреро, Дж. М., «Проектирование и настройка
модифицированной системы ФАПЧ на основе питания для однофазной сети —
Connected Power Conditioning Systems», IEEE Trans.on Power
Electronics, vol.27, no.8, pp.3639-3650, август 2012 г.
[10] Clarke, D.W .; Park, JW, «Фазовая синхронизация для настройки оборудования и мониторинга
«, IEE Proceedings Control Theory and Applications, vol.150,
No. 2, pp.155-169, March 2003
[11] Silva, SM; Lopes, B.M .; Filho, B.JC; Campana, R.P .; Bosventura,
W.C., «Оценка производительности алгоритмов PLL для однофазных сетей —
подключенных систем», IEEE IAS’04, vol.4, pp.2259-2263, 3-7 октября 2004 г.
[12] Ciobotaru, M .; Teodorescu, R .; Блаабьерг, Ф., «Новая однофазная структура ФАПЧ
на основе обобщенного интегратора второго порядка», IEEE-PESC
’06, стр. 1-6, 18-22 июня 2006 г.
[13] Blanco, C .; Reigosa, D .; Бриз, Ф .; Герреро, Дж. М., «Синхронизация в
трехфазных сетях с сильными искажениями с использованием селективных режекторных фильтров», IEEE
ECCE 2013, стр. 2641-2648, 15-19 сентября 2013 г.
[14] Бланко, К.; Reigosa, D .; Бриз, Ф .; Герреро, J.M .; Гарсия, П., «Сетка
,, синхронизация трехфазных преобразователей с использованием каскадного комплексного векторного фильтра
PLL, 2012 IEEE ECCE, стр. 196, 203, 15-20 сентября 2012 г. V., «Линейное уменьшение динамического диапазона музыкального звука
с использованием цепочки фильтров Allpass», Письма об обработке сигналов IEEE,
, том 20, номер 7, стр. 669-672, июль 2013 г.,
[16] Sah , SP; Xinmin Yu; Deukhyoun Heo, «Проектирование и анализ широкополосного квадратурного фазовращателя на 15–35 ГГц
с индуктивной нагрузкой
«, IEEE Transactions on Microwave Theory and Techniques,
vol.61, номер 8, стр. 3024-3033, август 2013 г.
a)
b)
c)
d)
Рис. 13 — Экспериментальные результаты, показывающие реакцию на 3-е, 5-е и 7-е места
инжекция гармоник при t = 1 с: a) фактическое напряжение сети vg и расчетное напряжение сети
vμg, b) ошибка величины, c) ошибка частоты, d) ошибка фазы.
À1
À0,5
0
0,5
1
о.е.
0,2
0,1
0
0.1
0,2
о.е.
0,3
0,2
0,1
0
0,1
0,2
0,3
о.е.
0,95 11,05 1,1
15
10
5
0
5
10
15
т (с)
deg
Phase erro
Fre
. erro
Ма
. erro
v
v
RL low pass, онлайн-калькулятор
Калькулятор и формулы для расчета параметров ФНЧ КЛ
RL онлайн-калькулятор низких частот
Эта функция вычисляет свойства фильтра нижних частот, состоящего из резистора и катушки.Выходное напряжение, затухание и фазовый сдвиг рассчитываются для данной частоты.
\ (\ Displaystyle L \) = Индуктивность [H]
\ (\ Displaystyle R \) = Сопротивление [Ом]
\ (\ displaystyle U_1 \) = Входное напряжение [В]
\ (\ displaystyle U_2 \) = Выходное напряжение [В]
\ (\ Displaystyle X_L \) = Реактивное сопротивление [Ом]
\ (\ displaystyle f_g \) = частота среза [Гц]
\ (\ Displaystyle φ \) = фазовый угол [°]
Формулы низкочастотного прохода RL
Рассчитать коэффициент напряжений
Выходное напряжение U 2 нижнего прохода RL рассчитывается по следующей формуле.2}} \)
\ (\ Displaystyle X_L = 2 π · е · L \)
Затухание в децибелах
На резонансной частоте затухание составляет 3 дБ. Его можно рассчитать для различных частот, используя приведенные ниже формулы. Если входное и выходное напряжение известны, затухание можно легко рассчитать по следующей формуле.
\ (\ Displaystyle V_u = 20 · lg \ влево (\ гидроразрыва {U_2} {U_1} \ right) \)
Если напряжения неизвестны, используется следующая формула.2}} \ справа) \)
Фазовый сдвиг
В проходе нижних частот RL выходное напряжение отстает от входного на 0–90 °, в зависимости от частоты. На резонансной частоте фазовый сдвиг -45 °. На низких частотах он стремится к 0. На высоких частотах фаза поворачивается в сторону -90 °. Фазовый сдвиг можно рассчитать по следующей формуле.
\ (\ Displaystyle φ = acos \ влево (\ гидроразрыва {U_2} {U_1} \ вправо) \)
\ (\ Displaystyle φ = arctan \ влево (ω · \ гидроразрыва {L} {R} \ вправо) \)
Частота среза
На частоте среза f g или ω g значение амплитудно-частотной характеристики (т.е. величина передаточной функции) равна 0.707, г. что соответствует -3 дБ.
\ (\ Displaystyle 0.707 = \ гидроразрыва {1} {\ sqrt {2}} \)
Формулы частоты среза
\ (\ Displaystyle ω_g = \ гидроразрыва {R} {L} ⇒ f_g = \ frac {R} {2 · π · L} \)
\ (\ Displaystyle R = 2 · π · f_g · L \)
\ (\ Displaystyle L = \ гидроразрыва {R} {2 · π · f_g} \)
|
Классификация, характеристики, типы, применения и преимущества
Фильтры — это электронные схемы, которые удаляют любые нежелательные компоненты или функции из сигнала.Проще говоря, вы можете понять это, поскольку схема отклоняет определенную полосу частот и позволяет проходить другим. Они широко используются в измерительных приборах, электронике и системах связи, особенно в системах обработки сигналов и изображений. Этот пост даст вам краткое представление о том, что такое фильтры, их классификации, характеристиках, типах, приложениях, преимуществах и недостатках.
Что такое фильтрыФильтры являются важными строительными блоками любых электронных и коммуникационных систем, которые изменяют амплитудные и / или фазовые характеристики сигнала относительно частоты.Фильтр — это в основном линейная схема, которая помогает удалить из входного сигнала нежелательные компоненты, такие как шум, помехи и искажения. В идеале фильтр изменяет относительные амплитуды различных частотных компонентов и фазовые характеристики, а его «усиление» полностью зависит от частоты сигнала.
Рис. 1 — Знакомство с фильтром
Фильтр определяется их воздействием на сигналы в частотной области, которое часто математически описывается в терминах его передаточной функции и выражается в соотношении преобразований Лапласа. его выходных и входных сигналов.
Функция передачи напряжения H (s) схемы фильтра записывается как:
Где,
- V IN (s) = входной сигнал
- V OUT (s) = выходной сигнал
- S = комплексная частотная переменная.
Заменив переменную «S» в приведенном выше уравнении на jὠ, где j равно, а ὠ — частота в радианах (2ᴨf), мы можем найти влияние фильтра на величину и фазу входного сигнала.
Величина находится, взяв абсолютное значение уравнения (1):
Рис.2 — Блок-схема цепи фильтра
Классификация фильтровФильтр в основном подразделяется на два типа:
- Активный фильтр
- Пассивный фильтр
Цепь фильтра, состоящая из активных компонентов Подобно транзисторам и операционным усилителям в дополнение к резисторам и конденсаторам, он называется Активный фильтр .
Пассивные фильтрыСхема фильтра, состоящая из пассивных компонентов, таких как резисторы, конденсаторы и катушки индуктивности, называется пассивным фильтром .Диапазон рабочих частот фильтров на компонентах, используемых для построения схемы. Следовательно, фильтр можно дополнительно разделить на категории в зависимости от рабочей частоты конкретной цепи. Это:
- Фильтр низких частот
- Фильтр высоких частот
- Полосовой фильтр
- Полосовой стоп-фильтр
- Полнопроходный фильтр
Это тип фильтра, который ослабляет все частоты выше частот среза.Он обеспечивает постоянный выходной сигнал (усиление) от нуля до частоты среза.
Рис. 3 — Характеристики фильтра низких частот (a) Фактические (b) Идеальные
Фильтры высоких частотЭто тип фильтра, который ослабляет все частоты ниже частот среза. Он обеспечивает постоянный выход (усиление) выше частоты среза.
Рис.4 — Характеристики фильтра верхних частот (a) Фактические (b) Ideal
Узнайте больше о фильтре верхних частот - типы, применения, преимущества и недостатки
Полосовые фильтры
Это тип фильтра, который позволяет пропускать определенную полосу частот, а все другие частоты за ее пределами ослабляются.
Рис. 5 — Характеристики полосового фильтра
Ограничивающие полосовые фильтрыОпределенная полоса частот отклоняется и позволяет пропускать частоты за пределами полосы.
Рис. 6 — Характеристики полосового стоп-фильтра
Все проходные фильтрыЭто тип фильтра, который одинаково пропускает все частоты. Он также известен как фильтр фазового сдвига, фильтр с временной задержкой, поскольку выходное напряжение сдвигается по фазе относительно входного напряжения, но они равны по величине.
Рис. 7 — Всепроходный фильтр Характеристики
Применения фильтров
Применения включают:
- Цепи фильтров используются для устранения фонового шума
- Они используются при настройке радио на определенную частоту
- Используется в предварительном усилении, эквализации, управлении тоном в аудиосистемах
- Они также используются в схемах обработки сигналов и преобразования данных
- Схемы фильтров широко используются в медицинских электронных системах
Преимущества фильтров
Преимущества: :
- Они экономичны или рентабельны
- В отличие от схем пассивных фильтров, схемы активных фильтров требуют источника питания
Недостатки:
- Цепи громоздкие
- Ограниченная полоса пропускания
- Повышенная чувствительность к вариациям ci Параметры схемы
Также читайте: Усилитель класса C - принцип работы, применение, преимущества и недостатки Волновод - классификация, режимы, принцип работы, применение, преимущество Широтно-импульсная модуляция (ШИМ) - создание, применение и преимущества.




 д.
д. .. Статьи об Hi-End ламповых усилителях, радиолампах, акустических системах
.. Статьи об Hi-End ламповых усилителях, радиолампах, акустических системах И еще хорошо, если (относительно других полос) фазу динамика для восстановления синфазности полос нужно просто перевернуть на 180 градусов, а вот если значение некруглое, необходима какая-то линия задержки, дополнительно сдвигающая фазу до круглых знчений 0 или 180.. Причем, в результате разность фаз сигналов СЧ и ВЧ полос может стать 360 градусов, то есть ВЧ-динамик отстанет на один период граничной частоты.
И еще хорошо, если (относительно других полос) фазу динамика для восстановления синфазности полос нужно просто перевернуть на 180 градусов, а вот если значение некруглое, необходима какая-то линия задержки, дополнительно сдвигающая фазу до круглых знчений 0 или 180.. Причем, в результате разность фаз сигналов СЧ и ВЧ полос может стать 360 градусов, то есть ВЧ-динамик отстанет на один период граничной частоты.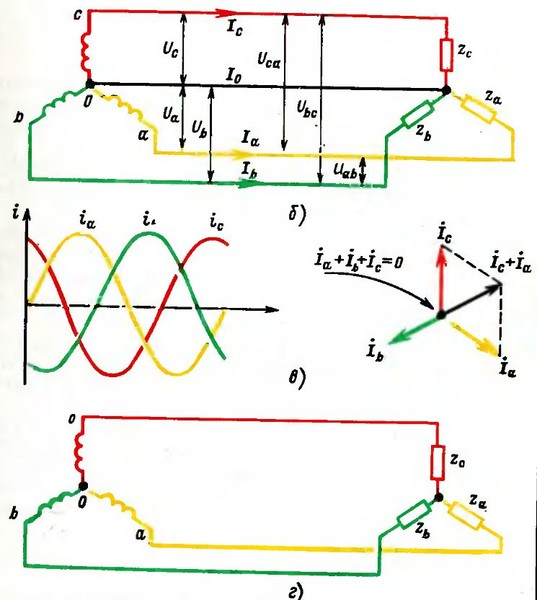
 А значит, есть широкое поле для деятельности, и можно не только ухудшить характеристики и звук, а и улучшить, если конечно постараться. 😉 И еще — фаза у динамика обычно помечается жирной точкой или плюсиком. Что означает, что при подведении к этой клемме напряжения положительной полярности диффузор смещается вперед.
А значит, есть широкое поле для деятельности, и можно не только ухудшить характеристики и звук, а и улучшить, если конечно постараться. 😉 И еще — фаза у динамика обычно помечается жирной точкой или плюсиком. Что означает, что при подведении к этой клемме напряжения положительной полярности диффузор смещается вперед. функции g (ω).Передаваемая мощность обычно идет как
коэффициент усиления возведен в квадрат, поэтому фильтр передает 50% максимальной мощности при f o .
Теперь уменьшение мощности на коэффициент двух означает снижение на 3 дБ.
(см. Что такое децибел?).
Сигнал с частотой f = f o = 1 / 2πRC
ослабляется на 3 дБ, низкие частоты ослабляются меньше и высокие
частоты более приглушенные.
функции g (ω).Передаваемая мощность обычно идет как
коэффициент усиления возведен в квадрат, поэтому фильтр передает 50% максимальной мощности при f o .
Теперь уменьшение мощности на коэффициент двух означает снижение на 3 дБ.
(см. Что такое децибел?).
Сигнал с частотой f = f o = 1 / 2πRC
ослабляется на 3 дБ, низкие частоты ослабляются меньше и высокие
частоты более приглушенные.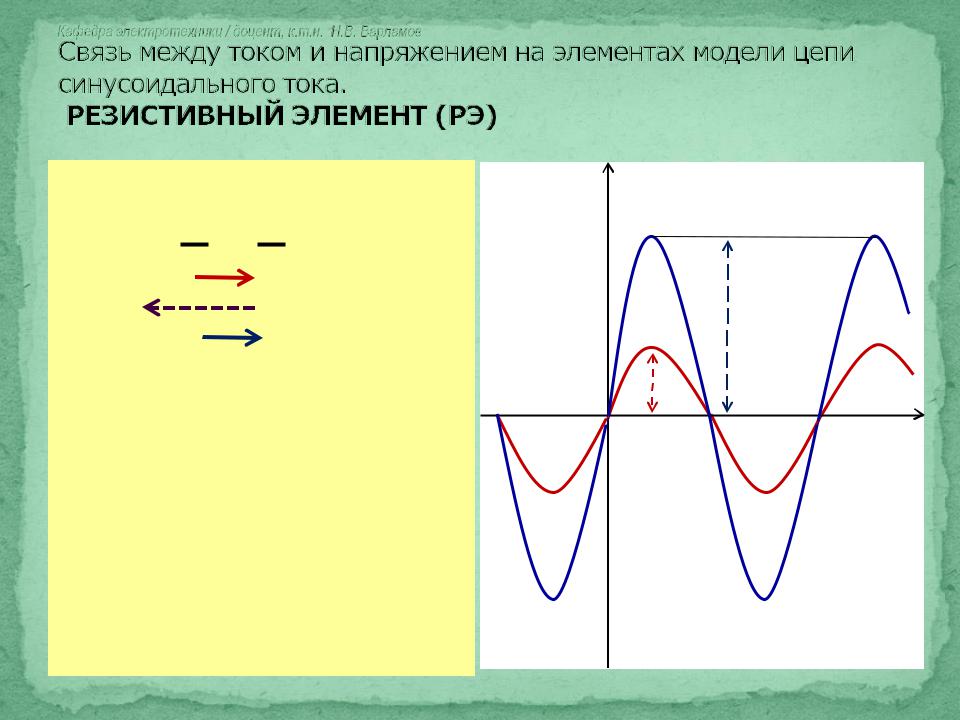


 Выход — это напряжение на конденсаторе.
Мы рассматриваем только высоких частот w >> 1 / RC, так что конденсатора недостаточно.
время зарядки, его напряжение небольшое, поэтому входное напряжение приблизительно
равно напряжению на резисторе.
Выход — это напряжение на конденсаторе.
Мы рассматриваем только высоких частот w >> 1 / RC, так что конденсатора недостаточно.
время зарядки, его напряжение небольшое, поэтому входное напряжение приблизительно
равно напряжению на резисторе. Здесь показано влияние нескольких распространенных типов фильтров на входной сигнал с качающейся частотой.
Здесь показано влияние нескольких распространенных типов фильтров на входной сигнал с качающейся частотой.