Магнитный поток из своего определения равен:
$Ф=\int\limits_S {\vec{B}\bullet d\vec{S}\left( 5 \right),}$
где $S$ – площадь поверхности контура с током. Вектор индукции магнитного поля запишем через векторный потенциал магнитного поля ($\vec A$), который создается током $I$:
$\vec{B}=rot\, \vec{A}\left( 6 \right)$
Тогда выражение (5) приведем к виду:
$Ф=\int\limits_S {rot\, \vec{A}} d\vec{S}=\int\limits_L \vec{A} \bullet d\vec{l}\left( 7 \right)$.
где $L$ — контур тока.
В выражении (7) векторный потенциал поля $\vec{A}$ создан током, который течет в этом контуре, получается, что замкнутый ток взаимодействует с собственным магнитным полем.
Физическая сущность данного взаимодействия заключается в том, что всякий элемент тока $I\vec dl$ порождает в пространстве магнитное поле. С этим полем входят во взаимодействие все остальные элементы контура.
Подставим выражение для магнитного потока (7) в формулу для энергии (2), найдем:
$E_{m}=\frac{I}{2}\int\limits_L \vec{A} \bullet d\vec{l}=\frac{1}{2}\int\limits_V \vec{A} \vec{j}dV\left( 8 \right)$,
где сделан переход к объемным токам при помощи соотношения:
$\vec{j}dV\leftrightarrow Id\vec{l}\left( 9 \right)$,
$\vec j$ – вектор плотности тока.
Замечание 1
Стрелка в выражении (9) показывает, что данная замена дает возможность перейти от формул для объемных токов к формулам линейных токов и в обратную сторону.
Преобразуем выражение под интегралом так, чтобы в него входили только векторы поля и векторный потенциал. Используем формулы (6) и
$\vec{j}=rot\, \vec{H\, }\left( 10 \right).$
Вспомним известное соотношение для дивергенции векторного произведения:
$div(\vec{A}\times \, \vec{H})=\vec{H}rot\, \vec{A}-\vec{A}rot\vec{H\,}\left( 11 \right)$.
Получим в результате:
$\vec{A}\vec{j}=\vec{H}\vec{B}-div(\vec{A}\times \vec{H})\left( 12 \right)$.
тогда выражение для энергии примет вид:
$E_{m}=\frac{1}{2}\int {\vec{H}\vec{B}dV} -\int {div(\vec{A}\times \vec{H})}dV\left( 13 \right)$
Интеграл $\int {div(\vec{A}\times \vec{H})} dV$ в соответствии с теоремой Гаусса – Остроградского преобразуем в интеграл по поверхности, которая ограничивает объем интегрирования:
$\int\limits_V {div(\vec{A}\times \vec{H})dV} =\int\limits_S {(\vec{A}\times\vec{H})dS\, \left( 14 \right).
$E_{m}=\frac{1}{2}\int {\vec{H}\vec{B}dV} \left( 15 \right)$.
Из выражения (15) следует, что объемная плотность распределения энергии магнитного поля равна:
$w=\frac{1}{2}\vec{H}\vec{B}\left( 16 \right)$.
Определение 1
Плотностью энергии магнитного поля называют его энергию, сосредоточенную в единице объема этого поля.
$w=\frac{E_{m}}{V}$
Представленное выражение справедливо для равномерного распределения энергии поля по объему.
Формула (16) говорит нам о том, что объемная плотность энергии магнитного поля в каждой его точке определяют значения векторов поля в этой точке, и не имеет значение каковы источники поля.
Для однородного изотропного магнетика мы имеем следующую связь между векторами поля:
$\vec{B}=\mu \mu_{0}\vec{H}\left( 17 \right)$. 3$ ).
3$ ).
Энергия магнитного поля при наличии магнетиков
Допустим, что все пространство заполняет однородный магнетик. В этом случае создаваемая токами индукция будет изменяться в $\frac{\mu }{\mu_{0}}$ раз в сравнении с индукцией в вакууме. ($\mu$ – магнитная проницаемость вещества; $\mu_{0}$ – магнитная постоянная). Это означает, что во столько же раз изменятся потоки $Ф$ и $dФ$. Из формулы (2) заключим, что индуктивность контура и взаимные индуктивности увеличатся в $\frac{\mu }{\mu_{0}}$ раз. Формула (1) для энергии магнитного поля не изменится, но в ней индуктивность изменится в $\frac{\mu }{\mu_{0}}$ раз.
Можно сделать вывод о том, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменится в $\frac{\mu }{\mu_{0}}$ раз в сравнении с энергией поля этих же самых токов в вакууме. Аналогичный вывод можно сделать относительно плотности энергии.
Ограниченность формул для вычисления плотности энергии
- Мы предполагали, что вещество, в котором токи создают магнитные поля, является магнитоизотропным.
 {2}}{2\mu \mu_{0}}lS\, \left( 21 \right)$.
{2}}{2\mu \mu_{0}}lS\, \left( 21 \right)$.где присутствуют параметры самого соленоида и характеристика магнитного поля ($B$), что говорит о том, что энергия поля распределена по объему поля.
Для постоянных магнитных полей эта непонятность вызвана тем, что токи и поля существуют неразрывно, образуя систему.
При переходе к переменным магнитным полям приемлемой становится только полевая концепция магнитной энергии, так как переменные магнитные поля входят как компоненты электромагнитных полей и могут существовать самостоятельно от токов. Электромагнитные волны переносят энергию, значит, сделаем вывод о том, что энергия магнитного поля распределена в объеме поля.
Электричество и магнетизм
Обратимся снова к процессу замыкания цепи на рис. 8.33-1. Умножая правую и левую части уравнения (8.23) на , получим
(8.
 29)
29)Левая часть уравнения (8.29) выражает работу, совершаемую источником тока за время . В правой части первое слагаемое есть величина работы, расходуемой на выделение джоулева тепла в проводнике. Ясно, что перед нами — уравнение закона сохранения энергии в рассматриваемой цепи. Каков же смысл второго слагаемого? Оно связано с катушкой, о чем свидетельствует множитель L, и представляет собой работу, затраченную на преодоление противодействия ЭДС самоиндукции. Куда же девается эта работа? В процессе замыкания цепи в катушкой создается магнитное поле. Значит, указанная работа аккумулируется именно в катушке как запасенная в ней энергия её магнитного поля. Ток возрастает от нуля до некого установившегося значения
(8.
 30)
30)Поскольку
этот же результат можно записать в формах
(8.31)
Эти формулы очень похожи на выражения для энергии конденсатора как функции его заряда или разности потенциалов на обкладках. Мы помним, что их можно привести к виду, где явно выделен объем конденсатора. Это позволило нам связать плотность энергии электрического поля с его напряженностью. Выполним аналогичную программу и для магнитного поля, используя в качестве «катушки» достаточно длинный соленоид.
Индуктивность соленоида дается выражением (8.21)
Магнитная индукция в соленоиде определяется по формуле (7.18)
Выразим плотность числа витков в соленоиде через магнитное поле в нем
 Получим
ПолучимНаконец, подставим это выражение в формулу (17.28) для энергии поля в катушке
(8.32)
Мы достигли своей цели: параметры соленоида, с которого мы начали, не присутствуют в этой формуле. Мы все выразили через магнитную индукцию поля, и энергия в катушке оказалась пропорциональной ее объему. Отсюда следует выражение для плотности энергии магнитного поля (неважно, чем и как созданного)
(8.33)
Вспоминая связь напряженности магнитного поля с магнитной индукцией
находим эквивалентные представления для плотности энергии магнитного поля:
(8.

Для магнитного поля в вакууме следует положить во всех этих формулах . Нетрудно заметить сходство (8.34) с аналогичными формулами (3.35), (3.36) для электрического поля (рис. 8.36, рис. 8.37).
Рис. 8.36. Мощное магнитное поле Солнца производит выбросы плазмы
Рис. 8.37. Мощное магнитное поле нейтронной звезды
Пример. Сравнить энергии, содержащиеся в объеме 1 л, если он пронизан: 1) однородным электрическим полем с напряженностью Е = 100 кВ/м; 2) однородным магнитным полем с индукцией
Решение. Энергия электрического поля равна
Энергия магнитного поля равна
Оба указанных поля считаются достаточно сильными, но могут быть созданы без особых проблем. Задача демонстрирует, что практически выгоднее накапливать энергию в магнитном поле: в данном примере отношение энергий равно
Магнитное поле проводника: определение плотности энергии
Одной из характеристик магнитного излучения, показывающей распределение его энергии в объеме пространства, является плотность энергии магнитного поля.
 При изучении электромагнетизма необходимо усвоить, что это за величина, что она характеризует и как измеряется.
При изучении электромагнетизма необходимо усвоить, что это за величина, что она характеризует и как измеряется.Катушка или дроссель генерирует вокруг себя магнитное поле
Объемная плотность магнитной энергии
Формула нахождения объемной плотности энергии имеет такой вид:
ω=W/V.
Под ω здесь подразумевается собственно искомая плотность, под W – энергия имеющегося поля, под V – объем пространства, в котором поле проявляет активность. Если выразить значение W через магнитную проницаемость µ и индукцию В и подставить в формулу, она приобретет следующий вид:
ω=В2/2* µ0* µ (здесь µ0 – это магнитная постоянная).
Преобразование с использованием вектора индукции применяется, чтобы исключить привязку активного магнитного поля к особенностям дросселя. Формула для вычисления индукционной характеристики выглядит так:
B= µ0* µ*I*n.
I здесь – токовая сила в катушечной цепочке, через n выражается такая величина, как плотность обмотки.
 Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W:
Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W:W= В2*V/2* µ0* µ.
Подставив выражение в основную формулу плотности, можно привести его к ранее обозначенному виду.
Наличие магнитного поля вокруг проводника или катушки с током
При подключении соленоида (катушки) в электрическую цепь вокруг нее формируется поле. Характеристики поля зависят от ряда параметров: от средовых особенностей окружения, токовой силы (она измеряется в амперах) и материала, из которого изготовлен проводник или обмотка катушки. В полевом пространстве могут образовываться электромагнитные волны. Так как на полевой энергетический потенциал, прежде всего, оказывает влияние сила текущего в системе электротока, можно сделать вывод, что работа тока по генерированию магнитного пространства будет эквивалентной энергии последнего. Если в систему подключена катушка с магнитным сердечником, то на энергетическую плотность будет влиять полевая энергия в вакууме и в материале, из которого сделан сердечниковый элемент.

Подключение индуктивной катушки к источнику тока
Для изучения динамики явления можно рассмотреть электроцепь, включающую в себя дроссель, лампу, замыкающий ключ и источник постоянного электротока. Когда ключик замыкается, токовый путь будет идти от «положительного» зажима источника через лампу и индуктивную катушку. Поначалу лампа накаливания загорится ярче, что связано со значительной величиной сопротивления дроссели. По мере того, как сопротивление будет падать, а проходящий через обмотку ток увеличиваться, интенсивность горения лампочки будет понижаться. Связано это с тем, что первое время подаваемый на дроссель ток имеет значение, пропорциональное току высокой частоты.
Чтобы практически построить цепь, подходящую для расчета, нужно, чтобы энергетический ресурс источника питания затрачивался на генерирование магнитного поля. Поэтому параметрами внутреннего сопротивления дроссели и питательного источника допустимо пренебрегать.
Важно! Согласно второму закону Кирхгофа, сумма подсоединенных к электрической цепи напряжений равняется сумме снижений напряжения для всех компонентов цепочки.

Второй закон Кирхгофа
Измерение плотности энергии магнитных полей
Данная величина показывает энергию, содержащуюся в единице объема окружающей среды, подпадающей под влияние поля. Обозначается она греческой буквой ω. Для вычисления применяется формула:
ω=W/V, в данном случае W – это полевая энергия в объеме пространства V.
Единица измерения плотности поля в международной системе СИ тоже выглядит как частное единиц, в которых измеряются эти величины: джоулей и кубических метров (Дж/м3). Показатель для аккумуляторов (ионных, свинцово-кислотных и других) указывают в прилагающейся документации.
Для соленоида, подсоединенного в электрическую цепь, оба составляющих этого частного можно выразить через следующие единицы:
- Значение энергетического ресурса поля будет равным уполовиненному произведению индуктивности соленоида на квадрат токовой силы в его обмотке:
W=L*I2/2.
- В качестве «пространства» рассматривается сама катушка, тогда V=S*l, где S – площадь сечения катушечного элемента в поперечнике, а l – его длина.

Тогда конечная формула принимает следующий облик:
ω=L*I2/2*S*l.
Формула индуктивного сопротивления катушки
Вычислить величину сопротивления дросселя XL можно, воспользовавшись следующей формулой:
XL=2πfL.
Здесь буква L обозначает параметр индуктивности дроссели, а f – токовую частоту. Исходя из этого выражения, поначалу попадающий на обмотку ток будет пропорциональным электротоку большой чистоты. В это время дроссель проявляет поведение, аналогичное ситуации цепного разрыва, с сильным повышением индуктивного сопротивления. С течением времени последнее падает до нулевого значения.
Вмонтированная в лампу нитка отличается высоким показателем сопротивления, тогда как активный показатель обмотки, напротив, стремится к нулю. Из-за этого возникает ситуация, когда почти весь цепной ток проходит через дроссель. Когда цепь размыкают при помощи ключа, лампа не затухает постепенно. Напротив, она сначала резко начинает гореть интенсивно, потом – медленно угасать.
 Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.
Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.В рассмотренном примере катушка с обмотками, подключенная в цепь, выступает как источник магнитного поля. Поскольку в такой ситуации это поле не является однородным, для выполнения расчетов необходимо использование показателя, характеризующего концентрацию и распределение энергии в поле. Можно заключить, что смысл введения параметра плотности поля состоит именно в этом.
Видео
Персональный сайт — 45. Энергия магнитного поля. Плотность энергии магнитного поля.
Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока.
 Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.
Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна
Значит, энергия магнитного поля, которое связано с контуром,
(1)
Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем
Так как I=Bl/(μ0μN) и В=μ0μH , то
(2)
где Sl = V — объем соленоида.

Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью
(3)
Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.
Плотность энергии магнитного поля — Энциклопедия по машиностроению XXL
Объемная плотность энергии магнитного поля [c.403]Плотность энергии магнитного поля зависит от характеристик последнего [c.219]
Плотность энергии магнитного поля W Джоуль на метр, Дж/м кубический Эрг на кубический сантиметр, Эрг/см 1 Дж мЗ Ю Эрг/сц [c.
 136]
136]Энергия магнитного поля, заключенная в единице объема поля, называется объемной плотностью энергии магнитного поля [c.105]
Объемная плотность энергии магнитного поля вн ВН ВН ВН [c.28]
Найти отношение / объемной плотности энергии магнитного поля волны к объемной плотности энергии электрического поля в проводящей среде. [c.115]Плотность энергии магнитного поля и,т 8л [c.251]
Из соотношения (1.31) следует также, что объемная плотность энергии электрического поля Шз (1.42) в бегущей электромагнитной волне в каждой точке и в любой момент времени равна плотности энергии магнитного поля Шм (1.43). Поэтому выражаемую формулой (1.52) плотность потока энергии можно записать как произведение полной плотности энергии ш = Шэ + Шм электромагнитного поля бегущей волны на скорость волны с [c.
 32]
32]Плотность энергии магнитного поля в вакууме (ц = 1) в системе единиц СИ может быть вычислена по формуле [c.12]
Магнитотвердые материалы — это сплавы и химические соединения, относящиеся к классу ферро- и ферримагнетиков и характеризуемые большой коэрцитивной силой (условно свыше 4 кА/м) и максимальной объемной плотностью энергии магнитного поля (более 800 Дж/м ). К ним относятся сплавы и соединения на основе Ре —Со—V, Ре —Со —Сг, Ре —N1—А1, Ре—№—Си, Ре —Со — Си, Ре—Со—М—А1—Си, 1-Со, Мп—А1—С, Мп—В1, Со—редкоземельные материалы (РЗМ), Со —Си —РЭМ, ферриты бария и стронция, а также другие вещества, обладающие высокой остаточной намагниченностью. [c.117]
Плотность энергии электромагнитного поля представляет энергию, сосредоточенную в единице объёма. В том случае, когда магнитная проницаемость постоянна, что для ферромагнитных материалов справедливо лишь при малых насыщениях, плотность энергии магнитного поля будет [c.
 485]
485]При распространении электромагнитной волны происходит перенос (течение) энергии, подобно тому как это имеет место при распространении упругой волны. Вопрос о течении энергии в упругой волне был впервые (1874 г.) рассмотрен Н. А. Умовым ), который доказал общую теорему о потоке энергии в любой среде. Поток энергии в упругой волне может быть вычислен через величины, характеризующие потенциальную энергию упругой деформации и кинетическую энергию движения частиц упругой среды. Плотность потока энергии выражается с помощью специального вектора (вектор Умова). Аналогичное. рассмотрение плодотворно и для электромагнитных волн. До известной степени можно уподобить энергию электрического поля потенциальной энергии упругой деформации, а энергию магнитного поля — кинетической энергии движения частей деформированного тела. Так же как и в случае упругой деформации, передача энергии от точки к точке в электромагнитной волне связана с тем обстоятельством, что волны электрической и магнитной напряженностей находятся в одной фазе.
 Такая волна называется бегущей. Движение энергии в бегущей упругой или электро-магнитной
[c.37]
Такая волна называется бегущей. Движение энергии в бегущей упругой или электро-магнитной
[c.37]
Действительно, пусть ао — искомый угол между вектором напряженности поля и вектором силы Oi, а а — угол между вектором намагниченности насыщения / и тем же вектором силы. Тогда величина анизотропного магнитоупругого эффекта может быть найдена из условия минимума магнитоупругой энергии и энергии магнитного поля. Плотность магнитоупругой энергии для случая изотропной магнитострикции Xs может быть записана следующим образом [c.204]В большей части этой главы мы будем считать, что среда является однородной, непоглощающей и магнитно-изотропной. Плотность энергии электрического поля, запасенной в анизотропной среде, равна [c.80]
Совершенно аналогично в монохроматической волне в каждой точке осциллируют на частоте 2ы плотность энергии электрического поля [см.
 (1.42)], пропорциональная (г, t), и равная ей плотность энергии Wy магнитного поля [см. (1.43)]. Их средние по времени значения во всех точках одинаковы и пропорциональны квадрату амплитуды
[c.32]
(1.42)], пропорциональная (г, t), и равная ей плотность энергии Wy магнитного поля [см. (1.43)]. Их средние по времени значения во всех точках одинаковы и пропорциональны квадрату амплитуды
[c.32]Магнитно-твердые материалы оценивают еще величиной максимальной энергии магнитного поля, создаваемого магнитом в воздушном зазоре (между полюсами магнита отнесенной к единице объема магнита (рис. 80). Это удельная объемная плотность энергии [c.215]
Энергия электромагнитного поля связана с распределением в пространстве векторов электрич. и магнитного поля. Плотность энергии электрич. поля (безразлично, будет ли поле статическим или нет) определяется в W k/ m по ф-ле [c.212]
Максимумы для плотности электрической энергии н плотности магнитной энергии сдвинуты во времени на V4 периода и в пространстве па V4 длины волны. Покажите сами (задача 7.36), что в любой области длиной полная энергия постоянна. Энергия электрического поля совершает гармонические колебания относительно среднего значения с частотой 2м, достигая предельных значений — пуля и двойного среднего значения.
 То же происходит с энергией магнитного поля. Таким образом, энергия колеблется от чисто электрической, имеющей максимум плотности з одном месте, до чисто магнитной с максимумом плотности энергии, смещенным на Это напоминает поведение гармонического осциллятора (колебательного контура). Полная энергия осциллятора постоянна, но колеблется, переходя из чисто потенциальной энергии в одном положении массы в чисто кинетическую энергию в другом положении массы. Как потенциальная, так и кинетическая энергии гармонически колеблются относительно их среднего значения с частотой 2со. Двойка появляется потому, что потенциальная энергия дважды (за период) положительна и дважды достигает максимального зна-че[П1Я (то же справедливо и для кинетической энергии). Электрическое поле Ех в стоячей волне аналогично смещению массы гармонического осциллятора от положения равновесия, в то время как магнитное поле Ву аналогично скорости этой массы.
[c.324]
То же происходит с энергией магнитного поля. Таким образом, энергия колеблется от чисто электрической, имеющей максимум плотности з одном месте, до чисто магнитной с максимумом плотности энергии, смещенным на Это напоминает поведение гармонического осциллятора (колебательного контура). Полная энергия осциллятора постоянна, но колеблется, переходя из чисто потенциальной энергии в одном положении массы в чисто кинетическую энергию в другом положении массы. Как потенциальная, так и кинетическая энергии гармонически колеблются относительно их среднего значения с частотой 2со. Двойка появляется потому, что потенциальная энергия дважды (за период) положительна и дважды достигает максимального зна-че[П1Я (то же справедливо и для кинетической энергии). Электрическое поле Ех в стоячей волне аналогично смещению массы гармонического осциллятора от положения равновесия, в то время как магнитное поле Ву аналогично скорости этой массы.
[c.324]Если одновременно существуют электрическое и магнитное поля, то объемная плотность энергии электромагнитного поля W в изотропной среде, не обладающей ферромагнитными (П1.
 6.5.1°) и сегнетоэлектрическими (III.1.6.9 ) свойствами, равна сумме объемных плотностей энергий электрического (111.1.12.7 ) и магнитного полей
[c.274]
6.5.1°) и сегнетоэлектрическими (III.1.6.9 ) свойствами, равна сумме объемных плотностей энергий электрического (111.1.12.7 ) и магнитного полей
[c.274]Как и обычные гидродинамические уравнения, уравнения магнитной гидродинамики для идеальной среды (т) = С = у. = 0, а=оо) допускают разрывные решения, в которых характеристики среды и поля на некоторых поверхностях испытывают скачкообразное изменение. В обычной гидродинамике существует два типа таких поверхностей разрыва тангенциальный разрыв и ударная волна. В магнитной гидродинамике картина значительно усложняется. Впервые ударные волны в магнитной гидродинамике рассматривались Гофманом и Теллером ), исходя из релятивистского тензора энергии — импульса для среды и электромагнитного поля. Как следует из этой работы, релятивистское рассмотрение необходимо лишь в том случае, если плотность магнитной энергии по порядку величины сравнима с плотностью полной энергии среды, включая энергию покоя (ср. (1.18)). Во всех практически важных случаях энергия магнитного поля значительно меньше полной энергии среды, поэтому ниже будут рассмотрены только нерелятивистские ударные волны.
 [c.14]
[c.14]
Предположение, высказанное Бэтчелором з, состоит в том, что рост-энергии магнитного поля продолжается до тех пор, пока средняя плотность магнитной энергии не становится сравнимой с плотностью кинетической энергии для наименьших масштабов турбулентности. Так как в силу (7,3) последняя равна p(ev) , то, по Бэтчелору, в стационарном. состоянии [c.48]Для увеличения плотности энергии в луче после выхода электронов из первого анода электроны фокусируются магнитным полем в специальной магнитной линзе 4. Сфокусированные в плотный пучок летящие электроны ударяются с большой скоростью о малую, резко ограниченную площадку (пятно нагрева) на изделии 6, при этом кинетическая энергия электронов, вследствие торможения превращается в теплоту, нагревая металл до очень высоких температур. Для перемещения,луча по свариваемому изделию на пути электронов помещают магнитную отклоняющую систему 5, позволяющую устанавливать луч точно по линии стыка.
 [c.16]
[c.16]Собственное магнитное поле, охватывая область высоких концентраций зарядов наподобие футляра, уменьшает диффузионные потери частиц. Благодаря этому возможна высокая концентрация частиц и энергии над микроучастками (ячейками) катода, что приводит к высокой плотности тока, испарению металла и эмиссии электронов. [c.73]
Перемычка движется под действием сил давления, создаваемых, магнитным полем. Пусть р — объемная плотность энергии магнитного поля проводяш,ей линии. Тогда dWldx = pS, где 5 — площадь бокового сечения перемычки. Подставляя m=pSd (р — плотность материала перемычки), получим ускорение a=p/pd. Величину pd называют эффективной толщиной. Положим pdt=10 кг/м . Значению р = 400 атм соответствует fi=10 Тл. При этих условиях а = 4-10 = м/с —4-10 g. Скорость о=10 км/с достигается на длине s=125 м. Время разгона —2,5-10- с. Перемычка массой т = 2 кг приобретает энергию 100 МДж. [c.93]
Для определения стеиенп охлаждения при адиабатическом размагничивании рассчитаем энергию Гельмгольца F единицы объема магнетика в магнитном поле.
 Плотность энергии магнитного поля 1И 18л, где Н — напряженность магнитного поля, представляет собой составляющую энергии Гельмгольца. Так как магнитная индукция В = iH, то энергию Гельмгольца можно представить в виде
[c.296]
Плотность энергии магнитного поля 1И 18л, где Н — напряженность магнитного поля, представляет собой составляющую энергии Гельмгольца. Так как магнитная индукция В = iH, то энергию Гельмгольца можно представить в виде
[c.296]Характеристики — магнитнотвердых материалов. Свойства таких материалов во многом определяются кривой размагничивания это участок предельной петли гистерезиса, расположенный во втором квадранте (рис. 20.1). К характеристикам магнитнотвердых,материалов относятся остаточная индукция и коэрцитивная сила Не, а также удвоенная максимальная объемная плотность энергии магнитного поля в воздушном зазоре она измеряется в дж1м , если В [c.262]
Пусть р — объемная плотность энергии магнитного поля. Тогда dW/dx = = pS, где S — площадь бокового сечения перемычки. Из (3) находим ускорение а = рЗ/т. Величину m/S называют эффективной толпщной. Положим m/s = 10 кг/м , р = 400 атм. При таких условиях а = 4 х X 10 м/с = 4 10 g. Скорость v = 10 км/с достигается на длине s = = 125 м.
 Время разгона 2,5 10 с. Перемычка массой w = 2 кг
[c.242]
Время разгона 2,5 10 с. Перемычка массой w = 2 кг
[c.242]Рационализация уравнений повлияла на численные значения ряда электрических п магнитных величин электрической н магнитной постоянных, напряженности маипгг-ного поля, магнитного сопротивления и магнитной проводимости цепей, мaгнитoдвпжyIцei силы, плотности энергии магнитного поля, магнитного момента, интенсивности намагничивания, мап[итной восприимчивости. [c.106]
Энергая магантного поля. Плотность энергии магнитного поля в вакууме [c.136]
Объемная плотность энергии м-згнитного поля Ь-1МТ-2 джоуль на кубический метр Джоуль на кубический метр равен объемной плотности энергии магнитного поля, в котором энергия 1 Дж равномерно распределена по объему 1 м ДК 111.5.7.4° дж лг Дж/мЗ Л/гпз М-1-КГ-С- [c.552]
Плотность потока энергии волн описывается вектором Пойнтинга (3.1). Следовательно, поток энергии отсутствует в точках, где либо Е, либо В равнь нулю.
 Это означает, что поток энергии в стоячей электромагнитной волне отсутствует через узлы и пучности в волне, поскольку пучность напряженности электрического поля совпадает с узлом индукции магнитного поля и наоборот. Поэтому с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии магнитного поля в энергию электрического поля и обратно. С помощью (4.11) и (4.14), пользуясь формулой для объемной плотности энергии электромагнитного поля
[c.36]
Это означает, что поток энергии в стоячей электромагнитной волне отсутствует через узлы и пучности в волне, поскольку пучность напряженности электрического поля совпадает с узлом индукции магнитного поля и наоборот. Поэтому с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии магнитного поля в энергию электрического поля и обратно. С помощью (4.11) и (4.14), пользуясь формулой для объемной плотности энергии электромагнитного поля
[c.36]Энергия магнитного поля (IV), Б магнитном поле содержится энергия, которая с большей или меньшей плотностью распределяется по всему пространству, занимаемому магнитным полем. Энергия магнитного поля получается за счёт той электрической работы, которая совершается электрическим током во время создания л агнитного поля t ф ==l — eL)idt= J 1йФ дж. (35) [c.485]
На начальной стадии (/ ,. > 0.3) влияние магнитного поля несущественно и развитие процесса происходит газодинамически.
 Ударная волна и среда за фронтом ускоряются, плотность, давление и температура растут, причем для всех режимов одинаково (фиг. 2, кривые / и 2). Параметр Re , монотонно растет, т.е. остается > 1 (фиг. 3, кривая /), магнитное поле, вмораживаясь в среду частично уносится из неразрушенной части монокристалла так, что магнитный поток Ф в ней падает, хотя напряженность магнитного поля растет (фиг. 2, кривые 3—5). Динамический параметр Л мал, то есть величина кинетической энергии ударной волны и среды за ней гораздо больше, чем энергия магнитного поля в неразрушенной части кристалла. При этом для различных режимов его величина различается 2 порядка. Для режимов 1 и 2 параметр Л монотонно убывает, а для режима 3 достигает минимума на / = 0.5 (фиг. 3, кривые J-3).
[c.151]
Ударная волна и среда за фронтом ускоряются, плотность, давление и температура растут, причем для всех режимов одинаково (фиг. 2, кривые / и 2). Параметр Re , монотонно растет, т.е. остается > 1 (фиг. 3, кривая /), магнитное поле, вмораживаясь в среду частично уносится из неразрушенной части монокристалла так, что магнитный поток Ф в ней падает, хотя напряженность магнитного поля растет (фиг. 2, кривые 3—5). Динамический параметр Л мал, то есть величина кинетической энергии ударной волны и среды за ней гораздо больше, чем энергия магнитного поля в неразрушенной части кристалла. При этом для различных режимов его величина различается 2 порядка. Для режимов 1 и 2 параметр Л монотонно убывает, а для режима 3 достигает минимума на / = 0.5 (фиг. 3, кривые J-3).
[c.151]
Для фокусирования электронного луча в электронгюй пушке обычно используется система диафрагм и магнитных линз. Магнитная линза 4 представляет собой соленоид с магнитопроводом, создающий специальной формы магнитное поле, которое при взаимодействии с электроном изменяет его траекторию и искривляет ее в направлении к оси системы. При этом можно добиться сходимости электронов на достаточно малой площади поверхности и в фокусе электронный луч может обладать весьма высокой плотностью энергии, достигающей 5-10 Bт/мм . Такая плотность энергии достаточна для осуществления целого ряда технологических процессов, причем в результате измене ния фокусировки она может быть плавно изменена до минимальных значений.
[c.108]
При этом можно добиться сходимости электронов на достаточно малой площади поверхности и в фокусе электронный луч может обладать весьма высокой плотностью энергии, достигающей 5-10 Bт/мм . Такая плотность энергии достаточна для осуществления целого ряда технологических процессов, причем в результате измене ния фокусировки она может быть плавно изменена до минимальных значений.
[c.108]44. Энергия магнитного поля, её плотность.
Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI.
 Но для изменения магнитного
потока на величину dФ следует совершить
работу dА=IdФ=LIdI. Тогда работа по созданию
магнитного потока Ф равна
Но для изменения магнитного
потока на величину dФ следует совершить
работу dА=IdФ=LIdI. Тогда работа по созданию
магнитного потока Ф равна
Значит, энергия магнитного поля, которое связано с контуром, (1)
Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем
Так как I=Bl/(μ0μN) и В=μ0μH , то (2)
где Sl = V — объем соленоида.
Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью (3)
Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными.
 Формула (3) выводилась
для однородного поля, но она верна и для
неоднородных полей. Формула (3) справедлива
только для сред, для которых линейная
зависимость В
от Н , т.е. оно относится только к пара-
и диамагнетикам.
Формула (3) выводилась
для однородного поля, но она верна и для
неоднородных полей. Формула (3) справедлива
только для сред, для которых линейная
зависимость В
от Н , т.е. оно относится только к пара-
и диамагнетикам. 45. Магнитное поле в веществе. Намагниченность. Магнитная проницаемость. Напряженность магнитного поля, её связь с магнитной индукцией.
Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.
Физическая величина, показывающая, во сколько раз индукция В магнитного поля в однородной среде отличается по модулю от индукции В0 магнитного поля в вакууме, называется магнитной проницаемостью:
Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов.
 В настоящее
время установлено, что магнитные свойства
протонов и нейтронов почти в 1000 раз слабее
магнитных свойств электронов. Поэтому
магнитные свойства веществ в основном
определяются электронами, входящими в
состав атомов.
В настоящее
время установлено, что магнитные свойства
протонов и нейтронов почти в 1000 раз слабее
магнитных свойств электронов. Поэтому
магнитные свойства веществ в основном
определяются электронами, входящими в
состав атомов.Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.
Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля.
 Поэтому у
парамагнетиков μ > 1,
а у диамагнетиков μ < 1.
Отличие μ от единицы у пара- и диамагнетиков
чрезвычайно мало. Например, у алюминия,
который относится к
парамагнетикам, μ – 1 ≈ 2,1·10–5,
у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3.
К парамагнетикам относятся также
платина, воздух и многие другие вещества.
К диамагнетикам относятся
медь (μ – 1 ≈ –3·10–6),
вода (μ – 1 ≈ –9·10–6),
висмут (μ – 1 ≈ –1,7·10–3)
и другие вещества. Образцы из пара- и
диамагнетика, помещенные в неоднородное
магнитное поле между полюсами
электромагнита, ведут себя по-разному
– парамагнетики втягиваются в область
сильного поля, диамагнетики – выталкиваются
(рис. 1.19.1).
Поэтому у
парамагнетиков μ > 1,
а у диамагнетиков μ < 1.
Отличие μ от единицы у пара- и диамагнетиков
чрезвычайно мало. Например, у алюминия,
который относится к
парамагнетикам, μ – 1 ≈ 2,1·10–5,
у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3.
К парамагнетикам относятся также
платина, воздух и многие другие вещества.
К диамагнетикам относятся
медь (μ – 1 ≈ –3·10–6),
вода (μ – 1 ≈ –9·10–6),
висмут (μ – 1 ≈ –1,7·10–3)
и другие вещества. Образцы из пара- и
диамагнетика, помещенные в неоднородное
магнитное поле между полюсами
электромагнита, ведут себя по-разному
– парамагнетики втягиваются в область
сильного поля, диамагнетики – выталкиваются
(рис. 1.19.1).Рисунок 1.19.1.
Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле
Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле.
 У атомов диамагнитных веществ в
отсутствие внешнего поля собственные
магнитные поля электронов и поля,
создаваемые их орбитальным движением,
полностью скомпенсированы. Возникновение
диамагнетизма связано с действием силы
Лоренца на электронные орбиты. Под
действием этой силы изменяется характер
орбитального движения электронов и
нарушается компенсация магнитных полей.
Возникающее при этом собственное
магнитное поле атома оказывается
направленным против направления
индукции внешнего поля.
У атомов диамагнитных веществ в
отсутствие внешнего поля собственные
магнитные поля электронов и поля,
создаваемые их орбитальным движением,
полностью скомпенсированы. Возникновение
диамагнетизма связано с действием силы
Лоренца на электронные орбиты. Под
действием этой силы изменяется характер
орбитального движения электронов и
нарушается компенсация магнитных полей.
Возникающее при этом собственное
магнитное поле атома оказывается
направленным против направления
индукции внешнего поля.В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по направлению индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной.
 При усилении внешнего
поля ориентационный эффект возрастает,
так что индукция собственного магнитного
поля парамагнитного образца растет
прямо пропорционально индукции внешнего
магнитного поля. Полная индукция
магнитного поля в образце складывается
из индукции внешнего магнитного поля
и индукции собственного магнитного
поля, возникшего в процессе намагничивания.
Механизм намагничивания парамагнетиков
очень похож на механизм поляризации
полярных диэлектриков.
Диамагнетизм не имеет аналога среди
электрических свойств вещества.
При усилении внешнего
поля ориентационный эффект возрастает,
так что индукция собственного магнитного
поля парамагнитного образца растет
прямо пропорционально индукции внешнего
магнитного поля. Полная индукция
магнитного поля в образце складывается
из индукции внешнего магнитного поля
и индукции собственного магнитного
поля, возникшего в процессе намагничивания.
Механизм намагничивания парамагнетиков
очень похож на механизм поляризации
полярных диэлектриков.
Диамагнетизм не имеет аналога среди
электрических свойств вещества.Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем в 1845 г.
Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 102–105. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.

К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.
Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.
Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.
Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы.
 Эти материалы применяются в
приборах переменного тока, в которых
происходит непрерывное перемагничивание,
то есть изменение направления магнитного
поля (трансформаторы, электродвигатели
и т. п.).
Эти материалы применяются в
приборах переменного тока, в которых
происходит непрерывное перемагничивание,
то есть изменение направления магнитного
поля (трансформаторы, электродвигатели
и т. п.).Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовленияпостоянных магнитов.
Магнитная проницаемость μ ферромагнетиков не является постоянной величиной; она сильно зависит от индукции B0 внешнего поля. Типичная зависимость μ (B0) приведена на рис.Рисунок 1.19.2.
Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля
 1.19.2. В таблицах
обычно приводятся значения максимальной
магнитной проницаемости.
1.19.2. В таблицах
обычно приводятся значения максимальной
магнитной проницаемости.Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции B магнитного поля в ферромагнетике от индукции B0внешнего магнитного поля. Характерной особенностью процесса намагничивания ферромагнетиков является так называетмый гистерезис, то есть зависимость намагничивания от предыстории образца. Кривая намагничивания B (B0) ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 1.19.3).
Рисунок 1.19.3.
Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции B0 внешнего магнитного поля
Из рис.
 1.19.3 видно, что при наступает
магнитное насыщение – намагниченность
образца достигает максимального
значения.
1.19.3 видно, что при наступает
магнитное насыщение – намагниченность
образца достигает максимального
значения.Если теперь уменьшать магнитную индукцию B0 внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно Br. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию B0 до значения –B0c, которое принято называтькоэрцитивной силой. Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 1.19.3.
У магнито-мягких материалов значения коэрцитивной силы B0c невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.

Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка 10–2–10–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.
В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем оказывается ненамагниченным. При наложении внешнего магнитного поля происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается.
 С увеличением
индукции внешнего поля возрастает
магнитная индукция намагниченного
вещества. В очень сильном внешнем поле
домены, в которых собственное магнитное
поле совпадает по направлению с внешним
полем, поглощают все остальные домены,
и наступает магнитное насыщение.
Рис. 1.19.4 может служить качественной
иллюстрацией процесса намагничивания
ферромагнитного образца.
С увеличением
индукции внешнего поля возрастает
магнитная индукция намагниченного
вещества. В очень сильном внешнем поле
домены, в которых собственное магнитное
поле совпадает по направлению с внешним
полем, поглощают все остальные домены,
и наступает магнитное насыщение.
Рис. 1.19.4 может служить качественной
иллюстрацией процесса намагничивания
ферромагнитного образца.Рисунок 1.19.4.
Намагничивание ферромагнитного образца. (1) B0 = 0; (2) B0 = B01; (3) B0 = B02 > B01
4.6.Энергия магнитного поля. Объемная плотность энергии магнитного поля в веществе
Рассмотрим цепь, состоящую из соленоида, замкнутого на источник тока (рис.4.8), находящуюся в неферромагнитной среде.
 В соленоиде
течет ток
,
который образует магнитный поток,
сцепленный с соленоидом. Если отключить
соленоид от источника и замкнуть его
на сопротивление,
по цепи пойдет постепенно убывающий
ток. Работа, совершаемая этим током за
времяравна
В соленоиде
течет ток
,
который образует магнитный поток,
сцепленный с соленоидом. Если отключить
соленоид от источника и замкнуть его
на сопротивление,
по цепи пойдет постепенно убывающий
ток. Работа, совершаемая этим током за
времяравна.
Если индуктивность соленоида остается постоянной, , то, и
. (4.3)
Эта работа идет на нагревание проводников. Вследствие совершения этой работы происходит исчезновение магнитного поля, и так как никаких изменений в окружающей цепь среде не происходит, следует заключить, что работа совершается за счет энергии магнитного поля, а выражения (4.3) как раз и определяет эту работу. Вся работа, произведенная током при убывании магнитного поля до нуля равна
,
и энергия магнитного поля .
Объемной плотностью энергии магнитного поля называется энергия этого поля, отнесенная к его объему:
.

Однако ( поле соленоида однородно), согласно закону полного тока в случае поля соленоида получаем, где- длина соленоида,- число витков соленоида, тогда
.
Энергия , локализованная во всем объеме магнитного поля равна:
.
Если поле в данной точке пространства создано несколькими контурами с током, то энергия результирующего магнитного поля равна:
,
где — сила тока в-том контуре,- потокосцепление- того контура, равное сумме потокосцепления самоиндукции (магнитного потока самоиндукции)—того контура и магнитного потока взаимоиндукции -того контура с остальными ,. Поэтому энергия магнитного поля равна
,
–взаимная индуктивность -того иi— того контуров с токами и.
4.7. Закон сохранения энергии в неферромагнитной среде
Энергия магнитного поля, создаваемого какой-либо системой тел (проводящих контуров с токами) изменяется, если контуры с токами перемещаются, или, если изменяются токи в них.

При этом совершают работу внешние силы, приложенные к телам системы, источники электрической энергии, включенные в цепи токов.
Если температура системы постоянна, и плотность среды не меняется, то закон сохранения энергии можно записать в виде:
,
здесь — работа внешних сил в рассматриваемом процессе,- работа источников электрической энергии,- изменение энергии магнитного поля,- изменение кинетической энергии тел системы,- теплота Джоуля-Ленца.
Если тела системы перемещаются очень медленно (квазистатически), то можно пренебречь изменением кинетической энергии системы, =0, и можно считать, где- работа сил, действующих на тела системы в магнитном поле. Это пондемоторные силы. Тогда закон сохранения энергии примет вид:
.
Если система содержит n проводящих контуров с токами, работа источников электрической энергии за малый промежуток времени dt равна:
,
где – алгебраическая сумма ЭДС всех источников электрической энергии, включенных в-тый контур,– сила тока в этом контуре.

Рассмотрим некоторые примеры.
Неподвижный контур с током.
а) Если ток в контуре остается постоянным, то энергия магнитного поля не изменяется,, а пондемоторные силы не совершают работы:, поэтому
— вся работа источника электрической энергии преобразуется в контуре в тепло Джоуля-Ленца.
б) Пусть ток в контуре растет от 0 до . Работа пондемоторных сил равна нулю и работа источника электрической энергии в контуре расходуется на изменение знергии магнитного поля и на выделение тепла Джоуля-Ленца:, или, где- ЭДС источника,R — сопротивление, L – индуктивность контура, I -сила тока в нем.
Работа пондемоторных сил при очень медленной деформации контура с током. Закон сохранения энергии имеет вид: . Сила токаI в контуре изменяется под влиянием ЭДС самоиндукции , где– ЭДС источника постоянного тока в контуре, тогда работа источников электрической энергии
При очень медленной деформации контура ЭДС самоиндукции мала по сравнению с , поэтому теплота, выделяемая по закону Джоуля-_Ленца, равна, и.

Таким образом, элементарная работа пондемоторных сил . Полная работа пондемоторных сил, где– изменение индуктивности контура при его деформации,– постоянный ток в контуре до и после его деформации.
Лекция 9
Плотность магнитного потока— обзор
Электродвигатели Приводы
Возможно, самый важный электромеханический привод в автомобилях — это электродвигатель. Электродвигатели уже давно используются в автомобилях, начиная со стартера, который использует электроэнергию, подаваемую аккумуляторной батареей, для вращения двигателя с частотой вращения, достаточной для запуска двигателя. Двигатели также использовались для подъема или опускания окон, положения сидений, а также для исполнительных механизмов управления воздушным потоком на холостом ходу (см. Главу 7).В последнее время электродвигатели используются для обеспечения основной движущей силы транспортного средства в гибридных или электрических транспортных средствах.

Существует большое количество типов электродвигателей, которые классифицируются по типу возбуждения (например, постоянного или переменного тока), физической структуре (например, гладкий воздушный зазор или явный полюс) и типу структуры магнита для вращающийся элемент (ротор), который может быть постоянным магнитом или электромагнитом. Однако между всеми электродвигателями есть определенные фундаментальные общие черты, которые обсуждаются ниже.Еще одно различие между типами электродвигателей основано на том, получает ли ротор электрическое возбуждение от скользящего механического переключателя (т.е. коммутатора и щетки) или от индукции. Независимо от конфигурации двигателя, каждый из них способен производить механическую мощность за счет крутящего момента, прилагаемого к ротору за счет взаимодействия магнитных полей между ротором и неподвижной конструкцией (статором), которая поддерживает ротор вдоль его оси вращения.
Подробное рассмотрение всех типов двигателей выходит за рамки данной книги.
 Скорее, мы представляем базовую физическую структуру и разрабатываем аналитические модели, которые могут быть применены ко всем вращающимся электромеханическим машинам. Кроме того, мы ограничиваем наше обсуждение линейными, не зависящими от времени моделями, которых достаточно для анализа производительности, подходящего для большинства автомобильных приложений.
Скорее, мы представляем базовую физическую структуру и разрабатываем аналитические модели, которые могут быть применены ко всем вращающимся электромеханическим машинам. Кроме того, мы ограничиваем наше обсуждение линейными, не зависящими от времени моделями, которых достаточно для анализа производительности, подходящего для большинства автомобильных приложений.Мы представляем конструкции различных электродвигателей на Рисунке 6.34, который представляет собой очень упрощенный эскиз, изображающий только самые основные характеристики электродвигателя.
Рисунок 6.34. Схематическое изображение электродвигателя.
Этот двигатель имеет катушки, намотанные вокруг статора (имеющего N 1 витков) и ротора (имеющего N 2 витков), которые размещены в пазах по периферии в машине с равномерным зазором. На этом упрощенном чертеже изображены только две катушки. На практике их больше двух с одинаковым количеством как в статоре, так и в роторе.
 Каждая обмотка статора или ротора называется «полюсом» двигателя.И статор, и ротор изготовлены из ферромагнитного материала с очень высокой проницаемостью (см. Обсуждение ферромагнетизма выше). Целесообразно разработать модель этого упрощенного идеализированного двигателя, чтобы обеспечить основу для понимания относительно сложной конструкции практического двигателя. На рисунке 6.34 статор представляет собой цилиндр длиной, а ротор представляет собой цилиндр меньшего размера, поддерживаемый соосно со статором, так что он может вращаться вокруг общей оси. Угол между плоскостями двух катушек обозначен как θ , а угловая переменная относительно оси, измеренная от плоскости катушки статора, обозначена как α .Радиальный воздушный зазор между ротором и статором обозначен как г . При проектировании любой вращающейся электрической машины (включая двигатели) важно поддерживать этот воздушный зазор настолько малым, насколько это практически осуществимо, поскольку сила связанных магнитных полей изменяется обратно пропорционально г .
Каждая обмотка статора или ротора называется «полюсом» двигателя.И статор, и ротор изготовлены из ферромагнитного материала с очень высокой проницаемостью (см. Обсуждение ферромагнетизма выше). Целесообразно разработать модель этого упрощенного идеализированного двигателя, чтобы обеспечить основу для понимания относительно сложной конструкции практического двигателя. На рисунке 6.34 статор представляет собой цилиндр длиной, а ротор представляет собой цилиндр меньшего размера, поддерживаемый соосно со статором, так что он может вращаться вокруг общей оси. Угол между плоскостями двух катушек обозначен как θ , а угловая переменная относительно оси, измеренная от плоскости катушки статора, обозначена как α .Радиальный воздушный зазор между ротором и статором обозначен как г . При проектировании любой вращающейся электрической машины (включая двигатели) важно поддерживать этот воздушный зазор настолько малым, насколько это практически осуществимо, поскольку сила связанных магнитных полей изменяется обратно пропорционально г . Напряжения на клеммах этих двух катушек обозначены как v 1 и v 2 . Токи обозначены i 1 и i 2 , а магнитная индукционная связь для каждого обозначена λ 1 и λ 2 соответственно.Предполагая для упрощения, что прорези, несущие катушки, пренебрежимо малы, напряженность магнитного поля H направлена радиально и положительна, когда направлена наружу, и отрицательна, когда направлена внутрь.
Напряжения на клеммах этих двух катушек обозначены как v 1 и v 2 . Токи обозначены i 1 и i 2 , а магнитная индукционная связь для каждого обозначена λ 1 и λ 2 соответственно.Предполагая для упрощения, что прорези, несущие катушки, пренебрежимо малы, напряженность магнитного поля H направлена радиально и положительна, когда направлена наружу, и отрицательна, когда направлена внутрь.Напряжения возбуждения выводов определяются по формуле:
v1 = λ˙1v2 = λ˙2
Плотность магнитного потока в воздушном зазоре B r также радиально направлена и определяется как
(85) Br = μoHr
, где μ o — проницаемость воздуха.
Эта плотность магнитного потока непрерывна через ферромагнитную структуру, но поскольку проницаемость статора и ротора ( мкм, ) очень велика по сравнению с проницаемостью воздуха, напряженность магнитного поля внутри как ротора, так и статора пренебрежимо мала:
H ≃ 0 внутри ферромагнитного материала.
Контурный интеграл вдоль любого пути (например, контура C на рис. 6.34), охватывающего две катушки, определяется как
(86) IT = ∮CH¯ · d¯ℓ¯ = 2gHr (α)
Плотность магнитного потока B r ( α ) также направлена радиально и равна
Br (α) = μoHr (α)
Эта напряженность магнитного поля является кусочно-непрерывной функцией α как указано ниже:
2gHr (α) = N1i1 − N2i20≤α <θ = N1i1 + N2i2θ <α <π = −N1i1 + N2i2π <α <π + θ = −N1i1 − N2i2π + θ <α <2π
Магнитный поток для двух катушек λ 1 и λ 2 задается формулой
λ1 = N1∫oπBr (α) ℓRrⅆα
(87) λ2 = N2∫θπ + θBr (α) ℓRrⅆα
, где R r — радиус ротора.
В интегралах для λ 1 и λ 2 предполагается, что так называемый окаймляющий магнитный поток за пределами осевой длины ℓ ротора / статора пренебрежимо мал. Используя концепцию индуктивности для каждой катушки, представленную при обсуждении соленоидов, эту потокосцепление можно записать как линейную комбинацию вкладов от i 1 и i 2 :
(88) λ1 = L1i1 + Lmi2
(89) λ2 = Lmi1 + L2i2
, где
(90) L1 = N12Lo = собственная индуктивность катушки 1
(91) L2 = N22Lo = собственная индуктивность катушки 2
(92) Lo = μoℓRrπ2g
Параметр L м — это взаимная индуктивность для двух катушек, которая определяется как потокосцепление, индуцированное в каждой катушке из-за тока в другой, деленное на этот ток, и выражается как
Лм = LoN1N2 (1−2θπ) 0 <θ <π = LoN1N2 (1 + 2θπ) −π <θ <0
Приведенные выше формулы для этих индуктивностей обеспечивают достаточную модель для получения соотношений напряжения / тока на клеммах, а также электромеханических модели для расчета характеристик двигателя.Собственные индуктивности для каждой катушки не зависят от θ , но взаимная индуктивность изменяется в зависимости от θ , так что L м ( θ ) является симметричной функцией θ . Его можно формально разложить в ряд Фурье по θ , имеющий только косинусные члены в нечетных гармониках, как показано ниже:
(93) Lm (θ) = M1cos (θ) + M3cos (3θ) + M5cos (5θ) +…
В любом практическом двигателе будет такое распределение обмоток, при котором преобладает основной компонент M 1 ; то есть взаимная индуктивность равна примерно
(94) Lm≃Mcos (θ)
Для удобства записи индекс 1 на M 1 опущен.Любой двигатель, состоящий из нескольких совпадающих пар катушек в статоре и роторе, будет иметь набор клеммных соотношений в потокосцеплении для статора и ротора λ s и λ r , соответственно, заданные как
λs = Lsis + Mircosθ
λr = Lrir + Miscosθ
Крутящий момент электрического происхождения, действующий на ротор T e , определяется как
Te = ∂WmM∂θ
где, для линейной системы без потерь , энергия взаимной связи Вт мМ составляет
WmM = isirLm (θ)
Крутящий момент T e определяется как
Te = −isirMsinθ
Механическая динамика двигателя определяется выражением
Te = Jrⅆ2θⅆt2 + Bvⅆθⅆt + Ccsgn (ⅆθⅆt)
где J r — момент инерции ротора относительно его оси, B v — коэффициент демпфирования вращения из-за вращательного вязкого трения, а С 900 17 c — коэффициент кулоновского трения.
Представляет интерес оценить характеристики двигателя путем расчета механической мощности двигателя P m для заданного возбуждения. Пусть возбуждение статора и ротора происходит от идеальных источников тока, таких что
(95) is = Issin (ωst) ir = Irsin (ωrt) θ (t) = ωmt + γ
, где ω m — частота вращения ротора (рад / сек) и γ выражают произвольный параметр фазы времени. Мощность двигателя определяется как
(96) Pm = Teωm
(97) = — ωmIsIrMsin (ωst) sin (ωrt) sin (ωmt + γ)
Это уравнение можно переписать, используя хорошо известные тригонометрические тождества в форма
(98) Pm = −ωmIsIrM4 {sin [(ωm + ωs − ωr) t + γ] + sin [(ωm − ωs + ωr) t + γ] −sin [(ωm + ωs + ωr) t + γ] −sin [(ωm − ωs − ωr) t + γ]}
Среднее по времени значение любой синусоидальной функции времени равно нулю.Единственные условия, при которых двигатель может производить ненулевую среднюю мощность, задаются частотными соотношениями ниже:
(99) ωm = ± ωs ± ωr
Например, всякий раз, когда ω m = ω s + ω r , средняя временная мощность двигателя Pmav равна
(100) Pmav = ωmIsIrM4sinγ
В таком двигателе работа в равновесии будет достигнута, когда Pmav = PL, где P L = Мощность нагрузки.Таким образом, фаза между полями ротора и статора определяется выражением
(101) sinγ = 4PLωmIsIrM
при условии
(102) PL≤ωmIsIrM4
Вышеупомянутые частотные условия (уравнение (99)) являются фундаментальными для всех вращающихся машин и должны выполняться для любой ненулевой средней механической выходной мощности. Каждый тип двигателя имеет уникальный способ удовлетворения частотных условий. Мы проиллюстрируем это на конкретном примере, который использовался в некоторых гибридных транспортных средствах.Этот пример — асинхронный двигатель. Однако, прежде чем перейти к этому примеру, важно рассмотреть вопрос о моторных характеристиках. Обычно электродвигатели, которые предназначены для выработки значительного количества энергии (например, для применения в гибридных транспортных средствах), являются многофазными машинами; то есть, в дополнение к обмоткам, связанным с возбуждением статора, многофазная машина будет иметь один или несколько дополнительных наборов обмоток, которые возбуждаются с одинаковой частотой, но с разными фазами. Хотя трехфазные двигатели широко используются, анализ двухфазных асинхронных двигателей иллюстрирует основные принципы многофазных двигателей с помощью относительно упрощенной модели и предполагается в следующем обсуждении.
Двухфазный двигатель имеет два набора обмоток, смещенных на 90 ° в направлении θ и возбуждаемых токами с фазой 90 ° как для статора, так и для ротора. Так называемый сбалансированный двухфазный двигатель будет иметь катушку, возбуждаемую токами i как , i bs для фаз a и b, соответственно, где
(103) ias = Iscos (ωst)
ibs = Issin (ωst)
Ротор также состоит из двух наборов обмоток, физически смещенных на 90 ° и возбуждаемых токами i ar и i br со сдвигом фазы 90 °:
( 104) iar = Ircos (ωrt)
ibr = Irsin (ωrt)
Двухфазный асинхронный двигатель — это двигатель, в котором обмотки статора возбуждаются токами, указанными выше (т.е., i как и i bs ). Цепи ротора закорочены таким образом, что v ar = v br = 0, где v ar — напряжение на клеммах для обмоток фазы a, а v br — это напряжение на клеммах. напряжение на клеммах для фазы b. Токи в роторе возникают за счет индукции полей статора. В расширении анализа однофазного возбуждения концевые потокосцепления задаются формулой
(105) λas = Lsias + Miarcosθ − Mibrsinθλbs = Lsibs + Miarsinθ + Mibrcosθλar = Lriar + Miascosθ + Mibssinθλbr = Lribr − Miscosinθ
Крутящий момент T e и мгновенная мощность P m для двухфазного асинхронного двигателя равны
(106) Te = M [(iaribs-ibrias) cosθ− (iarias + ibribs) sinθ ]
Pm = ωmMIsIrsin [(ωm − ωs + ωr) t + γ]
Средняя мощность P av не равна нулю, когда ω м = ω s — ω r и определяется как
Па = ωmMIsIrsinγ
Поскольку выводы ротора закорочены, имеем
(107) λarⅆt = ⅆλbrⅆt = 0
Таким образом, два тока ротора удовлетворяют следующим уравнениям:
(108) 0 = Rriar + Lrⅆiarⅆt + MIsⅆⅆt [cos (ωst) cos (ωmt + γ) + sin (ωst) sin (ωmt + γ)]
(109) 0 = Rribr + Lrⅆi brⅆt + MIsⅆⅆt [−cos (ωst) sin (ωmt + γ) + sin (ωst) cos (ωmt + γ)]
, где R r и L r — сопротивление и самоиндукция. двух наборов (предполагаемой) идентичной структуры).Эти уравнения можно переписать как
(110) Lrⅆiarⅆt + Rriar = MIs (ωs − ωm) sin [(ωs − ωm) t − γ]
(111) Lrⅆibrⅆt + Rribr = −MIs (ωs − ωm) cos [ (ωs − ωm) t − γ]
Текущее значение i ab идентично i ar , за исключением фазового сдвига на 90 °, как видно из уравнения (111). Обратите внимание, что ток для обеих фаз находится на частоте ω r , где
ωr = (ωs − ωm)
Таким образом, асинхронный двигатель удовлетворяет условию частоты, имея токи на разнице между возбуждением и частотой вращения ротора.Текущее значение i ar определяется как
(112) iar = (ωs − ωm) MIsRr2 + (ωs − ωm) 2Lr2cos [(ωs − ωm) t − α]
, где
α = — (π2 + γ + β)
и
(113) β = tan − 1 [(ωs − ωm) RrLr]
Ток в фазе b идентичен, за исключением фазового сдвига на 90 °. Подстановка токов для ротора и статора в уравнение для крутящего момента T e дает замечательный результат: этот крутящий момент не зависит от θ и определяется как
(114) Te = (ωs − ωm) M2RrIs2Rr2 + ( ωs − ωm) 2Lr2
Механическая выходная мощность P m определяется как
Pm = ωmTe = [ωs2M2Is2 (Rr / s) 2 + ωs2Lr2] (1 − ss) Rr
, где s — называется скольжением и определяется как
(115) s = ωs − ωmωs
Индукционная машина имеет три режима работы, которые характеризуются значениями s .Для 0 < с <1 он действует как двигатель и вырабатывает механическую энергию. Для -1 < с <0 он действует как генератор, и механическая входная мощность ротора преобразуется в выходную электрическую мощность. Для с > 1 индукционная машина действует как тормоз, при этом электрическая входная и механическая входная мощность рассеивается в роторе i r 2 R r потерь. Благодаря своей универсальности асинхронный двигатель имеет большой потенциал в силовых установках гибридных / электрических транспортных средств.Однако это требует, чтобы система управления включала в себя твердотельную электронику переключения мощности, чтобы иметь возможность управлять необходимыми токами. Кроме того, требуется точный контроль тока возбуждения.
Применение асинхронного двигателя для обеспечения необходимого крутящего момента для движения гибридного или электрического транспортного средства зависит от изменения крутящего момента в зависимости от скорости вращения ротора. Изучение уравнения (114) показывает, что двигатель создает нулевой крутящий момент при синхронной скорости (т.е. ω m — ω s ).Крутящий момент асинхронного двигателя первоначально увеличивается от его значения при ω м = 0 достигает максимального крутящего момента ( T max ) при скорости ωm> ωm ∗, когда
0≤ωm ∗ ≤ωs
Крутящий момент имеет отрицательный наклон, определяемый как
ⅆTeⅆωm <0ωm> ωm ∗
Обычно асинхронный двигатель работает в области отрицательного наклона T м ( ω м ) (т. Е. Ωm ∗ > ωm <ωs) для стабильной работы. Равновесие достигается при скорости вращения двигателя ω, м , при которой крутящий момент двигателя T и и крутящий момент нагрузки T L равны, т.е.е. T e ( ω м ) = T L ( ω м ).
Эта точка проиллюстрирована для гипотетического крутящего момента нагрузки, который является линейной функцией скорости двигателя, так что крутящий момент нагрузки задается как
(116) TL = KLωm
На рисунке 6.35 показаны крутящие моменты двигателя и нагрузки для изменяющейся нагрузки. линейно с ω м .
Рисунок 6.35. Нормированный крутящий момент T м vs.нормализованные моменты нагрузки T L 1 T L 2 .
Для удобства представления на рисунке 6.35 представлены нормализованный крутящий момент двигателя и крутящий момент нагрузки, приведенные к максимальному крутящему моменту T max , где
(117) Tmax = maxωm (Te (ωm))
Этот максимум происходит при ωm = ωm ∗, который для данного гипотетического нормализованного примера задается как
ωm ∗ ωs≅.68
На рисунке 6.33 также представлены два момента нагрузки, нормированные на T max :
TL1 = KL1ωm / TmaxTL2 = KL2ωm / Tmax
, где
KL2> KL1
Рабочая скорость двигателя для этих двух моментов нагрузки — это две точки пересечения ω 01 и ω 02 , где
Tm (ω01) = TL1 (ω01 ) Tm (ω02) = TL2 (ω02)
Эти две точки пересечения представляют собой установившиеся рабочие условия для двух моментов нагрузки.Более высокая из двух нагрузок имеет установившуюся рабочую точку ниже, чем первая (т. Е. ω 02 < ω 01 ).
В главе 7 обсуждается управление асинхронным двигателем, который используется в гибридном электромобиле. Там разработана модель зависимости крутящего момента нагрузки от условий эксплуатации транспортного средства.
Бесщеточные двигатели постоянного тока
Далее мы рассмотрим относительно новый тип электродвигателя, известный как бесщеточный двигатель постоянного тока. Бесщеточный двигатель постоянного тока вообще не является двигателем постоянного тока в том смысле, что для возбуждения статора используется переменный ток.Однако свое название он получил из-за схожести по физическим характеристикам и характеристикам с шунтирующим двигателем постоянного тока с постоянным током возбуждения. Этот тип двигателя включает постоянный магнит в роторе и полюса электромагнита в статоре, как показано на рис. 6.36. Традиционно роторные двигатели с постоянными магнитами обычно использовались только в относительно маломощных приложениях. Недавняя разработка некоторых относительно мощных редкоземельных магнитов и разработка мощных переключающих твердотельных устройств существенно повысили мощность таких машин.
Рисунок 6.36. Бесщеточный двигатель постоянного тока.
Полюса статора возбуждаются так, что они имеют магнитные полюса N и S с полярностью, как показано на рисунке 6.36, токами I a и I b . Эти токи попеременно включаются и выключаются от источника постоянного тока с частотой, соответствующей скорости вращения. Переключение осуществляется электронным способом с помощью системы, которая включает датчик углового положения, прикрепленный к ротору. Это переключение выполняется таким образом, чтобы магнитное поле, создаваемое электромагнитами статора, всегда прикладывало крутящий момент к ротору в направлении его вращения.
Крутящий момент T¯m, приложенный к ротору вектором напряженности магнитного поля H¯, создаваемым обмотками статора, определяется следующим векторным произведением
(118) T¯m = γ (M¯ × H¯)
где M¯ — вектор намагниченности постоянного магнита, а γ — постоянная для конфигурации.
Направление этого крутящего момента таково, что постоянный магнит вращается в направлении параллельного совмещения с движущим полем H¯ (которое пропорционально току возбуждения).Величина крутящего момента T м определяется как
Tm = γMHsin (θ)
, где M = величина M¯, H = величина H¯ и θ = угол между M¯ и H¯.
Если бы ротор с постоянным магнитом мог вращаться в статическом магнитном поле, он бы вращался только до θ = 0 (т. Е. До выравнивания).
В бесщеточном двигателе постоянного тока, однако, поля возбуждения поочередно переключаются электронно, так что крутящий момент непрерывно прикладывается к магниту ротора.Чтобы этот двигатель продолжал иметь ненулевой крутящий момент, обмотки статора должны постоянно переключаться синхронно с вращением ротора. Хотя на рисунке 6.36 показаны только два набора обмоток статора (т. Е. Двухполюсная машина), обычно имеется несколько наборов обмоток, каждый из которых приводится в действие отдельно и синхронно с вращением ротора. Фактически, последовательное приложение токов статора создает вращающееся магнитное поле, которое вращается с частотой ротора ( ω r ).
Упрощенная блок-схема системы управления двухполюсным двигателем для двигателя, показанного на рис. 6.36a и b, показана на рис. 6.36c. Датчик S измеряет угловое положение θ ротора относительно осей магнитных полюсов статора. Контроллер определяет время включения токов , , , и , , , , а также продолжительность. Время переключения определяется таким образом, чтобы к ротору прилагался крутящий момент в направлении вращения.
В соответствующее время транзистор A, включается, и электроэнергия от бортового источника постоянного тока (например, аккумуляторной батареи) подается на полюса A двигателя. Продолжительность этого тока регулируется контроллером C для выработки желаемой мощности (по команде драйвера). После поворота примерно на 90 ° ток I b включается путем активации транзистора B через сигнал, отправляемый контроллером C.
Постоянный магнит ротора эквивалентен электромагниту с возбуждением постоянного тока (т.е., ω r = 0). Частота, с которой переключаются токи в обмотках статора, всегда синхронна со скоростью вращения. Таким образом, условие частоты для двигателя выполняется, поскольку ω s = ω m . Эта скорость определяется механической нагрузкой на двигатель и мощностью, управляемой контроллером. Когда команда мощности увеличивается, контроллер реагирует увеличением длительности импульса тока, подаваемого на каждую обмотку статора.Мощность, выдаваемая двигателем, пропорциональна доле каждого цикла, в котором находится ток (т. Е. Так называемого рабочего цикла).
Разница между измерением магнитного потока и магнитных полей
Проще говоря, магнитное поле аналогично электрическому напряжению, а магнитный поток аналогичен электрическому току. Магнитная цепь аналогична электрической цепи с важными отличиями. Электродвижущая сила в электрической цепи соответствует магнитодвижущей силе.Сопротивление и обратная ему проводимость в электрической цепи соответствуют сопротивлению и его обратной магнитной проницаемости в цепи магнита. Но есть тонкие способы, в которых силы соответствуют лишь приблизительно, а сравнения несовершенные.
Другими словами, напряженность магнитного поля (H в амперах на метр) — это величина силы намагничивания. Эта сила прямо пропорциональна току, переносимому проводником, и длине проводника. Плотность магнитного потока (B в теслах или Вебер / м 2 ) — это величина магнитной силы, наведенной на данное тело из-за силы намагничивания H.Величина индуцированной магнитной силы зависит от силы H и природы среды.
Намагниченное тело имеет северный и южный полюсы, и эти полюса всегда существуют в связанных парах. Если разрезать стержневой магнит пополам, чтобы сделать два более коротких стержневых магнита, каждый из новых магнитов будет иметь северный и южный полюса. Магнитный монополь так и не был обнаружен.
Железные опилки образуют магнитомагнитные силовые линии.Магнитное поле, связанное с постоянным магнитом, можно продемонстрировать, поместив лист бумаги поверх магнита и беспорядочно посыпав его железными опилками.Каждая частица быстро намагничивается своим собственным северным и южным полюсами, и поскольку их противоположные полюса притягиваются, они образуют линии, представляющие магнитное поле. Плотность линий (количество линий на миллиметр) и направление линий показывают, что магнитное поле является векторным полем. Линии меняют направление и становятся ближе друг к другу или дальше друг от друга по мере изменения плотности поля.
Железные опилки могут показывать направление и напряженность магнитного поля, но это не само векторное поле.Они похожи на следы на песке или рябь в движущемся потоке, а не на воду. B и H пропорциональны в вакууме, но расходятся внутри магнитных материалов. Намагниченность, обозначаемая буквой M в верхнем регистре, является мерой степени реакции материалов на приложенное поле B. Диамагнитные материалы создают намагниченность, противодействующую приложенному полю. Парамагнитные материалы создают намагниченность в том же направлении, что и приложенное поле.
В обоих случаях M обычно пропорционально приложенному магнитному полю.Связь между B и H: B = μH, где μ — проницаемость среды, через которую проходит поток. Проницаемость различается для разных материалов и часто является гистерезисной, что означает, что она демонстрирует гистерезис в своей реакции на магнитные поля. Железо очень проницаемо для магнитного потока.
Магнитный поток сначала определяется количественно путем создания воображаемой поверхности. Эта поверхность представляет собой строго математическую конструкцию и может совпадать с поверхностью магнита или пересекать ее. Магнитный поток — это величина потока, протекающего через поверхность.В частности, это большее количество линий, проходящих через поверхность в одном направлении, за вычетом небольшого количества линий, проходящих через поверхность в противоположном направлении, или ноль, если они равны.
Соответствующее уравнение для плотности магнитного потока Φ: Φ = BA cosθ. A представляет собой площадь поверхности. Если поверхность перпендикулярна магнитному полю, cosθ = 1. Если поверхность расположена под углом к силовым линиям, cosθ меньше единицы. Единица измерения магнитного потока в системе СИ — Вебер.Плотность магнитного потока — это магнитный поток, деленный (векторно, если он находится под углом) на площадь поверхности в единицах тесла.
Электрический ток в проводке, созданной человеком, протекает по изолированным проводникам. В магнитной области нет абсолютных изоляторов, но вместо этого все материалы имеют большее или меньшее сопротивление, то есть меньшую или большую магнитную проницаемость. Вот почему в эксперименте с железными опилками линии, представляющие магнитное поле, выходят далеко за пределы реального магнита. В двигателях, трансформаторах и подобных устройствах магнитный поток проходит через железные сердечники для выполнения желаемой работы.
Магнитный поток, передаваемый через магнитную цепь приложенной магнитодвижущей силой, выражается как F = ϕR, где F — магнитодвижущая сила, действующая во всей или части магнитной цепи, ϕ — магнитный поток, проходящий через данный сегмент, а R — магнитный поток. сопротивление сегмента.
Определяющее различие между электрической цепью и цепью магнитодвижущей силы состоит в том, что рассеяние мощности связано с сопротивлением, а не с реактивным сопротивлением. Электрическое поле заставляет ток следовать по пути наименьшего сопротивления, а магнитное поле заставляет магнитный поток следовать по пути наименьшего сопротивления.
Уравнения Максвелла утверждают, что магнитный поток всегда образует замкнутый контур. Магнитные цепи нелинейны. Сопротивление различается в зависимости от магнитного поля. Когда магнитный поток поднимается выше определенного уровня, проницаемый материал насыщается, поэтому не может быть дальнейшего увеличения магнитного потока, который ограничен сопротивлением убегающему сопротивлению. В резистивной электрической цепи такого явления не происходит.
Земной магнитометр в действии.Типичный способ измерения магнитных полей — с помощью магнитометра.Векторные магнитометры измеряют векторные компоненты магнитного поля, тогда как магнитометры полного поля или скалярные магнитометры измеряют только величину векторного магнитного поля.
В магнитометрах используется несколько технологий. Обычный компас — это, по сути, простой магнитометр. Стрелка измеряет направление поля. Частота колебаний намагниченной иглы пропорциональна квадратному корню из силы окружающего магнитного поля.
Одной из самых простых технологий магнитометров является индуктивная считывающая катушка, которая измеряет намагниченность путем определения тока, индуцированного в катушке, вызванного изменением магнитного момента образца.Намагниченность образца можно изменить, приложив небольшое переменное магнитное поле (или быстро меняющееся постоянное поле), как в импульсных магнитах с конденсаторным приводом. Эти измерения требуют различения магнитного поля, создаваемого образцом, и внешнего приложенного поля, часто за счет использования катушек компенсации. Обычно половина приемной катушки намотана в одном направлении, а другая половина — в другом. Образец находится только в одной половине. Внешнее однородное магнитное поле обнаруживается обеими половинами катушки.Поскольку они намотаны встречной намоткой, внешнее магнитное поле не производит чистого сигнала.
Существует множество более экзотических технологий магнитометров. Магнитометры с вибрирующим образцом (VSM) обнаруживают намагниченность образца путем механической вибрации образца внутри индукционной измерительной катушки или катушки SQUID. Измеряется наведенный ток или изменяющийся магнитный поток в катушке. Магнитометрия с извлечением импульсного поля также использует считывающие катушки для измерения намагниченности. Здесь образец закреплен, и внешнее магнитное поле быстро изменяется.Затем необходимо использовать один из нескольких методов, чтобы нейтрализовать внешнее поле, создаваемое образцом. К ним относятся катушки с противообмоткой, которые нейтрализуют внешнее однородное поле и измерения фона при удалении образца из катушки.
Флюксметр.Магнитный поток обычно измеряется с помощью измерителя потока, который содержит измерительные катушки и электронику, которая оценивает изменение напряжения в измерительных катушках для расчета измерения магнитного потока.
Флюксметры— это в основном интеграторы, используемые из-за физической взаимосвязи между катушками проволоки и магнитным потоком.Мгновенное напряжение, создаваемое на катушке, пропорционально количеству витков в катушке, умноженному на скорость изменения магнитного потока. Проблематично использовать это соотношение скорости изменения непосредственно для измерений постоянного тока, потому что напряжение исчезает, как только поток перестает изменяться. Напряжение также пропорционально скорости изменения магнитного потока, а не общему изменению магнитного потока, которое обычно является параметром, представляющим интерес.
Если напряжение на катушке интегрировать, чтобы посмотреть на область под ней в зависимости от времени, вышеуказанные проблемы исчезнут.Выход интегратора пропорционален общему изменению потока, и скорость изменения не имеет значения.
Магнитное поле, напряженность поля и плотность потока
В физике есть два различных атрибута магнитного поля:
- «Сила магнитного поля». Обычно обозначается символом H. Измеряется в амперах на метр (А / м).
- «Плотность магнитного потока». Обычно обозначается символом B. Измеряется в теслах (микротеслах или гауссах).
В теории электромагнетизма совершенно очевидно, что это разные величины, и вам нужно точно указать, какие измерения вы измеряете.
Но для многих практических целей они связаны простым числовым соотношением:
B = μ 0 H
, где μ 0 — постоянная величина — она называется проницаемостью свободного пространства и имеет значение ( в СИ) 4π.10 -7
Чтобы быть более точным, мы можем записать полное соотношение:
B = μ r μ 0 H
Эта вторая константа, которую мы ввели, μ r , называется относительной проницаемостью.Для немагнитных материалов — воздуха, большинства строительных материалов, человеческого тела и т. Д. — он имеет значение почти 1. Вот почему обычно достаточно правильно просто сказать B = μ 0 H. Только рядом с железом или стали или других магнитных материалов, нам нужно немного углубиться в физику, потому что именно тогда μ r начинает принимать разные значения.
Итак, в большинстве случаев на самом деле не имеет большого значения, измеряем ли мы B, плотность магнитного потока в микротеслах, или H, напряженность магнитного поля в амперах на метр.Вы можете просто преобразовать одно в другое, как мы это делаем в нашей таблице единиц.
Иногда люди очень точны и говорят либо о плотности магнитного потока, либо о напряженности магнитного поля. Но на самом деле «магнитное поле» прекрасно подходит для описания любого из них — и плотность магнитного потока, и напряженность магнитного поля являются примерами магнитного поля. И просто использовать «магнитное поле» намного проще … так что мы делаем это большую часть времени на этом сайте.
Если вы думаете, что мы немного работаем над этим вопросом, то это потому, что иногда люди видели, как мы используем «магнитное поле», и предполагали, что мы действительно имели в виду «напряженность магнитного поля», а затем поняли, что на самом деле мы говорили о плотность магнитного потока », поэтому критиковали нас за то, что мы запутали эти две величины.Но это немного ложный педантизм — то, что мы делаем, совершенно правильно с точки зрения университетского физика, а также с точки зрения попыток сделать наши коммуникации как можно более простыми.
Запутались? Суть в том, что большую часть времени, когда вы видите «магнитное поле», это все, о чем вам нужно беспокоиться.
Плотность магнитного потока
Плотность магнитного потока
В Международной системе (СИ) единицей измерения плотности магнитного потока является тесла (Тл).
Магнитное поле в один тесла относительно велико. Вот почему магнитные поля также выражаются в милтеслах (мТл) и микротеслах (мкТл).
1 T = 1 000 мТл = 1 000 000 мкТл
Для облегчения сравнений GreenFacts систематически использовал единицу mT в своих сводках статических полей.
Типичные значения для статических магнитных полей
(наиболее часто используемые единицы отмечены серым цветом)Магнитный поле Т мТ мкТл Земли напряженность магнитного поля при его поверхность 0.035-
0,070 мТл35 — 70 мкТл Внутри электропоезда до 0,002 Т до 2 mT до 2000 мкТл Алюминий производство вверх до 0.06 Т до 60 mT до 60000 мкТл Магнитный Резонансная томография (МРТ) сканер, используемый в клинических условиях 0,2 —
3 т200-
3000 мТПоля Сообщается, что вызывает головокружение и фосфены
в людях, перемещающихся в нихвыше 2-3 Т выше 2000-3000 mT Поля для которых последствия для здоровья имеют изучено на данный момент вверх к 8 Т до 8000 mT Самый сильный поля, которые сейчас разрабатываются для клиническая визуализация до 9.4 Т до 9400 mT В Международной системе (СИ) одна тесла (1 Тл) определяется как напряженность поля, генерирующая один ньютон силы на ампер тока на метр проводника:
T = Nw · A-1 · м-1 = кг · с-2 · A-1
Международное бюро мер и весов (BIPM) предоставляет дополнительную информацию о Международной системе единиц (SI) на сайте www.bipm.org/en/si/ и префиксы Международной системы единиц (СИ) на www.bipm.fr/en/si/prefixes.html
Связанная публикация :
Другие рисунки и таблицы в этой публикации :
Таблица 1: Рекомендации по исследованию
Статические электрические поля телевизоров и экранов компьютеров
Плотность магнитного потока
Напряженность магнитного поля
Магнитные поля, создаваемые токами и рассчитываемые по закону Ампера или закону Био-Савара, характеризуются магнитным полем B, измеряемым в теслах.Но когда генерируемые поля проходят через магнитные материалы, которые сами вносят вклад во внутренние магнитные поля, могут возникнуть неоднозначности относительно того, какая часть поля исходит от внешних токов, а какая — от самого материала. Обычной практикой было определение другой величины магнитного поля, обычно называемой «напряженностью магнитного поля», обозначенной Н. Ее можно определить соотношением
H = B / μ м = B / μ 0 — Mи имеет значение однозначного определения управляющего магнитного воздействия от внешних токов в материале, независимо от магнитного отклика материала.Отношение для B можно записать в эквивалентной форме
B = μ 0 (H + M)H и M будут иметь одинаковые единицы измерения, ампер / метр. Чтобы еще больше отличить B от H, B иногда называют плотностью магнитного потока или магнитной индукцией. Величина M в этих соотношениях называется намагниченностью материала.
Другая часто используемая форма отношения между B и H —
. B = μ м Hгде
μ = μ м = K м μ 0μ 0 — магнитная проницаемость пространства, а K м — относительная проницаемость материала.Если материал не реагирует на внешнее магнитное поле, создавая какую-либо намагниченность, тогда K m = 1. Другой обычно используемой магнитной величиной является магнитная восприимчивость, которая указывает, насколько относительная проницаемость отличается от единицы.
Магнитная восприимчивость χ м = K м — 1Для парамагнитных и диамагнитных материалов относительная проницаемость очень близка к 1, а магнитная восприимчивость очень близка к нулю. Для ферромагнитных материалов эти количества могут быть очень большими.
Единица измерения напряженности магнитного поля H может быть получена из ее отношения к магнитному полю B, B = мкГн. Поскольку единица магнитной проницаемости μ — N / A 2 , то единица измерения напряженности магнитного поля:
T / (N / A 2 ) = (N / Am) / (N / A 2 ) = A / mСтарая единица измерения напряженности магнитного поля — эрстед: 1 А / м = 0,01257 эрстед
Magnetic Fundamentals, Flux Density
Magnetic Fundamentals, Flux DensityЭксперименты с магнитами и окружающей средой
Двенадцать основ магнетизма
4.Плотность потока, В [тесла, Тл]
а. Ссылки по теме
http://en.wikipedia.org/wiki/Mintage_flux_de density
б. Что это?Плотность потока — это мера количества магнитных силовые линии (поток), перпендикулярные площади. Когда силовые линии магнитного поля плотно прижаты друг к другу, плотность потока больше, чем когда магнитное поле линии проводятся дальше друг от друга.
г. Единица
Единица измерения — тесла (T для сокращения) и То же, что и Wb / m 2 , количество веберов на квадратный метр. Одна тесла — это также равняется 10 000 Гаусс, с которыми вы, скорее всего, знакомы. В В магнитных уравнениях он обычно обозначается буквой B.
г.Плотность потока Земли
Плотность магнитного потока Земли составляет около 4 линий на кв. дюйм, или 0,5 Гаусс, или 5 * 10 -5 Тл. Итак, если вы коснетесь кончика ваш указательный палец до кончика большого пальца, у вас площадь около 1 кв. дюйма. Выровняйте его так, чтобы проходила линия с юга на север земли. через это отверстие, и у вас будет около 4 магнитных линий потока, протекающих через эту область.
эл.Плотность магнитного потока магнита
Плотность потока, близкая к редкоземельному магниту, составляет около 8000 Гаусс, или 0,8 тесла. Наибольшая плотность потока, достигнутая в лаборатории, составляет около 45 Тесла.
ф. Изменение плотности потока
Если определенное количество линий магнитного флюс течет в куске железа, и форма железа изменяется так, что его площадь поперечного сечения становится меньше, но остается то же количество линий то же самое, плотность потока увеличится. Это способ увеличить B без увеличения Φ. Посмотрим, где это пригодится.
Закон, связывающий напряженность магнитного поля H с его источник, плотность тока Дж , составляет
Отметим, что в отличие от интегральной формулировки закона Гаусса, (1.3.1), символы поверхностных интегралов справа не имеют кружков. Это означает, что интеграции производятся на открытых поверхностях с краями. Обозначается контуром C . Такая поверхность S , ограниченная контуром C , является показано на рис. 1.4.1. Другими словами, интегральный закон Ампера в формуле (1) требует, чтобы строка интеграл (циркуляция) магнитного поля интенсивность H по замкнутому контуру равна чистому току проходящей через поверхность, охватывающую контур плюс скорость изменение чистой плотности потока смещения o E через поверхность (ток смещения ).
Направление положительного d a определяется правилом правой руки, как также показано на рис. 1.4.1. Пальцами правой руки в направлении d s большой палец имеет направление d a . Как вариант, большим пальцем правой руки в направлении d s , пальцы будут в положительном направлении d a .
В законе Ампера H появляется без o .Этот закон поэтому устанавливает основные единицы H как кулон / (метр-секунда). В гл. 1.1, единицы плотности потока o H определяются силой Лоренца, поэтому второй эмпирический константа, проницаемость свободного пространства , составляет o = 4 x 10 -7 генри / м (генри = вольт-сек / ампер).
Постоянный ток в направлении z внутри кругового цилиндрическая область радиусом R , показанная на рис.1.4.2, простирается от до бесконечность до + бесконечность по оси z и представлена плотность
где J o и R — заданные константы. Связанное магнитное поле Интенсивность имеет только азимутальную составляющую.
Рисунок 1.4.2. Осесимметричный ток распределение и связанное с ним радиальное распределение азимутальных магнитных напряженность поля. Контур C используется для определения азимутального H , в то время как C ‘ используется, чтобы показать, что поле, направленное z , должно быть униформа.Чтобы увидеть, что в этом поле не может быть r составляющей, заметим, что вращение источника вокруг радиальной оси, как показано на рис. 1.4.2, меняет местами источник (тогда ток в направлении -z ) и следовательно, необходимо перевернуть поле. Но компонент поля r делает не переворачивается при таком повороте и, следовательно, должно быть равно нулю. В Этот аргумент не исключает компонентов H и H z . Однако если они существуют, они не должны зависеть от координат и z , потому что вращение источника вокруг оси z и перенос источника вдоль оси z не изменяет источник и, следовательно, не меняет поле.
Ток не зависит от времени, поэтому мы предполагаем, что поля тоже. Следовательно, последнее слагаемое в (1), смещение ток равен нулю. Затем закон используется с S , поверхность, имеющая охватывающий контур C на произвольном радиусе r , как показано на рис. 1.4.2. Тогда элементы площади и линии
и правая часть (1) принимает вид
Интегрирование в левой части сводится к умножению независимый H по длине C .
Эти последние два выражения используются для оценки (1) и получения
Таким образом, азимутальная напряженность магнитного поля имеет радиальную Распределение показано на рис. 1.4.2.
Компонент z в H в лучшем случае является однородным. Это видно по применяя интегральный закон к контуру C ‘ , также показанному на Рис. 1.4.2. Интеграция на верхних и нижних ножках дает ноль потому что H r = 0 .




 {2}}{2\mu \mu_{0}}lS\, \left( 21 \right)$.
{2}}{2\mu \mu_{0}}lS\, \left( 21 \right)$. 29)
29) 30)
30) Получим
Получим
 При изучении электромагнетизма необходимо усвоить, что это за величина, что она характеризует и как измеряется.
При изучении электромагнетизма необходимо усвоить, что это за величина, что она характеризует и как измеряется. Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W:
Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W:

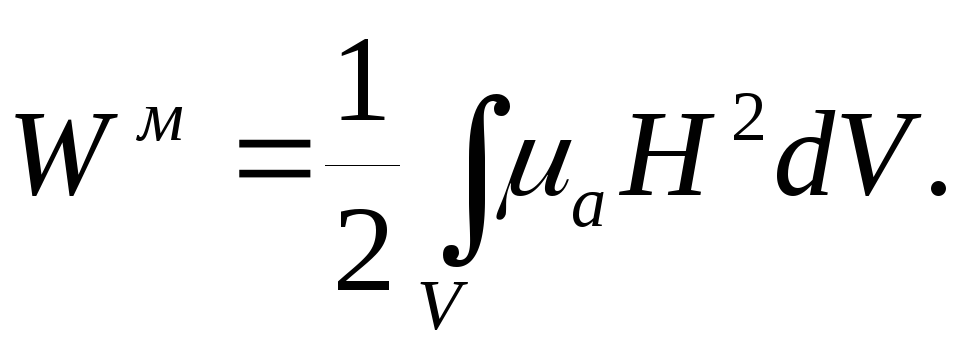
 Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.
Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.
Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. 
 136]
136] 32]
32] 485]
485] Такая волна называется бегущей. Движение энергии в бегущей упругой или электро-магнитной
[c.37]
Такая волна называется бегущей. Движение энергии в бегущей упругой или электро-магнитной
[c.37]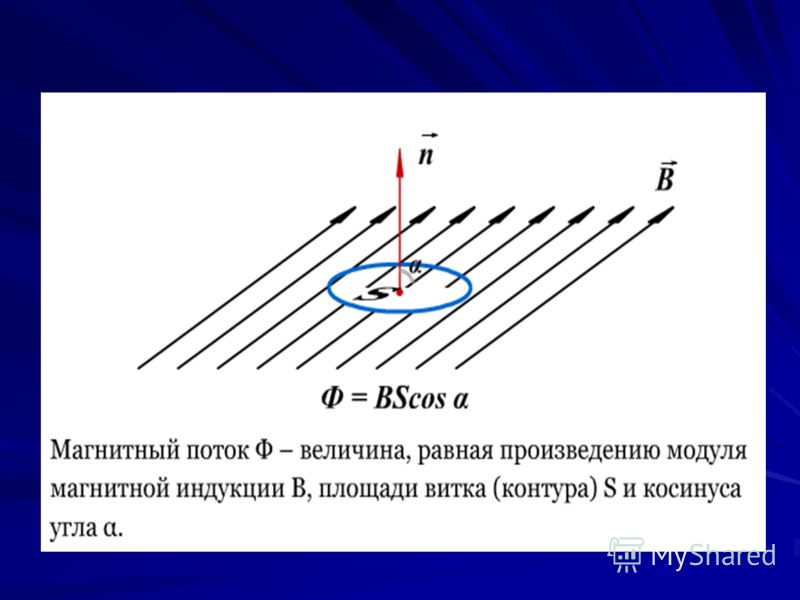 (1.42)], пропорциональная (г, t), и равная ей плотность энергии Wy магнитного поля [см. (1.43)]. Их средние по времени значения во всех точках одинаковы и пропорциональны квадрату амплитуды
[c.32]
(1.42)], пропорциональная (г, t), и равная ей плотность энергии Wy магнитного поля [см. (1.43)]. Их средние по времени значения во всех точках одинаковы и пропорциональны квадрату амплитуды
[c.32] То же происходит с энергией магнитного поля. Таким образом, энергия колеблется от чисто электрической, имеющей максимум плотности з одном месте, до чисто магнитной с максимумом плотности энергии, смещенным на Это напоминает поведение гармонического осциллятора (колебательного контура). Полная энергия осциллятора постоянна, но колеблется, переходя из чисто потенциальной энергии в одном положении массы в чисто кинетическую энергию в другом положении массы. Как потенциальная, так и кинетическая энергии гармонически колеблются относительно их среднего значения с частотой 2со. Двойка появляется потому, что потенциальная энергия дважды (за период) положительна и дважды достигает максимального зна-че[П1Я (то же справедливо и для кинетической энергии). Электрическое поле Ех в стоячей волне аналогично смещению массы гармонического осциллятора от положения равновесия, в то время как магнитное поле Ву аналогично скорости этой массы.
[c.324]
То же происходит с энергией магнитного поля. Таким образом, энергия колеблется от чисто электрической, имеющей максимум плотности з одном месте, до чисто магнитной с максимумом плотности энергии, смещенным на Это напоминает поведение гармонического осциллятора (колебательного контура). Полная энергия осциллятора постоянна, но колеблется, переходя из чисто потенциальной энергии в одном положении массы в чисто кинетическую энергию в другом положении массы. Как потенциальная, так и кинетическая энергии гармонически колеблются относительно их среднего значения с частотой 2со. Двойка появляется потому, что потенциальная энергия дважды (за период) положительна и дважды достигает максимального зна-че[П1Я (то же справедливо и для кинетической энергии). Электрическое поле Ех в стоячей волне аналогично смещению массы гармонического осциллятора от положения равновесия, в то время как магнитное поле Ву аналогично скорости этой массы.
[c.324] 6.5.1°) и сегнетоэлектрическими (III.1.6.9 ) свойствами, равна сумме объемных плотностей энергий электрического (111.1.12.7 ) и магнитного полей
[c.274]
6.5.1°) и сегнетоэлектрическими (III.1.6.9 ) свойствами, равна сумме объемных плотностей энергий электрического (111.1.12.7 ) и магнитного полей
[c.274] [c.14]
[c.14] [c.16]
[c.16] Плотность энергии магнитного поля 1И 18л, где Н — напряженность магнитного поля, представляет собой составляющую энергии Гельмгольца. Так как магнитная индукция В = iH, то энергию Гельмгольца можно представить в виде
[c.296]
Плотность энергии магнитного поля 1И 18л, где Н — напряженность магнитного поля, представляет собой составляющую энергии Гельмгольца. Так как магнитная индукция В = iH, то энергию Гельмгольца можно представить в виде
[c.296] Время разгона 2,5 10 с. Перемычка массой w = 2 кг
[c.242]
Время разгона 2,5 10 с. Перемычка массой w = 2 кг
[c.242] Это означает, что поток энергии в стоячей электромагнитной волне отсутствует через узлы и пучности в волне, поскольку пучность напряженности электрического поля совпадает с узлом индукции магнитного поля и наоборот. Поэтому с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии магнитного поля в энергию электрического поля и обратно. С помощью (4.11) и (4.14), пользуясь формулой для объемной плотности энергии электромагнитного поля
[c.36]
Это означает, что поток энергии в стоячей электромагнитной волне отсутствует через узлы и пучности в волне, поскольку пучность напряженности электрического поля совпадает с узлом индукции магнитного поля и наоборот. Поэтому с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии магнитного поля в энергию электрического поля и обратно. С помощью (4.11) и (4.14), пользуясь формулой для объемной плотности энергии электромагнитного поля
[c.36] Ударная волна и среда за фронтом ускоряются, плотность, давление и температура растут, причем для всех режимов одинаково (фиг. 2, кривые / и 2). Параметр Re , монотонно растет, т.е. остается > 1 (фиг. 3, кривая /), магнитное поле, вмораживаясь в среду частично уносится из неразрушенной части монокристалла так, что магнитный поток Ф в ней падает, хотя напряженность магнитного поля растет (фиг. 2, кривые 3—5). Динамический параметр Л мал, то есть величина кинетической энергии ударной волны и среды за ней гораздо больше, чем энергия магнитного поля в неразрушенной части кристалла. При этом для различных режимов его величина различается 2 порядка. Для режимов 1 и 2 параметр Л монотонно убывает, а для режима 3 достигает минимума на / = 0.5 (фиг. 3, кривые J-3).
[c.151]
Ударная волна и среда за фронтом ускоряются, плотность, давление и температура растут, причем для всех режимов одинаково (фиг. 2, кривые / и 2). Параметр Re , монотонно растет, т.е. остается > 1 (фиг. 3, кривая /), магнитное поле, вмораживаясь в среду частично уносится из неразрушенной части монокристалла так, что магнитный поток Ф в ней падает, хотя напряженность магнитного поля растет (фиг. 2, кривые 3—5). Динамический параметр Л мал, то есть величина кинетической энергии ударной волны и среды за ней гораздо больше, чем энергия магнитного поля в неразрушенной части кристалла. При этом для различных режимов его величина различается 2 порядка. Для режимов 1 и 2 параметр Л монотонно убывает, а для режима 3 достигает минимума на / = 0.5 (фиг. 3, кривые J-3).
[c.151] При этом можно добиться сходимости электронов на достаточно малой площади поверхности и в фокусе электронный луч может обладать весьма высокой плотностью энергии, достигающей 5-10 Bт/мм . Такая плотность энергии достаточна для осуществления целого ряда технологических процессов, причем в результате измене ния фокусировки она может быть плавно изменена до минимальных значений.
[c.108]
При этом можно добиться сходимости электронов на достаточно малой площади поверхности и в фокусе электронный луч может обладать весьма высокой плотностью энергии, достигающей 5-10 Bт/мм . Такая плотность энергии достаточна для осуществления целого ряда технологических процессов, причем в результате измене ния фокусировки она может быть плавно изменена до минимальных значений.
[c.108] Но для изменения магнитного
потока на величину dФ следует совершить
работу dА=IdФ=LIdI. Тогда работа по созданию
магнитного потока Ф равна
Но для изменения магнитного
потока на величину dФ следует совершить
работу dА=IdФ=LIdI. Тогда работа по созданию
магнитного потока Ф равна
 Формула (3) выводилась
для однородного поля, но она верна и для
неоднородных полей. Формула (3) справедлива
только для сред, для которых линейная
зависимость В
от Н , т.е. оно относится только к пара-
и диамагнетикам.
Формула (3) выводилась
для однородного поля, но она верна и для
неоднородных полей. Формула (3) справедлива
только для сред, для которых линейная
зависимость В
от Н , т.е. оно относится только к пара-
и диамагнетикам.  В настоящее
время установлено, что магнитные свойства
протонов и нейтронов почти в 1000 раз слабее
магнитных свойств электронов. Поэтому
магнитные свойства веществ в основном
определяются электронами, входящими в
состав атомов.
В настоящее
время установлено, что магнитные свойства
протонов и нейтронов почти в 1000 раз слабее
магнитных свойств электронов. Поэтому
магнитные свойства веществ в основном
определяются электронами, входящими в
состав атомов. Поэтому у
парамагнетиков μ > 1,
а у диамагнетиков μ < 1.
Отличие μ от единицы у пара- и диамагнетиков
чрезвычайно мало. Например, у алюминия,
который относится к
парамагнетикам, μ – 1 ≈ 2,1·10–5,
у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3.
К парамагнетикам относятся также
платина, воздух и многие другие вещества.
К диамагнетикам относятся
медь (μ – 1 ≈ –3·10–6),
вода (μ – 1 ≈ –9·10–6),
висмут (μ – 1 ≈ –1,7·10–3)
и другие вещества. Образцы из пара- и
диамагнетика, помещенные в неоднородное
магнитное поле между полюсами
электромагнита, ведут себя по-разному
– парамагнетики втягиваются в область
сильного поля, диамагнетики – выталкиваются
(рис. 1.19.1).
Поэтому у
парамагнетиков μ > 1,
а у диамагнетиков μ < 1.
Отличие μ от единицы у пара- и диамагнетиков
чрезвычайно мало. Например, у алюминия,
который относится к
парамагнетикам, μ – 1 ≈ 2,1·10–5,
у хлористого железа (FeCl3) μ – 1 ≈ 2,5·10–3.
К парамагнетикам относятся также
платина, воздух и многие другие вещества.
К диамагнетикам относятся
медь (μ – 1 ≈ –3·10–6),
вода (μ – 1 ≈ –9·10–6),
висмут (μ – 1 ≈ –1,7·10–3)
и другие вещества. Образцы из пара- и
диамагнетика, помещенные в неоднородное
магнитное поле между полюсами
электромагнита, ведут себя по-разному
– парамагнетики втягиваются в область
сильного поля, диамагнетики – выталкиваются
(рис. 1.19.1).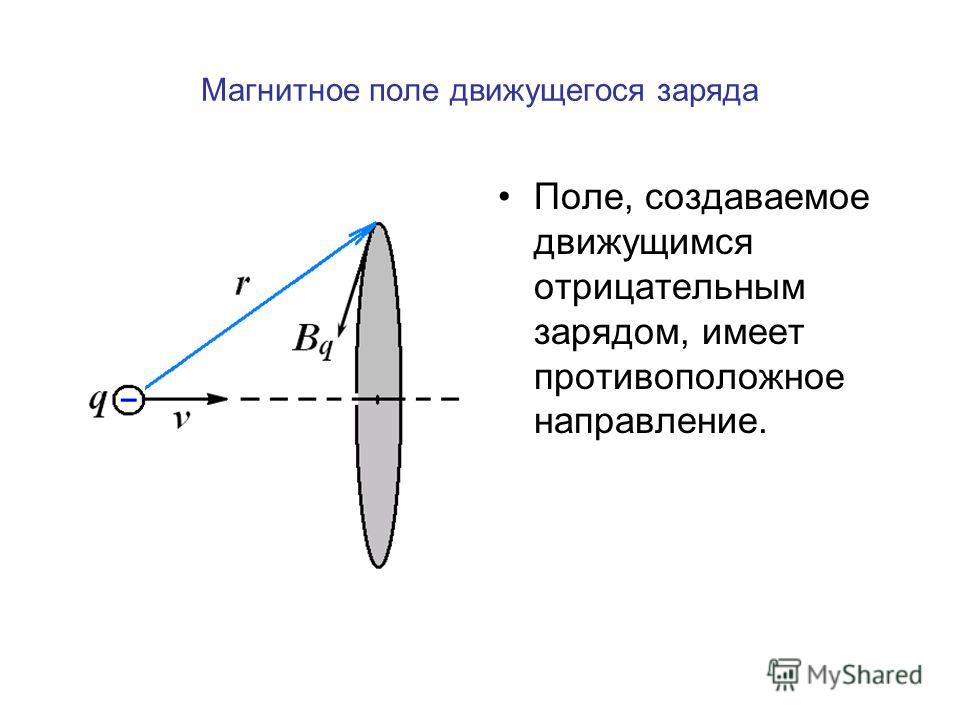 У атомов диамагнитных веществ в
отсутствие внешнего поля собственные
магнитные поля электронов и поля,
создаваемые их орбитальным движением,
полностью скомпенсированы. Возникновение
диамагнетизма связано с действием силы
Лоренца на электронные орбиты. Под
действием этой силы изменяется характер
орбитального движения электронов и
нарушается компенсация магнитных полей.
Возникающее при этом собственное
магнитное поле атома оказывается
направленным против направления
индукции внешнего поля.
У атомов диамагнитных веществ в
отсутствие внешнего поля собственные
магнитные поля электронов и поля,
создаваемые их орбитальным движением,
полностью скомпенсированы. Возникновение
диамагнетизма связано с действием силы
Лоренца на электронные орбиты. Под
действием этой силы изменяется характер
орбитального движения электронов и
нарушается компенсация магнитных полей.
Возникающее при этом собственное
магнитное поле атома оказывается
направленным против направления
индукции внешнего поля. При усилении внешнего
поля ориентационный эффект возрастает,
так что индукция собственного магнитного
поля парамагнитного образца растет
прямо пропорционально индукции внешнего
магнитного поля. Полная индукция
магнитного поля в образце складывается
из индукции внешнего магнитного поля
и индукции собственного магнитного
поля, возникшего в процессе намагничивания.
Механизм намагничивания парамагнетиков
очень похож на механизм поляризации
полярных диэлектриков.
Диамагнетизм не имеет аналога среди
электрических свойств вещества.
При усилении внешнего
поля ориентационный эффект возрастает,
так что индукция собственного магнитного
поля парамагнитного образца растет
прямо пропорционально индукции внешнего
магнитного поля. Полная индукция
магнитного поля в образце складывается
из индукции внешнего магнитного поля
и индукции собственного магнитного
поля, возникшего в процессе намагничивания.
Механизм намагничивания парамагнетиков
очень похож на механизм поляризации
полярных диэлектриков.
Диамагнетизм не имеет аналога среди
электрических свойств вещества.
 Эти материалы применяются в
приборах переменного тока, в которых
происходит непрерывное перемагничивание,
то есть изменение направления магнитного
поля (трансформаторы, электродвигатели
и т. п.).
Эти материалы применяются в
приборах переменного тока, в которых
происходит непрерывное перемагничивание,
то есть изменение направления магнитного
поля (трансформаторы, электродвигатели
и т. п.). 1.19.2. В таблицах
обычно приводятся значения максимальной
магнитной проницаемости.
1.19.2. В таблицах
обычно приводятся значения максимальной
магнитной проницаемости.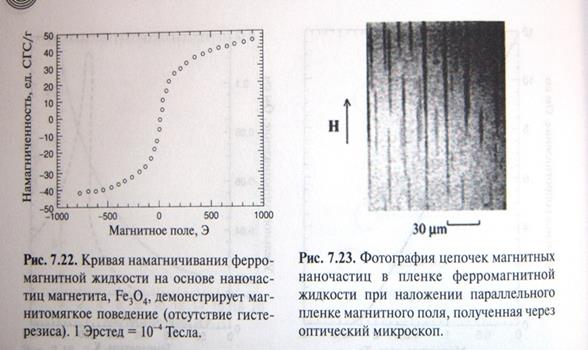 1.19.3 видно, что при наступает
магнитное насыщение – намагниченность
образца достигает максимального
значения.
1.19.3 видно, что при наступает
магнитное насыщение – намагниченность
образца достигает максимального
значения.
 С увеличением
индукции внешнего поля возрастает
магнитная индукция намагниченного
вещества. В очень сильном внешнем поле
домены, в которых собственное магнитное
поле совпадает по направлению с внешним
полем, поглощают все остальные домены,
и наступает магнитное насыщение.
Рис. 1.19.4 может служить качественной
иллюстрацией процесса намагничивания
ферромагнитного образца.
С увеличением
индукции внешнего поля возрастает
магнитная индукция намагниченного
вещества. В очень сильном внешнем поле
домены, в которых собственное магнитное
поле совпадает по направлению с внешним
полем, поглощают все остальные домены,
и наступает магнитное насыщение.
Рис. 1.19.4 может служить качественной
иллюстрацией процесса намагничивания
ферромагнитного образца. В соленоиде
течет ток
,
который образует магнитный поток,
сцепленный с соленоидом. Если отключить
соленоид от источника и замкнуть его
на сопротивление,
по цепи пойдет постепенно убывающий
ток. Работа, совершаемая этим током за
времяравна
В соленоиде
течет ток
,
который образует магнитный поток,
сцепленный с соленоидом. Если отключить
соленоид от источника и замкнуть его
на сопротивление,
по цепи пойдет постепенно убывающий
ток. Работа, совершаемая этим током за
времяравна

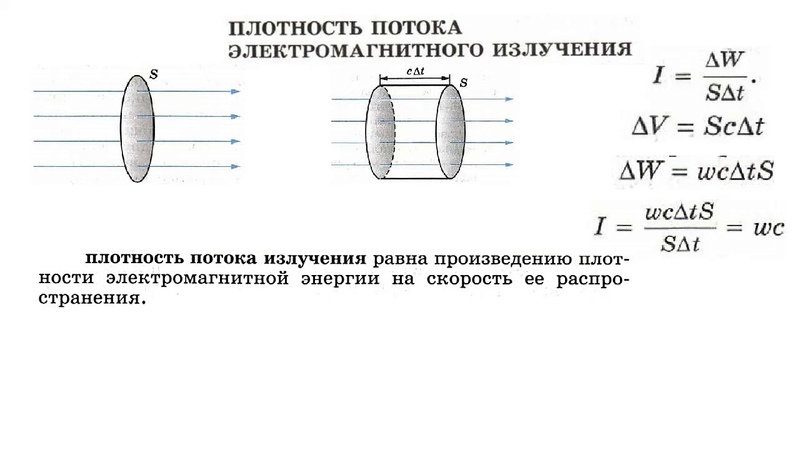


 Скорее, мы представляем базовую физическую структуру и разрабатываем аналитические модели, которые могут быть применены ко всем вращающимся электромеханическим машинам. Кроме того, мы ограничиваем наше обсуждение линейными, не зависящими от времени моделями, которых достаточно для анализа производительности, подходящего для большинства автомобильных приложений.
Скорее, мы представляем базовую физическую структуру и разрабатываем аналитические модели, которые могут быть применены ко всем вращающимся электромеханическим машинам. Кроме того, мы ограничиваем наше обсуждение линейными, не зависящими от времени моделями, которых достаточно для анализа производительности, подходящего для большинства автомобильных приложений. Каждая обмотка статора или ротора называется «полюсом» двигателя.И статор, и ротор изготовлены из ферромагнитного материала с очень высокой проницаемостью (см. Обсуждение ферромагнетизма выше). Целесообразно разработать модель этого упрощенного идеализированного двигателя, чтобы обеспечить основу для понимания относительно сложной конструкции практического двигателя. На рисунке 6.34 статор представляет собой цилиндр длиной, а ротор представляет собой цилиндр меньшего размера, поддерживаемый соосно со статором, так что он может вращаться вокруг общей оси. Угол между плоскостями двух катушек обозначен как θ , а угловая переменная относительно оси, измеренная от плоскости катушки статора, обозначена как α .Радиальный воздушный зазор между ротором и статором обозначен как г . При проектировании любой вращающейся электрической машины (включая двигатели) важно поддерживать этот воздушный зазор настолько малым, насколько это практически осуществимо, поскольку сила связанных магнитных полей изменяется обратно пропорционально г .
Каждая обмотка статора или ротора называется «полюсом» двигателя.И статор, и ротор изготовлены из ферромагнитного материала с очень высокой проницаемостью (см. Обсуждение ферромагнетизма выше). Целесообразно разработать модель этого упрощенного идеализированного двигателя, чтобы обеспечить основу для понимания относительно сложной конструкции практического двигателя. На рисунке 6.34 статор представляет собой цилиндр длиной, а ротор представляет собой цилиндр меньшего размера, поддерживаемый соосно со статором, так что он может вращаться вокруг общей оси. Угол между плоскостями двух катушек обозначен как θ , а угловая переменная относительно оси, измеренная от плоскости катушки статора, обозначена как α .Радиальный воздушный зазор между ротором и статором обозначен как г . При проектировании любой вращающейся электрической машины (включая двигатели) важно поддерживать этот воздушный зазор настолько малым, насколько это практически осуществимо, поскольку сила связанных магнитных полей изменяется обратно пропорционально г .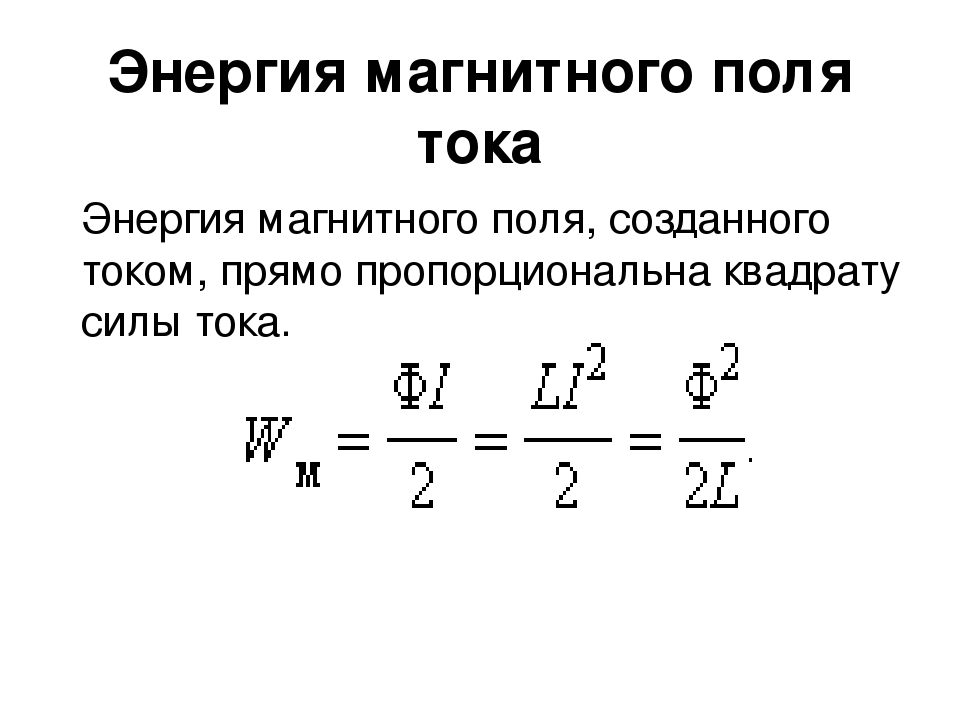 Напряжения на клеммах этих двух катушек обозначены как v 1 и v 2 . Токи обозначены i 1 и i 2 , а магнитная индукционная связь для каждого обозначена λ 1 и λ 2 соответственно.Предполагая для упрощения, что прорези, несущие катушки, пренебрежимо малы, напряженность магнитного поля H направлена радиально и положительна, когда направлена наружу, и отрицательна, когда направлена внутрь.
Напряжения на клеммах этих двух катушек обозначены как v 1 и v 2 . Токи обозначены i 1 и i 2 , а магнитная индукционная связь для каждого обозначена λ 1 и λ 2 соответственно.Предполагая для упрощения, что прорези, несущие катушки, пренебрежимо малы, напряженность магнитного поля H направлена радиально и положительна, когда направлена наружу, и отрицательна, когда направлена внутрь.