Важно! Согласно второму закону Кирхгофа, сумма подсоединенных к электрической цепи напряжений равняется сумме снижений напряжения для всех компонентов цепочки.

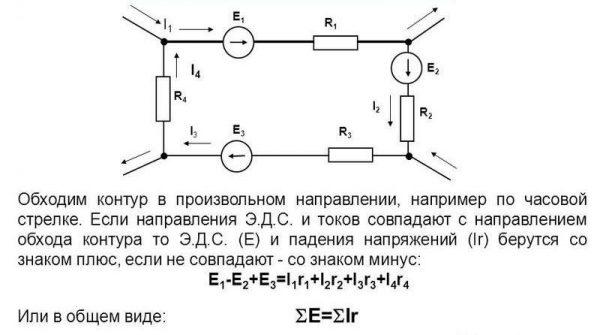
Второй закон Кирхгофа

Измерение плотности энергии магнитных полей

Данная величина показывает энергию, содержащуюся в единице объема окружающей среды, подпадающей под влияние поля. Обозначается она греческой буквой ω. Для вычисления применяется формула:

ω=W/V, в данном случае W – это полевая энергия в объеме пространства V.

Единица измерения плотности поля в международной системе СИ тоже выглядит как частное единиц, в которых измеряются эти величины: джоулей и кубических метров (Дж/м3). Показатель для аккумуляторов (ионных, свинцово-кислотных и других) указывают в прилагающейся документации.

Для соленоида, подсоединенного в электрическую цепь, оба составляющих этого частного можно выразить через следующие единицы:

1. Значение энергетического ресурса поля будет равным уполовиненному произведению индуктивности соленоида на квадрат токовой силы в его обмотке:

W=L*I2/2.

2. В качестве «пространства» рассматривается сама катушка, тогда V=S*l, где S – площадь сечения катушечного элемента в поперечнике, а l – его длина.

Тогда конечная формула принимает следующий облик:

ω=L*I2/2*S*l.

Формула индуктивного сопротивления катушки

Вычислить величину сопротивления дросселя XL можно, воспользовавшись следующей формулой:

XL=2πfL.

Здесь буква L обозначает параметр индуктивности дроссели, а f – токовую частоту. Исходя из этого выражения, поначалу попадающий на обмотку ток будет пропорциональным электротоку большой чистоты. В это время дроссель проявляет поведение, аналогичное ситуации цепного разрыва, с сильным повышением индуктивного сопротивления. С течением времени последнее падает до нулевого значения.

Вмонтированная в лампу нитка отличается высоким показателем сопротивления, тогда как активный показатель обмотки, напротив, стремится к нулю. Из-за этого возникает ситуация, когда почти весь цепной ток проходит через дроссель. Когда цепь размыкают при помощи ключа, лампа не затухает постепенно. Напротив, она сначала резко начинает гореть интенсивно, потом – медленно угасать. Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.

В рассмотренном примере катушка с обмотками, подключенная в цепь, выступает как источник магнитного поля. Поскольку в такой ситуации это поле не является однородным, для выполнения расчетов необходимо использование показателя, характеризующего концентрацию и распределение энергии в поле. Можно заключить, что смысл введения параметра плотности поля состоит именно в этом.

Видео

Плотность энергии магнитного поля

Энергия магнитного поля и плотность энергии

Магнитное поле, создаваемое токами, распределено в пространстве. Рассмотрим, какова плотность энергии поля изолированного контура с током. Используем выражение для энергии магнитного поля, которое создано контуром с током:

$E_{m}=\frac{LI^{2}}{2}\left( 1 \right)$.

где $I$ — сила тока в контуре; L – индуктивность контура.

Примем во внимание, что магнитный поток индукции через фиксированную неподвижную площадку пропорционален силе тока, а именно:

$Ф=LI\left( 2 \right)$.

Из формулы (2) получим, что индуктивность контура равна:

$L=\frac{Ф}{I}\left( 3 \right)$.

тогда энергия магнитного поля может быть представлена как:

$E_{m}=\frac{ФI^{2}}{2I}=\frac{ФI}{2}\left( 4 \right)$.

Магнитный поток из своего определения равен:

$Ф=\int\limits_S {\vec{B}\bullet d\vec{S}\left( 5 \right),}$

где $S$ – площадь поверхности контура с током. Вектор индукции магнитного поля запишем через векторный потенциал магнитного поля ($\vec A$), который создается током $I$:

$\vec{B}=rot\, \vec{A}\left( 6 \right)$

Тогда выражение (5) приведем к виду:

$Ф=\int\limits_S {rot\, \vec{A}} d\vec{S}=\int\limits_L \vec{A} \bullet d\vec{l}\left( 7 \right)$.

где $L$ — контур тока.

В выражении (7) векторный потенциал поля $\vec{A}$ создан током, который течет в этом контуре, получается, что замкнутый ток взаимодействует с собственным магнитным полем.

Физическая сущность данного взаимодействия заключается в том, что всякий элемент тока $I\vec dl$ порождает в пространстве магнитное поле. С этим полем входят во взаимодействие все остальные элементы контура.

Подставим выражение для магнитного потока (7) в формулу для энергии (2), найдем:

$E_{m}=\frac{I}{2}\int\limits_L \vec{A} \bullet d\vec{l}=\frac{1}{2}\int\limits_V \vec{A} \vec{j}dV\left( 8 \right)$,

где сделан переход к объемным токам при помощи соотношения:

$\vec{j}dV\leftrightarrow Id\vec{l}\left( 9 \right)$,

$\vec j$ – вектор плотности тока.

Замечание 1

Стрелка в выражении (9) показывает, что данная замена дает возможность перейти от формул для объемных токов к формулам линейных токов и в обратную сторону.

Преобразуем выражение под интегралом так, чтобы в него входили только векторы поля и векторный потенциал. Используем формулы (6) и

$\vec{j}=rot\, \vec{H\, }\left( 10 \right).$

Вспомним известное соотношение для дивергенции векторного произведения:

$div(\vec{A}\times \, \vec{H})=\vec{H}rot\, \vec{A}-\vec{A}rot\vec{H\,}\left( 11 \right)$.

Получим в результате:

$\vec{A}\vec{j}=\vec{H}\vec{B}-div(\vec{A}\times \vec{H})\left( 12 \right)$.

тогда выражение для энергии примет вид:

$E_{m}=\frac{1}{2}\int {\vec{H}\vec{B}dV} -\int {div(\vec{A}\times \vec{H})}dV\left( 13 \right)$

Интеграл $\int {div(\vec{A}\times \vec{H})} dV$ в соответствии с теоремой Гаусса – Остроградского преобразуем в интеграл по поверхности, которая ограничивает объем интегрирования:

$\int\limits_V {div(\vec{A}\times \vec{H})dV} =\int\limits_S {(\vec{A}\times\vec{H})dS\, \left( 14 \right).} $

Будем считать, что все токи находятся в конечной области пространства. Тогда на больших расстояниях ($r$) от области локализации токов мы будем иметь:

1. $A\sim \frac{1}{r};$
2. $H\sim \frac{1}{r^{2}}$.

В результате мы получаем, что подынтегральное выражение убывает пропорционально $\sim \frac{1}{r^{3}}$ . При этом поверхность интегрирования увеличивается пропорционально квадрату расстояния ($\sim \frac{1}{r^{2}}$). Вывод: с ростом расстояния от места расположения токов интеграл (14) убывает пропорционально расстоянию ($\sim \frac{1}{r}$). Следовательно, для всего пространства, когда $r\to \infty$ интеграл (4) стремится к нулю. Полную энергию магнитного поля представим в виде:

$E_{m}=\frac{1}{2}\int {\vec{H}\vec{B}dV} \left( 15 \right)$.

Из выражения (15) следует, что объемная плотность распределения энергии магнитного поля равна:

$w=\frac{1}{2}\vec{H}\vec{B}\left( 16 \right)$.

Определение 1

Плотностью энергии магнитного поля называют его энергию, сосредоточенную в единице объема этого поля.

$w=\frac{E_{m}}{V}$

Представленное выражение справедливо для равномерного распределения энергии поля по объему.

Формула (16) говорит нам о том, что объемная плотность энергии магнитного поля в каждой его точке определяют значения векторов поля в этой точке, и не имеет значение каковы источники поля.

Для однородного изотропного магнетика мы имеем следующую связь между векторами поля:

$\vec{B}=\mu \mu_{0}\vec{H}\left( 17 \right)$.

Используя формулу (17) выражения для нахождения плотности магнитного поля представим как:

$w=\mu \mu_{0}\frac{H^{2}}{2}\left( 18 \right)$.

Или

$w=\frac{B^{2}}{2\mu_{0}}\left( 19 \right)$..

В Международной системе единиц (СИ) плотность энергии магнитного поля измеряется в джоулях, деленных на кубометр ($Дж/м^3$ ).

Энергия магнитного поля при наличии магнетиков

Допустим, что все пространство заполняет однородный магнетик. В этом случае создаваемая токами индукция будет изменяться в $\frac{\mu }{\mu_{0}}$ раз в сравнении с индукцией в вакууме. ($\mu$ – магнитная проницаемость вещества; $\mu_{0}$ – магнитная постоянная). Это означает, что во столько же раз изменятся потоки $Ф$ и $dФ$. Из формулы (2) заключим, что индуктивность контура и взаимные индуктивности увеличатся в $\frac{\mu }{\mu_{0}}$ раз. Формула (1) для энергии магнитного поля не изменится, но в ней индуктивность изменится в $\frac{\mu }{\mu_{0}}$ раз.

Можно сделать вывод о том, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменится в $\frac{\mu }{\mu_{0}}$ раз в сравнении с энергией поля этих же самых токов в вакууме. Аналогичный вывод можно сделать относительно плотности энергии.

Ограниченность формул для вычисления плотности энергии

Допущения, сделанные нами, которые заставляют говорить об ограничениях применения формул, полученных нами для плотности энергии магнитного поля:

• Мы предполагали, что вещество, в котором токи создают магнитные поля, является магнитоизотропным. Магнитная проницаемость среды постоянная величина.
• Мы не учитывали, что поле осуществляет намагничивание вещества.

Вопрос о локализации энергии магнитного поля

Для постоянных магнитных полей, которые создаются неподвижными постоянными токами, непонятно, где локализуется энергия. Возьмем выражение для магнитной энергии соленоида:

$E_{m}=\frac{IѰ}{2}\left( 20 \right)$),

где $Ѱ=BSN$ – потокосцепление, то есть магнитный поток через витки соленоида. В этом энергия поля кажется энергией тока, так как он является носителем.

Однако энергию соленоида можно представить и так:

$E_{m}=\frac{B^{2}}{2\mu \mu_{0}}lS\, \left( 21 \right)$.

где присутствуют параметры самого соленоида и характеристика магнитного поля ($B$), что говорит о том, что энергия поля распределена по объему поля.

Для постоянных магнитных полей эта непонятность вызвана тем, что токи и поля существуют неразрывно, образуя систему.

При переходе к переменным магнитным полям приемлемой становится только полевая концепция магнитной энергии, так как переменные магнитные поля входят как компоненты электромагнитных полей и могут существовать самостоятельно от токов. Электромагнитные волны переносят энергию, значит, сделаем вывод о том, что энергия магнитного поля распределена в объеме поля.

44. Энергия магнитного поля, её плотность.

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.  Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна   

Значит, энергия магнитного поля, которое связано с контуром,   (1) 

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем   

Так как I=Bl/(μ₀μN) и В=μ₀μH , то   (2) 

где Sl = V — объем соленоида. 

Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью   (3) 

Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам. 

45. Магнитное поле в веществе. Намагниченность. Магнитная проницаемость. Напряженность магнитного поля, её связь с магнитной индукцией.

Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.

Физическая величина, показывающая, во сколько раз индукция В магнитного поля в однородной среде отличается по модулю от индукции В₀ магнитного поля в вакууме, называется магнитной проницаемостью: 

Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. В настоящее время установлено, что магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.

Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля. Собственное магнитное поле электрона называют спиновым (spin – вращение). Электрон создает магнитное поле также и за счет орбитального движения вокруг ядра, которое можно уподобить круговому микротоку. Спиновые поля электронов и магнитные поля, обусловленные их орбитальными движениями, и определяют широкий спектр магнитных свойств веществ.

Вещества крайне разнообразны по своим магнитным свойствам. У большинства веществ эти свойства выражены слабо. Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля. Поэтому у парамагнетиков μ > 1, а у диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало. Например, у алюминия, который относится к парамагнетикам, μ – 1 ≈ 2,1·10^–5, у хлористого железа (FeCl₃) μ – 1 ≈ 2,5·10^–3. К парамагнетикам относятся также платина, воздух и многие другие вещества. К диамагнетикам относятся медь (μ – 1 ≈ –3·10^–6), вода (μ – 1 ≈ –9·10^–6), висмут (μ – 1 ≈ –1,7·10^–3) и другие вещества. Образцы из пара- и диамагнетика, помещенные в неоднородное магнитное поле между полюсами электромагнита, ведут себя по-разному – парамагнетики втягиваются в область сильного поля, диамагнетики – выталкиваются (рис. 1.19.1).

Пара- и диамагнетизм объясняется поведением электронных орбит во внешнем магнитном поле. У атомов диамагнитных веществ в отсутствие внешнего поля собственные магнитные поля электронов и поля, создаваемые их орбитальным движением, полностью скомпенсированы. Возникновение диамагнетизма связано с действием силы Лоренца на электронные орбиты. Под действием этой силы изменяется характер орбитального движения электронов и нарушается компенсация магнитных полей. Возникающее при этом собственное магнитное поле атома оказывается направленным против направления индукции внешнего поля.

В атомах парамагнитных веществ магнитные поля электронов скомпенсированы не полностью, и атом оказывается подобным маленькому круговому току. В отсутствие внешнего поля эти круговые микротоки ориентированы произвольно, так что суммарная магнитная индукция равна нулю. Внешнее магнитное поле оказывает ориентирующее действие – микротоки стремятся сориентироваться так, чтобы их собственные магнитные поля оказались направленными по направлению индукции внешнего поля. Из-за теплового движения атомов ориентация микротоков никогда не бывает полной. При усилении внешнего поля ориентационный эффект возрастает, так что индукция собственного магнитного поля парамагнитного образца растет прямо пропорционально индукции внешнего магнитного поля. Полная индукция магнитного поля в образце складывается из индукции внешнего магнитного поля и индукции собственного магнитного поля, возникшего в процессе намагничивания. Механизм намагничивания парамагнетиков очень похож на механизм поляризации полярных диэлектриков. Диамагнетизм не имеет аналога среди электрических свойств вещества.

Следует отметить, что диамагнитными свойствами обладают атомы любых веществ. Однако во многих случаях диамагнетизм атомов маскируется более сильным парамагнитным эффектом. Явление диамагнетизма было открыто М. Фарадеем в 1845 г.

Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 10²–10⁵. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000.

К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.

Ферромагнетиками могут быть различные сплавы, содержащие ферромагнитные элементы. Широкое применение в технике получили керамические ферромагнитные материалы – ферриты.

Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C.

Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы. Магнито-мягкие ферромагнитные материалы почти полностью размагничиваются, когда внешнее магнитное поле становится равным нулю. К магнито-мягким материалам относится, например, чистое железо, электротехническая сталь и некоторые сплавы. Эти материалы применяются в приборах переменного тока, в которых происходит непрерывное перемагничивание, то есть изменение направления магнитного поля (трансформаторы, электродвигатели и т. п.).

Магнито-жесткие материалы в значительной мере сохраняют свою намагниченность и после удаления их из магнитного поля. Примерами магнито-жестких материалов могут служить углеродистая сталь и ряд специальных сплавов. Магнито-жесткие метериалы используются в основном для изготовленияпостоянных магнитов.

Непостоянство магнитной проницаемости приводит к сложной нелинейной зависимости индукции B магнитного поля в ферромагнетике от индукции B₀внешнего магнитного поля. Характерной особенностью процесса намагничивания ферромагнетиков является так называетмый гистерезис, то есть зависимость намагничивания от предыстории образца. Кривая намагничивания B (B₀) ферромагнитного образца представляет собой петлю сложной формы, которая называется петлей гистерезиса (рис. 1.19.3).

Из рис. 1.19.3 видно, что при  наступает магнитное насыщение – намагниченность образца достигает максимального значения.

Если теперь уменьшать магнитную индукцию B₀ внешнего поля и довести ее вновь до нулевого значения, то ферромагнетик сохранит остаточную намагниченность – поле внутри образца будет равно B_r. Остаточная намагниченность образцов позволяет создавать постоянные магниты. Для того, чтобы полностью размагнитить образец, необходимо, изменив знак внешнего поля, довести магнитную индукцию B₀ до значения –B_0c, которое принято называтькоэрцитивной силой. Далее процесс перемагничивания может быть продолжен, как это указано стрелками на рис. 1.19.3.

У магнито-мягких материалов значения коэрцитивной силы B_0c невелико – петля гистерезиса таких материалов достаточно узкая. Материалы с большим значением коэрцитивной силы, то есть имеющие широкую петлю гистерезиса, относятся к магнито-жестким.

Природа ферромагнетизма может быть до конца понята только на основе квантовых представлений. Качественно ферромагнетизм объясняется наличием собственных (спиновых) магнитных полей у электронов. В кристаллах ферромагнитных материалов возникают условия, при которых, вследствие сильного взаимодействия спиновых магнитных полей соседних электронов, энергетически выгодной становится их параллельная ориентация. В результате такого взаимодействия внутри кристалла ферромагнетика возникают самопроизвольно намагниченные области размером порядка 10^–2–10^–4 см. Эти области называются доменами. Каждый домен представляет из себя небольшой постоянный магнит.

В отсутствие внешнего магнитного поля направления векторов индукции магнитных полей в различных доменах ориентированы в большом кристалле хаотически. Такой кристалл в среднем оказывается ненамагниченным. При наложении внешнего магнитного поля  происходит смещение границ доменов так, что объем доменов, ориентированных по внешнему полю, увеличивается. С увеличением индукции внешнего поля возрастает магнитная индукция намагниченного вещества. В очень сильном внешнем поле домены, в которых собственное магнитное поле совпадает по направлению с внешним полем, поглощают все остальные домены, и наступает магнитное насыщение. Рис. 1.19.4 может служить качественной иллюстрацией процесса намагничивания ферромагнитного образца.

26. Энергия магнитного поля. Объемная плотность энергии

Продолжим рассмотрение размыкания цепи с точки зрения закона сохранения энергии. Поскольку после отключения источника (рис.6.15) ток в цепи не прекращается, то можно говорить, что работа по переносу зарядов в цепи совершается за счет самоиндукции. Величина работы определяется ЭДС самоиндукции. При переносе по цепи заряда dq работу можно найти так:

. (6.16)

Поскольку сила тока в цепи уменьшается, то ослабевает создаваемое током магнитное поле. С точки зрения закона сохранения энергии это означает, что работа по переносу зарядов при самоиндукции осуществляется за счет уменьшения энергии магнитного поля: . Последнее уравнение можно проинтегрировать, получив

.Поскольку по окончании процесса сила тока в цепи равна нулю, то . Подставим в это соотношение выражение (6.16):(6.17)

Можно рассмотреть и обратный процесс, осуществляемый при включении источника в цепь. При нарастании силы тока через катушку от 0 до I увеличивается и магнитный поток через катушку, поэтому возникает явление самоиндукции. Поскольку оно препятствует нарастанию тока в цепи, то источник тока будет совершать работу против сил индуцированного поля. Тогда работа источника тока переходит в энергию создаваемого магнитного поля:

.После интегрирования этого выражения получим(6.18)

Таким образом, как бы мы ни анализировали процесс, но результат его рассмотрения один и тот же: если в системе, обладающей индуктивностью L, существует ток I, то система создает магнитное поле с энергией (6.19)

Рассмотрим бесконечный соленоид, индуктивность которого выражается согласно (6.11). Если пропустить по соленоиду ток I, то внутри себя он создаст однородное магнитное поле, энергию которого можно определить по (6.19):

Преобразуем это выражение, учитывая, что – объем соленоида, т.е. объем той части пространства, в которой существует магнитное поле:

где индукция магнитного поля соленоида В определена в соответствии с (5.27). Введем понятие объемной плотности энергии магнитного поля так же, как мы вводили это понятие для электрического поля (3.15). Объемной плотностью энергии магнитного поля называется отношение энергии поля, заключенного в малом объеме пространства к этому объему: (6.20)

Следовательно, энергию однородного магнитного поля можно рассчитать так: .

Сделанный вывод можно распространить на случай неоднородного поля таким образом: 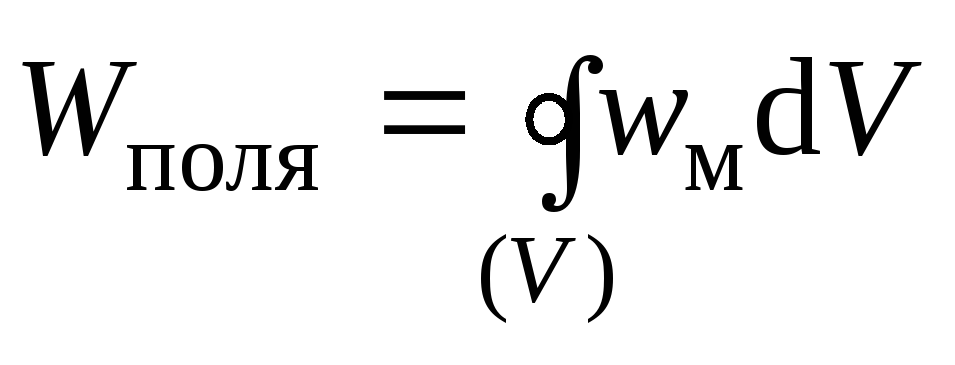,(6.21)

где– объем такой части пространства, чтобы в ее пределах поле можно было считать однородным.

27. Магнитное поле в веществе

Из сопоставления картин линий магнитной индукции соленоида и полосового магнита видно, что они очень похожи. Полная аналогия между магнитными полями полосовых магнитов и соленоидов позволила французскому физику А. Амперу в 1822 г. высказать гипотезу о том, что магнитные свойства постоянных магнитов обусловлены существующими в них микротоками. О природе и характер этих микротоков Ампер ничего не мог сказать, т.к. в то время учение о строении вещества только зарождалось. Лишь после открытия электрона и выяснения строения атомов и молекул, т.е. спустя почти 100 лет, гипотеза ампера была блестяще подтвержден и легла в основу современных представлений о магнитных свойствах вещества. Гипотетические микротоки Ампера получили простое и наглядное объяснение: они связаны с движением электронов в атомах, молекулах и ионах.

При помещении любого вещества в магнитное поле оно реагирует на него и создает собственное магнитное поле, т.е. вещество намагничивается. Существуют различные виды намагниченности, но везде и всегда она создается магнитными моментами микрочастиц вещества. Среди них можно выделить электронный орбитальный магнитный момент, электронный спиновой магнитный момент, ядерный магнитный момент. Мы при рассмотрении эффекта намагничивания материалов в магнитном поле ограничимся рассмотрением электронного орбитального магнитного момента.

16.2. Энергия магнитного поля. Плотность магнитной энергии

Возникает вопрос о том, где локализована энергия 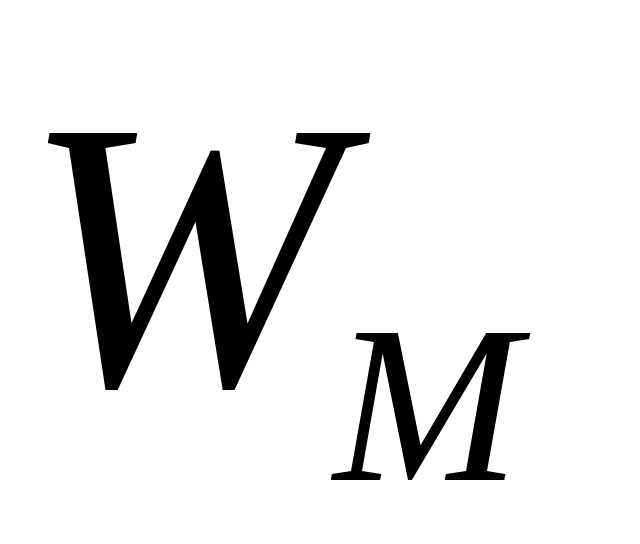контура с током. Эта энергия не меняется, если не меняется ток в данном контуре, однако ее нельзя сопоставить непосредственно с кинетической энергией движения электронов в контуре, поскольку контур с другой индуктивностью при том же токе будет иметь другую энергию.

Исследование свойств переменных магнитных полей показало, что энергия магнитного поля локализована в пространстве. Энергия элемента объема dV поля равна

(16.3)

где — плотность энергии магнитного поля, т.е. энергия единицы объёма магнитного поля.

Для вычисления этой характеристики рассмотрим простейший случай однородного поля внутри длинного соленоида. Подставив в формулу (16.1) выражение (15.11), получим магнитную энергию поля соленоида

(16.4)

Поскольку индукция магнитного поля внутри такого соленоида равна

(16.5)

то, подставив (16.5) в (16.4), получим

(16.6)

Поскольку произведение lS=V -объем однородного магнитного поля соленоида, то из сопоставления формул (16.6) и (16.3), с учетом формулы =, получим для объемной плотности магнитной энергии три эквивалентных формулы:

(16.7)

Выведенные для случая однородного поля эти выражения остаются справедливыми и для неоднородных полей.

В электростатике были получены аналогичные формулы для объемной плотности энергии электрического поля (§ 3):

При наличии в пространстве и электрического и магнитного поля объёмная плотность энергии равна

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенную в любом объёме V. Для этого надо вычислить интеграл:

§ 17. Обобщение законов электромагнетизма. Уравнения Максвелла

17.1. Обобщение закона электромагнитной индукции. Первое уравнение Максвелла

В § 15 отмечалось, что в явлении электромагнитной индукции электродвижущая сила зависит только от скорости изменения магнитного потока. Изменение магнитного потока может быть вызвано движением контура в стационарном магнитном поле, либо изменением во времени магнитного поля, если контур неподвижен. С учетом двух возможностей изменения потока магнитной индукции закон Фарадея может быть записан в обобщенной форме:

. (17.1)

Соотношение (17.1) первоначально было получено Максвеллом экспериментально для контура из тонкого проводника.

В этом частном случае Э.Д.С. индукции создает в проводнике электрический ток, который можно измерить прибором, включенным в контур, и тем самым обнаружить индуктированное переменным магнитным полем электрическое поле .

Таким образом, в явлении электромагнитной индукции проводящая цепь и возбуждаемый в ней ток не имеют принципиального значения.

Необходимо отметить, что обобщенный закон электромагнитной индукции (17.1) справедлив лишь для произвольного материального контура L.

При вычислении изменения потока магнитной индукции через опирающуюся на контур поверхность S необходимо считать, что в момент времени (t+dt) контур образуется теми же материальными точками среды, которыми он был образован в момент t. Поэтому при рассмотрении электромагнитных процессов в контурах, которые движутся вместе с вещественной средой относительно системы в которой измеряется поле, необходимо использовать обобщенный закон электромагнитной индукции в форме (17.1).

При исследовании электромагнитных процессов в средах, в которых контур покоится , формула (17.1) упрощается:

(17.2)

Закон (17.2), обобщенный на случай произвольного замкнутого контура, который может быть и воображаемым, проходящим через любые среды, называют первым уравнением Максвелла в интегральной форме.

Этот закон характеризует процессы, происходящие непосредственно в электромагнитном поле. В соответствии с (17.2) изменяющееся во времени магнитное поле порождает в той же области пространства электрическое поле.

Электрическое поле по своим свойствам отличается от электростатического поля, созданного неподвижными зарядами. Действительно, из теоремы Гаусса-Остроградского для вектора электрического смещения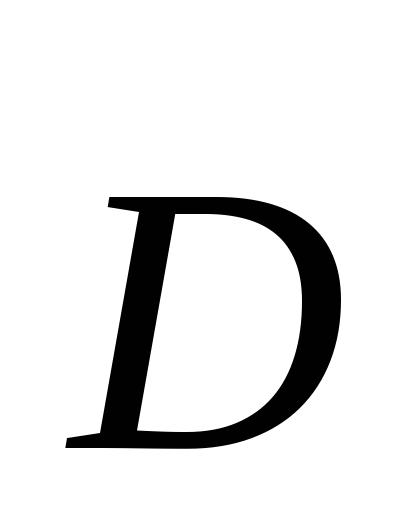

следует, что источником электростатического поля являются заряды, причем силовые линии поля начинаются на положительных зарядах и заканчиваются на отрицательных.

Циркуляция вектора по любому замкнутому контуру равна нулю, что является следствием потенциальности электростатического поля.

В отличие от поля , электрическое поле, созданное изменяющимся во времени магнитным полем, согласно (17.2) имеет отличную от нуля циркуляцию и, следовательно, являетсявихревым. Силовые линии такого поля замкнуты.

Из (17.2) так же следует, что циркуляция вектора напряженности вихревого электрического поля по произвольно выбранному контуру равна взятой со знаком минус скорости изменения магнитного потока через поверхность, опирающуюся на контур.

Исходя из закона Фарадея, можно дать интерпретацию первого уравнения Максвелла в интегральной форме:изменяющийся во времени магнитный поток через нормальную к нему воображаемую поверхность создает вихревое электрическое поле, направление силовых линий которого на поверхности определяется по правилу Ленца (рис. 17.1).

Правило Ленца утверждает, что должен создаваться новый магнитный поток, препят-ствующий изменению внеш-него магнитного потока.

Если среда, в которой выбран воображаемый контур L не является проводящей, то остается заключить, что новый магнитный поток (а, следо-вательно, и создающее его магнитное поле) должен порождаться вихревым электрическим полем. Это предположение лежит в основе второго уравнения Максвелла, которое будет рассмотрено ниже.

4.6.Энергия магнитного поля. Объемная плотность энергии магнитного поля в веществе

Рассмотрим цепь, состоящую из соленоида, замкнутого на источник тока (рис.4.8), находящуюся в неферромагнитной среде. В соленоиде течет ток , который образует магнитный поток, сцепленный с соленоидом. Если отключить соленоид от источника и замкнуть его на сопротивление, по цепи пойдет постепенно убывающий ток. Работа, совершаемая этим током за времяравна

.

Если индуктивность соленоида остается постоянной, , то, и

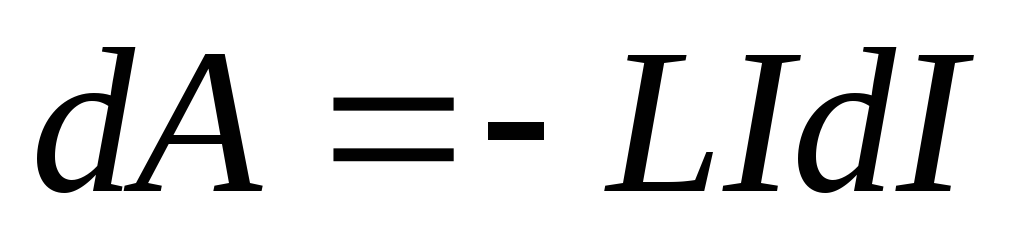. (4.3)

Эта работа идет на нагревание проводников. Вследствие совершения этой работы происходит исчезновение магнитного поля, и так как никаких изменений в окружающей цепь среде не происходит, следует заключить, что работа совершается за счет энергии магнитного поля, а выражения (4.3) как раз и определяет эту работу. Вся работа, произведенная током при убывании магнитного поля до нуля равна

,

и энергия магнитного поля .

Объемной плотностью энергии магнитного поля называется энергия этого поля, отнесенная к его объему:

.

Однако ( поле соленоида однородно), согласно закону полного тока в случае поля соленоида получаем, где— длина соленоида,— число витков соленоида, тогда

.

Энергия , локализованная во всем объеме магнитного поля равна:

.

Если поле в данной точке пространства создано несколькими контурами с током, то энергия результирующего магнитного поля равна:

,

где — сила тока в-том контуре,— потокосцепление— того контура, равное сумме потокосцепления самоиндукции (магнитного потока самоиндукции)—того контура и магнитного потока взаимоиндукции -того контура с остальными ,. Поэтому энергия магнитного поля равна

,

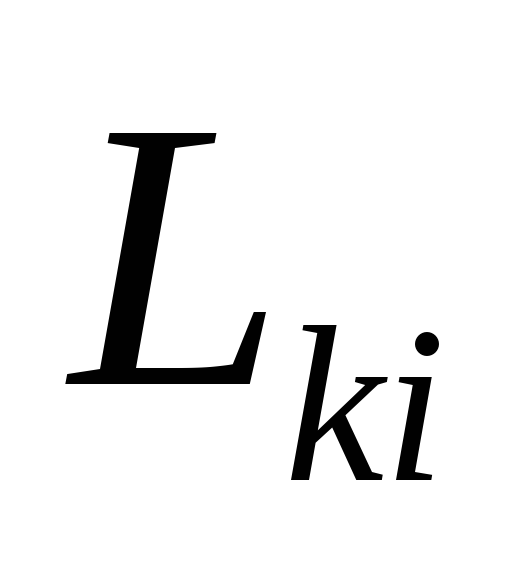–взаимная индуктивность -того иi— того контуров с токами и.

4.7. Закон сохранения энергии в неферромагнитной среде

Энергия магнитного поля, создаваемого какой-либо системой тел (проводящих контуров с токами) изменяется, если контуры с токами перемещаются, или, если изменяются токи в них.

При этом совершают работу внешние силы, приложенные к телам системы, источники электрической энергии, включенные в цепи токов.

Если температура системы постоянна, и плотность среды не меняется, то закон сохранения энергии можно записать в виде:

,

здесь — работа внешних сил в рассматриваемом процессе,— работа источников электрической энергии,— изменение энергии магнитного поля,— изменение кинетической энергии тел системы,— теплота Джоуля-Ленца.

Если тела системы перемещаются очень медленно (квазистатически), то можно пренебречь изменением кинетической энергии системы, =0, и можно считать, где— работа сил, действующих на тела системы в магнитном поле. Это пондемоторные силы. Тогда закон сохранения энергии примет вид:

.

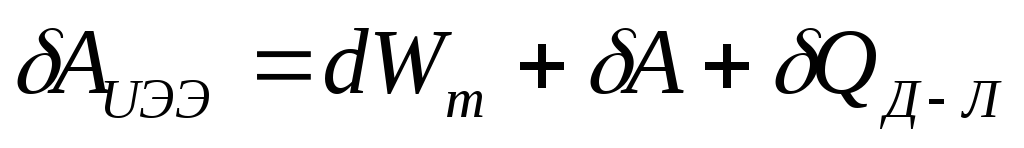Если система содержит n проводящих контуров с токами, работа источников электрической энергии за малый промежуток времени dt равна:

,

где – алгебраическая сумма ЭДС всех источников электрической энергии, включенных в-тый контур,– сила тока в этом контуре.

Рассмотрим некоторые примеры.

1. Неподвижный контур с током.

а) Если ток в контуре остается постоянным, то энергия магнитного поля не изменяется,, а пондемоторные силы не совершают работы:, поэтому

— вся работа источника электрической энергии преобразуется в контуре в тепло Джоуля-Ленца.

б) Пусть ток в контуре растет от 0 до . Работа пондемоторных сил равна нулю и работа источника электрической энергии в контуре расходуется на изменение знергии магнитного поля и на выделение тепла Джоуля-Ленца:, или, где— ЭДС источника,R — сопротивление, L – индуктивность контура, I -сила тока в нем.

2. Работа пондемоторных сил при очень медленной деформации контура с током. Закон сохранения энергии имеет вид: . Сила токаI в контуре изменяется под влиянием ЭДС самоиндукции , где– ЭДС источника постоянного тока в контуре, тогда работа источников электрической энергии

При очень медленной деформации контура ЭДС самоиндукции мала по сравнению с , поэтому теплота, выделяемая по закону Джоуля-_Ленца, равна, и.

Таким образом, элементарная работа пондемоторных сил . Полная работа пондемоторных сил, где– изменение индуктивности контура при его деформации,– постоянный ток в контуре до и после его деформации.

Лекция 9