Петля гистерезиса в электротехнике: Петля гистерезиса значение и нарисовать. Гистерезис в электротехнике. Механизм возникновения петли гистерезиса

Петля гистерезиса в электротехнике: Петля гистерезиса значение и нарисовать. Гистерезис в электротехнике. Механизм возникновения петли гистерезиса

Posted on

Содержание

Петля гистерезиса значение и нарисовать. Гистерезис в электротехнике. Механизм возникновения петли гистерезиса

Биологические и физические системы способны мгновенно откликаться на приложенное к ним воздействие. Если рассмотреть это явление на временной оси координат, то становится заметно, что отклик зависит от предыстории системы и ее текущего состояния. График, который наглядно демонстрирует это свойство систем, получил название петли гистерезиса, которая отличается остроугольной формой.

Оригинальная форма петли обусловлена эффектом насыщения и неравномерностью траектории между соседними расстояниями. Эффект гистерезиса имеет кардинальные отличия от инерционности, с которой его часто путают, забывая о том, что монотонное сопротивление существенно отличается от мгновенного сопротивления на воздействие.

Петля гистерезиса является циклом, в ходе которого часть свойств системы используются независимо от воздействий, а часть – отправляется на повторную проверку.

Явление гистерезиса в физике

В физике наиболее часто системы сталкиваются со следующими видами гистерезиса:

  • Магнитный – отражает зависимость между векторами напряжения магнитного поля и намагничивания в веществе. Это явление объясняет существование постоянных магнитов.
  • Сепнгетоэлектрический – зависимость между поляризацией сегнетоэлектриков и изменения внешнего электрического поля.
  • Упругий – зависимость деформации упругих материалов от воздействия высоких давлений. Это явление лежит в основе великолепных механических характеристик изделий из кованого метала.

Упругий гистерезис встречается двух основных видов – статический и динамический. В первом случае петля будет равномерной, во втором – постоянно меняющейся.

Применение гистерезиса в электронике

В электротехнике широко применяются устройства, в основе которых лежат магнитные взаимодействия. Наиболее распространение получили магнитные носители данных. Понимание гистерезиса необходимо для подавления в них шумов, таких как быстрые колебания или дребезжание контактов.

В большинстве электронных приборов наблюдается явление теплового гистерезиса. В процессе работы устройства нагреваются, а после охлаждения ряд характеристик уже не могут принять первоначальные явления.

Так, в процессе нагрева происходит расширение микросхем и печатных плат, полупроводниковых кристаллов. В результате развивается механическое напряжение, воздействие которого на элементы системы сохраняется после остывания. Особенно ярко тепловой гистерезис проявляется в высокоточных источниках опорного напряжения.

Гистерезис происходит от греческого слова, означающего запаздывание или отставание. С данным понятием связана такая физическая величина, как петля гистерезиса, определяющая одну из характеристик тела. Она определенным образом связана также и с физическими величинами, характеризующими внешние условия, такие как магнитное поле.

Общие понятия гистерезиса

Гистерезис можно наблюдать в те моменты, когда какое-либо тело в конкретный период времени будет находиться в зависимости от внешних условий.

Данное состояние тела рассматривается и в предыдущее время, после чего производится сравнение и выводится определенная зависимость.

Подобная зависимость хорошо просматривается на примере человеческого тела. Чтобы изменить его состояние потребуется какой-то отрезок времени на релаксацию. Поэтому реакция тела будет всегда отставать от причин, вызвавших измененное состояние. Данное отставание значительно уменьшается, если изменение внешних условий также будет заме для ться. Тем не менее, в некоторых случаях может не произойти уменьшения отставаний. В результате, возникает неоднозначная зависимость величин, известная как гистерезисная, а само явление называется гистерезисом.

Эта физическая величина может встречаться в самых разных веществах и процессах, однако чаще всего рассматриваются понятия диэлектрического, магнитного и упругого гистерезиса. Магнитный гистерезис как правило появляется в магнитных веществах, например, таких как ферромагнетики. Характерной особенностью этих материалов является самопроизвольная или спонтанная неоднородная намагниченность, наглядно демонстрирующая это физическое явление.

Механизм возникновения петли гистерезиса

Сам по себе гистерезис представляет собой кривую, отображающую измененный магнитный момент вещества, на которое воздействует периодически изменяющаяся напряженность поля. Когда магнитное поле воздействует на ферромагнетики, то изменение их магнитного момента наступает не сразу, а с определенной задержкой.

В каждом ферромагнетике изначально присутствует самопроизвольная намагниченность. Сам материал включает в свой состав отдельные фрагменты, каждый из которых обладает собственным магнитным моментом. При направленности этих моментов в разные стороны, значение суммарного момента оказывается равным нулю в результате взаимной компенсации.

Если на ферромагнетик оказать воздействие магнитным полем, то все моменты, присутствующие в отдельных фрагментах (доменах) будут развернуты вдоль внешнего поля. В итоге, в материале образуется некоторый общий момент, направленный в одну сторону. Если внешнее действие поля прекращается, то домены не все окажутся в изначальном положении.

Для этого потребуется воздействие достаточно сильного магнитного поля, предназначенного для разворота доменов. Такому развороту создают препятствия наличие примесей и неоднородность материала. Поэтому материал имеет некоторую остаточную намагниченность, даже при отключенном внешнем поле.

Для снятия остаточного магнитного момента, необходимо приложение действия поля в противоположном направлении. Напряженность поля должна иметь величину, достаточную, чтобы выполнить полное размагничивание материала. Такая величина известна как коэрцитивная сила. Дальнейшее увеличение магнитного поля приведет к перемагничиванию ферромагнетика в противоположную сторону.

Когда напряженность поля достигает определенного значения, материал становится насыщенным, то есть магнитный момент больше не увеличивается. При снятии поля вновь наблюдается наличие остаточного момента, который снова можно убрать. Дальнейшее увеличение поля приводит к попаданию в точку насыщения с противоположным значением.

Таким образом, на графике появляется петля гистерезиса, начало которой приходится на нулевые значение поля и момента. В дальнейшем, первое же намагничивание выводит начало петли гистерезиса из нуля и весь процесс начинает происходить по графику замкнутой петли.

В электротехнике есть разные приборы, принцип работы которых основан на электромагнитных явлениях. Где есть сердечник, на котором намотана катушка из проводящего материала, например, меди, наблюдаются взаимодействия за счёт магнитных полей. Это реле, пускатели, контакторы, электродвигатели и магниты. Среди характеристик сердечников есть такая характеристика как гистерезис. В этой статье мы рассмотрим, что это такое, а также какаие польза и вред от данного явления.

Определение понятия

У слова «Гистерезис» греческие корни, оно переводится как запаздывающий или отстающий. Этот термин используется в разных сферах науки и техники. В общем смысле понятие гистерезис отличает различное поведение системы при противоположных воздействиях.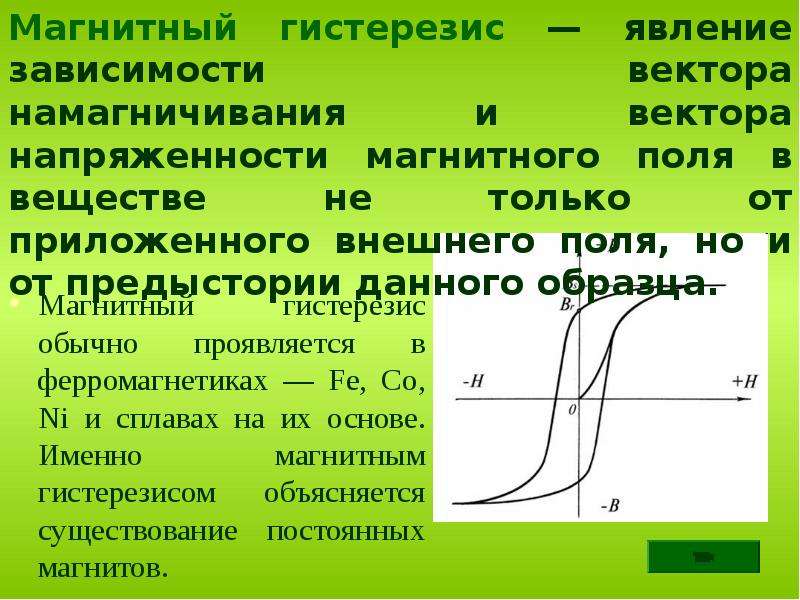

Это можно сказать и более простыми словами. Допустим есть какая-то система, на которую можно влиять в нескольких направлениях. Если при воздействии на неё в прямом направлении, после прекращения система не возвращается в исходное состояние, а устанавливается в промежуточном — тогда чтобы вернуть в исходное состояние нужно воздействовать уже в другом направлении с какой-то силой. В этом случае система обладает гистерезисом.

Иногда это явление используется в полезных целях, например, для создания элементов, которые срабатывают при определённых пороговых значениях воздействующих сил и для регуляторов. В других случаях гистерезис несёт пагубное влияние, рассмотрим это на практике.

Гистерезис в электротехнике

В электротехнике гистерезис — это важная характеристика для материалов, из которых изготавливаются сердечники электрических машин и аппаратов. Прежде чем приступать к объяснениям, давайте рассмотрим кривую намагничивания сердечника.

Изображение на графике подобного вида называют также петлей гистерезиса.

Важно! В данном случае речь идет о гистерезисе феромагнетиков, здесь это нелинейная зависимость внутренней магнитной индукции материала от величины внешней магнитной индукции, которая зависит от предыдущего состояния элемента.

При протекании тока через проводник вокруг последнего возникает магнитное и . Если смотать провод в катушку и пропустить через него ток, то получится электромагнит. Если поместить внутрь катушки сердечник, то её индуктивность увеличится, как и силы, возникающие вокруг неё.

Отчего зависит гистерезис? Соответственно сердечник изготавливается из металла, от его типа зависят его характеристики и кривая намагничивания.

Если использовать, например, каленную сталь, то гистерезис будет шире. При выборе так называемых магнитомягких материалов — график сузится. Что это значит и для чего это нужно?

Дело в том, что при работе такой катушки в цепи переменного тока ток протекает то в одном, то в другом направлении. В результате и магнитные силы, полюса постоянно переворачивается. В катушке без сердечника это происходит в принципе одновременно, но с сердечником дела обстоят иначе. Он постепенно намагничивается, его магнитная индукция возрастает и постепенно доходит до почти горизонтального участка графика, который называется участком насыщения.

После этого, если вы начнете изменять направление тока и магнитного поля, сердечник должен будет перемагнитится. Но если просто отключить ток и тем самым убрать источник магнитного поля, сердечник все равно останется намагниченным, хоть и не так сильно. На следующем графике это точка «А». Чтобы его размагнитить до исходного состояния нужно создать уже отрицательную напряженность магнитного поля. Это точка «Б». Соответственно ток в катушке должен протекать в обратном направлении.

Значение напряженности магнитного поля для полного размагничивания сердечника называется коэрцитивной силой и чем она меньше, тем лучше в данном случае.

Перемагничивание в обратном направлении будет проходить аналогично, но уже по нижней ветви петли. То есть при работе в цепи переменного тока часть энергии будет затрачиваться на перемагничивание сердечника. Это ведёт к тому что КПД электродвигателя и трансформатора снижается. Соответственно это приводит к его нагреву.

Важно! Чем меньше гистерезис и коэрцитивная сила, тем меньше потери на перемагничивание сердечника.

Кроме выше описанного гистерезис характерен и для работы реле и других электромагнитных коммутационных приборов. Например, ток отключения и включения. Когда реле выключено, чтобы оно сработало нужно приложить определённый ток. При этом ток его удержания во включенном состоянии может быть намного ниже тока включения. Оно отключится только тогда, когда ток опустится ниже тока удержания.

Гистерезис в электронике

В электронных устройствах гистерезис несёт в основном полезные функции. Допустим это используется в пороговых элементах, например, компараторах и триггерах Шмидта. Ниже вы видите график его состояний:

Это нужно в тех случаях, чтобы устройство сработало при достижении сигнала X, после чего сигнал может начать уменьшаться и устройство не отключилось до тех пор, пока сигнал не упадет до уровня Y.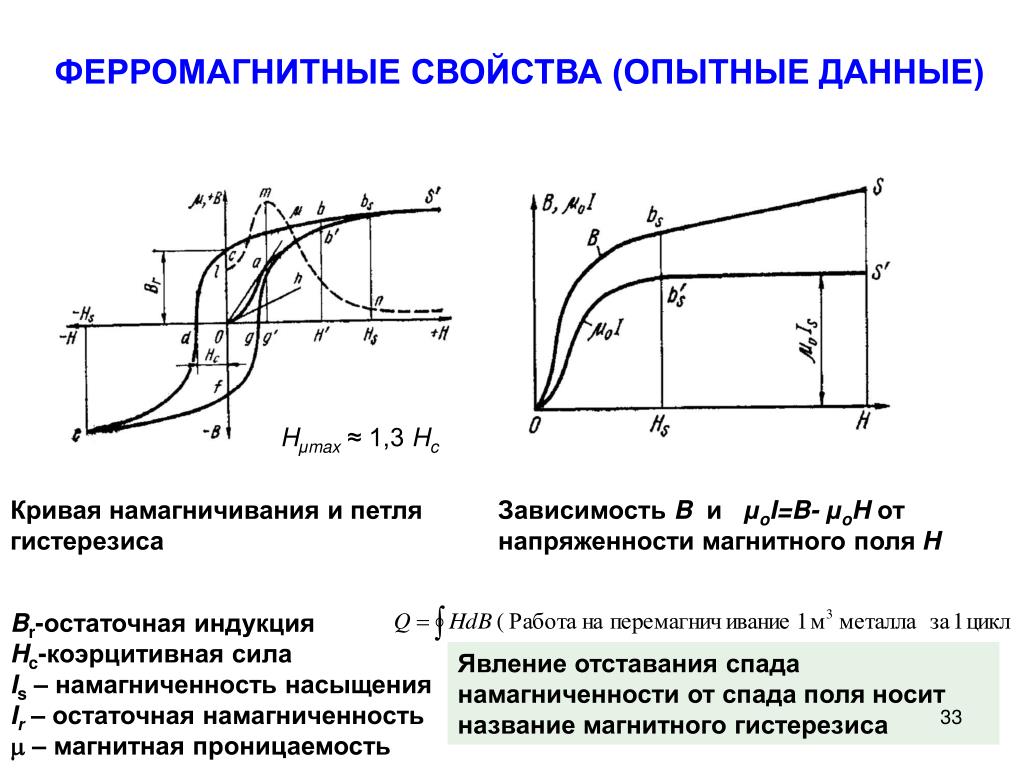 Такое решение используется для подавления дребезга контакта, и случайных всплесков, а также в различных регуляторах.

Например, термостат или регулятор температуры. Обычно его принцип действия заключается в том, чтобы отключить нагревательный (или охладительный) прибор в тот момент, когда температура в помещении или другом месте достигла заданного уровня.

Рассмотрим два варианта работы кратко и просто:

  1. Без гистерезиса. Включение и отключение при заданной температуре. При этом здесь есть нюансы. Если вы установили регулятор температуры на 22 градуса и обогреваете комнату до этого уровня, то как только в комнате будет 22 он выключится, а когда вновь опустится до 21 – включится. Это не всегда правильное решение, потому что ваш управляемый прибор будет слишком часто включаться и отключаться. К тому же в большинстве бытовых и многих производственных задачах нет нужды настолько четкой поддержки температуры.
  2. С гистерезисом. Чтобы сделать некий зазор в допустимом диапазоне регулируемых параметров применяют гистерезис. То есть, если вы установили температуру в 22 градуса, то, как только она будет достигнута, обогреватель отключится. Допустим, что гистерезис в регуляторе установлен на зазор в 3 градуса, то обогреватель вновь заработает только тогда, когда температура воздуха опустится до 19 градусов.

Иногда этот зазор регулируется на ваше усмотрение. В простых исполнениях используются биметаллические пластины.

Мы рассмотрели явление и применение гистерезиса в электрике. Итог следующий: в электроприводе и трансформаторах он несет пагубный эффект, а в электронике и разнообразных регуляторах находит и полезное применение. Надеемся, предоставленная информация была для вас полезной и интересной!

Материалы

Любой электромагнитный сердечник после действия электрического тока какое-то время сохраняет магнитное поле (остаточный магнетизм). Эта величина зависит от свойств материала, но остаточный магнетизм всегда имеется. Чтобы перемагнитить сердечник, необходим магнитный поток обратного направления. Изменение магнитной индукции не успевает за изменением магнитного потока. Эта задержка по времени намагничивания сердечника из-за изменения направления магнитных потоков и именуется как гистерезис.

Чтобы понять всю сущность этого явления, необходимо рассмотреть способность веществ к намагничиванию.

Магнитные свойства веществ

Все вещества в окружающей нас природе в той или иной мере обладают магнитными свойствами. Еще в глубокой древности была известна удивительная способность некоторых минералов притягивать железные предметы. Среди многочисленных навигационных приборов, необходимых для прокладывания курса корабля или самолета, обязательно присутствует магнитный компас.

В точнейших измерительных приборах к числу основных деталей относятся постоянные магниты. Известно, что сильными магнитными свойствами обладает не только железо. Сюда входят кобальт, никель, сплавы на их основе и некоторые редкоземельные элементы. Все эти вещества и сплавы называют ферромагнетиками. Объединяет их способность к самопроизвольной спонтанной намагниченности.

Это свойство ферромагнетиков используют при создании постоянных магнитов. Наличие в атомах вещества нескомпенсированных магнитных моментов является необходимым условием возникновения ферромагнетизма.

В опыте Эйнштейна по величине закручивания при намагничивании образца было доказано, что ферромагнетизм связан со спиновыми магнитными моментами электронов. Обменное взаимодействие электронов при определенных соотношениях диаметра атома и внутренней незаполненной оболочки приводят к параллельной ориентации спинов.

Она возможна только при положительном значении интеграла обменной энергии.

В конечном счете, в ферромагнетике устанавливается такая ориентация спинов, которая обеспечивает минимальное значение суммы энергий магнитного и обменного взаимодействия.

Область с однородной спонтанной намагниченностью называют доменом. Энергетически наиболее выгодно такое расположение доменов, при котором они создают замкнутую магнитную цепь.

Между соседними доменами с различным направлением намагниченности имеются переходные слои, называемые границами или стенками домена. В них происходит постепенный поворот вектора намагниченности.

Ферромагнитные свойства у веществ существуют только в определенной области температуры. Температура, при которой ферромагнетики полностью теряют ферромагнитные свойства, называют точкой Кюри. Форму и величину доменов на поверхности ферромагнетика можно увидеть под микроскопом

В элементарной кристаллической ячейке железа ребра куба соответствуют направлению наиболее легкого намагничивания кристалла железа. Диагонали граней определяют направление среднего намагничивания.

Направление наиболее трудного намагничивания совпадает с диагоналями куба. Площадь на графике характеризует энергию магнитной анизотропии.

При отсутствии внешнего поля магнитные моменты доменов ориентированы по направлениям легкого намагничивания. В целом образец размагничен.

В слабых полях происходит рост доменов, направление намагниченности которых составляет меньший угол с направлением внешнего поля.

Этот процесс обратим. Если внешнее поле убрать, образец размагнитится. При увеличении внешнего поля происходит дальнейший рост доменов, который приостанавливается из-за дефектов кристалла. Когда поле достигает определенной величины, стенки растущих доменов скачком преодолевают препятствие. За счет этого препятствия кривая намагниченности имеет ступенчатый характер.

Скачкообразные изменения намагниченности создают в катушке соленоида импульсы напряжения. С дальнейшим увеличением поля вектор намагниченности поворачивается от оси легкого намагничивания в сторону внешнего поля, пока они не совпадут.

Гистерезис

Этот участок называют областью технического насыщения ферромагнетика, а соответствующую величину поля, полем насыщения. Если от этой величины поле уменьшить до нуля, в образце сохранится остаточное намагничивание.

Гистерезис – это явление отставания намагниченности от напряженности внешнего поля. Замыкающие домены, создавая замкнутую магнитную цепь, снижают поля рассеивания и уменьшают свободную энергию образца.

Его определяют, как разность величин магнитного насыщения ферромагнетика и намагниченности замыкающих доменов. Чтобы размагнитить образец, необходимо приложить к нему отрицательное поле, называемое коэрцитивной силой. Когда поле достигнет величины насыщения, произойдет полное перемагничивание ферромагнетика.

На графике можно определить еще одно свойство, которое имеет гистерезис. При очередном изменении поля кривая намагничивания замыкает петлю, которую называют петлей гистерезиса.

Гистерезисная петля для условия насыщения называется предельной петлей. Ее площадь пропорциональна потерям энергии на перемагничивание образца. Ферромагнетики намагничиваясь, изменяют свои линейные размеры. Это явление называют магнитострикцией.

Выделяются две основные группы ферромагнитных материалов:

  1. Магнитотвердые.
  2. Магнитомягкие.

Одно из основных требований к магнитомягким материалам – их высокая коэрцитивная сила. Магнитомягкие материалы намагничиваются до насыщения при небольших полях и имеют малые потери на перемагничивание. От этих параметров зависит потеря энергии трансформатора.

Например, в линии электропередач мощностью 100 х 10 6 ВА с трансформаторами на концах, ежегодные потери составляют около 5 миллионов киловатт-часов. Одним из лучших представителей магнитомягких материалов считают пермаллой – сплав железа и никеля. Намагниченность пермаллоя в слабых полях в десятки раз превосходит намагниченность железа. Магнитные упорядоченные структуры в некоторых веществах отличаются от магнитной структуры ферромагнетиков.

Если в железе, кобальте и никеле спиновые магнитные моменты направлены параллельно, то в хроме и марганце – антипараллельно. Такие вещества называют антиферромагнетиками.

В данном случае магнитные подрешетки с самопроизвольной намагниченностью компенсированы. Если в кристаллах вещества нет полной компенсации магнитных подрешеток, то его называют ферримагнетиком. Феррит – один из примеров ферримагнетиков, который широко используют в технике. Структура ферритов подобна структуре минералов шпинели, в котором ионы неферромагнитных металлов заменены ферромагнитными.

Гистерезис в электротехнике и электронике

Из многообразия примеров использования ферромагнитных материалов расскажем о применении их в запоминающих устройствах. Для оперативного запоминания информации используют память на ферритовых кольцах. Одного ферритового сердечника достаточно для запоминания одного бита информации. В качестве долговременных запоминающих устройств большой емкости служат специальные магнитные диски (триггеры Шмидта).

Также он используется в специальных гистерезисных электромоторах, устройствах шумоподавления (дребезг контактов, колебания и т.д.) при коммутации логических схем.

Во многих электронных устройствах существует тепловой гистерезис. Во время работы приборы нагреваются, а после охлаждения некоторые свойства уже не принимают начальные значения. При нагреве микросхемы, печатной платы, кристаллы полупроводников расширяются, появляется механическое напряжение. При охлаждении это напряжение в какой-то мере остается.

Различные ферромагнитные материалы обладают неодинаковой способностью проводить магнитный поток. Основной характеристикой ферромагнитного материала является петля магнитного гистерезиса В(Н) . Эта зависимость определяет значение магнитной индукции, которая будет возбуждена в магнитопроводе из данного материала при воздействии некоторой напряженности поля.

Рассмотрим процесс перемагничивания ферромагнетика. Пусть первоначально он был полностью размагничен. Сначала индукция быстро возрастает за счет того, что магнитные диполи ориентируются по силовым линиям поля, добавляя свой магнитный поток к внешнему. Затем ее рост замедляется по мере того, как количество неориентированных диполей уменьшается и, наконец, когда практически все они ориентируются по внешнему полю рост индукции прекращается и наступает режим насыщения.

Если процесс циклического перемагничивания повторять при разных амплитудных значениях тока (Н ), то получим семейство петель магнитного гистерезиса. При некотором максимальном значении тока, а значит Н max , площадь петли гистерезиса практически не увеличивается. Наибольшая по площади петля называется предельной петлей гистерезиса.

Кривая, соединяющая вершины петель — на рисунке жирная линия, называется основной кривой намагничивания.

После нескольких (около 10) циклов изменения напряженности от положительного до отрицательного максимальных значений зависимость B =f (H ) начнет повторяться и приобретет характерный вид симметричной замкнутой кривой, называемой петлей гистерезиса . Гистерезисом называют отставание изменения индукции от напряженности магнитного поля .

Симметричная петля гистерезиса, полученная при максимальной напряженности поля H m , соответствующей насыщению ферромагнетика, называется предельным циклом .

Для предельного цикла устанавливают также значения индукции B r при H = 0, которое называется остаточной индукцией , и значение H c при B = 0, называемое коэрцитивной силой . Коэрцитивная (удерживающая) сила показывает, какую напряженность внешнего поля следует приложить к веществу, чтобы уменьшить остаточную индукцию до нуля.

Форма и характерные точки предельного цикла определяют свойства ферромагнетика. Вещества с большой остаточной индукцией, коэрцитивной силой и площадью петли гистерезиса (кривая 1 рис.8а) называются магнитнотвердыми .

Они используются для изготовления постоянных магнитов. Вещества с малой остаточной индукцией и площадью петли гистерезиса (кривая 2 рис.8а) называются магнитномягкими и используются для изготовления магнитопроводов электротехнических устройств, в особенности работающих при периодически изменяющемся магнитном потоке.

Свойства ферромагнитных материалов в переменных магнитных полях

При возбуждении переменного магнитного потока в магнитопроводах электротехнических устройств происходит непрерывное циклическое перемагничивание ферромагнитного материала.

В каждый момент времени магнитное состояние материала определяется точкой В (Н ) на симметричной петле (рис. 9), по конфигурации похожей на петлю магнитного гистерезиса. Получаемая при быстрых перемагничиваниях петля называется динамической петлей , и она отличается от статической петли магнитного гистерезиса, получаемой при медленных перемагничиваниях. Динамическая петля (показана пунктиром) шире статической.

Что такое гистерезис в температурах и давлениях?


Что такое гистерезис?

Говоря простым и понятным языком – гистерезис это ответная, запоздалая реакция некой системы на определённый раздражитель (воздействие). При устранении причины, вызвавшей ответную реакцию системы, либо в результате противоположного действия, она полностью или частично возвращается к первоначальному состоянию. Причём для такого явления характерно то, что поведение системы между крайними состояниями не одинаково. То есть: характеристики перехода от первоначального состояния и обратно – сильно отличаются.

Явление гистерезиса наблюдается:

  • в физике;
  • электротехнике и радиоэлектронике;
  • биологии;
  • геологии;
  • гидрологии;
  • экономике;
  • социологии.

Гистерезис может иметь как полезное, так и пагубное влияние на происходящие процессы. Это отчётливо просматривается в электротехнике и электронике, о чём речь пойдёт ниже.

Динамический гистерезис

Рассмотрим явление запаздывания ответной реакции во времени на примере механической деформации. Предположим у нас есть металлический стержень, обладающий упругой деформацией. Приложим к одному концу стержня силу, направленную в сторону другого конца, который покоится на опоре. Например, поставим стержень под пресс.

По мере возрастания давления, тело будет сжиматься. В зависимости от механических характеристик металла, реакция стержня на приложенную силу (напряжение) будет проявляться по-разному: вначале сила упругости постепенно будет возрастать, потом она резко устремится к пороговому значению. Достигнув порогового значения, сила упругого напряжения уже не сможет противодействовать возрастающему нагружению.

Если увеличивать силу давления, то в стержне произойдут необратимые изменения – он, либо изменит свою форму, либо разрушится. Но мы не будем доводить наш эксперимент до такого состояния. Начнём уменьшать силу давления. Реакция напряжения при этом будет меняться зеркально: вначале резко понизится, потом постепенно будет стремиться к нулю, по мере разгрузки.

Отставание процесса развития деформации во времени, под действием приложенного механического напряжения вследствие упругого гистерезиса описывается динамической петлей (см. рис. 2). Явление обусловлено особенностями перемещений дислокаций микрочастиц вещества.

Различают упругий гистерезис двух видов:

  1. Динамический, при котором напряжения изменяются циклически, а максимальная амплитуда напряжений не достигает пределов упругости.
  2. Статический, характерный для вязкоупругих или неупругих деформаций. При таких деформациях полностью, либо частично исчезают напряжения при снятии нагрузки.

Причиной динамического гистерезиса являются также силы термоупругости и магнитоупругости.

Как правильно настроить гистерезис

Что такое гистерезис в температурах и давлениях?
Гистере́зис

(в переводе с греческого — отстающий) — свойство систем (физических, логических, биологических и т. д.), мгновенный отклик которых на приложенные к ним воздействия зависит в том числе и от их текущего состояния, а поведение системы на интервале времени во многом определяется её предысторией.

Многие устройства по регулировке и контролю температуры систем отопления имеют настройку не только температуры, но и обязательную настройку гистерезиса, которая позволяет уменьшить количество переключения в единицу времени между двумя положениями: Вкл / Выкл. Гистерезис также позволяет повысить точность регулировки температуры уменьшением гистерезиса.

На сегодняшний день в основном существует только дуальный гистерезис, имеющий только два положения.

К примеру, мы рассмотрим два варианта:

1. Температурный гистерезис – для логики темростатов

2. Гистерезис давления – реле включения / отключения насосов

Как известно у них имеется только два варианта: Вкл / Выкл.

Данное понятие можно разделить на две составляющее:

1. Обозначить этим термином само явление, что существует гистерезис. Например, что данная система обладает гистерезисом.

2. Обозначить значение гистерезиса. Например, сказать, что гистерезис равен 2 градусам.

Исходя из этого

Гистерезисом называется или величина, при котором сигнал меняется на противоположный сигнал. Или сам эффект при котором, действие переключения на противоположный сигнал осуществляется с некоторой задержкой по величине влияния. (Например, при достижение нормы температуры и превышение этой нормы сигнал изменится не сразу, а по достижению той самой величины гистерезиса).

График температурного гистерезиса

Пример для термостата

Термостат настроен на 25 градусов с гистерезисом 2 градуса.

Предположим что температура помещения 20 градусов. Когда температура достигнет 27 градусов термостат переходит в положение отключения. После этого температура помещения будет падать. Когда температура достигнет 23 градусов, то термостат переходит в положение включения. Цикл замыкается.

Пример для реле давления

Реле настроено на два порога: Порог включения 1,2 Bar, порог отключения 3 Bar

Гистерезис при этом будет равен 0,9 Bar. (3-1,2)/2=0,9

Когда давление составляет 1 Bar, реле замыкает контакт. Когда давление достигает 3 Bar, реле размыкает контакт. Когда давление достигает 1,2 Bar, реле вновь замыкает контакт. Цикл повторяется.

Вот собственно так и нужно понимать логику гистерезиса.

Если бы давление включение и отключения имели одно значение, то гистерезиса бы не было. То есть если порог включения равен порогу отключения, то в такой системе отсутствует гистерезис.

А поскольку комнатные термостаты обладают разными порогами включения и отключения, то такая система обладает гистерезисом. Гистерезис в свою очередь позволяет реже производить переключение между двумя положениями: Вкл / Выкл. Но чем больше гистерезис, тем выше скачкообразное изменение температуры.

Существуют другие графики гистерезисов. Например, магнитный гистерезис

Источник



Петля гистерезиса

Кривая, характеризующая ход зависимости ответной реакции системы от приложенного воздействия называется петлёй гистерезиса (показана на рис. 1).


Рис. 1. Петля гистерезиса

Все петли, характеризующие циклический гистерезис, состоят из одной или нескольких замкнутых линий различной формы. Если после завершения цикла система не возвращается в первоначальное состояние, (например, при вязкоупругой деформации), то динамическая петля имеет вид кривой, показанной на рисунке 2.


Рис. 2. Динамическая петля

Анализ гистерезисных петель позволяет очень точно определить поведение системы в результате внешнего воздействия на неё.

Двухпозиционные регуляторы

Назначение. Принцип работы

Двухпозиционные регуляторы обеспечивают хорошее качество регулирования для инерционных объектов с малым запаздыванием, не требуют настройки и просты в эксплуатации. Эти регуляторы представляют обычный и наиболее широко распространенный метод регулирования.Двухпозиционные регуляторы используются для управления переключательными элементами -дискретными исполнительными устройствами:

  • электромеханическими реле,
  • контакторами,
  • транзисторными ключами,
  • симисторными или тиристорными устройствами,
  • твердотельными реле и др.

В простейшем случае (без обратной связи) двухпозиционный регулятор работает как двухпозиционный переключатель. Например, мощность, подаваемая на нагреватель, имеет только два значения — максимальное и минимальное (нулевое), две позиции (отсюда и название регулятора — двухпозиционный) — нагреватель полностью включен или полностью выключен. Структурная схема двухпозиционной системы регулирования приведена на рис. 1.

Рисунок 1 — Структурная схема двухпозиционной системы регулирования

где: АР

– двухпозиционный регулятор,
ОУ
– обьект управления,
SP
– узел формирования заданной точки(задания),
Е
– рассогласование регулятора,
PV=X
– регулируемая величина,
У
– управляющее воздействие,
Z
– возмущающее воздействие.

Для предотвращения «дребезга» управляющего выходного устройства (например, реле) иисполнительного механизма (например, нагревательного элемента) вблизи задания SP

(слишком частоговключения нагревателя), предусматривается гистерезис
Н
.Например, описание работы двухпозиционной системы регулирования температуры в печи спомощью нагревателя, может быть представлено следующим образом:

  • Нагреватель включен, пока температура в печи (X=PV
    ) не достигнет значения заданной точки
    SP
    . Выход регулятора
    Y
    (нагреватель) отключается, если регулируемая величина (температура) выше заданной точки
    SP
    .
  • Повторное включение нагревателя происходит после уменьшения температуры до значения SP-H
    , т.е. с учетом гистерезиса
    H
    переключательного элемента.

Алгоритмы двухпозиционного регулирования

Алгоритм двухпозиционных регуляторов определяется статической характеристикой: зависимостьювыходного сигнала Y

от входного
Х
(см. рис. 2).

Рисунок 2 — Статическая характеристика двухпозиционной системы регулирования

Выходная величина Y

равна максимальному воздействию — нагреватель включен:

  • Y = max
    при
    X, где H-значение гистерезиса.

Выходная величина Y

равна минимальному воздействию — нагреватель выключен:

  • Y = 0
    при
    X > SP
    , где
    H
    -значение гистерезиса.

Зона гистерезиса

Ширина зоны гистерезиса в современных двухпозиционных регуляторах является единственным программируемым параметром настройки. Представление зоны гистерезиса описывается в руководстве по эксплуатации на соответствующий тип регулятора или систему регулирования.Основные варианты представления зоны гистерезиса показаны на рис.3.

Рисунок 3 — Основные варианты представления зоны гистерезиса

Смысл вариантов представления зоны гистерезиса понятен из рисунка 3.Назначение гистерезиса Н

— предотвращение «дребезга» управляющего выходного устройства(например, реле) вблизи задания
SP
от слишком частого включения нагревателя. В литературе по автоматизации также встречаются другие наименования параметра зоны гистерезиса – зона нечувствительности, зона возврата, зона неравномерности, дифференциал.

Гистерезис (в некоторых типах регуляторов) может принимать как положительные, так и отрицательные значения. Отрицательные значения гистерезиса используются в основном для упреждения или задержки включения (выключения) выходных устройств.Например, включение выходного устройства по значению задания SP

меньшем на величину гистерезиса
Н
— включение с упреждением, или выключение выходного устройства по значению задания
SP
меньшем на величину гистерезиса
Н
— выключение с задержкой. Эти типы гистерезиса применяются для того,чтобы учесть инерционность обьектов регулирования.

Процессы регулирования с двухпозиционным законом

Процесс двухпозиционного регулирования является автоколебательным — регулируемая величинакак в переходном, так и в установившемся режиме периодически изменяется относительно заданногозначения (см. рис. 4), т.е. регулируемая величина PV

(X) подвержена незатухающим колебаниям.Показателями автоколебательного режима являются амплитуда автоколебаний
Ак
и периодавтоколебаний
Тк
.

  • Частота и амплитуда колебаний зависят и определяются следующими величинами:
  • от времени транспортного запаздывания ,
  • от постоянной времени обьекта Т
    (определяется инерционностью объекта),
  • от максимальной скорости R
    изменения параметра
    Х
    (определяется по переходной характеристике),
  • от величины гистерезиса H
    переключательного элемента регулятора.

Рисунок 4 — Процесс регулирования с двухпозиционным законом

Для объектов с большой инерционностью (большим значением постоянной времени обьекта Т

) и с малым запаздыванием
регулирование происходит с постоянными колебаниями до 5-15% от задания SP
.

  • Чем больше гистерезис Н
    , отношение /Т,
    R
    — тем больше амплитуда колебаний
    Ак
    .
  • Чем больше время запаздывания и постоянная времени обьекта Т
    — тем больше период колебаний
    Тк
    (см. рис.4).

Точность регулирования технологического параметра, например, температуры зависит от величины гистерезиса. Чем меньше гистерезис, тем точнее регулирование, но тем чаще включается нагреватель и тем самым больше износ коммутационных элементов (например, реле). Уменьшая гистерезис можно повысить качество регулирования до некоторого предела, определяемого параметрами обьекта регулирования(тепловой инерцией, мощностью нагревателя, тепловой связью нагревателя и обьекта и др.).

Гистерезис в электротехнике

Важными характеристиками сердечников электромагнитов и других электрических машин являются параметры намагничивания ферромагнитных материалов, из которых они изготавливаются. Исследовать эти материалы помогают петли ферромагнетиков. В данном случае прослеживается нелинейная зависимость внутренней магнитной индукции от величины внешних магнитных полей.

На процесс намагничивания (перемагничивания) влияет предыдущее состояние ферромагнетика. Кроме того, кривая намагничивания зависит от типа ферромагнитного образца, из которого состоит сердечник.

Если по катушке с сердечником циркулирует переменный ток, то намагничивания образца приводит к отставанию намагничивания. В результате намагничивания сердечника происходит сдвиг фаз в цепи с индуктивной нагрузкой. Ширина петли гистерезиса при этом зависит от гистерезисных свойств ферромагнетиков, применяемых в сердечнике.

Это объясняется тем, что при изменении полярности тока, ферромагнетик какое-то время сохраняет приобретённую ориентацию полюсов. Для переориентации этих полюсов требуется время и дополнительная энергия, которая израсходуется на нагревание вещества, что приводит к гистерезисным потерям. По величине потерь материалы подразделяются на магнитомягкие и магнитотвёрдые (см. рис. 3).


Рис. 3. Классификация магнитных материалов

Магнитный гистерезис в ферромагнетиках отображает зависимость вектора намагничивания от напряженности электрического поля (см. Рис. 3). Но не только изменение поля по знаку вызывает гистерезис. Вращение поля или (что, то же самое) магнитного образца, также сдвигает временные характеристики намагничивания.


Рис. 4. Петли гистерезиса под действием изменения напряжённости поля

Обратите внимание, что на рисунке изображены двойные петли. Такие петли характерны для магнитного гистерезиса.

В однодоменных ферромагнетиках, которые состоят из очень маленьких частиц, образование доменов не поддерживается (не выгодно с точки зрения энергетических затрат). В таких образцах могут происходить только процессы магнитного вращения.


Рис. 5. Механизм возникновения петли магнитного гистерезиса

В электротехнике гистерезисные свойства используются довольно часто:

  • в работе электромагнитных реле;
  • в конструкциях коммутационных приборов;
  • при создании электромоторов и других силовых механизмов.

Явления диэлектрического гистерезиса

У диэлектриков отсутствуют свободные заряды. Электроны тесно связаны со своими атомами и не могут перемещаться. Другими словами, у диэлектриков спонтанная поляризация. Такие вещества называются сегнетоэлектриками.

Однако под действием электрического поля заряды в диэлектриках поляризуются, то есть изменяют ориентацию в противоположные стороны. С увеличением напряжённости поля абсолютная величина вектора поляризации возрастает по нелинейному принципу. В определённый момент поляризация достигает насыщённости, что вызывает эффект диэлектрического гистерезиса.

На изменение поляризации уходит часть энергии, в виде диэлектрических потерь.

Гистерезис в электронике

При срабатывании различных пороговых элементов, часто применяемых в электронных устройствах, требуется задержка во времени. Например, гистерезис используется в компаратороах или триггерах Шмидта с целью стабилизации работы устройств, которые могут срабатывать в результате помех или случайных всплесков напряжения. Задержка по времени исключает случайные отключения электронных узлов.

На таком принципе работает электронный термостат. При достижении заданного уровня температуры устройство срабатывает. Если бы не было эффекта задерживания, частота срабатываний оказалась бы неоправданно высокой. Изменение температуры на доли градуса приводило бы к отключению термостата.

На практике часто разница в несколько градусов не имеет особого значения. Используя устройства, обладающего тепловым гистерезисом, позволяет оптимизировать процесс поддержания рабочей температуры.

Настройка гистерезиса

Гистерезис для всех блоков Кситал составляет 1 o С.

Это значение оптимально практически для всех применений. В случае особой необходимости его можно изменить.

Нижеприведенные рекомендации не актуальны для старых блоков, которые не реагируют на SMS-команды запроса и изменения констант в энергонезависимой памяти блока.

Когда Вы задаете термостату температуру поддержания, например, +23 o С, то при заводских значениях гистерезиса, управляющее реле будет включаться на 22,5 o С и отключаться на 23,5 o С, поддерживая тем самым температуру 23 o С±0,5 o С. Это оптимальная настройка для поддержания температуры воздуха.

Если Вам нужно, чтобы температура поддерживалась в других пределах или управляющее реле более редко включало и выключало бы отопитель, Вы можете подстроить гистерезис выбранного термостата.

Все буквы в командах — английские.

«пароль» в командах это актуальный пароль в системе. Значение по умолчанию 00000.

в командах это адрес константы половины гистерезиса нужного термостата:

  • 03D — адрес константы значения половины гистерезиса для реле №1 в полуградусах
  • 03E — адрес константы значения половины гистерезиса для реле №2 в полуградусах
  • 03F — адрес константы значения половины гистерезиса для реле №3 в полуградусах

Значения констант по умолчанию равны «01», т.е. половина гистерезиса равна 0,5 o С, а полный гистерезис каждого термостата равен 1 o С.

Чтобы подстроить гистерезис выбранного термостата

Узнайте текущее значение половины гистерезиса SMS-командой с телефона 00SMS:

Получите ответ типа:

Задайте новое значение половины гистерезиса в диапазоне 0,5 o С. 40 o С, что соответствует диапазону значений констант 01. 50 с помощью SMS-команды с телефона 00SMS:

Получите подтверждение типа:

Пример:

Необходимо, чтобы реле №2 включалось при +30 o С, а выключалось при +50 o С. В системе используется пароль по умолчанию.

Т.к. средняя температура между +30 o С и +50 o С равна +40 o С, то отправляем команду задания среднего порога регулирования для реле №2:

Т.к. половина гистерезиса (отклонение в одну сторону от порога регулирования) составляет 10 o С (в полуградусах это «20», а в шестнадцатеричном виде «14»), то отправляем команду:

Исследованы магнитные явления в нанокомпозитах

Детальный микромагнитный расчет этой зависимости выполнили для наночастиц, хаотически распределенных на плоскости, при этом средняя плотность частиц различалась. Также была учтена случайная ориентация осей легкого намагничивания частиц (это направление в ферро- или ферримагнетике, вдоль которого намагничивание образца до предельных значений происходит легче всего). Это соответствует условиям стандартных магнитометрических исследований порошков и некоторых приложений (частицы, распределенные в немагнитных матрицах). Оказалось, что диполь-дипольное взаимодействие изменяет зависимость коэрцитивной силы (напряженность магнитного поля, необходимая для полного размагничивания образца) от объемной концентрации частиц. Сначала она – нелинейная, но монотонная, а затем на ней появляется максимум. Это изменение определяется соотношением энергии магнитной анизотропии индивидуальной частицы (зависимости ее магнитных свойств от выбранного направления в образце) и удельной дипольной энергии.

«Рассмотренная модель хорошо описывает наногранулированные пленки, имеющие перспективы применения в магнитных датчиках, экранах и элементах магнитооптической памяти. Важно, что магнитные свойства пленок зависят от соотношения магнитной и немагнитной фазы. Проведенные расчеты позволяют подобрать концентрацию частиц, оптимальную для достижения необходимого уровня гистерезиса», — рассказывает Оксана Ли, доцент кафедры физики Сибирского федерального университета.

Гранулированные пленки с нанометровыми магнитными гранулами относятся к функциональным материалам. Их используют в радиоэлектронике, в высокочастотных устройствах микроэлектроники, вычислительной технике, при создании беспроводных сетей, где они увеличивают скорость передачи данных. Свойства гранулированных сред зависят от доли магнитных гранул: они обладают большой намагниченностью насыщения, высоким электрическим сопротивлением и исключительно широким диапазоном магнитной проницаемости.

Магнитные материалы — Пластмассы


Магнитные материалы

Категория:

Пластмассы



Магнитные материалы

По значению магнитной проницаемости материалы разделяются на пара-, диа- и ферромагнитные. При магнитной проницаемости, близкой к единице, материалы относятся к первым двум группам. Ферромагнитные материалы имеют магнитную проницаемость, равную десяткам и сотням тысяч единиц (гаусс/эрстед).

В электротехнике и радиотехнике особенно широко используются ферромагнитные материалы. Они хорошо намагничиваются в сравнительно слабых магнитных полях и сохраняют намагниченность при удалении внешнего поля. К числу ферромагнетиков относятся такие металлы, как железо, кобальт, никель, некоторые их сплавы и окислы.

Сущность ферромагнетизма сводится к следующему. Атомы ферромагнитных элементов имеют недостроенные внутренние электронные слои, а соотношение диаметров атома и незаполненного слоя у них больше 1,5. При таких условиях в кристалле ферромагнитного тела существуют области, называемые доменами, в которых спины электронов располагаются параллельно, обеспечивая самопроизвольную намагниченность этих областей. Векторы намагниченности соседних доменов различны, вследствие чего средняя намагниченность ферромагнитного тела равна нулю.

При внесении ферромагнетика в магнитное поле в нем постепенно происходят изменения (рис. 1), приводящие к состоянию, когда все домены имеют одинаковое направление спинов электронов, совпадающее с направлением внешнего магнитного поля, обозначенного стрелкой Н вверху слева рис. 2. Процесс намагничивания может быть проиллюстрирован хорошо известной из электротехники кривой намагничивания и петлей гистерезиса, представленными на рис. 2, где кривая 1 является начальной кривой намагничивания, а кривая 2 показывает изменение магнитной индукции при последующем размагничивании и намагничивании в зависимости от напряженности поля.

Рис. 1. Изменение положения доменов при намагничивании: а и б — при увеличении магнитного поля; в — материал намагничен до насыщения

Рис. 2. Петля гистерезиса (2) с первичной кривой намагничивания (1) и графиком магнитной проницаемости (3)

По кривой намагничивания и петле гистерезиса определяются такие основные магнитные характеристики, как магнитная проницаемость, остаточная индукция и коэрцитивная сила.

Перечисленные магнитные свойства характеризуют поведение магнитных материалов в постоянных или медленно изменяющихся магнитных полях. При работе в переменных полях, при перемагничивании ферромагнетиков наблюдаются потери энергии на гистерезис и на вихревые токи.

Потери на гистерезис за один цикл перемагничивания могут быть определены по площади петли гистерезиса (рис. 2).

Потери на вихревые токи численно пропорциональны квадрату частоты тока и обратно пропорциональны электрическому сопротивлению магнитного материала.

Необходимо отметить еще одну особенность поведения ферромагнетиков — явление магнитострикции, заключающееся в изменении линейных размеров ферромагнитных материалов при намагничивании и размагничивании их, происходящем за счет изменения характера движения электронов и энергии их взаимодействия.

Коэрцитивная сила, магнитная проницаемость и остаточная индукция ферромагнетиков зависят от химического состава, от фазового и структурного состояния, например, от дисперсности фаз, формы и размеров зерен, ориентировки и взаимного расположения их, от искажений кристаллической решетки. Не случайно магнитные сплавы часто называют прецизионными, точными. Высокие магнитные характеристики их достигаются не столько определенным легированием, сколько правильным и, главным образом, точно выполненным режимом обработки.

По характеру кривой гистерезиса магнитные материалы делятся на две группы: магнито-твердые и магнито-мягкие.

Рис. 3. Кривые гистерезиса магнито-твер-дого (а) и магиито-мягкого (б) материалов

Магнито-твердые материалы характеризуются широкой петлей гистерезиса (рис. 3,а). Высокие значения коэрцитивной силы и остаточной индукции этих материалов, а также неизменность указанных свойств во времени необходимы при создании постоянных магнитов.

Магнито-твердые материалы получаются путем легирования ферромагнитных металлов, при котором образуются избыточные вторые фазы. Получаемые сплавы подвергаются термической обработке, сообщающей материалу мелкозернистое строение осно вы, высокую дисперсность второй фазы и напряженность кри сталлической решетки. При этом полезно заметить, что обработ ка, вызывающая повышение магнитной твердости материала, со общает ему высокую механическую твердость.

В качестве материалов для постоянных магнитов исполь зуются углеродистые и легированные стали, а также сплавы ти па алнико, магнико и другие.

Углеродистые стали марок У10 и У12, закаленные на мартенсит, имеют высокую коэрцитивную силу (до 55 э), обусловленную искажениями решетки и остаточными напряжениями, возникающими в результате процесса превращения высокоуглероди-стого аустенита в мартенсит. Однако применение этих сталей для магнитов ограничено ввиду малой прокаливаемости их и невысокой стабильности мартенситной структуры в процессе нагрева.

Хромистые стали, содержащие 1—3% Сг, имеют тот же уровень магнитных характеристик, что и стали У10 и У12, но большая прокаливаемость их дает возможность изготавливать магниты больших размеров.

Кобальтовые стали ЕХ5К5, ЕХ9К15М, содержащие кроме хрома еще и кобальт, имеют высокие магнитные свойства, но дефицитность кобальта ограничивает применение этих материалов.

С целью обеспечения гетерогенного мелкодисперсного строения и напряженности, а следовательно, и высокой магнитной твердости хромистые и кобальтовые стали подвергают сложной термической обработке, состоящей из нормализации, закалки, обработки холодом и отпуска. При этом первый нагрев (1000— 1250 °С) обеспечивает растворение карбидов в аустените, закалка с температур 830—1050° придает сплаву мелкоигольчатую мартенситную структуру с некоторым количеством остаточного аустенита, обработка холодом вызывает превращение аустенита в мартенсит и придает стали однородную ферромагнитную мартенситную структуру с высокими характеристиками магнитных свойств. Отпуск при 100° повышает стабильность структуры, однако коэрцитивная сила при этом несколько снижается за счет частичного снятия искажений пространственной решетки.

Термическая обработка его состоит в нагреве до 1300° и охлаждении в межполюсном пространстве сильного электромагнита до 500°, дальнейшее охлаждение ведется обычным порядком на воздухе. После такой обработки материал обладает анизотропией магнитных свойств: в направлении действия внешнего поля они оказываются более высокими. Это объясняется тем, что при переходе из парамагнитного в ферромагнитное состояние в процессе закалки в магнитном поле происходит поворот микрообъемов спонтанного намагничивания в одном направлении, совпадающем с силовыми линиями поля.

Магиито-мягкие материалы в отличие от магнито-твердых характеризуются в первую очередь низкой коэрцитивной силой, а также высокой магнитной проницаемостью и малыми потерями при перемагничивании. Такие материалы применяются в качестве магнитопроводов, электромагнитных сердечников, трансформаторов, реле и т. д. Магнито-мягкий материал, отличающийся низкой коэрцитивной силой, должен иметь не искаженную как у магнито-твердых, а равновесную крупнозернистую структуру. Этому требованию удовлетворяют прежде всего технически чистые металлы, в частности железо, а также малоуглеродистые и легированные стали и сплавы на основе никеля и кобальта.

Техническое железо, используемое в качестве магнито-мяг-кого материала, может быть разным по содержанию примесей. Так, например, суммарное количество примесей С, Мп, Si, S, Р и Си в железе марки А составляет около 0,3%, а в железе Э — около 0,65%. Указанные примеси оказывают влияние на магнитные свойства железа; увеличение количества их вызывает снижение магнитной проницаемости и повышение коэрцитивной силы. Магнитные свойства зависят также и от структурного состояния железа. При наклепе магнитные свойства резко ухудшаются, а при укрупнении зерна улучшаются. С целью снятия наклепа и укрупнения зерна, а следовательно, уменьшения коэрцитивной силы и увеличения магнитной проницаемости железо подвергают отжигу при высокой температуре. Железо как магнито-мягкий материал используется в качестве сердечников, реле и электромагнитов постоянного тока. Наряду с хорошими магнитными свойствами железо имеет существенный недостаток, оно обладает высокими потерями мощности на вихревые токи вследствие малого электросопротивления.

Малоуглеродистые стали марок 10, 20 также могут быть использованы в качестве магнито-мягких материалов.

Электротехническая сталь представляет собой сплав железа с 0,5—4,5% Si. Кремний образует с железом твердый раствор, вследствие чего удельное электросопротивление получаемой стали (около 50 ом • см) значительно выше, чем железа (10 ом • см). Таким образом потери на вихревые токи в электротехнической стали по сравнению с железом существенно снижаются. Однако следует учитывать, что благодаря искажению решетки железо-кремнистый твердый раствор имеет более высокую коэрцитивную силу, чем железо. Поэтому электротехническую сталь подвергают высокому нагреву для выращивания зерна, что способствует снижению коэрцитивной силы. Эта сталь поставляется в виде тонких листов и используется для изготовления сердечников трансформаторов, магнитопроводов электрических машин переменного и постоянного тока.

Железоникелевые сплавы (пермаллои) характеризуются структурой твердого раствора. Они имеют высокое значение начальной магнитной проницаемости, что важно для приборов, работающих в слабых полях (радио, телефон, телеграф). Обычный пермаллой содержит 78,5% Ni и 21,5% Fe. Этот сплав необыкновенно чувствителен к наклепу, повышающему коэрцитивную силу его в десятки раз, и к скорости охлаждения в процессе термической обработки.

Кроме двойных железоникелевых сплавов применяют и более сложные, легированные молибденом, хромом и медью, повышающими электросопротивление и позволяющими применять сплавы при повышенных и высоких частотах тока. Кроме того, молибден снижает чувствительность к наклепу, а медь повышает стабильность свойств.

Альсифер представляет собой сплав состава 5,4% А1, 9,6% Si и 85% Fe. Он обладает высокой магнитной проницаемостью и вполне может заменить Дорогостоящий сплав пермаллой. Недостаток его — высокая хрупкость, вследствие чего изготовление листов из него не производится, сплав используется в виде порошка.

Электротехнические стали имеют маркировку Э11, Э12, Э21 и т. д., где Э — электротехническая, первая цифра — среднее значение кремния в процентах, вторая цифра — магнитные свойства (чем больше цифра, тем выше свойства), нуль после цифр— холоднокатанная текстурованная сталь, два нуля — холоднока-танная малотекстурованная сталь. Например, марка Э12 — электротехническая, горячекатанная сталь, с 1% Si; марка Э1200 — такая же сталь, но холоднокатанная малотекстурованная.

Пермендюр состоит из 50% Со, 1,8% V, остальное железо; имеет высокую индукцию насыщения; применяется для деталей, осуществляющих концентрацию магнитного потока в телефонах, микрофонах, осциллографах.

Для концентрации магнитного потока применяются также ферриты, являющиеся ферромагнитными полупроводниками с электронной проводимостью и представляющие собой поликристаллические вещества, состоящие из окислов металлов, например, магнитный феррит NiO • Fe203 состоит из окислов никеля и железа.


Реклама:

Читать далее:
Материалы для проводников тока и элементов сопротивления

Статьи по теме:

Петля гистерезиса — электрическое напряжение

Когда к материалу применяется переменное магнитное поле, материал намагничивается, и намагничивание образует петлю, называемую петлей гистерезиса . Петля гистерезиса представляет собой четырехквадрантный график B-H. Потери гистерезиса, удерживающая способность и коэрцитивная сила магнитного материала могут быть найдены с помощью петли гистерезиса.

Возьмем полностью размагниченный ферромагнитный материал. Полностью размагниченный ферромагнитный материал имеет B = H = 0.Катушка с числом витков N намотана на ферромагнитный материал. Катушка подключена к источнику постоянного тока последовательно с переменным резистором для изменения тока.

Сила намагничивания H пропорциональна току и количеству витков.

H = NI / л

Где,

N = количество витков катушки

л = Эффективная длина змеевика


Плотность магнитного потока B всегда отстает от силы намагничивания H.Это свойство магнитного материала известно как гистерезис магнитного материала.

Некоторые важные термины, относящиеся к намагничиванию

Коэрцитивная сила

Коэрцитивная сила — это мера способности ферромагнитного материала оставаться размагниченным под действием внешнего магнитного поля. Коэрцитивная сила — это противоположная сила, которая должна быть приложена к намагниченному материалу, чтобы полностью размагнитить его. При приложении отрицательной намагничивающей силы (-H) остаточный магнитный поток становится равным нулю.Эта отрицательная намагничивающая сила равна коэрцитивной силе магнитного материала.

Остаточная плотность потока

Магнитный материал имеет определенное значение магнитного потока на единицу площади, когда сила намагничивания H равна нулю.

Ретенитивность Плотность потока Удерживающая способность — это способность магнитного материала сохранять определенное количество магнитного поля после снятия намагничивающей силы после достижения насыщения. Петля гистерезиса или кривая B-H магнитного материала приведена ниже.


Шаг 1:
Исходная точка (o) кривой B-H находится там, где встречаются обе оси. В этот момент ток I = 0 и плотность магнитного поля B = 0.


Шаг 2:
Когда ток увеличивается от нуля до определенного значения, возникают намагничивающая сила (H) и магнитное поле (B). Путь, по которому идет кривая B-H, равен o-a.

Шаг 3:
Точка «а» называется точкой насыщения на кривой B-H. В этот момент при дальнейшем увеличении тока плотность магнитного потока не увеличивается, потому что все магнитные полюса уже идеально выровнены и нет возможности дальнейшего намагничивания магнитного материала.Точка «B» обозначена как Bm на кривой B-H, это точка магнитного насыщения.

Шаг 4:
Теперь, если ток уменьшается, сила намагничивания (H) уменьшается, и, соответственно, уменьшается плотность магнитного потока (B), но кривая B-H не следует по предыдущему пути (o-a). Он следует по пути o-b пути.

Шаг 5:

Точка «b» указывает, что H = 0, но плотность магнитного потока имеет положительное значение. Это отставание B от H называется гистерезисом.Точка «b» показывает, что после снятия тока магнитный материал имеет плотность магнитного потока (B) и его величина равна ob. Остаточный поток o-b обусловлен удерживающей способностью магнитного материала.

Шаг 6:

Если направление тока меняется на противоположное, то направление силы намагничивания меняется на противоположное. Когда ток увеличивается в обратном направлении, сила намагничивания (-Hc) сначала приводит к уменьшению остаточного потока (Br) до нуля, это называется коэрцитивной силой. .

Шаг 7:

С увеличением тока в отрицательном направлении сила намагничивания увеличивается в отрицательном направлении, а плотность магнитного потока (B) также увеличивается в отрицательном направлении. Кривая B-H следует по пути c-f. Плотность магнитного потока не увеличивается за пределами точки f и называется точкой насыщения в обратном направлении. В точке f B и H достигают максимального значения в обратном направлении.


Шаг 8:
При уменьшении тока в отрицательном направлении кривая B-H следует траектории f-g, и сила намагничивания достигает нулевого значения, когда ток равен нулю, но магнитный материал имеет остаточную плотность магнитного потока (-Br).O-g — это остаточный поток в обратном направлении.

Шаг 9:
Если направление H снова меняется на противоположное путем изменения направления тока, остаточный магнетизм (-Br) уменьшается до нуля в точке d по пути g-d. Если ток увеличивается, кривая B-H следует по пути d-a.
Таким образом, путь a-b-c-f-g-d-a образует петлю гистерезиса.

Важность петли гистерезиса

1. Малая площадь петли гистерезиса означает меньшие потери на гистерезис.

2. Остаточный магнетизм, удерживающая способность и коэрцитивная сила могут быть рассчитаны с использованием графика B-H.

Похожие сообщения

Модель магнитной цепи

с учетом магнитного гистерезиса — Танака — 2015 — Электротехника в Японии

РЕЗЮМЕ

Количественная оценка потерь в сердечнике с учетом свойства магнитного гистерезиса настоятельно необходима для разработки высокоэффективных электрических машин. В этой статье представлена ​​новая модель магнитной цепи с учетом магнитного гистерезиса.В предложенной модели гистерезисные потери на постоянном токе рассчитываются по уравнению Ландау – Лифшица – Гильберта (ЛЛГ), а классические и аномальные потери на вихревые токи рассчитываются в магнитной цепи. Показано, что петля гистерезиса при возбуждении ШИМ-волны может быть выражена предложенной моделью. Достоверность и эффективность метода подтверждены сравнением с измеренными значениями.

1. Введение

В контексте глобальной защиты окружающей среды и энергосбережения одной из недавних тенденций в области энергетики стал переход в сторону электричества, включая переход с автомобилей с бензиновым двигателем на электромобили.Но существует острая необходимость в сокращении потерь в двигателях электромобилей и другом электрическом оборудовании, таком как генераторы и трансформаторы.

Потери в электрических устройствах можно условно разделить на потери, связанные с электрическими и электронными цепями, и потери, связанные с магнитными устройствами. Последние могут быть далее разделены на потери в меди и потери в стали. В частности, потери в железе возникают из-за сложных магнитных явлений, таких как магнитный гистерезис и насыщение, и их количественная оценка не всегда проста.В настоящее время потери в стали часто рассчитываются путем последующей обработки обычного численного анализа магнитного поля, что может ухудшить оценку с высокой точностью.

Метод магнитной цепи — это метод макроанализа внутренних магнитных явлений, когда взаимосвязь между магнитодвижущей силой и магнитным потоком рассматривается так же, как взаимосвязь между напряжением и током в электрических цепях. Это позволяет понять работу устройства с помощью простых расчетов с учетом нелинейных характеристик железных сердечников.Кроме того, анализ может легко комбинировать электрические и магнитные цепи, а также тепловые эквивалентные схемы, так что можно анализировать и проектировать не только отдельные устройства, но и целые системы. Однако до сих пор не разработаны методы для тщательной оценки потерь в стали с учетом магнитного гистерезиса с помощью метода магнитной цепи.

В данном исследовании мы сосредоточили внимание на уравнении Ландау – Лифшица – Гильберта (ЛЛГ). Уравнение LLG формулирует поведение слабой намагниченности и взаимодействия внутри магнитных материалов, обеспечивая выражение таких сложных магнитных явлений, как магнитный гистерезис и насыщение 1.В этом исследовании мы разработали модель магнитной цепи, которая может включать магнитный гистерезис, объединив уравнение ЛЛГ с магнитной цепью. Кроме того, предполагая, что все более популярные устройства сочетают в себе схемы силовой электроники и магнитные цепи, мы попытались рассчитать петли гистерезиса при возбуждении ШИМ и сообщаем результаты здесь.

2. Обычная модель магнитной цепи

Тороидальный сердечник и его магнитопровод показаны на рис.1. Количество витков катушки Н , а ток катушки и . Площадь поперечного сечения и длина магнитного пути железного сердечника составляют, соответственно, S и l . Магнитный поток, текущий в сердечнике, обозначается ϕ.

Тороидальный сердечник и его магнитопровод.

Однако в этой схеме одна индуктивность представляет собой гистерезисные потери, пропорциональные первой степени частоты, и потери на вихревые токи, пропорциональные второй степени частоты.Следовательно, потери в стали можно точно оценить, если напряжение возбуждения представляет собой единственную форму волны на единственной частоте; но точная оценка невозможна, если форма волны и частота напряжения возбуждения меняются во времени.

Чтобы решить эту проблему, мы ранее предложили модель магнитной цепи, в которой потери на гистерезис постоянного тока и потери на гистерезис переменного тока были разделены 2. В частности, фактические значения потерь на гистерезис постоянного тока задаются табличной функцией и потерями на гистерезис переменного тока. делится на потери на вихревые токи и потери на аномальные вихревые токи.Таким образом, мы смогли оценить потери в стали, включая петли гистерезиса, с относительно высокой точностью при различных условиях возбуждения, таких как синусоидальные и прямоугольные волны. Однако все еще оставалась проблема, заключающаяся в том, что требовалось большое количество экспериментальных данных для того, чтобы составить табличную функцию для потерь на гистерезис постоянного тока.

Таким образом, в следующем разделе мы предлагаем модель магнитной цепи с гистерезисом постоянного тока, выраженным с помощью уравнения ЛЛГ.

3. Модель магнитной цепи, включающая уравнение ЛЛГ

3.1 Уравнение ЛЛГ

При расчете LLG Eq. 3 область анализа сначала разделяется на несколько элементов, и каждому элементу назначается магнитный вектор M , как показано на рис. 2. Распределение намагниченности затем может быть найдено путем решения уравнения ЛЛГ. (3) Первый член в правой части приведенного выше уравнения представляет собой прецессионное движение намагниченности, а второй член представляет потери в стали.В уравнении γ — гиромагнитное отношение электрона, α — коэффициент затухания Гильберта и — спонтанная намагниченность. Здесь магнитный вектор M выражается как нормированный магнитный вектор.

Принципиальная схема поведения магнитного вектора M .

Приложенное магнитное поле — это магнитное поле, приложенное извне к катушке и т. Д.

Используя эффективное магнитное поле, составленное из вышеуказанных компонентов, и решая уравнение ЛЛГ для каждого элемента, мы можем вычислить поведение и распределение магнитного вектора M внутри магнитного материала. В этой статье мы изменим формулу. 3 относительно следующего, чтобы решить уравнение ЛЛГ методом Рунге-Кутта: (7)

3.2 Модель магнитной цепи, включающая уравнение ЛЛГ

Напряженность магнитного поля H и плотность потока B , удовлетворяющие уравнению. 8 получаются следующим образом: (9) В приведенном выше уравнении первый член справа представляет потери на гистерезис постоянного тока, второй член представляет потери на вихревые токи, третий член представляет собой аномальные потери на вихревые токи, а γ 1 и γ 2 равны коэффициенты, полученные, как описано в разделе 3.4. Из уравнения. 9, получается следующая зависимость между магнитодвижущей силой и магнитным потоком ϕ: (10) Модель магнитной цепи, основанная на приведенном выше уравнении, показана на рисунке 3.

Модель магнитной цепи, включающая уравнение ЛЛГ.

В предложенной модели гистерезис постоянного тока выражается уравнением ЛЛГ, а потери на вихревые токи и аномальные потери на вихревые токи выражаются зависимыми источниками, которые регулируются, соответственно, магнитной индуктивностью и магнитным потоком ϕ.

LLG Eq. 7 фактически дает магнитный вектор M , а плотность потока B в предлагаемой модели задается следующим соотношением: (11) где μ 0 — проницаемость вакуума, а — среднее значение продольной составляющей магнитного вектора M . Намагниченность, найденная из уравнения ЛЛГ, является вектором; однако в этой магнитной цепи учитывается только продольная составляющая и используется для определения плотности магнитного потока B .Давайте теперь объясним связь между электрической и магнитной цепями на рис. 3. Электрическая цепь описывается следующим уравнением: (12) где v — напряжение, а r — сопротивление цепи, включая катушку. Подставляя уравнение. 10 в уравнение. 12, следующее дифференциальное уравнение получено для плотности потока B : (13) Следовательно, плотность потока B может быть определена, если задано напряжение v .Кроме того, текущее значение i находится путем подстановки плотности потока B в уравнение. 12. Таким образом, динамическое поведение тока, напряженности магнитного поля и плотности потока, соответствующее изменению напряжения источника, может быть рассчитано с использованием предложенной модели.

3.3 Выражение петель гистерезиса постоянного тока с использованием уравнения ЛЛГ

На рис. 4 показаны форма и размер ядра (анализируемого объекта) и аналитическое пространство уравнения ЛЛГ.Для простоты, когда уравнение ЛЛГ фактически используется для расчета распределения намагниченности в предлагаемом методе, учитывается только небольшой элемент сердечника, а найденное таким образом распределение экстраполируется на всю сердцевину. Аналитическое пространство уравнения ЛЛГ состоит из элементов, каждый из которых представляет собой куб со стороной 0,1 мм.

Анализируемый объект и аналитическое пространство уравнения ЛЛГ.

Параметры уравнения ЛЛГ находятся путем аппроксимации петель гистерезиса постоянного тока материала сердечника.Измеренные и аппроксимированные петли гистерезиса постоянного тока неориентированных листов кремнистой стали (35A440) при максимальных плотностях потока 0,4 Тл, 0,8 Тл и 1,2 Тл представлены на рис. 5. Как видно из диаграммы, гистерезис постоянного тока может быть точно определен. моделируется с использованием уравнения ЛЛГ. Здесь коэффициент затухания α равен 1, а спонтанная намагниченность составляет 1,4 Тл. Что касается направлений легкого намагничивания, случайное трехмерное (3D) распределение предполагается в случае неориентированных листов кремнистой стали; нормальное распределение применяется к коэффициенту поля анизотропии со средним значением и стандартным отклонением 120 А / м и 30 А / м, соответственно.Коэффициенты магнитной упругой энергии b 2 , b 4 и b 6 составляют 40 Дж, 30 Дж и 6,7 Дж соответственно.

петли гистерезиса постоянного тока и их аппроксимированные петли.

3.4 Вывод коэффициентов γ

1 и γ 2 Когда плотность потока B задана как синусоидальная волна (), потери в стали могут быть рассчитаны по формуле.9 следующим образом: (14) где T — цикл, а q — плотность железного ядра (7700 кг / м 3 в данном исследовании). Следующее получается, когда обе стороны уравнения. 14 делятся на частоту f : (15) Следовательно, γ 1 и γ 2 могут быть найдены аппроксимацией кривых методом наименьших квадратов. Фактические значения и их приближения для листов неориентированной кремнистой стали (35А440) показаны на рис.6; здесь коэффициенты γ 1 и γ 2 равны 0,020 и 0,392 соответственно. кривые и их приближения.

3.5 Схема предлагаемого метода

Блок-схема предлагаемого метода представлена ​​на рис. 7. В какой-то момент предполагается, что распределение намагниченности рассчитывается по формуле LLG. 7. Продольный компонент плотности потока затем находится из среднего значения продольного компонента намагниченности с помощью уравнения.11. Если уравнение. 13 справедливо для определенной таким образом плотности потока, расчет переходит к следующему моменту времени; в противном случае предполагается повторно использовать метод Ньютона до уравнения. 13 верно.

Блок-схема предлагаемой модели магнитопровода.

4. Сравнение результатов моделирования и экспериментов

4.1 Результаты для синусоидального возбуждения

Используя предложенную модель на рис.3 мы рассчитали ток, магнитное поле, магнитную индукцию и петлю гистерезиса для синусоидальных напряжений разной частоты и амплитуды и таким образом оценили потери в стали.

Измеренные и рассчитанные формы сигналов напряжения и тока возбуждения в случае синусоидального напряжения 50 Гц показаны на рис. 8 и 9. Как видно из диаграмм, осциллограммы тока хорошо согласуются между собой, что подтверждает справедливость предложенной модели магнитной цепи.

Измеренные формы сигналов при синусоидальном возбуждении (Гц, Тл). Формы сигналов напряжения возбуждения и расчетного тока (Гц, Тл).

Измеренные и рассчитанные петли гистерезиса при 50 Гц и 200 Гц сравниваются на рис. 10 и 11. Как видно из диаграмм, предложенная модель предлагает точное воспроизведение петель гистерезиса в широком диапазоне частот и максимальных плотностей потока, что указывает на соответствующее моделирование характеристик магнитного насыщения и гистерезиса железных сердечников.Небольшие различия можно объяснить ошибками аппроксимации гистерезиса постоянного тока на рис. 5 и кривых на рис. 6.

Петли гистерезиса при синусоидальном возбуждении (Гц). Петли гистерезиса при синусоидальном возбуждении (Гц).

Потери в стали, рассчитанные по предложенной модели, сравниваются с измеренными значениями на рис. 12. Эта диаграмма показывает хорошее соответствие между расчетными и измеренными значениями.

Сравнение расчетных и измеренных значений потерь в сердечнике.

4.2 Результаты для возбуждения ШИМ

Инверторы и другие схемы силовой электроники очень часто сочетаются с магнитными блоками в современных электрических устройствах, таких как источники питания и двигатели. Таким образом, в этом разделе мы сравниваем моделирование и эксперименты с железным сердечником, показанным на рис. 4, при двух различных схемах возбуждения ШИМ.

Измеренные и рассчитанные формы сигналов напряжения и тока возбуждения для тройного режима ШИМ показаны на рис. 13 и 14. Соответствующие петли гистерезиса показаны на рис. 15. Как можно заключить из этих диаграмм, предлагаемая модель обеспечивает точную оценку петель гистерезиса даже в случае сложных форм приложенного напряжения, таких как ШИМ.

Формы сигналов напряжения возбуждения и измеренного тока (тройной режим, Гц, Тл).Формы сигналов напряжения возбуждения и расчетного тока (тройной режим, Гц, Тл). Измеренные и рассчитанные петли гистерезиса при возбуждении ШИМ (тройной режим, Гц, Тл).

На рисунках 16 и 17 представлены измеренные и рассчитанные формы сигналов напряжения и тока возбуждения для режима двоичной ШИМ. Соответствующие петли гистерезиса показаны на рис. 18. Как видно из диаграмм, второстепенные петли также могут быть воспроизведены с относительно высокой точностью.Различия, наблюдаемые на рис. 15 и 18, помимо ошибок аппроксимации в предлагаемой модели, можно отнести к ошибкам измерения, вызванным искажением формы сигналов напряжения и тока.

Формы сигналов напряжения возбуждения и измеренного тока (двоичный режим, Гц, Тл). Формы сигналов напряжения возбуждения и расчетного тока (двоичный режим, Гц, Тл). Измеренные и рассчитанные петли гистерезиса при возбуждении ШИМ (бинарный режим, Гц, Тл).

Петли гистерезиса для синусоидального возбуждения и возбуждения ШИМ сравниваются на рис. 19. Как видно из диаграммы, предложенная модель может воспроизводить увеличение потерь, вызванное возбуждением ШИМ.

Сравнение петель гистерезиса при синусоидальном и ШИМ-возбуждении (Гц, Тл).

5. Заключение

Мы предложили модель магнитной цепи, которая может включать магнитный гистерезис, комбинируя уравнение ЛЛГ с магнитной цепью.Мы показали, что петли гистерезиса и потери в стали можно точно оценить с помощью относительно простой модели, путем определения гистерезиса постоянного тока с использованием уравнения ЛЛГ и определения потерь на вихревые токи и аномальных потерь на вихревые токи в магнитной цепи.

Кроме того, предполагая устройство, объединяющее силовую электронику и магнитные цепи, мы попытались оценить петли гистерезиса при возбуждении ШИМ и получили хорошие результаты, включая второстепенные петли.

В будущем мы планируем проверить предложенный метод на примере листа ориентированной кремнистой стали, аморфных сплавов и других материалов, а также оценить эффективность системы инверторов и преобразователей с помощью предложенного метода.

Биографии

  • Хидэаки Танака (студент-член) получил степень бакалавра в области информации и интеллектуальных систем в Университете Тохоку в 2012 году и поступил на докторскую программу по электротехнике в Высшей школе инженерии. Научные интересы Танаки включают анализ и проектирование магнитных устройств.

  • Кенджи Накамура (член) получил степень бакалавра электротехники в Университете Тохоку в 1998 году, завершил первый этап докторской программы по электротехнике и технике связи в Высшей инженерной школе в 2000 году и поступил на факультет того же университета, что и научный сотрудник (Д.Eng.) В 2007 г. Накамура в настоящее время является доцентом Университета Тохоку. Научные интересы Накамуры включают анализ и проектирование магнитных устройств. Членство: MSJ, JSAEM, IEEE.

  • Осаму Ичинокура (член) закончил докторскую программу в области электротехники и коммуникаций в Университете Тохоку (Высшая школа инженерии) в 1980 году и поступил на факультет того же университета в качестве научного сотрудника, в 1988 году стал адъюнкт-профессором и профессором. в 1995 г.Сфера научных интересов Ичинокура — силовая магнетика и силовая электроника (D.Eng.). Членство: MSJ, SICE, IEEJ, IEEE.

ССЫЛКИ