Гистерезис при Площади — Энциклопедия по машиностроению XXL

Для многих материалов экспериментально установлено, что скорость процесса деформирования практически не влияет на очертание ветвей петли гистерезиса, поэтому площадь петли, служащая мерой рассеяния энергии при колебаниях за один цикл, для любого данного материала определяется только амплитудой перемещения. В частности, широко используется зависимость, предложенная Н. Н. Давиденковым  [c.50]

На рис. 7 представлена схема установки для определения площади статической петли гистерезиса. При оп -ределении декремента для различных форм колебаний искусственно создавались формы прогиба образца, приближающиеся к его формам прогибов при колебаниях.  [c.22]

Для соединений с сосредоточенным трением характерны петли гистерезиса, составленные из отрезков прямых. Данные для трех систем такого типа приведены в табл. 1. Площадь петли гистерезиса при возрастании коэффициента трения (или для случаев 1 и 2 — силы прижатия) изменяется немонотонно и имеет максимум. Форма петли гистерезиса в случае 3 типична и для рессорных пакетов, в которых сила прижатия листов возрастает вместе с увеличением переменной нагрузки.  [c.144]

Площадь петли гистерезиса при симметричном цикле нагружения  [c.146]

С увеличением гетерогенности явления гистерезиса увеличи-«ваются. В частности, наклепанные металлы дают больший гистерезис. При повторении нагружения и разгружения ниже некоторого критического напряжения наблюдается постепенное уменьшение площади петли гистерезиса, в то время как при повышении нагрузки площадь петли может увеличиваться. Указанное изменение площади и ширины петли гистерезиса весьма важно при  

[c.320]

Только после этого муфта начнет перемещаться в сторону положения которое и будет достигнуто при угловой скорости Рассуждая подобным образом дальше, можно замкнуть петлю гистерезиса (заштрихованная площадь), внутри которой и заключена область нечувствительности.  [c.199]

Собственные колебания — см. Свободные колебания Соединения деталей — Гистерезис при циклическом нагружении — Площади петли 341, 343—346 —Уравнения ветвей петли 342  

[c.563]

II ниже) петля представляет собой эллипс, потому что и индукция, и напряженность поля практически синусоидальны. При средних индукциях и низких частотах площадь динамической петли определяется в основном потерями на гистерезис и по форме напоминает петлю гистерезиса. При высоких индукциях, близких к индукции насыщения, изменяется форма носика петли из острого ои постепенно превращается в закругленный, что связано с ростом потерь на вихревые токи. Увеличение частоты вызывает более быстрый рост потерь на вихревые токи (пропорционально квадрату частоты). Это ведет сначала к закруглению носика петли, а при более высоких частотах (порядка сотен килогерц) форма петли постепенно переходит в эллипсовидную, Увеличение толщины листов, из которых изготовлен образец, ведет к росту потерь на вихревые токи, а следовательно, к изменению формы петли (уширению при низких частотах и большему закруглению носика по сравнению с петлей образца из тонколистового материала при больших частотах).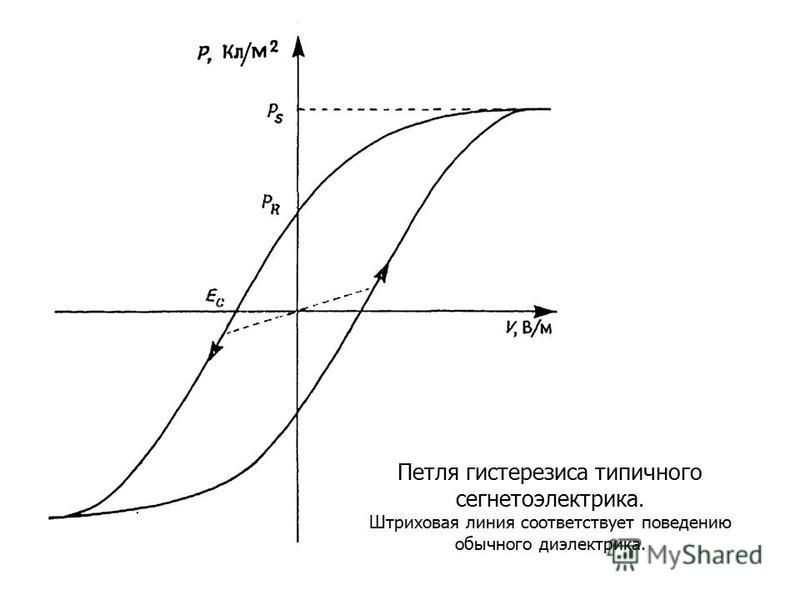

 [c.34]

Определение потерь производится планиметрированием площади петли гистерезиса при заданной индукции, величину которой определяют по известной чувствительности прибора.  [c.250]

Потому от сплавов этой группы требуется высокая остаточная магнитная индукция и высокая коэрцитивная сила, или, иными словами, максимальная площадь петли гистерезиса при намагничивании Практически величина й, находится в пределах 6000—10 000  

[c.129]

Экспериментально установлено, что скорость деформирования практически или пренебрежимо мало влияет на очертания ветвей петли гистерезиса, поэтому площадь петли, служащая мерой рассеяния энергии при колебаниях за один цикл нагружения, для любого данного материала определяется только амплитудой перемещения, поэтому на практике широко используют зависимость, предложенную Н. Н. Давиденковым [22]  [c.119]

Наибольшей долговечностью обладают элементы из резины марки 7842, проработавшие на стенде более 4,0-10 циклов.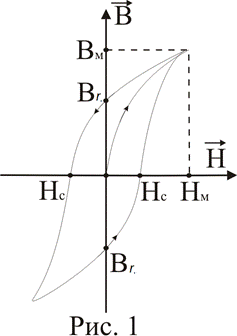

Математическое ожидание жесткости у новых резинометаллических элементов 2200 Н/мм, а у изношенных 2550 Н/мм. Характеристики вязкости определялись экспериментально по отношению площади петли гистерезиса к площади, лежащей между линией нагружения и осью абсцисс. Коэффициент демпфирования КМБ при 12 упругих элементах 8,24 кН-с/м.  [c.79]

Внешние силы при деформации тела от П до Л совершают работу, большую работы, совершаемой внутренними силами при спаде деформации от А до В. Разность этих работ графически равна площади верхней части петли гистерезиса  

[c.162]

Указанная зависимость может быть также оправдана на основании следующих рассуждений. При неподвижном катке (рис. 9.5, а), согласно теории Герца, контактные напряжения распределяются по закону эллипса, ось которого проходит через середину полоски контакта. При этом реакция R, определяемая суммированием по площади контакта удельных давлений, равна общей силе нормального давления N и направлена в обратную сторону. При качении цилиндра симметрия поля контактных напряжений нарушается в силу явлений гистерезиса напряжения в зоне нарастающих деформаций больше, чем в зоне уменьшающихся (рис. 9.5,6). Таким образом, линия действия общей составляющей реакции Я = Ы смещается за линию симметрии полоски контакта на величину к, которая и называется плечом трения качения (таково второе представление о сопротивлении при качении).  

[c.314]

Таким образом, в этом случае влияние примесей заключается в заметном повышении средней величины критического поля. При уменьшении ноля наблюдается петля гистерезиса большой площади замороженный момент составляет почти 50% ). Такая резко выраженная необратимость характерна скорее для сверхпроводящих колец, чем для сплошных образцов, имеющих эллипсоидальную форму. Поскольку небольшие количества примесей ока. зы-вают значительное влияние на магнитные свойства, можно иредполож1гть, что некоторая необратимость, наблюдаемая у номинально чистых образцов, связана с наличием небольших загрязнений как физического, так и химического ироисхождения.

 [c.626]

Настольные машины для испытания на растяжение с электромеханическим приводом фирмы Instron (Англия) мод. 1026 (диапазон нагрузок от 0,1 Н до 5 кН) и 1101 (диапазон нагрузок от 0,02 Н до 1 кН) снабжены механизмом для создания циклического нагружения как при заданных напряжениях, так и при заданных деформациях, с различными частотами и амплитудами, с записью петли гистерезиса. Машины могут быть укомплектованы интегратором, позволяющим вычислить площадь диаграммы деформации при растяжении и площадь петель гистерезиса при циклическом нагружении, термостатом и нагревательной печью для испытания при повышенных и пониженных температурах.  

[c.164]

Существует интересная корреляция между энергией разрыва эластомера 11 (площадью под кривой напряжение—деформация) и гистерезисом при разрыве—энергией Я , рассеянной за счет механических- потерь при амплитуде деформации, несколько меньщей деформации при разрыве ь 171—72]. Эта связь описывается эмпирическим уравнением  

[c. 166]

ЦИКЛИЧЕСКАЯ вязкость — способность материала при циклич, нагружении поглощать энергию деформации в необратимой форме характеризуется площадью иетли гистерезиса. При установившемся режиме циклич. нагружения Ц. в. характеризуется шириной петли гистерезиса Д. Характер и скорость изменения Л с увеличением числа циклов N у разпых материалов различны и зависят от частоты и параметров цикла напряжений. При макс. напряжениях цикла, превышающих предел выносливо-Д / — сти материала, ши-  [c.429]

В машине Инстрон имеется механизм для создания циклического нагружения как при заданных напряжениях, так и при заданных деформациях, с различными частотами и амплитудами напряжений и деформаций, с записью петли гистерезиса. Машина снабжена интегратором, позволяющим вычислить площадь диаграммы деформации при растяжении и площадь петель гистерезиса при циклическом нагружении. На ней можно проводить статические и циклические испытания по заданной программе. Машина снабжена термостатом для испытания при различных температурах (от —50 до +300° С), нагревательной печью до 1300° С и вакуумной камерой. Машина позволяет испытывать материалы на релаксацию напряжений.   [c.93]

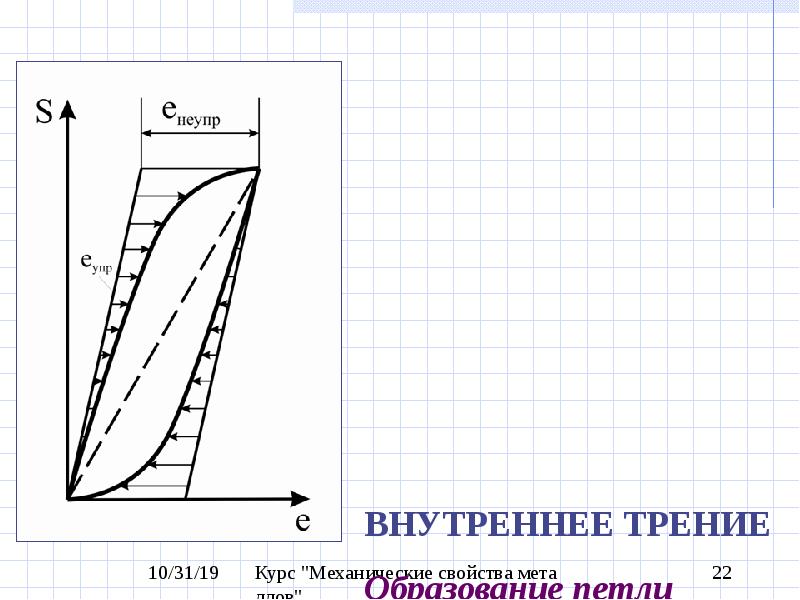
Первый тип процесса зависит непосредственно от неупругого поведения тела. Если кривая напряжение — деформация для единичного цикла колебаний имеет вид петли гистерезиса, то площадь, заключенная внутри этой петли, представляет ту механическую энергию, которая теряется в форме тепла. Когда образец совершает замкнутый цикл напряжений статически , определенное количество энергии рассеивается и эти потери представляют часть специфического рассеяния при колебаниях образца. Как показали Джемант и Джексон [40], даже в том случае, когда петля гистерезиса настолько узкая, что не может быть измерена статически, она оказывает существенное влияние на затухание колебаний, так как в опыте на колебания образец может совершать большое число замкнутых циклов гистерезиса.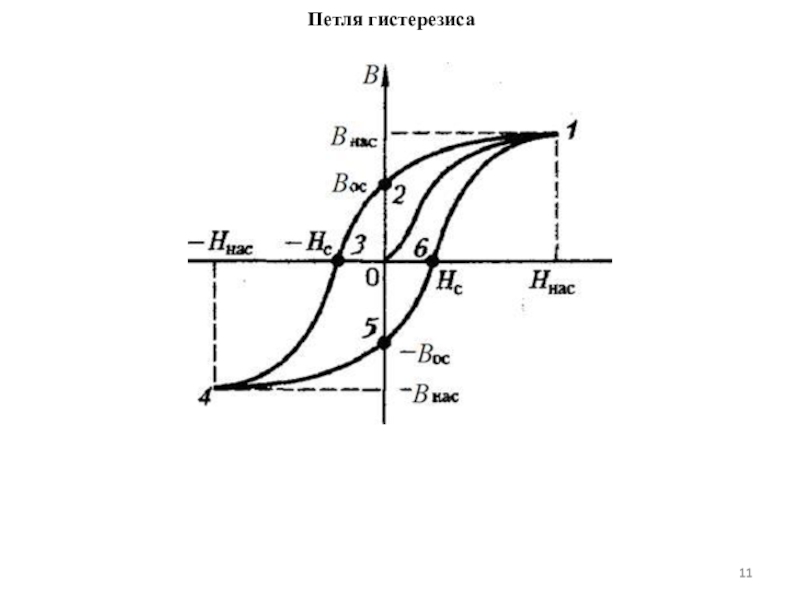 Потеря энергии за один цикл постоянна, так что специфическое рассеяние и, следовательно, логарифмический декремент не зивисят от частоты. Джемант и Джексон нашли, что для многих материалов логарифмический декремент действительно постоянен в довольно широкой области частот, и пришли к заключению, что основная причина внутреннего трения в этих случаях может быть связана просто со статической нелинейностью зависимости напряжение — деформация материала. Аналогичные результаты были получены Вегелем и Уолтером [155] при высоких частотах.  [c.117]

В расчетах затухания используются логарифмический декремент колебаний 0 и неоднозначная зависимость силы сопротивления от перемещения за цикл нагружения или за период колебания, представляющая собой петлю гистерезиса. Н. Н. Давиден-ков, один из основоположников теории демпфирования, считал, что для металлов площадь петли гистерезиса при колебаниях не зависит от частоты, а следовательно, не зависит от частоты и относительное рассеяние энергии гр, равное отношению работы сил сопротивления за цикл к амплитудному значению потенциальной энергии.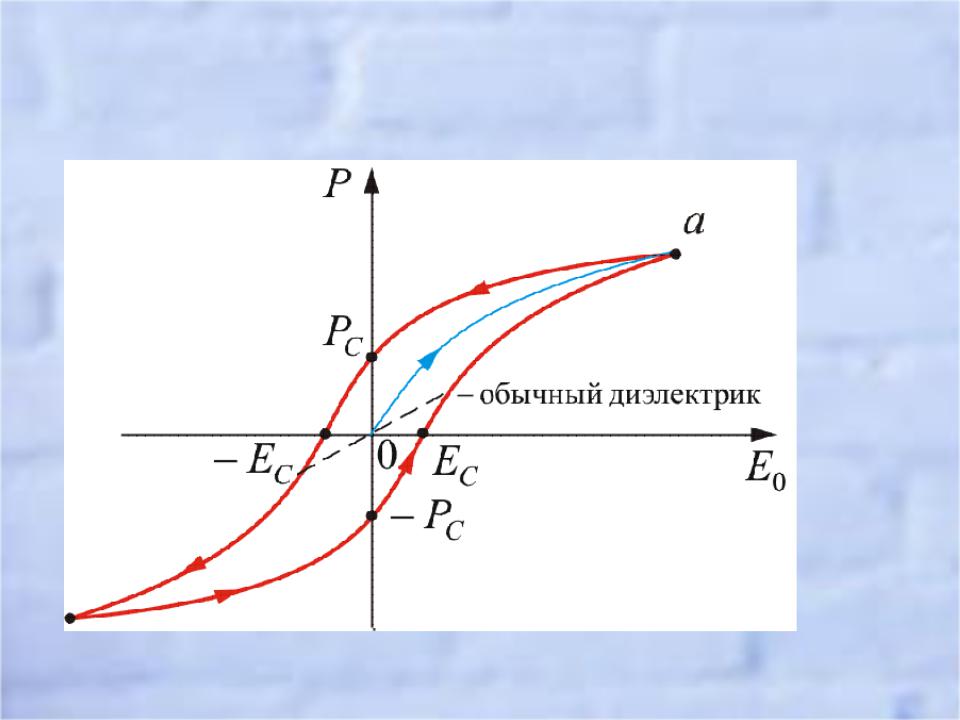  [c.13]

При увеличении значения максимальной напряженности поля Ямакс для дзнной петли гистерезиса ее площадь увеличивается и при некотором 3 ШЧенИИ Ямакс достигает наибольших размеров. Эта наибольшая петля называется предельной петлей гистерезиса. При дальнейшем увеличении намагничивающего поля форма и размеры петли уже не. меняются, а увеличиваются лишь ее безгистерезисные части (участки АБ и А Б на рис. 1-2).  [c.12]

В тяжелых весах в основном применяют открытые призмы. В этом случае h/j 1. Следует отметить,что принимаемый уровень напряжений в рычагах не превыщает I Стд кгс/см = 100 МПа для стальных рычагов, хотя из условия прочности эти напряжения можно было бы увеличить в 1,6 — 1,8 раза. Для решения вопроса о возможности компенсации погрешности, возникающей вследствие деформации рычагов, определим ее случайную составляющую. Источником случайной погрешности являются упругие несовершенства рычагов (последействие, ползучесть, внутреннее трение), приводящие к уходу нуля и появлению петли гистерезиса при нагрузке-разгрузке ВУ.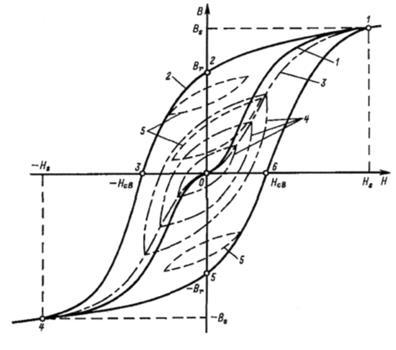 Рассмотрим задачу определения погрешности вследствие внутреннего трения. Как известно, внутреннее трение определяется из энергетических условий и представляет собой отношение необратимо поглощенной телом за один цикл части энергии циклических деформаций к потенциальной энергии тела, которая соответствует амплитуде деформаций за тот же цикл. Графически это может быть представлено как отношение площади петли гистерезиса к площади треугольника ОАС (рис. 16), равное коэффициенту поглощения ф. Форма петли гистерезиса при циклической деформации может быть достаточно точно аппроксимирована уравнением эллипса. Рассматривая петлю гистерезиса в безразмерных координатах Р/РтахИ ///max,где / и /т ах — текущая и максимальная деформации, определим ф  [c.42]

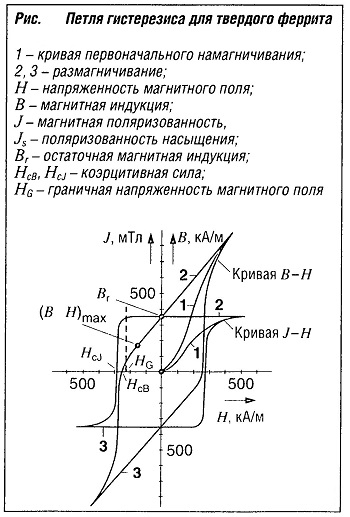
Основные сведения о магнитных свойствах дают кривые намагничивания, приведенные на рис. 399. Кривая 2 является начальной кривой намагничивания, кривая / показывает изменение магнитной индукции в зависимости от напряженности поля при последующем намагничивании и размагничивании. Площадь, ограниченная этой кривой (которая называется гистере-зисной петлей), представляет собой так называемые потери на гистерезис, т. е. энергию, которая затрачена на намагничивание. Важнейшими являются следующие магнитные характеристики, определяемые по кривой намагничивания.  [c.540]

Важным свойством упругой муфты является ее демпфирующая способность, которая характеризуется энергией, необратимо поглощаемой муфтой за один цикл (рис. 17.10) нагрузка (OAI) и разгрузка (1ВС). Kai известно, эта энергия измеряется площадью петли гистерезиса OAW . Энергия в муфтах расходуется на внутреннее и внеи)-нее трение при деформировании упругих элементов.  [c.307]

Демпфирование колебаний онределяют следующими способами по загуханию свободных колебаний форме резонансной кривой мощности, затрачиваемой на колебания теплообразованию при циклическом деформировании площади петли гистерезиса.  [c.482]

Из-за трения между витками характеристики при нагрузке и разгрузке не совпадают, образуя на диаграмме петлю гистерезиса, которая зависит от состояния поверхности ленты, длины ее отожженных концов, условий их закрепления и смазки пружины. Площадь диаграммы ОпСКО (см. рис. 19) пропорциональна работе при заводе пружины, площадь СтОКС — полезной работе, пружины при ее разворачивании.  [c.723]

Здесь ] — намагниченность, достигаемая при поле Н. Полная накопленная энергия пропорциональна площади заштрихованного участка на рис. 10.19,а. При уменьшении поля до нуля кривая /(Я) идет так, как показано на рис. 10.19,6. Выделяющаяся при размагничении энергия пропорциональна площади, заштрихованной на этом рисунке. Разность этих двух площадей, т. е. площадь, заштрихованная на рис. 10.19,6, пропорциональна энергии, оставшейся в ферромагнетике. Аналогичные рассуждения можно провести и для других участков петли гистерезиса. Таким образом, петля гистерезиса является очень важной характеристикой ферромагнитных материалов, так как она позволяет рассчитать энергетические потери в устройствах, в которых используются эти материалы.  [c.346]

Зависимость магнитной индукции В от Н при изменении Н не представляет собой единой кривой, а характеризуется летлей гистерезиса. Площадь петли соответствует работе, необходимой для проведения одногр цикла перемагничивания образца. Форма петли, максимальное значение индукции, положение точек пересечения с осями KoqpAHHaT зависят от условий термообработки ферромагнитного материала, его химического состава и других факторов.  [c.11]

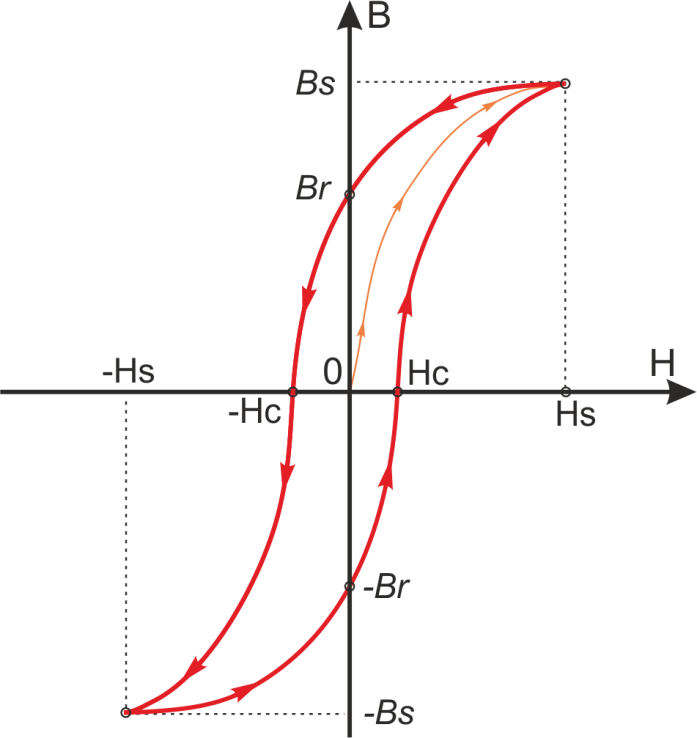
На рис. 11.3 показана кривая полного цикла перемагничипания ферромагнетика. Из рис. 11.3 видно, что при перемагничивании изменение В отстает от изменения Я и при Я = О оказывается равным не нулю, а Явление такого отставания В от Н называют магнитным гистерезисом, а индукцию Sr — остаточной индукцией или остаточным магнетизмом. Для ее уничтожения требуется приложение размагничивающего поля которое называют коэрцитивной силой. Замкнутая петля ABj-H A В Н А, описывающая цикл перемагничивания, называется петлей гистерезиса. Площадь петли пропорциональна работе перемагничивания единицы объема ферромагнетика. В процессе перемагничивания эта работа целиком переходит в тепло.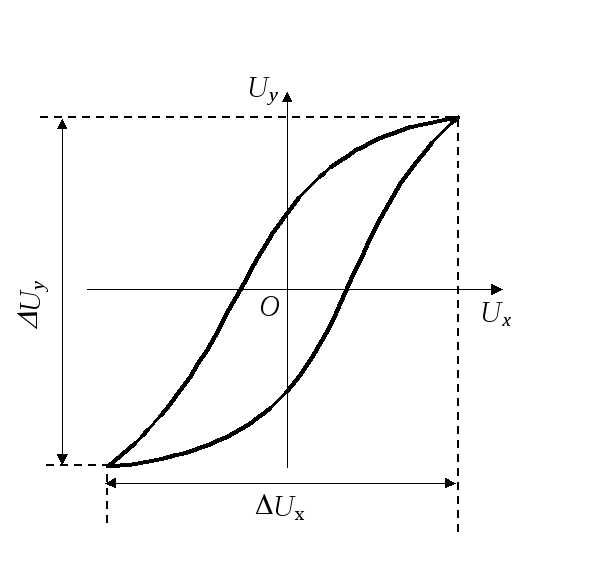 Поэтому при многократном перемагничивании ферромагнетики нагреваются.  [c.287]

В условиях одноосного напряженного состояния для определения рассеянной энергии можно использовать площадь проявляющегося при циклическом пагружешш на определенном уровне напряжения гистерезиса между напряжением и соответствующей ему деформацией. При сложном напряженном состоянии рассеянную энергию можно определить аналогичным способом, регистрируя петли гистерезиса для каждого главного направления, что предполагает наличие сигнала напряжения. По этой причине такой подход к реальной конструкции или даже только к определенному конструкционному элементу встречает серьезные затруднения. Их можно избежать, если учитывать, что как при одноосном, так и при сложном напряженном состоянии можно наблюдать гистерезис не только между напряжениями и соответствующими им деформациями, но и между деформациями по двум направлениям, в частности между деформациями по главным направлениям (деформационный гистерезис) 12]. Для циклического нагружения с пропорциональным изменением компонентов тензора напряжений существует свя.зь между площадями деформационного и механического гистерезиса. В качестве отправной точки вывода этой СВЯ.ЗИ служит предположение, что тензор деформации представляет сумму упругой и неупругой компонент или если глав-  [c.81]

---

Гистерезиса петля формула — Энциклопедия по машиностроению XXL

Задача 3-7. Петля гистерезиса описывается формулой Релея  [c.155]

Если намагниченный до насыщения образец начать размагничивать, уменьшая внешнее поле Я, то изменение намагниченности будет описываться уже другой кривой (рис. 4.9). Из-за необратимого смещения границ доменов при Н-О сохраняется некоторая намагниченность М называемая остаточной. Для достижения нулевой намагниченности необходимо приложить размагничивающее поле противоположной направленности Не, называемое коэрцитивной силой. При достижении больших значений размагничивающего поля образец намагничивается до насыщения в противоположном направлении. Последующее размагничивание уже этого направления происходит по аналогичной кривой, симметричной предыдушей относительно точки М = 0 Я = 0). В результате полный цикл перемагничивания при изменении поля от — Ятах ДО Ятах описывается петлей гистерезиса (ПГ) (рис. 4.9). Петля гистерезиса наглядно показывает, что процесс размагничивания отстает от уменьшения поля. Это означает, что энергия, полученная ферромагнетиком при намагничивании, не полностью отдается в процессе размагничивания. Часть энергии теряется. Теряемая за один полный цикл энергия в единице объема материала (потери на гистерезис) выражается формулой  [c.287]

Наконец, в случае циклически стабильных материалов (например, среднеуглеродистые и аустенитные стали) ширина петли упру-го-пластического гистерезиса практически не зависит от числа циклов деформирования. При различной ширине петель в четных и нечетных полуциклах происходит одностороннее накопление деформации. Для таких материалов, стабилизирующихся при определенном числе полуциклов k = k, ширина петли определяется по формуле (22.29) при k = k.  [c.686]

Длину и сечение постоянного магнита можно определить, пренебрегая рассеянием по экспериментально определенной спинке петли гистерезиса для данного материала, воспользовавшись приведенными выше формулами. В идеальном случае В и Я должны быть координатами точки (Во и Яо на рис. 141), которой соответствует максимальная магнитная энергия. Значения Во и Но, соответствующие максимальной магнитной энергии, зависят от формы кривой размагничивания. Форма кривой размагничивания между точками В, и характеризуется так называемым коэффициентом выпуклости  [c.200]

Выходная э. д. с. накладного датчика. Для решения задачи необходимо знать аналитическую зависимость между магнитной индукцией и намагничивающим магнитным полем с учетом петли магнитного гистерезиса. Эту связь для области средних и сильных полей представим формулой [1]  [c. 7]

Гармоники э.д.с. накладного датчика, связанные однозначно с магнитными параметрами петли гистерезиса ферромагнетика, находятся из формул (11), (28 ), (28″). Таким образом, поставленная задача полностью решена.  [c.17]

Формулы (3) — (10) дают возможность описывать кривую упрочнения, ветви петли механического гистерезиса, определять остаточную деформацию и рассчитывать потери на механический гистерезис. Аналогичными рассуждениями можно получить уравнения ветвей петель механического гистерезиса последующих циклов нагружения.  [c.164]

На рис. 2 изображена петля гистерезиса с учетом компенсации для образца из стали ШХ-15. Как видно из рисунка, результаты измерений хорошо согласуются с результатами, измеренными на БУ-3, и с результатами, рассчитанными по формуле (7).  [c.156]

В этих формулах еа и уа — амплитуды деформаций Аен и Ау — неупругие деформации за цикл В — удельная энергия, необратимо рассеянная за цикл /сф — коэффициент формы петли гистерезиса.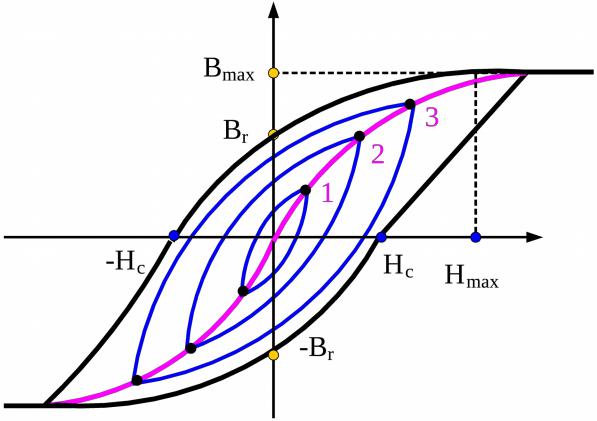 В случае неоднородного напряженного состояния в приведенных выше формулах, как уже отмечалось, использовались действительные значения напряжений и неупругих деформаций.  [c.4]

Площадь петли гистерезиса определим по формуле  [c.167]

Сколько-нибудь достоверное математическое описание гистерезисных потерь в виде аналитической зависимости силы неупругого сопротивления от текущих (мгновенных) Рис. 3. Петля гистерезиса параметров деформации (величины деформации, ее скорости) не представляется возможным. Зависимость вида (а, а) не может согласовать такие экспериментально наблюдаемые факты, как независимость силы неупругого сопротивления от скорости деформации и существенное влияние амплитуды деформации на ширину гистерезисной петли. Некоторыми авторами предложены формулы,выражающие зависимость силы внутреннего неупругого сопротивления от амплитуды гармонической деформации [69]. Эти зависимости имеют нелинейный характер и правомерны лишь при исследовании колебательных процессов, близких к моногармоническим.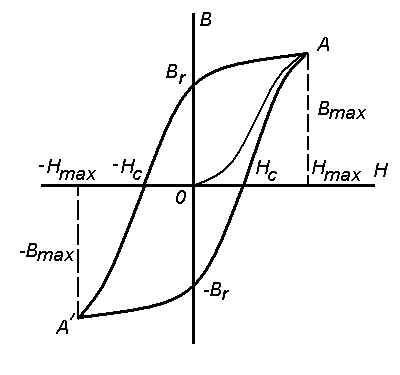  [c.12]

Если в системе с одной степенью свободы имеется слабое демпфирование, то значения k, т w ц (или С) можно определить при резонансных частотах с помощью методов, описанных в разд. 4.3. Например, по значению ширины резонансной амплитуды можно определить коэффициент потерь т] (выражения (4.37) или (4.39)), коэффициент усиления при резонансе (4.42) или (4.44), диаграмму Найквиста, петлю гистерезиса, ширину полосы A(Oq (см. выражение (4.61)). Так как коэффициент y.q мал, то при использовании формулы (4.68), в которую входит динамическая жесткость, могут встретиться трудности, если демпфирование в конструкции очень мало. Итак, в результате измерений получим характеристики демпфирования в виде набора некоторых числовых величин  [c.191]

Формулы (5.6)—(5.8) позволяют построить диаграмму деформирования материала при первичном нагружении из исходного естественного состояния материала и диаграмму дальнейшего циклического деформирования при заданных силовых характеристиках цикла. Как показано ниже на примерах, диаграмма деформирования при первичном нагружении даже теоретически несколько отличается от соответствующей диаграммы в одном из последующих полуциклов нагружения. Однако фактически эти расхождения бывают значительно больше, чем это предсказывает используемая структурная модель материала. Постоянные и fji можно подбирать как по экспериментальной диаграмме первичного нагружения из условия ее наилучшей аппроксимации с помощью ломаной линии, определяемой соотношениями (5.6)— (5.8), так и по экспериментальной диаграмме циклического деформирования, т. е. по очертанию петли пластического гистерезиса. Второй путь является предпочтительным.  [c.174]

Диаграмма циклического деформирования строится на основании формул (5.6)—(5.8) в виде ломаной, состоящей из трех линейных участков (рис. 5.10) (мгновенно-упругая деформация е(1) = ( >, не влияющая на петли пластического гистерезиса, на этом рисунке не показана). Эта аппроксимирующая ломаная вписывается в реальную диаграмму деформирования, причем может быть любой коэффициент асимметрии R. Величины Са, и С, отвечают переломам аппроксимирующей линии, причем j может рассматриваться как технический предел текучести при циклическом деформировании. Коэффициент жесткости Ез представляет собой тангенс угла наклона первого линейного участка теоретической кривой деформирования, а два других коэффициента жесткости 4 и определяются по фактической диаграмме циклического деформирования с учетом формул (5.7) и (5.8) как  [c.174]

Если задан размах одной пластической деформации, то i-+ с . Из формул (5.17) и (5.18) видно, что при расчете требуется предварительно назначить интервал, в который попадает искомое значение а ах- После этого нужно вычислить это значение и проверить по (5.17), попало ли оно действительно в указанный интервал. Учет циклической нестабильности через коэффициент а приводит к соответствующему упрочнению, когда коэффициенты жесткости возрастают, или к разупрочнению материала, если коэффициенты жесткости уменьшаются. Заметим также, что для построения петли пластического гистерезиса (см. рис. 5.10) достаточно вычислить напряжения прямого хода. После расчета напряжения о или а» (рис. 5.19) размах Да, т. е. высота петли гистерезиса, находится как сумма ст + Сг, после чего может быть найдена также и площадь а.  [c.198]

Размах интенсивности напряжений Aaj = Oj + j (аналогично размаху напряжения при линейном напряженном состоянии), а вся необратимая работа пластического деформирования при пропорциональном нагружении определяется площадью петли гистерезиса в координатах а,еР . Как и в случае линейного напряженного состояния, расчет начинается с попытки применения какой-либо одной из вышеприведенных формул для постоянных А и В с последующей проверкой соответствующего неравенства для  [c.199]

Определение декрементов колебаний при помощи статической петли гистерезиса производилось, исходя из соотношения (4). Входящую в это выражение величину потенциальной энергии деформации можно найти по формуле  [c.21]

Обратимся к рассмотрению систем, для которых петля гистерезиса имеет вид параллелограмма (фиг. 5, а). Площадь петли гистерезиса в этом случае определяется по формуле  [c.229]

Полученное выражение совпадает с коэффициентом гармонической линеаризации диссипативных характеристик (см т. 2). Формулой (22) пользуются в том случае, когда диссипативные характеристики заданы соотношениями типа (2)—(4) либо кон фигурацией петли гистерезиса. Зависимость (19) удобно использовать, если рассей-  [c.130]

Выражение (6.16) обладает следующей особенностью если одновременно увеличить параметры Dp и DJ на произвольную величину и на ту же величину уменьшить Dp и Dj, значение не изменится. Это означает, что при изотермическом нагружении одну из четырех констант необходимо задать произвольно, например, принять ее равной нулю. Естественно, ч го ни из каких испытаний при замкнутой петле пластического гистерезиса (когда изменения в полу-цикл ах, отвечающих 9 > О и 0 начала отсчета относится и к общему случаю, когда определяемая из опыта функция D (0) не аппроксимируется кусочно-постоянной. Отсюда следует, что для идентификации упрощенного варианта модели при изотермическом нагружении достаточны испытания при трех различных комбинациях характеристик х+. Х > если для показателя m а + 1 принять обычно используемую в формуле Коффина константу. В противном случае минимально необходимы четыре испытания, т. е. вдвое больше, чем при отсутствии выдержек в цикле.  [c.136]

Были определены пределы изменения напряжений для случая г = О (условно симметричный цикл) в соответствии с формулой (А5.25). При этих значениях петля гистерезиса действительно оставалась неподвижна (рис. А5.33, а). Изменения среднего напряжения в ту или другую сторону, даже незначительные, приводили к накоплению деформации соответствующего знака (рис. А5.33, б, в).  [c.199]

Основные расчетные соотношения. Из рассмотренных методов лучше других всей совокупности перечисленных требований отвечает метод, предполагающий прямое измерение неупругой деформации за цикл на основе ее равенства ширине динамической петли гистерезиса. Зная неупругую деформацию за цикл А н, характеристики Z) и можно рассчитать с применением формул (П.5) и (II.6). Некоторые ограничения при использовании этого метода накладывает разрешающая способность метода. Приняв, что минимальная относительная неупругая деформация, которая может  [c.99]

Как показывают опыты [Л. 31, гармонической нагрузке отвечает эллиптическая петля гистерезиса. Коэффициент поглощения ф в этом случае можно определить по формуле  [c.183]

Измерения на участке АВг начинают с точки с координатами В24 и (рис. 4), для чего в положении 1 (см. рис. 3) переключателя П и при замкнутом ключе реостатами устанавливают намагничивающий ток, соответствующий максимальной для данной петли гистерезиса напряженности намагничивающего поля (обычно эта последняя измеренная точка основной кривой индукции петля гистерезиса может быть определена так, чтобы ее вершина совпадала с любой точкой основной кривой индукции). Затем ключ К , размыкают и с помощью реостатов Гд по амперметру Лз устанавливают значение тока, соответствующее напряженности намагничивающего поля, несколько меньшей, чем Яд1 (точка Я1 на рис. 4). После этого ключ замыкают, производят коммутирование тока, соответствующего напряженности поля и оставляют переключатель П в положении 1. Включают измеритель и отмечают отклонение его стрелки или светового пятна или цифровой отсчет при размыкании ключа Яг. Отклонение а, пропорционально разности индукции Вщ — В1, рассчитываемой по формуле  [c.19]

Влияние гистерезиса. То же соотношение энергетического баланса может бьггь положено в основу исследования вынужденных колебаний при наличии частотно-независимого гистерезиса. Для этого нужно приравнять площадь петли гистерезиса, определяемую формулой (2.43)  [c.142]

По механизму возникновения различают потери на гистерезис и динамические. Потери на гистерезис связаны с явлением магни ного гистерезиса и с необратимым перемещением границ доменов Они пропорциональны площади петли гистерезиса и частоте пере менного поля. Мощность потерь, расходуемая на гистерезис, определяется следующей формулой  [c.91]

Циклическую деформацию (лолную и неупругую) при условии постоянства коэффициента усиления аппаратуры по горизонтальной оси Кх можно определить по формулам Аг=КхЛх, Ва=КхХа, где Д — ширина петли гистерезиса по экрану осциллографа Хг. — амплитуда по экрану осциллографа.  [c.144]

На рис. 5.3.5 приведены экспериментальные данные по коэффициенту р(з-Е), полученные при установившейся петле гистерезиса для различных чисел циклов нагружения стали Х18Н10Т и вычисленные по формуле (5.3.5) при р = 0,275 и рр = 0,475 (сплошные линии), при Це = 0,25 и рр = 0,5 (пунктир). Соответствие интерполяционной формулы и эксперимента достаточно хорошее можно отметить повышенный разброс экспериментальных данных, связанный со сложностью проведения опыта.  [c.242]

Отметим, что выражения передаваемых сил лучше отражают реальные петли гистерезиса, так как степень косинусов обеспечивает появление высших гармоник у сил внутреннего трения. За счет резкого уменьшения второго члена вблизи фазы a>t = nl2 петли получают острые вершины (табл. 2.3, д, ж), наблюдаемые и в экспериментах. Максимальные напряжения при этом можно определять без поправок на силы трения, как это делалось пофиг. 2. 1 и формулам (2. 3) и (2. 6), прямо по закону Гука. = Bbq и Yoi  [c.100]

Основные и вспомогательные параметры (см. рис. 220 и 221), характеризующие рабочие свойства ферритов с ППГ (прямоугольной петлей гистерезиса), принято делить на статические и динамические. К статическим параметрам относятся коэффициент прямо-угольности а и коэффициент квадрат-ности К, к динамическим — коэффициент переключения и время пере-магничивания Тц. Коэффициент прямо-угольности вычисляют по формуле а=Вг В . Коэффициент квадратности определяют по графику предельной петли гистерезиса, снятой при изменении намагничивающего поля в пределах Шс и вычисляют по формуле  [c.203]

При изучении процессов накопления повреждений и термопластического деформирования, а также сопоставлении термоциклической долговечности новых материалов следует рассматривать величину пластической деформации за цикл. В этом случае для точного определения е л. а также Лег необходимо осуществить запись петель упругопластического гистерезиса, что значительно усложняет эксперимент. Для расчета пластической деформации часто используют формулу (1), принимая в соответствии с идеализированной петлей гистерезиса величину уругой деформации при максимальной температуре  [c.6]

В этом выражешш для скорости деформации (е,,) учтено, что = j -ь /, а вдоль JHiHHH = orist, согласно (2.12), при > =0 выполнен баланс импульсов в проекции на ОХ, Для фиксированною значения х вблизи критической точки формулы (2,16), (2,17), зависящие параметрически от /, дают возможность построить в плоскости «напряжение — деформация» петлю динамического гистерезиса.  [c.47]

Во внешнем магнитном поле Н частицы приобретают дополнительную энергию —МН = —МН os ф, которая изменяет энергетический барьер Ев и время релаксации т [1034, 1053]. В тех случаях, когда эффектами анизотропии можно пренебречь МН KV или к-вТ KV), ориентации векторов М отдельных частиц стохастически изменяются под действием тепловых флуктуаций, вследствие чего исчезают внешние признаки ферромагнетика петля гистерезиса вырождается в одиночную кривую намагничивания (коэрцитивная сила Не и остаточная намагниченность равны нулю), описываемую формулой Ланжевена [1033, 1034]  [c.320]

В алюминатах редких земель ИК-диэлектрический вклад несколько меньше, чем в оксидах висмута e gjj=20—30. Эти кристаллы с общей формулой ЬпАЮз, где Ln = La, Рг, Nd, Ей, Gd, Sm, обладают положительным ТКе. Однако в них уже получены весьма низкие диэлектрические потери tg6 = = 10- —10 . Положительный ТКе и большая величина диэлектрического ИК-вклада дают основание предполагать, как и в антисегнетоэлектриках, существование сильного внутреннего поля. Однако в этих кристаллах фазовые переходы при высоких температурах обна1ружить не удалось и петли диэлектрического гистерезиса не наблюдались. Аномальные свойства ИК-поляризации в этом случае не находят традиционного объяснения.  [c.92]

В заключение отметим, что собственное атомное разупорядо-чение существенным образом влияет на магнитные свойства ферритов и это обстоятельство надо учитывать, когда надо получить материал со строго повторяющимися параметрами. В качестве технологического приема, стабилизирующего магнитную индукцию и квадратность термостабильной петли гистерезиса, иногда рекомендуют дополнительные к основной термообработке отжиги при температурах 700—800°С в течение времени, достаточном для равновесного перераспределения ионов по подрешеткам (продолжительность отжига зависит от природы феррита 2]). Примером значительного влияния собственно атомного разупорядочения на магнитные свойства является поведение феррита никеля, резко закаленного с высоких температур и обладающего определенной концентрацией ионов Ni + в Л-узлах решетки (при 1300°С в формуле Fe » [Ni Fe2ij ]04 JT = 0,9955). Как показали измерения [142], появление Ni + в тетраэдрических узлах шпинельной структуры приводит к изменению анизотропии кристалла и ширины линии ферромагнитного резонанса.  [c.116]

В слабых полях с амплитудами напряженности, меньшими коэрцитивной силы , зависимость Я от практически линейна, доменная поляризация осуществляется только за счет обратимого смещения доменных стенок (область / на рис. 21,10), С приближением к Е (область II) появляется переполяризация доменов путем необратимого смещения доменных стенок, две ветви петли гистерезиса разделяются и дополнительный механизм доменной поляризации приводит к увеличению е ф (21.11). При Е > Е,. (область III) переполяри-зуется весь объем образца, доменная поляризованность достигает насыщения (при этом для монокристаллов она равна Р , а снижается с ростом за счет увеличения знаменателя в формуле (21.11) при почти постоянном числителе. Максимального значения е ф достигает при амплитуде напряженности поля, близкой к коэрцитивной силе данного материала.  [c.219]

Интенсивность изменения петли гистерезиса с ростом числа полуциклов нагружения определяется по формуле (9.7) е учетом (9.10) и (9.11). При любом полуцикле ширина петли гистерезиса вычисляется [192] так для аустенитной стали 1Х18Н9Т  [c.246]

Из рис. 9.7 видно, как результаты приближаются к кривой (9.48) в пределе (9.44). Участки кривых с отрицательным наклоном неустойчивы, так что возникают петли гистерезиса. Кривая е на рис. 9.7, а построена по формуле (9.48) при С = 50, Д = 0 = О (чисто абсорбционный случай) кривая е на рис. 9.7, б построена по формуле (9.48) при С = 50, Д = 10, 0 = 2,25 (дисперсионный случай). На обоих рис. 9.7, а н б кривыми а, Ь, с, й представлено точное решение уравнений (9.39) А (9.42) при разных значениях aL и пропускания, выбранных таким образом, чтобы отношение С = аЫ 2Т) было постоянным и равнялось 50. При больших значениях аЬ и Т, как на кривой а, бистабильность отсутствует, а при уменьшении а1 и Т бистабильное поведение усиливается. При этом мы подходим все ближе к результату (9.48) ( среднее поле ), который оказывается хорошим приближением уже при aL I. При фиксированных С и Г кривая среднего поля дает более точное приближение в дисперсионном случае (рис. 9.7, б), чем в абсорбционном (рис. 9.7, а). Это объясняется тем, что в дисперсионном случае поглощение уменьшаете и изменения амплитуды поля в пространстве даже при больших aL оказываются не очень сильными. В следующих двух подразделах мы проанализируем уравнение состояния в приближении среднего поля (9.48), которое выражает интенсивность падающего света через интенсивность прошедшего. Оно зависит от трех параметров параметра кооперативности С, атомной расстройки Д и расстрой-  [c.242]

---

Петля гистерезиса, теория и примеры задач

Основные понятия гистерезиса. Петля гистерезиса

Важное свойство сегнетоэлектриков обнаруживается при изучении зависимости электрического смещения (D) от напряженности поля (E). Смещение является не прямо пропорциональным полю. Диэлектрическая проницаемость вещества () зависит от напряженности поля. Кроме того, величина диэлектрического смещения зависит не только от значения напряженности электрического поля в настоящий момент, но и от предыстории состояний поляризации. Это явление носит название диэлектрического гистерезиса. Зависимость смещения D от напряженности поля E для сегнетоэлектриков графически изображается петлей гистерезиса (рис.1).

Между обкладками плоского конденсатора поместим сегнетоэлектрик. Будем изменять напряженность (E) внешнего электрического поля по гармоническому закону. При этом станем проводить измерение диэлектрической проницаемости сегнетоэлектрика (). При этом используется схема, которая состоит из двух конденсаторов, соединенных последовательно. К крайним клеммам конденсаторов присоединен генератор, который создает разность потенциалов, которая изменяется по гармоническому закону. Один из имеющихся конденсаторов заполнен сегнетоэлектриком (его емкость обозначим C), в другом диэлектрик отсутствует (). Считаем, что площади обкладок конденсаторов равны, расстояния между обкладками – d. Тогда напряженности полей конденсаторов:

   

тогда разности потенциалов между обкладками соответствующих конденсаторов:

   

где – плотность заряда на пластинах конденсатора. Тогда отношение равно:

   

Если напряжение U подают на горизонтальную развертку осциллографа, а напряжение на вертикальную развертку, то на экране осциллографа отобразится, при изменении E, кривая, абсцисса точек которой в некотором масштабе равна , а ордината – . Данная кривая будет петлей гистерезиса (рис.1).

Рис. 1

Стрелки на представленной кривой указывают направления изменения напряженности поля. Отрезок ОВ – отображает величину остаточной поляризации сегнетоэлектрика. Это поляризация диэлектрика при внешнем поле равном нулю. Чем больше отрезок ОВ, тем больше остаточная поляризация. Отрезок ОС отображает величину напряженности, противоположного направления к вектору поляризации, при которой сегнетоэлектрик полностью деполяризован (остаточная поляризация равна нулю). Чем больше длина отрезка ОС, тем лучше остаточную поляризацию удерживает сегнетоэлектрик.

Петлю гистерезиса можно получить, если производить перемагничивание ферромагнетика в периодическом магнитном поле. Кивая зависимости магнитной индукции магнетика от напряженности внешнего магнитного поля (B(H)) будет иметь вид аналогичный рис.1. Демонстрация петли гистерезиса для ферромагнетиков проводится по выше описанной схеме, но при замене конденсаторов на катушки.

Примеры решения задач

Физический смысл площади фигуры ограниченной петлей гистерезиса. Гистерезис для инженеров. Петля гистерезиса. Прерванные процессы на петле гистерезиса. Смена направления процесса

В электротехнике есть разные приборы, принцип работы которых основан на электромагнитных явлениях. Где есть сердечник, на котором намотана катушка из проводящего материала, например, меди, наблюдаются взаимодействия за счёт магнитных полей. Это реле, пускатели, контакторы, электродвигатели и магниты. Среди характеристик сердечников есть такая характеристика как гистерезис. В этой статье мы рассмотрим, что это такое, а также какаие польза и вред от данного явления.

Определение понятия

У слова «Гистерезис» греческие корни, оно переводится как запаздывающий или отстающий. Этот термин используется в разных сферах науки и техники. В общем смысле понятие гистерезис отличает различное поведение системы при противоположных воздействиях.

Это можно сказать и более простыми словами. Допустим есть какая-то система, на которую можно влиять в нескольких направлениях. Если при воздействии на неё в прямом направлении, после прекращения система не возвращается в исходное состояние, а устанавливается в промежуточном — тогда чтобы вернуть в исходное состояние нужно воздействовать уже в другом направлении с какой-то силой. В этом случае система обладает гистерезисом.

Иногда это явление используется в полезных целях, например, для создания элементов, которые срабатывают при определённых пороговых значениях воздействующих сил и для регуляторов. В других случаях гистерезис несёт пагубное влияние, рассмотрим это на практике.

Гистерезис в электротехнике

В электротехнике гистерезис — это важная характеристика для материалов, из которых изготавливаются сердечники электрических машин и аппаратов. Прежде чем приступать к объяснениям, давайте рассмотрим кривую намагничивания сердечника.

Изображение на графике подобного вида называют также петлей гистерезиса.

Важно! В данном случае речь идет о гистерезисе феромагнетиков, здесь это нелинейная зависимость внутренней магнитной индукции материала от величины внешней магнитной индукции, которая зависит от предыдущего состояния элемента.

При протекании тока через проводник вокруг последнего возникает магнитное и . Если смотать провод в катушку и пропустить через него ток, то получится электромагнит. Если поместить внутрь катушки сердечник, то её индуктивность увеличится, как и силы, возникающие вокруг неё.

Отчего зависит гистерезис? Соответственно сердечник изготавливается из металла, от его типа зависят его характеристики и кривая намагничивания.

Если использовать, например, каленную сталь, то гистерезис будет шире. При выборе так называемых магнитомягких материалов — график сузится. Что это значит и для чего это нужно?

Дело в том, что при работе такой катушки в цепи переменного тока ток протекает то в одном, то в другом направлении. В результате и магнитные силы, полюса постоянно переворачивается. В катушке без сердечника это происходит в принципе одновременно, но с сердечником дела обстоят иначе. Он постепенно намагничивается, его магнитная индукция возрастает и постепенно доходит до почти горизонтального участка графика, который называется участком насыщения.

После этого, если вы начнете изменять направление тока и магнитного поля, сердечник должен будет перемагнитится. Но если просто отключить ток и тем самым убрать источник магнитного поля, сердечник все равно останется намагниченным, хоть и не так сильно. На следующем графике это точка «А». Чтобы его размагнитить до исходного состояния нужно создать уже отрицательную напряженность магнитного поля. Это точка «Б». Соответственно ток в катушке должен протекать в обратном направлении.

Значение напряженности магнитного поля для полного размагничивания сердечника называется коэрцитивной силой и чем она меньше, тем лучше в данном случае.

Перемагничивание в обратном направлении будет проходить аналогично, но уже по нижней ветви петли. То есть при работе в цепи переменного тока часть энергии будет затрачиваться на перемагничивание сердечника. Это ведёт к тому что КПД электродвигателя и трансформатора снижается. Соответственно это приводит к его нагреву.

Важно! Чем меньше гистерезис и коэрцитивная сила, тем меньше потери на перемагничивание сердечника.

Кроме выше описанного гистерезис характерен и для работы реле и других электромагнитных коммутационных приборов. Например, ток отключения и включения. Когда реле выключено, чтобы оно сработало нужно приложить определённый ток. При этом ток его удержания во включенном состоянии может быть намного ниже тока включения. Оно отключится только тогда, когда ток опустится ниже тока удержания.

Гистерезис в электронике

В электронных устройствах гистерезис несёт в основном полезные функции. Допустим это используется в пороговых элементах, например, компараторах и триггерах Шмидта. Ниже вы видите график его состояний:

Это нужно в тех случаях, чтобы устройство сработало при достижении сигнала X, после чего сигнал может начать уменьшаться и устройство не отключилось до тех пор, пока сигнал не упадет до уровня Y. Такое решение используется для подавления дребезга контакта, и случайных всплесков, а также в различных регуляторах.

Например, термостат или регулятор температуры. Обычно его принцип действия заключается в том, чтобы отключить нагревательный (или охладительный) прибор в тот момент, когда температура в помещении или другом месте достигла заданного уровня.

Рассмотрим два варианта работы кратко и просто:

1. Без гистерезиса. Включение и отключение при заданной температуре. При этом здесь есть нюансы. Если вы установили регулятор температуры на 22 градуса и обогреваете комнату до этого уровня, то как только в комнате будет 22 он выключится, а когда вновь опустится до 21 – включится. Это не всегда правильное решение, потому что ваш управляемый прибор будет слишком часто включаться и отключаться. К тому же в большинстве бытовых и многих производственных задачах нет нужды настолько четкой поддержки температуры.
2. С гистерезисом. Чтобы сделать некий зазор в допустимом диапазоне регулируемых параметров применяют гистерезис. То есть, если вы установили температуру в 22 градуса, то, как только она будет достигнута, обогреватель отключится. Допустим, что гистерезис в регуляторе установлен на зазор в 3 градуса, то обогреватель вновь заработает только тогда, когда температура воздуха опустится до 19 градусов.

Иногда этот зазор регулируется на ваше усмотрение. В простых исполнениях используются биметаллические пластины.

Мы рассмотрели явление и применение гистерезиса в электрике. Итог следующий: в электроприводе и трансформаторах он несет пагубный эффект, а в электронике и разнообразных регуляторах находит и полезное применение. Надеемся, предоставленная информация была для вас полезной и интересной!

Материалы

Гистере́зис (от греч. hysteresis — отставание) — физическое явление, при котором наблюдается запаздывание изменения состояния системы от изменения физической величины, определяющей внешние условия.
Например, запаздывание изменения намагниченности ферромагнетика от изменения напряженности магнитного поля; запаздывание изменения поляризации сегнетоэлектрика от изменения электрического поля.
Наблюдается в тех случаях, когда состояние системы определяется внешними условиями не только в данный момент времени, но и в предшествующие моменты. Гистерезис наблюдается в разных разделах физики. Наиболее важны: магнитный гистерезис, сегнетоэлектрический гистерезис и упругий гистерезис.

Суть данного явления можно пояснить на примере работы термостата.
Рассмотрим термостат, настроенный на поддержание температуры 20 °С с помощью электрического нагревателя. Если бы управляющая нагревателем биметаллическая пластина, деформирующаяся при изменении температуры, не обладала гистерезисом, нагреватель включался бы и выключался очень часто, что приведет к быстрому износу контактов. В действительности регулятор включается при 19 °С, а выключается примерно при 21 °С. При этом механическая инерционность биметаллической пластины и тепловая инерционность нагревателя порождают явление гистерезиса, переключение режимов происходит с небольшой частотой, а температура в термостате колеблется в некотором интервале вблизи заданного значения (рис. 1 ).

Рисунок 1

Для гистерезиса характерно явление «насыщения», а также неодинаковость траекторий между крайними состояниями, отсюда наличие остроугольной петли на графиках, именуемой петлей гистерезиса. Неоднозначная зависимость состояния системы от физической величины (при циклическом изменении) изображается петлей гистерезиса (рис. 2 )

Рисунок 2

В электронике и электротехнике используются устройства, обладающие магнитным гистерезисом — различные магнитные носители информации, или электрическим гистерезисом, например, триггер Шмитта или гистерезисный двигатель. Гистерезис используется для подавления шумов (быстрых колебаний, дребезга контактов) в момент переключения логических сигналов. Например, для подавления дребезга контактов часто применяется триггер Шмитта (рис. 3 ).

Рисунок 3. Петля гистерезиса для триггера Шмитта имеет прямоугольный вид
В электронных приборах всех видов наблюдается явление теплового гистерезиса: после нагрева прибора и его последующего охлаждения до начальной температуры его параметры не возвращаются к начальным значениям. Из-за неодинакового теплового расширения кристаллов полупроводников, кристаллодержателей, корпусов микросхем и печатных плат в кристаллах возникают механические напряжения, которые сохраняются и после охлаждения. Явление теплового гистерезиса наиболее заметно в прецизионных источниках опорного напряжения, используемых в измерительных аналого-цифровых преобразователях. В современных микросхемах относительный сдвиг опорного напряжения вследствие теплового гистерезиса составляет порядка 10-100

Гистерезис происходит от греческого слова, означающего запаздывание или отставание. С данным понятием связана такая физическая величина, как петля гистерезиса, определяющая одну из характеристик тела. Она определенным образом связана также и с физическими величинами, характеризующими внешние условия, такие как магнитное поле.

Общие понятия гистерезиса

Гистерезис можно наблюдать в те моменты, когда какое-либо тело в конкретный период времени будет находиться в зависимости от внешних условий. Данное состояние тела рассматривается и в предыдущее время, после чего производится сравнение и выводится определенная зависимость.

Подобная зависимость хорошо просматривается на примере человеческого тела. Чтобы изменить его состояние потребуется какой-то отрезок времени на релаксацию. Поэтому реакция тела будет всегда отставать от причин, вызвавших измененное состояние. Данное отставание значительно уменьшается, если изменение внешних условий также будет заме для ться. Тем не менее, в некоторых случаях может не произойти уменьшения отставаний. В результате, возникает неоднозначная зависимость величин, известная как гистерезисная, а само явление называется гистерезисом.

Эта физическая величина может встречаться в самых разных веществах и процессах, однако чаще всего рассматриваются понятия диэлектрического, магнитного и упругого гистерезиса. Магнитный гистерезис как правило появляется в магнитных веществах, например, таких как ферромагнетики. Характерной особенностью этих материалов является самопроизвольная или спонтанная неоднородная намагниченность, наглядно демонстрирующая это физическое явление.

Механизм возникновения петли гистерезиса

Сам по себе гистерезис представляет собой кривую, отображающую измененный магнитный момент вещества, на которое воздействует периодически изменяющаяся напряженность поля. Когда магнитное поле воздействует на ферромагнетики, то изменение их магнитного момента наступает не сразу, а с определенной задержкой.

В каждом ферромагнетике изначально присутствует самопроизвольная намагниченность. Сам материал включает в свой состав отдельные фрагменты, каждый из которых обладает собственным магнитным моментом. При направленности этих моментов в разные стороны, значение суммарного момента оказывается равным нулю в результате взаимной компенсации.

Если на ферромагнетик оказать воздействие магнитным полем, то все моменты, присутствующие в отдельных фрагментах (доменах) будут развернуты вдоль внешнего поля. В итоге, в материале образуется некоторый общий момент, направленный в одну сторону. Если внешнее действие поля прекращается, то домены не все окажутся в изначальном положении. Для этого потребуется воздействие достаточно сильного магнитного поля, предназначенного для разворота доменов. Такому развороту создают препятствия наличие примесей и неоднородность материала. Поэтому материал имеет некоторую остаточную намагниченность, даже при отключенном внешнем поле.

Для снятия остаточного магнитного момента, необходимо приложение действия поля в противоположном направлении. Напряженность поля должна иметь величину, достаточную, чтобы выполнить полное размагничивание материала. Такая величина известна как коэрцитивная сила. Дальнейшее увеличение магнитного поля приведет к перемагничиванию ферромагнетика в противоположную сторону.

Когда напряженность поля достигает определенного значения, материал становится насыщенным, то есть магнитный момент больше не увеличивается. При снятии поля вновь наблюдается наличие остаточного момента, который снова можно убрать. Дальнейшее увеличение поля приводит к попаданию в точку насыщения с противоположным значением.

Таким образом, на графике появляется петля гистерезиса, начало которой приходится на нулевые значение поля и момента. В дальнейшем, первое же намагничивание выводит начало петли гистерезиса из нуля и весь процесс начинает происходить по графику замкнутой петли.

Петля гистерезиса. При циклическом изменении напряженности постоянного магнитного поля от 0 до +Н, от +Н до –Н и снова от –Н до +Н кривая изменения индукции (кривая перемагничивания) имеет форму замкнутой кривой – петли гистерезиса. Для слабых полей петля имеет вид эллипса. При увеличении значения напряженности магнитного поля Н получают серию заключенных одна в другую петель гистерезиса. Когда все векторы намагниченности доменов сориентируются вдоль направления поля, процесс намагничивания закончится состоянием технического насыщения намагниченности материала. Петлю гистерезиса, полученную при условии насыщения намагничивания, называют предельной петлей гистерезиса. Она характеризуется максимально достигнутым значением индукции Bs, называется индукцией насыщения. При уменьшении напряженности магнитного поля от +Н до 0 магнитная индукция сохраняет остаточную индукцию Вс. Чтобы получить остаточную магнитную индукцию, равную 0, необходимо приложить противоположно направленное размагничивающее поле определенной напряженности -Нс. Отрицательная напряженность магнитного поля -Нс называется коэрцитивной силой материала. При достижении напряженности магнитного поля значения –Н, а затем 0 вновь возникает остаточная индукция –Вс. Если повысить напряженность магнитного поля до +Нс, то остаточная магнитная индукция Вс будет равна 0. Площадь гистерезисных петель в промежуточных и предельных состояниях характеризует рассеивание электрической энергии в процессе перемагничивания материала, т.е. потери на гистерезис. Площадь гистерезисной петли зависит от свойств материала, его геометрических размеров и частоты перемагничивания. По предельной петле гистерезиса определяют такие характеристики магнитных материалов, как индукцию насыщения Bs, остаточную индукцию Вс, коэрцитивную силу Нс.

Кривая намагничивания

Кривая намагничивания. Это важнейшая характеристика магнитных материалов, она показывает зависимость намагниченности или магнитной индукции материала от напряженности внешнего поля Н. Магнитная индукция материала Bi измеряется в теслах (Тл) и связана с намагниченностью. Основная (коммутационная) кривая намагничивания представляет собой геометрическое место вершин петель гистерезиса, полученных при циклическом перемагничивании и отражает изменение магнитной индукции В в зависимости от напряженности магнитного поля Н, которое создается в материале при намагничивании. Напряженность магнитного поля в образце в виде тороида, когда магнитная цепь замкнута, равна напряженности внешнего поля Нв. В разомкнутой магнитной цепи на концах образца появляются магнитные полюса, создающие размагничивающее поле Нр. Разница между магнитными напряженностями внешнего и размагничивающего полей определяют внутреннюю магнитную напряженность Hi материала. Основная кривая намагничивания имеет ряд характерных участков, которые можно условно выделить при намагничивании монокристалла ферромагнетика. Первый участок кривой намагничивания соответствует процессу смещения границ менее благоприятно ориентированных доменов. На втором участке происходит поворот векторов намагниченности доменов в направлении внешнего магнитного поля. Третий участок соответствует парапроцессу, т.е. завершающему этапу процесса намагничивания, когда сильное магнитное поле поворачивает в направлении своего действия не сориентированные магнитные моменты доменов ферромагнетика.

Чтобы лучше понять, что такое магнитный гистерезис, нужно разобраться, где и при каких условиях он возникает.

Основные понятия

Магнитное поле – это одна из составляющих электромагнитного поля, характеризующаяся своим силовым действием на движущиеся заряженные частицы.

Вектор магнитной индукции B – это основная силовая величина магнитного поля.

Намагниченность M – это величина, которая характеризует магнитное состояние вещества.

Напряженность магнитного поля – это характеристика магнитного поля, которая равна разности магнитной индукции и намагниченности.

Ферромагнитный материал – это материал, намагниченность которого зависит от напряженности внешнего магнитного поля.

Допустим, мы имеем катушку, внутри которой имеется сердечник из ферромагнитного материала. Обычно такой сердечник состоит из железа, никеля, кобальта и различных соединений на их основе. Если подключить её к источнику переменного тока , то вокруг катушки образуется магнитное поле, которое будет изменяться по закону

График зависимости B (H)

Участок 0-1 называется кривой первоначального намагничивания. Благодаря ей мы можем увидеть, как меняется магнитная индукция в размагниченной катушке.

После насыщения (то есть точки 1) с уменьшением напряженности магнитного поля до нуля (участок 1-2), мы видим, что сердечник остался намагниченным на величину остаточной намагниченности Br. Это и называется явлением магнитного гистерезиса.

С точки зрения физики остаточная намагниченность объясняется тем, что в ферромагнетиках существуют сильные магнитные связи между молекулами, благодаря которым создаются беспорядочно направленные магнитные моменты. Под воздействием внешнего поля, они принимают направления поля, а после его снятия, часть магнитных моментов остаются направленными. Поэтому вещество остается намагниченным.

После изменения направления тока в катушке размагничивание продолжается (участок 2-3) до пересечения оси абсцисс. Участок 3-0 называется коэрцитивной силой Hc. Это величина, которая необходима для уничтожения поля в сердечнике. Далее аналогично происходит намагничивание сердечника до насыщения (участок 3-4) и обратно размагничивание на участке 4-5 и 5-6, с последующим намагничиванием до точки 1. Весь этот график называется петлей магнитного гистерезиса.

Если многократно намагнитить сердечник с напряженностью и индукцией магнитного поля, меньшими чем при насыщении, то можно получить семейство кривых, из которых в дальнейшем можно построить основную кривую намагничивания (0-1-2). Эта кривая зачастую требуется при электротехнических расчетах магнитных систем.

В зависимости от ширины петли гистерезиса, ферромагнитные материалы делят на магнитотвердые и магнитомягкие. Магнитотвердые вещества обладают большими значениями остаточной намагниченности и коэрцитивной силы. Магнитомягкие вещества, такие как электротехническая сталь применяют в трансформаторах, электрических машинах,электромагнитах , благодаря небольшой коэрцитивной силе и большому значению магнитной проницаемости.

Тематические материалы:

Обновлено: 28.09.2019

103583

Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter

Магнитный гистерезис

Если предварительно размагниченный образец ферромагнитного материала подвергнуть намагничиванию до состояния технического насыщения, то с увеличением напряженности магнитного поля Н магнитная индукция образца В будет изменяться в соответствии с кривой ОАБ (рисунок 2.2).

Рисунок 2.2 – Предельная петля магнитного гистерезиса

В точке А при H = H_s магнитная индукция образца достигнет индукции насыщения B_s. При уменьшении напряженности поля Н намагниченность образца уменьшается по кривой БАB_r, и при Н = 0 образец будет обладать некоторой индукцией, величина которой будет отлична от нуля. Эта индукция называется остаточной и обозначается Вr. Остаточная индукция (остаточная намагниченность) обусловлена тем, что при размагничивании, когда Н = 0, магнитные моменты доменов оказываются ориентированными вдоль оси легкого намагничивания, направление которой близко к направлению внешнего.

Для достижения полного размагничивания образца к нему необходимо приложить противоположное по знаку поле определенной напряженности. Напряженность такого поля называют коэрцитивной силой Н_с. При дальнейшем усилении отрицательного поля магнитная индукция тоже становится отрицательной и в точке A’ при H = –H_s достигает значения индукции технического насыщения (B = –B_s). После уменьшения отрицательного поля, а затем увеличения положительного поля кривая перемагничивания опишет петлю, называемую предельной петлей магнитного гистерезиса, которая является важной технической характеристикой магнитных материалов.

Таким образом, предельная петля магнитного гистерезиса – это кривая изменения магнитной индукции при изменении внешнего магнитного поля от +H_s до –H_s и обратно. Пользуясь предельной петлей магнитного гистерезиса можно определить основные параметры материала: коэрцитивную силу Нс, индукцию насыщения B_s, остаточную индукцию Br и др.

Такие характеристики материала, как точка Кюри и индукция насыщения, зависят только от химического состава магнитных материалов. Коэрцитивная сил Н_с, магнитная проницаемость M и площадь петли гистерезиса являются структурночувствительными. Чем больше размер зерна (меньше суммарная удельная поверхность зерен) и более совершенна структура кристаллической решетки (меньше дислокаций, внутренних напряжений, примесей и других дефектов), тем меньше Н_с и больше M, а материал легче намагничивается и перемагничивается.

По величине коэрцитивной силы магнитные материалы подразделяются на магнитомягкие и магнитотвердые. Материалы, у которых Нс с > 4 кА/м – к магнитответдым (ГОСТ 19693 – 74).

Для магнитомягких материалов характерно малое значение коэрцитивной силы. У промышленных образцов наименьшая Н_с = 0,4 А/м. Поэтому они намагничиваются до индукции технического насыщения при невысоких напряженностях поля. У магнитомягких материалов высокая магнитная проницаемость, малые потери на перемагничивание и узкая петля гистерезиса при высоких значениях магнитной индукции.

Для магнитотвердых материалов характерна широкая петля гистерезиса с большой коэрцитивной силой. У промышленных образцов наибольшая Нс = 800 кА/м. Магнитотвердые материалы намагничиваются при высокой напряженности внешнего магнитного поля, но зато длительное время сохраняют сообщенную энергию.

В каких координатных осях строится петля гистерезиса. Что такое петля гистерезиса

Петля гистерезиса. При циклическом изменении напряженности постоянного магнитного поля от 0 до +Н, от +Н до –Н и снова от –Н до +Н кривая изменения индукции (кривая перемагничивания) имеет форму замкнутой кривой – петли гистерезиса. Для слабых полей петля имеет вид эллипса. При увеличении значения напряженности магнитного поля Н получают серию заключенных одна в другую петель гистерезиса. Когда все векторы намагниченности доменов сориентируются вдоль направления поля, процесс намагничивания закончится состоянием технического насыщения намагниченности материала. Петлю гистерезиса, полученную при условии насыщения намагничивания, называют предельной петлей гистерезиса. Она характеризуется максимально достигнутым значением индукции Bs, называется индукцией насыщения. При уменьшении напряженности магнитного поля от +Н до 0 магнитная индукция сохраняет остаточную индукцию Вс. Чтобы получить остаточную магнитную индукцию, равную 0, необходимо приложить противоположно направленное размагничивающее поле определенной напряженности -Нс. Отрицательная напряженность магнитного поля -Нс называется коэрцитивной силой материала. При достижении напряженности магнитного поля значения –Н, а затем 0 вновь возникает остаточная индукция –Вс. Если повысить напряженность магнитного поля до +Нс, то остаточная магнитная индукция Вс будет равна 0. Площадь гистерезисных петель в промежуточных и предельных состояниях характеризует рассеивание электрической энергии в процессе перемагничивания материала, т.е. потери на гистерезис. Площадь гистерезисной петли зависит от свойств материала, его геометрических размеров и частоты перемагничивания. По предельной петле гистерезиса определяют такие характеристики магнитных материалов, как индукцию насыщения Bs, остаточную индукцию Вс, коэрцитивную силу Нс.

Кривая намагничивания

Кривая намагничивания. Это важнейшая характеристика магнитных материалов, она показывает зависимость намагниченности или магнитной индукции материала от напряженности внешнего поля Н. Магнитная индукция материала Bi измеряется в теслах (Тл) и связана с намагниченностью. Основная (коммутационная) кривая намагничивания представляет собой геометрическое место вершин петель гистерезиса, полученных при циклическом перемагничивании и отражает изменение магнитной индукции В в зависимости от напряженности магнитного поля Н, которое создается в материале при намагничивании. Напряженность магнитного поля в образце в виде тороида, когда магнитная цепь замкнута, равна напряженности внешнего поля Нв. В разомкнутой магнитной цепи на концах образца появляются магнитные полюса, создающие размагничивающее поле Нр. Разница между магнитными напряженностями внешнего и размагничивающего полей определяют внутреннюю магнитную напряженность Hi материала. Основная кривая намагничивания имеет ряд характерных участков, которые можно условно выделить при намагничивании монокристалла ферромагнетика. Первый участок кривой намагничивания соответствует процессу смещения границ менее благоприятно ориентированных доменов. На втором участке происходит поворот векторов намагниченности доменов в направлении внешнего магнитного поля. Третий участок соответствует парапроцессу, т.е. завершающему этапу процесса намагничивания, когда сильное магнитное поле поворачивает в направлении своего действия не сориентированные магнитные моменты доменов ферромагнетика.

Биологические и физические системы способны мгновенно откликаться на приложенное к ним воздействие. Если рассмотреть это явление на временной оси координат, то становится заметно, что отклик зависит от предыстории системы и ее текущего состояния. График, который наглядно демонстрирует это свойство систем, получил название петли гистерезиса, которая отличается остроугольной формой.

Оригинальная форма петли обусловлена эффектом насыщения и неравномерностью траектории между соседними расстояниями. Эффект гистерезиса имеет кардинальные отличия от инерционности, с которой его часто путают, забывая о том, что монотонное сопротивление существенно отличается от мгновенного сопротивления на воздействие.

Петля гистерезиса является циклом, в ходе которого часть свойств системы используются независимо от воздействий, а часть – отправляется на повторную проверку.

Явление гистерезиса в физике

В физике наиболее часто системы сталкиваются со следующими видами гистерезиса:

• Магнитный – отражает зависимость между векторами напряжения магнитного поля и намагничивания в веществе. Это явление объясняет существование постоянных магнитов.
• Сепнгетоэлектрический – зависимость между поляризацией сегнетоэлектриков и изменения внешнего электрического поля.
• Упругий – зависимость деформации упругих материалов от воздействия высоких давлений. Это явление лежит в основе великолепных механических характеристик изделий из кованого метала.

Упругий гистерезис встречается двух основных видов – статический и динамический. В первом случае петля будет равномерной, во втором – постоянно меняющейся.

Применение гистерезиса в электронике

В электротехнике широко применяются устройства, в основе которых лежат магнитные взаимодействия. Наиболее распространение получили магнитные носители данных. Понимание гистерезиса необходимо для подавления в них шумов, таких как быстрые колебания или дребезжание контактов.

В большинстве электронных приборов наблюдается явление теплового гистерезиса. В процессе работы устройства нагреваются, а после охлаждения ряд характеристик уже не могут принять первоначальные явления.

Так, в процессе нагрева происходит расширение микросхем и печатных плат, полупроводниковых кристаллов. В результате развивается механическое напряжение, воздействие которого на элементы системы сохраняется после остывания. Особенно ярко тепловой гистерезис проявляется в высокоточных источниках опорного напряжения.

Гистерезис в общем понятии (от греческого – отстающий) — это свойство определенных физических, биологических и иных систем, которые реагируют на соответствующие воздействия с учетом текущего состояния, а также предыстории.

Гистерезис характерен т.н. «насыщением», и различными траекториями соответствующих графиков, отмечающих состояние системы в данный момент времени. Последние, в итоге, имеют форму остроугольной петли.

Если же рассматривать конкретно электротехнику, то каждый электромагнитный сердечник после окончания воздействия электрического тока в течение некоторого времени сохраняет собственное магнитное поле, называемое остаточным магнетизмом.

Его величина зависит, прежде всего, от свойств материала: у закаленной стали она существенно выше, чем у мягкого железа.

Но, в любом случае, явление остаточного магнетизма всегда присутствует при перемагничивании сердечника, когда необходимо размагнитить его до нуля, а затем изменить полюс на противоположный.

Любое изменение направления тока в обмотке электромагнита предусматривает (из-за наличия вышеуказанных свойств материала) предварительное размагничивание сердечника. Только после этого он может поменять свою полярность — это известный закон физики.

Для перемагничивания в обратном направлении необходим соответствующий магнитный поток.

Другими словами: изменение сердечника не «поспевает» за соответствующими изменениями магнитного потока, которое оперативно создает обмотка.

Вот эта временная задержка намагничивания сердечника от изменений магнитных потоков и получило название в электротехнике как гистерезис.

Каждое перемагничивание сердечника предусматривает избавление от остаточного магнетизма путем воздействия противонаправленным магнитным потоком. На практике это приводит к определенным потерям электроэнергии, которые тратятся на преодоление «неправильной» ориентации молекулярных магнитиков.

Последние проявляются в виде выделения тепла, и представляют так называемые затраты на гистерезис.

Таким образом, стальные сердечники, например, статоров или якорей электродвигателей или генераторов, а также , должны иметь по возможности наименьшую корреляционную силу . Это позволит снизить гистерезисные потери, повысив в итоге КПД соответствующего электрического агрегата или прибора.

Сам процесс намагничивания определяется соответствующим графиком – так называемой петлей гистерезиса. Она представляет замкнутую кривую, отображающую зависимость скорости намагничивания от изменения динамики напряженности внешнего поля.

Большая площадь петли подразумевает, соответственно, и большие затраты на перемагничивание.

Также практически во всех электронных приборах наблюдается и такое явление, как тепловой гистерезис – невозвращение после прогрева аппаратуры к изначальному состоянию.

В и явление гистерезиса используется в различных магнитных носителях информации (например, триггерах Шмидта), или в специальных гистерезисных электродвигателях.

Широкое распространение этот физический эффект нашел также в различных устройствах, предназначенных для подавления различных шумов (дребезг контактов, быстрые колебания и т. п.) в процессе переключения логических схем.

В сердечнике любого электромагнита после выключения тока всегда сохраняется часть магнитных свойств, называемая остаточным магнетизмом. Величина остаточного магнетизма зависит от свойств материала сердечника и достигает большего значения у закаленной стали и меньшего у мягкого железа.

Однако, как бы ни было мягко железо, остаточный магнетизм все же будет оказывать известное влияние в том случае, если по условиям работы прибора необходимо перемагничивание его сердечника, т. е. размагничивание до нуля и намагничивание в противоположном направлении.

Действительно, при всяком изменении направления тока в обмотке электромагнита необходимо (благодаря наличию в сердечнике остаточного магнетизма) сначала размагнитить сердечник, и только после этого он может быть намагничен в новом направлении. Для этого потребуется какой-то магнитный поток противоположного направления.

Иначе говоря, изменение намагничивания сердечника (магнитной индукции) всегда отстает от соответствующих изменений магнитного потока (), создаваемого обмоткой.

Это отставание магнитной индукции от напряженности магнитного поля носит название гистерезиса . При каждом новом намагничивании сердечника для уничтожения его остаточного магнетизма приходится действовать на сердечник магнитным потоком противоположного направления.

Практически это будет означать затрату какой-то части электрической энергии на преодоление коэрцитивной силы, затрудняющей поворот молекулярных магнитиков в новое положение. Затраченная на это энергия выделяется в железе в виде тепла и представляет потери на перемагничивание, или, как говорят, потери на гистерезис .

Исходя из сказанного, железо, подверженное в том или ином приборе непрерывному перемагничиванию (сердечники якорей генераторов и электродвигателей , сердечники трансформаторов), должно выбираться всегда мягкое, с очень небольшой коэрцитивной силой. Это дает возможность уменьшить потери на гистерезис и тем самым повысить коэффициент полезного действия электрической машины или прибора.

Петля гистерезиса

Петля гистерезиса — кривая, изображающая ход зависимости намагничивания от напряженности внешнего поля. Чем больше площадь петли, тем большую работу на перемагничивание надо затратить.

Представим себе простой электромагнит с железным сердечником. Проведем его через полный цикл намагничивания, для чего будем менять намагничивающий ток от нуля до величины ОМ в обоях направлениях.

Начальный момент: сила тока равна нулю, железо не намагничено, магнитная индукция В=0.

1-ая часть: намагничивание изменением тока от 0 до величины — + ОМ. Индукция в железе сердечника будет возрастать сначала быстро, затем медленнее. К концу операции, в точке А железо так насыщено магнитными силовыми линиями, что дальнейшее усиление тока (свыше + ОМ) может дать самые незначительные результаты, почему операцию намагничивания можно считать законченной.

Намагничивание до насыщения означает, что имеющиеся в сердечнике молекулярные магниты, находящиеся в начале процесса намагничивания в полном, а затем лишь в частичном беспорядке, почти все расположились теперь стройными рядами, северными полюсами в одну сторону, южными в другую, почему на одном конце сердечника мы имеем теперь северную полярность, на другом — южную.

2-я часть: ослабление магнетизма вследствие уменьшения тока от + ОМ до 0 и полное размагничивание при токе — OD. Магнитная индукция, изменяясь по кривой АС, дойдет до значения ОС, в то время как ток уже будет равен нулю. Эту магнитную индукцию называют остаточным магнетизмом, или остаточной магнитной индукцией. Для уничтожения ее, для полного, следовательно, размагничивания, необходимо дать в электромагнит ток обратного направления и довести его до значения, соответствующего на чертеже ординате OD.

3-я часть: намагничивание в обратную сторону путем изменения тока от — OD до — ОМ1. Магнитная индукция, возрастая по кривой DE, дойдет до точки Е, соответствующей моменту насыщении.

4-я часть: ослабление магнетизма постепенным уменьшением тока от — ОМ1, до нуля (остаточный магнетизм OF) и последующее размагничивание путем перемены направления тока и доведения его до величины + ОН.

5-я часть: намагничивание, соответствующее процессу 1-й части, доведение магнитной индукции от нуля до + МА путем изменении тока от + ОН до + ОМ.

При уменьшении размагничивающего тока до нуля не все элементарные или молекулярные магниты приходят в прежнее беспорядочное состояние, но часть их сохраняет свое положение, соответствующее последнему направлению намагничивания. Это явление запаздывания или задерживания магнетизма и носит название гистерезиса.

Гистерезис

Явление магнитного гистерезиса наблюдается не только при изменении поля H по величине и знаку, но также и при его вращении (гистерезис магнитного вращения), что соответствует отставанию (задержке) в изменении направления M с изменением направления H . Гистерезис магнитного вращения возникает также при вращении образца относительно фиксированного направления H .

Теория явления гистерезиса учитывает конкретную магнитную доменную структуру образца и её изменения в ходе намагничивания и перемагничивания. Эти изменения обусловлены смещением доменных границ и ростом одних доменов за счёт других, а также вращением вектора намагниченности в доменах под действием внешнего магнитного поля. Всё, что задерживает эти процессы и способствует попаданию магнетиков в метастабильные состояния, может служить причиной магнитного гистерезиса.

В однодоменных ферромагнитных частицах (в частицах малых размеров, в которых образование доменов энергетически невыгодно) могут идти только процессы вращения M . Этим процессам препятствует магнитная анизотропия различного происхождения (анизотропия самого кристалла, анизотропия формы частиц и анизотропия упругих напряжений). Благодаря анизотропии, M как-будто удерживается некоторым внутренним полем (эффективным полем магнитной анизотропии) вдоль одной из осей лёгкого намагничивания, соответствующей минимуму энергии. Магнитный гистерезис возникает из-за того, что два направления M (по и против) этой оси в магнитоодноосном образце или несколько эквивалентных (по энергии) направлений М в магнитомногоосном образце соответствуют состояниям, отделённым друг от друга потенциальным барьером (пропорциональным ). При перемагничивании однодоменных частиц вектор M рядом последовательных необратимых скачков поворачивается в направлении H . Такие повороты могут происходить как однородно, так и неоднородно по объёму. При однородном вращении M коэрцитивная сила . Более универсальным является механизм неоднородного вращения M . Однако наибольшее влияние на он оказывает в случае, когда основную роль играет анизотропия формы частиц. При этом может быть существенно меньше эффективного поля анизотропии формы.

Сегнетоэлектрический гистерезис — неоднозначная петлеобразная зависимость поляризации P сегнетоэлектриков от внешнего электрического поля E при его циклическом изменении. Сегнетоэлектрические кристаллы обладают в определенном температурном интервале спонтанной (самопроизвольной, то есть возникающей в отсутствие внешнего электрического поля) электрической поляризацией P c . Направление поляризации может быть изменено электрическим полем. При этом зависимость P (E ) в полярной фазе неоднозначна, значение P при данном E зависит от предыстории, то есть от того, каким было электрическое поле в предшествующие моменты времени. Основные параметры сегнетоэлектрического гистерезиса:

• остаточная поляризация кристалла P ост, при E = 0
• значение поля E Kt (коэрцитивное поле) при котором происходит переполяризация

Упругий гистерезис

Гистерезис используется для подавления шумов (быстрых колебаний, дребезга контактов) в момент переключения логических сигналов.

В электронных приборах всех видов наблюдается явление теплового гистерезиса : после нагрева прибора и его последующего охлаждения до начальной температуры его параметры не возвращаются к начальным значениям. Из-за неодинакового теплового расширения кристаллов полупроводников, кристаллодержателей, корпусов микросхем и печатных плат в кристаллах возникают механические напряжения , которые сохраняются и после охлаждения. Явление теплового гистерезиса наиболее заметно в прецизионных , используемых в измерительных аналого-цифровых преобразователях . В современных микросхемах относительный сдвиг опорного напряжения вследствие теплового гистерезиса составляют порядка 10-100 ppm .

В биологии

Гистерезисные свойства характерны для скелетных мышц млекопитающих.

В почвоведении

Одно из них указывает на взаимосвязь приложенных усилий субъектом влияния и достигнутым результатом. Уровень затраченной субъектом просветительской и пропагандистской работы можно соотносить с уровнем «намагниченности» (степенью вовлеченности в новую идею) объекта-носителя общественного мнения, социальную группу, коллектив, социальную общность или общество в целом; при этом может обнаружиться некоторое отставание объекта от субъекта. Переубеждение, в том числе с предполагаемыми деструктивными последствиями, далеко не всегда проходит успешно. Оно зависит от собственных моральных ценностей, обычаев, традиций, характера предыдущего воспитания, от этических норм, доминирующих в обществе и т. д.

Второе обстоятельство связано с тем, что новый этап формирования общественного мнения можно соотносить с историей объекта, его опытом, его оценкой теми, кто ранее выступал объектом формирования общественного мнения. При этом можно обнаружить, что «точка отсчета» времени формирования общественного мнения смещается относительно прежней, что является характеристикой самой системы и ее текущего состояния.

Литература по теме

• Раддай Райхлин Гражданская война, террор и бандитизм. Систематизация социологии и социальная динамика . Раздел «Борьба с толпой»
• Капустин Валерий Сергеевич Введение в теорию социальной самоорганизации . Тема 11. Явление гистерезиса в формировании национальных форм и способов самоорганизации. Современные парадоксы и загадки «начала»

В философии

Математические модели гистерезиса

Появление математических моделей гистерезисных явлений обуславливалось достаточно богатым набором прикладных задач (прежде всего в теории автоматического регулирования), в которых носители гистерезиса нельзя рассматривать изолированно, поскольку они являлись частью некоторой системы. Создание математической теории гистерезиса относится к 60-м годам XX-го века, когда в Воронежском университете начал работать семинар под руководством М. А. Красносельского , «гистерезисной» тематики. Позднее, в 1983 году появилась монография , в которой различные гистерезисные явления получили формальное описание в рамках теории систем: гистерезисные преобразователи трактовались как операторы, зависящие от своего начального состояния как от параметра, определённые на достаточно богатом функциональном пространстве (например, в пространстве непрерывных функций), действующие в некотором функциональном пространстве. Простое параметрическое описание различных петель гистерезиса можно найти в работе (замена в данной модели гармонических функций на прямоугольные, треугольные или трапецеидальные импульсы позволяет также получить кусочно-линейные петли гистерезисы, которые часто встречаются в дискретной автоматике, см. пример на Рис. 2).

Литература

Примечания

Wikimedia Foundation . 2010 .

Синонимы :

Смотреть что такое «Гистерезис» в других словарях:

— (от греч. hysteresis отставание) запаздывание изменения физической величины, характеризующей состояние вещества (намагниченности М ферромагнетика, поляризации P сегнетоэлектрика и т. п.), от изменения другой физической величины, определяющей… … Большой Энциклопедический словарь

Сдвиг, отставание Словарь русских синонимов. гистерезис сущ., кол во синонимов: 2 отставание (10) … Словарь синонимов

ГИСТЕРЕЗИС, явление, характерное для упругих тел; заключается в том, что ДЕФОРМАЦИЯ тела при увеличении НАПРЯЖЕНИЯ меньше, чем при его уменьшении из за задержки эффекта деформации. Когда механическое напряжение удалено полностью, остается… … Научно-технический энциклопедический словарь

— (от греческого hysteresis отставание, запаздывание) 1) Г. в аэродинамике неоднозначность структуры поля течения и, следовательно, аэродинамических характеристик обтекаемого тела при одних и тех же значениях кинематических параметров, но при… … Энциклопедия техники

Гистерезис — «Энциклопедия»

ГИСТЕРЕЗИС (от греческого ?στ?ρησις — отставание, запаздывание), запаздывание изменения физической величины, характеризующей состояние вещества, от изменения другой физической величины, определяющей внешние условия. Гистерезис имеет место в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. В результате для циклического процесса (рост и уменьшение внешнего воздействия) получается петлеобразная (неоднозначная) диаграмма, которая называется петлёй гистерезиса. Возникает гистерезис в различных веществах и при разных физических процессах. Наибольший интерес представляют магнитный, сегнетоэлектрический и упругий гистерезис.

Магнитный гистерезис — неоднозначная зависимость намагниченности М магнитоупорядоченного вещества (магнетика, например, ферро- или ферримагнетика) от внешнего магнитного поля Н при его циклическом изменении (увеличении и уменьшении). Причиной существования магнитного гистерезиса является наличие в определённом интервале изменения Н среди состояний магнетика, отвечающих минимуму термодинамического потенциала, метастабильных состояний (наряду со стабильными) и необратимых переходов между ними. Магнитный гистерезис можно также рассматривать как проявление магнитных ориентационных фазовых переходов 1-го рода, для которых прямой и обратный переходы между фазами в зависимости от Н происходят, в силу указанной метастабильности состояний, при различных значениях Н.

Реклама

На рисунке 1 схематически показана типичная зависимость М от Н в ферромагнетике; из состояния М = 0 при Н = 0 с увеличением Н значение М растёт (основная кривая намагничивания, а) и в достаточно сильном поле Н ≥ H_m М становится практически постоянной и равной намагниченности насыщения M_s. При уменьшении Н от значения Н_m намагниченность изменяется вдоль ветви б и при Н = 0 принимает значение М = M_R (остаточная намагниченность). Для размагничивания вещества (М = 0) необходимо приложить обратное поле Н = -Н_с, называемое коэрцитивной силой. Далее при Н = -Н_m образец намагничивается до насыщения (М = -M_s) в обратном направлении. При изменении Н от -Н_m до +Н_m намагниченность изменяется вдоль кривой в. Ветви б и в, получающиеся при изменении Н от +Н_m до -H_m и обратно, образуют замкнутую кривую, называемую максимальной (или предельной) петлёй гистерезиса. Ветви б и в называются, соответственно, нисходящей и восходящей ветвями петли гистерезиса. При изменении Н на отрезке [-Н₁, Н₁] с Н₁ <Н_m зависимость М(Н) описывается замкнутой кривой (частной петлёй гистерезиса), целиком лежащей внутри максимальной петли гистерезиса.

Описанные петли гистерезиса характерны для достаточно медленных (квазистатических) процессов перемагничивания. Отставание М от Н при намагничивании и размагничивании приводит к тому, что энергия, приобретаемая магнетиком при намагничивании, не полностью отдаётся при размагничивании. Теряемая за один цикл энергия определяется площадью петли гистерезиса. Эти потери энергии называются гистерезисными. При динамическом перемагничивании образца переменным магнитным полем Н~ петля гистерезиса оказывается шире статической вследствие того, что к квазиравновесным гистерезисным потерям добавляются динамические, которые могут быть связаны с вихревыми токами (в проводниках) и релаксационными явлениями.

Форма петли гистерезиса и наиболее важные характеристики магнитного гистерезиса (гистерезисные потери, Н_с, M_R и др.) зависят от химического состава вещества, его структурного состояния и температуры, от характера и распределения дефектов в образце, а следовательно, от технологии его приготовления и последующих физических обработок (тепловой, механической, термомагнитной и др.). С магнитным гистерезисом связано гистерезисное поведение целого ряда других физических свойств, например гистерезис магнитострикции, гистерезис гальваномагнитных и магнитооптических явлений и так далее.

Сегнетоэлектрический гистерезис — неоднозначная зависимость величины вектора электрической поляризации Р сегнетоэлектриков от напряжённости Е внешнего электрического поля при циклическом изменении последнего. Сегнетоэлектрики обладают в определённом температурном интервале спонтанной (т. е. самопроизвольной, возникающей в отсутствие внешнего поля) поляризацией Р_сп. Направление поляризации может быть изменено электрическим полем, при этом значение Р при данном Е зависит от предыстории, т. е. от того, каким было электрическое поле в предшествующие моменты времени. Сегнетоэлектрический гистерезис имеет вид характерной петли (петля гистерезиса), основными параметрами которой являются остаточная поляризация Р_ост при Е= 0 и коэрцитивное поле Е_к, при котором происходит изменение направления (переключение) вектора Р_сп. Для совершенных монокристаллов петля гистерезиса имеет форму, близкую к прямоугольной, и Р_ОСТ = Р_СП. В реальных кристаллах остаточная поляризация меньше спонтанной из-за разбиения кристалла на домены.

Существование сегнетоэлектрического гистерезиса следует из феноменологической теории сегнетоэлектрических явлений, в соответствии с которой равновесным значениям Р_сп при любой температуре ниже температуры сегнетоэлектрического фазового перехода отвечают два симметричных минимума термодинамического потенциала, разделённые потенциальным барьером. При Е= + Е_к один из минимумов исчезает, и кристалл оказывается в состоянии с определённым направлением вектора Р_сп. При циклическом переключении спонтанной поляризации площадь петли гистерезиса определяет гистерезисные потери — количество энергии электрического поля, переходящей в теплоту. Величина коэрцитивного поля связана также с процессами зарождения и эволюции в электрическом поле сегнетоэлектрических доменов — областей кристалла с выделенным электрическим полем направлением вектора спонтанной поляризации.

Упругий гистерезис — неоднозначная зависимость механического напряжения от деформации упругого тела при циклическом приложении и снятии нагрузки. График зависимости напряжения σ от деформации ε отличается от отрезка прямой линии, соответствующей закону Гука, и представляет собой петлю гистерезиса (рис. 2).

Площадь этой петли пропорциональна механической энергии, которая рассеялась (превратилась в теплоту) во время цикла.

Появление упругого гистерезиса в металлах связано с тем, что в некоторых зёрнах поликристалла микронапряжения существенно превышают средние напряжения в образце, что приводит к появлению пластических деформаций и тем самым к рассеянию механической энергии. В некоторых случаях вклад в упругий гистерезис дают электромагнитные явления.

Упругий гистерезис как проявление отличия реального упругого тела от идеально упругого наблюдается у всех твёрдых тел, даже при весьма низких температурах. Упругий гистерезис является причиной затухания свободных колебаний упругих тел, затухания в них звука, уменьшения коэффициента восстановления при неупругом ударе и др. В общем случае отклонение упругости от идеальной включается в понятие внутреннего трения.

Лит.: Ильюшин А. А., Ленский В. С. Сопротивление материалов. М., 1959; Постников В. С. Внутреннее трение в металлах. 2-е изд. М., 1974. Вонсовский С. В. Магнетизм. М., 1984; Филиппов Б. Н., Танкеев А. П. Динамические эффекты в ферромагнетиках с доменной структурой. М., 1987; Струков Б. А., Леванюк А. П. Физические основы сегнетоэлектрических явлений в кристаллах. М., 1995.

Б. Н. Филиппов, Б. А. Струков, В. Н. Кузнецов.

Петля гистерезиса — обзор

XII Ферромагнитные материалы и их применение

Петля гистерезиса ферромагнитного материала предоставляет информацию о ее полезности в технических приложениях, как описано в Разделе IV. Петля гистерезиса зависит от физического состояния, состава и чистоты образца. В зависимости от области применения ферромагнитного материала важными свойствами являются «проницаемость» и «коэрцитивность».

При холодной деформации материала без деформации проницаемость материала снижается, а гистерезисные потери увеличиваются.Термическая обработка для снятия напряжения холоднодеформированного образца снова возвращает исходные магнитные свойства, например, увеличивается проницаемость и уменьшаются гистерезисные потери. В целом кристаллы без деформации демонстрируют минимальные гистерезисные потери.

Присутствие примесей углерода, кислорода, азота, серы и т.д. влияет на проницаемость и гистерезисные потери ферромагнитного материала. В общем, материалы с высокой проницаемостью и низкими гистерезисными потерями являются чистыми материалами.

Состав ферромагнитного материала также влияет на его магнитные свойства. Добавление кремния к железу увеличивает проницаемость и снижает потери на гистерезис. Однако высокие концентрации кремния уменьшают намагниченность насыщения. Следовательно, сплавы железо-кремний с низкой концентрацией кремния желательны для таких применений, как сердечники трансформаторов, а также электродвигатели и генераторы.

Сплавы железо-никель обладают высокими значениями начальной и максимальной проницаемости и очень низкими потерями на гистерезис по сравнению со сплавами железо-кремний.Сплав состава с 78,5% никеля и 21,5% железа называется пермаллоем и имеет начальную относительную проницаемость ~ 10 000 по сравнению с 250 для чистого железа. Эти сплавы обычно используются для магнитного экранирования электронного оборудования. Небольшие добавки металлов, хрома или молибдена, дополнительно изменяют магнитные свойства этих материалов, которые используются в качестве сердечников в трансформаторах или индукторах, работающих на звуковых или более высоких частотах. Например, магнитопроводы катушек индуктивности и трансформаторов, работающих на радиочастотах (~ 100 Мгц / сек), демонстрируют высокие потери на вихревые токи.Здесь используются ферриты, которые обладают высоким удельным сопротивлением (в ∼10 ⁶ раз больше, чем у металлов) и высокой проницаемостью. В других приложениях требуются ферромагнитные материалы с высоким значением «коэрцитивной силы» и большой площадью петли гистерезиса. Эти материалы обладают жестким магнетизмом по сравнению с уже рассмотренным мягким магнетизмом. Добавление углерода к железу увеличивает потери на гистерезис. Углеродистая сталь раньше использовалась в качестве материала для постоянных магнитов. Однако старение ухудшает магнитные свойства магнитов из углеродистой стали.Добавление металлов, таких как кобальт, хром или вольфрам, улучшает магнитные свойства, и эти материалы менее подвержены старению. Было разработано большое количество сплавов, состоящих из железа, никеля, кобальта, алюминия, меди, платины, марганца и оксидов железа и редкоземельных металлов, которые показывают высокие значения коэрцитивной силы и подходят для постоянных магнитов.

Некоторые оксиды, такие как γ-Fe ₂ O ₃ и CrO ₂ , обладают высокой коэрцитивной силой и используются в качестве записывающих лент в виде слоев тонких порошков.Пермаллои используются для создания индуктивных магнитных головок для записи сигналов в виде остаточной намагниченности на лентах или для воспроизведения электрических сигналов с намагниченных лент. Также используются магниторезистивные считывающие головки на основе пермаллоя. Значительный прогресс был достигнут в разработке очень чувствительных и малых считывающих головок на основе магнитно-немагнитных многослойных систем. Магнитные диски или барабаны производятся для систем памяти в компьютерах. Разработка модификации магнитных свойств путем быстрого затвердевания сплавов из расплава создала новую область.Быстрое затвердевание может повлиять на микроструктуру — в некоторых случаях фазы могут быть мелкодисперсными, а в других сплавы могут стать некристаллическими или аморфными. Аморфные сплавы не имеют кристаллической решетки и магнитной анизотропии.

В этих некристаллических материалах нет протяженных дефектов, которые в противном случае сильно взаимодействовали бы с доменными стенками. В некоторых некристаллических сплавах на основе кобальта магнитострикция может быть доведена до нуля, так что внутренние и приложенные напряжения оказывают минимальное влияние на магнитные свойства.Аморфные магнитные сплавы обладают высокой твердостью, пределом текучести и магнитомягкостью. В частности, кобальтсодержащие сплавы обладают исчезающе малой магнитострикцией. Сочетая в себе хорошие механические и магнитные свойства, они являются очень полезными материалами. Их можно упруго деформировать в широких пределах, они нечувствительны к необратимым магнитным повреждениям и являются очень подходящими материалами, где желательна упругая деформируемость. Они также являются полезными материалами для изготовления записывающих головок в системах записи звука, видео и данных из-за их хорошей высокочастотной характеристики и износостойкости.

Магнитомягкие и высокоэластичные механические свойства привели к разработке гибкого магнитного экранирования.

Аморфные магнитные материалы состоят из двух основных групп. В одной группе материалы состоят из переходных металлов и металлоидов; во второй группе они состоят только из разных металлов. Некоторые аморфные материалы, используемые в качестве магнитомягких материалов: Fe ₈₁ (Si B, C) ₁₉ ; (FeNi) ₇₈ (Mo, Si, B) ₂₂ ; (Co, Fe) ₇₀ … ₇₆ (Mo, Si, B) ₃₀ … ₂₄ ; и (Co, Mn) ₇₀ … ₇₆ (Mo, Si, B) ₃₀ … ₂₄ .

Магнитотвердые материалы также могут быть произведены методами быстрого затвердевания. Например, магнитный материал состава Fe ₁₄ Nd ₂ B, полученный путем быстрого затвердевания, превосходит материал Co-Sm. Другие магнитотвердые материалы (некоторые переходные и редкоземельные металлы, а также бор) также производятся путем быстрого охлаждения. Метод быстрого охлаждения также дешевле по сравнению с обычными методами.

Магнитный гистерезис — Engineering LibreTexts

1. Последнее обновление

2. Сохранить как PDF

1. Структура петли гистерезиса
2. Вариации петель гистерезиса
3. Важность петель гистерезиса
4. Вопросы
5. Ответы
6. Ссылки
7. Участники и атрибуты

A Магнитный гистерезис петля, иначе известная как петля гистерезиса , иначе известная как петля гистерезиса представляет собой зависимость силы намагничивания (H) от плотности магнитного потока (B) ферромагнитного материала.Кривизна гистерезиса характерна для типа наблюдаемого материала и может различаться по размеру и форме (то есть узкая или широкая). Петля может быть создана с помощью датчика Холла для измерения величины магнитного поля в различных точках — в присутствии магнитного поля, когда оно удаляется из магнитного поля и когда прикладывается сила, приводящая к магнитному полю. поток обратно к нулю. Эти петли важны для емкости памяти устройств для аудиозаписи или магнитного хранения данных на дисках компьютера.

Рисунок \ (\ PageIndex {1} \): б). Эти дипольные моменты настолько упорядочены, что при удалении от магнитного поля остается некоторая остаточная намагниченность. Чтобы уменьшить магнитный поток до нуля, необходимо применить коэрцитивную силу, при которой дипольные моменты компенсируют друг друга. Таким образом, эта петля гистерезиса суммирует путь, который проходит ферромагнитный материал от добавления и удаления намагничивающей силы.

Структура петли гистерезиса

Рисунок 3, на котором спины начинают дезориентироваться, затем выравниваются с магнитным полем и, наконец, смещаются до тех пор, пока моменты не уравняются друг с другом, чтобы не создавать результирующий магнитный момент.Также обратите внимание, что кривая никогда не возвращается в начало координат (B и H = 0). Чтобы вернуться к этому моменту, материал необходимо размагнитить (то есть вернуться к парамагнитным свойствам), ударив материал по поверхности, изменив направление намагничивающего поля или нагревая его до температуры Нееля. При этой температуре ферромагнитный материал становится парамагнитным из-за тепловых флуктуаций магнитных дипольных моментов, которые дезориентируют спины.

Варианты петель гистерезиса

Таблица 1.Температура насыщения ферромагнитных материалов Fe, Co и Ni при 0 К.

Металл	Hs [А / м]
Fe	1,75 х 10 6
Co	1,45 x 10 6
Ni	0,51 х 10 6

Рисунок \ (\ PageIndex {4} \):.

Важность петель гистерезиса

Петли гистерезиса важны в конструкции нескольких электрических устройств, которые подвержены быстрому изменению магнетизма или требуют хранения в памяти.Магнитомягкие материалы (то есть материалы с меньшими и более узкими областями гистерезиса) и их быстрое изменение магнетизма полезны в электрическом оборудовании, которое требует минимального рассеивания энергии. Трансформаторы и сердечники, используемые в электродвигателях, получают выгоду от использования этих материалов, поскольку они теряют меньше энергии в виде тепла. Твердые магнитные материалы (т. Е. Петли с большей площадью) имеют гораздо более высокую удерживающую способность и коэрцитивную силу. Это приводит к более высокой остаточной намагниченности, полезной в постоянных магнитах, где трудно добиться размагничивания.Жесткие магнитные материалы также используются в устройствах памяти, таких как аудиозаписи, дисководы компьютеров и кредитные карты. Высокая коэрцитивная сила этих материалов не позволяет легко стереть память.

Вопросы

1. Обозначьте следующую петлю гистерезиса.

2. Какими 3 способами размагнитить ферромагнитный материал?

3. Какой из этих элементов (Fe, Co, Cr, Ni) не будет создавать петлю гистерезиса? Почему?

ответы

1.а) Точка насыщения — HS

б) Точка удержания —

руб.

c) Точка коэрцитивности — Hc

2. Ударьте ферромагнитным материалом о поверхность, чтобы дезориентировать магнитные дипольные моменты, изменить направление петли гистерезиса, нагреть материал выше его критической температуры.

3. Cr не создает петли гистерезиса, потому что он антиферромагнитен. Fe, Co и Ni являются ферромагнитными и поэтому создают петлю гистерезиса.

Список литературы

1. Хаммель, Рольф Э. Электронные свойства материалов: введение для инженеров. Берлин: Springer-Verlag, 1985. Печать.
2. Чиказуми, Сошин и К.Д. Грэм. Физика ферромагнетизма. Оксфорд: Кларедон, 1997. Печать.
3. Раллс, Кеннет М., Томас Х. Кортни и Джон Вульф. Введение в материаловедение и инженерию. Нью-Йорк: Wiley, 1976. Печать.
4. Бертотти, Джорджо. Гистерезис в магнетизме: для физиков, материаловедов и инженеров. Сан-Диего: Академический, 1998. Печать.

Авторы и авторство

• Саманта Дрис (бакалавр материаловедения и инженерии, Калифорнийский университет в Дэвисе | июнь 2016 г.)

Что такое петля гистерезиса? Что такое потеря гистерезиса?

Что такое петля гистерезиса, потеря гистерезиса

В этом посте давайте посмотрим, что подразумевается под петлей гистерезиса и что подразумевается под потерей гистерезиса ….
Перед этим настоятельно рекомендуется прочитать термины, относящиеся к магнитным цепям.
Нажмите здесь, чтобы узнать больше о терминологии магнитных цепей

Что такое петля гистерезиса?

Рассмотрим полностью размагниченный ферромагнитный материал. [Полностью размагниченный материал — это материал, в котором B = H = 0].
Он будет подвергаться воздействию возрастающих значений напряженности магнитного поля H и соответствующей измеренной плотности магнитного потока B.

Результат показан на рисунке ниже кривой o-a-b.
В точке b, если напряженность поля (H) будет увеличиваться дальше, плотность потока (B) больше не будет увеличиваться.
Это называется насыщением (материал называется насыщенным). На этом рисунке b-y называется плотностью потока насыщения.

Теперь, если напряженность поля (H) уменьшится, плотность потока (B) будет следовать кривой b-c.
Когда напряженность поля (H) уменьшается до нуля, магнитный поток остается в железе.
Это называется остаточной магнитной индукцией или остаточной магнитной индукцией.
Обозначается на рисунке как o-c.

• Теперь, если H увеличивается в противоположном направлении, плотность потока уменьшается.
• Уменьшится до точки d. Здесь плотность потока (B) равна нулю.
• Напряженность магнитного поля (точки от 0 до d), необходимая для удаления остаточного магнетизма, т.е. уменьшения B до нуля. Это называется принудительной силой.
• Теперь, если H увеличивается дальше в обратном направлении, плотность магнитного потока увеличивается в обратном направлении до точки насыщения (здесь точка-е).
• Если H изменяется в обратном направлении от 0x до 0y, плотность потока (B) следует кривой e-f-g-b, аналогично кривой b-c-d-e.
• Из рисунка видно, что изменение плотности потока отстает от изменения напряженности магнитного поля.
• Этот эффект называется Гистерезис.
• Замкнутая фигура b-c-d-e-f-g-b называется петлей гистерезиса (или петлей B / H) .

Потеря гистерезиса:

Что означает потеря гистерезиса?

Нарушение выравнивания доменов (домены — это не что иное, как группы атомов. Домены микроскопических размеров, но достаточно велики, чтобы вмещать от 1017 до 1021 атома) ферромагнитного материала вызывает расход энергии на его прохождение через цикл намагничивания.


(Если поля доменов в ферромагнитном материале совпадают, материал намагничивается; если они ориентированы случайным образом, тогда ферромагнитный материал не намагничивается.)
Эта энергия проявляется в образце в виде тепла и называется потерей гистерезиса .

Потери энергии, связанные с гистерезисом, пропорциональны площади петли гистерезиса.

• Площадь петли гистерезиса зависит от типа материала.
• Для твердых материалов площадь петли гистерезиса велика и, следовательно, потери на гистерезис также больше.
• Петля гистерезиса для твердых материалов имеет высокую намагничиваемость (0-c) и большую коэрцитивную силу (0-d).
• Для мягких материалов площадь петли гистерезиса мала, и поэтому потери на гистерезис меньше.
• Петля гистерезиса для мягкой стали имеет большую намагничиваемость и небольшую коэрцитивную силу.
• Для твердых материалов площадь и, следовательно, потери энергии намного больше, чем потери энергии для мягких материалов.
• Потери на гистерезис для феррита (оксидов алюминия, железа, кобальта, магния, никеля и маргенеза очень малы.

Петля гистерезиса для устройств, возбуждаемых переменным током, повторяется каждый цикл переменного тока.
Таким образом, материал с большой площадью петли гистерезиса не подходит, так как потери энергии больше.
Кремниевая сталь имеет небольшую площадь петли гистерезиса, поэтому потери на гистерезис меньше.
Подходит для сердечников трансформаторов и якоря вращающихся машин.

Подробнее:
Методы управления скоростью асинхронного двигателя
Как работает звонок Bell?
В чем разница между диодом Шоттки и диодом с PN переходом?
555 Идеи для простых проектов на основе таймера

Спасибо за чтение… Пожалуйста, оставляйте свои комментарии ниже …. Пожалуйста, подпишитесь, чтобы получать новые сообщения на свой электронный адрес ..

Петля гистерезиса

Петля гистерезиса
Далее: Домены Up: Микромагнитные системы Предыдущий: Микромагнитные системы Содержание

Петля гистерезиса Отличительной чертой магнитной системы является петля гистерезиса . Этот традиционно представляется графически как общая намагниченность образца против некоторого приложенного магнитного поля.Значение приложенное поле, в котором петля пересекает нулевую намагниченность, известно как коэрцитивное поле или , и, следовательно, представляет собой величина приложенного поля, необходимого для обратного намагничивания направление магнита. Остаточная намагниченность намагничивание, которое сохраняется, когда приложенное поле уменьшается до нуля. Коэрцитивное поле т.е. приложенное поле где общая намагниченность образца равна нулю Коэрцитивное поле i.е. прикладное поле где общая намагниченность образца равна нулю ( ) Остаточная намагниченность , т.е. величина намагничивание образца при нулевом приложенном магнитном поле

Сравнение петель гистерезиса, показанных на рисунке 2.10, из мягкого и жесткого магнита можно обратите внимание, что более мягкий магнит будет иметь узкую петля гистерезиса, т.е. приложенное поле, необходимое для реверсирования намагничивание относительно низкое, и жесткий магнит будет обладают сравнительно широкой петлей гистерезиса.

Точка, в которой общая намагниченность образца больше не может быть увеличенным (так как вся намагниченность полностью направлена ​​в один направление) — насыщенность точка или — идентифицируется как плато на крайних точках приложенного поля в петле гистерезиса. Точка насыщения , т.е. величина максимально возможного намагничивания образца

Также следует отметить, что площадь под петлей гистерезиса составляет эквивалентной энергии, которая при изменении поля на противоположное равна превращается в тепло.

Для длительного хранения данных желательно наличие материала с широкой петлей гистерезиса и, следовательно, большим коэрцитивным полем, так как это затрудняет потерю указанного материала состояние намагниченности. Узкая петля гистерезиса — характеристика полезно для таких приложений, как записывающие головки, как в этих временное намагничивание способствует легкому переключению между намагничиванием состояния. Идеальные петли гистерезиса для приложений с магнитными носителями можно увидеть на рисунке 2.11.

.

Рисунок 2.10: Две типичные петли гистерезиса — левая петля показывает какой-то постоянный магнитный материал, правая петля — более мягкий магнит. Сплошная синяя линия указывает на уменьшающееся поле, пунктирная красная линия указывает на увеличивающееся поле

Рисунок 2.11: Идеалы магнитной записи. Квадратный цикл с высокой коэрцитивностью хорош для длительного хранения данных; бесконечно узкая петля с диагональными характеристиками желательна для переключения поля, необходимого для считывающих головок в магнитных носителях

---

Далее: Домены Up: Микромагнитные системы Предыдущий: Микромагнитные системы Содержание

Ричард Бордман 2006-11-28

Область, ограниченная петлей гистерезиса, соответствует физическому классу 12 CBSE

Подсказка: Петля гистерезиса проявляется только в ферромагнитных материалах.Он показывает, как магнитное поле в ферромагнитном материале изменяется в соответствии с магнитной напряженностью. Материал многократно намагничивается и размагничивается, что приводит к потере энергии.

Полный пошаговый ответ.
Шаг 1. Нарисуйте петлю гистерезиса ферромагнитного материала.
На приведенном ниже рисунке изображена петля гистерезиса ферромагнитного материала.

На приведенном выше рисунке $ B $ — это магнитное поле в материале, а $ H $ — магнитная напряженность.Кривая $ {\ text {ob}} $ отмечает рост и насыщение магнитного поля $ B $ в материале. Затем поле уменьшается по $ {\ text {bc}} $ по мере уменьшения $ H $. Точка $ c $ представляет магнитное поле в материале, когда $ H = 0 $. Это называется сохраняемостью. Чтобы получить $ B = 0 $, интенсивность меняется на противоположную и увеличивается вдоль $ {\ text {cd}} $. При $ d $ имеем $ B = 0 $. Это называется принуждением. Теперь, чтобы достичь насыщения в обратном направлении, интенсивность увеличивают в отрицательном направлении вдоль $ {\ text {de}} $.Уменьшение обратной интенсивности дает удерживающую способность $ f $ в отрицательном направлении, а увеличение в положительном направлении сделает поле нулевым при $ g $. Снова насыщенность достигается по $ {\ text {gb}} $. Это составляет один цикл.

Таким образом, материал намагничивается и размагничивается за один цикл. При этом теряется энергия. Потерянная энергия выделяется как тепло и называется гистерезисными потерями. Площадь петли представляет собой потерю энергии за один цикл.

Следовательно, правильный вариант — D.

Примечание: Узкая петля гистерезиса указывает на меньшую потерю энергии, а широкая петля указывает на большую потерю энергии. Сердечник трансформатора должен иметь минимальные потери энергии, поэтому для него предпочтительны материалы с узким гистерезисом, такие как мягкое железо. Однако для изготовления постоянных магнитов мы выбираем материалы с высокой удерживающей способностью, чтобы они были сильными, и с высокой коэрцитивной силой, чтобы их нельзя было легко размагнитить.

Важность петли гистерезиса — Inst Tools

Потеря гистерезиса:

Когда магнитный материал подвергается циклу намагничивания (сначала намагничивается в одном направлении, а затем циклически намагничивается в противоположном направлении), происходит потеря энергии.Эта потеря энергии происходит из-за молекулярного трения в материале. То есть домены (или молекулярные магниты) материала сначала поворачиваются в одном направлении, а затем в другом. Таким образом, на преодоление этого противостояния в материале расходуется энергия. Эта потеря происходит в виде тепла и называется потерей гистерезиса .

Потери на гистерезис присутствуют во всех электрических машинах, железные части которых подвергаются циклу намагничивания, например, трансформаторы, асинхронные двигатели и другие машины, работающие от источника переменного тока.Когда на электрические машины подается переменное питание, магнитный поток в железе этих машин изменяется как в направлении, так и в величине поочередно. Во время этого процесса теряется энергия, и эти потери составляют потери в сердечнике машины. Очевидным эффектом потери гистерезиса является повышение температуры машины

• Трансформаторы и большинство электрических машин работают на переменном токе. В таких устройствах поток в железе непрерывно изменяется как по величине, так и по направлению.Следовательно, в этих машинах возникают потери на гистерезис
• Потери на гистерезис также возникают, когда железные части вращаются в постоянном магнитном поле, например, машины постоянного тока

Петля гистерезиса или область петли B-H:

Петля гистерезиса получается путем построения графика B-H (B: плотность потока, H: сила намагничивания) железа для одного цикла намагничивания.

Когда сердечник машины, такой как трансформатор, асинхронные двигатели, намагничивается силой намагничивания (H) за счет приложения напряжения, плотность магнитного потока (B) увеличивается, как показано на рисунке (пунктирные линии), и насыщается (первый квадрант).Область насыщения в той, в которой увеличение силы намагничивания (H) не приведет к дальнейшему заметному увеличению плотности магнитного потока (B) в материале.

Когда приложенное напряжение возвращается к нулевому положению от пика (первый полупериод), сила намагничивания также становится нулевой. Однако плотность магнитного потока в сердечнике не будет достигать нуля, а будет иметь некоторое конечное значение. Это свойство магнитного материала удерживать некоторый поток (B), когда сила намагничивания становится равной нулю, называется удерживающей способностью .

В течение следующего полупериода все домены в магнитопроводе пытаются выровняться в противоположном направлении по мере изменения полярности приложенного напряжения и, следовательно, приложенной силы намагничивания. С увеличением намагничивающей силы (H) достигается точка, в которой плотность магнитного потока (B) становится равной нулю. Эта точка называется коэрцитивной силой . За пределами этой точки магнитный поток будет в противоположном направлении с увеличением напряженности поля и достигнет насыщения, как показано на рисунке (третий квадрант).

Далее приложенное магнитное поле начнет уменьшаться от пика до нуля. Это уменьшение магнитного потока с уменьшением напряженности поля можно увидеть на рисунке (третий квадрант) и возвращается при изменении полярности напряжения.

Это образует петлю B-H петли гистерезиса магнитного материала машин

Важность или значение петли B-H:

Форма и размер петли гистерезиса во многом зависят от природы магнитного материала.Выбор магнитного материала, необходимого для конкретного применения, часто зависит от формы и размера петли гистерезиса.

• Чем меньше площадь петли гистерезиса магнитного материала, тем меньше потери на гистерезис. Например, площадь петли гистерезиса для кремнистой стали очень мала, по этой причине кремнистая сталь широко используется для изготовления сердечников трансформаторов и вращающихся машин, которые подвержены быстрому изменению магнетизма.
• Петля гистерезиса для твердой стали (большая площадь петли гистерезиса) указывает на то, что материал имеет высокую удерживающую способность и коэрцитивную силу.Поэтому твердая сталь очень полезна для изготовления постоянных магнитов. Но из-за большой площади гистерезисные потери довольно велики. По этой причине твердая сталь не используется для изготовления электрических машин.

Методы уменьшения петли гистерезиса или петли B-H:

Петля гистерезиса может быть выполнена за счет использования магнитомягких материалов (например, магнитного материала сердечника CRGO в трансформаторах), имеющего меньшую петлю для уменьшения потерь на гистерезис.

% PDF-1.6 % 133 0 объект > эндобдж xref 133 119 0000000016 00000 н. 0000003616 00000 н. 0000003853 00000 н. 0000003976 00000 н. 0000004370 00000 н. 0000004397 00000 н. 0000004536 00000 н. 0000004696 00000 н. 0000004909 00000 н. 0000005139 00000 п. 0000005591 00000 н. 0000005759 00000 п. 0000005796 00000 н. 0000006209 00000 н. 0000006287 00000 н. 0000007799 00000 н. 0000008219 00000 п. 0000008300 00000 н. 0000008677 00000 н. 0000008795 00000 н. 0000008872 00000 н. 0000011592 00000 п. 0000015327 00000 п. 0000047500 00000 п. 0000048688 00000 н. 0000051973 00000 п. 0000052260 00000 п. 0000057786 00000 п. 0000058069 00000 п. 0000067147 00000 п. 0000067430 00000 п. 0000069181 00000 п. 0000069454 00000 п. 0000072051 00000 п. 0000072312 00000 п. 0000072574 00000 п. 0000072980 00000 п. 0000073199 00000 п. 0000073510 00000 п. 0000073566 00000 п. 0000076293 00000 п. 0000076627 00000 н. 0000076684 00000 п. 0000076793 00000 п. 0000076865 00000 п. 0000077018 00000 п. 0000077136 00000 п. 0000077191 00000 п. 0000077321 00000 п. 0000077376 00000 п. 0000077558 00000 п. 0000077646 00000 п. 0000077701 00000 п. 0000077898 00000 п. 0000077985 00000 п. 0000078040 00000 п. 0000078239 00000 п. 0000078339 00000 п. 0000078394 00000 п. 0000078495 00000 п. 0000078678 00000 п. 0000078779 00000 п. 0000078834 00000 п. 0000078934 00000 п. 0000079114 00000 п. 0000079216 00000 п. 0000079271 00000 п. 0000079371 00000 п. 0000079535 00000 п. 0000079622 00000 п. 0000079677 00000 п. 0000079842 00000 п. 0000079942 00000 н. 0000079997 00000 н. 0000080097 00000 п. 0000080243 00000 п. 0000080298 00000 п. 0000080479 00000 п. 0000080568 00000 п. 0000080623 00000 п. 0000080772 00000 п. 0000080827 00000 п. 0000080957 00000 п. 0000081012 00000 п. 0000081142 00000 п. 0000081197 00000 п. 0000081326 00000 п. 0000081374 00000 п. 0000081503 00000 п. 0000081551 00000 п. 0000081713 00000 п. 0000081761 00000 п. 0000081927 00000 н. 0000082015 00000 н. 0000082062 00000 н. 0000082110 00000 п. 0000082165 00000 п. 0000082220 00000 н. 0000082334 00000 п. 0000082389 00000 п. 0000082444 00000 п. 0000082499 00000 н. 0000082554 00000 п. 0000082609 00000 п. 0000082664 00000 п. 0000082777 00000 н. 0000082832 00000 н. 0000082887 00000 п. 0000082942 00000 п. 0000082997 00000 п. 0000083052 00000 п. 0000083107 00000 п. 0000083209 00000 п. 0000083256 00000 п. 0000083358 00000 п.