Равномерное движение материальной точки по окружности. Период вращения » Народна Освіта

Более 5000 лет назад жрецы древнего Вавилона, наблюдая за Луной, определили такой хорошо известный нам интервал времени, как неделя. Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение? В данном параграфе вы найдете ответы на эти и многие другие вопросы.

 

Знакомимся с движением по окружности

Попробуйте представить линию, вдоль которой движутся ребенок, кружащийся на карусели, носок в барабане стиральной машины во время отжима, кончик ножа блендера при изготовлении коктейля или смузи. Уверены, что вы легко определили: этой линией является окружность. Итак, в перечисленных случаях имеем дело с движением по окружности; простейшим является равномерное движение по окружности. Далее, говоря о равномерном движении по окружности любого физического тела, будем считать это тело материальной точкой.

Равномерно по окружности движутся, например, кабинки колеса обозрения. Близким к равномерному движению по окружности является движение планет вокруг Солнца (рис. 12.1, а), естественного спутника (Луны) или искусственных спутников вокруг Земли* (рис. 12.1, б).

Приведите примеры движения по окружности. В каких случаях это движение можно считать равномерным? Можно ли считать движение точек обода колеса велосипеда относительно его рамы равномерным движением по окружности? Обоснуйте свой ответ.

 

Точнее — планеты и спутники движутся по эллиптическим орбитам.

 

 

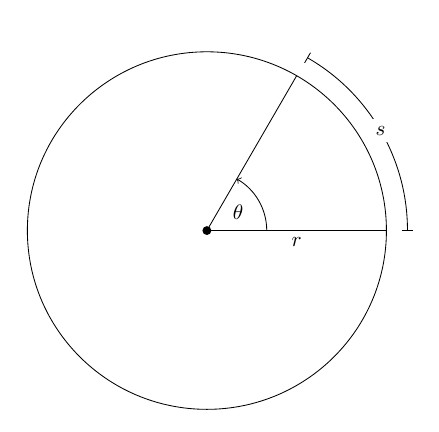
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь.

Определяем период вращения

Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные равные интервалы времени. Например, кончик секундной стрелки часов, двигаясь равномерно вдоль циферблата, повторяет свое движение через каждые 60 с (рис. 12.2).

Любое периодическое движение характеризуется такими физическими величинами, как период и частота. При равномерном движении по окружности говорят о периоде вращения и частоте вращения.

Период вращения — это физическая величина, равная времени, за которое материальная точка, равномерно движущаяся по окружности, совершает один оборот.

Период вращения обозначают символом T.

Единица периода вращения в СИ — секунда:

Период вращения равен одной секунде, если за одну секунду совершается один оборот.

Кончик секундной стрелки часов совершает один оборот за 60 с, поэтому период его вращения, как и каждой точки секундной стрелки, равен 60 с (( = 60 с).

Подумайте, каковы периоды вращения точек минутной и часовой стрелок часов. Когда взбивают молочный коктейль блендером, каждая точка его ножа за 30 с делает 6000 оборотов (рис. 12.3). Чтобы определить время одного оборота, нужно

 

Вращательное движение тела. Закон вращательного движения :: SYL.ru

В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».

Основные понятия кинематики вращательного движения

Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.

Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.

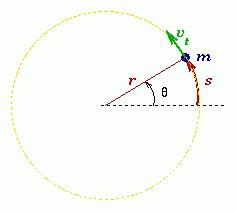
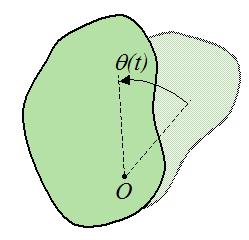
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.

Через некоторое время радиус повернется относительно исходного положения на угол Δφ.

За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:

φ = φ(t).

Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:

ΔS = Δφr.

Основные элементы кинематики равномерного вращательного движения

Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.

Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:

ω = dφ/dt.

Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле

ω = φ/t.

Согласно предварительной формуле размерность угловой скорости

[ω] = 1 рад/с.

Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то

ω = 2π/T,

поэтому период вращения определим следующим образом:

T = 2π/ω.

Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:

ν = 1/T.

Единицы измерения частоты: [ν]= 1/c = 1 c^-1 = 1 Гц.

Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:

ω = 2πν.

Основные элементы кинематики неравномерного вращательного движения

Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.

Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:

ε = dω/dt.

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.

Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.

Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).

Связь величин, характеризующих поступательное и вращательное движение

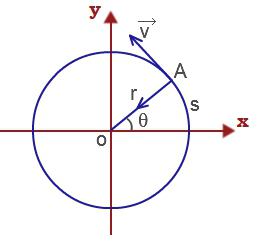
Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением

ΔS = Δφ r.

Тогда линейная скорость материальной точки, выполняющей вращательное движение

υ = ΔS/Δt = Δφr/Δt = ωr.

Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:

a = υ²/r = ω²r²/r.

Итак, в скалярном виде

a = ω²r.

Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение

a = ε r.

Момент импульса материальной точки

Векторное произведение радиуса-вектора траектории материальной точки массой m_i на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.

Момент импульса материальной точки (L_i) направлен перпендикулярно плоскости, проведенной через r_i и υ_i, и образует с ними правую тройку векторов (то есть при движении с конца вектора r_iк υ_i правый винт покажет направление вектора L_i).

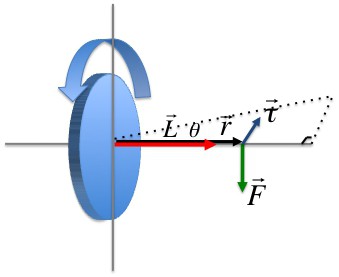
В скалярной форме

L = m_iυ_ir_isin(υ_i,r_i).

Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,

sin(υ_i,r_i) = 1.

Так что момент импульса материальной точки для вращательного движения примет вид

L = m_iυ_ir_i.

Момент силы, которая действует на i-ю материальную точку

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме

M_i = r_iF_isin(r_i, F_i).

Считая, что r_isinα = l_i, M_i = l_iF_i.

Величина l_i, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы F_i.

Динамика вращательного движения

Уравнение динамики вращательного движения записывается так:

M = dL/dt.

Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.

Момент импульса и момент инерции

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой

L_i = m_iυ_ir_i.

Если вместо линейной скорости подставить ее выражение через угловую:

υ_i = ωr_i,

то выражение для момента импульса примет вид

L_i = m_ir_i²ω.

Величина I_i = m_ir_i² называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:

L_i = I_iω.

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:

L = Iω.

Момент силы и момент инерции

Закон вращательного движения гласит:

M = dL/dt.

Известно, что представить момент импульса тела можно через момент инерции:

L = Iω.

Тогда

M = Idω/dt.

Учитывая, что угловое ускорение определяется выражением

ε = dω/dt,

получим формулу для момента силы, представленного через момент инерции:

M = Iε.

Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.

Теорема Штейнера. Закон сложения моментов инерции

Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I₀ + ma²,

где I₀ — начальный момент инерции тела; m — масса тела; a — расстояние между осями.

Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).

Период вращения — Википедия. Что такое Период вращения

Материал из Википедии — свободной энциклопедии

«»

Период вращения космического объекта — это время, которое требуется объекту для совершения полного оборота вокруг своей оси(относительно звезд)

Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.

Период вращения Земли относительно точки весеннего равноденствия называется звёздными сутками^[1].

Периоды вращения некоторых объектов:

Объект	Период
Солнце	25,379995 дня[2][3]	25.379995
Меркурий	58,6462 дня[4]	58.6462
Венера	243,0187 дня (ретроградное)[4]	243.0187
Земля	0,99726968 дня[4]	0.99726968
Луна	27,321661 дня[5]	27.321661
Марс	1,02595675 дня[4]	1.02595675
Юпитер	0,41354 дня[4]	0.41354
Сатурн	0,44401 дня[4]	0.44401
Уран	0,71833 дня (ретроградное)[4]	0.71833
Нептун	0,67125 дня[4]	0.67125
Плутон	6,38718 дня (ретроградное)[4]	6.38718

См. также

Примечания

1. ↑ К. В. Куимов. Вращение Земли и продолжительность суток (рус.). ГАИШ, Москва (6 февраля 2008). Проверено 20 июля 2010. Архивировано 3 марта 2012 года.
2. ↑ P. K. Seidelmann, V. K. Abalakin, M. Bursa, M. E. Davies, C. de Bergh, J. H. Lieske, J. Oberst, J. L. Simon, E. M. Standish, P. Stooke, P. C. Thomas (2002). «Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites: 2000». Celestial Mechanics and Dynamical Astronomy 82 (1): 86.
3. ↑ Равен 360° делить на коэффициент при d в выражении для W.
4. ↑ ^{1 2 3 4 5 6 7 8 9} Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — P. 296. — ISBN 0-387-98746-0.
5. ↑ Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities. — Springer, 2000. — P. 308. — ISBN 0-387-98746-0.

Период вращения Википедия

Период вращения космического объекта — время, которое требуется объекту для совершения полного оборота вокруг своей оси относительно звёзд.

Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.

Период вращения Земли относительно точки весеннего равноденствия называется звёздными сутками^[1].

Периоды вращения некоторых объектов:

Объект	Период
Солнце	25,379995 дня[2][3]	25.379995
Меркурий	58,6462 дня[4]	58.6462
Венера	243,0187 дня (ретроградное)[4]	243.0187
Земля	0,99726968 дня[4]	0.99726968
Луна	27,321661 дня[5]	27.321661
Марс	1,02595675 дня[4]	1.02595675
Юпитер	0,41354 дня[4]	0.41354
Сатурн	0,44401 дня[4]	0.44401
Уран	0,71833 дня (ретроградное)[4]	0.71833
Нептун	0,67125 дня[4]	0.67125
Плутон	6,38718 дня (ретроградное)[4]	6.38718

См. также[ | ]

Примечания[ | ]

1. ↑ К. В. Куимов. Вращение Земли и продолжительность суток (рус.). Астронет (6 февраля 2008). Дата обращения 20 июля 2010.
2. ↑ P. K. Seidelmann, V. K. Abalakin, M. Bursa, M. E. Davies, C. de Bergh, J. H. Lieske, J. Oberst, J. L. Simon, E. M. Standish, P. Stooke, P. C. Thomas. Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites: 2000 (англ.) // Celestial Mechanics and Dynamical Astronomy : journal. — 2002. — Vol. 82, no. 1. — P. 86.
3. ↑ Равен 360° делить на коэффициент при d в выражении для W.
4. ↑ ^{1 2 3 4 5 6 7 8 9} Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities (неопр.). — Springer, 2000. — С. 296. — ISBN 0-387-98746-0.
5. ↑ Clabon Walter Allen, Arthur N. Cox. Allen’s Astrophysical Quantities (неопр.). — Springer, 2000. — С. 308. — ISBN 0-387-98746-0.

Прецессия — Википедия

Прецессия земной оси вокруг Северного полюса эклиптики

Преце́ссия — явление, при котором момент импульса тела меняет своё направление в пространстве.

Следует, однако, понимать, что ось вращения — не то же самое, что направление момента импульса; хотя момент импульса тела имеет свойство сохраняться (в отсутствие внешних воздействий), вращение твёрдого тела может происходить либо вокруг этого вектора (например, у тел, обладающих определённой симметрией), либо ось вращения будет постоянно менять своё направление.

Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем она постепенно отклоняется от вертикали и начинает описывать конус. Это движение, выполняемое помимо собственного вращения вокруг оси волчка, и называется прецессией оси волчка.^[1] С уменьшением скорости вращения волчка его верхняя точка постепенно опускается и движется по расходящейся спирали.

Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а ось вращения волчка займёт неподвижное положение в пространстве. В примере с волчком, вращающимся в гравитационном поле Земли, этого не произойдёт, поскольку вызывающее прецессию воздействие — комбинация гравитации Земли и давления поверхности стола — постоянно действует.

Можно получить эффект прецессии, не дожидаясь замедления вращения волчка: толкните его ось (приложите силу) — начнётся прецессия. С прецессией напрямую связан другой эффект, показанный на иллюстрации ниже: это нутация — колебательные движения оси прецессирующего тела. Скорость прецессии и амплитуда нутации связаны со скоростью вращения тела (изменяя параметры прецессии и нутации в случае, если есть возможность приложить силу к оси вращающегося тела, можно изменить скорость его вращения).

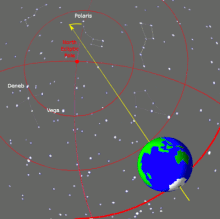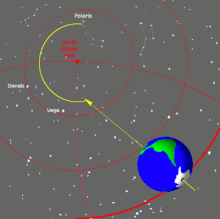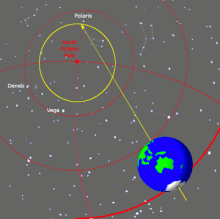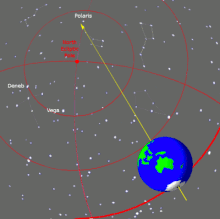
Подобное движение совершает ось вращения Земли, что было отмечено Гиппархом как предварение равноденствий. По современным данным, полный цикл земной прецессии (прецессионный тур) составляет около 25 765 лет, что соответствует частоте прецессии 1,23 пикогерц.

Колебание оси вращения Земли влечёт изменение положения звёзд относительно экваториальной системы координат. В частности, через некоторое время Полярная звезда перестанет быть ближайшей к северному полюсу мира яркой звездой, а Турайс будет Южной Полярной звездой примерно в 8100 году н. э.

Предположительно^[2], с прецессией связано периодическое изменение климата Земли^[3].

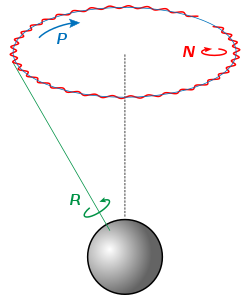
Рис.1 Прецессия велосипедного колеса

В основе объяснения явления прецессии лежит экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела L→{\displaystyle {\vec {L}}} прямо пропорциональна величине приложенного к телу момента силы M→{\displaystyle {\vec {M}}}:

dL→dt=M→{\displaystyle {\frac {d{\vec {L}}}{dt}}={\vec {M}}}

Пример[править | править код]

На рис. 1 изображено вращающееся велосипедное колесо, висящее на двух нитях a{\displaystyle a}и b{\displaystyle b}. Вес колеса уравновешивается силами, вызванными деформациями нитей. Колесо обладает моментом импульса L→{\displaystyle {\vec {L}}}, направленным по его оси, и в том же направлении направлен вектор угловой скорости вращения колеса ω→{\displaystyle {\vec {\omega }}}.

Пусть в некоторый момент времени нить b{\displaystyle b} будет разрезана. В таком случае, вопреки ожиданиям, вращающееся колесо не изменит горизонтального направления своей оси и, подобно маятнику, не будет качаться на нити a{\displaystyle a}. Но его ось начнёт поворачиваться в горизонтальной плоскости благодаря действию на него момента M→{\displaystyle {\vec {M}}} силы тяжести P{\displaystyle P}:

 r→×P→=M→{\displaystyle \ {\vec {r}}\times {\vec {P}}={\vec {M}}}, где r→{\displaystyle {\vec {r}}}- радиус-вектор центра масс вращающегося тела относительно точки крепления на нити a{\displaystyle a}.

Поскольку

dL=dφL(t){\displaystyle dL={d\varphi }{L(t)}} и dL=Mdt{\displaystyle dL=Mdt} , то dφdt=ML{\displaystyle {\frac {d\varphi }{dt}}={\frac {M}{L}}}

и, так как угловая скорость прецессии: ωp{\displaystyle \omega _{p}} равна: dφdt=ωp{\displaystyle {\frac {d\varphi }{dt}}=\omega _{p}}, получаем: ωp=ML{\displaystyle \omega _{p}={\frac {M}{L}}} или, с учётом того, что L=Iω{\displaystyle L=I\omega }, где I{\displaystyle I} есть момент инерции колеса: ωp=MIω{\displaystyle \omega _{p}={\frac {M}{I\omega }}}^[4]

Формальное объяснение такого поведения вращающегося колеса заключается в том, что вектор приращения момента количества движения dL{\displaystyle dL} всегда перпендикулярен вектору L→{\displaystyle {\vec {L}}}, кроме того, он всегда параллелен вектору момента силы тяжести M→{\displaystyle {\vec {M}}}, находящегося в горизонтальной плоскости перпендикулярно плоскости чертежа, так как сила тяжести P→{\displaystyle {\vec {P}}} вертикальна. Поэтому ось колеса прецессирует в данном случае в горизонтальной плоскости.

Приведённое объяснение показывает, как происходит прецессия, но не даёт ответа, почему, который состоит в том, что в начальный момент под действием силы тяжести ось колеса всё же немного наклоняется в плоскости чертежа и вектор количества движения меняет своё положение в пространстве, становясь L→′{\displaystyle {\vec {L}}^{\prime }}. Однако сила тяжести не создаёт никакого момента в вертикальной плоскости, и поэтому направление и величина вертикальной составляющей момента количества движения должна оставаться прежними, что может быть достигнуто только появлением дополнительного момента количества движения δL→{\displaystyle \delta {\vec {L}}} в выражении:

L→{\displaystyle {\vec {L}}} = L→′{\displaystyle {\vec {L}}^{\prime }} + δL→{\displaystyle \delta {\vec {L}}}.

Такой дополнительный момент соответствует направленной горизонтально перпендикулярно плоскости чертежа силе, которая и вызывает прецессию^[5].