Расчёт перегрузки
В данной статье репетитор по физике и математике рассказывает о том, как рассчитать перегрузку, которую испытывает тело в момент разгона или торможения. Данный материал очень плохо рассматривается в школе, поэтому школьники очень часто не знают, как осуществлять расчёт перегрузки, а ведь соответствующие задания встречаются на ЕГЭ и ОГЭ по физике. Так что дочитайте эту статью до конца или посмотрите прилагающийся видеоурок. Знания, которые вы получите, пригодятся вам на экзамене.
Начнём с определений. Перегрузкой называется отношение веса тела к величине силы тяжести, действующей на это тело у поверхности земли. Вес тела — это сила, которая действует со стороны тела на опору или подвес. Обратите внимание, вес — это именно сила! Поэтому измеряется вес в ньютонах, а не в килограммах, как некоторые считают.
Таком образом, перегрузка — это безразмерная величина (ньютоны делятся на ньютоны, в результате ничего не остаётся). Однако, иногда эту величину выражают в ускорениях свободного падения. Говорят, к примеру, что перегрузка равна 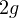 , имея ввиду, что вес тела вдвое больше силы тяжести.
, имея ввиду, что вес тела вдвое больше силы тяжести.
Примеры расчёта перегрузки
Покажем, как осуществлять расчёт перегрузки на конкретных примерах. Начнём с самых простых примеров и перейдём далее к более сложным.
| Пример 1. Чему равна перегрузка человека, стоящего на земле? Чему равна перегрузка человека, свободно падающего с некоторой высоты? |
Очевидно, что человек, стоящий на земле, не испытывает никаких перегрузок. Поэтому хочется сказать, что его перегрузка равна нулю. Но не будем делать поспешных выводов. Нарисуем силы, действующие на этого человека:
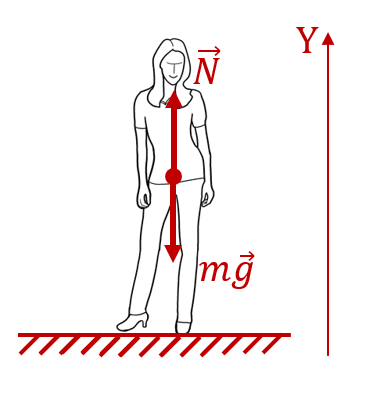
К человеку приложены две силы: сила тяжести 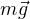
 , направленная вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.
, направленная вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.Вес человека 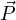
 . Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.
. Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.Поскольку человек стоит на месте и не проваливается сквозь землю, то силы, которые на него действуют скомпенсированы. То есть 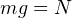
 . То есть расчёт перегрузки в этом случае даёт следующий результат:
. То есть расчёт перегрузки в этом случае даёт следующий результат: ![Rendered by QuickLaTeX.com \[ \frac{P}{mg} = \frac{mg}{mg} = 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-30c6b72fcb234535995262bea256f512_l3.png)
Запомните это! При отсутствии перегрузок перегрузка равна 1, а не 0. Как бы странно это не звучало.
Определим теперь, чему равна перегрузка человека, который находится в свободном падении.

Если человек пребывает в состоянии свободного падения, то на него действует только сила тяжести, которая ничем не уравновешивается. Силы реакции опоры нет, как нет и веса тела. Человек находится в так называемом состоянии невесомости. В этом случае перегрузка равна 0.
| Пример 2. Определите перегрузку космонавтов, находящихся в ракете, движущейся на небольшой высоте вверх с ускорением 40 м/с2. |
Космонавты находятся в горизонтальном положении в ракете во время её старта. Только так они могут выдержать перегрузки, которые они испытывают, не потеряв при этом сознания. Изобразим это на рисунке:

В этом состоянии на них действует две силы: сила реакции опоры  и сила тяжести
и сила тяжести 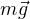
 . Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением
. Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением 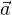 . С этим же ускорением синхронно с ракетой ускоряются и космонавты.
. С этим же ускорением синхронно с ракетой ускоряются и космонавты.Тогда в соответствии со 2-м законом Ньютона в проекции на ось Y (см. рисунок), получаем следующее выражение: 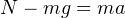
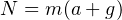 . То есть искомая перегрузка равна:
. То есть искомая перегрузка равна: ![Rendered by QuickLaTeX.com \[ \frac{P}{mg} = \frac{m(a+g)}{mg} = \frac{a+g}{g} = \frac{40+10}{10} = 5. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e9a9a6b267fc1ab6bd7f1028cc516fe4_l3.png)
Надо сказать, что это не самая большая перегрузка, которую приходится испытывать космонавтам во время старта ракеты. Перегрузка может доходить до 7. Длительное воздействие таких перегрузок на тело человека неминуемо приводит к летальному исходу.
| Пример 3. Рассчитайте перегрузку, которую испытывает пилот самолёта, выполняющего «мёртвую петлю» в нижней точке траектории. Скорость самолёта в этой точке составляет 360 км/ч. Радиус «мёртвой петли» составляет 200 м. |
В нижней точке «мёртвой петли» на пилота будут действовать две силы: вниз — сила 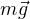
 (со стороны кресла, в котором сидит пилот):
(со стороны кресла, в котором сидит пилот):
Туда же будет направлено центростремительное ускорение пилота 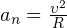 , где
, где  км/ч
км/ч 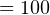 м/с — скорость самолёта,
м/с — скорость самолёта, 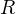 — радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:
— радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:
![Rendered by QuickLaTeX.com \[ N-mg = ma_n = \frac{m\upsilon^2}{R}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-da2862b088975ab67d22919e568ab5b6_l3.png)
Тогда вес равен 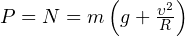 . Итак, расчёт перегрузки даёт следующий результат:
. Итак, расчёт перегрузки даёт следующий результат:
![Rendered by QuickLaTeX.com \[ \frac{m\left(g+\frac{\upsilon^2}{R}\right)}{mg} = 1+\frac{\upsilon^2}{gR} = 1+\frac{100^2}{10\cdot 200} = 6. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bd0d66979d42352b265faec5a2a13b2e_l3.png)
Весьма существенная перегрузка. Спасает жизнь пилота только то, что действует она не очень длительно.
Ну и напоследок, рассчитаем перегрузку, которую испытывает водитель автомобиля при разгоне.
| Пример 4. Рассчитайте перегрузку, которую испытывает водитель автомобиля, разгоняющегося с места до скорости 180 км/ч за 10 с. |
Итак, конечная скорость автомобиля равна 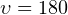 км/ч
км/ч 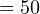 м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за
м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за 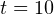 c, то его ускорение равно
c, то его ускорение равно  м/с2.
м/с2.
На водителя в процессе ускорения действуют две составляющие силы реакции опоры: со стороны седушки кресла (вертикальная составляющая)  и со стороны спинки кресла (горизонатльная составляющая)
и со стороны спинки кресла (горизонатльная составляющая)  :
:

Автомобиль движется горизонтально, следовательно, вертикальная составляющая силы реакции опоры уравновешена силой тяжести, то есть  . В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна
. В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна 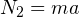 .
.
Величину общей силы реакции опоры найдём по теореме Пифагора:  . Она будет равна модулю веса. То есть искомая перегрузка будет равна:
. Она будет равна модулю веса. То есть искомая перегрузка будет равна:
![Rendered by QuickLaTeX.com \[ \frac{P}{mg} = \frac{N}{mg} = \frac{m\sqrt{g^2+a^2}}{mg} = \sqrt{1+\frac{a^2}{g^2}} \approx 1.12. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-57f6de2348b1dde4ac2ab7c3c900e407_l3.png)
Сегодня мы научились рассчитывать перегрузку. Запомните этот материал, он может пригодиться при решении заданий из ЕГЭ или ОГЭ по физике, а также на различных вступительных экзаменах и олимпиадах.
Материал подготовил репетитор по физике в Москве, Сергей Валерьевич
Смотрите также:
Вес тела в физике. Невесомость и перегрузка
Вес , как и любая другая сила, в системе СИ измеряется в Ньютонах.
Следы на снегу или на песке свидетельствуют о том, что человек или животное, проходя, давит на снежную или песчаную опору с некоторой силой.
Вес тела во время движения. Состояния невесомости и перегрузки
Вес тела зависит от ускорения, с которым движется тело, а потому может быть различным:
- Если тело покоится или движется равномерно прямолинейно, т.е. ускорение тела равно нулю, вес тела равен силе тяжести.
По второму закону Ньютона:
или в проекции на ось :
откуда
По третьему закону Ньютона:
- Если тело движется с ускорением, направленным вертикально вверх, вес тела увеличивается. Такое состояние тела называется перегрузкой.
По второму закону Ньютона:
или в проекции на ось :
откуда
По третьему закону Ньютона:
Перегрузки испытывают космонавты при взлете и на участках торможения космического корабля, летчики при выполнении фигур высшего пилотажа, пассажиры лифта при разгоне или торможении лифта и т.д.
- Если тело движется с ускорением, направленным вертикально вниз, вес тела уменьшается.
По второму закону Ньютона:
или в проекции на ось :
откуда
По третьему закону Ньютона:
Если ускорение тела в этом случае будет равно ускорению свободного падения, вес тела равен нулю, т.е. тело будет находиться в состоянии невесомости.
Поскольку вес покоящегося тела равен силе тяжести, часто считают, что вес и сила тяжести – это одна и та же сила. Однако это неверно. Во-первых, вес и сила тяжести приложены к разным телам: сила тяжести приложена к телу, а вес – к опоре или подвесу. Во-вторых, вес и сила тяжести имеют различную физическую природу: вес, как правило, является силой упругости, а сила тяжести – это сила гравитационного взаимодействия. Наконец, как было показано выше, вес тела изменяется с изменением ускорения и может быть равен нулю, когда сила тяжести нулю не равна.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Перегрузка — физика
Во время старта космического корабля космонавты испытывают перегрузок. Этот термин означает, что вес космонавта по модулю становится больше силу тяжести. Выясним, почему это происходит.
После включения ракетного двигателя, когда ракета начинает разгоняться, ее движение и движение космонавта осуществляются с ускорением, направленным вертикально вверх. При этом вес космонавта будет больше силу тяготения:
P = m (g + a)> mg.
^ Отношение силы, с которой тело давит на опору в случае ускоренного движения вверх, к его весу в инерциальной системе отсчета называют перегрузкой. Когда вес тела больше силы тяжести, говорят, что тело испытывает перегрузки. Перегрузка испытывают пассажиры лифтов, космонавты при взлете на ракете в космос, летчики при выходе из пикирования и т.д.. Вследствие перегрузки увеличивается не только вес человека в целом, но и каждого ее органа. Здоровый человек может без вреда для своего здоровья выдерживать кратковременные трехкратные перегрузки, т.е. увеличение веса втрое. Космонавтам же во время старта и посадки космического корабля приходится выдерживать многократные перегрузки.
Вопрос к ученикам во время изложения нового материала
1. При каких условиях вес тела равен по модулю силе тяжести, действующей на это тело?
2. Ли вес гиря, висит на нитке? Чему равна вес, если нить перерезать?
3. Ли вес у дерева, растущего во дворе?
4. Камень бросили вертикально вверх. В какие моменты полета он находится в состоянии невесомости, если можно пренебречь сопротивлением воздуха? Изменится ответ, если камень бросить под углом к горизонту?
5. Почему необходимо учитывать перегрузки?
6. Что общего в падении тел на Землю, вращении Луны вокруг Земли, приливах и отливах?
Закрепление изученного материала
1. Тренируемся решать задачи
1. В лифте установили динамометр, на котором подвесили тело массой 1 кг. Что покажет динамометр, если:
а) лифт движется равномерно;
б) лифт поднимается вверх с ускорением 5 м/с2;
в) лифт опускается вниз с ускорением 5 м/с2?
2. Самолет делает «мертвую петлю», описывая в вертикальной плоскости окружность радиусом 250 м. Во сколько раз вес летчика в нижней части траектории больше силы тяжести, если скорость самолета — 100 м / с?
3. Ученик утверждает, что вес человека, находящегося в лифте, обязательно увеличивается, когда лифт движется вверх, и уменьшается, когда лифт движется вниз. Согласны ли вы с этим утверждением? Решение
Утверждение неверно: вес зависит не от скорости лифта, а от его ускорения.
4. Космический корабль сразу же после старта движется вертикально вверх с ускорением 40 м/с2. С какой силой космонавт массой 70 кг давит на кресло кабины? Чему равна в этом случае коэффициент перегрузки?
2. Контрольные вопросы
1. Приведите примеры движений, когда вес тела равен силе тяжести, действующей на это тело.
2. Приведите примеры движений, при которых вес тела меньше силу тяжести, действующая на него (больше силы тяжести, действующей на него).
3. Или исчезает сила притяжения тела к Земле во время перехода тела в состояние невесомости?
4. Когда возникают перегрузки?
5. Зависит вес тела от его местонахождения?
Сила тяжести. Вес, невесомость, перегрузки
Вы уже знакомы с понятием силы тяжести — это сила, с которой Земля притягивает тело, находящееся на её поверхности (или вблизи этой поверхности). Именно под действием силы тяжести, тела могут находиться в свободном падении. Находясь в свободном падении можно ясно ощутить состояние невесомости, то есть, отсутствие веса. Рассмотрим эти явления более подробно.
Еще в седьмом классе вы познакомились с весом тела. Вес тела — это сила, с которой тело действует на горизонтальную опору или растягивает подвес. Надо сказать, что вес — это частный случай силы упругости. Рассмотрим простой пример. В помещении вы видите сидящего человека, горшки с растениями, часы, висящие на стене и так далее. На все эти тела, несомненно, действует сила тяжести.

Несмотря на это, все тела находятся в состоянии покоя. Дело в том, что опора, по третьему закону Ньютона, действует, например, на горшок, с той же силой, что и горшок давит на неё. Эта сила называется реакцией опоры. Итак, мы выяснили что, исходя из третьего закона Ньютона, реакция опоры равна по модулю весу тела. Поскольку тело покоится, равнодействующая сила равна нулю. Следовательно, реакция опоры должна уравновешивать силу тяжести (в противном случае, тело бы падало по направлению к центру Земли).
Таким образом, если тело покоится на горизонтальной поверхности, или двигается равномерно и прямолинейно, то вес тела равен силе тяжести.
А теперь, давайте рассмотрим, что произойдет, если опора будет двигаться с ускорением. Классический пример подобной ситуации — это движение лифта. При начальном движении лифта вверх, ускорение, конечно, направлено вверх.

Применим второй закон Ньютона:


Из этого уравнения, мы видим, что вес тела увеличивается при ускоренном движении опоры вверх. Это явление называется перегрузкой. Действительно, при рывке лифта вверх, мы чувствуем некое давление.
Нетрудно догадаться, что при ускоренном движении вниз, происходит противоположное явление: вес тела уменьшается.

В этом можно убедиться, если вновь применить второй закон Ньютона:

Как
видно, из уравнения, при движении вниз с ускорением свободного падения, вес
тела обратится в ноль: 
Это явление называется невесомостью. И правда, при рывке лифта вниз, мы ощущаем некую легкость.
Так, космонавты, находящиеся на космической станции, испытывают состояние невесомости. Они, фактически находятся в свободном падении, но падают, как бы, вокруг Земли. Дело, конечно, в их орбитальной скорости, достаточной для того, чтобы находиться на околоземной орбите.
Приведем пару примеров. Допустим, вы поставите стакан с водой на поднос. Очевидно, что стакан будет действовать на поднос с силой: Fт = mg. Но, как вы знаете, если вы отпустите поднос, то и стакан, и поднос будут находиться в свободном падении.

При этом, стакан не будет оказывать никакого воздействия на поднос, то есть не будет обладать весом. Точно также, мотоциклист, едущий с постоянной скоростью, будет действовать на сиденье мотоцикла силой тяжести. Но после прыжка на трамплине, и мотоциклист, и мотоцикл будут находиться в свободном падении.

Таким образом, вес мотоциклиста будет равен нулю, до тех пор, пока он не приземлится.
Примером перегрузки может быть выход пилота из пике.

В нижней точке, его центростремительное ускорение будет направлено вверх, что приведет увеличению веса пилота. Пилоты истребителей испытывают перегрузки до 30g. Перегрузки часто измеряются в единицах измерения g. То есть, например, перегрузка 5g означает, что вес пилота увеличился в 6 раз (в состоянии покоя наша перегрузка равна g). Иногда перегрузку обозначают буквой n, и она является безразмерной величиной, равной отношению ускорения движения к ускорению свободного падения.

Таким
образом, вес тела при перегрузках можно вычислить по формуле:  .
.
Для примера вычислим перегрузку, которую испытывает пилот в нижней точке пике в вертикальной плоскости, если радиус кривизны траектории полёта равен 400 м, а скорость самолёта равна 1080 км/ч.

1.3. Перегрузки и невесомость
В обычных условиях на животное действуют сила тяжести и сила реакции опоры. При отсутствии ускорения эти силы равны и противоположено направлены. Такое состояние естественно.
При ускоренном движении системы могут возникнуть особые состояния, называемые перегрузками и невесомостью.
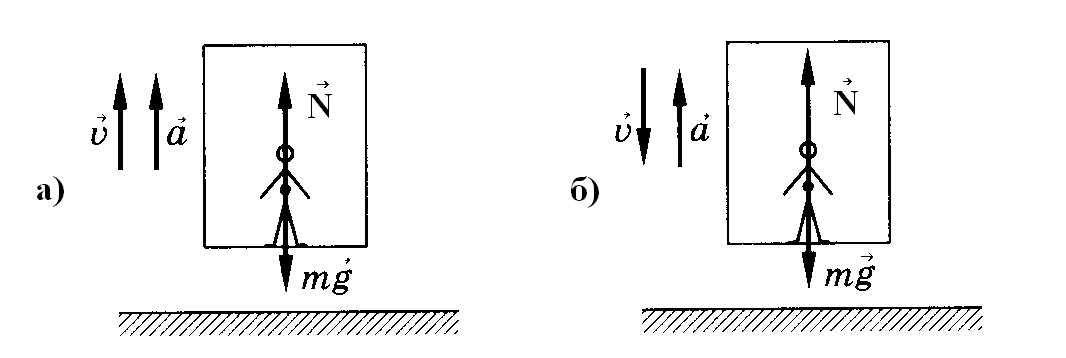
Рисунок 1.
Рассмотрим некоторые примеры.
Пусть человек находится в кабине лифта (в ракете), который поднимается вверх с ускорением а (рисунок 1а). На человека действует сила тяжести mg и сила реакции опоры N. По второму закону Ньютона
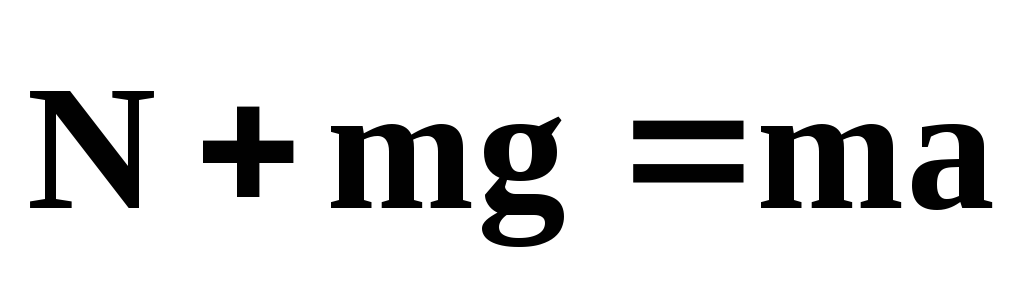
или в скалярной форме с учетом направления сил
В этом случае сила реакции опоры больше силы тяжести, и возникают перегрузки. Перегрузка выражается отношением
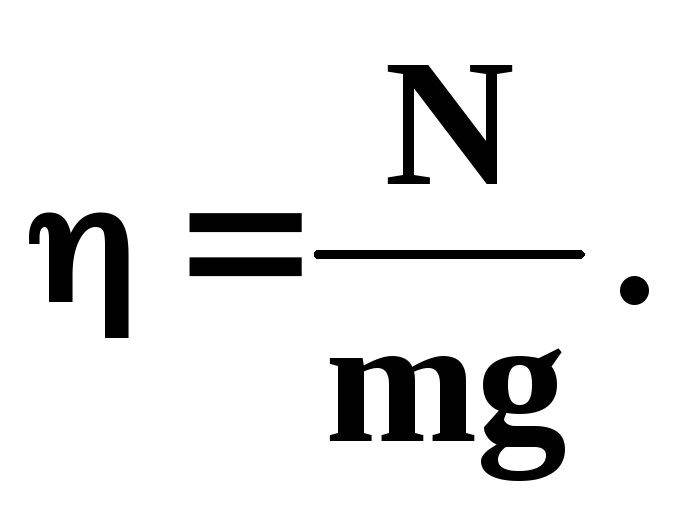
Перегрузки могут оказывать существенное влияние на организм, так как в этих состояниях происходит отток крови, изменяется взаимное давление внутренних органов друг на друга, возникает их деформация и т.п. Поэтому животные способны выдерживать лишь ограниченные перегрузки.
Если лифт (или космический корабль) ускоренно движется вниз (рис.1б) или замедленно вверх, то
 или
или 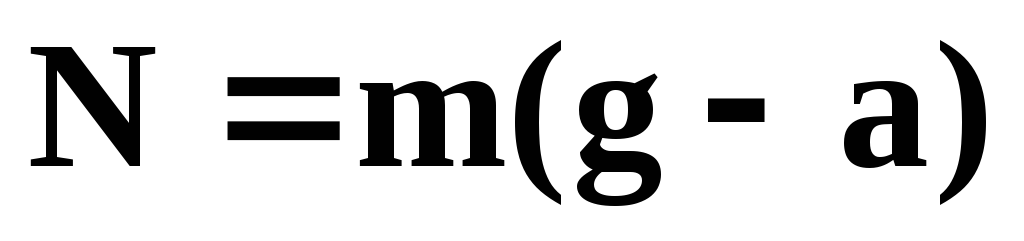 .
.
Как видно, сила реакции опоры меньше чем сила тяжести. Если а=g, то N=0 – состояние невесомости. Это такое состояние, при котором действующие на систему внешние силы не вызывают взаимных давлений частиц системы друг на друга.
Для биологических объектов невесомость – необычное состояние, хотя в обыденной жизни встречается кратковременные периоды частичной невесомости: прыжки, качели, начало движения вниз скоростного лифта и т.п.
Отсутствие действия опоры при невесомости приводит к общей детренированности организма и связанному с этим снижению работоспособности. При этом уменьшается мышечная масса, происходит деминерализация костной ткани, кров равномерно распределяется в организме, это означает, что верхняя часть тела переполнена кровью по сравнению с обычным состоянием, ощущается тяжесть в голове, появляется отечность лица.
1.4. Вестибулярный аппарат как инерциальная система ориентации
Удобным индикатором ускорения является устройство, изображенное на рисунке 2, — тело известной массы укреплено на шести пружинах. По деформации пружин можно определить значение и направление силы действующей на тело, а отсюда и ускорение системы, если учесть ускорение свободного падения. Такого рода индикаторы используются в инерциальной навигации, получившей развитие в связи с решением космических задач. Соответствующие устройства называются
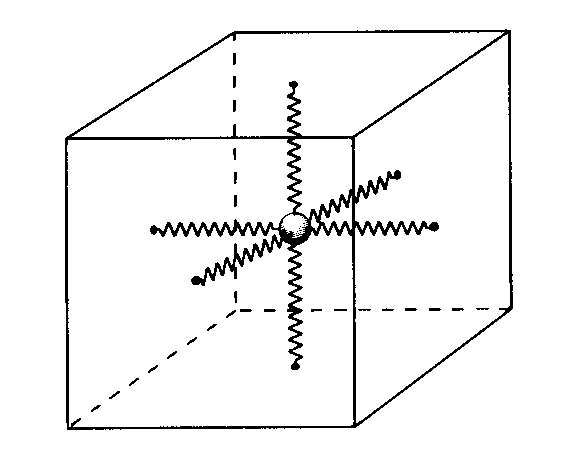

Рисунок 2. Рисунок 3.
В человеческом организме имеется орган, который тоже, по существу, является инерциальной системой ориентации – это вестибулярный аппарат. Он расположен во внутреннем ухе и состоит из трех взаимно перпендикулярных полукружных каналов К и полости преддверия В (рис.3). На внутренней поверхности стенок преддверия и в части полукружных каналов находятся группы чувствительных нервных клеток, имеющих свободные окончания в форме волосков. Внутри преддверия и полукружных каналов ест студенистая масса (эндолимфа), содержащая мелкие кристаллы фосфорнокислого и углекислого кальция (отолиты). Ускоренное перемещение головы вызывает перемещение эндолимфы и отолитов, что воспринимается нервными клетками (через волоски). Вестибулярный аппарат, как и любая другая физическая система, не отличает гравитационное воздействие от воздействий, возникающих при ускоренном движении системы.
Единицы силы. Вес. Перегрузка — Факты программы «Аполлон»
Единицы силы. Вес. Перегрузка
Сила, приложенная к телу, в системе единиц СИ измеряется в ньютонах (1 Н = 1 кг·м/с2). В технических дисциплинах в нередко качестве единицы измерения силы традиционно используют килограмм-силу (1 кгс, 1 кГ) и аналогичные единицы: грамм-силу (1 гс, 1 Г), тонна-силу (1 тс, 1 Т). 1 килограмм-сила определена как сила, сообщающая телу массой 1 кг нормальное ускорение, равное по определению 9,80665 м/с2 (это ускорение приблизительно равно ускорению свободного падения). Таким образом, по второму закону Ньютона, 1 кгс = 1 кг · 9,80665 м/с2 = 9,80665 Н. Можно сказать также, что тело массой 1 кг, покоящееся на опоре, имеет вес 1 кгс Часто ради краткости килограмм-силу называют просто «килограммом» (а тонна-силу, соответственно, «тонной»), что порождает порой путаницу у людей, не привыкших к использованию разных единиц.
Русская терминология, сложившаяся в ракетостроении, традиционно использует «килограммы» и «тонны» (точнее, килограмм-силы и тонна-силы) в качестве единиц тяги ракетных двигателей. Таким образом, когда говорят о ракетном двигателе с тягой 100 тонн, имеют в виду, что данный двигатель развивает тягу 105кг · 9,80665 м/с2 $\approx$ 106Н.
Частая ошибка
Путая ньютоны и килограмм-силы, некоторые считают, что сила в 1 килограмм-силу сообщает телу массой 1 килограмм ускорение 1 м/с2, т. е. пишут ошибочное «равенство» 1 кгс / 1 кг = 1 м/с2. В то же время очевидно, что на самом деле 1 кгс / 1 кг = 9,80665 Н / 1 кг = 9,80665 м/с2 — таким образом, допускается ошибка почти в 10 раз.
Пример
Ю. И. Мухин в книге «Антиаполлон. Лунная афера США» (2006) ведет расчет ускорения частиц песка под воздействием газов из двигателя лунного модуля:
<…> Соответственно, сила которая давит на частицы в пределах средневзвешенного радиуса будет равна: 0,74 Гс/мм2 · 0,00024 = 0,00018 Гс/мм2 или 0,18 мГс/мм2. Соответственно, на среднюю частицу с поперечным сечением в 0,01 мм2 будет давить сила в 0,0018 мГс.
Эта сила придаст частице ускорение, равное ее отношению к массе средней частицы: 0,0018 мГс / 0,0014 мГ = 1,3 м/сек2. <…>
(Выделение apollofacts.) Разумеется, сила величиной 0,0018 миллиграмм-сил сообщила бы частице массой 0,0014 миллиграмм ускорение почти в 10 раз больше того, что насчитал Мухин: 0,0018 миллиграмм-сил / 0,0014 миллиграмм = 0,0018 мг · 9,81 м/с2 / 0,0014 мг $\approx$ 13 м/сек2. (Можно заметить, что с исправлением одной только этой ошибки насчитанная Мухиным глубина кратера, который якобы должен был бы образоваться под лунным модулем при посадке, сразу упадет с 1,9 м, которые требует Мухин, до 20 см; однако весь остальной расчет настолько нелеп, что эта поправка не способна его исправить).
По определению, вес тела есть сила, с которой тело давит на опору или подвес. Вес тела, покоящегося на опоре или подвесе (т. е. неподижного относительно Земли или иного небесного тела) равен
(1)\begin{align} \mathbf{W} = m \cdot \mathbf{g}, \end{align}
где $\mathbf{W}$ — вес тела, $m$ — масса тела, $\mathbf{g}$ — ускорение свободного падения в данной точке. На поверхности Земли ускорение свободного падения близко к нормальному ускорению (часто округляемому до 9,81 м/с2). Тело массой 1 кг имеет вес $\approx$ 1 кг · 9,81 м/с2 $\approx$ 1 кгс. На поверхности Луны ускорение свободного падения примерно в 6 раз меньше, чем у поверхности Земли (точнее, близко к 1,62 м/с2). Таким образом, на Луне тела примерно в 6 раз легче, чем на Земле.
Частая ошибка
Путают вес тела и его массу. Масса тела не зависит от небесного тела, она постоянна (если пренебречь релятивистскими эффектами) и всегда равна одной и той же величине — и на Земле, и на Луне, и в невесомости
Пример
В газете «Дуэль», № 47, 2005 г. «объясняется», почему лунный модуль якобы не мог взлететь с Луны [2]:
<…> на такую фразу хиви (добровольного помощника) NASA: «Достаточно комфортные условия были и при взлёте с Луны. Сухая (т.е. без топлива) масса взлётной ступени — 2,2 тонны, а сила тяги ее двигателя — 1,6 тонны (1590 кг). Поэтому взлетная ступень не может развить ускорение свыше 7,3 м/с2, а это значит, что вес находящихся в ней астронавтов опять-таки менее их земного веса».
Эту фразу я бы назвал шедевром тупости хиви, не требующим других доказательств лунной аферы NASA. Какое ускорение может развить взлётная ступень, если ее тяговооруженность (отношение тяги двигателя к ее весу) меньше единицы и равна 1590 кг/ 2200 кг = 0,72. При взлете с Земли тяговооруженность ракеты (имеется в виду «Сатурн-5» — apollofacts) составляла 3 470 000 кг/ 2 913 000 кг = 1,19. Да она бы просто не сумела оторваться от поверхности Луны, это же школьная физика, закон Ньютона. Любой желающий может это проверить дома.
Разумеется, в своем разоблачительском порыве автор этого «опровержения» позабыл, что масса и вес — это разные вещи. Вес сухой взлетной ступени составляет $\approx$ 2200 кг · 1,62 м/с2$\approx$ 3560 Н $\approx$ 360 кгс. Топливо и астронавты увеличивали эту цифру примерно до 800 кгс, поэтому стартовая тяговооруженность составляла около $\approx$ 1590 кгс/800 кгс $\approx$ 2 — эта величина больше, чем у большинства ракет-носителей на земле.
Перегрузкой называется вес тела, выраженный в единицах его нормального веса, т. е. веса этого тела, покоящегося при нормальном ускорении свободного падения $\approx$ 9,81 м/с2. Единицей измерения перегрузки традиционно является 1 g (1 «же»). Фактически, g есть безразмерная величина. Если вес тела меньше его нормального веса, то величина перегрузки меньше единицы, и можно условно говорить о «недогрузке» (термин не употребляется). Например, двигатель лунного модуля тягой $\approx$ 10 тс сообщает модулю массой $\approx$ 15 т [1] ускорение $\approx$ 9,81·104Н / 15·103кг $\approx$ 6,5 м/с2 (это верно как в совершенно пустом пространстве, так и вблизи Луны: гравитация не оказывает прямого влияния на вес тел). Таким образом лунный модуль и находящиеся в нем астронавты под воздействием этого двигателя испытывают перегрузку $\approx$ 6,5 / 9,81 $\approx$ 0,66 g — то есть их вес при этом меньше, чем их вес на земле.
Частые ошибки
Иногда путают вес тела и его силу тяжести (силу, действующую на тело со стороны планеты). При этом приходят к абсурдному выводу о том, что корабль, движущийся в поле тяжести планеты с выключенным двигателем, все-таки испытывает перегрузку из-за действия на корабль гравитационной силы. Гравитационная сила сама по себе не может вызывать перегрузки. Ее вызывает лишь действие на тело опоры (подвеса). Для ракеты и космического корабля перегрузка обычно связана либо с действием тяги его двигателя, либо с тормозящим действием атмосферы (или суммой этих действий).
Другая распространенная ошибка — путают ускорение тела и перегрузку. Однако даже когда речь идет об ускорениях, связанных с работой двигателя (или торможением атмосферой), перегрузка должна рассчитываться в единицах нормального ускорения; таким образом, перегрузка в $\approx$ 9,81 раза меньше ускорения.
Пример
В газете «Дуэль», № 20, 2002 г. автор живописует страдания, которые должны испытывать астронавты лунного модуля при посадке на Луну, и настаивает на невозможности такой посадки [3]:
Космонавты <…> испытывают длительную перегрузку, максимальное значение которой — 5. Перегрузка направлена вдоль позвоночника (самая опасная перегрузка). Спросите у военных летчиков, можно ли устоять в самолете в течение 8 мин. при пятикратной перегрузке да еще и управлять им. Представьте себе, что после трех дней пребывания в воде (три дня полета к Луне в невесомости) вы выбрались на сушу, вас поместили в Лунную кабину, а ваш вес стал 400 кг (перегрузка 5), комбинезон на вас — 140 кг, а рюкзак за спиной — 250 кг. Чтобы вы не упали, вас держат тросом, прикрепленным к поясу, 8 минут, а затем еще 1,5 мин. (никаких кресел, ложементов нет). Не подгибайте ноги, опирайтесь на подлокотники (руки должны быть на органах управления). Кровь отлила от головы? Глаза почти не видят? Не умирайте и не падайте в обморок <…>
уж совсем плохо заставлять космонавтов управлять посадкой в положении «стоя» при длительной 5-кратной перегрузке — это просто НЕВОЗМОЖНО.
Однако, как уже было показано, в начале спуска астронавты испытывали перегрузку $\approx$ 0,66 g — то есть заметно меньше их нормального земного веса (и никакого рюкзака за спиной у них не было — они были непосредственно подключены к системе жизнеобеспечения корабля). Перед посадкой тяга двигателя почти уравновешивала вес корабля на Луне, поэтому связанное с ней ускорение составляет $\approx$ 1/6 g — таким образом, в течение всей посадки они испытывали меньшую нагрузку, чем при простом стоянии на земле. По сути, одна из задач описыванной тросовая системы как раз и была в том, чтобы помочь астронавтам удержаться на ногах в условиях пониженного веса.
Ссылки
2. «Тяга», В. Б. Селиванчик, «Дуэль», 47, 2005Перегрузка (техника) Википедия
Акробатический манёвр с увеличением угла тангажа (например, ввод в горку) сопровождается положительной перегрузкой — тело весит больше, чем обычно У этого термина существуют и другие значения, см. Перегрузка.Перегру́зка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности Земли. Будучи отношением двух ускорений, перегрузка является безразмерной величиной[1], однако часто перегрузка указывается в единицах стандартного ускорения свободного падения g (произносится как «же»), равного 9,80665 м/с²[2][3]. Перегрузка в 0 g испытывается телом, находящемся в состоянии свободного падения под воздействием только гравитационных сил, то есть в состоянии невесомости[1]. Перегрузка, испытываемая телом, покоящимся на поверхности Земли на уровне моря, равна 1[1].
Перегрузка — векторная величина[1]. Для живого организма очень важно направление действия перегрузки. При перегрузке органы человека стремятся оставаться в прежнем состоянии (равномерного прямолинейного движения или покоя). При положительной перегрузке (ускорение направлено от ног к голове, а вектор перегрузки — от головы к ногам) кровь уходит от головы в ноги, желудок опускается вниз. При отрицательной перегрузке увеличивается приток крови к голове. Наиболее благоприятное положение тела человека, при котором он может воспринимать наибольшие перегрузки — лёжа на спине, лицом к направлению ускорения движения, наиболее неблагоприятное для перенесения перегрузок — в продольном направлении ногами к направлению ускорения. При столкновении автомобиля с неподвижной преградой сидящий в автомобиле человек испытает перегрузку спина — грудь. Такая перегрузка переносится без особых трудностей. Обычный человек может выдерживать перегрузки до 15 g около 3—5 секунд без потери сознания. Перегрузки от 20—30 g и более человек может выдерживать без потери сознания не более 1—2 секунд и зависимости от величины перегрузки.
Одно из основных требований к военным летчикам и космонавтам — способность организма переносить перегрузки. Тренированные пилоты в противоперегрузочных костюмах могут переносить перегрузки от −3…−2 g до +12 g[4]. Обычно при положительной перегрузке 7—8 g в глазах «краснеет», пропадает зрение, и человек постепенно теряет сознание из-за отлива крови от головы. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Космонавты во время взлёта переносят перегрузку лёжа. В этом положении перегрузка действует в направлении грудь — спина, что позволяет выдержать несколько минут перегрузку в несколько единиц g. Существуют специальные противоперегрузочные костюмы, задача которых — облегчить действие перегрузки. Костюмы представляют собой корсет со шлангами, надувающимися от воздушной системы и удерживающими наружную поверхность тела человека, немного препятствуя оттоку крови.
Перегрузка увеличивает нагрузку на конструкцию машин и может привести к их поломке или разрушению, а также к перемещению не закреплённого или плохо закреплённого груза. Разрешённая эксплуатационной документацией величина перегрузки для пассажирских самолётов[каких?] составляет 2,5 g.
Примеры перегрузок и их значения:
| Пример перегрузки | Значение, g |
|---|---|
| Человек (или любой предмет), в неподвижном состоянии относительно Земли | 1 |
| Пассажир в самолёте при взлёте | 1,5 |
| Парашютист при приземлении со скоростью 6 м/с | 1,8 |
| Парашютист при раскрытии парашюта | до 10,0 (По-16, Д1-5У) до 16 (Ут-15 сер. 5) |
| Космонавты при спуске в космическом корабле «Союз» | до 3,0—4,0 |
| Лётчик спортивного самолёта при выполнении фигур высшего пилотажа | от −7 до +12 |
| Перегрузка (длительная), соответствующая пределу физиологических возможностей человека | 8,0—10,0 |
| Рекорд при несмертельном аварийном спуске космического корабля «Союз» | 20—26 (по разным данным)[5]:37[6][7] |
| Предыдущий рекорд (кратковременной) перегрузки автомобиля, при которой человеку удалось выжить[8][9] | 179,8 |
| Наибольшая (кратковременная) перегрузка, при которой человеку удалось выжить. Кенни Брак, IRL IndyCar, авария в последней гонке сезона в Форт-Уорте | 214 |
| Перегрузка, которую испытала автоматическая межпланетная станция «Венера-7» при торможении в плотных слоях атмосферы Венеры. | 350 |
| Перегрузка, которую может выдержать твёрдотельный накопитель (SSD-диск) | 1500 |
| Перегрузка снаряда при выстреле (в начале ствола) | 47 000 |
Ссылки
Литература
- Статья Перегрузка // Большая политехническая энциклопедия / сост. В. Д. Рязанцев. — М.: Мир и Образование, 2011. — 704 с. — ISBN 978-5-94666-621-3.



