Параллельное соединение элементов
Параллельное соединение элементов характеризуется тем, что каждый из элементов находится под действием одного и того же напряжения источника энергии (рис. 20). В результате величина тока каждого параллельно включенного элемента зависит только от величины его сопротивления.
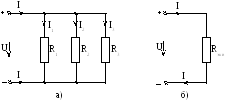
Рис. 20
Действительно, согласно закону Ома для участка цепи (1) применительно к схеме (рис. 20а) можно записать:
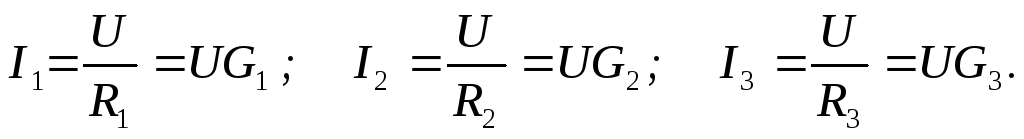
В соответствии с первым законом Кирхгофа втекающий ток Iв неразветвленной части цепи (рис. 20а) равен сумме токов, вытекающих из узла (показанные на схеме узлы являются «устраняемыми»).
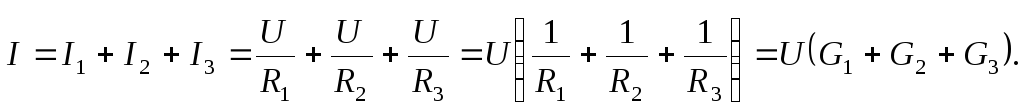
(44а)
При замене параллельной цепи (рис. 20а) эквивалентной (рис. 20б) необходимо сохранить величины напряжения Uи токаI.
Для эквивалентной схемы согласно закону Ома
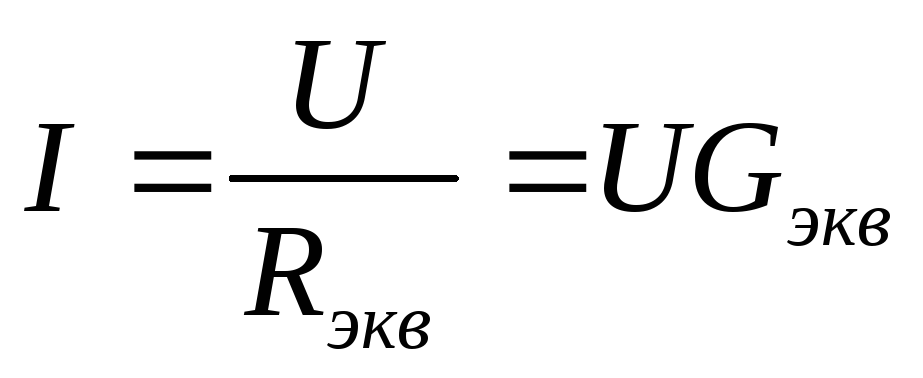
(44б)
.Приравняв правые части равенств (44а) и (44б) и сократив их на величину напряжения U, получим
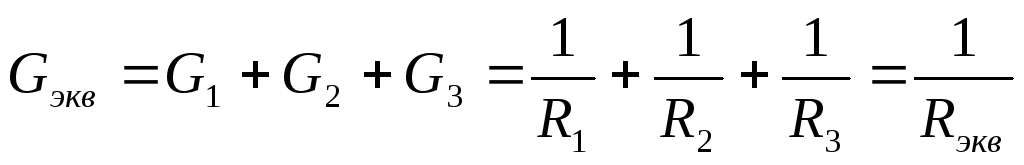 ,
,
В общем случае для числа nпараллельных ветвей можно получить формулу эквивалентной проводимости

(45)
или формулу для расчета эквивалентного сопротивления
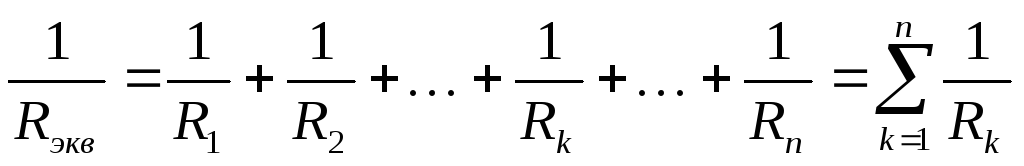
(46)
. Например, сделав в эту формулу подстановки
для схемы на рисунке 20а, получим 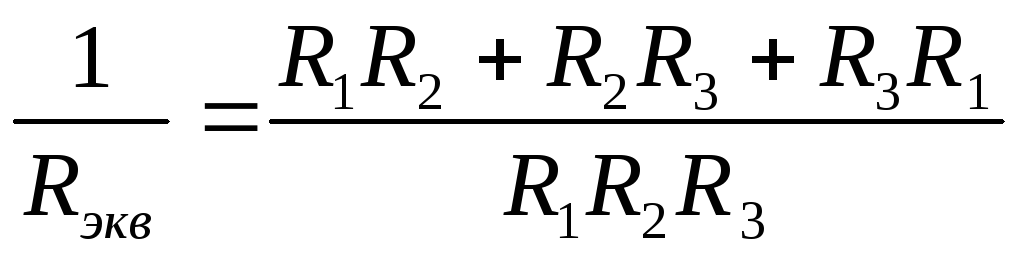
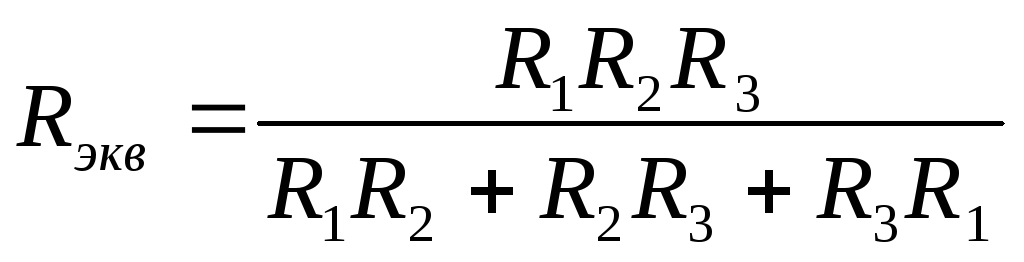
(47)
.В отличие от последовательной цепи (рис. 19а) при параллельном включении (рис.20а)приемники электроэнергии работают независимо друг от друга,поскольку величина тока конкретного приемника Ik зависит только от его сопротивления Rk и не влияет на токи остальных приемников.
Поэтому все осветительные и электробытовые приборы включаются в питающую сеть всегда параллельно
Смешанное соединение элементов
На рисунке 21а показана простейшая электрическая цепь со смешанным соединением резисторов. Резисторы R2иR3соединены параллельно друг с другом, а сама разветвленная цепь – последовательно с резисторомR1.
Чтобы заменить эти резистора одним эквивалентным Rэкв(рис. 21б) необходимо сначала заменить разветвленную цепь эквивалентным сопротивлениемR23, которое оказывается включенным последовательно с резисторомR1.

Рис. 21
В результате эквивалентное сопротивление всей цепи (рис. 21б) будет равно
(48)
.Эквивалентные соединения резистивных элементов по схеме треугольника и звезды
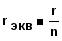
При расчете схемы встречаются сложные соединения, части которых нельзя отнести ни к последовательным, ни к параллельным соединениям. В частности рассмотрим часть схемы в виде треугольника (рис. 22а), вершинами которого А,В,С являются три узла, а сторонами – три резистора RАВ, RВС, RСА, включенные между этими узлами.
Для упрощения подобных схем во многих случаях бывает удобным заменить треугольник эквивалентной трехлучевой звездой(рис. 22б). Такое преобразование широко применяется при расчетах сложных цепей постоянного тока и цепей трехфазного тока.

Рис. 22
Эквивалентность схем в виде треугольника и звезды получается приравниванием значений сопротивлений или проводимостей между узлами этих схем, отсоединенных от остальной части цепи.
При заданной схеме треугольника (рис. 22а) сопротивления RА, RВ, RСэквивалентной звезды (рис. 22б) рассчитываются по формулам:
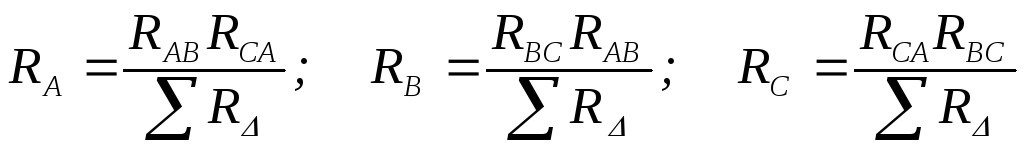 ,
,
где RАВ, R
∑RΔ = RАВ + RВС + RСА сумма сопротивлений треугольника.
Возможно обратное преобразование звезды из резистивных элементов в эквивалентный треугольник по формулам:
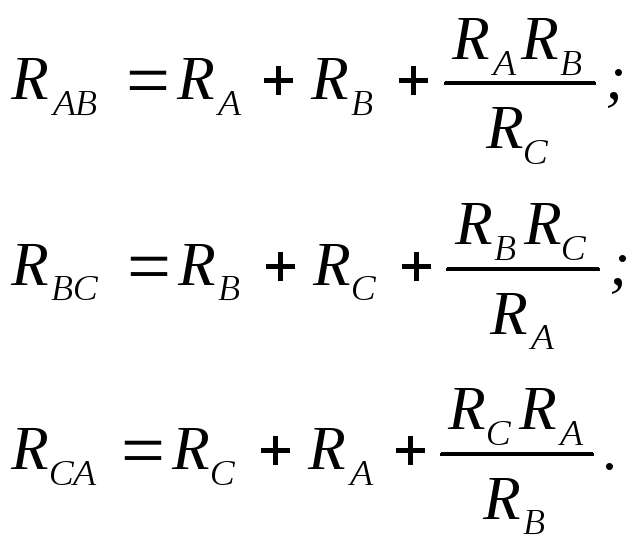
Подробный вывод формул взаимного эквивалентного преобразования треугольника и звезды приведен в [4].
Примером упрощения расчетов может служить преобразование мостовой схемы соединения резистивных элементов (рис. 23а).
После замены одного из треугольников эквивалентной звездой всю цепь (рис. 23б) можно рассматривать как смешанное соединение резистивных элементов.

Рис. 23
Параллельное соединение элементов r,l,c
Рассмотрим параллельное соединение разнородных элементов R,
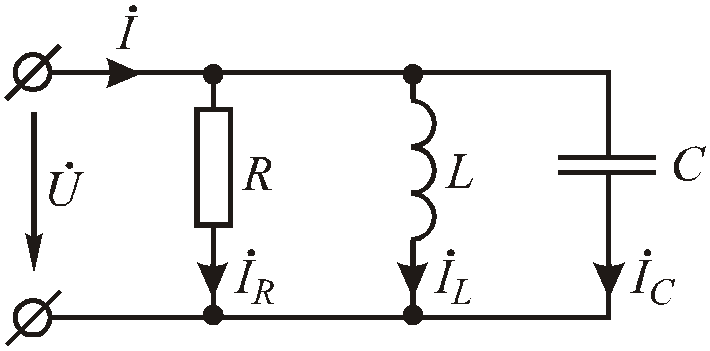
Рис.2.28. Схема параллельного соединения элементовR, L, C
Пусть на вход цепи подано напряжение u = Umsin(t+u),тогда по первому закону Кирхгофа:
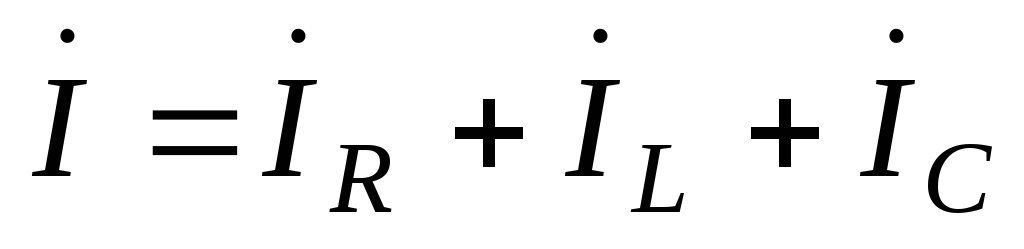
Комплексное изображение входного напряжения:
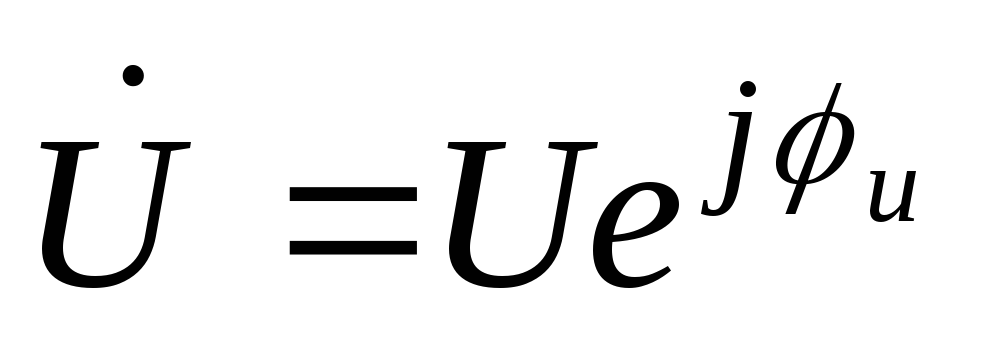
Для определения комплекса общего тока найдем его составляющие:
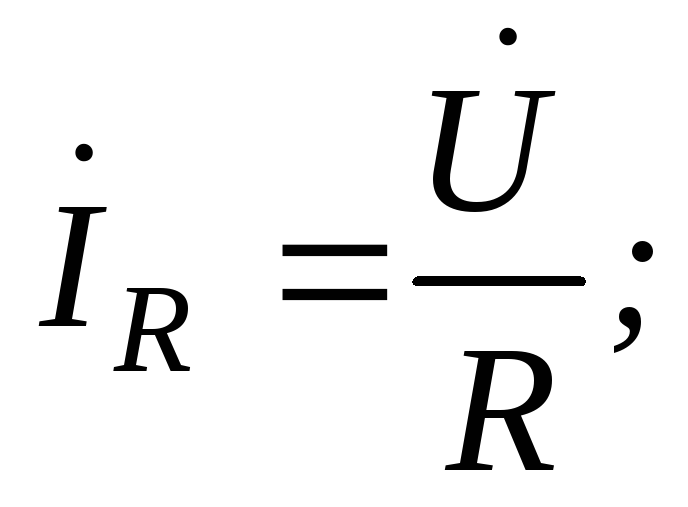
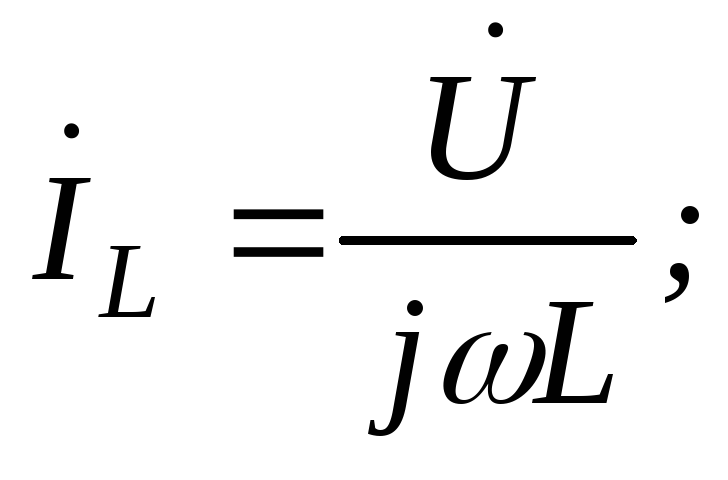
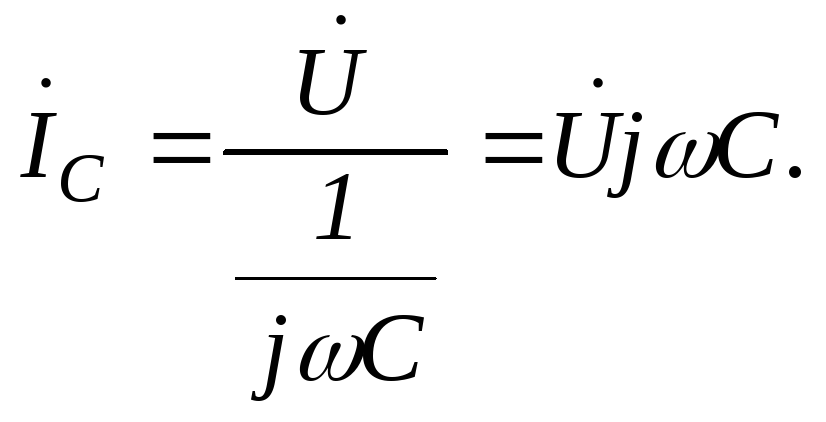
тогда комплекс общего тока:
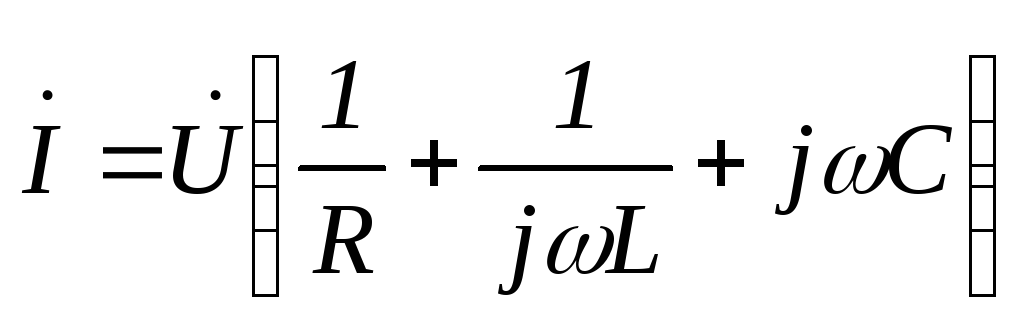 .54(2.47)
.54(2.47)
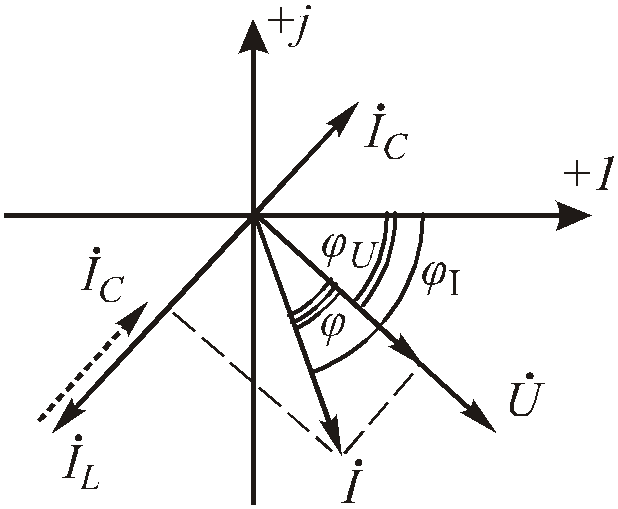
Построим векторную диаграмму для параллельного соединения (Рис. 2 .29).
Пусть φu < 0,
Выражение в круглых скобках ( 2 .47) имеет размерность 1/Ом или См (симменс) и носит название комплексной проводимости цепи:
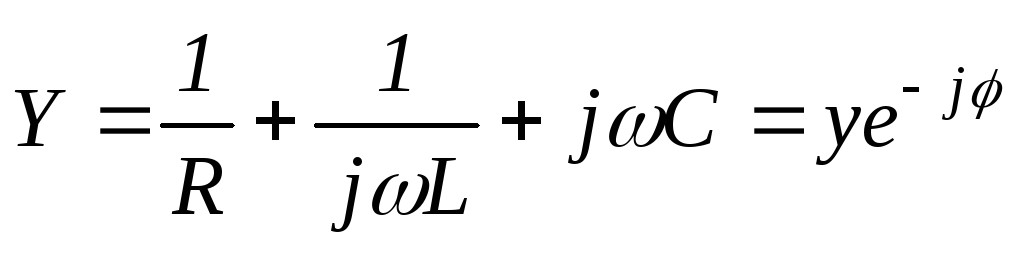 ,55(2.48)
,55(2.48)
где y– модуль комплексной проводимости, а– угол сдвига фаз между током и напряжением.
Комплексная амплитуда общего тока:
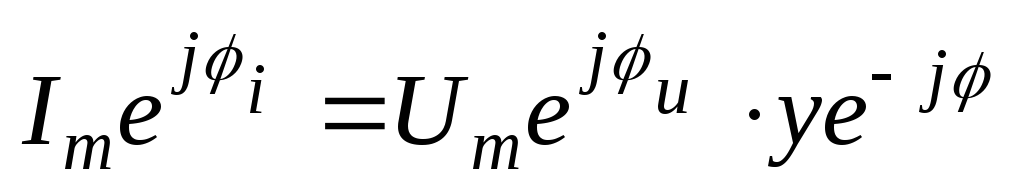 .56(2.49)
.56(2.49)
Её модуль:
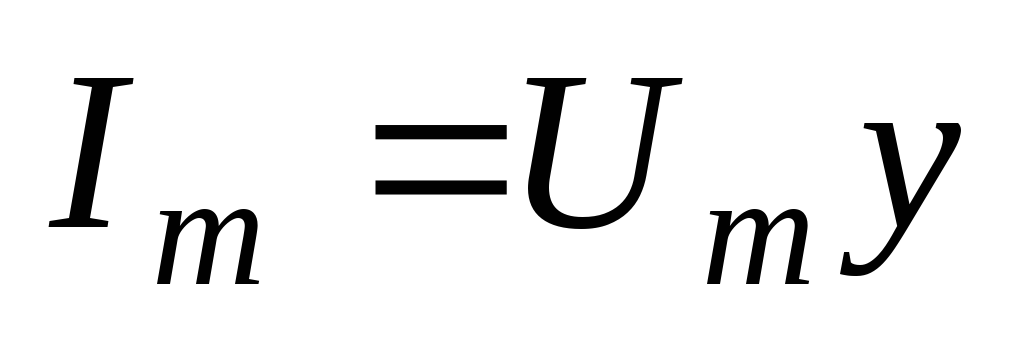 .
.
Её фаза:
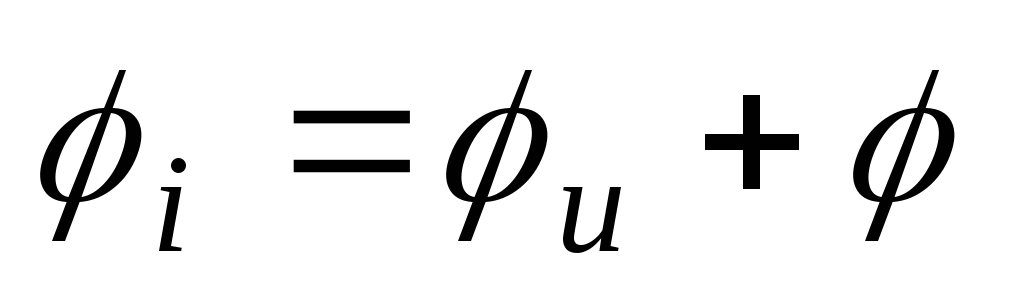 ;
;
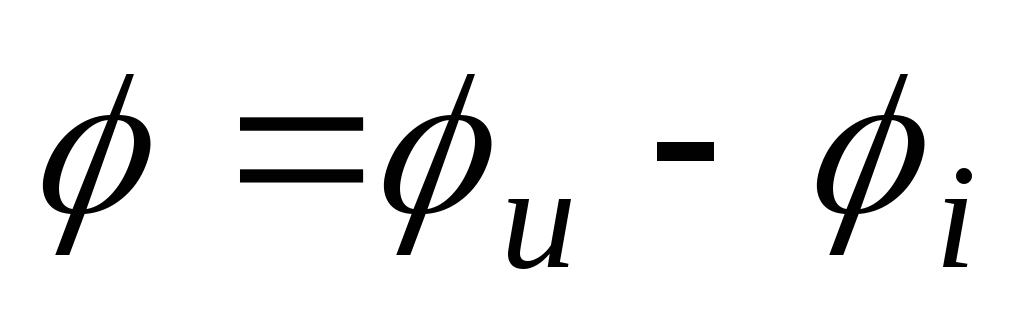
Мгновенное значение общего тока:
i = Imsin(t + φu – ).
Проводимости
Под комплексной проводимостью любой цепи понимается величина обратная ее полному комплексному сопротивлению:
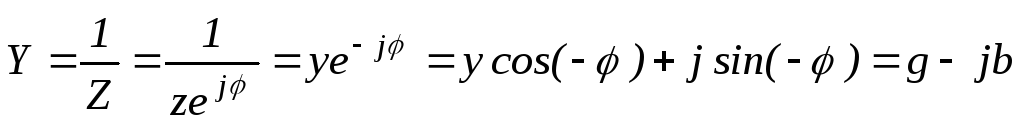 ,57(2.50)
,57(2.50)
где g– активная проводимость данной цепи;
b– результирующая реактивная проводимость.
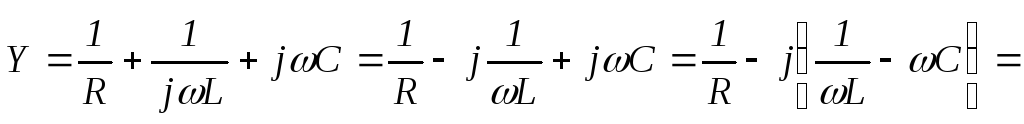
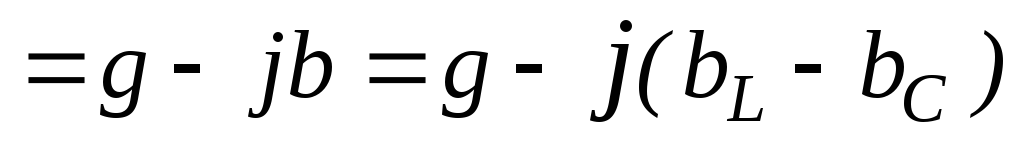 ,58(2.51)
,58(2.51)
где bLиbC– индуктивная и емкостная проводимости соответственно.
Понятие проводимости приобретает особый смысл в том случае, если ветвь содержит активные и реактивные элементы. На ветви, изображенной на Рис. 2 .30, определим ее активную и реактивную проводимости:
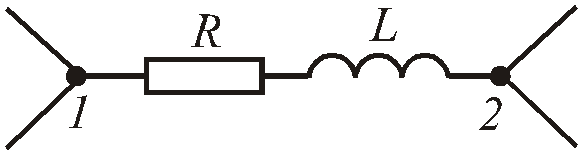
Рис.2.30. Участок цепи с активно-индуктивным сопротивлением
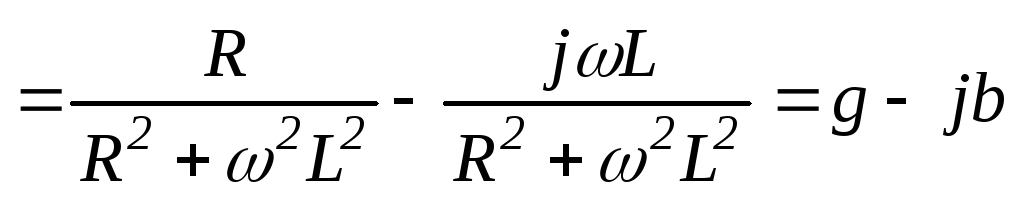 .59(2.52)
.59(2.52)
Из векторной диаграммы (Рис. 2 .29) можно выделить треугольник токов:
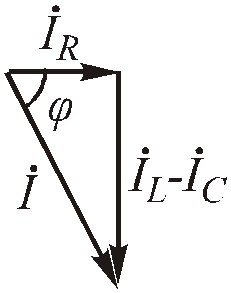
Рис.2.31. Векторный треугольник токов
Разделив стороны векторного треугольника токов на вектор напряжения, получим скалярный треугольник проводимостей.
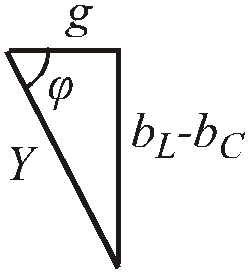
Рис.2.32. Скалярный треугольник проводимостей
Резонанс токов
Резонансный режим, возникающий при параллельном соединении R, L, C,называется резонансом токов. В отличие от рассмотренного ранее режима резонанса напряжений, данный режим не столь однозначен.
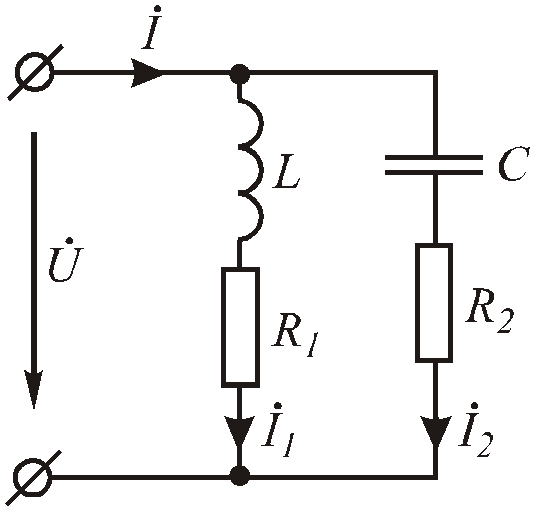
Рис.2.33. Цепь с параллельным соединением разнородных приемников
В цепи (Рис. 2 .33) режим резонанса токов возникает при условии равенства нулю результирующей реактивной проводимости этой цепи:
b = b1+ b2 = 0. 60(2.53)
Реактивные проводимости ветвей:
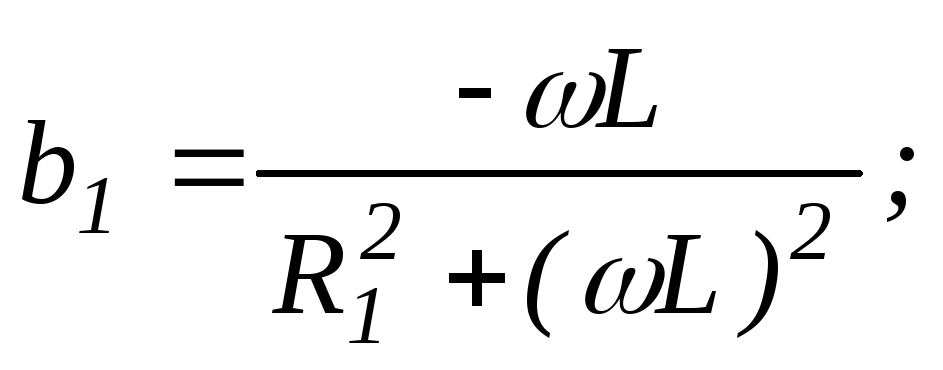
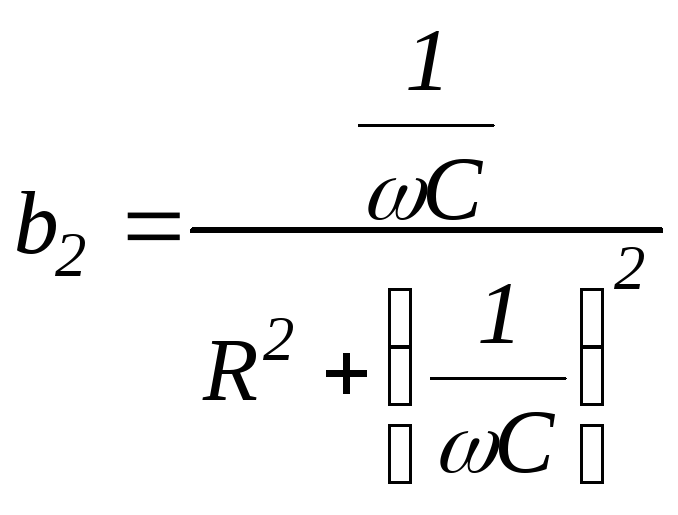 .
.
Подставим выражения b1иb2в ( 2 .53):
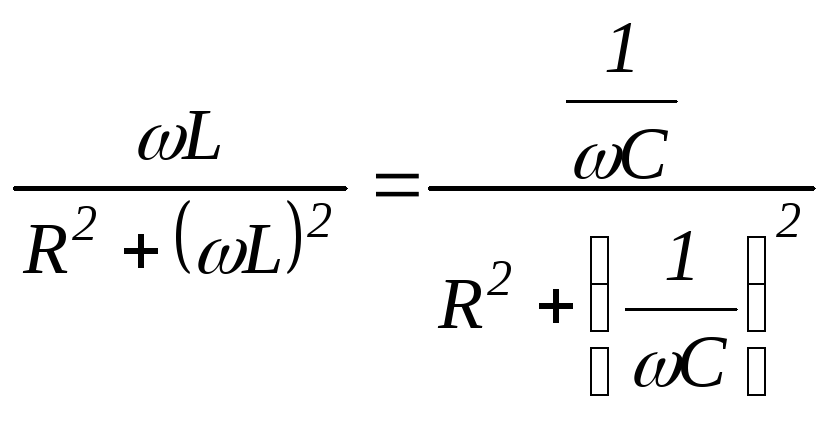
и после преобразования
получим резонансную частоту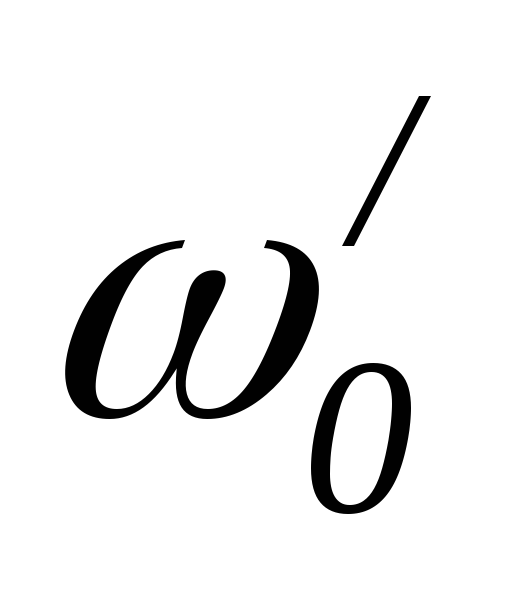 :
:
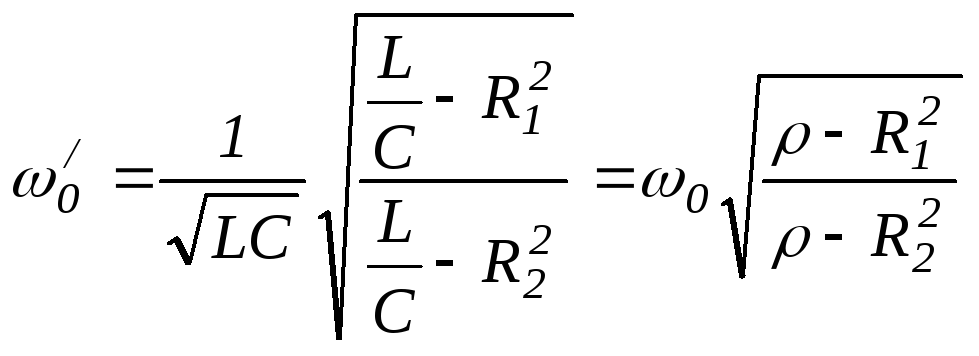 .61(2.54)
.61(2.54)
Структура
полученного уравнения показывает, что
существует четыре варианта частоты 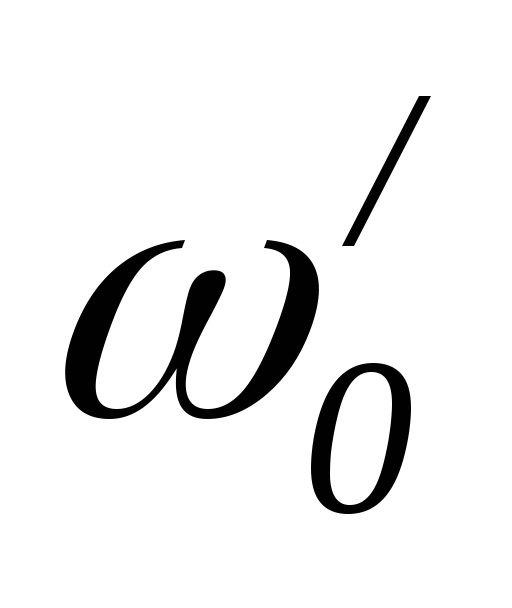 :
:
Если R1 = R2 ,то
 =0
=0Если R1 = R2 = ,то
 =0
=0 – с физической точки зрения это означает,
что входное сопротивление данного
контура равно ее волновому, которое не
зависит от частоты, значит, резонанс
будет иметь место при любой частоте.Для доказательства этого положения
определим входное сопротивление цепи:
– с физической точки зрения это означает,
что входное сопротивление данного
контура равно ее волновому, которое не
зависит от частоты, значит, резонанс
будет иметь место при любой частоте.Для доказательства этого положения
определим входное сопротивление цепи:
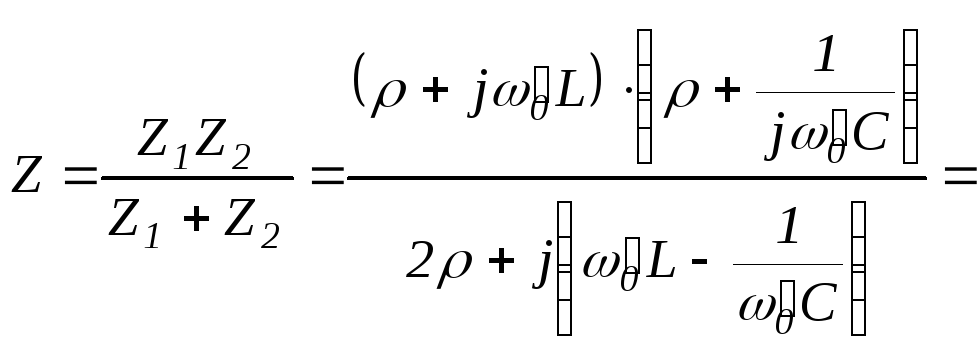
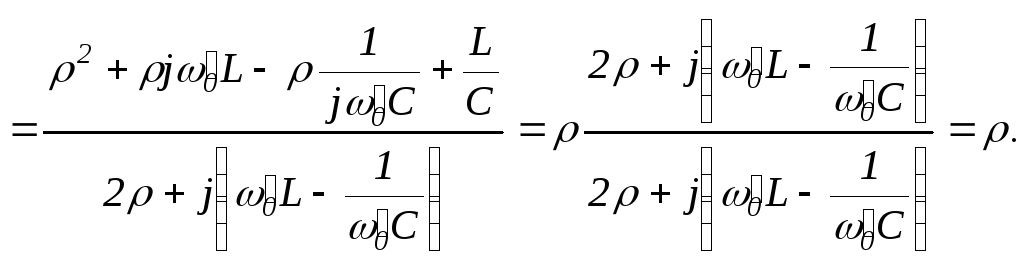
Если под корнем получилось отрицательное число, значит, резонансной частоты не существует для данных параметров R1, R2, , L, C.
Если под корнем положительное число, то получаем
 — единственную резонансную частоту.
— единственную резонансную частоту.
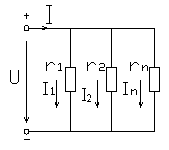
Параллельное соединение элементов.
Соединение групп элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным (рис.1.20). Согласно первому Кирхгофа, ток всей цепи I равен алгебраической сумме токов в параллельных ветвях, т.е.
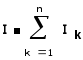
 (1.31)
(1.31)
На основании этого уравнения с учетом (1.8) для параллельного соединения резистивных элементов получаем:
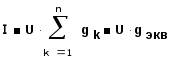
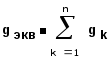
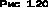
где -эквивалентная проводимость. (1.32)
Токи и мощности параллельно соединенных ветвей при U=const (рис. 1.20) не зависят друг от друга и определяются по формулам:
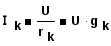
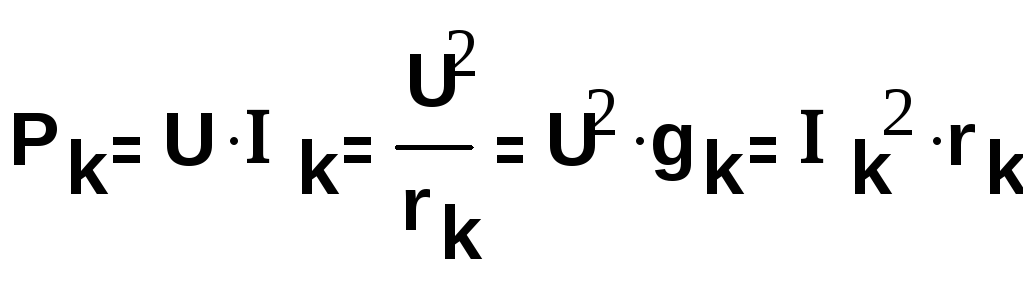 (1.33)
(1.33)
Мощность всей цепи равна :
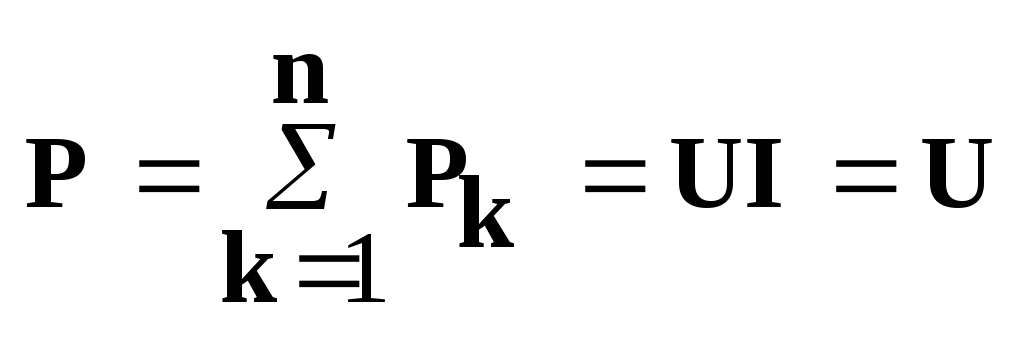 ,
, 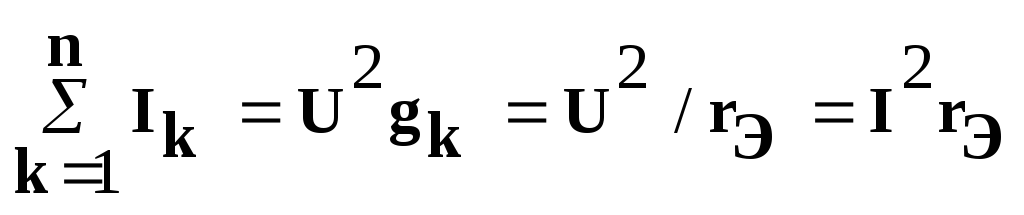 (1.34)
(1.34)
где rэ=1/gэ -эквивалентное сопротивление цепи.
При увеличении числа параллельных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление соответственно уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность Р. Токи и мощности ранее включенных ветвей не изменяются.
Рассмотрим частные случаи параллельного соединения резистивных элементов.
а) параллельное соединение двух элементов
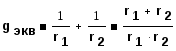
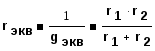 (1.35)
(1.35)
б) параллельное соединение n ветвей с одинаковыми сопротивлениями
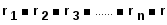
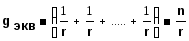
 (1.36)
(1.36)
Эквивалентное преобразование резистивноготреугольника в звезду.
Под
соединением треугольником (рис.1.21.а) понимается такое, при к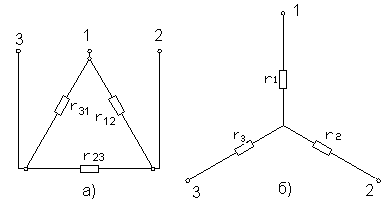 отором
конец одного элемента соединяется с
началом второго, конец второго- с началом
третьего, а конец третьего — с началом
первого. Узловые точки 1,2,3 подключаются
к остальной
отором
конец одного элемента соединяется с
началом второго, конец второго- с началом
третьего, а конец третьего — с началом
первого. Узловые точки 1,2,3 подключаются
к остальной
Рис 1.21 части электрической цепи. Соединение звездой получается при объединении начал или концов сопротивлений в одну точку (рис.1.21.б).
При расчете электрических цепей оказывается полезно преобразовать треугольник в звезду или совершить преобразование звезды в треугольник.
Замена треугольника эквивалентной звездой должна производиться таким образом, чтобы после указанной замены токи в остальной части цепи, а также напряжения между точками 1 и 2 , 2 и 3,3 и 1 остались без изменения.
С помощью законов Кирхгофа можно получить следующие формулы для определения сопротивлений эквивалентной звезды:
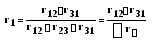
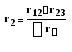
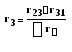 (
1.37)
(
1.37)
При замене резистивных элементов, соединенных звездой, эквивалентным треугольником, пользуются следующими формулами
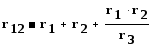
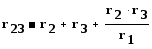 (1.38)
(1.38)
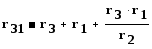
1.8.3. Метод контурных токов.
М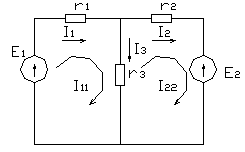 етод
контурных токов дает возможность
упростить расчет электрических цепей
по сравнению с методом расчета по законам
Кирхгофа за счет уменьшения числа
уравнений, которые приходится решать
совместно.Этот
метод заключается в том, что вместо
токов в ветвях определяются на основании
второго закона Кирхгофа так Рис
1.22 называемые контурные токи,
етод
контурных токов дает возможность
упростить расчет электрических цепей
по сравнению с методом расчета по законам
Кирхгофа за счет уменьшения числа
уравнений, которые приходится решать
совместно.Этот
метод заключается в том, что вместо
токов в ветвях определяются на основании
второго закона Кирхгофа так Рис
1.22 называемые контурные токи,
замыкающиеся в контурах. На рис.1.22. в виде примера показана двухконтурная цепь, в которой I11 и I22 — контурные токи. Токи в сопротивлениях r1 и r2 равны соответствующим контурным токам; ток в сопротивлении r3 являющемся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви r3 встречно.
Число уравнений , записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы p-q +1 уравнений. Так, в схеме рис.1.22 q = 2 p = 3; следовательно, число уравнений равно 3-2+1=2 (число уравнений независимых контуров).
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от заданного контурного тока в сопротивлениях, входящих в контур, берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис.1.22., где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис.1.22) могут быть записаны два уравнения по второму закону Кирхгофа, а
именно:
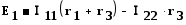 ,
, 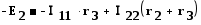 ,
,
здесь (r1 + r3) и (r2 + r3) — собственные сопротивления контуров 1 и 2, r3 —
общее сопротивление контуров 1 и 2. После определения контурных токов, легко найти и токи всех ветвей.
I1 = I11; I2 = I22 ; I3 = I11 — I22 .
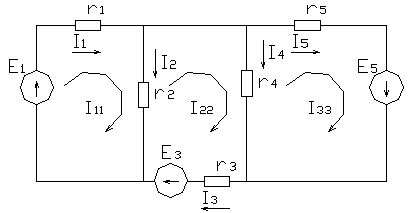
Рис 1.23
Пример 1.2.
Найти токи в схеме (рис. 1.23) при помощи метода контурных токов.
r1 = r2 = r3 = r4 = r5 = 10 Ом; E1 = E5= 50 В; E3 = 90 В.
Решение:
Выбираем направление всех контурных токов I11, I22 , I33 по часовой стрелке.
Записываем систему уравнений:
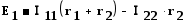
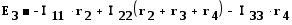
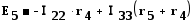
После подстановки численных значений:
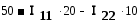
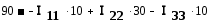 ,
, 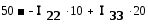
выразим I11 и I33 через I22 :
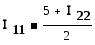 ,
, 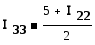
и подставим во второе уравнение системы
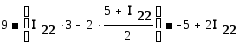
получаем в итоге I22 = 7А ; I11 = I33 = 6А.
В соответствии с выбранным положительным направлением токов в ветвях окончательно получим:
I1=I11=6A; I2=I11-I22=6-7= —1A; I3=I22=6A
I4=I22-I33=1A; I5=I33=6A
Параллельное соединение элементов r, l, c

На вход электрической цепи (рис. 2.14), состоящей из соединенных параллельно элементов R,L,C, подано синусоидальное напряжение
u(t)=Umsin(ωt+ψu).
Запишем уравнение по первому закону Кирхгофа для мгновенных значений токов цепи:
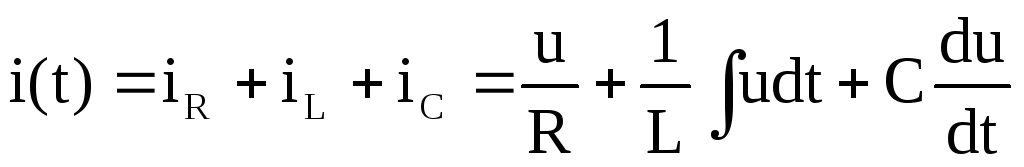 .
.
Сумме синусоидальных токов соответствует сумма изображающих их комплексных величин. И для действующих комплексных значений можно записать
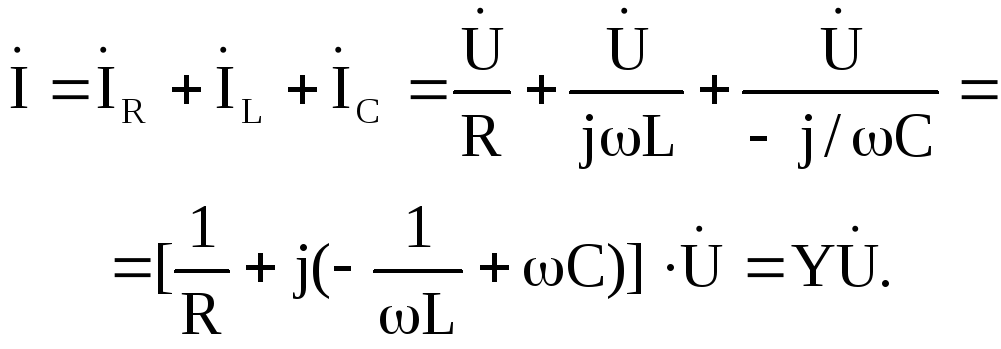
Величину 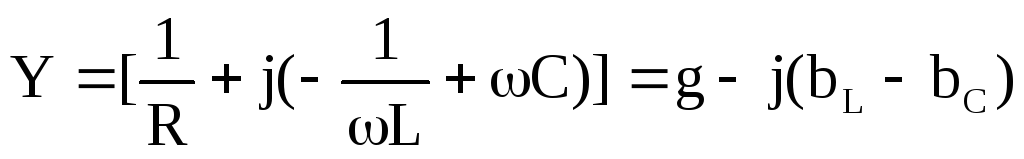 —
называют комплексной проводимостью
цепи с параллельным соединением элементовR,L,C,
которая определяется как сумма
проводимостей параллельных ветвей;
—
называют комплексной проводимостью
цепи с параллельным соединением элементовR,L,C,
которая определяется как сумма
проводимостей параллельных ветвей;
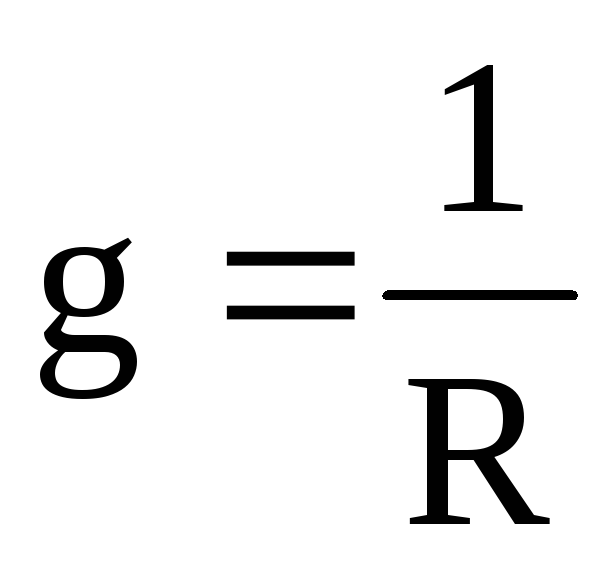 активная составляющая
проводимости;
активная составляющая
проводимости;
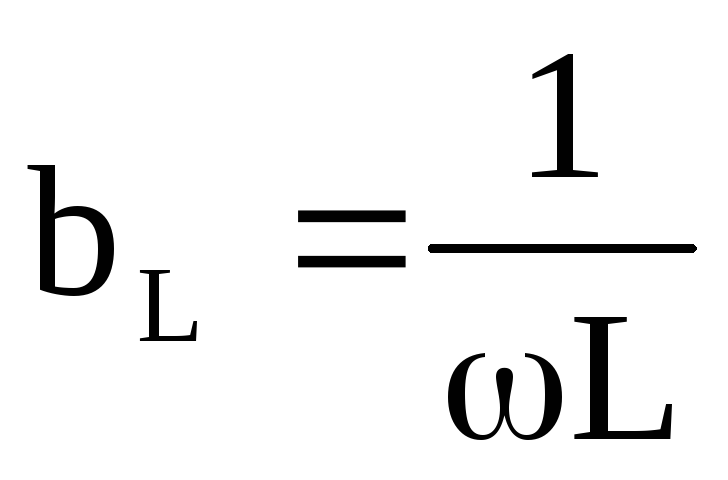 — реактивная
индуктивная составляющая проводимости;
— реактивная
индуктивная составляющая проводимости;
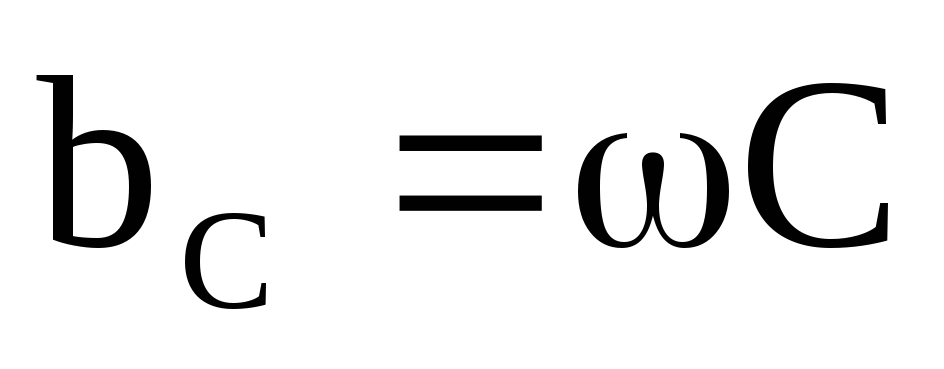 — реактивная
емкостная составляющая проводимости.
— реактивная
емкостная составляющая проводимости.
Запишем комплексную проводимость в показательной форме:
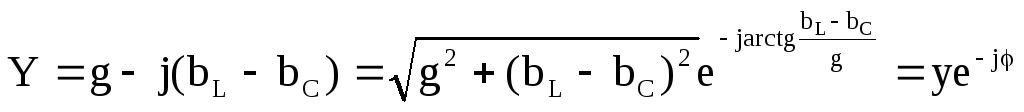 .
.
Тогда комплексный ток
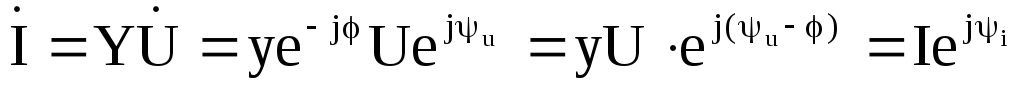 ,
,
где 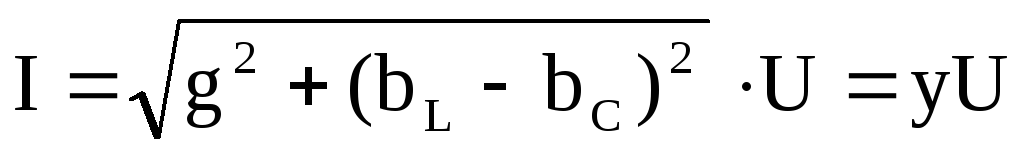 — действующее значение входного тока;
— действующее значение входного тока;
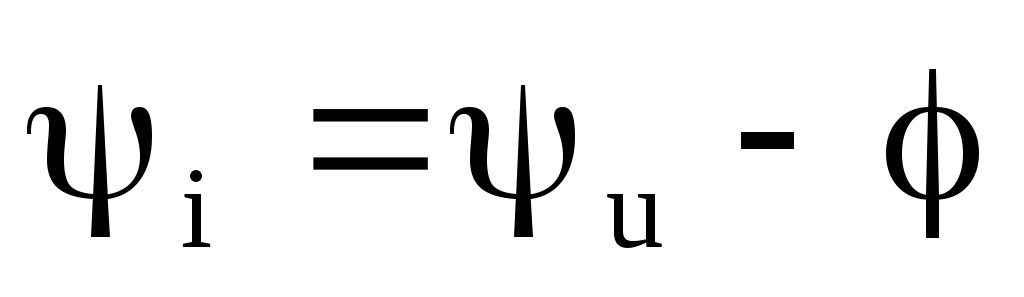 — начальная фаза тока;
— начальная фаза тока;
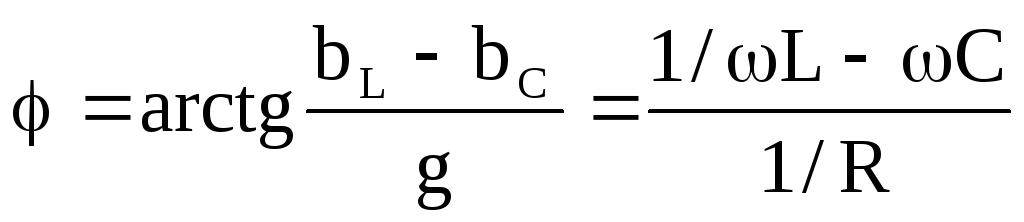 — угол сдвига фаз между напряжением на
зажимах цепи и входным током, который
определяется соотношением активной и
реактивной проводимостей.
— угол сдвига фаз между напряжением на
зажимах цепи и входным током, который
определяется соотношением активной и
реактивной проводимостей.
Построим векторную диаграмму токов и напряжений (рис. 2.15) на зажимах цепи, приняв начальную фазу напряжения за ноль.
Ток активного элемента совпадает по фазе с напряжением, поэтому на векторной диаграмме вектор этого тока изображается параллельно вектору напряжения. Ток индуктивного элемента отстает от напряжения на 90 градусов, поэтому на векторной диаграмме индуктивный ток повернут относительно вектора напряжения на 90 градусов по направлению движения часовой стрелки. Ток емкостного элемента опережает напряжение на 90 градусов, поэтому емкостный ток повернут относительно вектора напряжения против направления часовой стрелки на 90 градусов.
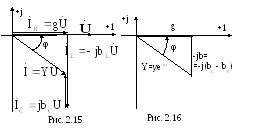 Необходимо
отметить, что ток индуктивного и
емкостного элементов находятся в
противофазе, вследствие чего в цепи
переменного тока при параллельном
соединении этих элементов могут
создаваться условия, невозможные для
цепей постоянного тока, когда токи
отдельных элементов будут значительно
превышать входной ток.
Необходимо
отметить, что ток индуктивного и
емкостного элементов находятся в
противофазе, вследствие чего в цепи
переменного тока при параллельном
соединении этих элементов могут
создаваться условия, невозможные для
цепей постоянного тока, когда токи
отдельных элементов будут значительно
превышать входной ток.
Треугольник, образованный векторами токов, принято называть треугольником токов.
Если каждую сторону треугольника токов поделить на вектор напряжения, то получим треугольник (рис. 2.16), подобный исходному и называемый треугольником проводимостей.
Как видно из полученных векторных диаграмм (рис. 2.15 и 2.16), угол сдвига фаз зависит от соотношения параметров цепи:
при IL>IC ( )
угол φ>0, ток отстает по фазе от
напряжения;
)
угол φ>0, ток отстает по фазе от
напряжения;
при IL<IC (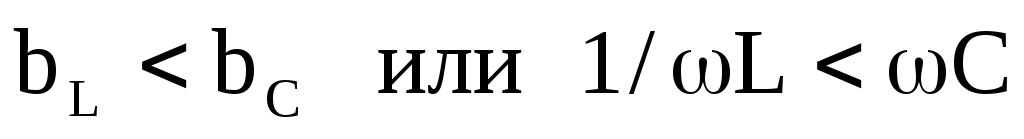 )
угол φ<0, ток опережает по фазе напряжение;
)
угол φ<0, ток опережает по фазе напряжение;
при IL=IC ( )
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление; такой режим работы цепи
называется режимомрезонанса токов.
)
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление; такой режим работы цепи
называется режимомрезонанса токов.
Расчет токов и напряжений при смешанном
соединении приемников
Расчет цепи переменного тока существенно облегчается, если синусоидально изменяющиеся токи, напряжения, ЭДС и т.д. изображать векторами и комплексными числами. Тогда для расчета цепей синусоидального тока можно применять все те методы, которые использовались для расчета цепей постоянного тока, только все токи, напряжения и сопротивления необходимо записывать в комплексной форме записи.
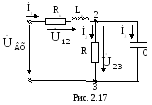
Рассмотрим решение прямой и обратной задачи для цепи с одним источником энергии рис. 2.17.
Прямая задача: при известных параметрах цепи R, Rк, Lк, C и токе третьей ветви I2 определить все остальные токи и напряжения. Частота питающей сети f. Расчет синусоидальных токов и напряжений удобно выполнять в комплексной форме записи.
Примем начальную фазу тока второй ветви равной нулю
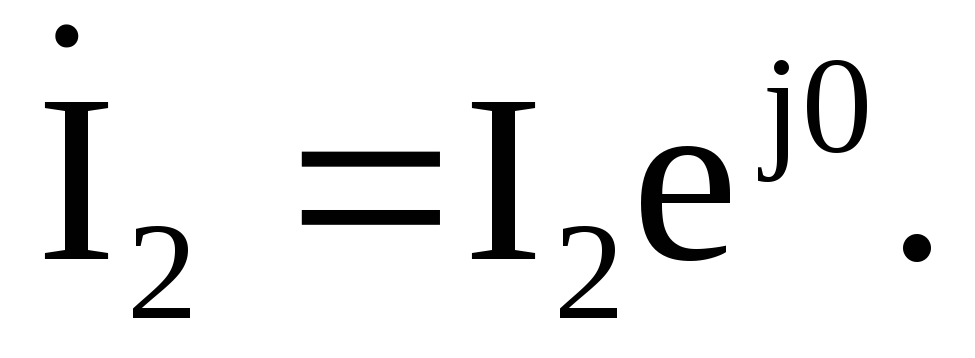
Комплексные сопротивления ветвей:
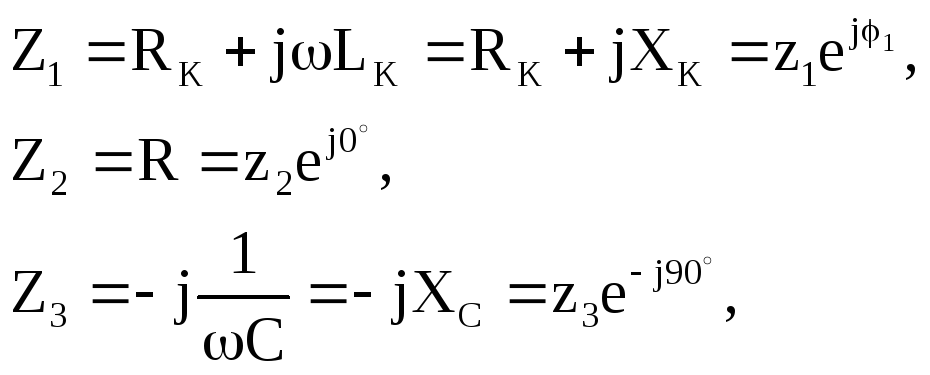
где 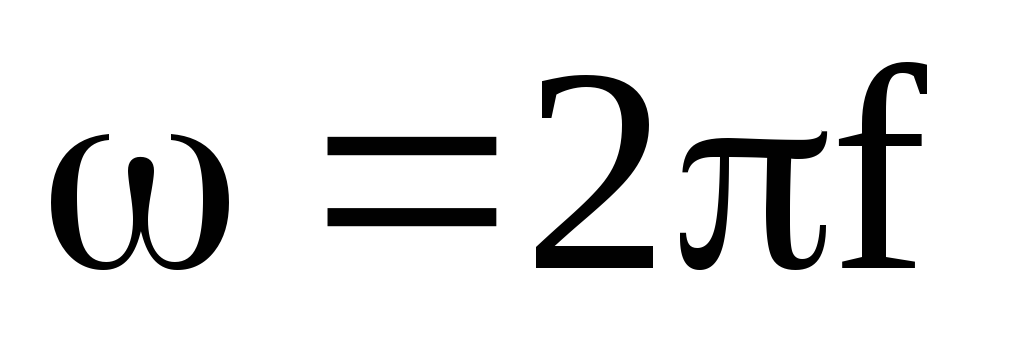 —
угловая частота.
—
угловая частота.
Зная ток I2 в одной из параллельных ветвей,
найдем напряжение на зажимах этих ветвей
по закону Ома: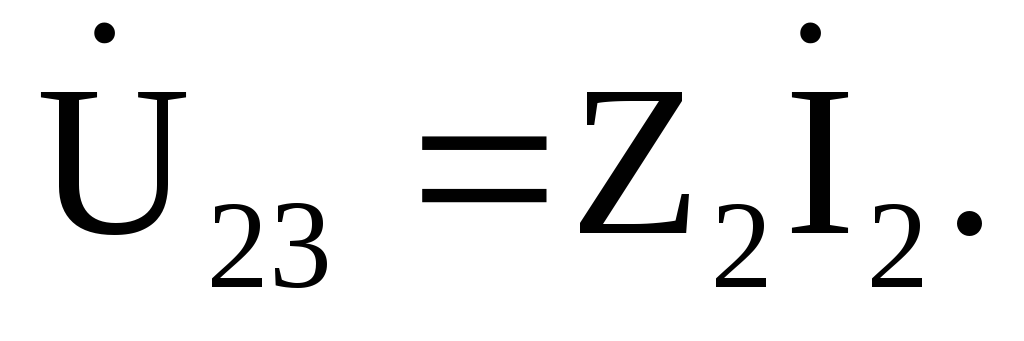
Ток третьей ветви
найдем: 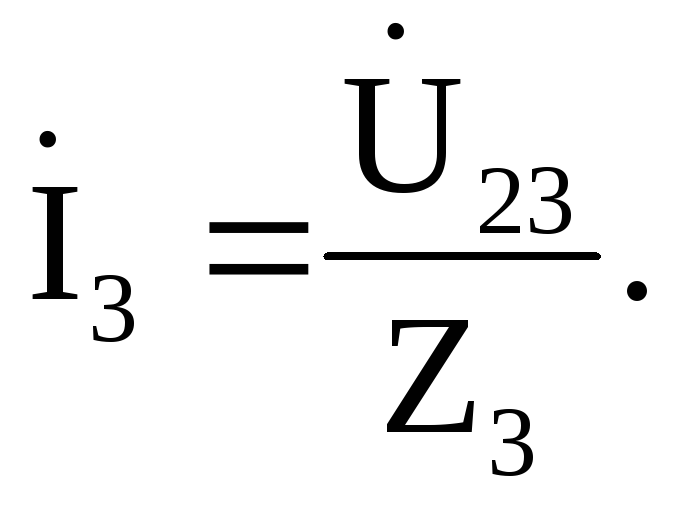
Ток I1 в неразветвленной части цепи найдем, составив уравнение по первому закону Кирхгофа для узла «2»:
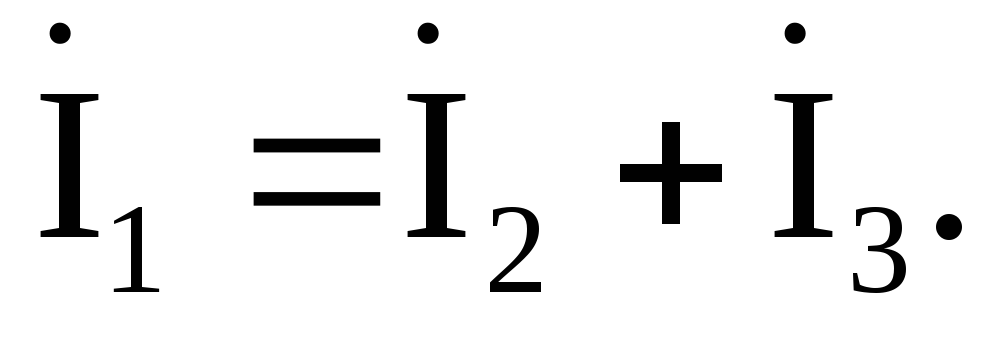
Напряжение на
зажимах первой ветви 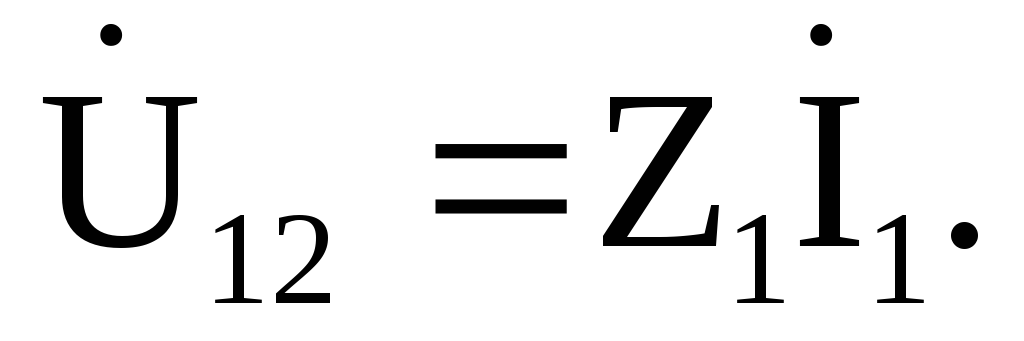
Напряжение на
зажимах цепи найдем, составив уравнение
по второму закону Кирхгофа: 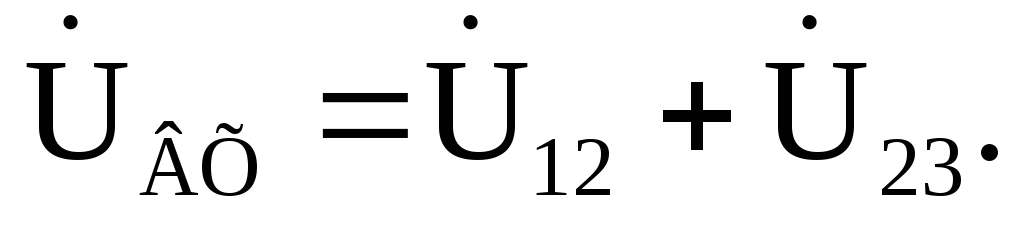
Построение векторной диаграммы удобно начинать с вектора тока второй ветви. Длины векторов токов и напряжений на векторной диаграмме откладываются в соответствующих масштабах по току miи напряжениюmu.
Начальная фаза
тока равна нулю 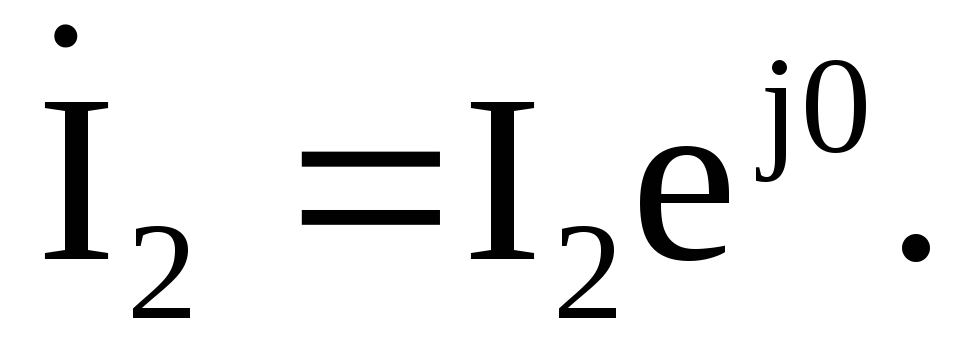 В соответствующем масштабе токов
изобразим вектор на комплексной
плоскости, совпадающим с осью действительных
чисел (рис. 2.18).
В соответствующем масштабе токов
изобразим вектор на комплексной
плоскости, совпадающим с осью действительных
чисел (рис. 2.18).
Н апряжение
апряжение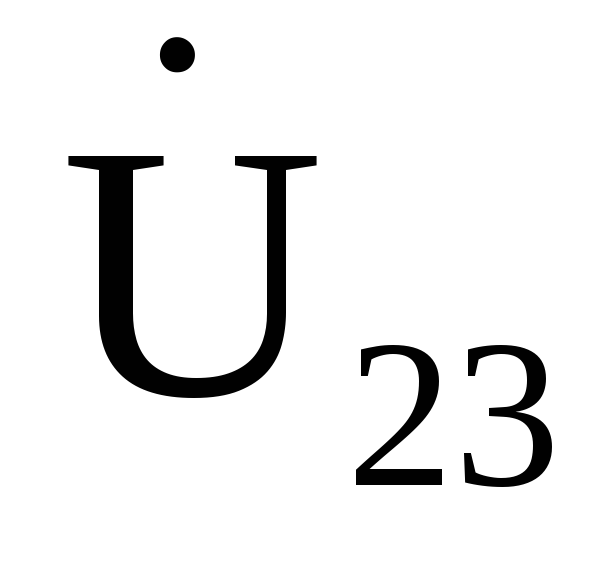 изображаем на векторной диаграмме
совпадающим по фазе с током второй
ветви, так как сопротивление этой ветви
чисто активное. Ток третьей ветви İ3, в которую включенидеальныйконденсатор, опережает напряжение
параллельных ветвей на угол 90°.
изображаем на векторной диаграмме
совпадающим по фазе с током второй
ветви, так как сопротивление этой ветви
чисто активное. Ток третьей ветви İ3, в которую включенидеальныйконденсатор, опережает напряжение
параллельных ветвей на угол 90°.
Согласно первому
закону Кирхгофа 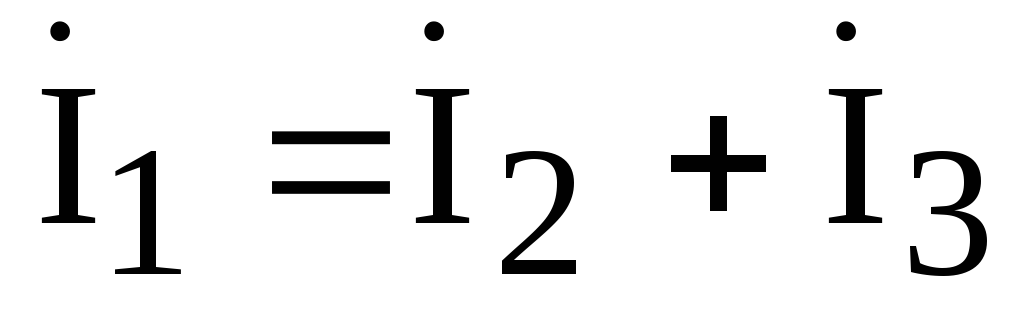 .
По правилу параллелограмма складываем
вектора токов İ2, İ3 и получаем
вектор тока İ1.
.
По правилу параллелограмма складываем
вектора токов İ2, İ3 и получаем
вектор тока İ1.
Напряжение 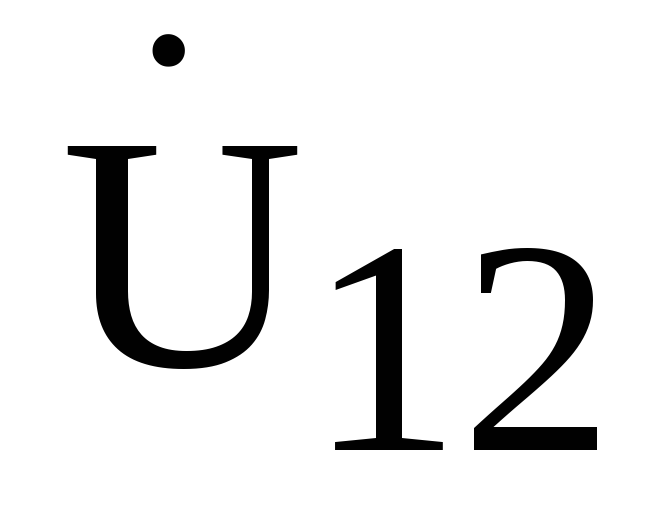 опережает
ток этого участка на угол φ1. Вектор
входного напряжения получаем путем
суммирования векторов согласно второму
закону Кирхгофa
опережает
ток этого участка на угол φ1. Вектор
входного напряжения получаем путем
суммирования векторов согласно второму
закону Кирхгофa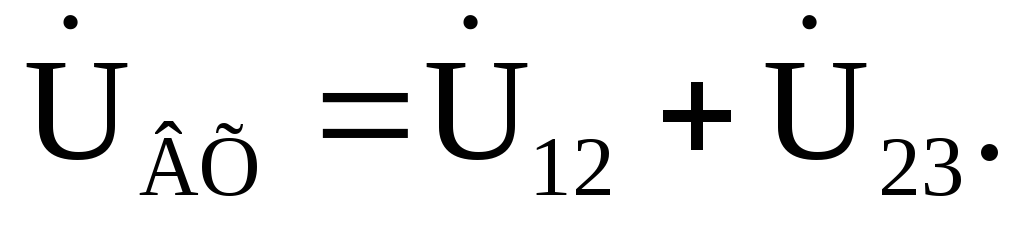
Начальные фазы, построенных токов и напряжений, должны совпадать с расчетными. Длины векторов в масштабе тока или напряжения должны соответствовать действующим значениям рассчитанных величин.
Обратная задача. Рассчитать токи и напряжения на всех участках электрической цепи, схема которой показана на рис. 2.7, питающейся от источника синусоидального напряжения с частотойf.
Известны параметры
цепи R,Rк,Lк,Cи величина напряжения на источнике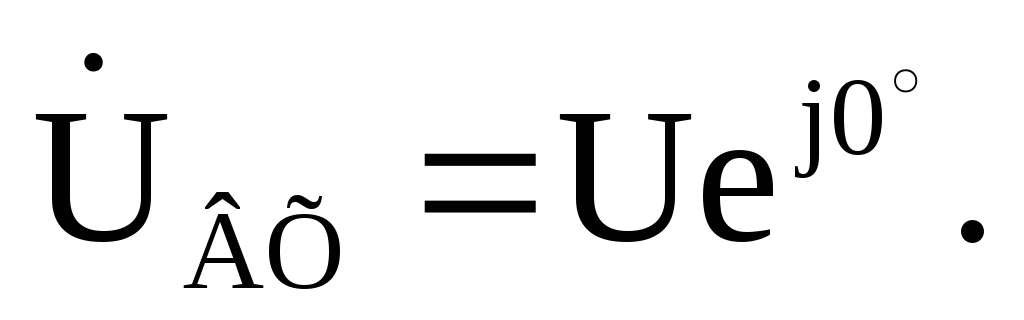
Комплексные сопротивления ветвей определяем аналогично предыдущей задаче:

Для того, чтобы по закону Ома определить ток на входе цепи, необходимо рассчитать комплексное сопротивление цепи относительно входных зажимов.
Сопротивления второй и третьей ветвей соединены параллельно, поэтому эквивалентное сопротивление относительно зажимов «23» можно рассчитать:
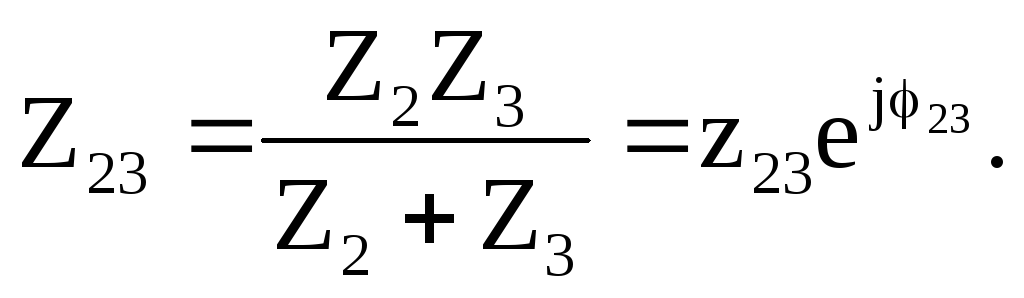
Относительно
входных зажимов сопротивление катушки
и сопротивление участка «23» соединены
последовательно, поэтому входное
сопротивление всей цепи можно определить
как сумму комплексных сопротивлений 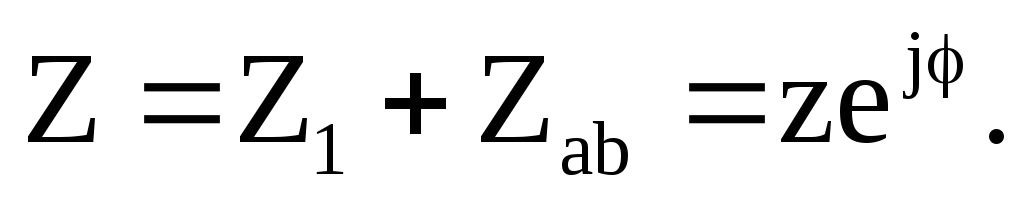
Определим входной
ток по закону Ома 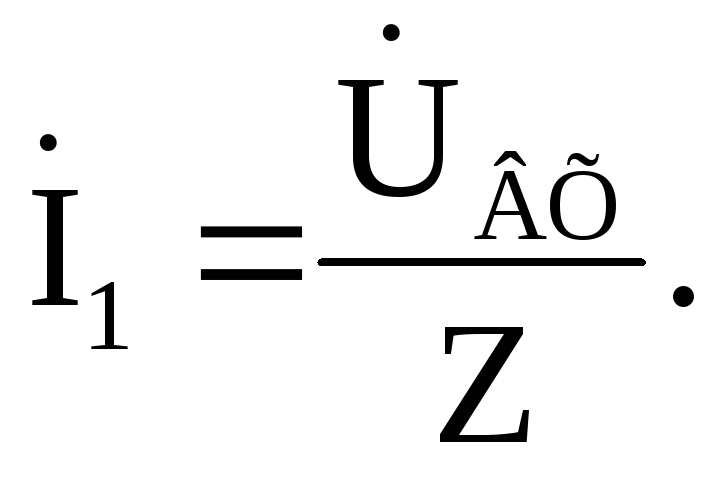
Напряжения на
участках цепи: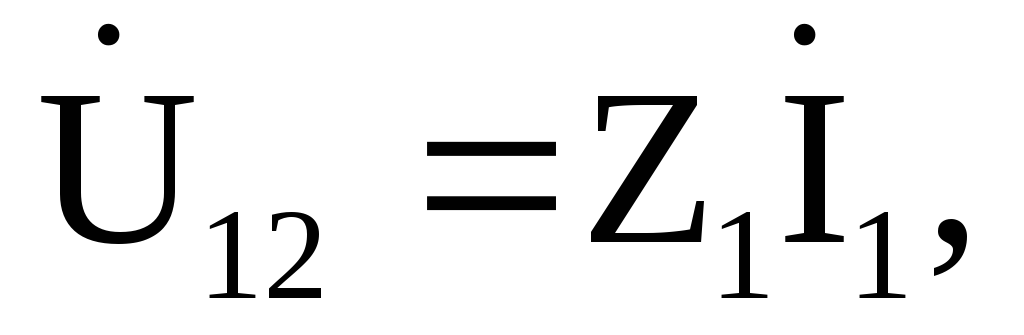
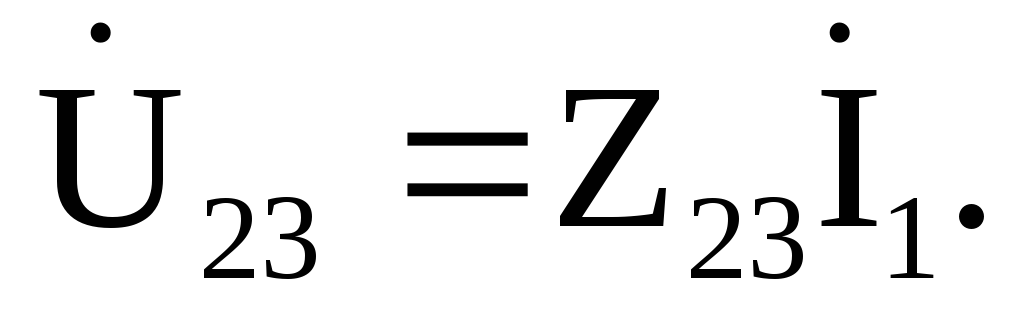
Т оки
параллельных ветвей определим по закону
Ома:
оки
параллельных ветвей определим по закону
Ома:
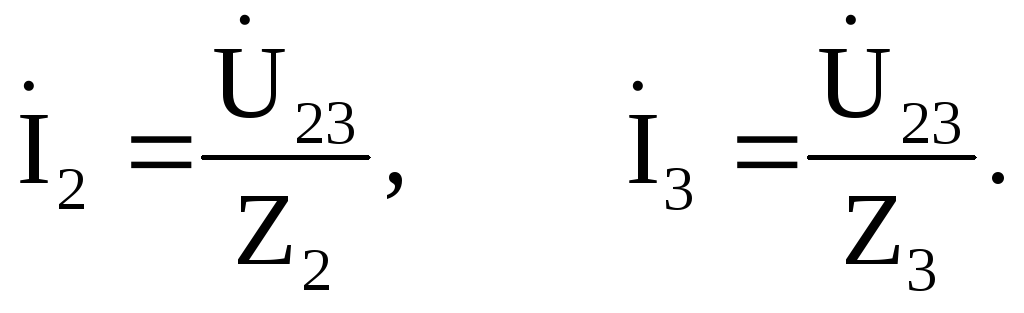
Построим векторную диаграмму токов и напряжений участков цепи (рис. 2.18). Для этого на комплексной плоскости в соответствующих масштабах тока miи напряженияmuпостроим вектора рассчитанных напряжений и токов со своими начальными фазами. На векторной диаграмме покажем выполнение законов Кирхгофа:
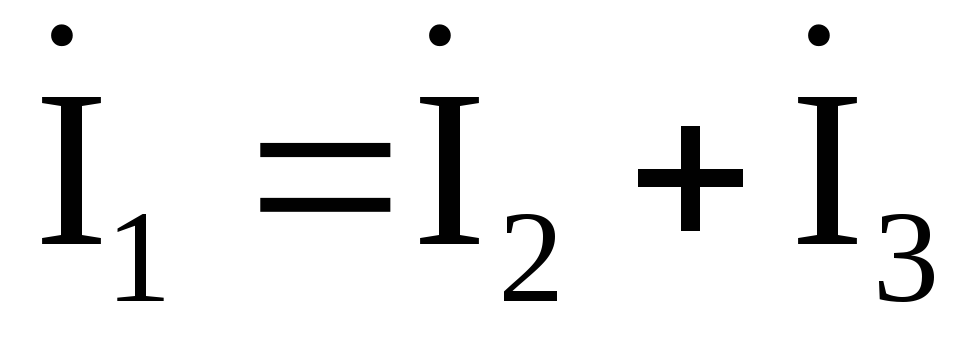 ,
, 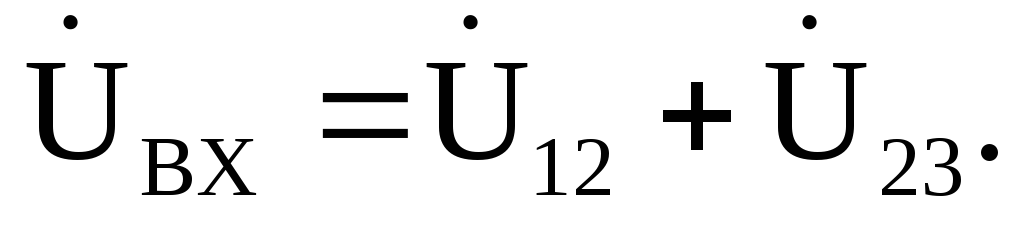
25
Способы соединения элементов
В электрических цепях применяют последовательное, параллельное и смешанное соединение резисторов.
Последовательным соединениемрезисторов — (приемников энергии) называется такое соединение, при котором резисторы соединены один за другим без разветвлений (рис. 2,а)ипри наличии источника питания по ним проходит один и тот же ток.
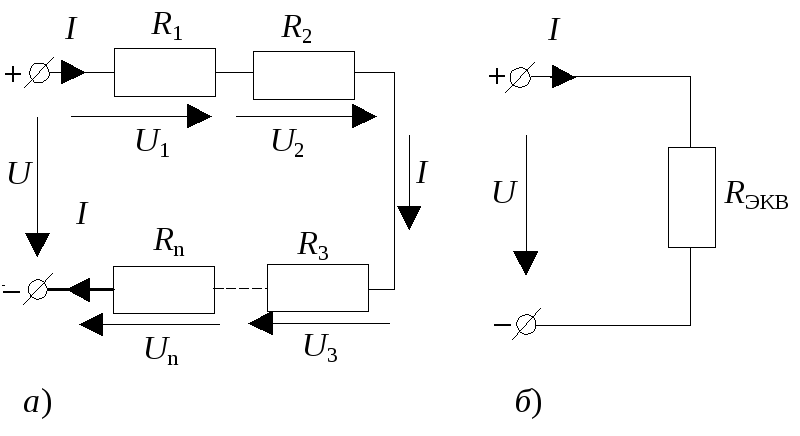
Рис. 2
При последовательном соединении nрезисторов токи заданной (рис. 2,а) и эквивалентной (рис. 2,б) схем будут одинаковыми. Поэтому, для них по второму закону Кирхгофа можно написать уравнения
U1 + U2 + U3 + … + Un = U
или
R1I + R2I + R3I + … + RnI = RэквI
и определить эквивалентное сопротивление
Rэкв = R1 + R2 + R3 + … + Rn.
Таким образом, эквивалентное сопротивление последовательно соединенных пассивных элементов равно сумме сопротивлений этих элементов.
При расчете цепи с последовательным соединением элементов при заданных напряжении источника питания и сопротивлениях элементов ток в цепи рассчитывают по закону Ома:
I = U/Rэкв.
Параллельное соединениехарактеризуется тем,что все элементы присоединяются к одной и той же паре узлов (рис. 3,а). При этом ко всем элементам приложено одно и тоже напряжениеU.
Для схемы (см. рис. 3, а) на основании первого закона Кирхгофа можно записать:
I = I1 + I2 + I3 + … + In
или, учитывая, что для каждой ветви по закону Ома Iк = U/Rк,
I = U/R1 + U/R2 + U/R3 + … + U/Rn = U(1/R1 + 1/R2 + 1/R3 + … + 1/Rn).
Заменим параллельно соединенные резисторы одним эквивалентным Rэкв(рис. 3,б). Для схемы рис. 3,бтокI = U/Rэкв.
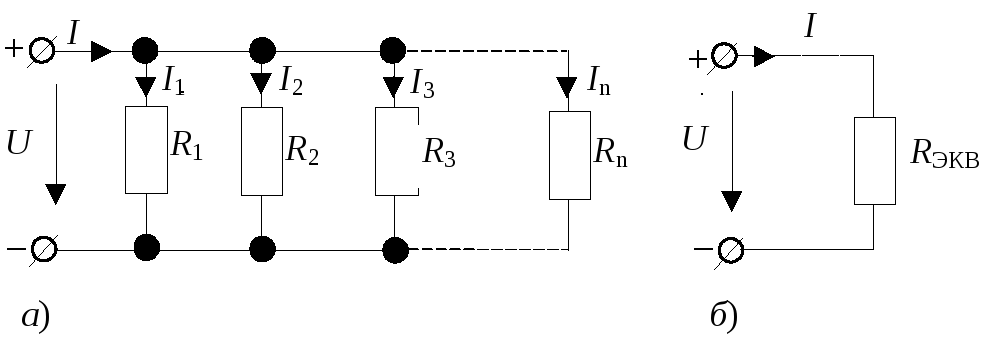
Рис. 3
По условиям эквивалентности при одном и том же напряжении Uв схемах (см. рис. 3,а,б), токи должны быть одинаковы. Поэтому
1/Rэкв = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn.
Величина, обратная сопротивлению, называется проводимостью G = 1/R :
Gэкв = G1 + G2 + G3 + … + Gn = 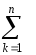 Gk ,
Gk ,
т.е. эквивалентная проводимость параллельно соединенных резистивных элементов равна сумме их проводимостей.Эквивалентная проводимость всегда больше проводимости любой части параллельных ветвей. Эквивалентной проводимостиGэквсоответствует эквивалентное сопротивлениеRэкв= 1/Gэкв, которое всегда меньше наименьшего из сопротивлений ветвей.
В частном случае, если параллельно соединены два резистора R1иR2, их эквивалентная проводимость 1/Rэкв=1/R1+ 1/R2, а эквивалентное сопротивлениеRэкв=(R1R2)/(R1+R2) (равно произведению этих сопротивлений, деленному на их сумму).
Если R1= R2, эквивалентное сопротивление будет в 2 раза меньше.
В общем случае, при nветвях с одинаковыми сопротивлениями резисторовR, включенных между двумя узлами, эквивалентное сопротивление между узламиRэкв= R/n.
Ток в неразветвленной части цепи с параллельным соединением резисторов может быть определен по закону Ома:I = U/Rэкв= GэквU.
Следует ясно представлять, что при подключении нового потребителя электроэнергии к сети образуется дополнительная параллельная ветвь, общая проводимость цепи при этом увеличивается, ее эквивалентное сопротивление уменьшается, ток в неразветвленной части цепи (ток источника питания) увеличивается.
Смешанное соединениепредставляет собой сочетание последовательного и параллельного соединений. Эквивалентное сопротивление находится путем постепенного упрощения схемы и “свертывания” ее таким образом, чтобы получилось одно сопротивление. При расчете токов в отдельных ветвях схему “развертывают” в обратном порядке.
5 Эквивалентные преобразования схем. Последовательное и параллельное соединение элементов электрических цепей
Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы,
где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.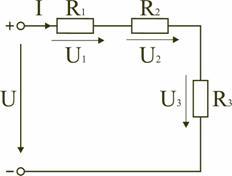
Электрическая цепь с последовательным соединением элементов
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I.
На основании второго закона Кирхгофа общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3,
откуда следует Rэкв = R1 + R2 + R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв.
После этого расчет цепи сводится к
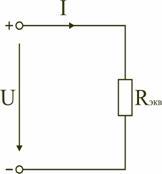
определению тока I
всей цепи по закону Ома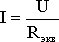 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи.
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением.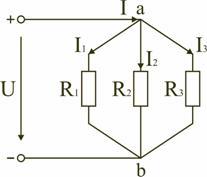
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I
= I1 + I2 + I3,
т.е. 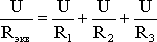 ,откуда
следует, что
,откуда
следует, что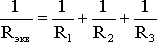 .
.
В
том случае, когда параллельно включены
два сопротивления R1 и R2,
они заменяются одним эквивалентным
сопротивлением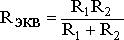 .
.
Из соотношения, следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв = g1 + g2 + g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями
U = IRэкв = I1R1 = I2R2 = I3R3.
Отсюда
следует, что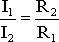
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Параллельное соединение элементов в цепи синусоидального тока
В электрических цепях переменного тока имеются цепи с параллельным соединением потребителей электроэнергии, при котором все потребители находятся под одним и тем же напряжением. При этом на ток в цепи каждого из потребителей не влияет их число. Значение тока в каждом из них определяется только значениями соответствующих сопротивлений и значением подводимого напряжения. Наличие на различных участках цепей переменного тока как активных, так и реактивных элементов приводит к тому, что сопротивление этих участков имеет комплексный характер. В качестве примера рассмотрим цепь, представленную на рис. 8, а. Данная цепь состоит из двух параллельно соединенных ветвей, характер сопротивлений которых различен. Эта схема может рассматриваться как схема замещения реальной цепи, содержащей неидеальные катушку индуктивности и конденсатор. СопротивлениеR1 учитывает наличие потерь в витках обмотки катушки, аR2 – потери энергии в диэлектрике конденсатора.
Анализ работы данной цепи проведем на основе построения векторной диаграммы токов и напряжений. Вначале рассмотрим графоаналитический метод расчета. Определим действующие значения токов ветвей, используя закон Ома:
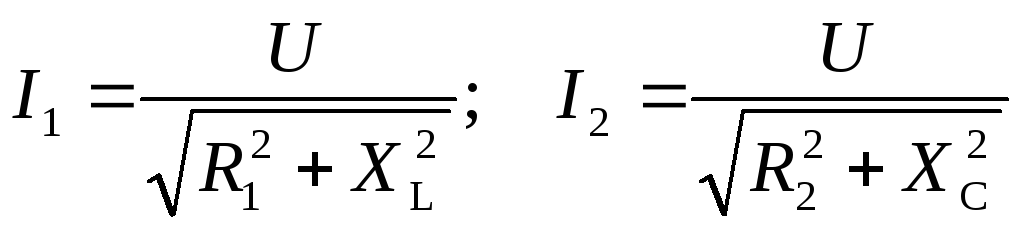 .
.
Данные соотношения позволяют определить длины векторов токов на комплексной плоскости. Для построения вектора тока на комплексной плоскости необходимо, помимо длины вектора, знать его ориентацию относительно вектора напряжения на соответствующем участке цепи (угол сдвига фаз). Углы сдвига фаз 1и2 между напряжением и токами ветвей могут быть определены из следующих соотношений:
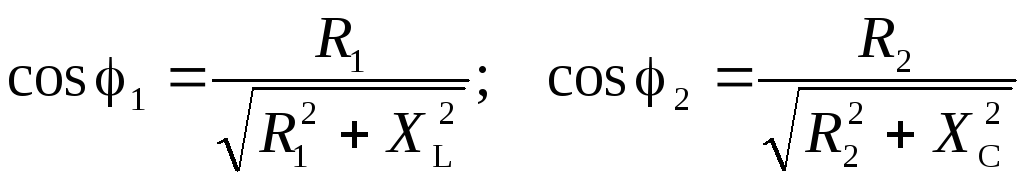 .
.
Примем начальную фазу напряжения uна входе рассматриваемой цепи равной
нулю, что соответствует ориентации
вектора напряжения, совпадающей с
положительным направлением оси
вещественных чисел (рис. 8,б).
Рассчитанные выше углы сдвига фаз1и2 представляют
собой углы между соответствующими
векторами токов (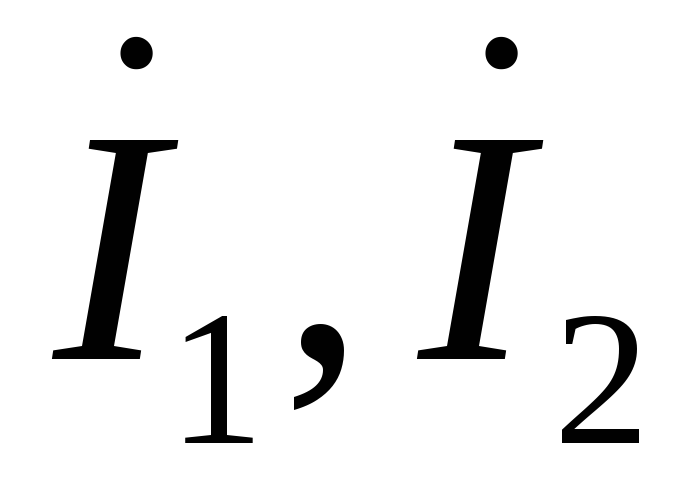 )
и напряжения
)
и напряжения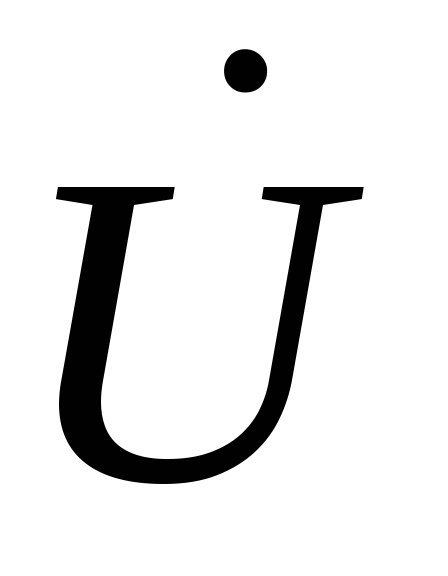 на
комплексной плоскости. Причем, при
активно-индуктивном характере
сопротивления (в данной схеме первая
ветвь) напряжение опережает ток на угол1, а при
активно-емкостном сопротивлении (вторая
ветвь) – напротив, напряжение отстает
по фазе от тока на угол2.
Вектор общего тока цепи в соответствии
с первым законом Кирхгофа равен
геометрической сумме векторов токов
ветвей:
на
комплексной плоскости. Причем, при
активно-индуктивном характере
сопротивления (в данной схеме первая
ветвь) напряжение опережает ток на угол1, а при
активно-емкостном сопротивлении (вторая
ветвь) – напротив, напряжение отстает
по фазе от тока на угол2.
Вектор общего тока цепи в соответствии
с первым законом Кирхгофа равен
геометрической сумме векторов токов
ветвей:
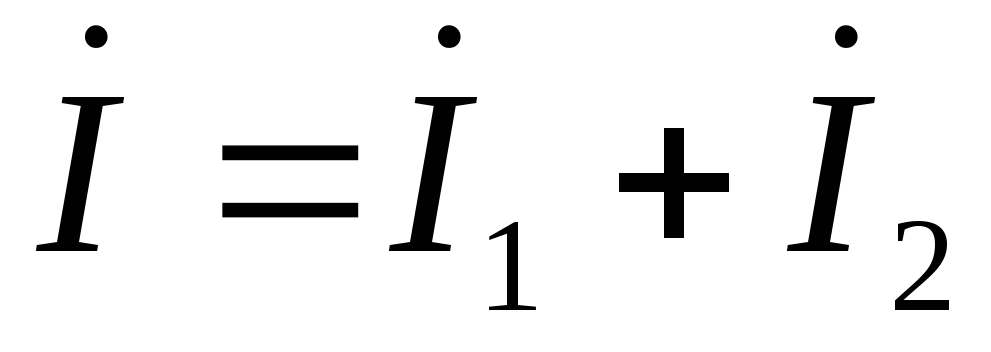 .
.
Действующее значение общего тока Iопределяется графически по векторной
диаграмме как длина вектора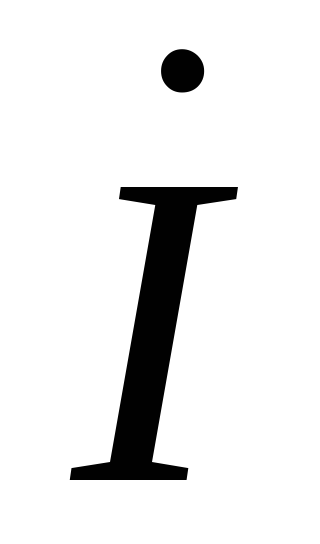 .
.
Графоаналитический метод не удобен для расчета разветвленных цепей: он отличается громоздкостью и невысокой степенью точности. Более эффективным является использование комплексного метода расчета с использованием проводимостей. Под комплексной проводимостью участка цепи (ветви) Yпонимают величину, обратную комплексному сопротивлению этого участкаZ:
Y=1/Z = G – jB = Ye–j
Единица измерения проводимости – (Ом-1) или (См) (читается: сименс). Вещественная часть комплексной проводимостиG называется активной проводимостью участка цепи, а мнимая часть комплексной проводимостиB называется реактивной (индуктивной или емкостной) проводимостью. Учитывая что комплексное сопротивление участка цепи в общем виде может быть представлено в видеZ = R+jX, запишем выражение для комплексной проводимости через активную и реактивную составляющие комплексного сопротивления участка цепи:
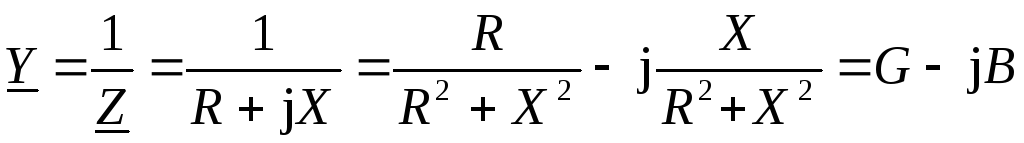 ;
;
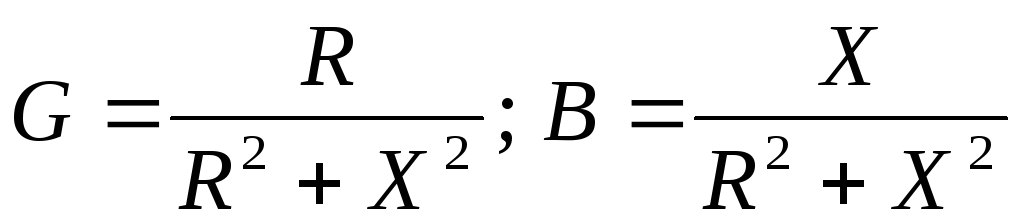 .
.
Если комплексное сопротивление участка цепи имеет индуктивный характер, то B> 0, если же характер комплексного сопротивления емкостный, тоB< 0. Для рассматриваемой схемы проводимости ветвей имеют вид
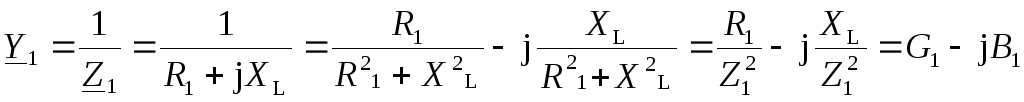 ;
;
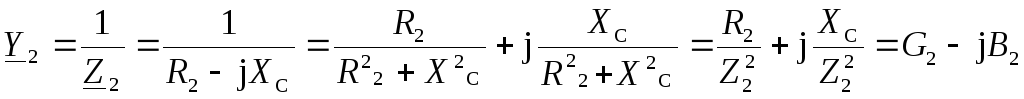 .
.
Таким образом, выражения для активных (G1иG2) и реактивных (B1иB2) проводимостей ветвей рассматриваемой цепи имеют вид
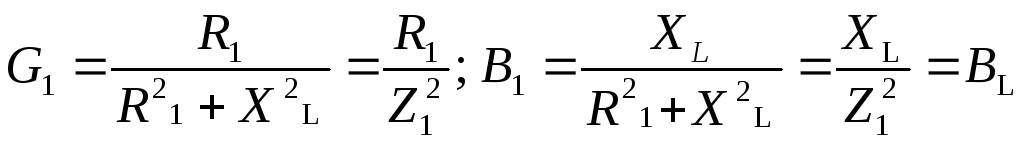 ;
;
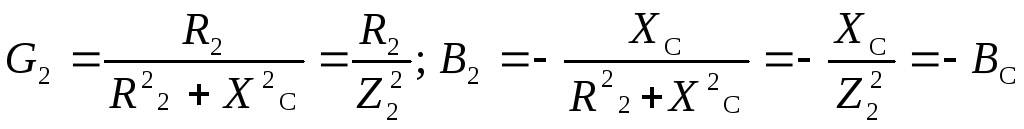 .
.
Здесь через Z1иZ2обозначены модули комплексных сопротивлений ветвей. Токи ветвей на основе закона Ома могут быть представлены в виде
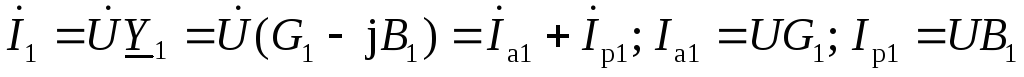 ;
;
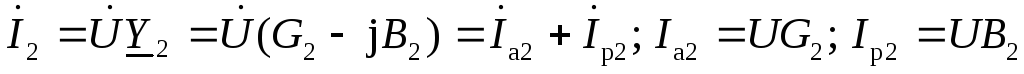 .
.
Анализ полученных выражений показывает,
что ток любого участка цепи может быть
представлен в виде суммы двух составляющих.
Векторы активных составляющих токов
ветвей (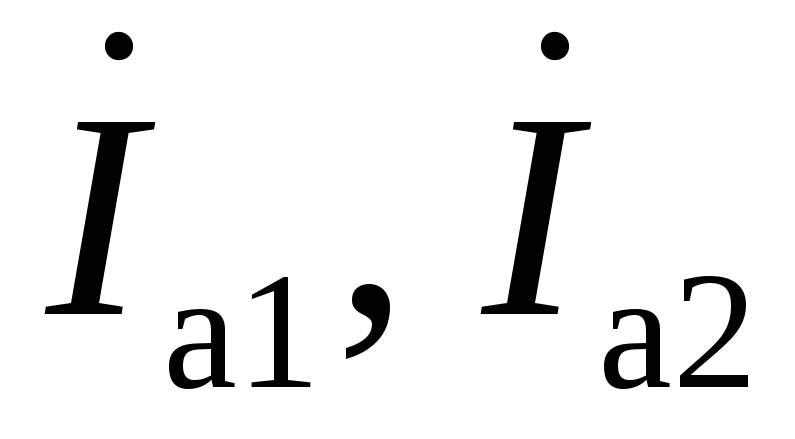 )
параллельны вектору напряженияU,
тогда как векторы реактивных составляющих
токов ветвей (
)
параллельны вектору напряженияU,
тогда как векторы реактивных составляющих
токов ветвей (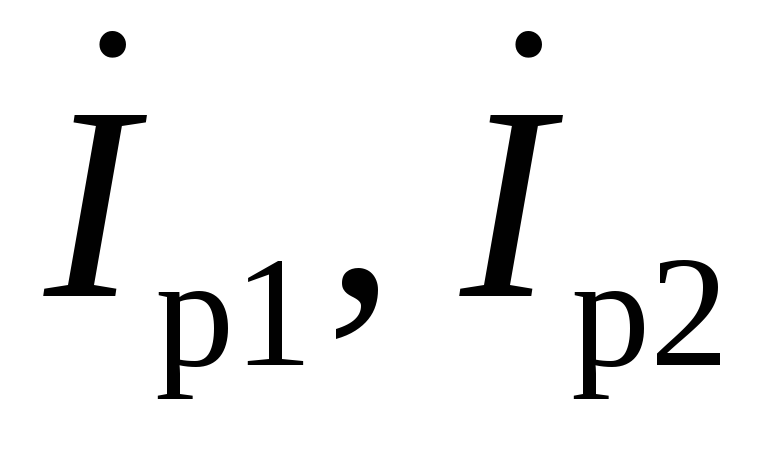 )
ему перпендикулярны. Представление
токов ветвей в виде суммы двух составляющих
является удобным математическим приемом,
непосредственному измерению они
недоступны. На векторной диаграмме
(см. рис. 8,б) реактивная составляющая
тока первой ветви
)
ему перпендикулярны. Представление
токов ветвей в виде суммы двух составляющих
является удобным математическим приемом,
непосредственному измерению они
недоступны. На векторной диаграмме
(см. рис. 8,б) реактивная составляющая
тока первой ветви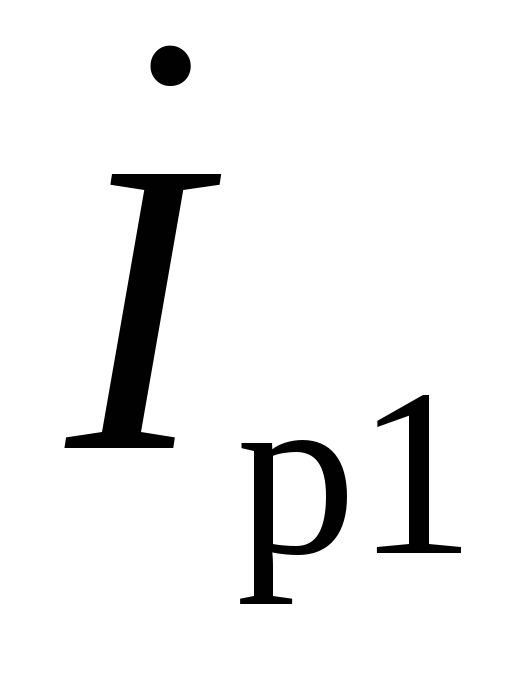 отстает по фазе от вектора напряжения
на угол 90, а реактивная
составляющая тока второй ветви
отстает по фазе от вектора напряжения
на угол 90, а реактивная
составляющая тока второй ветви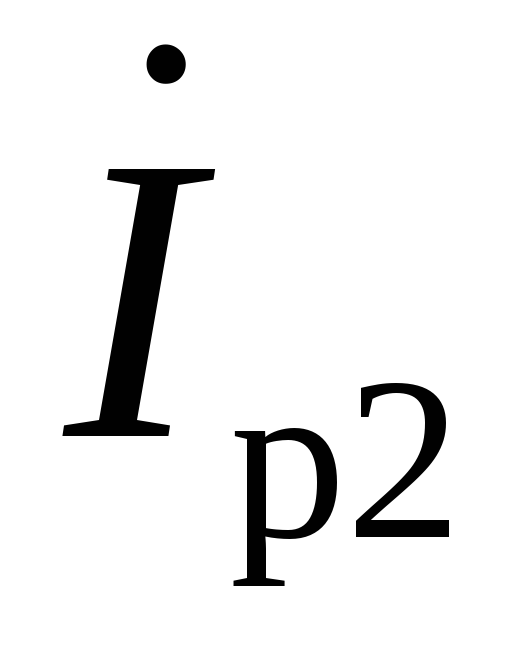 опережает вектор напряжения на такой
же угол.
опережает вектор напряжения на такой
же угол.
На основании первого закона Кирхгофа, составленного для точки разветвления, получим выражение для общего тока Iв неразветвленном участке цепи:
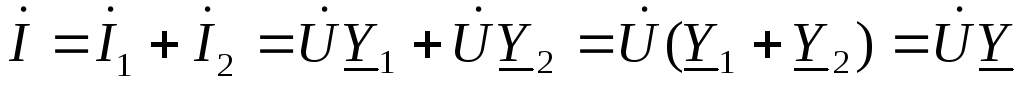 .
.
Из этого выражения следует, что комплексная проводимость электрической цепи при параллельном соединении сопротивлений оказывается равной сумме комплексных проводимостей соответствующих параллельных ветвей:
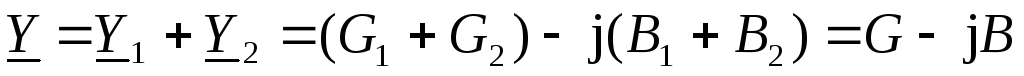 .
.
Отсюда в общем случае для произвольного числа параллельных ветвей активная проводимость электрической цепи оказывается равной сумме активных проводимостей всех параллельных ветвей, а реактивная проводимость цепи – равной алгебраическойсумме реактивных проводимостей всех параллельных ветвей, входящих в данную электрическую цепь.
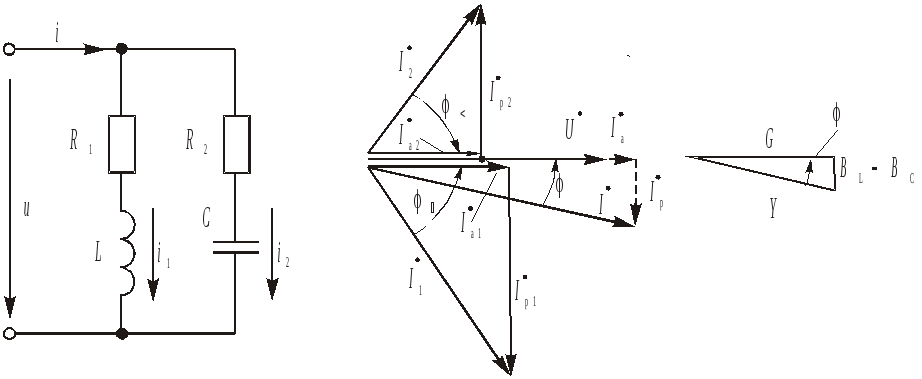
а)б)в)
Рис. 8
Модуль полной проводимости цепи определяется из выражения
Y = 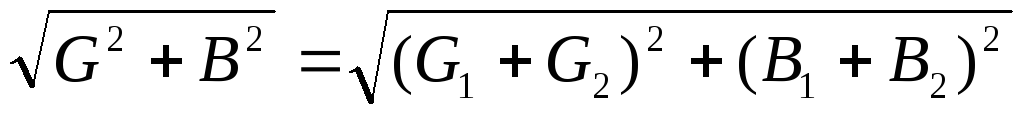 .
.
Полная проводимость цепи в то же время является и величиной, обратной ее полному сопротивлению Y= 1/Z.
Из треугольника токов, представленного
на векторной диаграмме (см. рис. 8, б),
можно получить треугольник проводимостей
для рассматриваемой цепи, разделив
стороны этого треугольника на комплексное
напряжение (см.
рис. 8,в).
(см.
рис. 8,в).
Из треугольника проводимостей следует, что cos=G/Y, а sin=B/Y= (BLBC)/Y.
С учетом этого полная, активная и реактивная мощности цепи могут быть определены через соответствующие проводимости:
S = UI = U 2Y; P = UIcos = U2G ; Q = UIsin = U2B.




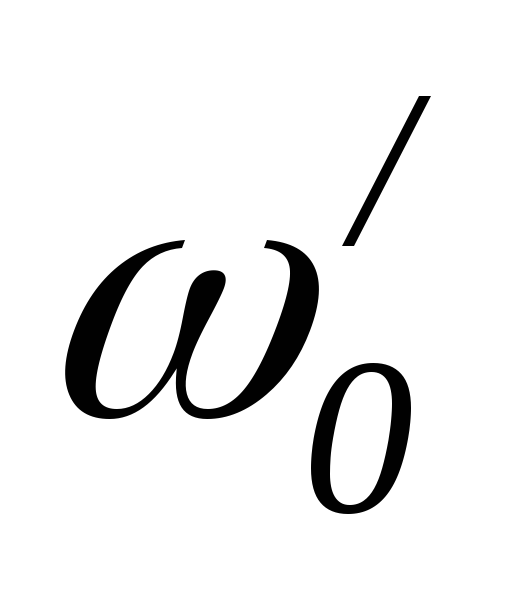 =0
=0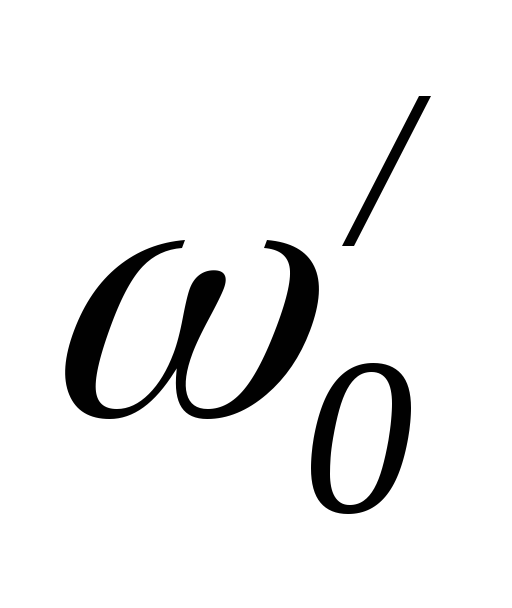 =0
=0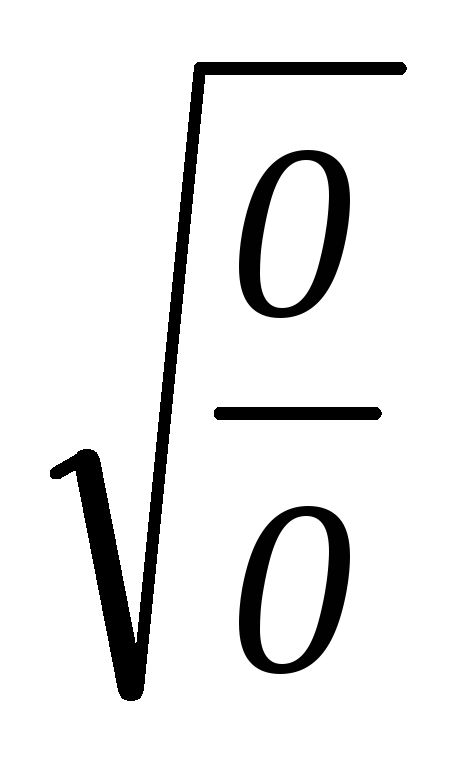 – с физической точки зрения это означает,
что входное сопротивление данного
контура равно ее волновому, которое не
зависит от частоты, значит, резонанс
будет иметь место при любой частоте.Для доказательства этого положения
определим входное сопротивление цепи:
– с физической точки зрения это означает,
что входное сопротивление данного
контура равно ее волновому, которое не
зависит от частоты, значит, резонанс
будет иметь место при любой частоте.Для доказательства этого положения
определим входное сопротивление цепи: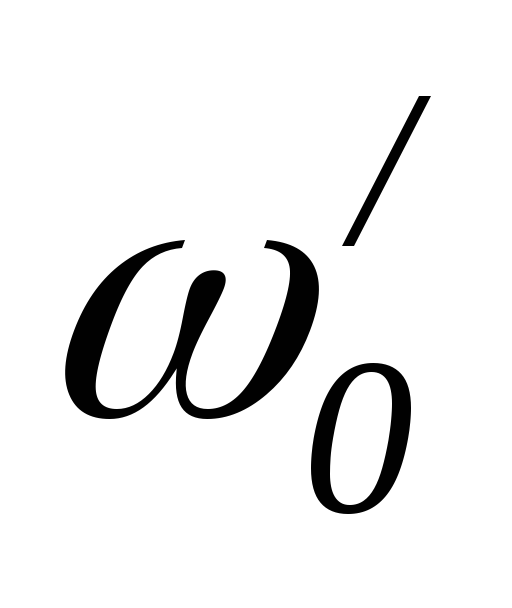 — единственную резонансную частоту.
— единственную резонансную частоту.