29.Падение и потеря напряжения в лэп

Потеря напряжения это алгебраическая разность межу абсолютной величиной напряжения в начале и конце линии. ΔU = U_к ± U_н. Потеря напряжения – это алгебраическая разность значения напряжения, измеренные вольтметром в начале и конце. ± стоит из-за того что напряжение в конце линии может быть больше, так и меньше чем в начале линии.

Допустимые потери напряжения:

1) для сетей напряжения 220 – 380 в 5-6,5%

2) для ВЛ 6-35 кВ 8%, для КЛ 6%.

3) в аварийном режиме 10-12%.

Вектор падения напряжения – это геометрическая разность между векторами комплексами напряжений в начале и конце линии.

Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линий. Это AB

Продольная составляющая падения U АС=∆ U

12^k, k – означает проекция на напряжение конца линии U_2. Поперечная составляющая:

5.Понятие о пропускной способности электропередачи

Пропускная способность электропередачи – наибольшая активная мощность трех фазной электропередачи, которую можно передавать длительно-установившемся режиме с учетом режима технического ограничения. Наибольшая передаваемая мощность электропередачи ограничена условием статической устойчивости генератора, передающих и принимающих частей энергосистемы, которые связанны с номинальным напряжением.

На практике эксплуатации электрических систем следует, что 500 – 700 кВ ограничена только работой генераторов, а электропередачи ниже по условию допустимого нагрева проводов.

Иногда предельная передаваемая мощность характеризуется коэффициентом изменения фаз волны, а также длиной линий.

Пропускная способность линий.

Напряжение, кВ	Наибольшая передаваемая мощность, МВт	Наибольшее расстояние передачи, км
0,38	0,05 — 0,15	0,5 — 1,0
10	2,0 — 3,0	10 — 15
35	5 — 10	30 — 50
110	25 — 50	50 — 150
150	40 — 70	100 — 200
220	100 — 200	150 -250
330	200 — 300	300 — 400
500	700 — 900	800 — 1200
750	1800 — 2200	1000 — 1500
1150	4000 — 6000	2000 — 3000

Повышение пропускной способности: увеличение напряжения, уменьшение сопротивления проводов (расщепление фаз на несколько проводов, до 25% снижение).

30.Выбор номинального напряжения сети

Величиной напряжения определяются параметры линий электропередачи и выбираются электрооборудование подстанций и сетей, а следовательно, раз­меры капиталовложений, расход цветного металла, потери электроэнергии и эксплуатационные расходы.

Номинальное напряжение определяется передаваемой активной мощностью и длиной линий электропередачи.

Для предварительной оценки номинального напряжения можно воспользоваться данными таблицы или провести расчет по эмпирическим формулам.

UH0M, к В	1, км		Р.МВт
35	5…20		5…20
110	50…100		15…60
150	75…150		50…100
220	150…300		150…300

Для определения длины линий надо учитывать, что длина трассы из-за непрямолинейности и неровностей рельефа местности на 5… 15% больше расстояний по прямой между рассматриваемыми пунктами.

Номинальное напряжение можно предварительно определить по известной передаваемой мощности Р, МВт и длине линии 1, км, по формуле Стилла:

Эта формула применима для линий длиной до 250 км и передаваемых мощностей, не превышающих 60 МВт. В случае больших мощностей, передаваемых на расстояние до 1000 км, используется формула А.М.Зелеского:

Удовлетворительные результаты для всей шкалы номинальных напряжений от 35 до 1150 кВ дает формула Г.А.Илларионова:

Варианты проектируемой электрической сети или отдельные ее участки могут иметь разные номинальные напряжения. Обычно сначала определяют номинальное напряжение головных, более загруженных участков. Участки кольцевой сети, как правило, необходимо выполнять на одно номинальное напряжение.

В результате расчетов будут получены значения нестандартных напряжений отдельных линий сети. Выбираем ближайшее.

3.4. Падение и потеря напряжения в линии

На рис. 3.2, е приведена векторная диаграмма для ли­- нейных напряжений в начале и в конце линии и . Эта диаграмма аналогична диаграмме на рис. 3.2, в.

Падение напряжения—геометрическая (векторная) разность между комплексами напряжений начала и конца линии. На рис. 3.2, е падение напряжения — это вектор

, т. е.

. (3.26)

Продольной составляющей падения напряжения называют проекцию падения напряжения на действитель­- ную ось или на напряжение , =АС на рис. 3.2, е. Индекс «к» означает, что — проекция на напряжение конца линии

. Обычно выражается через данные в конце линии: , , .

Поперечная составляющая падения напряжения — это проекция падения напряжения на мнимую ось, ==СВ на рис. 3.2, е. Таким образом,

. (3.27)

Часто используют понятие потеря напряжения — это ал- гебраическая разность между модулями напряжений на­- чала и конца линии. На рис. 3.2,е . Если попе­- речная составляющая мала (например, в сетях кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения на­- пряжения.

Расчет режимов электрических сетей ведется в мощно­- стях, поэтому выразим падение напряжения и его состав­- ляющие через потоки мощности в линии.

Известны мощность и напряжение в конце линии (рас- чет напряжения в начале линии по данным конца). Выра­- зим ток в линии в (3.27) через мощность в конце про­- дольной части линии и напряжение :

. (3 28)

В результате получим

. (3.29)

Приравняв в (3.29) действительные и мнимые части, по­- лучим выражения продольной и поперечной составляющих падения напряжения по данным конца:

; (3.30)

. (3.31)

Напряжение в начале линии

, (3.32)

где 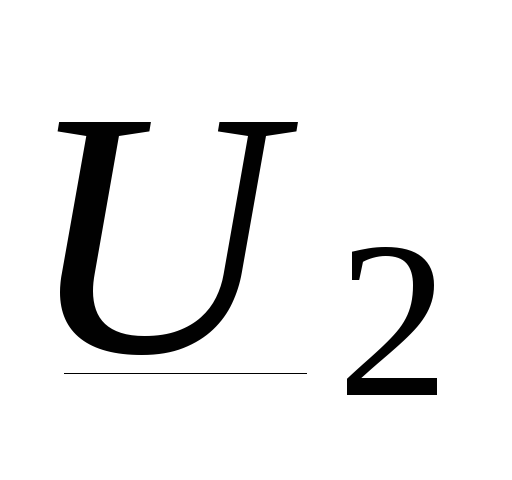известно; , определяем из (3.30) и (3.31).

Соответственно модуль и фаза напряжения в начале ли­- нии (см. рис. 3.2, е)

; (3.33)

. (3.34)

Определение напряжения в начале линии по данным конца по выражениям (3.32), а также (3.30), (3.31) экви­- валентно использованию закона Ома.

Пример 3.2. Определим падение и потерю напряжения в линии, рас­- смотренной в примере 3.1, по известным мощности нагрузки =15+ +j10 МВА и напряжению в конце линии j2,65 кВ.

Используя параметры линии, а также мощность в конце линии , приведенные в примере 3.1, по (3.30), (3.31) найдем продольную и поперечную составляющие падения напряжения по данным конца:

кВ ;

кВ .

Напряжения иприведены на рис. 3.2, з. В большем мас­- штабе продольная и поперечная составляющие падения напряжения изображены на рис 3.2, и.

Напряжение в начале линии по (3.32) равно

кВ.

Модуль напряжения в начале линии

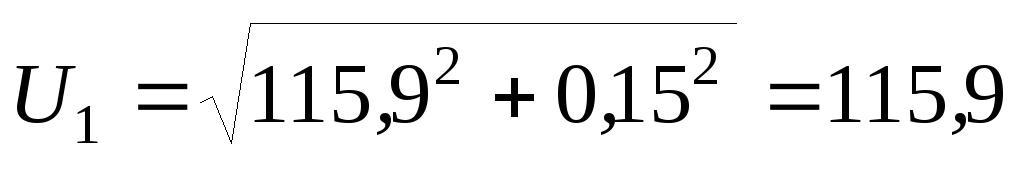кВ.

Потеря напряжения

кВ.

Известны мощность и напряжение в начале линии (рас- чет напряжения в конце линии по данным начала). Напра­- вим по действительной оси, т.е. примем, что (рис. 3.2, ж). На рис. 3.2, ж изменилось положение осей в сравнении с рис. 3.2, е. Продольная составляющая паде­- ния напряжения =ВС‘—это проекция падения на­- пряжения на действительную ось или на . Поперечная составляющая падения напряжения =АС’—это про­- екция падения напряжения на мнимую ось. Один и тот же вектор падения напряжения проектируется на различ­- ные оси. Поэтому

,.

Если выразить ток в линии аналогично (3.28) через известные в данном случае мощность в начале продольной ветви линии и , то получим выражения, аналогичные (3.30), (3.31):

; (3.35)

. (3.36)

Напряжение в конце линии

, (3.37)

где известно; , определяются из(3.35), (3.36). Модуль и фаза равны

; (3.38)

. (3.39)

Определение напряжения в конце линии по данным на­- чала по выражениям (3.37), а также (3.35), (3.36) эквива­- лентно применению закона Ома в виде (3.25).

Пример 3.3. Определим падение и потерю напряжения в линии, рассмотренной в примере 3.1, по известным мощности в начале линии =15,61+j9,6 МВА и напряжению в начале линии кВ; = 115,9 кВ.

Используя параметры линии, приведенные в примере 3.1, по выра­- жениям (3.35), (3.36) найдем продольную и поперечную составляющие падения напряжения по данным начала:

кВ:

кВ.

Напряжение в конце линии по (3.37)

кВ.

Модуль напряжения в конце линии

кВ.

Потеря напряжения кВ.

Результаты определения напряжений в примерах 3.1, 3.2 и 3.3 раз­- личаются на погрешность округления, в примере 3.1 кВ, а в примере 3.2 кВ. Соответственно в примерах 3.2, 3.3 потери напряжения равны 6,1 и 6,2 кВ. При проведении расчетов напряжений с четырьмя значащими цифрами погрешность округления при опреде­- лении, например, в данных примерах равна 116—115,9=0,1 кВ. Ес­- ли проводить расчеты с восемью значащими цифрами, то результаты определения и различаются на 0,00094 кВ, т. е. погрешность ок­- ругления равна 0,001 кВ.

Справочник электрика. Потери напряжения, мощности и энергии

Основной причиной появления отклонений напряжения в электрической сети являются потери напряжения в линиях электропередачи и силовых трансформаторах, причем, главное значение имеют потери напряжения в линиях. На рис. 1, а приведены электрическая схема, включающая в себя источник питания С и две подстанции, связанные линией W без ответвлений. Здесь U₁ — напряжение в начале, U₂ — в конце линии.

Векторная диаграмма электрических величин для линии W, построенная на основе ее схемы замещения (рис. 1, б), приведена на рис. 1, в. Обычно нагрузка линии имеет активно-индуктивный характер, поэтому вектор тока İ отстает по фазе от вектора напряжения Ú₂ конца линии на угол φ. Вектор напряжения в начале линии Ú₁, получается в результате суммирования вектора напряжения в конце линии Ú₂ с активной ΔÚ_wa =İR и реактивной ΔÚ_wp = _jİX составляющими падения напряжения на линии İZ_w, где R, jX, Z — соответственно активное, индуктивное и полное сопротивления линии.

Модуль (длину) вектора İZ_w называют падением напряжения на линии. Вектор падения напряжения на линии можно разложить на две составляющие:

направленную по вектору Ú₂ — продольную составляющую падения напряжения ΔÚ_w;

направленную перпендикулярно вектору Ú₂ — поперечную составляющую падения напряжения δÚ_w.

Рис. 1. Потеря напряжения в линии

Из точки 0 на рис. 1, в радиусом, равным длине вектора 0, можно провести дугу окружности до пересечения в точке b с прямой Оα (по направлению вектора Ú₂). Отрезок 0b равен модулю вектора Ú₁ т. е. напряжению в начале линии. Потеря напряжения в линии равна длине отрезка cb, т. е. арифметической разности U₁ – U₂ Для упрощения потерю напряжения вычисляют приближенно и полагают ее равной не отрезку cb, а отрезку cd. Ошибка, получающаяся в результате такой замены, относительно невелика и допустима в расчетах. Тогда можно получить следующее выражение для потери напряжения в линии:

 

где Р, Q — соответственно, активная Р и реактивная Q мощности нагрузки в конце линии; U₂ — напряжение в конце линии.

Таким образом, нужно различать падение напряжения и потерю напряжения на линии. Падение напряжения — это модуль геометрической разности векторов напряжения по концам линии

|ΔÚ_w| = |Ú₁ — Ú₂|.

Потеря напряжения — это арифметическая разность напряжений по концам линии, т. е. ΔUw = U₁ — U₂.

Потеря напряжения показывает, насколько напряжение в конце линии отличается от напряжения в ее начале. Падение напряжения обычно больше потери напряжения из-за сдвига по фазе векторов Ú₁ и Ú₂. Практику в ГРС интересует потеря напряжения, а не падение напряжения, потому что потеря напряжения связывает наиболее простой формулой напряжения в начале и конце линии.

Потеря напряжения в проводах линий электропередач

     Передача электроэнергии на расстояния выполняется с помощью линии электропередач (ЛЭП), которые делятся на воздушные и кабельные. При передаче энергии часть ее расходуется на нагрев проводов, образование

электромагнитных полей. Эти потери электроэнергии нужно толковать как технологические потери электроэнергии на ее передачу, а не как в других отраслях — потери от брака, когда нарушается технологический процесс. В основном электроэнергию в одного потребителя передают по двум одинаковым по параметрам ЛЭП для обеспечения надежности сетей. То есть, когда аварийно отключится одна из ЛЭП второй останется питать потребитель.

     ЛЭП состоят из проводов, которые в свою очередь изготавливаются из проводников, в основном из меди или алюминия. Все материалы, даже проводники, имеют сопротивление. При передаче электроэнергии по проводам длиной более 10 м сопротивлением провода пренебрегать нельзя, так как ток в них вызывает заметное падение напряжения согласно закону Ома.

 

С целью экономии энергии и обеспечения незначительного колебания напряжения на зажимах приемника при изменении сопротивления или тока приемника потеря напряжения должна быть невелика при сравнении с номинальным напряжением приемника. Ток потребителя (или нагрузки) при различных сопротивлениях приемника изменяется от нуля до наибольшего своего значения. Потеря напряжения при этом тоже колеблется от нуля до своего максимального значения.

 

В электрических сетях напряжением до 20 кВ отклонения напряжения на зажимах потребителей в нормальном режиме не должны превышать ± 5%, а в аварийном — ± 10%.

     Отклонение напряжения нежелательны как в сторону увеличения так и в сторону уменьшения по отношению к номинальной напряжения. При больших отклонениях напряжения наблюдается потерь мощности и энергии, изменяются нагрузки потребителей, ухудшается качество продукции, возможно браковки продукции, сокращение срока работы элементов сети и оборудование, нарушение нормальной деятельности устройств автоматики и релейной защиты, что может привести к авариям и отключениям потребителей. Например, для ламп накаливания при освещенность возрастает на 40%, а срок работы уменьшается в 3 раза, при освещенность уменьшается на 30%, а срок работы увеличивается в 2 раза, но уменьшается производительность труда и ухудшается состояние и здоровье человека.

     В случае если сеть имеет несколько приемников, присоединенных к разным городам линии, потерю напряжения во всей сети определяется как сумма потерь напряжения на отдельных ее участках:

     Под наибольшей потерей напряжения понимают потерю напряжения на пути от источника питания до наиболее удаленного потребителя электроэнергии сети одного класса напряжения. Причем определяют наибольшую потерю напряжения как в нормальном режиме работы электросети, так и в аварийном (например, при отключении одного ЛЭП из двух параллельных). Расчетные наибольшие потери напряжений должны быть меньше наиболее допустимые, как в нормальном, так и в аварийном режиме.

§12.4. Падение и потеря напряжения в линиях электроснабжения

ущерб (доменные цехи, котельные производственного пара, подъемные и вентиляционные установки шахт, аварийное освещение и др.). Они должны работать непрерывно. Для потребителей второй категории (самых многочисленных) допускаются перерывы в питании на ограниченное время. К потребителям третьей категории относятся вспомогательные цехи и другие объекты, для которых допускается перерыв в электроснабжении до одних суток.

Для повышения надежности энергоснабжения предусматривается питание потребителей от двух независимых сетей и автоматически включаемого резервного источника электроэнергии. Различают «горячий» и «холодный» резервные источники. «Горячий» резервный источник обеспечивает немедленное аварийное питание, его используют для безаварийной остановки потребителя.

Дальнейшее улучшение систем электроснабжения промышленных предприятий связано с повышением напряжения питания (с 220 до 380В, с 6 до 10кВ и т.д.) при максимально возможном приближении высокого напряжения к потребителям (глубокий ввод) и уменьшении числа ступеней трансформации.

Карточка № 12.3 (220).

Электроснабжение промышленных предприятий

Что составляет основу ЕЭС СССР?	ТЭС			35
	ГЭС			148
	АЭС			69
	ЛЭП			178
Какое свойство не относится к достоинствам ЕЭС?	Надежность питания потребителей			94
	Возможность менять		направление	13
	потоков энергии в течение суток
	Постоянство напряжения и частоты			63
	Возможность получения высоких и			243
	сверхвысоких напряжений
Какое напряжение допустимо в особо опасных	660В			29
условиях?
	36В			185
	12В			27
	380/220В			219
К какой категории потребителей следует отнести	К первой категории			59
компрессорные установки шахт?
	Ко второй категории			188
	К третьей категории			92
Какое электропитание обеспечивает безаварийную	От	резервного	источника,	222
остановку агрегата?	подготовленного к запуску
	От	резервного	источника,	213
	работающего вхолостую

В проводах возникает падение напряжения, пропорциональное току и сопротивлению линии. Напряжение на зажимах потребителя U меньше напряжения на зажимах источника U1. Разность DU=U1—U называют потерей напряжения.

Потерю напряжения часто выражают в процентах от номинального значения напряжения потребителя: DUU ×100

При заданном напряжении источника от потери напряжения зависит напряжение на зажимах потребителя, поэтому значение потери напряжения строго регламентируется. В линиях, по которым осуществляется питание силовой (электродвигатели, гальванические ванны и др.) нагрузки, допускается потеря напряжения, не превышающая 6% от номинального напряжения потребителя. В осветительных сетях допускается потеря напряжения не более 2,5%. В

зависимости от конкретных условий могут быть установлены и другие предельные значения потери напряжения.

Несоблюдение норм потери напряжения приводит к нарушению работы потребителей, уменьшению пусковых и вращающих моментов двигателей, изменению светового потока осветительных установок. Например, при уменьшении напряжения на 10% световой поток ламп накаливания уменьшается на 1/3. Незначительное превышение напряжения относительно номинального приводит к резкому сокращению срока службы ламп накаливания.

Нетрудно видеть, что в цепях постоянного тока понятия падения и потери напряжения совпадают: U=IRпр, где I — ток в линии; Rпр — сопротивление провода линии.

Несколько сложнее выглядят эти зависимости в цепях переменного тока.

Рассмотрим векторную диаграмму токов и напряжений, изображенную на рис. 12.4. Проходящий по линии ток нагрузки I сдвинут по фазе относительно напряжения U на угол ϕ, определяемый коэффициентом мощности нагрузки. Падение напряжения на активном сопротивлении линии IR совпадает по фазе с током I, а падение напряжения на реактивном сопротивлении линии Iх опережает по фазе ток I на 90° (считаем, что емкостное сопротивление линии меньше ее индуктивного сопротивления). В этом случае падением напряжения считают

g g g

векторную разность напряжений в начале и конце линии: U =U1 −U = I Z , где Z — комплекс полного сопротивления линии.

Рис. 12.4. Связь векторов напряжений на входе и	Рис. 12.5. Приближенное выражение потери напряжения
выходе линии	отрезком аб

Для потребителя важно значение напряжения, поэтому целесообразно ввести понятие потери напряжения U как разности действующих значений напряжений U1 и U.

Потерю напряжения U можно выразить через модуль		g
		вектора U . В практических
расчетах принимают потерю напряжения (отрезок ас на рис.		12.5) равной проекции вектора
g g	g
падения напряжения U = I Z на вектор U (отрезок ab).

Рис. 12.6. Вид векторной диаграммы,если пренебречь реакт

При расчете сетей напряжением до 1000В считают, что реактивное сопротивление линии мало по сравнению с ее активным сопротивлением и им можно пренебречь. Векторная диаграмма токов и напряжений для этого случая представлена на рис. 12.6. Полагая ab≈ac, находим U≈ab=IRcosϕ, где U — потеря напряжения в линии; I — ток нагрузки, проходящий в проводах линии; R=Rпр — активное сопротивление проводов линии; cosϕ — коэффициент мощности

потребителя электроэнергии.

Карточка № 12.4 (183).

Падение и потеря напряжения в линиях электроснабжения

Напряжение на зажимах источника электроэнергии в сети					1%			193
постоянного тока 26В. Напряжение на зажимах
					2%			21
потребителя 25В. Определить потерю напряжения в
					4%			228
процентах
Сопротивление одного провода двухпроводной линии					0,5В			53
постоянного тока 0,05Ом. Через нагрузку течет ток 10А.
					1В			200
Рассчитать потерю напряжения
					2В			88
					Для	решения	задачи	234
					недостаточно данных
Напряжение источника		сети	переменного	тока 230В,	а) 10В; б) определить нельзя			117
напряжение на зажимах потребителя 220В. Определить: а)
потерю напряжения; б) падение напряжения					а) Определить нельзя;			206
					б) 10В
					а) 10В; б) 10В			8
Активное сопротивление одного провода двухпроводной					0,5В			240
линии	переменного	тока	0,05Ом.	Реактивным
					1В			46
сопротивлением пренебречь. Через нагрузку течет ток 10А.
					2В			122
Найти потерю напряжения
					Для	решения	задачи	83
					недостаточно данных
В условиях предыдущей задачи сдвиг фаз между током и					0,5В			155
напряжением равен 60°. Определить потерю напряжения
					1В			112
					2В			128
					Для	решения	задачи	2
					недостаточно данных

§12.5. Расчет проводов по допустимой потере напряжения в линиях постоянного, однофазного и трехфазного тока

Схема цепи постоянного тока изображена на рис. 12.7. Выразим потерю напряжения через ток в линии и сопротивление проводов:

DU=Ul-U=IRnp.

Рис. 12.7. Схема сети постоянного тока	Рис. 12.8. Схема сети однофазного переменного тока
Сопротивление проводов

Rпр=2l/(δS), где l — длина линии, м; S — площадь поперечного сечения провода, мм2; δ — удельная электропроводность материала провода, м/(Ом×мм2).

Для меди δм=53м/(Ом×мм2), для алюминия δа=32м/(Ом×мм2). Поскольку линия двухпроводная, то в формулу введен коэффициент 2.

Таким образом,

DU=I2l/(δS), откуда S =I2l/(δΔU).

Для удобства расчетов последнюю формулу преобразуют, для чего числитель и знаменатель умножают на напряжение U:

S = 2Il U = 2lP δDU U δDUU

Здесь потеря напряжения DU выражена в вольтах. Кроме того, в формулу вводят процентную потерю напряжения. В результате получают

S = 200lP δDUU 2

где S — в мм; l — в м; Р — в Вт, U — в В; DU— в %.

На рис. 12.8 изображена электрическая цепь однофазного тока. Реактивное сопротивление линии не учитываем. Согласно § 12.4, DU=IRпpcosj.

	Введем процентную потерю напряжения:
		DUU	=	I 2l	cosϕ
		100
	Отсюда			δ S
		2Il cosϕ ×100
	S =
	где DU — в %.	δDUU
						200lUI cosϕ		200lP
	Умножив числитель и знаменательна U, получим S =						=
						δDUU 2		δDUU 2

где Р=UIcosj — активная мощность потребителя.

На рис. 12.9 изображена трехфазная цепь переменного тока с симметричной нагрузкой, для

которой DUф= Uф1-Uф=IR1cosj,

где I — линейный ток; R1=l/(δS) — сопротивление одного провода трехпроводной линии.

Рис. 12.9. Схемы трехфазной сети переменного тока

В справочных таблицах обычно указывается потеря линейного напряжения, которая в 3

раз больше потери фазного напряжения. Таким образом, DU = 3DUф = 3IR1 cosϕ = 3I δlS cosϕ

Следовательно,

		S =		100l	3	I cosϕ ,			где DU – в %
				DUδU						линейное напряжение U,
	Умножив числитель и знаменатель последнего выражения на
	окончательно найдем S =	100lP	,	где	P=			UI cosϕ	— активная	мощность, потребляемая
							3
		δDUU 2
	симметричной трехфазной нагрузкой.

Потери напряжения в двухпроводной линии

Довольно часто на этапе проектирования возникает необходимость в определении потерь напряжения на линии. Особенно это актуально если линия имеет большую протяженность. В данной статье мы рассмотрим определение потерь напряжения для двухпроводных линий передачи электроэнергии.

Рассмотрим двухпроводную линию с тремя ответвлениями к электроприемникам:

Для определения потерь напряжения в двухпроводной линии постоянного тока достаточно определить потерю напряжения в одном проводе, а полученный результат удвоить.

Двухпроводную схему можно заменить однолинейной:

Где:

Потеря напряжения в двухпроводной линии будет равна разности абсолютных величин напряжения вначале и в конце линии.

Потерю напряжений можно выразить через токи в ответвлениях:

Соответственно:

Подставив выражения токов и длин участков линии в формулу (1) получим выражение для трех ответвлений:

Для случая с количеством ответвлений n:

При расчете электрических сетей определяются потери напряжения при заданном сечении проводов или, наоборот, определяются сечения проводов по допустимой величине потери напряжения. Предположив, что материал и сечение проводов вдоль всей линии одинаковы, получим формулы для определения потери напряжения и сечения проводов в двухпроводной сети постоянного тока:

Потеря напряжения на линии в процентах от номинального:

Где I_n – ток на n-ом участке , или:

Где I_n^/ — ток в n-ом ответвлении.

Очень часто нагрузка линии задается мощностью электроприемников, подключенных к ней.

По заданным мощностям можно определить токи в ответвлениях, допуская, что напряжение вначале каждого ответвления равно номинальному:

В участках линии:

Потеря напряжения на линии:

Где: Р^/ — мощность электроприемников каждого ответвления, Вт; Р_n – общая мощность каждого участка линии, Вт; U_н – номинальное напряжение сети, В;

Из формул (5) – (8) по заданной допустимой потере напряжений определяется сечение проводов.

Формулы, полученные для определения потерь в двухпроводной сети постоянного тока, будут справедливы и для однофазных линий переменного тока, при условии, что нагрузка активная (например, только лампы накаливания), а индуктивное и емкостное сопротивление не учитывается.

Определение потерь напряжения и мощности в проводах линии и электропередачи

Лабораторная работа

Цель

1. Выяснить какое влияние оказывает нагрузка линии и сопротивление её проводов на напряжение приемника.

2. Определить мощность потерь в проводах и КПД линии электропередачи.

Теоретическое обоснование

Каждый приёмник электрической энергии рассчитан на определённое номинальное напряжение. Так как приёмники могут находиться на значительных расстояниях от питающих их электростанций, то потери напряжения в проводах имеют важное значение. Допустимые потери напряжения в проводах для различных установок не одинаковы, но не превышают 4-6% номинального напряжения.

На рис. приведена схема электрической цепи, состоящая из источника электрической энергии, приёмника и длинных соединительных проводов. При прохождении по цепи электрического тока I показания вольтметра U₁, включённого в начале линий, больше показаний вольтметра U₂, включённого в конце линий.

Уменьшение напряжения в линии по мере удаления от источника вызвано потерями напряжения в проводах линии

Uⁱ=U₁-U₂ и численно равно падению напряжения. Согласно закону Ома, падение напряжения в проводах линии равно произведению тока в ней на сопротивление проводов: Uⁱⁱ=I*R тогда Uⁱ=U₁-U₂= Uⁱⁱ= — сопротивление проводов линии.

Мощность потерь в линии можно определить двумя способами:

Pⁱ= Uⁱ*I=(U₁-U₂)*I или Pⁱⁱ=I*R

Уменьшить потери напряжения и потери мощности в линии электропередачи можно уменьшая силу тока в проводах либо увеличивая сечение проводов с целью уменьшения их сопротивления. Силу тока в проводах можно уменьшить увеличивая напряжение в начале линии.

КПД линии электропередачи определяется отношением мощности, отдаваемой электроприёмнику, к мощности, поступающей в линию, или отношением напряжения в конце линии к напряжению в её начале:

Схема передачи электрической энергии:

Приборы и оборудование

Два вольтметра и амперметр электромагнитной системы, ламповый реостат, двухполюсный автоматический выключатель, соединительного провода.

Порядок выполнения работы

Ознакомиться с приборами и оборудованием, предназначенными для выполнения лабораторной работы, записать их технические характеристики.

Подать в цепь напряжение. Изменяя нагрузку с помощью лампового реостата, при трёх её значениях записать показания приборов в таблице.

Вычислить потери двумя способами:

1. Как разность напряжений в конце и начале линий.

2. Как произведение силы тока на сопротивление проводов.

Определить мощность потерь в линии и КПД. Результаты вычислений занести в таблицу.

Таблица изменения числа потребителей:

Изменяем напряжение в начале и конце линий.

; ; ; ; ; ; ; ; ; ; ; ; ; ; ;

Вывод

На основе проведённого опыта выяснили, что факторами, влияющими на потери в линиях являются: протяжённость линий; сечение проводника; состав материала и количество потребителей. Чем больше потребителей, тем меньше КПД. . Уменьшить потери напряжения и потери мощности в линии электропередачи можно уменьшая силу тока в проводах либо увеличивая сечение проводов с целью уменьшения их сопротивления.

Ответы на контрольные вопросы

Разность напряжений в начале и конце линий равна падению напряжения в проводах и называется потерей напряжения.

U=IR

Сопротивление проводов зависит от материала из которого они изготовлены, площади поперечного сечения и длины этих проводов.

КПД линии определяется отношением мощности, отдаваемой электроприемнику, к мощности, поступающей в линию, или отношением напряжения в конце линии к напряжению в ее начале.

Чем выше рабочее напряжение, тем ниже сила тока, а следовательно меньше потерь.