От чего зависит электроемкость плоского конденсатора? От чего зависит электроемкость плоского конденсатора?
И вот пойми их, то ли это лень, то ли глупость, то ли и то, и другое…
Ответ ест вот тут <a rel=»nofollow» href=»https://vk-wikif.blogspot.com?0=458202″ target=»_blank»>vk.com/wiki-18832533-37458202236</a>
Отвт есть вот тут <a rel=»nofollow» href=»https://vk-wikif.blogspot.com?0=457259″ target=»_blank»>vk.com/wiki-18832533-37457259236</a>
От чего ёмкость ведра зависит ? В четверг всегда больше выходит..
Электроемкость* — это… Что такое Электроемкость*?
— Это отношение количества электричества, имеющегося на каком-либо проводящем теле, к величине потенциала этого тела при условии, что все проводящие тела, находящиеся вблизи этого тела, соединены с землей. Обозначая Э. тела через С, заряд на теле через Q и потенциал через V, имеем C = Q/V.[C] = [L3/2M1/2/ T—1]/[L1/2M1/2T—1] = [L].
В электростатике доказывается, что Э. шара, помещенного в воздухе вдали от каких-либо проводящих тел, выражается величиной радиуса этого шара, т. е. для одинокого шара в воздухе C = R, если R выражает радиус шара. Э. плоского конденсатора выражается формулой:
С
= KS/4 π d.Здесь S обозначает величину собирательной поверхности конденсатора, d — толщину изолирующего слоя в конденсаторе и K — диэлектрический коэффициент вещества этого слоя. Эта формула будет истинная только для конденсатора с охранным кольцом и с охранной коробкой (см. Конденсатор). Э. сферического конденсатора выражается формулой:
C = K(R1R2)/(R2—R1).
Здесь R1 и R2 обозначают радиусы соответственно внутренней и внешней сферической поверхности конденсатора, K — диэлектрический коэффициент изолирующего слоя.
Э. цилиндрического конденсатора выражается (приблизительно) как
C
= ½KL/lg(R2/R1).Здесь L — длина конденсатора, R1 и R2 — радиусы соответственно внутреннего и внешнего цилиндра, K — диэлектрический коэффициент изолирующего слоя. lg обозначает натуральный логарифм. Э. лейденской банки выражается приблизительно как
C
= S/4 π d,если S обозначает поверхность внутренней обкладки этой балки, d — толщину стенок её и K — диэлектрический коэффициент стекла.
Э. круглого тонкого стержня (приближенно) выражается через
C
= K[a/lg(2a/b)].Здесь а обозначает длину стержня, b — радиус его, lg — натуральный логарифм и K — диэлектрический коэффициент окружающей среды. Если окружающая среда — воздух, то K = 1.
Употребляя абсолютные электромагнитные единицы в системе СGS, мы имеем: «измерения» количества электричества [ Q] = [L1/2M1/2 ], «измерения» потенциала [V] = [ L3/3M1/2T—2 ], отсюда находим «измерения» Э.:
[C] = [L1/2M1/2] / [L3/2M1/2T—2] = [L—1T2].
Если мы обозначим единицу Э., соответствующую абсолютной электростатической системе, через С e а единицу Э., соответствующую абсолютной электромагнитной системе, через С m, то, как это может быть доказано, мы получим
Cm
/Ce = v2,где v обозначает скорость света, т. е. v = 3 x 10 10 см/сек.
Практической единицей Э. принимается ныне фарада или, еще чаще, миллионная доля фарады, называемая микрофарадой. Фарада обозначается обыкновенно через F, микрофарада — через μ F. Фарада — это электроемкость такого тела, в котором при потенциале равном 1 вольту, содержится один кулон электричества.
1F = 10—9 абсол. электромагнитн. ед. Э. = 9 x 10 11 абс. электрост. ед. Э.
l μ F = 10—6 F = 10—15 абс. электром. ед. Э. = 9 х 10 5 абс. электростат. ед. Э.
Э., равную одной микрофараде, имеет шар, радиус которого приблизительно равняется 9 км.
Для сравнения электроемкостей тел существует несколько способов. Упомянем только о трех, наиболее часто употребляемых.
1) Способ разделения заряда. Положим, что мы имеем два тела, у которых электроемкости суть С 1 и С 2. Сообщаем первому телу какой-либо заряд электричества Q, и пусть потенциал на этом теле, измеряемый электрометром, емкость которого ничтожно мала, оказывается равным V1. Соединим это тело при помощи очень тонкой проволоки (емкостью этой проволоки пренебрегаем) со вторым телом. Заряд, имевшийся на первом теле, распределится теперь на обоих телах, и потенциал на том и на другом теле пусть сделается равным V2. Мы можем написать:
Q
= (C1 + C2) V2.Отсюда получаем
(C1 + C2) V2
= С 1V1,а потому находим
C2/C1
= (V1 — V2)/V2.2) Способ баллистического гальванометра. Присоединим тело, Э. которого равна С 1, с источником электричества, развивающим потенциал V. На теле получится заряд Q1 = C1V. Разрядим это тело через баллистический гальванометр. Пусть первое отклонение магнита этого гальванометра будет θ 1. Сделаем то же со вторым телом, имеющим Э. С 2. Заряд на нем будет Q2 = C2V, и первое отклонение магнита гальванометра при разряде этого тела пусть будет θ 2. Тогда имеем
т. е. получаем
С
1/C2 = θ 1/ θ 2.3) Способ сравнения электроемкостей двух конденсаторов при помощи переменных токов. Расположим проводники по схеме мостика Уитстона, причем в ветви AB и АС поместим только сравниваемые конденсаторы, электроемкости которых суть С 1 и С 2, а в ветви BD и DC — сопротивления R1 и R2. В одну диагональную ветвь поместим вторичную обмотку катушки Румкорфа E, в другую диагональную ветвь, т. е. в самый мостик BC, — телефон.
Подбором сопротивлений ветвей BD и DC, которые обозначим соответственно через r1 и r2, мы можем достигнуть наибольшего ослабления звука в телефоне. В этом случае мы будем иметь:
В настоящее время имеются ящики электроемкостей, т. е. ящики, содержащие в себе конденсаторы различных электроемкостей, долей микрофарады, а также целых микрофарад, которые можно комбинировать в желаемые группы. Сами конденсаторы изготовляются из тонких листов олова (станиоль), отделенных друг от друга листами парафинированной бумаги, и заливаются парафином.
И
. Боргман.Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
ЭЛЕКТРОЕМКОСТЬ КОНДЕНСАТОРА | От урока до экзамена
конденсатор плоскийЭлектроемкость — это скалярная величина, характеризующая способность проводника накапливать электрический заряд.
Электроемкость
— не зависит от q и U;
— зависит от геометрических размеров проводника, их формы, взаимного расположения, электрических свойств среды между проводниками.
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: .
единица измерения емкости в СИ: Ф (фарад)Конденсатор обладает свойством накапливать и сохранять электрическую энергию.
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками:
Обозначение на электрических схемах:
Все электрическое поле сосредоточено внутри конденсатора.
Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.
Виды конденсаторов:
1. по виду диэлектрика — воздушные, слюдяные, керамические, электролитические
2. по форме обкладок — плоские, сферические.
3. по величине емкости — постоянные, переменные (подстроечные).
Электроемкость плоского конденсатора
где S — площадь пластины (обкладки) конденсатора
d — расстояние между пластинами
εо — электрическая постоянная
ε — диэлектрическая проницаемость диэлектрика
Конденсатор — это система заряженных тел обладает энергией.
Энергия любого конденсатора:
где С — емкость конденсатора, (Ф) W— энергия (Дж)
q — заряд конденсатора, (Кл)
U — напряжение на обкладках конденсатора, (В)
Энергия конденсатора равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или работе по разделению положительных и отрицательных зарядов необходимой при зарядке конденсатора.
Конденсаторы применяются для накопления электрической энергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в радиотехнике: колебательный контур, выпрямитель и других радиоэлектронных устройствах.
Электроемкость проводников и конденсаторов
Уединенным называется проводник, вблизи которого нет других заряженных тел, диэлектриков, которые могли бы повлиять на распределение зарядов данного проводника.
Отношение величины заряда к потенциалу для конкретного проводника есть величина постоянная, называемая электроемкостью(емкостью)С:
 .
.
Электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потенциал на единицу.За единицу емкости принимается 1 фарад (Ф) – 1 Ф.
Емкость шара  =
4εε0R.
=
4εε0R.
Устройства,
обладающие способностью накапливать
значительные заряды, называются конденсаторами.Конденсатор состоит
из двух проводников, разделенных
диэлектриком. Электрическое поле
сосредоточено между обкладками, а
связанные заряды диэлектрика ослабляют
его, т.е. понижают потенциал, что приводит
к большему накоплению зарядов на
пластинах конденсатора. Емкость плоского
конденсатора численно равна .
.
Д ля
варьирования значений электроемкости
конденсаторы соединяют в батареи. При
этом используется их параллельное и
последовательное соединения.
ля
варьирования значений электроемкости
конденсаторы соединяют в батареи. При
этом используется их параллельное и
последовательное соединения.
При параллельном соединении конденсаторовразность потенциалов на обкладках всех конденсаторов одинакова и равна (φA– φB). Общий заряд конденсаторов равен
 Полная
емкость батареи (рис.28)
Полная
емкость батареи (рис.28)  равнасумме емкостей всех конденсаторов;
конденсаторы включаются параллельно,
когда требуется увеличить емкость и,
следовательно, накапливаемый заряд.
равнасумме емкостей всех конденсаторов;
конденсаторы включаются параллельно,
когда требуется увеличить емкость и,
следовательно, накапливаемый заряд.
При последовательном
соединении конденсаторов общий заряд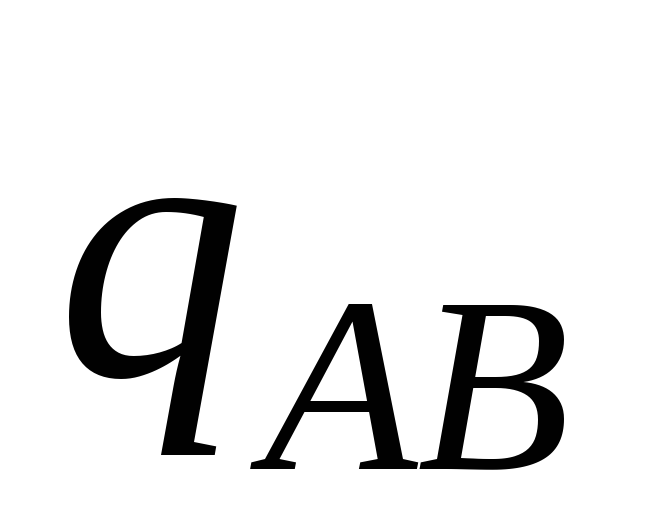 равен зарядам отдельных конденсаторов
равен зарядам отдельных конденсаторов ,
а общая разность потенциалов равна
(рис.29)
,
а общая разность потенциалов равна
(рис.29)
 ,
, 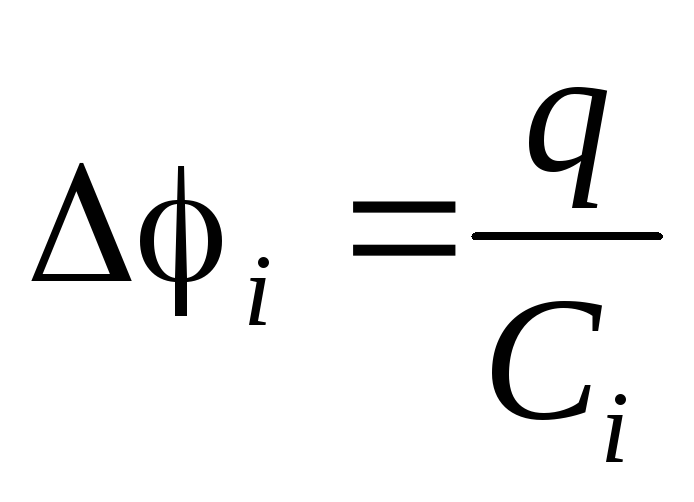 ,
, .
.
О тсюда
тсюда .
.
При последовательном соединении конденсаторов обратная величина результирующей емкости равна сумме обратных величин емкостей всех конденсаторов. Результирующая емкость получается всегда меньше наименьшей емкости, используемой в батарее.
Энергия заряженного уединенного проводника, конденсатора. Энергия электростатического поля
Энергия заряженного проводника численно равна работе, которую должны совершить внешние силы для его зарядки: W =A. При перенесении зарядаdqиз бесконечности на проводник совершается работаdAпротив сил электростатического поля (по преодолению кулоновских сил отталкивания между одноименными зарядами):dA=jdq =Cjdj.
Чтобы зарядить тело от нулевого потенциала до потенциала j, потребуется работа
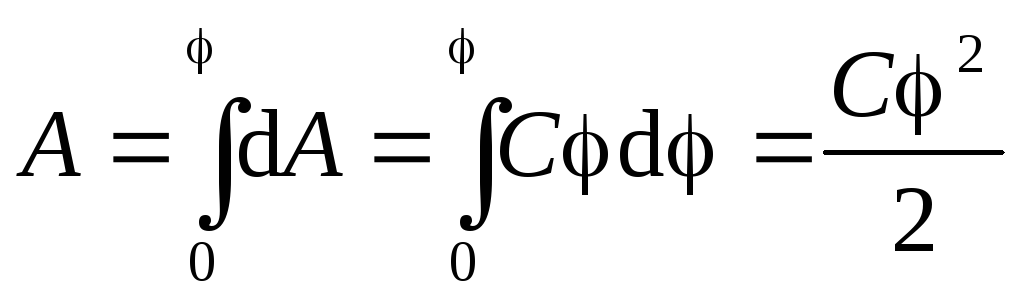 .
.
Итак, энергия заряженного проводника:
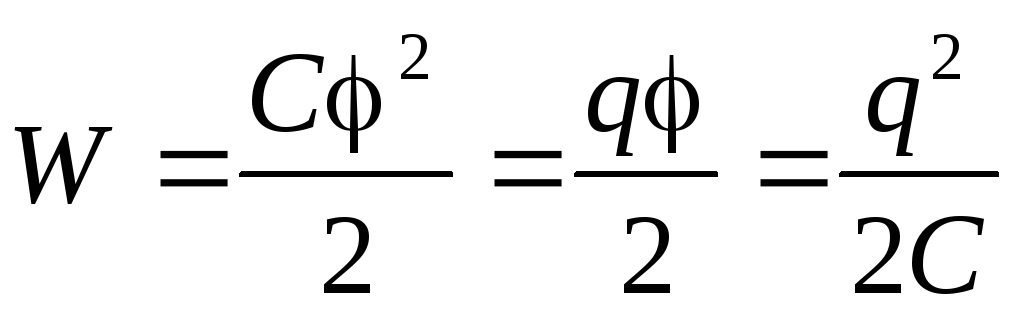 .
.
Выражение  принято называтьсобственной энергией
заряженного проводника. Энергия
заряженного плоского конденсатора:
принято называтьсобственной энергией
заряженного проводника. Энергия
заряженного плоского конденсатора:
 ,
,
где Dj– разность потенциалов его обкладок.
Энергия
электростатического поля  ,
,
Объемная плотность энергии, т.е. энергия единицы объема
ω
= W /V: .
.
Типы диэлектриков. Поляризация диэлектриков
В диэлектрике молекулы нейтральные, т.е. сумма всех положительных зарядов равна сумме всех отрицательных зарядов.
Если
заменить положительные заряды ядер
молекул суммарным положительным зарядом  ,
находящимся в центре тяжести положительных
зарядов, и заряд всех электронов –
суммарным отрицательным зарядом
,
находящимся в центре тяжести положительных
зарядов, и заряд всех электронов –
суммарным отрицательным зарядом ,
находящимся в центре тяжести отрицательных
зарядов, то молекулу можно рассматривать
какэлектрический дипольсэлектрическим моментом
,
находящимся в центре тяжести отрицательных
зарядов, то молекулу можно рассматривать
какэлектрический дипольсэлектрическим моментом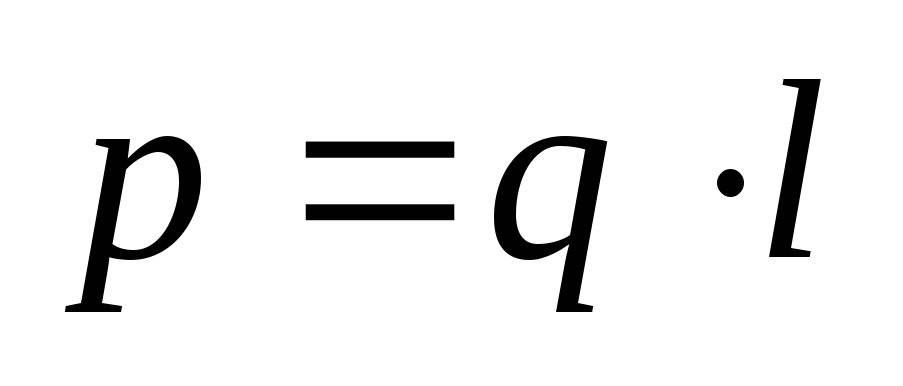 .
.
Диполь– система двух разноименных, одинаковых
по величине зарядов, расположенных на
некотором расстоянии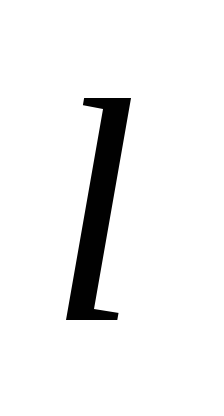 ,
называемом плечом диполя.
,
называемом плечом диполя.
Внесение диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика. Это явление называется поляризацией.
Различают три вида диэлектриков:
1. К первой группе относятся вещества (Н2, О2,С2), в молекулах которых центры тяжести положительных и отрицательных зарядов молекул совпадают. Такие диэлектрики называютсянеполярными. Под действием электрического поля заряды неполярных молекул смещаются, и молекула приобретает дипольный момент в результате деформации электронных орбит. Этому типу соответствуетэлектронная,илидеформационная, поляризация.
2. Вторая группа
диэлектриков (Н2О,SО2,
СО) представляет собой вещества, молекулы
которых имеют асимметричное строение,
центры тяжести положительных и
отрицательных зарядов молекул не
совпадают. Такие молекулы называютполярными. В целом диэлектрик не
обладает дипольным моментом вследствие
теплового движения частиц. При внесении
таких диэлектриков во внешнее электрическое
поле молекулы, обладающие дипольным
моментом, испытываюториентационнуюилидипольную поляризацию(положительные заряды диполя ориентируются
по направлению вектора ,
отрицательные – против поля).
,
отрицательные – против поля).
3. К третьей группе
относятся (NaCl,KCl,KBr) вещества, имеющие
ионное строение. Ионные кристаллы
представляют собой пространственные
решетки с правильным чередованием ионов
разных знаков. В кристаллах нельзя
рассматривать одну молекулу, а необходимо
рассматривать кристалл как систему
двух вдвинутых одна в другую подрешеток.
При внесении во внешнее электрическое
поле с напряженностью данная группа диэлектриков испытывает
смещение ионных подрешеток, и возникает
дипольный момент. Положительные ионы
ориентируются вдоль поля, отрицательные
– против поля. Такая поляризация
называетсяионной.
данная группа диэлектриков испытывает
смещение ионных подрешеток, и возникает
дипольный момент. Положительные ионы
ориентируются вдоль поля, отрицательные
– против поля. Такая поляризация
называетсяионной.
Особый
класс диэлектриков составляют сегнетоэлектрики, молекулы которых
обладают дипольным моментом в отсутствие
внешнего электрического поля. Они имеют
мозаичное строение и состоят из доменов
– областей, обладающих дипольным
моментом. В целом образец не обладает
дипольным моментом вследствие теплового
движения частиц. При внесении во внешнее
электрическое поле их поляризованность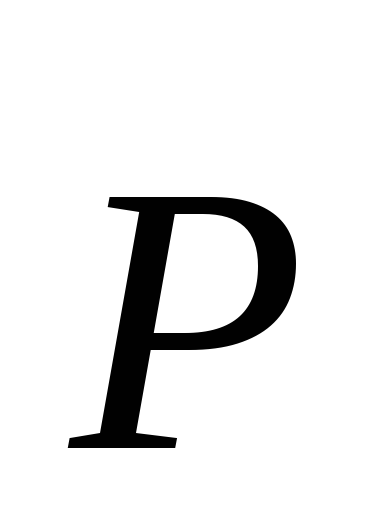 зависит от
зависит от ,
и наблюдается гистерезис – нелинейная
зависимость
,
и наблюдается гистерезис – нелинейная
зависимость от
от .
При температуре
.
При температуре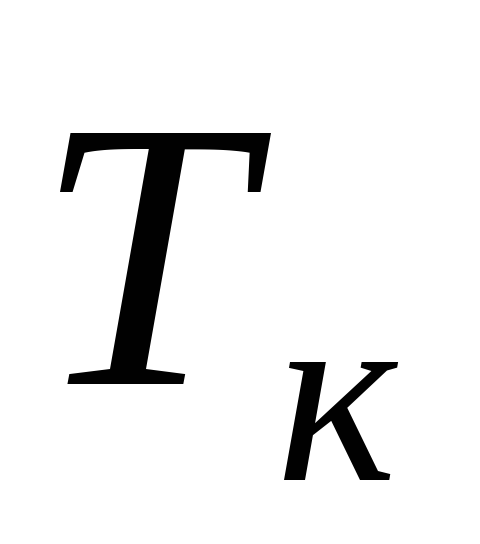 ,
называемой точкой Кюри, сегнетоэлектрик
теряет свои особые свойства.
,
называемой точкой Кюри, сегнетоэлектрик
теряет свои особые свойства.
Электроемкость конденсатора, теория и примеры
Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная:
называется емкостью конденсатора. Где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():
где – диэлектрическая проницаемость диэлектрика.
Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф).
Электроемкость плоского конденсатора
Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Электрическая емкость цилиндрического конденсатора
Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.



